Time-Dependent Hamiltonian Mechanics on a Locally Conformal Symplectic Manifold

Abstract

In this paper we aim at presenting a concise but also comprehensive study of time-dependent (t-dependent) Hamiltonian dynamics on a locally conformal symplectic (lcs) manifold. We present a generalized geometric theory of canonical transformations in order to formulate an explicitly time-dependent geometric Hamilton-Jacobi theory on lcs manifolds, extending our previous work with no explicit time-dependence. In contrast to previous papers concerning locally conformal symplectic manifolds, the introduction of the time dependency that this paper presents, brings out interesting geometric properties, as it is the case of contact geometry in locally symplectic patches. To conclude, we show examples of the applications of our formalism, in particular, we present systems of differential equations with time-dependent parameters, which admit different physical interpretations as we shall point out.

1. Introduction

Symplectic geometry has been widely developed since its beginnings in the 1940s, the literature on this topic is vast, and there exist very complete anthologies on it [1,2,3]. On the contrary, the studies on locally conformal symplectic structures (lcs, henceforth) are not so developed. Except for the works of Libermann in 1955 [4] and Jean Lefebvre from 1966 to 1969 [5,6], the subject remained untouched until Vaisman revived the topic in the 1970s [7,8]. One can notice, though, that recently, the topic of lcs manifolds has become increasingly popular. For an extended description of the revival of lcs geometry and a comprehensive discussion of its relations to other topics, we refer the reader to [9].

Let us refresh the memory of the reader with a brief recalling of the setting of lcs geometry more explicitly. The advent of lcs was rooted in Hwa-Chung Lee’s works in 1941 [10], which reconsider the general setting of a manifold endowed with a non-degenerate two-form $\omega$. First, he discussed the symplectic case, and then the problem of a pair of two-forms ${\omega }_1$ and ${\omega }_2$, which are conformal to one another [9]. Later, in 1985, Vaisman [8] defined an lcs manifold as an even dimensional manifold endowed with a non-degenerate two-form such that for every point $p\in M$ there is an open neighborhood U in which the following equation is satisfied:

$$d\left(e^{-\sigma }{\omega |}_U\right)=0,$$

(1)

where $\sigma :U\to \mathbb{R}$ is a smooth function. If (1) holds for a constant function $\sigma$, then $(M,\omega )$ is a symplectic manifold. The work of Lee proposes an equivalent definition with the aid of a compatible one-form, named the Lee form [10], that we will introduce in subsequent sections.

It is important to notice that at a local scale, a symplectic manifold cannot be distinguished from an lcs manifold. Thus, not only do all symplectic manifolds locally look alike, but there exist manifolds which behave like symplectic manifolds locally, but they fail to do so globally [8,9].

Locally conformal symplectic structures of the first kind are strictly related to contact structures. Recall that a (co-orientable) contact manifold is the pair $(P,\alpha )$, where P is an odd dimensional manifold, such that $dimP\ge 3$, and $\alpha$ is a one-form such that $\alpha \wedge {\left(d\alpha \right)}^n\ne 0$ at every point [11,12]. Frobenius’ integrability theorem shows that the distribution $\xi =ker\alpha$ is then maximally non-integrable. Let $(P,\alpha )$ be a contact manifold and consider a strict contactomorphism, that is, a diffeomorphism $\varphi :P\to P$ satisfying ${\varphi }^{*}\alpha =\alpha$. Then, as observed, for instance, by Banyaga in [13], the mapping torus $P_{\varphi }$ admits a locally conformal symplectic structure of the first kind. A similar result, in which the given lcs structure is preserved, is proved in [14].

It is interesting to notice that contact and locally conformal symplectic structures converge towards Jacobi structures too. Indeed, a transitive Jacobi manifold is a contact manifold if it is odd-dimensional, and an lcs manifold if it is even-dimensional [15]. Therefore, locally conformal symplectic structures may be seen as the even-dimensional counterpart of contact geometry.

Concerning the physical applications of lcs structures, it has been proven that they form a very successful geometric model for certain physical problems. In [16], Maciejewski, Przybylska and Tsiganov considered conformal Hamiltonian vector fields in the theory of bi-Hamiltonian systems in order to reproduce examples of completely integrable systems. In [17], Marle used conformal Hamiltonian vector fields to study a certain diffeomorphism between the phase space of the Kepler problem and an open subset of the cotangent bundle of $S^3$ (resp. of a two-sheeted hyperboloid, according to the energy of the motion). In [18], Wojtkowski and Liverani apply lcs structures in order to model concrete physical situations such as Gaussian isokinetic dynamics with collisions, and Nosé–Hoover dynamics. More precisely, the authors show that such systems are tractable by means of conformal Hamiltonian dynamics and explain how one deduces properties of the symmetric Lyapunov spectrum. Another interesting role of lcs geometry is its appearance in dissipative systems.

Another important structure having a close connection with lcs structures are contact pairs, which we shall discuss in the last section of the paper. Contact pairs were introduced in [19], although they had been previously discussed in [20] with the name bicontact structures in the context of Hermitian geometry [21]. In short, a contact pair on a manifold is a pair of one-forms, ${\alpha }_1$ and ${\alpha }_2$, of constant and complementary classes, for which ${\alpha }_1$ induces a contact form on the leaves of the characteristic foliation of ${\alpha }_2$, and viceversa. In [19,22,23], it is shown how a locally conformal symplectic structure can be constructed out of a contact pair. This fact is quite remarkable, and establishes physical interpretations. Indeed, our modus operandi consists of identifying Lie algebras that admit a contact pair and construct a Lie system [24,25,26,27,28] from such Lie algebras. Lie systems are time-dependent systems of differential equations that admit finite-dimensional Lie algebras, and they usually find a plethora of applications in biology, economics, cosmology, control theory and engineering. Furthermore, some of these systems admit a Hamiltonian. In this line, one is able to construct time-dependent Hamiltonians that are locally conformal symplectic. The last section of this manuscript is dedicated to applications that will illustrate the mentioned constructions.

The aim of this paper is to present a comprehensive formulation of a time-dependent (t-dependent) Hamiltonian dynamics on a locally conformal symplectic manifold. We extend the time-independent formalism explained in [8] to the time-dependent case. Subsequently, we extend the theory of canonical transformations and the Hamilton–Jacobi theory (HJ theory) for time-dependent Hamiltonian systems through lcs geometry. All these new results open a path to studying physical systems such as the ones mentioned above when one considers their time-dependent version, altogether with the application of advanced methods such as canonical transformations and HJ theory. We approach our study from a local and a global point of view and see the relation between both approaches.

The extension of the notion of time-dependent canonical transformations to lcs structures is naturally led by the relation between the symplectic and the lcs case. What is more, the notion of a canonical transformation is strongly related to HJ theory, which is another problem of our paper. HJ theory is a powerful tool in mechanics which has many applications both in classical and quantum physics. The Hamilton–Jacobi equation is one of the most elegant approaches to Hamiltonian systems such as geometric optics and classical mechanics, establishing the duality between trajectories and waves and paving the way naturally for quantum mechanics. It is particularly useful in identifying conserved quantities for mechanical systems, which may be possible even when the mechanical problem itself cannot be solved completely. In quantum mechanics, it provides a relation between classical and quantum mechanics by means of the correspondence principle, although we shall restrict ourselves to the classical approach here. Indeed, we will take the classical geometric detour, in which the solution to the Hamilton–Jacobi equation is interpreted as a section of the cotangent bundle.

Let us explain this pictorically in the simplest case of a symplectic manifold. Let $X_H$ be the Hamiltonian vector field of a Hamiltonian $H:T^{*}Q\to \mathbb{R}$ and $W:Q\to \mathbb{R}$, a smooth function. Recall that $X_H$ is a vector field on $T^{*}Q$. We define the projected vector field as

$$X_H^{dW}=T\pi \circ X_H\circ dW,$$

(2)

where $T\pi :T{T}^{*}Q\to T^{*}Q$ is the tangent map of the canonical projection $\pi :T^{*}Q\to Q$. The construction of $X_H^{dW}$ can be seen on a commutative diagram

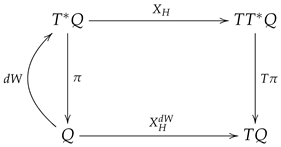
Notice that the image of $dW$ is a Lagrangian submanifold, since it is exact and, consequently, closed. Indeed, one can change $dW$ by a closed one-form $\gamma$ [12,29,30]. Lagrangian submanifolds are very important objects in Hamiltonian mechanics, since the dynamical equations (Hamiltonian or Lagrangian) can be described as Lagrangian submanifolds of convenient (symplectic) manifolds. We enunciate the following theorem.

Theorem 1.

For a closed one-form $\gamma =dW$ on Q, the following conditions are equivalent:

1. 

The vector fields $X_H$ and $X_H^{\gamma }$ are γ-related, that is

$$T\gamma \circ X_H^{\gamma }=X_H\circ \gamma .$$

(3)

2. 

The following equation is fulfilled

$$d\left(H\circ \gamma \right)=0.$$

Theorem 1 is a geometric formulation of the (time-independent) HJ theory from classical mechanics. The first item in the theorem says that if $\left(q^i\left(t\right)\right)$ is an integral curve of $X_H^{\gamma }$, then $\left(q^i\left(t\right),{\gamma }_j\left(t\right)\right)$ is an integral curve of the Hamiltonian vector field $X_H$ and, hence, a solution of the Hamilton equations. Such a solution of the Hamiltonian equations is called horizontal since it is on the image of a one-form on Q. In the local picture, the second condition implies that the exterior derivative of the Hamiltonian function on the image of $\gamma$ is closed; that is, $H\circ \gamma$ is constant. Under the assumption that $\gamma$ is closed, we can find (at least locally) a function W on Q satisfying $dW=\gamma$ [12,29,30]. The pioneer of this purpose was Tulczyjew, who characterized the image of local Hamiltonian vector fields on a symplectic manifold $(M,\omega )$ as Lagrangian submanifolds of a symplectic manifold $(TM,{\omega }^T)$, where ${\omega }^T$ is the tangent lift of $\omega$ to $TM$ [31]. This result was later generalized to Poisson manifolds [32]. In our paper, we generalize this result to time-dependent lcs manifolds and show that HJ theory is naturally related to canonical transformations in the time-dependent and lcs frame, in a fashion similar to the symplectic case.

The paper is organised as follows. In Section 2, we review the geometric fundamentals of time-dependent Hamiltonian formalism on a symplectic manifold. We recall how the time-dependency is introduced to Hamiltonian mechanics within its main objects: Hamiltonian vector fields, integral curves and Hamilton equations. Next, we discuss canonical transformations in the context of Hamiltonian mechanics. Section 3 contains a review of the geometric fundamentals of lcs manifolds and recalls some introductory objects such as musical mappings, the Lichnerowicz–deRham differential, and the construction of lcs structures on the cotangent bundle. Alongside this, we remind the reader of the concept of Lagrangian submanifolds on lcs structures, since these will play a crucial role in describing the dynamics on lcs cotangent bundles. Section 4 is the core of our paper. We present the time-dependent Hamiltonian formalism on lcs manifolds, we extend the theory of canonical transformations to the lcs case and, subsequently, formulate a Hamilton–Jacobi theory on lcs manifolds for explicitly time-dependent Hamiltonians. Section 5 contains one of the possible applications of our formalism, which is concerned with differential equations that admit finite-dimensional Lie algebras of vector fields, i.e., the well-known Lie systems (see, e.g., [28] for details on Lie systems). We provide a physical interpretation for these systems out of the construction of time-dependent lcs two-forms with the properties of the Lie algebra that are compatible with the system of differential equations.

2. Fundamentals on Time-Dependent Hamiltonian Systems

2.1. Time-Dependent Systems

We will briefly present, now, fundamentals on time-dependent systems based on [33]. Let Q be a smooth manifold. We will denote by $TQ$ and $T^{*}Q$ the tangent and cotangent bundle on Q, respectively. We say that a map

$$X:\mathbb{R}\times Q\to TQ,(t,q)⟼X(t,q)$$

(4)

is a time-dependent vector field if for each $t\in \mathbb{R}$; the map $X_t:Q\to TQ,q⟼X(t,q)$ is a vector field on Q. Therefore, each time-dependent vector field on a manifold can be understood as a family of time-independent vector fields ${\left\{X_t\right\}}_{t\in \mathbb{R}}$ that depends in a smooth way on a parameter $t\in \mathbb{R}$. Notice that one can also understand (4) as a vector field along the projection ${\mathrm{pr}}_2:\mathbb{R}\times Q\to Q$. With each time-dependent vector field we can associate in a unique way a vector field on $\mathbb{R}\times Q$ given by

$$\tilde{X}:\mathbb{R}\times Q\to T(\mathbb{R}\times Q)\simeq T\mathbb{R}\times TQ,(t,q)⟼((t,1),(q,X(q,t))$$

so that

$$\tilde{X}=\frac{\partial }{\partial t}+X(t,q).$$

We refer to $\tilde{X}$ as the suspension or autonomization of the time-dependent vector field X. A curve $b:I\to Q$ on a manifold Q is an integral curve of X if

$$\dot{b}\left(t\right)=X(t,b\left(t\right)),\forall t\in I,$$

where we used a notation $\dot{b}\left(t\right)={\frac{d}{ds}}_{|s=0}b(t+s).$

Let $(P,\omega )$ be an exact symplectic manifold, i.e., P is a smooth manifold and $\omega$ is a closed, exact and nondegenerate two-form on P. We consider the product $\mathbb{R}\times P$ and the projection ${\pi }_2:\mathbb{R}\times P\to P$ onto the second factor. We will denote by $\tilde{\omega }$ the pull-back of $\omega$ with respect to ${\pi }_2$, namely, $\tilde{\omega }={\pi }_2^{*}\omega$. A pair $(\mathbb{R}\times P,\tilde{\omega })$ is then a contact manifold with a contact form $\tilde{\omega }$. Let us recall that a contact manifold is a pair $(M,\eta )$, where M is a smooth manifold of odd dimension $2n+1$ and $\eta$ stands for a differential one-form that is non-degenerate in the sense that [12]

$$\eta \wedge {\left(d\eta \right)}^n\ne 0,\mathrm{where}{\left(d\eta \right)}^n:=\underset{n-\mathrm{times}}{\underbrace{d\eta \wedge \dots \wedge d\eta }}.$$

One can show that there exists a a unique vector field $\mathcal{R}$ (called a Reeb vector field) such that

$$i_{\mathcal{R}}d\eta =0,i_{\mathcal{R}}\eta =1.$$

The characteristic line bundle of $\tilde{\omega }$ is generated by the vector field $X=\frac{\partial }{\partial t}$. A time-dependent Hamiltonian is a smooth function $H:\mathbb{R}\times P\to \mathbb{R}$ such that for each $t\in \mathbb{R}$, H defines the function $H_t:P\to \mathbb{R}$, $H_t\left(m\right)=H(t,m).$ From this, we see that a time-dependent Hamiltonian can be viewed as a family of time-independent Hamiltonians $\left\{H_t\right\}$ for each $t\in \mathbb{R}$. Since each element of this family $H_t$ is a smooth function on a symplectic manifold, we can associate with it a Hamiltonian vector field $X_{H_t}$ with respect to $\omega$, namely,

$$\omega (·,X_{H_t})=d{H}_t.$$

(5)

By collecting Hamiltonian vector fields $X_{H_t}$ in (5), for each $t\in \mathbb{R}$ we obtain a family of vector fields $\left\{X_{H_t}\right\}$ on P. In light of the discussion above, this family defines a time-dependent vector field given by

$$X_H:\mathbb{R}\times P\to TP,(t,p)⟼X_{H_t}\left(p\right).$$

We will call $X_H$ a time-dependent Hamiltonian vector field of the (time-dependent) Hamiltonian H with respect to the form $\omega$. As usual, we are interested in the integral curves of $X_H$ that represent phase trajectories of the system. It is a matter of straightforward calculations to show that the integral curve b of $X_{H_t}$ is given by the time-dependent Hamilton equations

$$\begin{array}{cc}\hfill \frac{d}{dt}{q}^i\left(b\left(t\right)\right)& =\frac{\partial H}{\partial p_i}(t,b\left(t\right)),\hfill \\ \hfill \frac{d}{dt}{p}_i\left(b\left(t\right)\right)& =-\frac{\partial H}{\partial q^i}(t,b\left(t\right)).\hfill \end{array}$$

Let us recall that in the time-independent case we have ${\mathcal{L}}_{X_H}H=0$, where $\mathcal{L}$ is the Lie derivative. In the time-dependent case we have, instead, ${\mathcal{L}}_{X_H}H=\partial H/\partial t.$ If $\partial H/\partial t=0$, then all of the above structures reduce to the standard Hamiltonian formalism on a symplectic manifold.

To finish this section let us notice that the existence of the function $H:\mathbb{R}\times P\to \mathbb{R}$ allows us to define a new two-form

$${\omega }_H=\tilde{\omega }+dH\wedge dt,$$

which will be important in our work later on. One can show that ${\tilde{X}}_H$, associated with H, is the unique vector field satisfying

$$i_{{\tilde{X}}_H}{\omega }_H=0,i_{{\tilde{X}}_H}dt=1.$$

Moreover, if F is the flow of $X_H$, then $F^{*}\omega =\tilde{\omega }-dH\wedge dt$.

In the end, let us mention that there are alternative approaches to the geometric description of time-dependent systems based for instance on the cosymplectic or presymplectic structures (see e.g., [34,35,36,37,38] for details).

2.2. Canonical Transformations

In Hamiltonian mechanics, a canonical transformation is a transformation of coordinates that preserves the form of Hamilton equations. The notion of a canonical transformation is an important concept in symplectic geometry itself but it also plays a crucial role in Hamilton–Jacobi theory (as a useful method for calculating conserved quantities) and in Liouville’s theorem in classical statistical mechanics. Let us stress that although a canonical transformation preserves the form of Hamilton equations, it does not need to preserve the form of the Hamiltonian itself. We will briefly recall now the geometric basics of the theory of canonical transformations. The structures presented here will be generalised to the lcs case in Section 4.

Let $(P_1,{\omega }_1)$ and $(P_2,{\omega }_2)$ be exact symplectic manifolds and $(\mathbb{R}\times P_1,{\tilde{\omega }}_1)$ and $(\mathbb{R}\times P_2,{\tilde{\omega }}_2)$ be the corresponding contact manifolds. A smooth map $F:\mathbb{R}\times P_1\to \mathbb{R}\times P_2$ is called a canonical transformation if each of the following holds

(i) 

F is a diffeomorphism

(ii) 

F preserves time, i.e., $F^{*}t=t$ or, equivalently, the following diagram is commutative

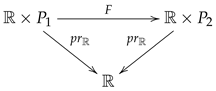
(iii) 

There exists a function $K_F\in C^{\infty }(\mathbb{R}\times P_1)$ such that

$$F^{*}{\tilde{\omega }}_2={\omega }_{K_F}\mathrm{where}{\omega }_{K_F}={\tilde{\omega }}_1+d{K}_F\wedge dt.$$

From now on, we will say that a diffeomorphism $F:\mathbb{R}\times P_1\to \mathbb{R}\times P_2$ has the so-called S property if for each t, the map $F_t:P_1\to P_2,F_t\left(p_1\right):=F(t,p_1)$ is a symplectomorphism. One can show that the map F has the S property if and only if there exists a one-form $\alpha$ on $\mathbb{R}\times P_1$ such that $F^{*}{\tilde{\omega }}_2={\tilde{\omega }}_1+\alpha \wedge dt.$ The most important properties of canonical transformations are expressed in the following theorem.

Theorem 2.

Assume that conditions $\left(i\right)$ and $\left(ii\right)$ hold. Then, $\left(iii\right)$ is equivalent to each of the following three statements

(a) 

For each function $H\in C^{\infty }(\mathbb{R}\times P_2)$, there exists a function $K\in C^{\infty }(\mathbb{R}\times P_1)$ such that

$$F^{*}{\omega }_H={\omega }_K$$

(b) 

For all $H\in C^{\infty }(\mathbb{R}\times P_2)$, there exists a $K\in C^{\infty }(\mathbb{R}\times P_1)$ such that

$$F_{*}{\tilde{X}}_K={\tilde{X}}_H$$

where ${\tilde{X}}_K$ and ${\tilde{X}}_H$ are the suspensions of Hamiltonian vector fields $X_K$ and $X_H$, respectively.

(c) 

If ${\omega }_1=d{\Theta }_1$ and ${\omega }_2=d{\Theta }_2$, then there exists a function $K_F$ such that

$$d(F^{*}{\tilde{\Theta }}_2-{\Theta }_{K_F})=0$$

where

$${\tilde{\Theta }}_1={\pi }_2^{*}{\Theta }_1+dt,{\tilde{\Theta }}_2={\pi }_2^{*}{\Theta }_2+dtand{\Theta }_{K_F}={\tilde{\Theta }}_1-K_{F}dt.$$

Proof of the above theorem may be found, for instance, in [33]. We will omit it here since in Section 4 we will prove Theorem 4, which is a generalization of Theorem 2. Notice that condition (b) implies that F preserves the form of Hamilton equations.

2.3. Generating Functions of Canonical Transformations

It is an interesting fact that each canonical transformation $F:\mathbb{R}\times P_1\to \mathbb{R}\times P_2$ can be obtained from a real-valued function on $\mathbb{R}\times P_1$, the so-called generating function of F. We will briefly present here the basic properties of generating functions, which play a crucial role in Hamilton–Jacobi theory, which will be the main subject of Section 4.3. Let $F:\mathbb{R}\times P_1\to \mathbb{R}\times P_2$ be a canonical transformation and ${\omega }_1,{\omega }_2$ symplectic forms of $P_1$ and $P_2$, respectively. Let us assume that both $P_1$ and $P_2$ are exact, i.e., there exist one-forms ${\theta }_1$ and ${\theta }_2$ such that ${\omega }_1=d{\theta }_1$ and ${\omega }_2=d{\theta }_2$. Then, from condition $\left(c\right)$ in Theorem 2, we have that $d(F^{*}{\tilde{\theta }}_2-{\theta }_{K_F})=0,$ which means that, locally, there exists a function $W:\mathbb{R}\times P_1\to \mathbb{R}$ such that $F^{*}{\tilde{\theta }}_2-{\theta }_{K_F}=dW.$ We will call W a generating function for a canonical transformation F. Let us stress that the local existence of W is equivalent to F being canonical. Let us denote by $\dot{F}$ the coefficient of $dt$ in $F^{*}{\pi }_2^{*}{\theta }_2$. The following theorem provides a relation between generating functions and Theorem 2.

Theorem 3.

If $F:\mathbb{R}\times P_1\to \mathbb{R}\times P_2$ is a canonical transformation with a local generating function $W:\mathbb{R}\times P_1\to \mathbb{R}$, then

$$K_F=\frac{\partial W}{\partial t}-\dot{F}$$

and for a Hamiltonian H on $\mathbb{R}\times P_2$

$$F_{*}{\tilde{X}}_K={\tilde{X}}_{H}whereK=H\circ F+\left(\frac{\partial W}{\partial t}-\dot{F}\right)$$

where K and $K_F$ are the ones displayed in Theorem 2.

3. Geometry of Locally Conformal Symplectic Manifolds

3.1. Basics on Locally Conformal Symplectic Manifolds

The pair $(M,\Omega )$, where $\Omega$ is a non-degenerate two-form and is called an almost symplectic manifold, and $\Omega$ is an almost symplectic two-form. If $\Omega$ is, additionally, closed, then the manifold turns out to be a symplectic manifold [30]. There is an intermediate step between symplectic manifolds and almost symplectic manifolds: these are the so-called locally conformal symplectic manifolds [8]. An almost symplectic manifold $(M,\Omega )$ is an lcs manifold if the two-form is closed locally up to a conformal parameter, i.e., if there exists an open neighborhood, say $U_{\alpha }$, around each point x in M, and a function ${\sigma }_{\alpha }$ such that the exterior derivative $d(e^{-{\sigma }_{\alpha }}\Omega {|}_{\alpha })$ vanishes identically on $U_{\alpha }$ [9]. Here, ${\Omega |}_{\alpha }$ denotes the restriction of the almost symplectic structure $\Omega$ to the open set $U_{\alpha }$. The positive character of the exponential function implies that the local two-form $e^{-{\sigma }_{\alpha }}{\Omega |}_{\alpha }$ is non-degenerate as well. Being closed and non-degenerate,

$${\Omega }_{\alpha }=e^{-{\sigma }_{\alpha }}{\Omega |}_{\alpha }$$

(6)

is a symplectic two-form. That is, the pair $(U_{\alpha },{\Omega }_{\alpha })$ is a symplectic manifold [30].

The question now is how to glue the behavior in all local open charts to arrive at a global definition for lcs manifolds. Notice that ${\Omega |}_{\alpha }$ is a local realization of the global two-form $\Omega$, whereas, up to now, ${\Omega }_{\alpha }$ is defined only on $U_{\alpha }$. In another local chart, say, $U_{\beta }$, a local symplectic two-form is defined to be ${\Omega }_{\beta }:=e^{-{\sigma }_{\beta }}{\Omega |}_{\beta }$. This gives that, for overlapping charts, the local symplectic two-forms are related by ${\Omega }_{\beta }=e^{-({\sigma }_{\beta }-{\sigma }_{\alpha })}{\Omega }_{\alpha }$. Accordingly, this conformal relation determines scalars

$${\lambda }_{\beta \alpha }=e^{{\sigma }_{\alpha }}/e^{{\sigma }_{\beta }}=e^{-({\sigma }_{\beta }-{\sigma }_{\alpha })}$$

(7)

satisfying the cocycle condition

$${\lambda }_{\beta \alpha }{\lambda }_{\alpha \gamma }={\lambda }_{\beta \gamma }.$$

(8)

This way, one can glue the local symplectic two-forms ${\Omega }_{\alpha }$ to a line bundle $L\to M$ valued two-form $\tilde{\Omega }$ on M. To sum up, we say that there are two global two-forms $\Omega$ (real valued) and $\tilde{\Omega }$ (line-bundle valued) on M with local realizations ${\Omega |}_{\alpha }$ and ${\Omega }_{\alpha }$, respectively. These local two-forms are related as in (6). Now, recalling (6) once more, it is easy to see that ${d\Omega |}_{\alpha }=d{\sigma }_{\alpha }{\wedge \Omega |}_{\alpha }$, but, equally, ${d\Omega |}_{\beta }=d{\sigma }_{\beta }{\wedge \Omega |}_{\beta }$ on an overlapping region $U_{\alpha }\cap U_{\beta }$. This implies that $d({\sigma }_{\beta }-{\sigma }_{\alpha }){\wedge \Omega |}_{U_{\alpha }\cap U_{\beta }}=0,$ and since $\Omega$ is nondegenerate, necessarily, $d{\sigma }_{\alpha }=d{\sigma }_{\beta }$. Thus, $\theta =d{\sigma }_{\alpha }$ is a well-defined one-form on M that satisfies $d\Omega =\theta \wedge \Omega$. Such a one-form $\theta$ is called the Lee one-form [10]. Since $\theta$ is locally exact, it is closed. An lcs manifold $(M,\Omega ,\theta )$ is a globally conformal symplectic (gcs) manifold if the Lee form $\theta$ is an exact one-form. Since it is fulfilled that in two-dimensional manifolds every closed form is exact, two-dimensional lcs manifolds are gcs manifolds. Notice that the Lee form $\theta$ is completely determined by $\Omega$ for manifolds with a dimension 4 or higher. We can, likewise, denote an lcs manifold by a triple $(M,\Omega ,\theta )$. Equivalently, this realization of locally conformal symplectic manifolds reads that an lcs manifold is a symplectic manifold if and only if the Lee form $\theta$ vanishes identically. Conversely, if $(M,\Omega ,\theta )$ is a triple such that $\Omega$ is an almost symplectic form, and $\theta$ is a closed one-form such that $d\Omega =\theta \wedge \Omega$, then one can find an open cover $\left\{U_{\alpha }\right\}$ of M such that, on each chart $U_{\alpha }$, $\theta =d{\sigma }_{\alpha }$ for some functions ${\sigma }_{\alpha }$. It is clear now that $e^{-{\sigma }_{\alpha }}{\Omega |}_{\alpha }$ is symplectic on $U_{\alpha }$ [30].

Musical mappings. Consider an almost symplectic manifold $(M,\omega )$. The non-degeneracy of the two-form $\Omega$ leads us to define a musical isomorphism

$${\Omega }^{♭}:\mathfrak{X}\left(M\right)⟶{\Lambda }^1\left(M\right):X\mapsto {\iota }_X\omega ,$$

(9)

where ${\iota }_X$ is the interior derivative. Here, $\mathfrak{X}\left(M\right)$ is the space of vector fields on M whereas ${\Lambda }^1\left(M\right)$ is the space of one-form sections on M. We denote the inverse of the isomorphism (9) by ${\Omega }^{♯}$. When pointwise evaluated, the musical mappings ${\Omega }^{♭}$ and ${\Omega }^{♯}$ induce isomorphisms from $TM$ to $T^{*}M$, and from $T^{*}M$ to $TM$, respectively. We shall use the same notation for the induced isomorphisms [30].

Let us now concentrate on the particular case of lcs manifolds. Assume an lcs manifold $(M,\Omega )$ with a Lee form $\theta$. Referring to the ${\Omega }^{♯}$, we define the so-called Lee vector field

$$Z_{\theta }:={\Omega }^{♯}\left(\theta \right),{\iota }_{Z_{\theta }}\Omega =\theta$$

(10)

where $\theta$ is the Lee form. By applying ${\iota }_{Z_{\theta }}$ to both sides of the second equation, one obtains that ${\iota }_{Z_{\theta }}\theta =0$. Further, by a direct calculation, we see that ${\mathcal{L}}_{Z_{\theta }}\theta =0$ and that ${\mathcal{L}}_{Z_{\theta }}\Omega =0$. Here, ${\mathcal{L}}_{Z_{\theta }}$ is the Lie derivative.

The Lichnerowicz–deRham differential. Consider now an arbitrary manifold M equipped with a closed one-form $\theta$. The Lichnerowicz–deRham differential (LdR) on the space of differential forms $\Lambda \left(M\right)$ is defined as

$$d_{\theta }:{\Lambda }^k\left(M\right)\to {\Lambda }^{k+1}\left(M\right):\beta \mapsto d\beta -\theta \wedge \beta ,$$

(11)

where d denotes the exterior (deRham) derivative. Notice that $d_{\theta }$ is a differential operator of order 1. That is, if $\beta$ is a k form then $d_{\theta }\beta$ is the $k+1$ form. The closure of the one-form $\theta$ reads that $d_{\theta }^2=0$. This allows the definition of cohomology as the $d_{\theta }$ cohomology in $\Lambda \left(M\right)$ [39]. We represent this with the pair $(\Lambda \left(M\right),d_{\theta })$. A direct computation shows that an almost symplectic manifold $(M,\Omega )$ equipped with a closed one-form $\theta$ is an lcs manifold if and only if $d_{\theta }\Omega =0$ [9].

Lagrangian Submanifolds of lcs manifolds. Consider an almost symplectic manifold $(M,\Omega )$. Let L be a submanifold of M [30]. The complement $T{L}^{\perp }$ is defined with respect to $\Omega$. For a point $x\in L$,

$$T_x{L}^{\perp }=\{u\in T_{x}M|\Omega (u,w)=0,\forall w\in T_{x}L\}.$$

(12)

We say that L is isotropic if $TL\subset T{L}^{\perp }$, it is coisotropic if $T{L}^{\perp }\subset TL$ and it is Lagrangian if $T{L}^{\perp }=TL$. Accordingly a submanifold is Lagrangian if it is both isotropic and coisotropic. Observe that the definition is exactly the same as in the symplectic case, since they are obtained at the linear level.

3.2. Locally Conformal Symplectic Structures on Cotangent Bundles

We shall depict the lcs framework on cotangent bundles. Start with the canonical symplectic manifold $(T^{*}Q,{\omega }_Q)$. Here, the canonical symplectic two-form ${\omega }_Q=-d{\Theta }_Q$ is minus the exterior derivative of the canonical Liouville one-form ${\Theta }_Q$ on $T^{*}Q$. Let $\vartheta$ be a closed one-form on the base manifold Q and pull it back to $T^{*}Q$ by means of the cotangent bundle projection ${\pi }_Q$. This gives us a closed semi-basic one-form $\theta ={\pi }_Q^{*}\left(\vartheta \right)$. By means of the Lichnerowicz-de Rham differential, we define a two-form

$${\Omega }_{\theta }=-d_{\theta }\left({\Theta }_Q\right)=-d{\Theta }_Q+\theta \wedge {\Theta }_Q={\omega }_Q+\theta \wedge {\Theta }_Q$$

(13)

on the cotangent bundle $T^{*}Q$. Since $d{\Omega }_{\theta }=\theta \wedge {\Omega }_{\theta }$ holds, the triple

$$T_{\theta }^{*}Q=(T^{*}Q,{\Omega }_{\theta },\theta )$$

(14)

determines a locally conformal symplectic manifold with Lee-form $\theta$. In short, we denote this lcs manifold by, simply, $T_{\theta }^{*}Q$. This structure is conformally equivalent to a symplectic manifold if and only if $\vartheta$ lies in the zeroth class of the first deRham cohomology on Q. Notice that $T_{\theta }^{*}Q$ is an exact locally conformal symplectic manifold since ${\Omega }_{\theta }$ is defined to be minus of the Lichnerowicz–deRham differential $d_{\theta }$ of the canonical one-form ${\Theta }_Q$. It is important to note that all lcs manifolds locally look like $T_{\theta }^{*}Q$ for some Q and for a closed one-form $\vartheta$.

Consider the lcs manifold $T_{\theta }^{*}Q$ in (14) with Lee form $\theta ={\pi }_Q^{*}\vartheta$. Let $\gamma$ be a section of the cotangent bundle or, in other words, a one-form on Q. A direct computation shows that the pull-back of the lcs structure is $d_{\theta }$ exact, that is

$${\gamma }^{*}{\Omega }_{\theta }=-d_{\vartheta }\gamma$$

(15)

where $d_{\vartheta }$ denotes the LdR differential defined by the one-form $\vartheta$ on Q. This implies that the image space of $\gamma$ is a Lagrangian submanifold of $T_{\theta }^{*}Q$ if and only if $d_{\vartheta }\gamma =0$. Since $d_{\vartheta }^2$ is identically zero, the image space of the one-form $d_{\vartheta }f$ is a Lagrangian submanifold of $T_{\theta }^{*}Q$ for some function f defined on Q.

3.3. Dynamics on Locally Conformal Symplectic Manifolds

Let us now concentrate on Hamiltonian dynamics on lcs manifolds [40], which was presented in [30]. Here, we briefly remind the reader about the main crucial points of Hamiltonian dynamics on lcs manifolds [30]. As discussed previously, there are two equivalent definitions of lcs manifolds. One is local, and the other is global. First consider the local definition by recalling the local symplectic manifold $(U_{\alpha },{\Omega }_{\alpha })$. For a Hamiltonian function $h_{\alpha }$ on this chart, we write the Hamilton equations by

$${\iota }_{X_{\alpha }}{\Omega }_{\alpha }=d{h}_{\alpha }.$$

(16)

Here, $X_{\alpha }$ is the local Hamiltonian function associated to this framework. In terms of the Darboux coordinates $(q_{\left(\alpha \right)}^i,p_i^{\left(\alpha \right)})$ on $U_{\alpha }$. The local symplectic two-form is ${\Omega }_{\alpha }=d{q}_{\left(\alpha \right)}^i\wedge d{p}_i^{\left(\alpha \right)}$, and the Hamilton Equation (16) becomes

$$\frac{d{q}_{\alpha }^i}{dt}=\frac{\partial h_{\alpha }}{\partial p_i^{\alpha }},\frac{d{p}_i^{\alpha }}{dt}=-\frac{\partial h_{\alpha }}{\partial q_{\alpha }^i}.$$

(17)

We have discussed the gluing problem of the local symplectic manifolds but we have not addressed this problem for the local Hamiltonian functions. We wish to define a global realization of the local Hamiltonian functions in such a way that the structure of the local Hamilton equation (17) does not change under transformations of coordinates. This can be rephrased as to establish a global realization of the local Hamiltonian function $h_{\alpha }$ by preserving the local Hamiltonian vector fields $X_{\alpha }$ in (16). A direct observation reads that multiplying both sides of (16) by the scalars ${\lambda }_{\beta \alpha }$ defined in (7) leaves the dynamics invariant. Thus, the transition $h_{\beta }=e^{{\sigma }_{\alpha }-{\sigma }_{\beta }}{h}_{\alpha }$ is needed for the preservation of the structure of the equations. In the light of the cocyle character of the scalars shown in (8), we can glue the local Hamiltonian functions $h_{\alpha }$ to define a section $\tilde{h}$ of the line bundle $L\to M$. On the other hand, in light of the identity $e^{{\sigma }_{\alpha }}{h}_{\alpha }=e^{{\sigma }_{\beta }}{h}_{\beta }$, one arrives at a real valued Hamiltonian function

$${h|}_{\alpha }=e^{{\sigma }_{\alpha }}{h}_{\alpha }.$$

(18)

on $U_{\alpha }$ that defines a real valued function h on the whole M. Recall the discussion in Section 3.1 about the local and global character of the two-forms. Similarly, we argue that there exist two global functions $\tilde{h}$ (line-bundle valued) and h (real valued) on the manifold M. On a chart $U_{\alpha }$, these functions reduce to $h_{\alpha }$ and ${h|}_{\alpha }$, respectively, and they satisfy relation (18).

In order to recast the global picture of the Hamilton equation (16), we first substitute identity (18) into (16). Hence, a direct calculation turns the Hamilton equations into the following form

$${\iota }_{X_{\alpha }}{\Omega |}_{\alpha }=dh{{|}_{\alpha }-h|}_{\alpha }d{\sigma }_{\alpha }$$

(19)

where we employed the identity (6) on the left-hand side of this equation. Notice that all the terms in Equation (19) have global realizations. Thus, we can write

$${\iota }_{X_h}\Omega =dh-h\theta ,$$

(20)

where $X_h$ is the vector field obtained by gluing all the vector fields $X_{\alpha }$. That is, we have $X_h{|}_{\alpha }=X_{\alpha }$. Notice that (20) can also be written as

$${\iota }_{X_h}\Omega =d_{\theta }h,$$

(21)

where $d_{\theta }$ is the Lichnerowicz–deRham differential given in (11). The vector field $X_h$ defined in (21) is called a Hamiltonian vector field for the Hamiltonian function h. In terms of the Lee vector field $Z_{\theta }$ defined in (10), the Hamiltonian vector field is computed to be

$$X_h={\Omega }^{♯}\left(dh\right)+h{Z}_{\theta },$$

(22)

where ${\Omega }^{♯}$ is the musical isomorphism induced by the almost symplectic two-form $\Omega$. From this, one can easily see that, apart from the classical symplectic framework, for the constant function $h=1$ the corresponding Hamiltonian vector field is not zero but the Lee vector in (10), that is $Z_{\theta }=X_1$. More generally, a vector field X is called a locally conformal Hamiltonian vector field if

$$d_{\theta }({\iota }_X\Omega )=0.$$

(23)

It is clear to see that a Hamiltonian vector field is a locally Hamiltonian vector field, since $d_{\theta }^2=0$.

3.4. Morphisms of lcs Manifolds

Let $(M_1,{\Omega }_1,{\theta }_1)$ and $(M_2,{\Omega }_2,{\theta }_2)$ be lcs manifolds of the same dimension. We say that the diffeomorphism $F:M_1\to M_2$ is a strict morphism of lcs manifolds if $F^{*}{\Omega }_2={\Omega }_1.$ Notice that this condition implies that

$$d{\Omega }_1=d\left(F^{*}{\Omega }_2\right)=F^{*}d{\Omega }_2=F^{*}{\theta }_2\wedge F^{*}{\Omega }_2=F^{*}{\theta }_2\wedge {\Omega }_1,$$

which means that $F^{*}{\theta }_2={\theta }_1.$ In a local context, we have that if ${\theta }_1=d{\sigma }_1$ and ${\theta }_2=d{\sigma }_2$ for some ${\sigma }_1:M_1\to \mathbb{R}$ and ${\sigma }_2:M_2\to \mathbb{R}$, then $F\circ {\sigma }_2={\sigma }_1$. From now on, we will call F a morphism of locally conformal symplectic manifolds or, in short, an lcs-morphism.

4. Time-Dependent Hamiltonian Formalism on an Lcs Framework

In this section, we present the main result of our paper, which consists of the formulation of time-dependent Hamiltonian mechanics on an lcs manifold and the subsequent discussion of canonical transformations and Hamilton–Jacobi theory in the context of lcs manifolds.

In [41], one can find a brief discussion of lcs structures in relation to a cosymplectic framework. In our approach, we prefer a more direct and physical approach in the spirit of [33] starting directly from a phase space of the form $\mathbb{R}\times M$, where M is an lcs manifold. In physical applications, $\mathbb{R}\times M$ represents the phase space of a time-dependent system on an lcs manifold. Subsequently, we present a generalization of the theory of canonical transformations to an lcs structure. We discuss it in both the local and the global picture and show how this theory naturally arises as an extension of the cosymplectic case. We finish our study by setting a Hamilton–Jacobi theory in the context of time-dependent lcs manifolds. For a review of the time-independent case, we refer the reader to [30].

4.1. Time-Dependent Hamiltonian Dynamics in an Lcs Framework

The time-dependent Hamiltonian formalism on an lcs manifold may be constructed from the time-independent one in similar fashion as it is performed in the symplectic case. Since, locally, an lcs manifold resembles a symplectic manifold, we can use the results from Section 2 for each chart $U_{\alpha }$ in M and find the transition conditions on double overlaps $U_{\alpha }\cap U_{\beta }\subset M$.

Let $(M,\Omega ,\theta )$ be an lcs manifold. Locally, we have a family of open charts $U_{\alpha }$ and functions ${\sigma }_{\alpha }:U_{\alpha }\to \mathbb{R}$. Let us recall that each $(U_{\alpha },{\Omega }_{\alpha })$, where ${\Omega }_{\alpha }=e^{-{\sigma }_{\alpha }}\Omega |{}_{\alpha }$ is a symplectic manifold, which means that we can construct a time-dependent Hamiltonian structure on it, applying the constructions from Section 2. Let $H_{t\alpha }:\mathbb{R}\times U_{\alpha }\to \mathbb{R}$ be a time-dependent Hamiltonian function for a given $t\in \mathbb{R}$. Then, according to (5), the dynamics on a local chart $U_{\alpha }$ is given by the equation ${\iota }_{X_{t\alpha }}{\Omega }_{\alpha }=d{H}_{t\alpha },$ where $X_{t\alpha }$ is a time-dependent vector field representing the dynamics on $U_{\alpha }$. The global time-dependent Hamiltonian H may be obtained from gluing local time-dependent Hamiltonians on $U_{\alpha }\cap U_{\beta }$ through the condition $e^{{\sigma }_{\alpha }}{H}_{t\alpha }=e^{{\sigma }_{\beta }}{H}_{t\beta }$, for each $t\in \mathbb{R}$. Therefore, we obtain a global Hamiltonian function

$$H:\mathbb{R}\times M\to \mathbb{R},H_t|{}_{\alpha }=e^{{\sigma }_{\alpha }}{H}_{t\alpha },$$

where $H_t\left(m\right):=H(t,m)$. We have the diagram

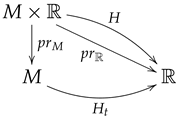
The dynamics of the system is given by the equation

$${\iota }_{X_{H_t}}\Omega =d_{\theta }{H}_t,$$

(24)

where $X_{H_t}$ is a Hamiltonian vector field on M associated with the Hamiltonian $H_t$. Equation (24) constitutes a generalization of the time-dependent Hamilton Equation (5) to an lcs framework. The family of vector fields $\left\{X_{H_t}\right\}$ defines a time-dependent vector field

$$X_H:\mathbb{R}\times M\to TM,(t,m)⟼X_{H_t}\left(m\right),$$

which represents the phase dynamics of the system, where the phase space is represented by $\mathbb{R}\times M$. The solutions of $X_H$ are integral curves $b:\mathbb{R}\to M$ of $X_H$ that represent the phase trajectory of the system. The equations for the integral curves $b:\mathbb{R}\to M$ read

$$\begin{array}{ccc}\hfill \frac{d}{dt}{q}^i\left(b\left(t\right)\right)& =& \frac{\partial H}{\partial p_i}(t,b\left(t\right)),\hfill \\ \hfill \frac{d}{dt}{p}_i\left(b\left(t\right)\right)& =& -\frac{\partial H}{\partial q^i}(t,b\left(t\right))+\frac{\partial H}{\partial p_k}(t,b\left(t\right))\left({\theta }_k\left(b\left(t\right)\right)p_i\left(b\left(t\right)\right)-p_k\left(b\left(t\right)\right){\theta }_i\left(b\left(t\right)\right)\right)+\hfill \\ & & +{\theta }_i\left(b\left(t\right)\right)H(t,b\left(t\right)).\hfill \end{array}$$

(25)

Let us notice that for $\theta =0$, the above equations reduce to standard time-dependent Hamilton equations.

In the following sections, we will need the pull-backs of objects defined on M by means of the projection $p{r}_2:\mathbb{R}\times M\to M$. For an lcs manifold $(M_{,}\Omega ,\theta )$ we define the pull-backs $\tilde{\Omega }:=p{r}_2^{*}\Omega ,$ $\tilde{\theta }:=p{r}_2^{*}\theta .$ See that, locally, we have ${\theta |}_{\alpha }=d{\sigma }_{\alpha }$, so that

$$\tilde{\theta }{|}_{\alpha }=d{\tilde{\sigma }}_{\alpha },$$

where ${\tilde{\sigma }}_{\alpha }:\mathbb{R}\times U_{\alpha }\to \mathbb{R}$, ${\tilde{\sigma }}_{\alpha }={\sigma }_{\alpha }\circ p{r}_2.$ Furthermore, for an exact $\Omega$, i.e., $\Omega =d_{\theta }\Theta$, we obtain

$$\tilde{\Omega }=p{r}_2^{*}{d}_{\theta }\Theta =d_{p{r}_2^{*}\theta }p{r}_2^{*}\Theta =d_{\tilde{\theta }}\tilde{\Theta }.$$

At the end of this section, we will point out that, similarly to the symplectic case, the existence of the function $H:\mathbb{R}\times M\to \mathbb{R}$ allows us to define a new two-form

$${\Omega }_H=\tilde{\Omega }+d_{\tilde{\theta }}H\wedge dt,$$

(26)

which will be important in our work later on. One can show that ${\tilde{X}}_H$, associated with H, is the unique vector field satisfying

$$i_{{\tilde{X}}_H}{\Omega }_H=0,i_{{\tilde{X}}_H}dt=1.$$

(27)

4.2. Canonical Transformations on Lcs Manifolds

We will present now one of the main results of this paper, which is the notion of canonical transformations on lcs manifolds. Before we arrive at the global definition, we will take a look at the local picture. Let $(M_1,{\Omega }_1,{\theta }_1)$ and $(M_2,{\Omega }_2,{\theta }_2)$ be two different lcs manifolds. Let us choose open subsets $U_1\subset M_1$ and $U_2\subset M_2$. Then $(U_{1\alpha },{\Omega }_{1\alpha },{\sigma }_{1\alpha })$ and $(U_{2\alpha },{\Omega }_{2\alpha },{\sigma }_{2\alpha })$ are, by definition, symplectic manifolds. We can consider a canonical transformation between these two symplectic manifolds, i.e., a diffeomorphism $F_{\alpha }:\mathbb{R}\times U_{1\alpha }\to \mathbb{R}\times U_{2\alpha }$ satisfying

$$F_{\alpha }^{*}{\tilde{\Omega }}_{2\alpha }={\tilde{\Omega }}_{1\alpha }+d{K}_{\alpha }\wedge dt,$$

where ${\tilde{\Omega }}_1{|}_{\alpha }$ and ${\tilde{\Omega }}_2{|}_{\alpha }$ are pull-backs of the forms ${\Omega }_1{|}_{\alpha }$ and ${\Omega }_2{|}_{\alpha }$ with respect to the projections $\mathbb{R}\times U_{1\alpha }\to U_{1\alpha }$ and $\mathbb{R}\times U_{2\alpha }\to U_{2\alpha },$ respectively, and $K_{\alpha }$ is a function on $\mathbb{R}\times U_{1\alpha }$. By definition of the forms ${\Omega }_1$ and ${\Omega }_2$, we have that ${\tilde{\Omega }}_{1\alpha }=e^{-{\tilde{\sigma }}_{1\alpha }}{\tilde{\Omega }}_1{|}_{\alpha }$ and ${\tilde{\Omega }}_{2\alpha }=e^{-{\tilde{\sigma }}_{2\alpha }}{\tilde{\Omega }}_2{|}_{\alpha }$, so we can write

$$F_{\alpha }^{*}{e}^{-{\tilde{\sigma }}_{2\alpha }}{\tilde{\Omega }}_2{{|}_{\alpha }=e^{-{\tilde{\sigma }}_{1\alpha }}{\tilde{\Omega }}_1|}_{\alpha }+d{K}_{\alpha }\wedge dt.$$

The global definition of a canonical transformation on an lcs manifold should come from the gluing of local canonical transformations on charts of $M_1$ and $M_2$. Therefore, let us multiply the above formula by $e^{{\tilde{\sigma }}_{1\alpha }}$ so that

$$e^{{\tilde{\sigma }}_{1\alpha }}{F}_{\alpha }^{*}{e}^{-{\tilde{\sigma }}_{2\alpha }}{\tilde{\Omega }}_2{{|}_{\alpha }={\tilde{\Omega }}_1|}_{\alpha }+e^{{\tilde{\sigma }}_{1\alpha }}d{K}_{\alpha }\wedge dt.$$

(28)

Now we can make a few observations. First of all, let us assume that

$${\tilde{\sigma }}_{1\alpha }={\tilde{\sigma }}_{2\alpha }\circ F_{\alpha }.$$

(29)

Then, we can write

$$e^{{\tilde{\sigma }}_{1\alpha }}{F}_{\alpha }^{*}{e}^{-{\tilde{\sigma }}_{2\alpha }}{\tilde{\Omega }}_2{|}_{\alpha }=e^{{\tilde{\sigma }}_{1\alpha }}{e}^{-{\tilde{\sigma }}_{2\alpha }\circ F_{\alpha }}{F}_{\alpha }^{*}{\tilde{\Omega }}_2{{|}_{\alpha }=F_{\alpha }^{*}{\tilde{\Omega }}_2|}_{\alpha },$$

where the last equality comes from (29). On the other hand, it is easy to check that $e^{{\tilde{\sigma }}_{1\alpha }}d{K}_{\alpha }=d_{d{\tilde{\sigma }}_{1\alpha }}\left(e^{{\tilde{\sigma }}_{1\alpha }}{K}_{\alpha }\right)$, where $d_{d{\tilde{\sigma }}_{1\alpha }}$ is the Lichnerowicz–deRham differential with respect to a form $d{\tilde{\sigma }}_{1\alpha }$. Locally, we have ${\tilde{\theta }}_1{|}_{\alpha }=d{\tilde{\sigma }}_{1\alpha }$ so finally we can rewrite (28) as

$$F_{\alpha }^{*}{\tilde{\Omega }}_2{{|}_{\alpha }={\tilde{\Omega }}_1|}_{\alpha }+d_{{\tilde{\theta }}_1{|}_{\alpha }}\left(e^{{\tilde{\sigma }}_{1\alpha }}{K}_{\alpha }\right)\wedge dt.$$

From the above equation, it is easy to see the global version of the equation, which reads

$$F^{*}{\tilde{\Omega }}_2={\tilde{\Omega }}_1+d_{{\tilde{\theta }}_1}K\wedge dt,$$

where ${F|}_{\alpha }=F_{\alpha }$ and K is a function on $\mathbb{R}\times M_1$, such that, locally, ${K|}_{\alpha }=e^{{\tilde{\sigma }}_{1\alpha }}{K}_{\alpha }$. Notice that by imposing condition (29) in every chart, we obtain the global condition $F^{*}{\tilde{\theta }}_2={\tilde{\theta }}_1$. Furthermore, it is obvious that F preserves time, i.e., $F^{*}t=t$.

Considering the above conclusions, we arrive at the following global definition of a canonical transformation on an lcs manifold.

Definition 1.

Let $(M_1,{\Omega }_1,{\theta }_1)$ and $(M_2,{\Omega }_2,{\theta }_2)$ be lcs manifolds and ${\tilde{\Omega }}_1=p{r}_2^{*}{\Omega }_1$ and ${\tilde{\Omega }}_2=p{r}_2^{*}{\Omega }_2,$ be the corresponding two-forms on $\mathbb{R}\times M_1$ and $\mathbb{R}\times M_2$, respectively. A smooth map

$$F:\mathbb{R}\times M_1\to \mathbb{R}\times M_2$$

is called a (strict) canonical transformation if the following statements hold

(i) 

F is a diffeomorphism;

(ii) 

F preserves time, i.e., $F^{*}t=t$ or, equivalently, the following diagram is commutative

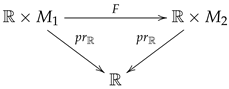
(iii) 

F satisfies $F^{*}{\tilde{\theta }}_2={\tilde{\theta }}_1$;

(iv) 

There exists a function $K_F\in C^{\infty }(\mathbb{R}\times M_1)$ such that

$$F^{*}{\tilde{\Omega }}_2={\Omega }_{K_F}\mathrm{where}{\Omega }_{K_F}={\tilde{\Omega }}_1+d_{{\tilde{\theta }}_1}{K}_F\wedge dt.$$

Notice that in comparison with the definition of canonical transformations given in Section 2.2, we have an extra condition stating that $F^{*}{\tilde{\theta }}_2={\tilde{\theta }}_1$. The map F reduced to a subset $U_{1\alpha }\subset M_1$ is a canonical transformation between the symplectic manifolds $(U_{1\alpha },{\Omega }_{1\alpha })$ and $(U_{2\alpha },{\Omega }_{2\alpha })$, where $U_{2\alpha }:=F\left(U_{1\alpha }\right)$. Condition (iii) ensures that these local canonical transformations glue up to a global map that establishes a canonical transformation from $M_1$ to $M_2$.

The following theorem defines the concept of canonical transformations for Hamiltonian mechanics on lcs manifolds.

Theorem 4.

Let $\left(i\right),\left(ii\right),\left(iii\right)$ hold. Then, the following conditions are equivalent.

0. 

The condition (iv) is satisfied.

1. 

For each function $H\in C^{\infty }(\mathbb{R}\times M_2)$, there exists a function $K\in C^{\infty }(\mathbb{R}\times M_1)$, such that

$$F^{*}{\Omega }_H={\Omega }_K,where{\Omega }_H=\tilde{\Omega }+d_{{\tilde{\theta }}_2}H\wedge dt.$$

2. 

For each $H\in C^{\infty }(\mathbb{R}\times M_2)$, there exists a $K\in C^{\infty }(\mathbb{R}\times M_1)$ such that

$$F_{*}{\tilde{X}}_K={\tilde{X}}_H,$$

where ${\tilde{X}}_K$ and ${\tilde{X}}_H$ is a suspension of a Hamiltonian vector field $X_K$ and $X_H$, respectively.

Additionally, if ${\Omega }_1=d_{{\theta }_1}{\Theta }_1$ and ${\Omega }_2=d_{{\theta }_2}{\Theta }_2$ then 0., 1. and 2. are equivalent to

3. 

If ${\Omega }_1=d_{{\theta }_1}{\Theta }_1$ and ${\Omega }_2=d_{{\theta }_2}{\Theta }_2$, then there exists a function $K_F$ such that

$$d_{{\tilde{\theta }}_1}(F^{*}{\tilde{\Theta }}_2-{\Theta }_{K_F})=0$$

where

$${\tilde{\Theta }}_1={\pi }_2^{*}{\Theta }_1+dt,{\tilde{\Theta }}_2={\pi }_2^{*}{\Theta }_2+dt\mathrm{and}{\Theta }_{K_F}={\tilde{\Theta }}_1-K_{F}dt.$$

Proof. 

$0⟺1.$

Let us take $K=H\circ F+K_F$, then:

$$F^{*}{\Omega }_H=F^{*}({\tilde{\Omega }}_2+d_{{\tilde{\theta }}_2}H\wedge dt)=F^{*}{\tilde{\Omega }}_2+F^{*}\left(d_{{\tilde{\theta }}_2}H\right)\wedge F^{*}dt=F^{*}{\tilde{\Omega }}_2+d_{{\tilde{\theta }}_1}(H\circ F)\wedge dt=$$

$$={\tilde{\Omega }}_1+d_{{\tilde{\theta }}_1}{K}_F\wedge dt+d_{{\tilde{\theta }}_1}(H\circ F)\wedge dt={\tilde{\Omega }}_1+d_{{\tilde{\theta }}_1}(K_F+H\circ F)\wedge dt={\Omega }_K$$

The converse implication is trivial since by taking $H=0$ and $K=K_F$, we obtain, exactly, (iv).

$1⟺2.$

Again, we have $K=H\circ F+K_F$. We show first that 1 implies 2. We know that ${\tilde{X}}_H$ is the unique vector field satisfying

$$i_{{\tilde{X}}_H}{\Omega }_H=0,i_{{\tilde{X}}_H}dt=1.$$

Therefore, we have to prove that

$$i_{{\left(F^{-1}\right)}_{*}{\tilde{X}}_H}{\Omega }_K=0,i_{{\left(F^{-1}\right)}_{*}{\tilde{X}}_H}dt=1.$$

Indeed, we have

$$i_{{\left(F^{-1}\right)}_{*}{\tilde{X}}_H}{\Omega }_K=i_{{\left(F^{-1}\right)}_{*}{\tilde{X}}_H}{F}^{*}{\Omega }_H=F^{*}{i}_{X_H}{\Omega }_H=0$$

and

$$i_{{\left(F^{-1}\right)}_{*}{\tilde{X}}_H}dt=i_{{\left(F^{-1}\right)}_{*}{\tilde{X}}_H}{F}^{*}dt=F^{*}{i}_{X_H}dt=F^{*}1=1,$$

which proves ${\left(F^{-1}\right)}_{*}{\tilde{X}}_H={\tilde{X}}_K$. Reversing arguments, it is straightforward to prove that 2 implies 1.

$0⟺3.$

From condition (iv), we have $F^{*}{\tilde{\Omega }}_2-{\Omega }_{K_F}=0$. Moreover, we have

$$F^{*}{\tilde{\Omega }}_2-{\Omega }_{K_F}=F^{*}{\tilde{\Omega }}_2-{\tilde{\Omega }}_1-d_{{\tilde{\theta }}_1}{K}_F\wedge dt=F^{*}{d}_{{\tilde{\theta }}_2}{\tilde{\Theta }}_2-d_{{\tilde{\theta }}_1}{\tilde{\Theta }}_1-d_{{\tilde{\theta }}_1}{K}_F\wedge dt=$$

$$=d_{{\tilde{\theta }}_1}(F^{*}{\tilde{\Theta }}_2-{\tilde{\Theta }}_1-K_{F}dt),$$

so that

$$F^{*}{\tilde{\Omega }}_2-{\Omega }_{K_F}=0⟺d_{{\tilde{\theta }}_1}(F^{*}{\tilde{\Theta }}_2-{\tilde{\Theta }}_1-K_{F}dt)=0.$$

□

Notice that Theorem 2 is a special case of Theorem 4, when ${\theta }_1={\theta }_2=0$. Condition 2 in Theorem 4 implies that F preserves the form of generalized Hamilton equations on the lcs manifold given by Theorem 25. On the other hand, condition 3 leads us to the notion of generating functions for canonical transformations. Indeed, from

$$d_{{\tilde{\theta }}_1}(F^{*}{\tilde{\Theta }}_2-{\tilde{\Theta }}_1-K_{F}dt)=0,$$

we immediately obtain that, locally,

$$F^{*}{\tilde{\Theta }}_2-{\tilde{\Theta }}_1-K_{F}dt=d_{{\tilde{\theta }}_1}W,$$

where $W:\mathbb{R}\times M_1\to \mathbb{R}$. We will call the function W a generating function of a canonical transformation F.

4.3. Hamilton–Jacobi Theory on Lcs Manifolds

We will present now an extension of HJ theory to the time-dependent lcs framework. The standard HJ theory is usually related to a symplectic or cosymplectic structure (see, e.g., [29]). A time-independent HJ theory for lcs manifolds can be found, for instance, in [30]. Here, we present its time-dependent version, which can be seen as a generalization containing both approaches from [29,30]. Since we are interested in mechanics, we will restrict ourselves to the case $M=T_{\theta }^{*}Q$. The generalisation of the results below to the general case where M is $\theta$-exact and fibered over Q is straightforward.

Consider the fibration $\pi :T_{\theta }^{*}Q\times \mathbb{R}\to Q\times \mathbb{R}$ and a section $\gamma$ of $\pi :T_{\theta }^{*}Q\times \mathbb{R}\to Q\times \mathbb{R}$, which preserves time. In local coordinates, $\gamma$ can be written as

$$\gamma :Q\times \mathbb{R}\to T_{\theta }^{*}Q\times \mathbb{R},\gamma (q^i,t)=(q^i,{\gamma }^i(q^i,t),t).$$

We can associate with $\gamma$ a family of sections ${\gamma }_t:Q\to T_{\theta }^{*}Q\times \mathbb{R}$, such that ${\gamma }_t\left(q^i\right):=\gamma (q^i,t)$. We have the diagram

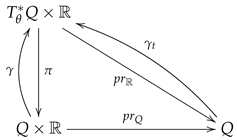
Similarly, we can define a (q-dependent) family of maps ${\gamma }_q\left(t\right):=p{r}_{T_{\theta }^{*}Q}\circ \gamma (q,t)$.

In the following, we will assume that $\gamma$ is $\theta$-closed, i.e., $d_{\theta }\gamma =0$. Consider a Hamiltonian vector field ${\tilde{X}}_H$ defined through Equation (24). We can use a section $\gamma$ to define a projected vector field on $Q\times \mathbb{R}$ as

$${\tilde{X}}_H^{\gamma }=T\pi \circ {\tilde{X}}_H\circ \gamma .$$

The following diagram summarizes the above construction

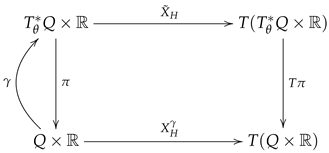
The last necessary tool for the construction of an HJ theory is the vertical lift of a one-form [42]. Let us recall the concept of vertical lift. Consider $\alpha$ a one-form on $T_{\theta }^{*}Q$, which, in local coordinates, reads $\alpha ={\alpha }_{i}d{q}^i$. We say that a vector field ${\alpha }^V$ is a vertical lift of $\alpha$ if

$$i_{{\alpha }^V}{\Omega }_{\theta }=\alpha .$$

In local coordinates, we have ${\alpha }^V=-{\alpha }_i\frac{\partial }{\partial p_i}$. Since ${\Omega }_{\theta }$ is nondegenerate, the map $\alpha \to {\alpha }^V$ is an isomorphism. The following theorem constitutes a time-dependent Hamilton–Jacobi theory for lcs manifolds.

Theorem 5.

Let $M=T_{\theta }^{*}Q$ be an lcs manifold and let ${\tilde{X}}_H$ be a time-dependent Hamiltonian vector field on $\mathbb{R}\times T_{\theta }^{*}Q$ associated with the Hamiltonian $H:\mathbb{R}\times T_{\theta }^{*}Q\to \mathbb{R}$. Consider a section $\gamma :Q\times \mathbb{R}\to T_{\theta }^{*}Q\times \mathbb{R}$, such that $d_{\theta }\gamma =0$. Then, the following conditions are equivalent:

(i) 

The two vector fields ${\tilde{X}}_H$ and ${\tilde{X}}_H^{\gamma }$ are γ-related, i.e.,

$$T\gamma \left({\tilde{X}}_H^{\gamma }\right)={\tilde{X}}_H\circ \gamma ,where{\tilde{X}}_H^{\gamma }=T\pi \circ {\tilde{X}}_H\circ \gamma .$$

(ii) 

The following equation is fulfilled

$${[d(H\circ {\gamma }_t)+{\dot{\gamma }}_q]}^V=0.$$

(30)

Proof. 

We know that $X_H$ is a unique vector field satisfying $i_{X_H}{\Omega }_{\theta H}=0,i_{X_H}dt=1,$ where ${\Omega }_{\theta H}={\Omega }_{\theta }+d_{\theta }H\wedge dt$. It is a matter of calculation to check that for

$${\Omega }_{\theta }=d{q}^i\wedge d{p}_i+{\theta }_i{p}_{j}d{q}^i\wedge d{q}^j,{\tilde{X}}_H=\frac{\partial }{\partial t}+a^i\frac{\partial }{\partial q^i}+b^j\frac{\partial }{\partial p_j}$$

one obtains

$$a^i=\frac{\partial H}{\partial p_i},b^i=-\frac{\partial H}{\partial q^i}+\frac{\partial H}{\partial p_j}({\theta }_j{p}_i-{\theta }_i{p}_j)+{\theta }_{i}H,$$

so that

$${\tilde{X}}_H=\frac{\partial }{\partial t}+\frac{\partial H}{\partial p_i}\frac{\partial }{\partial q^i}+\left(-\frac{\partial H}{\partial q^i}+\frac{\partial H}{\partial p_j}({\theta }_j{p}_i-{\theta }_i{p}_j)+{\theta }_{i}H\right)\frac{\partial }{\partial p_i}.$$

Now, we take a curve $\gamma :Q\times \mathbb{R}\to T_{\theta }^{*}Q\times \mathbb{R}$, $\gamma (t,q^i)=(t,q^i,{\gamma }^k(t,q^i))$, which satisfies $d_{\theta }\gamma =0$. In coordinates, we have

$$d_{\theta }\gamma =0⟺\frac{\partial {\gamma }^i}{\partial q^j}={\theta }_j{\gamma }_i.$$

(31)

The next step is to compare ${\tilde{X}}_H$ with $T\gamma \left({\tilde{X}}_H^{\gamma }\right)$. For $T\gamma \left({\tilde{X}}_H^{\gamma }\right)$, we have

$${\tilde{X}}_H^{\gamma }=\frac{\partial }{\partial t}+\frac{\partial H}{\partial p_i}\frac{\partial }{\partial q^i}$$

and

$$T\gamma \left(\frac{\partial }{\partial t}\right)=\frac{\partial }{\partial t}+\frac{\partial {\gamma }^j}{\partial t}\frac{\partial }{\partial p_j},T\gamma \left(\frac{\partial }{\partial q^i}\right)=\frac{\partial }{\partial q^i}+\frac{\partial {\gamma }^j}{\partial q^i}\frac{\partial }{\partial p_j}$$

so that

$$T\gamma \left({\tilde{X}}_H^{\gamma }\right)=\frac{\partial }{\partial t}+\frac{\partial H}{\partial p_i}\frac{\partial }{\partial q^i}+\left(\frac{\partial {\gamma }^j}{\partial t}+\frac{\partial H}{\partial p_i}\frac{\partial {\gamma }^j}{\partial q^i}\right)\frac{\partial }{\partial p_j}.$$

Therefore, the condition $T\gamma \left({\tilde{X}}_H^{\gamma }\right)={\tilde{X}}_H$ in coordinates reads

$$-\frac{\partial H}{\partial q^i}+\frac{\partial H}{\partial p_j}({\theta }_j{\gamma }_i-{\theta }_i{\gamma }_j)+{\theta }_{i}H=\left(\frac{\partial {\gamma }^i}{\partial t}+\frac{\partial H}{\partial p_j}\frac{\partial {\gamma }^i}{\partial q^j}\right).$$

(32)

On the other hand, from (ii) we have ${\left[d_{\theta }(H\circ {\gamma }_t)\right]}^V=-{\dot{\gamma }}_q^V$. In coordinates, one has

$${\left[d_{\theta }(H\circ {\gamma }_t)\right]}^V=-\left(\frac{\partial H}{\partial q^i}+\frac{\partial H}{\partial p_j}\frac{\partial {\gamma }^j}{\partial q^i}-{\theta }_{i}H\right)\frac{\partial }{\partial p_i},{\dot{\gamma }}_q^V=-\frac{\partial {\gamma }^i}{\partial t}\frac{\partial }{\partial p_i}$$

so that

$$\frac{\partial {\gamma }^i}{\partial t}=-\frac{\partial H}{\partial q^i}-\frac{\partial H}{\partial p_j}\frac{\partial {\gamma }^j}{\partial q^i}+{\theta }_{i}H.$$

(33)

Now, it is a matter of straightforward computation to see that (32) and (33) are equivalent if and only if (31) is satisfied. □

Let us notice that the condition ${[d_{\theta }(H\circ {\gamma }_t)+{\dot{\gamma }}_q]}^V=0$ holds if and only if $d_{\theta }(H\circ {\gamma }_t)+{\dot{\gamma }}_q=0$. In coordinates, we have

$$\frac{\partial {\gamma }^i}{\partial t}+\frac{\partial H}{\partial q^i}+\frac{\partial H}{\partial p_j}\frac{\partial {\gamma }^j}{\partial q^i}-{\theta }_{i}H=0.$$

(34)

We will refer to (34) as the Hamilton–Jacobi equation on a locally conformal symplectic manifold.

4.4. Lcs Manifolds and Jacobi Structures

A locally conformal symplectic manifold is a particular example of a Jacobi structure [29]. A Jacobi manifold is a smooth manifold equipped with a bracket of functions $\{·,·\}$ that is bilinear, skew-symmetric and satisfies both the weak Leibniz rule and the Jacobi identity. It is a generalization of the Poisson manifold in the sense that the bracket does not necessarily satisfy the Leibniz rule. It is interesting to see how the Poisson bracket in the symplectic and cosymplectic case deforms into the Jacobi bracket in the lcs generalization.

Let us consider a symplectic manifold $(M,\omega )$. The form $\omega$ defines a bracket

$$\{f,g\}:=\omega (X_f,X_g).$$

In the symplectic case, the Jacobi identity comes from the closedness of the form $\omega$. Indeed, if $f,g,h\in C^{\infty }\left(M\right)$ and $X_f,X_g,X_h$ are Hamiltonian vector fields of $f,g$ and h, respectively, then we have

$$0=d\omega (X_f,X_g,X_h)=\{\{g,h\},f\}+\{\{h,f\},g\}+\{\{f,g\},h\}.$$

On the other hand, to prove the Leibniz rule we write

$$\{fg,h\}=\omega (X_{fg},X_h)=X_h\left(fg\right)=g{X}_h\left(f\right)+f{X}_h\left(g\right)=\{f,h\}g+f\{g,h\}$$

so that

$$\{fg,h\}=\{f,h\}g+f\{g,h\}.$$

In the same way one can prove the Jacobi identity and the Leibniz rule in the cosymplectic setting. If $(M,\Omega ,\eta )$ is a cosymplectic manifold then the we have a canonical isomorphism [29]

$$♭:\left(M\right)\to {\Omega }^1\left(M\right),♭\left(X\right)=i_X\Omega +\eta \left(X\right)\eta .$$

The Poisson bracket on $C^{\infty }\left(M\right)$ is given by

$$\{f,g\}:=\Omega (\#df,\#dg),$$

where $\#:={♭}^{-1}$. Notice that the above bracket defines a map ${\#}_{\Lambda }\left(df\right):=\Omega (·,df)$, which, in general, is not an isomorphism. To prove the Leibniz rule, we compute

$$\{fg,h\}=\Omega (X_{fg},X_h)={\#}_{\Lambda }\left(dh\right)\left(fg\right)={\#}_{\Lambda }\left(dh\right)\left(f\right)g+f{\#}_{\Lambda }\left(dh\right)\left(g\right)=\{f,h\}g+f\{g,h\}.$$

Notice that in the lcs realm we also have the bracket, which is given by

$${\{f,g\}}_{\theta }:={\Omega }_{\theta }(X_f,X_g)=X_g\left(f\right)-f⟨\theta ,X_g⟩,f,g\in C^{\infty }\left(M\right),$$

where M is an lcs manifold. From simple computations, we have

$${\Omega }_{\theta }(X_f,X_g)=⟨d_{\theta }f,X_g⟩=⟨df,X_g⟩-⟨\theta f,X_g⟩=X_g\left(f\right)-f⟨\theta ,X_g⟩$$

so that

$${\{f,g\}}_{\theta }=X_g\left(f\right)-f⟨\theta ,X_g⟩.$$

It is straightforward to check that ${\{·,·\}}_{\theta }$ is bilinear and skew-symmetric. One can also show that it satisfies the Jacobi identity. However, it turns out that it does not satisfy the Leibniz rule. Indeed, we have

$${\{fg,h\}}_{\theta }={\Omega }_{\theta }(X_{fg},X_h)=X_h\left(fg\right)-fg⟨\theta ,X_h⟩=g{X}_h\left(f\right)+f{X}_h\left(g\right)-fg⟨\theta ,X_h⟩=$$

$$=f{X}_h\left(g\right)-fg⟨\theta ,X_h⟩+fg⟨\theta ,X_h⟩+g{\{f,h\}}_{\theta }=f{\{g,h\}}_{\theta }+g{\{f,h\}}_{\theta }+fg⟨\theta ,X_h⟩.$$

One can see that the reason for the violation of the Leibniz rule comes form the factor $fg⟨\theta ,X_h⟩$ in the above expression. In the case $\theta =0$ (i.e., for the symplectic structure), the above formula reduces to the standard Leibniz rule for symplectic manifolds.

4.5. Comparison with Locally Conformal Cosymplectic Structures

Let us stress that in [41], M. de Leon et al. performed a similar study to the one presented in our paper. It is interesting to compare the advantages and disadvantages of both approaches.

The idea behind [41] is to generalize cosymplectic geometry to its locally conformal counterpart in the same way as symplectic geometry can be extended to lcs structures. The authors called this new structure a locally conformal cosymplectic manifold (lcc manifold, henceforth). Let us recall that a cosymplectic manifold is a triple $(M,\Omega ,\eta )$, where M is a manifold of the dimension $2n+1$, $\eta$ is a closed one-form and $\Omega$ is a closed two-form such that $\eta \wedge {\Omega }^n\ne 0$. In [41], the authors define an lcc manifold as an almost cosymplectic manifold $(M,\Omega ,\eta )$ equipped with a closed one-form $\theta$ such that

$$d\Omega =-2\Omega \wedge \theta ,d\eta =\eta \wedge \theta .$$

We have to admit that the approach taken by [41] is more general since it allows work on an arbitrary lcc manifold instead of just $M\times \mathbb{R}$, where M is lcs. Another advantage of this approach is that it clearly shows its relation with the cosymplectic setting. However, in our paper, we are more interested in time-dependent Hamiltonian mechanics on an lcs manifold than in lcs manifolds themselves. In particular, our aim is to extend the theory of canonical transformations and HJ theory to the time-dependent lcs case.

In our opinion, starting from $\mathbb{R}\times M$ seems much more natural in order to formulate both problems. Notice that in the famous book of Abraham and Marsden [33], the authors present the same approach we used to deal with canonical transformations, i.e., they consider the product $\mathbb{R}\times M$ instead of a cosymplectic manifold. In our paper, we wanted to show how the ideas contained in that book have the natural generalisation to the lcs case. Since $M\times \mathbb{R}$ usually represents spacetime, our structures can be possibly applied to problems employing Cauchy hypersurface spacetimes. However, it seems to us pretty obvious that the results concerning canonical transformations obtained within our work can be generalised to the lcc setting from [41].

Regarding HJ theory, we started from the approach in [30] and we extended it to the time-dependent case presented in this paper. However, one can think of other ways to approach HJ theory in that context. One can start with an HJ theory for cosymplectic manifolds [29] and extend these results to the case presented in [41]. As we have already mentioned, in our paper we chose the first path described.

5. Applications: Contact Structures and Lcs HJ

In order to shed some light on the applications of time-dependent locally conformal symplectic structures, we introduce the concept of contact pairs in the frame of contact geometry and previously introduced in [19,22].

A contact pair of type $(h,k)$ on a $(2h+2k+2)$-dimensional manifold is a pair of one-forms $(\alpha ,\beta )$, such that $\alpha \wedge {\left(d\alpha \right)}^h\wedge \beta \wedge {\left(d\beta \right)}^k$ is a volume form and

$${\left(d\alpha \right)}^{h+1}=0,{\left(d\beta \right)}^{k+1}=0.$$

To this pair there are two associated Reeb vector fields, A and B, uniquely determined by the following conditions: $\alpha \left(A\right)=\beta \left(B\right)=1$, $\alpha \left(B\right)=\beta \left(A\right)=0$ and $i_{A}d\alpha =i_{A}d\beta =i_{B}d\alpha =i_{B}d\beta =0$. It turns out that a contact pair $(\alpha ,\beta )$ of type $(h,0)$ gives rise to the lcs form

$$\Omega =d\alpha +\alpha \wedge \beta .$$

(35)

Let us provide now a necessary and sufficient condition for an lcs form to arise from a contact pair. Considering contact pairs of type $(h,0)$, so that $\beta$ is a closed one-form, and the dimension of the manifold is $2h+2$, more generally, we can provide pairs of one-forms $(\alpha ,\beta )$ such that $d\beta =0$ and $\alpha \wedge {\left(d\alpha \right)}^h\wedge \beta$ is a volume form. We shall refer to these pairs as generalized contact pairs of type $(h,0)$. For a generalized contact pair, one defines a Reeb distribution $\mathcal{R}$ consisting of tangent vectors Y satisfying the equation $\left(i_{Y}d\alpha \right){|}_{ker\left(\alpha \right)\cap ker\left(\beta \right)}=0$.

Suppose that $\Omega$ is an lcs form, and X is a vector field satisfying ${\mathcal{L}}_X\Omega =0$. Then, we have $d{\mathcal{L}}_X\Omega =0$, which by the nondegeneracy of $\Omega$ implies ${\mathcal{L}}_X\theta =0$. It means that $d\left(\theta \right(X\left)\right)=0$, since $\theta$ is a closed form. Thus, $\theta \left(X\right)=1$ is (locally) a constant that we normalized. The following result is discussed in detail in [8].

Theorem 6.

Let M be a smooth manifold of dimension $2h+2$. There is a bijection between contact pairs $(\alpha ,\beta )$ of type $(h,0)$ and lcs forms Ω with Lee form θ, that admit a vector field X satisfying ${\mathcal{L}}_X\Omega =0$ and $\theta \left(X\right)=1$. The bijection maps are the Reeb vector fields A and B of $(\alpha ,\beta )$ to L and X, respectively. Moreover, ${\Omega }^{h+1}$ and $\alpha \wedge {\left(d\alpha \right)}^h\wedge \beta$ define the same orientation on M.

There is a partial generalization of this result to the case of generalized contact pairs in place of contact pairs [19,22].

It turns out that on a closed manifold, every generalized contact pair $(\alpha ,\beta )$ of type $(h,0)$ gives rise to an lcs form

$$\Omega =d\alpha +c\alpha \wedge \beta$$

(36)

when $c\in \mathbb{R}$ is large. The Lee form $\theta$ of $\Omega$ equals $c\beta$. It is straightforward to check that $d\Omega =\Omega \wedge c\beta$. To check nondegeneracy, we compute

$${\Omega }^{h+1}={(d\alpha +c\alpha \wedge \beta )}^{h+1}={\left(d\alpha \right)}^{h+1}+c(h+1)\alpha \wedge {\left(d\alpha \right)}^h\wedge \beta .$$

For a large c, the second summand dominates the first summand, so the right-hand side is a volume form. In this case, the equality $A=L$ no longer holds; in fact, L in general is not proportional to the Reeb vector field A. The other Reeb vector field B does not give an infinitesimal automorphism X of the lcs form. If a closed manifold M admits a (possibly generalized) contact pair $(\alpha ,\beta )$, then the existence of the closed non-vanishing one-form $\beta$ implies that M fibers over the circle.

We would like to now show some physical examples related to the existence of an lcs structure associated with contact pairs. Nilpotent Lie groups provide interesting examples of contact pairs [43], from which one can build a locally conformal symplectic two-form, as it is shown in the examples below. In order to describe the Lie algebra of a Lie group, we give only the non-zero ordered brackets of the fundamental fields $X_i$. The dual forms of $X_i$ will be denoted by ${\eta }^i$.

In particular, we will focus on general Lie systems that are related with control systems. From the theory of Lie systems [28], we know that some physical systems, such as nonlinear oscillators, control systems, etc., can be described in terms of a curve taking values in a finite-dimensional Lie algebra of vector fields. These systems depend on some explicitly time-dependent functions, as well as the finite-dimensional Lie algebra of vector fields, aka., Vessiot–Guldberg Lie algebra. The following examples are based on the general construction of Lie systems with the underlying Lie algebras that we expose, in particular, ${\mathfrak{g}}_{4,1}$ and three different representations. The interest of these Lie algebras is that one may construct lcs structures from them, and, hence, they provide a physical interpretation of our time-dependent lcs Hamiltonian systems.

In particular, our examples are based on control systems on ${\mathbb{R}}^5\times \mathbb{R}$ when one reduces the system by the symmetry coordinate $x_5$. For example, in System 1, the functions $a_3\left(t\right)$ and $a_4\left(t\right)$ are the controls allowing the dynamics to connect two points in ${\mathbb{R}}^4$ while optimizing a cost functional depending on the controls. These systems, under certain particular considerations, are equivalent to plate-ball systems with respect to the optimization problem [44].

5.1. Examples: Coupled Linear Differential Equations

Consider the indecomposable nilpotent Lie algebra ${\mathfrak{g}}_{4,1}$ with nontrivial commutators

$$[X_1,X_4]=X_3,[X_1,X_3]=X_2.$$

(37)

The pair $({\eta }^2,{\eta }^4)$ determines a contact pair of type $(1,0)$ on the corresponding Lie group, where ${\eta }^i$ are the dual forms of the vector fields $X_i$ in (37). One can construct a locally conformally symplectic form, which is

$$\Omega =d{\eta }^2+{\eta }^2\wedge {\eta }^4.$$

(38)

and the Lee form is $\theta ={\eta }^4$. The Lie algebra (37) admits different representations depending on the dimension of the space we are working on [45]. Let us select one that is convenient for the time-dependent lcs case.

Using the representations $\mathbf{1}$, $\mathbf{2}$ and $\mathbf{4}$ given in [45] to complete the basis for the Lie algebra ${\mathfrak{g}}_{4,1}$, we can build up linear systems of differential equations in the five-dimensional manifold coordinated by $(t,x_1,x_2,x_3,x_4)$.

5.1.1. System 1

Using representation $\mathbf{1}$, given by

$$\{X_1={\partial }_{x_2},X_2={\partial }_{x_1},X_3=x_2{\partial }_{x_1}+x_3{\partial }_{x_2}+{\partial }_{x_4},X_4={\partial }_{x_3}\}$$

(39)

we obtain a time-dependent vector field

$$X_t=a_1\left(t\right){\partial }_{x_1}+a_2\left(t\right){\partial }_{x_2}+a_3\left(t\right){\partial }_{x_3}+a_4\left(t\right)\left(x_2{\partial }_{x_1}+x_3{\partial }_{x_2}+{\partial }_{x_4}\right),$$

which can be rewritten as

$$X_t=\left(a_1\left(t\right)+a_4\left(t\right)x_2\right){\partial }_{x_1}+\left(a_2\left(t\right)+a_4\left(t\right)x_3\right){\partial }_{x_2}+a_3\left(t\right){\partial }_{x_3}+a_4\left(t\right){\partial }_{x_4}$$

(40)

and whose integral curves correspond with the system

$$\left\{\begin{array}{c}{\dot{x}}_1=a_1\left(t\right)+a_4\left(t\right)x_2,\hfill \\ {\dot{x}}_2=a_2\left(t\right)+a_4\left(t\right)x_3,\hfill \\ {\dot{x}}_3=a_3\left(t\right),\hfill \\ {\dot{x}}_4=a_4\left(t\right).\hfill \end{array}\right.$$

The dual basis of one-forms reads

$$\{{\eta }^1=d{x}_2-x_{3}d{x}_4,{\eta }^2=d{x}_1-x_{2}d{x}_4,{\eta }^3=d{x}_4,{\eta }^4=d{x}_3\}$$

(41)

Using the above forms, we can construct a locally conformal symplectic two-form as in (38). In this case, it reads

$${\Omega }_{\mathbf{1}}=-d{x}_2\wedge d{x}_4+d{x}_1\wedge d{x}_3-x_{2}d{x}_4\wedge d{x}_3.$$

(42)

It is straightfoward to see that (42) fulfills $d{\Omega }_{\mathbf{1}}={\eta }^4\wedge {\Omega }_{\mathbf{1}}$. Therefore, it is an lcs form with a Lee form $\theta ={\eta }^4$.

5.1.2. System 2

Using representation $\mathbf{2}$, which reads

$$\{X_1={\partial }_{x_2},X_2={\partial }_{x_1},X_3=x_2{\partial }_{x_1}+x_3{\partial }_{x_2}+x_4{\partial }_{x_3}+{\partial }_{x_4},X_4={\partial }_{x_3}\}$$

(43)

we obtain a time-dependent vector field

$$X_t=a_1\left(t\right){\partial }_{x_1}+a_2\left(t\right){\partial }_{x_2}+a_3\left(t\right){\partial }_{x_3}+a_4\left(t\right)\left(x_2{\partial }_{x_1}+x_3{\partial }_{x_2}+x_4{\partial }_{x_3}+{\partial }_{x_4}\right),$$

which can be rewritten as

$$X_t=\left(a_1\left(t\right)+a_4\left(t\right)x_2\right){\partial }_{x_1}+\left(a_2\left(t\right)+a_4\left(t\right)x_3\right){\partial }_{x_2}+(a_3\left(t\right)+a_4\left(t\right)x_4){\partial }_{x_3}+a_4\left(t\right){\partial }_{x_4}$$

(44)

and whose integral curves correspond with the system

$$\left\{\begin{array}{c}{\dot{x}}_1=a_1\left(t\right)+a_4\left(t\right)x_2,\hfill \\ {\dot{x}}_2=a_2\left(t\right)+a_4\left(t\right)x_3,\hfill \\ {\dot{x}}_3=a_3\left(t\right)+a_4\left(t\right)x_4,\hfill \\ {\dot{x}}_4=a_4\left(t\right).\hfill \end{array}\right.$$

The dual basis of one-forms is

$$\{{\eta }^1=d{x}_2-x_{3}d{x}_4,{\eta }^2=d{x}_1-x_{2}d{x}_4,{\eta }^3=d{x}_4,{\eta }^4=d{x}_3-x_{4}d{x}_4\}$$

(45)

Again, we can construct a locally conformal symplectic two-form according to (38)

$${\Omega }_{\mathbf{2}}=-d{x}_2\wedge d{x}_4+d{x}_1\wedge d{x}_3-x_{4}d{x}_1\wedge d{x}_4+x_{2}d{x}_3\wedge d{x}_4$$

(46)

with a Lee form $\theta ={\eta }^4$. It is easy to check that $d{\Omega }_{\mathbf{2}}=\theta \wedge {\Omega }_{\mathbf{2}}$.

5.1.3. System 3

We use representation $\mathbf{4}$, which reads

$$\{X_1={\partial }_{x_2},X_2={\partial }_{x_1},X_3=x_2{\partial }_{x_1}+x_4{\partial }_{x_3}-{\partial }_{x_4},X_4=x_3{\partial }_{x_1}+x_4{\partial }_{x_2}+{\partial }_{x_3}\}.$$

(47)

Again, we obtain a t-dependent vector field

$$X_t=a_1\left(t\right){\partial }_{x_1}+a_2\left(t\right){\partial }_{x_2}+a_3\left(t\right)\left(x_3{\partial }_{x_1}+x_4{\partial }_{x_2}+{\partial }_{x_3}\right)+a_4\left(t\right)\left(x_2{\partial }_{x_1}+x_4{\partial }_{x_3}-{\partial }_{x_4}\right)$$

which can be rewritten as

$$X_t=\left(a_1\left(t\right)+a_3\left(t\right)x_3+a_4\left(t\right)x_2\right){\partial }_{x_1}+\left(a_2\left(t\right)+a_3\left(t\right)x_4\right){\partial }_{x_2}+(a_3\left(t\right)+a_4\left(t\right)x_4){\partial }_{x_3}-a_4\left(t\right){\partial }_{x_4}$$

and whose integral curves correspond with the system

$$\left\{\begin{array}{c}{\dot{x}}_1=a_1\left(t\right)+a_3\left(t\right)x_3+a_4\left(t\right)x_2,\hfill \\ {\dot{x}}_2=a_2\left(t\right)+a_3\left(t\right)x_4,\hfill \\ {\dot{x}}_3=a_3\left(t\right)+a_4\left(t\right)x_4,\hfill \\ {\dot{x}}_4=-a_4\left(t\right).\hfill \end{array}\right.$$

In this case, the basis of dual one-forms is

$$\{{\eta }^1=d{x}_2-x_{4}d{x}_3-x_4^{2}d{x}_4,{\eta }^2=d{x}_1-x_{3}d{x}_3-(x_3{x}_4-x_2)d{x}_4,{\eta }^3=-d{x}_4,{\eta }^4=d{x}_3+x_{4}d{x}_4\}$$

and the associated lcs two-form $\Omega =d{\eta }^2+{\eta }^2\wedge {\eta }^4$ reads

$${\Omega }_{\mathbf{4}}=d{x}_1\wedge d{x}_3+x_{4}d{x}_1\wedge d{x}_4+d{x}_2\wedge d{x}_4-(x_4+x_2)d{x}_3\wedge d{x}_4$$

(48)

where the Lee form is $\theta ={\eta }^4$.

5.2. HJ Equation for a System with a Time-Dependent Potential

In addition to the previous example, we will consider a toy model, whose aim is to familiarize the reader with our construction of a time-dependent lcs HJ theory through a theoretical physical model.

Consider a planar Euclidean space $Q={\mathbb{R}}^n$. In order to define an lcs manifold structure on the cotangent bundle, we assume that we have a closed one-form $\theta ={\theta }_{i}d{q}^i$, which is the pull-back of the one-form $\vartheta$ on Q. Then $T_{\theta }^{*}Q\times \mathbb{R}={\mathbb{R}}^{2n}\times \mathbb{R}$ and

$${\Omega }_{\theta }={\Omega }_Q+\theta \wedge {\theta }_Q=d{q}^i\wedge d{p}_i-{\theta }_i{p}_{j}d{q}^i\wedge d{q}^j.$$

(49)

Let us consider a system described by the following Hamiltonian including an explicitly time-dependent potential [30]

$$H=\frac{1}{2m}{p}_i{p}^i+V(q,t).$$

(50)

Applying the time-dependent lcs HJ equation, we obtain a solution $\gamma (t,q^i)=(t,q^i,{\gamma }^k(t,q^i))$ for the Hamilton Equation (25) associated with (50). From (34), we have that the lcs HJ equation for $\gamma$ reads

$$\frac{\partial {\gamma }^i}{\partial t}+\frac{1}{2m}{p}_j\frac{\partial {\gamma }^j}{\partial q^i}+\frac{\partial V}{\partial q^i}-{\theta }_i\left(\frac{1}{2m}{p}_i{p}^i+V(q,t)\right)=0.$$