Abstract
Transcription factors (TFs) and microRNAs (miRNAs) are co-actors in genome-scale decoding and regulatory networks, often targeting common genes. To discover the symmetries and invariants of the transcription and regulation at the scale of the genome, in this paper, we introduce tools of infinite group theory and of algebraic geometry to describe both TFs and miRNAs. In TFs, the generator of the group is a DNA-binding domain while, in miRNAs, the generator is the seed of the sequence. For such a generated (infinite) group , we compute the character variety, where is simultaneously a ‘space-time’ (a Lorentz group) and a ‘quantum’ (a spin) group. A noteworthy result of our approach is to recognize that optimal regulation occurs when looks similar to a free group ( to 3) in the cardinality sequence of its subgroups, a result obtained in our previous papers. A non-free group structure features a potential disease. A second noteworthy result is about the structure of the Groebner basis of the variety. A surface with simple singularities (such as the well known Cayley cubic) within is a signature of a potential disease even when looks similar to a free group in its structure of subgroups. Our methods apply to groups with a generating sequence made of two to four distinct DNA/RNA bases in . We produce a few tables of human TFs and miRNAs showing that a disease may occur when either is away from a free group or contains surfaces with isolated singularities.
1. Introduction
Again since the one face, constant in symmetry, appears sometimes fair and sometimes not, can we doubt that beauty is something more than symmetry, that symmetry itself owes its beauty to a remoter principle?[1] (Ennead I, Sixt Tractate, p66).
The remote principle envisaged by Plotinus is still a symmetry principle but in a modern definition involving group theory and algebraic geometry. Recently, we wrote a paper about a common algebra possibly ruling the beauty and structure in poems, music and proteins [2]. We found that free groups govern the structure of such disparate topics where a language emerges from pure randomness. We coined the concept of ‘syntactical freedom’ for qualifying the occurrence of symbols and rules organized according to group theory and aperiodicity [3,4]. One favorite decomposition of the secondary structure of proteins is in term of -helices, -sheets and coils [5] but this decomposition and the resulting syntax is model dependent [2]. According to our view, at the genome scale, the escape to ‘syntactical freedom’ means a lack of harmony and the signature of a potential disease. The secondary structures in the sequence of proteins or viruses are, most of the time, organized according to the rules of free groups and, otherwise they may be a witness of a potential aberrant topology.
Of course, there are other techniques to identify a potential disease in the DNA/RNA structures. The loose of homochirality of DNA may indicate an age-related disease [6]. Data mining techniques may be employed to identify cancer in gene expression [7]. The role of miRNAs in the regulation of pathogenesis during infection is investigated in [8].
Apart from the canonical double helix B-DNA we now know that there exists a diversity of non-canonical coding/decoding sequences organized in structures such as Z-DNA (often encountered in transcription factors [9,10]), G-quadruplex (in telomeres) and other types that are single-stranded, two-stranded, or multistranded [11]. RNA is usually a single-stranded molecule in a short chain of nucleotides, as is the case for a messenger RNA (mRNA) or a (non-coding) microRNA (miRNA).
In our approach, the investigated sequences define a finitely generated group whose structure of subgroups is close or away from a free group of rank r, where is the number of distinct amino acids in the sequence (or the number of distinct secondary structures considered in the protein chain) [4]. Recently, we also introduced concepts for representing the groups over the Lie group . The character variety of and its Groebner basis are topological ingredients, they feature algebraic geometric properties of the group under question [12,13,14]. A reminder of the theory is given in the next section.
In this paper, we focus upon transcription factors and miRNAs, both serve at properly decoding and regulating the genes and their action, either independently of each other or together by targeting common genes [15]. Figure 1 (Left) is a picture of the pluripotent transcription factor Nanog. Figure 1 (Right) is an example of a pre-miRNA associated to a disease [16]. Both are investigated in detail in this paper.
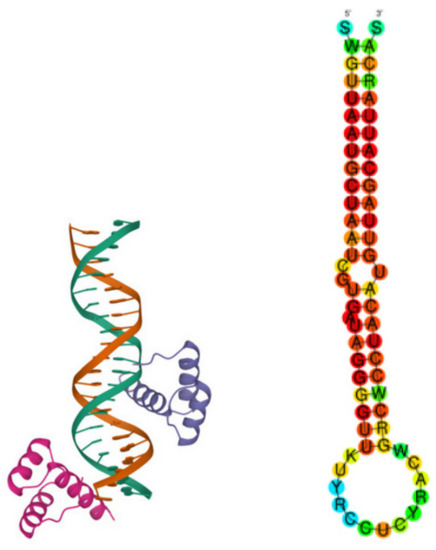
Figure 1.
Left: the Nanog transcription factor (PDB 9ANT). Right: the pre-miR-155 secondary structure [16].
In Section 2, we describe the mathematical methods and the software needed for describing the algebraic surfaces relevant to DNA/RNA sequences. This includes the definition of infinite groups under question, of the free groups of rank to 3 corresponding to 2- to 4-base sequences and the calculation of representation of such groups. A special care is needed to compute a Groebner basis of the character variety.
Section 3 is a discussion about the type of singular surfaces encountered in this research. They play an important role in our view of the discrimination of a potential disease.
In Section 4, the methods are applied to representative examples of sequences taken from transcription factors and microRNAs whose group is close or away from a free group, and whose Groebner basis of the variety contains simple singularities. Our theory applies to many TFs and miRNAs that are known to be related to an identified disease.
Section 5 summarizes our paper and opens a few perspectives.
2. Theory
2.1. Finitely Generated Groups, Free Groups and Their Conjugacy Classes
Let be the free group on r generators (r is called the rank).
The number of conjugacy classes of of a given index d is known and is a signature of the isomorphism, or the closeness, of a group to [4,17]. The cardinality structure of conjugacy classes of index d in will be called the card seq of . We need the cases from r = 1 to 3 that correspond to the number of distinct bases in a DNA/RNA sequence. The card seq of is in Table 1 for the 3 sequences of interest in the context of DNA/RNA.

Table 1.
The counting of conjugacy classes of subgroups of index d in the free group of rank r = 1 to 3. The last column is the index of the sequence in the on-line encyclopedia of integer sequences [18].
The free group of rank 1 may be defined as (with one generator a and no relation) or (with two generators a and b and the relation ). Similarly, the free group of rank 2 is and so on for higher rank r.
Next, given a finitely generated group with a relation (rel) given by a sequence motif, we are interested in the number of conjugacy classes of subgroups of index d (the card seq of ). Often, for a selected DNA/RNA motif taken as the generator of a finitely generated group , the card seq that is obtained is close to that of a free group , with being the number of distinct bases involved in the motif.
The closeness of to can be checked by its signature in the finite range of indices of the card seq.
To illustrate our methodology, let us consider the seed UCCUACA of the microRNA sequence mir-155-3p that is investigated in detail in Section 4.3; see also Figure 2. The finitely generated group is . The card seq of is found to be the series . The group is of rank 2 and the card seq corresponds to that of the group we call in the tables of Section 4. In this case, the card seq of is ‘away’ from the card seq of the free group of the same rank and the two groups and are of course ‘away’ to each other. However, if we omit the last nucleotide A of the seed in the generator of , then the group obtains the same card seq than (at least in the finite range of the card seq series that we can check) and, in this sense, both groups and become ‘close’ to each other.
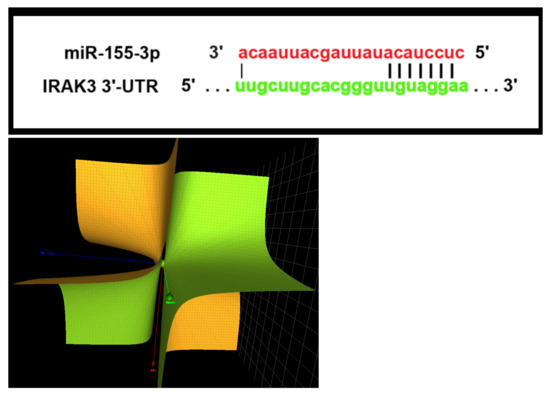
Figure 2.
(Up): Complementary base-pairing between miR-155-3p and the human Irak3 (interleukin-1 receptor-associated kinase 3) mRNA ([16], Figure 5). The requisite‘seed sequence’ base-pairing is denoted by the bold dashes. (Down): the surface .
2.2. The Character Variety of a Finitely Generated Group and a Groebner Basis
Let be a finitely generated group, we describe the representations of in , the group of matrices with complex entries and determinant 1. The group may be seen simultaneously as a ‘space-time’ (a Lorentz group) and a ‘quantum’ (a spin) group.
Such a group describes representations as degrees of freedom for all quantum fields and is the gauge group for Einstein–Cartan theory. The later contains the Einstein–Hilbert action and Einstein’s field equations [19]. The so-called Holst action used in loop quantum gravity has quantum gravity states given in terms of representations [20].
Representations of in are homomorphisms with character , . The notation means the trace of the matrix . The set of characters allows to determine an algebraic set by taking the quotient of the set of representations by the group , that acts by conjugation on representations [21,22].
Such an algebraic set is called the character variety of . The set is made of a sequence of multivariate polynomials called a scheme X. The ideal is defined by the vanishing of polynomials living in the scheme X. Below, we use a particular basis of the polynomial ring , called a Groebner basis. The Groebner basis has to follow algorithmic rules (similar to the Euclidean division for univariate polynomials) [14].
For the effective calculations of the character variety, we make use of a software on Sage [23]. We also need Magma [24] for the calculation of a Groebner basis, at least for 3- and 4-base sequences.
2.3. Algebraic Geometry and Topology of DNA/RNA Sequences
2.3.1. Two-Base Sequences
Following [25], in this section, we are interested by the special case of representations for the once punctured torus and the relevance of the extended mapping class group in its action on surfaces of type , .
The fundamental group of , that we denote , is the free group on two generators a and b. The boundary component of consists of a single loop around the puncture expressed by the commutator with and . Taking the traces , , , the trace of the commutator is the surface [21,25]
According to the Dehn–Nielsen–Baer theorem [26], for a surface of genus , we have
where is the mapping class group. It denotes the group of isotopy classes of orientation-preserving diffeomorphisms of S.
The extended mapping class group is the group of isotopy classes of all homeomorphisms of S (including the orientation-reversing ones). The outer automorphism group of is denoted . This leads to the (topological) action of on the once punctured torus as follows
The automorphism group acts by composition on the representations and induces an action of the extended mapping class group on the character variety by polynomial diffeomorphisms of the surface defined by [25]
Within the family , the Cayley surface is obtained from the character variety for the fundamental group of the Hopf link (the link of two unknotted curves). For the Hopf link, the fundamental group is
where the notation is for the 3-sphere and means that a small tubular neighborhood around the Hopf link is removed from to define the corresponding Hopf link 3-manifold.
The Cayley surface possesses 4 simple (isolated) singularities. At these points, the surface loses its smoothness. We already showed that it plays a role in the context of Z-DNA conformations of transcription factors ([13], Tables 2 and 5); see also, Section 4 below, and notably Figure 3 (Left).
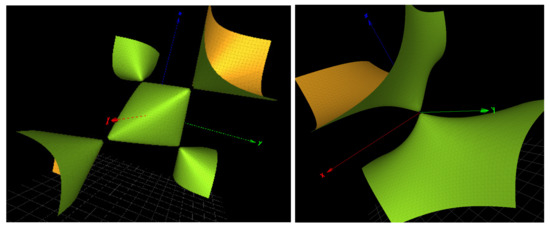
Figure 3.
(Left): the Cayley cubic . (Right): the surface .
The surface lies within the character variety for the fundamental group of the link L6a1 [27]. We show below that this surface also lies in the generic Groebner basis obtained for 4-base sequences; see Section 4 below.
2.3.2. Three-Base Sequences
Our main object in this section is the four punctured sphere for which the fundamental group is the free group of rank 3 whose character variety generalizes the Fricke cubic surface (2) to the surface in . From now, a and b are no longer generators of a group but belong to the set of parameters of the surface V.
We follow the work of references [21,25,28].
Let be the quadruply punctured sphere. The fundamental group for can be expressed in terms of the boundary components , , , as .
A representation is a quadruple
Let us associate the seven traces
where a, b, c, d are boundary traces and x, y and z are traces of elements , and representing simple loops on .
The character variety for satisfies the equation ([21], Section 5.2), ([25], Section 2.1), ([28], Section 3B), ([29], Equation (1.9)) or ([30], Equation (39)).
with , , and
The 4-punctured sphere, whose fundamental group is the free group with generator the product of the 4 letters, is a generic topology. It is straightforward to check that the Groebner basis for contains (among other surfaces and depending on the choice of parameters) a single copy of the generic surfaces , and , a surface we also denote because it contains 3 simple singularities of type as shown in Figure 4 and Figure 5.
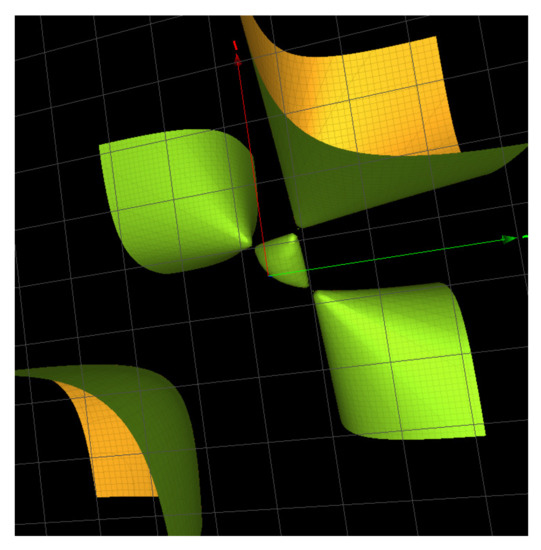
Figure 4.
The Fricke surface (with three simple singularities of type ).
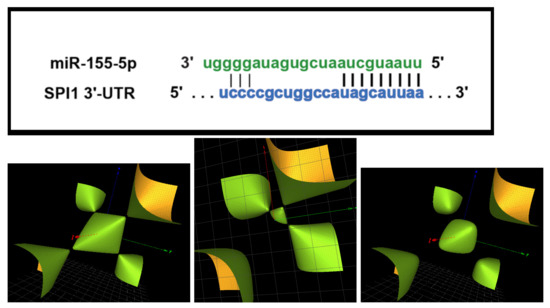
Figure 5.
(Up): Complementary base-pairing between miR-155-5p and the human Spi1 (spleen focus forming virus proviral integration oncogene) ([16], Figure 4). The requisite ‘seed sequence’ base-pairing is denoted by the bold dashes. (Down (from left to right)): the surfaces , and , four copies of them are contained within the Groebner basis for the character variety.
There are other surfaces encountered in our study of the Groebner basis for transcription factors and miRNAs when the generated group is close or away from the free group (for 3-base sequences) or the free group (for 4 base sequences). These surfaces are described in Section 4.
2.3.3. Four-Base Sequences
There does not exist a huge difference in the structure of a Groebner basis of the character variety in the case of a 4-base sequence compared to the case of a 3-basis sequence. One difference is that one has to manage a 14-dimensional hypersurface in (instead of a 7-dimensional one as in the previous subsection). In general, after the appropriate choice of the 8 parameters , the Groebner basis contains more than one copy of the generic Groebner basis. Each copy S of a relevant surface may be of the form , , or .
3. Discussion
Given an ordinary projective surface S in the projective space over a number field, when S is birationally equivalent to a rational surface, the software Magma [24] determines the map to such a rational surface and returns its type within five categories. The returned type of S is for the projective plane, a quadric surface (for a degree 2 surface in ), a rational ruled surface, a conic bundle or a degree p Del Pezzo surface where .
One important attribute of a projective surface is its degree of singularity. Most surfaces S of interest below are almost not singular in the sense that they have at worst simple (isolated) singularities. A simple singularity is referred to as an A-D-E singularity [31]. It has to be of the type , , , , , or .
The type and the number of simple singularities are denoted in an exponent such as for l singularities of type . All such surfaces are degree 3 del Pezzo surfaces. For the Cayley cubic , the exponent means .
There are additional facilities offered by Magma for studying a singular scheme. As already mentioned, a scheme is any geometric object defined by a set of polynomials in a projective space. An algebraic surface is a scheme. If the scheme has simple singularities, one can calculate the degree and the support of the reduced singular subscheme that are signatures of the scheme. In the examples of this paper, for a surface , the degree is l and the support contains l simple singular points. Otherwise, we add a lower index to to qualify the index and the support of the singular subscheme. The notation means that there are l singularities of type , that the degree of the singular subscheme is m and that the support is the empty set.
Most of the time, the surfaces in the character variety attached to a transcription factor or a microRNA only contain isolated singularities.
This contrasts with some sequences encountered in another context. For instance, a complete turn of A-DNA (PDB; 2D47) defines the dodecamer sequence CCCCCGCGGGGG whose attached character variety contains the surface ([13], Figure 5).
This surface contains many non isolated singularities (that cannot be resolved by blow ups). Methods to desingularize a surface of such a type are presented in a companion paper [32].
To summarize the important issues below, a noteworthy result of our approach is to recognize that optimal regulation occurs when the group underlying the sequence looks similar to a free group ( to 3) in the cardinality sequence of its subgroups, a result obtained in our previous papers. A non-free group structure features a potential disease. A second noteworthy result is about the structure of the Groebner basis of the variety. A surface with simple singularities (such as the well known Cayley cubic) within the Groebner basis is a signature of a potential disease even when the generated group looks similar to a free group in its structure of subgroups. Our methods apply to groups with a generating sequence made of two to four distinct DNA/RNA bases in . Several human TFs and miRNAs are investigated in detail thanks to our approach. We summarize this discussion in the diagram presented in Figure 6.
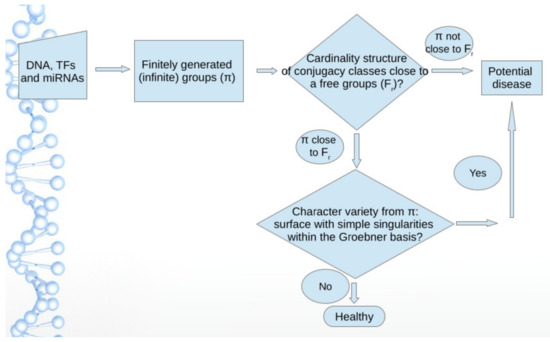
Figure 6.
A diagram with the main results discussed in the main text.
4. Results
In this section, we apply the representation theory to groups generated by DNA/RNA sequences occurring in transcription factors and microRNAs. Both play a leading role in the decoding of the genome and in genome-scale regulatory networks. Two-letter transcription factors (TFs) whose structure is close or away from the free group were already investigated in ([13], Table 2). The occurrence of the Cayley cubic in the Groebner basis of the character variety was found to be a signature in the former case. In this case, this surface seems to possess a regulatory action that may be lost in the latter case. In ([13], Table 3), the potential diseases associated with a non-free group structure are mentioned. In the present section, one explores, in Table 2, the case of a 3-letter sequence of a TF and in Table 3, the case of 3-letter sequence of a miRNA. The case of a 4-letter sequence of a miRNA is summarized in Table 4. The role of surfaces with simple singularities in the Groebner basis is emphasized.
4.1. Algebraic Morphology of the Transcription Factor Prdm1
The transcriptional repressor PR domain containing 1 (Prdm1), also known as B-lymphocyte-induced maturation protein-1 (Blimp1), is essential for normal development and immunity [33]. It is of a zinc finger type. The consensus sequence ACTTTC corresponds to the code MA0508.2 in [34].
4.1.1. The Character Variety
The ideal for the character variety for a few values of the parameters is
where , are Fricke surfaces [27] and is the surface drawn in Figure 4. The subscript is for featuring the three singularities of type .
4.1.2. The Groebner Basis
The singular surfaces found in the Groebner basis of the ideal are not similar to those in the ideal. One of them is obtained at values featuring two simple singularities of type and with a singular subscheme of degree 3 and the singular point of type in its support. The other surface obtained in the Groebner basis at values is a conic bundle of the type whose singular subscheme is non zero dimensional and of degree 1.
These two surfaces are non standard in our context of TFs and miRNAs. The formal desingularization of the surface is given in [32].
4.2. Algebraic Morphology of Homeodomains for Nanog and Xvent
The pluripotency in embryonic stem cells and their regulation is characterized by the expression of several transcription factors [35,36]. Among them, the transcription factor Nanog is present in the embryonic stages of life of several vertebrate species. Nanog binds to promoter elements of hundreds of target genes as a regulatory element. It has a conserved DNA-binding homeodomain with consensus sequence TAATGG. The closest homolog of Nanog is the (nonmammalia) Xenopus, a Xvent transcription factor with consensus sequence CTAATT [36]. In this subsection, we investigate the algebraic morphology of both transcription factors Nanog and Xvent thanks to their consensus sequences.

Table 2.
A few (three-base) transcription factors whose group structure is away from a free group or whose Groebner basis of the character variety contains a (possibly almost) singular surface. The symbol gene is for the identification of the transcription factor in the Jaspar database [34], motif is for the consensus sequence of the transcription factor, card seq is for the cardinality sequence of conjugacy classes of subgroups of the group whose motif is the generator, simple sing is for the identification of a surface with simple singularities within the Groebner basis and the last column is for a reference paper and the corresponding disease. The group is the free group of rank two. The card seq for is , close to the card seq of the group . The latter group is found as governing the structure of many transcription factors and is associated to the link found in ([13], Figure 2). The card seq for is . The surface (not defined in the text) is part of the character variety for the genes Pitx1, OTX1, etc.
Table 2.
A few (three-base) transcription factors whose group structure is away from a free group or whose Groebner basis of the character variety contains a (possibly almost) singular surface. The symbol gene is for the identification of the transcription factor in the Jaspar database [34], motif is for the consensus sequence of the transcription factor, card seq is for the cardinality sequence of conjugacy classes of subgroups of the group whose motif is the generator, simple sing is for the identification of a surface with simple singularities within the Groebner basis and the last column is for a reference paper and the corresponding disease. The group is the free group of rank two. The card seq for is , close to the card seq of the group . The latter group is found as governing the structure of many transcription factors and is associated to the link found in ([13], Figure 2). The card seq for is . The surface (not defined in the text) is part of the character variety for the genes Pitx1, OTX1, etc.
| Gene | Motif | Card Seq | Simple Sing | Ref & Disease |
|---|---|---|---|---|
| Prdm1 | ACTTTC | [34], MA0508.2 lupus, rheumatoid arthritis MA1549.1 lung adenocarcinoma MA0076.2 gastric cancer [MA0712.2, MA0883.1] medulloblastomas [37] drug sensitivity | ||
| POU6F1 | TAATGAG | no | ||
| ELK4 | CTTCCGG | . | no, Fricke | |
| OTX2 | GGATTA | no | ||
| N-box | TTCCGG | . | no, Fricke | |
| Pitx1,OTX1,⋯ | TAATCC | . | [34], [MA0682.1,MA0711.1] autism, epilepsy, ⋯ | |
| Nanog | TAATGG | . | [35] cancer cells | |
| Xvent | CTAATT | F2 | [36] |
The Groebner basis for Xvent takes the form
where is the Cayley cubic (with its 4 simple singularities) and (a surface with a single simple singularity of type ) as shown in Figure 3 (Right). The forgotten factors are factors for planes or trivial smooth surfaces.
The Groebner basis for Xvent takes the form
where (a surface with three simple singularity of type ). The missing term does not contain surfaces with singularities. The character variety contains the cubic surface (with two simple singularities of type ) and other factors for planes or trivial smooth surfaces. Both surfaces and are pictured in Figure 7.
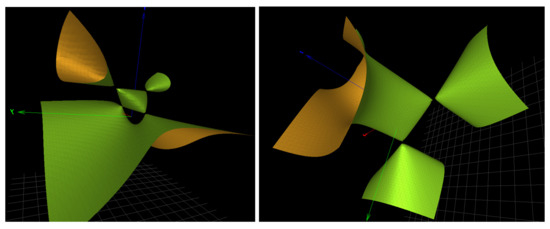
Figure 7.
(Left): the cubic surface . (Right): the cubic surface .
Table 2 lists a few selected transcription factors, their card seq and the corresponding singular surfaces, if any. As announced, in the selected transcription factors, there exists a correlation between the lack of ‘syntactical freedom’, or the presence of a surface with isolated singularities in the character variety, with an identified disease.
4.3. Algebraic Morphology of microRNAs
MicroRNAs (miRNAs) are important players of the expression and regulation of genes by targeting specific messenger RNAs (mRNAs) for degradation or translational repression [38,39]. The miRNAs are approximately 22 nt (where nt is for nucleotide) long single-stranded RNA molecules. The genes encoding miRNAs have a length much longer than the processed mature miRNA molecule. Many miRNAs reside in introns of their pre-mRNA host genes. They share their regulatory elements, primary transcript and have a similar expression profile. MicroRNAs are transcribed by RNA polymerase II as large RNA precursors called pri-miRNAs. The pre-miRNAs are approximately 70-nucleotides in length and are folded into imperfect stem-loop structures; see Figure 1 (Right) for an example.
Each miRNA is synthesized as a miRNA duplex comprising two strands (-5p and -3p). However, only one of the two strands is selectively incorporated into the RNA-induced silencing complex to act as a template for the transcript of a complementary mRNA [40,41]. For details about the mirRNA sequences, we use the Mir database [42,43].
Plant miRNAs usually have near-perfect pairing with their mRNA targets so that gene repression proceeds through cleavage of the target transcripts. In contrast, animal miRNAs are able to recognize their target mRNAs by using as few as 6 to 8 nucleotides (the seed region), which is not enough pairing for leading to cleavage of the target mRNAs. A given miRNA may have hundreds of different mRNA targets, and a given target might be regulated by multiple miRNAs.
Disregulation of miRNAs may lead to a disease such as cancer. A key microRNA known as an oncommir (involved in immunity and cancer) is mir-155.
Specifically the -3p strand is mir-155-3p. Figure 2 (top) illustrates the complementary base-pairing between miR-155-3p and the human IRAK3 (interleukin-1 receptor-associated kinase 3) mRNA ([16], Figure 4) and the relevant seed sequence UCCUAC. The card seq for this sequence is the two-letter free group and the Groebner basis for the corresponding character variety contains the surface that has a single simple singularity as shown in Figure 2 (down). If one retains the full seed sequence is UCCUAC(A) then the card seq passes to that of the free group to the group and the singular surface is lost. This is a case where the ‘bandwidth’ of the seed is critical in the (dis)regulation of the miRNA. These results are transcribed in Table 3.

Table 3.
A few human (prefix ‘hsa’) microRNAs whose group structure is away from a free group or whose Groebner basis of the character variety contains a singular surface. The symbol mir is for the identification in the Mir database [43], seed is for the seed of the miRNA, card seq is for the cardinality sequence of conjugacy classes of subgroups of the group whose seed is the generator, sing is the identification of a singular surface within the Groebner basis and the last column is for a reference paper and the corresponding disease [40]. The card seq for and are given in ([4], Table 5). The card seq for is . For hsa-mir-124-1-3p, one encounters the Fricke surface in the character variety.
Table 3.
A few human (prefix ‘hsa’) microRNAs whose group structure is away from a free group or whose Groebner basis of the character variety contains a singular surface. The symbol mir is for the identification in the Mir database [43], seed is for the seed of the miRNA, card seq is for the cardinality sequence of conjugacy classes of subgroups of the group whose seed is the generator, sing is the identification of a singular surface within the Groebner basis and the last column is for a reference paper and the corresponding disease [40]. The card seq for and are given in ([4], Table 5). The card seq for is . For hsa-mir-124-1-3p, one encounters the Fricke surface in the character variety.
| mir | Seed | Card Seq | Simple Sing | Ref & Disease |
|---|---|---|---|---|
| hsa-mir-193b-5p | GGGGUU | no | [40,43] lung cancer | |
| GGGGUUU | no | |||
| hsa-mir-155-3p | UCCUAC | [40,41,43] multiple sclerosis | ||
| UCCUACA | no | |||
| hsa-mir-193a-5p | GGGUCUU | [40,43] breast cancer | ||
| hsa-mir-223-5p | GUGUAUU | . | . | . |
| hsa-mir-133-3p | UUGGUC | [40,43] atrial fibrillation | ||
| UUGGUCC | no | |||
| hsa-mir-124-3p | AAGGCA | [43,44] | ||
| AAGGCAC | . | no sing | Alzheimer’s disease |
For the case of -5p strand mir-155-3p, the seed sequence UUAAUGCUA contains four distinct letters. This case is similar to generic Groebner bases obtained from four letter seeds. Depending on the choices of parameters , the Groebner basis contains the Cayley cubic , the Fricke surface (that is related to the link L6a1 ([27], Figure 2)), the surface shown in Figure 4 and other surfaces. In this generic case, the surface is found with (at most) 4 copies where each copy is attached to a distinct puncture of the 4-punctured 4-sphere .
In Table 3, this generic case is denoted (or for mir-133-5p). These results are transcribed in Table 4.

Table 4.
The opposite strand of the microRNA considered in Table 3. The seed sequence is made of 4 distinct bases and the corresponding card seq is the free group of rank 3. The Groebner basis contains 4 copies of the generic collection of surfaces , , , etc., as shown in Figure 5, except for the -5p strand of mir-133, where there are only 3 copies of the generic surfaces.
Table 4.
The opposite strand of the microRNA considered in Table 3. The seed sequence is made of 4 distinct bases and the corresponding card seq is the free group of rank 3. The Groebner basis contains 4 copies of the generic collection of surfaces , , , etc., as shown in Figure 5, except for the -5p strand of mir-133, where there are only 3 copies of the generic surfaces.
| mir | Seed | Card Seq | Sing | Ref & Disease |
|---|---|---|---|---|
| hsa-mir-193b-3p | ACUGGCC | generic | [40,43] | |
| hsa-mir-155-5p | UUAAUGCUA | . | . | [40,41,43] |
| hsa-mir-193a-3p | ACUGGCC | . | . | [40,43] |
| hsa-mir-223-3p | GUCAGUU | . | . | . |
| hsa-mir-124-5p | GUGUUCA | . | . | . |
| hsa-mir-133-5p | GCUGGUA | . | generic | [43,44] |
A small list of huma miRNAs is investigated in Table 3 and Table 4 corresponding to 3-letter and 4-letter seeds. the prefix ‘hsa’ is for the human species. Similar to transcription factors in Table 2, the lack of ‘syntactical freedom’, or the occurrence of a singular surface in the character variety, is symptomatic of a disease.
5. Conclusions
We found, in this work, that a signature of a disease may be given in terms of the group structure of a DNA/RNA sequence and the related character variety representing the group. The DNA motif of a transcription factor, or the seed of a microRNA, defines the generator of a group . As soon as is away from a free group (with the number of distinct bases in the sequence) or the character variety of contains singular surfaces with isolated singularities, a potential disease is on sight, as shown in Figure 6.
For example, for mir-155-3p, examined in much detail in Section 4.3, the seed UCCUAC serves as the generator of the group whose card seq is that of the free group and whose Groebner basis of the variety contains the surface possessing an isolated singularity of type . The potential disease is multiple sclerosis. Note that a longer seed (with A added at the right hand side) is not appropriate to the detection. A partial list of other potential diseases identified from the structure of a miRNA seed can be seen in Table 3. The diseases are a lung cancer associated with mir-193b-5p, a breast cancer associated with mir-194a-5p or mir-223-5p, an atrial fibrillation associated with mir-133-3p and an Alzheimer’s disease associated with mir-124-3p.
One would like to be more predictive in identifying the potential disease with peculiar groups or singular surfaces. First of all, most of the time, the surfaces encountered in the context of TFs and miRNAs are degree 3 del Pezzo, in contrast to surfaces obtained from other DNA sequences, as in Equation (4). However, the degree 3 del Pezzo family is very rich. For instance, the singular surface (see Figure 2) is part of the character variety of TF Pitx1 (see Table 2) and of miRNAs 155-3p and 193a-5p (in Table 3). Then, the singular surface is part of the character variety of mirRNA 133-3p. Both surfaces have a simple singular point of type but distinct singular subschemes (see Section 3 for the notation).
An exception to the degree 3 del Pezzo rule was found in investigating the character variety for the Prdm1 transcription factor in Section 4.1. Do these features and other ones to be described later help for the diagnostic of a potential disease? There is room for much work in the future along these lines, as shown in our recent new paper [32].
In a separate direction, the work of Reference [45] about biochirality and the CPT theorem may be possibly related to the space-time-spin group that served as a prism of DNA/RNA structure in our approach. Related ideas about the concept of a time crystal are also worthwhile to be pointed out, e.g., Reference [46].
Author Contributions
Conceptualization, M.P.; methodology, M.P and M.M.A.; software, M.P.; validation, M.M.A. and K.I.; formal analysis, M.P.; investigation, M.M.A.; resources, K.I.; data curation, M.P.; writing—original draft preparation, M.P.; writing—review and editing, M.P. and M.M.A.; visualization, M.M.A.; supervision, M.P.; project administration, K.I.; funding acquisition, K.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available from the authors after a reasonable demand.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Uždavinys, A. The Heart of Plotinus. The Essential Enneads; World Wisdom, Inc.: Bloomington, IN, USA, 2009. [Google Scholar]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Fang, F.; Irwin, K. Graph coverings for investigating non local structures in protein, music and poems. Science 2021, 3, 39. [Google Scholar] [CrossRef]
- Irwin, K. The code-theoretic axiom; the third ontology. Rep. Adv. Phys. Sci. 2019, 3, 39. [Google Scholar] [CrossRef]
- Planat, M.; Amaral, M.M.; Fang, F.; Chester, D.; Aschheim, R.; Irwin, K. Group theory of syntactical freedom in DNA transcription and genome decoding. Curr. Issues Mol. Biol. 2022, 44, 1417–1433. [Google Scholar] [CrossRef] [PubMed]
- Dang, Y.; Gao, J.; Wang, J.; Heffernan, R.; Hanson, J.; Paliwal, K.; Zhou, Y. Sixty-five years of the long march in protein secondary structure prediction: The final strech? Brief. Bioinform. 2018, 19, 482–494. [Google Scholar]
- Dyakin, V.V.; Wisniewski, T.M.; Lajtha, A. Racemization in Post-Translational Modifications Relevance to Protein Aging, Aggregation and Neurodegeneration: Tip of the Iceberg. Symmetry 2021, 13, 455. [Google Scholar] [CrossRef]
- Abd El Nabi, M.L.R.; Jasim, M.W.; El-Bakry, H.M.; Taha, M.H.N.; Khalifa, N.E.M. Breast and colon cancer classification from gene expression profiles using data mining techniques. Symmetry 2020, 12, 408. [Google Scholar] [CrossRef]
- Milhem, Z.; Chroi, P.; Nutu, A.; Ilea, M.; Lipse, M.; Zanoaga, O.; Berindan-Neagoe, I. Non-coding RNAs and reactive oxygen species—Symmetric players of the pathogenesis associated with bacterial and viral infections. Symmetry 2021, 13, 1307. [Google Scholar] [CrossRef]
- Aldrich, P.R.; Horsley, R.K.; Turcic, S.M. Symmetry in the language of gene expression: A survey of gene promoter networks in multiple bacterial species and non-regulons. Symmetry 2011, 3, 750–766. [Google Scholar] [CrossRef]
- Heinemann, U.; Roske, Y. Symmetry in nucleic-acid double helices. Symmetry 2020, 12, 737. [Google Scholar] [CrossRef]
- Bansal, A.; Kaushik, S.; Kukreti, S. Non-canonical DNA structures: Diversity and disease association. Front. Genet. 2022, 13, 959258. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Fang, F.; Chester, D.; Irwin, K. Character varieties and algebraic surfaces for the topology of quantum computing. Symmetry 2022, 14, 915. [Google Scholar] [CrossRef]
- Planat, M.; Amaral, M.M.; Fang, F.; Chester, D.; Aschheim, R.; Irwin, K. DNA sequence and structure under the prism of group theory and algebraic surfaces. Int. J. Mol. Sci. 2022, 23, 13290. [Google Scholar] [CrossRef]
- Gröbner Basis. Available online: https://en.wikipedia.org/wiki/Gröbner_basis (accessed on 1 August 2022).
- Martinez, N.J.; Walhout, A.J.M. The interplay between transcription factors and microRNAs in genome-scale regulatory networks. Bioessays 2009, 31, 435–445. [Google Scholar] [CrossRef]
- miR-155. Available online: https://en.wikipedia.org/wiki/MiR-155 (accessed on 18 November 2022).
- Kwak, J.H.; Nedela, R. Graphs and their coverings. Lect. Notes Ser. 2007, 17, 118. [Google Scholar]
- The On-Line Encyclopedia of Integer Sequences. Available online: https://oeis.org/book.html (accessed on 1 November 2022).
- Hehl, F.W.; von der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. Covariant Loop Quantum Gravity, 1st ed.; Cambridge University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Goldman, W.M. Trace coordinates on Fricke spaces of some simple hyperbolic surfaces. Eur. Math. Soc. 2009, 13, 611–684. [Google Scholar]
- Ashley, C.; Burelle, J.P.; Lawton, S. Rank 1 character varieties of finitely presented groups. Geom. Dedicata 2018, 192, 1–19. [Google Scholar] [CrossRef]
- Python Code to Compute Character Varieties. Available online: http://math.gmu.edu/~slawton3/main.sagews (accessed on 1 May 2021).
- Bosma, W.; Cannon, J.J.; Fieker, C.; Steel, A. (Eds.) Handbook of Magma Functions, 2.23rd ed.; University of Sydney: Sydney, Australia, 2017; 5914p. [Google Scholar]
- Cantat, S. Bers and Hénon, Painlevé and Schrödinger. Duke Math. J. 2009, 149, 411–460. [Google Scholar] [CrossRef]
- Farb, B.; Margalit, D. A Primer on Mapping Class Groups; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Planat, M.; Chester, D.; Amaral, M.; Irwin, K. Fricke topological qubits. Quant. Rep. 2022, 4, 523–532. [Google Scholar] [CrossRef]
- Benedetto, R.L.; Goldman, W.M. The topology of the relative character varieties of a quadruply-punctured sphere. Exp. Math. 1999, 8, 85–103. [Google Scholar] [CrossRef]
- Iwasaki, K. An area-preserving action of the modular group on cubic surfaces and the Painlevé VI. Comm. Math. Phys. 2003, 242, 185–219. [Google Scholar] [CrossRef]
- Inaba, M.; Iwasaki, K.; Saito, M.H. Dynamics of the sixth Painlevé equation. arXiv 2005, arXiv:math.AG/0501007. [Google Scholar]
- ADE Classification. Available online: https://en.wikipedia.org/wiki/ADE_classification (accessed on 1 August 2022).
- Planat, M.; Amaral, M.M.; Chester, D.; Irwin, K. SL(2,ℂ) scheme processsing of singularities in quantum computing and genetics. Axioms 2023, 12, 233. [Google Scholar] [CrossRef]
- Doody, G.M.; Care, M.A.; Burgoyne, N.J.; Bradford, J.R.; Bota, M.; Bonifer, C.; Westhead, D.R.; Tooze, R.M. An extended set of PRDM1/BLIMP1 target genes links binding motif type to dynamic repression. Nucl. Acids Res. 2010, 38, 5336–5350. [Google Scholar] [CrossRef] [PubMed]
- Sandelin, A.; Alkema, W.; Engstrom, P.; Wasserman, W.W.; Lenhard, B. JASPAR: An open-access database for eukaryotic transcription factor binding profiles. Nucleic Acids Res. 2004, 32, D91–D94. Available online: https://jaspar.genereg.net/ (accessed on 1 November 2022). [CrossRef]
- Jauch, R. Crystal tructure and DNA inding of the homeodomain of the stem cell transcription factor Nanog. J. Mol. Biol. 2008, 376, 758–770. [Google Scholar] [CrossRef]
- Schuff, M.; Siegel, D.; Philipp, M.; Bunsschu, K.; Heymann, N.; Donow, C.; Knöchel, W. Characterization of Danio rerio Nanog and Functional Comparison to Xenopus Vents. Stem Cells Devt. 2012, 21, 1225–1238. [Google Scholar] [CrossRef]
- Schaeffer, L.N.; Huchet-Dymanus, M.; Changeux, J.P. Implication of a multisubunit Ets-related transcription factor in synaptic expression of the nicotinic acetylcholine receptor. EMBO J. 1998, 17, 3078–3090. [Google Scholar] [CrossRef]
- microRNA. Available online: https://en.wikipedia.org/wiki/MicroRNA (accessed on 1 September 2022).
- Fang, Y.; Pan, X.; Shen, H.B. Recent deep learning methodology development for RNA-RNA interaction prediction. Symmetry 2022, 14, 1302. [Google Scholar] [CrossRef]
- Medley, C.M.; Panzade, G.; Zinovyeva, A.Y. MicroRNA stran selection: Unwinding the rules. WIREs RNA 2021, 12, e1627. [Google Scholar] [CrossRef]
- Dawson, O.; Piccinini, A.M. miR-155-3p: Processing by-product or rising star in immunity and cancer? Open Biol. 2022, 12, 220070. [Google Scholar] [CrossRef]
- Kozomara, A.; Birgaonu, M.; Griffiths-Jones, S. miRBase: From microRNA sequences to function. Nucl. Acids Res. 2019, 47, D155–D162. [Google Scholar] [CrossRef]
- miRBase: The microRNA Database. Available online: https://www.mirbase.org/ (accessed on 1 November 2022).
- Kou, X.; Chen, D.; Chen, N. The regulation of microRNAs in Alzheimer’s disease. Front. Neurol. 2020, 11, 288. [Google Scholar] [CrossRef]
- Dyakin, V.V. Fundamental Cause of Bio-Chirality: Space-Time Symmetry—Concept Review. Symmetry 2023, 15, 79. [Google Scholar] [CrossRef]
- Sbitnev, V. Relativistic Fermion and Boson Fields: Bose-Einstein Condensate as a Time Crystal. Symmetry 2023, 15, 275. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).