Some New Hermite-Hadamard Type Inequalities Pertaining to Fractional Integrals with an Exponential Kernel for Subadditive Functions

Abstract

The class of symmetric function interacts extensively with other types of functions. One of these is the class of convex functions, which is closely related to the theory of symmetry. In this paper, we obtain some new fractional Hermite–Hadamard inequalities with an exponential kernel for subadditive functions and for their product, and some known results are recaptured. Moreover, using a new identity as an auxiliary result, we deduce several inequalities for subadditive functions pertaining to the new fractional integrals involving an exponential kernel. To validate the accuracy of our results, we offer some examples for suitable choices of subadditive functions and their graphical representations.

1. Introduction

Hille and Phillips’ work [1] is the key contribution to the general theory of subadditive functions. In addition, a portion of Rosenbaum’s [2] research on subadditive functions involving many variables is included. Measure theory, a number of mathematical disciplines, and mathematical inequalities all make use of the ideas of additivity, subadditivity, and superadditivity. Numerous examples of additive, subadditive, and superadditive functions, including error functions, norms, growth rates, differential equations, square roots, and integral means, can be found in a variety of mathematical contexts. One of the most developed areas in theoretical and practical mathematics, physics, and other applied disciplines is inequality theory, specifically subadditive function theory. Here, we highlight the findings of [3,4,5,6,7,8,9].

Definition 1.

A function $\mathsf{{\rm Y}}:\mathrm{I}\subset \mathrm{R}\to [0,\infty )$ is said to be subadditive on $\mathrm{I},$ if for all ${\mathtt{r}}_1,{\mathtt{r}}_2\in \mathrm{I}$ such that ${\mathtt{r}}_1+{\mathtt{r}}_2\in \mathrm{I},$ we have

$$\mathsf{{\rm Y}}({\mathtt{r}}_1+{\mathtt{r}}_2)\le \mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right).$$

(1)

If the equality holds, Υ is called additive; if the Inequality (1) is reversed, Υ is called superadditive.

Theory of convexity played a significant role in the development of theory of inequalities. Symmetric convex sets have a variety of significant characteristics. The fact that we can work on one and then apply it to the other is an important aspect of the relationship between symmetry and convexity.

Definition 2 ([10]).

A function $\mathsf{{\rm Y}}:\mathrm{I}\subset \mathrm{R}\to \mathrm{R}$ is said to be convex, if

$$\mathsf{{\rm Y}}(\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\le \mathsf{s}\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)+(1-\mathsf{s})\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)$$

(2)

holds for all ${\mathtt{r}}_1,{\mathtt{r}}_2\in \mathrm{I}$ and $\mathsf{s}\in [0,1].$

The following Hermite-Hadamard’s inequality (H-H) is one of the well-known studied results involving convex functions.

Theorem 1 

([11,12]). Let $\mathsf{{\rm Y}}:\mathrm{I}\to \mathrm{R}$ be a convex function on $\mathrm{I}$ for ${\mathtt{r}}_1,{\mathtt{r}}_2\in \mathrm{I}$ and ${\mathtt{r}}_1<{\mathtt{r}}_2,$ then

$$\mathsf{{\rm Y}}\left(\frac{{\mathtt{r}}_1+{\mathtt{r}}_2}{2}\right)\le \frac{1}{{\mathtt{r}}_2-{\mathtt{r}}_1}{\int }_{{\mathtt{r}}_1}^{{\mathtt{r}}_2}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s}\le \frac{\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)}{2}.$$

(3)

The convexity property of the functions can be used to obtain many well-known inequalities. Some improvements to the H-H inequality on convex functions have been thoroughly studied since then; for more information, see the articles [13,14,15,16,17,18,19], as well as the references therein.

Recently, Sarikaya and Ali [20] proved the following interesting integral inequalities of H-H type for continuous subadditive functions.

Theorem 2. 

Let $\mathsf{{\rm Y}}:\mathrm{I}\to \mathrm{R}$ be a continuous subadditive function with ${\mathtt{r}}_1,{\mathtt{r}}_2\in {\mathrm{I}}^{\circ }$ and ${\mathtt{r}}_1<{\mathtt{r}}_2,$ then the following inequality holds true:

$$\frac{1}{2}\mathsf{{\rm Y}}({\mathtt{r}}_1+{\mathtt{r}}_2)\le \frac{1}{{\mathtt{r}}_2-{\mathtt{r}}_1}{\int }_{{\mathtt{r}}_1}^{{\mathtt{r}}_2}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s}\le \frac{1}{{\mathtt{r}}_1}{\int }_0^{{\mathtt{r}}_1}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s}+\frac{1}{{\mathtt{r}}_2}{\int }_0^{{\mathtt{r}}_2}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s}.$$

(4)

Theorem 3. 

Let $\omega ,\Phi :\mathrm{I}\to \mathrm{R}$ be two continuous subadditive functions with ${\mathtt{r}}_1,{\mathtt{r}}_2\in {\mathrm{I}}^{\circ }$ and ${\mathtt{r}}_1<{\mathtt{r}}_2,$ then the following inequalities hold true:

$$\begin{array}{cc}\hfill & \frac{1}{2}\omega ({\mathtt{r}}_1+{\mathtt{r}}_2)\Phi ({\mathtt{r}}_1+{\mathtt{r}}_2)\le \frac{1}{{\mathtt{r}}_2-{\mathtt{r}}_1}{\int }_{{\mathtt{r}}_1}^{{\mathtt{r}}_2}\omega \left(\mathsf{s}\right)\Phi \left(\mathsf{s}\right)d\mathsf{s}\hfill \\ \hfill & +{\int }_0^1\left[\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)\right]d\mathsf{s}\hfill \\ \hfill & +{\int }_0^1\left[\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)+\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)\right]d\mathsf{s}\hfill \end{array}$$

(5)

and

$$\begin{array}{cc}\hfill & \frac{1}{{\mathtt{r}}_2-{\mathtt{r}}_1}{\int }_{{\mathtt{r}}_1}^{{\mathtt{r}}_2}\omega \left(\mathsf{s}\right)\Phi \left(\mathsf{s}\right)d\mathsf{s}\le \frac{1}{{\mathtt{r}}_1}{\int }_0^{{\mathtt{r}}_1}\omega \left(\mathsf{s}\right)\Phi \left(\mathsf{s}\right)d\mathsf{s}+\frac{1}{{\mathtt{r}}_2}{\int }_0^{{\mathtt{r}}_2}\omega \left(\mathsf{s}\right)\Phi \left(\mathsf{s}\right)d\mathsf{s}\hfill \\ \hfill & +{\int }_0^1\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right)d\mathsf{s}+{\int }_0^1\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)d\mathsf{s}.\hfill \end{array}$$

(6)

Finally, let us recall the following definition regarding fractional integral operators with exponential kernels that will be used in the sequel.

Definition 3 

([21,22]). Let $\mathsf{{\rm Y}}\in \mathrm{L}[{\mathtt{r}}_1,{\mathtt{r}}_2],$ where $0\le {\mathtt{r}}_1<{\mathtt{r}}_2.$ Then the fractional integrals with exponential kernel ${\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }$ and ${\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }$ of order $\alpha \in (0,1)$ are defined as

$${\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left(\mathrm{x}\right):=\frac{1}{\alpha }{\int }_{{\mathtt{r}}_1}^{\mathrm{x}}{e}^{\frac{\alpha -1}{\alpha }(\mathrm{x}-\mathsf{s})}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s},(\mathrm{x}>{\mathtt{r}}_1)$$

(7)

and

$${\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left(\mathrm{x}\right):=\frac{1}{\alpha }{\int }_{\mathrm{x}}^{{\mathtt{r}}_2}{e}^{\frac{\alpha -1}{\alpha }(\mathsf{s}-\mathrm{x})}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s},(\mathrm{x}<{\mathtt{r}}_2),$$

(8)

respectively.

It is crucial to stress that Leibniz and L’Hospital are responsible for developing the concept of fractional calculus (1695). Other mathematicians have significantly contributed to the topic of fractional calculus and its many applications, including Riemann, Liouville, Erdéli, Grünwald, Letnikov, and Kober. Due to its behaviour and ability to deal with real-world problems, fractional calculus is of interest to many physical and engineering professionals. The study of so-called fractional order integral and derivative functions over real and complex domains, as well as its applications, are currently the focus of fractional calculus. Since fractional mathematical models are specific instances of fractional order mathematical models, they produce more conclusive and accurate conclusions than classical mathematical models. Different mathematical models are used to explain the endemics’ distinctive transmission dynamics and gain understanding of how infection affects a new population. In order to increase the precision and accuracy of real phenomenons, non-integer order fractional differential equations (FDEs) are used (see [23,24,25,26,27]). Furthermore, Refs. [28,29,30] contains other intriguing results for fractional calculus. However, fractional calculation allows us to take any number of orders and create far more measurable goals. Mathematicians have grown increasingly interested in employing a range of novel theories of fractional integral operators to illustrate well-known inequalities in recent years.

There are many published articles regarding inequalities but in our paper we have done the numerical analysis and their graphical representations for suitable choices of subadditive functions. For the correctness of the presented results, we discussed some examples and validate those via numerical estimations and graphs with the change of the parameter $0<\alpha <1$. The results presented in this study are substantial generalizations of previous findings given by Sarikaya et al. [20]. Additivity, subadditivity and superadditivity functions play an important role both in measure theory and in different fields of mathematics. Here, we have obtained some new fractional Hermite–Hadamard inequalities with an exponential kernel for subadditive functions and for the product of two such functions. Our results obtained here deviate moderately from the recent research directions.

Motivated from above results and literature, this work includes the following sections: In Section 2, we will obtain some new fractional H-H inequalities with an exponential kernel for subadditive functions and for their product, and some known results will be recaptured. In Section 3, using a new identity as an auxiliary result, we will deduce several inequalities for subadditive functions pertaining to fractional integrals with an exponential kernel. To validate the accuracy of our results, we will offer some examples for suitable choices of subadditive functions and their graphical representations. The conclusion and future research will be given in Section 4.

2. Main Results

For the simplicity of notations, let

$$\varpi :=\frac{\alpha -1}{\alpha }({\mathtt{r}}_2-{\mathtt{r}}_1),\mathrm{and}\mathrm{Q}=[0,\infty ).$$

Additionally, we mark ${\mathrm{Q}}^{\circ }$ as the interior of $\mathrm{Q}$ and $\mathrm{L}\left(\mathrm{Q}\right)$ as the set of all Lebesgues integrable functions on $\mathrm{Q}$. The fractional H-H type inequalities with an exponential kernel for subadditive functions are given as follows:

Theorem 4. 

Let $\mathsf{{\rm Y}}:\mathrm{Q}\to \mathrm{R}$ be a continuous subadditive function with ${\mathtt{r}}_1,{\mathtt{r}}_2\in {\mathrm{Q}}^{\circ }$ and ${\mathtt{r}}_1<{\mathtt{r}}_2.$ Then for $\alpha \in (0,1),$

$$\begin{array}{cc}\hfill & \frac{\left(e^{\varpi }-1\right)}{\varpi }\mathsf{{\rm Y}}({\mathtt{r}}_1+{\mathtt{r}}_2)\le \frac{\alpha }{{\mathtt{r}}_2-{\mathtt{r}}_1}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)\right]\hfill \\ \hfill & \le \frac{1}{{\mathtt{r}}_1}{\int }_0^{{\mathtt{r}}_1}\left(e^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_1}}+e^{\varpi \left(1-\frac{\mathsf{s}}{{\mathtt{r}}_1}\right)}\right)\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s}+\frac{1}{{\mathtt{r}}_2}{\int }_0^{{\mathtt{r}}_2}\left(e^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_2}}+e^{\varpi \left(1-\frac{\mathsf{s}}{{\mathtt{r}}_2}\right)}\right)\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s},\hfill \end{array}$$

(9)

holds true.

Proof. 

Since $\mathsf{{\rm Y}}$ is a subadditive function on $\mathrm{Q},$ we have

$$\mathsf{{\rm Y}}({\mathtt{r}}_1+{\mathtt{r}}_2)\le \mathsf{{\rm Y}}(\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\mathsf{{\rm Y}}((1-\mathsf{s}){\mathtt{r}}_1+\mathsf{s}{\mathtt{r}}_2).$$

(10)

After multiplying both sides of the Equation (10) by $e^{\varpi \mathsf{s}},$ integrating the resulting inequality with respect to $\mathsf{s}$ over $[0,1]$ and altering the integration’s variables, we get

$$\begin{array}{cc}\hfill & \frac{\left(e^{\varpi }-1\right)}{\varpi }\mathsf{{\rm Y}}({\mathtt{r}}_1+{\mathtt{r}}_2)\le {\int }_0^1{e}^{\varpi \mathsf{s}}\mathsf{{\rm Y}}(\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)d\mathsf{s}+{\int }_0^1{e}^{\varpi \mathsf{s}}\mathsf{{\rm Y}}((1-\mathsf{s}){\mathtt{r}}_1+\mathsf{s}{\mathtt{r}}_2)d\mathsf{s}\hfill \\ \hfill & =\frac{1}{{\mathtt{r}}_2-{\mathtt{r}}_1}\left[{\int }_{{\mathtt{r}}_1}^{{\mathtt{r}}_2}{e}^{\frac{\alpha -1}{\alpha }({\mathtt{r}}_2-\mathsf{s})}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s}+{\int }_{{\mathtt{r}}_1}^{{\mathtt{r}}_2}{e}^{\frac{\alpha -1}{\alpha }(\mathsf{s}-{\mathtt{r}}_1)}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s}\right]\hfill \\ \hfill & =\frac{\alpha }{{\mathtt{r}}_2-{\mathtt{r}}_1}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)\right].\hfill \end{array}$$

hence,

$$\begin{array}{cc}\hfill & \frac{\left(e^{\varpi }-1\right)}{\varpi }\mathsf{{\rm Y}}({\mathtt{r}}_1+{\mathtt{r}}_2)\le \frac{\alpha }{{\mathtt{r}}_2-{\mathtt{r}}_1}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)\right].\hfill \end{array}$$

with this, the left side inequality of Equation (9) has been fully demonstrated. Next, we observe that $\mathsf{{\rm Y}}$ is a subadditive function on $\mathrm{Q}$, and for $\mathsf{s}\in [0,1],$ we have

$$\mathsf{{\rm Y}}(\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\le \mathsf{{\rm Y}}\left(\mathsf{s}{\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left((1-\mathsf{s}){\mathtt{r}}_2\right)$$

(11)

and

$$\mathsf{{\rm Y}}((1-\mathsf{s}){\mathtt{r}}_1+\mathsf{s}{\mathtt{r}}_2)\le \mathsf{{\rm Y}}\left((1-\mathsf{s}){\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left(\mathsf{s}{\mathtt{r}}_2\right).$$

(12)

By adding Inequalities (11) and (12), we obtain

$$\mathsf{{\rm Y}}(\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\mathsf{{\rm Y}}((1-\mathsf{s}){\mathtt{r}}_1+\mathsf{s}{\mathtt{r}}_2)\le \mathsf{{\rm Y}}\left(\mathsf{s}{\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left(\mathsf{s}{\mathtt{r}}_2\right)+\mathsf{{\rm Y}}\left((1-\mathsf{s}){\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left((1-\mathsf{s}){\mathtt{r}}_2\right).$$

(13)

The right side inequality in Equation (9) is obtained by multiplying both sides of Equation (13) by $e^{\varpi \mathsf{s}},$ integrating the resulting inequality with respect to $\mathsf{s}$ over $[0,1]$ and applying the change of variables. Theorem 4 has been fully proven. □

Corollary 1. 

Under the assumptions of Theorem 4, taking $\alpha \to 1^{-},$ then we get ([20], Theorem 2).

Example 1. 

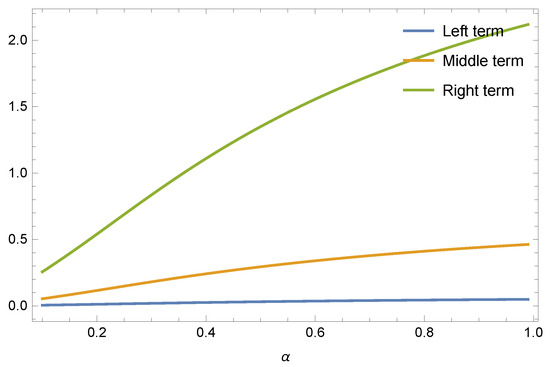
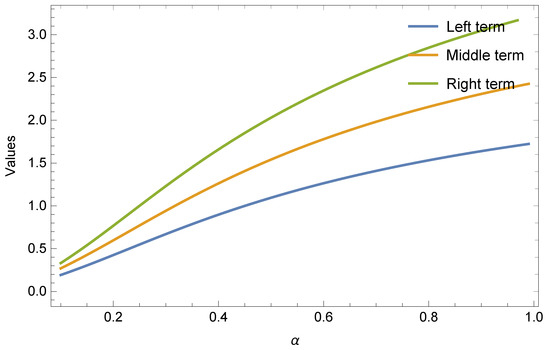
If we take subadditive functions $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=e^{-\mathsf{s}}$ and $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\sqrt{\mathsf{s}},$ respectively, in Theorem 4 for all $\mathsf{s}>0$, $0<\alpha <1,$${\mathtt{r}}_1=1$ and ${\mathtt{r}}_2=2$, then we have the following results given in Table 1 and Table 2 and Figure 1 and Figure 2.

Table 1. Numerical validation of Theorem 4 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=e^{-\mathsf{s}},\forall \mathsf{s}>0$.

Values of $\mathit{\alpha }$	Value of the Left Term	Value of the Middle Term	Value of the Right Term
$0.1$	0.00553121	0.0536975	0.256189
$0.2$	0.0122188	0.115946	0.539937
$0.3$	0.0192682	0.181173	0.835309
$0.4$	0.0257854	0.241573	1.10934
$0.5$	0.0314714	0.294381	1.34949
$0.6$	0.0363383	0.339659	1.55579
$0.7$	0.0404923	0.378354	1.73237
$0.8$	0.0440514	0.411544	1.88399
$0.9$	0.0471208	0.440188	2.01497

Table 2. Numerical validation of Theorem 4 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\sqrt{\mathsf{s}},\forall \mathsf{s}>0$.

Values of $\mathit{\alpha }$	Value of the Left Term	Value of the Middle Term	Value of the Right Term
$0.1$	0.192426	0.269591	0.331513
$0.2$	0.425082	0.597198	0.767753
$0.3$	0.670324	0.94277	1.23139
$0.4$	0.897052	1.26219	1.65864
$0.5$	1.09486	1.54081	2.03003
$0.6$	1.26418	1.77924	2.34697
$0.7$	1.40869	1.98271	2.61686
$0.8$	1.53251	2.15703	2.84769
$0.9$	1.63929	2.30734	3.04647

Figure 1. Graphical behaviour of Theorem 4 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=e^{-\mathsf{s}},\forall \mathsf{s}>0$ and $0<\alpha <1$.

Figure 2. Graphical behaviour of Theorem 4 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\sqrt{\mathsf{s}},\forall \mathsf{s}>0$ and $0<\alpha <1$.

Theorem 5. 

Let $\omega ,\Phi :\mathrm{Q}\to \mathrm{R}$ be two continuous subadditive functions with ${\mathtt{r}}_1,{\mathtt{r}}_2\in {\mathrm{Q}}^{\circ }$ and ${\mathtt{r}}_1<{\mathtt{r}}_2.$ Then for $\alpha \in (0,1),$

$$\begin{array}{cc}\hfill & \frac{\left(e^{\varpi }-1\right)}{\varpi }\omega ({\mathtt{r}}_1+{\mathtt{r}}_2)\Phi ({\mathtt{r}}_1+{\mathtt{r}}_2)\le \frac{\alpha }{{\mathtt{r}}_2-{\mathtt{r}}_1}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\omega \left({\mathtt{r}}_2\right)\Phi \left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\omega \left({\mathtt{r}}_1\right)\Phi \left({\mathtt{r}}_1\right)\right]\hfill \\ \hfill & +{\int }_0^1\left(e^{\varpi \mathsf{s}}+e^{\varpi \left(1-\mathsf{s}\right)}\right)\left[\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)+\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)\right]d\mathsf{s}\hfill \\ \hfill & +\frac{1}{{\mathtt{r}}_1}{\int }_0^{{\mathtt{r}}_1}{e}^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_1}}\left[\omega \left(\mathsf{s}\right)\Phi ({\mathtt{r}}_1-\mathsf{s})+\omega ({\mathtt{r}}_1-\mathsf{s})\Phi \left(\mathsf{s}\right)\right]d\mathsf{s}\hfill \\ \hfill & +\frac{1}{{\mathtt{r}}_2}{\int }_0^{{\mathtt{r}}_2}{e}^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_2}}\left[\omega \left(\mathsf{s}\right)\Phi ({\mathtt{r}}_2-\mathsf{s})+\omega ({\mathtt{r}}_2-\mathsf{s})\Phi \left(\mathsf{s}\right)\right]d\mathsf{s}\hfill \end{array}$$

(14)

and

$$\begin{array}{cc}\hfill & \frac{\alpha }{{\mathtt{r}}_2-{\mathtt{r}}_1}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\omega \left({\mathtt{r}}_2\right)\Phi \left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\omega \left({\mathtt{r}}_1\right)\Phi \left({\mathtt{r}}_1\right)\right]\hfill \\ \hfill & \le {\int }_0^1{e}^{\varpi \mathsf{s}}\left[\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)+\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)\right]d\mathsf{s}\hfill \\ \hfill & +\frac{1}{{\mathtt{r}}_1}{\int }_0^{{\mathtt{r}}_1}\left(e^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_1}}+e^{\varpi \left(1-\frac{\mathsf{s}}{{\mathtt{r}}_1}\right)}\right)\omega \left(\mathsf{s}\right)\Phi \left(\mathsf{s}\right)d\mathsf{s}+\frac{1}{{\mathtt{r}}_2}{\int }_0^{{\mathtt{r}}_2}\left(e^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_2}}+e^{\varpi \left(1-\frac{\mathsf{s}}{{\mathtt{r}}_2}\right)}\right)\omega \left(\mathsf{s}\right)\Phi \left(\mathsf{s}\right)d\mathsf{s},\hfill \end{array}$$

(15)

hold true.

Proof. 

Since $\omega$ and $\Phi$ are subadditive functions on $\mathrm{Q},$ we have

$$\begin{array}{cc}\hfill & \omega ({\mathtt{r}}_1+{\mathtt{r}}_2)=\omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2+\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\hfill \\ \hfill & \le \omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\omega (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill & \Phi ({\mathtt{r}}_1+{\mathtt{r}}_2)=\Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2+\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\hfill \\ \hfill & \le \Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\Phi (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1).\hfill \end{array}$$

(17)

From Inequalities (16) and (17), we get

$$\begin{array}{cc}\hfill & \omega ({\mathtt{r}}_1+{\mathtt{r}}_2)\Phi ({\mathtt{r}}_1+{\mathtt{r}}_2)\hfill \\ \hfill & \le \left[\omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\omega (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\right]\left[\Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\Phi (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\right]\hfill \\ \hfill & =\omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\Phi (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\hfill \\ \hfill & +\omega (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\omega (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\Phi (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\hfill \\ \hfill & \le \omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\omega (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\Phi (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\hfill \\ \hfill & +\left[\omega \left(\mathsf{s}{\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\right]\left[\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)+\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)\right]+\left[\omega \left(\mathsf{s}{\mathtt{r}}_2\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_1\right)\right]\left[\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)+\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right)\right]\hfill \\ \hfill & =\omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\omega (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\Phi (\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\hfill \\ \hfill & +\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)+\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)\hfill \\ \hfill & +\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)+\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right).\hfill \end{array}$$

(18)

We generate Inequality (14) by multiplying both sides of Equation (18) by $e^{\varpi \mathsf{s}},$ integrating the resulting inequality with respect to $\mathsf{s}$ over $[0,1]$ and using the change in variables.

Since $\omega$ and $\Phi$ are subadditive functions on $\mathrm{Q},$ we have

$$\begin{array}{cc}\hfill & \omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\le \omega \left(\mathsf{s}{\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\hfill \end{array}$$

(19)

and

$$\begin{array}{cc}\hfill & \Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\le \Phi \left(\mathsf{s}{\mathtt{r}}_1\right)+\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right).\hfill \end{array}$$

(20)

From inequalities (19) and (20), we get

$$\begin{array}{cc}\hfill & \omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\le \omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)+\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right)\hfill \\ \hfill & +\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right).\hfill \end{array}$$

(21)

Similarly,

$$\begin{array}{cc}\hfill & \omega ((1-\mathsf{s}){\mathtt{r}}_1+\mathsf{s}{\mathtt{r}}_2)\Phi ((1-\mathsf{s}){\mathtt{r}}_1+\mathsf{s}{\mathtt{r}}_2)\le \omega \left((1-\mathsf{s}){\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)\hfill \\ \hfill & +\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)+\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right).\hfill \end{array}$$

(22)

Adding Inequalities (21) and (22), we obtain

$$\begin{array}{cc}\hfill & \omega (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)\Phi (\mathsf{s}{\mathtt{r}}_1+(1-\mathsf{s}){\mathtt{r}}_2)+\omega ((1-\mathsf{s}){\mathtt{r}}_1+\mathsf{s}{\mathtt{r}}_2)\Phi ((1-\mathsf{s}){\mathtt{r}}_1+\mathsf{s}{\mathtt{r}}_2)\hfill \\ \hfill & \le \omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)+\omega \left(\mathsf{s}{\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_2\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_2\right)\hfill \\ \hfill & +\omega \left((1-\mathsf{s}){\mathtt{r}}_1\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)+\omega \left((1-\mathsf{s}){\mathtt{r}}_1\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right)+\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left((1-\mathsf{s}){\mathtt{r}}_1\right)+\omega \left(\mathsf{s}{\mathtt{r}}_2\right)\Phi \left(\mathsf{s}{\mathtt{r}}_2\right).\hfill \end{array}$$

(23)

We generate Inequality (15) by multiplying both sides of Equation (23) by $e^{\varpi \mathsf{s}},$ integrating the resulting inequality with respect to $\mathsf{s}$ over $[0,1]$ and using the change in variables. This completely proves Theorem 5. □

Corollary 2. 

Under the assumptions of Theorem 5, letting $\alpha \to 1^{-},$ then we obtain ([20], Theorem 3).

Example 2. 

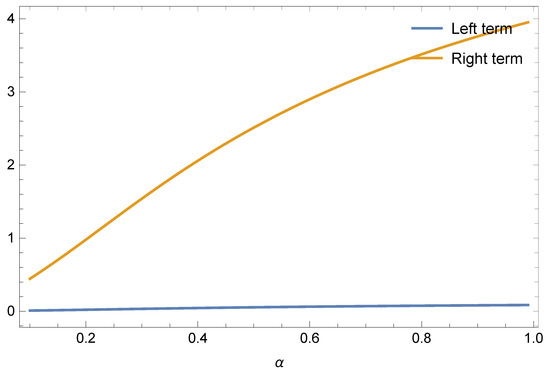
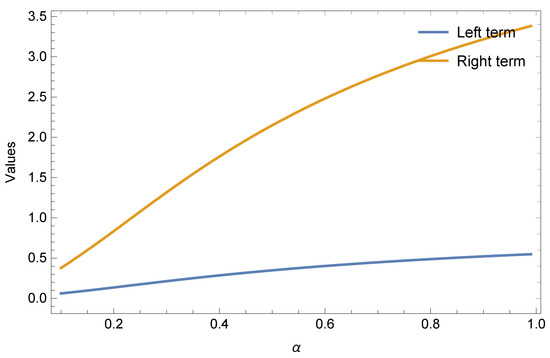
If we choose subadditive functions $\omega \left(\mathsf{s}\right)=e^{-\mathsf{s}}$ and $\Phi \left(\mathsf{s}\right)=\sqrt{\mathsf{s}},$ respectively, in Theorem 5 for all $\mathsf{s}>0$, $0<\alpha <1,$${\mathtt{r}}_1=1$ and ${\mathtt{r}}_2=2$, then we get the following results given in Table 3 and Table 4 and Figure 3 and Figure 4 for Inequalities (14) and (15), separately.

Table 3. Numerical validation of Theorem 5 for $\omega \left(\mathsf{s}\right)=e^{-\mathsf{s}}\mathrm{and}\Phi \left(\mathsf{s}\right)=\sqrt{\mathsf{s}},\forall \mathsf{s}>0$.

Values of $\mathit{\alpha }$	Value of the Left Term	Value of the Right Term
$0.1$	0.00958034	0.444685
$0.2$	0.0211636	0.979074
$0.3$	0.0333735	1.54003
$0.4$	0.0446616	2.05865
$0.5$	0.0545101	2.51138
$0.6$	0.0629398	2.89908
$0.7$	0.0701347	3.23013
$0.8$	0.0762993	3.51386
$0.9$	0.0816156	3.75862

Table 4. Numerical validation of Theorem 5 for $\omega \left(\mathsf{s}\right)=e^{-\mathsf{s}}\mathrm{and}\Phi \left(\mathsf{s}\right)=\sqrt{\mathsf{s}},\forall \mathsf{s}>0$.

Values of $\mathit{\alpha }$	Value of the Left Term	Value of the Right Term
$0.1$	0.0616893	0.37773
$0.2$	0.135673	0.835708
$0.3$	0.213566	1.31664
$0.4$	0.285599	1.7611
$0.5$	0.348471	2.14896
$0.6$	0.402303	2.48101
$0.7$	0.448262	2.76447
$0.8$	0.487647	3.00739
$0.9$	0.521618	3.2169

Figure 3. Graphical behaviour of Theorem 5 for $\omega \left(\mathsf{s}\right)=e^{-\mathsf{s}}\mathrm{and}\Phi \left(\mathsf{s}\right)=\sqrt{\mathsf{s}},\forall \mathsf{s}>0$ and $0<\alpha <1$.

Figure 4. Graphical behaviour of Theorem 5 for $\omega \left(\mathsf{s}\right)=e^{-\mathsf{s}}\mathrm{and}\Phi \left(\mathsf{s}\right)=\sqrt{\mathsf{s}},\forall \mathsf{s}>0$ and $0<\alpha <1$.

3. Further Results

Lemma 1. 

Let $\mathsf{{\rm Y}}:\mathrm{Q}\to \mathrm{R}$ be a differentiable function with ${\mathtt{r}}_1,{\mathtt{r}}_2\in {\mathrm{Q}}^{\circ }$ and ${\mathtt{r}}_1<{\mathtt{r}}_2.$ If ${\mathsf{{\rm Y}}}^{\prime }\in \mathrm{L}\left(\mathrm{Q}\right),$ then for $\alpha \in (0,1),$

$$\begin{array}{cc}\hfill & \frac{\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)}{2}-\frac{1-\alpha }{2\left(1-e^{\varpi }\right)}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)\right]\hfill \\ \hfill & =\frac{{\mathtt{r}}_2-{\mathtt{r}}_1}{2\left(1-e^{\varpi }\right)}{\int }_0^1\left(e^{\varpi \left(1-\mathsf{s}\right)}-e^{\varpi \mathsf{s}}\right){\mathsf{{\rm Y}}}^{\prime }(\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)d\mathsf{s},\hfill \end{array}$$

(24)

holds true.

Proof. 

Let

$$\begin{array}{cc}\hfill {\mathrm{I}}_1& :={\int }_0^1{e}^{\varpi \left(1-\mathsf{s}\right)}{\mathsf{{\rm Y}}}^{\prime }(\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)d\mathsf{s}\hfill \\ \hfill & =\frac{\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)-e^{\varpi }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)}{{\mathtt{r}}_2-{\mathtt{r}}_1}+\frac{\varpi }{{({\mathtt{r}}_2-{\mathtt{r}}_1)}^2}{\int }_{{\mathtt{r}}_1}^{{\mathtt{r}}_2}{e}^{-\frac{1-\alpha }{\alpha }({\mathtt{r}}_2-\mathsf{s})}\mathsf{{\rm Y}}\left(\mathsf{s}\right)d\mathsf{s}\hfill \\ \hfill & =\frac{\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)-e^{\varpi }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)}{{\mathtt{r}}_2-{\mathtt{r}}_1}-\frac{1-\alpha }{{\mathtt{r}}_2-{\mathtt{r}}_1}{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right).\hfill \end{array}$$

(25)

Similarly,

$$\begin{array}{cc}\hfill {\mathrm{I}}_2& :={\int }_0^1{e}^{\varpi \mathsf{s}}{\mathsf{{\rm Y}}}^{\prime }(\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)d\mathsf{s}\hfill \\ \hfill & =\frac{e^{\varpi }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)}{{\mathtt{r}}_2-{\mathtt{r}}_1}+\frac{1-\alpha }{{\mathtt{r}}_2-{\mathtt{r}}_1}{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right).\hfill \end{array}$$

(26)

Now, simplifying the following computation

$$\begin{array}{c}\hfill \frac{{\mathtt{r}}_2-{\mathtt{r}}_1}{2\left(1-e^{\varpi }\right)}\left[{\mathrm{I}}_1-{\mathrm{I}}_2\right]\end{array}$$

(27)

and using Equalities (25) and (26), we get the desired Equality (24). □

Theorem 6. 

Let $\mathsf{{\rm Y}}:\mathrm{Q}\to \mathrm{R}$ be a differentiable function with ${\mathtt{r}}_1,{\mathtt{r}}_2\in {\mathrm{Q}}^{\circ }$ and ${\mathtt{r}}_1<{\mathtt{r}}_2.$ If ${\mathsf{{\rm Y}}}^{\prime }\in \mathrm{L}\left(\mathrm{Q}\right)$ and $|{\mathsf{{\rm Y}}}^{\prime }{|}^{\mathrm{q}}$ is subadditive function with $\mathrm{p}>1$ and $\frac{1}{\mathrm{p}}+\frac{1}{\mathrm{q}}=1,$ then for $\alpha \in (0,1),$

$$\begin{array}{cc}\hfill & \left|\frac{\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)}{2}-\frac{1-\alpha }{2\left(1-e^{\varpi }\right)}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)\right]\right|\hfill \\ \hfill & \le \frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\mathrm{C}}^{\frac{1}{\mathrm{p}}}(\varpi ,\mathrm{p}){\left[\frac{1}{{\mathtt{r}}_1}{\int }_0^{{\mathtt{r}}_1}|{\mathsf{{\rm Y}}}^{\prime }{\left(\mathsf{s}\right)|}^{\mathrm{q}}d\mathsf{s}+\frac{1}{{\mathtt{r}}_2}{\int }_0^{{\mathtt{r}}_2}{\left|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}\right)\right|}^{\mathrm{q}}d\mathsf{s}\right]}^{\frac{1}{\mathrm{q}}},\hfill \end{array}$$

(28)

holds true, where

$$\mathrm{C}(\varpi ,\mathrm{p}):={\int }_0^{\frac{1}{2}}{\left(e^{\varpi \mathsf{s}}-e^{\varpi \left(1-\mathsf{s}\right)}\right)}^{\mathrm{p}}d\mathsf{s}+{\int }_{\frac{1}{2}}^1{\left(e^{\varpi \left(1-\mathsf{s}\right)}-e^{\varpi \mathsf{s}}\right)}^{\mathrm{p}}d\mathsf{s}.$$

Proof. 

Employing Lemma 1, Hölder’s inequality, subadditivity of $|{\mathsf{{\rm Y}}}^{\prime }{|}^{\mathrm{q}}$ on $\mathrm{Q},$ changing the variables of integration and properties of modulus, we have

$$\begin{array}{cc}\hfill & \left|\frac{\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)}{2}-\frac{1-\alpha }{2\left(1-e^{\varpi }\right)}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)\right]\right|\hfill \\ \hfill & \le \frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\int }_0^1\left|e^{\varpi \left(1-\mathsf{s}\right)}-e^{\varpi \mathsf{s}}\right|\left|{\mathsf{{\rm Y}}}^{\prime }(\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\right|d\mathsf{s}\hfill \\ \hfill & \le \frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\left({\int }_0^1{\left|e^{\varpi \left(1-\mathsf{s}\right)}-e^{\varpi \mathsf{s}}\right|}^{\mathrm{p}}d\mathsf{s}\right)}^{\frac{1}{\mathrm{p}}}{\left({\int }_0^1{\left|{\mathsf{{\rm Y}}}^{\prime }(\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\right|}^{\mathrm{q}}d\mathsf{s}\right)}^{\frac{1}{\mathrm{q}}}\hfill \\ \hfill & \le \frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\mathrm{C}}^{\frac{1}{\mathrm{p}}}(\varpi ,\mathrm{p}){\left[{\int }_0^1|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}{\mathtt{r}}_2\right){|}^{\mathrm{q}}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left((1-\mathsf{s}){\mathtt{r}}_1\right)\right|}^{\mathrm{q}}d\mathsf{s}\right]}^{\frac{1}{\mathrm{q}}}\hfill \\ \hfill & =\frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\mathrm{C}}^{\frac{1}{\mathrm{p}}}(\varpi ,\mathrm{p}){\left[\frac{1}{{\mathtt{r}}_1}{\int }_0^{{\mathtt{r}}_1}|{\mathsf{{\rm Y}}}^{\prime }{\left(\mathsf{s}\right)|}^{\mathrm{q}}d\mathsf{s}+\frac{1}{{\mathtt{r}}_2}{\int }_0^{{\mathtt{r}}_2}{\left|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}\right)\right|}^{\mathrm{q}}d\mathsf{s}\right]}^{\frac{1}{\mathrm{q}}}.\hfill \end{array}$$

This concludes the proof of Theorem 6. □

Example 3. 

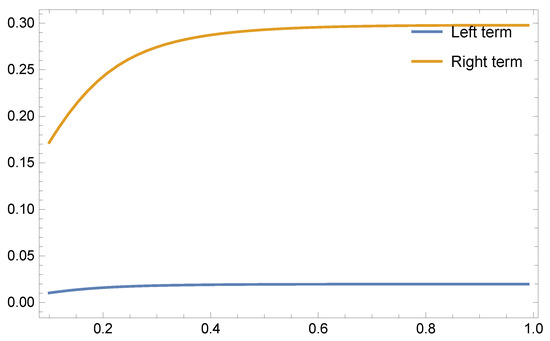
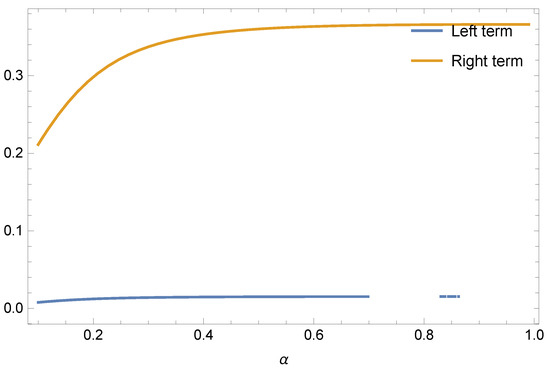
If we take functions $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\mathrm{q}{e}^{\frac{-\mathsf{s}}{\mathrm{q}}}$ and $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\frac{{\mathsf{s}}^{\frac{\mathtt{m}}{\mathrm{q}}+1}}{\frac{\mathtt{m}}{\mathrm{q}}+1}$ for fixed $\mathtt{m}=\frac{1}{2}$ and $\mathrm{q}=2,$ respectively, then $|{\mathsf{{\rm Y}}}^{\prime }{|}^{\mathrm{q}}$ are both subadditive functions for all $\mathsf{s}>0.$ Applying Theorem 6 for $\mathrm{p}=2$, $0<\alpha <1,$${\mathtt{r}}_1=1$ and ${\mathtt{r}}_2=2$, we have the following results given in Table 5 and Table 6 and Figure 5 and Figure 6.

Table 5. Numerical validation of Theorem 6 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\mathrm{q}{e}^{\frac{-\mathsf{s}}{\mathrm{q}}}and\mathrm{q}=2,\forall \mathsf{s}>0$.

Values of $\mathit{\alpha }$	Value of the Left Term	Value of the Right Term
$0.1$	0.010286	0.171784
$0.2$	0.0159689	0.242684
$0.3$	0.0182159	0.274321
$0.4$	0.0191014	0.287313
$0.5$	0.0194834	0.293001
$0.6$	0.0196603	0.295653
$0.7$	0.019745	0.296926
$0.8$	0.0197847	0.297523
$0.9$	0.0198012	0.297772

Table 6. Numerical validation of Theorem 6 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\frac{{\mathsf{s}}^{\frac{\mathtt{m}}{\mathrm{q}}+1}}{\frac{\mathtt{m}}{\mathrm{q}}+1}$, $\mathtt{m}=\frac{1}{2}and\mathrm{q}=2,\forall \mathsf{s}>0$.

Values of $\mathit{\alpha }$	Value of the Left Term	Value of the Right Term
$0.1$	0.00775404	0.211233
$0.2$	0.0122236	0.298415
$0.3$	0.0139898	0.337317
$0.4$	0.0146857	0.353292
$0.5$	0.0149858	0.360287
$0.6$	0.0151249	0.363548
$0.7$	0.0151914	0.365113
$0.8$	0.0152226	0.365847
$0.9$	0.0152356	0.366153

Figure 5. Graphical behaviour of Theorem 6 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\mathrm{q}{e}^{\frac{-\mathsf{s}}{\mathrm{q}}}and\mathrm{q}=2,\forall \mathsf{s}>0$ and $0<\alpha <1$.

Figure 6. Graphical behaviour of Theorem 6 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\frac{{\mathsf{s}}^{\frac{\mathtt{m}}{\mathrm{q}}+1}}{\frac{\mathtt{m}}{\mathrm{q}}+1}$, $\mathtt{m}=\frac{1}{2}and\mathrm{q}=2,\forall \mathsf{s}>0$ and $0<\alpha <1$.

Theorem 7. 

Let $\mathsf{{\rm Y}}:\mathrm{Q}\to \mathrm{R}$ be a differentiable function with ${\mathtt{r}}_1,{\mathtt{r}}_2\in {\mathrm{Q}}^{\circ }$ and ${\mathtt{r}}_1<{\mathtt{r}}_2.$ If ${\mathsf{{\rm Y}}}^{\prime }\in \mathrm{L}\left(\mathrm{Q}\right)$ and $|{\mathsf{{\rm Y}}}^{\prime }{|}^{\mathrm{q}}$ is subadditive function with $\mathrm{q}\ge 1,$ then for $\alpha \in (0,1),$

$$\begin{array}{cc}\hfill & \left|\frac{\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)}{2}-\frac{1-\alpha }{2\left(1-e^{\varpi }\right)}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)\right]\right|\le \frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\left[\frac{2{\left(e^{\frac{\varpi }{2}}-1\right)}^2}{-\varpi }\right]}^{1-\frac{1}{\mathrm{q}}}\hfill \\ \hfill & \times {\left[{\mathrm{F}}_{{\mathtt{r}}_1}(\mathsf{{\rm Y}};\varpi ,\mathrm{q})+{\mathrm{F}}_{{\mathtt{r}}_2}(\mathsf{{\rm Y}};\varpi ,\mathrm{q})+{\mathrm{G}}_{{\mathtt{r}}_1}(\mathsf{{\rm Y}};\varpi ,\mathrm{q})+{\mathrm{G}}_{{\mathtt{r}}_2}(\mathsf{{\rm Y}};\varpi ,\mathrm{q})\right]}^{\frac{1}{\mathrm{q}}},\hfill \end{array}$$

(29)

holds true, where

$$\begin{array}{c}\hfill {\mathrm{F}}_{{\mathtt{r}}_1}(\mathsf{{\rm Y}};\varpi ,\mathrm{q}):=\frac{1}{{\mathtt{r}}_1}{\int }_0^{\frac{{\mathtt{r}}_1}{2}}\left(e^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_1}}-e^{\varpi \left(1-\frac{\mathsf{s}}{{\mathtt{r}}_1}\right)}\right){\left|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}\right)\right|}^{\mathrm{q}}d\mathsf{s};\\ \hfill {\mathrm{F}}_{{\mathtt{r}}_2}(\mathsf{{\rm Y}};\varpi ,\mathrm{q}):=\frac{1}{{\mathtt{r}}_2}{\int }_0^{\frac{{\mathtt{r}}_2}{2}}\left(e^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_2}}-e^{\varpi \left(1-\frac{\mathsf{s}}{{\mathtt{r}}_2}\right)}\right){\left|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}\right)\right|}^{\mathrm{q}}d\mathsf{s};\\ \hfill {\mathrm{G}}_{{\mathtt{r}}_1}(\mathsf{{\rm Y}};\varpi ,\mathrm{q}):=\frac{1}{{\mathtt{r}}_1}{\int }_{\frac{{\mathtt{r}}_1}{2}}^{{\mathtt{r}}_1}\left(e^{\varpi \left(1-\frac{\mathsf{s}}{{\mathtt{r}}_1}\right)}-e^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_1}}\right){\left|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}\right)\right|}^{\mathrm{q}}d\mathsf{s};\\ \hfill {\mathrm{G}}_{{\mathtt{r}}_2}(\mathsf{{\rm Y}};\varpi ,\mathrm{q}):=\frac{1}{{\mathtt{r}}_2}{\int }_{\frac{{\mathtt{r}}_2}{2}}^{{\mathtt{r}}_2}\left(e^{\varpi \left(1-\frac{\mathsf{s}}{{\mathtt{r}}_2}\right)}-e^{\varpi \frac{\mathsf{s}}{{\mathtt{r}}_2}}\right){\left|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}\right)\right|}^{\mathrm{q}}d\mathsf{s}.\end{array}$$

Proof. 

Employing Lemma 1, power-mean inequality, subadditivity of $|{\mathsf{{\rm Y}}}^{\prime }{|}^{\mathrm{q}}$ on $\mathrm{Q},$ changing the variables of integration and properties of modulus, we have

$$\begin{array}{cc}\hfill & \left|\frac{\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)+\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)}{2}-\frac{1-\alpha }{2\left(1-e^{\varpi }\right)}\left[{\mathrm{I}}_{{\mathtt{r}}_1^{+}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_2\right)+{\mathrm{I}}_{{\mathtt{r}}_2^{-}}^{\alpha }\mathsf{{\rm Y}}\left({\mathtt{r}}_1\right)\right]\right|\hfill \\ \hfill & \le \frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\int }_0^1\left|e^{\varpi \left(1-\mathsf{s}\right)}-e^{\varpi \mathsf{s}}\right|\left|{\mathsf{{\rm Y}}}^{\prime }(\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\right|d\mathsf{s}\hfill \\ \hfill & \le \frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\left({\int }_0^1\left|e^{\varpi \left(1-\mathsf{s}\right)}-e^{\varpi \mathsf{s}}\right|d\mathsf{s}\right)}^{1-\frac{1}{\mathrm{q}}}\hfill \\ \hfill & \times {\left({\int }_0^1\left|e^{\varpi \left(1-\mathsf{s}\right)}-e^{\varpi \mathsf{s}}\right|{\left|{\mathsf{{\rm Y}}}^{\prime }(\mathsf{s}{\mathtt{r}}_2+(1-\mathsf{s}){\mathtt{r}}_1)\right|}^{\mathrm{q}}d\mathsf{s}\right)}^{\frac{1}{\mathrm{q}}}\hfill \\ \hfill & \le \frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\left[\frac{2{\left(e^{\frac{\varpi }{2}}-1\right)}^2}{-\varpi }\right]}^{1-\frac{1}{\mathrm{q}}}\hfill \\ \hfill & \times \{{\left({\int }_0^{\frac{1}{2}}\left(e^{\varpi \mathsf{s}}-e^{\varpi \left(1-\mathsf{s}\right)}\right)\left[|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}{\mathtt{r}}_2\right){|}^{\mathrm{q}}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left((1-\mathsf{s}){\mathtt{r}}_1\right)\right|}^{\mathrm{q}}\right]d\mathsf{s}\right)}^{\frac{1}{\mathrm{q}}}\hfill \\ \hfill & +{\left({\int }_{\frac{1}{2}}^1\left(e^{\varpi \left(1-\mathsf{s}\right)}-e^{\varpi \mathsf{s}}\right)\left[|{\mathsf{{\rm Y}}}^{\prime }\left(\mathsf{s}{\mathtt{r}}_2\right){|}^{\mathrm{q}}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left((1-\mathsf{s}){\mathtt{r}}_1\right)\right|}^{\mathrm{q}}\right]d\mathsf{s}\right)}^{\frac{1}{\mathrm{q}}}\}\hfill \\ \hfill & =\frac{({\mathtt{r}}_2-{\mathtt{r}}_1)}{2\left(1-e^{\varpi }\right)}{\left[\frac{2{\left(e^{\frac{\varpi }{2}}-1\right)}^2}{-\varpi }\right]}^{1-\frac{1}{\mathrm{q}}}\hfill \\ \hfill & \times {\left[{\mathrm{F}}_{{\mathtt{r}}_1}(\mathsf{{\rm Y}};\varpi ,\mathrm{q})+{\mathrm{F}}_{{\mathtt{r}}_2}(\mathsf{{\rm Y}};\varpi ,\mathrm{q})+{\mathrm{G}}_{{\mathtt{r}}_1}(\mathsf{{\rm Y}};\varpi ,\mathrm{q})+{\mathrm{G}}_{{\mathtt{r}}_2}(\mathsf{{\rm Y}};\varpi ,\mathrm{q})\right]}^{\frac{1}{\mathrm{q}}},\hfill \end{array}$$

which completes the proof of Theorem 7. □

Example 4. 

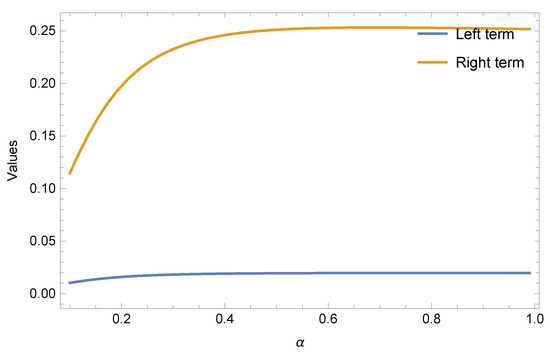
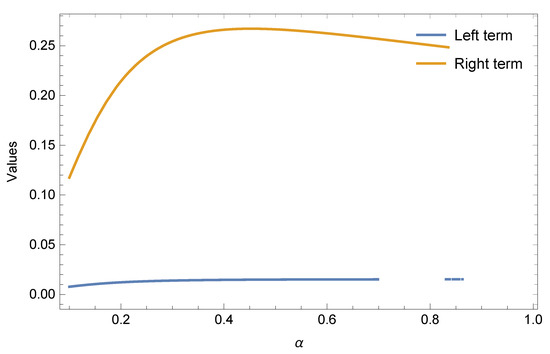
If we choose functions $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\mathrm{q}{e}^{\frac{-\mathsf{s}}{\mathrm{q}}}$ and $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\frac{{\mathsf{s}}^{\frac{\mathtt{m}}{\mathrm{q}}+1}}{\frac{\mathtt{m}}{\mathrm{q}}+1}$ for fixed $\mathtt{m}=\frac{1}{2}$ and $\mathrm{q}=2,$ respectively, then $|{\mathsf{{\rm Y}}}^{\prime }{|}^{\mathrm{q}}$ are both subadditive functions for all $\mathsf{s}>0.$ Applying Theorem 7 for $0<\alpha <1,$${\mathtt{r}}_1=1$ and ${\mathtt{r}}_2=2$ we get the following results given in Table 7 and Table 8 and Figure 7 and Figure 8.

Table 7. Numerical validation of Theorem 7 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\mathrm{q}{e}^{\frac{-\mathsf{s}}{\mathrm{q}}}and\mathrm{q}=2,\forall \mathsf{s}>0$.

Values of $\mathit{\alpha }$	Value of the Left Term	Value of the Right Term
$0.1$	0.010286	0.114528
$0.2$	0.0159689	0.197689
$0.3$	0.0182159	0.232613
$0.4$	0.0191014	0.245951
$0.5$	0.0194834	0.251064
$0.6$	0.0196603	0.252851
$0.7$	0.019745	0.253198
$0.8$	0.0197847	0.252898
$0.9$	0.0198012	0.252308

Table 8. Numerical validation of Theorem 7 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\frac{{\mathsf{s}}^{\frac{\mathtt{m}}{\mathrm{q}}+1}}{\frac{\mathtt{m}}{\mathrm{q}}+1}$, $\mathtt{m}=\frac{1}{2}and\mathrm{q}=2,\forall \mathsf{s}>0$.

Values of $\mathit{\alpha }$	Value of the Left Term	Value of the Right Term
$0.1$	0.00775404	0.117499
$0.2$	0.0122236	0.21428
$0.3$	0.0139898	0.254368
$0.4$	0.0146857	0.266062
$0.5$	0.0149858	0.266483
$0.6$	0.0151249	0.262478
$0.7$	0.0151914	0.256803
$0.8$	0.0152226	0.250629
$0.9$	0.0152356	0.244468

Figure 7. Graphical behaviour of Theorem 7 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\mathrm{q}{e}^{\frac{-\mathsf{s}}{\mathrm{q}}}and\mathrm{q}=2,\forall \mathsf{s}>0$ and $0<\alpha <1$.

Figure 8. Graphical behaviour of Theorem 7 for $\mathsf{{\rm Y}}\left(\mathsf{s}\right)=\frac{{\mathsf{s}}^{\frac{\mathtt{m}}{\mathrm{q}}+1}}{\frac{\mathtt{m}}{\mathrm{q}}+1}$, $\mathtt{m}=\frac{1}{2}and\mathrm{q}=2,\forall \mathsf{s}>0$ and $0<\alpha <1$.

4. Conclusions

In this paper, we established some new fractional H-H inequalities with an exponential kernel for subadditive functions, for product of two such functions and some known results are recaptured as well. Moreover, we proved a new identity, that acts as an auxiliary result for the derivation of further inequalities involving subadditive functions via fractional integrals. To validate the accuracy of our results, we give some examples for suitable choices of subadditive functions and their graphical representations with $0<\alpha <1$. We believe that our results using fractional integral operators with exponential kernels open many avenues for interested researchers working in this field and they can discover further approximations for different kinds of fractional integral operators and functions as well. Moreover, we can apply the obtained results in special functions, quantum calculus, applied mathematics, etc, in related future research works.