Chiral Restoration of Nucleons in Neutron Star Matter: Studies Based on a Parity Doublet Model

Abstract

We review the chiral variant and invariant components of nucleon masses and the consequence of their existence on the chiral restoration in extreme conditions, particularly in neutron star matter. We consider a model of linear realization of chiral symmetry with the nucleon parity doublet structure that permits the chiral invariant mass, $m_0$, for positive and negative parity nucleons. The nuclear matter is constructed with the parity doublet nucleon model coupled to scalar fields $\sigma$, vector fields $(\omega ,\rho )$, and mesons with strangeness through the U(1)${}_A$ anomaly. In models with a large $m_0$, the nucleon mass is insensitive to the medium, and the nuclear saturation properties can be reproduced without demanding strong couplings of the nucleons to the scalar fields $\sigma$ and vector fields $\omega$. We confront the resulting nuclear equations of state with nuclear constraints and neutron star observations and delineate the chiral invariant mass and effective interactions. To further examine the nuclear equations of state beyond the saturation density, we supplement quark models to set the boundary conditions from the high-density side. The quark models are constrained by the two-solar-mass conditions, and such constraints are transferred to nuclear models through the causality and thermodynamic stability conditions. We also calculate various condensates and the matter composition from nuclear to quark matter in a unified matter by constructing a generating functional that interpolates the nuclear and quark matter with external fields. Two types of chiral restoration are discussed: one due to the positive scalar charges of nucleons and the other triggered by the evolution of the Dirac sea. We found that the U(1)${}_A$ anomaly softens equations of state from low to high density.

1. Introduction

The quest for the origin of hadron masses is one of the most interesting problems in low-energy hadron physics. Spontaneous chiral symmetry breaking (S$\chi$SB) is known to generate a part of hadron masses. A typical model in this context is the linear $\sigma$ model [1,2] where the Lagrangian contains nucleons, N, and the meson fields $\sigma$, $\overrightarrow{\pi }$, which are grouped into a chiral invariant form. The fields in such models are the linear realization of the chiral symmetry which transforms linearly under chiral transformations, e.g., $N_i\to N_i^{\prime }=U_{ij}(\overrightarrow{\theta })N_j$, ${\pi }_i\to {\pi }_i^{\prime }=V_{i0}(\overrightarrow{\theta })\sigma +V_{ij}(\overrightarrow{\theta }){\pi }_j$ ($\overrightarrow{\theta }$: some constant vector). The model is arranged to yield the nonzero expectation value of the $\sigma$ fields, $⟨\sigma ⟩$, which breaks the chiral symmetry and generates the nucleon mass term that couples nucleon fields of the left- and right-chirality. The nucleon mass ($\propto ⟨\sigma ⟩$) is not chiral invariant and is entirely generated by the S$\chi$SB.

The more general and systematic construction of models is based on the non-linear realization of chiral symmetry for which chiral transformations act on fields non-linearly, e.g., ${\pi }_i\to U_{ij}(\overrightarrow{\pi },\overrightarrow{\theta }){\pi }_j$ [3]. Such pions accompany space–time derivatives, which enable us to power count in pion momenta and greatly systematize the construction of an effective Lagrangian [4]. The $\sigma$ field does not manifestly appear as a dynamical degree of freedom and is not necessary to make the Lagrangian chiral invariant. In fact, we can allow the chiral invariant mass term of the form, $\sim \overline{N}{M}_{\mathrm{inv}}{U}_5(\overrightarrow{\pi })N=M_{\mathrm{inv}}\overline{\mathcal{N}}\mathcal{N}$ where $\mathcal{N}\equiv U_5^{1/2}N$ expresses the nucleons (with a “pion cloud”) in the non-linear realization. If we start with a linear $\sigma$ model, the chiral invariant mass $M_{\mathrm{inv}}$ appears as $\sim {(⟨{\sigma }^2+{\overrightarrow{\pi }}^2⟩)}^{1/2}$, but models of non-linear realization do not necessarily require such identification; this draws our attention to dynamical mechanisms, not necessarily related to the S$\chi$SB, for the origin of $M_{\mathrm{inv}}$.

While the non-linear realization allows for a more general construction of nucleonic models than the linear realization, the descriptions without $\sigma$ fields, in practice, have difficulties in the extension to the domain of the chiral symmetry restoration; there, $\overrightarrow{\pi }$ and $\sigma$ should together form a chiral multiplet, since the physical states in a symmetrical unbroken vacuum must belong to irreducible representations of the chiral symmetry. We note here that it is not trivial that such mesonic excitations exist in the chiral symmetric phase, but it would be useful to include $\sigma$ in an effective model to approach the restoration point from the broken phase. Furthermore, if the chiral restoration is not a first-order phase transition, one may observe the consequence of the symmetry restoration even before reaching the complete restoration. For this purpose, the linear realization with $\sigma$ has a greater advantage over the non-linear realization (where $\sigma$ must be generated dynamically from the pion dynamics). Such chiral restoration may happen at a high temperature and high density and has phenomenological impacts on descriptions of the physics of relativistic heavy-ion collision and neutron stars (NSs) [5].

A model of linear realization may be improved by supplementing the concept of Weinberg’s mended symmetry [6,7]. His mended symmetry states that, even in a spontaneously broken vacuum, superposing the linear representations of the original symmetry may be used to describe the physical spectra. Based on this picture, Weinberg described low-lying mesons $(\sigma ,\pi ,\rho ,a_1)$ as the superposition of chiral multiplets and then obtained reasonable mass relations and decay widths for these states. This success encourages us to consider models of linear realization for nucleons, including several chiral multiplets.

In this review, we consider a parity doublet model (PDM) of nucleons as a model of linear realization and examine its feature through the phenomenology of dense QCD, especially neutron star matter. The PDM includes two nucleon fields, $N_1$ and $N_2$, whose left- and right-handed components (defined through the $(1\pm {\gamma }_5)/2$ projections) transform differently as $N_{1R/L}\to g_{R/L}{N}_{1R/L}$ and $N_{2R/L}\to g_{L/R}{N}_{2R/L}$ under the U($N_{\mathrm{f}}$)${}_L\otimes$ U($N_{\mathrm{f}}$)${}_R$ chiral transformations (mirror assignment). The mass term of $\sim m_0\left({\overline{N}}_{1R}{N}_{2L}+{\overline{N}}_{1L}{N}_{2R}\right)$ is now possible without breaking the U($N_{\mathrm{f}}$)${}_L\otimes$ U($N_{\mathrm{f}}$)${}_R$ symmetry, and the mass $m_0$ is chiral invariant. This chiral invariant mass term and the conventional Yukawa coupling term are diagonalized together, yielding spectra of positive and negative parity nucleons. For a sufficiently large $m_0$, the overall magnitude of the physical nucleon masses is primarily set by the $m_0$, while the chiral variant mass $\propto ⟨\sigma ⟩$ is mainly responsible for mass splitting between the positive and negative parity nucleons. Such a model was first constructed by DeTar and Kunihiro [8], where $N(939)$ and $N^{*}(1535)$ are regarded as partners.

The size of $m_0$ is of great concern when predicting the properties of nucleons near the chiral restoration. In a minimal PDM, the decay width of $N^{*}(1535)$ is used to set the constraint $m_0\lesssim 500$ MeV [9]. However, as in the standard $\sigma$ model, such estimates can be easily affected by ∼30% if we permit non-renormalizable terms of dimension five, and a larger value of $m_0$ is possible (see, e.g., Ref. [10]). Further evidence of a large $m_0$ comes from a lattice QCD study at a finite temperature for a nucleon and its parity partner [11]. The mass gap between $N(939)$ and $N^{*}(1535)$ is reduced together with a reduction of the chiral condensates, while the substantial mass of $N(939)$ can remain; this suggests that $m_0$ may be as large as the mass of $N(939)$ itself.

The nucleon mass, which is relatively insensitive to the chiral restoration, has important consequences on the dense nuclear matter at a density relevant to neutron star (NS) phenomenology. In the past ∼20 years, there has been dramatic progress in the measurements of NS mass–radius (M-R) relations, which have a one-to-one correspondence with the QCD equation of state (EOS). The key question is whether the EOS is stiff or soft; a stiffer EOS has a larger pressure at a given energy density and prevents a star from gravitational collapse into a blackhole. The relevant NS constraints are the existence of $2M_{\odot }$ NS [12,13,14,15,16,17], and the radii of $1.4M_{\odot }$ [18,19,20] and $\simeq 2.1M_{\odot }$ NS [21,22]. In short, the NS EOS is relatively soft at the baryon density $n_B$ around 1-2$n_0$ ($n_0\simeq 0.16{\mathrm{fm}}^{-3}$: nuclear saturation density) but evolves into a very stiff EOS at ∼$5n_0$. The density ≃1-$2n_0$ is usually regarded as the domain of nuclear theories, while the domain at ≳$5n_0$, where nucleons of the radii ∼0.5–$0.8$ fm begin to overlap, likely demands quark matter descriptions. The EOS constraints at 1-2$n_0$ obviously give important information about the chiral invariant mass, but the EOS constraints on ≳$5n_0$ also impose indirect but powerful constraints on the nuclear territory through the causality condition that the sound velocity, $c_s={(\partial P/\partial \epsilon )}^{1/2}$ (P: pressure, $\epsilon$: energy density), is less than the light velocity ($c=1$ in our unit); see, e.g., Ref. [23]. In order to describe the domain between nuclear and quark matter in a way that is consistent with the observed soft-to-stiff evolution of EOS, the simplest scenario is the quark–hadron crossover (QHC) [24,25,26,27,28]. Unlike models with first-order phase transitions, gradual quark matter formation does not accompany a strong softening of the EOS and even leads to stiffening [29,30,31,32,33]. Based on this picture, we build unified equations of state that utilize nuclear models at $n_B\lesssim 2n_0$ and quark models at $n_B\gtrsim 5n_0$ and interpolate them for the EOS at $2n_0\lesssim n_B\lesssim 5n_0$. We confront the unified EOS with M-R relations constrained by observations and also calculate the chiral condensates and matter composition. All of these quantities are examined from the nuclear to quark matter domains, and the correlation between low and high densities gives us global insights into the chiral properties of nucleons.

For the construction of the nuclear EOS, we implement a PDM into the Walecka-type mean field model with $\sigma$, $\omega$, and $\rho$ [34,35,36]. The strangeness is included at the level of the $U{(1)}_A$ anomaly where the scalar mesons with strangeness, ${\sigma }_s$, couple to a $\sigma$ made of up- and down-quarks. For a neutron star EOS based on the PDM, see, e.g., Refs. [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62]. The most notable feature of the PDM is the density dependence of the nucleon mass. The chiral invariant mass allows nucleons to stay massive during the reduction in $⟨\sigma ⟩$. In the dilute regime, the $⟨\sigma ⟩$ decreases linearly as a function of $n_B$, as does the nucleon mass $\propto ⟨\sigma ⟩$ if $m_0$ is absent; the nucleon mass at $n_0$ is ≃30–50% smaller than the vacuum mass. With a larger $m_0$, the mass reduction becomes more modest. In addition, nucleon fields need not couple to $\sigma$ very strongly to reproduce the nucleon mass $m_N\simeq 939$ MeV; in the Walecka-type model, this results in a weaker coupling between the nucleons and $\omega$ fields because such models have been arranged to balance the attractive $\sigma$ and repulsive $\omega$ contributions to reproduce the nuclear matter properties at $n_0$. Beyond $n_0$, the attractive $\sigma$ contributions decrease while the repulsive $\omega$ contributions keep growing. Thus, a greater $m_0$ makes the overall magnitude of the $\sigma$ and $\omega$ contributions smaller, and the resulting softer $\omega$ repulsion improves the consistency with the radius constraints on $1.4M_{\odot }$ NS, for which the EOS at $n_B=1$-$2n_0$ is most important.

The PDM as a hadronic model does not describe the chiral restoration at the quark level, such as the modification in the quark Dirac sea. In order to supply such a qualitative trend, the quark matter EOS plays a role as a high-density boundary condition. For the quark matter, a three-flavor Nambu–Jona-Lasinio (NJL)-type model, which leads to the color-flavor locked (CFL) color-superconducting matter (for a review, see Ref. [63]), is adopted. The effective interactions are examined to fulfill the two-solar-mass ($2M_{\odot }$) constraint [27,28,64,65]. In Refs. [58,61], they construct an effective model combining a PDM and an NJL-type model with two flavors assuming no color-superconductivity.

This article is mostly a review of our works, Refs. [66,67,68], and it also presents improvements to the analyses of Refs. [66,68] with the up-to-date version of our PDM. In Ref. [66], we used the PDM without the U(1)${}_A$ anomaly to construct a unified EOS and obtained the constraint $600\mathrm{MeV}\lesssim m_0\lesssim 900\mathrm{MeV}$. The lower bound is primarily determined by the tidal deformability constraint from the GW170817, which is a detection of gravitational waves from an NS merger event. Later, in Ref. [67], we updated the PDM by adding the $U{(1)}_A$ anomaly effects, or the Kobayashi–Maskawa–’t Hooft (KMT) interactions [69], to the meson sector. Even though we stop using the PDM at ≲$2n_0$ before hyperons appear, the strangeness does affect the chiral condensates in the up- and down-sectors through the KMT interactions. The $U{(1)}_A$ effects enhance the energy difference between the chiral symmetric and broken vacua, leading to a stronger softening in the EOS when the chiral symmetry is restored. This is found to be true for both hadronic and quark matter. In particular, the chiral restoration with the $U{(1)}_A$ anomaly makes the EOS at 1-$2n_0$ softer and leads to small radii for $1.4M_{\odot }$ NS. In effect, the lower bound $m_0\gtrsim 600$ MeV, given in Ref. [66], is relaxed to $m_0\gtrsim 400$ MeV.

While the seminal works [24,25,27,64,66,70,71,72] utilize the interpolation to construct a unified EOS, the microscopic quantities have not been calculated in a unified way. To utilize the full potential of the interpolation framework, in Ref. [68], three of the present authors (T.M., T.K., and M.H.) extend the interpolation to unified generating functionals with external fields coupled to the quantities of interest and differentiated the functionals to extract the chiral and diquark condensates as well as the matter composition. The condensates in the interpolated domain are affected by the physics of both the hadronic and quark matter through the boundary conditions for the interpolation; for $m_0\gtrsim 500$ MeV, the significant chiral condensate remains at $n_B\sim 2$-$3n_0$ and smoothly approaches the condensate in the quark matter at $n_B\gtrsim 5n_0$. In this review, we update these analyses, including the effects of the $U{(1)}_A$ anomaly.

This review is structured as follows. In Section 2, we first review the PDM with mesonic potentials in Ref. [67] and show how to constrain the model parameters to satisfy the hadron properties in a vacuum and the saturation properties in nuclear matter. Section 3 is the review of quark matter construction. With these hadronic and quark matter models, in Section 4, we construct unified generating functionals as introduced in Ref. [68] and calculate various condensates. Section 6 is devoted to a summary.

2. Hadronic Matter from a Parity Doublet Model

In this section, we review the construction of the PDM in Ref. [67]. The fields appearing in the Lagrangian are the linear realization of chiral symmetry, classified by the chiral representation as (SU(3)${}_L$, SU(3)${}_R$)${}_{{\mathrm{U}(1)}_A}$. We determine the model parameters to reproduce the hadronic properties in a vacuum and the saturation properties of nuclear matter.

2.1. Scalar and Pseudoscalar Mesons

We introduce a $3\times 3$ matrix field $\Phi$ for the scalar and pseudoscalar mesons, which belong to ${(\mathbf{3},\overline{\mathbf{3}})}_{-2}$ under (SU(3)${}_L$, SU(3)${}_R$)${}_{{\mathrm{U}(1)}_A}$ symmetry. The Lagrangian is given by

$$\begin{array}{c}\hfill {\mathcal{L}}_M^{\mathrm{scalar}}=\frac{1}{4}tr\left[{\partial }_{\mu }\Phi {\partial }^{\mu }{\Phi }^{†}\right]-V_M-V_{\mathrm{SB}}-V_{\mathrm{Anom}},\end{array}$$

(1)

where

$$\begin{array}{cc}\hfill V_M=& -\frac{1}{4}{\overline{\mu }}^{2}tr\left[\Phi {\Phi }^{†}\right]+\frac{1}{8}{\lambda }_{4}tr\left[{\left(\Phi {\Phi }^{†}\right)}^2\right]-\frac{1}{12}{\lambda }_{6}tr\left[{\left(\Phi {\Phi }^{†}\right)}^3\right]\hfill \\ & +{\lambda }_{8}tr\left[{\left(\Phi {\Phi }^{†}\right)}^4\right]+{\lambda }_{10}tr\left[{\left(\Phi {\Phi }^{†}\right)}^5\right],\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill V_{\mathrm{SB}}=& -\frac{1}{2}ctr\left[{\widehat{m}}_q^{†}\Phi +{\widehat{m}}_q{\Phi }^{†}\right],\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill V_{\mathrm{Anom}}=& -B\left[det(\Phi )+det\left({\Phi }^{†}\right)\right],\hfill \end{array}$$

(4)

with B and c being the coefficients for the axial anomaly term and the explicit chiral symmetry breaking term, respectively, and ${\widehat{m}}_q=\mathrm{diag}\{m_u,m_d,m_s\}$. In the above, we include only the terms with one trace in $V_M$ since they are of leading order in the $1/N_c$ expansion.

The present hadronic model is used up to $2n_0$ assuming no appearance of hyperons. In the mean field approximation, the $\Phi$ field can be reduced to

$$\begin{array}{c}\hfill \Phi \to {\left(\begin{array}{cc}M& 0\\ 0& {\sigma }_s\end{array}\right)}_{3\times 3},\end{array}$$

(5)

where M is a $2\times 2$ matrix field transforming as $M\to g_{L}M{g}_R^{†}$ with $g_{L,R}\in {\mathrm{SU}(2)}_{L,R}$. While we apply the mean field, here, we keep a matrix representation for the two-flavor part to clarify the symmetry of the two-flavor part. The field ${\sigma }_s$ corresponds to the scalar condensate made of a strange and an anti-strange quark, $⟨\overline{s}s⟩$. The reduced Lagrangian is now given by

$$\begin{array}{c}\hfill {\mathcal{L}}_M^{\mathrm{scalar}}=\frac{1}{4}\left(\mathrm{tr}\left[{\partial }_{\mu }M{\partial }^{\mu }{M}^{†}\right]+({\partial }_{\mu }{\sigma }_s{\partial }^{\mu }{\sigma }_s)\right)-V_M-V_{SB}-V_{\mathrm{Anom}},\end{array}$$

(6)

where

$$\begin{array}{cc}\hfill V_M=& -\frac{1}{4}{\overline{\mu }}^2\left(\mathrm{tr}\left[M{M}^{†}\right]+{\sigma }_s^2\right)+\frac{1}{8}{\lambda }_4\left(\mathrm{tr}\left[{(M{M}^{†})}^2\right]+{\sigma }_s^4\right)\hfill \\ \hfill & -\frac{1}{12}{\lambda }_6\left(\mathrm{tr}\left[{(M{M}^{†})}^3\right]+{\sigma }_s^6\right)+{\lambda }_8\left(\mathrm{tr}\left[{(M{M}^{†})}^4\right]+{\sigma }_s^8\right)\hfill \\ \hfill & +{\lambda }_{10}\left(\mathrm{tr}\left[{(M{M}^{†})}^5\right]+{\sigma }_s^{10}\right),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill V_{\mathrm{S}\mathrm{B}}=& -\frac{c}{2}\left[\mathrm{tr}\left[{\widehat{m}}_{2\times 2}(M+M^{†})\right]+2m_s{\sigma }_s\right],\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill V_{\mathrm{Anom}}=& -B{\sigma }_s\left[\det (M)+\det (M^{†})\right],\hfill \end{array}$$

(9)

with ${\widehat{m}}_{2\times 2}=\mathrm{diag}\{m_u,m_d\}$. In the mean field treatment, the two-flavor matrix field M is reduced to $\mathrm{diag}(\sigma ,\sigma )$.

Here, one might wonder why the $(\Phi {\Phi }^{†})$ terms are included up to the fifth powers. In fact, the potential of the two-flavor model in the analyses [49,59,66] is not bounded from below at a very large value of $(\Phi {\Phi }^{†})$ and has only a local minimum. There, very large values of $(\Phi {\Phi }^{†})$ are simply discarded because they are not supposed to be within the domain applicability of the model. For three-flavor models with the KMT interactions, however, it turns out that reasonable local minima do not exist, as depicted by the black curve in Figure 1. We add higher-order terms to stabilize the potential and fine tune the models to reproduce the nuclear saturation properties. Note that these higher-order terms do not modify the potentials at a small ${\sigma }_s$.

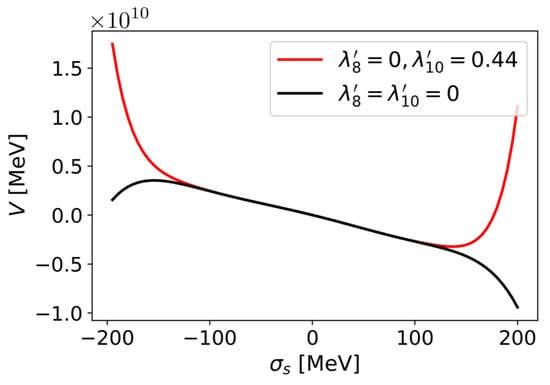
Figure 1. Potential for ${\sigma }_s$ in the vacuum with $m_0=800$ MeV. Here, ${\lambda }_8^{\prime }$ and ${\lambda }_{10}^{\prime }$ are dimensionless quantities defined by ${\lambda }_8^{\prime }={\lambda }_8{f}_{\pi }^4$ and ${\lambda }_{10}^{\prime }={\lambda }_{10}{f}_{\pi }^6$.

2.2. Nucleon Parity Doublet and Vector Mesons

In the analysis performed in Refs. [66,67,68], hadronic models are used only up to $2n_0$ with the assumption that the hyperons are not populated. Therefore, although the mesonic sector includes three-flavors, we include only nucleons in the baryon sector. The nucleons and the chiral partners belong to the ${(\mathbf{2},\mathbf{1})}_{+1}$ and ${(\mathbf{1},\mathbf{2})}_{-1}$ representations under ${({\mathrm{SU}(2)}_L,{\mathrm{SU}(2)}_R)}_{{\mathrm{U}(1)}_A}$:

$$\begin{array}{c}\hfill {\psi }_1^L:{(\mathbf{2},\mathbf{1})}_{-1},{\psi }_1^R:{(\mathbf{1},\mathbf{2})}_{+1},{\psi }_2^L:{(\mathbf{1},\mathbf{2})}_{+1},{\psi }_2^R:{(\mathbf{2},\mathbf{1})}_{-1}.\end{array}$$

(10)

We note that ${\psi }_1$ and ${\psi }_2$ carry the positive and negative parities, respectively:

$$\begin{array}{c}\hfill {\psi }_1\underset{P}{\to }{\gamma }_0{\psi }_1,{\psi }_2\underset{P}{\to }-{\gamma }_0{\psi }_2.\end{array}$$

(11)

Relevant Lagrangian for nucleons and their Yukawa interactions in the field M are given by

$$\begin{array}{cc}\hfill {\mathcal{L}}_N^{\mathrm{scalar}}=& \sum _{i=1,2}{\overline{\psi }}_{i}i{\gamma }^{\mu }{D}_{\mu }{\psi }_i-m_0\left({\overline{\psi }}_1^L{\psi }_2^R-{\overline{\psi }}_1^R{\psi }_2^L-{\overline{\psi }}_2^L{\psi }_1^R+{\overline{\psi }}_2^R{\psi }_1^L\right)\hfill \\ \hfill & -g_1\left({\overline{\psi }}_1^L{\tau }^2{(M^{†})}^{\mathrm{T}}{\tau }^2{\psi }_1^R+{\overline{\psi }}_1^R{\tau }^2{M}^{\mathrm{T}}{\tau }^2{\psi }_1^L\right)\hfill \\ \hfill & -g_2\left({\overline{\psi }}_2^L{\tau }^2{M}^{\mathrm{T}}{\tau }^2{\psi }_2^R+{\overline{\psi }}_2^R{\tau }^2{(M^{†})}^{\mathrm{T}}{\tau }^2{\psi }_2^L\right),\hfill \end{array}$$

(12)

where the covariant derivatives on the nucleon fields are defined as

$$\begin{array}{c}\hfill D_{\mu }{\psi }_{1,2}=({\partial }_{\mu }-i{V}_{\mu }){\psi }_{1,2},\end{array}$$

(13)

with

$$\begin{array}{c}\hfill V_{\mu }=\left(\begin{array}{cc}{\mu }_B+{\mu }_Q& 0\\ 0& {\mu }_B\end{array}\right){\delta }_{\mu }^0.\end{array}$$

(14)

Following Ref. [49], the vector mesons $\omega$ and $\rho$ are included based on the framework for hidden local symmetry (HLS) [73,74]. Here, instead of showing the forms as manifestly invariant under the HLS, we only show the relevant interaction terms among the baryons and vector mesons:

$$\begin{array}{cc}\hfill {\mathcal{L}}_N^{\mathrm{vector}}=& -\sum _{i=1,2}{\overline{\psi }}_i{\gamma }^{\mu }\left(g_{\omega NN}{\omega }_{\mu }+g_{\rho NN}\frac{\overrightarrow{\tau }}{2}{\overrightarrow{\rho }}_{\mu }\right){\psi }_i,\hfill \end{array}$$

(15)

where $\overrightarrow{\tau }$ is the Pauli matrix for isospin symmetry. The relevant potential terms for the vector mesons are expressed as

$$\begin{array}{cc}\hfill {\mathcal{L}}_V=& \frac{1}{2}{m}_{\omega }^2{\omega }_{\mu }{\omega }^{\mu }+\frac{1}{2}{m}_{\rho }^2{\overrightarrow{\rho }}_{\mu }·{\overrightarrow{\rho }}^{\mu }+{\lambda }_{\omega \rho }{g}_{\omega }^2{g}_{\rho }^2{\omega }_{\mu }{\omega }^{\mu }{\overrightarrow{\rho }}_{\nu }·{\overrightarrow{\rho }}^{\nu }.\hfill \end{array}$$

(16)

In the presence of $\omega$, the attractive ${\omega }^2$-${\rho }^2$ coupling with ${\lambda }_{\omega \rho }>0$ assists the appearance of the $\rho$ fields, reducing the symmetry energy associated with the isospin asymmetry, as discussed below. (Note that ${\lambda }_{\omega \rho }>0$ is needed for the VEVs of the $\omega$ and $\rho$ fields not to have a non-zero value in a vacuum.)

In the mean field approximation, the meson fields take

$$\begin{array}{cc}\hfill ⟨\sigma ⟩& =\sigma ,⟨{\omega }^{\mu }⟩=\omega {\delta }_0^{\mu },⟨{\rho }^{\mu }⟩=\rho \frac{{\tau }_3}{2}{\delta }_0^{\mu },\hfill \end{array}$$

(17)

where each mean field is assumed to be independent of the spatial coordinates. The thermodynamic potential in the hadronic matter is calculated as [49]

$$\begin{array}{cc}\hfill {\Omega }_{\mathrm{PDM}}=& V(\sigma ,{\sigma }_s)-V({\sigma }_0,{\sigma }_{s0})-\frac{1}{2}{m}_{\omega }^2{\omega }^2-\frac{1}{2}{m}_{\rho }^2{\rho }^2\hfill \\ \hfill & -{\lambda }_{\omega \rho }{\left(g_{\omega }\omega \right)}^2{\left(g_{\rho }\rho \right)}^2-2\sum _{i=\pm }\sum _{\alpha =p,n}{\int }_{\mathbf{p}}^{k_F^{\alpha ,i}}({\mu }_{\alpha }^{*}-E_{\mathbf{p}}^i),\hfill \end{array}$$

(18)

where $i=+$ and − label the ordinary nucleon $N(939)$ and the excited nucleon $N^{*}(1535)$, respectively. The energies of these nucleons are $E_{\mathbf{p}}^i=\sqrt{{\mathbf{p}}^2+m_i^2}$ with the momenta $\mathbf{p}$ and masses obtained by diagonalizing the Lagrangian (12),

$$\begin{array}{c}\hfill m_{\pm }=\sqrt{m_0^2+{\left(\frac{g_1+g_2}{2}\sigma \right)}^2}\mp \frac{g_2-g_1}{2}\sigma ,\end{array}$$

(19)

where $g_2>g_1$ is assumed so that $m_{+}<m_{-}$. The effective chemical potentials ${\mu }_p^{*}$ and ${\mu }_n^{*}$ are defined as

$$\begin{array}{c}\hfill {\mu }_p^{*}={\mu }_B+{\mu }_Q-g_{\omega NN}\omega -\frac{1}{2}{g}_{\rho NN}\rho ,{\mu }_n^{*}={\mu }_B-g_{\omega NN}\omega +\frac{1}{2}{g}_{\rho NN}\rho .\end{array}$$

(20)

In the integration above, the integral region is restricted as $\left|\mathbf{p}\right|<k_F^{\alpha ,i}$ where $k_F^{\alpha ,i}=\sqrt{{({\mu }_{\alpha }^{*})}^2-m_i^2}$ is the Fermi momentum for a nucleon i. In the above expression, we implicitly used the so-called “no-sea approximation”, assuming that the structure of the Dirac sea remains the same for the vacuum and medium for $n_B\lesssim 2n_0$. $V(\sigma ,{\sigma }_s)$ is the potential of the scalar mean fields given by

$$\begin{array}{cc}\hfill V(\sigma ,{\sigma }_s)=& -\frac{1}{2}{\overline{\mu }}^2\left({\sigma }^2+\frac{1}{2}{\sigma }_s^2\right)+\frac{1}{4}{\lambda }_4\left({\sigma }^4+\frac{1}{2}{\sigma }_s^4\right)-\frac{1}{6}{\lambda }_6\left({\sigma }^6+\frac{1}{2}{\sigma }_s^6\right)\hfill \\ \hfill & +{\lambda }_8\left(2{\sigma }^8+{\sigma }_s^8\right)+{\lambda }_{10}\left(2{\sigma }^{10}+{\sigma }_s^{10}\right)-2B{\sigma }^2{\sigma }_s-\left(2c{m}_u\sigma +c{m}_s{\sigma }_s\right).\hfill \end{array}$$

(21)

In Equation (18), we subtracted the potential in the vacuum $V({\sigma }_0,{\sigma }_{s0})$, for which the total potential in the vacuum is zero. Here, ${\sigma }_0$ and ${\sigma }_{s0}$ are related with the decay constants $f_{\pi }$ and $f_K$ as

$$\begin{array}{c}\hfill {\sigma }_0=f_{\pi },{\sigma }_{s0}=2f_K-f_{\pi }.\end{array}$$

(22)

Finally, we include leptons for the charge neutrality realized in NSs. The total thermodynamic potential of the hadronic matter for NSs takes the form

$$\begin{array}{c}\hfill {\Omega }_{\mathrm{H}}={\Omega }_{\mathrm{PDM}}+\sum _{l=e,\mu }{\Omega }_l,\end{array}$$

(23)

where ${\Omega }_l$ ($l=e,\mu$) are the thermodynamic potentials for leptons given by

$$\begin{array}{c}\hfill {\Omega }_l=-2{\int }_{\mathbf{p}}^{k_F^l}({\mu }_l-E_{\mathbf{p}}^l),k_F^l=\sqrt{{\mu }_l^2-m_l^2}.\end{array}$$

(24)

Here, the mean fields are determined by the following stationary conditions:

$$\begin{array}{c}\hfill 0=\frac{\partial {\Omega }_{\mathrm{H}}}{\partial \sigma }=\frac{\partial {\Omega }_{\mathrm{H}}}{\partial \omega }=\frac{\partial {\Omega }_{\mathrm{H}}}{\partial \rho }.\end{array}$$

(25)

In neutron stars, we impose the beta equilibrium and the charge neutrality condition represented as

$$\begin{array}{cc}\hfill {\mu }_e& ={\mu }_{\mu }=-{\mu }_Q,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill \frac{\partial {\Omega }_{\mathrm{H}}}{\partial {\mu }_Q}& =n_p-n_l=0.\hfill \end{array}$$

(27)

The mean fields and charge chemical potential are determined as functions of ${\mu }_B$. After substituting these values into ${\Omega }_{\mathrm{H}}$, we obtain the pressure in the hadronic matter as a function of ${\mu }_B$,

$$P_{\mathrm{H}}({\mu }_B)=-{\Omega }_{\mathrm{H}}({\mu }_B).$$

(28)

2.3. Determination of Model Parameters

In this subsection, we determine the parameters in the PDM to reproduce the masses and decay constants in a vacuum and the saturation properties in nuclear matter. In nuclear matter, the energy per nucleon (energy density) $\epsilon$ is given as a function of the baryon number density $n_B$ and the isospin asymmetry $\delta =\frac{n_p-n_n}{n_p+n_n}$. The energy density is expanded around the normal nuclear density $n_0=0.16{\mathrm{fm}}^{-3}$ and the symmetric matter $\delta =0$ as

$$\begin{array}{c}\hfill \epsilon =-B_0+\frac{K_0}{2}{\left(\frac{n_B-n_0}{3n_0}\right)}^2+{\delta }^2\left(S_0+L_0\frac{n_B-n_0}{3n_0}\right)+\mathrm{higher}\mathrm{order},\end{array}$$

(29)

where $B_0,K_0,S_0,L_0$ denote the binding energy, incompressibility, symmetry energy, and slope parameter, respectively, as shown in Figure 2. The parameter $K_0$ measures the curvature of the energy density at the normal nuclear density:

$$\begin{array}{c}\hfill K_0=9n_0^2\frac{{\partial }^2\epsilon }{\partial n_B^2}{|}_{n_B=n_0,\delta =0}.\end{array}$$

(30)

The symmetry energy $S_0$ is calculated as

$$\begin{array}{c}\hfill S_0=\frac{1}{2}\frac{{\partial }^2\epsilon }{\partial {\delta }^2}{|}_{n_B=n_0,\delta =0}.\end{array}$$

(31)

The parameter $L_0$ characterizes the slope of the symmetry energy at a normal nuclear density:

$$\begin{array}{c}\hfill L=\frac{3n_0}{2}\frac{{\partial }^3\epsilon }{\partial n_B\partial {\delta }^2}{|}_{n_B=n_0,\delta =0}.\end{array}$$

(32)

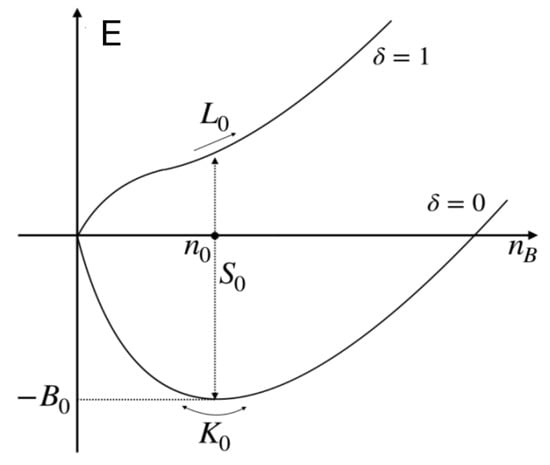
Figure 2. Density dependence of energy per nucleon for the symmetric matter (indicated by $\delta =0$) and the pure neutron matter ($\delta =1$).

We summarize the input values that we used in this review in Table 1 and Table 2.

Table 1. Physical inputs in a vacuum in units of MeV.

${\mathit{m}}_{\mathit{\pi }}$	${\mathit{m}}_{\mathit{K}}$	${\mathit{f}}_{\mathit{\pi }}$	${\mathit{f}}_{\mathit{K}}$	${\mathit{m}}_{\mathit{\omega }}$	${\mathit{m}}_{\mathit{\rho }}$	${\mathit{m}}_{+}$	${\mathit{m}}_{-}$
140	494	92.4	109	783	776	939	1535

Table 2. Saturation properties used to determine the model parameters: the saturation density $n_0$, the binding energy $B_0$, the incompressibility $K_0$, symmetry energy $S_0$, and the slope parameter $L_0$.

${\mathit{n}}_0$ [fm−3]	${\mathit{E}}_{\mathbf{Bind}}$ [MeV]	${\mathit{K}}_0$ [MeV]	${\mathit{S}}_0$ [MeV]	${\mathit{L}}_0$ [MeV]
0.16	16	240	31	57.7

We first use the masses of the $\omega$ and $\rho$ mesons to fix $m_{\omega }$ and $m_{\rho }$ in Equation (16). The parameters $c{m}_u=c{m}_d$ and $c{m}_s$ are fixed from $m_{\pi }{f}_{\pi }$ and $m_K{f}_K$ as

$$\begin{array}{c}\hfill 2c{m}_u=m_{\pi }^2{f}_{\pi }^2,c(m_u+m_s)=m_K^2{f}_K^2.\end{array}$$

(33)

The values of $g_1$ and $g_2$ are determined from the masses of the nucleons in a vacuum through Equation (19) with $\sigma$ replaced by $f_{\pi }$. There are still nine parameters to be determined:

$${\overline{\mu }}^2,{\lambda }_4,{\lambda }_6,{\lambda }_8,{\lambda }_{10},B,{\lambda }_{\omega \rho },g_{\omega NN},g_{\rho NN}.$$

(34)

These parameters are tuned to reproduce the saturation properties listed in Table 2. It turns out that there are some degeneracies related to the choice of parameters ${\lambda }_8,{\lambda }_{10}$, and B.

In Figure 3, we show the range between ${\lambda }_8$ and ${\lambda }_{10}$ needed to satisfy the saturation properties. Finally, we fit parameter B to reproduce the masses of the $\eta$ and ${\eta }^{\prime }$ mesons. Here, we omit the details and show the determined values of the model parameters only for $m_0=700$ MeV as a typical example in Table 3. We refer to Ref. [67] for the details of the determination and the values of the model parameters for other choices of $m_0$.

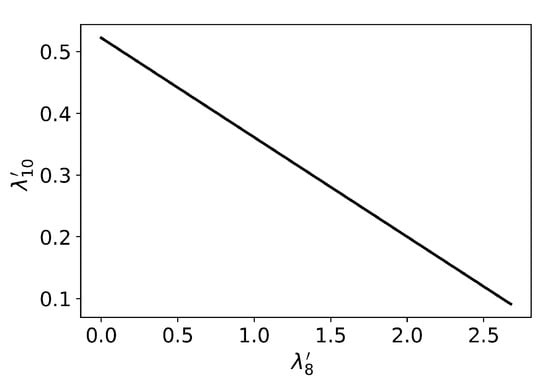
Figure 3. Restricted combination of ${\lambda }_8$ and ${\lambda }_{10}$ after fixing the value of ${\sigma }_s$ with $m_0=700\mathrm{MeV}$. We normalize the couplings as ${\lambda }_8^{\prime }={\lambda }_8{f}_{\pi }^4$ and ${\lambda }_{10}^{\prime }={\lambda }_{10}{f}_{\pi }^6$.

Table 3. Model parameters determined from the saturation properties. When $B=600$ MeV, solutions satisfying the saturation properties can be found only in the range: $0\le {\lambda }_8^{{}^{\prime }}\le 2.677$. Here, we list the boundary values as typical examples; ${\lambda }_8^{\prime }=0$ is the minimum boundary, and ${\lambda }_8^{\prime }=2.677$ is the maximum boundary.

	${\mathit{m}}_0=700$ [MeV]	${\mathit{\lambda }}_8^{\prime }=0$	${\mathit{\lambda }}_8^{\prime }=2.677$
	$g_1$	$7.81$	$7.81$
	$g_2$	$14.26$	$14.26$
	${\overline{\mu }}^2/f_{\pi }^2$	$23.21$	$41.35$
	${\lambda }_4$	$133.4$	$194.7$
$B=600$ [MeV]	${\lambda }_6{f}_{\pi }^2$	$82.71$	$160.1$
	${\lambda }_{\omega \rho }$	$0.3047$	$0.3636$
	${\lambda }_{10}{f}_{\pi }^6$	$0.5221$	$0.09091$
	$g_{\omega NN}$	$5.437$	$5.142$
	$g_{\rho NN}$	$9.577$	$9.541$
	$g_1$	$7.81$	$7.81$
	$g_2$	$14.26$	$14.26$
	${\overline{\mu }}^2/f_{\pi }^2$	$39.98$	$55.24$
	${\lambda }_4$	$94.02$	$149.3$
$B=0$ [MeV]	${\lambda }_6{f}_{\pi }^2$	$62.23$	$136.4$
	${\lambda }_{\omega \rho }$	$0.2442$	$0.2988$
	${\lambda }_{10}{f}_{\pi }^6$	$0.5221$	$0.09091$
	$g_{\omega NN}$	$6.287$	$5.957$
	$g_{\rho NN}$	$10.19$	$10.21$

2.4. Softening of the EOS by the Effect of Anomaly

Here, we briefly explain the mechanism for the effect of anomaly to soften the EOS in the PDM. We refer to Ref. [67] for the details.

One of the key features is that both the condensate $\sigma$ and ${\sigma }_s$ are enhanced when the effect of anomaly is included. Their values in a vacuum are actually increased with an increasing B. Since the mass of the $\sigma$ meson, $m_{\sigma }$, is proportional to $\sigma$, the mass is increased, as shown in Figure 4. In the potential picture for nucleons, the $\sigma$ meson mediates the attractive force among nucleons in the matter so that the larger $m_{\sigma }$ leads to a shorter effective range of the attraction with a weaker overall strength. The repulsive $\omega$ interaction should be weaker to balance the weaker attraction. As a result, the weaker repulsion for a larger B makes the softer EOS in the density region higher than the normal nuclear density.

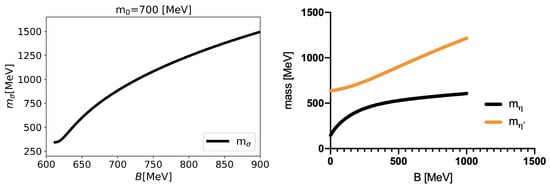
Figure 4. B dependence of $m_{\sigma }$ (left panel), $m_{\eta }$, and $m_{{\eta }^{\prime }}$ (right panel) for $m_0=700\mathrm{MeV}$.

3. Quark Matter from an NJL-Type Model

Following Ref. [27], we construct quark matter from an NJL-type effective model of quarks with the four-Fermi interactions that cause color-superconductivity as well as the spontaneous chiral symmetry breaking. The Lagrangian is given by

$$\begin{array}{cc}{\mathcal{L}}_{\mathrm{CSC}}\hfill & ={\mathcal{L}}_0+{\mathcal{L}}_{\sigma }+{\mathcal{L}}_{\mathrm{d}}+{\mathcal{L}}_{\mathrm{KMT}}+{\mathcal{L}}_{\mathrm{vec}},\hfill \end{array}$$

(35)

where

$$\begin{array}{ll}\hfill {\mathcal{L}}_0& =\overline{q}(i{\gamma }^{\mu }{\partial }_{\mu }-{\widehat{m}}_q+{\gamma }_{\mu }{\widehat{A}}^{\mu })q,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\sigma }& =G\sum _{A=0}^8[{(\overline{q}{\tau }_{A}q)}^2+{(\overline{q}i{\gamma }_5{\tau }_{A}q)}^2],\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{d}}& =H\sum _{A,B=2,5,7}\left[(\overline{q}{\tau }_A{\lambda }_{B}C{\overline{q}}^t)(q^{t}C{\tau }_A{\lambda }_{B}q)\right.+\left.(\overline{q}i{\gamma }_5{\tau }_A{\lambda }_{B}C{\overline{q}}^t)(q^{t}Ci{\gamma }_5{\tau }_A{\lambda }_{B}q)\right],\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{KMT}}& =-K[\underset{f}{det}\overline{q}(1-{\gamma }_5)q+\underset{f}{det}\overline{q}(1+{\gamma }_5)q],\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{vec}}& =-g_V(\overline{q}{\gamma }^{\mu }q)(\overline{q}{\gamma }_{\mu }q),\hfill \end{array}$$

(40)

with ${\widehat{A}}^{\mu }$ being the collection of chemical potentials

$$\begin{array}{c}\hfill {\widehat{A}}^{\mu }=({\mu }_q+{\mu }_3{\lambda }_3+{\mu }_8{\lambda }_8+{\mu }_{Q}Q){\delta }_0^{\mu }.\end{array}$$

(41)

Here, ${\lambda }_a$ are Gell-Mann matrices in color space, where ${\tau }_0={\mathbf{1}}_{3\times 3}\sqrt{2/3}$ and ${\tau }_A(A=1\cdots 8)$ are the Gell-Mann matrices, and $Q=\frac{1}{2}{\tau }_3+\frac{1}{2\sqrt{3}}{\tau }_8=\mathrm{diag}(2/3,-1/3,-1/3)$ is a charge matrix in flavor space. Meanwhile, ${\tau }_0={\mathbf{1}}_{3\times 3}\sqrt{2/3}$ and ${\tau }_A(A=1\cdots 8)$ are the Gell-Mann matrices for the flavor. For the coupling constants G and K, as well as the cutoff $\Lambda$, we use $G{\Lambda }^2=1.835$, $K{\Lambda }^5=9.29$, and $\Lambda =631.4$ MeV, which successfully reproduce the hadron phenomenology at a low energy [26,75]. The mean fields are introduced as

$$\begin{array}{cc}\hfill {\sigma }_f& =⟨{\overline{q}}_f{q}_f⟩,(f=u,d,s),\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill d_j& =⟨q^{t}C{\gamma }_5{R}_{j}q⟩,(j=1,2,3),\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill n_q& =\sum _{f=u,d,s}⟨q_f^{†}{q}_f⟩,\hfill \end{array}$$

(44)

where $(R_1,R_2,R_3)=({\tau }_7{\lambda }_7,{\tau }_5{\lambda }_5,{\tau }_2{\lambda }_2)$. The resultant thermodynamic potential is calculated as

$$\begin{array}{cc}\hfill {\Omega }_{\mathrm{CSC}}& ={\Omega }_s-{\Omega }_s[{\sigma }_f={\sigma }_f^0,d_j=0,{\mu }_q=0]+{\Omega }_c-{\Omega }_c[{\sigma }_f={\sigma }_f^0,d_j=0],\hfill \end{array}$$

(45)

where

$$\begin{array}{cc}\hfill {\Omega }_s& =-2\sum _{\alpha =1}^{18}{\int }_{\mathbf{p}}^{\Lambda }\frac{{\epsilon }_{\alpha }}{2},\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\Omega }_c& =\sum _{f=u,d,s}2G{\sigma }_i^2+\sum _{j=1,2,3}H{d}_j^2-4K{\sigma }_u{\sigma }_d{\sigma }_s-g_V{n}_q^2.\hfill \end{array}$$

(47)

In Equation (46), ${\epsilon }_{\alpha }$ are energy eigenvalues of the inverse propagator in the Nambu–Gor’kov basis given by

$$\begin{array}{c}\hfill S^{-1}(k)=\left(\begin{array}{cc}{\gamma }_{\mu }{k}^{\mu }-\widehat{M}+{\gamma }^0\widehat{\mu }& \hfill {\gamma }_5\sum _i{\Delta }_i{R}_i\\ \hfill -{\gamma }_5\sum _i{\Delta }_i^{*}{R}_i& {\gamma }_{\mu }{k}^{\mu }-\widehat{M}-{\gamma }^0\widehat{\mu }),\hfill \end{array}\right)\end{array}$$

(48)

where

$$\begin{array}{cc}\hfill M_i& =m_i-4G{\sigma }_i+K\sum _{j,k=u,d,s}\left|{ϵ}_{ijk}\right|{\sigma }_j{\sigma }_k,(i=u,d,s),\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill {\Delta }_j& =-2H{d}_j,(j=1,2,3),\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill \widehat{\mu }& ={\mu }_q-2g_V{n}_q+{\mu }_3{\lambda }_3+{\mu }_8{\lambda }_8+{\mu }_{Q}Q.\hfill \end{array}$$

(51)

The inverse propagator $S^{-1}(k)$ in Equation (48) is a $72\times 72$ matrix in terms of the color, flavor, spin, and Nambu–Gorkov basis and has 72 eigenvalues. $M_{u,d,s}$ are the constituent masses of the $u-,d-,s$-quarks, and ${\Delta }_{1,2,3}$ are the color-superconducting gap energies. In the high-density region, $n_B\gtrsim 5n_0$, and their ranges are $M_{u,d}\approx 50$–100 MeV, $M_s\approx$ 250–300 MeV, and ${\Delta }_{1,2,3}\approx$ 200–250 MeV [26]. We note that the inverse propagator matrix does not depend on the spin and that the charge conjugation invariance relates two eigenvalues. Then, there are 18 independent eigenvalues at most.

The entire thermodynamic potential is constructed by adding the lepton contribution in Equation (24) as

$$\begin{array}{c}\hfill {\Omega }_{\mathrm{Q}}={\Omega }_{\mathrm{CSC}}+\sum _{l=e,\mu }{\Omega }_l.\end{array}$$

(52)

The chiral condensates ${\sigma }_i$ ($i=u,d,s$) and the diquark condensates $d_j$ ($j=1,2,3$) are determined from the gap equations:

$$\begin{array}{c}\hfill \frac{\partial {\Omega }_{\mathrm{Q}}}{\partial {\sigma }_i}=0,\frac{\partial {\Omega }_{\mathrm{Q}}}{\partial d_j}=0.\end{array}$$

(53)

The relevant chemical potentials, other than the baryon number density, are determined from the beta equilibrium condition in Equation (26) combined with the conditions for electromagnetic charge neutrality and color charge neutrality expressed as

$$\begin{array}{c}\hfill n_j=-\frac{\partial {\Omega }_{\mathrm{Q}}}{\partial {\mu }_j}=0,(j=3,8,Q).\end{array}$$

(54)

The baryon number density $n_B$ is equal to three times the quark number density given by

$$\begin{array}{c}\hfill n_q=-\frac{\partial {\Omega }_{\mathrm{Q}}}{\partial {\mu }_q},\end{array}$$

(55)

where ${\mu }_q$ is the quark number chemical potential, which is $1/3$ of the baryon number chemical potential. Substituting the above conditions, we obtain the pressure of the system as

$$P_{\mathrm{Q}}=-{\Omega }_{\mathrm{Q}}.$$

(56)

Softening of the EOS by the Effect of Anomaly in NJL-Type Model

Here, we briefly explain how the anomaly softens the EOS in the NJL-type quark model. For simplicity, we set $H=0$ and omit the effects of diquarks. In the KMT interaction in Equation (39), the coefficient K represents the strength of the U(1)${}_A$ anomaly. The anomaly assists the chiral symmetry breaking and lowers the ground-state energy in a vacuum; a larger K leads to chiral condensates that are greater in magnitude, as shown in the left panel of Figure 5.

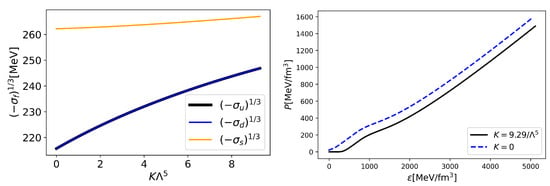
Figure 5. K dependence of chiral condensates (left panel) and the energy dependence of pressure for $H/G=0$ and $g_V/G=0.1$ (right panel).

With the chiral restoration, the system loses the energetic benefit of having the chiral condensates. Such release of the energy is more radical with the anomaly than without it. As one can see from the thermodynamic relation $P=-\epsilon +{\mu }_q{n}_q$, a larger energy $\epsilon$ with a stronger anomaly leads to a smaller pressure, i.e., softening. In other words, with the anomaly, we have to add a larger “bag constant” to the energy density, but we must subtract it from the pressure. We show the resulting EOSs for $H/G=0$ and $g_V/G=0.1$ in the right panel of Figure 5.

4. Interpolated EOSs and M-R Relations of NSs

4.1. Interpolation of EOSs

In this subsection, we briefly explain how to interpolate the EOS for the hadronic matter to that for the quark matter constructed in previous sections. Following Ref. [26], we assume that the hadronic matter is realized in the low-density region $n_B<2n_0$ and use the pressure constructed in Equation (28). In the high-density region $n_B>5n_0$, the pressure given in Equation (56) for the quark matter is used. In the intermediate region $2n_0<n_B<5n_0$, we assume that the pressure is expressed by a fifth-order polynomial of ${\mu }_B$ as (It is important to create interpolation for the correct set of variables, either $P({\mu }_B)$ or $\epsilon (n_B)$, from which one can deduce all the thermodynamic quantities by taking derivatives [26]. Other combinations, e.g., $P(\epsilon )$, can not be used to derive $n_B$ and hence would miss some constraints.)

$$\begin{array}{c}\hfill P_{\mathrm{I}}({\mu }_B)=\sum _{i=0}^5{C}_i{\mu }_B^i.\end{array}$$

(57)

Following the quark–hadron continuity scenario, we demand that the interpolating EOS matches the quark and hadronic EOSs up to the second derivatives (otherwise, we would have the first- or second-order phase transitions at the boundaries). The six parameters $C_i$ ($i=1,\dots ,6$) are determined from the boundary conditions given by

$$\begin{array}{c}\hfill \frac{{\mathrm{d}}^n{P}_{\mathrm{I}}}{{(\mathrm{d}{\mu }_B)}^n}{|}_{{\mu }_{BL}}=\frac{{\mathrm{d}}^n{P}_{\mathrm{H}}}{{(\mathrm{d}{\mu }_B)}^n}{|}_{{\mu }_{BL}},\frac{{\mathrm{d}}^n{P}_{\mathrm{I}}}{{\mathrm{d}({\mu }_B)}^n}{|}_{{\mu }_{BU}}=\frac{{\mathrm{d}}^n{P}_{\mathrm{Q}}}{{(\mathrm{d}{\mu }_B)}^n}{|}_{{\mu }_{BU}},(n=0,1,2),\end{array}$$

(58)

where ${\mu }_{BL}$ is the chemical potential corresponding to $n_B=2n_0$ and ${\mu }_{BU}$ to $n_B=5n_0$.

In addition to these boundary conditions, the interpolated pressure must obey the causality constraint, i.e., the sound velocity,

$$\begin{array}{c}\hfill c_s^2=\frac{\mathrm{d}P}{\mathrm{d}\epsilon }=\frac{n_B}{{\mu }_B{\chi }_B},\end{array}$$

(59)

where $n_B=\frac{\mathrm{d}P}{\mathrm{d}{\mu }_B}$ and ${\chi }_B=\frac{{\mathrm{d}}^{2}P}{\mathrm{d}{\mu }_B^2}$ to be less than the light velocity. This condition is more difficult to satisfy for the combination of a softer nuclear EOS and a stiffer quark matter EOS, since such a soft-to-stiff combination requires a larger slope in $P(\epsilon )$.

We show an example of the interpolated pressure in Figure 6 with the parameter set ${\lambda }_8^{\prime }=2.677,{\lambda }_{10}^{\prime }=0.09091$ for $m_0=700$ MeV, and $B=600\mathrm{MeV}$ for the PDM and the two parameter sets $(H/G,g_V/G)=(1.45,0.4)$ and $(1.45,0.5)$ for the quark matter. Both plots (a) and (b) in Figure 6 are smoothly connected by the construction, but the set $(H/G,g_V/G)=(1.45,0.4)$ violates causality, as seen in Figure 7, and, therefore, must be excluded.

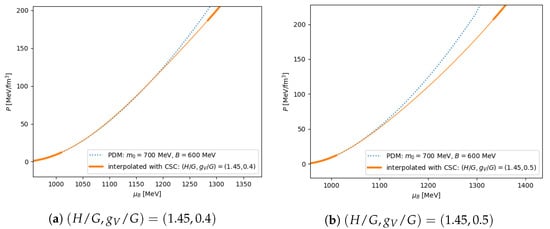
Figure 6. Pressure $P({\mu }_B)$ of the PDM and the unified equations of state. For the PDM, we chose ${\lambda }_8^{\prime }=2.677,{\lambda }_{10}^{\prime }=0.09091$ for $m_0=700$ MeV, and $B=600\mathrm{MeV}$ as a typical parameter set and, for the quark models, we used $(H/G,g_V/G)=(1.45,0.4)$ and $(1.45,0.5)$. The thick curves in the unified equations of state are used to mark the pure hadronic and quark parts.

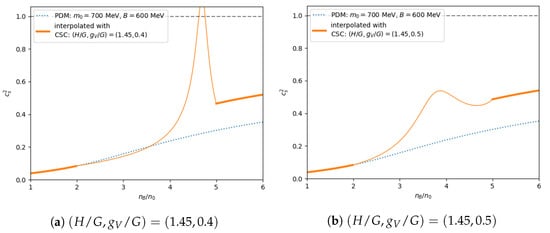
Figure 7. Squared speed of sound $c_s^2$ for $(H/G,g_V/G)=(1.45,0.4)$ and (1.45, 0.5). Curves are same as in Figure 6.

The $c_s^2$ exceeding the conformal value, $c_s^2=1/3$ and the subsequent reduction within the interval 2-$5n_0$ are the characteristic features of the crossover models [24,25,26,27,28]. In the nuclear domain, the sound velocity is small, $c_s^2\sim 0.1$, while the natural size is $c_s^2\sim 1/3$ in the quark matter. In the intermediate region, $c_s^2$ makes a peak. How to approach the conformal limit is a subject under intensive discussions (see Refs. [76,77,78,79,80]).

Figure 8 shows the allowed combinations of $(H,g_V)$ for several choices of $m_0$.

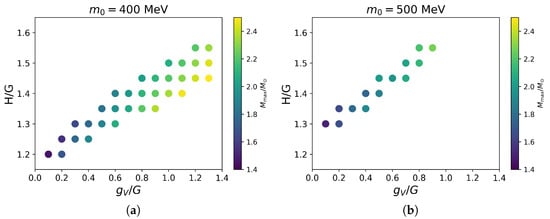
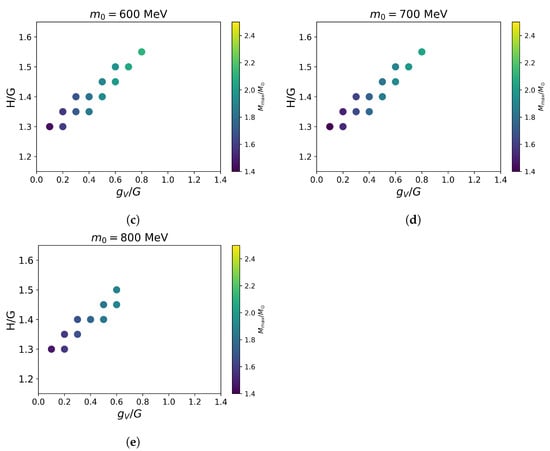
Figure 8. Allowed combinations of $(H,g_V)$ for $m_0=400–800\mathrm{MeV}$. The color of the circle shows the maximum mass of neutron stars obtained from the corresponding parameters, as indicated by a vertical bar on the right side of each figure.

Here, we fix the parameters in the PDM to $B=600$ MeV and ${\lambda }_8^{\prime }=0$, which determines the value of ${\lambda }_{10}^{\prime }$ as summarized in Section 2.3 (e.g., ${\lambda }_{10}^{\prime }=0.5221$ for $m_0=700$ MeV). The parameter ${\lambda }_{\omega \rho }$ is set to reproduce the slope parameter as $L_0=57.7$ MeV. In all cases, the allowed values of H and $g_V$ have a positive correlation; for a larger $g_V$, we need to increase the value of H [27]. For $m_0=800$ MeV, the maximum masses for all the combinations are below $2M_{\odot }$, leading to the conclusion that $m_0=800$ MeV should be excluded from the current setup of the PDM parameters. The details of the positive correlation between H and $g_V$ depend on the low-density constraint and the choice of $m_0$. As we mentioned in Introduction, the EOS in hadronic matter is softer for a larger $m_0$. Correspondingly, the parameter $g_V$, which makes the quark matter EOS stiff, should not be too large for causal interpolations; for a larger $m_0$, the acceptable $g_V$ tends to appear at lower values. The typical values of $(H,g_V)$ are greater than expected from the Fierz transformation for which $(H,g_V)=(0.5,0.5)G$ (see, e.g., Ref. [81]). Such choices were used in the hybrid quark–hadron matter EOS with first-order phase transitions, but they tend to lead to predictions that are incompatible with the $2M_{\odot }$ constraints.

4.2. M-R Relations of NSs

With the unified EOS explained so far, we now calculate the M-R relations of NSs by solving the Tolman–Oppenheimer–Volkoff (TOV) equation [82,83],

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathrm{d}P}{\mathrm{d}r}& =-G\frac{(\epsilon +P)(m+4\pi r^{3}P)}{r^2-2Gmr},\hfill \\ \hfill \frac{\mathrm{d}m}{\mathrm{d}r}& =4\pi r^2\epsilon ,\hfill \end{array}\end{array}$$

(60)

where G is the Newton constant; r is the distance from the center of a neutron star; and P, m, and $\epsilon$ are the pressure, mass, and energy density as functions of r:

$$\begin{array}{c}\hfill P=P(r),m=m(r),\epsilon =\epsilon (r).\end{array}$$

(61)

The radius R is determined by the condition $P(R)=0$ and the mass M by $M=m(R)$. To estimate the radii of NSs with an accuracy of better than ∼0.5 km, we need to include the crust EOS. We use the BPS EOS [84] for the outer and inner crust parts. (The BPS EOS is usually referred to as the EOS for the outer crust, but it also contains the BPP EOS [84] for the inner crust. At $n_B\le 0.1{\mathrm{fm}}^{-3}$ and at $n_B\ge 0.1{\mathrm{fm}}^{-3}$, we use our unified EOS from nuclear liquid to quark matter. For a given central density, we obtain the corresponding M-R point, and the sequence of such points forms the M-R curves.)

In order to study the relation between microscopic parameters and M-R relations, below, we examine the impacts of the PDM EOS, the dependence on the ${\omega }^2{\rho }^2$ coupling (${\lambda }_{\omega \rho }$), the chiral invariant mass $m_0$, and the anomaly strength B for a given set of quark matter parameters $(H,g_V)$.

We first study the effect of the ${\omega }^2{\rho }^2$ interaction. We fix $m_0=500$ MeV and $B=600$ MeV and vary ${\lambda }_{\omega \rho }$, which leads to changes in the slope parameter $L_0$ in the symmetry energy. We examine the cases with $L_0=40,57.7$ and 80 MeV since the value of $L_0$ still has uncertainty, which is being intensively studied [85]. The resultant M-R relation is shown in Figure 9. The M-R relations with a core density smaller than $2n_0$ (and larger than 5$n_0$) are emphasized by thick curves in the low (high) mass region. The ${\lambda }_{\omega \rho }>0$ corresponds to attractive correlations that reduce $L_0$ and soften the EOS in the nuclear domain. For $L_0=40,57.7$ and 80 MeV, the radii of $1.4M_{\odot }$ NS are $\simeq 11.05$ km, $\simeq 11.2$ km, and ≃12.1 km, respectively A precise determination of the slope parameter in the future will help us to further constrain the NS properties, especially the radii.

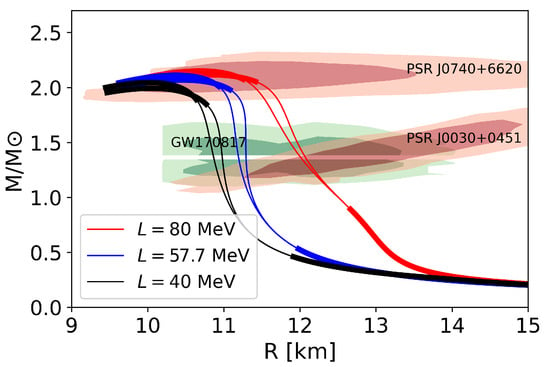
Figure 9. Dependence of M-R relations for $m_0=500$ MeV on the slope parameter. Red curves are connected to the NJL parameters $(H,g_V)/G=$ (1.55, 1.0), (1.50, 0.9); blue curves to (1.55, 0.9), (1.50, 0.8); black curves to (1.55, 0.8), (1.50, 0.7).

In the following analysis, we fix the value $L_0=57.7$ MeV and the parameter ${\lambda }_8^{\prime }=0$. The value of ${\lambda }_{10}^{\prime }$ is determined as explained in Section 2.3. For example, ${\lambda }_{10}^{\prime }=0.5221$ is obtained for the $m_0=700$ MeV below. Then, we examine the effects of the U(1)${}_A$ anomaly on the M-R relation. In Figure 10a, we show the M-R curves for several values of the anomaly strength B, with the NJL parameters $(H,g_V)$ leading to the largest and second largest maximum masses for a given set of the PDM parameters. This shows that, due to the softening effect of the anomaly, as explained in Section 2.4, even the stiffest connection for $m_0=800$ MeV with $B=600$ MeV is unable to satisfy the maximum mass constraints. The effect of the anomaly in general softens the EOS from low to high densities and increasing B from 0 to 600 MeV (while retuning the other parameters to reproduce the nuclear saturation properties) reduces both the M and R by a few percents. In Figure 10b, we set $B=600$ MeV to fit the ${\eta }^{\prime }$ mass and examine several values of $m_0$. These results should be regarded as the representatives of the present review.

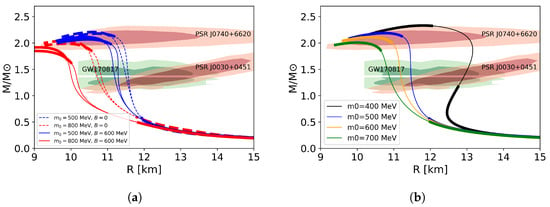
Figure 10. Mass–radius relations for different $m_0$ in different parameter setting. (a) $B=$ 0, 600 MeV for $m_0=$ 500, 800 MeV; (b) $B=600$ MeV for different $m_0$. NJL parameters $(H,g_V)/G$ are chosen to be (1.45, 1.3)${}_{m_0=400\mathrm{MeV}}$, (1.6, 1.3)${}_{m_0=500\mathrm{MeV}}$, (1.6, 1.3)${}_{m_0=600\mathrm{MeV}}$, and (1.6, 1.2)${}_{m_0=700\mathrm{MeV}}$.

In this review, the mass of the millisecond pulsar PSR J0740+6620 [16]

$$\begin{array}{c}\hfill M_{\mathrm{TOV}}^{\mathrm{lowest}}={2.08}_{-0.07}^{+0.07}{M}_{\odot },\end{array}$$

(62)

is regarded as the lower bound for the maximum mass, which is shown by upper red-shaded area in Figure 9 and Figure 10. Actually, the lower bound may be even significantly higher; the recent analyses for the black-widow binary pulsar PSR J0952-0607 suggest a maximum mass of $2.35\pm 0.17M_{\odot }$ [86]. Meanwhile, there are constraints, $M_{\max }\lesssim {2.16}_{-0.15}^{+0.17}{M}_{\odot }$, from the gamma-ray burst GRB170817A associated with the GW170817 event (under the assumption that the post-merger of GW170817 is a hypermassive NS). If the maximum mass is indeed $\sim 2.3M_{\odot }$ or higher, we will need to allow for a much stiffer low-density EOS with which a much stiffer quark EOS becomes possible. The analyses based on another criterion will be presented elsewhere.

Another important constraint comes from NS radii. We show that the constraints on the radii obtained from the LIGO-Virgo [87,88] as green-shaded areas on the middle left (More precisely, the LIGO-Virgo constrains the tidal deformability $\tilde{\Lambda }$, which is the function of the tidal deformability of each neutron star (${\Lambda }_1$ and ${\Lambda }_2$) and the mass ratio $q=M_2/M_1$. However, for EOSs which do not lead to a large variation in radii for $M\gtrsim 1M_{\odot }$, $\tilde{\Lambda }$ is insensitive to q. In fact, the radii of neutron stars and $\tilde{\Lambda }$ can be strongly correlated (for more details, see Refs. [89,90]), and, for our purposes, it is sufficient to directly use the estimates on the radii given in Ref. [88], rather than $\tilde{\Lambda }$.) and from the NICER in Ref. [19] as red-shaded areas on the middle right. The inner contour of each area contains $68\%$ of the posterior probability ($1\sigma$), and the outer one contains $95\%$ ($2\sigma$). These values (plus another NICER result in Ref. [20]) are summarized in Table 4.

Table 4. Radius constraints for neutron stars for $\simeq 1.4M_{\odot }$ and $\simeq 2.1M_{\odot }$ NSs.

	Radius [km]	Mass [${\mathit{M}}_{\odot }$]
GW170817 (primary)	${11.9}_{-1.4}^{+1.4}$	${1.46}_{-0.10}^{+0.12}$
GW170817 (second)	${11.9}_{-1.4}^{+1.4}$	${1.27}_{-0.09}^{+0.09}$
J0030+0451 (NICER [19])	${13.02}_{-1.06}^{+1.24}$	${1.44}_{-0.14}^{+0.15}$
J0030+0451 (NICER [20])	${12.71}_{-1.19}^{+1.14}$	${1.34}_{-0.16}^{+0.15}$
PSR J0740+6620 (NICER [21])	${12.35}_{-0.75}^{+0.75}$	${2.08}_{-0.07}^{+0.07}$
PSR J0740+6620 (NICER [22])	${12.39}_{-0.98}^{+1.30}$	${2.08}_{-0.07}^{+0.07}$

From all the constraints, we restrict the chiral invariant mass as

$$\begin{array}{c}\hfill 400\mathrm{MeV}\lesssim m_0\lesssim 700\mathrm{MeV}.\end{array}$$

(63)

which is updated from those in the the original work of Ref. [66], 600 MeV $\lesssim m_0\lesssim 900$ MeV, which corresponds to the set ${\lambda }_8^{\prime }={\lambda }_{10}^{\prime }=0$ and $B=0$ in the present model.

5. Chiral Condensates in Crossover

The method of interpolation can be used not only to construct a unified EOS but also to calculate microscopic quantities, such as condensates and matter composition. In the hadronic and quark matter domains, we consider the generating functional with external fields coupled to the quantities of interest and then interpolate two functionals. The microscopic quantities are then extracted by differentiating the unified generating functional. We first review the computations in the hadronic and quark matter domains and then turn to computations in the crossover region.

5.1. Chiral Condensates in the PDM

The chiral condensate in the PDM can be calculated by differentiating a thermodynamic potential with respect to the current quark mass. In the present model, the explicit chiral symmetry breaking enters only through the $V_{SB}$ term in Equation (8), which leads to $-\left(2c{m}_u\sigma +c{m}_s{\sigma }_s\right)$ as in Equation (21). There may be mass dependence in the other coupling constants in front of the higher powers in the meson fields, but such couplings exist already at $m_q=0$, and the finite $m_q$ is supposed to give only minor corrections. Hence, we neglect the $m_q$ dependence, except for the terms in $V_{SB}$. Using the Gell-Mann–Oakes–Renner relation, the explicit symmetry breaking term can be written as

$$\begin{array}{c}\hfill {\Omega }_{\mathrm{ESB}}=-\left(2c{m}_u\sigma +c{m}_s{\sigma }_s\right)=m_q{⟨(\overline{u}u+\overline{d}d)⟩}_0\frac{\sigma }{f_{\pi }}+m_s{⟨\overline{s}s⟩}_0\frac{{\sigma }_s}{{\sigma }_{s0}},\end{array}$$

(64)

where ${⟨(\overline{u}u+\overline{d}d)⟩}_0$ and ${⟨\overline{s}s⟩}_0$ are the chiral condensates in a vacuum. The in-medium chiral condensates are obtained as

$$\begin{array}{cc}\hfill & ⟨(\overline{u}u+\overline{d}d)⟩\equiv \frac{\partial {\Omega }_{\mathrm{ESB}}}{\partial m_q}={⟨(\overline{u}u+\overline{d}d)⟩}_0\frac{\sigma }{f_{\pi }},\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill & ⟨\overline{s}s⟩\equiv \frac{\partial {\Omega }_{\mathrm{ESB}}}{\partial m_s}={⟨\overline{s}s⟩}_0\frac{{\sigma }_s}{{\sigma }_{s0}},\hfill \end{array}$$

(66)

where we neglected the $m_q$ and $m_s$ dependences of ${⟨(\overline{u}u+\overline{d}d)⟩}_0$ and ${⟨\overline{s}s⟩}_0$, which are of higher orders in $m_q/M_q$ and $m_s/M_s$.

In the following Section 5.1.1, we examine how $\sigma$ varies as the baryon density increases, and we study the in-medium $⟨(\overline{u}u+\overline{d}d)⟩$ condensate in Section 5.1.2. We postpone discussions on the strange quark condensate $⟨\overline{s}s⟩$ to Section 5.3 since changes in $⟨\overline{s}s⟩$ at $n_B\le 2n_0$, which are induced only through the anomaly, are very small in the hadronic region.

5.1.1. Chiral Scalar Density in A Nucleon

To set up the baseline for the estimate of in-medium chiral condensates, we consider the scalar charge, $N_{\sigma }$, for a nucleon in a vacuum. It is defined as

$$\begin{array}{cc}\hfill N_{\sigma }& ={\int }_{\mathbf{x}}⟨N|(\overline{u}u+\overline{d}d)(x)|N⟩=⟨N|\frac{\partial H_{\mathrm{QCD}}}{\partial m_q}|N⟩=\frac{\partial m_N^{\mathrm{vac}}}{\partial m_q},\hfill \end{array}$$

(67)

where $H_{\mathrm{QCD}}$ is the QCD Hamiltonian. In the last step, we used the Hellmann–Feynman theorem [91].

In the PDM, the current quark masses affect nucleon masses only through the modification of $\sigma$. The nucleon’s chiral scalar charge in a vacuum is given as

$$\begin{array}{c}\hfill N_{\sigma }\equiv \frac{\partial m_N^{\mathrm{vac}}}{\partial m_q}=\frac{\partial {\sigma }_0}{\partial m_q}{\left(\frac{\partial m_N}{\partial \sigma }\right)}_{\sigma ={\sigma }_0}.\end{array}$$

(68)

The mass derivative of ${\sigma }_0$ is related to the chiral susceptibility, which is given by the (connected) scalar correlator at zero momentum,

$$\begin{array}{cc}\hfill \frac{\partial ⟨\overline{q}q(x)⟩}{\partial m_q}& \sim \int \mathcal{D}q\mathcal{D}\overline{q}\left[\overline{q}q(x)\right]\frac{\partial }{\partial m_q}\left({\mathrm{e}}^{-{\int }_{x^{\prime }}{m}_q\overline{q}q(x^{\prime })+\cdots }/Z\right)\hfill \\ \hfill & \sim {\int }_{x^{\prime }}{⟨\left[\overline{q}q(x)\right]\left[\overline{q}q(x^{\prime })\right]⟩}_{\mathrm{conn}.}\sim \underset{q\to 0}{lim}\frac{1}{q^2+m_{\sigma }^2}.\hfill \end{array}$$

(69)

Then, a smaller scalar meson mass enhances $N_{\sigma }$.

Multiplication of $m_q$ by the scalar charge leads to the so-called nucleon sigma term:

$$\begin{array}{c}\hfill {\Sigma }_N\equiv m_q{N}_{\sigma }={\int }_{\mathbf{x}}⟨N|m_q(\overline{u}u+\overline{d}d)|N⟩,\end{array}$$

(70)

which is renormalization group invariant and has direct access to experimental quantities. The traditional estimate [92] gives ${\Sigma }_N\simeq 45$ MeV. However, precise determination is difficult, and the possible range is $40–70$ MeV, according to the lattice QCD analyses or the combined analyses of the lattice QCD and the chiral perturbation theory. (See Ref. [91] for a review and the references therein.) Here, we take $m_q\simeq 5$ MeV, which leads to obtaining $N_{\sigma }\simeq 8–14$, and the scalar density is given by

$$\begin{array}{c}\hfill \frac{N_{\sigma }}{\frac{4}{3}\pi R_N^3}={\left(0.24–0.30\mathrm{GeV}\times \frac{1\mathrm{fm}}{R_N}\right)}^3,\end{array}$$

(71)

where $R_N\sim 1$ fm is the size of a nucleon. (Note that the scalar isoscalar radius is estimated as $⟨r_s^2⟩\simeq {(0.7–1.2\mathrm{fm})}^2$ [93].) Note that the magnitude is roughly the same order as that of the vacuum, but the sign is opposite. Therefore, the nucleon scalar charges tend to cancel that of the vacuum and reduce the net value of $\sigma$. Therefore, the appearance of nucleons inevitably reduces the magnitude of the chiral condensates.

In Table 5, for several choices of $m_0$, we summarize the values of the Yukawa coupling:

$$\begin{array}{c}\hfill \frac{\partial m_N}{\partial \sigma }=\frac{{(g_1+g_2)}^2\sigma }{2\sqrt{4m_0^2+{(g_1+g_2)}^2{\sigma }^2}}-\frac{g_2-g_1}{2},\end{array}$$

(72)

together with the scalar meson mass ($m_{\sigma }$) obtained as the smallest eigenvalue of the following matrix

$$\begin{array}{c}\hfill \left(\begin{array}{cc}\frac{{\partial }^{2}V}{\partial {\sigma }^2}& \frac{{\partial }^{2}V}{\partial \sigma \partial {\sigma }_s}\\ \frac{{\partial }^{2}V}{\partial \sigma \partial {\sigma }_s}& \frac{{\partial }^{2}V}{\partial {\sigma }_s^2}\end{array}\right).\end{array}$$

(73)

We also show the values of the nucleon sigma term (${\Sigma }_N$) calculated from the PDM using Equation (70).

Table 5. Yukawa coupling, the scalar meson mass, and the nucleon sigma term predicted by the PDM in a vacuum.

${\mathit{m}}_0$ [MeV]	400	500	600	700
${(\partial m_N/\partial \sigma )}_{\mathrm{vac}.}$	8.79	7.97	7.01	5.87
$m_{\sigma }$ [MeV]	607	664	688	599
${\Sigma }_N$ [MeV]	51.12	48.71	51.39	62.01

The estimates of $m_{\sigma }$ and ${\Sigma }_N$ are reasonably consistent with the hadron phenomenology; $m_{\sigma }$ are consistent with the mass of the scalar meson $f_0(500)$ (with the width ∼500 MeV) (it is not a trivial issue whether one can identify $\sigma$ in mean field models with the physical scalar meson), and the estimates for the nucleon sigma term, ${\Sigma }_N\simeq$ 40–70 MeV, are within the ball park of several theoretical estimates.

5.1.2. Dilute Regime

In the dilute regime (Figure 11), the nucleons are widely separated. In a good approximation, the in-medium scalar density is simply the sum of the negative scalar charges from the chiral condensates and the positive scalar charges from the nucleons (linear density approximation (LDA)),

$$\begin{array}{c}\hfill ⟨(\overline{u}u+\overline{d}d)⟩\simeq {⟨(\overline{u}u+\overline{d}d)⟩}_0+n_B{N}_{\sigma },\end{array}$$

(74)

which can be rewritten as

$$\begin{array}{c}\hfill \sigma \simeq f_{\pi }\left(1+n_B\frac{N_{\sigma }}{{⟨(\overline{u}u+\overline{d}d)⟩}_0}\right).\end{array}$$

(75)

In this LDA, the $\sigma$ decreases linearly as a function of $n_B$.

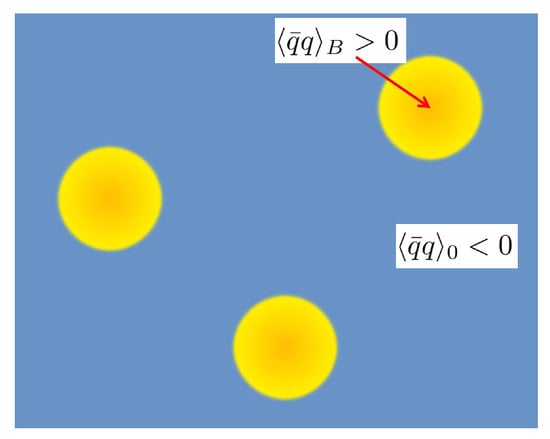
Figure 11. Schematic picture of the chiral condensates in the dilute regime. The chiral scalar charge is negative where the vacuum chiral condensate dominates, while nucleons contribute to the positive scalar charges to cancel the vacuum’s contributions.

The linear density approximation is violated when the density increases and nonlinear effects set in. Shown in Figure 12 is the ratio of the quark condensate, $⟨\overline{u}u⟩/⟨{\overline{u}u}_0⟩=\sigma /f_{\pi }$, as a function of the neutron number density $n_n$ in pure neutron matter. The result of the linear density approximation is also shown for comparison. Our mean field results are consistent with the linear density approximation with ${\Sigma }_N=45$ MeV in the low-density region. Our predictions start to deviate from the LDA around $n_B=0.5n_0$, signaling the importance of higher powers of $n_B$.

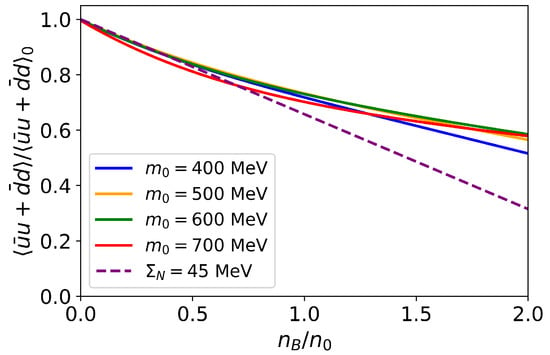
Figure 12. Dependence of the quark condensate in the PDM $⟨\overline{u}u⟩/⟨{\overline{u}u}_0⟩=\sigma /f_{\pi }$ on the baryon number density $n_B$ for $m_0=$ 400, 500, 600, and 700 MeV. Here, the condensate is normalized by the vacuum’s counterpart.

We stress that, in the PDM, while the chiral restoration or reduction in $\sigma$ occurs rather quickly with the increasing density, such changes do not immediately mean structural changes in the nucleons or in the nucleon or quark Dirac sea. The nucleon mass in the PDM is relatively modest (Figure 13), and this feature is welcomed for the commonly used no-sea approximation for the thermodynamic potential (see Equation (18)) which is justified only when modifications in the Dirac sea are small. Another hint regarding the chiral condensates and hadron structures comes from a high temperature transition in which a hadron resonance gas (HRG) transforms to a quark–gluon plasma (QGP). There, the chiral condensates begin to drop before the temperature reaches the critical temperature, but the HRG model with the vacuum hadron masses remains valid in reproducing the lattice data even after the chiral condensates are substantially reduced [94,95]. Chiral restoration, beyond cancellations of the negative and positive scalar charges, will be discussed in the next section on quark matter models.

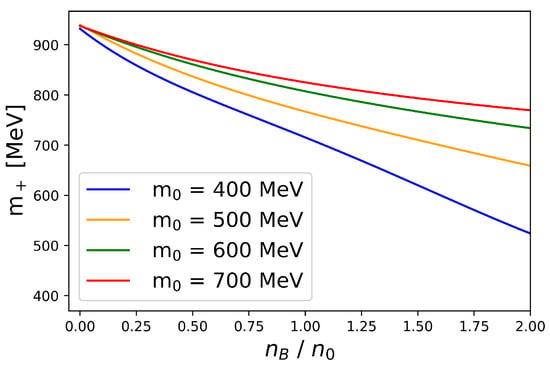
Figure 13. Dependence of the nucleon masses in the PDM on the baryon number density $n_B$, for $m_0=$ 400, 500, 600, and 700 MeV.

5.2. Chiral Condensates in the CFL Quark Matter

In terms of quarks, the chiral condensates are triggered by the attractive quark–antiquark pairing. At a high density, such a pairing is disfavored by the presence of the quark Fermi sea; as shown in Figure 14, creating an antiquark costs approximately the quark Fermi energy since it is necessary to bring a particle in the Dirac sea to the domain beyond the Fermi sea. Therefore, the chiral condensates made of quarks and antiquarks naturally dissociate as the density increases. Instead, the particle–particle [63] or particle–hole pairings [96,97,98] near the Fermi surface do not have such energetic disadvantages. The method of these computations is given in Section 3.

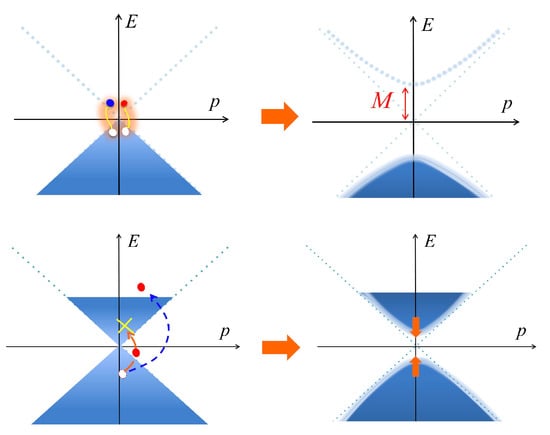
Figure 14. Chiral symmetry breaking by condensation of quark–antiquark pairs; (upper) in a vacuum; (lower) in the medium. In the latter, the pairing is blocked by the quark Fermi sea.

We note that, unlike the chiral restoration in the dilute nuclear matter as a mere consequence of cancellations between the positive and negative charges, in quark matter, the magnitude of each contribution is reduced together with the chiral restoration in the quark Dirac sea. This extra energy from the Dirac sea modification is important in the quark matter EOS and must be taken into account. The softening of the quark EOS due to the U(1)${}_A$ anomaly is related to the Dirac sea modifications associated with the chiral restoration. If we consider the anomaly term for couplings between diquark and chiral condensates [99], then the EOS can be stiffer; see Figure 7 in Ref. [64].).

5.3. Condensates in a Unified EOS

In this subsection, we review the interpolating method of generating functionals, which is introduced in Ref. [68]. We use it to calculate the chiral and diquark condensates from the nuclear to quark matter and also to examine the composition of matter with ($u-,d-,s$)-quarks and charged leptons (electrons and muons, $e,\mu$).

5.3.1. Unified Generating Functional

For computations of condensate $\varphi$, we first construct a generating functional $P({\mu }_B;J)$ with the external field J coupled to the $\varphi$. A condensate $\varphi$ at a given ${\mu }_B$ is obtained by differentiating $P({\mu }_B;J)$ with respect to J and then set $J=0$,

$$\begin{array}{c}\hfill \varphi =-\frac{\partial P}{\partial J}{|}_{J=0}.\end{array}$$

(76)

The generating functional for the nuclear domain, $n_B\le 2n_0$, is given by the PDM, and for the quark matter domain, $n_B\ge 5n_0$, by the NJL-type model. We interpolate these functionals with the constraints that the interpolating curves match up to the second derivatives at each boundary, $2n_0$ and $5n_0$. For the interpolating function, we adopt a polynomial function of ${\mu }_B$ with six coefficients $a_n(J)$,

$$\begin{array}{cc}\hfill P_{\mathrm{I}}({\mu }_B;J)& =\sum _{n=0}^5{a}_n(J){\mu }_B^n.\hfill \end{array}$$

(77)

We determine the chemical potentials at the boundaries, ${\mu }_B^L$ and ${\mu }_B^U$, as

$$\begin{array}{c}\hfill n_B({\mu }_B^L;J)=2n_0,n_B({\mu }_B^U;J)=5n_0.\end{array}$$

(78)

The resulting ${\mu }_B^L$ and ${\mu }_B^U$ depend on J. The six boundary conditions

$$\begin{array}{c}\hfill \frac{{\partial }^k{P}_{\mathrm{I}}}{{(\partial {\mu }_B)}^k}{|}_{{\mu }_B^L({\mu }_B^U)}=\frac{{\partial }^k{P}_{\mathrm{PDM}(\mathrm{NJL})}}{{(\partial {\mu }_B)}^k}{|}_{{\mu }_B^L({\mu }_B^U)},\end{array}$$

(79)

with $k=0,1,2$ uniquely fix $a_n$’s. As in the EOS construction, the generating functional must satisfy the causality condition. Such constraints are transferred to the evaluation of the condensates; condensates in the crossover domain are correlated with those in the nuclear and quark matter.

5.3.2. An Efficient Method for Computations of Many Condensates

While the generating functional in the previous section is general, the calculations become cumbersome when we need to compute many condensates. Each condensate requires the corresponding external field and generating functional. Fortunately, for the interpolating function Equation (77), we can use a more efficient method in Ref. [68], which does not demand the construction of $P({\mu }_B,J)$ and utilizes only the ${\mu }_B$-dependence of the condensate at $J=0$ for each interpolating boundary.

In the interpolated domain, the condensate $\varphi$ can be expressed as

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{I}}=-\frac{\partial P_{\mathrm{I}}}{\partial J}{|}_{J=0}=-\sum _{n=0}^5\frac{\partial a_n}{\partial J}{|}_{J=0}{\mu }_B^n.\end{array}$$

(80)

This implies the equivalence between the determination of ${\varphi }_{\mathrm{I}}$ and that of the six constants $\partial a_n/\partial J{|}_{J=0}$. Taking the ${\mu }_B$-derivatives in Equation (79), we obtain

$$\begin{array}{c}\hfill \frac{\partial }{\partial J}\left(\frac{{\partial }^k{P}_{\mathrm{I}}}{{(\partial {\mu }_B)}^k}{|}_{{\mu }_B^L({\mu }_B^U)}\right)=\frac{\partial }{\partial J}\left(\frac{{\partial }^k{P}_{\mathrm{PDM}(\mathrm{NJL})}}{{(\partial {\mu }_B)}^k}{|}_{{\mu }_B^L({\mu }_B^U)}\right),\end{array}$$

(81)

where $k=0,1,2$. Only the quantities at a given ${\mu }_B$ and $J=0$ are necessary to construct all of these derivatives at $J=0$. Hence, this method speeds up our analyses considerably.

5.3.3. Numerical Results

Using the method explained above, we calculate the light quark chiral condensate $⟨(\overline{u}u+\overline{d}d)⟩$, the strange quark condensate $⟨\overline{s}s⟩$, the diquark gaps ${\Delta }_j$ ($j=1,2,3$), and the quark number densities $n_f$ ($f=u,d,s$) from the nuclear to quark matter domain. Below, we adopt three values of the chiral invariant mass ($m_0=500$, 600, 700 MeV) as samples and fix the anomaly coefficient B to 600 MeV and the NJL parameters $(H/G,g_V/G)$ to $(1.45,0.5)$. The presence of the anomaly term in the PDM is the difference between the results in this review and in Ref. [68] whose impacts are just few percents in magnitude. The EOS for these parameter sets satisfies $0\le c_s^2\le 1$. For comparisons, the extrapolation of the PDM results are shown by black dotted curves.

Light Quark Chiral Condensates

Figure 15 shows the density dependences of the in-medium chiral condensate normalized by the vacuum value, $⟨(\overline{u}u+\overline{d}d)⟩/⟨{(\overline{u}u+\overline{d}d)⟩}_0$. Clearly, the condensate at the boundaries affects the condensate in the crossover region. We note that, when the EOS from the PDM is extrapolated to the high-density region ($n_B\ge 2n_0$) as indicated by black dotted curves, the chiral condensate rapidly decreases in the range $n_B\simeq 3.8$–$4.5$ for $m_0=500$ MeV as well as $n\gtrsim 5.5n_0$ for $m_0=600$ MeV, which corresponds to the phase transition brought by the entering of $N^{*}$(1535).

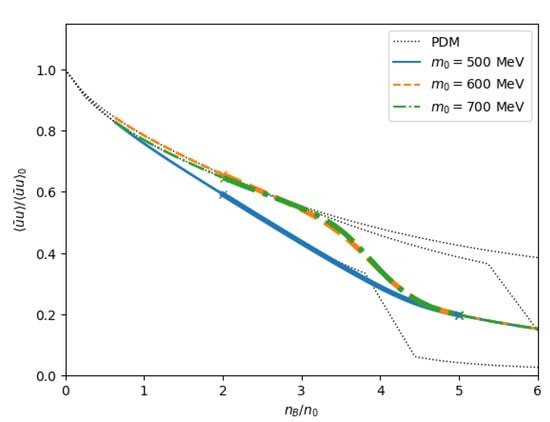
Figure 15. Density dependence of the chiral condensates normalized by the vacuum counterpart. The parameters are chosen as $B=600$ MeV and $(H/G,g_V/G)=(1.45,0.5)$.

The condensates in the hadronic matter strongly depend on the choice of $m_0$: for $m_0=500$ MeV, the nucleon mass $m_N=939$ MeV gains a large contribution from the chiral condensate, and the Yukawa coupling of nucleons to $\sigma$ is large; accordingly, the chiral condensate drops quickly as the baryon density increases. For a larger $m_0$, the nucleons have fewer impacts on the chiral condensates, and the chiral restoration takes place more slowly.

As mentioned in Section 5.1, the PDM may underestimate the chiral restoration effects as they do not describe the chiral restoration at the quark level. By putting the quark matter constraints from the high density and using the causality constraints for the interpolated domain, we can gain qualitative insights into how the chiral restoration should occur toward a high density. Taking into account the nuclear and quark matter effects, interpolation offers reasonable descriptions for the crossover domain.

Strange Chiral Condensates

The density dependence of the strange quark condensate is shown in Figure 16. In the present PDM model, the ${\sigma }_s$ field corresponding to the strange quark condensate does not directly couple to the nucleons, but it does couple, only through the anomaly term in the meson potential, to Equation (9). As a result, the density dependence is mild in the hadronic matter ($n_B\le 2n_0$). In the interpolated region, the condensate starts to decrease rapidly toward that of the quark matter, which is about $40\%$ of the vacuum value at $n_B=5n_0$. There are at least two effects responsible for this chiral restoration. The first is the reduction in the anomaly contribution, $\sim ⟨\overline{u}u⟩⟨\overline{d}d⟩(\overline{s}s)$, which is due to the chiral restoration for the light quark sectors. The other is due to the evolution of the strange quark Fermi sea. In our unified model, the strangeness sector significantly deviates from the prediction of the PDM at $n_B\simeq 3n_0$ due to the constraints from the quark matter boundary conditions.

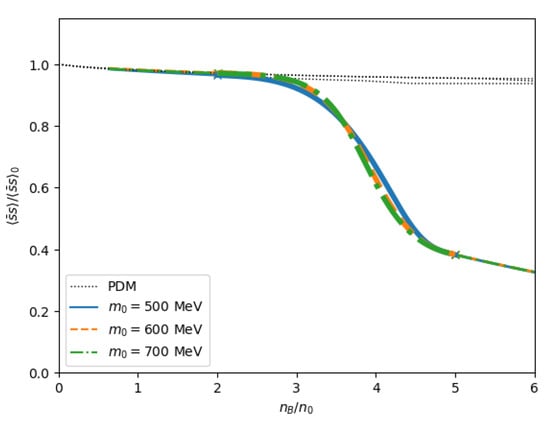
Figure 16. Density dependence of the strange quark condensate normalized by the vacuum counterpart. The parameters B and $(H/G,g_V/G)$ are as in Figure 15.

Diquark Gaps and Number Density

Shown in Figure 17 are the diquark gaps in the $ud$-pairing channel (left panel) and $ds$-pairing channel (right panel) at various densities. We set the diquark condensates to zero at $n_B\le 2n_0$. Meanwhile, the isospin symmetry holds in the CFL quark matter, so, in the whole region, ${\Delta }_{ds}\simeq {\Delta }_{us}$ holds in good accuracy.

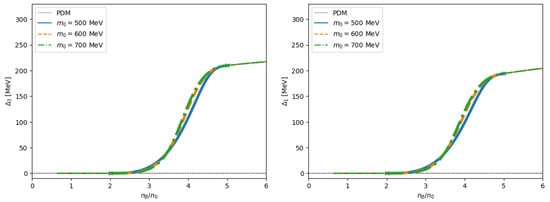
Figure 17. Diquark condensates as functions of density; (left) ${\Delta }_3={\Delta }_{ud}$ and (right) ${\Delta }_1={\Delta }_{ds}$. The parameters B and $(H/G,g_V/G)$ are as in Figure 15.

Next, we study the density dependence of the diquark condensates on the quark number density (Figure 18). The quark densities in the nuclear domain are calculated as $n_u=2n_p+n_n$, $n_d=n_p+2n_n$, and $n_s=0$. As seen from Figure 17 and Figure 18, there are clear correlations between the growth of the diquark condensates and the quark number densities. These two quantities assist each other: more diquark pairs are possible for a larger quark Fermi sea, while the resulting energy reduction, in turn, enhances the quark density. The flavor composition is also affected by these correlations: the substantial $u,d$-quark Fermi sea and the pairing to strange quarks favor the formation of the strange quark Fermi sea, even before the quark chemical potential reaches the threshold of the vacuum strange quark mass.

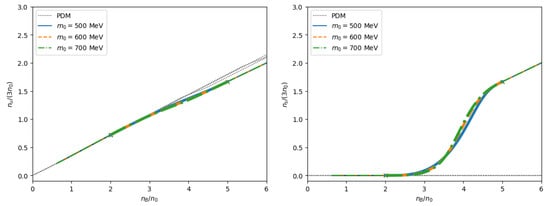
Figure 18. Number density for (left) up-quarks and (right) strange quarks. The parameters B and $(H/G,g_V/G)$ are as in Figure 15.

Quark and Lepton Compositions

The present framework can be extended for computations of the matter composition in NS matter with leptons. We simply impose the charge neutrality and $\beta$-equilibrium conditions on the generating functionals. Shown in Figure 19 are the quark flavor $n_f/n_B$ with $f=u,d,s$ and the lepton fraction $n_l/n_B$ with l referring to the electrons or muons.

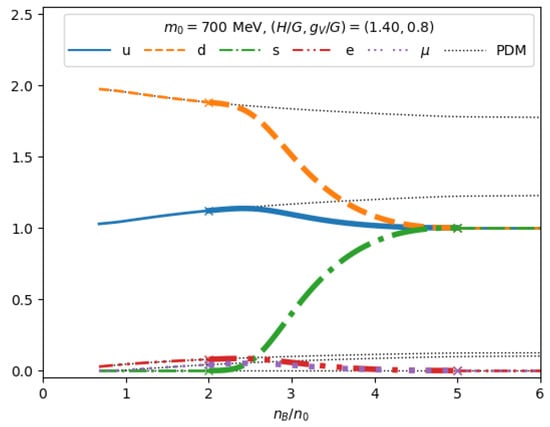
Figure 19. Matter composition $n_f/n_B$ ($f=u,d,s$) and $n_l/n_B$ as functions of the baryon density.

The quick evolution of the strangeness fraction, taking off around $n_B\simeq 2.5n_0$ and becoming as abundant as up- and down-quarks at $n_B\gtrsim 4.5n_0$, and the associated reduction in lepton fractions, are one of distinct features of our unified model. Beyond $5n_0$, in the CFL quark matter, the charge neutrality is satisfied by quarks, and no charged leptons are necessary.

6. A Summary

In this review article, we summarized the main points of Refs. [66,67,68] and updated some of the analyses, including the U(1)${}_A$ anomaly effects. In Section 2, we explained how to construct the EOS in hadronic matter for $n_B\le 2n_0$ using an effective hadron model based on the parity doublet structure. In the analysis, we focused on the effect of the U(1)${}_A$ axial anomaly included as the KMT-like interaction among scalar and pseudoscalar mesons and showed that the effect makes the EOS softer. In Section 3, following Ref. [27], we briefly reviewed how to construct a quark matter EOS for $n_B\ge 5n_0$ using an NJL-type model. Then, in Section 4, we built a unified EOS in the density region of $2n_0\le n_B\le 5n_0$ by interpolating the hadronic and quark EOS. For the given microscopic parameters, we calculated the M-R relations of NSs, confronted them with the observational constraints, and then obtained constraints on the chiral invariant mass and quark model parameters. In Section 5 we determined the density dependence of the chiral condensate in the interpolated region using a method proposed in Ref. [68]. The boundary conditions from the hadronic and quark matter affect the condensates in the intermediate region and give a balanced description.

We want to stress that our method provides some connection from microscopic physical quantities, such as the chiral invariant mass, the chiral condensates, and diquark gaps, to macroscopic observables, such as the masses and radii of NSs. Actually, our analysis implies that a rapid decrease in the nucleon mass, even near the normal nuclear density, which can occur when the chiral invariant mass $m_0$ is very small, provides a too-soft EOS to satisfy the radius constraint of NSs with a mass of about $1.4M_{\odot }$. In other words, the radius constraint of the NSs obtained from recent observations indicates that the nucleon mass should include a certain amount of chiral invariant mass, from which the nucleon keeps a large portion of its mass even in the high-density region in which the chiral symmetry restoration is expected to occur.

Our density dependence of the chiral condensate in the low-density region is consistent with the linear density approximation. We should note that the reduction of the chiral condensate there is achieved by the contribution of the positive scalar charge of the nucleon without changing the nucleon properties drastically. This is due to our construction of hadronic matter in the PDM: We adopted the so-called “no-sea approximation” where we neglect the effect of the nucleon Dirac sea and use fixed nucleon–meson couplings for $n_B\lesssim 2n_0$. In the present treatment, the intrinsic properties of nucleons start to change at $n_B\gtrsim 2n_0$, drastically, where the quark exchanges among the baryons become frequent; since baryons are made of quarks, the quark exchanges are supposed to change the baryon structure. Such intrinsic dependence would be able to be included through the introduction of the density- (and/or temperature-) dependent coupling constants in effective hadronic models as completed in, e.g., Refs. [100,101]. This is a reflection of the partially released quarks, which are affected by the medium. The inclusion of such effects into coupling constants is very difficult. Our interpolation scheme provides a practical way to implement some restrictions through the quark matter constraints at a high density.

In the present model for hadronic matter, we did not explicitly include the hyperons, assuming that they are not populated in the low-density region $n_B\lesssim 2n_0$. The hyperons may enter into matter around $n_B\sim 2$-$3n_0$, which is not far from present choice for the hadronic boundary. It would be interesting to conduct an analysis explicitly including the hyperons based on the parity doublet structure (see, e.g., Ref. [102]).

In the present analysis, we assume that the anomaly has a stronger impact in the mesonic sectors than in the baryonic sectors and included the anomaly B term only in the mesonic sector. It would be interesting to include some Yukawa interactions, which also break the U(1)${}_A$ symmetry.