Abstract
The offset as the average value of a variable plays an important role in signal processing and system design. Offset boosting can be realized by a non-bifurcation parameter or an initial condition. In this work, symmetric coexisting attractors with opposite polarity and a 2D hyperchaotic map with multiple modes of offset boosting are proposed, where the offset can be controlled both by the initial condition and system parameter, and as a result, multiple alternatives of offset boosting and offset competition show up. Consequently, the final offset is determined eventually by the balance of two factors. The theoretical findings are verified through the hardware experiment based on the STM32. Finally, a pseudo-random number generator (PRNG) is constructed based on the newly proposed hyperchaotic map, demonstrating its high performance in engineering applications.
1. Introduction
Chaos control, including amplitude control [1,2,3] and offset boosting [4,5,6,7], is a hot topic in the nonlinear community, which becomes more important for a multistable system since it hosts many coexisting attractors [8,9,10,11,12]. Offset boosting of a chaotic attractor brings great convenience for chaotic signal conditioning and thus brings increasing interest. The introduction of a periodic function drives attractor self-reproduction, where any of the coexisting attractors locates at a definite position in phase space and can be extracted out by an initial condition [13]. A periodically forced megastable chaotic system may give birth to countless embedded coexisting attractors [14]. In Chua’s memristive multi-double-scroll system, the internal parameter of the memristor can be employed to construct the desired number of multi-double-scroll chaotic attractors [15]. All the phenomena resort to the technology of offset boosting. However, the associated research on offset control in the field of the discrete map is relatively poor, which leaves a significant margin [16,17,18]. It has been proved that offset boosting plays an important role in the discrete map for the desired multistability [19,20]. Zhou et al. proposed homogenous multistability in a 3D map, in which the chaotic attractor structure and the distance between any two petals can be controlled by initial conditions [21]. Offset boosting can be applied to construct a discrete multi-cavity [22]. A self-reproduction hyperchaotic map may exhibit compound lattice dynamics associated with offset boosting [23]. Offset boosting shows its specific function in discrete systems for attractor control.
Offset boosting can be realized by a non-bifurcation parameter or an initial condition. Therefore, sometimes it is difficult to determine how exactly offset boosting happens since the final derived offset may be the balanced result from the competition of a parameter and an initial start. In this work, a 2D hyperchaotic map with symmetric coexisting attractors is designed, where hyperchaotic sequences with opposite polarities are obtained, and multiple modes of offset boosting controlled both by the initial condition and system parameter are found. As a result, multiple alternatives of offset boosting and offset competition show up. The main contributions are summarized as follows:
- (1)
- A new control knob is found, which can control the interval and direction of attractor self-reproduction.
- (2)
- Various alternatives of offset boosting are systematically explored, which include initially controlled offset boosting, parameter-oriented offset boosting and competitive offset boosting.
- (3)
- Competitive offset boosting is firstly discussed, where the newly introduced constants show the function of offset boosting determining the direction of the shifted attractor in the phase space, and as a result, based on the constant, the bipolar and unipolar chaotic signals can be switched accordingly.
- (4)
- Periodic windows are caught by the plot of the bifurcation diagram, which poses a great threat to engineering applications. However, competitive offset boosting can be easily applied to cross this interval and reach hyperchaos.
- (5)
- An STM32-based circuit implementation is constructed to prove two different offset boosting regimes. PRNG is employed to demonstrate the practical application of the proposed map.
The rest of this paper is organized as follows. A basic analysis of the 2D hyperchaotic map, including stability of fixed points and bifurcation are provided in Section 2. In Section 3, various mechanisms of offset boosting are exhaustively explored. In Section 4, STM32-based circuit implementation is set up for physical verification, and PRNG is derived to explore its chaos-based applications. Discussions and conclusions are presented in Section 5.
2. A 2D Hyperchaotic Map
2.1. Model Description
By introducing a periodic nonlinearity [23], a novel 2-D discrete map is proposed,
where n represents a natural number, xn and yn respectively denote the nth states. System parameters are represented by the symbol a. When xn+1 →–xn+1, yn+1 →–yn+1, xn →–xn, yn →–yn, map (1) keeps its polarity balance indicating that map (1) is of inversion symmetry.
2.2. Bifurcation Analysis
The Lyapunov exponent is a direct theoretical description and widely used criteria indicating the existence of chaos, which is widely accepted in nonlinearity community. The Lyapunov exponent of a differential equation xi+1 = f(xi), denoted as λf(x), is mathematically defined as
where ε is a very small positive value nearing zero. One positive value indicates chaos, and more positive values show hyperchaos.
When (x0, y0) = (1, 0) and a varies in (−3.4, 2.5), several kinds of evolution including period, chaos, and hyperchaos are found in map (1) [24,25,26], as depicted in Figure 1. When a is in (−2.7, −2.248), hyperchaos shows up; when a varies in (−2.248, −2.03), map (1) is chaotic; when a increases in (−2.03, −2.01), a small range periodic window is captured; when a increases in (1.758, 1.882), quasi-periodic oscillation behavior is exhibited; when the parameter a varies in (1.892, 2.5), map (1) is chaotic, and two separate periodic windows (1.99, 2.115) and (2.333, 2.365) are embedded. Typical dynamical behaviors of map (1) are summarized in Table 1, corresponding phase orbits are shown in Figure 2. When x0 →–x0, y0 →–y0, the polarity in map (1) is switched and its symmetrical attractors are produced, as shown in Figure 2d–f, their symmetrical waveforms are displayed in Figure 3.
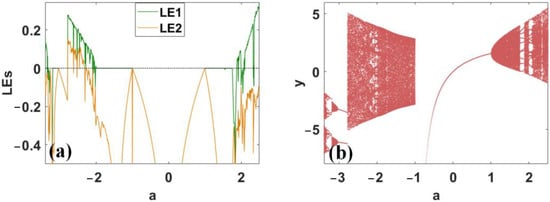
Figure 1.
Dynamical evolution of hyperchaotic map (1) under the initial condition (x0, y0) = (1, 0) when a varies in (−3.4, 2.5): (a) Lyapunov exponents, (b) bifurcation diagram.

Table 1.
Typical dynamics of map (1) when (x0, y0) = (1, 0).
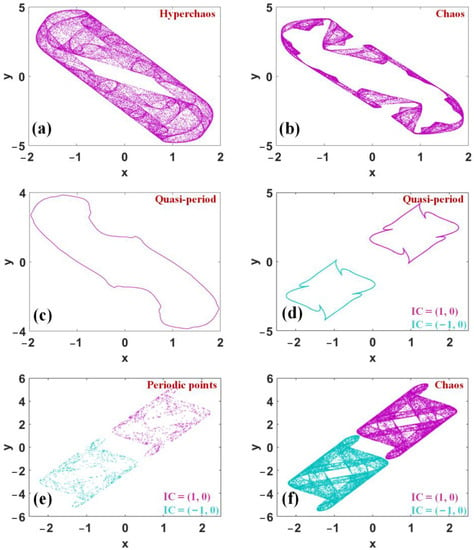
Figure 2.
Typical phase trajectories of map (1): (a) a = −2.6, (b) a = −2.2, (c) a = −1.96, (d) a = 1.887, (e) a = 2.336, (f) a = 2.5, where (a–c) under the initial condition (x0, y0) = (1, 0).
Figure 3.
Symmetrical waveforms of map (1): (a) a = 1.887, (b) a = 2.336, (c) a = 2.5.
3. Multiple Alternatives of Offset Boosting
3.1. Initially Controlled Offset Boosting
Discrete map (1) is a dynamic system with self-reproduction. According to the iterative relationship, suppose the initial data of xn receives the offset boosting, and the properties of the attractor are not disturbed by the value of offset boosting. For the periodicity of the sine function, the attractor is shifted in phase space with inconsistent steps, and the coexisting attractors are arranged by the polarity of x0 and a.
Case I: x0 > 0, a < 0: when x0 > 0, a < 0, attractor self-reproducing is heading in the negative direction of y, as shown in Figure 4a,b.
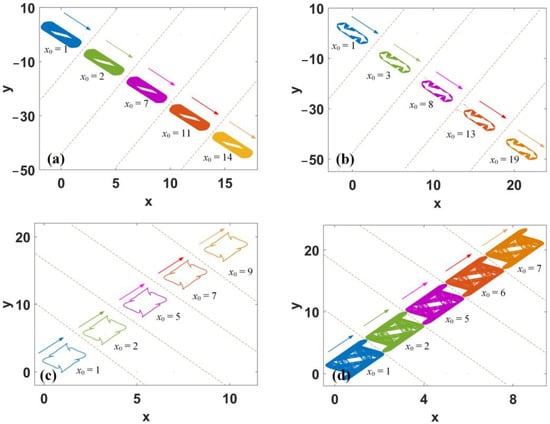
Figure 4.
Coexisting phase trajectories of map (1) under various initial conditions: (a) a = −2.6, (b) a = −2.2, (c) a = 1.887, (d) a = 2.5.
Case II: x0 > 0, a > 0: when x0 > 0, a > 0, coexisting attractors are arranged in the positive direction of y, as plotted in Figure 4c,d.
Case III: x0 < 0, a < 0: when x0 < 0, a < 0, the direction of attractor self-reproduction is in the negative direction of y, which is the same as that of case I.
Case IV: x0 < 0, a > 0: when x0 < 0, a > 0, self-reproducing attractors are extracted in the phase space in the positive direction of y, as in case II.
The initial condition x0 controls the position of coexisting attractors in two-dimensional space. As depicted in Figure 5a, the plot of Lyapunov exponents with many periodic windows indicates the nonsmooth switch from one state to another when a = −2.6 and x0 varies in [0, 15]. When a = −2.6 and x0 varies on the negative side of the coordinate axis, in pace with the change in x0 in the positive direction, the dynamic behavior is also accompanied by mutations. Correspondingly, when a = 2.5 and x0 varies in [0, 8], Figure 5b shows that the dynamic evolution is relatively smooth without a change in state. Moreover, when a = 2.5 and x0 > 0, a similar smooth dynamic evolution will also appear. The basins of attraction of the coexisting attractors plotted in Figure 6 also prove this phenomenon. When a = −2.6, the separate basins are nonsmooth, while when a = 2.5, the boundary of the basins is smooth. The rule of attractor reproduction agrees with the evolution of the square plot of bifurcation.
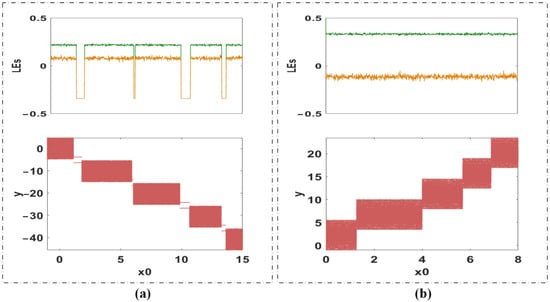
Figure 5.
Bifurcation of map (1) under the initial value x0: (a) a = −2.6, (b) a = 2.5.
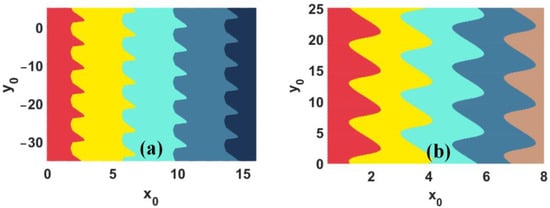
Figure 6.
Basins of attraction of the coexisting attractors: (a) a = −2.6, (b) a = 2.5.
3.2. Parameter-Oriented Offset Boosting
Suppose the sequence xn has the offset shift l while sequence yn obtains offset boosting with −l, map (1) turns out to be,
set d = al + l = (a + 1) l, Equation (3) turns out to be,
It means that the constant d in Equation (4) indicates the offset boosting l = d/(a + 1) in the opposite direction along the axis of x and y. Shifted attractors of map (4) are arranged in phase space along a specific direction defined by the parameters a and d.
Case I: a < −1, d < 0 or a > −1, d > 0: when a < −1, d < 0 or a > −1, d > 0, then l > 0, so the sequence xn is given a positive offset boosting (PX), and the sequence yn is offered a negative offset boosting (NY).
Case II: a > −1, d < 0 or a < −1, d > 0: when a > −1, d > 0 or a < −1, d > 0, then l < 0, and then the sequence xn is assigned with negative offset boosting (NX), and the sequence yn is equipped with positive offset boosting (PY).
As shown in Figure 7, the attractor is constantly shifted on the y-axis as well as moved in a certain interval on the x-axis. Four different modes of offset boosting are revealed in Table 2.
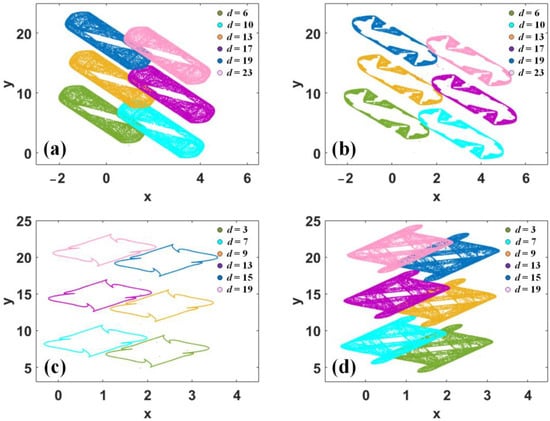
Figure 7.
Phase trajectories of map (4) under (x0, y0) = (1, 0): (a) a = −2.6, (b) a = −2.2, (c) a = 1.887, (d) a = 2.5.

Table 2.
Various modes of offset boosting in the map (4).
When a < −1, d > 0, and l < 0, the chaotic signal xn is shifted in the positive direction, and the signal yn is moved in the negative direction. The dynamical evolution of d is accompanied by many periodic windows, indicating the threat to engineering can be effectively diagnosed by competitive offset boosting. Different from the above-mentioned offset boosting, when a > −1, d > 0, and l > 0, the attractor moves in the negative direction of x and the positive direction of y. The dynamical behavior of d is non-bifurcation without revising Lyapunov exponents, as plotted in Figure 8b. From Figure 8, it is obvious that the evolution of parameter d makes the offset boosting of the signals xn and yn different according to the period of 2π. Further explanation will be discussed later.
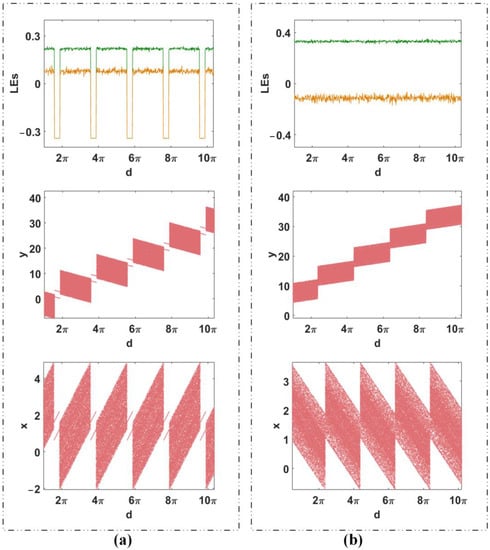
Figure 8.
Bifurcation of map (4) under (x0, y0) = (1, 0): (a) a = −2.6, (b) a = 2.5.
Suppose the sequence of xn receives offset boosting with p while the offset of yn is revised by q, map (1) turns out to be,
When q = ap, and let p + q = h, Equation (5) turns out to be,
It indicates that the constant h in Equation (6) implies the offset boosting p = h/(a + 1) in various combinations of movement in the axis of x and y when a and h are located in different regions, respectively. When a < −1 and h > 0, then p < 0 and q > 0, the sequence xn is given a negative offset boosting, and the sequence yn is offered a positive offset boosting. Conversely, when a > 0 and h > 0, then p > 0 and q > 0, the sequence xn and yn are assigned with positive offset boosting. Six different modes of competitive offset boosting are revealed in Table 3. As shown in Figure 9, the attractors are arranged in a certain interval on the x-axis and y-axis.

Table 3.
Regulated directions of offset boosting in the map (6).
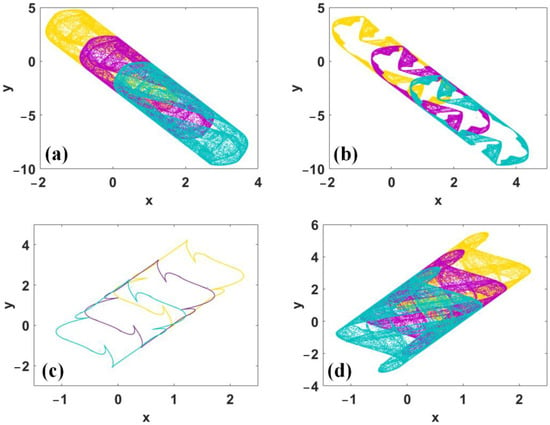
Figure 9.
Phase trajectories of map (6) with a different offset constant h under (x0, y0) = (1, 0), where gold: h = 0, violet red: h = 1.5, turquoise: h = 3: (a) a = −2.6, (b) a = −2.2, (c) a = 1.887, (d) a = 2.5.
The starting position of the chaotic signal can be regulated by the offset constant h, as shown in Figure 10a. When a < −1, h > 0, p < 0, and q > 0, the dynamical evolution of h is accompanied by many periodic windows, and signal xn and yn have migrations in the opposite direction, as shown in Figure 10b–d.
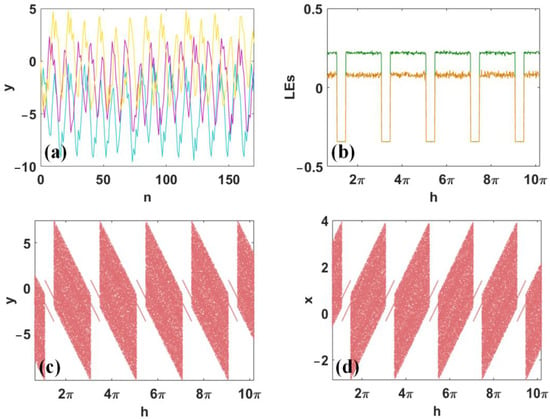
Figure 10.
Feature of competitive offset boosting of map (6) with a = −2.6 under (x0, y0) = (1, 0): (a) discrete sequences, (b) Lyapunov exponents, (c,d) bifurcation diagram.
Because the periodic function appears in the iterative equation of map (1) in the first dimension, offset boosting of map (1) becomes more flexible and shows multiple patterns. According to parameter d in Equation (4), the offset boosting of the signal xn oscillates periodically with the interval of 2π, but that of the signal yn climbs periodically, as shown in Figure 8. According to parameter h in Equation (6), the offset boosting with signals xn and yn oscillates periodically with a period of 2π, as shown in Figure 10. The multiple alternatives of offset boosting controlled by parameters are summarized in Table 4. Average values of chaotic sequences xn and yn are shown in Figure 11.

Table 4.
Multiple parameter-oriented patterns of offset boosting.
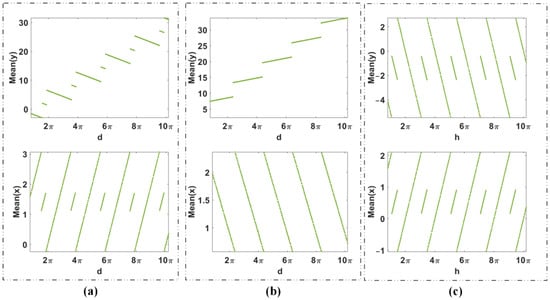
Figure 11.
Average values of xn and yn: (a) a = −2.6 and d varies in [0, 10π], (b) a = 2.5 and d varies in [0, 10π], (c) a = −2.6 and h varies in [0, 10π].
As shown in Figure 8a and Figure 11a, according to parameter d, the offset of signal yn climbs globally but falls locally with a period of 2π, the offset of signal xn oscillates periodically with a period of 2π, as plotted in Figure 8b and Figure 11b. That is to say, there are two different offset evolutions in a large scope of initial conditions. Specifically, when a < −1, the offset of xn increases in the period but totally remains at the same level according to parameter d in Equation (4). The offset of yn decreases in the period but grows globally, as shown in Figure 8a and Figure 11a. The evolution of offset boosting according to h in Equation (6) seems to be similar. Here, the offset of yn decreases periodically while the offset of xn increases periodically, as shown in Figure 10c,d and Figure 11c.
3.3. Competitive Offset Boosting
Suppose map (1) is given constants d and h at the same time, map (1) turns out to be,
As proved above, the offset boosting in the dimensions x and y can be defined by the newly introduced constants d and h along with the initial conditions. This can be called offset competition. In the map (7), due to the existence of the periodic function, the parameters d and h and the initial value of x0 influence the offset of coexisting attractors, as shown in Figure 12, which means that to obtain a desired offset, the parameter and the initial condition should match each other. From Figure 12, we also know that in map (7) the power of offset boosting of parameter d seems stronger than parameter h, which is because parameter h is in the sinusoidal function. More demonstrations based on Lyapunov exponents can verify this phenomenon further. As shown in Figure 13, when a < −1 and x0 varies with constants d and h, respectively, in different ranges, the largest 2D Lyapunov exponent under the mixture control of a parameter and initial condition is given, showing the strength of offset boosting under the evolutions of a parameter or an initial condition.
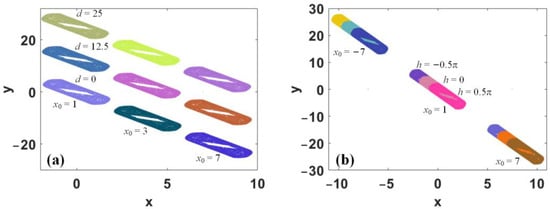
Figure 12.
Competitive offset boosting of map (7) when a = −2.6 and y0 = 0: (a) d = 0, 12.5 and 25, x0 = 1, 3 and 7, (b) h = −0.5π, 0 and 0.5π, x0 = −7, 1 and 7.
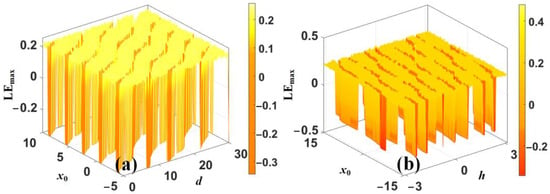
Figure 13.
The largest Lyapunov exponent of map (7) when a = −2.6 and y0 = 0: (a) x0 varies in [−5, 10] and d varies in [0, 30], (b) x0 varies in [−15, 15] and h varies in [−π, π].
4. Hardware Implementation and Application
4.1. Hardware Implementation Based on STM32
In this section, the implementation of chaotic signal acquisition and transmission using the STM32F103 microcontroller as the core and the TLV5618 module for digital-to-analog conversion are obtained. The resulting waveforms are displayed on an oscilloscope of SDS1102X [27,28]. The TLV5618 is a 12-bit voltage output digital-to-analog converter. The hardware implementation for map (1) is presented in Figure 14. The waveform of map (1) under the initial condition of (x0, y0) = (1, 0) is shown in Figure 15. Coexisting phase orbits of map (1) observed from the oscilloscope under various initial conditions are presented in Figure 16. Phase trajectories of map (1) observed from the oscilloscope with competitive offset boosting under (x0, y0) = (1, 0) are illustrated in Figure 17. Phase orbits of map (1) with different offset constant h under (x0, y0) = (1, 0) are shown in Figure 18. All figures from the hardware implementation based on the STM32 microcontroller and TLV5618 module are consistent with the numerical simulation.

Figure 14.
The hardware implementation based on STM32 for map (1).
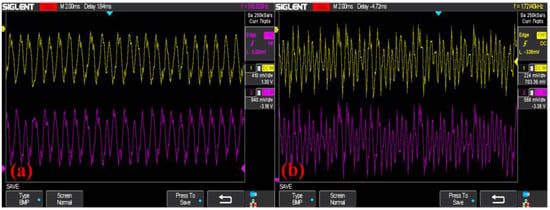
Figure 15.
The hardware-implemented waveform of in map (1) under (x0, y0) = (1, 0): (a) hyperchaos: a = −2.6, (b) chaos: a = 2.5.
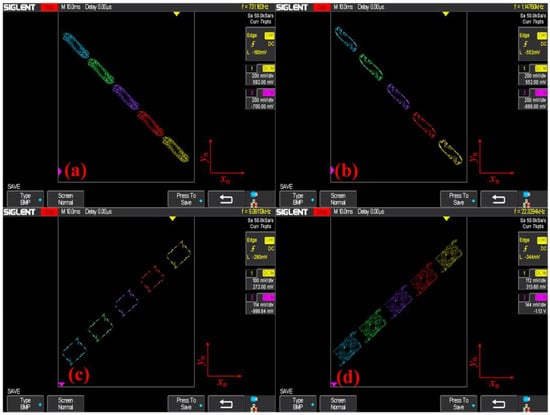
Figure 16.
Coexisting phase trajectories of map (1) observed from the oscilloscope under different initial conditions: (a) a = −2.6, (b) a = −2.2, (c) a = 1.887, (d) a = 2.5.
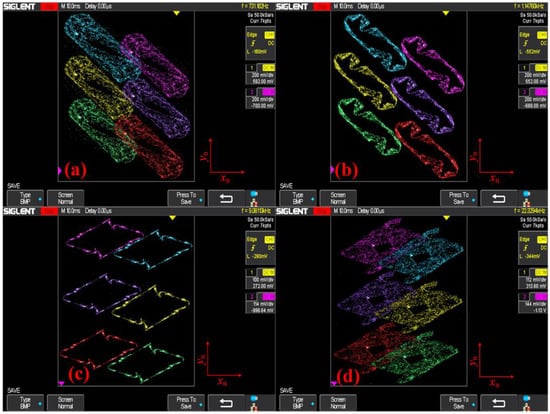
Figure 17.
Phase trajectories of map (4) from the oscilloscope under (x0, y0) = (1, 0): (a) a = −2.6, (b) a = −2.2, (c) a = 1.887, (d) a = 2.5.
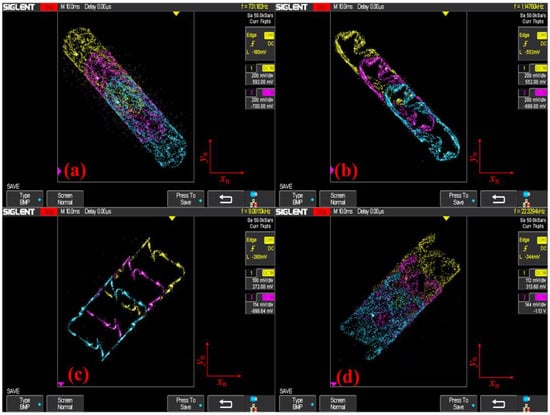
Figure 18.
Phase trajectories of map (6) with different offset constant h under (x0, y0) = (1, 0), where gold: h = 0, violet red: h = 1.5, turquoise: h = 3: (a) a = −2.6, (b) a = −2.2, (c) a = 1.887, (d) a = 2.5.
4.2. Application in PRNG
Assuming that the chaotic sequence generated by map (1) is denoted as X = {x1, x2, …, xn} or Y = {y1, y2, …, yn} [29,30]. The quantization function Pi employed in this experiment can be expressed as follows
let K = 107 and N = 256 in this paper.
In this experiment, we utilized the hyperchaotic sequence generated by map (1) with parameters a = −2.6 and initial condition (x0, y0) = (1, 0), the National Institute of Standards and Technology (NIST) test suite is used to measure its performance. To ensure high precision in detection, each sequence set should consist of no less than 1 × 106 bits. By setting the number of test groups as m = 128, the proportion (Prop) of passing test groups can indicate the pseudo-randomness of the sequence, thereby demonstrating the potential value for engineering applications of map (1). The results of the NIST statistical test of PRNG are illustrated in Table 5.

Table 5.
NIST statistical test of the proposed PRNG.
5. Discussion and Conclusions
In this paper, a new symmetric hyperchaotic map with multiple regimes of offset boosting is proposed and exhaustively explored. Multiple alternatives of offset boosting are proposed by two parameters and initial conditions. Offset competition is disclosed, where offset is determined by two parameters and initial conditions. In this case, infinitely many coexisting phase orbits are born, which are arranged by the coefficient-matched initial conditions. Therefore, the location of the coexisting hyperchaotic attractor is flexibly selected by the offset parameter and a matched initial condition. This elegant hyperchaotic map with multiple alternatives of offset boosting definitely shows greater potential in other relevant research fields and chaos-based applications, including Brownian movement, neural networks, and image encryption [31,32,33,34,35], which could be our future work.
Author Contributions
Conceptualization, X.G.; data curation, X.G. and C.L.; funding acquisition, C.L.; investigation, X.G. and Y.L.; methodology, C.Z.; project administration, X.G.; resources, Y.L.; software, X.G., Y.L. and C.Z.; supervision, X.G.; validation, C.T.; writing—original draft, X.G.; writing—review and editing, X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported financially by the National Natural Science Foundation of China (Grant Nos.: 61871230, 51974045) and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
We declare that we have no known competing financial interest or personal relationship that could have appeared to influence the work reported in this paper.
References
- Sheng, S.; Wen, H.; Xie, G.; Li, Y. The Reappearance of Poetic Beauty in Chaos. Symmetry 2022, 14, 2445. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.; Bao, H.; Chen, M.; Bao, B. Generating multi-scroll Chua’s attractors via simplified piecewise-linear Chua’s diode. IEEE Trans. Circuits Syst. I Reg. Pap. 2019, 66, 4767–4779. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Zhao, Y.; Liu, S. Memristor-type chaotic mapping. Chaos 2022, 32, 021104. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lei, T.; Liu, Z. Offset parameter cancellation produces countless coexisting attractors. Chaos 2022, 32, 121104. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Ren, X.; Wu, H.; Xu, Q.; Bao, B. Periodically varied initial offset boosting behaviors in a memristive system with cosine memductance. Front. Inf. Technol. Electron. Eng. 2019, 20, 1706–1716. [Google Scholar] [CrossRef]
- Gu, H.; Li, C.; Li, Y.; Ge, X.; Lei, T. Various patterns of coexisting attractors in a hyperchaotic map. Nonlinear Dyn. 2023, 1–12. [Google Scholar] [CrossRef]
- Ma, M.; Xiong, K.; Li, Z.; Sun, Y. Dynamic behavior analysis and synchronization of memristor-coupled heterogeneous discrete neural networks. Mathematics 2023, 11, 375. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Yao, Z.; Ma, J. A feasible neuron for estimating the magnetic field effect. Nonlinear Dyn. 2020, 102, 1849–1867. [Google Scholar] [CrossRef]
- Wang, S.; Wang, C.; Xu, C. An image encryption algorithm based on a hidden attractor chaos system and the Knuth–Durstenfeld algorithm. Opt. Lasers Eng. 2020, 128, 105995. [Google Scholar] [CrossRef]
- Panda, A.K.; Ray, K.C. A coupled variable input LCG method and its VLSI architecture for pseudorandom bit generation. IEEE Trans. Instrum. Meas. 2019, 69, 1011–1019. [Google Scholar] [CrossRef]
- Kong, S.; Li, C.; Jiang, H.; Zhao, Y.; Wang, Y. Asymmetry Evolvement and Controllability of a Symmetric Hyperchaotic Map. Symmetry 2021, 13, 1039. [Google Scholar] [CrossRef]
- Lei, T.; Zhou, Y.; Fu, H.; Huang, L.; Zang, H. Multistability dynamics analysis and digital circuit implementation of entanglement-chaos symmetrical memristive system. Symmetry 2022, 14, 2586. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Wang, N.; Zhu, L.; Chen, M.; Bao, B. Initials-boosted coexisting chaos in a 2D sine map and its hardware implementation. IEEE Trans. Ind. Informat. 2020, 17, 1132–1140. [Google Scholar] [CrossRef]
- Sprott, J.C.; Jafari, S.; Khalaf, A.J.M.; Kapitaniak, T. Megastability: Coexistence of a countable infinity of nested attractors in a periodically-forced oscillator with spatially-periodic damping. Eur. Phys. J.-Spec. Top. 2017, 226, 1979–1985. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Zheng, J.; Wang, X.; Zeng, Z.; Peng, X. Generating any number of initial offset-boosted coexisting Chua’s double-scroll attractors via piecewise-nonlinear memristor. IEEE Trans. Ind. Electron. 2021, 69, 7202–7212. [Google Scholar] [CrossRef]
- Jafari, S.; Pham, V.T.; Golpayegani, S.M.R.H.; Moghtadaei, M.; Kingni, S.T. The relationship between chaotic maps and some chaotic systems with hidden attractors. Int. J. Bifurc. Chaos 2016, 26, 1650211. [Google Scholar] [CrossRef]
- Panahi, S.; Sprott, J.C.; Jafari, S. Two simplest quadratic chaotic maps without equilibrium. Int. J. Bifurc. Chaos 2018, 28, 1850144. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Sun, J.; Zhang, X.; Sun, Y.; Iu, H.H. Memristor-coupled asymmetric neural networks: Bionic modeling, chaotic dynamics analysis and encryption application. Chaos Solitons Fractals 2023, 166, 112905. [Google Scholar] [CrossRef]
- Chen, M.; Ren, X.; Wu, H.; Xu, Q.; Bao, B. Interpreting initial offset boosting via reconstitution in integral domain. Chaos Solitons Fractals 2020, 131, 109544. [Google Scholar] [CrossRef]
- Iskakova, K.; Alam, M.M.; Ahmad, S.; Saifullah, S.; Akgül, A.; Yılmaz, G. Dynamical study of a novel 4D hyperchaotic system: An integer and fractional order analysis. Math. Comput. Simul. 2023, 208, 219–245. [Google Scholar] [CrossRef]
- Zhou, X.; Li, C.; Li, Y.; Lu, X.; Lei, T. An amplitude-controllable 3-D hyperchaotic map with homogenous multistability. Nonlinear Dyn. 2021, 105, 1843–1857. [Google Scholar] [CrossRef]
- Liang, Z.; Sun, K.; He, S. Design and dynamics of the multicavity hyperchaotic map based on offset boosting. Eur. Phys. J. Plus 2022, 137, 51. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Zhang, S.; Chen, G.; Zeng, Z. A Self-reproduction hyperchaotic map with compound lattice dynamics. IEEE Trans. Ind. Electron. 2022, 69, 10564–10572. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Xu, C.; Hong, Q.; Yao, W.; Sun, Y. An ex-tremely simple multiwing chaotic system: Dynamics analysis, encryption application, and hardware implementation. IEEE Trans. Ind. Electron. 2021, 68, 12708. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, K.; He, S. A discrete memristor model and its application in henon map. Chaos Solitons Fractals 2020, 137, 109873. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Zheng, J.; Wang, X.; Zeng, Z.; Chen, G. Memristive Autapse-Coupled Neuron Model With External Electromagnetic Radiation Effects. IEEE Trans. Ind. Electron. 2022, 1–9. [Google Scholar] [CrossRef]
- Lai, Q.; Lai, C. Design and implementation of a new hyperchaotic memristive map. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2331–2335. [Google Scholar] [CrossRef]
- He, S.; Natiq, H.; Banerjee, S.; Sun, K. Complexity and chimera states in a network of fractional-order laser systems. Symmetry 2021, 13, 341. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine chaotification model for enhancing chaos and its hardware implementation. IEEE Trans. Ind. Electron. 2018, 66, 1273–1284. [Google Scholar] [CrossRef]
- Zhou, Y.; Hua, Z.; Pun, C.M.; Chen, C.P. Cascade chaotic system with applications. IEEE Trans. Cybern. 2014, 45, 2001–2012. [Google Scholar] [CrossRef]
- Ahmad, M.; Al Solami, E.; Wang, X.Y.; Doja, M.N.; Beg, M.S.; Alzaidi, A.A. Cryptanalysis of an image encryption algorithm based on combined chaos for a BAN system, and improved scheme using SHA-512 and hyperchaos. Symmetry 2018, 10, 266. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, W.; Aouiti, C.; Liu, Z.; Yao, L. Bifurcation insight for a fractional-order stage-structured predator–prey system incorporating mixed time delays. Math. Meth. Appl. Sci. 2023, 1–16. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Cao, Y.; Xiong, L.; Chen, X. An effective multiple-image encryption algorithm based on a 3D cube and hyperchaotic map. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1535–1551. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Li, P.; Yan, J.; Yao, L. Bifurcation mechanism for fractional-order three-triangle multi-delayed neural networks. Neural Process. Lett. 2022, 1–27. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Liu, Z.; Pang, Y.; Liao, M.; Aouiti, C. New insight into bifurcation of fractional-order 4D neural networks incorporating two different time delays. Commun. Nonlinear Sci. 2023, 118, 107043. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).