Nonlinear T-symmetry Quartic, Sextic, Octic Oscillator Models under Real Spectra

Abstract

We propose nonlinear model T-symmetry operators having quartic, sextic, octic anharmonicity and inverse quadratics under real spectra. In fact, the model operator is non-Hermitian but real in nature. A comparison with the corresponding hermitian counterpart shows higher energy levels (E^T ≫ E^hermitian).

1. Introduction

Since the discovery of $PT$-symmetry, real spectra of quantum operators are now confined to hermiticity, the space–time invariance property [1,2]. However, complex quantum systems can be $PT$ symmetry ($[PT,H]=0$) or T-symmetry ($[T,H]=0$). In the above, P stands for the parity operator having the behavior: $Px{P}^{-1}=-x$ and a time reversal operator (T) transformation nature, i.e., $Ti{T}^{-1}=-i$. The real spectra study under T-symmetry is very limited [3,4], unlike in PT-symmetry [2,5]. In fact, Hatano and Nelson [3] proposed a model theoretical analysis on localization transition in superconductors relating to Meissner’s transverse effect using imaginary vector potential. Later on, T-symmetry analysis involving a mod operator ($\left|x\right|$) and a harmonic oscillator was considered in the literature, e.g., [4].

Till now, all the discussions are pertaining to linear models only. In fact, nonlinear quantum systems are not exactly solvable, so spectral studies are not yet an industry [6]. In this paper, we propose a model of a nonlinear T-symmetry operator using the mean field models reported earlier by Ciosloski [6] and study its spectral nature as follows.

2. Non-Hermitian Models Having Real Eigenvalues

2.1. Operator Model

Here, we present a simple non-hermitian Hamiltonian using a simultaneous coordinate $\left(x\right)$ and momentum $\left(p\right)$ transformation in real and complex space as

$$x=x^{\prime }=x+1$$

(1)

and

$$p=p^{\prime }=p+i$$

(2)

Now applying the same to Harmonic oscillator, we have

$$H^{\prime }={(p+i)}^2+{(x+1)}^2$$

(3)

In a simplified form, this is written as

$$H^{{}^{\prime }}=p^2+x^2+2(x+ip)$$

(4)

In fact, energy levels of this operator $H^{{}^{\prime }}$ are

$$E_n^{{}^{\prime }}=2n+1$$

(5)

which remains the same as a simple harmonic oscillator. In fact, the above operator is linear, and the corresponding nonlinear operator can be written as [6]

$$H_N^{{}^{\prime }}|\psi >=[p^2+\int {\psi }^{*}\left(x\right)x^2\psi \left(x\right)dx+2(x+ip)]|\psi >$$

(6)

In short, this is expressed as [6]

$$H_N^{{}^{\prime }}=p^2+<x^2>+2(x+ip)$$

(7)

here, we use $<x^2>$ as $\int {\psi }^{*}\left(x\right)x^2\psi \left(x\right)dx$. It should be kept in mind that the energy levels of $H_N^{{}^{\prime }}$ are complex, and it is a case of broken T-symmetry. However, energy levels of

$$H_N=p^2+x^2+<x^2>+2(x+ip)$$

(8)

are real. Below, we cite the first four energy levels in Table 1.

Table 1. First four energy levels of the T-symmetry operator (Equation (8)).

${\mathit{H}}_{\mathit{N}}$
1.0379
3.1139
5.1387
7.1570

In this context, we would like to compare the present ground state energy with that of Cioslowski [6] on Hamiltonian

$$H_{Cioslowski}=p^2+x^2+\alpha <x^2>x^2$$

(9)

in Table 2.

Table 2. Ground state energy comparison.

Energy	$\mathit{\alpha }$	Present	Previous [6]
	0.5	0.59574	0.59574
	1	0.66235	0.66235
$<x^2>$	0.5	0.41964	0.41964
	1	0.37743	0.37743

For the interested reader, we present the ground state wave function for $\alpha =1$ in Figure 1.

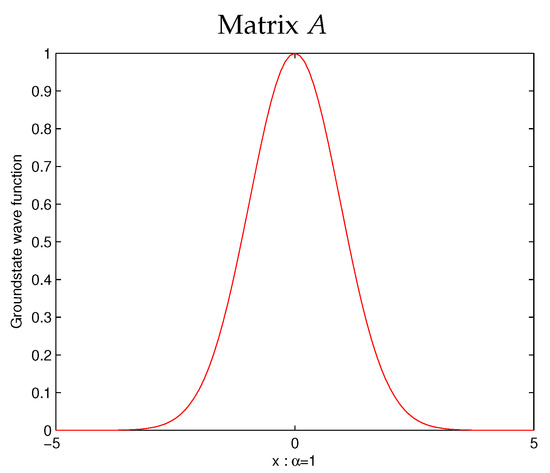
Figure 1. Ground state wave function for $\alpha =1$ (Equation (9)).

In the above, we present a simple model of a T-symmetry operator using the coordinate space. However, in terms of a matrix, the above analysis can be reflected as follows.

2.2. Real Non-Hermitian Matrix Having Real Eigenvalues

Here, we present a model (2 × 2) matrix reflecting the non-hermiticity character satisfying the condition as $H\ne H^{†}$. It should be kept in mind that the present non-Hermitian matrix is nothing but a T-symmetry Hamiltonian in a matrix representation [4]. Here, we present a (2 × 2) matrix as

$$A=\left[\begin{array}{cc}60& 11\\ -11& 30\end{array}\right]$$

(10)

with eigenvalues ${\lambda }_1=55.1980$ and ${\lambda }_2=34.8020$. The above-suggested matrix can also be presented pictorially, as in Figure 2.

Figure 2. Pictorial view of the T-symmetry matrix.

3. Momentum Transformation in Complex Space: Quartic Operator

Consider the transformation,

$$e^{f\left(x\right)}p{e}^{-f\left(x\right)}=p+i\frac{df\left(x\right)}{dx}$$

(11)

If $f\left(x\right)$ is an odd function of x, then the said Hamiltonian is T-symmetry. However, for an even function, the Hamiltonian is generally $PT$-symmetry in nature [5].

3.1. Invariance in Commutation Relation

Under the above transformation, the commutation relation between the coordinate and momentum remains invariant. Mathematically,

$$[x,p]=i$$

(12)

$$[x,p+i\frac{df}{dx}]=[x,p]+[x,\frac{df}{dx}]=[x,p]=i$$

(13)

Let us consider that $f\left(x\right)=\lambda x^3$ and $\lambda =1/3$. Now, we consider the quartic anharmonic oscillator Hamiltonian as

$$H=p^2+\beta x^4$$

(14)

3.2. Hamiltonian on Momentum Transformation

Here, we transform the momentum as $p\to p+i{x}^2$ and use the same in hamiltonian H. After transformation, the resulting Hamiltonian is written as

$$H=p^2+i{x}^{2}p+ip{x}^2+(\beta -1)x^4$$

(15)

On selecting $\beta =2$, we have

$$H=p^2+i{x}^{2}p+ip{x}^2+x^4$$

(16)

It is seen that in the above equation, $ip$ and $x^2$ are in a mixed form. The term $x^2$ can be separated from $ip$ using the mean field approximation [6] as

$$H=p^2+i<x^2>p+ip<x^2>+x^4$$

(17)

After the mean field approximation, the equation becomes nonlinear in nature [6]. Here, $<x^2>$ means $\int {\psi }^{*}{x}^2\psi dx$.

Instead of a complex space transformation, one can have a real space transformation as $p\to p+x^2$

$$H^{†}=p^2+x^{2}p+p{x}^2+3x^4$$

(18)

However, considering the T-symmetry operator, we present the first 10 energy levels of

$$H^{†}=p^2+<x^2>p+p<x^2>+x^4$$

(19)

and make a possible comparison. Interestingly, we find that the energy levels of the T-symmetry operator are higher compared to its Hermitian counterpart. In fact, both of the two are strongly nonlinear. Using the matrix diagonalization method [2], we present the first ten energy levels in Table 3, as given below.

Table 3. First ten energy levels of T-symmetry and Hermiticity operators.

H	${\mathit{H}}^{†}$
1.2628	0.9293
4.0021	3.6686
7.6581	7.3246
11.8472	11.5136
16.4642	16.1307
21.4408	21.1073
26.7309	26.3974
32.3031	31.9675
38.1254	37.7919
44.1836	43.8500

4. Nonlinear Sextic Hamiltonian with Quadratic Nonlinearity

Now, we consider the Hamiltonian as

$$H=p^2+i<x^2>p+ip<x^2>+x^6-x^4$$

(20)

Using the matrix diagonalization method [2], we present the first ten energy levels in Table 4, as given below.

Table 4. First, the ten energy levels of the T-symmetry sextic nonlinear operator (Equation (19)).

Quantum No.	Sextic Operator
0	1.0681
1	3.6568
2	7.8084
3	13.1266
4	19.3569
5	26.3947
6	34. 1618
7	42. 5987
8	51.6585
9	61.3030

5. Nonlinear Octic Hamiltonian with Quadratic Nonlinearity

Now, we consider the Hamiltonian as

$$H=p^2+i<x^2>p+ip<x^2>+x^8-x^4$$

(21)

Using the matrix diagonalization method [2], we present the first ten energy levels in Table 5 as given below.

Table 5. First ten energy levels of the T-symmetry octic nonlinear operator (Equation (20)).

Quantum No.	Sextic Operator
0	1.1305
1	4.2463
2	9.3934
3	16.2161
4	24.4188
5	33.8533
6	44.4223
7	56.0506
8	68.6778
9	82.2541

6. Nonlinear Quartic, Octic Hamiltonian with Quartic Nonlinearity

Now, we consider the Hamiltonian as

$$H=p^2+i<x^4>p+ip<x^4>+x^8$$

(22)

Using the matrix diagonalization method [6], we present the first ten energy levels in Table 6, as given below.

Table 6. Energy levels of T-symmetry octic with a quartic nonlinear operator (Equation (21)).

Quantum No.	Sextic Operator
0	1.2677
1	4.7978
2	10.2869
3	17.3850
4	25.8509
5	35.5398
6	46.3547
7	58.2216
8	71.0812
9	84.8845

7. Nonlinear Singular Model Nonlinearity in Quartic Operator

In the above models, we have considered non-singular models. Here, we focus our attention on a singular model quartic operator as

$$H=p^2+i<\frac{1}{x^2}>p+ip<\frac{1}{x^2}>+x^4$$

(23)

Using the matrix diagonalization method [2], we present the first ten energy levels in Table 7, as given below.

Table 7. Energy levels of T-symmetry singular model quartic operator (Equation (22)).

Quantum No.	Sextic Operator
0	1.0627
1	3.8020
2	7.4580
3	11.6471
4	16.2640
5	21.2407
6	26.5308
7	32.1009
8	37.9253
9	43.9835

8. Method of Calculation

Here, we use the matrix diagonalization method to solve the eigenvalue relation

$$H|\Phi >=E|\Phi >$$

(24)

where

$$|\Phi >=\sum A_m|m>$$

(25)

in which $|m>$ satisfies the eigenvalue relation [2]

$$[p^2+x^2]|m>=(2m+1)|m>$$

(26)

with $m=0,1,2,3,4\cdots$

Below, we present matrix elements using the above method. The numerical matrix element of (4 × 4) matrix is given below (Equation (17))

$$H(4\times 4)=\left[\begin{array}{cccc}5/4& 1694/1977& 1393/985& 0\\ -1694/1977& 21/4& 1482/1223& 4801/980\\ 1393/985& -1482/1223& 49/4& 981/661\\ 0& 4801/980& -981/661& 69/4\end{array}\right]$$

(27)

Interested readers can check the diagonal element from the relation

$$H_{n,n}=1.25+3.5n+1.5n^2$$

(28)

9. Conclusions

In this paper, we present a model of a nonlinear quartic, sextic and oscillator with singular as well as non-singular models satisfying a T-symmetry condition under a mean field approximation [6]. The models are unbroken in nature. However, if T-symmetry is incorrectly selected, it may give complex spectra (see Equation (7)). In other words, real spectra in quantum operators are not only confined to Hermiticity, PT-symmetry but also to T-symmetry. It should be kept in mind that the suggested models can be extended to fractional operators also. As the topic of T-symmetry is not yet an industry, we found minimal literature on it. We believe one can propose hybrid models as

$$H=p^2+x^2+i<x^2>p+ip<x^2>+x^2<x^2>+x^2<x^4>$$

(29)

and many more.