On Statistical Modeling Using a New Version of the Flexible Weibull Model: Bayesian, Maximum Likelihood Estimates, and Distributional Properties with Applications in the Actuarial and Engineering Fields

Abstract

In this article, we present a new statistical modification of the Weibull model for updating the flexibility, called the generalized Weibull-Weibull distribution. The new modification of the Weibull model is defined and studied in detail. Some mathematical and statistical functions are studied, such as the quantile function, moments, the information generating measure, the Shannon entropy and the information energy. The joint distribution functions of the two marginal univariate models via the Copula model are provided. The unknown parameters are estimated using the maximum likelihood method and Bayesian method via Monte Carlo simulations. The Bayesian approach is discussed using three different loss functions: the quadratic error loss function, the LINEX loss function, and the general entropy loss function. We perform some numerical simulations to show how interesting the theoretical results are. Finally, the practical application of the proposed model is illustrated by analyzing two applications in the actuarial and engineering fields using corporate data to show the elasticity and advantage of the proposed generalized Weibull-Weibull model. The practical applications show that proposed model is very suitable for modeling actuarial and technical data sets and other related fields.

1. Introduction

Statistical methods play a crucial role in analysis of measurement system errors [1], test data [2], sports data [3], reliability [4], medical data [5], robust analysis [6], educational data [7], risk assessment [8], social data [9], and other important fields in the tech world. In addition to the areas already mentioned, the application of statistical methods to data analysis in the world of engineering [10] and actuarial data [11] has attracted the interest of researchers. Due to the crucial role that statistical models play in data analysis in the technology industry, many new statistical approaches have been proposed and implemented. These methods are very useful to update the distribution elasticity for statistical distributions [12].

Many applications in the world need statistical description to be more understandable to the reader, but there is no specific statistical distribution that describes all these phenomena. Recently, many attempts have aroused the interest of researchers in the statistical literature to define new flexible distributions for modeling and analyzing data in different domains. Thus, several families have been proposed in the statistical literature that generate novel models by adding one or more parameters to improve other flexible models [13,14,15,16,17,18,19]. These distributions are usually derived from existing distributions by introducing new parameters or making some modifications to the existing probability density functions. Each of these distributions has its own advantages and disadvantages and can be used for different types of data analysis. However, in many applied fields, there is a clear need for modified forms of these models, since the basic models do not provide an adequate fit to real data in many practical situations.

In general, actuarial and technical data are positively skewed [20,21] or unimodally shaped [22] and have heavy tails [23]. In [24], it is shown that right-skewed data sets can be modeled by skewed statistical distributions. Therefore, some unimodal and right-skewed distributions have been used to analyze such data [25,26]. In the letters, most modifications of the Weibull model have been discussed by introducing new families of models.

The Weibull distribution is used to simulate many probabilistic applications. The Weibull distribution has many useful physical explanations and nice and desirable properties. Over the last half century, the Weibull model has become remarkably important in the field of durability and reliability testing. Let X be a random variable (R.V.) that follows the three-parameters Weibull $(\beta ,\sigma ,\mu )$, then its cumulative distribution function (CDF) is given by

$$\begin{array}{c}\hfill G(x;\beta ,\sigma ,\mu )=1-e^{-{\left(\frac{x-\mu }{\sigma }\right)}^{\beta }},x\ge \mu ; \beta ,\sigma ,\mu >0.\end{array}$$

(1)

where $x\ge \mu$, $\sigma >0$ is the scale parameter and $\beta >0$ is the shape parameter. The probability density function (PDF) is

$$\begin{array}{c}\hfill g(x;\beta ,\sigma ,\mu )=\frac{\beta }{\sigma }{\left(\frac{x-\mu }{\sigma }\right)}^{\beta -1}{e}^{-{\left(\frac{x-\mu }{\sigma }\right)}^{\beta }},x\ge \mu ; \beta ,\sigma ,\mu >0.\end{array}$$

(2)

A generalized family of univariate distributions with two additional positive parameters $\tau$ and $\lambda$ was generated by Weibull random variables, proposed by Cordeiro et al. [27] and called the generalized Weibull family. The CDF and PDF of the generalized Weibull family for any baseline CDF $G\left(x\right)$ (for $x\in \mathbb{R}$) and PDF $g\left(x\right)$ are given, respectively, by

$$\begin{array}{c}\hfill F(x;\tau ,\lambda )=1-exp\left[-\tau {(-log[1-G\left(x\right)])}^{\lambda }\right],\end{array}$$

(3)

and

$$\begin{array}{c}\hfill f(x;\tau ,\lambda )=\frac{\tau \lambda g\left(x\right)}{1-G\left(x\right)}{(-log[1-G\left(x\right)])}^{\lambda -1}exp\left(-\tau {\left(-log\left(1-G\left(x\right)\right)\right)}^{\lambda }\right).\end{array}$$

(4)

In this article, we propose a new approach to update the level of the distributional flexibility of the Weibull model. The new flexible distribution, called the generalized Weibull-Weibull model. The extended model is more flexible and can provide a reasonable fit when modeling actuarial and technical data sets and other related fields. Some key motivations for using the new generalized Weibull-Weibull distribution ($GWWD$) modification:

(i)

improve the flexibility and distribution properties of Weibull model.

(ii)

the evolution has added only one parameter to the Weibull distribution in this way, although the family was originally built from two parameters. As the number of parameters increases, many difficulties arise, from which, sequences of estimation problems arise, and more computational effort is required to obtain the basic mathematical properties, etc.

(iii)

a convenient and very simple way to mutate the Weibull model-only one parameter addition.

(iv)

can take several forms: a right-skewed form, a left-skewed form, a decreasing form, a curved form, and a symmetric form. The failure rate function also can take a variety of forms, so it has important standing in reliability analysis.

(v)

the model functions have simple and closed forms.

The rest of this work was presented as follows. The $GWWD$ is provided in Section 2. In Section 3, some mathematical properties and information generating measures are reported. The maximum likelihood estimators as well as the bootstrap confidence intervals: Boot-p Algorithm of the proposed model parameters are obtained in Section 4. The Bayesian estimation of the model parameters under three loss functions are discussed in Section 5. In Section 6, the performance of the introduced estimators ar evaluated via numerical simulations. A real business data sets are analysed in Section 7. Section 8 show the discussion and future works. Some conclusions are provided in Section 9.

2. The $\mathit{GWWD}$

This section provides the $GWWD$ sub-model from Cordeiro generalized Weibull family.

Consider X is R.V. follow (∼) the three-parameters Weibull $(\beta ,\sigma ,\mu )$ with CDF that given in Equation (1). For location parameter $\mu \in {\mathbb{R}}^{+}$, scale parameter $\delta \in {\mathbb{R}}^{+}$, two shape parameters $\tau ,\sigma \in {\mathbb{R}}^{+}$, and $X\ge \mu$, the $GWWD$ can be formed by replacing $g\left(x\right)$ and $G\left(x\right)$ in Equations (4) and (3) by $g(x;\beta ,\sigma ,\mu )$ and $G(x;\beta ,\sigma ,\mu )$ that given in Equations (2) and (1), respectively. The CDF and PDF of the $GWWD$ are given, respectively, by

$$\begin{array}{c}\hfill F(x;\tau ,\delta ,\sigma ,\mu )=1-e^{-\tau {\left(\frac{x-\mu }{\sigma }\right)}^{\delta }},x\ge \mu ; \tau ,\delta ,\sigma ,\mu >0,\end{array}$$

(5)

and

$$\begin{array}{c}\hfill f(x;\tau ,\delta ,\sigma ,\mu )=\frac{\tau \delta }{\sigma }{\left(\frac{x-\mu }{\sigma }\right)}^{\delta -1}{e}^{-\tau {\left(\frac{x-\mu }{\sigma }\right)}^{\delta }},x\ge \mu ; \tau ,\delta ,\sigma ,\mu >0.\end{array}$$

(6)

The hazard rate function (HRF) and survival function (SF) of time t are

$$\begin{array}{c}\hfill H(t;\tau ,\delta ,\sigma ,\mu )=\frac{\tau \delta }{\sigma }{\left(\frac{t-\mu }{\sigma }\right)}^{\delta -1}.\end{array}$$

(7)

and

$$\begin{array}{c}\hfill S(t;\tau ,\delta ,\sigma ,\mu )=e^{-\tau {\left(\frac{t-\mu }{\sigma }\right)}^{\delta }},\end{array}$$

(8)

where $\delta =\lambda \times \beta$. Thus, we find compatibility between the generalized Weibull family and the Weibull model and note that evolution has added only one parameter to the Weibull distribution in this way, although the family was originally built from two parameters $F(x;\tau ,\lambda ,\beta ,\sigma ,\mu )\equiv F(x;\tau ,\lambda \beta ,\sigma ,\mu )$. For $\tau =\lambda =1$, the three-parameter Weibull model $(\beta ,\sigma ,\mu )$ follows as a special sub-model from the $GWWD$ model. For $\tau =\lambda =1$ and $\mu =0$, the two-parameter Weibull model $(\beta ,\sigma )$ follows as a special sub-model from the $GWWD$ model. The one parameter Weibull model $\left(\beta \right)$ follows as a special sub-model from the $GWWD$ when $\tau =\lambda =1$ and $\sigma =\mu =0$. The exponential model $\left(\sigma \right)$ follows as a special sub-model from the $GWWD$ model when $\beta =\tau =\lambda =1$ and $\mu =0$.

For selected parameters values of the $GWWD$ model, Figure 1 show different visual illustrations for the PDF of $GWWD$ model. The corresponding HRF are showed in Figure 2, respectively. The illustrations of the PDF are obtained for (i) $GWWD$ (10.2, 10.9, 0.50, 1.9, 0.20) (blue curve line), (ii) $GWWD$ (02.2, 10.9, 0.50, 1.9, 0.20) (orange curve line), (iii) $GWWD$ (10.2, 06.9, 0.50, 1.9, 0.20) (green curve line), (iv) $GWWD$ (10.2, 10.9, 0.65, 1.9, 0.20) (red curve line), and (v) $GWWD$ (0.20, 12.9, 0.30, 1.1, 0.01) (purple curve line) in the left panel plot. Figure 1 (right panel plot) is for (i) $GWWD$ (0.90, 0.90, 0.90, 0.9, 0.20) (blue curve line), (ii) $GWWD$ (1.20,1.90, 0.45, 1.9, 0.40) (orange curve line), (iii) $GWWD$ (8.20, 6.00, 0.15, 1.9, 0.20) (green curve line), (iv) $GWWD$ (10.2, 1.90, 0.65, 1.9, 0.20) (red curve line), and (v) $GWWD$ (5.20, 13.0, 0.30, 1.1, 0.01) (purple curve line).

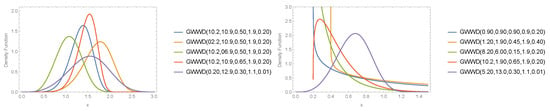
Figure 1. Visual illustration of PDF for the $GWWD (\tau ,\delta ,\sigma ,\mu )$.

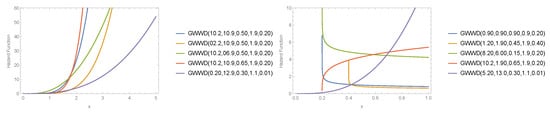
Figure 2. Visual illustration of HRF for the $GWWD (\tau ,\delta ,\sigma ,\mu )$.

Figure 1 show the flexibility of the $GWWD$ model. These modified model can provide heavy tail shaped, reversed-J shaped, decreasing, modified bathtub, increasing, symmetric, asymmetric, and unimodal density shapes. From Figure 2, it can be seen that $GWWD$ has monomodal characteristics and an increased failure rate. The monomodal failure rate and increased modal properties are another advantage of the proposed model along with the heavy tail behaviour. Therefore, the proposed model is suitable for modeling actuarial and technical data sets and other related fields that have corresponding behaviour.

3. Properties of the $\mathit{GWWD}$

Some mathematical quantities and information generating measures of the $GWWD$ were introduced in this section.

3.1. Quantile Function

With reference to a continuous and strictly monotonic CDF. Let $Q_{GWWD}\left(u\right)$ be the quantile function of $GWWD (\tau ,\delta ,\sigma ,\mu )$, then

$$\begin{array}{c}\hfill Q_{GWWD}\left(u\right)=X_q=F^{-1}(u;\tau ,\delta ,\sigma ,\mu ),\end{array}$$

(9)

where $0<u<1$. Inverting $F(x;\tau ,\delta ,\sigma ,\mu )=u$ in (5), the $Q_{GWWD}\left(u\right)$ of $X\sim GWWD (\tau ,\delta ,\sigma ,\mu )$ is

$$\begin{array}{c}\hfill X_q=\sigma {\left(\frac{-1}{\tau }log[1-u]\right)}^{\frac{1}{\delta }}+\mu .\end{array}$$

(10)

The median (Me) of $X\sim GWWD (\tau ,\delta ,\sigma ,\mu )$ when $u=\frac{1}{2}$ is obtained as

$$\begin{array}{c}\hfill Me=\sigma {\left(\frac{0.693147}{\tau }\right)}^{\frac{1}{\delta }}+\mu .\end{array}$$

(11)

Setting $u\sim uniform(0,1)$, we also (10) can be used for simulating $GWWD (\tau ,\delta ,\sigma ,\mu )$ R.V.s.

3.2. Moments

Let $X\sim$GWWD $(\tau ,\delta ,\sigma ,\mu )$, and $r\in \mathbb{Z}$ an optional constant, the expectation of ${\left(\frac{x-\mu }{\sigma }\right)}^r$, can be written as

$$\begin{array}{c}\hfill E\left({\left(\frac{x-\mu }{\sigma }\right)}^r\right)=\frac{\tau \delta }{\sigma }{\int }_{\mu }^{\infty }{\left(\frac{x-\mu }{\sigma }\right)}^{r+\delta -1}{e}^{-\tau {\left(\frac{x-\mu }{\sigma }\right)}^{\delta }}dx,\end{array}$$

(12)

using the integral transformation $z={\left(\frac{x-\mu }{\sigma }\right)}^{\delta }$, we have

$$\begin{array}{ccc}\hfill E\left({\left(\frac{x-\mu }{\sigma }\right)}^r\right)& =& \hfill \tau {\int }_0^{\infty }{z}^{\frac{r}{\delta }}{e}^{-\tau z}dz\hfill \\ & =& \hfill {\tau }^{-\frac{r}{\delta }}\Gamma \left(1+\frac{r}{\delta }\right),\hfill \end{array}$$

(13)

where $\Gamma \left(.\right)$ is gamma constant. Explicit expressions for moments can be produced using (13). In particular, the 1st and 2nd moments, can be derived by sitting $r=1$ and $r=2$, respectively

$$\begin{array}{c}\hfill {\mu }_1^{\prime }=E\left(x\right)=\mu +\sigma {\tau }^{-\frac{1}{\delta }}\Gamma \left(1+\frac{1}{\delta }\right),\end{array}$$

(14)

and

$$\begin{array}{c}\hfill {\mu }_2^{\prime }=E\left(x^2\right)=2\mu {\mu }_1^{\prime }-{\mu }^2+{\sigma }^2{\tau }^{-\frac{2}{\delta }}\Gamma \left(1+\frac{2}{\delta }\right).\end{array}$$

(15)

Using Equation (14) and (15), the variance of $GWWD$, take the form

$$\begin{array}{c}\hfill Var\left(X\right)=\mu +\sigma {\tau }^{-\frac{r}{\delta }}\Gamma \left(1+\frac{1}{\delta }\right)-{\left(2\mu {\mu }_1^{\prime }-{\mu }^2+{\sigma }^2{\tau }^{-\frac{2}{\delta }}\Gamma \left(1+\frac{2}{\delta }\right)\right)}^2.\end{array}$$

(16)

The Skewness and Kurtosis Functions.

By using Equation (10), we can derive (i) the skewness and (ii) the kurtosis. The Skewness ($S_k$) (see, Bowley [28]) and Kurtosis (K) (See, Moor [29]) formulas are, respectively, given by

$$S_k=\frac{2X_{1/2}-X_{3/4}-X_{1/4}}{X_{1/4}-X_{3/4}},\mathrm{and}K=\frac{X_{1/8}-X_{3/8}+X_{5/8}-X_{7/8}}{X_{2/8}-X_{6/8}}.$$

And by using Equation (10), we can write

$$\begin{array}{c}\hfill S_k\left(\delta \right)=\frac{log{\left(\frac{4}{3}\right)}^{\frac{1}{\delta }}-2log{\left(2\right)}^{\frac{1}{\delta }}+log{\left(4\right)}^{\frac{1}{\delta }}}{-log{\left(\frac{4}{3}\right)}^{\frac{1}{\delta }}+log{\left(4\right)}^{\frac{1}{\delta }}},\end{array}$$

(17)

$$\begin{array}{c}\hfill K\left(\delta \right)=\frac{log{\left(\frac{8}{7}\right)}^{\frac{1}{\delta }}-log{\left(\frac{8}{5}\right)}^{\frac{1}{\delta }}+log{\left(\frac{8}{3}\right)}^{\frac{1}{\delta }}-log{\left(8\right)}^{\frac{1}{\delta }}}{log{\left(\frac{4}{3}\right)}^{\frac{1}{\delta }}-log{\left(4\right)}^{\frac{1}{\delta }}},\end{array}$$

(18)

Based on Equations (17) and (18) and as expected, the new shape parameter $\delta$ is the only one that affects the form and value of both $S_k$ and K. Table 1 represent some numerical values of the $X_p$ via $p=0.50, \tau =1.1, \sigma =1.01, \mu =1.1)$, $S_k$ and K for $\delta =0.05,0.2,0.4,0.6,0.8,1,3.288,3.285,3.289,7,20,60,80$.

Table 1. Some numerical values of the $X_p$, $S_k$ and K for some $\delta$ values.

$\mathit{\delta }$	${\mathit{X}}_{\mathit{p}}$	${\mathit{S}}_{\mathit{k}}$	K
0.05	1.1001	0.999998	3325.26
0.2	1.20034	0.938246	7.42379
0.4	1.41835	0.679392	2.44666
0.6	1.56778	0.477511	1.66985
0.8	1.66704	0.347893	1.41426
1	1.73644	0.26186	1.30627
3.288	1.97765	1.12 × 10${}^{-5}$	1.21002
3.285	1.97765	0	1.21002
3.289	1.97769	−2.4 × 10${}^{-5}$	1.21003
7	2.04552	−0.0628706	1.23677
20	2.08695	−0.099024	1.26168
40	2.09841	−0.108735	1.26962
60	2.10226	−0.111969	1.27239
80	2.10419	−0.113586	1.2738

Based on Table 1, Figure 1 plots the $S_k$ (left panel) and K (right panel). Figure 1 shows that, the model $S_k$ is positive (right skew) $\forall \delta <3.285$ then the model $S_k$ become negative (left skew) while the K is positive (leptokurtic) and the Kurtosis effect increase as $\delta$ decrease.

3.3. The Information Generating Function

The information generating function is a mathematical tool used to measure the amount of information contained in a given set of data. It is defined as the sum of the logarithms of all possible outcomes, weighted by their respective probabilities. Finally, the information generating function can be used to compare different models or algorithms for predicting outcomes based on data. By calculating the IGF for each model or algorithm, we can determine which one has better predictive power and thus contains more information about the underlying data.

Let $X\sim f\left(x\right)$, the information generating function ${\mathrm{\Omega }}_{\gamma }\left(X\right)$, for any $\gamma >0$ (See, Golomb [30]), is defined as

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{\gamma }\left(X\right)={\int }_X{\left(f\left(x\right)\right)}^{\gamma }dx.\end{array}$$

(19)

Suppose the R.V. $X\sim$GWWD $(\tau ,\delta ,\sigma ,\mu )$. By substituting (6) in (19), ${\mathrm{\Omega }}_{\gamma }\left(X\right)$ become

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{\gamma }\left(X\right)={\int }_{\mu }^{\infty }{\left(\frac{\tau \delta }{\sigma }{\left(\frac{x-\mu }{\sigma }\right)}^{\delta -1}{e}^{-\tau {\left(\frac{x-\mu }{\sigma }\right)}^{\delta }}\right)}^{\gamma }dx.\end{array}$$

(20)

By using the integral transformation $y=\tau \gamma {\left(\frac{x-\mu }{\sigma }\right)}^{\delta }$, we get

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{\gamma }\left(X\right)={\left(\gamma \tau \right)}^{\frac{\gamma -1}{\delta }}{\left(\frac{\delta }{\sigma }\right)}^{\gamma -1}{\gamma }^{-\gamma }\Gamma \left(\gamma +\frac{1-\gamma }{\delta }\right).\end{array}$$

(21)

In particular ${\mathrm{\Omega }}_1\left(X\right)=1$. Let $X^{\left(n\right)}=(X_1,...,X_n)$ be a simple random sample (SRS) of size n, where $X\sim f\left(x\right)$. Then, the information generating measure of vector $X^{\left(n\right)}$ is given by

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{\gamma }\left(X^{\left(n\right)}\right)& =& \hfill {\int }_{X_n}...{\int }_{X_1}{f}^{\gamma }\left(x_1\right)...f^{\gamma }\left(x_n\right)d{x}_1...d{x}_n\hfill \\ & =& \hfill \prod _{i=1}^n{\int }_{X_i}{f}^{\gamma }\left(x_i\right)d{x}_i={\left({\int }_X{f}^{\gamma }\left(x\right)dx\right)}^n={\left({\mathrm{\Omega }}_{\gamma }\left(X\right)\right)}^n.\hfill \end{array}$$

(22)

Then, the corresponding ${\mathrm{\Omega }}_{\gamma }\left(X^{\left(n\right)}\right)$ based on $GWWD(\tau ,\delta ,\sigma ,\mu )$, is given by

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{\gamma }\left(X^{\left(n\right)}\right)={\gamma }^{-n\gamma }{\left(\gamma \tau \right)}^{n\left(\frac{1-\gamma }{\delta }\right)}{\left(\frac{\delta }{\sigma }\right)}^{n(1-\gamma )}{\left(\Gamma \left(\gamma +\frac{1-\gamma }{\delta }\right)\right)}^n.\end{array}$$

(23)

For more details about the IGF and its extensions one may see López-Ruiz et al. [31].

3.4. The Shannon Entropy (H)

The information generating function can be used to calculate measures of uncertainty such as Shannon entropy. The Shannon entropy measure is useful for quantifying how uncertain we are about a given set of data or how much uncertainty there is in a system. The Shannon entropy, or Information entropy was introduced by Claude Shannon [32], and is defined as

$$\begin{array}{c}\hfill H=-{\int }_{X}f\left(x\right)log\left(f\left(x\right)\right)dx.\end{array}$$

(24)

H can obtain from ${\mathrm{\Omega }}_{\gamma }\left(X\right)$ as

$$\begin{array}{ccc}\hfill H& =& \hfill {\left.-\frac{\partial {\mathrm{\Omega }}_{\gamma }\left(X\right)}{\partial \gamma }\right|}_{\gamma =1}\hfill \\ & =& \hfill 1+ϵ\left(1-\frac{1}{\delta }\right)-log\left(\frac{\delta }{\sigma }\right)-\frac{log\left(\tau \right)}{\delta },\hfill \end{array}$$

(25)

where $\epsilon$ is Euler’ s constant $(\cong 0.577216)$.

3.5. The Informational Energy (IE)

Many series of computational intelligence tools are based on the informational energy (IE). IE for any $X\sim f\left(x\right)$, is given by

$$\begin{array}{c}\hfill IE=-{\int }_X{f}^2\left(x\right)dx.\end{array}$$

(26)

In particular, ${\mathrm{\Omega }}_{\gamma }\left(X\right)$ is simply IE when $\gamma =2$, and is given by

$$\begin{array}{c}\hfill IE=\frac{2^{-2+\frac{1}{\delta }}\delta {\tau }^{\frac{1}{\delta }}\Gamma \left(2-\frac{1}{\delta }\right)}{\sigma }.\end{array}$$

(27)

For some applications and the usefulness on IE, see, Cataron and Andonie [33].

4. Maximum Likelihood Estimation (MLE)

Consider $x_1,x_2,...,x_n$ are observed values of $X_{1:n},X_{2:n},\dots X_{r:n}$ that is an ordered random sample from the $GWWD (\tau ,\delta ,\sigma ,\mu )$ given in (6). The $GWWD (\tau ,\delta ,\sigma ,\mu )$ likelihood is

$$\begin{array}{c}\hfill l={\left(\frac{\tau \delta }{{\sigma }^{\delta }}\right)}^n\left(\prod _{i=1}^n{\left(x_i-\mu \right)}^{\delta -1}\right)e^{-\tau {\sum }_{i=1}^n{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta }},\end{array}$$

(28)

and the log-likelihood function $\left(L\right)$ is

$$\begin{array}{c}\hfill L=nlog\left[\tau \delta \right]-n\delta log\left[\sigma \right]+(\delta -1)\sum _{i=1}^{n}log\left[x_i-\mu \right]-\tau \sum _{i=1}^n{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta }.\end{array}$$

(29)

The first partial derivatives of (29) w.r.t $\tau ,\delta ,\sigma ,\mu$ are

$$\begin{array}{ccc}\frac{\partial L}{\partial \tau }& =& \hfill \frac{n}{\tau }-\sum _{i=1}^n{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta },\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\frac{\partial L}{\partial \delta }& =& \hfill \frac{n}{\delta }-nlog\left[\sigma \right]+\sigma \sum _{i=1}^n\left(log\left[x_i-\mu \right]-\tau {\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta }log\left[\frac{-\mu +x_i}{\sigma }\right]\right),\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\frac{\partial L}{\partial \sigma }& =& \hfill \frac{\delta }{\sigma }\left(-n+\frac{\tau }{\sigma }\sum _{i=1}^n\left(x_i-\mu \right){\left(\frac{x_i-\mu }{\sigma }\right)}^{-1+\delta }\right),\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\frac{\partial L}{\partial \mu }& =& \hfill (\delta -1)\sum _{i=1}^n\left(\frac{\tau \delta }{\sigma }{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta -1}-\frac{1}{x_i-\mu }\right).\hfill \end{array}$$

(33)

The maximum likelihood estimators ${\widehat{\tau }}_{ML},{\widehat{\delta }}_{ML},{\widehat{\sigma }}_{ML},$ and ${\widehat{\mu }}_{ML}$ of the $GWWD (\tau ,\delta ,\sigma ,\mu )$ parameters are the solutions of the Equations (30)–(33).

The asymptotic confidence intervals of the parameters $\tau ,\delta ,\sigma$ and $\mu$. Then $\widehat{V}=V$$({\widehat{\tau }}_{ML},{\widehat{\delta }}_{ML},{\widehat{\sigma }}_{ML},{\widehat{\mu }}_{ML})=\left[{\sigma }_{i,j}\right],i,j=1,2,3,4$ is the variance covariance matrix, such that

$$\begin{array}{c}\hfill V(\tau ,\delta ,\sigma ,\mu )=-{\left[\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{2}L}{\partial {\tau }^2}\frac{{\partial }^{2}L}{\partial \tau \partial \delta }\frac{{\partial }^{2}L}{\partial \tau \partial \sigma }\frac{{\partial }^{2}L}{\partial \tau \partial \mu }}\hfill \\ \\ \hfill {\displaystyle \frac{{\partial }^{2}L}{\partial \delta \partial \tau }\frac{{\partial }^{2}L}{\partial {\beta }^{{}^{\prime }2}}\frac{{\partial }^{2}L}{\partial \delta \partial \sigma }\frac{{\partial }^{2}L}{\partial \delta \partial \mu }}\hfill \\ \\ \hfill {\displaystyle \frac{{\partial }^{2}L}{\partial \sigma \partial \tau }\frac{{\partial }^{2}L}{\partial \sigma \partial \delta }\frac{{\partial }^{2}L}{\partial {\sigma }^2}\frac{{\partial }^{2}L}{\partial \sigma \partial \mu }}\hfill \\ \\ \hfill {\displaystyle \frac{{\partial }^{2}L}{\partial \mu \partial \tau }\frac{{\partial }^{2}L}{\partial \mu \partial \delta }\frac{{\partial }^{2}L}{\partial \mu \partial \sigma }\frac{{\partial }^{2}L}{\partial {\mu }^2}}\hfill \end{array}\right]}^{-1},\end{array}$$

(34)

where

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial {\tau }^2}& =& \hfill -\frac{n}{{\tau }^2},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial \tau \partial \delta }& =& \hfill -\sum _{i=1}^n{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta }log\left[\frac{x_i-\mu }{\sigma }\right],\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial \tau \partial \sigma }& =& \hfill \frac{\delta }{{\sigma }^{\delta +2}}\sum _{i=1}^n{\left(x_i-\mu \right)}^{\delta },\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial \tau \partial \mu }& =& \hfill \frac{\delta }{\sigma }\sum _{i=1}^n{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta -1},\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial {\delta }^2}& =& \hfill -\frac{n}{{\beta }^{{}^{\prime }2}}-\tau \sum _{i=1}^n{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta }log{\left[\frac{x_i-\mu }{\sigma }\right]}^2,\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial \delta \partial \sigma }& =& \hfill \frac{1}{\sigma }\left(-n+\tau \sum _{i=1}^n{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta }\left(1+\delta log\left[\frac{x_i-\mu }{\sigma }\right]\right)\right),\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial \delta \partial \mu }& =& \hfill \sum _{i=1}^n\left(-\frac{1}{x_i-\mu }+\tau \left(\frac{{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta }}{x_i-\mu }+\frac{\delta log\left[\frac{x_i-\mu }{\sigma }\right]{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta -1}}{\sigma }\right)\right),\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial {\sigma }^2}& =& \hfill \frac{\delta }{{\sigma }^2}\left(n+\tau \sum _{i=1}^n(\delta -\frac{2}{{\sigma }^2}-1){(x_i-\mu )}^{\delta }\right),\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial \sigma \partial \mu }& =& \hfill -\tau {\left(\frac{\delta }{\sigma }\right)}^2\sum _{i=1}^n{\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta -1},\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}L}{\partial {\mu }^2}& =& \hfill (\delta -1)\sum _{i=1}^n-\frac{1}{{\left(x_i-\mu \right)}^2}+\tau \delta \left(\frac{1-\delta }{{\sigma }^2}\right){\left(\frac{x_i-\mu }{\sigma }\right)}^{\delta -2}.\hfill \end{array}$$

(44)

A $100(1-ϵ)\%$ two-sided approximate confidence intervals for the parameters $\tau ,\delta ,\sigma$ and $\mu$ are then given by $\widehat{\tau }\pm z_{ϵ/2}\sqrt{V\left(\widehat{\tau }\right)},$ $\widehat{\delta }\pm z_{ϵ/2}\sqrt{V\left(\widehat{\delta }\right)},$ $\widehat{\sigma }\pm z_{ϵ/2}\sqrt{V\left(\widehat{\sigma }\right)},$ and $\widehat{\mu }\pm z_{ϵ/2}\sqrt{V\left(\widehat{\mu }\right)},$ respectively, where $V\left(\widehat{\tau }\right),$ $V\left(\widehat{\delta }\right),$ $V\left(\widehat{\sigma }\right),$ and $V\left(\widehat{\mu }\right)$ are the estimated variances of ${\widehat{\tau }}_{ML},$ ${\widehat{\delta }}_{ML},$ ${\widehat{\sigma }}_{ML},$ and ${\widehat{\mu }}_{ML},$ which are given by the diagonal elements of $\widehat{V}$, and $z_{ϵ/2}$ is the upper $\left(\frac{ϵ}{2}\right)$ percentile of Z(0,1).

The Bootstrap Confidence Intervals: Boot-p Algorithm

Next, obtain the bootstrap confidence intervals for boot-p for $\lambda =(\tau ,\delta ,\sigma ,\mu$), using the algorithms

1.

Generate sample $\left\{x_i\right\}$ from the GWWD $(\tau ,\delta ,\sigma ,\mu )$ of size n and estimate a $\widehat{\lambda }$.

2.

Generate another sample $\left\{x_i^{*}\right\}$ of size n using $\widehat{\lambda }$. Then estimate ${\widehat{\lambda }}^{*}$.

3.

Repeat step 2 B times.

4.

Via $\widehat{F}\left(x\right)=P({\widehat{\lambda }}^{*}\le x)$, that is, the CDF of ${\widehat{\lambda }}^{*}$, the $100(1-\epsilon )\%$ C.I. of $\lambda$ is given by

$$\left({\widehat{\lambda }}_{Boot-p}\left(\frac{ϵ}{2}\right),{\widehat{\lambda }}_{Boot-p}(1-\frac{ϵ}{2})\right),$$

where ${\widehat{\lambda }}_{Boot-p}\left(\tau \right)={\widehat{F}}^{-1}\left(\tau \right)$ and x is prefixed.

For more details about the bootstrap confidence intervals, one may refer to Kundu and Joarder [34].

5. Bayesian Estimation

Bayesian estimation is a method of statistical inference that uses Bayes’ theorem to calculate the probability of an event based on prior knowledge of conditions that might be related to the event. It is a way of combining prior beliefs with new data to arrive at an updated belief. This updated belief is called the posterior probability. Bayesian estimation can be used to estimate parameters in a statistical model, such as the mean and variance of a normal distribution, or to make predictions about future events, see, [35]. We assume that $\tau ,\delta ,\sigma ,$ and $\mu$ are R.V.s that follow the prior PDFs Gamma $(\tau ;a_1,b_1)$, Gamma $(\delta ;a_2,b_2)$, Gamma $(\sigma ;a_3,b_3)$ and Gamma $(\mu ;a_4,b_4)$, respectively, are given by

$$\begin{array}{c}\hfill {\pi }_1\left(\tau \right)=\frac{b_1^{a_1}}{\tau \left(a_1\right)}{\tau }^{a_1-1}exp\left[-b_1\tau \right],\tau ,a_1,b_1>0,\end{array}$$

(45)

$$\begin{array}{c}\hfill {\pi }_2\left(\delta \right)=\frac{b_2^{a_2}}{\tau \left(a_2\right)}{\delta }^{a_3-1}exp\left[-b_3\delta \right],\delta ,a_2,b_2>0,\end{array}$$

(46)

$$\begin{array}{c}\hfill {\pi }_3\left(\sigma \right)=\frac{b_3^{a_3}}{\tau \left(a_3\right)}{\sigma }^{a_3-1}exp\left[-b_3\sigma \right],\sigma ,a_3,b_3>0.\end{array}$$

(47)

and

$$\begin{array}{c}\hfill {\pi }_4\left(\mu \right)=\frac{b_4^{a_4}}{\tau \left(a_4\right)}{\mu }^{a_4-1}exp\left[-b_4\mu \right],\mu ,a_4,b_4>0.\end{array}$$

(48)

Then, the posterior density of $\tau ,\delta ,\sigma ,\mu$ and the data is given by

$$\begin{array}{ccc}\hfill {\pi }^{*}(\tau ,\delta ,\sigma ,\mu |\mathbf{x})& =& \hfill J^{-1}{\tau }^{n+a_1-1}{\delta }^{n+a_2-1}{\sigma }^{a_3-n\delta -1}{\mu }^{a_4-1}\left(\prod _{i=1}^n{\left(x_i-\mu \right)}^{\delta -1}\right)\hfill \\ & \times & \hfill e^{-\left(\tau \left(b_1+{\sum }_{i=1}^n{\left(\frac{x-\mu }{\sigma }\right)}^{\delta }\right)+\left(b_2\delta +b_3\sigma +b_4\mu \right)\right)},\hfill \end{array}$$

(49)

where J is the normalizing constant.

MCMC Method

We use Metropolis Hastings procedure as:

1.

Set start values ${\tau }^{\left(0\right)}=10.025, {\delta }^{\left(0\right)}=0.027, {\sigma }^{\left(0\right)}=0.5$ and ${\mu }^{\left(0\right)}=1.16$. Then, simulate sample of size n from GWWD $({\tau }^{\left(0\right)},{\delta }^{\left(0\right)},{\sigma }^{\left(0\right)},{\mu }^{\left(0\right)})$, next set $l=1$.

2.

Simulate ${\tau }^{(*)},{\delta }^{(*)},{\sigma }^{(*)}$ and ${\mu }^{(*)}$. using the proposal distributions $N({\tau }^{(l-1)},V\left(\widehat{\tau }\right))$, $N({\delta }^{(l-1)},V\left(\widehat{\delta }\right))$, $N({\sigma }^{(l-1)},V\left(\widehat{\sigma }\right))$ and $N({\mu }^{(l-1)},V\left(\widehat{\mu }\right))$.

3.

Calculate r = min$\left(\frac{{\pi }^{*}({\tau }^{(*)},{\delta }^{(*)},{\sigma }^{(*)},{\mu }^{(*)})}{{\pi }^{*}({\tau }^{(l-1)},{\delta }^{(l-1)},{\sigma }^{(l-1)},{\mu }^{(l-1)})},1\right)$.

4.

Simulate U from Uniform (0, 1).

5.

If $U<r$, then $\left({\tau }^{\left(l\right)},{\delta }^{\left(l\right)},{\sigma }^{\left(l\right)},{\mu }^{\left(l\right)}\right)=\left({\tau }^{(*)},{\delta }^{(*)},{\sigma }^{(*)},{\mu }^{(*)}\right)$.

If $U\ge r$, then $\left({\tau }^{(l-1)},{\delta }^{(l-1)},{\sigma }^{(l-1)},{\mu }^{(l-1)}\right)=\left({\tau }^{(*)},{\lambda }^{(*)},{\delta }^{(*)},{\sigma }^{(*)},{\mu }^{(*)}\right)$.

6.

Set $l=l+1$.

7.

Iterate Steps 2–6, M repetitions, and get ${\tau }^{\left(l\right)},{\delta }^{\left(l\right)},{\sigma }^{\left(l\right)}$ and ${\mu }^{\left(l\right)}$ for $l=1,$…$,M$.

Suppose the squared error loss function for the parameter $\lambda =\tau ,\delta ,\sigma$ and $\mu$, given by $L_{SE}(\lambda ,\widehat{\lambda })={(\lambda -\widehat{\lambda })}^2.$ By using the generated random samples from the M-H technique and for N is the nburn. Then, the Bayes estimator of $\lambda$ against the squared error loss function, is given by

$$\begin{array}{c}\hfill {\widehat{\lambda }}_{SE}=E_{\lambda }\left[\lambda |\mathbf{x}\right]=\frac{1}{M-N}\sum _{l=N+1}^M{\lambda }^{\left(l\right)}.\end{array}$$

(50)

Next, suppose the LINEX (LE) loss function, given by

$$L_{LE}\left(\lambda ,\widehat{\lambda }\right)=exp\left[\rho \left(\lambda -\widehat{\lambda }\right)\right]-\rho \left(\lambda -\widehat{\lambda }\right)-1,\rho \ne 0.$$

(51)

The approximate Bayes estimate of $\lambda$ under LE loss function, is given by

$$\begin{array}{c}\hfill {\widehat{\lambda }}_{LE}=\frac{-1}{\rho }log\left(E_{\lambda }\left[exp\left(-\rho \lambda \right)|\mathbf{x}\right]\right)=\frac{-1}{\rho }log\left(\frac{{\sum }_{l=N+1}^{M}exp\left(-\rho {\lambda }^{\left(l\right)}\right)}{M-N}\right),\end{array}$$

(52)

Finally, suppose the general entropy (GE) loss function, given by

$$L_{GE}\left(\lambda ,\widehat{\lambda }\right)={\left(\frac{\widehat{\lambda }}{\lambda }\right)}^{\epsilon }-\epsilon log\left(\frac{\widehat{\lambda }}{\lambda }\right)-1.$$

(53)

The approximate Bayes estimate of the parameters, given by

$${\widehat{\lambda }}_{GE}={\left.\left(E_{\lambda }\left[{\lambda }^{-\epsilon }\right|\mathbf{x}\right]\right)}^{\frac{-1}{\epsilon }}={\left(\frac{1}{M-N}\sum _{l=N+1}^M{\left({\lambda }^{\left(l\right)}\right)}^{-\epsilon }\right)}^{\frac{-1}{\epsilon }},$$

(54)

MCMC HPD Credible Interval Algorithm

1.

Arrange ${\tau }^{(*)},{\delta }^{(*)},{\sigma }^{(*)}$ and ${\mu }^{(*)}$ in rising values.

2.

The lower bounds of $\tau ,\delta ,\sigma ,$ and $\mu$ is in the rank $(M-N)\times \epsilon /2$.

3.

The Upper bounds of $\tau ,\delta ,\sigma ,$ and $\mu$ is in the rank $(M-N)\times (1-\epsilon /2)$.

4.

Iterate the previous steps M times. Get the average value of the lower and upper bounds of $\tau ,\delta ,\sigma ,$ and $\mu$.

6. Simulation Study

In this section, we show the usefulness of the theatrical findings in this paper by conducting series of simulation experiments. The simulations show the bias and estimated risk of bayesian and the maximum likelihood estimates. The simulation experiments can be explained though the following steps:

• We generate sample of sizes n = 25, 50, 100, 200, 400, and 600 from the $GWWD(\tau ,\delta ,\sigma ,\mu )$ via initial parameter values are ${\tau }^{\left(0\right)}=10.025, {\delta }^{\left(0\right)}=0.027, {\sigma }^{\left(0\right)}=0.5$ and ${\mu }^{\left(0\right)}=1.16$.
• Again use each of the cases in step (1) for calculating the Bayesian estimates for both cases of GE, LINEX and SE loss functions. The parameter $\rho$ in LINEX is chosen as −3 and 7. The parameter $\epsilon$ in general entropy is chosen as 0.5.
• For the Bayesian analysis, we take small values for the hyper-parameters as $a_i,b_i\in U(0,1),\forall i=1,2,3$.
• The steeps (1)–(3) are repeated M= 3000 times, then the estimate, bias and estimated risk (ER) in each cases are calculated in Table 2. Obtain the point estimation of the parameter using MLE and MCMC methods (with 10,000 repetitions and 200 burns).
  Table 2. Point and Interval estimation of the parameters $\tau ,\delta ,\sigma ,$ and $\mu$.

  Par.		$\mathit{Point}$					$\mathit{Intrval}$
  		$\mathit{ML}$	$\mathit{SE}$	$\mathit{LE}1$	$\mathit{LE}2$	$\mathit{GE}$	$\mathit{ML}$	$\mathit{Boot}$ $\mathit{strap}$	${\mathit{HPD}}_{\mathit{SE}}$	${\mathit{HPD}}_{\mathit{LE}1}$	${\mathit{HPD}}_{\mathit{LE}2}$	${\mathit{HPD}}_{\mathit{GE}}$
  n = 25	$\tau$	6.3181	10.3431	10.3719	10.2251	10.3209	4.8457 7.7905	4.074 12.802	6.084 13.773	6.1198 13.7789	5.9828 13.7537	6.0457 13.7704
  		−3.7073	0.3177	0.3465	0.1997	0.2955	2.9448	8.728	7.689	7.6591	7.7709	7.7247
  		0.5643	3.3109	3.3618	3.0911	3.2849	5.0785 7.5576	4.105 11.067	7.4 13.714	7.4354 13.7226	7.2949 13.5131	7.3673 13.6937
  							2.4791	6.962	6.314	6.2872	6.2183	6.3264
  	$\delta$	1.0574	0.7607	0.763	0.7508	0.7334	0.7306 1.3843	0.028 3.857	0.248 1.416	0.2481 1.4163	0.2481 1.3778	0.248 1.3543
  		1.03	0.7333	0.7355	0.7234	0.706	0.6537	3.829	1.168	1.1682	1.1297	1.1063
  		0.0278	0.6421	0.6469	0.6215	0.5927	0.7823 1.3326	0.07 2.864	0.331 1.356	0.3319 1.3622	0.3294 1.3177	0.319 1.2817
  							0.5503	2.794	1.025	1.0303	0.9883	0.9627
  	$\sigma$	0.8828	0.5237	0.5238	0.5234	0.5224	0.8025 0.9631	0.268 2.03	0.371 0.632	0.3714 0.6324	0.3712 0.6321	0.3708 0.6319
  		0.3611	0.002	0.0021	0.0017	0.0007	0.1606	1.762	0.261	0.2611	0.2608	0.2611
  		0.0017	0.0049	0.0049	0.0049	0.0049	0.8152 0.9504	0.331 1.705	0.412 0.631	0.4116 0.6309	0.4114 0.6309	0.4108 0.6303
  							0.1352	1.374	0.219	0.2194	0.2195	0.2195
  	$\mu$	4.371	0.1072	0.1132	0.089	0.0312	3.3328 5.4092	0.736 7.05	0.004 0.442	0.0044 0.4616	0.0044 0.3357	0.0015 0.1187
  		3.2126	−1.0512	−1.0452	−1.0694	−1.1272	2.0764	6.314	0.438	0.4572	0.3314	0.1172
  		0.2806	1.1208	1.1116	1.1515	1.2715	3.497 5.245	1.081 6.924	0.009 0.366	0.009 0.4048	0.009 0.2666	0.0026 0.0923
  							1.748	5.843	0.357	0.3958	0.2576	0.0897
  n = 50	$\tau$	6.4887	10.1651	10.1893	10.0699	10.1456	5.4776 7.4997	4.08 13.449	7.103 12.454	7.1026 12.5488	7.1026 12.1554	7.1026 12.3822
  		−3.5368	0.1397	0.1639	0.0445	0.1202	2.0221	9.369	5.351	5.4462	5.0528	5.2795
  		0.2661	1.6401	1.656	1.5826	1.6381	5.6375 7.3398	4.134 11.872	8.057 12.057	8.198 12.1842	7.9144 11.9608	7.9333 12.0548
  							1.7023	7.738	4	3.9862	4.0464	4.1215
  	$\delta$	1.306	0.7934	0.7956	0.7836	0.7683	1.0508 1.5612	0.045 4.306	0.255 1.503	0.2555 1.507	0.2509 1.4554	0.2414 1.396
  		1.2785	0.766	0.7682	0.7561	0.7408	0.5103	4.261	1.248	1.2516	1.2044	1.1546
  		0.0169	0.6945	0.6991	0.6741	0.649	1.0912 1.5208	0.102 3.469	0.317 1.308	0.3177 1.3087	0.3161 1.304	0.3042 1.3018
  							0.4296	3.367	0.991	0.9909	0.988	0.9976
  	$\sigma$	0.9169	0.518	0.5181	0.5178	0.5171	0.8625 0.9712	0.252 2.228	0.366 0.653	0.3665 0.6536	0.3661 0.6531	0.365 0.6523
  		0.3952	−0.0038	−0.0037	−0.004	−0.0047	0.1087	1.976	0.287	0.2871	0.287	0.2874
  		0.0008	0.0044	0.0044	0.0044	0.0045	0.8711 0.9626	0.325 1.885	0.404 0.628	0.4043 0.629	0.4041 0.6261	0.4035 0.6205
  							0.0915	1.56	0.224	0.2247	0.222	0.217
  	$\mu$	4.3197	0.1427	0.1506	0.1163	0.0276	3.6536 4.9858	0.55 7.035	0.003 0.789	0.0026 0.8551	0.0026 0.5736	0.0019 0.1317
  		3.1613	−1.0156	−1.0078	−1.0421	−1.1308	1.3322	6.485	0.786	0.8525	0.571	0.1298
  		0.1155	1.0707	1.0605	1.1081	1.2799	3.7589 4.8804	0.99 6.941	0.006 0.513	0.006 0.5699	0.006 0.3466	0.0023 0.1133
  							1.1215	5.951	0.507	0.5639	0.3406	0.111
  n = 100	$\tau$	6.6441	10.2021	10.2187	10.1356	10.1887	5.968 7.3202	4.063 14.199	6.799 12.282	6.8126 12.3097	6.7487 12.147	6.7835 12.2636
  		−3.3813	0.1767	0.1933	0.1102	0.1633	1.3522	10.136	5.483	5.4971	5.3983	5.4801
  		0.119	1.2782	1.2829	1.2505	1.2797	6.075 7.2133	4.123 12.487	8.245 11.876	8.2567 11.9168	8.1858 11.7579	8.2297 11.8457
  							1.1383	8.364	3.631	3.6601	3.5722	3.6159
  	$\delta$	1.6427	0.7726	0.7748	0.7632	0.7467	1.4372 1.8482	0.055 4.769	0.313 1.293	0.3128 1.2965	0.3127 1.2798	0.3125 1.1974
  		1.6152	0.7451	0.7474	0.7358	0.7193	0.411	4.714	0.98	0.9837	0.9671	0.8849
  		0.011	0.6226	0.6268	0.6051	0.5783	1.4697 1.8157	0.104 4.138	0.366 1.203	0.3686 1.2057	0.3616 1.1889	0.3514 1.1748
  							0.346	4.034	0.837	0.8371	0.8273	0.8234
  	$\sigma$	0.9418	0.5157	0.5158	0.5155	0.5149	0.9056 0.978	0.275 2.37	0.426 0.61	0.4262 0.61	0.4261 0.6098	0.4259 0.6096
  		0.4201	−0.006	−0.006	−0.0062	−0.0068	0.0724	2.095	0.184	0.1838	0.1837	0.1837
  		0.0003	0.0028	0.0028	0.0028	0.0028	0.9114 0.9723	0.348 1.893	0.431 0.601	0.4313 0.6008	0.431 0.6007	0.4295 0.6004
  							0.0609	1.545	0.17	0.1695	0.1696	0.1709
  	$\mu$	4.384	0.232	0.2442	0.19	0.0368	3.9463 4.8216	0.732 7.062	0.009 0.785	0.009 0.8254	0.0082 0.6529	0.0003 0.2209
  		3.2256	−0.9264	−0.9142	−0.9684	−1.1216	0.8753	6.33	0.776	0.8164	0.6447	0.2206
  		0.0499	0.906	0.8896	0.968	1.2624	4.0156 4.7524	1.159 6.969	0.014 0.71	0.014 0.7237	0.0139 0.5954	0.0007 0.1041
  							0.7369	5.81	0.696	0.7097	0.5815	0.1034
  n = 200	$\tau$	6.7887	10.2314	10.2422	10.1876	10.2227	6.3275 7.2499	4.075 14.026	8.125 12.06	8.1681 12.0764	7.9705 11.9846	8.0848 12.0483
  		−3.2367	0.206	0.2168	0.1621	0.1973	0.9224	9.951	3.935	3.9083	4.014	3.9636
  		0.0554	0.7143	0.7158	0.704	0.7145	6.4004 7.1769	4.129 12.796	8.995 11.776	9.0071 11.7941	8.9532 11.6652	8.9856 11.7619
  							0.7765	8.667	2.781	2.787	2.7121	2.7764
  	$\delta$	1.8115	0.6668	0.6696	0.655	0.6279	1.6635 1.9594	0.05 5.23	0.264 1.158	0.2646 1.1606	0.2625 1.1272	0.2527 1.0693
  		1.784	0.6394	0.6422	0.6276	0.6004	0.2959	5.18	0.894	0.896	0.8647	0.8166
  		0.0057	0.4555	0.4599	0.4372	0.4015	1.6869 1.936	0.091 4.817	0.331 1.108	0.3311 1.1208	0.3293 1.0721	0.3208 1.0233
  							0.2491	4.726	0.777	0.7897	0.7428	0.7025
  	$\sigma$	0.9484	0.5123	0.5123	0.5121	0.5119	0.9246 0.9723	0.261 2.43	0.421 0.595	0.4207 0.5951	0.4206 0.595	0.4203 0.5948
  		0.4267	−0.0095	−0.0094	−0.0096	−0.0099	0.0477	2.169	0.174	0.1744	0.1744	0.1744
  		0.0001	0.0017	0.0017	0.0017	0.0017	0.9284 0.9685	0.331 1.968	0.453 0.583	0.453 0.5831	0.4525 0.5829	0.4511 0.5825
  							0.0402	1.637	0.13	0.13	0.1304	0.1315
  	$\mu$	4.1174	0.3197	0.3323	0.2738	0.067	3.8483 4.3864	0.403 7.037	0.024 0.96	0.0248 0.9792	0.0225 0.8627	0.0012 0.5413
  		2.959	−0.8387	−0.8261	−0.8846	−1.0914	0.5381	6.634	0.936	0.9544	0.8402	0.5401
  		0.0188	0.7605	0.7429	0.8281	1.214	3.8909 4.3439	0.664 6.906	0.041 0.84	0.0415 0.8843	0.0391 0.7398	0.0015 0.1768
  							0.453	6.242	0.799	0.8427	0.7007	0.1754
  n = 400	$\tau$	6.9837	10.1202	10.1299	10.0817	10.1126	6.6582 7.3092	4.095 14.269	9.117 11.188	9.126 11.1972	9.0864 11.1518	9.1103 11.1814
  		-3.0417	0.0948	0.1045	0.0563	0.0872	0.651	10.174	2.071	2.0712	2.0653	2.0711
  		0.0276	0.3253	0.3287	0.3134	0.3233	6.7097 7.2577	4.151 13.153	9.229 11.057	9.2409 11.06	9.1831 11.0046	9.2188 11.0555
  							0.548	9.002	1.828	1.819	1.8216	1.8366
  	$\delta$	1.9108	0.5999	0.6029	0.5873	0.5508	1.8052 2.0165	0.029 5.514	0.297 0.97	0.297 0.9733	0.2951 0.9582	0.2851 0.9249
  		1.8834	0.5724	0.5755	0.5599	0.5234	0.2113	5.485	0.673	0.6762	0.6632	0.6398
  		0.0029	0.355	0.359	0.3387	0.2978	1.8219 1.9998	0.074 4.987	0.354 0.913	0.3542 0.9171	0.353 0.8986	0.341 0.8709
  							0.1779	4.913	0.559	0.5628	0.5456	0.5299
  	$\sigma$	0.9527	0.513	0.5131	0.513	0.5127	0.9363 0.9692	0.282 2.319	0.444 0.557	0.4441 0.5575	0.4441 0.5572	0.4441 0.5567
  		0.431	−0.0087	−0.0087	−0.0088	−0.009	0.033	2.037	0.113	0.1134	0.1131	0.1127
  		0.0001	0.0009	0.0009	0.0009	0.0009	0.9389 0.9666	0.35 2.014	0.46 0.555	0.46 0.5552	0.4595 0.5552	0.4581 0.5552
  							0.0278	1.664	0.095	0.0952	0.0957	0.0971
  	$\mu$	4.103	0.5107	0.5225	0.4656	0.2524	3.9184 4.2876	0.388 7.018	0.06 1.25	0.0602 1.2675	0.0584 1.2317	0.0043 1.2211
  		2.9446	−0.6477	−0.6359	−0.6928	-0.906	0.3692	6.63	1.19	1.2073	1.1733	1.2168
  		0.0089	0.5143	0.4997	0.5724	0.953	3.9476 4.2584	0.764 6.867	0.097 1.146	0.0995 1.148	0.0867 1.1402	0.0054 1.0922
  							0.3108	6.103	1.049	1.0486	1.0535	1.0868
  n = 600	$\tau$	7.058	10.1735	10.1822	10.1382	10.1667	6.7917 7.3242	4.064 14.518	9.206 11.574	9.2141 11.6015	9.1754 11.3311	9.1988 11.5544
  		−2.9674	0.1481	0.1568	0.1128	0.1413	0.5324	10.454	2.368	2.3874	2.1557	2.3556
  		0.0184	0.3736	0.382	0.342	0.3681	6.8339 7.2821	4.125 13.313	9.296 11.245	9.2976 11.2547	9.2714 11.2005	9.2924 11.2372
  							0.4482	9.188	1.949	1.957	1.9291	1.9448
  	$\delta$	1.8777	0.5827	0.5865	0.5669	0.5185	1.7953 1.9601	0.025 5.605	0.317 0.834	0.3181 0.8409	0.3126 0.8068	0.2643 0.7471
  		1.8503	0.5552	0.5591	0.5395	0.491	0.1648	5.58	0.517	0.5228	0.4942	0.4828
  		0.0018	0.3266	0.3314	0.3076	0.2572	1.8083 1.9471	0.06 4.97	0.356 0.827	0.3567 0.8342	0.354 0.7973	0.3023 0.7436
  							0.1388	4.91	0.471	0.4775	0.4433	0.4413
  	$\sigma$	0.9365	0.5151	0.5151	0.515	0.5149	0.9237 0.9494	0.247 2.501	0.469 0.558	0.4694 0.5577	0.4691 0.5576	0.4686 0.5572
  		0.4148	−0.0066	−0.0066	−0.0067	−0.0068	0.0257	2.254	0.089	0.0884	0.0884	0.0886
  		0	0.0005	0.0005	0.0005	0.0005	0.9257 0.9474	0.323 1.894	0.483 0.548	0.4826 0.5482	0.4824 0.548	0.4817 0.5477
  							0.0217	1.571	0.065	0.0656	0.0657	0.066
  	$\mu$	3.8824	0.7874	0.7952	0.7561	0.626	3.7438 4.021	0.345 6.939	0.202 1.215	0.2073 1.22	0.182 1.1943	0.0051 1.1814
  		2.724	−0.371	−0.3632	−0.4023	−0.5324	0.2772	6.594	1.013	1.0127	1.0123	1.1764
  		0.005	0.2101	0.203	0.2401	0.433	3.7657 3.9991	0.658 6.754	0.357 1.168	0.3735 1.1817	0.2946 1.1593	0.0135 1.1406
  							0.2333	6.096	0.811	0.8082	0.8647	1.127

  Point estimate: first line represents estimate and second line represents ER. Interval estimate: 95% and 90% interval estimate, respectively. The first and second lines show the credible HPD interval and the corresponding width of the parameter, respectively.
• The $90\%$ and $95\%$ approximate confidence, bootstrap HPD credible intervals with their width are calculated.
• The biases and ERs are given, respectively, by

  $$Bias\left(\widehat{\lambda }\right)=\frac{1}{1000}\sum _{i=1}^{1000}\left({\widehat{\lambda }}_i-\lambda \right),$$

  and

  $$ER\left(\widehat{\lambda }\right)=\frac{1}{1000}\sum _{i=1}^{1000}{\left({\widehat{\lambda }}_i-\lambda \right)}^2,$$
• Coverage probabilities (CPs) are also calculated at the 95% and 90% HPD credible intervals. The simulation results are presented in Table 2 for the parameters $\tau ,\delta ,\sigma ,$ and $\mu$, respectively.

The simulation experiments can be explained though the following steps:

• In most cases, the Bayesian estimates of $\tau$ are overestimated, while the MLE estimates is underestimated.
• In most cases, the estimates of $\delta$ are overestimated.
• In most cases, the Bayesian estimates of $\mu$ and $\sigma$ are underestimated, while the MLE estimates is overestimated.
• In most cases, the Bayesian estimates of $\tau$ is overestimated, while the MLE estimates is underestimated.
• The results shows that the Bayesian estimate based Linex with negative $\rho$ approach gives better estimates other Bayesian estimators.
• The performance of MLE was also good even when the small sample sizes.
• At the level of confidence intervals, there is a significant superiority the Bayesian approach.

7. Application of the $\mathit{GWWD}$

In this section, the flexibility in practice of the $GWWD$ model was illustrated by analyzing two practical data sets. Example 1: The actuarial data that introduced by Wong [36]. The point and interval estimation are presented in Table 3 and Table 4. Example 2: The Civil Engineering Cement Manufacturing Dataset of size 16 was taken from the engineering field that represent the cement measured in $kg$ in a $m^3$ mixture and is given by: 141.3, 168.9, 250, 266, 154.8, 255, 166.8, 251.4, 296, 155, 151.8, 173, 385, 237.5, 167, 213.8.

Table 3. Point estimation of the actuarial data.

			$\mathit{Point}$
Par.	a	b	$\mathit{ML}$	$\mathit{SE}$	$\mathit{LE}1$	$\mathit{LE}2$	$\mathit{GE}$
$\tau$	0.578219	0.74522	0.0108	0.1947	0.1953	0.1923	0.158
			−3.2434	−3.0594	−3.0588	−3.0618	−3.0962
			0.0027	9.3677	9.3641	9.3822	9.5934
$\gamma$	0.774842	0.22833	0.0154	2.626	2.6799	2.399	2.4024
			−0.4222	2.1883	2.2422	1.9613	1.9648
			0.1582	5.1654	5.4436	4.1231	4.2406
$\delta$	0.866376	0.039942	0.5483	0.5499	0.5499	0.5499	0.5499
			−1.9734	−1.9718	−1.9718	−1.9718	−1.9718
			0.001	3.8882	3.8881	3.8882	3.8884
$\sigma$	0.536458	0.645524	0.0046	0.0034	0.0034	0.0034	0.0025
			−1.8343	−1.8355	−1.8355	−1.8355	−1.8364
			0.001	3.369	3.3689	3.3689	3.3724

First line represents estimate, second line represents bias, and third line represents ER.

Table 4. Interval estimation of the actuarial data.

			$\mathit{Interval}$
Par.	a	b	$\mathit{ML}$	${\mathit{HPD}}_{\mathit{S}}$	${\mathit{HPD}}_{\mathit{LE}1}$	${\mathit{HPD}}_{\mathit{LE}2}$	${\mathit{HPD}}_{\mathit{GE}}$
$\tau$	0.578219	0.74522	0.001 0.1123	0.051 0.348	0.0515 0.3487	0.0507 0.3439	0.019 0.3077
			0.1113	0.297	0.2972	0.2932	0.2887
			0.001 0.0962	0.06 0.331	0.0607 0.3314	0.0595 0.3272	0.0328 0.3004
			0.0952	0.271	0.2707	0.2677	0.2676
$\gamma$	0.774842	0.22833	0.001 0.795	1.568 3.846	1.5815 4.0513	1.4289 3.443	1.2721 3.5939
			0.794	2.278	2.4698	2.0141	2.3218
			0.001 0.6717	1.719 3.787	1.7276 3.8726	1.6032 3.3122	1.3592 3.4139
			0.6707	2.068	2.145	1.709	2.0546
$\delta$	0.866376	0.039942	0.5377 0.5589	0.515 0.58	0.5148 0.5802	0.5148 0.5802	0.5147 0.5802
			0.0213	0.065	0.0654	0.0654	0.0655
			0.5393 0.5572	0.525 0.575	0.5249 0.5752	0.5249 0.5751	0.5248 0.5749
			0.0179	0.05	0.0503	0.0502	0.0501
$\sigma$	0.536458	0.645524	0.0017 0.0074	0.001 0.01	0.0002 0.0104	0.0002 0.0104	0.001 0.0102
			0.0057	0.009	0.0102	0.0102	0.0092
			0.0022 0.007	0.001 0.01	0.0002 0.0099	0.0002 0.0099	0.001 0.0097
			0.0048	0.009	0.0097	0.0097	0.0087

The first and second lines show the credible HPD interval and the corresponding width of the parameter, respectively. 95% and 90% interval estimate, respectively.

The data are analysed and the maximum likelihood and Bayesian estimates of the model parameters are obtained. Table 3 shows the result of the point estimation of the actuarial data and Table 4 shows the result of the corresponding interval estimations. To decide about the best fitting among the competitive distributions, One-sample Kolmogorov-Smirnov test statistic with its corresponding p-value are taken calculated. The comparison of the $GWWD$ distribution is made with some important distributions including generalized Weibull two-parameter Weibull distribution (GW-OWD), exponentiated distribution (EXP-WD) and two-parameter Weibull distribution (TW-D). The CDF of the competing probability models are, respectively, given by

$$\begin{array}{c}\hfill F(x;\tau ,\delta ,\sigma )=1-e^{-\tau {\left(\frac{x}{\sigma }\right)}^{\delta }},x\ge 0; \tau ,\delta ,\sigma ,>0,\end{array}$$

(55)

$$\begin{array}{c}\hfill F(x;\tau ,\delta ,\sigma )={\left(1-e^{-{\left(\delta x\right)}^{\sigma }}\right)}^{\tau },x\ge 0; \tau ,\delta ,\sigma >0.\end{array}$$

(56)

$$\begin{array}{c}\hfill F(x;\delta ,\sigma )=1-e^{-\delta x^{\sigma }},x\ge 0; \delta ,\sigma >0.\end{array}$$

(57)

Table 5 shows the one-sample Kolmogorov-Smirnov test of the actuarial data. Table 6 shows the result of the point estimation of the engineering data and Table 7 shows the result of the corresponding interval estimations. The one-sample Kolmogorov-Smirnov test of the engineering data is presented in Table 8.

Table 5. One-sample Kolmogorov-Smirnov test of the actuarial data.

Model	KS	p-Value
$GWWD$	0.15252	0.9476
GW-OWD	0.21753	0.6559
EXP-CD	0.22573	0.6116
TW-D	0.26447	0.4142

Table 6. Point estimation of the engineering data.

			$\mathit{Point}$
Par.	a	b	$\mathit{ML}$	$\mathit{SE}$	$\mathit{LE}1$	$\mathit{LE}2$	$\mathit{GE}$
$\tau$	0.241816	0.521228	0.4401	0.1312	0.1318	0.1292	0.1068
			−2.814	−3.1229	−3.1223	−3.125	−3.1473
			0.3444	9.7559	9.7525	9.7687	9.9083
$\gamma$	0.104293	0.476433	0.1949	0.4171	0.4181	0.4135	0.4034
			1.4649	0.9716	0.9684	0.9837	0.9958
			0.0001	1.2135	1.2084	1.233	1.2613
$\delta$	0.020871	0.796755	1.61	1.4092	1.5439	1.0328	0.7481
			1.1723	0.9715	1.1062	0.5952	0.3105
			2169.2	1.4276	1.7777	0.648	0.4358
$\sigma$	0.764295	0.747721	0.5833	0.8495	0.8565	0.8213	0.7738
			−1.2555	−0.9894	−0.9824	−1.0176	−1.065
			0.0853	1.2636	1.2578	1.2885	1.4146

First line represents estimate, second line represents bias, and third line represents ER.

Table 7. Interval estimation of the engineering data.

			$\mathit{Interval}$
Par.	a	b	$\mathit{ML}$	${\mathit{HPD}}_{\mathit{S}}$	${\mathit{HPD}}_{\mathit{LE}1}$	${\mathit{HPD}}_{\mathit{LE}2}$	${\mathit{HPD}}_{\mathit{GE}}$
$\tau$	0.241816	0.521228	−0.7101 1.5903	0.039 0.268	0.0386 0.2701	0.0383 0.2571	0.0237 0.2036
			2.3003	0.229	0.2315	0.2188	0.1798
			−0.5282 1.4084	0.043 0.241	0.0433 0.2424	0.0433 0.2344	0.031 0.1875
			1.9365	0.198	0.1991	0.1911	0.1565
$\gamma$	0.104293	0.476433	0.0568 0.3928	0.1497 0.8421	0.1503 0.8439	0.1495 0.8371	0.1468 0.8244
			0.3359	0.6924	0.6935	0.6876	0.6775
			0.0747 0.3576	0.1800 0.8080	0.1798 0.8112	0.1792 0.7962	0.1748 0.7854
			0.2828	0.6279	0.6313	0.6169	0.6106
$\delta$	0.020871	0.796755	-89.67 92.89	0.016 2.582	0.0159 2.8682	0.0159 2.1998	0.0134 2.103
			182.574	2.566	2.8523	2.1839	2.0896
			−75.2386 78.45	0.369 2.504	0.418 2.6762	0.2734 1.92	0.0386 1.8855
			153.697	2.135	2.2583	1.6467	1.8469
$\sigma$	0.764295	0.747721	0.011 1.1556	0.188 1.976	0.1964 1.9812	0.1638 1.9556	0.0951 1.9545
			1.1446	1.788	1.7848	1.7918	1.8594
			0.1015 1.0651	0.276 1.703	0.2779 1.7123	0.2657 1.6623	0.1272 1.6482
			0.9636	1.427	1.4345	1.3966	1.5209

The first and second lines show the credible HPD interval and the corresponding width of the parameter, respectively. 95% and 90% interval estimate, respectively.

Table 8. One-sample Kolmogorov-Smirnov test of the engineering data.

Model	KS	p-Value
$GWWD$	0.52541	0.0001215
GW-OWD	0.57143	1.797 × 10${}^{-5}$
EXP-WD	0.85718	6.106 × 10${}^{-14}$
TW-D	0.53245	9.201 × 10${}^{-5}$

8. Discussion and Future Works

The use of the Weibull distribution with the generalized Weibull distribution family used resulted in the generation of a new distribution with desirable properties that had not been studied previously. Generating new distributions from the existing ones is useful if the new distribution has sufficiently novel, and interesting properties. Applying this distribution to new domains and using it to model processes not described in the statistical literature is not straightforward. In this work, we applied a new $GWWD$ model to new domains and used the distribution in modeling processes that differ from those in the statistical literature. We have presented a new application to actuarial and engineering data using several different methods. Sometimes the development of a basic model such as the Weibull distribution, exponential distribution, or other basic distributions using a particular family is not sufficient and leads to some problems that need to be considered. Sometimes the developed model lacks a scale or location parameter, which proves to be a weakness when modeling different data. One of the strengths of the proposed $GWWD$ is that it has a location parameter $\mu$, a scale parameter $\sigma$, and two shape parameters $\tau$ and $\delta$. Increasing the number of parameters leads to problems in the estimation and complexity of the shape of the distribution and its equations, which leads to difficulties in the application of the new distribution. This study showed a match between the family used and the Weibull distribution, resulting in a new distribution to which only one shape parameter $\tau$ was added, increasing flexibility even though the family used had two parameters. The Kolmogorov-Smirnov test is a test that can be used to check whether a data set comes from a particular distribution. It is a non-parametric test. It is applicable for continuous distributions. The basic idea is to compare the empirical CDF and the actual CDF of the distribution and find out how far the empirical CDF is from the ideal CDF. The test works by calculating the maximum difference between the two cumulative distribution functions. If this maximum difference is greater than a certain threshold, the null hypothesis is rejected. The null hypothesis states that the two samples are from the same distribution. The Kolmogorov-Smirnov test is used to compare two samples and determine if they are from the same distribution. It can also be used to compare a sample to a theoretical distribution. From the results in Table 5 and Table 8, it can be seen that the $GWWD$ model could be selected as the best model among the fitted models because the proposed model has the highest values for the Kolmogorov-Smirnov p-value. Other methods can be used to estimate the parameters, extend the practical application of data from other areas, and use the proposed distribution as a new family to generate new models and improve the properties of the distribution.

9. Concluding Remarks

In this paper, a new extension of the Weibull distribution, the generalized Weibull-Weibull distribution with four parameters, is proposed and studied in detail. The proposed model changes the properties of the distribution. In addition, the flexibility of the density shapes of the model was improved. It can take a heavy tail shape, an inverted J-shape, a decreasing modified bathtub shape, an increasing symmetric, asymmetric and unimodal shape. The failure rate function can take a variety of forms and therefore occupies an important place in reliability analysis. All the functions obtained have a closed form, which has the advantage that the distribution can be studied scientifically as well as used in practical applications for control, prediction and decision making. The quantile function, moments, information generating function, information generating measure, Shannon entropy, information energy, and joint CDF of the two marginal univariate distributions were provided in simple and closed forms. Maximum likelihood estimators for the intended model parameters and a Bayesian study were used to estimate the parameters. Performance is evaluated against the detailed classified simulation results to determine the best estimation approach for the model parameters. The one-sample Kolmogorov-Smirnov test is used to compare the generalized Weibull-Weibull distribution and other competing distributions. After analyzing these two data sets, the results indicate that the generalized Weibull-Weibull distribution provides a better fit than other competing models and could be chosen as an appropriate model for analyzing the actuarial and technical data.