The Ascending Ramsey Index of a Graph

Abstract

Let G be a graph with a given red-blue coloring c of the edges of G. An ascending Ramsey sequence in G with respect to c is a sequence $G_1$, $G_2$, …, $G_k$ of pairwise edge-disjoint subgraphs of G such that each subgraph $G_i$ ($1\le i\le k$) is monochromatic and $G_i$ is isomorphic to a proper subgraph of $G_{i+1}$ ($1\le i\le k-1$). The ascending Ramsey index $A{R}_c\left(G\right)$ of G with respect to c is the maximum length of an ascending Ramsey sequence in G with respect to c. The ascending Ramsey index $AR\left(G\right)$ of G is the minimum value of $A{R}_c\left(G\right)$ among all red-blue colorings c of G. It is shown that there is a connection between this concept and set partitions. The ascending Ramsey index is investigated for some classes of highly symmetric graphs such as complete graphs, matchings, stars, graphs consisting of a matching and a star, and certain double stars.

1. Introduction

One of the major topics in graph theory involving edge colorings takes place in Ramsey theory where typically for each red-blue edge coloring of a given graph, one of two prescribed monochromatic subgraphs occur. Here, our goal is to determine, for each red-blue edge coloring of certain graphs, the existence of a maximum number of monochromatic pairwise edge-disjoint subgraphs satisfying conditions that were initially specified in what is now a well-known conjecture addressing graph decompositions. In order to present a solution to this problem for two particular classes of graphs, we first consider a question involving sets and then apply the symmetry of the resulting concepts.

Let S be a set such that $\left|S\right|=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$ for some integer $k\ge 2$. Since ${\sum }_{i=1}^{k}i=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$, the set S can be partitioned into k subsets $S_1,S_2,\dots ,S_k$ such that $|S_i|=i$ for $i=1,2,\dots ,k$. Now, suppose that we are given a partition $\{S^{\prime },S^{″}\}$ of S into two subsets. A question here is the following:

Is there also a partition of S into k subsets $S_1,S_2,\dots ,S_k$ such that $|S_i|=i$ for $i=1,2,\dots ,k$ with the added property that either $S_i\subseteq S^{\prime }$ or $S_i\subseteq S^{″}$ for each integer i with $1\le i\le k$?

We show that this question has an affirmative answer. This is obvious if $k=2$, in which case $\left|S\right|=\left(\genfrac{}{}{0pt}{}{2+1}{2}\right)=3$. Let us assume such is the case for every set T with $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$ elements and every partition $\{T^{\prime },T^{″}\}$ of T. Let S be a set such that $\left|S\right|=\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$ and let $\{S^{\prime },S^{″}\}$ be an arbitrary partition of S into two subsets. Since $k\ge 2$, it follows that $(k+2)(k+1)\ge 4(k+1)$ and so $\frac{1}{2}\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)\ge k+1$. Consequently, in any partition of S into two subsets $S^{\prime }$ and $S^{″}$, at least one of these two sets contains at least $k+1$ elements. We may assume that $S^{\prime }$ contains a subset $S_{k+1}$ of $k+1$ elements. Let $S^{*}=S-S_{k+1}$. Thus, $|S^{*}|=|S|-|S_{k+1}|=\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)-(k+1)=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$.

We now partition the set $S^{*}$ into two subsets $S_1^{*}=S^{\prime }-S_{k+1}$ and $S_2^{*}=S^{″}$. By the induction hypothesis, $S^{*}$ contains k pairwise disjoint subsets $S_1,S_2,\dots ,S_k$ such that $|S_i|=i$ for $i=1,2,\dots ,k$ and either $S_i\subseteq S_1^{*}$ or $S_i\subseteq S_2^{*}$ for each integer i with $1\le i\le k$. Therefore, for the partition $\{S^{\prime },S^{″}\}$ of S into two subsets, there are $k+1$ pairwise disjoint subsets $S_1,S_2,\dots ,S_{k+1}$ of S such that $|S_i|=i$ for $1\le i\le k+1$ where either $S_i\subseteq S^{\prime }$ or $S_i\subseteq S^{″}$ for each integer i with $1\le i\le k+1$.

If S is a set such that $\left|S\right|=m$ for some integer $m\ge 3$, then there is an integer $k\ge 2$ such that $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$. By the discussion above, the following observation can now be made.

Let S be a set with $\left|S\right|=m\ge 3$ such that $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$ for some integer $k\ge 2$ and let $\{S^{\prime },S^{″}\}$ be a partition of S into two subsets. Then, there exist k pairwise disjoint subsets $S_1,S_2,\dots ,S_k$ of S such that $|S_i|=i$ for $i=1,2,\dots ,k$ and either $S_i\subseteq S^{\prime }$ or $S_i\subseteq S^{″}$ for each integer i with $1\le i\le k$.

From this, a more general question arises.

Let S be a set with $\left|S\right|=m\ge 3$ where $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$ for some integer $k\ge 2$ such that there is some prescribed structure among the elements of S. If $\{S^{\prime },S^{″}\}$ is a partition of S into two subsets, do there exist k pairwise disjoint subsets $S_1,S_2,\dots ,S_k$ of S such that (1) $|S_i|=i$ for $i=1,2,\dots ,k$, (2) either $S_i\subseteq S^{\prime }$ or $S_i\subseteq S^{″}$ for each integer i with $1\le i\le k$, and (3) for each integer i with $2\le i\le k$, there is a substructure of $i-1$ elements of $S_i$ identical with that of $S_{i-1}$? If there exists no such k subsets of S with these properties, then what is the maximum number of pairwise disjoint subsets of S having all three properties?

In order to investigate this problem, we turn to the area of graph theory.

2. Ascending Subgraph Sequences

A popular area of study in graph theory is graph decompositions. One problem in this area involves determining graphs that can be decomposed into subgraphs, every two of which are isomorphic, referred to as isomorphic decompositions. For example, it is well known that every complete graph of odd order 3 or more can be decomposed into Hamiltonian cycles and every complete graph of even order as well as every regular bipartite graph can be decomposed into perfect matchings.

In [1], the question was posed for a graph G of determining the maximum number of subgraphs (without isolated vertices) of G into which G can be decomposed where no two subgraphs are isomorphic. One way to look at this problem is the following. For a positive integer k, let $f:E\left(G\right)\to \left[k\right]=\{1,2,\dots ,k\}$ be a labeling of the edges of G such that each label in $\left[k\right]$ is assigned to at least one edge of G. For $1\le i\le k$, let $G_i$ be the subgraph of G induced by the edges labeled i. What is the maximum positive integer k of such a labeling for which $G_i\ncong G_j$ for every pair $i,j$ of integers? The maximum such positive integer k is referred to as the irregular decomposition index of the graph G. For example, the irregular decomposition indices of the graphs $G=K_4-e$ and $H=K_7$ in Figure 1 are 3 and 8, respectively. The three subgraphs in the decomposition $\{G_1,G_2,G_3\}$ of G are $G_1=2K_2$, $G_2=P_3$, and $G_3=K_2$, while the eight subgraphs in the decomposition $\{H_1,H_2,\dots ,H_8\}$ of H are $H_1=K_3$, $H_2=P_3$, $H_3=K_{1,3}$, $H_4=P_3+K_2$, $H_5=3K_2$, $H_6=P_5$, $H_7=2K_2$, and $H_8=K_2$. In fact, G and H are the unique graphs of smallest order and smallest size having irregular decomposition indices of 3 and 8, respectively.

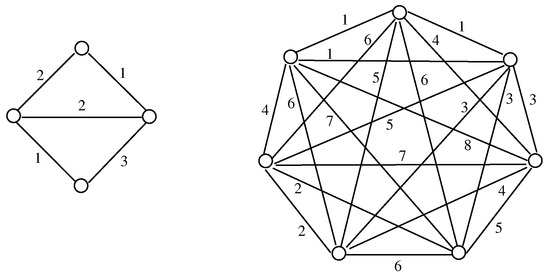
Figure 1. Irregular decompositions of $K_4-e$ and $K_7$.

The path $P_{35}$ of order 35 and size 34 has an irregular decomposition index of 11, as does the cycle $C_{34}$. No path or cycle of smaller order has an irregular decomposition index of 11. The eleven subgraphs in the decomposition $\mathcal{F}=\{F_1,F_2,\dots ,F_{11}\}$ of $P_{35}$ are $F_1=4K_2$, $F_2=2K_2+P_3$, $F_3=3K_2$, $F_4=K_2+P_4$, $F_5=2P_3$, $F_6=K_2+P_3$, $F_7=2K_2$, $F_8=P_5$, $F_9=P_4$, $F_{10}=P_3$, and $F_{11}=K_2$. An irregular decomposition $\{G_1,G_2,\dots ,G_{11}\}$ of $C_{34}$, where $G_i\cong F_i$ for $1\le i\le 11$, can be obtained from the decomposition $\mathcal{F}$ of $P_{35}$ by identifying the two end-vertices of $P_{35}$ in Figure 2.

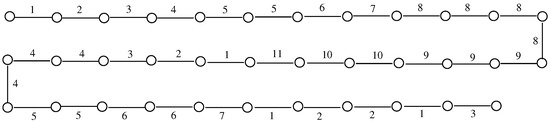
Figure 2. An irregular decomposition of $P_{35}$.

The question posed in [1] led to another concept introduced in [1]. A sequence $G_1$, $G_2$, …, $G_k$ of subgraphs (all without isolated vertices) of a graph G (without isolated vertices) is an ascending subgraph sequence in G if $G_i$ is isomorphic to a proper subgraph of $G_{i+1}$ for $i=1,2,\dots ,k-1$. If {$G_1$, $G_2$, …, $G_k$} is also a decomposition of G, then this is an ascending subgraph decomposition of G. If G has size m, then $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$ for some positive integer k and k is the maximum possible length of an ascending subgraph sequence in G. Furthermore, if G has an ascending subgraph sequence of length k, then there is such a sequence $G_1$, $G_2$, …, $G_k$ where $G_i$ has size i for $1\le i\le k$. The following conjecture was stated in [2].

Conjecture 1

(The Ascending Subgraph Decomposition Conjecture). Every graph has an ascending subgraph decomposition.

Upon learning the statement of this conjecture, the famous mathematician Paul Erdős doubted its truth and immediately offered USD 5 for a counterexample. He then participated in a study of the conjecture (see [2]). This conjecture remains unresolved today. Information on this conjecture is presented in [3,4].

3. Ascending Ramsey Sequences

We now change the topic briefly. A well-known area in graph theory is Ramsey theory and one of the most familiar concepts in this theory is Ramsey numbers. In a red-blue coloring of a graph G, every edge of G is colored red or blue. For two graphs F and H (without isolated vertices), the Ramsey number $R(F,H)$ is the minimum positive integer n such that for every red-blue coloring of the complete graph $K_n$ of order n, there is either a subgraph of $K_n$ isomorphic to F all edges of which are colored red (a red F) or a subgraph of $K_n$ isomorphic to H all edges of which are colored blue (a blue H). It is a consequence of a theorem of Ramsey [5] that the number $R(F,H)$ exists for every two graphs F and H. If $F\cong H$, then $R(F,H)=R(F,F)$ is the minimum positive integer n such that every red-blue coloring of $K_n$ results in a monochromatic F. If F and H are both complete graphs, then $R(F,H)$ is called a classical Ramsey number. For example, it is well known that $R(K_3,K_3)=6$, $R(K_4,K_4)=18$, and $R(K_5,K_5)$ are unknown. Not only does every red-blue coloring of $K_6$ produce a monochromatic $K_3$, every red-blue coloring of $K_6$ produces at least two monochromatic subgraphs $K_3$. Additional information involving edge colorings and Ramsey numbers is presented in [6,7,8,9], for example.

In [1], a concept was introduced that deals with both ascending subgraph sequences and monochromatic subgraphs resulting from red-blue colorings of the edges of a graph. Let G be a graph (without isolated vertices) of size m with a red-blue coloring c of G. An ascending subgraph sequence $G_1$, $G_2$, …, $G_k$ of subgraphs of G is an ascending Ramsey sequence (with respect to c) in G if each subgraph $G_i$ ($1\le i\le k$) in the sequence is monochromatic. The ascending Ramsey index $A{R}_c\left(G\right)$ of G with respect to c is the maximum length of an ascending Ramsey sequence of G. The ascending Ramsey index$AR\left(G\right)$ of G itself is

$$AR\left(G\right)=min\{A{R}_c\left(G\right):c \mathrm{i}\mathrm{s} \mathrm{a} \mathrm{r}\mathrm{e}\mathrm{d}-\mathrm{b}\mathrm{l}\mathrm{u}\mathrm{e} \mathrm{c}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{o}\mathrm{f}G\}.$$

This number exists for every graph without isolated vertices. Since $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$ for a unique positive integer k, it follows that $1\le AR\left(G\right)\le k$. It was shown in [1] that $AR\left(K_4\right)=AR(3K_2+K_{1,7})=3$. The ascending Ramsey index of certain matchings and stars were determined in [1] as well.

Theorem 1.

For each positive integer n, $AR((\genfrac{}{}{0pt}{}{n+1}{2})K_2)=AR\left(K_{1,\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)}\right)=n$.

The goal here is to investigate the ascending Ramsey index in more detail for some classes of highly symmetric graphs such as complete graphs, matchings, stars, and graphs consisting of a matching and a star. In order to illustrate a technique used to determine the value of the ascending Ramsey index of a graph, we also present results on double stars (trees of diameter 3) in which only one vertex has degree greater than 3. To prove for a graph G without isolated vertices that the ascending Ramsey index of G has the value ℓ, say, it is required to show that (1) every red-blue coloring of G results in an ascending Ramsey sequence $G_1,G_2,\dots ,G_{\ell }$ of ℓ subgraphs of G where $G_i$ has size i for $i=1,2,\dots \ell$ and (2) there exists some red-blue coloring of G such that no such sequence of $\ell +1$ subgraphs exists.

4. Complete Graphs

If G is a graph of size $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$ for some positive integer k, then, as we mentioned, $AR\left(G\right)\le k$. In fact, if $AR\left(G\right)=k$, then G not only has an ascending sequence of length k, it has an ascending Ramsey sequence of length k for every red-blue coloring of G. Perhaps the best known class of graphs possessing such a size is that of complete graphs $K_n$ which have a size $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$. Since $K_n$ can be decomposed into stars $K_{1,i}$ for $i=1,2,\dots ,n-1$, these graphs have an ascending sequence of length $n-1$. This brings up the problem of determining the value of $AR\left(K_n\right)$. Clearly, $AR\left(K_n\right)\le n-1$. We mentioned that it was shown in [1] that $AR\left(K_4\right)=3$. We show that $AR\left(K_n\right)=n-1$ when $n=5$ as well.

Theorem 2.

$AR\left(K_5\right)=4$.

Proof. 

Since the size of $K_5$ is 10, it suffices to show that every red-blue coloring of $G=K_5$ results in an ascending Ramsey sequence of length 4 in G. If the edges of G are assigned the same color, then the statement is immediate since the decomposition of G into the stars $G_i=K_{1,i}$ ($i=1,2,3,4$) form an ascending Ramsey sequence $G_1,G_2,G_3,G_4$ of G. Hence, we may assume that there is at least one edge of each color. We may further assume that the number of red edges in a red-blue coloring of G is at most the number of blue edges. Let r be the number of red edges in a red-blue coloring of G. Thus, $1\le r\le 5$. Let $G_R$ be the red subgraph in a red-blue coloring of G. Again, since G can be decomposed into stars, as described above, it follows that if $G_R$ is a star, then there is an ascending Ramsey sequence of size 4 in G. Hence, we only need to address the situation where in any red-blue coloring of G, the subgraph $G_R$ is not a star and $r=2,3,4,5$. We consider these four possibilities. Let $V\left(G\right)=\{v_1,v_2,v_3,v_4,v_5\}$.

Case 1. $r=2$. Then, $G_R=2K_2$, say $E\left(G_R\right)=\{v_2{v}_5,v_3{v}_4\}$. Let $G_1=K_2=(v_2,v_4)$, $G_2=G_R$, $G_3=K_2+P_3$ where $K_2=(v_2,v_3)$ and $P_3=(v_4,v_1,v_5)$, and let $G_4=P_5=(v_2,v_1,v_3,v_5,v_4)$. Then, $G_1,G_2,G_3,G_4$ is an ascending Ramsey sequence of G.

Case 2. $r=3$. Then $G_R\in \{K_3,K_2+P_3,P_4\}$. We construct an ascending Ramsey sequence $G_1,G_2,G_3,G_4$ of G by considering three subcases.

Subcase $2.1$. $G_R=K_3$, say $E\left(G_R\right)=\{v_1{v}_2,v_2{v}_5,v_5{v}_1\}$. Let $G_1=K_2=(v_2,v_4)$, $G_2=P_3=(v_3,v_1,v_4)$, $G_3=G_R$, and let $G_4=K_3🟉K_1$ (a graph obtained by adding a pendant edge at a vertex of $K_3$) with $E\left(G_4\right)$ = {$v_2{v}_3$, $v_3{v}_4$, $v_4{v}_5$, $v_5{v}_3$}.

Subcase $2.2$. $G_R=K_2+P_3$, say $E\left(G_R\right)=\{v_1{v}_2,v_1{v}_5,v_3{v}_4\}$. Let $G_1=K_2=(v_3,v_5)$, $G_2=P_3=(v_4,v_2,v_5)$, $G_3=G_R$, and let $G_4=P_5=(v_2,v_3,v_1,v_4,v_5)$.

Subcase $2.3$. $G_R=P_4$, say $E\left(G_R\right)=\{v_2{v}_3,v_3{v}_4,v_4{v}_5\}$. Let $G_1=K_2=(v_2,v_5)$, $G_2=P_3=(v_2,v_1,v_5)$, $G_3=G_R$, and let $G_4=P_5=(v_2,v_4,v_1,v_3,v_5)$.

Case 3. $r=4$. Then, $G_R\in \{K_3🟉K_1,P_5,S_{2,3},C_4,K_3+K_2\}$, where $S_{2,3}$ is the double star whose central vertices have degrees of 2 and 3. We construct an ascending Ramsey sequence $G_1,G_2,G_3,G_4$ of G by considering five subcases.

Subcase $3.1$. $G_R=K_3🟉K_1$. The result follows from Subcase 2.1 by letting $G_4=G_R$. That is, let $G_1=K_2=(v_2,v_4)$, $G_2=P_3=(v_3,v_1,v_4)$, $G_3=K_3=(v_1,v_2,v_5,v_1)$, and let $G_4=G_R$ with $E\left(G_4\right)$ = {$v_2{v}_3$, $v_3{v}_4$, $v_4{v}_5$, $v_5{v}_3$}.

Subcase $3.2$. $G_R=P_5$. The result follows from Subcase 2.3 by letting $G_4=G_R$. That is, $G_1=K_2=(v_2,v_5)$, $G_2=P_3=(v_2,v_1,v_5)$, $G_3=P_4=(v_2,v_3,v_4,v_5)$, and let $G_4=G_R=(v_2,v_4,v_1,v_3,v_5)$.

Subcase $3.3$. $G_R=S_{2,3}$, say $E\left(G_R\right)=\{v_1{v}_2,v_1{v}_4,v_1{v}_5,v_3{v}_4\}$. Let $G_1=K_2=(v_4,v_5)$, $G_2=P_3=(v_1,v_3,v_2)$, $G_3=P_4=(v_3,v_5,v_2,v_4)$, and let $G_4=G_R$.

Subcase $3.4$. $G_R=C_4$, say $G_R=(v_2,v_3,v_4,v_5,v_2)$. Let $G_1=K_2=(v_2,v_4)$, $G_2=P_3=(v_2,v_1,v_5)$, $G_3=P_4=(v_4,v_1,v_3,v_5)$, and let $G_4=G_R$.

Subcase $3.5$. $G_R=K_3+K_2$, say $E\left(G_R\right)=\{v_1{v}_2,v_2{v}_5,v_5{v}_1,v_3{v}_4\}$. Let $G_1=K_2=(v_2,v_3)$, $G_2=P_3=(v_1,v_4,v_5)$, $G_3=P_3+K_2$ with $E\left(G_3\right)=\{v_1{v}_3,v_3{v}_5,v_2{v}_4\}$, and let $G_4=G_R$.

Case 4. $r=5$. Then $G_R\in \{C_5,K_4-e,C_4🟉K_1,F_1,F_2,F_3\}$, where $F_1$ is the graph obtained by adding a pendant edge at two vertices of $K_3$, $F_2$ is the graph obtained adding a pendant path $P_3$ at a vertex of $K_3$, and $F_3$ is the graph obtained adding two pendant edges at a vertex of $K_3$. We construct an ascending Ramsey sequence $G_1,G_2,G_3,G_4$ of G by considering six subcases.

Subcase $4.1$. $G_R=C_5$, say $G_R=(v_1,v_2,v_3,v_4,v_5,v_1)$. Let $G_1=K_2=(v_2,v_5)$, $G_2=P_3=(v_2,v_1,v_5)$, $G_3=P_4=(v_2,v_3,v_4,v_5)$, and let $G_4=P_5=(v_2,v_4,v_1,v_3,v_5)$.

Subcase $4.2$. $G_R=K_4-e$, say $K_4=G\left[\{v_2,v_3,v_4,v_5\}\right]$ and $e=v_3{v}_5$. Let $G_1=K_2=(v_3,v_5)$, $G_2=P_3=(v_3,v_2,v_5)$, $G_3=K_{1,3}$ with $E\left(G_3\right)=\{v_4{v}_3,v_4{v}_2,v_4{v}_5\}$, and let $G_4=K_{1,4}$ with $E\left(G_4\right)=\{v_1{v}_2,v_1{v}_3,v_1{v}_4,v_1{v}_5\}$.

Subcase $4.3$. $G_R=C_4🟉K_1$, say $E\left(G_R\right)=\{v_1{v}_2,v_2{v}_3,v_3{v}_4,v_4{v}_5,v_5{v}_2\}$. Let $G_1=K_2=(v_1,v_5)$, $G_2=P_3=(v_2,v_5,v_4)$, $G_3=P_4=(v_1,v_2,v_3,v_4)$, and let $G_4=P_5=(v_2,v_4,v_1,v_3,v_5)$.

Subcase $4.4$. $G_R=F_1$, say $E\left(G_R\right)=\{v_3{v}_2,v_2{v}_1,v_1{v}_5,v_5{v}_4,v_2{v}_5\}$. Let $G_1=K_2=(v_3,v_4)$, $G_2=P_3=(v_2,v_5,v_4)$, $G_3=P_4=(v_5,v_1,v_2,v_3)$, and let $G_4=P_5=(v_2,v_4,v_1,v_3,v_5)$.

Subcase $4.5$. $G_R=F_2$, say $E\left(G_R\right)=\{v_4{v}_3,v_3{v}_2,v_2{v}_1,v_1{v}_5,v_2{v}_5\}$. Let $G_1=K_2=(v_4,v_5)$, $G_2=P_3=(v_2,v_1,v_5)$, $G_3=P_4=(v_4,v_3,v_2,v_5)$, and let $G_4=P_5=(v_2,v_4,v_1,v_3,v_5)$.

Subcase $4.6$. $G_R=F_3$, say $E\left(G_R\right)=\{v_1{v}_2,v_2{v}_5,v_5{v}_1,v_3{v}_5,v_4{v}_5\}$. Let $G_1=K_2=(v_1,v_3)$, $G_2=P_3=(v_3,v_5,v_4)$, $G_3=K_3=(v_1,v_2,v_5,v_1)$, and let $G_4=K_3🟉K_1$ with $E\left(G_4\right)=\{v_2{v}_3,v_3{v}_4,v_4{v}_2,v_4{v}_1\}$. □

While it can be shown that $AR\left(K_6\right)=5$ using an extensive a case-by-case analysis, whether $AR\left(K_n\right)=n-1$ when $n\ge 7$ is not known.

5. Matchings and Stars

Next, we determine the value of the ascending Ramsey index $AR\left(m{K}_2\right)$ for the matching $m{K}_2$ for every positive integer m. First, we make an observation.

Observation 1.

If H and G are graphs without isolated vertices such that $\mathit{H}\subseteq G$, then $AR\left(H\right)\le AR\left(G\right)$.

Theorem 3.

Let m be a positive integer. If n is the integer such that $\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)\le m<\left(\genfrac{}{}{0pt}{}{n+2}{2}\right)$, then $AR\left(m{K}_2\right)=AR\left(K_{1,m}\right)=n$.

Proof. 

Let $G\in \{m{K}_2,K_{1,m}\}$. Since $m<\left(\genfrac{}{}{0pt}{}{n+2}{2}\right)$, there exists no ascending subgraph sequence of length $n+1$ in G. Thus, there is no red-blue coloring of G that produces an ascending Ramsey sequence of length $n+1$. So, $AR\left(G\right)\le n$. Let there be given a red-blue coloring of G.

🟉

If $G=m{K}_2$, then let $H=\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)K_2$.

🟉

If $G=K_{1,m}$, then let $H=K_{1,\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)}$.

Since $H\subseteq G$, it follows by Theorem 1 and Observation 1 that $AR\left(G\right)\ge AR\left(H\right)=n$. □

The following is a consequence of Theorem 3.

Corollary 1.

If $G\in \{m{K}_2,K_{1,m}\}$ for some positive integer m, then

$$AR\left(G\right)=⌊\frac{-1+\sqrt{1+8m}}{2}⌋.$$

Proof. 

Let $G\in \{m{K}_2,K_{1,m}\}$ where n is the largest integer for which $\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)\le m$. By Theorem 3, it follows that $AR\left(G\right)=n$. Thus, $n^2+n\le 2m$ and so $n=⌊\frac{-1+\sqrt{1+8m}}{2}⌋.$ □

We mentioned that it was shown in [1] that $AR(3K_2+K_{1,7})=3$. We now determine the ascending Ramsey index of a graph consisting of a matching of any size and a star of any size, namely the graph $a{K}_2+K_{1,b}$ where $a,b\ge 1$. Since $a{K}_2+K_{1,1}\cong (a+1)K_2$, we may assume that $b\ge 2$.

Theorem 4.

For integers $a\ge 1$ and $b\ge 2$,

$$AR(a{K}_2+K_{1,b})=\left\{\begin{array}{cc}AR\left((a+1)K_2\right)& if b\le a\hfill \\ AR\left(K_{1,b}\right)& if b\ge a+2\hfill \\ AR\left(K_{1,b+1}\right)& if b=a+1.\hfill \end{array}\right.$$

Proof. 

Let $G=a{K}_2+K_{1,b}$. We consider three cases, according to whether (1) $b\le a$, (2) $b\ge a+2$ or (3) $b=a+1$.

Case 1. $b\le a$. Let ℓ be the largest integer such that $\left(\genfrac{}{}{0pt}{}{\ell +1}{2}\right)\le a+1$. Then, $AR\left((a+1)K_2\right)=\ell$ by Theorem 3. We show that $AR\left(G\right)=\ell$. Since $(a+1)K_2\subset G$, it follows that $\ell =AR\left((a+1)K_2\right)\le AR\left(G\right)$. Next, we show that there is a red-blue coloring of G for which there is no ascending Ramsey sequence of length $\ell +1$. Let c be the red-blue coloring of G such that $G_R=a{K}_2$ and $G_B=K_{1,b}$. We show that $A{R}_c\left(G\right)=\ell$. Let us assume, to the contrary, that there is an ascending Ramsey sequence $H_1,H_2,\dots ,H_{\ell +1}$ of length $\ell +1$ in G. Then, $H_1=K_2$ and $H_2\in \{2K_2,K_{1,2}\}$. If $H_2=2K_2$, then each $H_i=i{K}_2$ ($2\le i\le \ell +1$) is a red matching; while if $H_2=K_{1,2}$, then each $H_i=K_{1,i}$ ($2\le i\le \ell +1$) is a blue star. Hence,

$$a=max\{a,b\}\ge \sum _{i=2}^{\ell +1}\left|E\left(H_i\right)\right|=\sum _{i=2}^{\ell +1}i=\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)-1$$

and so $\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)\le a+1$, which contradicts the choice of ℓ. Thus, $A{R}_c\left(G\right)=\ell$ and so $AR\left(G\right)\le \ell$. Therefore, $AR\left(G\right)=\ell =AR\left((a+1)K_2\right)$ if $b\le a$.

Case 2. $b\ge a+2$. Let ℓ be the largest integer such that $\left(\genfrac{}{}{0pt}{}{\ell +1}{2}\right)\le b$. Then, $AR\left(K_{1,b}\right)=\ell$ by Theorem 3. We show that $AR\left(G\right)=\ell$. Since $K_{1,b}\subset G$, it follows that $\ell =AR\left(K_{1,b}\right)\le AR\left(G\right)$. Next, we show that there is a red-blue coloring of G for which there is no ascending Ramsey sequence of length $\ell +1$. Let c be the red-blue coloring of G such that $G_R=(a+1)K_2$ and $G_B=K_{1,b-1}$. We show that $A{R}_c\left(G\right)=\ell$. Let us assume, to the contrary, that there is an ascending Ramsey sequence $H_1,H_2,\dots ,H_{\ell +1}$ of length $\ell +1$ in G. Then, $H_1=K_2$ and $H_2\in \{2K_2,K_{1,2}\}$. If $H_2=2K_2$, then each $H_i=i{K}_2$ ($2\le i\le \ell +1$) is a red matching. Since

$$b-1\ge a+1\ge \sum _{i=2}^{\ell +1}\left|E\left(H_i\right)\right|=\sum _{i=2}^{\ell +1}i=\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)-1,$$

it follows that $\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)\le b$, which contradicts the choice of ℓ. Thus, $H_2=K_{1,2}$ and so each $H_i=K_{1,i}$ ($2\le i\le \ell +1$) is a blue star. Hence,

$$b-1\ge \sum _{i=2}^{\ell +1}\left|E\left(H_i\right)\right|=\sum _{i=2}^{\ell +1}i=\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)-1$$

and so $\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)\le b$, which contradicts the choice of ℓ. Thus, $A{R}_c\left(G\right)=\ell$ and so $AR\left(G\right)\le \ell$. Therefore, $AR\left(G\right)=\ell =AR\left(K_{1,b}\right)$ if $b\ge a+2$.

Case 3. $b=a+1$. Let ℓ be the largest integer such that $\left(\genfrac{}{}{0pt}{}{\ell +1}{2}\right)\le a+2=b+1$. Then, $AR\left(K_{1,b+1}\right)=\ell$ by Theorem 3. We show that $AR\left(G\right)=\ell$. First, we show that $AR\left(G\right)\le \ell$. Let c be the red-blue coloring of G such that $G_R=a{K}_2$ and $G_B=K_{1,b}$. We show that $A{R}_c\left(G\right)=\ell$. Let $H=K_{1,b+1}$ with $E\left(H\right)=E\left(G_B\right)\cup \left\{e\right\}$, where $e\in E\left(G_R\right)$ and where the edges of H are colored the same as in G. Since $AR\left(K_{b+1}\right)=\ell$, there is an ascending Ramsey sequence $H_1,H_2,\dots ,H_{\ell }$ of length ℓ in H, where $H_i=K_{1,i}$ for $1\le i\le \ell$. If the edge e belongs to some subgraph in this sequence, then $E\left(H_1\right)=\left\{e\right\}$ since e is the only red edge in this red-blue coloring of H. In any case, this sequence is also an ascending Ramsey sequence of length ℓ in G. Thus, $A{R}_c\left(G\right)\ge \ell$. It remains to show that $A{R}_c\left(G\right)\le \ell$. Let us assume, to the contrary, that there is an ascending Ramsey sequence $G_1,G_2,\dots ,G_{\ell +1}$ of length $\ell +1$ in G. Then, $G_2\in \{2K_2,K_{1,2}\}$. If $G_2=2K_2$, then each $G_i=i{K}_2$ ($2\le i\le \ell +1$) is a red matching in $G_R=a{K}_2$. Thus,

$$a\ge \sum _{i=2}^{\ell +1}\left|E\left(G_i\right)\right|=\sum _{i=2}^{\ell +1}i=\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)-1$$

and so $\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)\le a+1=b$. On the other hand, if $G_2=K_{1,2}$, then each $G_i=K_{1,i}$ ($2\le i\le \ell +1$) is a blue star in $G_B=K_{1,b}$. Thus,

$$b\ge \sum _{i=2}^{\ell +1}\left|E\left(G_i\right)\right|=\sum _{i=2}^{\ell +1}i=\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)-1 \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{s}\mathrm{o}\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)\le b+1=a+2.$$

Hence, the maximum possible length of an ascending Ramsey sequence in G with the red-blue coloring c is the largest integer ℓ such that $\left(\genfrac{}{}{0pt}{}{\ell +2}{2}\right)\le b+1=a+2$, which contradicts the defining property of ℓ. Therefore, $A{R}_c\left(G\right)\le \ell$ and so $A{R}_c\left(G\right)=\ell$. This implies that $AR\left(G\right)\le A{R}_c\left(G\right)=\ell$.

To show that $AR\left(G\right)\ge \ell$, it is required to show that for every red-blue coloring distinct from c, there is an ascending Ramsey sequence of length ℓ in G. Thus, let $c^{\prime }$ be a red-blue coloring of G distinct from c. In this coloring, there are edges $e\in E\left(a{K}_2\right)$ and $f\in E\left(K_{1,b}\right)$ that are colored the same, say red. Let $f^{\prime }$ be another edge in $K_{1,b}$, where then $f^{\prime }\ne f$. The edge $f^{\prime }$ may be colored red or blue. Let $F=(a+2)K_2$ where $E\left(F\right)=E\left(a{K}_2\right)\cup \{f,f^{\prime }\}$ and where the edges of F are colored the same as in G. Since $AR\left(F\right)=\ell$ by Theorem 3, there is an ascending Ramsey sequence $F_1,F_2,\dots ,F_{\ell }$ of length ℓ in F, where $F_i=i{K}_2$ for $1\le i\le \ell$. If f and $f^{\prime }$ do not belong to the same subgraph in the sequence, then this sequence is also an ascending Ramsey sequence in G.

Thus, we may assume that f and $f^{\prime }$ belong to the same subgraph $F_j$ in the sequence where then $2\le j\le \ell$. Since f is red and $F_j$ is monochromatic, the edge $f^{\prime }$ is also red. If the edge e belongs to no subgraph in this sequence, then we can replace $f^{\prime }$ by e, obtaining a new red matching $F_j^{\prime }$ of size j. Then, $F_1,F_2,\dots ,F_{j-1},F_j^{\prime },F_{j+1},\dots ,F_{\ell }$ is an ascending Ramsey sequence of length ℓ in G. Therefore, we may assume that e belongs to a subgraph $F_i$ in the sequence, where $1\le i\le \ell$. If $i\ne j$, then we may interchange the edges e and $f^{\prime }$ in $F_i$ and $F_j$, obtaining new red matchings $F_i^{\prime }$ and $F_j^{\prime }$, where the resulting sequence is an ascending Ramsey sequence of length ℓ in G.

Therefore, we may assume that $e\in E\left(F_j\right)$ where then $3\le j\le \ell$. Therefore, $F_1$ and $F_{j-1}$ are two distinct matchings in the sequence. If either of $F_1$ and $F_{j-1}$ is red, then we may interchange a red edge in one of them with the edge $f^{\prime }$ in $F_j$ to produce an ascending Ramsey sequence of length ℓ in G, where no matching contains both f and $f^{\prime }$. Hence, we may assume that $F_1$ and $F_{j-1}$ are both blue matchings. Let $F_j^{\prime }$ be the blue matching where $E\left(F_j^{\prime }\right)=E\left(F_1\right)\cup E\left(F_{j-1}\right)$. Let $F_1^{\prime }$ be a red matching where $E\left(F_1^{\prime }\right)=\left\{f^{\prime }\right\}$ and let $F_{j-1}^{\prime }$ be a red matching where $E\left(F_{j-1}\right)=E\left(F_j\right)-\left\{f^{\prime }\right\}$. Then, $F_1^{\prime },F_2,\cdots ,F_{j-2},F_{j-1}^{\prime },F_j^{\prime },F_{j+1},\dots ,F_{\ell }$ is an ascending Ramsey sequence of length ℓ in G. Therefore, $A{R}_{c^{\prime }}\left(G\right)\ge \ell$ and so $AR\left(G\right)\ge \ell$. Thus, $AR\left(G\right)=\ell$. □

6. Double Stars

We saw in Theorem 3 that $AR\left(K_{1,m}\right)=n$ for the positive integer n with $\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)\le m<\left(\genfrac{}{}{0pt}{}{n+2}{2}\right)$. The stars are those trees of diameter 2 (where only one vertex has degree greater than 1). We now turn to another well-known class of trees, namely the double stars. A double star is a tree of diameter 3. For integers a and b with $2\le a\le b$, let $S_{a,b}$ denote the double star of order $n=a+b$ and size $m=a+b-1$ whose central vertices u and v have degrees a and b, respectively. In order to illustrate a technique that can be used to determine the value of the ascending Ramsey index of graphs, we present results giving the values of $AR\left(S_{2,b}\right)$ for all $b\ge 2$ and $AR\left(S_{3,b}\right)$ for all $b\ge 3$. We begin with a general result on $AR\left(S_{a,b}\right)$ for all integers a and b with $2\le a\le b$.

Proposition 1.

For integers a and b with $2\le a\le b$, let $S_{a,b}$ be the double star of size $m=a+b-1$. If k is the integer such that $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+(a-1)\le m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$, then $AR\left(S_{a,b}\right)=k$.

Proof. 

Let $G=S_{a,b}$ where $2\le a\le b$. Since $m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$, there exists no ascending subgraph sequence of length $k+1$ in G. Thus, there is no red-blue coloring of G that produces an ascending Ramsey sequence of length $k+1$. Hence, $AR\left(G\right)\le k$. On the other hand, since $K_{1,m-a+1}\subset G$ and $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le m-a+1<m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$ for each integer $a\ge 2$, it follows by Observation 1 and Theorem 3 that $k=AR\left(K_{1,m-a+1}\right)\le AR\left(G\right)$. Therefore, $AR\left(G\right)=k$. □

For the double star $S_{2,b}$ of size $m=b+1\ge 3$, it is evident that $AR\left(S_{2,b}\right)=2$ for $b=2,3,4$. Thus, we may assume that $b\ge 5$. If k is the integer such that

$$\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+1\le m=b+1<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right),$$

then $AR\left(S_{2,b}\right)=k$ by Proposition 1. We now consider $AR\left(S_{2,b}\right)$ when (i) $m=b+1=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\ge 6$ or (ii) $m=b+1=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+1\ge 6$ for some integer $k\ge 3$. We begin with the first situation when $m=b+1=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$ or $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-1\ge 5$. The double star $S_{2,5}$ has a size $m=6=\left(\genfrac{}{}{0pt}{}{3+1}{2}\right)$ and so $k=3$. In the red-blue coloring of $S_{2,5}$ shown in Figure 3 where a solid edge indicates a red edge and a thin edge indicates a blue edge, the maximum length of an ascending Ramsey sequence in $S_{2,5}$ is 2 and so $AR\left(S_{2,5}\right)=2=k-1$. In fact, $AR\left(S_{2,b}\right)=k-1$ for all double stars $S_{2,b}$ where $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-1\ge 5$.

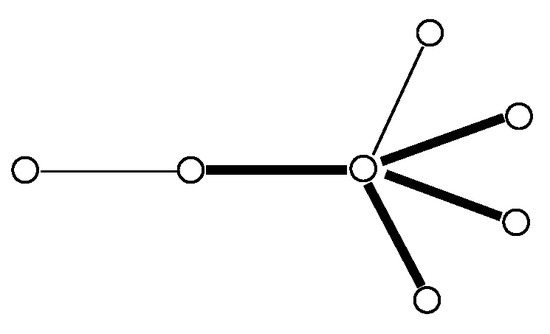
Figure 3. A red-blue coloring of $S_{2,5}$.

Proposition 2.

If $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-1\ge 5$ for some integer k, then $AR\left(S_{2,b}\right)=k-1$.

Proof. 

Let $G=S_{2,b}$ where $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-1\ge 5$. Thus, the size of G is $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$. Since $K_{1,b}\subset G$ and $\left(\genfrac{}{}{0pt}{}{k}{2}\right)\le b<\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$, it follows by Observation 1 and Theorem 3 that $AR\left(G\right)\ge AR\left(K_{1,b}\right)=k-1$. It remains to show that $AR\left(G\right)\le k-1$. That is, it is necessary to show that there is a red-blue coloring of G for which there is no ascending Ramsey sequence of length k. Let u and v be the central vertices of G where u is adjacent to the end-vertex w as well as v, and v is adjacent to the $b-1$ end-vertices $v_1,v_2,\dots ,v_{b-1}$. Define the red-blue coloring c of G that assigns the color blue to $uw$ and $v{v}_1$ and the color red to the remaining edges of G. This coloring is shown in Figure 3 for $b=5$ where a solid edge indicates a red edge and a thin edge indicates a blue edge. Thus, $G_B=2K_2$ and $G_R=K_{1,b-1}$. Let us assume, to the contrary, that there exists an ascending Ramsey sequence $G_1,G_2,\dots ,G_k$ of length k with respect to the red-blue coloring c of G. Since the size of G is $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$, it follows that $\{G_1,G_2,\dots ,G_k\}$ is a decomposition of G. Thus, $G_1=K_2$, $G_2=G_B=2K_2$ and $G_i=K_{1,i}$ for $3\le i\le k$. However, then, $G_2\not\subset G_3$, which is impossible. Therefore, $AR\left(G\right)\le k-1$ and so $AR\left(G\right)=k-1$. □

Next, we consider the situation where $m=b+1=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+1\ge 6$ and so $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\ge 5$.

Proposition 3.

If $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\ge 5$ for some integer k, then $AR\left(S_{2,b}\right)=k$.

Proof. 

Let $G=S_{2,b}$ where $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$. Since the size of G is $b+1=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+1<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$, it follows that $AR\left(S_{2,b}\right)\le k$. Next, we show that there is an ascending Ramsey sequence of length k for every red-blue coloring of G. Let u and v be the central vertices of G where w is the end-vertex of G that is adjacent to u and $v_1,v_2,\dots ,v_{b-1}$ are the end-vertices of G adjacent to v. Let c be a red-blue coloring of G and let $G^{\prime }=G-w$. Since $G^{\prime }=K_{1,b}$, it follows by Observation 1 and Theorem 3 that there is an ascending Ramsey sequence of length k in $G^{\prime }$, which is also an ascending Ramsey sequence of length k in G. Thus, $AR\left(G\right)\ge k$ and so $AR\left(G\right)=k$. □

With the aid of Propositions 1–3, we are now able to present necessary and sufficient conditions on the values of b for which $AR\left(S_{2,b}\right)=k$ for each integer $b\ge 2$.

Corollary 2.

Let $b\ge 2$. Then $AR\left(S_{2,b}\right)=k$ if and only if

$$\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le b\le \left(\genfrac{}{}{0pt}{}{k+2}{2}\right)-1.$$

We now turn our attention to the double stars $S_{3,b}$ of size $m=b+2\ge 5$. It can be shown that $AR\left(S_{3,3}\right)=2$ and $AR\left(S_{3,4}\right)=3$. Thus, we assume that $b\ge 5$. If k is the integer such that

$$\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+2\le m=b+2<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right),$$

then $AR\left(S_{3,b}\right)=k$ by Proposition 1. We now consider $AR\left(S_{3,b}\right)$ when (i) $m=b+2=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$ or (ii) $m=b+2=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+1$. We begin with the first situation when $m=b+2=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$ and so $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-2\ge 5$. Since $b\ge 5$, it follows that $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\ge 10$ and so $k\ge 4$.

Proposition 4.

If $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-2\ge 5$ for some integer k, then $AR\left(S_{3,b}\right)=k-1$.

Proof. 

Let u and v be the central vertices of $G=S_{3,b}$ where u is adjacent to the two end-vertices $u_1$ and $u_2$ and v is adjacent to the $b-1$ end-vertices $v_1,v_2,\dots ,v_{b-1}$. Let us define the red-blue coloring c of G that assigns the color blue to $u{u}_1$ and $v{v}_1$ and the color red to the remaining edges of G. Thus, $G_B=2K_2$ and $G_R=S_{2,b-1}$. We claim that there is no ascending Ramsey sequence $G_1,G_2,\dots ,G_k$ of length k with respect to this red-blue coloring c of G. Let us assume, to the contrary, that there exists such a sequence. Since the size of G is $b+2=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)$, it follows that $\{G_1,G_2,\dots ,G_k\}$ is a decomposition of G, where $G_1=K_2$ and $G_2=G_B=2K_2$. Then, $E\left(G_2\right)=\{u{u}_1,v{v}_1\}$ and $G_3\in \{P_4,K_{1,2}+K_2\}$.

🟉

If $G_3=P_4$, then $\{u{u}_2,uv\}\subseteq E\left(G_3\right)$ and so $G-[E\left(G_1\right)\cup E\left(G_2\right)\cup E\left(G_3\right)]$ is a star. Thus, $G_4$ is star. Since $G_3=P_4\not\subset G_4$, this is a contradiction.

🟉

If $G_3=K_{1,2}+K_2$, then $u{u}_2\in E\left(G_3\right)$ and so $G-[E\left(G_1\right)\cup E\left(G_2\right)\cup E\left(G_3\right)]$ is a star. Thus, $G_4$ is a star. Since $G_3=K_{1,2}+K_2\not\subset G_4$, this is a contradiction.

Therefore, $AR\left(G\right)\le k-1$. Next, we show that $AR\left(G\right)\ge k-1$. Since $K_{1,b}\subset G=S_{3,b}$ and $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-2>\left(\genfrac{}{}{0pt}{}{k}{2}\right)$, it follows by Observation 1 and Theorem 3 that $AR\left(G\right)\ge AR\left(K_{1,b}\right)=k-1$. Thus, $AR\left(G\right)=k-1$. □

Next, we consider the situation where $m=b+2=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+1$ and so $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-1\ge 5$ for some integer k. Since $b\ge 5$, it follows that $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\ge 6$ and so $k\ge 3$.

Theorem 5.

If $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-1\ge 5$ for some integer k, then $AR\left(S_{3,b}\right)=k$.

Proof. 

Let $b=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)-1\ge 5$ where $k\ge 3$. The size of $S_{3,b}$ is $m=b+2=\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+1$. Since $S_{2,b}\subset S_{3,b}$ and $m<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$, it follows by Observation 1 and Proposition 2 that $k-1\le AR\left(S_{3,b}\right)\le k$. Let $G=S_{3,b}$ with central vertices u and v, where u is adjacent to the two end-vertices $u_1$ and $u_2$ and v is adjacent to the $b-1\ge 4$ end-vertices $v_1,v_2,\dots ,v_{b-1}$. Let $g=uv$, $f_1=u{u}_1$, $f_2=u{u}_2$, and $e_i=v{v}_i$ for $1\le i\le b-1$. We show that $AR\left(S_{3,b}\right)=k$. Thus, it is necessary to show that for every red-blue coloring of G, there is an ascending Ramsey sequence of length k in G. Let c be a red-blue coloring of G. We may assume that g is colored red.

Let $F=K_{1,b+2}$ be the star whose central vertex v is adjacent to the $b+2$ end-vertices u, $u_1$, $u_2$, $v_1$, $v_2$, …, $v_{b-1}$, where the $b+2$ edges of F are denoted by $g=uv$, $f_1=u{u}_1$, $f_2=u{u}_2$, and $e_i=v{v}_i$ for $1\le i\le b-1$. Let the edges of F be colored the same as these edges of G, producing a red-blue coloring c of F. Since $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)<\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)+1=b+2<\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)$, it follows by Theorem 3 that $AR\left(K_{1,b+2}\right)=k$. Thus, there is an ascending Ramsey sequence of length k in F. Let $X=\{f_1,f_2\}$ and $Y=\{e_1,e_2,\dots ,e_{b-1}\}$. If there is no subgraph in this sequence that contains both an edge in X and an edge in Y, then this sequence is also an ascending Ramsey sequence in G. Thus, we may assume that there is at least one subgraph in this sequence that contains at least one edge in X and at least one edge in Y. There are two possibilities, namely

(1)

Both $f_1$ and $f_2$ appear in every ascending Ramsey sequence of length k in F;

(2)

One of $f_1$ and $f_2$ does not appear in some ascending Ramsey sequences of length k in F.

We consider these two cases.

Case 1. Both $f_1$ and $f_2$ appear in every ascending Ramsey sequence of length k in F. Let $F_1,F_2,\dots ,F_k$ be an ascending Ramsey sequence of length k in F. Let $c\left(F_i\right)$ denote the color of $F_i$ for $1\le i\le k$. Necessarily, $F_i=K_{1,i}$ for $1\le i\le k$. Then, (i) both $f_1$ and $f_2$ appear in this sequence and (ii) there is an edge e in $\left\{g\right\}\cup Y$ that does not appear in this sequence. We refer to this edge e as the missing edge of the sequence. Our goal here is to replace each $F_i\ncong K_{1,i}$ in G by a new subgraph $F_i^{*}\cong K_{1,i}$ in G (where possibly $F_i^{*}=F_i)$ in such a way to produce an ascending Ramsey sequence of length k in G. We now make three observations.

(A)

If $c\left(e\right)=c\left(f_1\right)$ or $c\left(e\right)=c\left(f_2\right)$, say the former, then we can interchange e and $f_1$ to produce a new ascending Ramsey sequence of length k in F that does not contain $f_1$, which is impossible in this case. Thus, $c\left(e\right)\ne c\left(f_i\right)$ for $i=1,2$ and so $c\left(f_1\right)=c\left(f_2\right)$.

(B)

If $E\left(F_1\right)\cup E\left(F_2\right)=\{f_1,f_2,g\}$, or $E\left(F_2\right)=\{f_1,f_2\}$, or $E\left(F_3\right)=\{f_1,f_2,g\}$, then this sequence is also an ascending Ramsey sequence in G. Therefore, we can assume that

$$E\left(F_1\right)\cup E\left(F_2\right)\ne \{f_1,f_2,g\},E\left(F_2\right)\ne \{f_1,f_2\},\mathrm{and}E\left(F_3\right)\ne \{f_1,f_2,g\}.$$

(C)

If $\{f_1,f_2\}\subset E\left(F_p\right)$ where $3\le p\le k$ and $c\left(F_2\right)=c\left(F_p\right)$, then we can interchange $E\left(F_2\right)$ and $\{f_1,f_2\}$ to produce $F_2^{*}\cong K_{1,2}$ and $F_p^{*}\cong K_{1,p}$ in G. Therefore, we can assume that $c\left(F_2\right)\ne c\left(F_p\right)$.

We consider two subcases, according to whether $f_1$ and $f_2$ belong to the same subgraph in the sequence or $f_1$ and $f_2$ belong to two different subgraphs in the sequence.

Subcase $1.1$. $f_1,f_2\in E\left(F_p\right)$ where $3\le p\le k$. Thus, $c\left(e\right)=c\left(F_2\right)\ne c\left(F_p\right)$ by (A) and (C). We consider two possibilities here according to whether $p=3$ or $p=4$.

Subcase $1.1.1$. $f_1,f_2\in E\left(F_3\right)$. We may assume that $E\left(F_3\right)=\{f_1,f_2,e_r\}$ by (B), where $e_r\in Y$.

🟉

First, suppose that the missing edge $e=g$. Since g is red, it follows by (A) that $F_2$ is red and $F_3$ is blue. We construct $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$ and $F_3^{*}\cong K_{1,3}$ in G with $E\left(F_3^{*}\right)=E\left(F_2\right)\cup \left\{g\right\}$.

🟉

Next, suppose that the missing edge $e=e_t\in Y$. First, let us suppose that $F_3$ is red. Since the red edge g appears in this sequence, say $g\in E\left(F_i\right)$ where $i\in \left[k\right]-\left\{3\right\}$, we can interchange g and $e_r$ to produce $F_3^{*}\cong K_{1,3}$, $F_i^{*}\cong K_{1,i}$, and an ascending Ramsey sequence of length k in G. Next, suppose that $F_3$ is blue. Therefore, $e_t$ and $F_2$ are red. Then, we construct $F_1^{*}$ in G with $E\left(F_1^{*}\right)=\left\{e_r\right\}$, $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$, and $F_3^{*}=K_{1,3}$ in G with $E\left(F_3^{*}\right)=\left\{e_t\right\}\cup E\left(F_2\right)$. Thus, in this situation as well, there is an ascending Ramsey sequence of length k in G.

Subcase $1.1.2$. $f_1,f_2\in E\left(F_p\right)$ for some $p\ge 4$. Thus, $E\left(F_p\right)=\{f_1,f_2\}\cup Z$ where $Z\subset \left\{g\right\}\cup Y$ with $\left|Z\right|=p-2$. Let $e\in \left\{g\right\}\cup Y$ be the missing edge. Then, $c\left(e\right)=c\left(F_2\right)\ne c\left(F_p\right)$ by (A) and (B). We may now assume that $c\left(e\right)=c\left(F_2\right)$ is blue and $c\left(F_p\right)$ is red (since the proof for the situation when $c\left(e\right)=c\left(F_2\right)$ is red and $c\left(F_p\right)$ is blue is the same by interchanging red and blue).

🟉

First, suppose that $F_{p-1}$ is red. Let q be the largest integer in $\{2,3,\dots ,p-2\}$ such that $F_q$ is blue. Since $c\left(F_{p-1}\right)=c\left(F_p\right)$ is red, it follows that $c\left(F_{q+1}\right)=c\left(F_{q+2}\right)$ is red. Let $e_r,e_s\in E\left(F_{q+2}\right)$. We define $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$, $F_q^{*}\cong K_{1,q}$ in G with $E\left(F_q^{*}\right)=E\left(F_{q+2}\right)-\{e_r,e_s\}$, $F_{q+2}^{*}\cong K_{1,q+2}$ in G with $E\left(F_q^{*}\right)=E\left(F_q\right)\cup E\left(F_2\right)$, and $F_p^{*}\cong K_{1,p}$ in G with $E\left(F_p^{*}\right)=(E\left(F_p\right)-\{f_1,f_2\})\cup \{e_r,e_s\}$.

🟉

Next, suppose that $F_{p-1}$ is blue.

⚬

If $F_{p-2}$ is blue, then we define $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$, $F_{p-2}^{*}\cong K_{1,p-2}$ in G with $E\left(F_{p-2}^{*}\right)=E\left(F_p\right)-\{f_1,f_2\}$, $F_p^{*}\cong K_{1,p}$ in G with $E\left(F_p^{*}\right)=E\left(F_{p-2}\right)\cup E\left(F_2\right)$. Thus, we may assume that $F_{p-2}$ is red. Thus, $p\ge 5$.

⚬

If $F_{p-3}$ is blue, then we define $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$, $F_{p-3}^{*}\cong K_{1,p-3}$ in G with $E\left(F_{p-3}^{*}\right)=E\left(F_p\right)-\{f_1,f_2,z\}$ where $z\in E\left(F_p\right)-\{f_1,f_2\}$, $F_p^{*}\cong K_{1,p}$ in G with $E\left(F_p^{*}\right)=E\left(F_{p-3}\right)\cup E\left(F_2\right)\cup \left\{e\right\}$. Here, z is the missing edge. Thus, we may assume that $F_{p-3}$ is red. Thus, $p\ge 6$.

Let q be the largest integer in $\{2,3,\dots ,p-4\}$ such that $F_q$ is blue. Since $c\left(F_{p-2}\right)=c\left(F_{p-3}\right)$ is red, it follows that $c\left(F_{q+1}\right)=c\left(F_{q+2}\right)$ is red. Let $e_r,e_s\in E\left(F_{q+2}\right)$. We define $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$, $F_q^{*}\cong K_{1,q}$ in G with $E\left(F_q^{*}\right)=E\left(F_{q+2}\right)-\{e_r,e_s\}$, $F_{q+2}^{*}\cong K_{1,q+2}$ in G with $E\left(F_{q+2}^{*}\right)=E\left(F_q\right)\cup E\left(F_2\right)$, and $F_p^{*}\cong K_{1,p}$ in G with $E\left(F_p^{*}\right)=(E\left(F_p\right)-\{f_1,f_2\})\cup \{e_r,e_s\}$. The edge e remains the missing edge.

Thus, there is an ascending Ramsey sequence of length k in G where $f_1,f_2\in E\left(F_p\right)$ for $p\ge 4$.

Subcase $1.2$. $f_1\in E\left(F_a\right)$ and $f_2\in E\left(F_b\right)$ where $1\le a<b\le k$. Thus, $c\left(F_a\right)=c\left(F_b\right)\ne c\left(e\right)$. If $a=2$, say $E\left(F_2\right)=\{f_1,e_r\}$, then we can interchange $e_r$ and $f_2$ to produce $F_2^{*}=K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$ and $F_b^{*}\cong K_{1,b}$ in G with $E\left(F_b^{*}\right)=(E\left(F_b\right)-\left\{f_2\right\})\cup \left\{e_r\right\}$. Thus, we can assume that $a\ne 2$ and so $a=1$ or $a\ge 3$. We consider these two subcases.

Subcase $1.2.1$. $a=1$. Then, $E\left(F_1\right)=\left\{f_1\right\}$. If $f_2\in E\left(F_2\right)$, then $E\left(F_2\right)=\{f_2,h\}$ where $f\in \left\{g\right\}\cup Y$. Since $c\left(F_1\right)=c\left(F_2\right)$, we can interchange h and $f_1$ to produce $F_1^{*}$ in G with $E\left(F_1^{*}\right)=\left\{h\right\}$ and $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$. Thus, we may assume that $f_2\in E\left(F_b\right)$ where $3\le b\le k$. Since $c\left(e\right)\ne c\left(F_1\right)=c\left(F_b\right)$, we may further assume that e is red and $c\left(F_1\right)=c\left(F_b\right)$ is blue (since the proof for the situation where e is blue and $c\left(F_1\right)=c\left(F_b\right)$ is red is the same by interchanging red and blue).

🟉

First, suppose that $F_2$ is blue with $E\left(F_2\right)=\{e_r,e_s\}$. Define $F_1^{*}$ with $E\left(F_1^{*}\right)=\left\{e_r\right\}$, $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$, and $F_b^{*}\cong K_{1,b}$ in G with $E\left(F_b^{*}\right)=(E\left(F_b\right)-\left\{f_2\right\})\cup \left\{e_s\right\}$.

🟉

Next, let us suppose that $F_2$ is red. Let q be the largest integer in $\{2,3,\dots ,b-1\}$ such that $F_q$ is red. If $q=b-1$, then we define $F_{b-1}^{*}\cong K_{1,b-1}$ in G with $E\left(F_{b-1}^{*}\right)=E\left(F_p\right)-\left\{f_2\right\}$ and $F_b^{*}=K_{1,b}$ in G with $E\left(F_b^{*}\right)=E\left(F_{b-1}\right)\cup \left\{e\right\}$. If $2\le q\le b-2$, then $F_{q+1}$ is blue. Let us define $F_{q+1}^{*}\cong K_{1,q+1}$ in G with $E\left(F_{q+1}^{*}\right)=E\left(F_q\right)\cup \left\{e\right\}$, $F_q^{*}\cong K_{1,q}$ in G with $E\left(F_q^{*}\right)=E\left(F_{q+1}\right)-\left\{e_j\right\}$ where $e_j\in E\left(F_{q+1}\right)$, and $F_b^{*}\cong K_{1,b}$ in G with $E\left(F_b^{*}\right)=(E\left(F_b\right)-\left\{f_2\right\})\cup \left\{e_j\right\}$.

Subcase $1.2.2$. $a\ge 3$. First, we make an observation.

(D)

If $c\left(F_2\right)=c\left(F_a\right)=c\left(F_b\right)$, say $E\left(F_2\right)=\{e_1,e_2\}$, then we can define $F_2^{*}\cong K_{1,2}$ in G with $E\left(F_2^{*}\right)=\{f_1,f_2\}$, $F_a^{*}\cong K_{1,a}$ in G with $E\left(F_a^{*}\right)=(E\left(F_a\right)-\left\{f_1\right\})\cup \left\{e_1\right\}$, and $F_b^{*}\cong K_{1,b}$ in G with $E\left(F_b^{*}\right)=(E\left(F_b\right)-\left\{f_b\right\})\cup \left\{e_2\right\}$. Thus, we can assume that $c\left(F_2\right)\ne c\left(F_a\right)=c\left(F_b\right)$ and so $c\left(e\right)=c\left(F_2\right)$.

🟉

If $f_1\in E\left(F_3\right)$, say $E\left(F_3\right)=\{f_1,g,e_r\}$ or $E\left(F_3\right)=\{f_1,e_r,e_s\}$, then we define $F_2^{*}=K_{1,2}$ in G with $E\left(F_2^{*}\right)=E\left(F_3\right)-\left\{f_1\right\}$ and $F_3^{*}=K_{1,3}$ in G with $E\left(F_3^{*}\right)=\left\{e\right\}\cup E\left(F_2\right)$, producing an ascending Ramsey sequence of length k in G.

🟉

If $f_1\in E\left(F_a\right)$ where $a\ge 4$, then we construct a new ascending Ramsey sequence $F_1^{*}$, $F_2^{*}$, …, $F_k^{*}$ of length k in F by defining $F_a^{*}$ with $E\left(F_a^{*}\right)=(E\left(F_a\right)-\left\{z\right\})\cup \left\{f_2\right\}$ where $z\in E\left(F_a\right)-\left\{f_1\right\}$, $F_b^{*}$ with $E\left(F_b^{*}\right)=(E\left(F_b\right)-\left\{f_2\right\})\cup \left\{z\right\}$, and $F_i^{*}=F_i$ if $i\ne a,b$ and $1\le i\le k$. Thus, $f_1,f_2\in F_a^{*}$ where $a\ge 4$. The argument used in Subcase 1.1.2 shows that there is an ascending Ramsey sequence of length k in G.

Case 2. One of $f_1$ and $f_2$ does not appear in some ascending Ramsey sequence of length k in F. Let $H_1,H_2,\dots ,H_k$ be an ascending Ramsey sequence of length k in F where $H_i=K_{1,i}$ for $1\le i\le k$ such that one of $f_1$ and $f_2$ does not appear in this sequence, say $f_1$ is the missing edge and $f_2\in E\left(H_p\right)$ where $1\le p\le k$. First, we make two observations.

(E)

If $E\left(H_1\right)=\left\{f_2\right\}$ or $E\left(H_2\right)=\{f_2,g\}$, then this sequence is also an ascending Ramsey sequence of length k in G. Thus, we may assume that $p\ge 2$ and $E\left(H_2\right)\ne \{f_2,g\}$.

(F)

If $c\left(H_1\right)=c\left(H_p\right)$ where $E\left(H_1\right)=\left\{z\right\}$ and $p\ge 2$, then we can interchange z and $f_2$ to produce an ascending Ramsey sequence of length k in G. Thus, we may assume that $c\left(H_1\right)\ne c\left(H_p\right)$.

We consider two cases, according to whether $c\left(f_1\right)=c\left(f_2\right)$ or $c\left(f_1\right)\ne c\left(f_2\right)$.

Subcase $2.1$. $c\left(f_1\right)=c\left(f_2\right)$. Since $f_2\in E\left(H_p\right)$ where $p\ge 2$, there is $z\in E\left(H_p\right)-\left\{f_2\right\}$. We interchange z and $f_1$ to define $H_p^{*}\cong K_{1,p}$ in G such that $f_1,f_2\in E\left(H_p^{*}\right)=(E\left(H_p\right)-\left\{z\right\})\cup \left\{f_1\right\}$ and z is the missing edge. We now consider the ascending Ramsey sequence $H_1^{*},H_2^{*},\dots ,H_k^{*}$ in F where $H_i^{*}=H_i$ for $1\le i\le k$ and $i\ne p$. We may assume that $E\left(H_2^{*}\right)\ne \{f_1,f_2\}$, $E\left(H_1^{*}\right)\cup E\left(H_2^{*}\right)\ne \{f_1,f_2,g\}$, and $E\left(H_3^{*}\right)\ne \{f_1,f_2,g\}$ (for otherwise, $H_1^{*},H_2^{*},\dots ,H_k^{*}$ is also an ascending Ramsey sequence in G). Thus, $p\ge 3$. If $c\left(H_2^{*}\right)=c\left(H_p^{*}\right)$, then we can interchange $E\left(H_2^{*}\right)$ and $\{f_1,f_2\}\subset E\left(H_p^{*}\right)$ to produce an ascending Ramsey sequence of length k in G. Thus, we may assume that $c\left(H_2^{*}\right)\ne c\left(H_p^{*}\right)$. Hence, $c\left(H_1^{*}\right)=c\left(H_2^{*}\right)\ne c\left(H_p^{*}\right)$ by (F).

🟉

First, let us suppose that $p=3$. Let $E\left(H_3^{*}\right)=\{f_1,f_2,e_r\}$ where $e_r\in Y$. Since $c\left(H_1^{*}\right)=c\left(H_2^{*}\right)$, we can define $H_1^{\prime }$ with $E\left(H_1^{\prime }\right)=\left\{e_r\right\}$, $H_2^{\prime }\cong K_{1,2}$ with $E\left(H_2^{\prime }\right)=\{f_1,f_2\}$, and $H_3^{\prime }\cong K_{1,3}$ with $E\left(H_3^{\prime }\right)=E\left(H_1^{*}\right)\cup E\left(H_2^{*}\right)$, producing an ascending Ramsey sequence $H_1^{\prime },H_2^{\prime },\dots ,H_k^{\prime }$ of length k in G where $H_i^{\prime }=H_i^{*}$ for $3\le i\le k$.

🟉

Next, let us suppose that $p\ge 4$. Let us recall that $c\left(H_1^{*}\right)=c\left(H_2^{*}\right)\ne c\left(H_p^{*}\right)=c\left(z\right)$ where z is the missing edge. Let $E\left(H_1^{*}\right)=\left\{e\right\}$. We now interchange e and z such that $E\left(H_1^{\prime }\right)=\left\{z\right\}$ and e is the missing edge in the new ascending Ramsey sequence $H_1^{\prime },H_2^{\prime },\dots ,H_k^{\prime }$ of length k in G where $H_i^{\prime }=H_i^{*}$ for $2\le i\le k$. Hence, $c\left(e\right)=c\left(H_2^{\prime }\right)\ne c\left(H_p^{\prime }\right)$ where $p\ge 4$ and $f_1,f_2\in E\left(H_p^{\prime }\right)$ (which are the conditions in the proof of Subcase 1.1.2). Therefore, the argument used in Subcase 1.1.2 shows that there is an ascending Ramsey sequence of length k in G.

Subcase $2.2$. $c\left(f_1\right)\ne c\left(f_2\right)$. Since $f_2\in E\left(H_p\right)$ where $p\ge 2$ and $c\left(H_1\right)\ne c\left(H_p\right)$ by (E) and (F), it follows that $c\left(H_1\right)=c\left(f_1\right)\ne c\left(H_p\right)$.

🟉

First, let us suppose that $p=2$. Then, $E\left(H_2\right)=\{f_2,e_r\}$ where $e_r\in Y$ by (E). Let $g\in H_t$ where $t\ne 2$. If $c\left(g\right)=c\left(H_2\right)$, then we can define $H_2^{*}=\{f_2,g\}$ and $H_t^{*}\cong K_{1,t}$ in G with $E\left(H_t^{*}\right)=(E\left(H_t\right)-\left\{g\right\})\cup \left\{e_r\right\}$. Thus, we may assume that $c\left(g\right)\ne c\left(H_2\right)$ and so $c\left(g\right)=c\left(H_1\right)=c\left(f_1\right)$. If $E\left(H_1\right)=\left\{g\right\}$, then we can define $H_1^{*}$ with $E\left(H_1^{*}\right)=\left\{f_2\right\}$, $H_2^{*}=\{f_1,g\}$, and $e_r$ is the missing edge. If $g\in E\left(H_t\right)$ where $t\ge 3$, then we can define $H_1^{*}=\left\{f_2\right\}$, $H_2^{*}=\{f_1,g\}$, $E\left(H_t^{*}\right)=(E\left(H_t\right)-\left\{g\right\})\cup E\left(H_1\right)$, and $e_r$ is the missing edge.

🟉

Next, suppose that $p\ge 3$. We may assume that $c\left(f_1\right)$ is blue and $c\left(H_p\right)$ is red (since the proof for the situation when $c\left(f_1\right)$ is red and $c\left(H_p\right)$ is blue is the same by interchanging red and blue). Let us recall that $c\left(f_1\right)=c\left(H_1\right)$ is blue and $c\left(H_p\right)$ is red. Let $q\in \{1,2,\dots ,p-1\}$ be the maximum integer such that $c\left(H_q\right)$ is blue. Thus, $c\left(H_{q+1}\right)=c\left(H_p\right)$ is red where possibly $H_{q+1}=H_p$. Let $h\in E\left(H_{q+1}\right)$. We now define $H_1^{*}$ with $E\left(H_1^{*}\right)=\left\{f_2\right\}$, $H_q^{*}\cong K_{1,q}$ with $E\left(H_q^{*}\right)=E\left(H_{q+1}\right)-\left\{h\right\}$, $H_{q+1}^{*}\cong K_{1,q+1}$ with $E\left(H_{q+1}^{*}\right)=E\left(H_q\right)\cup E\left(H_1\right)$, and $H_p^{*}\cong K_{1,p}$ with $E\left(H_p^{*}\right)=(E\left(H_p\right)-\left\{f_2\right\})\cup \left\{h\right\}$.

□

Therefore, there is an an ascending Ramsey sequence of length k in G in Subcase $2.2$.

The following is a consequence of Propositions 1 and 4 and Theorem 5.

Corollary 3.

Let $b\ge 3$ be an integer such that $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le b\le \left(\genfrac{}{}{0pt}{}{k+2}{2}\right)-1$ for some integer k.

🟉

If $\left(\genfrac{}{}{0pt}{}{k+1}{2}\right)\le b\le \left(\genfrac{}{}{0pt}{}{k+2}{2}\right)-2$, then $AR\left(S_{3,b}\right)=k$.

🟉

If $b=\left(\genfrac{}{}{0pt}{}{k+2}{2}\right)-1$, then $AR\left(S_{3,b}\right)=k+1$.