Abstract
The antiferromagnetic ordering that MnBiTe shows makes it invariant with respect to the combination of the time-reversal and primitive-lattice translation symmetries, giving rise to its topologically nontrivial nature and a number of fundamental phenomena. At the same time, the possibility to control the electronic and magnetic properties of this system can provide new effective ways for its application in devices. One of the approaches to manipulate MnBiTe properties is the partial substitution of magnetic atoms in the compound with atoms of non-magnetic elements, which inevitably affect the interplay of magnetism and band topology in the system. In this work, we have carried out theoretical modelling of changes in the electronic structure that occur as a result of increasing the concentration of Sn atoms at Mn positions in the (MnSn)BiTe compound both using Korringa–Kohn–Rostoker (KKR) Green’s function method as well as the widespread approach of using supercells with impurity in DFT methods. The calculated band structures were also compared with those experimentally measured by angle-resolved photoelectron spectroscopy (ARPES) for samples with x values of 0, , , and . We assume that the complex hybridization of Te-p and Bi-p orbitals with Sn and Mn ones leads to a non-linear dependence of band gap on Sn content in Mn positions, which is characterized by a plateau with a zero energy gap at some concentration values, suggesting possible topological phase transitions in the system.
1. Introduction
A three-dimensional topological insulator (TI) is characterized by surface states that are protected by time-reversal (TR) symmetry [1]. Introducing magnetism into topological insulators breaks time-reversal symmetry, and the magnetic exchange interaction can open a gap in the otherwise gapless topological surface states [2]. This can give rise to a number of quantum effects, such as quantum anomalous Hall effect (QAHE), topological magnetoelectric effect [1,2,3,4,5], and in the case of contact with a superconductor, to the realization of Majorana fermions [2,6]. The above-mentioned effects make magnetic TIs perspective for the development of new quantum memory and data processing devices based on them [7]. Currently, the most promising platform for studying the interaction of magnetism and topology is the intrinsic antiferromagnetic TI MnBiTe [8,9,10,11,12]. The antiferromagnetic ordering that MnBiTe shows makes it invariant with respect to the combination of the time-reversal and primitive-lattice translation symmetries, giving rise to its topologically nontrivial nature. In this compound, the magnetic atoms are embedded directly into the crystal structure. This simultaneously solves two problems: it enables a significant increase in concentration of magnetic material in the TI without violating the crystal structure, and provides a better interaction between the magnetic atoms (Mn) and the atoms on which the topological surface state (TSS) is localized (Bi, Te). As a result, it is possible to open the band gap at the Dirac point of the TSS in MnBiTe significantly larger than in any other known magnetic TI. Indeed, the calculations reveal the value of the band gap to be in the range of 70–90 meV [8,9,10,11]. Experimentally measured values of the band gap, however, vary widely and range from almost zero to the theoretically predicted one [13,14,15,16,17,18,19,20,21]. It has been shown that this variation of the gap value is related to defects in the crystal structure of MnBiTe such as point mutual substitutions between TI atoms [21] as well as changes in the interlayer and interblock (van der Waals) distances [14,15,16,17] and thus cannot be controlled. Despite the ambiguity with the experimental estimates of the band gap at the Dirac point, the realization of QAHE for MnBiTe thin films has been confirmed, and indeed, the transition to the QAHE state has been observed at significantly higher temperatures than in magnetically doped TI [22,23].
In order to effectively apply magnetic TIs in devices, it is necessary to be able to control their electronic and magnetic properties. For example, MnBiTe is strongly n-doped and for the realization of QAHE it is necessary to shift the Dirac point to Fermi level. This can be achieved by partial substitution of Bi atoms with Sb atoms [24,25,26]. The electronic structure of the TSS and the magnetic properties of the TI are preserved during such substitution. Furthermore, the magnetic properties should be controlled. In the ground state, MnBiTe is in the antiferromagnetic state, and the remagnetization field is very high: about 3.5 T [8]. The reduction of this remagnetization field, from a practical point of view, would make it possible to create systems in which the transition from the axion insulator state to the Chern insulator state as well as changing the direction of the edge current in the QAHE state is possible by applying significantly lower external magnetic fields [27,28]. This field can be reduced by decreasing the magnetic interaction in the TI. This can be achieved by partial substitution of Mn atoms with non-magnetic elements (Sn, Pb, Ge) which are components of ternary TIs SnBiTe [29], PbBiTe [30], GeBiTe [31,32] with crystal structures similar to MnBiTe. In addition, recent studies of the MnPbBiTe system [27] have shown that at certain values of x, topological phase transitions (TPTs) can occur in it.
In [28,33], the magnetic and transport properties of (MnSn)BiTe TI for concentrations of Sn from to were studied. It was shown that the critical field decreases almost linearly and the Néel temperature decreases as well when Sn concentration increases. The AFM ordering is preserved up to but turns into a paramagnetic state for larger values of x [33]. It is important to note that substitution of Mn with Sn does not change the crystal structure of TI [28] so it is possible to obtain TI crystals with any Sn/Mn ratio, allowing for a smooth variation of magnetic properties. Transport measurements have shown that Sn concentration also affects the system conductivity: the density of charge carriers increases almost two-fold at [29]. The Sn substitution thus affects both the magnetic and electronic properties of MnBiTe.
In this work, we have carried out theoretical modeling of changes in the electronic structure resulting from an increase in the concentration of Sn atoms at Mn positions in the compound (MnSn)BiTe both using Korringa–Kohn–Rostoker (KKR) Green’s function method [34] with the coherent potential approximation (CPA) [35] as well as the widespread approach of using supercells with impurity in density functional theory (DFT) methods. The calculated band structures were also compared with those experimentally measured via angle-resolved photoelectron spectroscopy (ARPES) for samples with x values of 0, , , and . The obtained results indicate the possibility of TPTs in this system at several x values.
2. Materials and Methods
The crystals were grown using the Bridgman method under state assignment contract of IGM and ISP SB RAS. ARPES and XPS measurements were made using a SPECS GmbH ProvenX-ARPES system equipped with ASTRAIOS 190 electron energy analyzer and 2D-CMOS electron detector. The photoemission was excited by monochromated Al emission with eV for XPS and non-monochromated He I light with eV for ARPES. The energy scale of the spectrometer was calibrated by setting the measured Ag line binding energy of eV with respect to the Fermi energy. For XPS and ARPES measurements the crystals were cleaved under UHV conditions in the preparation chamber. Samples were measured at the temperature of 77 K.
The electronic structure supercell calculations with impurities were performed using the OpenMX code which provides a fully relativistic DFT implementation with localized pseudoatomic orbitals [36,37,38] and norm-conserving pseudopotentials [39]. The exchange-correlation energy in the PBE version of generalized gradient approximation was employed [40]. The surface calculations were performed using 6 septuple layers slabs of MnBiTe with the vacuum layer of 12 Å. For impurity calculations slab supercells, which provide 4 non-equivalent positions of Mn atoms in each layer, were used. The Sn concentrations of 25, 50 and 75% were obtained by replacing one, two and three Mn atoms with Sn atoms, respectively. The accuracy of the real-space numerical integration was specified by the cutoff energy of 450 Ry, the total energy convergence criterion was eV. The k-mesh for Brillouin zones were specified as follows: mesh for bulk calculations, mesh for pristine MnBiTe slab and mesh for supercells. The basis functions were taken as Bi8.0—s3p2d2f1, Te7.0—s3p2d2f1, Mn6.0—s3p2d1, Sn7.0—s3p2d2 (the pseudopotential cutoff radius is followed by a basis set specification). The Mn states were treated within the DFT + U approach [41] within the Dudarev scheme [42] where U parameter equals 5.4 eV [8].
The band structure of (MnSn)BiTe with fully disordered impurities from first-principles calculations was obtained utilizing the spin polarized relativistic Korringa–Kohn–Rostoker (SPR-KKR) code, version 7.7 [43]. The generalized gradient approximation (GGA) in the Perdew, Burke, and Ernzerhof parametrization was used [40] with U correction and the atomic-sphere approximation (ASA) in the fully-relativistic approach. The coherent potential approximation (CPA) [35] was used to simulate chemical disorder. We used the basis functions up to , a regular k-point grid with 250 points, and 30 energy points.
3. Results and Discussion
The main purpose of this work is the investigation of the (MnSn)BiTe electronic structure under x variation. Several alternative theoretical approaches were used to solve this problem, such as conventional DFT calculations (with bulk supercells and slabs) and the KKR method with CPA which provides a unique opportunity to calculate band structure of a crystal with fully disordered impurities. The results of theoretical calculations using both methods were compared with each other as well as with ARPES data.
3.1. Infinite Crystal Calculations
Figure 1 demonstrates the KKR-calculated bulk electronic structure of (MnSn)BiTe along path in the first Brillouin zone and its variation under gradual substitution of magnetic Mn atoms with non-magnetic Sn atoms. CPA provides the possibility to account for a disordered distribution of these substitutions throughout the crystal as well as the possibility to change x smoothly without the need of large supercells typical for conventional DFT. Figure 1a–f show the data for x values of 0, , , , , , and , respectively. According to these calculations, the bulk gap decreases down to zero when x increases from 0 to , remains closed for x between and and reopens with further increase of x. A general view of the bulk gap value as a function of Sn content is shown in Figure 1g. It can be seen that this function is non-linear and shows some plateau with a zero energy gap at Sn concentration values of 35–40%.

Figure 1.
The KKR–calculated bulk band structure of (MnSn)BiTe along path in the first Brillouin zone for (a), (b), (c), (d), (e), (f). The general dependence of bulk gap as a function of Sn content is plotted on (g).
The collapse of the bulk gap at might be a sign of a TPT from a topological to a trivial phase or a Weyl semimetal state with a zero bulk gap. At the same time, it may be supposed that a further increase in the Sn concentration above 50% returns the system into a TI. Thus, the observed dependence of the bulk gap value on the parameter x can be explained by the presence of the TPTs realized in this system with changing the concentration of Sn atoms in the positions of Mn atoms.
A similar behaviour of the bulk gap value was observed for MnPbBiTe in [27] with a decreasing bulk gap for , zero gap plateau for and an increasing bulk gap for . The authors in [27] also suggested that such nonlinear character of the bulk gap value dependence on the Pb concentration may be associated with possible TPTs in the system.
In order to test the idea of correlation between Sn content and bulk gap value as well as its connection with possible TPTs in (MnSn)BiTe, supercell DFT calculations of the electronic structure along path were performed. These results are shown on Figure 2. Figure 2a–e presents the electronic structures for x values of 0, , , and 1, respectively. The crystal structure used for these calculations is that of pristine MnBiTe taken from [17] (cell parameters unaltered) with partial Sn substitution of Mn atoms.
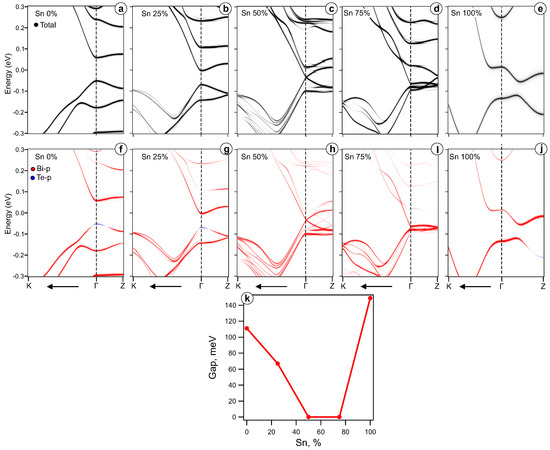
Figure 2.
DFT–calculated bulk band structure of (MnSn)BiTe supercell along path in the first Brillouin zone, corresponding concentrations are (a,f), (b,g), (c,h), (d,i), (e,j). General plot of the bulk band gap value as a function of Sn content x is on the panel (k). The total spectral weight unfolded to primitive cell is shown in black. Red and blue colours indicate regions of Bi-p and Te-p orbital weight dominance, respectively.
The bulk gap dependence on Sn concentration calculated by the supercell method is shown in Figure 2k where a behaviour similar to the KKR method results is evident (see Figure 1). A gradual decrease of the value of the bulk gap at in the range is followed by a zero-gap plateau for . The bulk gap then increases again during the transition to the SnBiTe stoichiometry. When the concentration of Sn atoms reaches 50%, the energy gap closes at the point but remains finite at the Z point. However, when the Sn concentration reaches 75%, the energy gap at the Z point closes but opens at the point instead. The full substitution of Mn with Sn is characterized by finite bulk gaps at both (normal gap) and Z (inverted gap) points. It is indeed typical for SnBiTe or PbBiTe compounds which are TI as well [27,29,30,33].
A possibility of TPTs realization was assessed by performing a more detailed analysis of the obtained bulk gap dependence. The lower panel in Figure 2f–j presents the Bi-p and Te-p orbital contribution difference for the corresponding (MnSn)BiTe band structures. Red and blue colours reflect the predominance of Bi-p or Te-p contribution into each electron state. The inversion of these contributions at both and Z high symmetry points can be interpreted as evidence that MnBiTe and SnBiTe, respectively, are both TI (Figure 2f,j). Hence, this indicator may be of particular interest in intermediate (MnSn)BiTe systems with , and substitution ratios. The case of in Figure 2g is very similar to the pure MnBiTe crystal where Bi-p and Te-p contributions are inverted at the point, the only difference being the reduced value of the energy gap. However, the and cases show drastic changes of the electronic structure compared to pristine MnBiTe. In these systems, the inversion of the Bi-p and Te-p no longer exists and the energy gap is also completely closed (at the point for and at the Z point for , see Figure 2h,i). At last, the case of corresponds to SnBiTe stoichiometry with nonzero bulk gap. Thus, the x-dependence of the bulk gap has a plateau-like character, which is similar to the KKR calculation results. We suppose that bulk gap closing at the and Z points together with a Bi-p and Te-p contribution ratio change at the gap edges can serve as a definite mark of occurring TPTs.
The main difference between KKR and DFT calculation results in Figure 1 and Figure 2 lies in the Sn concentration range which delivers the bulk gap plateau: 50–75% for DFT supercell calculations and 35–45% for KKR calculations. The most probable reason for this discrepancy may be the presence of a regular intralayer ordering of the Sn substitutes (common drawback of the supercell impurity calculations) which is not the case for the KKR method. Another difference stems from the usage of a cell with experimental parameters for the KKR calculations while the DFT calculations were performed using the structurally-optimized cell from [16] (with regular partial replacement of Mn atoms with Sn atoms in a supercell and unaltered cell parameters). Nevertheless, these distinctions do not influence the general conclusion regarding the bulk band gap dependence on x which was obtained by both methods simultaneously.
Based on the discussion above, the Sn concentration variation should lead to the realization of TPTs in the (MnSn)BiTe system: the first transition (presumably from the TI phase into another phase: trivial or a Weyl semimetal state) occurs at lower Sn concentrations of about 50% defined by closing the bulk gap at the point and the second transition (back into the TI state) occurs at higher Sn concentrations accompanied by the bulk gap reopening at the Z point. These TPTs are accompanied by the disappearance of the Te-p and Bi-p contributions inversion when bulk gap is closed, with its subsequent occurrence at the Z point when bulk gap is reopened.
3.2. Experimental Results
Experimentally measured band dispersions at different concentrations of Sn atoms are presented in Figure 3 to support the theoretical results shown in Figure 1 and Figure 2.
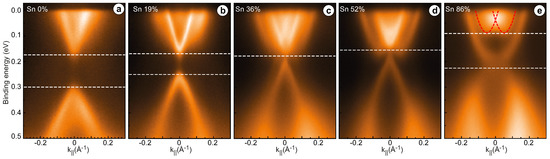
Figure 3.
Band structure of valence and conduction states in ARPES spectra taken from (MnSn)BiTe crystal for x = 0 (a), 0.19 (b), 0.36 (c), 0.52 (d) and 0.86 (e). White dotted horizontal lines indicate the approximate positions of the edges of bulk band gap. Sn–derived states in panels (e) are marked by red dotted parabolas.
This figure illustrates the results of an ARPES experiment. The ARPES spectra were taken at eV (He-I ). It is worth noting that at this excitation energy, TSS in the ARPES data are poorly distinguishable. The maximum intensity is found for bulk states in case of pure MBT [44] or compounds with low Sn content. The Sn concentration values in the measured samples (the ARPES data for which are presented on the different panels of Figure 3) were estimated from the XPS data (Figure S1 in Supplementary Materials) based on the ratio of intensities of the core levels of Mn2p and Sn3d. The size of the bulk gap for pure MnBiTe is about 195 meV, which matches well with the presented calculations of the bulk electronic structure and corresponds to the experimental results of other work [44]. Increasing the Sn concentration from 0% (Figure 3a) to 19% (Figure 3b) leads to a noticeable decrease of the bulk band gap. At a concentration of Sn atoms of about 36% (Figure 3c), the value of the bulk gap decreases to its minimum, which close to zero within the experimental error. When the concentration increases up to 52% (Figure 3d), the bulk band gap does not change. At concentrations of about 86% (Figure 3e), the obtatined electronic strucure resambles one for SnBiTe [29]. Comparig our results with theoretical [29,45] and experimental [33,45] studies of SnBiTe system, we can suppose that ARPES data for the sample with high Sn concentration in Figure 3e present the picture of TSS that are localized within the bulk band gap. The edges of bulk band gap for all Sn concentrations are shown by white dotted lines in Figure 3.
This behavior of the bulk gap as a function of the Sn atomic concentration, namely a decrease in the bulk gap down to zero with increasing concentrations (at 36% Sn) followed by a plateau near zero up to concentrations of about 52%, is (at least qualitatively) similar to the corresponding theoretical dependencies (Figure 1 and Figure 2). It confirms the accuracy of the bulk calculations performed and the conclusions drawn from them.
3.3. Surface Calculations
Slab DFT calculations of (MnSn)BiTe system along the path were carried out to obtain surface electronic structures in Figure 4a–d corresponding to different Sn concentrations (, , and , respectively). The positions of the bulk band gap edges are marked with black horizontal dashed lines and the edges of the TSS gap are marked with green solid lines (if applicable). When Sn content increases from 0% (Figure 4a) to 25% (Figure 4b), the bulk band gap and the TSS gap both decrease almost by one half; further increase up to 50% closes the bulk gap at the point (Figure 4c) and this gapless dispersion persists up to 75% of Sn content (Figure 4d). The bulk band gap dependence on the x parameter in the slab calculations thus matches well with that of the bulk crystal calculations presented in Figure 2. Moreover, they also agree qualitatively with the ARPES data in Figure 3 where a similar bulk gap decreases almost to zero value can be seen. Further, the bulk band gap on ARPES spectra reopens at large Sn concentrations. The overall electronic structure of (MnSn)BiTe with large x strongly resembles that of SnBiTe [29], PbBiTe [30] and GeBiTe [29,31].
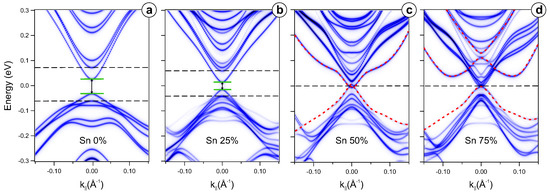
Figure 4.
Calculated electronic structure of the TSSs and the nearest valence and conduction band states for different Sn concentrations: 0% (a), 25% (b), 50% (c), 75% (d). The positions of the edges of the bulk band gap are marked with horizontal dotted lines, and the energy gap in the TSS (where they are present) is marked with green solid lines indicating its magnitude. Sn–derived states in panels (c,d) are marked by red dotted lines.
In the case of slab DFT calculations, one can observe additional Sn-derived states that are absent in the bulk crystal calculations in Figure 2. They appear as additional dispersion branches in both bulk valence and conduction band regions entering the bulk gap when Sn concentration is 50% (they are more pronounced for greater concentrations). A further increase in Sn concentration leads to a deformation of the energy dispersion of these additional Sn-derived states. In the case of , one may observe a structure that resembles two -shifted parabolic branches (these states are marked by dashed red lines in Figure 4d) with an avoided crossing feature at the point. The formation of similar additional states is also visible in the experimental ARPES data in Figure 3.
These theoretical calculations generally follow the tendencies revealed by the experimental spectra and emphasize the fact that the Sn orbitals introduced in the system by impurity doping substantially modify the electronic structure of (MnSn)BiTe. We assume that both in the case of the bulk calculations in Figure 2 and in the case of the slab calculations in Figure 3, the reason for the decrease in the band gap value with an increase in Sn concentration may be a change in the mutual hybridization of Te- and Bi- states with each other and the orbitals of Sn and Mn atoms. Moreover, in both of these cases one can observe the collapse of the band gap when Sn content reaches 50%, indicating the TPT to trivial or a Weyl semimetal state.
4. Conclusions
To summarize, we have analyzed in detail possible changes in the electronic structure of the TSSs and the nearest valence and conduction band states for (MnSn)BiTe system produced by partial substitution of Mn atoms by Sn atoms under x variation in the compound.
Theoretical calculations for both (MnSn)BiTe bulk and slab crystal models for different x values were performed by KKR (bulk) and DFT (both) methods. It was shown that partial substitution of Mn atoms with Sn atoms leads to a gradual bulk gap decrease at the point down to zero at (depending on the calculation method). When x is in the range , the bulk gap remains zero (i.e., forms the so-called zero-gap plateau in its dependence on the value of the parameter x). Finally, the bulk gap reopens again at the highest Sn concentrations (). Despite the KKR and DFT methods being conceptually different, they both qualitatively predict the existence of the zero-gap plateau, differing only quantitatively on the corresponding x range estimates.
The bulk gap closure and its subsequent reopening should be associated with two TPTs occurring in this system at different Sn concentrations: from the TI with inverted bulk gap at the point to a Weyl semimetal state at lower x and then the reverse transition to the TI phase with inverted bulk gap at the Z point at higher x. This is confirmed by electronic structure calculations along the path in the first Brillouin zone, where the inversion of Bi-p and Te-p orbital contributions can be clearly seen at the edges of the bulk gap at the point for x below the plateau range and at the Z point for x above the plateau range.
The experimentally measured band structure also agrees qualitatively with the calculations regarding the x-dependence of the bulk gap: when x increases, the bulk gap magnitude gradually decreases down to zero, and then the zero-gap plateau ensues and finally the bulk gap reopens at high x, when the band structure typical for SnBiTe TI is observed. These experimental observations form a sound basis for the computational investigation of topological phase transitions in (MnSn)BiTe presented in this work.
Strong changes in the electronic structure of (MnSn)BiTe with an increase in the parameter x are also demonstrated by the slab calculations, in which additional Sn-derived states that are absent in the calculations of the bulk crystal, can be easily identified for high concentrations of Sn atoms. These additional states are located in valence band, conduction band and the bulk gap regions; they correlate well to similar features in the experimental spectra.
Finally, Sn concentration dependence of the bulk gap in (MnSn)BiTe should be primarily determined by a complex mixing of Te- and Bi- orbitals with Mn and Sn ones. The character of this hybridization leads to the collapse of the bulk gap at the Sn concentrations of approximately 40–50%, which indicates a TPT from a topological to a trivial or a Weyl semimetal state. When the stoichiometry of (MnSn)BiTe approaches its SnBiTe limit at , the system reaches the TI phase characteristic of this compound. Although the details of these TPTs mechanism are yet to be revealed, it provides a path of a gradual modification of the (MnSn)BiTe electronic properties by controlling the Sn substitution ratio.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/sym15020469/s1, Figure S1: XPS data for Mn2p and Sn3d core levels for samples with different Sn concentrations.
Author Contributions
Conceptualization, A.V.T. and A.M.S.; methodology, A.V.T., A.V.E., V.A.G., K.A.K. and O.E.T.; software, A.V.T. and A.V.E.; validation, A.V.T., T.P.M., D.A.E., A.V.E., I.I.K. and A.M.S.; formal analysis, A.V.T., T.P.M., D.A.E., A.V.E. and A.M.S.; investigation, A.V.T., T.P.M., D.A.E., A.V.E., I.I.K., V.A.G., K.A.K., O.E.T. and A.M.S.; resources, I.I.K., V.A.G., K.A.K., O.E.T. and A.M.S.; data curation, A.V.T., T.P.M., D.A.E., A.V.E., V.A.G., K.A.K., O.E.T. and A.M.S.; writing—original draft preparation, A.V.T., T.P.M., D.A.E., A.V.E. and A.M.S.; writing—review and editing, A.V.T., T.P.M., A.V.E. and A.M.S.; visualization, A.V.T., T.P.M. and A.M.S.; supervision, A.V.T.; project administration, A.M.S.; funding acquisition, I.I.K. and A.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge support by the Saint Petersburg State University (Grant No. 94031444), Russian Science Foundation (Grant No. 22-72-10074) in the part of theoretical calculations and ARPES measurements and Grant No. 22-12-20024 in the part of the crystal growth.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qi, X.L.; Hughes, T.L.; Zhang, S.C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 2008, 78, 195424. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Chang, C.Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.L.; et al. Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Yasuda, K.; Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 2019, 1, 126–143. [Google Scholar] [CrossRef]
- Chang, C.; Zhao, W.; Kim, D.; Zhang, H.; Assaf, B.; Heiman, D.; Zhang, S.; Liu, C.; Chan, M.; Moodera, J. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 2015, 14, 473–477. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef]
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194–198. [Google Scholar] [CrossRef]
- Otrokov, M.M.; Klimovskikh, I.I.; Bentmann, H.; Estyunin, D.A.; Zeugner, A.; Aliev, Z.S.; Gaß, S.; Wolter, A.U.B.; Koroleva, A.V.; Shikin, A.M.; et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 2019, 576, 416. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, M.; Zhu, T.; Xing, D.; Zhang, H.; Wang, J. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys. Rev. Lett. 2019, 122, 206401. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Du, S.; Wang, Z.; Gu, B.L.; Zhang, S.C.; He, K.; Duan, W.; Xu, Y. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci. Adv. 2019, 5, eaaw5685. [Google Scholar] [CrossRef]
- Gong, Y.; Guo, J.; Li, J.; Zhu, K.; Liao, M.; Liu, X.; Zhang, Q.; Gu, L.; Tang, L.; Feng, X.; et al. Experimental realization of an intrinsic magnetic topological insulator. Chin. Phys. Lett. 2019, 36, 076801. [Google Scholar] [CrossRef]
- Aliev, Z.S.; Amiraslanov, I.R.; Nasonova, D.I.; Shevelkov, A.V.; Abdullayev, N.A.; Jahangirli, Z.A.; Orujlu, E.N.; Otrokov, M.M.; Mamedov, N.T.; Babanly, M.B.; et al. Novel ternary layered manganese bismuth tellurides of the MnTe-Bi2Te3 system: Synthesis and crystal structure. J. Alloy Compd. 2019, 789, 443–450. [Google Scholar] [CrossRef]
- Estyunin, D.; Klimovskikh, I.I.; Shikin, A.M.; Schwier, E.; Otrokov, M.; Kimura, A.; Kumar, S.; Filnov, S.; Aliev, Z.S.; Babanly, M.; et al. Signatures of temperature driven antiferromagnetic transition in the electronic structure of topological insulator MnBi2Te4. APL Mater. 2020, 8, 021105. [Google Scholar] [CrossRef]
- Shikin, A.M.; Estyunin, D.; Klimovskikh, I.I.; Filnov, S.; Schwier, E.; Kumar, S.; Miyamoto, K.; Okuda, T.; Kimura, A.; Kuroda, K.; et al. Nature of the Dirac gap modulation and surface magnetic interaction in axion antiferromagnetic topological insulator MnBi2Te4. Sci. Rep. 2020, 10, 13226. [Google Scholar] [CrossRef]
- Shikin, A.M.; Estyunin, D.; Zaitsev, N.L.; Glazkova, D.; Klimovskikh, I.I.; Filnov, S.; Rybkin, A.G.; Schwier, E.; Kumar, S.; Kimura, A.; et al. Sample-dependent Dirac-point gap in MnBi2Te4 and its response to applied surface charge: A combined photoemission and ab initio study. Phys. Rev. B 2021, 104, 115168. [Google Scholar] [CrossRef]
- Shikin, A.; Makarova, T.; Eryzhenkov, A.; Usachov, D.; Estyunin, D.; Glazkova, D.; Klimovskikh, I.; Rybkin, A.; Tarasov, A. Routes for the topological surface state energy gap modulation in antiferromagnetic MnBi2Te4. Phys. B Condens. Matter 2023, 649, 414443. [Google Scholar] [CrossRef]
- Shikin, A.; Estyunin, D.; Zaitsev, N.; Glazkova, D.; Klimovskikh, I.; Fil’nov, S.; Rybkin, A.; Kokh, K.; Tereshchenko, O.; Zvezdin, K.; et al. Modulation of the Dirac Point Band Gap in the Antiferromagnetic Topological Insulator MnBi2Te4 due to the Surface Potential Gradient Change. J. Exp. Theor. Phys. 2022, 134, 103–111. [Google Scholar] [CrossRef]
- Hao, Y.J.; Liu, P.; Feng, Y.; Ma, X.M.; Schwier, E.F.; Arita, M.; Kumar, S.; Hu, C.; Zeng, M.; Wang, Y.; et al. Gapless surface Dirac cone in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. X 2019, 9, 041038. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, L.; Li, J.; Li, Y.; Wang, H.; Zhang, C.; Li, H.; Wu, Y.; Liang, A.; Chen, C.; et al. Topological electronic structure and its temperature evolution in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. X 2019, 9, 041040. [Google Scholar] [CrossRef]
- Swatek, P.; Wu, Y.; Wang, L.L.; Lee, K.; Schrunk, B.; Yan, J.; Kaminski, A. Gapless Dirac surface states in the antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. B 2020, 101, 161109. [Google Scholar] [CrossRef]
- Garnica, M.; Otrokov, M.; Aguilar, P.C.; Klimovskikh, I.; Estyunin, D.; Aliev, Z.; Amiraslanov, I.; Abdullayev, N.; Zverev, V.; Babanly, M.; et al. Native point defects and their implications for the Dirac point gap at MnBi2Te4 (0001). Quantum Mater. 2022, 7, 1–9. [Google Scholar] [CrossRef]
- Deng, Y.; Yu, Y.; Shi, M.Z.; Guo, Z.; Xu, Z.; Wang, J.; Chen, X.H.; Zhang, Y. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 2020, 367, 895–900. [Google Scholar] [CrossRef]
- Lee, S.H.; Zhu, Y.; Wang, Y.; Miao, L.; Pillsbury, T.; Yi, H.; Kempinger, S.; Hu, J.; Heikes, C.A.; Quarterman, P.; et al. Spin scattering and noncollinear spin structure-induced intrinsic anomalous Hall effect in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. Res. 2019, 1, 012011. [Google Scholar] [CrossRef]
- Riberolles, S.X.M.; Zhang, Q.; Gordon, E.; Butch, N.P.; Ke, L.; Yan, J.Q.; McQueeney, R.J. Evolution of magnetic interactions in Sb-substituted MnBi2Te4. Phys. Rev. B 2021, 104, 064401. [Google Scholar] [CrossRef]
- Chen, B.; Fei, F.; Zhang, D.; Zhang, B.; Liu, W.; Zhang, S.; Wang, P.; Wei, B.; Zhang, Y.; Zuo, Z.; et al. Intrinsic magnetic topological insulator phases in the Sb doped MnBi2Te4 bulks and thin flakes. Nat. Commun. 2019, 10, 4469. [Google Scholar] [CrossRef] [PubMed]
- Glazkova, D.A.; Estyunin, D.A.; Klimovskikh, I.I.; Makarova, T.P.; Tereshchenko, O.E.; Kokh, K.A.; Golyashov, V.A.; Koroleva, A.V.; Shikin, A.M. Electronic Structure of Magnetic Topological Insulators Mn(Bi1−xSbx)2Te4 with Various Concentration of Sb Atoms. JETP Lett. 2022, 115, 286–291. [Google Scholar] [CrossRef]
- Qian, T.; Yao, Y.T.; Hu, C.; Feng, E.; Cao, H.; Mazin, I.I.; Chang, T.R.; Ni, N. Magnetic dilution effect and topological phase transitions in (Mn1-xPbx)Bi2Te4. Phys. Rev. B 2022, 106, 045121. [Google Scholar] [CrossRef]
- Zhu, J.; Naveed, M.; Chen, B.; Du, Y.; Guo, J.; Xie, H.; Fei, F. Magnetic and electrical transport study of the antiferromagnetic topological insulator Sn-doped MnBi2Te4. Phys. Rev. B 2021, 103, 144407. [Google Scholar] [CrossRef]
- Li, Y.; Huang, C.; Wang, G.; Hu, J.; Duan, S.; Xu, C.; Lu, Q.; Jing, Q.; Zhang, W.; Qian, D. Topological Dirac surface states in ternary compounds GeBi2Te4, SnBi2Te4 and Sn0.571Bi2.286Se4*. Chin. Phys. B 2021, 30, 127901. [Google Scholar] [CrossRef]
- Kuroda, K.; Miyahara, H.; Ye, M.; Eremeev, S.V.; Koroteev, Y.M.; Krasovskii, E.E.; Chulkov, E.V.; Hiramoto, S.; Moriyoshi, C.; Kuroiwa, Y.; et al. Experimental Verification of PbBi2Te4 as a 3D Topological Insulator. Phys. Rev. Lett. 2012, 108, 206803. [Google Scholar] [CrossRef]
- Arita, M.; Sato, H.; Shimada, K.; Namatame, H.; Taniguchi, M.; Sasaki, M.; Kitaura, M.; Ohnishi, A.; Kim, H.J. Angle resolved photoemission study of GeBi2Te4. In Proceedings of the 12th Asia Pacific Physics Conference (APPC12), Makuhari, Japan, 14–19 July 2013. [Google Scholar] [CrossRef]
- Okamoto, K.; Kuroda, K.; Miyahara, H.; Miyamoto, K.; Okuda, T.; Aliev, Z.S.; Babanly, M.B.; Amiraslanov, I.R.; Shimada, K.; Namatame, H.; et al. Observation of a highly spin-polarized topological surface state in GeBi2Te4. Phys. Rev. B 2012, 86, 195304. [Google Scholar] [CrossRef]
- Changdar, S.; Ghosh, S.; Vijay, K.; Kar, I.; Routh, S.; Maheswari, P.K.; Ghorai, S.; Banik, S.; Thirupathaiah, S. Effect on the Electronic and Magnetic Properties of Antiferromagnetic Topological Insulator MnBi2Te4 with Sn Doping. arXiv 2022, arXiv:2207.13595. [Google Scholar]
- Weinberger, P. Electron Scattering Theory for Ordered and Disordered Matter; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Liechtenstein, A.I.; Katsnelson, M.I.; Gubanov, V.A. Exchange interactions and spin-wave stiffness in ferromagnetic metals. J. Phys. F Met. Phys. 1984, 14, L125. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Efficient projector expansion for the ab initio LCAO method. Phys. Rev. B 2005, 72, 045121. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Han, M.J.; Ozaki, T.; Yu, J. O(N) LDA + U electronic structure calculation method based on the nonorthogonal pseudoatomic orbital basis. Phys. Rev. B 2006, 73, 045110. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Ebert, H.; Ködderitzsch, D.; Minár, J. Calculating condensed matter properties using the KKR-Green’s function method—Recent developments and applications. Rep. Prog. Phys. 2011, 74, 096501. [Google Scholar] [CrossRef]
- Vidal, R.C.; Bentmann, H.; Peixoto, T.R.F.; Zeugner, A.; Moser, S.; Min, C.H.; Schatz, S.; Kißner, K.; Ünzelmann, M.; Fornari, C.I.; et al. Surface states and Rashba-type spin polarization in antiferromagnetic MnBi2Te4(0001). Phys. Rev. B 2019, 100, 121104. [Google Scholar] [CrossRef]
- Fragkos, S.; Baringthon, L.; Tsipas, P.; Xenogiannopoulou, E.; Le Fèvre, P.; Kumar, P.; Okuno, H.; Reyren, N.; Lemaitre, A.; Patriarche, G.; et al. Topological surface states in epitaxial (SnBi 2Te4)n(Bi 2Te3)m natural van der Waals superlattices. Phys. Rev. Mater. 2021, 5, 014203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).