Abstract
This numerical analysis aims to observe and analyze the combined convection characteristics of the micropolar tri-hybrid nano-liquid that moves around a cylindrical object, and, in addition, to compare its thermal behavior to that of hybrid and mono nano-fluids. For this purpose, the problem is modeled by developing the Tiwari and Das models, then the governing model is converted into dimensionless expressions, and finally, the problem is solved using the Keller box approximation. The current findings are compared with previously published results to show that the present method is sufficiently accurate for physical and engineering applications. By examining and analyzing the extent to which skin friction, the Nusselt number, velocity, angular velocity, and temperature are affected by some critical factors, the following points are revealed: A greater value of the micropolar and magnetic factors can result in curtailing the heat transmission rate, velocity, and angular velocity. Higher values of the mixed convection factor can contribute to a better rate of energy transfer and can grant the micropolar tri-hybrid nano-liquid a higher velocity. Regardless of the influencing factors, the maximum value of all considered physical groups is achieved by using ternary hybrid nano-liquids.
1. Introduction
Micropolar liquids are polar liquids with an asymmetrical pressure sensor, and they are commonly represented as complex liquids with a microstructure. They are liquids that are suspended in an adhesive medium, and they are vital for scientific researchers and industry practitioners operating with hydrodynamic liquid issues and phenomena, as well as having a wide range of applications such as in polymeric solutions, lubricating fluids, animal blood, liquid crystals, and others. The microfluidic theory and its extensions were first introduced by Eringen et al. [1,2]. In their studies, they highlighted the local micromotions and described the case in which microdeformation rates are linear, in addition to including heat conduction and dissipation impacts. Recently, Abbas et al. [3] provided a numerical analysis of a magneto-micropolar nano-liquid in a porous medium over a cylindrical object possessing a sinusoidally varying radius. Swalmeh et al. [4] computationally explored the convection that is produced by natural means in a micropolar nano-liquid moving about a spherical object. Alkasasbeh et al. [5] looked into the thermal performance of kerosene oil and a micropolar fluid host of metallic nano-solids across a cylindrical surface was studied. El-Zahar et al. [6] analyzed the influence of a combined free and forced convection flow of micropolar nano-fluid along an orthogonal cylindrical object. Alwawi et al. [7] observed the thermal behavior of a micropolar liquid enhanced with nano-particles moving around a cylindrical surface subjected to Lorentz force. Yaseen et al. [8] presented a report on the thermal performance of a magnetized micropolar nano-liquid moving around a spherical object.
The development of mechanisms and technologies in the field of energy transfer through liquids is an essential goal because of its tangible impact on the development of many food and pharmaceutical industries, as well as countless fields with physics and engineering applications. To this end, large-scale experiments and studies have been conducted in an attempt to identify the fundamental and critical factors that influence energy transmission and are controlled via new and innovative methods and technologies. Among the most effective of these techniques, which are supported by earlier studies, are those that have been concerned with promoting the thermal conductivity performance of liquids by including solid nano-particles to obtain a composition of liquid and solid nano-particles, which are known as nano-fluids. The inclusion of those nano-particles in the world of energy transport is credited to Choi and Eastman [9]. Their study demonstrated the extent of metallic nano-particles’ ability to raise the thermal conductivity performance of the host fluid. Furthermore, the host fluid became able to overcome previous problems caused by the researchers’ use of micrometer-sized particles, such as clogging and instability. Eastman et al. [10] published a research paper showing the great ability and superiority of copper nano-solids in raising the thermal conductivity of liquid ethylene glycol over copper and aluminum oxides. Thereafter, many simulation investigations were held in an attempt to predict the behavior of these upgraded fluids. Kuznetsov and Nield [11] have used the Buongiorno nano-liquid model to upgrade earlier studies on regular liquids past a vertical plate. Dinarvand et al. [12] presented a report on the combined convection of a nano-liquid moving around a vertical cylindrical surface with the aid of the homotopy approximation. Rashad and Nabwey [13] looked into the combined bio-convection of a nano-liquid involving motile gyrotactic microorganisms moving past a cylindrical surface. Alwawi et al. [14] examined the combined and free convection flow of magneto-micropolar and magneto-Casson nano-liquids around a cylinder. Alsulami et al. [15] investigates the MHD energy transport produced by a sodium alginate liquid motion about a stretching sheet in a porous media. More studies can be found in [16,17,18]. A second generation of nano-substances, known as hybrid nano-substances, has emerged and spread as a result of extensive experimental research. The concept of hybrid nano-composites is centered on the fabrication of two nano-materials to generate a nano-combination with better features [19,20,21,22,23]. Nadeem [24] considered the influence of thermal slip on hybrid nano-liquid flow via the cylindrical surface. Dinarvand [25] optimized the Tiwari–Das’s model to examine the combined convection flow of a hybrid nano-liquid over a porous cylindrical shape. Rashad et al. [26] looked into the energy transport performance of a hybrid polar nano-liquid around a cylindrical shape in a saturated porous medium. Alharbi et al. [27] explored the effect of hybrid nano-materials on the thermal performance of a moving magneto-liquid around a cylindrical surface. More recent comprehensive contributions are reported in [28,29,30,31,32,33]. The experiments did not appear to end there, and they are still ongoing in order to find the ideal fluid on which to rely. This motivated the availability of the third generation of nano-fluids (ternary hybrid nano-fluids), in which three different types of nano-solids with integrated physical and chemical features are suspended in the ternary hybrid nano-particles. Experimental studies [34,35,36] demonstrate that these advanced nano-particles outperform the previous generation in terms of thermal performance. The heat transfer characteristics of a Cu/Fe3O4/SiO2-polymer-based tri-hybrid nano-liquid past a heated stretching/shrinking cylindrical shape were investigated by Mahmood et al. [37]. A numerical study was carried out by Alharbi et al. [38] to analyze the heat and mass transfer of a magneto-tri-hybrid nano-liquid moving about a stretching cylinder. In their comprehensive study, Nazir et al. [39] observed the impact of the application of a magnetic field on the flow of the tri-hybrid toward a heated cylindrical object. Khan et al. [40] analyzed the flow of tri-hybrid nano-fluid characteristics around a rotating sphere in the context of trying to cool rotating spherical industrial products. Sarada et al. [41] examined the heat transport of tri-hybrid nano-liquids in motion past a curved stretching sheet, considering the non-Fourier heat flux model. In their investigation, Kumar et al. [42] provided a comparative analysis of energy transport in time-dependent MHD tri-hybrid nano-liquids, considering the conveyance of three variously shaped nano-solids. Other relevant works are included in [43,44,45,46,47].
The combination of natural and forced convection is referred to as combined (mixed) convection. It is caused by both an external force and a difference in the fluid density that is caused by temperature gradients. In a mixed convection, there are two types of fluid flow: assisting, where forced convection and convection produced by natural means are in the same direction, and opposing, where natural and forced convections are in opposite directions. The wide range of engineering and physical applications of mixed convection, such as cooling in electronic devices, nuclear reactors, many mantle-driven cavities, and others, have gained the utmost importance and have attracted many researchers. Magnetohydrodynamics (MHDs), on the other hand, are critical in regulating energy transmission in many industrial applications, such as the role of fluid metals in cooling nuclear reactors and controlling metallurgical procedures. Dhanai et al. [48] presented a study on the transfer of energy and mass through a magneto-nano-fluid moving around an inclined cylinder in combined convection. Alizadeh et al. [49] provided a numerical study on the entropy generation of magnetized nano-fluid flow over a cylinder in a porous medium in the case of combined convection. In their study, Patil and Kulkarni [50] analyzed the thermal behavior of second-generation nano-fluids flowing around a cylinder in a magnetized mixed convection. Ullah et al. [51] analyzed the slip velocity impact on MHDs mixed convection flow past a non-conducting cylindrical surface within a porous medium. Depending on the Buongiorno model in their investigation, Umavathi et al. [52] examined MHDs that squeezed Cassonian nano-liquid flow between parallel convectively heated disks. See also [53,54].
The wide-ranging applications of tri-hybrid nano-fluids, micropolar fluids, combined convection, and magnetohydrodynamics mentioned in the earlier literature may lend weight to this study. In addition, in scrutiny of the previous literature, it appears that our gap appears to have not been deliberated previously. Additionally, our study is an improvement and an expansion of many previous studies, and it can be relied upon in many experimental and numerical studies. All of the foregoing prompted us to present a computational simulation and parametric analysis of the effectiveness of ternary nano-composites for improving the performance of micropolar liquid heat transport. To this end, the well-known Tiwari–Das model is expanded to include a ternary hybrid micropolar nano-liquid, considering magnetic force. The dimensional governing equations of the studied model are transformed into nondimensional, partial differential equations, and then, the Keller box scheme is employed to solve these partial differential equations. The obtained numerical results are compared to the previous literature and are found to be highly compatible.
2. Formulating the Governing Model
This section develops the mathematical formulations for heat transfer in the case of combined convection in magnetized micropolar ternary hybrid nano-fluids. The magnetic field strength is indicated by . The problem considers a horizontal circular cylinder with a radius of a. It depends on the constant heat flux boundary condition , as presented in Figure 1. , , and are ambient temperatures, free-stream velocity, and the gravitation. The perpendicular coordinates ζ and are measured along the circumference of the horizontal cylinder, starting from the lower stagnation point .
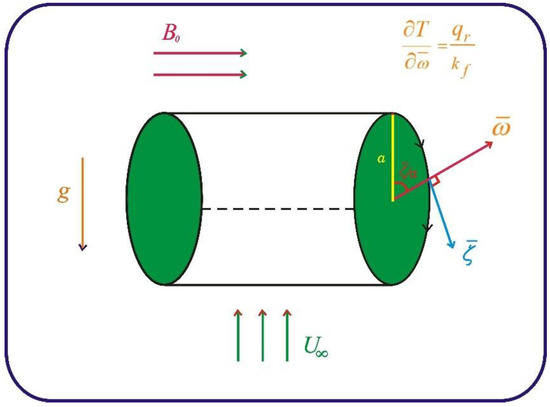
Figure 1.
Physical model and coordinate system.
Relying on the above assumptions, and by including the ternary hybrid nano-fluid characteristics [55,56,57], applying a magnetic field [7] and microrotation equations [4,58], the governing dimensional equations can be represented as:
The isoflux surface boundary condition for single-phase flows is considered in this study, which means that the heat flux at the boundary is constant. It can be stated mathematically as follows (see [57]):
and indicate the velocity components in the and directions, respectively. are angular velocity and the temperature. , and stand for the thermal conductivity of the fluid, the microinertia density, and the vortex viscosity. The physical properties represent the density, dynamic viscosity, and thermal expansion coefficient. , , and symbolize thermal diffusivity, electrical conductivity, and the spin gradient viscosity of the fluid, respectively. refers to the local free-stream velocity. Additionally, the subscript thnf denotes the ternary hybrid nano-fluid. Taking into account the ternary hybrid nano-fluid characteristics, their physical properties can be obtained, as displayed in Table 1.

Table 1.
Tri-hybrid nano-fluid physical properties [56,59].
Where denotes the volume fraction of the studied nano-particles. Based on the model characterization, the nondimensional variables are introduced as the following:
is called the Reynolds number and represents the kinematic viscosity of the fluid. Invoking the dimensionless variables (6) and ternary hybrid nano-fluid physical properties (Table 1), the dimensional governing Equations (1)–(4) and boundary conditions (5) can be expressed into a dimensionless form as follows:
subject to the following:
The stream function can be defined as the following:
Now, assume the following variables:
Substituting these variables (12) and (13) into Equations (7)–(11). The dimensionless equations can be rewritten as partial differential equations:
The above partial differential Equations (14)–(16), at the stagnation point , can be determined as the following:
The local skin friction coefficient Cf and the Nusselt number Nu can be written as the following [59]:
3. Numerical Approximation and Validation
The Keller box numerical method is exceedingly applicable since it has been flexibly programmed. The method’s numerical outcomes possess remarkable accuracy [60,61]. Consequently, all these properties give it adaptability compared to other methods for dealing with convection boundary layer flow problems. The Keller box method comprises the following procedures: Initially, the system was reduced from third-order to first-order equations via the finite differences method. After that, the converted difference equations were linearized using Newton’s scheme. Finally, the linear system of equations was solved by a block elimination process. Moreover, the numerical outcomes are gained, as shown in the figures and tables, by programming the algorithm of a linear system performed by MATLAB software. Furthermore, they are checked to see if the current results are correct by comparing the results of (bold results) the local skin friction and temperature, at a fixed value (, Pr ), with the previously reported literature (Italic results), as shown in Table 2 and Table 3. According to the tables, the present numerical results are in excellent agreement with the results of Nazar et al. [59] On the other hand, Table 4 displays the thermo-physical properties of the used nano-particles and fluid.

Table 2.
Comparing the results of skin friction with previous results.

Table 3.
Comparing the results of with previous results.

Table 4.
Thermo-physical characteristics of ethylene glycol and studied nano-particles [47,62,63,64].
4. Results and Discussion
In this section, the thermal behavior of micropolar tri-hybrid nano-liquids is presented. Additionally, insights and physical interpretations of the responses of physical groups when they are exposed to critical factors related to energy transfer are provided. The pertinent factors values have been taken into account as −0.5 ≤ λ ≤ 2, 1 ≤ K ≤ 5, 0.1 ≤ M ≤ 3, and 0.01 ≤ ψ ≤ 0.03. Figure 2, Figure 3, Figure 4 and Figure 5 represent the impacts of the studied parameters on the skin friction Cf, when enlarging values of mixed convection λ, micropolar K, and volume fraction ψ are the parameters. Figure 2 confirms that as the mixed convection values escalate, so do the drag forces. The skin friction increases with an increase in velocity, and previous studies confirm that for larger values of the mixed convection factor, the velocity is increased and, accordingly, there is a growth in the drag forces. Figure 3 describes that skin friction increases for micropolar factor boosting. The perceptions are that the viscosity appears to grow while the rising upsides of micropolar factor are utilized. Mathematically, Equation (22) shows that skin friction is an increasing function of the micropolar factor. As a result, the coefficient of skin friction increases. In Figure 4, it is evident that increasing the intensity of the magnetic field forces negatively affected the skin friction. This negative effect can be linked to an inhibition in the velocity of the fluid and the transport of energy, which are caused by the intensification of the magnetic field. Figure 5 is plotted to describe the tendency of skin friction when it is exposed to the volume fraction factor. Skin friction shows a positive tendency when the volume fraction factor increases, because, by increasing this factor, the thermal conductivity of the host fluid improves. In addition, looking closely at Equation (22), we find that the skin friction has a positive relationship with the nano-particle volume fraction if its values are between 0 and 1, and because this study relied on a range of volume fraction values between 0 and 0.2 (as recommended in the previous studies), the relationship will be positive, which leads to an improvement in the drag forces. The Nusselt number behaviors that result from the impacts of mixed convection, micropolar, magnetic, and volume fraction factors are captured in Figure 6, Figure 7, Figure 8 and Figure 9. Figure 6 shows how the Nusselt number behaves when the values of the mixed convection factor are escalating. The buoyant forces will undoubtedly improve as the combined convective factor values rise, and as a result, the Nusselt number value will also obviously improve. The inverse relationship between the Nusselt number and the micropolar factor is clearly visible in Figure 7. With the improvement of the micropolar factor, the resistance of the fluid to movement increases, and this means that its velocity is slowed, which causes an inhibition of energy transfer. The Nusselt number shows in Figure 8 a reverse response when exposed to a magnetic field of increasing intensity. This response is explained by the braking that occurs at the velocity of the tri-hybrid nano-fluid, which causes an inhibition of energy transfer. It is clear from Figure 9 that the Nusselt number is an increasing function of the volume fraction factor, which agrees with the fact that has been supported in several previous numerical and experimental studies, namely, that the thermal conductivity of the host fluid increases with the increase in the volume fraction factor, and accordingly, the rate of the energy transport increases.
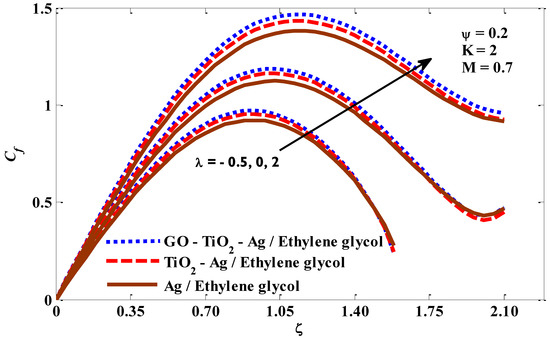
Figure 2.
Mixed convection factor against skin friction.
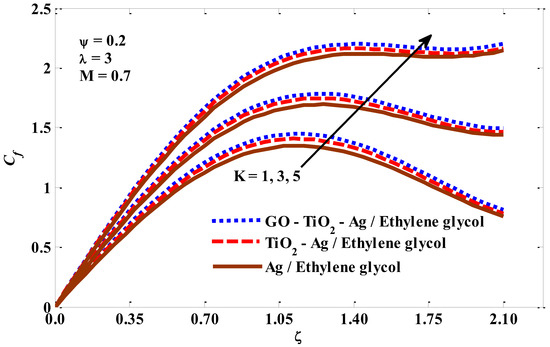
Figure 3.
Micropolar factor against skin friction.
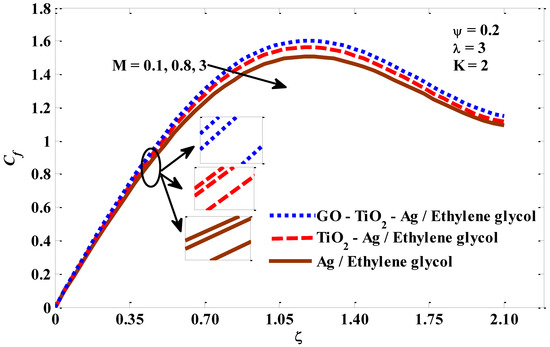
Figure 4.
Magnetic parameter against skin friction.
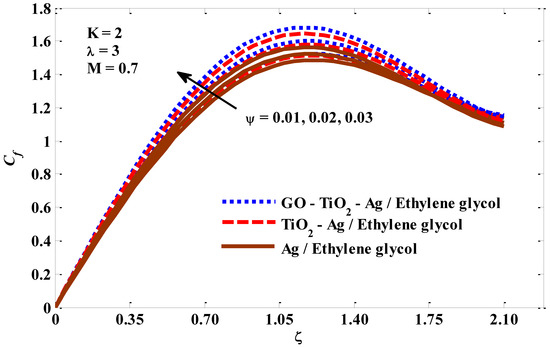
Figure 5.
Volume fraction factor against skin friction.
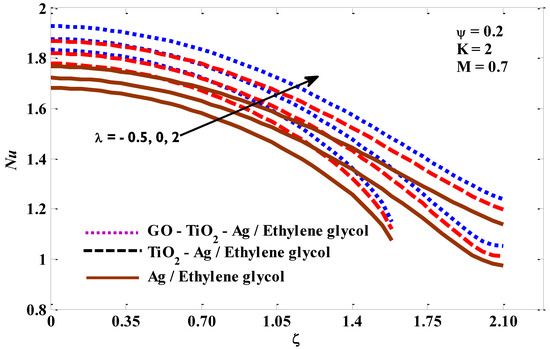
Figure 6.
Mixed convection parameter against Nusselt number.
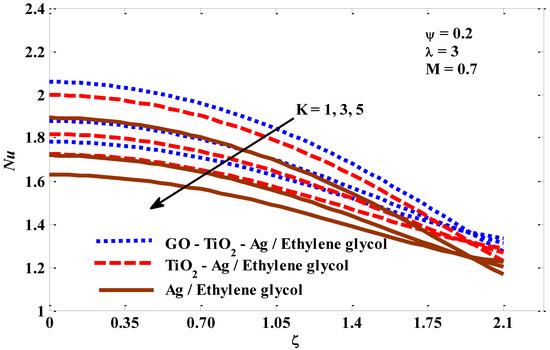
Figure 7.
Micropolar factor against Nusselt number.
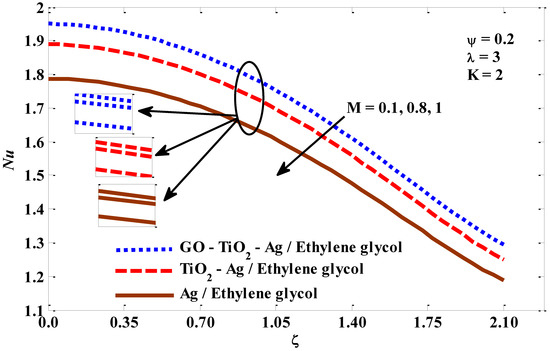
Figure 8.
Magnetic parameter against Nusselt number.
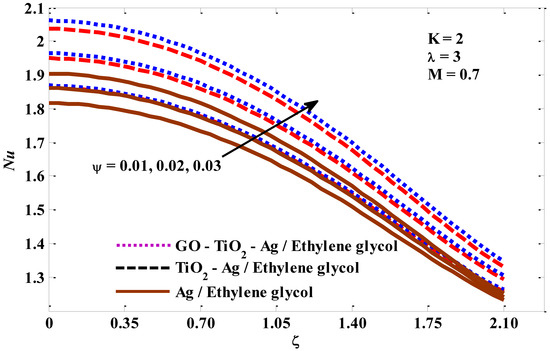
Figure 9.
Volume fraction factor against Nusselt number.
Figure 10, Figure 11, Figure 12 and Figure 13 depict the temperature profile’s response when subjected to the effects of a mixed convection factor, micropolar factor, magnetic factor, and a volume fraction factor. It is noted from Figure 10 that the temperature profile decreases owing to magnification in the mixed convection factor. The rise in the factor of mixed convection contributes significantly to a reduction in thermal diffusivity, which means low-energy capabilities and a thermal boundary layer thickness. Consequently, a decrease in the temperature of the micropolar tri-hybrid fluid occurs. In Figure 11, the incremental change in the micropolar factor leads to an improvement in the temperature contour of the micropolar tri-hybrid fluid. This positive behavior of tri-hybrid fluid temperature can be explained by the increase in viscosity caused by the incremental change in the micropolar factor. Figure 12 demonstrates the positive impact of the magnetic field factor on the temperature contour. The increasing change in the magnetic field factor leads to the stimulation of the frictional forces (Lorentz force), which means that more energy is generated inside the fluid, leading to an enhanced micropolar tri-hybrid fluid temperature. Figure 13 depicts the significant growth in the temperature profile as the volume fraction factor values improve. Physically, an increase in the volume fraction factor promotes heat transport between the exterior of the object wall and the host fluid, which assists in expanding the thickness of the thermal layer. The response of the velocity to the impacts of the combined convection factor, magnetic factor, micropolar factor, and volume fraction factor is graphically represented in Figure 1. There is a noticeable improvement in the velocity of the host fluid when the values of the mixed convection factor rise, which is evident in Figure 14. The reasons for these increased changes in the velocity of the host fluid are the improvement in the buoyant forces resulting from the rise in the values of the mixed convection factor. From Figure 15 it can be seen that the velocity of the tri-hybrid fluid is slowed down by the growth in the micropolar factor values. The suppression in the fluid velocity is expected to occur because the increase in the values of the micropolar factor improves the viscosity of the fluid, and this leads to an increase in the fluid’s resistance to movement, thereby limiting its velocity. Figure 16 depicts the negative effect of the Lorentz force on the velocity of the micropolar mono, hybrid, and tri-hybrid nano-fluids. The high value of the magnetic factor leads to a stimulation of the emergence of the Lorentz force, which in turn, works to enhance the resistance of the fluid to moving. As a result, its velocity actually declines. Figure 17 confirms that there is a positive relationship between the volume fraction factor and the velocity of the host fluid, in which both the fluid’s velocity and x move in tandem. It is well recognized that growth in the volume fraction factor leads to better energy transmission, contributing to more rapid fluid movement.
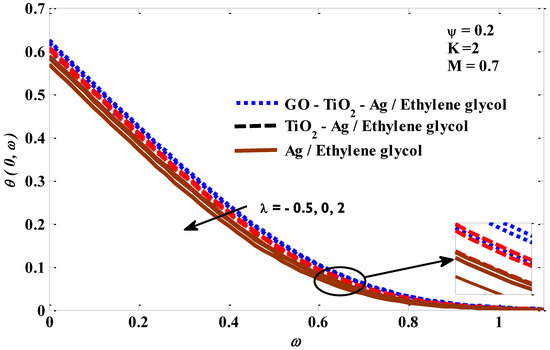
Figure 10.
Mixed convection factor against temperature.
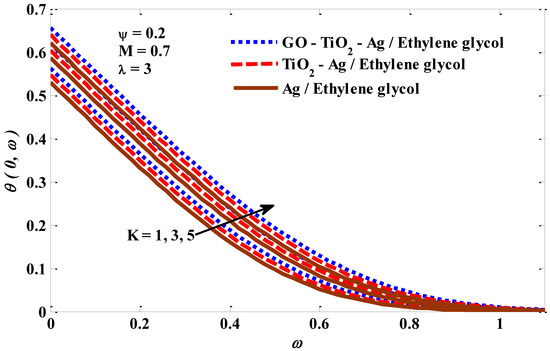
Figure 11.
Micropolar factor against temperature.
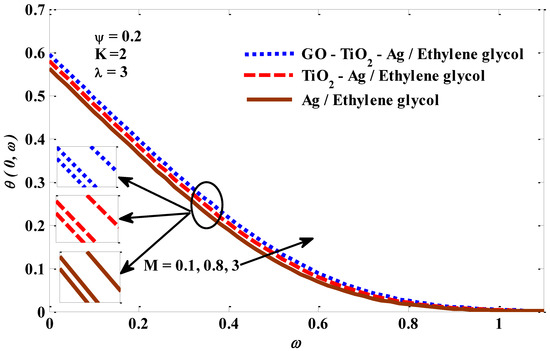
Figure 12.
Magnetic factor against temperature.
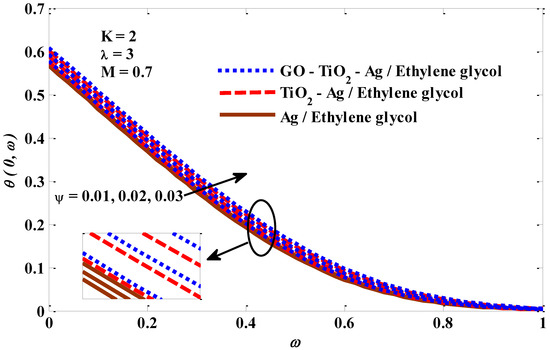
Figure 13.
Volume fraction factor against temperature.
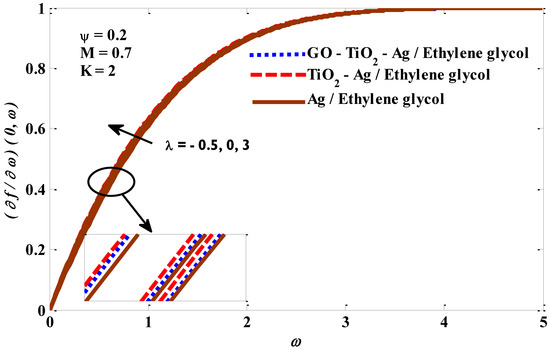
Figure 14.
Mixed convection factor against velocity.
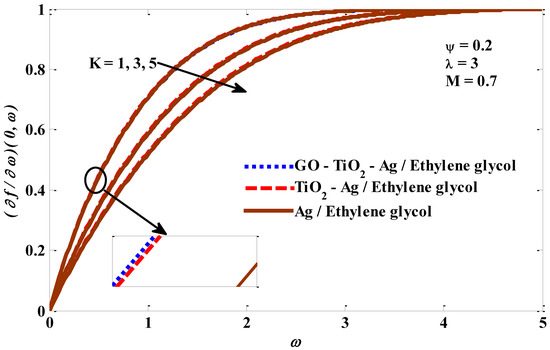
Figure 15.
Micropolar factor against velocity.
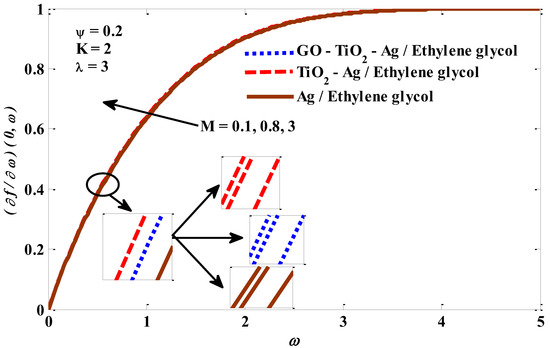
Figure 16.
Magnetic factor against velocity.
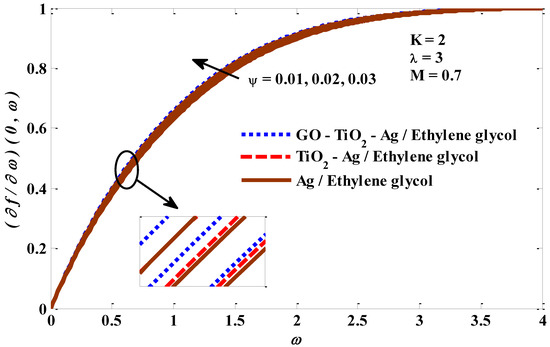
Figure 17.
Volume fraction factor against velocity profile.
Figure 18, Figure 19, Figure 20 and Figure 21 expose the impressions of the mixed convection factor, micropolar factor, magnetic factor, and volume fraction factor on the angular velocity. Figure 18 emphasizes that there is a direct association between the angular velocity and mixed convection factors. As the values of the mixed convection factor are raised, the buoyant forces are promoted, potentially causing the tri-hybrid nano-fluid’s angular velocity to rise. Figure 19 is portrayed to examine the impact of the micropolar factor on a tri-hybrid nano-fluid’s angular velocity. The enhancement in the micropolar factor values is accompanied by the improvement in the tri-hybrid nano-fluid’s resistance to flow, which leads to a reduction in its angular velocity. Figure 20 exemplifies the influence of the magnetic factor on a tri-hybrid nano-fluid’s angular velocity. It is exposed that the force exerted by the magnetic field resists the angular velocity. In Figure 21, the angular velocity shows a positive reaction to the growth in the values of the volume fraction factor. In fact, this behavior should occur owing to the increase in energy transfer resulting from the upgrade in the thermal conductivity of the host liquid. Furthermore, a combination of silver Ag, titanium oxide TiO2, and graphene oxide GO is considered as a ternary hybrid nano-particle. The combination of aluminum oxide Al2O3 and silver Ag is utilized as a hybrid nano-particle, whereas silver Ag is used as a mono nano-particle. All these nano-solids are suspended in ethylene glycol. It has been noticed that ternary hybrid nano-fluids have maximum local skin friction compared with hybrid fluids or mono nano-fluids. The ternary hybrid nano-fluid heat transfer performance is better than that of the hybrid nano-fluid and the mono nano-fluid. Hence, it can be concluded that the ternary hybrid nano-particles are more reliable for the development and growth of energy transfer rates. Lastly, the graphical findings for velocity, angular velocity, and temperature satisfy the considered boundary conditions.
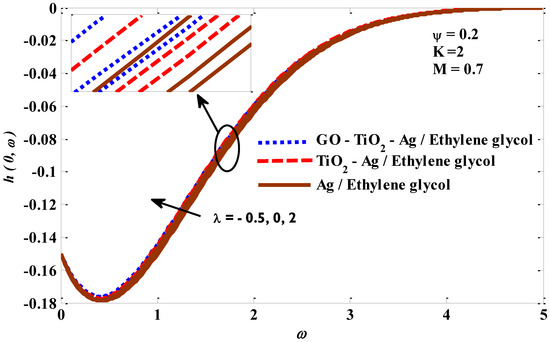
Figure 18.
Mixed convection factor versus angular velocity profile.
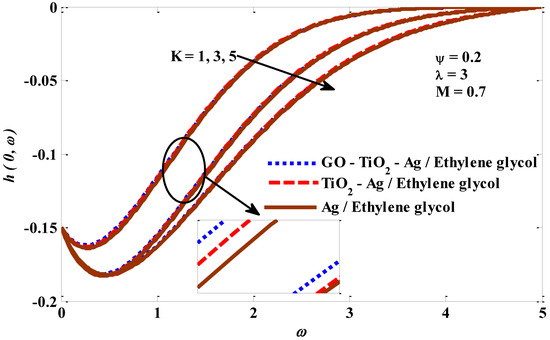
Figure 19.
Micropolar factor versus angular velocity profile.
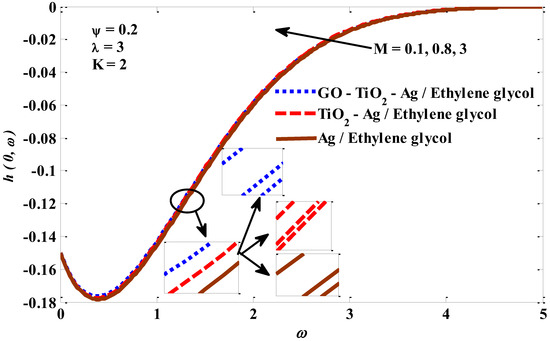
Figure 20.
Magnetic factor versus angular velocity profile.
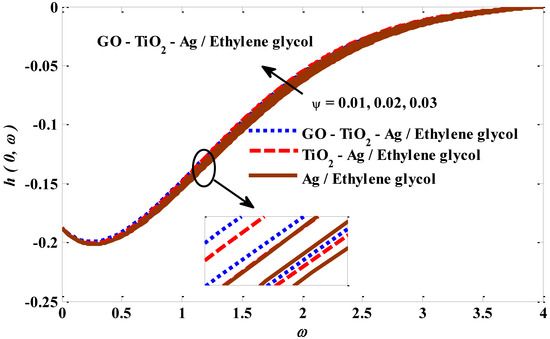
Figure 21.
Volume fraction factor versus angular velocity profile.
5. Conclusions
In this analysis, the thermal performance of a micropolar tri-hybrid fluid was investigated and numerically assessed using the Keller box approximation. The following are the main conclusions of this analysis:
- 1-
- Regardless of the influencing factors, the tri-hybrid nano-fluid, represented by GO-TiO2-Ag-ethylene glycol, produced the maximum value of the rate of energy transfer, velocity, angular velocity, skin friction, and temperature.
- 2-
- Elevating the value of the mixed convection factor improves heat transport, velocity, and angular velocity.
- 3-
- The volume fraction factor of tri-hybrid nano-particles has the potential to enhance all of the physical groups investigated in this study.
- 4-
- The velocity of the tri-hybrid nano-fluids and their ability to transfer energy are significantly suppressed when the magnetic field strength is increased.
- 5-
- Greater values of the micropolar factor have the ability to improve skin friction and temperature while inhibiting velocity, angular velocity, and energy transfer.
The combined convection boundary layer flow of ternary hybrid micropolar nano-fluids is studied under the magnetic field effect, with the constant heat flux boundary conditions over a horizontal circular cylinder. There are numerous aspects that can be addressed in future research, such as studying the flow characteristics and heat transfer in the presence of radiation, heat generation, and absorption, including other models such as Casson, Maxwell, and so on. This issue can also be seen in the case of unsteady state flow.
Author Contributions
F.A.A.: formal analysis, investigation, writing—review and editing; M.Z.S.: methodology, software; A.S.H.: writing—review and editing, writing draft, review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IF2/PSAU/2022/01/21396).
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on a reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eringen, A.C. Simple microfluids. Int. J. Eng. Sci. 1964, 2, 205–217. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of thermomicrofluids. J. Math. Anal. Appl. 1972, 38, 480–496. [Google Scholar] [CrossRef]
- Abbas, N.; Saleem, S.; Nadeem, S.; Alderremy, A.; Khan, A. On stagnation point flow of a micro polar nanofluid past a circular cylinder with velocity and thermal slip. Res. Phys. 2018, 9, 1224–1232. [Google Scholar] [CrossRef]
- Swalmeh, M.Z.; Alkasasbeh, H.T.; Hussanan, A.; Mamat, M. Heat transfer flow of Cu-water and Al2O3-water micropolar nanofluids about a solid sphere in the presence of natural convection using Keller-box method. Res. Phys. 2018, 9, 717–724. [Google Scholar] [CrossRef]
- Alkasasbeh, H.T.; Swalmeh, M.Z.; Hussanan, A.; Mamat, M. Effects of mixed convection on methanol and kerosene oil based micropolar nanofluid containing oxide nanoparticles. CFD Lett. 2019, 11, 55–68. [Google Scholar]
- EL-Zahar, E.R.; Mansour, M.A.; Rashad, A.; EL-Mky, H.A.; EL-Hakiem, A.M. Micropolar nanoliquid flow via mixed convective over an orthogonal cylinder. Heat Transf. 2021, 50, 6425–6443. [Google Scholar] [CrossRef]
- Alwawi, F.; Sulaiman, I.M.; Swalmeh, M.Z.; Yaseen, N. Energy transport boosters of magneto micropolar fluid flowing past a cylinder: A case of laminar combined convection. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2022, 236, 10902–10913. [Google Scholar] [CrossRef]
- Yaseen, N.; Shatat, F.; Alwawi, F.A.; Swalmeh, M.Z.; Kausar, M.S.; Sulaiman, I.M. Using Micropolar Nanofluid under a Magnetic Field to Enhance Natural Convective Heat Transfer around a Spherical Body. J. Adv. Res. Fluid Mech. Therm. Sci. 2022, 96, 179–193. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Eastman, J.A.; Choi, S.; Li, S.; Yu, W.; Thompson, L. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Dinarvand, S.; Abbassi, A.; Hosseini, R.; Pop, I. Homotopy analysis method for mixed convective boundary layer flow of a nanofluid over a vertical circular cylinder. Therm. Sci. 2015, 19, 549–561. [Google Scholar] [CrossRef]
- Rashad, A.; Nabwey, H.A. Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. J. Taiwan Inst. Chem. Eng. 2019, 99, 9–17. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Hamarsheh, A.S.; Alkasasbeh, H.T.; Idris, R. Mixed Convection Flow of Magnetized Casson Nanofluid over a Cylindrical Surface. Coatings 2022, 12, 296. [Google Scholar] [CrossRef]
- Alsulami, M.; Naveen Kumar, R.; Punith Gowda, R.; Prasannakumara, B. Analysis of heat transfer using Local thermal non-equilibrium conditions for a non-Newtonian fluid flow containing Ti6Al4V and AA7075 nanoparticles in a porous media. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 2022, e202100360. [Google Scholar] [CrossRef]
- Zaher, A.; Ali, K.K.; Mekheimer, K.S. Electroosmosis forces EOF driven boundary layer flow for a non-Newtonian fluid with planktonic microorganism: Darcy Forchheimer model. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2534–2559. [Google Scholar] [CrossRef]
- Abbas, W.; Mekheimer, K.S.; Ghazy, M.; Moawad, A. Thermal radiation effects on oscillatory squeeze flow with a particle-fluid suspension. Heat Transf. 2021, 50, 2129–2149. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Ramadan, S.F. New insight into gyrotactic microorganisms for bio-thermal convection of Prandtl nanofluid over a stretching/shrinking permeable sheet. SN Appl. Sci. 2020, 2, 1–11. [Google Scholar] [CrossRef]
- Turcu, R.; Darabont, A.; Nan, A.; Aldea, N.; Macovei, D.; Bica, D.; Vekas, L.; Pana, O.; Soran, M.; Koos, A. New polypyrrole-multiwall carbon nanotubes hybrid materials. J. Optoelectron. Adv. Mater. 2006, 8, 643–647. [Google Scholar]
- Suresh, S.; Venkitaraj, K.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surf. A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Baghbanzadeh, M.; Rashidi, A.; Rashtchian, D.; Lotfi, R.; Amrollahi, A. Synthesis of spherical silica/multiwall carbon nanotubes hybrid nanostructures and investigation of thermal conductivity of related nanofluids. Thermochim. Acta 2012, 549, 87–94. [Google Scholar] [CrossRef]
- Leong, K.; Ahmad, K.K.; Ong, H.C.; Ghazali, M.; Baharum, A. Synthesis and thermal conductivity characteristic of hybrid nanofluids—A review. Renew. Sustain. Energy Rev. 2017, 75, 868–878. [Google Scholar] [CrossRef]
- Muneeshwaran, M.; Srinivasan, G.; Muthukumar, P.; Wang, C.-C. Role of hybrid-nanofluid in heat transfer enhancement—A review. Int. Commun. Heat Mass Transf. 2021, 125, 105341. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Khan, A. Characteristics of three dimensional stagnation point flow of Hybrid nanofluid past a circular cylinder. Res. Phys. 2018, 8, 829–835. [Google Scholar] [CrossRef]
- Dinarvand, S.; Nademi Rostami, M. Mixed convection of a Cu-Ag/water hybrid nanofluid along a vertical porous cylinder via modified Tiwari-Das model. J. Theor. Appl. Mech. 2019, 49, 149–169. [Google Scholar] [CrossRef]
- Rashad, A.M.; Khan, W.A.; EL-Kabeir, S.M.; EL-Hakiem, A.M. Mixed convective flow of micropolar nanofluid across a horizontal cylinder in saturated porous medium. Appl. Sci. 2019, 9, 5241. [Google Scholar] [CrossRef]
- Alharbi, S.O.; Nawaz, M.; Nazir, U. Thermal analysis for hybrid nanofluid past a cylinder exposed to magnetic field. AIP Adv. 2019, 9, 115022. [Google Scholar] [CrossRef]
- Shah, Z.; Saeed, A.; Khan, I.; Selim, M.M.; Ikramullah; Kumam, P. Numerical modeling on hybrid nanofluid (Fe3O4+MWCNT/H2O) migration considering MHD effect over a porous cylinder. PLoS ONE 2021, 16, e0251744. [Google Scholar] [CrossRef]
- John Christopher, A.; Magesh, N.; Punith Gowda, R.J.; Naveen Kumar, R.; Varun Kumar, R.S. Hybrid nanofluid flow over a stretched cylinder with the impact of homogeneous–heterogeneous reactions and Cattaneo–Christov heat flux: Series solution and numerical simulation. Heat Transf. 2021, 50, 3800–3821. [Google Scholar] [CrossRef]
- Alwawi, F.; Swalmeh, M.; Sulaiman, I.; Yaseen, N.; Alkasasbeh, H.; Al Soub, T. Numerical investigation of heat transfer characteristics for blood/water-based hybrid nanofluids in free convection about a circular cylinder. J. Mech. Eng. Sci. 2022, 16, 8931–8942. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Al Faqih, F.M.; Swalmeh, M.Z.; Ibrahim, M.A.H. Combined Convective Energy Transmission Performance of Williamson Hybrid Nanofluid over a Cylindrical Shape with Magnetic and Radiation Impressions. Mathematics 2022, 10, 3191. [Google Scholar] [CrossRef]
- Alzu’bi, O.A.S.; Alwawi, F.A.; Swalmeh, M.Z.; Sulaiman, I.M.; Hamarsheh, A.S.; Ibrahim, M.A.H. Energy Transfer through a Magnetized Williamson Hybrid Nanofluid Flowing around a Spherical Surface: Numerical Simulation. Mathematics 2022, 10, 3823. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Swalmeh, M.Z.; Qazaq, A.S.; Idris, R. Heat Transmission Reinforcers Induced by MHD Hybrid Nanoparticles for Water/Water-EG Flowing over a Cylinder. Coatings 2021, 11, 623. [Google Scholar] [CrossRef]
- Xuan, Z.; Zhai, Y.; Ma, M.; Li, Y.; Wang, H. Thermo-economic performance and sensitivity analysis of ternary hybrid nanofluids. J. Mol. Liq. 2021, 323, 114889. [Google Scholar] [CrossRef]
- Cakmak, N.K.; Said, Z.; Sundar, L.S.; Ali, Z.M.; Tiwari, A.K. Preparation, characterization, stability, and thermal conductivity of rGO-Fe3O4-TiO2 hybrid nanofluid: An experimental study. Powder Technol. 2020, 372, 235–245. [Google Scholar] [CrossRef]
- Souby, M.M.; Bargal, M.H.; Wang, Y. Thermohydraulic performance improvement and entropy generation characteristics of a microchannel heat sink cooled with new hybrid nanofluids containing ternary/binary hybrid nanocomposites. Energy Sci. Eng. 2021, 9, 2493–2513. [Google Scholar] [CrossRef]
- Mahmood, Z.; Iqbal, Z.; Alyami, M.A.; Alqahtani, B.; Yassen, M.F.; Khan, U. Influence of suction and heat source on MHD stagnation point flow of ternary hybrid nanofluid over convectively heated stretching/shrinking cylinder. Adv. Mech. Eng. 2022, 14, 16878132221126278. [Google Scholar] [CrossRef]
- Alharbi, K.A.M.; Ahmed, A.E.-S.; Ould Sidi, M.; Ahammad, N.A.; Mohamed, A.; El-Shorbagy, M.A.; Bilal, M.; Marzouki, R. Computational valuation of darcy ternary-hybrid nanofluid flow across an extending cylinder with induction effects. Micromachines 2022, 13, 588. [Google Scholar] [CrossRef] [PubMed]
- Nazir, U.; Saleem, S.; Al-Zubaidi, A.; Shahzadi, I.; Feroz, N. Thermal and mass species transportation in tri-hybridized Sisko martial with heat source over vertical heated cylinder. Int. Commun. Heat Mass Transf. 2022, 134, 106003. [Google Scholar] [CrossRef]
- Khan, U.; Kumar, R.N.; Zaib, A.; Prasannakumara, B.; Ishak, A.; Galal, A.M.; Gowda, R.P. Time-dependent flow of water-based ternary hybrid nanoparticles over a radially contracting/expanding and rotating permeable stretching sphere. Therm. Sci. Eng. Prog. 2022, 36, 101521. [Google Scholar] [CrossRef]
- Sarada, K.; Gamaoun, F.; Abdulrahman, A.; Paramesh, S.; Kumar, R.; Prasanna, G.; Gowda, R.P. Impact of exponential form of internal heat generation on water-based ternary hybrid nanofluid flow by capitalizing non-Fourier heat flux model. Case Stud. Therm. Eng. 2022, 38, 102332. [Google Scholar]
- Kumar, R.N.; Gamaoun, F.; Abdulrahman, A.; Chohan, J.S.; Gowda, R.P. Heat transfer analysis in three-dimensional unsteady magnetic fluid flow of water-based ternary hybrid nanofluid conveying three various shaped nanoparticles: A comparative study. Int. J. Mod. Phys. B 2022, 36, 2250170. [Google Scholar] [CrossRef]
- Sarangi, M.; Thatoi, D.; Nayak, M.; Prakash, J.; Ramesh, K.; Azam, M. Rotational flow and thermal behavior of ternary hybrid nanomaterials at small and high Prandtl numbers. Int. Commun. Heat Mass Transf. 2022, 138, 106337. [Google Scholar] [CrossRef]
- Puneeth, V.; Manjunatha, S.; Ganesh Kumar, K.; Gnaneswara Reddy, M. Perspective of multiple slips on 3D flow of Al2O3–TiO2–CuO/H2O ternary nanofluid past an extending surface due to non-linear thermal radiation. Waves Random Complex Media 2022, 1–19. [Google Scholar] [CrossRef]
- Sajid, T.; Ayub, A.; Shah, S.Z.H.; Jamshed, W.; Eid, M.R.; El Din, E.S.M.T.; Irfan, R.; Hussain, S.M. Trace of Chemical Reactions Accompanied with Arrhenius Energy on Ternary Hybridity Nanofluid Past a Wedge. Symmetry 2022, 14, 1850. [Google Scholar] [CrossRef]
- Hafeez, M.B.; Krawczuk, M.; Nisar, K.S.; Jamshed, W.; Pasha, A.A. A finite element analysis of thermal energy inclination based on ternary hybrid nanoparticles influenced by induced magnetic field. Int. Commun. Heat Mass Transf. 2022, 135, 106074. [Google Scholar] [CrossRef]
- Rauf, A.; Shah, N.A.; Botmart, T. Hall current and morphological effects on MHD micropolar non-Newtonian tri-hybrid nanofluid flow between two parallel surfaces. Sci. Rep. 2022, 12, 16608. [Google Scholar] [CrossRef]
- Dhanai, R.; Rana, P.; Kumar, L. MHD mixed convection nanofluid flow and heat transfer over an inclined cylinder due to velocity and thermal slip effects: Buongiorno’s model. Powder Technol. 2016, 288, 140–150. [Google Scholar] [CrossRef]
- Alizadeh, R.; Karimi, N.; Arjmandzadeh, R.; Mehdizadeh, A. Mixed convection and thermodynamic irreversibilities in MHD nanofluid stagnation-point flows over a cylinder embedded in porous media. J. Therm. Anal. Calorim. 2019, 135, 489–506. [Google Scholar] [CrossRef]
- Patil, P.; Kulkarni, M. Analysis of MHD mixed convection in a Ag-TiO2 hybrid nanofluid flow past a slender cylinder. Chin. J. Phys. 2021, 73, 406–419. [Google Scholar] [CrossRef]
- Ullah, Z.; Ehsan, M.; Ahmad, H.; Ilyas, A. Combined effects of MHD and slip velocity on oscillatory mixed convective flow around a non-conducting circular cylinder embedded in a porous medium. Case Stud. Therm. Eng. 2022, 38, 102341. [Google Scholar] [CrossRef]
- Umavathi, J.; Prakasha, D.; Alanazi, Y.M.; Lashin, M.M.; Al-Mubaddel, F.S.; Kumar, R.; Gowda, R.P. Magnetohydrodynamic squeezing Casson nanofluid flow between parallel convectively heated disks. Int. J. Mod. Phys. B 2023, 37, 2350031. [Google Scholar] [CrossRef]
- Sharma, B.; Khanduri, U.; Mishra, N.K.; Mekheimer, K.S. Combined effect of thermophoresis and Brownian motion on MHD mixed convective flow over an inclined stretching surface with radiation and chemical reaction. Int. J. Mod. Phys. B 2022, 2350095. [Google Scholar] [CrossRef]
- Shahid, A.; Bhatti, M.; Ellahi, R.; Mekheimer, K.S. Numerical experiment to examine activation energy and bi-convection Carreau nanofluid flow on an upper paraboloid porous surface: Application in solar energy. Sustain. Energy Technol. Assess. 2022, 52, 102029. [Google Scholar] [CrossRef]
- Prasad, V.R.; Gaffar, S.A.; Bég, O.A. Heat and mass transfer of nanofluid from horizontal cylinder to micropolar fluid. J. Thermophys. Heat Transf. 2015, 29, 127–139. [Google Scholar] [CrossRef]
- Hou, E.; Wang, F.; Nazir, U.; Sohail, M.; Jabbar, N.; Thounthong, P. Dynamics of tri-hybrid nanoparticles in the rheology of pseudo-plastic liquid with dufour and soret effects. Micromachines 2022, 13, 201. [Google Scholar] [CrossRef]
- Nazir, U.; Sohail, M.; Kumam, P.; Sitthithakerngkiet, K.; Mousa, A.A.A.; Khan, M.J.; Galal, A.M. A dynamic assessment of various non-Newtonian models for ternary hybrid nanomaterial involving partially ionized mechanism. Sci. Rep. 2022, 12, 10306. [Google Scholar] [CrossRef]
- Swalmeh, M.; Alkasasbeh, H.; Hussanan, A.; Mamat, M. Numerical study of mixed convection heat transfer in methanol based micropolar nanofluid about a horizontal circular cylinder. J. Phys. Conf. Ser. 2019, 1366, 012003. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Mixed convection boundary-layer flow from a horizontal circular cylinder with a constant surface heat flux. Heat Mass Transf. 2004, 40, 219–227. [Google Scholar] [CrossRef]
- Cebeci, T.; Bradshaw, P. Physical and Computational Aspects of Convective Heat Transfer; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Swalmeh, M.Z.; Shatat, F.; Alwawi, F.A.; Ibrahim, M.A.H.; Sulaiman, I.M.; Yaseen, N.; Naser, M.F. Effectiveness of Radiation on Magneto-Combined Convective Boundary Layer Flow in Polar Nanofluid around a Spherical Shape. Fractal Fract. 2022, 6, 383. [Google Scholar] [CrossRef]
- Swalmeh, M.Z. Numerical solutions of hybrid nanofluids flow via free convection over a solid sphere. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 83, 34–45. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.; Idris, R. Heat transfer analysis of ethylene glycol-based Casson nanofluid around a horizontal circular cylinder with MHD effect. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2020, 234, 2569–2580. [Google Scholar] [CrossRef]
- Mahdy, A. Simultaneous impacts of MHD and variable wall temperature on transient mixed Casson nanofluid flow in the stagnation point of rotating sphere. Appl. Math. Mech. 2018, 39, 1327–1340. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).