Investigation of Special Type-Π Smarandache Ruled Surfaces Due to Rotation Minimizing Darboux Frame in E³

Abstract

This study begins with the construction of type-$\Pi$ Smarandache ruled surfaces, whose base curves are Smarandache curves derived by rotation-minimizing Darboux frame vectors of the curve in ${\mathbf{E}}^{\mathbf{3}}$. The direction vectors of these surfaces are unit vectors that convert Smarandache curves. The Gaussian and mean curvatures of the generated ruled surfaces are then separately calculated, and the surfaces are required to be minimal or developable. We report our main conclusions in terms of the angle between normal vectors and the relationship between normal curvature and geodesic curvature. For every surface, examples are provided, and the graphs of these surfaces are produced.

1. Introduction

One of the branches of classical differential geometry that has been explored by a number of researchers is the theory of ruled surfaces. A ruled surface is one that has at least one straight line passing through each point on the surface that is also on the surface. One way to conceptualize a ruled surface is as one that is “swept out” by a moving straight line in space. Cones and cylinders are basic instances of ruled surfaces. Architects are interested in more intricate ruled surfaces, particularly when it comes to free-form building and intricate designs. In contemporary design, there are several instances of ruled surface structures, such as saddle roofs (hyperbolic paraboloid) and cooling towers (hyperboloid). A ruled surface is often described as a collection of a family of straight lines that are reliant on the parameters, called the rulings, of the ruled surface. The parametric representation of a ruled surface is $\Gamma (s,\upsilon )=r\left(s\right)+\upsilon X\left(s\right)$, where $r\left(s\right)$ is the base curve and $X\left(s\right)$ specifies the rulings directions [1]. Many practical uses arise out of the study of developable surfaces. Studies on developable surfaces are widely available. A surface that can be developed into a plane without changing the surface metric is called a developable surface. Studies of developable surfaces of space curves from the perspective of singularity theory have been documented in the literature. The governed surface that results from the tangent lines of a space curve is called the tangent developable surface. Tantent developable surfaces are crucial to the duality theory of algebraic geometry. From differential calculus, singularity theory is a branch of mathematics that has applications in physics, astronomy, and geometry. Some of key investigations on the submanifold theory and singularity theory have been presented in [2,3,4,5]. The developability and minimalist principles of surfaces are two of its key characteristics. The investigation of ruled surfaces with various moving frames provides one of the most fascinating features (see [6,7,8,9,10,11]).

In Euclidean and Minkowski spaces, the Smarandache curve is the curve whose position vector is created by Frenet frame vectors on another regular curve [12,13,14]. Recent studies on Smarandache curves in Minkowski and Euclidean spaces have been conducted by a number of researchers [15].

In this study, the requirements of type-$\Pi$ Smarandache ruled surfaces are specified by using the rotation minimizing Darboux frame in ${\mathbf{E}}^{\mathbf{3}}$. Furthermore, we address the geometric analysis of a particular kind of ruled surface, namely the type-$\Pi$ Smarandache ruled surfaces associated with the space curves as a basic example for studying the manifolds with the largest dimensions in Euclidean 3-space. We examine the sufficient and necessary requirements for these surfaces to be minimal and developable. We report our main conclusions in terms of the angle between normal vectors and the relationship between normal curvature and geodesic curvature. The organization of this work is as follows: In Section 2, we review the concepts of ruled surfaces in Euclidean space, Smarandache curves, Frenet frame, and Darboux frame. In Section 3, we derive some of the geometric characteristics of the type-$\Pi$ Smarandache ruled surfaces, which we define due to rotation minimizing Darboux frame whose a director curve and base curve are Smarandache curves. We give an example in Section 4 that emphasizes the most significant findings in this work.

2. Preliminaries

Let $\phi \left(s\right)=M\left(u\right(s),\upsilon (s\left)\right)$ be a unit speed regular curve lying on a surface $M(u,v)$ in ${\mathbf{E}}^{\mathbf{3}}$. Let $\{T,N,B\}$ denotes the moving Frenet frame of $\phi$, then $\{T,N,B\}$ satisfying [1]:

$${\displaystyle \frac{d}{ds}}\left(\begin{array}{c}T\left(s\right)\\ N\left(s\right)\\ B\left(s\right)\end{array}\right)=\left(\begin{array}{ccc}0& \kappa \left(s\right)& 0\\ -\kappa \left(s\right)& 0& \tau \left(s\right)\\ 0& -\tau \left(s\right)& 0\end{array}\right)\left(\begin{array}{c}T\left(s\right)\\ N\left(s\right)\\ B\left(s\right)\end{array}\right),$$

(1)

where $⟨T,T⟩=⟨N,N⟩=⟨B,B⟩=1$ and $⟨T,N⟩=⟨T,B⟩=⟨N,B⟩=0$.

For any arbitrary curve $\phi$ with $\tau \ne 0$ in ${\mathbf{E}}^{\mathbf{3}}$, the Darboux frame of $\phi$ is given by [16]:

$${\displaystyle \frac{d}{ds}}\left(\begin{array}{c}T\left(s\right)\\ \mathbb{N}\left(s\right)\\ G\left(s\right)\end{array}\right)=\left(\begin{array}{ccc}0& {\kappa }_g\left(s\right)& {\kappa }_n\left(s\right)\\ -{\kappa }_g\left(s\right)& 0& {\tau }_g\left(s\right)\\ -{\kappa }_n\left(s\right)& -{\tau }_g\left(s\right)& 0\end{array}\right)\left(\begin{array}{c}T\left(s\right)\\ \mathbb{N}\left(s\right)\\ G\left(s\right)\end{array}\right),$$

(2)

where $\mathbb{N}$ is the surface normal and $G=\mathbb{N}\times T$. The geodesic curvature ${\kappa }_g$, normal curvature ${\kappa }_n$, and geodesic torsion ${\tau }_g$ that connects the curve $\phi$ on M are given as

$${\kappa }_g=⟨T^{\prime },G⟩,{\kappa }_n=⟨T^{\prime },\mathbb{N}⟩,{\tau }_g=⟨G^{\prime },\mathbb{N}⟩.$$

(3)

The rotation minimizing Darboux frame (RMDF) $\{T,P_1,P_2\}$ of curve $\phi$ on the surface M is defined by [17,18]:

$${\displaystyle \frac{d}{ds}}\left(\begin{array}{c}T\left(s\right)\\ P_1\left(s\right)\\ P_2\left(s\right)\end{array}\right)=\left(\begin{array}{ccc}0& {\zeta }_1\left(s\right)& {\zeta }_2\left(s\right)\\ -{\zeta }_1\left(s\right)& 0& 0\\ -{\zeta }_2\left(s\right)& 0& 0\end{array}\right)\left(\begin{array}{c}T\left(s\right)\\ P_1\left(s\right)\\ P_2\left(s\right)\end{array}\right),$$

(4)

where the RMDF curvatures are obtained as follows:

$$\begin{array}{cc}& {\zeta }_1={\kappa }_{g}sin\vartheta +{\kappa }_{n}cos\vartheta ,\hfill \\ & {\zeta }_2={\kappa }_{n}sin\vartheta -{\kappa }_{g}cos\vartheta ,\hfill \end{array}$$

(5)

where ${\displaystyle \vartheta \left(s\right)={\int }_0^s{\tau }_{g}ds}$ is the angle between vectors $\mathbb{N}$ and $P_1$. The relation matrix between frames may be expressed as:

$$\left(\begin{array}{c}T\left(s\right)\\ P_1\left(s\right)\\ P_2\left(s\right)\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& sin\vartheta \left(s\right)& cos\vartheta \left(s\right)\\ 0& -cos\vartheta \left(s\right)& sin\vartheta \left(s\right)\end{array}\right)\left(\begin{array}{c}T\left(s\right)\\ \mathbb{N}\left(s\right)\\ G\left(s\right)\end{array}\right).$$

(6)

The surface formed by a line moving depending on the parameter of a curve is called a ruled surface and its parametric expression is as follows:

$$\mathrm{{\rm Y}}(s,\upsilon )=\phi \left(s\right)+\upsilon X\left(s\right).$$

(7)

The normal vector field, the Gaussian and mean curvatures of $\mathrm{{\rm Y}}(s,\upsilon )$ are given by

$$\mathbb{N}={\displaystyle \frac{{\mathrm{{\rm Y}}}_s\times {\mathrm{{\rm Y}}}_{\upsilon }}{\parallel {\mathrm{{\rm Y}}}_s\times {\mathrm{{\rm Y}}}_{\upsilon }\parallel }},K={\displaystyle \frac{eg-f^2}{EG-F^2}},H={\displaystyle \frac{Eg-2fF+Ge}{2(EG-F^2)}}.$$

We also know that

$$E=⟨{\mathrm{{\rm Y}}}_s,{\mathrm{{\rm Y}}}_s⟩,F=⟨{\mathrm{{\rm Y}}}_s,{\mathrm{{\rm Y}}}_{\upsilon }⟩,G=⟨{\mathrm{{\rm Y}}}_{\upsilon },{\mathrm{{\rm Y}}}_{\upsilon }⟩,$$

and

$$e=⟨{\mathrm{{\rm Y}}}_{ss},\mathbb{N}⟩,f=⟨{\mathrm{{\rm Y}}}_{s\upsilon },\mathbb{N}⟩,g=⟨{\mathrm{{\rm Y}}}_{\upsilon \upsilon },\mathbb{N}⟩,$$

where E, F, G are the first fundamental coefficients and e, f, and g are the second fundamental coefficients of $\mathrm{{\rm Y}}$.

The Smarandache curves of the curve $\phi \left(s\right)$ is defined as follows:

$$T{P}_1-\mathrm{Smarandache} \mathrm{curve} {\gamma }_1\left(s\right)={\displaystyle \frac{1}{\sqrt{2}}}\left(T\left(s\right)+P_1\left(s\right)\right).$$

$$T{P}_2-\mathrm{Smarandache} \mathrm{curve} {\gamma }_2\left(s\right)={\displaystyle \frac{1}{\sqrt{2}}}\left(T\left(s\right)+P_2\left(s\right)\right).$$

$$P_1{P}_2-\mathrm{Smarandache} \mathrm{curve} {\gamma }_3\left(s\right)={\displaystyle \frac{1}{\sqrt{2}}}\left(P_1\left(s\right)+P_2\left(s\right)\right).$$

$$T{P}_1{P}_2-\mathrm{Smarandache} \mathrm{curve} {\gamma }_4\left(s\right)={\displaystyle \frac{1}{\sqrt{3}}}\left(T\left(s\right)+P_1\left(s\right)+P_2\left(s\right)\right).$$

3. Type-Π Smarandache Ruled Surfaces Due to RMDF

The curve $\phi \left(s\right)$ on the surface M caused by RMDF serves as the parametric representation of type-Π Smarandache ruled surfaces in this section. In addition, we assess the prerequisites that make it possible for these surfaces to be minimum and developable.

3.1. Type-Π Smarandache Ruled Surfaces along ${\gamma }_1$-Smarandache Curve

Definition 1. 

The type-Π Smarandache ruled surfaces due to RMDF in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_1$ along ${\gamma }_1$-Smarandache curve is defined by

$$\Psi (s,\upsilon )={\gamma }_1\left(s\right)+\upsilon {\gamma }_1\left(s\right).$$

(8)

Theorem 1. 

The type-Π Smarandache ruled surface $\Psi =\Psi (s,\upsilon )$ is developable.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\Psi =\Psi (s,\upsilon )$ given by (8), then the velocity vectors of $\Psi$ are given by

$$\left\{\begin{array}{c}{\Psi }_s={\displaystyle \frac{\upsilon +1}{\sqrt{2}}}\left[-{\zeta }_{1}T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ {\Psi }_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(T+P_1\right).\hfill \end{array}\right.$$

(9)

Then, the normal vector field ${\mathbb{N}}_{\Psi }$ of the surface $\Psi$ is obtained as

$${\mathbb{N}}_{\Psi }={\displaystyle \frac{{\Psi }_s\times {\Psi }_{\upsilon }}{\parallel {\Psi }_s\times {\Psi }_{\upsilon }\parallel }}={\displaystyle \frac{-{\zeta }_{2}T+{\zeta }_2{P}_1-2{\zeta }_1{P}_2}{\sqrt{2}\sqrt{{\zeta }_1^2+{\kappa }^2}}}.$$

Hence, it can be easily seen that the first fundamental coefficients of $\Psi$ are

$$\begin{array}{cc}& E={\displaystyle \frac{{(\upsilon +1)}^2}{2}}\left[{\zeta }_1^2+{\kappa }^2\right],\hfill \\ & F=0,G=1.\hfill \end{array}$$

(10)

Taking the derivative of (9) with respect to s and $\upsilon$, we find

$$\begin{array}{cc}& {\Psi }_{ss}={\displaystyle \frac{\upsilon +1}{\sqrt{2}}}\left[-({\zeta }_1^{\prime }+\kappa )T+({\zeta }_1^{\prime }-{\zeta }_1^2)P_1+({\zeta }_2^{\prime }-{\zeta }_1{\zeta }_2)P_2\right],\hfill \\ & {\Psi }_{s\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left[-{\zeta }_{1}T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ & {\Psi }_{\upsilon \upsilon }=0.\hfill \end{array}$$

(11)

Hence, it can be seen that the coefficients of second fundamental form of $\Psi$ are

$$\begin{array}{cc}& e={\displaystyle \frac{\upsilon +1}{2\sqrt{{\zeta }_1^2+{\kappa }^2}}}\left[{\zeta }_2(\kappa +{\zeta }_1^2)+2({\zeta }_1^{\prime }{\zeta }_2-{\zeta }_1{\zeta }_2^{\prime })\right],\hfill \\ & f=0,g=0.\hfill \end{array}$$

(12)

As a consequence, we obtain

$$\begin{array}{cc}& K_{\Psi }=0,\hfill \\ & H_{\Psi }={\displaystyle \frac{{\zeta }_2(\kappa +{\zeta }_1^2)+2({\zeta }_1^{\prime }{\zeta }_2-{\zeta }_1{\zeta }_2^{\prime })}{2(\upsilon +1){({\zeta }_1^2+{\kappa }^2)}^{\frac{3}{2}}}},\hfill \end{array}$$

(13)

which concludes the proof. □

From Theorem 1, we have the following immediate results.

Corollary 1. 

Let $\Psi =\Psi (s,\upsilon )$ be a type-Π Smarandache ruled surface. Then, the s-parameter curves of Ψ are not geodesic but υ-parameter curves are geodesic.

Proof. 

Let $\Psi =\Psi (s,\upsilon )$ defined by (8) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ be the type-$\Pi$ Smarandache ruled surface. Since

$$\begin{array}{cc}\hfill {\Psi }_{ss}\times {\mathbb{N}}_{\Psi }=& {\displaystyle \frac{\upsilon +1}{2\sqrt{{\zeta }_1^2+{\kappa }^2}}}\{\left[{\zeta }_2({\zeta }_2^{\prime }-{\zeta }_1{\zeta }_2)-2{\zeta }_1({\zeta }_1^{\prime }-{\zeta }_1^2)\right]T-\left[2{\zeta }_1({\zeta }_1^{\prime }+{\zeta }_2)+{\zeta }_2({\zeta }_2^{\prime }-{\zeta }_1{\zeta }_2)\right]P_1\hfill \\ & +\left[{\zeta }_2({\zeta }_1^{\prime }-{\zeta }_1^2)-{\zeta }_2({\zeta }_1^{\prime }+{\zeta }_2)\right]P_2\}\ne 0,\hfill \end{array}$$

and ${\Psi }_{\upsilon \upsilon }\times {\mathbb{N}}_{\Psi }=0$. Then, the s-parameter curves of $\Psi$ surface simultaneously are not geodesic and the $\upsilon$-parameter curves of $\Psi$ simultaneously are geodesic. □

Corollary 2. 

Let $\Psi =\Psi (s,\upsilon )$ be a type-Π Smarandache ruled surface. Then, the s-parameter curves of Ψ are not asymptotic but υ-parameter curves are asymptotic.

Proof. 

Let $\Psi =\Psi (s,\upsilon )$ defined by (8) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ be the type-$\Pi$ Smarandache ruled surface. Since

$$⟨{\Psi }_{ss},{\mathbb{N}}_{\Psi }⟩={\displaystyle \frac{(\upsilon +1)\left[{\zeta }_2(2{\zeta }_1^{\prime }-{\zeta }_1^2+\kappa )-2{\zeta }_1({\zeta }_2^{\prime }-{\zeta }_1{\zeta }_2)\right]}{2\sqrt{{\zeta }_1^2+{\kappa }^2}}}\ne 0,$$

and $⟨{\Psi }_{\upsilon \upsilon },{\mathbb{N}}_{\Psi }⟩=0$. Thus, the s-parameter curves of $\Psi$ surface simultaneously are not asymptotic but the $\upsilon$-parameter curves of $\Psi$ simultaneously are asymptotic. □

Corollary 3. 

Let $\Psi =\Psi (s,\upsilon )$ be a type-Π Smarandache ruled surface. Then, the s and υ-parameter curves are principal curves.

Proof. 

Let $\Psi =\Psi (s,\upsilon )$ defined by (8) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ be the type-$\Pi$ Smarandache ruled surface. Since

$$⟨{\Psi }_s,{\Psi }_{\upsilon }⟩=⟨{\Psi }_{s\upsilon },{\mathbb{N}}_{\Psi }⟩=0.$$

Therefore, it is clear that both s and $\upsilon$-parameter curves are principal curves. □

Definition 2. 

The type-Π Smarandache ruled surfaces due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_2$ along ${\gamma }_1$-Smarandache curve is defined as follows

$$\Gamma (s,\upsilon )={\gamma }_1\left(s\right)+\upsilon {\gamma }_2\left(s\right).$$

(14)

Theorem 2. 

The type-Π Smarandache ruled surface $\Gamma =\Gamma (s,\upsilon )$ together with ${\kappa }_g\left(s\right)\ne {\kappa }_n\left(s\right)$ is developable iff one of the following conditions holds

i. 

$\vartheta \left(s\right)=-{tan}^{-1}\left({\displaystyle \frac{{\kappa }_n}{{\kappa }_g}}\right)$,

ii. 

$\vartheta \left(s\right)={tan}^{-1}\left({\displaystyle \frac{{\kappa }_n+{\kappa }_g}{{\kappa }_n-{\kappa }_g}}\right)$.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\Gamma =\Gamma (s,\upsilon )$ given by (14), then the velocity vectors of $\Gamma$ are given by:

$$\left\{\begin{array}{c}{\Gamma }_s={\displaystyle \frac{1}{\sqrt{2}}}\left[-({\zeta }_1+\upsilon {\zeta }_2)T+(\upsilon +1){\zeta }_1{P}_1+(\upsilon +1){\zeta }_2{P}_2\right],\hfill \\ {\Gamma }_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(T+P_2\right).\hfill \end{array}\right.$$

(15)

Then, the normal vector field ${\mathbb{N}}_{\Gamma }$ of the surface $\Gamma$ is obtained as:

$${\mathbb{N}}_{\Gamma }={\displaystyle \frac{(\upsilon +1){\zeta }_{1}T+\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]P_1-(\upsilon +1){\zeta }_1{P}_2}{\sqrt{2{(\upsilon +1)}^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2}}}.$$

Hence, it can be easily seen that the first fundamental coefficients of $\Gamma$ are:

$$\begin{array}{cc}& E={\displaystyle \frac{1}{2}}\left[{({\zeta }_1+\upsilon {\zeta }_2)}^2+{(\upsilon +1)}^2{\kappa }^2\right],\hfill \\ & F={\displaystyle \frac{1}{2}}\left[{\zeta }_2-{\zeta }_1\right],G=1.\hfill \end{array}$$

(16)

Taking the derivative of (15) with respect to s and $\upsilon$, we find

$$\begin{array}{cc}& {\Gamma }_{ss}={\displaystyle \frac{1}{\sqrt{2}}}\{-\left[{\zeta }_1^{\prime }+\upsilon {\zeta }_2^{\prime }+(\upsilon +1){\kappa }^2\right]T+\left[(\upsilon +1){\zeta }_1^{\prime }-{\zeta }_1({\zeta }_1+\upsilon {\zeta }_2)\right]P_1\hfill \\ & +\left[(\upsilon +1){\zeta }_2^{\prime }-{\zeta }_1({\zeta }_1+\upsilon {\zeta }_2)\right]P_2\},\hfill \\ & {\Gamma }_{s\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left[-{\zeta }_{2}T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ & {\Gamma }_{\upsilon \upsilon }=0.\hfill \end{array}$$

(17)

Thus, it can be seen that the coefficients of the second fundamental form of $\Gamma$ are:

$$\begin{array}{cc}& e={\displaystyle \frac{1}{\sqrt{2}\sqrt{2{(\upsilon +1)}^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2}}}\{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]\left[(\upsilon +1){\zeta }_1^{\prime }-{\zeta }_1({\zeta }_1+\upsilon {\zeta }_2)\right]\hfill \\ & -(\upsilon +1){\zeta }_1\left[{\zeta }_1^{\prime }+(2\upsilon +1){\zeta }_2^{\prime }+{\zeta }_2({\zeta }_1+\upsilon {\zeta }_2)+(\upsilon +1){\kappa }^2\right]\},\hfill \\ & f={\displaystyle \frac{{\zeta }_1({\zeta }_1-{\zeta }_2)}{\sqrt{2}\sqrt{2{(\upsilon +1)}^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2}}},\hfill \\ & g=0.\hfill \end{array}$$

(18)

As a result, we derive

$$\begin{array}{cc}& K_{\Gamma }=-{\displaystyle \frac{{\zeta }_1^2{({\zeta }_1-{\zeta }_2)}^2}{\left[{\zeta }_1^2+{\upsilon }^2{\zeta }_2^2+(\upsilon +1)(\upsilon {\kappa }^2+2{\zeta }_1{\zeta }_2)\right]\left[2{(\upsilon +1)}^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2\right]}},\hfill \\ & H_{\Gamma }={\displaystyle \frac{\left\{\begin{array}{c}\left[{\zeta }_1+(\upsilon +2){\zeta }_2\right]\left[(\upsilon +1){\zeta }_1^{\prime }-{\zeta }_1({\zeta }_1+{\zeta }_2)\right]-(\upsilon +1){\zeta }_1[{\zeta }_1^{\prime }+(\upsilon +2){\zeta }_2^{\prime }\\ +{\zeta }_2({\zeta }_1+{\zeta }_2)+(\upsilon +1){\kappa }^2]-{\zeta }_1({\zeta }_1+{\zeta }_2)(\upsilon {\zeta }_2-{\zeta }_1)\end{array}\right\}}{\sqrt{2}\sqrt{2{(\upsilon +1)}^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2}\left[{\zeta }_1^2+{\upsilon }^2{\zeta }_2^2+(\upsilon +1)(\upsilon {\kappa }^2+2{\zeta }_1{\zeta }_2)\right]}}.\hfill \end{array}$$

(19)

Combining the above equation with (5), we conclude the proof. □

As a consequence of Theorem 2, we obtain the following results:

Corollary 4. 

Let $\Gamma =\Gamma (s,\upsilon )$ be a type-Π Smarandache ruled surface. Then, the Γ has constant Gauss curvature iff ${\zeta }_1({\zeta }_1+{\zeta }_2)=c$ for some non-zero constant c.

Corollary 5. 

Let $\Gamma =\Gamma (s,\upsilon )$ be a type-Π Smarandache ruled surface. Then, the s-parameter curves of Γ are not asymptotic but υ-parameter curves are asymptotic curves.

Remark 1. 

The proof of Corollary 4 and 5 is similar to the proof of Corollaries 1–3.

Definition 3. 

The type-Π Smarandache ruled surfaces due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_3$ along ${\gamma }_1$-Smarandache curve is defined as follows

$$\Lambda (s,\upsilon )={\gamma }_1\left(s\right)+\upsilon {\gamma }_3\left(s\right).$$

(20)

Theorem 3. 

The type-Π Smarandache ruled surface $\Lambda =\Lambda (s,\upsilon )$ defined by (20) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$. If ${\kappa }_g\left(s\right)\ne \pm {\kappa }_n\left(s\right)$, then Λ is developable iff one of the following conditions holds

i. 

$\vartheta \left(s\right)={tan}^{-1}\left({\displaystyle \frac{{\kappa }_n+{\kappa }_g}{{\kappa }_n-{\kappa }_g}}\right)$,

ii. 

$\vartheta \left(s\right)=-{tan}^{-1}\left({\displaystyle \frac{{\kappa }_n-{\kappa }_g}{{\kappa }_n+{\kappa }_g}}\right)$.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\Lambda =\Lambda (s,\upsilon )$ given by (20), then $\Lambda$’s velocity vectors are given by:

$$\left\{\begin{array}{c}{\Lambda }_s={\displaystyle \frac{1}{\sqrt{2}}}\left[-\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ {\Lambda }_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(P_1+P_2\right).\hfill \end{array}\right.$$

(21)

The normal vector field of the surface $\Lambda (s,\upsilon )$ may be ascertained by taking the cross-product of the partial derivatives of the surface given by Equation (21). Then, we have

$${\mathbb{N}}_{\Lambda }={\displaystyle \frac{({\zeta }_1-{\zeta }_2)T-\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right](P_1+P_2)}{\sqrt{{({\zeta }_1-{\zeta }_2)}^2+2{\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]}^2}}}.$$

From Equation (21), we can obtain the $\Lambda$’s quantities of first fundamental form are:

$$\begin{array}{cc}& E={\displaystyle \frac{1}{2}}\left[{\kappa }^2+{\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]}^2\right],\hfill \\ & F={\displaystyle \frac{1}{2}}\left[{\zeta }_1+{\zeta }_2\right],G=1.\hfill \end{array}$$

(22)

Using (21)’s second derivative with regard to s and $\upsilon$, we have

$$\begin{array}{cc}& {\Lambda }_{ss}={\displaystyle \frac{1}{\sqrt{2}}}\{-\left[{\kappa }^2+\upsilon {\zeta }_2^{\prime }+(\upsilon +1){\zeta }_1^{\prime }\right]T+\left[{\zeta }_1^{\prime }-{\zeta }_1\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]\right]P_1\hfill \\ & +\left[{\zeta }_2^{\prime }-{\zeta }_2\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]\right]P_2\},\hfill \\ & {\Lambda }_{s\upsilon }={\displaystyle \frac{-1}{\sqrt{2}}}\left[{\zeta }_1+{\zeta }_2\right]T,\hfill \\ & {\Lambda }_{\upsilon \upsilon }=0.\hfill \end{array}$$

(23)

Then, $\Lambda$’s quantities of second fundamental form are:

$$\begin{array}{cc}& e={\displaystyle \frac{-1}{\sqrt{2}\sqrt{{({\zeta }_1-{\zeta }_2)}^2+2{\left[{\zeta }_1+(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]}^2}}}\{({\zeta }_1-{\zeta }_2)\left[{\kappa }^2+\upsilon {\zeta }_2^{\prime }+(\upsilon +1){\zeta }_1^{\prime }\right]\hfill \\ & -\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]\left[{\zeta }_1^{\prime }+{\zeta }_2^{\prime }-({\zeta }_1+{\zeta }_2)\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]\right]\},\hfill \\ & f={\displaystyle \frac{{\zeta }_2^2-{\zeta }_1^2}{\sqrt{2}\sqrt{{({\zeta }_1-{\zeta }_2)}^2+2{\left[{\zeta }_1+(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]}^2}}},\hfill \\ & g=0.\hfill \end{array}$$

(24)

As a result, given the facts above, we are able to $K_{\Lambda }$ and $H_{\Lambda }$ are given by:

$$\begin{array}{cc}& K_{\Lambda }={\displaystyle \frac{{({\zeta }_1^2-{\zeta }_2^2)}^2}{\left[{\kappa }^2+{\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]}^2-{\displaystyle \frac{1}{2}}{\left[{\zeta }_1+{\zeta }_1\right]}^2\right]\left[{({\zeta }_1-{\zeta }_2)}^2+2{\left[{\zeta }_1+(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]}^2\right]}},\hfill \\ & H_{\Lambda }={\displaystyle \frac{\left\{\begin{array}{c}({\zeta }_1-{\zeta }_2)\left[{\kappa }^2+{({\zeta }_1+{\zeta }_2)}^2+\upsilon {\zeta }_2^{\prime }+(\upsilon +1){\zeta }_1^{\prime }\right]\\ -\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]\left[{\zeta }_1^{\prime }+{\zeta }_2^{\prime }-({\zeta }_1+{\zeta }_2)\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]\right]\end{array}\right\}}{\sqrt{2}\sqrt{{({\zeta }_1-{\zeta }_2)}^2+2{\left[{\zeta }_1+(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]}^2}\left[{\kappa }^2+{\left[(\upsilon +1){\zeta }_1+\upsilon {\zeta }_2\right]}^2-{\displaystyle \frac{1}{2}}{\left[{\zeta }_1+{\zeta }_1\right]}^2\right]}}.\hfill \end{array}$$

(25)

So, from Equation (5) the proof is ended. □

In the same way, as for the proof of Corollaries 1–3, we can prove the following results:

Corollary 6. 

Let $\Lambda =\Lambda (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (20) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the Λ has constant Gauss curvature iff $\vartheta =\pm \frac{\pi }{4}$.

Corollary 7. 

Let $\Lambda =\Lambda (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (20) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Λ are not asymptotic but υ-parameter curves are asymptotic curves.

3.2. Type-$\Pi$ Smarandache Ruled Surfaces along ${\gamma }_2$-Smarandache Curve

Definition 4. 

The type-Π Smarandache ruled surfaces due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_1$ along ${\gamma }_2$-Smarandache curve is defined as follows

$$\Theta (s,\upsilon )={\gamma }_2\left(s\right)+\upsilon {\gamma }_1\left(s\right).$$

(26)

Theorem 4. 

The type-Π Smarandache ruled surface $\Theta =\Theta (s,\upsilon )$ defined by (26) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$. If ${\kappa }_g\left(s\right)\ne {\kappa }_n\left(s\right)$ then Θ is developable iff one of the following conditions holds

i. 

$\vartheta \left(s\right)=-{tan}^{-1}\left({\displaystyle \frac{{\kappa }_g}{{\kappa }_n}}\right)$,

ii. 

$\vartheta \left(s\right)={tan}^{-1}\left({\displaystyle \frac{{\kappa }_n+{\kappa }_g}{{\kappa }_n-{\kappa }_g}}\right)$.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\Theta =\Theta (s,\upsilon )$ given by (26), then $\Theta$’s velocity vectors are given by:

$$\left\{\begin{array}{c}{\Theta }_s={\displaystyle \frac{1}{\sqrt{2}}}\left[-(\upsilon {\zeta }_1+{\zeta }_2)T+(\upsilon +1){\zeta }_1{P}_1+(\upsilon +1){\zeta }_2{P}_2\right],\hfill \\ {\Theta }_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(T+P_1\right).\hfill \end{array}\right.$$

(27)

The normal vector field of the surface $\Theta (s,\upsilon )$ may be ascertained by taking the cross-product of the partial derivatives of the surface given by Equation (27). Then, we have

$${\mathbb{N}}_{\Theta }={\displaystyle \frac{-(\upsilon +1){\zeta }_{1}T+(\upsilon +1){\zeta }_2{P}_1-{[}_2+(2\upsilon +1){\zeta }_1]P_2}{\sqrt{{(\upsilon +1)}^2{\kappa }^2+{[}_2+(2\upsilon +1){\zeta }_1{]}^2}}}.$$

From Equation (27), we can obtain the $\Theta$’s quantities of first fundamental form are:

$$\begin{array}{cc}& E={\displaystyle \frac{1}{2}}\left[{(\upsilon +1)}^2{\kappa }^2+{(\upsilon {\zeta }_1+{\zeta }_2)}^2\right],\hfill \\ & F={\displaystyle \frac{1}{2}}\left({\zeta }_1+{\zeta }_2\right),G=1.\hfill \end{array}$$

(28)

Using (27)’s second derivative with regard to s and $\upsilon$, we have

$$\begin{array}{cc}& {\Theta }_{ss}={\displaystyle \frac{1}{\sqrt{2}}}[-\left[{\zeta }_2^{\prime }+\upsilon {\zeta }_1^{\prime }+(\upsilon +1){\kappa }^2\right]T+\left[(\upsilon +1){\zeta }_1^{\prime }-{\zeta }_1(\upsilon {\zeta }_1+{\zeta }_2)\right]P_1\hfill \\ & +\left[(\upsilon +1){\zeta }_2^{\prime }-{\zeta }_2(\upsilon {\zeta }_1+{\zeta }_2)\right]P_2],\hfill \\ & {\Theta }_{s\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left[-{\zeta }_{1}T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ & {\Theta }_{\upsilon \upsilon }=0.\hfill \end{array}$$

(29)

Then, $\Theta$’s quantities of second fundamental form are:

$$\begin{array}{cc}& e={\displaystyle \frac{\left\{\begin{array}{c}(\upsilon +1){\zeta }_2\left[{\zeta }_2^{\prime }+(2\upsilon +1){\zeta }_1^{\prime }+(\upsilon +1){\kappa }^2-{\zeta }_1(\upsilon {\zeta }_1+{\zeta }_2)\right]\\ -\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\left[(\upsilon +1){\zeta }_2^{\prime }-{\zeta }_2(\upsilon {\zeta }_1+{\zeta }_2)\right]\end{array}\right\}}{\sqrt{2}\sqrt{2{(\upsilon +1)}^2{\kappa }^2+{\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]}^2}}},\hfill \\ & f={\displaystyle \frac{{\zeta }_2({\zeta }_1-{\zeta }_2)}{\sqrt{2}\sqrt{2{(\upsilon +1)}^2{\kappa }^2+{\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]}^2}}},\hfill \\ & g=0.\hfill \end{array}$$

(30)

As a result, given the facts above, we are able to see that $K_{\Theta }$ and $H_{\Theta }$ are given by:

$$\begin{array}{cc}& K_{\Theta }=-{\displaystyle \frac{{\zeta }_2^2{({\zeta }_1-{\zeta }_2)}^2}{\left[{(\upsilon +1)}^2{\kappa }^2+{(\upsilon {\zeta }_1+{\zeta }_2)}^2-\frac{1}{2}{\left({\zeta }_1+{\zeta }_2\right)}^2\right]\left[2{(\upsilon +1)}^2{\kappa }^2+{\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]}^2\right]}},\hfill \\ & H_{\Theta }={\displaystyle \frac{\left\{\begin{array}{c}{\zeta }_2({\zeta }_2^2-{\zeta }_1^2)+(\upsilon +1){\zeta }_2\left[{\zeta }_2^{\prime }+(2\upsilon +1){\zeta }_1^{\prime }+(\upsilon +1){\kappa }^2-{\zeta }_1(\upsilon {\zeta }_1+{\zeta }_2)\right]\\ -\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\left[(\upsilon +1){\zeta }_2^{\prime }-{\zeta }_2(\upsilon {\zeta }_1+{\zeta }_2)\right]\end{array}\right\}}{2\sqrt{2}\left[{(\upsilon +1)}^2{\kappa }^2+{(\upsilon {\zeta }_1+{\zeta }_2)}^2-\frac{1}{2}{\left({\zeta }_1+{\zeta }_2\right)}^2\right]{\left[2{(\upsilon +1)}^2{\kappa }^2+{\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]}^2\right]}^{\frac{3}{2}}}}.\hfill \end{array}$$

(31)

So, from Equation (5) the proof is ended. □

In the same way, as for the proof of Corollary 2, we can prove the following result:

Corollary 8. 

Let $\Theta =\Theta (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (26) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Θ are not asymptotic but υ-parameter curves are asymptotic curves.

Definition 5. 

The type-Π Smarandache ruled surfaces due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_2$ along ${\gamma }_2$-Smarandache curve is defined as follows

$$\mathrm{{\rm Y}}(s,\upsilon )={\gamma }_2\left(s\right)+\upsilon {\gamma }_2\left(s\right).$$

(32)

Theorem 5. 

The type-Π Smarandache ruled surface $\mathrm{{\rm Y}}=\mathrm{{\rm Y}}(s,\upsilon )$ defined by (32) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ is developable iff one of the following conditions holds

i. 

$\vartheta \left(s\right)=-{tan}^{-1}\left({\displaystyle \frac{{\kappa }_n}{{\kappa }_g}}\right)$,

ii. 

$\vartheta \left(s\right)={tan}^{-1}\left({\displaystyle \frac{{\kappa }_g}{{\kappa }_n}}\right)$.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\mathrm{{\rm Y}}=\mathrm{{\rm Y}}(s,\upsilon )$ given by (32), then $\mathrm{{\rm Y}}$’s velocity vectors are given by:

$$\left\{\begin{array}{c}{\mathrm{{\rm Y}}}_s={\displaystyle \frac{\upsilon +1}{\sqrt{2}}}\left[-{\zeta }_{2}T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ {\mathrm{{\rm Y}}}_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(T+P_2\right).\hfill \end{array}\right.$$

(33)

The normal vector field of the surface $\mathrm{{\rm Y}}(s,\upsilon )$ may be ascertained by taking the cross-product of the partial derivatives of the surface given by Equation (33). Then, we have

$${\mathbb{N}}_{\mathrm{{\rm Y}}}={\displaystyle \frac{{\zeta }_{1}T+2{\zeta }_2{P}_1+{\zeta }_1{P}_2}{\sqrt{2}\sqrt{2{\zeta }_2^2+{\zeta }_1^2}}}.$$

From Equation (33), we can obtain the $\mathrm{{\rm Y}}$’s quantities of first fundamental form are:

$$\begin{array}{cc}& E={\displaystyle \frac{1}{2}}\left[{(\upsilon +1)}^2({\zeta }_1^2+2{\zeta }_2^2)\right],\hfill \\ & F=0,G=1.\hfill \end{array}$$

(34)

Using (33)’s second derivative with regard to s and $\upsilon$, we have

$$\begin{array}{cc}& {\mathrm{{\rm Y}}}_{ss}={\displaystyle \frac{(\upsilon +1)}{\sqrt{2}}}\left[-({\kappa }^2+{\zeta }_2^{\prime })T+({\zeta }_1^{\prime }-{\zeta }_1{\zeta }_2)P_1+({\zeta }_2^{\prime }-{\kappa }^2)P_2\right],\hfill \\ & {\mathrm{{\rm Y}}}_{s\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left[-{\zeta }_{2}T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ & {\mathrm{{\rm Y}}}_{\upsilon \upsilon }=0.\hfill \end{array}$$

(35)

Then, $\mathrm{{\rm Y}}$’s quantities of second fundamental form are:

$$\begin{array}{cc}& e={\displaystyle \frac{(\upsilon +1)\left[{\zeta }_1{\zeta }_2^{\prime }+2{\zeta }_1^{\prime }{\zeta }_2-{\zeta }_1({\kappa }^2+{\zeta }_2^{\prime }+3{\zeta }_2^2)\right]}{2\sqrt{{\zeta }_1^2+2{\zeta }_2^2}}},\hfill \\ & f={\displaystyle \frac{{\zeta }_1{\zeta }_2}{\sqrt{{\zeta }_1^2+2{\zeta }_2^2}}},\hfill \\ & g=0.\hfill \end{array}$$

(36)

As a result, given the facts above, we are able to find that $K_{\mathrm{{\rm Y}}}$ and $H_{\mathrm{{\rm Y}}}$ are given by:

$$\begin{array}{cc}& K_{\mathrm{{\rm Y}}}=-{\displaystyle \frac{2{\zeta }_1^2{\zeta }_2^2}{{(\upsilon +1)}^2({\zeta }_1^2+2{\zeta }_2^2)}},\hfill \\ & H_{\mathrm{{\rm Y}}}={\displaystyle \frac{2{\zeta }_1^{\prime }{\zeta }_2+{\zeta }_1{\zeta }_2^{\prime }-3{\zeta }_1{\zeta }_2^2-{\zeta }_1({\kappa }^2+{\zeta }_2^{\prime })}{2(\upsilon +1){[{\zeta }_1^2+2{\zeta }_2^2]}^{\frac{3}{2}}}}.\hfill \end{array}$$

(37)

So, from Equation (5) the proof is ended. □

In the same way, as for the proof of Corollaries 1–3, we can prove the following results:

Corollary 9. 

Let $\mathrm{{\rm Y}}=\mathrm{{\rm Y}}(s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (32) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the Υ has constant Gauss curvature iff ${\kappa }_n$ and ${\kappa }_g$ satisfying the condition $2{\kappa }_n{\kappa }_g-({\kappa }_n^2+{\kappa }_g^2)sin2\vartheta =c$ for some non-zero constant c.

Corollary 10. 

Let $\mathrm{{\rm Y}}=\mathrm{{\rm Y}}(s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (32) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Υ are not asymptotic but υ-parameter curves are asymptotic curves.

Corollary 11. 

Let $\mathrm{{\rm Y}}=\mathrm{{\rm Y}}(s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (32) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Υ are principal curves but υ-parameter curves are not principal curves.

Definition 6. 

The type-Π Smarandache ruled surfaces due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_3$ along ${\gamma }_2$-Smarandache curve is defined as follows

$$\Omega (s,\upsilon )={\gamma }_2\left(s\right)+\upsilon {\gamma }_3\left(s\right).$$

(38)

Theorem 6. 

The type-Π Smarandache ruled surface $\Omega =\Omega (s,\upsilon )$ defined by (38) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$. If ${\kappa }_g\left(s\right)\ne \pm {\kappa }_n\left(s\right)$, then Ω is developable iff one of the following conditions holds

i. 

$\vartheta \left(s\right)={tan}^{-1}\left({\displaystyle \frac{{\kappa }_n+{\kappa }_g}{{\kappa }_n-{\kappa }_g}}\right)$,

ii. 

$\vartheta \left(s\right)=-{tan}^{-1}\left({\displaystyle \frac{{\kappa }_n-{\kappa }_g}{{\kappa }_n+{\kappa }_g}}\right)$.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\Omega =\Omega (s,\upsilon )$ given by (38), then $\Omega$’s velocity vectors are given by:

$$\left\{\begin{array}{c}{\Omega }_s={\displaystyle \frac{1}{\sqrt{2}}}\left[-\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ {\Omega }_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(P_1+P_2\right).\hfill \end{array}\right.$$

(39)

The normal vector field of the surface $\Omega (s,\upsilon )$ may be ascertained by taking the cross-product of the partial derivatives of the surface given by Equation (39). Then, we have

$${\mathbb{N}}_{\Omega }={\displaystyle \frac{({\zeta }_1-{\zeta }_2)T+\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right](P_1+P_2)}{\sqrt{{({\zeta }_1-{\zeta }_2)}^2+{\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2}}}.$$

From Equation (39), we can obtain the $\Omega$’s quantities of first fundamental form are:

$$\begin{array}{cc}& E={\displaystyle \frac{1}{2}}\left[{\kappa }^2+{\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2\right],\hfill \\ & F={\displaystyle \frac{1}{2}}\left[{\zeta }_1+{\zeta }_2\right],G=1.\hfill \end{array}$$

(40)

Using (39)’s second derivative with regard to s and $\upsilon$, we have

$$\begin{array}{cc}& {\Omega }_{ss}={\displaystyle \frac{1}{\sqrt{2}}}\{-\left[{\kappa }^2+\upsilon {\zeta }_1^{\prime }+(\upsilon +1){\zeta }_2^{\prime }\right]T+\left[{\zeta }_1^{\prime }-{\zeta }_1\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]\right]P_1\hfill \\ & +\left[{\zeta }_2^{\prime }-{\zeta }_2\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]\right]P_2\},\hfill \\ & {\Omega }_{s\upsilon }={\displaystyle \frac{-({\zeta }_1+{\zeta }_2)T}{\sqrt{2}}},\hfill \\ & {\Omega }_{\upsilon \upsilon }=0.\hfill \end{array}$$

(41)

Then, $\Omega$’s quantities of second fundamental form are:

$$\begin{array}{cc}& e={\displaystyle \frac{\left\{\begin{array}{c}({\zeta }_2-{\zeta }_1)\left[{\kappa }^2+\upsilon {\zeta }_1^{\prime }+(\upsilon +1){\zeta }_2^{\prime }\right]+\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]\\ \left[{\zeta }_1^{\prime }+{\zeta }_2^{\prime }-({\zeta }_1+{\zeta }_2)\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]\right]\end{array}\right\}}{\sqrt{2}\sqrt{{({\zeta }_1-{\zeta }_2)}^2+2{\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2}}},\hfill \\ & f={\displaystyle \frac{{\zeta }_2^2-{\zeta }_1^2}{\sqrt{2}\sqrt{{({\zeta }_1-{\zeta }_2)}^2+2{\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2}}},\hfill \\ & g=0.\hfill \end{array}$$

(42)

As a result, given the facts above, we are able to $K_{\Omega }$ and $H_{\Omega }$ are given by:

$$\begin{array}{cc}& K_{\Omega }={\displaystyle \frac{-2{({\zeta }_1^2-{\zeta }_2^2)}^2}{\left[{\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2-{\kappa }^2-2{\zeta }_1{\zeta }_2\right]\left[{({\zeta }_1-{\zeta }_2)}^2+2{\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2\right]}},\hfill \\ & H_{\Omega }={\displaystyle \frac{4\left\{\begin{array}{c}({\zeta }_1+{\zeta }_2)({\zeta }_1^2-{\zeta }_2^2)+({\zeta }_2-{\zeta }_1)\left[{\kappa }^2+\upsilon {\zeta }_1^{\prime }+(\upsilon +1){\zeta }_2^{\prime }\right]\\ +\left[\upsilon {\zeta }_1(\upsilon +1){\zeta }_2\right]\left[{\zeta }_1^{\prime }+{\zeta }_2^{\prime }-({\zeta }_1+{\zeta }_2)\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]\right]\end{array}\right\}}{\sqrt{2}\left[{\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2-{\kappa }^2-2{\zeta }_1{\zeta }_2\right]{\left[{({\zeta }_1-{\zeta }_2)}^2+2{\left[\upsilon {\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2\right]}^{\frac{3}{2}}}}.\hfill \end{array}$$

(43)

So, from Equation (5) the proof is ended. □

In the same way, as for the proof of Corollary 2, we can prove the following result:

Corollary 12. 

Let $\Omega =\Omega (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (38) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Ω are not asymptotic but υ-parameter curves are asymptotic curves.

3.3. Type-$\Pi$ Smarandache Ruled Surfaces along ${\gamma }_3$-Smarandache Curve

Definition 7. 

The type-Π Smarandache ruled surfaces due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_1$ along ${\gamma }_3$-Smarandache curve is defined as follows

$$\Xi (s,\upsilon )={\gamma }_3\left(s\right)+\upsilon {\gamma }_1\left(s\right).$$

(44)

Theorem 7. 

The type-Π Smarandache ruled surface $\Xi =\Xi (s,\upsilon )$ defined by (44) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ is developable iff one of the following conditions holds

i. 

$\vartheta \left(s\right)={tan}^{-1}\left({\displaystyle \frac{{\kappa }_g}{{\kappa }_n}}\right)$,

ii. 

$\vartheta \left(s\right)={tan}^{-1}\left({\displaystyle \frac{{\kappa }_g+(\upsilon +1){\kappa }_n}{{\kappa }_n-(\upsilon +1){\kappa }_g}}\right)$.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\Xi =\Xi (s,\upsilon )$ given by (44), then $\Xi$’s velocity vectors are given by:

$$\left\{\begin{array}{c}{\Xi }_s={\displaystyle \frac{1}{\sqrt{2}}}\left[-\left[(\upsilon +1){\zeta }_1+{\zeta }_2\right]T+\upsilon {\zeta }_1{P}_1+\upsilon {\zeta }_2{P}_2\right],\hfill \\ {\Xi }_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(T+P_1\right).\hfill \end{array}\right.$$

(45)

The normal vector field of the surface $\Xi (s,\upsilon )$ may be ascertained by taking the cross-product of the partial derivatives of the surface given by Equation (45). Then, we have

$${\mathbb{N}}_{\Xi }={\displaystyle \frac{\upsilon {\zeta }_2(T+P_1)+\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]P_2}{\sqrt{{\upsilon }^2{\kappa }^2+{\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]}^2}}}.$$

From Equation (45), we can obtain the $\Xi$’s quantities of first fundamental form are:

$$\begin{array}{cc}& E={\displaystyle \frac{1}{2}}\left[{\upsilon }^2{\kappa }^2+{\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}^2\right],\hfill \\ & F={\displaystyle \frac{-1}{2}}\left({\zeta }_1+{\zeta }_2\right),G=1.\hfill \end{array}$$

(46)

Using (45)’s second derivative with regard to s and $\upsilon$, we have

$$\begin{array}{cc}& {\Xi }_{ss}={\displaystyle \frac{1}{\sqrt{2}}}[-\left[\upsilon {\kappa }^2+{\zeta }_2^{\prime }+(\upsilon +1){\zeta }_1^{\prime }\right]T+\left[\upsilon {\zeta }_1^{\prime }-{\zeta }_1\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\right]P_1\hfill \\ & +\left[\upsilon {\zeta }_2^{\prime }-{\zeta }_2\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\right]P_2],\hfill \\ & {\Xi }_{s\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left[-{\zeta }_{1}T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ & {\Xi }_{\upsilon \upsilon }=0.\hfill \end{array}$$

(47)

Then, $\Xi$’s quantities of second fundamental form are:

$$\begin{array}{cc}& e={\displaystyle \frac{\left\{\begin{array}{c}\upsilon {\zeta }_2\left[\upsilon {\kappa }^2+{\zeta }_2^{\prime }+(2\upsilon +1){\zeta }_1^{\prime }-{\zeta }_1\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\right]\\ +\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\left[\upsilon {\zeta }_2^{\prime }-{\zeta }_2\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\right]\end{array}\right\}}{\sqrt{2}\sqrt{{\upsilon }^2{\kappa }^2+{\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}^2}}},\hfill \\ & f={\displaystyle \frac{-{\zeta }_2\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}{\sqrt{2}\sqrt{{\upsilon }^2{\kappa }^2+{\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}^2}}},\hfill \\ & g=0.\hfill \end{array}$$

(48)

As a result, given the facts above, we are able to find that $K_{\Xi }$ and $H_{\Xi }$ are given by:

$$\begin{array}{cc}& K_{\Xi }=-{\displaystyle \frac{-{\zeta }_2^2{\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}^2}{\left[{\upsilon }^2{\kappa }^2+{\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}^2-\frac{1}{2}{\left({\zeta }_1+{\zeta }_2\right)}^2\right]\left[{\upsilon }^2{\kappa }^2+{\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}^2\right]}},\hfill \\ & H_{\Xi }={\displaystyle \frac{\left\{\begin{array}{c}{\zeta }_2({\zeta }_1+{\zeta }_2)\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]+\upsilon {\zeta }_2[\upsilon {\kappa }^2+{\zeta }_2^{\prime }+(2\upsilon +1){\zeta }_1^{\prime }\\ -{\zeta }_1\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]]+\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\left[\upsilon {\zeta }_2^{\prime }-{\zeta }_2\left[{\zeta }_2+(2\upsilon +1){\zeta }_1\right]\right]\end{array}\right\}}{2\sqrt{2}\left[{\upsilon }^2{\kappa }^2+{\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}^2-\frac{1}{2}{\left({\zeta }_1+{\zeta }_2\right)}^2\right]{\left[{\upsilon }^2{\kappa }^2+{\left[{\zeta }_2+(\upsilon +1){\zeta }_1\right]}^2\right]}^{\frac{3}{2}}}}.\hfill \end{array}$$

(49)

So, from Equation (5) the proof is ended. □

In the same way, as for the proof of Corollary 2, we can prove the following result:

Corollary 13. 

Let $\Xi =\Xi (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (44) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Ξ are not asymptotic but υ-parameter curves are asymptotic curves.

Definition 8. 

The type-Π Smarandache ruled surfaces due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_2$ along ${\gamma }_3$-Smarandache curve is defined as follows:

$$\Sigma (s,\upsilon )={\gamma }_3\left(s\right)+\upsilon {\gamma }_2\left(s\right).$$

(50)

Theorem 8. 

The type-Π Smarandache ruled surface $\Sigma =\Sigma (s,\upsilon )$ defined by (50) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ is developable iff one of the following conditions holds

i. 

$\vartheta \left(s\right)=-{tan}^{-1}\left({\displaystyle \frac{{\kappa }_n}{{\kappa }_g}}\right)$,

ii. 

${\displaystyle \frac{{\zeta }_1}{{\zeta }_2}}={\displaystyle \frac{\upsilon -1}{2\upsilon +1}}$.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\Sigma =\Sigma (s,\upsilon )$ given by (50), then $\Sigma$’s velocity vectors are given by:

$$\left\{\begin{array}{c}{\Sigma }_s={\displaystyle \frac{1}{\sqrt{2}}}\left[-\left[{\zeta }_1+(\upsilon +1){\zeta }_2\right]T+\upsilon {\zeta }_1{P}_1+\upsilon {\zeta }_2{P}_2\right],\hfill \\ {\Sigma }_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(T+P_2\right).\hfill \end{array}\right.$$

(51)

The normal vector field of the surface $\Sigma (s,\upsilon )$ may be ascertained by taking the cross-product of the partial derivatives of the surface given by Equation (51). Then, we have

$${\mathbb{N}}_{\Sigma }={\displaystyle \frac{\upsilon {\zeta }_1(T+P_2)+\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]P_1}{\sqrt{2{\upsilon }^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2}}}.$$

From Equation (51), we can obtain the $\Sigma$’s quantities of first fundamental form are:

$$\begin{array}{cc}& E={\displaystyle \frac{1}{2}}\left[{\upsilon }^2{\kappa }^2+{\left[{\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2\right],\hfill \\ & F=-{\displaystyle \frac{1}{2}}\left({\zeta }_1-{\zeta }_2\right),G=1.\hfill \end{array}$$

(52)

Using (51)’s second derivative with regard to s and $\upsilon$, we have

$$\begin{array}{cc}& {\Sigma }_{ss}={\displaystyle \frac{1}{\sqrt{2}}}[-\left[\upsilon {\kappa }^2+{\zeta }_1^{\prime }+(\upsilon +1){\zeta }_2^{\prime }\right]T+\left[\upsilon {\zeta }_1^{\prime }-{\zeta }_1\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]\right]P_1\hfill \\ & +\left[\upsilon {\zeta }_2^{\prime }-{\zeta }_2\left[{\zeta }_1+(\upsilon +1){\zeta }_2\right]\right]P_2],\hfill \\ & {\Sigma }_{s\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left[-({\zeta }_1+{\zeta }_2)T+{\zeta }_1{P}_1+{\zeta }_2{P}_2\right],\hfill \\ & {\Sigma }_{\upsilon \upsilon }=0.\hfill \end{array}$$

(53)

Then, $\Sigma$’s quantities of second fundamental form are:

$$\begin{array}{cc}& e={\displaystyle \frac{\left\{\begin{array}{c}\upsilon {\zeta }_1\left[\upsilon ({\zeta }_2^2-{\kappa }^2)-(\upsilon +1)({\zeta }_2^2-{\zeta }_2^{\prime })-{\zeta }_1^{\prime }-{\zeta }_1{\zeta }_2\right]\\ +\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]\left[\upsilon {\zeta }_1^{\prime }-{\zeta }_1\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]\right]\end{array}\right\}}{\sqrt{2}\sqrt{2{\upsilon }^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2}}},\hfill \\ & f={\displaystyle \frac{{\zeta }_1\left[(1-\upsilon ){\zeta }_1+(2\upsilon +1){\zeta }_2\right]}{\sqrt{2}\sqrt{2{\upsilon }^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2}}},\hfill \\ & g=0.\hfill \end{array}$$

(54)

As a result, given the facts above, we are able to find that $K_{\Sigma }$ and $H_{\Sigma }$ are given by:

$$\begin{array}{cc}& K_{\Sigma }=-{\displaystyle \frac{{\zeta }_1^2{\left[(1-\upsilon ){\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2}{\left[{\upsilon }^2{\kappa }^2+{\left[{\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2-\frac{1}{2}{\left({\zeta }_1-{\zeta }_2\right)}^2\right]\left[2{\upsilon }^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2\right]}},\hfill \\ & H_{\Sigma }={\displaystyle \frac{\left\{\begin{array}{c}{\zeta }_1({\zeta }_1-{\zeta }_2)\left[(\upsilon -1){\zeta }_1+(2\upsilon +1){\zeta }_2\right]\upsilon {\zeta }_1[\upsilon ({\zeta }_2^2-{\kappa }^2)-(\upsilon +1)({\zeta }_2^2-{\zeta }_2^{\prime })\\ -{\zeta }_1^{\prime }-{\zeta }_1{\zeta }_2]+\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]\left[\upsilon {\zeta }_1^{\prime }-{\zeta }_1\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]\right]\end{array}\right\}}{\sqrt{2}\left[{\upsilon }^2{\kappa }^2+{\left[{\zeta }_1+(\upsilon +1){\zeta }_2\right]}^2-\frac{1}{2}{\left({\zeta }_1-{\zeta }_2\right)}^2\right]{\left[2{\upsilon }^2{\zeta }_1^2+{\left[{\zeta }_1+(2\upsilon +1){\zeta }_2\right]}^2\right]}^{\frac{3}{2}}}}.\hfill \end{array}$$

(55)

So, from Equation (5) the proof is ended. □

In the same way, as for the proof of Corollary 2, we can prove the following result:

Corollary 14. 

Let $\Sigma =\Sigma (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (50) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Σ are not asymptotic but υ-parameter curves are asymptotic curves.

Definition 9. 

The type-Π Smarandache ruled surfaces due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ generated by continuously moving vector ${\gamma }_3$ along ${\gamma }_3$-Smarandache curve is defined as follows

$$\Delta (s,\upsilon )={\gamma }_3\left(s\right)+\upsilon {\gamma }_3\left(s\right).$$

(56)

Theorem 9. 

The type-Π Smarandache ruled surface $\Delta =\Delta (s,\upsilon )$ defined by (56) due to RMDF (4) in ${\mathbf{E}}^{\mathbf{3}}$ is developable.

Proof. 

Consider the type-$\Pi$ Smarandache ruled surface $\Delta =\Delta (s,\upsilon )$ given by (56), then $\Delta$’s velocity vectors are given by:

$$\left\{\begin{array}{c}{\Delta }_s=-{\displaystyle \frac{(\upsilon +1)}{\sqrt{2}}}\left[{\zeta }_1+{\zeta }_2\right]T,\hfill \\ {\Delta }_{\upsilon }={\displaystyle \frac{1}{\sqrt{2}}}\left(P_1+P_2\right).\hfill \end{array}\right.$$

(57)

The normal vector field of the surface $\Delta (s,\upsilon )$ may be ascertained by taking the cross-product of the partial derivatives of the surface given by Equation (57). Then, we have

$${\mathbb{N}}_{\Delta }={\displaystyle \frac{P_1-P_2}{\sqrt{2}}}.$$

From Equation (57), we can obtain the $\Delta$’s quantities of first fundamental form are:

$$\begin{array}{cc}& E={\displaystyle \frac{1}{2}}\left(\upsilon +1\right){\left({\zeta }_1+{\zeta }_2\right)}^2,\hfill \\ & F=0,G=1.\hfill \end{array}$$

(58)

Using (57)’s second derivative with regard to s and $\upsilon$, we have

$$\begin{array}{cc}& {\Delta }_{ss}=-{\displaystyle \frac{(\upsilon +1)}{\sqrt{2}}}\left\{\left({\zeta }_1^{\prime }+{\zeta }_2^{\prime }\right)T+{\zeta }_1\left({\zeta }_1+{\zeta }_2\right)P_1+{\zeta }_2\left({\zeta }_1+{\zeta }_2\right)P_2\right\},\hfill \\ & {\Delta }_{s\upsilon }={\displaystyle \frac{-({\zeta }_1+{\zeta }_2)T}{\sqrt{2}}},\hfill \\ & {\Delta }_{\upsilon \upsilon }=0.\hfill \end{array}$$

(59)

Then, $\Delta$’s quantities of second fundamental form are:

$$\begin{array}{cc}& e={\displaystyle \frac{(\upsilon +1){\kappa }^2}{2}},\hfill \\ & f=0,g=0.\hfill \end{array}$$

(60)

As a result, given the facts above, we are able to find that $K_{\Delta }$ and $H_{\Delta }$ are given by:

$$\begin{array}{cc}& K_{\Delta }=0,\hfill \\ & H_{\Delta }={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\kappa }{{\zeta }_1+{\zeta }_2}}\right)}^2.\hfill \end{array}$$

(61)

Then, the proof is ended. □

In the same way, as for the proof of Corollaries 1–3, we can prove the following results:

Corollary 15. 

Let $\Sigma =\Sigma (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (56) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the Σ minimal surface iff $\kappa =0$.

Corollary 16. 

Let $\Delta =\Delta (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (56) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Δ are not geodesic curves but υ-parameter curves are geodesic curves.

Corollary 17. 

Let $\Sigma =\Sigma (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (56) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s-parameter curves of Σ are not asymptotic but υ-parameter curves are asymptotic curves.

Corollary 18. 

Let $\Sigma =\Sigma (s,\upsilon )$ be a type-Π Smarandache ruled surface defined by (56) in ${\mathbf{E}}^{\mathbf{3}}$ via to RMDF (4). Then, the s and υ-parameter curves of Σ are principal curves.

4. Example

Let consider a surface $M=M(s,\upsilon )$ parameterized by

$$M(s,\upsilon )=\left(cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)+\sqrt{2}sin\upsilon ,sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)+\sqrt{2}cos\upsilon ,{\displaystyle \frac{s}{\sqrt{2}}}\right).$$

The s-parameter curve $\phi \left(s\right)=\left(cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right),sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right),{\displaystyle \frac{s}{\sqrt{2}}}\right)$ lying on $M=M(s,\upsilon )$ (see Figure 1). Then, the Darboux frame of $\phi \left(s\right)$ on M are given, respectively, by

$$\begin{array}{cc}& T\left(s\right)=\frac{1}{\sqrt{2}}\left(-sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right),cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right),1\right),\hfill \\ & \mathbb{N}\left(s\right)=\frac{1}{\sqrt{2}}\left(-cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)+\frac{1}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right),-sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{1}{\sqrt{2}}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right),\frac{1}{\sqrt{2}}\right),\hfill \\ & G\left(s\right)=\frac{1}{\sqrt{2}}\left(cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)+\frac{1}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right),sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{1}{\sqrt{2}}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right),{\displaystyle \frac{1}{\sqrt{2}}}\right),\hfill \\ & {\kappa }_n={\kappa }_g={\displaystyle \frac{1}{\sqrt{2}}},{\tau }_g={\displaystyle \frac{1}{2}}.\hfill \end{array}$$

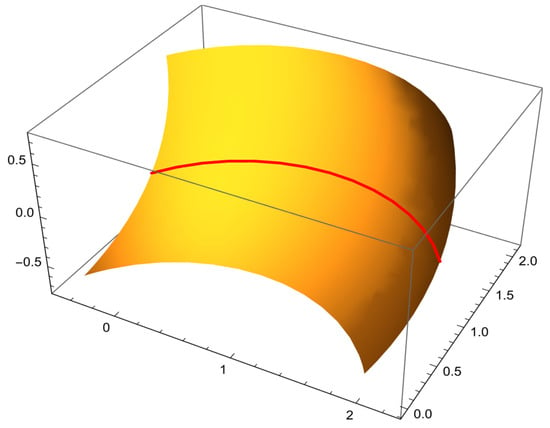
Figure 1. The curve $\phi \left(s\right)$ on $M(s,\upsilon )$.

Then, ${\displaystyle \vartheta \left(s\right)=-{\int }_0^2{\displaystyle \frac{1}{2}}ds=-{\displaystyle \frac{s}{2}}}$. So, we have

$$\begin{array}{cc}& P_1=\{\frac{1}{\sqrt{2}}\left[cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)+sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)\right],\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]sin\left(\frac{s}{\sqrt{2}}\right)\hfill \\ & -\frac{1}{\sqrt{2}}\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]cos\left(\frac{s}{\sqrt{2}}\right),\frac{1}{\sqrt{2}}\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]\},\hfill \\ & P_2=\{\frac{1}{\sqrt{2}}\left[cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)\right],\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]sin\left(\frac{s}{\sqrt{2}}\right)\hfill \\ & -\frac{1}{\sqrt{2}}\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]cos\left(\frac{s}{\sqrt{2}}\right),-\frac{1}{\sqrt{2}}\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]\}.\hfill \end{array}$$

Given the parametric equations below and these vectors and definitions, the graphs of type-$\Pi$ Smarandache ruled surface are shown in Figure 2, Figure 3, and Figure 4, respectively.

$$\begin{array}{cc}\hfill \Psi (s,\upsilon )=& \frac{\upsilon +1}{2}\{cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)+sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-sin\left(\frac{s}{\sqrt{2}}\right),cos\left(\frac{s}{\sqrt{2}}\right)\hfill \\ & +\sqrt{2}\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]sin\left(\frac{s}{\sqrt{2}}\right),1+cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Gamma (s,\upsilon )=& \{\frac{(\upsilon +1)}{2}cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)+\frac{(\upsilon -1)}{2}sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-\frac{(\upsilon +1)}{2}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\hfill \\ & ,\frac{(\upsilon +1)}{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)+\frac{(\upsilon +1)}{\sqrt{2}}\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\hfill \\ & -\frac{(\upsilon +1)}{\sqrt{2}}\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right),\frac{\upsilon +1}{2}\left[1+sin\left(\frac{s}{2}\right)\right]-\frac{(\upsilon -1)}{2}cos\left(\frac{s}{2}\right)\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Lambda (s,\upsilon )=& \{\frac{(\upsilon +1)}{2}cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)+\frac{1}{2}sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-\frac{1}{2}sin\left({\displaystyle \frac{s}{2}}\right),\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]\hfill \\ & \times \left[\frac{\upsilon }{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{(\upsilon +1)}{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right]+\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right][\frac{(\upsilon +1)}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\hfill \\ & -\frac{\upsilon }{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)],\frac{1}{2}\left[1+cos\left(\frac{s}{2}\right)\right]+\frac{(2\upsilon +1)}{2}sin\left(\frac{s}{2}\right)\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Theta (s,\upsilon )=& \{\frac{(\upsilon +1)}{2}cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-\frac{(\upsilon -1)}{\sqrt{2}}sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-\frac{(\upsilon +1)}{2}sin\left({\displaystyle \frac{s}{2}}\right)\hfill \\ & ,\frac{(\upsilon +1)}{2}cos\left({\displaystyle \frac{s}{2}}\right)+\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]\left[\frac{\upsilon }{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{1}{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right]\hfill \\ & +\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]\left[\frac{1}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{\upsilon }{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right],\frac{(\upsilon +1)}{2}sin\left({\displaystyle \frac{s}{2}}\right)\hfill \\ & +\frac{(\upsilon -1)}{2}cos\left({\displaystyle \frac{s}{2}}\right)\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathrm{{\rm Y}}(s,\upsilon )=& \frac{(\upsilon +1)}{2}\{cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-sin\left({\displaystyle \frac{s}{2}}\right),cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)+\sqrt{2}[cos\left(\frac{s}{2}\right)\hfill \\ & +sin\left(\frac{s}{2}\right)]sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right),1-cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Omega (s,\upsilon )=& \{\frac{(2\upsilon +1)}{2}cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)+\frac{1}{2}sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-\frac{1}{2}sin\left({\displaystyle \frac{s}{2}}\right)\hfill \\ & ,\frac{1}{2}cos\left({\displaystyle \frac{s}{2}}\right)+\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]\left[\frac{(\upsilon +1)}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{\upsilon }{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right]\hfill \\ & +\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]\left[\frac{\upsilon }{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{(\upsilon +1)}{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right],\frac{(2\upsilon +1)}{2}sin\left({\displaystyle \frac{s}{2}}\right)\hfill \\ & +\frac{1}{2}\left[1+cos\left({\displaystyle \frac{s}{2}}\right)\right]\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Xi (s,\upsilon )=& \{\frac{(2\upsilon +1)}{2}cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)+\frac{\upsilon }{2}sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-\frac{\upsilon }{2}sin\left({\displaystyle \frac{s}{2}}\right)\hfill \\ & ,\frac{\upsilon }{2}cos\left({\displaystyle \frac{s}{2}}\right)+\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]\left[\frac{1}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{(\upsilon +1)}{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right]\hfill \\ & +\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]\left[\frac{(\upsilon +1)}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{1}{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right],\frac{(\upsilon +2)}{2}sin\left({\displaystyle \frac{s}{2}}\right)\hfill \\ & +\frac{\upsilon }{2}\left[1+cos\left({\displaystyle \frac{s}{2}}\right)\right]\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Sigma (s,\upsilon )=& \{\frac{(\upsilon +2)}{2}cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-\frac{\upsilon }{2}sin\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right)-\frac{\upsilon }{2}sin\left({\displaystyle \frac{s}{2}}\right)\hfill \\ & ,\frac{\upsilon }{2}cos\left({\displaystyle \frac{s}{2}}\right)+\left[cos\left(\frac{s}{2}\right)+sin\left(\frac{s}{2}\right)\right]\left[\frac{(\upsilon +1)}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{1}{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right]\hfill \\ & +\left[cos\left(\frac{s}{2}\right)-sin\left(\frac{s}{2}\right)\right]\left[\frac{1}{\sqrt{2}}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)-\frac{(\upsilon +1)}{2}cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)\right],\frac{(\upsilon +2)}{2}sin\left({\displaystyle \frac{s}{2}}\right)\hfill \\ & +\frac{\upsilon }{2}\left[1-cos\left({\displaystyle \frac{s}{2}}\right)\right]\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Delta (s,\upsilon )=& (\upsilon +1)\left\{cos\left(\frac{s}{\sqrt{2}}-\frac{s}{2}\right),\sqrt{2}sin\left({\displaystyle \frac{s}{\sqrt{2}}}\right)cos\left(\frac{s}{2}\right)+cos\left({\displaystyle \frac{s}{\sqrt{2}}}\right)cos\left(\frac{s}{2}\right),sin\left(\frac{s}{2}\right)\right\}.\hfill \end{array}$$

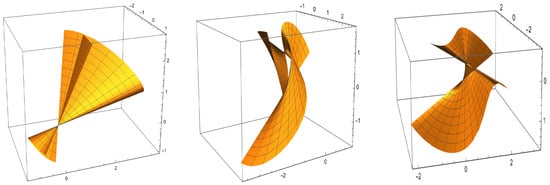
Figure 2. The type-$\Pi$ Smarandache ruled surfaces $\Psi$, $\Gamma$, and $\Lambda$ along ${\gamma }_1$.

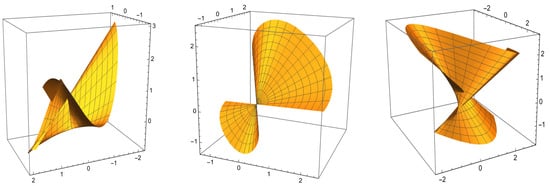
Figure 3. The type-$\Pi$ Smarandache ruled surfaces $\Theta$, $\mathrm{{\rm Y}}$, and $\Omega$ along ${\gamma }_2$.

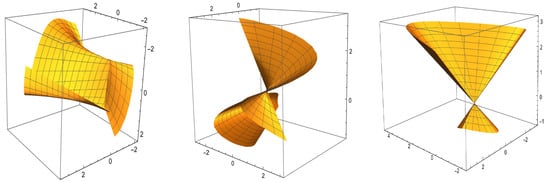
Figure 4. The type-$\Pi$ Smarandache ruled surfaces $\Xi$, $\Sigma$, and $\Delta$ along ${\gamma }_3$.

5. Conclusions

This study focused on the construction of type-$\Pi$ Smarandache ruled surfaces, with their base curves being Smarandache curves derived from rotation minimizing Darboux frame vectors of the curve in ${\mathbf{E}}^{\mathbf{3}}$. The direction vectors of these surfaces were unit vectors that transformed the Smarandache curves. The Gaussian and mean curvatures of the manufactured ruled surfaces were calculated separately with the requirement of being either minimum or developable. Graphs of these surfaces were generated, along with an example provided for each surface. Through this research, we have successfully examined and presented the characteristics and properties of these type-$\Pi$ Smarandache ruled surfaces, contributing to the understanding and exploration of this specific class of surfaces. Further investigations and applications of these surfaces in relevant fields are encouraged.