New Convergence Theorems for Pseudomonotone Variational Inequality on Hadamard Manifolds

Abstract

In this paper, we propose an efficient viscosity type subgradient extragradient algorithm for solving pseudomonotone variational inequality on Hadamard manifolds which is of symmetrical characteristic. Under suitable conditions, we obtain the convergence of the iteration sequence generated by the proposed algorithm to a solution of a pseudomonotone variational inequality on Hadamard manifolds. We also employ our main result to solve a constrained convex minimization problem and present a numerical experiment to illustrate the asymptotic behavior of the algorithm. Our results develop and improve some recent results.

1. Introduction

Let $\mathcal{C}$ be a non-empty closed and convex subset of a real Hilbert space $\mathcal{H}$ with inner product $⟨·,·⟩$ and $\mathcal{A}$ be an operator from $\mathcal{C}$ to $\mathcal{H}$. The variational inequality problem (in short, VIP) is to find a point $\mathfrak{x}\in \mathcal{C}$ such that

$$⟨\mathcal{A}\left(\mathfrak{x}\right),\mathfrak{x}-\mathfrak{y}⟩\le 0,\forall \mathfrak{y}\in \mathcal{C}.$$

(1)

VIP is an important problem of nonlinear analysis fields since many problems appear in these fields, such as the optimization problem, equilibrium and complementarity problem, and so on [1,2,3,4,5,6,7,8,9,10,11]. These may be translated into variational inequality problems. So, some researchers have focused on how to obtain the approximate solutions of the VIP (1) in the spaces with linear constructure and symmetrical characteristic, and have also proposed various iterative methods; see, for example, ref. [12,13,14,15,16,17,18] and the reference therein.

In the last decade, many problems occurring in the field of nonlinear analysis have been extended from the spaces with linear structure and symmetry to the symmetric Hadamard manifolds without linear structure. The main advantages of these extensions are that non- convex problems and constrained problems in spaces with linear structure and symmetry may be transformed into convex problems and unconstrained problems on Hadamard manifolds without linear structure, respectively. So, many nonlinear problems on symmetric Hadamard manifolds have been attracted and studied by some authors, see for example [19,20,21,22,23,24,25,26,27,28,29] and the reference therein.

The following VIP on Hadamard manifolds was first considered by Németh [30] in 2003:

$$\mathrm{find}\mathfrak{x}\in \mathcal{C}\mathrm{s}.\mathrm{t}.⟨\mathcal{A}\left(\mathfrak{x}\right),{\exp }_{\mathfrak{x}}^{-1}\mathfrak{y}⟩\ge 0, \forall \mathfrak{y}\in \mathcal{C}.$$

(2)

The author studied the existence of the solution for VIP (2) and provided a necessary and sufficient condition for a solution of an optimization problem in terms of VIP (2) on Hadamard manifolds; here, $\mathcal{C}$ is a non-empty, closed, and geodesic convex subset of Hadamard manifold $\mathcal{M},\mathcal{A}$ is a vector field from $\mathcal{C}$ to $\mathcal{TM}$, i.e., $\mathcal{A}\left(\mathfrak{x}\right)\in {\mathcal{T}}_{\mathfrak{x}}\mathcal{M}$ for each $\mathfrak{x}\in \mathcal{C}$, and ${\exp }^{-1}$ is the inverse of exponential map. The solution set of the VIP (2) is denoted by $\Omega$.

VIP (2) is an extension of VIP (1). In fact, the vector field $\mathcal{A}$ reduces to the operator $\mathcal{A}$ from $\mathcal{C}$ into ${\mathcal{R}}^n$ and VIP (2) reduces to VIP (1) when $\mathcal{M}={\mathcal{R}}^n$.

In 2005, Ferreira et al. [31] proposed an extragradient-type algorithm to solve single-valued monotone variational inequality on Hadamard manifolds. In 2012, in order to weaken the monotone assumption, Tang et al. [32,33] introduced Korpelevich’s method and the projection-type method to solve a pseudomonotone VIP (2). Furthermore, for solving non-monotone VIP (2), Ye and He [34] proposed a double projection algorithm to solve a quasi-monotone variational inequality problem in ${\mathcal{R}}^n$. Recently, Ansaril and Babu [35] proposed an Armijos type extragradient algorithm method to solve VIP (2), which does not require the monotonicity of the objective vector field on Hadamard manifolds.

Motivated and inspired by the works of Shehu et al. [16], Thong et al. [18], Ansaril et al. [35], Chen et al. [36] and the research in this direction, we propose a viscosity type subgradient-like method to solve the pseudomonotone VIP (2) on Hadamard manifolds. Here, the vector field $\mathcal{A}$ is a Lipschitz continuous pseudomonotone operator, but the Lipschitz constant need not be known in advance. Under suitable conditions, we prove that the sequence generated by the proposed algorithm converges to a solution of pseudomonotone VIP (2) on Hadamard manifolds. We also give an application of our main result to a constrained convex minimization problem and a numerical experiment to illustrate the effectiveness and the asymptotical behavior of the algorithm proposed. It is worth noting that our results can be viewed as a generalization of the corresponding results in [16].

2. Preliminaries

Let $\mathcal{M}$ be a finite dimensional differentiable manifold and ${\mathcal{T}}_{\mathfrak{p}}\mathcal{M}$ be a tangent space of $\mathcal{M}$ at $\mathfrak{p}\in \mathcal{M}$, $\mathcal{TM}={\cup }_{\mathfrak{p}\in \mathcal{M}}{\mathcal{T}}_{\mathfrak{p}}\mathcal{M}$ be the tangent bundle of $\mathcal{M}$. An inner product ${\mathcal{R}}_p⟨·,·⟩$ on ${\mathcal{T}}_{\mathfrak{p}}\mathcal{M}$ is said to be a Riemannian metric on ${\mathcal{T}}_{\mathfrak{p}}\mathcal{M}$. The norm induced by the inner product $\mathcal{R}\mathfrak{p}⟨·,·⟩$ on ${\mathcal{T}}_{\mathfrak{p}}\mathcal{M}$ is denoted by $\parallel ·\parallel \mathfrak{p}$; the subscript $\mathfrak{p}$ is omitted. A differentiable manifold $\mathcal{M}$ with a Riemannian metric $\mathcal{R}⟨·,·⟩$ is called a Riemannian manifold. Let $\mathfrak{p},\mathfrak{q}\in \mathcal{M}$ and $\gamma :[0,1]\to \mathcal{M}$ be a piecewise smooth curve connecting $\mathfrak{p}$ with $\mathfrak{q}$ (i.e., $\gamma \left(0\right)=\mathfrak{p}$ and $\gamma \left(1\right)=\mathfrak{q}$ ). The length of the curve $\gamma$ is defined by $L\left(\gamma \right)={\int }_0^1∥{\gamma }^{\prime }\left(t\right)∥dt,$ the Riemannian distance $d(\mathfrak{p},\mathfrak{q})$ is the minimum length of all such curves connecting $\mathfrak{p}$ with $\mathfrak{q}$. A Riemannian manifold $\mathcal{M}$ equipped with Riemannian distance d is a metric space $(\mathcal{M},d)$.

A Riemannian manifold $\mathcal{M}$ is complete if for every $\mathfrak{p}\in M$, all geodesics starting from $\mathfrak{p}$ are defined for all $t\in \mathcal{R}$. It has been shown in [37] that there exists only one minimal geodesic for any two points in $\mathcal{M}$ and $(\mathcal{M},d)$ is complete metric space when $\mathcal{M}$ is complete. A complete simply connected Riemannian manifold of nonpositive sectional curvature is called a Hadamard manifold.

Suppose that $\mathcal{M}$ is a complete Riemannian manifold; then, the exponential map ${\exp }_{\mathfrak{p}}:{\mathcal{T}}_{\mathfrak{p}}\mathcal{M}\to \mathcal{M}$ at $\mathfrak{p}\in \mathcal{M}$ is defined by

$${\exp }_{\mathfrak{p}}v={\gamma }_v(1,\mathfrak{p}), \mathit{for} \mathit{any} v\in {\mathcal{T}}_{\mathfrak{p}}\mathcal{M},$$

where ${\gamma }_v(·,\mathfrak{p})$ is the unique geodesic starting from $\mathfrak{p}$ with velocity v. It is well known that the mapping ${\exp }_{\mathfrak{p}}$ is diffeomorphism on ${\mathcal{T}}_{\mathfrak{p}}\mathcal{M}$ for any $\mathfrak{p}\in \mathcal{M}$. The exponential mapping ${\exp }_{\mathfrak{p}}$ owns the inverse ${\exp }_{\mathfrak{p}}^{-1}:\mathcal{M}\to {\mathcal{T}}_{\mathfrak{p}}\mathcal{M}$. Furthermore, for any $\mathfrak{p},\mathfrak{q}\in \mathcal{M}$, the equalities $∥{\exp }_{\mathfrak{p}}^{-1}\mathfrak{q}∥=∥{\exp }_{\mathfrak{q}}^{-1}\mathfrak{p}∥=$$d(\mathfrak{p},\mathfrak{q})$ hold. See [37].

The parallel transport $P_{\gamma ,\gamma \left(\mathfrak{b}\right),\gamma \left(\mathfrak{a}\right)}:{\mathcal{T}}_{\gamma \left(\mathfrak{a}\right)}\mathcal{M}\to {\mathcal{T}}_{\gamma \left(\mathfrak{b}\right)}\mathcal{M}$ on the tangent bundle $\mathcal{T}\mathcal{M}$ along $\gamma$: $[\mathfrak{a},\mathfrak{b}]\to \mathcal{M}$ with respect to Riemannian connection ∇ is defined as:

$$P_{\gamma ,\gamma \left(\mathfrak{b}\right),\gamma \left(\mathfrak{a}\right)}\left(v\right)=\mathcal{A}\left(\gamma \left(\mathfrak{b}\right)\right), \forall \mathfrak{a},\mathfrak{b}\in \mathbb{R} \mathrm{and} v\in {\mathcal{T}}_{\gamma \left(\mathfrak{a}\right)}\mathcal{M},$$

where $\mathcal{A}$ is the unique vector field such that ${\nabla }_{{\gamma }^{\prime }\left(t\right)}\mathcal{A}=\mathbf{0}$ for all $t\in [\mathfrak{a},\mathfrak{b}]$ and $\mathcal{A}\left(\gamma \right(\mathfrak{a}\left)\right)=v$. When $\gamma$ is the minimal geodesic joining $\mathfrak{x}$ to $\mathfrak{y}$, we write ${\mathcal{P}}_{\mathfrak{y},\mathfrak{x}}$ instead of ${\mathcal{P}}_{\gamma ,\mathfrak{y},\mathfrak{x}}$. Moreover, ${\mathcal{P}}_{\mathfrak{y},\mathfrak{x}}{\exp }_{\mathfrak{x}}^{-1}\mathfrak{y}=-{\exp }_{\mathfrak{y}}^{-1}\mathfrak{x}$. For further details, refer to [38]. Note that $P_{\mathfrak{y},\mathfrak{x}}$ is an isometry from ${\mathcal{T}}_{\mathfrak{x}}\mathcal{M}$ to ${\mathcal{T}}_{\mathfrak{y}}\mathcal{M}$. That is, the parallel transport preserves the inner product

$${⟨P_{\mathfrak{y},\mathfrak{x}}\left(u\right),P_{\mathfrak{y},\mathfrak{x}}\left(v\right)⟩}_{\mathfrak{y}}={⟨u,v⟩}_{\mathfrak{x}}, \forall u,v\in {\mathcal{T}}_{\mathfrak{x}}\mathcal{M}.$$

Definition 1 

([33,39]). Let $\mathcal{X}\left(\mathcal{M}\right)$ be a set of all single-valued vector fields $\mathcal{A}$ from $\mathcal{M}$ into $\mathcal{T}\mathcal{M}$ satisfying $\mathcal{A}\left(\mathfrak{x}\right)\in {\mathcal{T}}_{\mathfrak{x}}\mathcal{M}$ for each $\mathfrak{x}\in \mathcal{M}$ and $\mathcal{D}\left(\mathcal{A}\right)$ be the domain of $\mathcal{A}$, which is defined by $\mathcal{D}\left(\mathcal{A}\right)=\{\mathfrak{x}\in \mathcal{M}:\mathcal{A}\left(\mathfrak{x}\right)\in {\mathcal{T}}_{\mathfrak{x}}\mathcal{M}\}$. A single-valued vector field $\mathcal{A}\in \mathcal{X}\left(\mathcal{M}\right)$ is said to be

(i)

Monotone if

$$⟨\mathcal{A}\left(\mathfrak{x}\right),ex{p}_{\mathfrak{x}}^{-1}\mathfrak{y}⟩\le ⟨\mathcal{A}\left(\mathfrak{y}\right),-ex{p}_{\mathfrak{y}}^{-1}\mathfrak{x}⟩, \forall \mathfrak{x},\mathfrak{y}\in \mathcal{M};$$

(ii)

Pseudomonotone if

$$⟨\mathcal{A}\left(\mathfrak{x}\right),{\exp }_{\mathfrak{x}}^{-1}\mathfrak{y}⟩\ge 0\Rightarrow ⟨\mathcal{A}\left(\mathfrak{y}\right),{\exp }_{\mathfrak{y}}^{-1}\mathfrak{x}⟩\le 0, \forall \mathfrak{x}, \mathfrak{y}\in \mathcal{M};$$

(iii)

Lipschitz continuous if there exists a constant $L>0$ such that

$$∥{\mathrm{P}}_{\mathfrak{v},\mathfrak{u}}\mathcal{A}\left(\mathfrak{x}\right)-\mathcal{A}\left(\mathfrak{v}\right)∥\le Ld(\mathfrak{u},\mathfrak{v}), \forall \mathfrak{u},\mathfrak{v}\in \mathcal{M}.$$

Lemma 1 

([40]). If $▵(\mathfrak{u},\mathfrak{v},\mathfrak{w})$ is a geodesic triangle in a Hadamard manifold $\mathcal{M}$, then there exist $\overline{\mathfrak{u}},\overline{\mathfrak{v}},\overline{\mathfrak{w}}\in {\mathcal{R}}^2$ such that

$$d(\mathfrak{u},\mathfrak{v})=\parallel \overline{\mathfrak{u}}-\overline{\mathfrak{v}}\parallel ,d(\mathfrak{v},\mathfrak{w})=\parallel \overline{\mathfrak{v}}-\overline{\mathfrak{w}}\parallel ,d(\mathfrak{w},\mathfrak{u})=\parallel \overline{\mathfrak{w}}-\overline{\mathfrak{u}}\parallel .$$

(3)

The triangle $\Delta (\overline{\mathfrak{u}},\overline{\mathfrak{v}},\overline{\mathfrak{w}})$ is called a comparison triangle of geodesic-triangle $▵(\mathfrak{u},\mathfrak{v},\mathfrak{w})$, which is unique up to the isometry of $\mathcal{M}$.

Lemma 2 

([41]). Let $▵(\mathfrak{u},\mathfrak{v},\mathfrak{w})$ be a geodesic triangle in a Hadamard manifold $\mathcal{M},▵(\overline{\mathfrak{u}},\overline{\mathfrak{v}},\overline{r})$ be a its comparison triangle.

(i)

Suppose that $\alpha ,\theta ,\beta$ (resp., $\overline{\alpha },\overline{\theta },\overline{\beta })$ are the angles of $\Delta (\mathfrak{u},\mathfrak{v},r)$ (resp., $\Delta (\overline{\mathfrak{u}},\overline{\mathfrak{v}},\overline{r})$ at the vertices $\mathfrak{u},\mathfrak{v},r$ (resp., $\overline{\mathfrak{u}},\overline{\mathfrak{v}},\overline{r})$; then, the following inequalities hold:

$$\alpha \le \overline{\alpha }, \theta \le \overline{\theta }, \beta \le \overline{\beta };$$

(ii)

Suppose that $\mathfrak{z}$ is a point on the geodesic connecting $\mathfrak{u}$ with $\mathfrak{v}$ and $\overline{\mathfrak{z}}$ is its comparison point in the interval $[\overline{\mathfrak{u}}, \overline{\mathfrak{v}}]$, if $d(\mathfrak{z},\mathfrak{u})=\parallel \overline{\mathfrak{z}}-\overline{\mathfrak{u}}\parallel$ and $d(\mathfrak{z},\mathfrak{v})=\parallel \overline{\mathfrak{z}}-\overline{\mathfrak{v}}\parallel$; then,

$$d(\mathfrak{z},\mathfrak{w})\le \parallel \overline{\mathfrak{z}}-\overline{\mathfrak{w}}\parallel .$$

Lemma 3 

([37]). Let $▵\left({\mathfrak{u}}_1,{\mathfrak{u}}_2,{\mathfrak{u}}_3\right)$ be a geodesic triangle in a Hadamard manifold. For each $i=1,2,3\left(\mathrm{mod}3\right)$, ${\gamma }_i:\left[0,{\mathfrak{l}}_{\mathfrak{i}}\right]\to \mathcal{M}$ denotes the geodesic joining ${\mathfrak{u}}_i$ to ${\mathfrak{u}}_{i+1}$, and set ${\mathfrak{l}}_{\mathfrak{i}}=L\left({\gamma }_i\right)$, and ${\theta }_i=\angle \left({\gamma }_i^{\prime }\left(0\right),-{\gamma }_{i-1}^{\prime }\left(l_{i-1}\right)\right)$. Then,

(i)

$\pi \le {\theta }_1+{\theta }_2+{\theta }_3$;

(ii)

$l_{i-1}^2\ge l_i^2+l_{i+1}^2-2l_i{l}_{i+1}\cos {\theta }_{i+1}$;

(iii)

$l_{i+2}\le l_{i+1}\cos {\theta }_{i+2}+l_i\cos {\theta }_i$.

As in [25], the above inequalities (i), (ii), (iii) can be rewritten in the form of the Riemann distance and the exponential map as follows:

$$d^2\left({\mathfrak{u}}_i,{\mathfrak{u}}_{i+1}\right)+d^2\left({\mathfrak{u}}_{i+1},{\mathfrak{u}}_{i+2}\right)-2⟨{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_i,{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_{i+2}⟩\le d^2\left({\mathfrak{u}}_{i-1},{\mathfrak{u}}_i\right),$$

(4)

and

$$d^2\left({\mathfrak{u}}_i,{\mathfrak{u}}_{i+1}\right)\le ⟨{\exp }_{{\mathfrak{u}}_i}^{-1}{\mathfrak{u}}_{i+2},{\exp }_{{\mathfrak{u}}_i}^{-1}{\mathfrak{u}}_{i+1}⟩+⟨{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_{i+2},{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_i⟩.$$

(5)

Since

$$⟨{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_i,{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_{i+2}⟩=d\left({\mathfrak{u}}_i,{\mathfrak{u}}_{i+1}\right)d\left({\mathfrak{u}}_{i+1},{\mathfrak{u}}_{i+2}\right)\cos {\theta }_{i+1},$$

(6)

in (5), let ${\mathfrak{u}}_i={\mathfrak{u}}_{i+2}$; we have

$${∥{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_i∥}^2=⟨{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_i,{\exp }_{{\mathfrak{u}}_{i+1}}^{-1}{\mathfrak{u}}_i⟩=d^2\left({\mathfrak{u}}_{i+1},{\mathfrak{u}}_i\right).$$

(7)

Lemma 4 

([42]). Let $\mathcal{M}$ be a finite dimensional Hadamard manifold.

(i)

If $\gamma :[0,1]\to \mathcal{M}$ is a geodesic joining $\mathfrak{x}$ to $\mathfrak{y}$, then,

$$d\left(\gamma \left(t_1\right),\gamma \left(t_2\right)\right)=\left|t_1-t_2\right|d(\mathfrak{x},\mathfrak{y}),\forall t_1,t_2\in [0,1];$$

(ii)

For any $\mathfrak{x},\mathfrak{y},\mathfrak{z},u,w\in \mathcal{M}$ and $t\in [0,1]$, the following inequalities hold:

$$\begin{array}{c}d\left({\exp }_{\mathfrak{x}}(1-t){\exp }_{\mathfrak{x}}^{-1}\mathfrak{y},\mathfrak{z}\right)\le td(\mathfrak{x},\mathfrak{z})+(1-t)d(\mathfrak{y},\mathfrak{z}),\\ d^2\left({\exp }_{\mathfrak{x}}(1-t){\exp }_{\mathfrak{x}}^{-1}\mathfrak{y},\mathfrak{z}\right)\le t{d}^2(\mathfrak{x},\mathfrak{z})+(1-t)d^2(\mathfrak{y},\mathfrak{z})-t(1-t)d^2(\mathfrak{x},\mathfrak{y}),\\ d\left({\exp }_{\mathfrak{x}}(1-t){\exp }_{\mathfrak{x}}^{-1}\mathfrak{y},{\exp }_u(1-t){\exp }_u^{-1}w\right)\le td(\mathfrak{x},u)+(1-t)d(\mathfrak{y},w).\end{array}$$

Lemma 5 

([41]). Suppose that ${\mathfrak{x}}_0,y_0\in \mathcal{M}$ and $\left\{{\mathfrak{x}}_n\right\},\left\{y_n\right\}\subset \mathcal{M}$ satisfying ${\mathfrak{x}}_n\to {\mathfrak{x}}_0$, $y_n\to y_0$; then, the following results hold.

(i)

${\exp }_{{\mathfrak{x}}_n}^{-1}\mathfrak{y}⟶{\exp }_{{\mathfrak{x}}_0}^{-1}\mathfrak{y}, {\exp }_{\mathfrak{y}}^{-1}{\mathfrak{x}}_n⟶{\exp }_{\mathfrak{y}}^{-1}{\mathfrak{x}}_0 and ex{p}_{{\mathfrak{x}}_n}^{-1}{\mathfrak{y}}_n⟶{\exp }_{{\mathfrak{x}}_0}^{-1}{\mathfrak{y}}_0$, for any $\mathfrak{y}\in \mathcal{M}$, respectively;

(ii)

If $\left\{v_n\right\}$ is a sequence in ${\mathcal{T}}_{{\mathfrak{x}}_n}\mathcal{M}$ and $v_n\to v_0$, then $v_0\in {\mathcal{T}}_{{\mathfrak{x}}_0}\mathcal{M}$;

(iii)

If the sequences $\left\{u_n\right\}$ and $\left\{v_n\right\}$ satisfy $u_n,v_n\in {\mathcal{T}}_{{\mathfrak{x}}_n}\mathcal{M}$, $u_n\to u_0\in {\mathcal{T}}_{{\mathfrak{x}}_0}\mathcal{M}$ and $v_n\to v_0\in {\mathcal{T}}_{{\mathfrak{x}}_0}\mathcal{M}$, then

$$⟨u_n,v_n⟩⟶⟨u_0,v_0⟩.$$

Let $\mathcal{M}$ be a Hadamard manifold. A subset $\mathcal{C}\subset \mathcal{M}$ is said to be geodesic convex if for any two points $\mathfrak{x}$ and $\mathfrak{y}$ in $\mathcal{C}$, the geodesic joining $\mathfrak{x}$ to $\mathfrak{y}$ is contained in $\mathcal{C}$, which means that $\gamma (\mathfrak{x},\mathfrak{y};(1-t)a+tb)\in C$ for all $t\in [0,1]$, where $\gamma (\mathfrak{x},\mathfrak{y};·):[a,b]\to \mathcal{M}$ is a geodesic satisfing $\gamma (\mathfrak{x},\mathfrak{y},a)=\mathfrak{x}$ and $\gamma (\mathfrak{x},\mathfrak{y},b)=\mathfrak{y}$.

Lemma 6 

([43]). Let $\mathcal{M}$ be a Riemannian manifold with constant curvature. For given $\mathfrak{x}\in \mathcal{M}$ and $u\in {\mathcal{T}}_{\mathfrak{x}}\mathrm{M}$, the set

$${\mathcal{C}}_{\mathfrak{x},u}:=\left\{\mathfrak{z}\in \mathcal{M}:⟨{\exp }_{\mathfrak{x}}^{-1}\mathfrak{z},u⟩\le 0\right\},$$

is geodesic convex.

A function $f:\mathcal{C}\to (-\infty ,\infty ]$ is said to be geodesic convex if, for any geodesic $\gamma (\mathfrak{x},\mathfrak{y},\lambda )(0\le \lambda \le 1)$ joining $\mathfrak{x},\mathfrak{y}\in \mathcal{C}$, the function $f\circ \gamma$ is convex, that is,

$$f\left(\gamma \right(\mathfrak{x},\mathfrak{y},\lambda \left)\right)\le \lambda f\left(\gamma \right(\mathfrak{x},\mathfrak{y},0\left)\right)+(1-\lambda )f\left(\gamma \right(\mathfrak{x},\mathfrak{y},1\left)\right)=\lambda f\left(\mathfrak{x}\right)+(1-\lambda )f\left(\mathfrak{y}\right).$$

Let $\mathcal{C}$ be a non-empty, closed, and geodesic convex subset of a Hadamard manifold $\mathcal{M}$. The metric projection onto $\mathcal{C}$, denoted by $P_{\mathcal{C}}$, is defined as

$$P_{\mathcal{C}}\left(\mathfrak{x}\right)=\{\mathfrak{p}\in \mathcal{C}:d(\mathfrak{x},\mathfrak{p})\le d(\mathfrak{x},\mathfrak{q}),\forall \mathfrak{q}\in \mathcal{C}\}, \forall \mathfrak{x}\in \mathcal{M}.$$

Lemma 7 

([39]). Let $\mathcal{C}$ be a non-empty, closed geodesic convex subset of a Hadamard manifold $\mathcal{M}$. Then, for any $\mathfrak{x}\in \mathcal{M},P_{\mathcal{C}}\left(\mathfrak{x}\right)$ is a singleton, and the following inequality holds:

$$⟨{\exp }_{P_{\mathcal{C}}\left(\mathfrak{x}\right)}^{-1}\mathfrak{x},{\exp }_{P_{\mathcal{C}}\left(\mathfrak{x}\right)}^{-1}\mathfrak{q}⟩\le 0,\forall \mathfrak{q}\in \mathcal{C}.$$

Lemma 8 

([32]). Let $\mathcal{C}$ be a non-empty, closed, and geodesic convex subset of a Hadamard manifold $\mathcal{M}$ and $\mathcal{A}:\mathcal{C}\to \mathcal{T}\mathcal{M}$ be a single-valued vector field. For each $\mathfrak{x}\in \mathcal{C}$, the following statements are equivalent:

(i)

$\mathfrak{x}$ is a solution of VIP (2);

(ii)

$\mathfrak{x}=P_{\mathcal{C}}\left({\exp }_{\mathfrak{x}}(-\lambda \mathcal{A}\left(\mathfrak{x}\right))\right)$ for all $\lambda >0$;

(iii)

$r(\mathfrak{x},\lambda )=0$, where $r(\mathfrak{x},\lambda )$ is defined by $r(\mathfrak{x},\lambda ):={\exp }_{\mathfrak{x}}^{-1}\left[P_{\mathcal{C}}\left({\exp }_{\mathfrak{x}}(-\lambda \mathcal{A}\left(\mathfrak{x}\right))\right)\right]$.

Lemma 9 

([44]). Let $\left\{a_n\right\}$ be a sequence of nonnegative real numbers such that there exists a subsequence $\left\{a_{n_j}\right\}$ of $\left\{a_n\right\}$ such that $a_{n_j}<a_{n_j+1}$ for all $j\in \mathbb{N}$. Then, there exists a nondecreasing sequence $\left\{m_k\right\}\subseteq \mathbb{N}$ such that ${\lim }_{k\to \infty }{m}_k=\infty$ and the following properties are satisfied by all (sufficiently large) number $k\in \mathbb{N}$: $a_{m_k}\le a_{m_k+1}$ and $a_k\le a_{m_k+1}$. In fact, $m_k$ is the largest number n in the set $\{1,2,\dots ,k\}$ such that $a_n<a_{n+1}$.

Lemma 10 

([45]). Let $\left\{a_n\right\}$ be a sequence of nonnegative real numbers satisfying the following inequality:

$$a_{n+1}\le \left(1-{\theta }_n\right)a_n+{\theta }_n{\sigma }_n+{\gamma }_n,n\ge 1.$$

If (i) $\left\{{\theta }_n\right\}\subset [0,1], {\sum }_{n=1}^{\infty }{\theta }_n=\infty$; (ii) $\lim {\sup }_{n\to \infty }{\sigma }_n\le 0$; (iii) ${\gamma }_n\ge 0, n\ge 0, {\sum }_{n=1}^{\infty }{\gamma }_n<\infty$, then $a_n\to 0$ as $n\to \infty$.

3. Main Results

In this section, we need to make the following assumptions before we propose our algorithm:

(C1) $\mathcal{C}$ is a non-empty closed geodesic convex subset of a finite dimensional Hadamard manifold $\mathcal{M}$;

(C2) Mapping $\mathcal{A}:\mathcal{C}\to \mathcal{T}\mathcal{M}$ is a single valued vector field, that is, $\mathcal{A}\left(\mathfrak{x}\right)\in {\mathcal{T}}_{\mathfrak{x}}\mathcal{M}$ for each $\mathfrak{x}\in \mathcal{C}$;

(C3) Vector field $\mathcal{A}$ is pseudomonotone and L-Lipschitz continuous on $\mathcal{M}$;

(C4) The solution set $\Omega$ of the VIP (2) is non-empty;

(C5) Mapping $f:\mathcal{M}\to \mathcal{M}$ is a contraction mapping with constant $\rho \in [0,1)$.

Remark 1. 

It is worth noting that conditions (C1)–(C5) are popular assumptions both in Hadamard manifold and in Hilbert space. These conditions are applicable to problems from practical scenarios such as the linear equations due to image restorations and the Kojima–Shindo nonlinear complementary problem. For further real-world applications, refer to the complementary problems discussed in [46,47,48].

Lemma 11. 

The Armijo-like search rule (9) is well defined and

$$\min \left\{\gamma ,\frac{\mu \xi }{L}\right\}\le {\lambda }_n\le \gamma , n\ge 2$$

(8)

Proof. 

Since $\mathcal{A}$ is L-Lipschitz continuous on $\mathcal{M}$, we obtain

$$∥P_{{\mathfrak{y}}_n,{\mathfrak{x}}_n}\mathcal{A}\left({\mathfrak{x}}_n\right)-\mathcal{A}\left({\mathfrak{y}}_n\right)∥\le Ld\left({\mathfrak{x}}_n,{\mathfrak{y}}_n\right).$$

(9)

Due to $L>0$ and $\mu \in (0,1)$, we have $\frac{\mu }{L}∥P_{{\mathfrak{y}}_n,{\mathfrak{x}}_n}\mathcal{A}\left({\mathfrak{x}}_n\right)-\mathcal{A}\left({\mathfrak{y}}_n\right)∥\le \mu d\left({\mathfrak{x}}_n,{\mathfrak{y}}_n\right).$ Therefore, (9) holds for all $\lambda \le \mu /L$, so ${\lambda }_n$ is well defined.

If ${\lambda }_n=\gamma$, then this Lemma is proved; otherwise, if ${\lambda }_n<\gamma$, we know by the search rule (9) that ${\lambda }_n/\xi$ does not satisfy the inequality (9), that is

$$\begin{array}{cc}& ∥P_{{\mathfrak{y}}_n^{\prime },{\mathfrak{x}}_n}\mathcal{A}\left({\mathfrak{x}}_n\right)-\mathcal{A}\left({\mathfrak{y}}_n^{\prime }\right)∥=∥P_{{\mathfrak{y}}_n^{\prime },{\mathfrak{x}}_n}\mathcal{A}\left({\mathfrak{x}}_n\right)-\mathcal{A}\left(P_{\mathcal{C}}\left({\exp }_{{\mathfrak{x}}_n}\left(-\frac{{\lambda }_n}{\xi }\mathcal{A}\left({\mathfrak{x}}_n\right)\right)\right)\right)∥\hfill \\ & >\frac{\mu }{{\lambda }_n/\xi }d\left({\mathfrak{x}}_n,P_{\mathcal{C}}\left({\exp }_{{\mathfrak{x}}_n}\left(-\frac{{\lambda }_n}{\xi }\mathcal{A}\left({\mathfrak{x}}_n\right)\right)\right)\right)=\frac{\mu }{{\lambda }_n/\xi }d\left({\mathfrak{x}}_n,{\mathfrak{y}}_n\right).\hfill \end{array}$$

Consider that $\mathcal{A}$ is L-Lipschitz continuous on $\mathcal{M}$, we have ${\lambda }_n>\mu \xi /L$. The proof is completed.    □

Theorem 1. 

Assume that the assumptions $\left(\mathcal{C}1\right)-\left(\mathcal{C}5\right)$ hold. If $\left\{{\alpha }_n\right\}$ satisfies $li{m}_{n\to \infty }{\alpha }_n=0$ and ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$, then the sequence $\left\{{\mathfrak{x}}_n\right\}$ generated by Algorithm 1 converges to a solution of pseudomonotone VIP (2).

Algorithm 1: Viscosity type subgradient extragradient algorithm on Hadamard manifolds

Initialization: Give $0<\gamma <1, \xi \in (0,1), \mu \in (0,1)$; ${\lambda }_1>0$, $\left\{{\alpha }_n\right\}$ is a real sequence in $(0,1)$ and ${\mathfrak{x}}_1\in \mathcal{M}$ is arbitrarily chosen.       Iterative Steps: Calculate ${\mathfrak{x}}_{n+1}$ as follows:       Step 1. Compute $${\mathfrak{y}}_n=P_{\mathcal{C}}\left[ex{p}_{{\mathfrak{x}}_n}(-{\lambda }_n\mathcal{A}{\mathfrak{x}}_n)\right],$$ (10)       If ${\mathfrak{x}}_n={\mathfrak{y}}_n$, then stop and ${\mathfrak{y}}_n$ is a solution of pseudomontone VIP (2). Otherwise, go to $\mathbf{Step} \mathbf{2}.$       Step 2. Compute ${\lambda }_n$, which is chosen to be the largest $\lambda \in \{\gamma ,\gamma \xi ,\gamma {\xi }^2,\cdots \}$ satisfying $$\lambda ∥P_{{\mathfrak{y}}_n,{\mathfrak{x}}_n}\mathcal{A}{\mathfrak{x}}_n-\mathcal{A}{\mathfrak{y}}_n∥\le \mu d({\mathfrak{x}}_n,{\mathfrak{y}}_n).$$ (11)       Step 3. Compute $${\mathfrak{z}}_n=P_{{\mathcal{T}}_n}\left(ex{p}_{{\mathfrak{x}}_n}(-{\lambda }_n{P}_{{\mathfrak{x}}_n,{\mathfrak{y}}_n}\mathcal{A}{\mathfrak{y}}_n)\right),$$ where $${\mathcal{T}}_n:=\left\{\mathfrak{x}\in \mathcal{C}\mid ⟨ex{p}_{{\mathfrak{y}}_n}^{-1}ex{p}_{{\mathfrak{x}}_n}(-{\lambda }_n\mathcal{A}{\mathfrak{x}}_n),ex{p}_{{\mathfrak{y}}_n}^{-1}\mathfrak{x}⟩\le 0\right\}.$$       Step 4. Compute $${\mathfrak{x}}_{n+1}=ex{p}_{{\mathfrak{z}}_n}{\alpha }_{n}ex{p}_{{\mathfrak{z}}_n}^{-1}f\left({\mathfrak{x}}_n\right),\forall n\ge 1.$$ (12) Set $n:=n+1$ and go to Step 1.

Proof. 

Step 1. Now, we show that the sequences $\left\{{\mathfrak{x}}_n\right\}$, $\left\{f\left({\mathfrak{x}}_n\right)\right\}$, $\left\{{\mathfrak{y}}_n\right\}$ and $\left\{{\mathfrak{z}}_n\right\}$ are bounded.

It follows from Lemma 5, Lemma 6, and the definition of ${\mathcal{T}}_n$ that ${\mathcal{T}}_n$ is closed and geodesic convex and ${\mathcal{T}}_n\subset \mathcal{C}$. Furthermore, by the pseudomonotonicity of $\mathcal{A}$, we have $\mathsf{\Omega }\subset {\mathcal{T}}_n\subset \mathcal{C}$.

Let $\mathfrak{p}\in \mathsf{\Omega }\subset {\mathcal{T}}_n\subset \mathcal{C}$, $u_n=ex{p}_{{\mathfrak{x}}_n}(-{\lambda }_n\mathcal{A}{\mathfrak{y}}_n),$ $\Delta \left({\mathfrak{x}}_n,{\mathfrak{y}}_n,\mathfrak{p}\right)$ be a geodesic triangle, and $\Delta \left({\mathfrak{x}}_n^{\prime },{\mathfrak{y}}_n^{\prime },{\mathfrak{p}}^{\prime }\right)$ be its comparison triangle. By Lemma 1, we obtain

$$d\left({\mathfrak{x}}_n,\mathfrak{p}\right)=∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥, d\left({\mathfrak{y}}_n,\mathfrak{p}\right)=∥{\mathfrak{y}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥, d\left({\mathfrak{x}}_n,{\mathfrak{y}}_n\right)=∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{y}}_n^{\prime }∥.$$

By (ii) of Lemma 2 and Lemma 7, we obtain

$$\begin{array}{cc}{d}^2({\mathfrak{z}}_n,\mathfrak{p})\hfill & =d^2(P_{{\mathcal{T}}_n}{u}_n,\mathfrak{p})={∥P_{{\mathcal{T}}_n}{u}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2\hfill \\ & =⟨P_{{\mathcal{T}}_n}{u}_n^{\prime }-u_n^{\prime }+u_n^{\prime }-{\mathfrak{p}}^{\prime },P_{{\mathcal{T}}_n}{u}_n^{\prime }-u_n^{\prime }+u_n^{\prime }-{\mathfrak{p}}^{\prime }⟩\hfill \\ & ={∥u_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+{∥u_n^{\prime }-P_{{\mathcal{T}}_n}{u}_n^{\prime }∥}^2+2⟨P_{{\mathcal{T}}_n}{u}_n^{\prime }-u_n^{\prime },u_n^{\prime }-{\mathfrak{p}}^{\prime }⟩,\hfill \end{array}$$

(13)

where

$$2{∥u_n^{\prime }-P_{{\mathcal{T}}_n}{u}_n^{\prime }∥}^2+2⟨P_{{\mathcal{T}}_n}{u}_n^{\prime }-u_n^{\prime },u_n^{\prime }-{\mathfrak{p}}^{\prime }⟩=2⟨u_n^{\prime }-P_{{\mathcal{T}}_n}{u}_n^{\prime },{\mathfrak{p}}^{\prime }-P_{{\mathcal{T}}_n}{u}_n^{\prime }⟩\le 0.$$

(14)

This implies that

$${∥u_n^{\prime }-P_{{\mathcal{T}}_n}{u}_n^{\prime }∥}^2+2⟨P_{{\mathcal{T}}_n}{u}_n^{\prime }-u_n^{\prime },u_n^{\prime }-{\mathfrak{p}}^{\prime }⟩⩽-{∥u_n^{\prime }-P_{{\mathcal{T}}_n}{u}_n^{\prime }∥}^2.$$

(15)

Substituting (15) into (13), from (6), we have

$$\begin{array}{cc}\hfill d^2({\mathfrak{z}}_n,\mathfrak{p})& ⩽{∥u_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2-{∥u_n^{\prime }-P_{{\mathcal{T}}_n}{u}_n^{\prime }∥}^2\hfill \\ \hfill & ={∥{\mathfrak{x}}_n^{\prime }-{\lambda }_n\mathcal{A}{\mathfrak{y}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2-{∥{\mathfrak{x}}_n^{\prime }-{\lambda }_n\mathcal{A}{\mathfrak{y}}_n^{\prime }-{\mathfrak{z}}_n^{\prime }∥}^2\hfill \\ \hfill & ={∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+{∥{\lambda }_n\mathcal{A}{\mathfrak{y}}_n^{\prime }∥}^2-2⟨{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime },{\lambda }_n\mathcal{A}{\mathfrak{y}}_n^{\prime }⟩-{∥{\lambda }_n\mathcal{A}{\mathfrak{y}}_n^{\prime }∥}^2-{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{z}}_n^{\prime }∥}^2\hfill \\ \hfill & -2⟨{\mathfrak{x}}_n^{\prime }-{\mathfrak{z}}_n^{\prime },{\lambda }_n\mathcal{A}{\mathfrak{y}}_n^{\prime }⟩\hfill \\ \hfill & ={∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2-{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{z}}_n^{\prime }∥}^2+2{\lambda }_n⟨{\mathfrak{p}}^{\prime }-{\mathfrak{z}}_n^{\prime },\mathcal{A}{\mathfrak{y}}_n^{\prime }⟩\hfill \\ \hfill & ={∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2-{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{y}}_n^{\prime }+{\mathfrak{y}}_n^{\prime }-{\mathfrak{z}}_n^{\prime }∥}^2+2{\lambda }_n⟨{\mathfrak{p}}^{\prime }-{\mathfrak{z}}_n^{\prime },\mathcal{A}{\mathfrak{y}}_n^{\prime }⟩\hfill \\ \hfill & ={∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2-{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{y}}_n^{\prime }∥}^2-{∥{\mathfrak{y}}_n^{\prime }-{\mathfrak{z}}_n^{\prime }∥}^2-2⟨{\mathfrak{x}}_n^{\prime }-{\mathfrak{y}}_n^{\prime },{\mathfrak{y}}_n^{\prime }-{\mathfrak{z}}_n^{\prime }⟩\hfill \\ \hfill & +2{\lambda }_n⟨{\mathfrak{p}}^{\prime }-{\mathfrak{z}}_n^{\prime },\mathcal{A}{\mathfrak{y}}_n^{\prime }⟩\hfill \\ \hfill & ={∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2-{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{y}}_n^{\prime }∥}^2-{∥{\mathfrak{y}}_n^{\prime }-{\mathfrak{z}}_n^{\prime }∥}^2+2⟨{\mathfrak{x}}_n^{\prime }-{\mathfrak{y}}_n^{\prime },{\mathfrak{z}}_n^{\prime }-{\mathfrak{y}}_n^{\prime }⟩\hfill \\ \hfill & +2{\lambda }_n⟨{\mathfrak{p}}^{\prime }-{\mathfrak{z}}_n^{\prime },\mathcal{A}{\mathfrak{y}}_n^{\prime }⟩\hfill \\ \hfill & \le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)-d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n)+2d({\mathfrak{x}}_n,{\mathfrak{y}}_n)d({\mathfrak{z}}_n,{\mathfrak{y}}_n)cos\theta \hfill \\ \hfill & +2{\lambda }_n⟨\mathcal{A}{\mathfrak{y}}_n,ex{p}_{{\mathfrak{z}}_n}^{-1}\mathfrak{p}⟩\hfill \\ \hfill & \le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)-d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n)+2⟨ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{x}}_n,ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{z}}_n⟩\hfill \\ \hfill & +2{\lambda }_n⟨\mathcal{A}{\mathfrak{y}}_n,ex{p}_{{\mathfrak{z}}_n}^{-1}\mathfrak{p}⟩.\hfill \end{array}$$

(16)

Since $\mathfrak{p}\in \mathsf{\Omega }$ and ${\mathfrak{y}}_n\in \mathcal{C}$, we have $⟨ex{p}_p^{-1}{\mathfrak{y}}_n,\mathcal{A}\mathfrak{p}⟩\ge 0$. By the pseudomonotonicity of vector field $\mathcal{A}$, from Definition 1, we obtain that $⟨\mathcal{A}{\mathfrak{y}}_n,ex{p}_{{\mathfrak{y}}_n}^{-1}\mathfrak{p}⟩\le 0$. So,

$$\begin{array}{cc}\hfill ⟨\mathcal{A}{\mathfrak{y}}_n,ex{p}_{{\mathfrak{z}}_n}^{-1}\mathfrak{p}⟩& =⟨\mathcal{A}{\mathfrak{y}}_n,ex{p}_{{\mathfrak{y}}_n}^{-1}\mathfrak{p}⟩+⟨\mathcal{A}{\mathfrak{y}}_n,ex{p}_{{\mathfrak{z}}_n}^{-1}{\mathfrak{y}}_n⟩\hfill \\ \hfill & \le ⟨\mathcal{A}{\mathfrak{y}}_n,ex{p}_{{\mathfrak{z}}_n}^{-1}{\mathfrak{y}}_n⟩.\hfill \end{array}$$

(17)

From (16) and (17), we obtain

$$\begin{array}{cc}\hfill d^2({\mathfrak{z}}_n,\mathfrak{p}) & \le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)-d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n)+2⟨ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{x}}_n,ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{z}}_n⟩+2{\lambda }_n⟨\mathcal{A}{\mathfrak{y}}_n,ex{p}_{{\mathfrak{z}}_n}^{-1}{\mathfrak{y}}_n⟩\hfill \\ \hfill & =d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)-d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n)+2⟨ex{p}_{{\mathfrak{y}}_n}^{-1}ex{p}_{{\mathfrak{x}}_n}(-{\lambda }_n\mathcal{A}{\mathfrak{y}}_n),ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{z}}_n⟩.\hfill \end{array}$$

(18)

By the definition of ${\mathcal{T}}_n$, we know

$$\begin{array}{cc}\hfill ⟨ex{p}_{{\mathfrak{y}}_n}^{-1}ex{p}_{{\mathfrak{x}}_n}(-{\lambda }_n\mathcal{A}{\mathfrak{y}}_n),ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{z}}_n⟩& \le ⟨ex{p}_{{\mathfrak{y}}_n}^{-1}ex{p}_{{\mathfrak{x}}_n}(-{\lambda }_n\mathcal{A}{\mathfrak{x}}_n),ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{z}}_n⟩\hfill \\ & +⟨ex{p}_{{\lambda }_n\mathcal{A}{\mathfrak{y}}_n}^{-1}\left({\lambda }_n\mathcal{A}{\mathfrak{x}}_n\right),ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{z}}_n⟩\hfill \\ \hfill & \le ⟨ex{p}_{{\lambda }_n\mathcal{A}{\mathfrak{y}}_n}^{-1}\left({\lambda }_n\mathcal{A}{\mathfrak{x}}_n\right),ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{z}}_n⟩.\hfill \end{array}$$

(19)

It follows from Lemma 11, (6), (18), and (19) that

$$\begin{array}{cc}\hfill d^2({\mathfrak{z}}_n,\mathfrak{p}) & \le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)-d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n)+2⟨ex{p}_{{\lambda }_n\mathcal{A}{\mathfrak{y}}_n}^{-1}\left({\lambda }_n\mathcal{A}{\mathfrak{x}}_n\right),ex{p}_{{\mathfrak{y}}_n}^{-1}{\mathfrak{z}}_n⟩\hfill \\ \hfill & \le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)-d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n)+2d({\lambda }_n\mathcal{A}{\mathfrak{x}}_n,{\lambda }_n\mathcal{A}{\mathfrak{y}}_n)d({\mathfrak{y}}_n,{\mathfrak{z}}_n)\hfill \\ \hfill & \le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)-d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n)+{\lambda }_n^2(d^2(\mathcal{A}{\mathfrak{x}}_n,\mathcal{A}{\mathfrak{y}}_n)+d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n))\hfill \\ \hfill & \le d^2({\mathfrak{x}}_n,\mathfrak{p})-(1-{\gamma }^2)d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)-(1-{\gamma }^2)d^2({\mathfrak{z}}_n,{\mathfrak{y}}_n).\hfill \end{array}$$

(20)

This implies that

$$d({\mathfrak{z}}_n,\mathfrak{p})\le d({\mathfrak{x}}_n,\mathfrak{p}).$$

(21)

So,

$$\begin{array}{cc}\hfill d({\mathfrak{x}}_{n+1},\mathfrak{p})& =d(ex{p}_{{\mathfrak{z}}_n}{\alpha }_{n}ex{p}_{{\mathfrak{z}}_n}^{-1}f\left({\mathfrak{x}}_n\right),\mathfrak{p})\hfill \\ \hfill & \le {\alpha }_{n}d(f\left({\mathfrak{x}}_n\right),\mathfrak{p})+\left(1-{\alpha }_n\right)d({\mathfrak{z}}_n-\mathfrak{p})\hfill \\ \hfill & \le {\alpha }_{n}d(f\left({\mathfrak{x}}_n\right),f\left(\mathfrak{p}\right))+{\alpha }_{n}d(f\left(\mathfrak{p}\right),\mathfrak{p})+\left(1-{\alpha }_n\right)d({\mathfrak{z}}_n,\mathfrak{p})\hfill \\ \hfill & \le {\alpha }_n\rho d({\mathfrak{x}}_n,\mathfrak{p})+\left(1-{\alpha }_n\right)d({\mathfrak{x}}_n,\mathfrak{p})+{\alpha }_{n}df\left(\mathfrak{p}\right),\mathfrak{p})\hfill \\ \hfill & =\left(1-{\alpha }_n(1-\rho )\right)d({\mathfrak{x}}_n,\mathfrak{p})+{\alpha }_{n}d(f\left(\mathfrak{p}\right),\mathfrak{p})\hfill \\ \hfill & =\left(1-{\alpha }_n(1-\rho )\right)d({\mathfrak{x}}_n,\mathfrak{p})+{\alpha }_n(1-\rho )\frac{d(f\left(\mathfrak{p}\right),\mathfrak{p})}{1-\rho }\hfill \\ \hfill & \le \max \left\{d({\mathfrak{x}}_n,\mathfrak{p}),\frac{(f\left(\mathfrak{p}\right),\mathfrak{p})}{1-\rho }\right\}\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le \max \left\{d({\mathfrak{x}}_1,\mathfrak{p}),\frac{d(f\left(\mathfrak{p}\right),\mathfrak{p})}{1-\rho }\right\},\hfill \end{array}$$

(22)

which means that $\left\{{\mathfrak{x}}_n\right\}$ is bounded. So, $\left\{{\mathfrak{y}}_n\right\}$, $\left\{{\mathfrak{z}}_n\right\}$$\left\{f\left({\mathfrak{x}}_n\right)\right\}$ are also bounded.

Step 2. Next, we prove that for any $\mathfrak{p}\in \Omega$, the following inequality holds.

$$\left(1-{\alpha }_n\right)(1-{\gamma }^2)d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)\le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_{n+1},\mathfrak{p})+{\alpha }_n{d}^{2}f(\left({\mathfrak{x}}_n\right),\mathfrak{p}).$$

It follows from Lemma 4 and (20) that

$$\begin{array}{cc}\hfill d^2({\mathfrak{x}}_{n+1},\mathfrak{p})=& d^2(ex{p}_{{\mathfrak{z}}_n}{\alpha }_{n}ex{p}_{{\mathfrak{z}}_n}^{-1}f\left({\mathfrak{x}}_n\right),\mathfrak{p})\hfill \\ \hfill \le & {\alpha }_n{d}^2(f\left({\mathfrak{x}}_n\right),\mathfrak{p})+\left(1-{\alpha }_n\right)d^2({\mathfrak{z}}_n,\mathfrak{p})-{\alpha }_n\left(1-{\alpha }_n\right)d^2(f\left({\mathfrak{x}}_n\right),{\mathfrak{z}}_n)\hfill \\ \hfill \le & {\alpha }_n{d}^2(f\left({\mathfrak{x}}_n\right),\mathfrak{p})+\left(1-{\alpha }_n\right)[d^2({\mathfrak{x}}_n,\mathfrak{p})-(1-{\gamma }^2)d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)\hfill \\ & -(1-{\gamma }^2)d^2({\mathfrak{z}}_n,{\mathfrak{y}}_n)]-{\alpha }_n\left(1-{\alpha }_n\right)d^2(f\left({\mathfrak{x}}_n\right),{\mathfrak{z}}_n)\hfill \\ \hfill \le & \left(1-{\alpha }_n\right)d^2({\mathfrak{x}}_n,\mathfrak{p})+{\alpha }_n{d}^{2}f(\left({\mathfrak{x}}_n\right),\mathfrak{p})-\left(1-{\alpha }_n\right)(1-{\gamma }^2)d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)\hfill \\ & -\left(1-{\alpha }_n\right)(1-{\gamma }^2)d^2({\mathfrak{y}}_n,{\mathfrak{z}}_n).\hfill \end{array}$$

(23)

This implies that

$$\left(1-{\alpha }_n\right)(1-{\gamma }^2)d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n)\le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{x}}_{n+1},\mathfrak{p})+{\alpha }_n{d}^{2}f(\left({\mathfrak{x}}_n\right),\mathfrak{p}).$$

(24)

Step 3. Finally, we show that $\left\{{\mathfrak{x}}_n\right\}$ converges to some point $\mathfrak{q}\in \Omega$, where $\mathfrak{q}=P_{\Omega }f\left(\mathfrak{q}\right)$.

Let $\mathfrak{p}\in \Omega$, $\Delta \left({\mathfrak{x}}_n,{\mathfrak{y}}_n,\mathfrak{p}\right)$ be a geodesic triangle and $\Delta \left({\mathfrak{x}}_n^{\prime },{\mathfrak{y}}_n^{\prime },{\mathfrak{p}}^{\prime }\right)$ be its comparison triangle. From (10), we know that the comparison point of ${\mathfrak{x}}_{n+1}$ is ${\mathfrak{x}}_{n+1}^{\prime }=(1-{\alpha }_n){\mathfrak{z}}_n^{\prime }+{\alpha }_{n}f\left({\mathfrak{x}}_n^{\prime }\right)$. It follows from Lemma 1 that

$$\begin{array}{cc}\hfill d^2({\mathfrak{x}}_{n+1},\mathfrak{p})& ={∥{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }∥}^2={∥\left(1-{\alpha }_n\right)\left({\mathfrak{z}}_n^{\prime }-{\mathfrak{p}}^{\prime }\right)+{\alpha }_n\left(f\left({\mathfrak{x}}_n^{\prime }\right)-{\mathfrak{p}}^{\prime }\right)∥}^2\hfill \\ \hfill \le & {\left(1-{\alpha }_n\right)}^2{∥{\mathfrak{z}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+2{\alpha }_n⟨f\left({\mathfrak{x}}_n^{\prime }\right)-{\mathfrak{p}}^{\prime },{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }⟩\hfill \\ \hfill \le & {\left(1-{\alpha }_n\right)}^2{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+2{\alpha }_n⟨f\left({\mathfrak{x}}_n^{\prime }\right)-{\mathfrak{p}}^{\prime },{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }⟩\hfill \\ \hfill =& {\left(1-{\alpha }_n\right)}^2{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+2{\alpha }_n⟨f\left({\mathfrak{x}}_n^{\prime }\right)-f\left({\mathfrak{p}}^{\prime }\right),{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }⟩\hfill \\ \hfill & +2{\alpha }_n⟨f\left({\mathfrak{p}}^{\prime }\right)-{\mathfrak{p}}^{\prime },{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }⟩\hfill \\ \hfill \le & {\left(1-{\alpha }_n\right)}^2{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+2{\alpha }_n\rho ∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥∥{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }∥\hfill \\ \hfill & +2{\alpha }_n⟨f\left({\mathfrak{p}}^{\prime }\right)-{\mathfrak{p}}^{\prime },{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }⟩\hfill \\ \hfill \le & {\left(1-{\alpha }_n\right)}^2{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+{\alpha }_n\rho \left({∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+{∥{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }∥}^2\right)\hfill \\ \hfill & +2{\alpha }_n⟨f\left({\mathfrak{p}}^{\prime }\right)-{\mathfrak{p}}^{\prime },{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }⟩\hfill \\ \hfill =& \left(1-2{\alpha }_n+{\alpha }_n\rho \right){∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+{\alpha }_n^2{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+{\alpha }_n\rho {∥{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }∥}^2\hfill \\ \hfill & +2{\alpha }_n⟨f\left({\mathfrak{p}}^{\prime }\right)-{\mathfrak{p}}^{\prime },{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }⟩\hfill \\ \hfill \le & \left(1-\frac{2(1-\rho ){\alpha }_n}{1-{\alpha }_n\rho }\right){∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+\frac{2(1-\rho ){\alpha }_n}{1-{\alpha }_n\rho }\hfill \\ \hfill & \times \left[\frac{{\alpha }_n}{2(1-\rho )}{∥{\mathfrak{x}}_n^{\prime }-{\mathfrak{p}}^{\prime }∥}^2+\frac{1}{1-\rho }⟨f\left({\mathfrak{p}}^{\prime }\right)-{\mathfrak{p}}^{\prime },{\mathfrak{x}}_{n+1}^{\prime }-{\mathfrak{p}}^{\prime }⟩\right],\hfill \end{array}$$

(25)

which implies that

$$\begin{array}{cc}\hfill d^2({\mathfrak{x}}_{n+1},\mathfrak{p})\le & \left(1-\frac{2(1-\rho ){\alpha }_n}{1-{\alpha }_n\rho }\right)d^2({\mathfrak{x}}_n,\mathfrak{p})+\frac{2(1-\rho ){\alpha }_n}{1-{\alpha }_n\rho }\hfill \\ \hfill & \times \left[\frac{{\alpha }_n}{2(1-\rho )}{d}^2({\mathfrak{x}}_n,\mathfrak{p})+\frac{1}{1-\rho }⟨ex{p}_{\mathfrak{p}}^{-1}f\left(\mathfrak{p}\right),ex{p}_{\mathfrak{p}}^{-1}{\mathfrak{x}}_{n+1}⟩\right].\hfill \end{array}$$

(26)

The rest of the proof will be divided into two cases.

Case 1. Suppose that there exists $n_0\in N$ such that ${\left\{d({\mathfrak{x}}_n,\mathfrak{q})\right\}}_{n=n_0}^{\infty }$ is nonincreasing. Then, ${\left\{d({\mathfrak{x}}_n,\mathfrak{q})\right\}}_{n=1}^{\infty }$ is convergent. It follows from (24) that

$$\underset{n\to \infty }{\lim }d({\mathfrak{x}}_n,{\mathfrak{y}}_n)=0.$$

(27)

Similarly, from (20), (21), and (27), we have

$$(1-{\gamma }^2)d({\mathfrak{y}}_n,{\mathfrak{z}}_n)\le d^2({\mathfrak{x}}_n,\mathfrak{p})-d^2({\mathfrak{z}}_n,\mathfrak{p})-(1-{\gamma }^2)d^2({\mathfrak{x}}_n,{\mathfrak{y}}_n).$$

(28)

Hence,

$$\underset{n\to \infty }{\lim }d({\mathfrak{y}}_n,{\mathfrak{z}}_n)=0.$$

(29)

From Lemma 4 and (10), we have

$$d({\mathfrak{x}}_{n+1},{\mathfrak{z}}_n)\le {\alpha }_{n}d(f\left({\mathfrak{x}}_n\right),{\mathfrak{z}}_n)\to 0,n\to \infty .$$

(30)

So,

$$d({\mathfrak{x}}_{n+1},{\mathfrak{x}}_n)\le d({\mathfrak{x}}_{n+1},{\mathfrak{z}}_n)+d({\mathfrak{z}}_n,{\mathfrak{y}}_n)+d({\mathfrak{y}}_n,{\mathfrak{x}}_n).$$

(31)

It follows from (27), (29), (30), and (31) that

$$\underset{n\to \infty }{\lim }d({\mathfrak{x}}_{n+1},{\mathfrak{x}}_n)=0.$$

(32)

Since $\left\{{\mathfrak{x}}_n\right\}$ is bounded, there exists a subsequence $\left\{{\mathfrak{x}}_{n_j}\right\}$ of $\left\{{\mathfrak{x}}_n\right\}$ such that $\left\{{\mathfrak{x}}_{n_j}\right\}$ converges to some ${\mathfrak{x}}^{*}\in \mathcal{M}$. From Lemma 5, we have

$$\underset{n\to \infty }{\lim \sup }⟨ex{p}_{\mathfrak{p}}^{-1}f\left(\mathfrak{p}\right),ex{p}_{\mathfrak{p}}^{-1}{\mathfrak{x}}_n⟩=\underset{j\to \infty }{\lim }⟨ex{p}_{\mathfrak{p}}^{-1}f\left(\mathfrak{p}\right),ex{p}_{\mathfrak{p}}^{-1}{\mathfrak{x}}_{n_j}⟩=⟨ex{p}_{\mathfrak{p}}^{-1}f\left(\mathfrak{p}\right),ex{p}_{\mathfrak{p}}^{-1}{\mathfrak{x}}^{*}⟩.$$

(33)

Now, we show that ${\mathfrak{x}}^{*}\in \Omega$. In fact, by (27) we know that $\left\{{\mathfrak{y}}_{n_j}\right\}$ converges to ${\mathfrak{x}}^{*}\in \mathcal{C}$.

Since ${\mathfrak{y}}_{n_j}=P_{\mathcal{C}}\left[ex{p}_{{\mathfrak{x}}_{n_j}}(-{\lambda }_n\mathcal{A}{\mathfrak{x}}_{n_j})\right]$, by Lemma 7, for all $\mathfrak{x}\in \mathcal{C}$, we have

$$⟨ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}ex{p}_{{\mathfrak{x}}_{n_j}}(-{\lambda }_{n_j}\mathcal{A}{\mathfrak{x}}_{n_j}),ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}\mathfrak{x}⟩\le 0.$$

(34)

By Lemma 3, the inequality above becomes

$$\begin{array}{cc}\hfill 0\ge & ⟨ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}ex{p}_{{\mathfrak{x}}_{n_j}}(-{\lambda }_{n_j}\mathcal{A}{\mathfrak{x}}_{n_j}),ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}\mathfrak{x}⟩\hfill \\ \hfill =& ⟨ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}{\mathfrak{x}}_{n_j},ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}\mathfrak{x}⟩-{\lambda }_{n_j}⟨\mathcal{A}{\mathfrak{x}}_{n_j},ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}\mathfrak{x}⟩\hfill \\ \hfill \ge & ⟨ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}{\mathfrak{x}}_{n_j},ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}\mathfrak{x}⟩-{\lambda }_{n_j}⟨\mathcal{A}{\mathfrak{x}}_{n_j},ex{p}_{{\mathfrak{y}}_{n_j}}^{-1}{\mathfrak{x}}_{n_j}⟩\hfill \\ & -{\lambda }_{n_j}⟨\mathcal{A}{\mathfrak{x}}_{n_j},ex{p}_{{\mathfrak{x}}_{n_j}}^{-1}\mathfrak{x}⟩.\hfill \end{array}$$

By Lemma 11, we know that ${\lambda }_n>0$. It follows from Lemma 5 that

$$⟨\mathcal{A}{\mathfrak{x}}^{*},ex{p}_{{\mathfrak{x}}^{*}}^{-1}\mathfrak{x}⟩\ge 0,\forall \mathfrak{x}\in \mathcal{C}.$$

So, we have ${\mathfrak{x}}^{*}\in \Omega$. Since $\mathfrak{q}=P_{\Omega }f\left(\mathfrak{q}\right)\in \Omega$, from (33), we obtain

$$\begin{array}{cc}\hfill \underset{n\to \infty }{\lim \sup }⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_{\mathfrak{q}}^{-1}{\mathfrak{x}}_n⟩ & =\underset{j\to \infty }{\lim }⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_{\mathfrak{q}}^{-1}{\mathfrak{x}}_{n_j}⟩\hfill \\ \hfill & =⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_{\mathfrak{q}}^{-1}{\mathfrak{x}}^{*}⟩\hfill \\ \hfill & \le 0.\hfill \end{array}$$

(35)

It follows from (32) that

$$\underset{n\to \infty }{\lim \sup }⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_{\mathfrak{q}}^{-1}{\mathfrak{x}}_{n+1}⟩\le 0.$$

(36)

Since $li{m}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$, $0\le \rho <1$, and $\left\{{\mathfrak{x}}_n\right\}$ is bounded, it is obvious that $li{m}_{n\to \infty }\frac{2(1-\rho ){\alpha }_n}{1-{\alpha }_n\rho }=0$, ${\sum }_{n=1}^{\infty }\frac{2(1-\rho ){\alpha }_n}{1-{\alpha }_n\rho }=\infty$, and ${\lim \sup }_{n\to \infty }[\frac{{\alpha }_n}{2(1-\rho )}{d}^2({\mathfrak{x}}_n,\mathfrak{q})+\frac{1}{1-\rho }⟨ex{p}_q^{-1}f\left(\mathfrak{q}\right),ex{p}_q^{-1}{\mathfrak{x}}_{n+1}⟩]\le 0$. Due to the inequality (26) holding for any $\mathfrak{p}\in \Omega$, it follows from Lemma 10, (26), and (35) that $li{m}_{n\to \infty }d({\mathfrak{x}}_n,\mathfrak{q})=0$, which implies that the sequence $\left\{{\mathfrak{x}}_n\right\}$ converges to $\mathfrak{q}$.

Case 2. Assume that $\left\{d({\mathfrak{x}}_n,\mathfrak{q})\right\}$ is not a monotonically decreasing sequence.

It follows from Lemma 9 that there exists a nondecreasing sequence $\left\{m_k\right\}$ of $\mathbb{N}$ such that $li{m}_{n\to \infty }{m}_k=\infty$ and the following inequalities hold for all $k\in \mathbb{N}$:

$$d^2({\mathfrak{x}}_{m_k},\mathfrak{q})\le d^2({\mathfrak{x}}_{m_k+1},\mathfrak{q})\mathrm{and}{d}^2({\mathfrak{x}}_k,\mathfrak{q})\le d^2({\mathfrak{x}}_{m_k},\mathfrak{q}).$$

(37)

From (24), we have

$$\left(1-{\alpha }_{m_k}\right)(1-{\mu }^2)d^2({\mathfrak{x}}_{m_k},{\mathfrak{y}}_{m_k})\le d^2({\mathfrak{x}}_{m_k},\mathfrak{q})-d^2({\mathfrak{x}}_{m_k+1},\mathfrak{q})+{\alpha }_n{d}^{2}f({\mathfrak{x}}_{m_k},\mathfrak{q}).$$

(38)

So, we have

$$\underset{k\to \infty }{\lim }d({\mathfrak{x}}_{m_k},{\mathfrak{y}}_{m_k})=0.$$

(39)

Using the same arguments as in the proof of Case 1, we obtain

$$\underset{k\to \infty }{\lim }d({\mathfrak{y}}_{m_k},{\mathfrak{z}}_{m_k})=0,$$

(40)

$$\underset{k\to \infty }{\lim }d({\mathfrak{x}}_{m_k+1},{\mathfrak{z}}_{m_k})=0,$$

(41)

$$\underset{k\to \infty }{\lim }d({\mathfrak{x}}_{m_k+1},{\mathfrak{x}}_{m_k})=0,$$

(42)

and

$$\underset{n\to \infty }{\lim \sup }⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_{\mathfrak{q}}^{-1}{\mathfrak{x}}_{m_k+1}⟩\le 0.$$

(43)

Since ${\lim }_{k\to \infty }{\alpha }_{m_k}=0$, there exists $k_0\in \mathbb{N}$ such that $1-2{\alpha }_n(1-\rho )>0$ for all $k\ge k_0$. By Equation (25) we obtain

$$\begin{array}{cc}\hfill d^2({\mathfrak{x}}_{m_k+1},\mathfrak{q})& \le \left(1-\frac{2(1-\rho ){\alpha }_{m_k}}{1-{\alpha }_{m_k}\rho }\right)d^2({\mathfrak{x}}_{m_k},\mathfrak{q})+\frac{2(1-\rho ){\alpha }_{m_k}}{1-{\alpha }_{m_k}\rho }\hfill \\ \hfill & \times \left[\frac{{\alpha }_{m_k}}{2(1-\rho )}{d}^2({\mathfrak{x}}_{m_k},\mathfrak{q})+\frac{1}{1-\rho }⟨ex{p}_q^{-1}f\left(\mathfrak{q}\right),ex{p}_q^{-1}{\mathfrak{x}}_{m_k+1}⟩\right].\hfill \end{array}$$

(44)

Put ${\beta }_{m_k}=\frac{2(1-\rho ){\alpha }_{m_k}}{1-{\alpha }_{m_k}\rho }$, from (37) and (44); we have

$$\begin{array}{cc}\hfill {\beta }_{m_k}{d}^2({\mathfrak{x}}_{m_k},\mathfrak{q})& \le d^2({\mathfrak{x}}_{m_k},\mathfrak{q})-d^2({\mathfrak{x}}_{m_k+1},\mathfrak{q})\hfill \\ \hfill & +{\beta }_{m_k}\times \left[\frac{{\alpha }_{m_k}}{2(1-\rho )}{d}^2({\mathfrak{x}}_{m_k},\mathfrak{q})+\frac{1}{1-\rho }⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_q^{-1}{\mathfrak{x}}_{m_k+1}⟩\right]\hfill \\ \hfill & \le {\beta }_{m_k}\times \left[\frac{{\alpha }_{m_k}}{2(1-\rho )}{d}^2({\mathfrak{x}}_{m_k},\mathfrak{q})+\frac{1}{1-\rho }⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_{\mathfrak{q}}^{-1}{\mathfrak{x}}_{m_k+1}⟩\right].\hfill \end{array}$$

(45)

Further,

$$d^2({\mathfrak{x}}_{m_k},\mathfrak{q})\le \frac{{\alpha }_{m_k}}{2(1-\rho )}{d}^2({\mathfrak{x}}_{m_k},\mathfrak{q})+\frac{1}{1-\rho }⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_{\mathfrak{q}}^{-1}{\mathfrak{x}}_{m_k+1}⟩,$$

(46)

which means that

$$\underset{k\to \infty }{\lim \sup } d^2({\mathfrak{x}}_{m_k},\mathfrak{q})\le \underset{k\to \infty }{\lim \sup }[\frac{{\alpha }_{m_k}}{2(1-\rho )}{d}^2({\mathfrak{x}}_{m_k},\mathfrak{q})+\frac{1}{1-\rho }⟨ex{p}_{\mathfrak{q}}^{-1}f\left(\mathfrak{q}\right),ex{p}_{\mathfrak{q}}^{-1}{\mathfrak{x}}_{m_k+1}⟩].$$

(47)

Therefore,

$$\underset{k\to \infty }{\lim }d({\mathfrak{x}}_{m_k},\mathfrak{q})=0.$$

(48)

Meanwhile, it follows from (43), (45) and (47) that ${\lim \sup }_{k\to \infty }d({\mathfrak{x}}_{m_k+1},\mathfrak{q})\le 0$. Hence,

$$\underset{k\to \infty }{\lim }d({\mathfrak{x}}_{m_k+1},\mathfrak{q})=0.$$

(49)

Further, from (37) we obtain

$$\underset{k\to \infty }{\lim }d({\mathfrak{x}}_k,\mathfrak{q})=0.$$

(50)

Hence, $\left\{{\mathfrak{x}}_k\right\}$ converges to $\mathfrak{q}$. The proof is completed.    □

If $f\left(\mathfrak{x}\right)=u$, for any $\mathfrak{x}\in \mathcal{M}$, and u is a fixed vector in $\mathcal{M}$, then Theorem 1 reduces to the following corollary.

Corollary 1. 

Assume that the assumptions $\left(\mathcal{C}1\right)-\left(\mathcal{C}4\right)$ hold, and $\left\{{\alpha }_n\right\}\subseteq (0,1)$, $li{m}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$. Then, the sequence $\left\{{\mathfrak{x}}_n\right\}$ generated by Algorithm 1 with $f:=u$ converges to a solution of VIP (2).

Remark 2. 

1.

The main results obtained in this paper extend the main results in [16] from monotone VIP (1) on Hilbert spaces to more general pseudomonotone VIP (2) on Hadamard manifolds.

2.

In the algorithms proposed in [49,50], they are needed to compute two projections on the closed convex set $\mathcal{C}$ at each iteration step, which may affect the efficiency of the algorithm. To avoid this shortcoming, we use an easy calculated projection to replace the second projection in the algorithms in [49,50].

3.

In Algorithm 1, it works without prior knowledge of the Lipschitzian constant of the mapping involved.

4.

The generalization was made from the Hilbert spaces with linear structure to the Hadamard manifolds with nonlinear structure. See [16,49,50].

4. Application to Constrained Convex Minimization Problem

The so-called constrained convex minimization problem is to find $\mathfrak{x}\in \mathcal{C}$ such that

$$g\left(\mathfrak{x}\right)=\underset{\mathfrak{y}\in \mathcal{C}}{\min }g\left(\mathfrak{y}\right),$$

(51)

where $\mathcal{C}$ is a non-empty, closed, and geodesic convex subset of a Hadamard manifold $\mathcal{M}$ and g is a real-valued function from $\mathcal{C}$ to $\mathcal{R}$; the solution set of the convex minimization problem (51) is denoted by $\mathcal{C}MP(g,\mathcal{C})$, that is,

$$\mathcal{C}MP(g,\mathcal{C})=\{\mathfrak{x}\in \mathcal{M}:g(\mathfrak{x})\le g(\mathfrak{y}),\forall \mathfrak{y}\in \mathcal{C}\}.$$

(52)

The gradient $\nabla g$ of a differentiable real-valued function $g:\mathcal{M}\to \mathcal{R}$ at $\mathfrak{x}$ is defined by $⟨\nabla g\left(\mathfrak{x}\right),u⟩=g^{\prime }(\mathfrak{x},u),$ where $\mathcal{M}$ is a Hadamard manifold; $g^{\prime }(\mathfrak{x},u)$ is the directional derivative of g at $\mathfrak{x}$ in the direction $u\in {\mathcal{T}}_{\mathfrak{x}}\mathcal{M}$, which is defined as follows:

$$g^{\prime }(\mathfrak{x};u):=\underset{t\to 0^{+}}{\lim \inf }\frac{g\left({\exp }_{\mathfrak{x}}tu\right)-g\left(\mathfrak{x}\right)}{t}.$$

It is well known that $\nabla g$ is a continuous vector field on $\mathcal{M}$ (see [37]).

Lemma 12 

([30]). Let $\mathcal{C}$ be a non-empty, closed, and geodesic convex subset of a Hadamard manifold $\mathcal{M}$ and g be a differentiable convex function from $\mathcal{M}$ to $\mathcal{R}$. Then, $\mathfrak{p}\in \mathcal{C}\mathcal{M}P(g,\mathcal{C})$, if and only if $\mathfrak{p}$ solves the VIP $\left(2\right)$ with $\mathcal{A}=\nabla g$.

When the vector field $\mathcal{A}\equiv \nabla g$ in Algorithm 1, the sequence generated by Algorithm 1 converges to a solution of the minimization problem (51). So, we obtain the following result.

Theorem 2. 

Assume that the assumptions ${\mathcal{C}}_1-{\mathcal{C}}_5$ hold, where $\mathcal{A}$ is the gradient $\nabla g$ of a convex differentiable function g from $\mathcal{C}$ into R. If $li{m}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$, $\mathrm{error}(g,\mathcal{C})\ne \varnothing$, and $\nabla g$ is pseudomonotone and L-Lipschitz continuous, then the sequence $\left\{{\mathfrak{x}}_n\right\}$ generated by Algorithm 1 converges to a point $\mathfrak{p}\in \mathrm{error}(g,\mathcal{C})$.

Next, we will give a simple practical optimization case.

Electronics Supply Chain Inventory Optimization

An electronics retailer anticipates the launch of a new smartphone. Based on market analysis and pre-order data, the anticipated retail demand for the first month is 10,000 units. The current inventory level in the warehouse is 5000 units. The warehouse has a maximum capacity of 20,000 units. Given these parameters, the retailer aims to determine the optimal inventory level to stock up for the product launch.

Based on this problem, Algorithm 1 reduces to the following.

Based on the Algorithm 2, the new inventory level should be ${\mathfrak{x}}_{n+1}$ units. We choose the residual error $E_n=|{\mathfrak{x}}_{n+1}-{\mathfrak{x}}_n|$. If the residual error $E_n\le {10}^{-3}$ is met, we stop the iteration. Otherwise, we continue with the next step.

Algorithm 2: Iterative Inventory Optimization Algorithm

Initialization: Given initial inventory level, ${\mathfrak{x}}_0=5000$ units; Anticipated retail demand, ${\mathfrak{y}}_0=10,000$ units. Warehouse maximum capacity, $=20,000$ units. Decay factor, $\gamma =0.7$. Adjustment factor, $\xi =0.8$. Weight, $\alpha =0.5$.       Step 1. $d_n$ to denote demand function, that is, $d_n={\mathfrak{y}}_0-{\mathfrak{x}}_n$. Determine the desired inventory level: $${\mathfrak{y}}_n={\mathfrak{x}}_n+\gamma \times d_n.$$ Here, if ${\mathfrak{x}}_n={\mathfrak{y}}_n$, then stop and take ${\mathfrak{y}}_n$ as the optimal inventory level. Otherwise, proceed to the next step.       Step 2. Compute Adjustment Factor: ${\lambda }_n=\gamma$.       Step 3. Compute New Inventory Level: $${\mathfrak{z}}_n={\mathfrak{x}}_n+{\lambda }_n\times ({\mathfrak{y}}_0-{\mathfrak{y}}_n).$$       Step 4. Update Inventory Level: ${\mathfrak{x}}_{n+1}=(1-\alpha )\mathfrak{x}{}_n+\alpha {\mathfrak{z}}_n$. Repeat: Set $n:=n+1$ and return to Step 1.

In a word, the inventory levels at each iteration step are shown in Table 1. So, we can see that the residual error becomes smaller and smaller when the number of iterations increases, which indicates that the iteration scheme is convergent.

Table 1. Result of iterations.

Iteration	${\mathfrak{x}}_{\mathit{n}}$	${\mathfrak{z}}_{\mathit{n}}$	${\mathfrak{x}}_{\mathit{n}+1}$	${\mathit{E}}_{\mathit{n}}$
1	5000	8500	6750	1750
2	6750	9025	7887.5	1137.5
3	7887.5	9366.25	8626.875	739.38
4	8626.875	9588.063	9107.469	480.59
5	9107.46875	9732.241	9419.855	312.39
6	9419.854688	9825.956	9622.906	203.05
7	9622.905547	9886.872	9754.889	131.98
8	9754.888605	9926.467	9840.678	85.789
9	9840.677594	9952.203	9896.44	55.763
10	9896.440436	9968.932	9932.686	36.246
⋮	⋮	⋮	⋮	⋮
31	9999.9878	9999.996	9999.992	0.0042701
32	9999.99207	9999.998	9999.995	0.0027756
33	9999.994845	9999.998	9999.997	0.0018041
34	9999.996649	9999.999	9999.998	0.0011727
35	9999.997822	9999.999	9999.999	0.00076224

5. A Numerical Example

In this part, we provide a numerical example to illustrate the effectiveness and the convergence behavior of Algorithm 1. All codes were written with MATLAB 2020b computed on a Personal Computer (PC) Core i7.

Let ${\mathcal{R}}^{++}=\{\mathfrak{x}\in \mathcal{R}:\mathfrak{x}>0\}$ and $\mathcal{M}:={\mathcal{R}}^{++}$ the set of positive real numbers and $\left({\mathcal{R}}^{++},⟨·,·⟩\right)$ the Riemannian manifold, and let ${\mathcal{T}}_{\mathfrak{p}}\mathcal{M}$ be the tangent space at $\mathfrak{p}\in \mathcal{M}$, then

(i) the Riemannian metric $⟨·,·⟩$ is defined by

$$⟨\mathfrak{x},\mathfrak{y}⟩:=\frac{1}{{\mathfrak{p}}^2}\mathfrak{x}\mathfrak{y},\forall \mathfrak{x},\mathfrak{y}\in \mathcal{T}\mathfrak{p}\mathcal{M},$$

(53)

(ii) (see [51]) The Riemann distance $d:\mathcal{M}\times \mathcal{M}\to {\mathcal{R}}^{+}$ is defined by

$$\mathrm{d}(\mathfrak{x},\mathfrak{y})=\left|\ln \frac{\mathfrak{x}}{\mathfrak{y}}\right|, \forall \mathfrak{x},\mathfrak{y}\in \mathcal{M}.$$

(54)

Furthermore, the unique geodesic $c:\mathcal{R}\to \mathcal{M}$ with $c\left(0\right)=\mathfrak{x},u=c^{\prime }\left(0\right)\in {\mathcal{T}}_{\mathfrak{x}}\mathcal{M}$ is defined by $c\left(t\right):=$$\mathfrak{x}{e}^{\left(\frac{ut}{\mathfrak{x}}\right)}$. Thus

$${\exp }_{\mathfrak{x}}tu=\mathfrak{x}{e}^{\left(\frac{ut}{\mathfrak{x}}\right)}.$$

(55)

(iii) The inverse exponential map is defined by

$${\exp }_{\mathfrak{x}}^{-1}\mathfrak{y}=c^{\prime }\left(0\right)=\mathfrak{x}\ln \frac{\mathfrak{y}}{\mathfrak{x}}.$$

(56)

Example 1. 

Let $\mathcal{C}=[1,+\infty )$ be a geodesic convex subset of ${\mathcal{R}}^{+}$ and $\mathcal{A}:\mathcal{C}\to$$\mathcal{R}$ be a single-valued vector field defined by

$$\mathcal{A}\mathfrak{x}=\mathfrak{x}\ln \mathfrak{x}, \forall \mathfrak{x}\in \mathcal{C}.$$

(57)

Then, it is easy to see that $\mathcal{A}$ is pseudomonotone. Indeed, let $\mathfrak{x},\mathfrak{y}\in \mathcal{C}$ and assume $⟨\mathcal{A}\left(\mathfrak{x}\right),{\exp }_{\mathfrak{x}}^{-1}\mathfrak{y}⟩$$\ge 0$, from (53), (56) and (57); we easily see that

$$⟨\mathcal{A}\left(\mathfrak{x}\right),{\exp }_{\mathfrak{x}}^{-1}\mathfrak{y}⟩=⟨\mathfrak{x}\ln \mathfrak{x},\mathfrak{x}\ln (\mathfrak{y}/\mathfrak{x})⟩=1/{\mathfrak{x}}^2\times \mathfrak{x}\ln \mathfrak{x}\times \mathfrak{x}\ln (\mathfrak{y}/\mathfrak{x})\ge 0,$$

which implies that $\ln (\mathfrak{y}/\mathfrak{x})\ge 0$. Since

$$\begin{array}{cc}\hfill ⟨\mathcal{A}\mathfrak{y},{\exp }_{\mathfrak{y}}^{-1}\mathfrak{x}⟩& \le ⟨\mathcal{A}\mathfrak{y},{\exp }_{\mathfrak{y}}^{-1}\mathfrak{x}⟩+⟨\mathcal{A}\mathfrak{x},{\exp }_{\mathfrak{x}}^{-1}\mathfrak{y}⟩\hfill \\ & =\frac{1}{{\mathfrak{y}}^2}\times \mathfrak{y}\ln \mathfrak{y}\times \mathfrak{y}\ln \frac{\mathfrak{x}}{\mathfrak{y}}+\frac{1}{{\mathfrak{x}}^2}\times \mathfrak{x}\ln \mathfrak{x}\times \mathfrak{x}\ln \frac{\mathfrak{y}}{\mathfrak{x}}\hfill \\ & =-{(\ln \mathfrak{y}-\ln \mathfrak{x})}^2\hfill \\ & \le 0.\hfill \end{array}$$

So, $\mathcal{A}$ is pseudomonotone. Now, we prove that $\Omega \ne \varnothing$. Assume that $\mathfrak{p}\in \Omega$ and $\mathfrak{q}\in \mathcal{C}$, then

$$\begin{array}{cc}\hfill ⟨\mathcal{A}\mathfrak{p},{\exp }_{\mathfrak{p}}^{-1}\mathfrak{q}⟩& \ge \frac{1}{{\mathfrak{p}}^2}\left(\mathfrak{p}\ln \mathfrak{p}\right)·\mathfrak{p}·\ln \frac{\mathfrak{q}}{\mathfrak{p}}\hfill \\ & =\ln \mathfrak{p}\ln \frac{\mathfrak{q}}{\mathfrak{p}}\ge 0, \forall \mathfrak{q}\in \mathcal{C}\hfill \\ & \iff \mathfrak{p}=1,\hfill \end{array}$$

which implies that the solution of VIP (2) is 1.

Here, we choose $f\left(\mathfrak{x}\right)=\frac{\mathfrak{x}}{2}$, $\mathcal{A}\mathfrak{x}=\mathfrak{x}\ln \mathfrak{x}$, $\gamma =l=\mu =0.5$, and take two randomly initial points ${\mathfrak{x}}_1=0.5, {\mathfrak{x}}_1=8$. To show the effectiveness of Algorithm 1, we compare Algorithm 1 with the algorithm introduced in [36], which we named Algo*. In example 1, as $x_1$ = 0.5, the numbers of iteration of Algorithm 1 and Algo* are 23 and 28, respectively. As $x_1$ =8, the numbers of iteration of Algorithm 1 and Algo* are 297 and 350, respectively. We summarize the numerical experimental data in the Figure 1a–d, where Figure 1a,b illustrates the asymptotic behaviors of Algorithm 1 and Algo*. It can be seen that Algorithm 1 converges faster and owns better asymptotic behavior than Algo*. On the other hand, from Figure 1c,d, we may find that the residual error $E_n=\parallel {\mathfrak{x}}_{n+1}-{\mathfrak{x}}_n\parallel$ of Algorithm 1 is less than the residual error $E_n$ of Algo*.

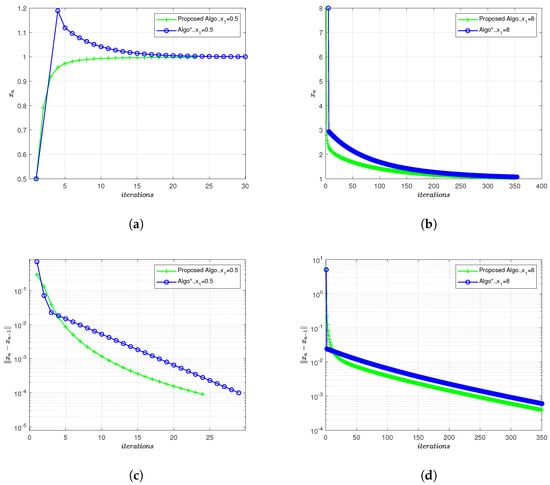
Figure 1. Comparison of Algorithms for Example 1. (a) The number of iterations; (b) The number of iterations; (c) Comparison of the residual error with $x_1=0.5$; (d) Comparison of the residual error with $x_1=8$.

6. Conclusions

In this paper, we proposed an efficient viscosity type subgradient extragradient algorithm to solve pseudomonotone variational inequality on Hadamard manifolds which is of symmetrical characteristic. Notably, the vector field $\mathcal{A}$ is characterized as a Lipschitz continuous pseudomonotone operator, with the advantage that its Lipschitz constant need not be predetermined. Under appropriate conditions, we prove that the sequence generated by the Algorithm 1 converges to a solution of the pseudomonotone VIP on Hadamard manifolds. Furthermore, we utilize our main result to solve a constrained convex minimization problem and give a practical example for an inventory optimization problem in an electronic supply chain. In addition, we also provide a numerical experiment to demonstrate the asymptotic behavior of the algorithm. It is noteworthy that our results presented in this paper extend the main results of [16] from monotone VIP on Hilbert spaces to the more general pseudomonotone VIP on Hadamard manifolds. In our Algorithm 1, although it is necessary to compute two projections at each iteration step, one of the projections is easily computed since it is a projection on a half-plane, which replaces the second projection in the algorithms in [49,50]. In summary, our new results in this paper are original. It is worth mentioning that part of our future research will focus on achieving the convergence results for the modifications of our proposed algorithms with low computational cost and fast convergence speed.