Abstract
Covariant integral quantization with rotational symmetry is established for quantum motion on this group manifold. It can also be applied to Gabor signal analysis on this group. The corresponding phase space takes the form of a discrete-continuous hypercylinder. The central tool for implementing this procedure is the Weyl–Gabor operator, a non-unitary operator that operates on the Hilbert space of square-integrable functions on . This operator serves as the counterpart to the unitary Weyl or displacement operator used in constructing standard Schrödinger–Glauber–Sudarshan coherent states. We unveil a diverse range of properties associated with the quantizations and their corresponding semi-classical phase-space portraits, which are derived from different weight functions on the considered discrete-continuous hypercylinder. Certain classes of these weight functions lead to families of coherent states. Moreover, our approach allows us to define a Wigner distribution, satisfying the standard marginality conditions, along with its related Wigner transform.
Keywords:
covariant Weyl–Heisenberg integral quantization; semi-discrete hypercylinder; coherent states; Weyl–Gabor operator; quantum models on SO(3); Wigner function; phase space portrait MSC:
46L65; 81S10; 81S30; 81R30
1. Introduction
The group is of particular interest in physics as it serves as the configuration space for the motion of a rigid body fixed at a point. It is also relevant in signal analysis and processing. The rigid rotor is a classic problem in classical and quantum mechanics, describing the dynamics of a rigid body with its center of mass held fixed [1,2,3,4]. On the quantum level, it provides a consistent framework for describing the rotational spectra of molecules [2,5,6,7,8,9,10,11,12,13,14,15,16]. Furthermore, utilizing as a configuration manifold has led to various applications, including texture analysis [17,18,19], protein–protein docking [20,21], air temperature control [22], the structure of interest rates in economics [23], the attitude determination of rigid bodies [24,25,26,27,28,29], quantum information [30], and spherical image analysis [31,32].
This work can be seen as a direct continuation of previous studies focused on the semi-discrete cylinder [33,34]. Our inspiration also stems from the insightful works of Mukunda et al. [35,36,37]. These authors were concerned with establishing a consistent Wigner function for compact Lie groups, and they illustrated their approach using the example of SU, the double covering of SO. For more recent and related works, please refer to, for instance, [38,39] and the references therein.
In [33], we implemented what is known as covariant quantization for the semi-discrete cylinder, considering it as the phase space for motion on a circle. Covariant integral quantizations linearly transform functions (referred to as “classical observables”) on phase spaces, in a broader sense, into operators (“quantum observables”) on specific Hilbert spaces of “quantum states”. These quantization methods are based on resolving the identity using continuous or discrete families of normalized positive-operator-valued measures (POVMs) that transform covariantly under certain symmetry group actions. In simple cases (see, for instance, [40]), these symmetries can be described by the Weyl–Heisenberg group, which includes projective representations of translations in the Euclidean plane, or by the affine groups, which involve translations of a subset of variables combined with dilations of the remaining subset of variables bounded below.
Starting with (quasi-)probability distributions in the phase spaces where the Weyl–Heisenberg or affine groups act (representing classical Hamiltonian models), these quantization methods produce their corresponding quantum models and associated probabilities (e.g., Husimi) or quasi-probabilities (e.g., Wigner) distributions. In turn, tracing the involved POVM with the operators provides semi-classical portraits of the quantum models, which act as a regularization of the original classical model. These quantization methods, with origins traceable to Klauder, Berezin, and Toeplitz, are relatively easier to manipulate compared to geometric or deformation quantizations. Importantly, they enable us to circumvent issues related to ordering (canonical quantization) and those arising from the presence of singularities in classical models.
In this study, our objective is to implement and investigate the covariant integral quantization of functions or distributions in the phase space , where is a discrete set denoted as , which labels the matrix elements of the unitary irreducible representations (UIR) of SO with respect to the spherical harmonic Hilbertian basis of .
In Section 2, we briefly describe the general method of covariant integral quantization.
In Section 3, we apply this method to the quantum description of the motion of a particle on the manifold.
Section 4 involves deriving the (non-unitary) Weyl–Gabor operator U acting on the Hilbert space of square-integrable functions on the manifold equipped with its Haar measure. This operator leads to a decomposition of the identity on the space .
In Section 5, we first define our quantization tools, which include a weight function defined in the phase space and the related integral operator that acts on the representation space. We then define the quantization map, which transforms a function or distribution f in the phase space into an operator acting on . We compute the quantization of separable functions in both position and momentum, only momentum, and only position.
In Section 6, we compute the so-called semi-classical portrait (or lower symbol) of the operator and study how closely they resemble the original function f.
Section 7 provides examples of quantum operators obtained through coherent state quantization.
In Section 8, we introduce a Wigner function built from what we define as the “squared rotation operator”.
Finally, concluding with Section 9, we present some appealing investigations in the continuation of the present work and provide insights about the application of our formalism to the analysis of signals defined on the manifold. Interesting formulas are included in Appendix A.
2. Resolution of the Identity as the Common Guideline
In this section, we provide an overview of integral quantization. For more comprehensive explanations, one can refer to [40,41] and, more recently, [42,43], along with their respective references.
2.1. Integral Quantization: The Essential
Given a measure space and a (separable) Hilbert space , an operator-valued function
resolves the identity operator in with respect the measure if
holds in a weak sense.
In signal analysis, analysis and reconstruction are grounded in the application of (1) on a signal, i.e., a vector in , where
In quantum formalism, integral quantization is grounded in the linear map of a function on X to an operator in :
2.2. Probabilistic Content of Integral Quantization: Semi-Classical Portraits
If the operators in
are nonnegative, i.e., for all , one says that they form a (normalized) positive-operator-valued measure (POVM) on X.
If they are further unit trace-class, i.e., for all , i.e., if the operatorsare density operators, then the map
is a local averaging of the original (which can be very singular, like the Dirac defined in (8) below) with respect to the probability distribution on X,
This averaging, or semi-classical portrait of the operator , is, in general, a regularization. It depends, of course, on the topological nature of the measure space and the functional properties of the operators.
2.3. Classical Limit
Consider a set of parameters and corresponding families of POVM solving the identity
One says that the classical limit holds at if
where the convergence is defined in the sense of a certain topology.
Otherwise said, tends to
where is a Dirac measure with respect to ,
Of course, these definitions should be rigorously mathematically formulated, and there is no guarantee of the existence of such a limit.
3. Overview: Scalar Fields on the Rotation Group SO(3) and Fourier and Gabor Transforms
In this section, we first introduce (Section 3.1) all the necessary mathematical objects with which we work, including the group SO and Hilbertian and harmonic analysis of it through its unitary irreducible representations (UIRs). Our primary source of reference for presenting this well-known material is Edmonds’ book (1957) [44]. We then proceed to describe the semi-discrete phase space in Section 3.2. Finally, in Section 3.3, we delve into the core of our work with the definition of the Weyl–Gabor operator, associated coherent states, Gabor transform, and relevant properties and provide a few illustrative examples.
3.1. Quantum Formalism on SO(3)
An element of SO can be parametrized in several ways.
- (a)
- In the Euler angles parametrization with ZYZ convention, and are rotation angles about the third axis and is rotation angle about the second axis, with , , and . The corresponding rotation matrix reads in terms of these one-dimensional matrices asThe related (non-normalized) Haar measure is given bywhich yields Vol.
- (b)
- In the axis-angle parametrization, belongs to the interval and represents the anticlockwise rotation angle (or follows the right-hand rule) about the oriented axis , which is determined by the usual angular spherical coordinates . Here, ranges from 0 to , and from 0 to .The matrix representation of is given bywhere is the orthogonal projector on , where , and linearly acts on asThe related unnormalized Haar measure is
We now consider the Hilbert space of square integrable functions on the rotation group SO, that is, functions satisfying the condition,
The group multiplication on the left induces the unitary action of the operator on :
The three basic generators (angular momentum components) of this action in the Euler angles parametrization (9) are given by [44]:
One can expand any function in terms of the Wigner -functions , with , and . Hence, these functions form an Hilbertian basis of , and the set of triplets of integers
form the Fourier dual of . The Wigner -functions are matrix elements of the irreducible unitary representation of SO with respect to the Hilbertian basis of normalized spherical harmonics in . Our convention concerning the latter is given by Edmonds [44]:
where comprises the associated Legendre functions [45].
In the Euler angle parametrization, the Wigner -functions appear in the expansion [5,44]:
and are given by
In this expression, the functions are expressed in terms of the Jacobi polynomials for and [45]:
The other cases give similar expressions after using symmetries of indexes for these polynomials. More precisely, from the general expression of the Jacobi polynomials
with
one can derive the Fourier series expansion of the Wigner d-functions (not trivial!):
where [46,47]. In terms of its matrix elements, the unitarity of the -matrix at fixed l reads
and so,
while the orthogonality relations obeyed by these -matrix elements read
Let us introduce the Dirac distribution on SO as having its support at the group identity :
for all test functions in some dense subspace of , e.g., infinitely differentiable. For any and from the invariance of the measure, we have
which entails the definition of the Dirac distribution with support at any point :
Using Dirac notations, we introduce kets and their dual bras , both labeled by the points , as obeying the following orthogonality and normalization (in the distributional sense) and resolution of the unity in :
From its construction, we derive the invariance property of the Dirac distribution on SO:
With these notations, one can write for any (or for suitably defined distributions)
With this formalism at hand, the completeness of the Hilbertian basis
in reads
On the other hand, as matrix elements of the unitary operator (irreducibly acting in the -dimensional subspace of ), they are uniformly bounded by
We now define the SO Fourier transform of as the orthogonal projection of on the basis , which is its Fourier coefficient:
and its inverse is consistently the Fourier series expansion:
3.2. Phase-Space Formalism
Inspired by the Mukunda et al.’s approach [35,36], we now consider the rotation as an element of the configuration space SO and the triple of its unitary (∼ Fourier) dual as momentum or frequency variables. Hence, we denote in the following:
with orthogonality relations and resolution of the identity
With these shortened notations, we write the Hilbertian basis as
3.3. SO(3)-Weyl–Gabor Operator, Coherent States, and Gabor Transform
In this subsection, we introduce the SO-Weyl–Gabor operator, an essential tool for comprehending the integral quantization formalism that is expounded upon in the subsequent sections. It serves as a pivotal link between the introductory exploration of functions, whether in the form of wavefunctions or signals, within the Hilbert space , as described above. It facilitates the transition from understanding these functions in their native Hilbert space to their representation in the phase space. This bridge is precisely established through the coherent states built from the action of the SO-Weyl–Gabor operator on fiducial vectors. The journey from the abstract space of functions to their manifestation in the phase space paves the way for a more profound grasp of the integral quantization framework that is to follow.
3.3.1. SO(3)-Weyl–Gabor Operator
Besides the unitary representation operator introduced in Equation (16), we define the non-unitary modulation operator by the momentum variable . This operator is a non-Hermitian, bounded multiplication operator:
Its adjoint is defined by
where the transpose of means
Combining these operators leads to the (non-unitary) “SO-Weyl-Gabor” operator
acting on as
Its adjoint acts on as
We then have the following actions on :
In particular, the lack of unitarity of and is obvious from the fact that and are nontrivial bounded multiplication operators:
3.3.2. Coherent States
Let us pick a normalized vector in and consider the family of family of states labeled by the elements of the phase space :
These states are named -coherent states with fiducial vector for the reason that they solve the identity in , as asserted in the following.
Proposition 1.
Let us equip the phase space Γ with the measure
Then, the states resolve the identity in with respect to this measure:
Proof.
Pick , , and compute
First, performing the sum on yields by the application of (46). By integrating the latter and using the invariance of the Haar measure , we end with
□
3.3.3. Gabor Transform
The Gabor transform, denoted by , maps to a function in the Hilbert space of square integrable functions on the phase space equipped with the measure :
Proposition 2.
The map satisfies the following properties:
- (i)
- It is an isometry:
- (ii)
- It can be inverted on its range:
- (iii)
- The closure of the range of is a reproducing kernel Hilbert space:
Proof.
All statements are straightforward consequences of the resolution of the identity (61). □
Proposition 3.
We have the following trace formulas for the SO-Weyl–Gabor operator:
3.4. Example of Fiducial Vectors and Coherent States
As seen above, any square-integrable function on SO, including the completely non-localized function on the manifold SO, can be viewed as a fiducial vector. Corresponding coherent states form the family of transported through the SO-Weyl–Gabor operator. It is, of course, interesting to consider fiducial vectors that are well “localized” in position and momentum. Although it is not the main purpose of this paper, we present a few fiducial vectors that can be of interest. Some of these examples are extracted from signal processing on SO as related to probability densities.
- Eigenfunctions of certain operators [48]. The first example is the free rotor fiducial vector, which is the eigenfunction of .The second example is the highest fiducial vector for . which is cancelled by , that is,
- Some radial fiducial vectors. Below, we give examples of fiducial vectors depending only onThe above expression defines a metric on , whose details can be found in [21].
- (a)
- The -dependent von Mises–Fisher Kernel fiducial vectors [21], their derivatives with respect to and , and their difference at two different :where , , denotes the modified Bessel functions of the first kind.In Appendix B, we give plots of these fiducial vectors in and variables at a fixed and for a few values of (Figure A1 and Figure A2).
- (b)
- The Abel–Poisson fiducial vector [21]:with .
4. Quantization Operators and the Quantization Map
In line with prior research [42,43], we select a function, denoted as , to serve as a weight in the phase space . However, this function is not necessarily positive. We then define the operator by
and we choose the weight such that the operator is bounded and symmetric, i.e., self-adjoint on the Hilbert of “physical states”.
In what follows, we compute the kernel of this operator and the related trace.
Proposition 4.
- (i)
- The operator is the integral operator:where the kernel is given bywhere is the partial inverse discrete Fourier transform (48) of ϖ with respect to the discrete variables.
- (ii)
- The operator is symmetric if and only the weight satisfies
- (iii)
- The trace of is given by
Proof.
- (i)
- The action of on is given by
- (ii)
- The action of on is given by
- (iii)
□
Furthermore, we demonstrate in the following proposition that the weight can be obtained from the quantization operator through a trace operation.
Proposition 5.
The trace of the operator is given by
Proof.
This relation trivially results from (67). □
As a helpful example, let us examine the case . Then, the operator is determined through its action on basis elements :
Let us introduce the squared rotation operator , defined by
5. SO(3)-Covariant Integral Quantization from Weight Function
We now introduce general formulae for quantizing a function in the phase space , resulting in a semi-classical phase space portrait represented as a new function on . The procedure’s outcome is contingent upon the choice of a weight. Different weight selections can give rise to two distinct quantizations. In practice, one weight may facilitate the regularization of singularities present in the classical model, while another weight may preserve these singularities intact.
5.1. General Results
We now establish general formulae for the integral quantization issued from a weight function on , yielding the bounded self-adjoint operator defined in (76). This allows us to build a family of operators obtained from the SO-Weyl–Gabor operator transport of :
Then, the corresponding integral quantization is given by the linear map:
We have the following result.
Proposition 6.
is the integral operator on :
and its kernel is given by
with a weighted version of the completeness relation
The requirement that is mapped to the unit operator imposes the following normalization condition on ϖ:
Proof.
The calculation of the kernel of the integral operator proceeds through the following steps, which are derived from the expressions in (85) and (57).
We then proceed with the change of variable
and use the SO invariance of the measures to obtain the form
with
We then proceed with the change of variables to obtain
This is Equation (88) with the notation (89).
5.2. Particular Quantizations
In the following discussion, we examine three simplified versions of functions, denoted as , on the phase space to make analytical calculations feasible. In more general cases, numerical computations may be required. Therefore, we begin with a function that depends solely on the angle variables, denoted as , allowing us to explore situations where singularities occur in the position variable. Similarly, a function that depends only on the momentum variable, denoted as , highlights the fact that SO is a curved manifold because of additional terms that appear in its quantized form. The next example involves the separable form, .
To facilitate the calculations, we begin by introducing the following function:
It obeys
We also introduce the notations
In Appendix A, we give examples of such calculations in the case of coherent states.
Of course, or, equivalently, should be understood as
and means the Euler angle of the rotation , etc. We also need the integral formulae (with suitable conditions on functions appearing in the integrand)
5.2.1. Separable Functions
In this case, in the integral factorizes as
with the notation
Hence,
5.2.2. Univariate Function
In this case the above, (102) simplifies to
Hence, the quantization of is the multiplication operator.
where the (noncommutative) convolution on the group SO is defined by
Let us give the quantizations of some basic Fourier or trigonometric functions . In the sequel, we put .
- For , we obtainwhere
- For ,where
- For ,where
- For ,where
5.2.3. Univariate Function
The integral kernel reads, in this case,
We know that the values of are constrained in a forward-rectangular discrete pyramid, which is the momentum space. We here work with Euler angle parameters and (for the sake of simplicity, we omit them and explicitly include them when necessary). Let us present the quantization of a few elementary functions .
- We haveThe kernel is then given byThe action of the quantum version of m on is then obtained through integration by part and the use of (92) and notation (93):Under mild conditions on the weight function, we have . Then, we exactly recover the angular momentum operator component . A similar result holds with the quantization of :
- We haveThe expression of the kernel then reads as follows:and for the quantum operator,i.e.,
- . We have to just use the eigenvalue property of the functionsor, equivalently, of the functions [44],and the results given in the above examples. The corresponding kernel is given bywhere [44]
6. Semi-Classical Portrait
Given a function in the phase space , normalized at and yielding a non-negative unit trace operator, i.e., a density operator, , the quantum phase space portrait of an operator A on is defined as
The most interesting aspect of this notion in terms of probabilistic interpretation holds when the operator A is precisely the integral quantized version of a classical with the same function (actually, we can define the transform with two different weights, one for the “analysis” and the other for the “reconstruction”). Then, with the use of the composition rule, let us compute the transform:
We successively have
Using the partial Fourier transform of , we obtain
Summing on gives
Hence, we can write
where the kernel is given by
Using the adjointness condition for , one obtains
where
Hence, we can conclude with the following result:
Proposition 7.
The semi-classical portrait of the operator with respect to the weight ϖ is given by
where the kernel is given by
This kernel satisfies the property
Below, we give the kernels and semi-classical portraits for two specific weights.
- (i)
- For the unit weight , the kernel readswhereFinally,
- (ii)
- For the squared rotation map weight ,andFor the univariate functions and ,
A third example of weight, namely that one corresponding to coherent states, is given in the next section.
7. Quantization and Semi-Classical Portraits with Coherent States with Non-Unit Fiducial States
The entire procedure of covariant integral quantization and the explanation of semi-classical phase-space portraits provided above are well-implemented in cases where the operator is a one-rank density operator, i.e., when we employ coherent-state quantization.
7.1. CS Quantization
Let us implement the quantization yielded by the weight , which corresponds, through Proposition 5, to the one-rank density operator , , . Particularizing Proposition 6 and subsequent derivations of various quantizations to the CS case allows us to state the following.
Let us implement the quantization defined by the weight , which corresponds to the one-rank density operator , where belongs to the Hilbert space and , as established in Proposition 5. By specializing Proposition 6 and subsequent quantization derivations to the coherent-state (CS) case, we can confidently present the following without going into a detailed proof:
Proposition 8.
Given a fiducial vector ϕ and the projector , the trace of the operator is given by (with the notations of (59))
In addition, we have
- (i)
- The partial inverse Fourier transform of with respect to is given by
- (ii)
In what follows, we compute the kernels or/and the corresponding operators for various simple cases of .
- (a)
- For ,
- (b)
- For ,Hence, the quantized of is the multiplication operator.
- (c)
- For ,
7.2. Semi-Classical Portraits Through CS
For the coherent state weight , the kernel is the probability distribution in the phase space:
Hence, is the local averaging of the original :
8. Squaring Rotation Operator for the Wigner Function
Based on the previoussection, let us consider the following phase portrait of a state :
where the operator is requested to yield marginality properties ‘a la Wigner for :
Let us assume that acts on through some differentiable transformation of the group manifold , namely,
where the factor has to also be determined.
With (54), (55), and the above definitions, we have
The completeness relation (46) combined with the above integral and change of variable allows us to write
The condition for achieving marginality with regard to summing on , namely,
thus imposes on the action and the function the following conditions:
Besides the constraint , possible solutions for are
since the group structure imposes that , i.e., should be one of the roots of the unity in SO. The most natural choice for n is obviously :
and we keep it in the sequel. Let us now examine the condition for getting marginality with regard to integrating on , namely,
where we recall that is the Fourier transform of :
With the solution (143) at hand, let us evaluate the l.h.s. of (144), assuming that inverting the order of integrations is legitimate.
Now, after changing the variable in the second integral and using the invariance of the measure , one obtains
In order to achieve marginality with regard to integrating on , the only possibility is that . Then, we obtain (144), and is precisely the squared rotation operator introduced in (83),
In summary and extending the above properties to mixed states in , we state the following.
Proposition 9.
To any density operator in , the squared rotation operator associates its Wigner-like function defined by
This function obeys the marginality properties:
- (i)
- where comprises the matrix elements of on the basis .
- (ii)
- (iii)
- For a pure state , these formulae simplify to
- (iv)
- From these two marginal properties, the normalization of results as a complex-valued quasi-distribution:
Let us discuss more about the properties of the squared rotation operator.
Proposition 10.
- (i)
- The operator is unit trace.
- (ii)
- (iii)
- The inverse partial Fourier transform of the weight with respect to the momentum is given byandand the kernel of the related quantum operator is given bywith the notations of (89).
Proof.
- (i)
- (ii)
- (iii)
- The proof is direct.
□
In the following, we calculate the kernels and/or the corresponding operators for various straightforward cases of . It is worth noting that we obtain our results quite easily, in contrast to the outcomes that would be obtained using alternative definitions of Wigner distributions , such as those discussed in [36] and [39].
- (a)
- For ,
- (b)
- For ,Hence, the quantized of is the multiplication operator.
- (c)
- For ,
9. Conclusions
In this paper, we introduce a covariant integral quantization approach for systems with a phase space, known as the semi-discrete hypercylinder , i.e., where the configuration space is and is defined by . This extends our prior work on the discrete cylinder , which addressed the motion of a particle on the circle . The phase space is not a coset arising from a group; we demonstrate that the Weyl–Gabor formalism is applicable.
First, we establish the concomitant resolution of the identity and its subsequent properties, including the Gabor transform on , its inversion, the reproducing kernel, and the crucial observation that any square-integrable function on the group can be considered a fiducial vector. Leveraging the decomposition of the identity, we define an integral operator based on a weight function defined on the phase space.
There are noticeable results related to the quantization of a point
in the phase space according to two standard choices of the weight.
- With the squared rotation weight, which yields the Wigner distribution, the quantization of the projection of momentum on the third axis is the expected angular momentum operator .while the quantization of the angle yields the multiplication operator by the angle:This is clearly not acceptable because of the discontinuity in the periodized angle function, as there is no regularization for this discontinuity.
- On the other hand, by using the squared rotation weight, we obtain a Wigner distribution that is more manageable than those derived in previous works [36,39]. We will demonstrate this through concrete examples in our future research.
- Using the coherent state weight, one can obtain the quantization of momentum, which includes the conventional operator along with an additional term. This additional term can be seen as a kind of covariant derivative along the circle within , taking into account the topology of this manifold,Furthermore, the quantization of the periodized function in the variable results in its smooth regularization.
In future studies, we intend to expand upon the findings of this work in various directions.
- We plan to extend this work to encompass all rotation groups , as well as the associated spheres . Additionally, we will explore the quantization of continuous phase space related to the Euclidean groups , , as described in the references [49,50].
- We plan to extend this work to the full configuration space of the rigid body, that is, the Euclidean motion group in three dimensions .
- We plan to apply our formalism to the case where the configuration space is a non-compact group, for example, or .
- We plan to explore the possibility of the covariant integral quantization in the situation where the phase space is This phase space is used in the context of quantum loop gravity [51,52].
- Finally, we plan to apply our approach to signal analysis on SO. We will investigate the robustness of the phase space representation of a signal in capturing salient futures in the signal. Various tools will be used. These tools include visualization of various partial energy densities of the Gabor transform, quantum operators related to various fiducial vectors, Husimi distributions, Wigner distribution, entropy, and sampling/frames on [46,53].
Author Contributions
Conceptualization, J.-P.G. and R.M.; methodology, J.-P.G. and R.M.; validation, J.-P.G. and R.M.; formal analysis, J.-P.G. and R.M.; investigation, J.-P.G. and R.M.; writing—original draft preparation, R.M.; writing—review and editing, J.-P.G. and R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
J.-P. Gazeau thanks ICTP Trieste for hosting him during the preparation of this work. We acknowledge discussions with Mladen Victor Wickerhauser.
Conflicts of Interest
The authors declare no conflict of interest. The ideas and opinions expressed in this article are those of the authors and do not necessary represent the view of UNESCO.
Abbreviations and Nomenclature
The following abbreviations are used in this manuscript:
| POVM | Positive operator-valued measure |
| UIR | Unitary irreducible representation |
| CS | Coherent state |
| Phase space | |
| Hilbert space | |
| Hilbert space | |
| Hilbert space | |
| ZYZ | Successive rotation about the z-axis, new x-axis, and new z-axis |
| Defined in (17) | |
| Dirac distribution with support the neutral element of SO, defined in (31) | |
| Dirac distribution with support the element of SO, defined in (33) | |
| Fourier transform of , defined in (41) | |
| Discrete momentum, defined in (43) | |
| Hilbertian basis element, defined in (45) | |
| Multiplication operator defined in (49) | |
| Transpose of , defined in (52) | |
| SO-Weyl–Gabor operator, defined in (53) | |
| Coherent state from fiducial vector , defined in (59) | |
| Gabor transform, defined in (62) | |
| Quantization operator defined in (76) | |
| Partial inverse discrete Fourier transform (48) of with respect to the discrete variables | |
| Squaring rotation operator defined in (83) | |
| SO-Weyl-Gabor operator transport of , defined in (85) | |
| Integral defined in (91) | |
| Defined in (93), (94), (95), respectively | |
| Weight corresponding to the one-rank density operator , defined in (10) |
Appendix A. Some Formulas for CS Quantization
In this appendix, we compute , for the coherent state weight for , using the following summation formulae [54]:
We therefore have
Let us now two types of fiducial vectors.
- Free rotor and highest weight fiducial vectors.For the free rotor with momentum , we obtain , andFor the highest weight state for , that is, with momentum , we obtain
- Radial fiducial vector.We consider a radial vector depending only on the distance to the origin . We have and [21].Finally,
Appendix B. Plot of Von Mises Fiducial Vector and Derivative
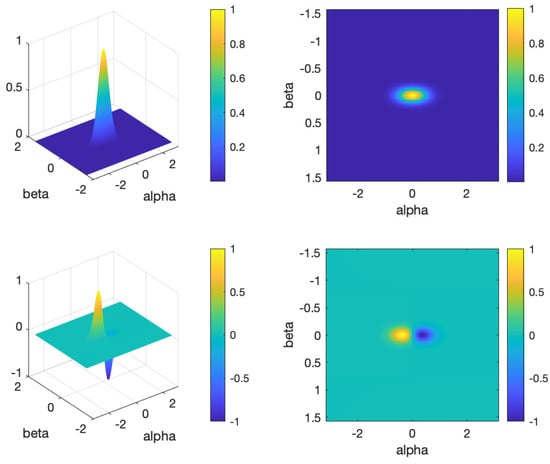
Figure A1.
Top left and right: Von Mises fiducial vector as a function of the Euler angles () at parameter and the third Euler angle . Bottom left and right: Derivative with respect to of the Von Mises fiducial vector as a function of the Euler angles () at and . Color bars indicate the values of these functions. The peaked and localized nature of these functions is evident.
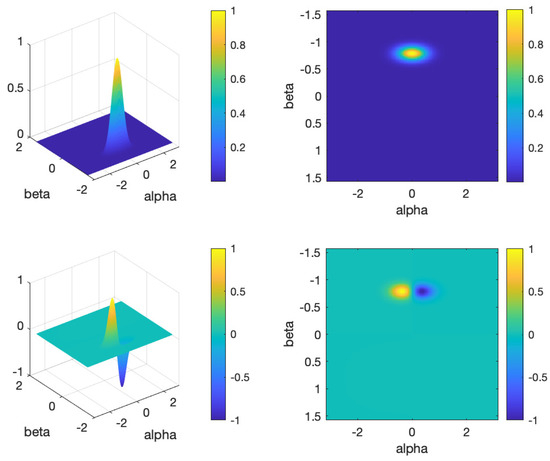
Figure A2.
Top left and right: Von Mises fiducial vector as a function of the Euler angles () at parameter and the third Euler angle . Bottom left and right: Derivative with respect to of the Von Mises fiducial vector as a function of the Euler angles () at and . The peaked and localized nature of these functions is also evident.
References
- Marle, C.-M. On Mechanical Systems with a Lie Group as Configuration Space. In Proceedings of the Jean Leray ’99 Conference Proceedings, the Karlskrona Conference in Honor of Jean Leray, Fairfield, OH, USA, 20–30 September 1999; pp. 183–203. [Google Scholar]
- Prieto, C.T. Quantization and spectral geometry of a rigid body in a magnetic monopole field. Differ. Geom. Appl. 2001, 14, 157–179. [Google Scholar]
- Khatua, S.; Ganesh, R. Berry phase in the rigid rotor: Emergent physics of odd antiferromagnets. Phys. Rev. B 2022, 105, 184401. [Google Scholar] [CrossRef]
- Casimir, H. Rotation of a Rigid Body in Quantum Mechanics. Ph.D. Thesis, University of Leiden, Leiden, The Netherlands, 1931. [Google Scholar]
- Breev, A.; Gitman, D. New Exact Solutions Describing Quantum Asymmetric Top. Symmetry 2023, 15, 503. [Google Scholar]
- Wells, T.; Raston, P.L. Concerning the asymmetric top rotational partition function in astronomical spectroscopy. J. Mol. Spectrosc. 2020, 370, 111292. [Google Scholar]
- Karczmarek, J.; Wright, J.; Corkum, P.; Ivanov, M. Optical Centrifuge for Molecules. Phys. Rev. Lett. 1999, 26, 3420–3423. [Google Scholar]
- Makito, O. Revisiting the Concept of Nuclear Rotation: Quantum and Classical Viewpoints. Bulg. J. Phys. 2022, 49, 97–107. [Google Scholar]
- Boscain, U.; Pozzoli, E.; Sigalotti, M. Classical and quantum controllability of a rotating 3D symmetric molecule. SIAM J. Control Optim. 2021, 59, 156–184. [Google Scholar]
- Koch, C.P.; Lemeshko, M.; Sugny, D. Quantum control of molecular rotation. Rev. Mod. Phys. 2019, 91, 035005. [Google Scholar]
- Thiamova, G.; Rowe, D.J.; Caprio, M.A. The relationship between the interacting boson model and the algebraic version of Bohr’s collective model in its triaxial limit. Nucl. Phys. A 2012, 895, 20–32. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Collective Nuclear Motion and the Unified Model. In Beta and Gamma Ray Spectroscopy; Siegbahn, K., Ed.; North Holland Publishing Co.: Amsterdam, The Netherlands, 1955; Chapter XVII; pp. 468–493. [Google Scholar]
- Dudek, J.; Gozdz, A.; Curien, D.; Pangona, V.; Schunc, N. Nuclear Tetrahedral Symmetry and Collective Rotation. Acta Phys. Pol. Ser. B 2006, 38, 1389–1404. [Google Scholar]
- Bohm, A.; Teese, R.B. Spectrum generating group of the symmetric top molecule. J. Math. Phys. 1976, 17, 94. [Google Scholar] [CrossRef]
- Bozic, M.; Arsenovic, D. Quantum magnetic top. In Quantization and Infinite-Dimensional Systems; Antoine, J.-P., Ali, S.T., Lisiecki, W., Mladenov, I.M., Odzijewicz, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Toth, J.A. Eigenfunction localization in the quantized rigid. J. Difer. Geom. 1996, 43, 844–858. [Google Scholar] [CrossRef]
- Yashnikov, V.P.; Bunge, H.J. Geometrical Foundations of Texture Analysis. Geodesic Curves and Motions in the group Space of Three-Dimensional Rotations. Textures Microstruct. 1997, 30, 959050. [Google Scholar] [CrossRef]
- Man, C.-S. Crystallographic Texture and Group Representations. J. Elast. 2022, 149, 3–445. [Google Scholar]
- Savyolova, T.I.; Filatov, S.V. About normal distribution on SO(3) group in texture analysis. J. Phys. Conf. Ser. 2017, 937, 012045. [Google Scholar]
- Chirikjian, G.S.; Kyatkin, A.B. Engineering Applications of Noncommutative Harmonic Analysis With Emphasis on Rotation and Motion Groups; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Vollrath, A. Nonequispaced Fast SO(3) Fourier Transform—Generalisations and Applications. Ph.D. Thesis, Lübeck University, Lübeck, Germany, 2010. [Google Scholar]
- Uçan, Y.; Bildirici, M. Air temperature measurement based on lie group SO(3). Therm. Sci. 2022, 26, 3089–3095. [Google Scholar] [CrossRef]
- Bildirici, M.; Ucan, Y.; Lousada, S. Interest Rate Based on The Lie Group SO(3) in the Evidence of Chaos. Mathematics 2022, 10, 3998. [Google Scholar]
- Markley, F. Attitude Filtering on SO(3). J. Astronaut. Sci. 2006, 54, 391–413. [Google Scholar] [CrossRef]
- Lee, T.; Leok, M.; McClamroch, N.H. Optimal Attitude Control of a Rigid Body Using Geometrically Exact Computations on SO(3). J. Dyn. Control Syst. 2008, 14, 465–487. [Google Scholar]
- Lee, T.; Leok, M.; McClamroch, N.H. Global Symplectic Uncertainty Propagation on SO(3). In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Berkane, S. Hybrid Attitude Control and Estimation On SO(3). Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, 2017. [Google Scholar]
- Lee, T. Bayesian Attitude Estimation With the Matrix Fisher Distribution on SO(3). IEEE Trans. Autom. Control 2018, 63, 18. [Google Scholar] [CrossRef]
- Berkane, S.; Tayebi, A. Construction of Synergistic Potential Functions on SO(3) With Application to Velocity-Free Hybrid Attitude Stabilization. IEEE Trans. Autom. Control 2017, 62, 495–501. [Google Scholar] [CrossRef]
- Albert, V.V.; Covey, J.P.; Preskill, J. Robust encoding of a qubit in a molecule. Phys. Rev. X 2020, 10, 031050. [Google Scholar] [CrossRef]
- Kazhdan, M.; Funkhouser, T.; Rusinkiewicz, S. Rotation invariant spherical harmonic representation of 3D shape descriptors. In Proceedings of the Eurographics Symposium on Geometry Processing, Aachen, Germany, 23–25 June 2003; pp. 156–164. [Google Scholar]
- Hoover, R.C.; Maciejewski, A.A.; Roberts, R.G. Pose detection of 3-D objects using images sampled on SO(3) spherical harmonics, and Wigner-D matrices. In Proceedings of the 2008 IEEE International Conference on Automation Science and Engineering, Arlington, VA, USA, 23–26 August 2008; pp. 47–52. [Google Scholar]
- Gazeau, J.-P.; Murenzi, R. Integral Quantization for the Discrete Cylinder. Quantum Rep. 2022, 4, 362–379. [Google Scholar] [CrossRef]
- Fabre, N.; Klimov, A.B.; Murenzi, R.; Gazeau, J.-P.; Sanchez-Soto, L.L. Majorana stellar representation of twisted photons. Phys. Rev. Res. 2023, 5, L032006. [Google Scholar] [CrossRef]
- Mukunda, N.; Arvind, S.; Chaturvedi, S.; Simon, R. Wigner distributions and quantum mechanics on Lie groups: The case of the regular representation. J. Math. Phys. 2004, 45, 114–148. [Google Scholar] [CrossRef]
- Mukunda, N.; Marmo, G.; Zampini, A.; Chaturvedi, S.; Simon, R. Wigner Weyl isomorphism for quantum mechanics on Lie groups. J. Math. Phys. 2005, 46, 012106. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Marmo, G.; Mukunda, N.; Simon, R.; Zampini, A. The Schwinger Representation of a Group: Concept and Applications. Rev. Math. Phys. 2006, 18, 887–912. [Google Scholar] [CrossRef]
- Fischer, T.; Gneiting, C.; Hornberger, K. Wigner function for the orientation state. New J. Phys. 2013, 15, 063004. [Google Scholar] [CrossRef]
- Grigorescu, M. Coherent distributions for the rigid rotator. J. Math. Phys. 2016, 57, 062702. [Google Scholar] [CrossRef]
- Bergeron, H.; Gazeau, J.P. Integral quantizations with two basic examples. Ann. Phys. 2014, 344, 43–68. [Google Scholar] [CrossRef]
- Ali, S.T.; Antoine, J.-P.; Gazeau, J.-P. Coherent States, Wavelets and their Generalizations. In Theoretical and Mathematical Physics, 2nd ed.; Springer: New York, NY, USA, 2014; Chapter 11. [Google Scholar]
- Gazeau, J.-P.; Murenzi, R. Covariant Affine Integral Quantization(s). J. Math. Phys. 2016, 57, 052102. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Koide, T.; Murenzi, R. 2-D Covariant Affine Integral Quantization(s). Adv. Oper. Theory 2020, 5, 901–935, Correction in Adv. Oper. Theory 2022, 7, 22. [Google Scholar] [CrossRef]
- Edmonds, A.R. Angular Momentum in Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Magnus, W.; Oberhettinger, F.; Soni, R.P. Formulas and Theorems for the Special Functions of Mathematical Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1966. [Google Scholar]
- McEwen, J.D.; Buttner, M.; Boris Leistedt, B.; Peiris, H.V.; Wiaux, Y.A. Novel sampling theorem on the rotation group. IEEE Signal Process. Lett. 2005, 22, 2425–2429. [Google Scholar] [CrossRef]
- Risbo, T. Fourier transform summation of Legendre series and D-functions. J. Geod. 2020, 70, 383–396. [Google Scholar] [CrossRef]
- Biedenharn, L.C.; Louck, J.D.; Carruthers, P.A. Standard Treatment of Angular Momentum in Quantum Mechanics. In Angular Momentum in Quantum Physics, Theory and Application; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Torresani, B. Position-frequency analysis for signals defined on spheres. Signal Process. 1995, 43, 341–346. [Google Scholar] [CrossRef]
- Fresneda, R.; Gazeau, J.-P.; Noguera, D. Quantum localisation on the circle. J. Math. Phys. 2018, 59, 052105. [Google Scholar] [CrossRef]
- Oriti, D.; Raasakka, M. Quantum Mechanics on SO(3) via Non-commutative Dual Variables. Phys. Rev. D 2011, 84, 025003. [Google Scholar] [CrossRef]
- Freidel, L.; Livine, E.R. Ponzano-Regge model revisited III: Feynman diagrams and Effective field theory. Class. Quantum Grav. 2006, 23, 2021–2061. [Google Scholar] [CrossRef]
- Murenzi, R. Ondelettes Multidimensionnelles et Applications à L’analyse d’Images. Ph.D. Thesis, Catholic University of Louvain, Louvain, Belgium, 1990. [Google Scholar]
- Lai, S.-T.; Palting, P.; Chiu, Y.-N.; Silverstone, H.J. On the summations involving Wigner rotation matrix elements. J. Math. Chem. 1998, 24, 123–132. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).