On a New Ma-Minda Class of Analytic Functions Created by a Roulette Curve Formula

Abstract

It is well known that there are two important classes of analytic functions of Ma-Minda type (MMT): Ma-Minda starlike and Ma-Minda convex functions. In this work, we suggest a new class of analytic functions, which is normalized in the open unit disk. The suggested class is generated by a roulette curve formula, which satisfies the symmetric behavior in the open unit disk. A roulette curve is shaped as the path outlined by the sum of two complex numbers, each affecting at a uniform rapidity in a circle. Special cases are illustrated involving special functions. Graphics of the curve are illustrated by using Mathematica 13.3.

1. Introduction

In mathematics, a roulette curve is a curve that is traced by a point on a curve as it moves along another curve. Generally, the location of this moving point in relation to the curve being rolled upon is fixed. The shape of the resulting curve, known as a roulette curve, is determined by the particular curves involved and the separation between them. A special case is one in which the center of the revolving circle always lies on the line. The curve that is produced as a result has intriguing mathematical characteristics and uses. Trigonometric functions and parametric equations are used in the equations which explain roulette curve structures, and they can be rather complex [1,2,3]. They are often utilized to mimic a variety of mechanical and geometric phenomena, including the actions of pendulums, the contours of the orbits of the planets, and the rotation of the gears. A special curve of the roulette curve structures is the centered trochoid curve. In mathematics, a curve is referred to as a “centered trochoid curve” when it is produced by a point rolling down a different curve, usually a straight line. The moving point’s subsequent curve is known as the roulette curve. There are many different kinds of roulette curves, and they can take on a variety of designs according to the individual curves and rolling action. A few usual instances are the trochoid, which is produced by a point on the circumference of a revolving circle, and the epitrochoid, which is produced by a point on a smaller circle rolling around the outside of a bigger stationary circle. We shall formulate the class of analytic functions based on the definition of the roulette curve between two analytic normalized functions.

Two significant classes of starlike and convex normalized functions, which are characterized by idea subordination, were introduced by Ma and Minda [4] in the open unit disk. Numerous studies have generalized and expanded on these groupings. Additionally, these classes were constructed by the researchers utilizing different types of operators, such as convoluted operators with derivatives and integration [4].

Define the class of normalized analytic functions as follows: $f\left(\xi \right)\in \wedge ,\xi \in \mathbb{k}:=\{\xi \in \mathbb{C}:|\xi |<1\}$ having the structure

$$f\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{\alpha }_n{\xi }^n,\xi \in \mathbb{k}.$$

(1)

Then, the MMT starlike class symbolizing by ${\mho }^{*}$ is formulated by the formula

$$\frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}\prec F\left(\xi \right),\xi \in \mathbb{k},$$

(2)

where F designates an analytic function with an optimistic real measure on $\mathbb{k}$, $F\left(0\right)=1,F^{\prime }\left(0\right)>0,$ and F maps $\mathbb{k}$ onto a starlike domain conforming to $\partial \mathbb{k}$ that is symmetric through deference to the real axis. And the representation ≺ designates the description of the subordination (see [5]). The MMT convex class symbolized by ${\mho }^c$ is framed by the subordination discrimination

$$1+\frac{\xi f^{″}\left(\xi \right)}{f^{\prime }\left(\xi \right)}\prec F\left(\xi \right),\xi \in \mathbb{k}.$$

(3)

Moreover, the linear combination of these two classes is defined in what is called an MMT $\alpha$convex class $\left({\mho }^{\alpha }\right)$ achieving the formula [6]

$$(1-\alpha )\frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}+\alpha \left(1+\frac{\xi f^{″}\left(\xi \right)}{f^{\prime }\left(\xi \right)}\right)\prec F\left(\xi \right),\xi \in \mathbb{k}.$$

(4)

Many researchers defined special cases by suggesting a specific formula of F such as Janowski function [7], integral operator [8], $1+sin\left(\xi \right)$ function [9], close to convex [10], quasi-subordination classes [11], $\tau$-class [12], Quantum classes (see [13,14]), Nephroid domain with parametric function [15], exponential function [16], lemniscate of Bernoulli [17], MMT starlike and convex of complex order [18], bi-pseudo-starlike functions [19,20], fractional calculus [21], linear operator [22], conformable fractional operator [23] and other combination and convolution classes which can be located in [24,25,26,27,28].

2. Preliminaries

We request the following result, which can be located in [5] (p. 132).

Lemma 1.

Suppose that $f_1$ is a univalent function in $\mathbb{k}$ and $f_2$ and $f_3$ are analytic in a domain Δ involving $f_1\left(\mathbb{k}\right)$ such that $f_3\left(\xi \right)\ne 0,$ where $\xi \in f_1\left(\mathbb{k}\right).$ By consuming

$$F_1\left(\xi \right)=\xi f_1^{\prime }\left(\xi \right).f_3\left[f_1\left(\xi \right)\right],F_2\left(\xi \right)=f_2\left[f_1\left(\xi \right)\right]+F_1\left(\xi \right)$$

and

• $F_1$ is starlike, or
• $F_2$ is convex, and
• $\Re \left(\frac{\xi F_2^{\prime }\left(\xi \right)}{F_1\left(\xi \right)}\right)=\Re \left(\frac{f_2^{\prime }\left[f_1\left(\xi \right)\right]}{f_3\left[f_1\left(\xi \right)\right]}+\frac{\xi F_1^{\prime }\left(\xi \right)}{F_1\left(\xi \right)}\right)>0.$

If ℘ is analytic in $\mathbb{k}$ such that $\wp \left(0\right)=f_1\left(0\right)$ and

$$f_2[\wp \left(\xi \right)]+\xi {\wp }^{\prime }\left(\xi \right)f_3[\wp \left(\xi \right)]\prec f_2\left[f_1\left(\xi \right)\right]+\xi f_1^{\prime }\left(\xi \right)f_3\left[f_1\left(\xi \right)\right]=F_2\left(\xi \right),$$

then $\wp \prec f_1$ and $f_1$ is the best dominant.

Definition 1.

A function $\phi \in H[a,n]$ where

$$H[a,n]=\{\varphi \in H\left(\mathbb{k}\right):\varphi \left(\xi \right)=a+{\varphi }_n{\xi }^n+{\varphi }_{n+1}{\xi }^{n+1}+...\}$$

is called a strongly Caratheodory function of order ν if it achieves

$$\left|arg\left\{\phi \left(\xi \right)\right\}\right|<\frac{\pi }{2}\nu ,\nu \in (0,1],\xi \in \mathbb{k}.$$

Moreover, a function $f\in \wedge$ is called a strongly starlike function of order ν if it satisfies

$$\left|\frac{\xi f^{\prime }\left(\xi \right)}{f\left(\xi \right)}\right|<\frac{\pi }{2}\nu ,\nu \in (0,1],\xi \in \mathbb{k}.$$

Note that when $\nu =1,$ then f is starlike. We have the following result, which can be found in [29]

Lemma 2.

Let the function $f\left(\xi \right)$ be analytic in $\mathbb{k}$ with

$$\mathsf{\Lambda }:=\underset{\xi \in \mathbb{k}}{inf}\{\Re \left(f\left(\xi \right)\right)sin\left(\frac{\pi }{2}\nu \right)-|\Im \left(f\left(\xi \right)\right)cos\left(\frac{\pi }{2}\nu \right)|>0,\nu \in (0,1]\}>0.$$

If $♭\in H[1,n],♭\ne 1$ is satisfying the inequality

$$\Re \left(♭\left(\xi \right)+f\left(\xi \right)\left(\xi {♭}^{\prime }\left(\xi \right)\right)\right)>\frac{1}{2n\mathsf{\Lambda }}[(sin\left(\frac{\pi }{2}\nu \right)+2n\mathsf{\Lambda }){cos}^2\left(\frac{\pi }{2}\nu \right)-n^2{\mathsf{\Lambda }}^{2}sin\left(\frac{\pi }{2}\nu \right)]$$

then ♭ is a strongly starlike function of order ν.

3. Ma-Minda Type (MMT) Generated by Roulette Curve

In this section, we present the definition of a new class of analytic functions using the formula of the roulette curve function.

Definition 2.

The function $\sigma \in \wedge$ is grouped in the class $M^{⊺}\left(\varsigma \right)$ if and only if there occur a normalized analytic function $\rho \in \wedge$ and analytic function ς with $\varsigma \left(0\right)=1,{\varsigma }^{\prime }\left(0\right)>0$ satisfying the inequality

$$\sigma \left(\xi \right)+\left(1-\rho \left(\xi \right)\right)\left(\frac{{\sigma }^{\prime }\left(\xi \right)}{{\rho }^{\prime }\left(\xi \right)}\right)\prec \varsigma \left(\xi \right),\xi \in \mathbb{k},$$

(5)

where σ is rolled on ρ such that

$$\sigma \left(0\right)=\rho \left(0\right),{\sigma }^{\prime }\left(0\right)={\rho }^{\prime }\left(0\right)\ne 0$$

and

$$\varsigma \left(\xi \right)=1+A_1\xi +A_2{\xi }^2+A_3{\xi }^3+...,A_1,A_2,...>0.$$

The left side of (5) is known as the roulette curve. The numerous roulette curve types and their potential shapes rely on the individual curves and rolling motions. The cycloid, which is produced by a point on a rotating circle, the trochoid, which is produced by a point on a rotating circle’s circumference, and the epitrochoid, which is produced by a point on a smaller circle rotating around a bigger fixed circle, are a few forms that are frequently used. These curves have intriguing qualities and can be applied to a variety of tasks in physics, mathematics, and the performing arts.

The physical meaning of the roulette curve is understood when a body moves in a curve under two forces: the centripetal force and the centrifugal. The force that pushes inward and maintains an object moving along a curving route is known as centripetal force. It serves to stop an object traveling in a straight line tangent to the curve and is aimed at the curve’s center. Centrifugal force is a projected force that appears to be pushing outward on an object traveling in a curve but is actually not a real force. It is a result of a thing’s propensity to move in straight lines and gravity. The object would actually prefer to proceed straight ahead, but the curved path prevents it from doing so. In some situations, it can be suggested as circular motion, in which an item moves in a circle around a center as the result of a constant force, which can be compared to roulette curves. Angular velocity, centripetal acceleration, and other kinematic variables can be used to describe this motion, satisfying the map

$$\xi \mapsto \sigma \left(\xi \right)+\left(1-\rho \left(\xi \right)\right)\left(\frac{{\sigma }^{\prime }\left(\xi \right)}{{\rho }^{\prime }\left(\xi \right)}\right).$$

For example, for the convex univalent function $\sigma \left(\xi \right)={\displaystyle \frac{\xi }{1-\xi }}$ and $\varsigma \left(\xi \right)={\displaystyle \frac{1+\xi }{1-\xi }},$ the rolled function is $\rho \left(\xi \right)=\xi .$ While for the starlike univalent function $\sigma \left(\xi \right)={\displaystyle \frac{\xi }{{(1-\xi )}^2}}$ and $\varsigma \left(\xi \right)={\displaystyle \frac{1+\xi }{1-\xi }},$ the rolled function is

$$\begin{array}{cc}\hfill \rho \left(\xi \right)& ={\displaystyle \frac{1}{{(1-\xi )}^2}}[{(2\xi +\sqrt{5}+1)}^{-2/\sqrt{5}}{\left({\displaystyle \frac{1+\sqrt{5}}{\sqrt{5}-1}}\right)}^{2/\sqrt{5}}{\xi }^2{(-2\xi +\sqrt{5}-1)}^{2\sqrt{5}}\hfill \\ \hfill & +{\xi }^2{(2\xi +\sqrt{5}+1)}^{2\sqrt{5}}+{\left({\displaystyle \frac{1+\sqrt{5}}{\sqrt{5}-1}}\right)}^{2\sqrt{5}}\xi {(-2\xi +\sqrt{5}-1)}^{2/\sqrt{5}}\hfill \\ \hfill & -{\left({\displaystyle \frac{1+\sqrt{5}}{\sqrt{5}-1}}\right)}^{2/\sqrt{5}}{(-2\xi +\sqrt{5}-1)}^{2/\sqrt{5}}\hfill \\ \hfill & -2\xi {(2\xi +\sqrt{5}+1)}^{2/\sqrt{5}}+{(2\xi +\sqrt{5}+1)}^{2/\sqrt{5}}]\hfill \\ \hfill & =\xi +...\hfill \end{array}$$

On this point, we proceed to investigate some geometric properties of the suggested class.

Theorem 1.

If the analytic normalized function

$$\sigma \left(\xi \right)=\xi +\sum _{n=2}^{\infty }{\alpha }_n{\xi }^n\in M^{⊺}\left(\varsigma \right)$$

then for

$$\rho \left(\xi \right)=\xi +\sum _{n=2}^{\infty }{\rho }_n{\xi }^n,\left|{\rho }_2\right|\le 1/4$$

the difference of connection bounds are

$$|{\alpha }_2-{\rho }_2|\le \frac{1}{2}{A}_1$$

and

$$|{\alpha }_3-{\rho }_3|\le \frac{1}{3}\left(A_1+A_2\right).$$

Proof. 

Since $\sigma \in M^{⊺}\left(\varsigma \right)$, then there occurs an analytic function $\omega \left(\xi \right)$ with the following properties:

$$\omega \left(0\right)=0,\left|\omega \right(\xi \left)\right|<1,\xi \in \mathbb{k}$$

and

$$\sigma \left(\xi \right)+\left(1-\rho \left(\xi \right)\right)\left(\frac{{\sigma }^{\prime }\left(\xi \right)}{{\rho }^{\prime }\left(\xi \right)}\right)=\varsigma \left(\omega \left(\xi \right)\right),\xi \in \mathbb{k}.$$

Define a function

$$\begin{array}{cc}\hfill \mathsf{{\rm Y}}\left(\xi \right)& =\frac{1+\omega \left(\xi \right)}{1-\omega \left(\xi \right)}\hfill \\ \hfill & =1+{\lambda }_1\xi +{\lambda }_2{\xi }^2+...\hfill \\ \hfill & \prec \frac{1+\xi }{1-\xi },\xi \in \mathbb{k}.\hfill \end{array}$$

Obviously, $\mathsf{{\rm Y}}\left(0\right)=1$ and has a positive real part in $\mathbb{k}.$ A calculation implies that

$$\begin{array}{cc}\hfill \omega \left(\xi \right)& =\frac{\mathsf{{\rm Y}}\left(\xi \right)-1}{\mathsf{{\rm Y}}\left(\xi \right)+1}\hfill \\ \hfill & =\frac{1}{2}\left({\lambda }_1\xi +({\lambda }_2-\frac{{\lambda }_1^2}{2}){\xi }^2+...,\right).\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}\hfill \sigma \left(\xi \right)+\left(1-\rho \left(\xi \right)\right)\left(\frac{{\sigma }^{\prime }\left(\xi \right)}{{\rho }^{\prime }\left(\xi \right)}\right)& =\varsigma \left(\omega \right(\xi \left)\right)\hfill \\ \hfill & =\varsigma \left(\frac{\mathsf{{\rm Y}}\left(\xi \right)-1}{\mathsf{{\rm Y}}\left(\xi \right)+1}\right)\hfill \\ \hfill & =1+\left(\frac{1}{2}{A}_1{\lambda }_1\right)\xi +\left(\frac{1}{2}{A}_1({\lambda }_2-\frac{{\lambda }_1^2}{2})+\frac{1}{4}{A}_2{\lambda }_1^2\right){\xi }^2+...\hfill \end{array}$$

(6)

By letting $\rho \left(\xi \right)=\xi +{\sum }_{n=2}^{\infty }{\rho }_n{\xi }^n,$ then we obtain

$$\begin{array}{cc}\hfill & \sigma \left(\xi \right)+\left(1-\rho \left(\xi \right)\right)\left(\frac{{\sigma }^{\prime }\left(\xi \right)}{{\rho }^{\prime }\left(\xi \right)}\right)\hfill \\ \hfill & =\left(\xi +\sum _{n=2}^{\infty }{\alpha }_n{\xi }^n\right)+\left(1-\xi -\sum _{n=2}^{\infty }{\rho }_n{\xi }^n\right)\left(\frac{1+{\sum }_{n=2}^{\infty }n{\alpha }_n{\xi }^{n-1}}{1+{\sum }_{n=2}^{\infty }n{\rho }_n{\xi }^{n-1}}\right)\hfill \\ \hfill & =\left(\xi +\sum _{n=2}^{\infty }{\alpha }_n{\xi }^n\right)+\left(1-\xi -\sum _{n=2}^{\infty }{\rho }_n{\xi }^n\right)\hfill \\ \hfill & \times \left(1+2({\alpha }_2-{\rho }_2)\xi +[3({\alpha }_3-{\rho }_3)-4{\rho }_2({\alpha }_2-{\rho }_2)]{\xi }^2+...\right)\hfill \\ \hfill & =\left(\xi +{\alpha }_2{\xi }^2+{\alpha }_3{\xi }^3+...\right)\hfill \\ \hfill & +\left(1-\xi -{\rho }_2{\xi }^2-{\rho }_3{\xi }^3-...\right)\left(1+2({\alpha }_2-{\rho }_2)\xi +[3({\alpha }_3-{\rho }_3)-4{\rho }_2({\alpha }_2-{\rho }_2)]{\xi }^2+...\right)\hfill \\ \hfill & =1+\left(2({\alpha }_2-{\rho }_2)\right)\xi +\left([3({\alpha }_3-{\rho }_3)-4{\rho }_2({\alpha }_2-{\rho }_2)]-({\alpha }_2-{\rho }_2)\right){\xi }^2\hfill \\ \hfill & +\left(({\alpha }_3-{\rho }_3)-[3({\alpha }_3-{\rho }_3)-4{\rho }_2({\alpha }_2-{\rho }_2)]-2{\rho }_2({\alpha }_2-{\rho }_2)\right){\xi }^3+...\hfill \end{array}$$

(7)

Equating the coefficients of (6) and (7), we have

$$\begin{array}{cc}\hfill & ({\alpha }_2-{\rho }_2)=\frac{1}{4}{A}_1{\lambda }_1\hfill \\ \hfill & [3({\alpha }_3-{\rho }_3)-4{\rho }_2({\alpha }_2-{\rho }_2)]-({\alpha }_2-{\rho }_2)=\frac{1}{2}{A}_1({\lambda }_2-\frac{{\lambda }_1^2}{2})+\frac{1}{4}{A}_2{\lambda }_1^2\hfill \\ \hfill & ⟹({\alpha }_3-{\rho }_3)=\frac{1}{3}({\alpha }_2-{\rho }_2)(4{\rho }_2+1)+\frac{1}{6}{A}_1({\lambda }_2-\frac{{\lambda }_1^2}{2})+\frac{1}{12}{A}_2{\lambda }_1^2\hfill \\ \hfill & ⟹({\alpha }_3-{\rho }_3)=\frac{1}{12}\left(A_1{\lambda }_1\right)(4{\rho }_2+1)+\frac{1}{6}{A}_1({\lambda }_2-\frac{{\lambda }_1^2}{2})+\frac{1}{12}{A}_2{\lambda }_1^2.\hfill \end{array}$$

(8)

Since $\mathsf{{\rm Y}}\in \mathcal{P}$ (the class of functions with a positive real part), then $|{\lambda }_1|\le 2$ implies that $|{\alpha }_2-{\rho }_2|\le \frac{1}{2}{A}_1.$ For the second difference, we have

$$\begin{array}{cc}\hfill & \frac{1}{12}\left(A_1{\lambda }_1\right)(4{\rho }_2+1)+\frac{1}{6}{A}_1({\lambda }_2-\frac{{\lambda }_1^2}{2})+\frac{1}{12}{A}_2{\lambda }_1^2\hfill \\ \hfill & =\frac{1}{12}\left(A_1{\lambda }_1\right)(4{\rho }_2+1)+\frac{1}{3}{A}_1+\frac{1}{12}{\lambda }_1^2\left(A_2-A_1\right)\hfill \\ \hfill & \le \frac{1}{6}\left(A_1\right)(4{\rho }_2+1)+\frac{1}{3}{A}_1+\frac{1}{3}\left(A_2-A_1\right)\hfill \\ \hfill & =\frac{1}{6}\left(A_1\right)(4{\rho }_2+1)+\frac{1}{3}{A}_2\hfill \\ \hfill & \le \frac{1}{6}\left(A_1\right)\left(4\right|{\rho }_2|+1)+\frac{1}{3}{A}_2\hfill \\ \hfill & \le \frac{1}{3}\left(A_1+A_2\right).\hfill \end{array}$$

(9)

This ends the proof. □

Definition 3.

A function ${\varsigma }_{Ne}:=1+\xi -{\xi }^3/3,$ (the Caratheodory function), which sings the boundary of the unit disk $\partial \mathbb{k}$ univalently onto a 2D curve, is called nephroid achieving

$${\left({(\mu -1)}^2+{\nu }^2-4/9\right)}^3=4/3{\nu }^2,$$

where ${\varsigma }_{Ne}:=\mu +i\nu .$ The function $\sigma \in \wedge$ is called in the class $M_{Ne}^{⊺}$ if and only if there occurs a normalized rolling function $\rho \in \wedge$ and analytic function ς with $\varsigma \left(0\right)=1,{\varsigma }^{\prime }\left(0\right)>0$ satisfying the inequality

$$\sigma \left(\xi \right)+\left(1-\rho \left(\xi \right)\right)\left(\frac{{\sigma }^{\prime }\left(\xi \right)}{{\rho }^{\prime }\left(\xi \right)}\right)\prec {\varsigma }_{Ne}\left(\xi \right),\xi \in \mathbb{k}.$$

(10)

In terms of geometry, a nephroid is the location of a stationary point on the perimeter of a moving ring of radius r that is fixed at one end. When the light basis is at infinity, the behavior of the nephroid curve which Huygens and Tschirnhausen first proposed in 1697 is revealed to be the envelope of rays emanating from a specified point in a ring. The nephroid is a cardioid’s cat-caustic for a bright cusp, according to Jakob Bernoulli’s 1692 observation. But Richard A. Proctor used the term “nephroid” for the first time in 1878 in his book The Geometry of Cycloids. To learn more information about the nephroid curve, one can see [30]. Finding the constraints on analytic function that are required to be in $M_{Ne}^{⊺}$ is the issue. We work with the Deltoid domain, which is maximized by the function, by merging a segment line with a length bigger than the deltoid arch (see Figure 1)

$$\mathrm{\Xi }\left(\xi \right)=\frac{1}{2}\left(e^{(1/2)i\xi }+e^{-i\xi }\right),\xi \in \mathbb{k}$$

$$=1-\frac{i}{4}\xi -\frac{5}{16}{\xi }^2+\frac{7i}{96}{\xi }^3+\frac{17}{768}{\xi }^4-\frac{31i}{7680}{\xi }^5+O\left({\xi }^6\right).$$

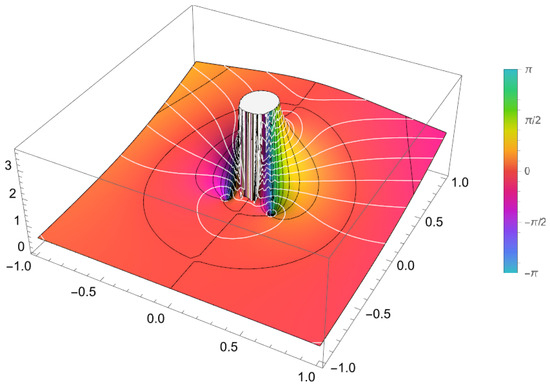
Figure 1. $\mathrm{\Xi }\left(\xi \right)=\frac{1}{2}\left(e^{i/2\xi }+e^{-i\xi }\right),\xi \in \mathbb{k}$ (the graph is given by Mathematica 13.3).

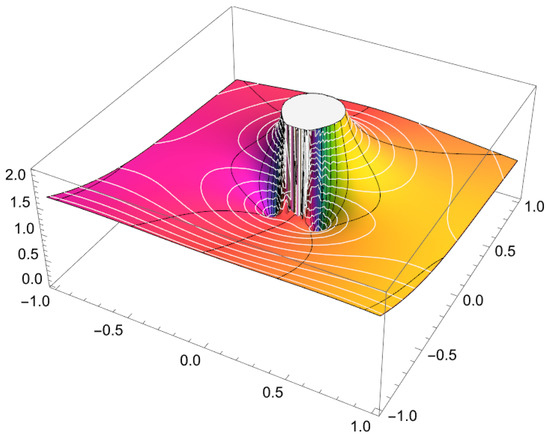
Moreover, we consider the special centered trochoid case, taking the formula (see Figure 2)

$$\mathsf{{\rm Y}}\left(\xi \right)=\frac{1}{2}\left(e^{i\xi }+e^{i/2\xi }\right)$$

$$=1+\left(3i\xi \right)/4-\left(5{\xi }^2\right)/16-\left(3i{\xi }^3\right)/32+\left(17{\xi }^4\right)/768+\left(11i{\xi }^5\right)/2560+O\left({\xi }^6\right).$$

Figure 2. $\mathrm{\Xi }\left(\xi \right)=\frac{1}{2}\left(e^{i\xi }+e^{i/2\xi }\right)$ (the graph is given by Mathematica 13.3).

Theorem 2.

Define the functional

$$\mathrm{\Theta }\left(\xi \right):=\sigma \left(\xi \right)+\left(1-\rho \left(\xi \right)\right)\left(\frac{{\sigma }^{\prime }\left(\xi \right)}{{\rho }^{\prime }\left(\xi \right)}\right)$$

and suppose that $\lambda \in \mathbb{C}$ is a complex constant. If one of the following subordination relations is satisfied

• $1+\lambda \left(\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)\right)\prec \mathrm{\Xi }\left(\xi \right),\frac{1}{2}\le \left|\lambda \right|\le 1;$
• $1+\lambda \left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{\mathrm{\Theta }\left(\xi \right)}\right)\prec \mathrm{\Xi }\left(\xi \right),\sqrt{\frac{6}{17}}\le \left|\lambda \right|\le 1;$
• $1+\lambda \left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{{\mathrm{\Theta }}^2\left(\xi \right)}\right)\prec \mathrm{\Xi }\left(\xi \right),1/(5/3+\sqrt{13}/2)\approx 0.288\le \left|\lambda \right|\le 1;$

where $\mathrm{\Xi }\left(\xi \right)=\frac{1}{2}\left(e^{i\xi /2}+e^{-i\xi }\right),$ then $\sigma \in M_{Ne}^{⊺}.$

Proof. 

Consider the differential equation

$$1+\lambda \xi Q^{\prime }\left(\xi \right)=\mathrm{\Xi }\left(\xi \right),\mathrm{\Xi }\left(\xi \right)=\frac{1}{2}\left(e^{i\xi /2}+e^{-i\xi }\right),$$

(11)

where $\mathrm{\Xi }\left(0\right)=1$ and $Q:\overline{\mathbb{k}}\to \mathbb{C}$ defining by

$$\begin{array}{cc}\hfill Q\left(\xi \right)& =1+\frac{1}{\lambda }\left({\int }_{\overline{\mathbb{k}}}\frac{\mathrm{\Xi }\left(\xi \right)-1}{\xi }d\xi \right)\hfill \\ \hfill & =1+1/2i\left(\right(-i((2\gamma -log\left(2\right))c+2(c-1)log\left(\xi \right))-\left(c\xi \right)/2+5/16ic{\xi }^2+\left(7c{\xi }^3\right)/144\hfill \\ \hfill & -\left(17ic{\xi }^4\right)/1536-\left(31c{\xi }^5\right)/19200+\left(13ic{\xi }^6\right)/55296+O\left({\xi }^7\right))+\pi c\lfloor \left(\right(\pi -2arg\left(\xi \right))/(4\pi \left)\right)\hfill \\ \hfill & -\pi c\lfloor \left(\right(2arg\left(\xi \right)+\pi )/(4\pi \left)\right)+\pi c\lfloor (3/4-arg(\xi )/(2\pi \left)\right)-\pi c\lfloor (arg(\xi )/(2\pi )+3/4))\hfill \\ \hfill & \approx 1+c\left(-\frac{i}{4}\xi -\frac{5}{32}{\xi }^2+\frac{7i}{288}{\xi }^3+...\right),\hfill \end{array}$$

where $c:=1/\lambda$ and $\gamma \approx 0.577$ is the Euler–Mascheroni number. Now, by assuming

$$f_1\left(\xi \right)=Q\left(\xi \right),f_2\left(\xi \right)=1,f_3\left(\xi \right)=\lambda$$

in Lemma 1, then we obtain

$$F_1\left(\xi \right)=\lambda \xi Q^{\prime }\left(\xi \right)=\mathrm{\Xi }\left(\xi \right)-1,F_2\left(\xi \right)=\mathrm{\Xi }\left(\xi \right)=1+\lambda \xi Q^{\prime }\left(\xi \right).$$

Subsequently, the appearance of $\mathbb{k}$ via the function $\mathrm{\Xi }\left(\xi \right)$ is a convex province; this infers that the function $F_2\left(\xi \right)$ is convex in $\mathbb{k}$. Then again, every convex function is starlike; therefore, the function $F_1\left(\xi \right)$ is starlike in $\mathbb{k}$. Thus, in virtue of the analytic description of starlike functions, it leads to

$$\Re \left(\frac{\xi F_2^{\prime }\left(\xi \right)}{F_1\left(\xi \right)}\right)=\Re \left(\frac{\xi F_1^{\prime }\left(\xi \right)}{F_1\left(\xi \right)}\right)>0$$

such that $\mathrm{\Theta }\left(0\right)=1=Q\left(0\right).$ But

$$1+\lambda \left(\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)\right)\prec \mathrm{\Xi }\left(\xi \right)=1+\lambda \left(\xi Q^{\prime }\left(\xi \right)\right),$$

then Lemma 1 indicates that $\mathrm{\Theta }\left(\xi \right)\prec Q\left(\xi \right).$ Now, by the majoran of the subordination, we obtain $Q\left(\xi \right)\prec {\varsigma }_{Ne}\left(\xi \right)$ under the necessary condition $\left|\lambda \right|\le 1.$ Since ${\varsigma }_{Ne}\left(\xi \right)$ is univalent in ∪ and $Q\left(0\right)=1={\varsigma }_{Ne}\left(0\right),$ then we have the subordination inequality

$$\mathrm{\Theta }\left(\xi \right)\prec Q\left(\xi \right)\prec {\varsigma }_{Ne}\left(\xi \right)\Rightarrow \mathrm{\Theta }\left(\xi \right)\prec {\varsigma }_{Ne}\left(\xi \right).$$

We conclude that $\sigma \in M_{Ne}^{⊺}.$

For the second case, we define a function $G:\overline{\mathbb{k}}\to \mathbb{C}$ by

$$G\left(\xi \right)=exp\left(\frac{1}{\lambda }\left({\int }_{\overline{\mathbb{k}}}\frac{\mathrm{\Xi }\left(\xi \right)-1}{\xi }d\xi \right)\right)$$

$$=1-1/4ic\xi -\left(c^2{\xi }^2\right)/32+1/384i{c}^3{\xi }^3+\left(c^4{\xi }^4\right)/6144-\left(i{c}^5{\xi }^5\right)/122880+O\left(c^6\right),$$

and

$$1+\lambda \left(\frac{\xi G^{\prime }\left(\xi \right)}{G\left(\xi \right)}\right)=1-\left(i{\xi }^2\right)/4-1/128i{c}^2{\xi }^4+\left(c^3{\xi }^5\right)/512+\left(i{c}^4{\xi }^6\right)/4096+O\left({\xi }^7\right),$$

where $c=1/\lambda ,G\left(0\right)=1=\mathrm{\Theta }\left(0\right)$ and achieves the equation $1+\lambda \left(\frac{\xi G^{\prime }\left(\xi \right)}{G\left(\xi \right)}\right)=\mathrm{\Xi }\left(\xi \right).$ By selecting $f_2\left(\xi \right)=1,f_3\left(\xi \right)=\lambda /\xi$ in Lemma 1, we have

$$F_1\left(\xi \right)=\left(\frac{\xi G^{\prime }\left(\xi \right)}{G\left(\xi \right)}\right)=\mathrm{\Xi }\left(\xi \right)-1,F_2\left(\xi \right)=1+F_1\left(\xi \right)=\mathrm{\Xi }\left(\xi \right).$$

The convexity of $\mathrm{\Xi }$ indicates the convexity of $F_2$ and $\Re \left(\xi F_1^{\prime }\left(\xi \right)/F_1\left(\xi \right)\right)>0.$ In view of Lemma 1, we have

$$1+\lambda \left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{\mathrm{\Theta }\left(\xi \right)}\right)\prec \mathrm{\Xi }\left(\xi \right)=1+\lambda \left(\frac{\xi G^{\prime }\left(\xi \right)}{G\left(\xi \right)}\right),$$

gives $\mathrm{\Theta }\left(\xi \right)\prec G\left(\xi \right).$ But $G\left(\xi \right)\prec {\varsigma }_{Ne}\left(\xi \right)$; then, by solving the equation

$$\frac{1}{128{\lambda }^2}=\frac{17}{768},$$

we obtain the condition $\sqrt{\frac{6}{17}}\le \left|\lambda \right|\le 1$, which implies that $\mathrm{\Theta }\left(\xi \right)\prec {\varsigma }_{Ne}\left(\xi \right).$

For the last case, we define a function $H:\overline{\mathbb{k}}\to \mathbb{C}$ by

$$\begin{array}{cc}\hfill H\left(\xi \right)& ={\left(1-\frac{1}{\lambda }\left({\int }_{\overline{\mathbb{k}}}\frac{\mathrm{\Xi }\left(\xi \right)-1}{\xi }d\xi \right)\right)}^{-1}\hfill \\ \hfill & =1+\left(ic\xi \right)/4+1/32(5-2c)c{\xi }^2-1/64i(c-5)c^2{\xi }^3+\left(c^2(4c^2-30c+25){\xi }^4\right)/1024\hfill \\ \hfill & +\left(i{c}^3(4c^2-40c+75){\xi }^5\right)/4096+O\left({\xi }^6\right),\hfill \end{array}$$

and

$$1+c\left(\frac{\xi H^{\prime }\left(\xi \right)}{H^2\left(\xi \right)}\right)=1+\left(i{\xi }^2\right)/4+\left(5{\xi }^3\right)/32+1/64ic(3c-10){\xi }^4+1/512c(8c^2-15c-25){\xi }^5$$

$$-\left(5i{c}^2(16c-45){\xi }^6\right)/4096+O\left({\xi }^7\right),$$

where $c=1/\lambda ,G\left(0\right)=1=\mathrm{\Theta }\left(0\right)$ and achieves the equation

$$1+\lambda \left(\frac{\xi H^{\prime }\left(\xi \right)}{H^2\left(\xi \right)}\right)=\mathrm{\Xi }\left(\xi \right).$$

under the condition $\left|\lambda \right|\le 1.$ By letting $f_2\left(\xi \right)=1,f_3\left(\xi \right)=\lambda /{\xi }^2$ in Lemma 1, we have

$$F_1\left(\xi \right)=\left(\frac{\xi H^{\prime }\left(\xi \right)}{H^2\left(\xi \right)}\right)=\mathrm{\Xi }\left(\xi \right)-1,F_2\left(\xi \right)=1+F_1\left(\xi \right)=\mathrm{\Xi }\left(\xi \right).$$

The convexity of $\mathrm{\Xi }$ indicates the convexity of $F_2$ and

$$\Re \left(\xi F_1^{\prime }\left(\xi \right)/F_1^2\left(\xi \right)\right)>0.$$

Moreover, the subordination

$$1+\lambda \left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{{\mathrm{\Theta }}^2\left(\xi \right)}\right)\prec \mathrm{\Xi }\left(\xi \right)\approx 1+\lambda \left(\frac{\xi H^{\prime }\left(\xi \right)}{H^2\left(\xi \right)}\right)$$

implies that $\mathrm{\Theta }\left(\xi \right)\prec H\left(\xi \right).$ Since under the condition on $\lambda ,$ which can be calculated form the equation

$$\frac{c(3c-10)}{64}=\frac{17}{768}$$

to obtain $0.288\le \left|\lambda \right|\le 1.$ Then, we have, $H\left(\xi \right)\prec {\varsigma }_{Ne}\left(\xi \right)$, and consequently, we attain $\mathrm{\Theta }\left(\xi \right)\prec {\varsigma }_{Ne}$ that is $\sigma \in M_{Ne}^{⊺}.$ □

In the similar manner of Theorem 2, we have the following result involving $\mathsf{{\rm Y}}\left(\xi \right).$

Theorem 3.

Let $\mathrm{\Theta }\left(\xi \right):=\sigma \left(\xi \right)+\left(1-\rho \left(\xi \right)\right)\left(\frac{{\sigma }^{\prime }\left(\xi \right)}{{\rho }^{\prime }\left(\xi \right)}\right)$ and a complex constant $\lambda \in \mathbb{C}.$ If one of the following subordination relations is satisfied

• $1+\lambda \left(\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)\right)\prec \mathsf{{\rm Y}}\left(\xi \right),\left|\lambda \right|\le 1;$
• $1+\lambda \left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{\mathrm{\Theta }\left(\xi \right)}\right)\prec \mathsf{{\rm Y}}\left(\xi \right),\frac{\sqrt{3}}{2}=0.866\le \left|\lambda \right|\le 1;$
• $1+\lambda \left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{{\mathrm{\Theta }}^2\left(\xi \right)}\right)\prec \mathsf{{\rm Y}}\left(\xi \right),1/3(5-\sqrt{29})\approx 0.128\le \left|\lambda \right|\le 1;$

then $\sigma \in M_{Ne}^{⊺}.$

The next result shows the upper bound of $\mathrm{\Theta }\left(\xi \right)$ by using a starlike function.

Theorem 4.

Consider Θ and Ξ in Theorem 2. Then

• $\left(\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)\right)\prec \xi \mathrm{\Xi }\left(\xi \right)\Rightarrow \mathrm{\Theta }\left(\xi \right)\prec \ell \left(\xi \right):=1+{\int }_0^{\xi }{\tau }^{-1}\mathrm{\Xi }\left(\tau \right)d\tau$ and ℓ is the best dominant.
• $\left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{\mathrm{\Theta }\left(\xi \right)}\right)\prec \xi \mathrm{\Xi }\left(\xi \right)\Rightarrow \mathrm{\Theta }\left(\xi \right)\prec \hslash \left(\xi \right):=exp\left({\int }_0^{\xi }{\tau }^{-1}\mathrm{\Xi }\left(\tau \right)d\tau \right)$ and ℏ is the best dominant.

Proof. 

Let

$$E\left(\xi \right):=\xi \mathrm{\Xi }\left(\xi \right)=\frac{\xi }{2}\left(e^{(1/2)i\xi }+e^{-i\xi }\right),$$

where $E\left(0\right)=0.$ Since ${\varsigma }_{Ne}=1+\xi -{\xi }^3/3$ is a Caratheodory function, then we obtain

$$\mathsf{\Lambda }=\underset{\xi \in \mathbb{k}}{inf}\left\{\Re \left({\varsigma }_{Ne}\left(\xi \right)\right)sin\left(\frac{\pi }{2}\right)-|\Im \left({\varsigma }_{Ne}\left(\xi \right)\right)cos\left(\frac{\pi }{2}\right)|\right\}>0.$$

Moreover, we have

$$\Re \left(E\left(\xi \right)+{\varsigma }_{Ne}\left(\xi \right)\left(\xi E^{\prime }\left(\xi \right)\right)\right)>0.$$

This leads to $\left|arg\left(E\left(\xi \right)\right)\right|<\frac{\pi }{4}$. Then, in view of Lemma 2, we conclude that $E\left(\xi \right)$ is starlike. Consequently, the subordination

$$\left(\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)\right)\prec \xi \mathrm{\Xi }\left(\xi \right)$$

and Theorem 3.1d [5] implies that

$$\mathrm{\Theta }\left(\xi \right)\prec \ell \left(\xi \right)=1+{\int }_0^{\xi }{\tau }^{-1}\mathrm{\Xi }\left(\tau \right)d\tau$$

and ℓ is the best dominant.

For the second part, in view of Corollary 3.1d.1, P76 [5], we indicate that

$$\left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{\mathrm{\Theta }\left(\xi \right)}\right)\prec \xi \mathrm{\Xi }\left(\xi \right)\Rightarrow \mathrm{\Theta }\left(\xi \right)\prec \hslash \left(\xi \right)=exp\left({\int }_0^{\xi }{\tau }^{-1}\mathrm{\Xi }\left(\tau \right)d\tau \right)$$

and ℏ is the best dominant. □

Similarly, we have the following result:

Theorem 5.

Consider Θ and Υ in Theorem 3. Then

• $\left(\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)\right)\prec \xi \mathsf{{\rm Y}}\left(\xi \right)\Rightarrow \mathrm{\Theta }\left(\xi \right)\prec \vartheta \left(\xi \right):=1+{\int }_0^{\xi }{\tau }^{-1}\mathsf{{\rm Y}}\left(\tau \right)d\tau$ and ϑ is the best dominant.
• $\left(\frac{\xi {\mathrm{\Theta }}^{\prime }\left(\xi \right)}{\mathrm{\Theta }\left(\xi \right)}\right)\prec \xi \mathsf{{\rm Y}}\left(\xi \right)\Rightarrow \mathrm{\Theta }\left(\xi \right)\prec h\left(\xi \right):=exp\left({\int }_0^{\xi }{\tau }^{-1}\mathsf{{\rm Y}}\left(\tau \right)d\tau \right)$ and h is the best dominant.

3.1. Examples

In this place, we introduce the roulette curve formula $\mathrm{\Theta }\left(\xi \right)$ by suggesting a well-known normalized analytic function $\sigma \left(\xi \right)$ and its rolled function $\rho \left(\xi \right)$ (see Figure 3).

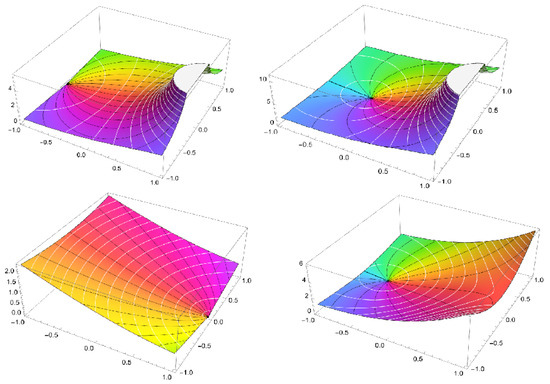
Figure 3. The 3D complex graphs of the roulette curve functional $(1+\xi )/(1-\xi ),(1+3\xi )/(1-\xi ),$$(2-\xi )\sqrt{1-\xi }/2,-e^{\xi }{\xi }^2+e^{\xi }\xi +e^{\xi }$ in Section 3.1, respectively (the graph is given by Mathematica 13.3).

• Assume the convex function $\sigma \left(\xi \right)=\frac{\xi }{1-\xi }$ and its rolled function $\rho \left(\xi \right)=\xi ,\xi \in \mathbb{k}.$ Then, the roulette curve is the Janowski function

  $$\mathrm{\Theta }\left(\xi \right)=\frac{1+\xi }{1-\xi }=1+2{\xi }^2+2{\xi }^3+...$$
• If $\sigma \left(\xi \right)=\xi \left(\frac{1+\xi }{1-\xi }\right)$ and its rolled function $\rho \left(\xi \right)=\xi ,\xi \in \mathbb{k}$, then the roulette curve is given by the function

  $$\mathrm{\Theta }\left(\xi \right)=\frac{1+3\xi }{1-\xi }=1+4{\xi }^2+4{\xi }^3+...$$
• Let $\sigma \left(\xi \right)=\xi \sqrt{(1-\xi )}$ and $\rho \left(\xi \right)=\xi ,\xi \in \mathbb{k}.$ Then, we have

  $$\mathrm{\Theta }\left(\xi \right)=\left({\displaystyle \frac{(2-\xi )}{2}}\right)\sqrt{1-\xi }=1-\xi +{\xi }^2/8-{\xi }^4/128+O\left({\xi }^5\right)...$$
• Suppose the analytic function $\sigma \left(\xi \right)=\xi e^{\xi }$ and its rolled function $\rho \left(\xi \right)=\xi ,\xi \in \mathbb{k}.$ Then, the roulette curve takes the formula

  $$\mathrm{\Theta }\left(\xi \right)=-e^{\xi }{\xi }^2+e^{\xi }\xi +e^{\xi }=1+2\xi +{\xi }^2/2-{\xi }^3/3-\left(7{\xi }^4\right)/24+O\left({\xi }^5\right)...$$

3.2. Application of the Rolled Function

The selecting of the rolled function $\rho \left(\xi \right)=\xi$ will reduce the roulette functional formula into the polarized derivative of order one for the corresponding polynomial, say $q\left(\xi \right)$ of of degree m, to be

$$\left[{\mathrm{\Theta }}_{m}q\right]\left(\xi \right)=mq\left(\xi \right)+(1-\xi )q^{\prime }\left(\xi \right).$$

This formula has many applications (see [31,32]). In the open unit disk, Aziz showed that [31] in Corollary 3, for any self-inversive polynomial:

$$q\left(\xi \right)={\xi }^m\overline{q(1/\overline{\xi })}$$

of degree m admitting the connection inequality

$$q_n=\epsilon q_{m-n},\left|\epsilon \right|\le 1,$$

with a maximum value equal to one at the boundary of the open unit disk, the upper bound of the polynomial satisfies the inequality

$$\begin{array}{c}\hfill |\left[{\mathrm{\Theta }}_{m}q\right]\left(\xi \right){|}_{\xi \in \partial \mathbb{k}}\le {\displaystyle \frac{m}{2}}\left(|{\xi }^{m-1}|+1\right),\xi \in \mathbb{k}\cup \partial \mathbb{k}\left(\right|\xi |\le 1).\end{array}$$

(12)

Meanwhile, $\left[{\mathrm{\Theta }}_{m}q\right]\left(\xi \right)$ achieves the inequality at the origin (see [31] (p. 4))

$$\begin{array}{c}\hfill |\left[{\mathrm{\Theta }}_{m}q\right]\left(\xi \right){|}_{\xi =0}\le {\displaystyle \frac{m}{2}}\underset{\xi \in \partial \mathbb{k}}{max}|q\left(\xi \right)|,\xi \in \mathbb{k}\cup \partial \mathbb{k}(\left|\xi \right|\le 1).\end{array}$$

(13)

Moreover, if q is a self-inversive polynomial, then [31] in Corollary 2, the upper bound of the coefficient $q_n$ is as follows:

$$\begin{array}{c}\hfill m|q_n|+|q_{n-1}|\le {\displaystyle \frac{m}{2}}\underset{\xi \in \partial \mathbb{k}}{max}\left|q\left(\xi \right)\right|,q\left(\xi \right)=\xi +\sum _{n=2}^m{q}_n{\xi }^n.\end{array}$$

(14)

4. Conclusions

As a conclusion, we presented a new class of analytic functions in $\mathbb{k}$ of MMT in a symmetric domain that takes a centered trochoid shape. The formula is suggested in terms of the roulette curve formula in the open unit disk. This formula involved two analytic normalized functions: the first one is the geometric function and the second is its rolled function. Several geometric studies are indicated by using the subordination concept to obtain the upper bound for formulas involving these functions. Examples are illustrated at the end of this study, and an application considering the polynomial that is generated by the partial sum of the formula $\mathrm{\Theta }\left(\xi \right)$ is investigated. This application yielded the upper bound of the coefficients of $\left[{\mathrm{\Theta }}_{m}q\right]\left(\xi \right).$

For the future works, one can extend this type of analytic function to classes of harmonic and meromorphic functions. They also can be generalized by using the differential and difference operators given in [33,34].