Asymptotic Constancy for the Solutions of Caputo Fractional Differential Equations with Delay

Abstract

In this paper, we aim to study the neutral-type delayed Caputo fractional differential equations of the form ${}^C{D}^{\alpha }\left(x\left(t\right)-g\left(t,x_t\right)\right)=f\left(t,x_t\right),t\in \left(t_0,\infty \right),t_0\ge 0$ with order $0<\alpha <1$, which can be used to describe the growth processes in real-life sciences at which the present growth depends on not only the past state but also the past growth rate. Our ultimate goal in this study is to concentrate on the convergence of the solutions to a predetermined constant by establishing a linkage between the delayed fractional differential equation and an integral equation. In our analysis, the sufficient conditions for the asymptotic results are obtained due to fixed point theory. The utilization of the contraction mapping principle is a convenient approach in obtaining technical conditions that guarantee the asymptotic constancy of the solutions.

1. Introduction

One of the current hot issues in applied mathematics is fractional calculus and fractional dynamic equations, which have a 300-year history. Researchers have learned that well-known mathematicians Liouville, Riemann, and Leibniz undertook research on fractional calculus in the past. For more information, see [1,2,3,4]. Researchers have focused on studying and developing the theory of fractional differential equations since the invention of the fractional derivative.

It came out that there are several unique and intriguing situations where fractional differential equations are favored over conventional differential equations. The applications of fractional differential equations are what make them a daunting and fundamental topic in the applied sciences, despite the fact that the theoretical solutions derived for them are intriguing and communicate profound implications. Applications of fractional differential equations have particularly found success in the fields of physics, biology, economics, and the medical and biological sciences (see [5,6,7,8,9]). Similar to the theory of ordinary differential equations, the theory of fractional differential equations has been separated into qualitative and quantitative categories. Stability analysis is one of the key areas in the qualitative examination of these equations. Numerous academics have thoroughly investigated the stability of the solutions to fractional differential equations. As a result, the stability theory of these equations has only recently been formed and still needs further refinement. We cite [10,11,12,13,14] for more readings on these two categories.

Studies concentrating on the existence of particular solutions, such as positive, periodic, nearly periodic, and affine periodic solutions, as well as oscillation of solutions, have gained a prominent place in the extant literature in the qualitative study of ordinary differential equations. Even if the idea of symmetry can be seen as a crucial component of the mathematical motivation for these studies, it is still unspoken in the field. It should be underlined that there is a vast amount of literature on the asymptotic behavior of the solutions of ordinary differential equations. There is also a substantial body of literature and comparable investigations for both discrete and hybrid temporal domains. In [15], Burton examined an ordinary differential equation with a delay which is used in biology and showed the asymptotic constancy and periodicity of the solutions with the help of fixed point theory. The authors of [16,17] were inspired by [15] and analyzed such equations, which are crucial in population dynamics, with constant and functional delays on discrete and hybrid time domains, respectively. To the best of our knowledge, the asymptotic constancy of fractional equations’ solutions has not yet been studied, despite the fact that stability analysis of fractional equations has grown rather quickly. Proposing sufficient conditions that assure that solutions converge to a preset constant, namely the asymptotic constancy of solutions, is an important topic from a mathematics perspective. By examining the asymptotic constancy of solutions to fractional equations, this study aims to close this gap. Furthermore, in our opinion, this study will launch a new line of inquiry based on symmetry-based asymptotic analysis of fractional differential equations. Functional differential equations containing the highest-order derivative in more than one term are called neutral differential equations. There are few results regarding the theory of fractional neutral equations, and we refer to the papers [18,19,20,21,22], which focus on the analysis of fractional neutral differential equations. We highlight that fractional neutral differential equations are challenging to study due to their complicated dynamics. However, their applications in various disciplines have intrinsically compelled and imposed on us to give them the deserved attention. Inspired by [23], we consider a neutral equation of order $0<\alpha <1$ with constant delay

$${}^C{D}^{\alpha }\left(x\left(t\right)-g\left(t,x_t\right)\right)=f\left(t,x_t\right),t\in \left(t_0,\infty \right),$$

and study the asymptotic constancy of its solutions. This approach enables us to adapt the possible outcomes of this study to biological models with a constant life span that are widely studied in biomathematics. By a quick literature review, it is possible to find significant biological models with a delay, such as the hematopoiesis model

$$\frac{d}{dt}\left(x\left(t\right)-cx\left(t-\tau \right)\right)=-a\left(t\right)x\left(t\right)+b\left(t\right)e^{-\beta \left(t\right)x\left(t-\tau \right)},t\in \mathbb{R},$$

and red blood cell production model

$$\frac{d}{dt}\left(x\left(t\right)-cx\left(t-\tau \right)\right)=-a\left(t\right)x\left(t\right)+b\left(t\right)\frac{1}{1+x^n\left(t-\tau \right)},n>0,t\in \mathbb{R}$$

(see [24,25], and references therein). The fractional analogues of the aforementioned equations have already gained importance in mathematics, because fractional differential equations are typically used to model real-world issues and are best suited for doing so. It is obvious that a connection between the equation we focus on and potential fractional analogs of neutral biological models may be made with ease. As a result, the major findings of our research have excellent application potential and will therefore advance the qualitative theory of fractional differential equations.

The next section is devoted to the presentation of the main results and illustrative examples. Also, a precise summary about fractional derivatives and integrals is provided in the Appendix A for the readers who are not familiar with fractional calculus.

2. Main Results

2.1. Setup

We consider the following neutral Caputo fractional differential equation with delay

$${}^C{D}^{\alpha }\left(x\left(t\right)-g\left(t,x_t\right)\right)=f\left(t,x_t\right),t\in \left(t_0,\infty \right),$$

(1)

with order $0<\alpha <1,$ where $f,g:\left(t_0,\infty \right)\times \mathbb{R}\to \mathbb{R},$ and $x_t\left(s\right)=x\left(t+s\right)$ if $s\in \left[t_0-\tau ,t_0\right]$ for $\tau >0.$ We set $\xi :\left[t_0-\tau ,t_0\right]\to \mathbb{R}$ as a continuous function, and the solution x of (1) is presented by $x^{\xi }=x\left(t,t_0,\xi \right)$ with $x^{\xi }\left(t\right)=\xi \left(t\right)$ on $\left[t_0-\tau ,t_0\right].$

Lemma 1.

The function x is a solution of (1) if and only if it satisfies the integral equation

$$x\left(t\right)=\xi \left(t_0\right)-g\left(t_0,\xi \right)+g\left(t,x_t\right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}f\left(s,x_s\right)ds.$$

(2)

Proof. 

This result can be obtained by applying the Caputo derivative on both sides of (2). For more on the details of its proof, we refer to ([23], Lemma 3.1). □

For the rest of this paper, we make the following assumptions:

A1 

For a constant $\beta ,$

$$f\left(t,\beta \right)={-}_{t_0}^C{D}_t^{\alpha }g\left(t,\beta \right).$$

A2 

The function g is Lipschitz in its second argument, i.e.,

$$\left|g\left(t,x_1\right)-g\left(t,x_2\right)\right|\le L_1\left|x_1-x_2\right|,\mathrm{for}\mathrm{all}{x}_1,x_2\in \mathbb{R}.$$

A3 

There exists a continuous function $p:\left[t_0,\infty \right)\to {\mathbb{R}}_{+}$, so that the inequality

$$\left|f\left(t,x_1\right)-f\left(t,x_2\right)\right|\le p\left(t\right)\left|x_1-x_2\right|$$

holds for all $x_1,x_2\in \mathbb{R}.$

A4 

There exists a constant $\gamma \in \left(0,1\right)$, so that $L_1+L_2<\gamma$ for $L_2=∥w\left(t\right)∥,$ where

$$w\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}p\left(s\right)ds,$$

and

$$∥w∥=\underset{t\in \left(t_0,\infty \right)}{sup}\left|w\left(t\right)\right|.$$

Lemma 2.

For a constant $\beta ,$

$$h\left(\beta \right)=g\left(t,\beta \right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}f\left(s,\beta \right)ds$$

(3)

is a constant.

Proof. 

We apply Caputo derivative on h

$${}_{t_0}^C{D}_t^{\alpha }\left[h\left(\beta \right)\right]{=}_{t_0}^C{D}_t^{\alpha }\left[g\left(t,\beta \right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}f\left(s,\beta \right)ds\right],$$

and use the identity

$$\left({}_{t_0}^C{D}_t^{\alpha }\left({}_{t_0}{I}_t^{\alpha }g\right)\right)\left(t\right)=g\left(t\right),\alpha >0$$

to obtain

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\alpha }\left[h\left(\beta \right)\right]& {=}_{t_0}^C{D}_t^{\alpha }\left[g\left(t,\beta \right)\right]{+}_{t_0}^C{D}_t^{\alpha }\left[{}_{t_0}{I}_t^{\alpha }\left(f\left(t,\beta \right)\right)\right]\hfill \\ \hfill & {=}_{t_0}^C{D}_t^{\alpha }\left[g\left(t,\beta \right)\right]+f\left(t,\beta \right)\hfill \\ \hfill & =0\hfill \end{array}$$

by A1. This indicates that $h\left(\beta \right)$ is a constant, and the proof is complete. □

2.2. Asymptotic Results

Theorem 1.

The unique solution $x^{\xi }$ of (1) satisfies the asymptotic property

$$\underset{t\to \infty }{lim}x\left(t,t_0,\xi \right)=\beta ,$$

where

$$\beta =\xi \left(t_0\right)-g\left(t_0,\xi \right)+h\left(\beta \right),$$

(4)

and $h\left(\beta \right)$ is given by (3).

Proof. 

First, we show that the mapping h given in (3) is a contraction. For ${\beta }_1,{\beta }_2\in \mathbb{R},$ we have

$$\begin{array}{cc}\hfill \left|h\left({\beta }_1\right)-h\left({\beta }_2\right)\right|& =\left|g\left(t,{\beta }_1\right)-g\left(t,{\beta }_2\right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}\left(f\left(s,{\beta }_1\right)-f\left(s,{\beta }_2\right)\right)ds\right|\hfill \\ \hfill & \le \left|g\left(t,{\beta }_1\right)-g\left(t,{\beta }_2\right)\right|+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}\left|f\left(s,{\beta }_1\right)-f\left(s,{\beta }_2\right)\right|ds\hfill \\ \hfill & \le L_1\left|{\beta }_1-{\beta }_2\right|+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}p\left(s\right)\left|{\beta }_1-{\beta }_2\right|ds\hfill \\ \hfill & =\left|{\beta }_1-{\beta }_2\right|\left(L_1+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}p\left(s\right)ds\right)\hfill \\ \hfill & <\gamma \left|{\beta }_1-{\beta }_2\right|.\hfill \end{array}$$

Thus, h is a contraction.

Next, we define the mapping

$$M_1\left(\beta \right)=\xi \left(t_0\right)-g\left(t_0,\xi \right)+h\left(\beta \right),$$

(5)

which is a contraction due to the mapping $h.$ Therefore, it has a unique fixed point $\beta .$ Subsequently, we construct the following set

$$\Phi =\left\{\varphi :\left[t_0-\tau ,\infty \right)\to \mathbb{R},\varphi \left(t\right)\to \beta \mathrm{as}t\to \infty ,\varphi \left(t\right)=\xi \left(t\right)\mathrm{for}\mathrm{all}t\in \left[t_0-\tau ,t_0\right]\right\},$$

(6)

which is a Banach space endowed by the supremum norm.

For $\varphi \in \Phi ,$ we define the mapping $M_2$ as follows:

$$\left(M_2\varphi \right)\left(t\right)=\left\{\begin{array}{c}\xi \left(t\right),t\in \left[t_0-\tau ,t_0\right]\\ \xi \left(t_0\right)-g\left(t_0,\xi \right)+g\left(t,{\varphi }_t\right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}f\left(s,{\varphi }_s\right)ds,t>t_0\end{array}\right..$$

(7)

We need to prove that $M_2:\Phi \to \Phi .$ To achieve this task, we show that

$$\underset{t\to \infty }{lim}\left[g\left(t,{\varphi }_t\right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}f\left(s,{\varphi }_s\right)ds\right]=h\left(\beta \right)$$

whenever $\varphi \left(t\right)\to \beta$ as $t\to \infty .$ Consider

$$\begin{array}{cc}\hfill & \left|g\left(t,{\varphi }_t\right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}f\left(s,{\varphi }_s\right)ds-h\left(\beta \right)\right|\hfill \\ \hfill & =\left|g\left(t,{\varphi }_t\right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}f\left(s,{\varphi }_s\right)ds-g\left(t,\beta \right)-\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}f\left(s,\beta \right)ds\right|\hfill \\ \hfill & \le \left|g\left(t,{\varphi }_t\right)-g\left(t,\beta \right)\right|+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}\left|f\left(s,{\varphi }_s\right)-f\left(s,\beta \right)\right|ds\hfill \\ \hfill & \le L_1\left|{\varphi }_t-\beta \right|+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}p\left(s\right)\left|{\varphi }_s-\beta \right|ds\hfill \\ \hfill & \le \left(L_1+L_2\right)\epsilon <\gamma \epsilon <\epsilon ,\hfill \end{array}$$

since $\left|{\varphi }_t-\beta \right|<\epsilon$ for sufficiently large $t.$ Then, we conclude that $\left(M_2\varphi \right)\left(t\right)\to \beta$ as $t\to \infty ,$ and consequentially, $M_2:\Phi \to \Phi .$ Finally, we show that $M_2$ is a contraction. To see this, we suppose $\phi ,\psi \in \Phi ,$ and write

$$\begin{array}{cc}\hfill \left|\left(M_2\phi \right)\left(t\right)-\left(M_2\psi \right)\left(t\right)\right|& \le \left|g\left(t,{\phi }_t\right)-g\left(t,{\psi }_t\right)\right|\hfill \\ & +\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}\left|f\left(s,{\phi }_s\right)-f\left(s,{\psi }_s\right)\right|ds\hfill \\ \hfill & \le L_1∥\phi -\psi ∥+\frac{∥\phi -\psi ∥}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}p\left(s\right)ds\hfill \\ \hfill & \le \left(L_1+L_2\right)∥\phi -\psi ∥<\gamma ∥\phi -\psi ∥.\hfill \end{array}$$

Thus, $M_2$ has a unique fixed point in $\Phi .$ As a result, the solution $x^{\xi }$ of (1) satisfies the asymptotic property $x^{\xi }\left(t\right)\to \beta$ as $t\to \infty .$ □

Theorem 2.

Every initial function ξ corresponding to $x^{\xi }$ of (2) is stable; that is, for every $\epsilon >0$, there exists a $\delta >0$, such that

$$\left|x\left(t,t_0,{\xi }_1\right)-x\left(t,t_0,{\xi }_2\right)\right|<\epsilon whenever\left|{\xi }_1-{\xi }_2\right|<\delta$$

for $t\ge t_0.$ Moreover, if $x\left(t,t_0,{\xi }_1\right)\to {\beta }_1$ and $x\left(t,t_0,{\xi }_2\right)\to {\beta }_2$ as $t\to \infty ,$ then $\left|{\beta }_1-{\beta }_2\right|<\epsilon .$

Proof. 

Let $M_2^{\left(1\right)}$ and $M_2^{\left(2\right)}$ be the mappings defined as in (7) corresponding to ${\xi }_1$ and ${\xi }_2,$ respectively. By Theorem 1, they have unique fixed points $x^{\left(1\right)}$ and $x^{\left(2\right)},$ i.e.,

$$M_2^{\left(1\right)}{x}^{\left(1\right)}=x^{\left(1\right)}\mathrm{and}{M}_2^{\left(2\right)}{x}^{\left(2\right)}=x^{\left(2\right)}$$

with the limit results $x^{\left(1\right)}\left(t\right)\to {\beta }_1$ and $x^{\left(2\right)}\left(t\right)\to {\beta }_2$ as $t\to \infty .$ Then, we consider

$$\begin{array}{cc}\hfill \left|x^{\left(1\right)}\left(t\right)-x^{\left(2\right)}\left(t\right)\right|& =\left|\left(M_2^{\left(1\right)}{x}^{\left(1\right)}\right)\left(t\right)-\left(M_2^{\left(2\right)}{x}^{\left(2\right)}\right)\left(t\right)\right|\hfill \\ \hfill & \le \left|{\xi }_1\left(t_0\right)-{\xi }_2\left(t_0\right)\right|+\left|g\left(t_0,{\xi }_1\right)-g\left(t_0,{\xi }_2\right)\right|\hfill \\ & +\left|g\left(t,x_t^{\left(1\right)}\right)-g\left(t,x_t^{\left(2\right)}\right)\right|\hfill \\ \hfill & +\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \underset{t_0}{\overset{t}{\int }}}{\left(t-s\right)}^{\alpha -1}\left|f\left(s,x_s^{\left(1\right)}\right)-f\left(s,x_s^{\left(2\right)}\right)\right|ds\hfill \\ \hfill & \le \left|{\xi }_1\left(t_0\right)-{\xi }_2\left(t_0\right)\right|+L_1\left|{\xi }_1-{\xi }_2\right|+L_1\left|x_t^{\left(1\right)}-x_t^{\left(2\right)}\right|\hfill \\ & +L_2∥x^{\left(1\right)}-x^{\left(2\right)}∥.\hfill \end{array}$$

This yields to

$$\begin{array}{cc}\hfill ∥x^{\left(1\right)}-x^{\left(2\right)}∥& \le \left(1+L_1\right)∥{\xi }_1-{\xi }_2∥+\left(L_1+L_2\right)∥x^{\left(1\right)}-x^{\left(2\right)}∥\hfill \\ \hfill & <\left(1+L_1\right)∥{\xi }_1-{\xi }_2∥+\gamma ∥x^{\left(1\right)}-x^{\left(2\right)}∥\hfill \end{array}$$

and

$$∥x^{\left(1\right)}-x^{\left(2\right)}∥<\frac{1+L_1}{1-\gamma }∥{\xi }_1-{\xi }_2∥.$$

If we set $\delta =\epsilon \frac{1-\gamma }{1+L_1},$ then the first part of the proof is complete.

Next, to prove the second assertion, we employ the limit results $x^{\left(1\right)}\to {\beta }_1$ and $x^{\left(2\right)}\to {\beta }_2$ as $t\to \infty$. We write

$$\begin{array}{cc}\hfill \left|{\beta }_1-{\beta }_2\right|& =\left|{\beta }_1-x^{\left(1\right)}\left(t\right)+x^{\left(1\right)}\left(t\right)-x^{\left(2\right)}\left(t\right)+x^{\left(2\right)}\left(t\right)-{\beta }_2\right|\hfill \\ \hfill & \le \left|{\beta }_1-x^{\left(1\right)}\left(t\right)\right|+∥x^{\left(1\right)}-x^{\left(2\right)}∥+\left|{\beta }_2-x^{\left(2\right)}\left(t\right)\right|\hfill \\ \hfill & <\epsilon \hfill \end{array}$$

when $t\to \infty .$ The proof is complete. □

Next, we give the following examples as an implementation of our asymptotic result.

Example 1.

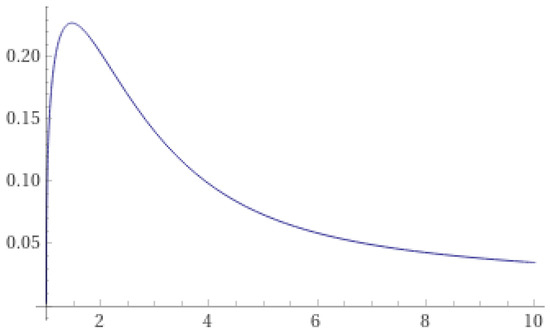
We set $\alpha =\frac{1}{3}$ and consider the neutral fractional differential equation with delay

$${}^C{D}^{\frac{1}{3}}\left(x\left(t\right)-\frac{1}{4}{e}^{-x\left(t-h\right)}\right)=e^{-t}arctan\left(x\left(t-h\right)\right),t\in \left(1,\infty \right),$$

(8)

where the solution of (8) is represented by $x^{\xi }=\xi \left(t\right)$ on $\left[1-h,1\right]$ with $\xi \left(1\right)=0.$ If we compare (1) with (8), then we deduce that

$$g\left(t,x\left(t\right)\right)=\frac{1}{4}{e}^{-x\left(t\right)},$$

and

$$f\left(t,x\left(t\right)\right)=e^{-t}arctan\left(x\left(t\right)\right).$$

We fix $\beta =0,$ and this results in (4) to hold true. Moreover, $f\left(t,0\right)=0={-}_1^C{D}_t^{\frac{1}{3}}g\left(t,0\right),$ which meansA1is satisfied. Next, we observe that the conditionsA2andA3are fulfilled, since

$$\left|\frac{1}{4}{e}^{-x_1}-\frac{1}{4}{e}^{-x_2}\right|\le \frac{1}{4}\left|x_1-x_2\right|,$$

and

$$\left|e^{-t}arctan\left(x_1\right)-e^{-t}arctan\left(x_2\right)\right|\le e^{-t}\left|x_1-x_2\right|,$$

with $L_1=\frac{1}{4}$ and $p\left(t\right)=e^{-t}.$ It remains to show thatA4holds. To achieve this task, we introduce

$$w\left(t\right)=\frac{1}{\Gamma \left(\frac{1}{3}\right)}{\displaystyle \underset{1}{\overset{t}{\int }}}{\left(t-s\right)}^{-2/3}{e}^{-s}ds,$$

(9)

and obtain

$$w\left(t\right)=\frac{\sqrt[3]{-1+t}\left(\Gamma \left(\frac{1}{3}\right)-\Gamma \left(\frac{1}{3},1-t\right)\right)}{e^t\left(\Gamma \left(\frac{1}{3}\right)\sqrt[3]{-1+t}\right)},$$

where $\Gamma \left(.,.\right)$ stands for the incomplete gamma function. We obtain $w\left(t\right)<0.3$ for all $t>1$ (see Figure 1). Thus, one may set $L_2=∥w\left(t\right)∥<0.3$, and this yields to $\gamma =0.55.$ Consequentially, Theorem 1 implies the solution $x^{\xi }$ of (8) has the asymptotic property

$$\underset{t\to \infty }{lim}x\left(t,1,\xi \right)=0.$$

Figure 1. Plot of the function $w\left(t\right)$.

Example 2.

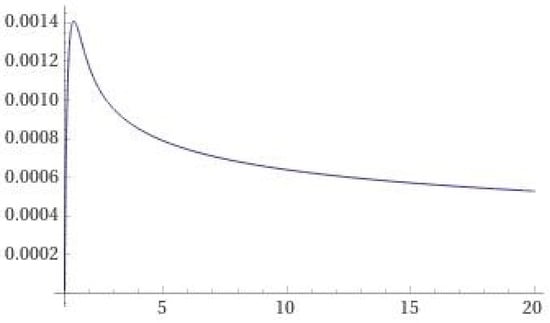
Fix $\alpha =\frac{3}{4},$ and consider the following neutral equation with delay

$${}^C{D}^{\frac{3}{4}}\left(x\left(t\right)-\frac{1}{2}cos\left(1-x\left(t-h\right)\right)\right)=e^{-5t}sin\left(1-x\left(t-h\right)\right),t\in \left(1,\infty \right),$$

(10)

where we define the solution of (10) as on $x^{\xi }=\xi \left(t\right)=1$$\left[1-h,1\right].$ A direct comparison of (1) with (10) results in

$$g\left(t,x\left(t\right)\right)=\frac{1}{2}cos\left(1-x\left(t\right)\right),$$

and

$$f\left(t,x\left(t\right)\right)=e^{-5t}sin\left(1-x\left(t\right)\right).$$

We set $\beta =1,$ and consequentially, $h\left(1\right)=\frac{1}{2}.$ Then, one may easily verify that the Equation (4) holds. Additionally, the conditionA1is satisfied since

$$f\left(t,1\right)=0={-}_1^C{D}_t^{\frac{3}{4}}g\left(t,1\right),$$

and the conditionsA2andA3hold with $L_1=\frac{1}{2},$ and $p\left(t\right)=e^{-5t},$ respectively. Next, we define

$$w\left(t\right)=\frac{1}{\Gamma \left(\frac{3}{4}\right)}{\displaystyle \underset{1}{\overset{t}{\int }}}{\left(t-s\right)}^{-1/4}{e}^{-5s}ds,$$

and direct computation gives the result

$$w\left(t\right)=\frac{e^{-5t}{\left(t-1\right)}^{3/4}\left(\Gamma \left(\frac{3}{4}\right)-\Gamma \left(\frac{3}{4},5-5t\right)\right)}{{\left(5-5t\right)}^{3/4}\Gamma \left(\frac{3}{4}\right)}.$$

Here, we obtain $w\left(t\right)<0.1$ for $t\in \left(1,\infty \right)$ (see Figure 2); therefore, we can take $L_2=0.1.$ Thus, the conditionA4is also satisfied. Subsequently, Theorem 1 implies that the solution $x^{\xi }$ of (10) has the long-term behavior

$$\underset{t\to \infty }{lim}x\left(t,1,\xi \right)=1.$$

Figure 2. Plot of the function $w\left(t\right)$.

3. Conclusions

In the present work, we concentrate on nonlinear neutral-type Caputo fractional differential equations with delay and study their asymptotic behavior under certain conditions. In our analysis, we rewrite the neutral fractional equation as an integral equation and then employ the contraction mapping principle to prove that the solution of the equation converges to a constant known in advance under sufficient conditions. To the best of our knowledge, our manuscript is the first one that focuses on the asymptotic constancy of solutions for fractional differential equations; thus, we believe our outcomes contribute to the ongoing theory of fractional differential equations. It should be pointed out that there are numerous promising research directions with symmetry background to accomplish a concrete survey on the qualitative analysis of fractional equations.