On Non-Symmetric Fractal-Fractional Modeling for Ice Smoking: Mathematical Analysis of Solutions
Abstract
1. Introduction
2. Description of the Ice-Smoking Model
3. Preliminaries
4. Existence Criteria
5. Unique Solution
6. Hyers–Ulam Stability
7. Numerical Algorithm
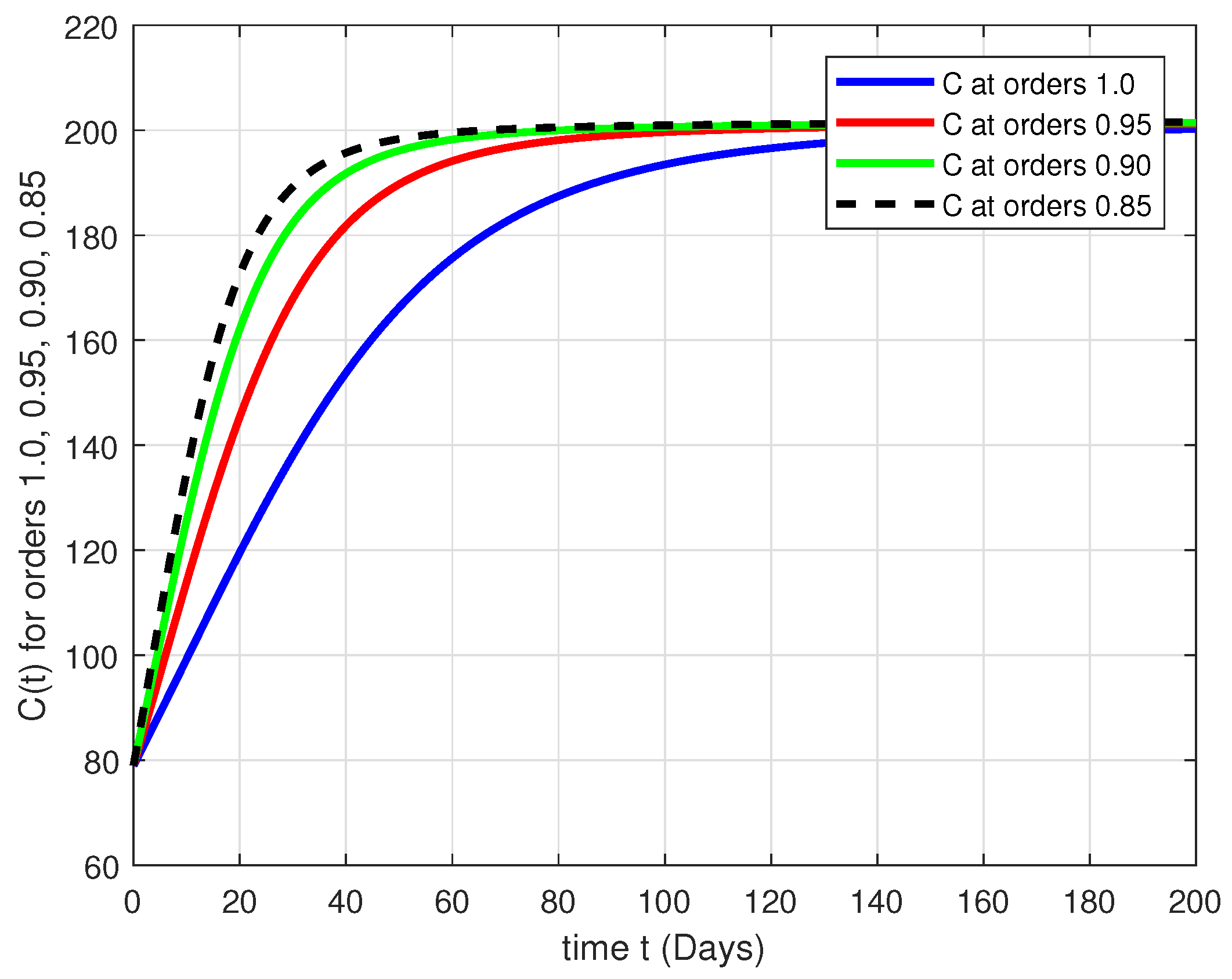
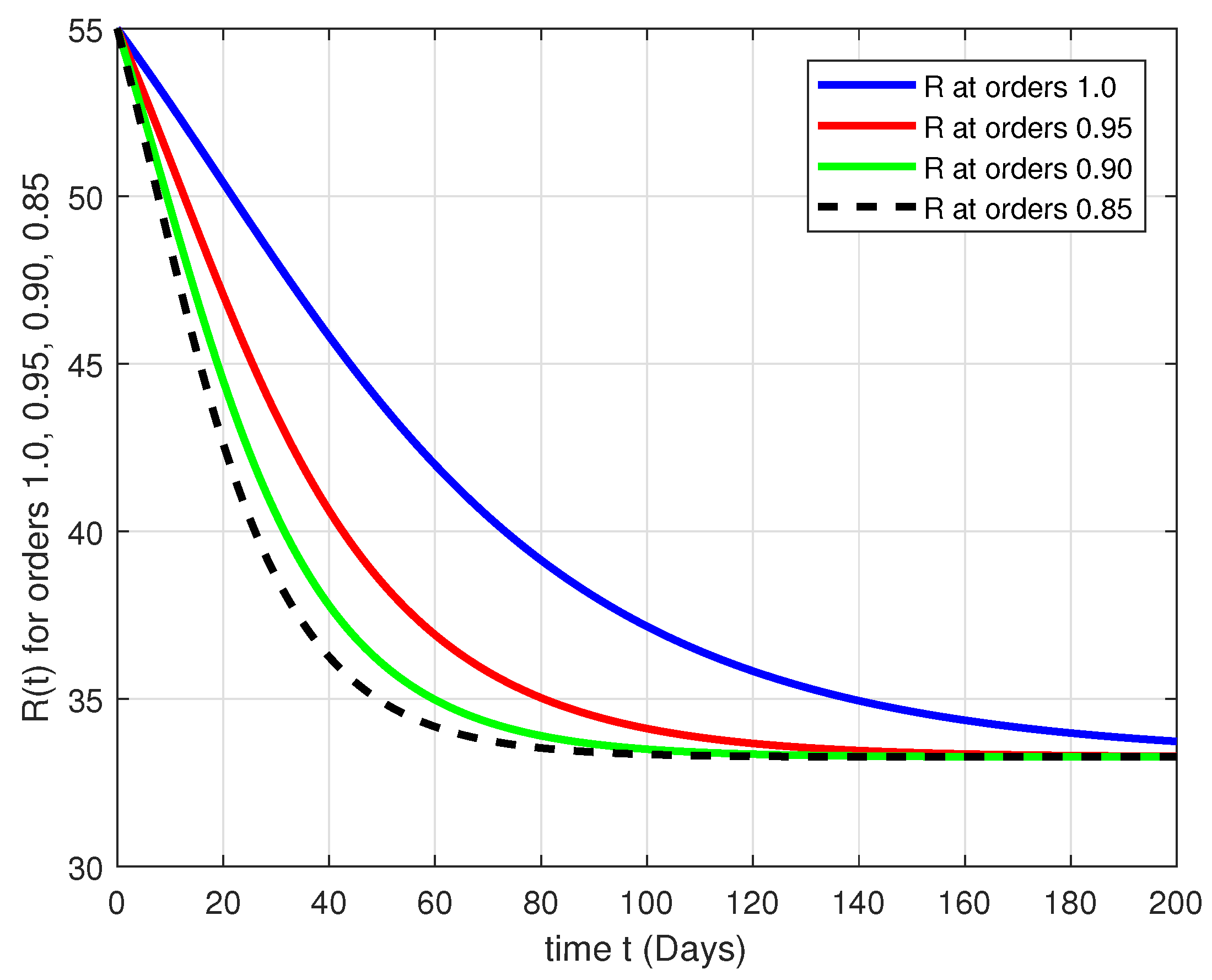
Computational Results
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McCoy, A. The Politics of Heroin in Southeast Asia; Harper and Row: New York, NY, USA, 1972. [Google Scholar]
- Cady, J.F. A History of Modern Burma; Cornell University Press: Ithaca, NY, USA, 1958. [Google Scholar]
- Khan, N.; Fahad, S. Review of Ice Drugs Utilization in Pakistan. 2019. Available online: https://ssrn.com/abstract=3511136 (accessed on 6 December 2022).
- Jenkins, P. “The ice age” the social construction of a drug panic. Justice Q. 1994, 11, 7–31. [Google Scholar] [CrossRef]
- Sharomi, O.; Gumel, A.B. Curtailing smoking dynamics: A mathematical modeling approach. Appl. Math. Comput. 2008, 195, 475–499. [Google Scholar] [CrossRef]
- Zaman, G. Qualitative behavior of giving up smoking models. Bull. Malays. Math. Sci. Soc. 2011, 34, 403–415. [Google Scholar]
- Swartz, J.B. Use of a multistage model to predict time trends in smoking induced lung cancer. J. Epidemiol. Community Health 1992, 46, 311–315. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zeb, A.; Zaman, G.; Momani, S. Square-root dynamics of a giving up smoking model. Appl. Math. Model. 2013, 37, 5326–5334. [Google Scholar] [CrossRef]
- Huo, H.F.; Zhu, C.C. Influence of relapse in a giving up smoking model. Abstr. Appl. Anal. 2013, 2013, 525461. [Google Scholar] [CrossRef]
- Zeb, A.; Bano, A.; Alzahrani, E.; Zaman, G. Dynamical analysis of cigarette smoking model with a saturated incidence rate. AIP Adv. 2018, 8, 045317. [Google Scholar] [CrossRef]
- Zeb, A.; Hussain, S.; Algatani, O.J.; Zaman, G. Global aspects of age-structured cigarette smoking model. Mediterr. J. Math. 2018, 15, 72. [Google Scholar] [CrossRef]
- Haidong, Q.; Rahman, M.U.; Arfan, M. Fractional model of smoking with relapse and harmonic mean type incidence rate under Caputo operator. J. Appl. Math. Comput. 2022. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Qurashi, M.A.; Baleanu, D. A new fractional model for giving up smoking dynamics. Adv. Differ. Equ. 2017, 2017, 88. [Google Scholar] [CrossRef]
- Khan, Z.A.; Rahman, M.U.; Shah, K. Study of a fractal-fractional smoking models with relapse and harmonic mean type incidence rate. J. Funct. Spaces 2021, 2021, 6344079. [Google Scholar] [CrossRef]
- Liu, C.; Sun, W.; Yi, X. Optimal control of a fractional smoking system. J. Ind. Manag. Opt. 2023, 19, 2936–2954. [Google Scholar] [CrossRef]
- Etemad, S.; Shikongo, A.; Owolabi, K.M.; Tellab, B.; Avci, I.; Rezapour, S.; Agarwal, R.P. A new fractal-fractional version of giving up smoking model: Application of Lagrangian piece-wise interpolation along with asymptotical stability. Mathematics 2022, 10, 4369. [Google Scholar] [CrossRef]
- Thaiprayoon, C.; Sudsutad, W.; Alzabut, J.; Etemad, S.; Rezapour, S. On the qualitative analysis of the fractional boundary valueproblem describing thermostat control model via ψ-Hilfer fractional operator. Adv. Differ. Equ. 2021, 2021, 201. [Google Scholar] [CrossRef]
- Rezapour, S.; Etemad, S.; Mohammadi, H. A mathematical analysis of a system of Caputo-Fabrizio fractional differential equationsfor the anthrax disease model in animals. Adv. Differ. Equ. 2020, 2020, 481. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Almusawa, H. Mathematical structure of mosaic disease using microbial biostimulants via Caputo and Atangana–Baleanu derivatives. Res. Phys. 2021, 24, 104186. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Okyere, E.; Yankson, E.; Opoku, A.A.; Adom-Konadu, A.; Acheampong, E.; Arthur, Y.D. Non-fractional and fractional mathematical analysis and simulations for Q fever. Chaos Solitons Fractals 2022, 156, 111821. [Google Scholar] [CrossRef]
- Deressa, C.T.; Etemad, S.; Rezapour, S. On a new four-dimensional model of memristor-based chaotic circuit in the context of nonsingular Atangana–Baleanu-Caputo operators. Adv. Differ. Equ. 2021, 2021, 444. [Google Scholar] [CrossRef]
- Mohammadi, H.; Kumar, S.; Rezapour, S.; Etemad, S. A theoretical study of the Caputo-Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solitons Fractals 2021, 144, 110668. [Google Scholar] [CrossRef]
- Khan, H.; Tunc, C.; Chen, W.; Khan, A. Existence theorems and Hyers–Ulam stability for a class of hybrid fractional differentialequations with p-Laplacial operator. J. Appl. Anal. Comput. 2018, 8, 1211–1226. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S. Environmental persistence influences infection dynamics for a butterfly pathogen via new generalised Caputo type fractional derivative. Chaos Solitons Fractals 2021, 144, 110672. [Google Scholar] [CrossRef]
- Zarin, R.; Khaliq, H.; Khan, A.; Khan, D.; Akgul, A.; Humphries, U.W. Deterministic and fractional modeling of a computer virus propagation. Res. Phys. 2022, 33, 105130. [Google Scholar] [CrossRef]
- Wongcharoen, A.; Ntouyas, S.K.; Tariboon, J. Nonlocal boundary value problems for Hilfer type pantograph fractional differentialequations and inclusions. Adv. Differ. Equ. 2020, 2020, 279. [Google Scholar] [CrossRef]
- Amara, A.; Etemad, S.; Rezapour, S. Topological degree theory and Caputo-Hadamard fractional boundary value problems. Adv. Differ. Equ. 2020, 2020, 1–22. [Google Scholar] [CrossRef]
- Omame, A.; Nwajeri, U.K.; Abbas, M.; Onyenegecha, C.P. A fractional order control model for Diabetes and COVID-19 co-dynamics with Mittag–Leffler function. Alex. Eng. J. 2022, 61, 7619–7635. [Google Scholar] [CrossRef]
- Jafari, H.; Mahmoudi, M.; Skandari, M.H.N. A new numerical method to solve pantograph delay differential equations with convergence analysis. Adv. Differ. Equ. 2021, 2021, 129. [Google Scholar] [CrossRef]
- Rashid, S.; Kubra, K.T.; Jafari, H.; Lehre, S.U. A semi-analytical approach for fractional order Boussinesq equation in a gradient unconfined aquifers. Math. Methods Appl. Sci. 2022, 45, 1033–1062. [Google Scholar] [CrossRef]
- Omame, A.; Ele Isah, M.; Abbas, M.; Abdel-Aty, A.H.; Onyenegecha, C.P. A fractional order model for Dual Variants of COVID-19 and HIV co-infection via Atangana-Baleanu derivative. Alex. Eng. J. 2022, 61, 9715–9731. [Google Scholar] [CrossRef]
- Omame, A.; Abbas, M.; Onyenegecha, C.P. Backward bifurcation and optimal control in a co-infection model for SARS-CoV-2 and ZIKV. Res. Phys. 2022, 37, 105481. [Google Scholar] [CrossRef]
- Omame, A.; Abbas, M.; Abdel-Aty, A.H. Assessing the impact of SARS-CoV-2 infection on the dynamics of dengue and HIV via fractional derivatives. Chaos Solitons Fractals 2022, 162, 112427. [Google Scholar] [CrossRef]
- Zeb, A.; Alzahrani, A. Non-standard finite difference scheme and analysis of smoking model with reversion class. Res. Phys. 2021, 21, 103785. [Google Scholar] [CrossRef] [PubMed]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Atangana, A.; Akgul, A.; Owolabi, K.M. Analysis of fractal fractional differential equations. Alex. Eng. J. 2020, 59, 1117–1134. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, A.; Khan, H.; De la Sen, M.; Alzabut, J.; Etemad, S.; Deressa, C.T.; Rezapour, S. On Non-Symmetric Fractal-Fractional Modeling for Ice Smoking: Mathematical Analysis of Solutions. Symmetry 2023, 15, 87. https://doi.org/10.3390/sym15010087
Shah A, Khan H, De la Sen M, Alzabut J, Etemad S, Deressa CT, Rezapour S. On Non-Symmetric Fractal-Fractional Modeling for Ice Smoking: Mathematical Analysis of Solutions. Symmetry. 2023; 15(1):87. https://doi.org/10.3390/sym15010087
Chicago/Turabian StyleShah, Anwar, Hasib Khan, Manuel De la Sen, Jehad Alzabut, Sina Etemad, Chernet Tuge Deressa, and Shahram Rezapour. 2023. "On Non-Symmetric Fractal-Fractional Modeling for Ice Smoking: Mathematical Analysis of Solutions" Symmetry 15, no. 1: 87. https://doi.org/10.3390/sym15010087
APA StyleShah, A., Khan, H., De la Sen, M., Alzabut, J., Etemad, S., Deressa, C. T., & Rezapour, S. (2023). On Non-Symmetric Fractal-Fractional Modeling for Ice Smoking: Mathematical Analysis of Solutions. Symmetry, 15(1), 87. https://doi.org/10.3390/sym15010087







