A Family of Higher Order Scheme for Multiple Roots

Abstract

We have developed a two-point iterative scheme for multiple roots that achieves fifth order convergence by using two function evaluations and two derivative evaluations each iteration. Weight function approach is utilized to frame the scheme. The weight function named as $R\left({\upsilon }_t\right)$ is used, which is a function of ${\upsilon }_t$, and ${\upsilon }_t$ is a function of ${\omega }_t$, i.e., ${\upsilon }_t=\frac{{\omega }_t}{1+a{\omega }_t},$ where a is a real number and ${\omega }_t={\left(\frac{g\left({\mathtt{y}}_t\right)}{g\left({\mathtt{x}}_t\right)}\right)}^{\frac{1}{\tilde{m}}}$ is a multi-valued function. The consistency of the newly generated methods is ensured numerically and through the basins of attraction. Four complex functions are considered to compare the new methods with existing schemes via basins of attraction, and all provided basins of attraction possess reflection symmetry. Further, five numerical examples are used to verify the theoretical results and to contrast the presented schemes with some recognized schemes of fifth order. The results obtained have proved that the new schemes are better than the existing schemes of the same nature.

2. Construction of the Fifth-Order Family

Here, we derive a fifth-order mechanism for multiple zeros $(\tilde{m}\ge 2)$ in the following, by considering the scheme:

$$\begin{array}{cc}\hfill {\mathtt{y}}_t& ={\mathtt{x}}_t-\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{x}}_{t+1}& ={\mathtt{y}}_t-\tilde{m}R\left({\upsilon }_t\right)\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{y}}_t\right)},\hfill \end{array}$$

(5)

where $\tilde{m}\ge 2$ is the multiplicity of the required zero and $R\left({\upsilon }_t\right)$ is a single variable weight function. Moreover, ${\upsilon }_t=\frac{{\omega }_t}{1+a{\omega }_t},$ where $a\in \mathbb{R}$ and ${\omega }_t={\left(\frac{g\left({\mathtt{y}}_t\right)}{g\left({\mathtt{x}}_t\right)}\right)}^{\frac{1}{\tilde{m}}}$ are multi-valued functions.

Theorem 1.

Let $\alpha \in D$ be a multiple root with multiplicity $\tilde{m}\ge 2$ of a holomorphic function $g:D\subset \mathbb{C}\to \mathbb{C}$ for an open interval $D.$ If $x_0$ is sufficiently close to α then the new Scheme (5) has fifth-order of convergence, provided

$$R\left(0\right)=1,R^{\prime }\left(0\right)=0,R^{″}\left(0\right)=2,\left|R^{‴}\left(0\right)\right|<\infty ,$$

(6)

and fulfils the aforementioned error equation,

$$e_{t+1}=\left(\frac{(18+12a+6\tilde{m}-R^{‴}\left(0\right))D_1^4-12\tilde{m}{D}_1^2{D}_2}{6{\tilde{m}}^4}\right)e_t^5+O\left(e_t^6\right).$$

(7)

Proof of Theorem 1.

If ${\mathtt{x}}_t$ and $e_t$ denote the approximate solution and the corresponding error in t–th iteration, then $e_t={\mathtt{x}}_t-\alpha .$

For the function $g\left({\mathtt{x}}_t\right),$ apply Taylor’s series expansion about $\mathtt{x}=\alpha ,$

$$g\left({\mathtt{x}}_t\right)=g\left(\alpha \right)+g^{\left(1\right)}\left(\alpha \right)e_t+\frac{g^{\left(2\right)}\left(\alpha \right)}{2!}{e}_t^2+...+\frac{g^{(\tilde{m}-1)}\left(\alpha \right)}{\tilde{m}-1!}{e}_t^{\tilde{m}-1}+\frac{g^{\left(\tilde{m}\right)}\left(\alpha \right)}{\tilde{m}!}{e}_t^{\tilde{m}}+\dots$$

(8)

since the root $\alpha$ has multiplicity $\tilde{m}$. Therefore, $g\left(\alpha \right)=g^{\left(1\right)}\left(\alpha \right)=g^{\left(2\right)}\left(\alpha \right)=\dots g^{(\tilde{m}-1)}\left(\alpha \right)=0$ and $g^{\left(\tilde{m}\right)}\left(\alpha \right)\ne 0.$ Thus, Equation (8) becomes

$$g\left({\mathtt{x}}_t\right)=\frac{g^{\left(\tilde{m}\right)}\left(\alpha \right)}{\tilde{m}!}{e}_t^{\tilde{m}}\left(1+D_1{e}_t+D_2{e}_t^2+D_3{e}_t^3+D_4{e}_t^4+D_5{e}_t^5+O\left(e_t^6\right)\right).$$

(9)

Here, the asymptotic error constants $D_i=\frac{\tilde{m}!}{(\tilde{m}+i)!}\frac{g^{(\tilde{m}+i)}\left(\alpha \right)}{g^{\left(\tilde{m}\right)}\left(\alpha \right)},i=1,2,3,\dots$

$$\begin{array}{c}\hfill g^{\prime }\left({\mathtt{x}}_t\right)=\frac{g^{\left(\tilde{m}\right)}\left(\alpha \right)}{(\tilde{m}-1)!}{e}_t^{\tilde{m}-1}[1+\left(\frac{1+\tilde{m}}{\tilde{m}}\right)D_1{e}_t+\left(\frac{2+\tilde{m}}{\tilde{m}}\right)D_2{e}_t^2+\left(\frac{3+\tilde{m}}{\tilde{m}}\right)D_3{e}_t^3\\ \hfill \left(\frac{4+\tilde{m}}{\tilde{m}}\right)D_4{e}_t^4+\left(\frac{5+\tilde{m}}{\tilde{m}}\right)D_5{e}_t^5+O\left(e_t^6\right)].\end{array}$$

(10)

Dividing (9) by (10), we obtain

$$\begin{array}{c}\hfill \frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)}=\frac{e_t}{\tilde{m}}-\frac{D_1}{{\tilde{m}}^2}{e}_t^2+\frac{[(1+\tilde{m})D_1^2-2\tilde{m}{D}_2]}{{\tilde{m}}^3}{e}_t^3+\frac{L^{\prime }}{{\tilde{m}}^4}{e}_t^4+\frac{L}{{\tilde{m}}^5}{e}_t^5+O\left(e_t^6\right),\end{array}$$

(11)

where $L^{\prime }=[-{(1+\tilde{m})}^2{D}_1^3+\tilde{m}(4+3\tilde{m})D_1{D}_2-3{\tilde{m}}^2{D}_3],$ $L=({(1+\tilde{m})}^3{D}_1^4-2\tilde{m}(3+5\tilde{m}+2{\tilde{m}}^2)D_1^2{D}_2+2{\tilde{m}}^2(3+2\tilde{m})D_1{D}_3$ $+2{\tilde{m}}^2[(2+\tilde{m})D_2^2-2\tilde{m}{D}_4]).$

Put (11) in the first step of (5),

$$\begin{array}{c}\hfill e_{{\mathtt{y}}_t}=\frac{D_1}{\tilde{m}}{e}_t^2+\left(\frac{2\tilde{m}{D}_2-(1+\tilde{m})D_1^2}{{\tilde{m}}^2}\right)e_t^3+\left(\frac{-L^{\prime }}{{\tilde{m}}^3}\right)e_t^4+O\left(e_t^5\right).\end{array}$$

(12)

Now, we have

$$\begin{array}{c}\hfill g\left({\mathtt{y}}_t\right)=\frac{g^{\left(\tilde{m}\right)}\left(x_0\right)}{\tilde{m}!}{e}_{{\mathtt{y}}_k}^{\tilde{m}}\left(1+D_1{e}_{{\mathtt{y}}_k}+D_2{e}_{{\mathtt{y}}_k}^2+D_3{e}_{{\mathtt{y}}_k}^3+D_4{e}_{{\mathtt{y}}_k}^4+D_5{e}_{{\mathtt{y}}_k}^5+O\left(e_{{\mathtt{y}}_k}^6\right)\right),\end{array}$$

(13)

and

$$\begin{array}{cc}\hfill g^{\prime }\left({\mathtt{y}}_t\right)=& \frac{g^{\left(\tilde{m}\right)}\left(\alpha \right)}{(\tilde{m}-1)!}{e}_{{\mathtt{y}}_k}^{\tilde{m}-1}[1+\left(\frac{1+\tilde{m}}{\tilde{m}}\right)D_1{e}_{{\mathtt{y}}_k}+\left(\frac{2+\tilde{m}}{\tilde{m}}\right)D_2{e}_{{\mathtt{y}}_k}^2+\left(\frac{3+\tilde{m}}{\tilde{m}}\right)D_3{e}_{{\mathtt{y}}_k}^3\hfill \\ \hfill & +\left(\frac{4+\tilde{m}}{\tilde{m}}\right)D_4{e}_{{\mathtt{y}}_k}^4+\left(\frac{5+\tilde{m}}{\tilde{m}}\right)D_5{e}_{{\mathtt{y}}_k}^5+O\left(e_{{\mathtt{y}}_k}^6\right)].\hfill \end{array}$$

(14)

Divide (13) by (9),

$$\begin{array}{cc}\hfill \frac{g\left({\mathtt{y}}_t\right)}{g\left(x_t\right)}=& \left(\frac{D_1}{\tilde{m}}\right)e^{\tilde{m}}\left(1+\frac{L_1}{D_1}{e}_t+\frac{L_2}{2\tilde{m}{D}_1^2}{e}_t^2+\frac{L_3}{6{\tilde{m}}^2{D}_1^3}{e}_t^3+o\left(e_t^4\right)\right),\hfill \end{array}$$

(15)

where $L_1=2\tilde{m}{D}_2-(2+\tilde{m})D_1^2,$ $L_2={(1+\tilde{m})}^2(3+\tilde{m})D_1^4-2\tilde{m}(3+5\tilde{m}+2{\tilde{m}}^2)D_1^2{D}_2+4{\tilde{m}}^2(\tilde{m}-1)D_2^2+6{\tilde{m}}^2{D}_1{D}_3,$ $L_3=-{(\tilde{m}+1)}^3({\tilde{m}}^2+6\tilde{m}+8)D_1^6+6\tilde{m}({\tilde{m}}^4+6{\tilde{m}}^3+13{\tilde{m}}^2+13\tilde{m}+4)D_1^4{D}_2+8{\tilde{m}}^3({\tilde{m}}^2-3\tilde{m}+2)D_2^3+6{\tilde{m}}^2{D}_1^3(3{\tilde{m}}^2+7\tilde{m}+4)D_3+36{\tilde{m}}^3(\tilde{m}-1)D_1{D}_2{D}_3-12{\tilde{m}}^3{D}_1^2[{(\tilde{m}+1)}^2{D}_2^2-2D_4].$

Also,

$$\begin{array}{cc}\hfill {\omega }_t={\left(\frac{g\left({\mathtt{y}}_t\right)}{g\left(x_t\right)}\right)}^{1/\tilde{m}}=& \frac{D_1}{\tilde{m}}{e}^{\tilde{m}}+\frac{L_1}{{\tilde{m}}^2}{e}_t^2+\frac{M_1}{2{\tilde{m}}^3}{e}_t^3+\frac{M_2}{6{\tilde{m}}^4}{e}_t^4+o\left(e_t^5\right),\hfill \end{array}$$

(16)

where $M_1=[(7+\tilde{m}(7+2\tilde{m}))D_1^3-2\tilde{m}(7+3\tilde{m})D_1{D}_2+6{\tilde{m}}^2{D}_3],$ $M_2=[-(2+\tilde{m})(17+\tilde{m}(17+6\mathsf{m}))D_1^4+6\tilde{m}(17+4\tilde{m}(4+\tilde{m}))D_1^2{D}_2-12{\tilde{m}}^2(5+2\tilde{m})D_1{D}_3+12{\tilde{m}}^2(-(3+\tilde{m})D_2^2+2\tilde{m}{D}_4)].$

From Scheme (5), we have ${\upsilon }_t=\frac{{\omega }_t}{1+a{\omega }_t}$. Using (16) in it, we obtain

$$\begin{array}{c}\hfill {\upsilon }_t=\frac{D_1}{\tilde{m}}{e}_t^{\tilde{m}}+\frac{2\tilde{m}{D}_2-(2+a+\tilde{m})D_1^2}{{\tilde{m}}^2}{e}_t^2+\frac{N_1}{2{\tilde{m}}^3}{e}_t^3+\frac{N_2}{6{\tilde{m}}^4}{e}_t^4+o\left(e_t^5\right),\end{array}$$

(17)

where $N_1=[(7+2a^2+\tilde{m}(7+2\tilde{m})+4a(2+\tilde{m}))D_1^3-2\tilde{m}(7+4a+3\tilde{m})D_1{D}_2+6{\tilde{m}}^2{D}_3],$ $N_2=[(34+6a^3+51\tilde{m}+29{\tilde{m}}^2+6{\tilde{m}}^3+18a^2(2+\tilde{m})+6a(11+11\tilde{m}+3{\tilde{m}}^2))D_1^4-6\tilde{m}(17+6a^2+16\tilde{m}+4{\tilde{m}}^2+2a(11+5\tilde{m}))D_1^2{D}_2+12{\tilde{m}}^2(5+3a+2\tilde{m})D_1{D}_3+12{\tilde{m}}^2((3+2a+\tilde{m})D_2^2-2\tilde{m}{D}_4)].$

Expanding weight function $R\left({\upsilon }_t\right)$ around the locality of origin, as follows,

$$R\left({\upsilon }_t\right)=R\left(0\right)+R^{\prime }\left(0\right){\upsilon }_t+\frac{1}{2!}{R}^{″}\left(0\right){\upsilon }_t^2+\frac{1}{3!}{R}^{‴}\left(0\right){\upsilon }_t^3+\dots$$

(18)

At last, using the result of step one of schemes (5), (13), ( 14) and (18) in the second step of Mechanism (5), we obtain

$$\begin{array}{cc}\hfill e_{t+1}& =-\frac{[-1+R\left(0\right)]D_1}{\tilde{m}}{e}_t^2+\frac{[-2(-1+R\left(0\right))\tilde{m}{D}_2+D_1^2((-1+R\left(0\right))(1+\tilde{m})-R^{\prime }\left(0\right)]}{{\tilde{m}}^2}{e}_t^3\hfill \\ & +\frac{Q_1}{2{\tilde{m}}^3}{e}_t^4+\frac{Q_2}{6{\tilde{m}}^4}{e}_t^5+O\left(e_t^6\right),\hfill \end{array}$$

(19)

where $Q_1=(-6(-1+R\left(0\right)){\tilde{m}}^2{D}_3+2\tilde{m}{D}_1{D}_2((-1+R\left(0\right))(4+3\tilde{m})-4R^{\prime }\left(0\right))+D_1^3(2+4\tilde{m}-4\tilde{m}(R\left(0\right)+2{\tilde{m}}^2-2R\left(0\right){\tilde{m}}^2+2(3+a+2\tilde{m})R^{\prime }\left(0\right)-R^{″}\left(0\right))),$ $Q_2=(12{\tilde{m}}^2(-2(-1+R\left(0\right))\tilde{m}{D}_4+D_2^2((-1+R\left(0\right))(2+\tilde{m})-2R^{\prime }\left(0\right)))+12{\tilde{m}}^2{D}_1{D}_3((-1+R\left(0\right))(3+2\tilde{m})-3R^{\prime }\left(0\right))+6\tilde{m}{D}_1^2{D}_2(2(-3+R\left(0\right)-5\tilde{m}+5R\left(0\right)\tilde{m}-2{\tilde{m}}^2+2R\left(0\right){\tilde{m}}^2)-(17+6a+10\tilde{m})R^{\prime }\left(0\right)+3R^{″}\left(0\right))+D_1^4(-6-6R\left(0\right)-18\tilde{m}+6R\left(0\right)\tilde{m}-18{\tilde{m}}^2+18R\left(0\right){\tilde{m}}^2-6{\tilde{m}}^3+6R\left(0\right){\tilde{m}}^3-3(11+2a^2+17\tilde{m}+6{\tilde{m}}^2+2a(5+3\tilde{m}))R^{\prime }\left(0\right)+3(5+2a+3\tilde{m})R^{″}\left(0\right)-R^{‴}\left(0\right)).$

Using the Expression (19), we can quickly determine that Mechanism (5) obtains the convergence of at least fifth-order, if

$$R\left(0\right)=1,R^{\prime }\left(0\right)=0,R^{″}\left(0\right)=2.$$

(20)

Next, by using (20) in (19), we obtain

$$e_{t+1}=\left(\frac{(18+12a+6\tilde{m}-R^{‴}\left(0\right))D_1^4-12\tilde{m}{D}_1^2{D}_2}{6{\tilde{m}}^4}\right)e_t^5+O\left(e_t^6\right),$$

(21)

Provided $\left|R^{‴}\left(0\right)\right|<\infty .$ Hence, Scheme (5) has fifth-order convergence.    □

3. Special Cases

This section provides the new methods of fifth order for multiple roots by making different choices of weight functions adhering the constraints of Theorem 1. A few special cases are stated in the preceding Table 1.

Table 1. Some special cases of Mechanism (5).

Cases (Naming)	Weight Functions	Equivalent Iterative Method
Case-1 (TM1)	$R\left({\upsilon }_t\right)=1+{\upsilon }_t^2$	${\mathtt{y}}_t={\mathtt{x}}_t-\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},$
		${\mathtt{x}}_{t+1}={\mathtt{y}}_t-\tilde{m}(1+{\upsilon }_t^2)\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{y}}_t\right)}$.
Case-2 (TM2)	$R\left({\upsilon }_t\right)=e^{-{\upsilon }_t}+{\upsilon }_t+\frac{{\upsilon }_t^2}{2}$	${\mathtt{y}}_t={\mathtt{x}}_t-\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},$
		${\mathtt{x}}_{t+1}={\mathtt{y}}_t-\tilde{m}(e^{-{\upsilon }_t}+{\upsilon }_t+\frac{{\upsilon }_t^2}{2})\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{y}}_t\right)}$.
Case-3 (TM3)	$R\left({\upsilon }_t\right)=(1-{\upsilon }_t)e^{{\upsilon }_t}+\frac{3}{2}{\upsilon }_t^2$	${\mathtt{y}}_t={\mathtt{x}}_t-\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},$
		${\mathtt{x}}_{t+1}={\mathtt{y}}_t-\tilde{m}((1-{\upsilon }_t)e^{{\upsilon }_t}+\frac{3}{2}{\upsilon }_t^2)\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{y}}_t\right)}$.
Case-4 (TM4)	$R\left({\upsilon }_t\right)=2-{\upsilon }_t-\frac{1}{1+{\upsilon }_t}+2{\upsilon }_t^2$	${\mathtt{y}}_t={\mathtt{x}}_t-\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},$
		${\mathtt{x}}_{t+1}={\mathtt{y}}_t-\tilde{m}(2-{\upsilon }_t-\frac{1}{1+{\upsilon }_t}+2{\upsilon }_t^2)\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{y}}_t\right)}$.

4. Basins of Attraction

The graphical images known as the basins of attraction of the roots of a polynomial $g\left(w\right)$ in the Complex plane are used to inspect the convergence of the scheme. The major significance of using the basins of attraction is that it widens the scope of inceptive guesses to obtain the zeros of an equation. These graphical images have been used by many researchers [34,35,36,37,38,39,40,41,42] to measure the stability and effectiveness of the iterative formulae. We use ${10}^{-3}$ as tolerance, with a maximum of 25 iterations to exhibit the basins. The procedure is closed down with the comment that the iteration method starting from $w_0$ is divergent, if the tolerance is not gained in the needed number of iterations. There are some basic rules that are used to draw the basins of attraction, given as below:

• The first rule is to select a rectangular area and make sure that every root of the considered polynomial lies inside this region.
• Each initial guess of a root is given a color in the basins of attraction. Similarly, another color is given to each initial guess of another root in the basins of attraction. For each of the complex polynomial’s roots, this operation is repeated.
• If the iterative formula which started with the initial approximation $w_0$ converges to a root, then the basins of attraction display the color which is allotted to the initial guess of that root at point $w_0.$ Otherwise, the initial guess $w_0$ is painted with black color.

We now proceed to compare our newly proposed methods, TM1, TM2, TM3 and TM4, with some existing schemes of the same nature. For comparison, we consider the three subcases of the scheme by Sharma et al. [40] and three subcases of the family presented by Chanu et al. [41]. The first method developed by Sharma et al. [40], which we denoted by SM1, is given as:

$$\begin{array}{cc}\hfill {\mathtt{y}}_t& ={\mathtt{x}}_t-\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{x}}_{t+1}& ={\mathtt{y}}_t-\tilde{m}(1+{\omega }_t^2)\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{y}}_t\right)}.\hfill \end{array}$$

(22)

We designate the second subcase of the method by Sharma et al. [40] as SM2, which is given below:

$$\begin{array}{cc}\hfill {\mathtt{y}}_t& ={\mathtt{x}}_t-\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{x}}_{t+1}& ={\mathtt{y}}_t-\tilde{m}\left(\frac{1+{\omega }_t+{\omega }_t^2}{1+{\omega }_t}\right)\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{y}}_t\right)}.\hfill \end{array}$$

(23)

Here, ${\omega }_t={\left(\frac{g\left({\mathtt{y}}_t\right)}{g\left({\mathtt{x}}_t\right)}\right)}^{\frac{1}{\tilde{m}}}$ is a multi-valued function in both the subcases SM1 and SM2.

We write the third subcase of the method by Sharma et al. [40] as SM3, which is given below:

$$\begin{array}{cc}\hfill {\mathtt{y}}_t& ={\mathtt{x}}_t-\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{x}}_{t+1}& ={\mathtt{y}}_t-\tilde{m}\left(\frac{{\left(g\left({\mathtt{x}}_t\right)\right)}^{\frac{2}{m}}-{\left(g\left({\mathtt{y}}_t\right)\right)}^{\frac{2}{m}}}{{\left(g\left({\mathtt{x}}_t\right)\right)}^{\frac{2}{m}}-2{\left(g\left({\mathtt{y}}_t\right)\right)}^{\frac{2}{m}}}\right)\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{y}}_t\right)},\hfill \end{array}$$

(24)

We denote the first subcase of the method by Chanu et al. [41] as NPM1. The scheme for NPM1 is:

$$\begin{array}{cc}\hfill {\mathtt{y}}_t& ={\mathtt{x}}_t+\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{z}}_t& ={\mathtt{x}}_t-\frac{\tilde{m}}{2^{\tilde{m}}}\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{x}}_{t+1}& ={\mathtt{z}}_t-\tilde{m}\left(1-\frac{2}{\tilde{m}}+\frac{4}{{\tilde{m}}^2}+\left(\frac{4}{\tilde{m}}-\frac{8}{{\tilde{m}}^2}\right)h+\left(\frac{4}{{\tilde{m}}^2}-\frac{2}{\tilde{m}}\right)h^2\right)\frac{g\left({\mathtt{z}}_t\right)}{g^{\prime }\left({\mathtt{z}}_t\right)},\hfill \end{array}$$

(25)

The second subcase of the method by Chanu et al. [41] is expressed as NPM2. This scheme is given by:

$$\begin{array}{cc}\hfill {\mathtt{y}}_t& ={\mathtt{x}}_t+\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{z}}_t& ={\mathtt{x}}_t-\frac{\tilde{m}}{2^{\tilde{m}}}\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{x}}_{t+1}& ={\mathtt{z}}_t-\tilde{m}\left(1+\frac{4(h^3-3h+2)}{3{\tilde{m}}^2}-\frac{2(h^3-3h+2)}{3\tilde{m}}\right)\frac{g\left({\mathtt{z}}_t\right)}{g^{\prime }\left({\mathtt{z}}_t\right)},\hfill \end{array}$$

(26)

The third subcase of the method by Chanu et al. [41] is denoted by NPM3. The method is presented by:

$$\begin{array}{cc}\hfill {\mathtt{y}}_t& ={\mathtt{x}}_t+\tilde{m}\frac{g\left({\mathtt{x}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{z}}_t& ={\mathtt{x}}_t-\frac{\tilde{m}}{2^{\tilde{m}}}\frac{g\left({\mathtt{y}}_t\right)}{g^{\prime }\left({\mathtt{x}}_t\right)},\hfill \\ \hfill {\mathtt{x}}_{t+1}& ={\mathtt{z}}_t-\tilde{m}\left(1+\frac{4{(h-1)}^2(2h+1)}{3{\tilde{m}}^2}-\frac{2{(h-1)}^2(2h+1)}{3\tilde{m}}\right)\frac{g\left({\mathtt{z}}_t\right)}{g^{\prime }\left({\mathtt{z}}_t\right)},\hfill \end{array}$$

(27)

where $h=2^{\tilde{m}}\frac{g\left({\mathtt{x}}_t\right)}{g\left({\mathtt{y}}_t\right)}$ is a multi-valued function in schemes NPM1, NPM2 and NPM3.

We compare our newly proposed methods TM1, TM2, TM3 and TM4 with SM1, SM2, SM3, NPM1, NPM2 and NPM3 by using the following four problems through basins of attraction. To view dynamical vision, we assume a rectangle $D=[-3,3]\times [-3,3]\in \mathbb{C}$ with $500\times 500$ grid points.

Problem 1.

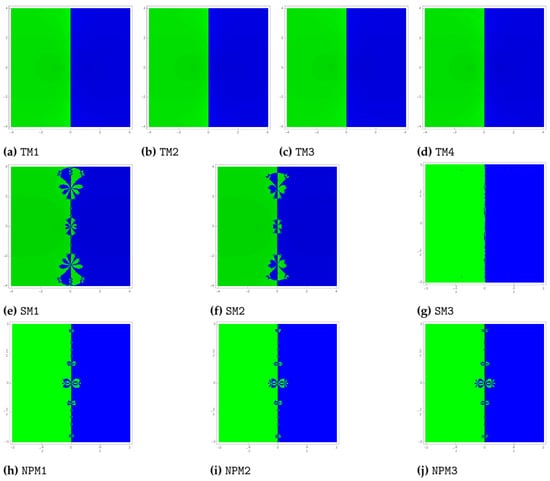
Let us assume the polynomial $g_1\left(w\right)={(w^2-1)}^3$, having zeros $w=1,-1$ with multiplicity 3. Distribute the colours blue and green among each starting point in the basins of attraction of roots $-1$ and $1,$ respectively. Figure 1 shows the basins that were obtained for the methods TM1, TM2, TM3, TM4, SM1, SM2, SM3, NPM1, NPM2 and NPM3. From Figure 1, one can easily observe that the methods TM1, TM2, TM3 and TM4 divide the complex plane into two equal halves without any disturbance in the regions, but in case of the methods SM1, SM2, SM3, NPM1, NPM2 and NPM3, the complex plane is divided into two equal halves, which have disturbances. Therefore, the basins of attraction for the proposed methods, TM1, TM2, TM3 and TM4, are more stable than those for SM1, SM2, SM3, NPM1, NPM2 and NPM3. Among the newly proposed methods, all performed equally well.

Figure 1. Basins of attraction of TM1–TM4, SM1–SM3 and NPM1–NPM3 for polynomial $g_1\left(w\right)$.

Problem 2.

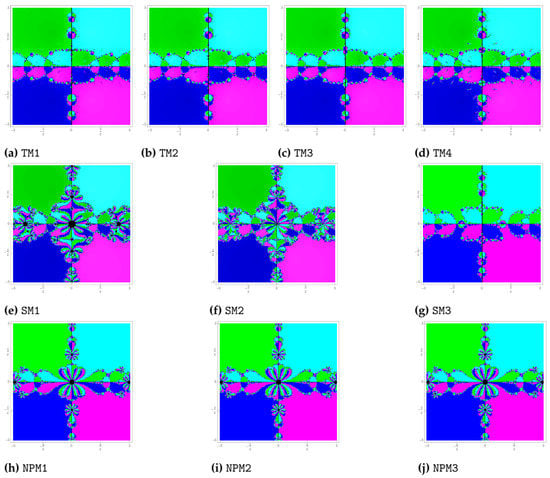
Now, consider the polynomial $g_2\left(w\right)={(w^4+4w^2+16)}^2$, having zeros $w=1+\sqrt{3}i,1-\sqrt{3}i,-1+\sqrt{3}i,-1-\sqrt{3}i$ with multiplicity $2.$ We have assigned the colors blue, green, magenta and cyan for each initial point in the basins of attraction of zeros $1+\sqrt{3}i,1-\sqrt{3}i,-1+\sqrt{3}i,-1-\sqrt{3}i,$ respectively. Figure 2 displays the basins created using the techniques TM1, TM2, TM3, TM4, SM1, SM2, SM3, NPM1, NPM2 and NPM3. Black spots in Figure 2 show the points which are not convergent to any of the roots. It is clear from Figure 2 that the convergence area is more for methods TM1, TM2, TM3, TM4 and SM3 as compared to the methods SM1, SM2, NPM1, NPM2 and NPM3. Furthermore, it can be seen that the new proposed methods, SM2 and SM3, do not contain any black spots which indicate the divergent points.

Figure 2. Basins of attraction of TM1–TM4, SM1–SM3 and NPM1–NPM3 for polynomial $g_2\left(w\right)$.

Problem 3.

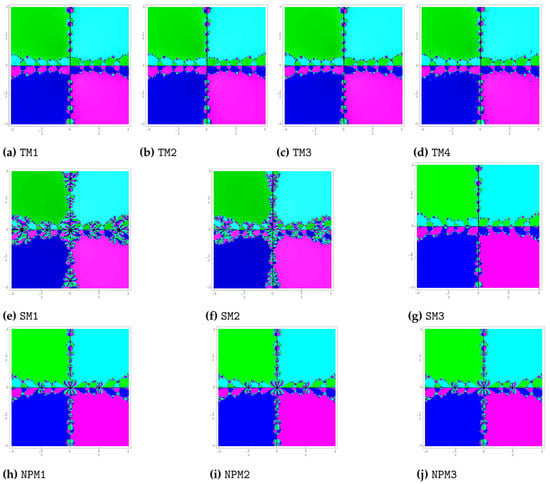
Consider the polynomial $g_3\left(w\right)={(w^4+w^2+1)}^2.$ The roots of this polynomial are $w=\frac{1-\sqrt{3}i}{2}$, $\frac{1+\sqrt{3}i}{2}$, $\frac{-1-\sqrt{3}i}{2}$ and $\frac{-1+\sqrt{3}i}{2}$ with multiplicity $2.$ Assign the colours green, blue, cyan, and magenta to each initial point on the roots $\frac{1-\sqrt{3}i}{2},\frac{1+\sqrt{3}i}{2},\frac{-1-\sqrt{3}i}{2}$ and $\frac{-1+\sqrt{3}i}{2}.$ It is observed from Figure 3 that the proposed methods TM1, TM2, TM3 and TM4, as well as the method SM3, are adequate to converge to all the roots, and the divergent points occur in case of the methods SM1, SM2, NPM1, NPM2 and NPM3.

Figure 3. Basins of attraction of TM1–TM4, SM1–SM3 and NPM1–NPM3 for polynomial $g_3\left(w\right)$.

Problem 4.

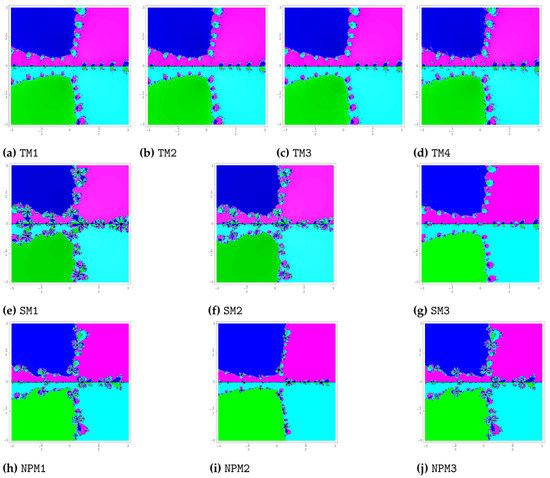
The fourth polynomial we consider is $g_4\left(w\right)={(w^4-w^3+w^2-w+1)}^3.$ For this polynomial, $w=e^{\frac{\pi i}{5}}$, $e^{\frac{-\pi i}{5}}$, $e^{\frac{3\pi i}{5}}$ and $e^{\frac{-3\pi i}{5}}$ are the roots of the polynomial with multiplicity $3.$ We assign the colors to each initial guess of zero $e^{\frac{\pi i}{5}}$, $e^{\frac{-\pi i}{5}}$, $e^{\frac{3\pi i}{5}}$ and $e^{\frac{-3\pi i}{5}}$ as green, blue, cyan and magenta, respectively. It is observed from Figure 4 that the methods TM1, TM2, TM3, TM4 and SM3 do not contain any black spots, but the methods SM1, SM2, NPM1, NPM2 and NPM3 do contain them, which means that the methods TM1, TM2, TM3, TM4 and SM3 have performed better than the methods SM1, SM2, NPM1, NPM2 and NPM3.

Figure 4. Basins of attraction of TM1–TM4, SM1–SM3 and NPM1–NPM3 for polynomial $g_4\left(w\right)$.

As is visible in all figures, the basins of attraction possess reflection symmetry, and one can even go further to provide a proof for their symmetry [42], while in other instances [3] the behavior was identified as near to symmetric.

5. Numerical Results

The convergence of the newly generated methods is ensured in this section, numerically. Some nonlinear problems are solved by the newly generated methods. Other existing schemes mentioned in the previous section are also considered for comparison.

Mathematica programming software [33] is used to bring off the computational work. The numerical results are summarized in tabular form. The table embraces the number of iterations necessary to procure the root with finishing benchmark $|{\mathtt{x}}_{t+1}-{\mathtt{x}}_t|+\left|f\left({\mathtt{x}}_t\right)\right|<{10}^{-200}$ and estimated error $|{\mathtt{x}}_{t+1}-{\mathtt{x}}_t|$ in the last three iterations, residual error of the considered function $\left|f\left({\mathtt{x}}_t\right)\right|$ and computational order of convergence (COC), by exerting the formula:

$$COC=\frac{log\left|\frac{{\mathtt{x}}_{t+2}-\alpha }{{\mathtt{x}}_{t+1}-\alpha }\right|}{log\left|\frac{{\mathtt{x}}_{t+1}-\alpha }{{\mathtt{x}}_t-\alpha }\right|},\mathrm{where}t=1,2,\dots$$

(28)

The CPU running time is also presented in numerical results. For all the numerical computations, we have used Mathematica 12.0 programming software on Windows 10 on Intel Core i3. The problems considered for comparison are mentioned in Table 2. For our methods, in all the problems we have taken $a=-1.$

Table 2. Test functions.

Test Functions	Root	p	${\mathtt{x}}_0$
$f_1\left(\mathtt{x}\right)={\left({\mathtt{sin}}^2\mathtt{x}-{\mathtt{x}}^2+1\right)}^2$	1.4044916	2	2
$f_2\left(\mathtt{x}\right)={\mathtt{x}}^3-5.22{\mathtt{x}}^2+9.0825\mathtt{x}-5.2675$	1.7500000	2	2.2
$f_3\left(\mathtt{x}\right)={(\mathtt{x}-2)}^{15}{(\mathtt{x}-4)}^5{(\mathtt{x}-3)}^{10}{(\mathtt{x}-1)}^{20}$	1.0000000	20	0.7
$f_4\left(\mathtt{x}\right)={\mathtt{x}}^9-29{\mathtt{x}}^8+349{\mathtt{x}}^7-2261{\mathtt{x}}^6+8455{\mathtt{x}}^5-17663{\mathtt{x}}^4+15927{\mathtt{x}}^3+6993{\mathtt{x}}^2-24732\mathtt{x}+12960$	3.0000000	4	2.5
$f_5\left(\mathtt{x}\right)={[{(\mathtt{x}-1)}^3-1]}^{50}$	2.0000000	50	2.1

The computational results in Table 3 and Table 4 show that the methods NPM1, NPM2 and NPM3 have the best residuals, but the major drawback of these methods is that they do not retain their order of convergence. Therefore, our proposed methods have performed better and possess lower residual error as well as low CPU-time for functions $f_1\left(\mathtt{x}\right)$ and $f_2\left(\mathtt{x}\right)$. They also preserve their fifth order of convergence. The numerical data for the function $f_3\left(\mathtt{x}\right)$ shown in Table 5 demonstrate that TM4 performs better than the existing methods, with low error and precise result estimations. Further, the elapsed CPU time is minimal in the case of TM3. The numerical results obtained for function $f_4\left(\mathtt{x}\right)$ are shown in Table 6. One can observe that each scheme has extremely high precision, with the lowest residual calculated by TM4. Table 7 shows the numerical results of the methods for function $f_5\left(\mathtt{x}\right)$. The best performer for this function is TM4. Furthermore, it is worth mentioning here that the methods NPM1–NPM3 do not converge to the required root for the problems $f_3\left(\mathtt{x}\right)$ and $f_5\left(\mathtt{x}\right)$, or we can say that they are divergent for these problems.

Table 3. Computational results for function $f_1\left(\mathtt{x}\right)$.

Methods	t	$\left|{\mathit{e}}_{\mathit{t}-2}\right|$	$\left|{\mathit{e}}_{\mathit{t}-1}\right|$	$\left|{\mathit{e}}_{\mathit{t}}\right|$	$\left|\mathit{f}\left({\mathtt{x}}_{\mathit{t}+1}\right)\right|$	COC	CPU Time
TM1	5	$9.65\times {10}^{-12}$	$5.42\times {10}^{-56}$	$3.03\times {10}^{-277}$	$1.66\times {10}^{-2765}$	5.00000	0.00186139
TM2	5	$1.21\times {10}^{-11}$	$1.87\times {10}^{-55}$	$1.64\times {10}^{-274}$	$4.44\times {10}^{-2738}$	5.00000	0.00216832
TM3	5	$1.57\times {10}^{-11}$	$7.36\times {10}^{-55}$	$1.67\times {10}^{-271}$	$6.13\times {10}^{-2708}$	5.00000	0.00231683
TM4	5	$1.87\times {10}^{-12}$	$6.12\times {10}^{-60}$	$2.32\times {10}^{-297}$	$2.00\times {10}^{-2967}$	5.00000	0.00247525
SM1	5	$6.71\times {10}^{-11}$	$1.90\times {10}^{-51}$	$3.48\times {10}^{-254}$	$3.11\times {10}^{-2534}$	5.00000	0.00279208
SM2	5	$1.17\times {10}^{-10}$	$3.82\times {10}^{-50}$	$1.45\times {10}^{-247}$	$8.09\times {10}^{-2468}$	5.00000	0.00278218
SM3	5	$5.76\times {10}^{-11}$	$8.90\times {10}^{-52}$	$7.82\times {10}^{-256}$	$1.03\times {10}^{-2550}$	5.00000	0.00263366
NPM1	5	$2.83\times {10}^{-15}$	$3.23\times {10}^{-88}$	$7.21\times {10}^{-526}$	$4.85\times {10}^{-6302}$	6.00000	0.00279208
NPM2	5	$2.83\times {10}^{-15}$	$3.23\times {10}^{-88}$	$7.21\times {10}^{-526}$	$4.85\times {10}^{-6302}$	6.00000	0.00279208
NPM3	5	$2.83\times {10}^{-15}$	$3.23\times {10}^{-88}$	$7.21\times {10}^{-526}$	$4.85\times {10}^{-6302}$	6.00000	0.00279208

Table 4. Computational results for function $f_2\left(\mathtt{x}\right)$.

Methods	t	$\left|{\mathit{e}}_{\mathit{t}-2}\right|$	$\left|{\mathit{e}}_{\mathit{t}-1}\right|$	$\left|{\mathit{e}}_{\mathit{t}}\right|$	$\left|\mathit{f}\left({\mathtt{x}}_{\mathit{t}+1}\right)\right|$	COC	CPU Time
TM1	6	$4.66\times {10}^{-12}$	$5.07\times {10}^{-52}$	$7.73\times {10}^{-252}$	$1.22\times {10}^{-2502}$	5.00000	0.00154455
TM2	6	$5.77\times {10}^{-12}$	$1.57\times {10}^{-51}$	$2.31\times {10}^{-249}$	$7.59\times {10}^{-2478}$	5.00000	0.00170297
TM3	6	$7.45\times {10}^{-12}$	$5.92\times {10}^{-51}$	$1.87\times {10}^{-246}$	$1.02\times {10}^{-2448}$	5.00000	0.00138614
TM4	6	$1.29\times {10}^{-12}$	$5.41\times {10}^{-55}$	$7.17\times {10}^{-267}$	$2.57\times {10}^{-2653}$	5.00000	0.00169307
SM1	6	$3.21\times {10}^{-11}$	$1.31\times {10}^{-47}$	$1.46\times {10}^{-229}$	$2.01\times {10}^{-2279}$	5.00000	0.00215842
SM2	6	$5.73\times {10}^{-11}$	$2.87\times {10}^{-46}$	$8.98\times {10}^{-223}$	$2.18\times {10}^{-2211}$	5.00000	0.00262376
SM3	6	$2.65\times {10}^{-11}$	$5.00\times {10}^{-48}$	$1.21\times {10}^{-231}$	$3.03\times {10}^{-2300}$	5.00000	0.00231683
NPM1	6	$1.48\times {10}^{-18}$	$1.03\times {10}^{-100}$	$1.16\times {10}^{-593}$	$1.72\times {10}^{-7103}$	6.00000	0.00232673
NPM2	6	$1.48\times {10}^{-18}$	$1.03\times {10}^{-100}$	$1.16\times {10}^{-593}$	$1.72\times {10}^{-7103}$	6.00000	0.00247525
NPM3	6	$1.48\times {10}^{-18}$	$1.03\times {10}^{-100}$	$1.16\times {10}^{-593}$	$1.72\times {10}^{-7103}$	6.00000	0.00200990

Table 5. Computational results for function $f_3\left(\mathtt{x}\right)$.

Methods	t	$\left|{\mathit{e}}_{\mathit{t}-2}\right|$	$\left|{\mathit{e}}_{\mathit{t}-1}\right|$	$\left|{\mathit{e}}_{\mathit{t}}\right|$	$\left|\mathit{f}\left({\mathtt{x}}_{\mathit{t}+1}\right)\right|$	COC	CPU Time
TM1	5	$1.52\times {10}^{-14}$	$2.00\times {10}^{-69}$	$7.74\times {10}^{-344}$	$1.03\times {10}^{-34298}$	5.00000	0.00139604
TM2	5	$2.12\times {10}^{-14}$	$1.15\times {10}^{-68}$	$5.39\times {10}^{-340}$	$1.13\times {10}^{-33913}$	5.00000	0.00139604
TM3	5	$3.08\times {10}^{-14}$	$8.08\times {10}^{-68}$	$9.98\times {10}^{-336}$	$3.42\times {10}^{-33486}$	5.00000	0.00108911
TM4	5	$1.46\times {10}^{-15}$	$7.05\times {10}^{-75}$	$1.84\times {10}^{-371}$	$2.49\times {10}^{-37068}$	5.00000	0.00154455
SM1	5	$2.29\times {10}^{-13}$	$3.26\times {10}^{-63}$	$1.92\times {10}^{-312}$	$9.26\times {10}^{-31153}$	5.00000	0.00262376
SM2	5	$4.77\times {10}^{-13}$	$1.62\times {10}^{-61}$	$7.34\times {10}^{-304}$	$2.06\times {10}^{-30292}$	5.00000	0.00247525
SM3	5	$1.84\times {10}^{-13}$	$1.08\times {10}^{-63}$	$7.68\times {10}^{-315}$	$1.82\times {10}^{-31392}$	5.00000	0.00171683
NPM1	Div	−	−	−	−	−	−
NPM2	Div	−	−	−	−	−	−
NPM3	Div	−	−	−	−	−	−

Here, Div means divergent.

Table 6. Computational results for function $f_4\left(\mathtt{x}\right)$.

Methods	t	$\left|{\mathit{e}}_{\mathit{t}-2}\right|$	$\left|{\mathit{e}}_{\mathit{t}-1}\right|$	$\left|{\mathit{e}}_{\mathit{t}}\right|$	$\left|\mathit{f}\left({\mathtt{x}}_{\mathit{t}+1}\right)\right|$	COC	CPU Time
TM1	5	$9.88\times {10}^{-24}$	$2.43\times {10}^{-117}$	$2.19\times {10}^{-585}$	$2.27\times {10}^{-11698}$	5.00000	0.00216832
TM2	5	$1.02\times {10}^{-23}$	$2.91\times {10}^{-117}$	$5.48\times {10}^{-585}$	$2.26\times {10}^{-11690}$	5.00000	0.00200990
TM3	5	$1.05\times {10}^{-23}$	$3.48\times {10}^{-117}$	$1.37\times {10}^{-584}$	$2.22\times {10}^{-11682}$	5.00000	0.00247525
TM4	5	$8.10\times {10}^{-24}$	$7.87\times {10}^{-118}$	$6.84\times {10}^{-588}$	$1.05\times {10}^{-11748}$	5.00000	0.00263366
SM1	5	$1.40\times {10}^{-23}$	$1.75\times {10}^{-116}$	$5.27\times {10}^{-581}$	$2.31\times {10}^{-11610}$	5.00000	0.00278218
SM2	5	$1.64\times {10}^{-23}$	$4.13\times {10}^{-116}$	$4.26\times {10}^{-579}$	$4.79\times {10}^{-11572}$	5.00000	0.00294059
SM3	5	$1.40\times {10}^{-23}$	$1.71\times {10}^{-116}$	$4.76\times {10}^{-581}$	$3.02\times {10}^{-11611}$	5.00000	0.00340595
NPM1	5	$2.50\times {10}^{-18}$	$3.16\times {10}^{-90}$	$1.02\times {10}^{-449}$	$1.21\times {10}^{-8984}$	5.00000	0.00309901
NPM2	5	$2.70\times {10}^{-18}$	$4.94\times {10}^{-90}$	$1.00\times {10}^{-448}$	$1.18\times {10}^{-8964}$	5.00000	0.00324752
NPM3	5	$2.90\times {10}^{-18}$	$7.52\times {10}^{-90}$	$8.78\times {10}^{-448}$	$1.04\times {10}^{-8945}$	5.00000	0.00308911

Table 7. Computational results for function $f_5\left(\mathtt{x}\right)$.

Methods	t	$\left|{\mathit{e}}_{\mathit{t}-2}\right|$	$\left|{\mathit{e}}_{\mathit{t}-1}\right|$	$\left|{\mathit{e}}_{\mathit{t}}\right|$	$\left|\mathit{f}\left({\mathtt{x}}_{\mathit{t}+1}\right)\right|$	COC	CPU Time
TM1	5	$1.11\times {10}^{-25}$	$2.25\times {10}^{-125}$	$7.74\times {10}^{-624}$	$1.96\times {10}^{-155748}$	5.00000	0.00200990
TM2	5	$2.01\times {10}^{-25}$	$4.90\times {10}^{-124}$	$4.26\times {10}^{-617}$	$8.03\times {10}^{-154061}$	5.00000	0.00170301
TM3	5	$3.61\times {10}^{-25}$	$1.02\times {10}^{-122}$	$1.82\times {10}^{-610}$	$1.64\times {10}^{-152400}$	5.00000	0.00200990
TM4	5	$4.50\times {10}^{-28}$	$6.15\times {10}^{-138}$	$2.92\times {10}^{-687}$	$2.36\times {10}^{-171634}$	5.00000	0.00170297
SM1	5	$1.08\times {10}^{-23}$	$4.79\times {10}^{-115}$	$8.42\times {10}^{-572}$	$2.36\times {10}^{-142719}$	5.00000	0.00247525
SM2	5	$3.65\times {10}^{-23}$	$2.79\times {10}^{-112}$	$7.39\times {10}^{-558}$	$6.33\times {10}^{-139228}$	5.00000	0.00231683
SM3	5	$8.89\times {10}^{-24}$	$1.85\times {10}^{-115}$	$7.26\times {10}^{-574}$	$1.87\times {10}^{-143235}$	5.00000	0.00757426
NPM1	Div	−	−	−	−	−	−
NPM2	Div	−	−	−	−	−	−
NPM3	Div	−	−	−	−	−	−

Here, Div means divergent.

6. Concluding Remarks

We have introduced a new multi-point iterative algorithm that can solve nonlinear equations having multiple zeros. The scheme is based on the weight function approach. Per iteration, the presented scheme requires two assessments of functions and two assessments of its derivatives to achieve the fifth order convergence. Some special cases of the new family are also presented. The presented basins of attraction have confirmed that the performance of the new methods is on par with or better than the established schemes in the literature. The theoretical results proved in the paper regarding the order of convergence are verified through various numerical examples. A comparison with the existing methods is also made. The results obtained have once again proved the robustness of the new schemes. Moreover, the CPU time is also evaluated, which is lesser for the newly proposed schemes. In a nutshell, we can say that the new methods have performed better than the existing methods in terms of basins of attraction, the number of iterations required to converge to the root, residual errors and CPU-time for the considered problems.