Abstract
The microscopic origins and the current predictions of the proxy-SU(3) symmetry model of atomic nuclei were reviewed. Beginning with experimental evidence for the special roles played by nucleon pairs with maximal spatial overlap, the proxy-SU(3) approximation scheme is introduced; its validity is demonstrated through Nilsson model calculations and its connection to the spherical shell model. The major role played by the highest weight-irreducible representations of SU(3) in shaping up the nuclear properties is pointed out, resulting in parameter-free predictions of the collective variables and for even–even nuclei in the explanation of the dominance of prolate over oblate shapes in the ground states of even–even nuclei, in the prediction of a shape/phase transition from prolate to oblate shapes below closed shells, and in the prediction of specific islands on the nuclear chart in which shape coexistence is confined. Further developments within the proxy-SU(3) scheme are outlined.
1. Introduction
The purpose of the present article is to discuss the ideas that led to the introduction of the proxy-SU(3) symmetry model, its microscopic justification, and its application to nuclear structural problems. Starting with a review of nuclear structure models based on the SU(3) symmetry in Section 2, we discuss nucleon pairs favoring deformation in Section 3, and show how these lead to the introduction of the proxy-SU(3) symmetry in Section 4. The approximation leading to the proxy-SU(3) symmetry is tested using Nilsson model calculations in Section 5 and is “translated” into spherical shell model language in Section 6. We point out (in Section 7) the crucial roles played by the highest weight-irreducible representations. Their consequences on providing parameter-free predictions for the collective variables and of even–even nuclei, explaining the dominance of prolate over oblate shapes in the ground states of even–even nuclei and the prediction of a prolate to oblate shape/phase transition are examined in Section 8; in Section 9, a mechanism predicting the nuclear chart’s specific islands (in which shape coexistence can appear) is discussed. Possible further work on parameter-free predictions of B(E2) transition rates, energy spectra, binding energies, and nucleon separation energies is outlined in Section 10. The literature was searched up until October 2022.
2. SU(3) Symmetry in Nuclear Structure
Symmetries have played major roles in nuclear structures since 1937, when Wigner [1] suggested that first approximation nuclear forces should be independent of the orientations of the spins and isospins of the nuclei constituting a nucleus, in a framework known as the SU(4) supermultiplet model [2,3].
In 1949, a major step forward in deciphering the experimental observations was made by Mayer and Jensen through the introduction of the shell model [4,5,6,7]; they interpreted the appearance of nuclear magic numbers in terms of a three-dimensional (3D) isotropic harmonic oscillator (HO), to which a crucial spin–orbit term was added. The 3D isotropic HO is known to possess shells labeled by the number of excitation quanta n, characterized by the unitary symmetries U((n + 1)(n + 2)/2), having SU(3) subalgebras [8,9,10,11]. Mayer, Jensen, and Wigner shared the Nobel Prize in Physics in 1963 [12].
The shell model was considered adequate for describing near-spherical nuclei in the vicinity of the magic numbers, away from which, however, large quadrupole moments were observed. In order to explain their appearance, Rainwater in 1950 suggested [13] that deformed shapes are energetically favored away from closed shells. In 1952, the collective model of Bohr and Mottelson was introduced [14,15], in which departures from the spherical shape and axial symmetry are described by the collective variables, and , respectively. Bohr, Mottelson, and Rainwater shared the Nobel Prize in Physics in 1975 [16].
In 1955, Nilsson introduced [17,18,19] a modified version of the shell model, in which axial-deformed nuclei with prolate (rugby ball-like) or oblate (pancake-like) shapes can be described through the use of a 3D anisotropic HO with cylindrical symmetry [20,21,22,23,24,25].
In 1958, Elliott proved that deformation within the nuclear shell with U(6) symmetry can be described in terms of its SU(3) subalgebra [26,27,28,29,30,31,32], thus building a bridge between the spherical shell model and the collective model for the case of light nuclei, in which the consequences of the spin–orbit interaction on the ordering of the single-particle nucleon levels are small. Beyond the nuclear shell, the spin–orbit force [4,5,6,7] is known to break the SU(3) symmetry of the 3D isotropic HO, by pushing within each HO shell the orbital possessing the highest angular momentum j to the shell below. As a result, each shell contains the orbitals left back after this removal, called the normal parity orbitals, plus the orbitals invading from the shell above with the opposite parity, called the intruder orbitals.
Efforts of extending the SU(3) symmetry to heavy nuclei [33,34,35,36] started in 1972, evolved gradually into the introduction of the vector boson model [37,38,39], while at the same time, the group’s theoretical structure of the Bohr–Mottelson model (with an overall U(5) symmetry possessing an O(5) subalgebra) was understood [40].
A major step forward in the extension of the SU(3) symmetry to heavy nuclei was taken in 1973, with the introduction of the pseudo-SU(3) symmetry [41,42,43,44,45,46,47]. Within the pseudo-SU(3) framework, a unitary transformation is used [48,49,50], through which the incomplete set of normal parity orbitals left in a shell is mapped onto the complete set of orbitals of the shell below, thus recovering the SU(3) symmetry of the 3D isotropic HO for the normal parity orbitals. This becomes possible by assigning to each orbital a pseudo-orbital angular momentum and a pseudo-spin, while the total angular momentum remains intact. As a result, within the pseudo-SU(3) scheme, each shell consists of a normal parity part, which possesses a U(n) symmetry and SU(3) subalgebra, and an intruder part which does not possess any SU(3) structure and has to be treated separately by shell model techniques [45,46]. The relativistic mean field origins of the pseudospin symmetry were later understood [51,52].
In 1974, it was realized that the nuclear quadrupole degree of freedom can be described in terms of SU(6) algebra [53] formed by five generalized coordinates, conjugated momenta, and their commutators.
Next year, the interacting boson model (IBM) [54,55,56,57,58,59,60] was introduced by Arima and Iachello. In the IBM, the monopole degree of freedom is taken into account in addition to the quadrupole one. IBM is characterized by an overall U(6) symmetry built by s-bosons of zero angular momentum and d-bosons of angular momentum two, possessing three limiting symmetries, U(5) [55] for vibrational nuclei, which correspond to the Bohr–Mottelson collective model, O(6) [57] for -unstable nuclei (which are soft towards triaxial deformation), and SU(3) [56] for deformed nuclei.
In 1977, the symplectic model [61,62,63,64,65] was introduced by Rowe and Rosensteel. The symplectic model, having an overall symmetry (called Sp(3,R) by Rowe and Rosensteel and Sp(6,R) by other authors [66,67]) is a generalization of the fermionic Elliott SU(3) model and includes many major oscillator shells in addition to core excitations. Its overall symmetry is characterized by non-compact algebra Sp(6,R), which does possess a compact SU(3) subalgebra along with other ones. A proton–neutron extension of the model, called the proton–neutron symplectic model (PNSM), is also developed [68,69,70].
In 1982, the interacting two-vector boson model [71,72] was introduced, in which two vector bosons of angular momentum are used as the building blocks, forming non-compact algebra Sp(12,R), of which the maximal compact subalgebra is U(6).
In 1987, the fermion dynamical symmetry model [73] was introduced, in which the total angular momentum of the nucleons is assumed to be split into active and inactive parts instead of orbital angular momentum and spin parts, the k-active part contains SU(3) subalgebra.
In 2000, an ab initio approach to a no-core shell model was introduced [74,75] for light nuclei. It was then realized that symplectic symmetry underlies the ab initio no-core shell model results, thus paving the way toward the development of the symplectic no-core shell model [76,77,78], which was extended to intermediate-mass nuclei [79,80,81,82]. The realization that nuclei are made of only a few equilibrium shapes [83] led to the introduction of the ab initio symmetry-adapted no-core shell model [84,85]. An SU(3)-adapted basis [80] plays a key role in this approach, taking advantage of the Elliott SU(3) symmetry underpinning the Sp(3,R) [61,62,63,64,65] (alias Sp(6,R) [66,67]) symplectic model.
The use of the SU(3) symmetry in the nuclear structure was reviewed in 2020 by Kota [86]. A historical account similar to the present section was given by some of the present authors in Reference [87].
In 2017, the proxy-SU(3) symmetry was suggested [88,89,90], which will be the subject of the present review. However, before describing the proxy-SU(3) symmetry itself, we will briefly review the physical motivation behind its introduction. A review similar to the next section was given by some of the present authors in Reference [87].
3. Nucleon Pairs Favoring Deformation
In 1953, deShalit and Goldhaber [91], in their studies on transition probabilities, noticed that within the proton–neutron pairs of orbitals (1p3/2, 1d5/2), (1d5/2, 1f7/2), (1f7/2, 1g9/2), (1g9/2, 1h11/2), (1h11/2, 1i13/2), the nucleons of one kind (protons, for example) have stabilizing effects on pairs of nucleons of the other kind (neutrons in the example), thus favoring the development of nuclear deformation. In the standard shell model notation , in which states are labeled by the number of oscillator quanta n, the orbital angular momentum l, the total angular momentum j, and its z-projection , the orbitals forming pairs differed by . We are going to call these pairs the spherical shell model pairs, or the pairs.
In 1962, a major step forward in our understanding of effective interactions and coupling schemes in nuclei was made by Talmi [92] through the introduction of seniority [92,93,94,95], representing the number of nucleon pairs coupled to non-zero angular momentum, which explained the linear dependence of neutron separation energies on the mass number within various series of isotopes.
In 1977, Federman and Pittel [96,97,98] realized that when adding valence protons and valence neutrons to a nucleus, the proton–neutron pairs (1d5/2, 1d3/2), (1g9/2, 1g7/2), (1h11/2, 1h9/2), and (1i13/2, 1i11/2) play major roles in the onset of deformation, while later on, deformation is reinforced by the proton–neutron pairs (1d5/2, 1f7/2), (1g9/2, 1h11/2), (1h11/2, 1i13/2), and (1i13/2, 1j15/2), as shown in Table 1. In the shell model notation, these sets correspond to , and , respectively, the latter set coinciding with the de Shalit–Goldhaber pairs.

Table 1.
Pairs of orbitals playing a leading role in the development of deformation in different mass regions of the nuclear chart according to Federman and Pittel [96,97,98]. The pairs on the left part of the table contribute to the beginning of the relevant shell, while the pairs on the right become important further within the shell, as adapted from Reference [87]. See Section 3 for further discussion.
In 1985, the decisive roles played by proton–neutron pairs were demonstrated by Casten through the introduction of the scheme [99,100], by showing the systematic dependence of several observables on the quadrupole–quadrupole interaction, measured through , where () is the number of valence protons (neutrons) counted from the nearest closed shell. In 1987, the P-factor, [101,102], was introduced, and the systematic dependence of several observables on it was demonstrated. The P-factor expresses the competition between the quadrupole deformation, “measured” by the quadrupole–quadrupole interaction through , and the pairing interaction, “measured” through .
In 1995, the quasi-SU(3) symmetry [103,104] was introduced, based on the proton–neutron pairs (1g9/2, 2d5/2), (1h11/2, 2f7/2), (1i13/2, 2g9/2), which lead to enhanced quadrupole collectivity [105]. The quasi-SU(3) pairs are expressed as in the shell model notation.
Following detailed studies of double differences in experimental binding energies [106,107,108,109], in 2010 it was realized (in Reference [110]) that proton–neutron pairs differed by in the Nilsson notation [17,18,19] , where N is the total number of oscillator quanta, is the number of quanta along the z-axis, and , K, are the projections along the z-axis of the orbital angular momentum and the total angular momentum, respectively, which play a major role in the development of nuclear deformation, due to the large spatial overlaps [111]. This effect was corroborated by nuclear density functional theory calculations [112]. We are going to call these pairs the Nilsson 0[110] pairs, or simply the 0[110] pairs. Notice the difference in the notation in comparison to the spherical shell model pairs.
As we shall see below, the Nilsson 0[110] pairs play crucial roles in the replacements made within the approximation leading to the proxy-SU(3) symmetry. Furthermore, the relation between the Nilsson 0[110] pairs and the spherical shell model pairs will be clarified through the connection of the proxy-SU(3) symmetry to the spherical shell model. Evidence supporting the formation of 0[110] pairs was found recently within Monte Carlo shell model calculations [113].
4. The Proxy-SU(3) Approximation
The proxy-SU(3) symmetry was born when the desire to reestablish the SU(3) symmetry of the 3D-HO in medium mass and heavy nuclei, described in Section 2, met the experimental hint of the 0[110] Nilsson pairs, described in Section 3. The 0[110] Nilsson pairs were discovered through experimental observation [110], where the proton–neutron pairs of this type maximize the proton–neutron interaction. This maximization was attributed to the large spatial overlaps of the two orbitals involved in such pairs [111]. In other words, 0[110] Nilsson pairs are very similar since they possess identical angular momentum and spin properties (identical projections of the orbital angular momentum, the spin, and the total angular momentum) and very similar spatial shapes since they differ only by one excitation quantum in the z-axis (and, therefore, also by one quantum in the total number of quanta). The similarity holds equally well if one considers a 0[110] pair of protons, or a 0[110] pair of neutrons. Such pairs will still have identical angular momentum and spin properties and very similar spatial shapes. Therefore, in the framework of an approximation needed for some reason, each member of a 0[110] pair could replace the other, i.e., acting as a proxy, with minimal changes inflicted in the physical system under study.
Such a situation appears in the shells of the shell model beyond 28 nucleons. The intruder orbitals, which come down from the shell above, form 0[110] pairs with the orbitals, which desert the shell by fleeing into the shell below. We can, therefore, think of replacing the intruder orbitals with their 0[110] counterparts, which are the deserting orbitals, expecting that the changes caused in the physical system under study would be minimal. In other words, the deserting orbitals can act as proxies of the intruder orbitals. However, in this way, the shell obtains the SU(3) symmetry of the 3D-HO, which it lost after the deserting of the orbitals, which fled to the shell below.
An example can be seen in Figure 1, in which the shell is depicted, consisting of the , , , , orbitals, having an overall symmetry of U(15), which possesses SU(3) subalgebra. The spin–orbit interaction pushes the orbital with the highest j, i.e., , to the shell below, while it brings down the orbital from the shell above. In this way, the 50–82 shell of the shell model is formed, in which the SU(3) symmetry is lost. Looking into the details of the orbitals, a sign of hope appears. The intruder orbital consists of the Nilsson orbitals 1/2[550], 3/2[541], 5/2[532], 7/2[523], 9/2[514], 11/2[505], while the deserting orbital consists of Nilsson orbitals 1/2[440], 3/2[431], 5/2[422], 7/2[413], 9/2[404]. We observe that the first five Nilsson orbitals of are 0[110] partners with the five orbitals making up . Therefore, it is plausible to replace the 1/2[550], 3/2[541], 5/2[532], 7/2[523], 9/2[514] orbitals by the 1/2[440], 3/2[431], 5/2[422], 7/2[413], 9/2[404] orbitals, hoping that the changes inflicted in the physical system would be minimal. In other words, the 1/2[440], 3/2[431], 5/2[422], 7/2[413], and 9/2[404] orbitals will act as proxies of the 1/2[550], 3/2[541], 5/2[532], 7/2[523], and 9/2[514] orbitals.
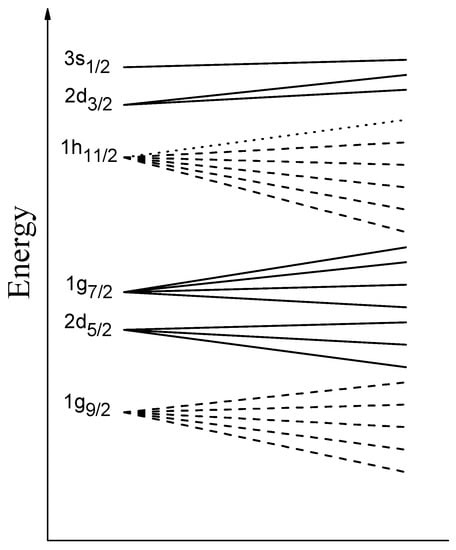
Figure 1.
Schematic representation of the 50–82 shell and the replacement leading to the proxy sdg shell, adapted from Reference [88]. See Section 4 for further discussion.
It is now time to consider the gains and losses of this replacement. The gain is that the SU(3) symmetry is re-established in the 50–82 shell since the shell will now contain all orbitals composing the shell. However, a couple of losses are lurking. First, the 11/2[505] Nilsson orbital has no 0[110] partner; thus, it is left behind within the 50–82 shell, where it stays outside the SU(3) symmetry, and in principle, it has to be treated separately by shell model techniques [45,46]. The good news in this case is that the 11/2[505] Nilsson orbital lies at the very top of the 50–82 shell, as one can see in the standard Nilsson diagrams [19,114]. Thus, it should be empty for most nuclei and, therefore, have little influence on the structures of most of them. The second problem arises from the fact that the intruder and deserting orbitals have opposite parities since they belong to adjacent shells differing by one unit in N. For even–even nuclei, this should not cause any trouble, since, for example, a pair of 9/2[514] particles will be replaced by a pair of 9/2[404] particles; therefore, no differences caused by parity should be seen. For odd nuclei, one would probably have to use projection techniques [115], a problem that has not been considered yet.
5. Corroboration of Proxy-SU(3) through Nilsson Model Calculations
The first test [88] of the accuracy of the proxy-SU(3) approximation described in the previous section was performed in the framework of the Nilsson model. In each shell of the shell model, two calculations were performed, one with the real orbitals composing the shell, and another one with the intruder orbitals replaced by their 0[110] counterparts. Numerical results for the 82–126 shell are shown in Table 2. In the upper part of the table, the matrix elements of the Nilsson Hamiltonian, using the standard set of parameters [15], are shown, while in the lower partm the matrix elements occurring within the shell (resulting after the proxy-SU(3) approximation) are reported. We remark that in the last seven columns of the upper part, corresponding to the orbitals, all non-diagonal matrix elements vanish, due to the fact that they connect orbitals of the opposite parity. On the contrary, in the last six columns of the lower part of the table, in which the proxies of the orbitals, i.e., the orbitals appear, not all off-diagonal matrix elements vanish since (in this case) they connect to orbitals of the same parity. However, the number of these off-diagonal matrix elements is small, and in addition, their sizes are small in comparison to the diagonal matrix elements; thus, they are not expected to affect the single-particle energy levels substantially. The diagonal matrix elements in the last six columns of the lower part of the table are also slightly modified in comparison to the corresponding matrix elements in the upper half of the table, but again the changes are small and are not expected to affect the single-particle energy levels radically. The evolution of the single-particle energy levels with deformation, depicted in Figure 2, shows that the changes caused in the Nilsson diagrams by the proxy-SU(3) approximation are minimal. Neither the order of the orbitals nor their dependence on the deformation (upward-sloping or downward-sloping) is modified. Similar tables and figures for other shells can be found in the supplemental material for Reference [88]. It can be seen there that the quality of the proxy-SU(3) approximation becomes better in higher shells.

Table 2.
Nilsson Hamiltonian matrix elements (in units of ) with for Nilsson orbitals in the 82–126 neutron shell (upper part) and in the full PFH neutron shell (lower part). Matrix elements in the lower part of the table, which differ from their counterparts in the upper part, are shown in boldface, adapted from Reference [88]. See Section 5 for further discussion.
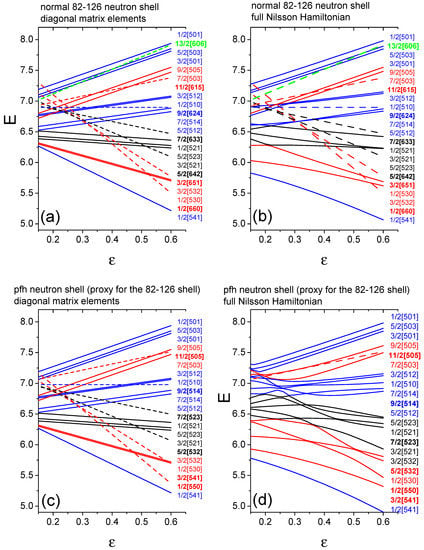
Figure 2.
Diagonal matrix elements (in units of ) of the Nilsson Hamiltonian for the 82–126 (a) and PFH (c) neutron shells compared to the results of the full diagonalization for the 82–126 (b) and PFH (d) neutron shells, as functions of the deformation parameter . The intruder orbitals are indicated by dashed lines and their labels appear in boldface. Orbitals are grouped in color only to facilitate visualizing the patterns of orbital evolution, adapted from Reference [88]. See Section 5 for further discussion.
6. Proxy-SU(3) Symmetry in the Spherical Shell Model Basis
The proxy-SU(3) symmetry is established in the nuclear shells beyond the shell in the framework of the Nilsson model by taking advantage of the 0[110] Nilsson pairs. The issue arises if such a process is possible within the framework of the spherical shell model, allowing for the replacement of certain orbitals by their proxies in order to reestablish the SU(3) symmetry.
In order to examine if such a possibility exists, we start with the Elliott model [26,27,28,30,31], in which the Cartesian basis of the 3D isotropic HO is used. This basis is labeled , in which the number of quanta along the z, x, y directions and the z-projection of the spin appear. The first step is to transform this basis into the spherical basis, in the l-s coupling, labeled by the principal quantum number n, the orbital angular momentum l, its z-projection (), and the z-projection of the spin (). This can be achieved through a unitary transformation [116,117,118]
the details of which can be found in Reference [119]. Using Clebsch–Gordan coefficients [120,121], the spherical basis can be recoupled from the l-s coupling to the j-j coupling in the following way
in which the total angular momentum j and its z-projection appear. Combining these two transformations, one obtains
i.e., the connection between the Cartesian Elliott basis and the spherical shell model basis in j-j coupling. Details of the calculations and transformation tables up to the shell can be found in Reference [119], while a succinct discussion of the approach, similar to the present section, was given by some of the present authors in Reference [87].
Using the above transformation, one sees that the Nilsson 0[110] replacements made within the proxy-SU(3) scheme are “translated” into replacements within the spherical shell model basis. The resulting correspondences between original shell model orbitals and proxy-SU(3) orbitals are summarized in Table 3. This correspondence paves the way for taking advantage of the proxy-SU(3) symmetry in shell model calculations for heavy nuclei, in a way similar to that of the symmetry-adapted no-core shell model approach [81,82] used in light nuclei.

Table 3.
Shell model orbitals of the original spin–orbit-like shells and of the proxy-SU(3) shells. The magic number 14 was proposed as a sub-shell closure in Reference [122]. The symmetry of each proxy-SU(3) shell is U() with . Orbitals being replaced are indicated in boldface, adapted from Reference [119]. See Section 6 for further discussion.
A unitary transformation connecting the orbitals being replaced within the proxy-SU(3) scheme was found [119] within the shell model basis, as depicted in Figure 3. This is reminiscent of the unitary transformation occurring in the framework of the pseudo-SU(3) symmetry [48,49,50].
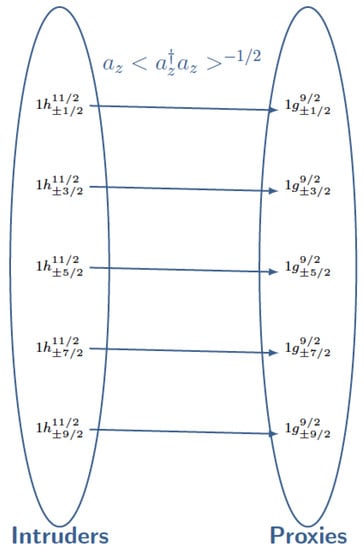
Figure 3.
Unitary transformation of the intruder orbitals (except for the ) in the 50–82 shell onto the orbitals , adapted from Reference [119]. See Section 6 for further discussion.
A by-product of the above transformation is that the 0[110] Nilsson pairs identified in Reference [110], and used within the proxy-SU(3) scheme [88,89,90], are identical to the de Shalit–Goldhaber pairs [91] and the Federman–Pittel pairs [96,97,98] within the spherical shell model basis, where they are expressed as pairs.
The correspondence between Nilsson pairs and shell model pairs was corroborated by calculations [123] within the Nilsson model, in which the first justification of the proxy-SU(3) scheme was found, as described in Section 5. As one can see in Table 4 and Table 5, the correspondence used in proxy-SU(3) works only for the Nilsson orbitals, which possess the highest total angular momentum j within their shell, which are exactly the orbitals, which are replaced within the proxy-SU(3) scheme.

Table 4.
Expansions of Nilsson orbitals in the shell model basis for three different values of the deformation . The Nilsson orbitals shown possess the highest total angular momenta j in their shells. The existence of a leading shell model eigenvector is evident at all deformations, adapted from Reference [123]. See Section 6 for further discussion.

Table 5.
Expansions of Nilsson orbitals in the shell model basis for three different values of the deformation . The Nilsson orbitals shown do not possess the highest total angular momenta j in their shells. The existence of leading shell model eigenvectors is evident in small deformations, but this is not the case anymore at higher deformations, at which several shell model eigenvectors make considerable contributions, adapted from Reference [123]. See Section 6 for further discussion.
7. The Dominance of the Highest Weight Irreducible Representations of SU(3)
In order to start examining the consequences of the existence of the proxy-SU(3) symmetry in medium mass and heavy nuclei, we should first consider a few properties of the irreducible representations (irreps) of SU(3).
In Elliott’s notation [26,27,28,29,30,31], the irreps of SU(3) are labeled by , where the Elliott quantum numbers and are connected to the number of boxes in the corresponding Young diagram through the relations
where () is the number of boxes in the first (second) line of the relevant Young diagram. Irreps with are known to correspond to prolate (rugby ball-like) shapes, while irreps with are known to describe oblate (pancake-like) shapes, with irreps corresponding to maximally triaxial shapes [124,125,126].
A quantity characterizing the SU(3) irreps is the eigenvalue of the second-order Casimir operator of SU(3), given by [8,10]
This quantity is known to be connected to the eigenvalues of the quadrupole–quadrupole interaction by [26,27,28,47]
where L is the eigenvalue of the orbital angular momentum. For the ground state bands of even–even nuclei, in which , it is clear that the eigenvalue of is proportional to the eigenvalue of the quadrupole–quadrupole interaction, . Since the quadrupole–quadrupole interaction is known to cause nuclear deformation, it is expected that the irrep with the highest value of should correspond to the preferred ground state with maximum deformation.
There is, however, another factor that should be taken into account. The nucleon–nucleon interaction is known to be attractive and of short-range [127], therefore favoring the maximal spatial overlap [111] among the nucleons, which can be achieved for the most symmetric SU(3) irrep. In the Young diagrams, it is known that boxes on the same line correspond to symmetrized particles, while boxes in the same column correspond to anti-symmetrized particles [8,10]. The degree of symmetrization of a given SU(3) irrep can, therefore, be measured by the ratio of the symmetrized boxes over the total number of boxes, which is
It was proved [128] that the irreps with the highest value of r, i.e., with the highest degree of symmetry, correspond to what is called the highest weight (hw) irreps of SU(3). As such, these irreps are favored by the nucleon–nucleon interaction and, therefore, dominate the related nuclear properties.
The irreps possessing the highest eigenvalues of the second-order Casimir operator, called the highest irreps, for brevity, and the highest hw irreps of SU(3) in the various nuclear shells, are shown in Table 6. It is clear that up to the mid-shell, the and hw irreps are identical, while in the upper half of each shell, the and hw irreps are different, with the exception of the last 5 particle numbers (which correspond to states with up to 4 holes at the top of the shell). Further mathematical details on the dominance of the hw irreps can be found in References [129,130].
8. Physical Consequences of the Dominance of the Highest Weight Irreps
8.1. Prolate over Oblate Dominance
One of the long-standing puzzles in a nuclear structure is the dominance of prolate (rugby ball-like) shapes over oblate (pancake-like) shapes in the ground state bands of even–even nuclei. In Elliott’s notation, prolate (oblate) irreps correspond to () [26,27,28,29,30,31,131], while irreps with correspond to maximal triaxiality. Despite several attempts [102,132,133,134,135] to resolve this puzzle, the issue is still considered open [136].
The dominance of the hw irreps over the highest irreps offers a simple, parameter-free justification of the prolate over oblate dominance. As an example, in Table 7, the hw irreps corresponding to the rare earth nuclei with valence protons in the 82–126 shell and valence neutrons in the 126–184 shell are shown. These hw irreps are obtained by adding up the hw irrep corresponding to the valence protons and the hw irrep and corresponding to the valence neutrons into the most stretched irrep [45]. We notice that prolate irreps are obtained over most of the table, with the exception of its lower right corner, near which, a few oblate irreps (underlined in Table 7) appear in nuclei lying below the tops of both the proton valence shell and the neutron valence shell. The same effect appears in other shells as well, as one can see using the irreps appearing in Table 6. For example, results for rare earth with valence protons in the 50–82 shell and valence neutrons within the 50–82 and the 82–126 shells are given in Reference [89]. The conclusion of this subsection was recently corroborated by a heuristic method in Reference [137].


Table 6.
Highest weight SU(3) irreps (labeled by hw) for U(n), n = 6, 10, 15, 21, 28, 36, and highest irreps (labeled by C) for n = 6, 10, 15, 21. The highest weight (hw) irreps differing from their highest counterparts are shown in boldface. The results were obtained by the code of Reference [138]; moreover, a new version exists [139] (see also Reference [140]), and were presented in [141]. An analytic formula for the calculation of the hw irreps was given in Reference [142]. Adapted from Reference [143]. See Section 7 for further discussion.
Table 6.
Highest weight SU(3) irreps (labeled by hw) for U(n), n = 6, 10, 15, 21, 28, 36, and highest irreps (labeled by C) for n = 6, 10, 15, 21. The highest weight (hw) irreps differing from their highest counterparts are shown in boldface. The results were obtained by the code of Reference [138]; moreover, a new version exists [139] (see also Reference [140]), and were presented in [141]. An analytic formula for the calculation of the hw irreps was given in Reference [142]. Adapted from Reference [143]. See Section 7 for further discussion.
| 8–20 | 8–20 | 28–50 | 28–50 | 50–82 | 50–82 | 82–126 | 82–126 | 126–184 | 184–258 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| sd | sd | pf | pf | sdg | sdg | PFH | PFH | sdgi | PFHj | ||
| M | irrep | U(6) | U(6) | U(10) | U(10) | U(15) | U(15) | U(21) | U(21) | U(28) | U(36) |
| hw | C | hw | C | hw | C | hw | C | hw | hw | ||
| 0 | (0,0) | (0,0) | (0,0) | (0,0) | (0,0) | (0,0) | (0,0) | (0,0) | (0,0) | (0,0) | |
| 1 | [1] | (2,0) | (2,0) | (3,0) | (3,0) | (4,0) | (4,0) | (5,0) | (5,0) | (6,0) | (7,0) |
| 2 | [2] | (4,0) | (4,0) | (6,0) | (6,0) | (8,0) | (8,0) | (10,0) | (10,0) | (12,0) | (14,0) |
| 3 | [21] | (4,1) | (4,1) | (7,1) | (7,1) | (10,1) | (10,1) | (13,1) | (13,1) | (16,1) | (19,1) |
| 4 | [] | (4,2) | (4,2) | (8,2) | (8,2) | (12,2) | (12,2) | (16,2) | (16,2) | (20,2) | (24,2) |
| 5 | [1] | (5,1) | (5,1) | (10,1) | (10,1) | (15,1) | (15,1) | (20,1) | (20,1) | (25,1) | (30,1) |
| 6 | [] | (6,0) | (0,6) | (12,0) | (12,0) | (18,0) | (18,0) | (24,0) | (24,0) | (30,0) | (36,0) |
| 7 | [1] | (4,2) | (1,5) | (11,2) | (11,2) | (18,2) | (18,2) | (25,2) | (25,2) | (32,2) | (39,2) |
| 8 | [] | (2,4) | (2,4) | (10,4) | (10,4) | (18,4) | (18,4) | (26,4) | (26,4) | (34,4) | (42,4) |
| 9 | [1] | (1,4) | (1,4) | (10,4) | (10,4) | (19,4) | (19,4) | (28,4) | (28,4) | (37,4) | (46,4) |
| 10 | [] | (0,4) | (0,4) | (10,4) | (4,10) | (20,4) | (20,4) | (30,4) | (30,4) | (40,4) | (50,4) |
| 11 | [1] | (0,2) | (0,2) | (11,2) | (4,10) | (22,2) | (22,2) | (33,2) | (33,2) | (44,2) | (55,2) |
| 12 | [] | (0,0) | (0,0) | (12,0) | (4,10) | (24,0) | (24,0) | (36,0) | (36,0) | (48,0) | (60,0) |
| 13 | [1] | (9,3) | (2,11) | (22,3) | (22,3) | (35,3) | (35,3) | (48,3) | (61,3) | ||
| 14 | [] | (6,6) | (0,12) | (20,6) | (20,6) | (34,6) | (34,6) | (48,6) | (62,6) | ||
| 15 | [1] | (4,7) | (1,10) | (19,7) | (7,19) | (34,7) | (34,7) | (49,7) | (64,7) | ||
| 16 | [] | (2,8) | (2,8) | (18,8) | (6,20) | (34,8) | (34,8) | (50,8) | (66,8) | ||
| 17 | [1] | (1,7) | (1,7) | (18,7) | (3,22) | (35,7) | (35,7) | (52,7) | (69,7) | ||
| 18 | [] | (0,6) | (0,6) | (18,6) | (0,24) | (36,6) | (36,6) | (54,6) | (72,6) | ||
| 19 | [1] | (0,3) | (0,3) | (19,3) | (2,22) | (38,3) | (38,3) | (57,3) | (76,3) | ||
| 20 | [] | (0,0) | (0,0) | (20,0) | (4,20) | (40,0) | (40,0) | (60,0) | (80,0) | ||
| 21 | [1] | (16,4) | (4,19) | (37,4) | (4,37) | (58,4) | (79,4) | ||||
| 22 | [] | (12,8) | (4,18) | (34,8) | (0,40) | (56,8) | (78,8) | ||||
| 23 | [1] | (9,10) | (2,18) | (32,10) | (3,38) | (55,10) | (78,10) | ||||
| 24 | [] | (6,12) | (0,18) | (30,12) | (6,36) | (54,12) | (78,12) | ||||
| 25 | [1] | (4,12) | (1,15) | (29,12) | (7,35) | (54,12) | (79,12) | ||||
| 26 | [] | (2,12) | (2,12) | (28,12) | (8,34) | (54,12) | (80,12) | ||||
| 27 | [1] | (1,10) | (1,10) | (28,10) | (7,34) | (55,10) | (82,10) | ||||
| 28 | [] | (0.8) | (0,8) | (28,8) | (6,34) | (56,8) | (84,8) | ||||
| 29 | [1] | (0,4) | (0,4) | (29,4) | (3,35) | (58,4) | (87,4) | ||||
| 30 | [] | (0,0) | (0,0) | (30,0) | (0,36) | (60,0) | (90,0) | ||||
| 31 | [1] | (25,5) | (2,33) | (56,5) | (87,5) | ||||||
| 32 | [] | (20,10) | (4,30) | (52,10) | (84,10) | ||||||
| 33 | [1] | (16,13) | (4,28) | (49,13) | (82,13) | ||||||
| 34 | [] | (12,16) | (4,26) | (46,16) | (80,16) | ||||||
| 35 | [1] | (9,17) | (2,25) | (44,17) | (79,17) | ||||||
| 36 | [] | (6,18) | (0,24) | (42,18) | (78,18) | ||||||
| 37 | [1] | (4,17) | (1,20) | (41,17) | (78,17) | ||||||
| 38 | [] | (2,16) | (2,16) | (40,16) | (78,16) | ||||||
| 39 | [1] | (1,13) | (1,13) | (40,13) | (79,13) | ||||||
| 40 | [] | (0,10) | (0,10) | (40,10) | (80,10) | ||||||
| 41 | [1] | (0,5) | (0,5) | (41,5) | (82,5) | ||||||
| 42 | [] | (0,0) | (0,0) | (42,0) | (84,0) | ||||||
| 43 | [1] | (36,6) | (79,6) | ||||||||
| 44 | [] | (30,12) | (74,12) | ||||||||
| 45 | [1] | (25,16) | (70,16) | ||||||||
| 46 | [] | (20,20) | (66,20) | ||||||||
| 47 | [1] | (16,22) | (63,22) | ||||||||
| 48 | [] | (12,24) | (60,24) | ||||||||
| 49 | [1] | (9,24) | (58,24) | ||||||||
| 50 | [] | (6,24) | (56,24) | ||||||||
| 51 | [1] | (4,22) | (55,22) | ||||||||
| 52 | [] | (2,20) | (54,20) | ||||||||
| 53 | [1] | (1,16) | (54,16) | ||||||||
| 54 | [] | (0,12) | (54,12) | ||||||||
| 55 | [1] | (0,6) | (55,6) | ||||||||
| 56 | [] | (0,0) | (56,0) |

Table 7.
Highest weight SU(3) irreps for nuclei with protons in the 82–126 shell and neutrons in the 126–184 shell. Oblate irreps are underlined, adapted from Reference [143]. See Section 8.1 for further discussion.
8.2. Parameter-Free Predictions for the Collective Variables and
Further consequences of the dominance of the hw irreps over the highest irreps become evident if one considers the connection between the Elliott quantum numbers , and the collective variables , of the Bohr–Mottelson model. This connection is obtained by employing a linear mapping between the invariant quantities of the two theories, which are the invariants and of the collective model [14,15] and the Casimir operators of the second and third order of SU(3) [8,10]. This mapping provides the angle collective variable of the expression [124,126]
while for the square of the deformation parameter , being proportional to the second-order Casimir operator of SU(3) [58], it gives [124,126]
where A is the mass number of the nucleus and is related to the dimensionless mean square radius [115], . The dimensionless mean square radius is obtained by dividing the mean square radius, which is proportional to , by the oscillator length, which grows as [115]. The constant is determined from a fit over a wide range of nuclei [144,145]. We stick to the value used in Reference [124], , in agreement with Reference [145].
A word of warning: since only the valence nucleons are taken into account in proxy-SU(3), the values of obtained from Equation (9) should be rescaled by multiplying them by a factor , where () is the size of the proton (neutron) valence shell. The need for this rescaling is discussed in detail in Section 5 of Reference [89]. In practice, this rescaling means that Equation (9), when used in the proxy-SU(3) framework, should read
Numerical results for the collective variable () for several rare earth nuclei are shown in Figure 4 and Figure 5 and are compared to other theoretical approaches, such as the D1S–Gogny interaction [146] and relativistic mean field theory [147], as well as experimental values [148]. By “Gogny D1S min”, we label the values of the deformation variables, and , at the HFB minimum energy (entries 4 and 5 in Reference [146]); “Gogny D1S mean” involves the mean ground state values (entries 11 and 12 in Reference [146]). It is seen that the parameter-free proxy-SU(3) predictions are in good agreement with both the theoretical approaches and the empirical values. Additional numerical results for and obtained within the proxy-SU(3) approach can be found in [149,150,151]. Additional comparisons of proxy-SU(3) predictions to covariant density functional theory can be found in References [152,153,154], while comparisons to recent experimental findings can be found in [155,156].
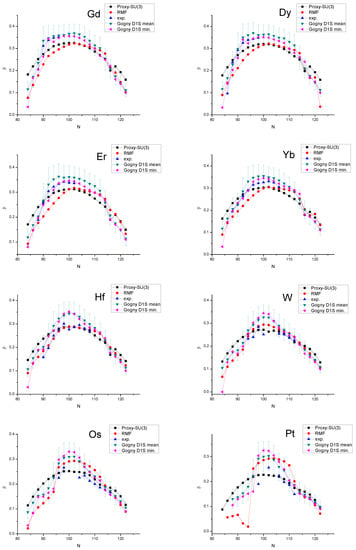
Figure 4.
Proxy SU(3) predictions for Gd-Pt isotopes for the collective variable , obtained from Equation (10), as described in detail in Reference [89], compared with results by the D1S–Gogny interaction (D1S–Gogny) [146] and by relativistic mean field theory (RMF) [147], as well as with empirical values (exp.) [148], adapted from Reference [157]. See Section 8.2 for further discussion.
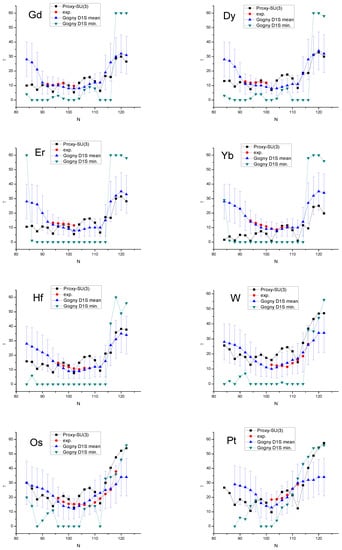
Figure 5.
The same as Figure 4, but for the collective variable , derived from Equation (8), adapted from Reference [157]. See Section 8.2 for further discussion.
In Figure 4, it is clear that the curve is not symmetric around the mid-shell, but it appears to exhibit higher values in the first half of the shell. The origin of this discrepancy can be traced in Figure 6, in which the square root of , which is proportional to , according to Equation (10), is shown. We see that the breaking of the symmetry around the mid-shell is due to the fact that in the upper half of the shell the highest weight irreps enter in the place of the highest irreps, as indicated by Table 6.
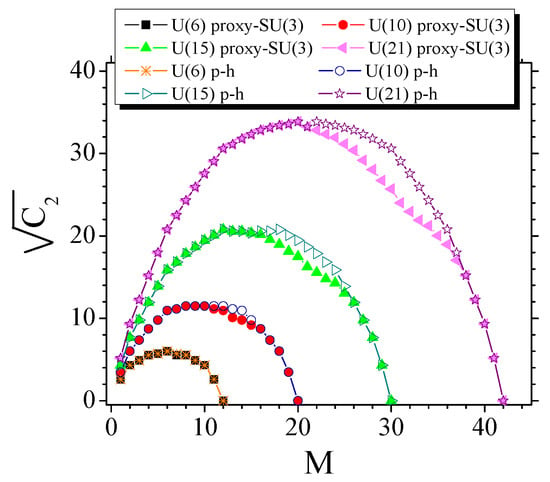
Figure 6.
Values of the square root of the second-order Casimir operator of SU(3), obtained from Equation (5), vs. particle number M, for different shells, obtained through proxy-SU(3) (columns hw in Table 6) or through the particle–hole symmetry assumption (columns C in Table 6), adapted from Reference [89]. See Section 8.2 for further discussion.
8.3. Prolate to Oblate Shape/Phase Transition
A second important consequence of the hw irreps dominance is seen in Figure 7, in which the proxy-SU(3) predictions for the collective variable for the rare earth with valence protons in the 50–82 shell and valence neutrons in the 82–126 shell are collected. The dip seen at signifies the occurrence of a shape/phase transition [158,159,160,161,162,163,164,165,166] from prolate to oblate shapes, for which extended experimental evidence exists [167,168,169,170,171], along with microscopic theoretical considerations [172,173,174,175,176,177,178], and relevant searches within the interacting boson model (IBM) [179,180,181,182,183,184] and the Bohr–Mottelson collective model [185,186]. In the framework of the Bohr Hamiltonian, this shape/phase transition is referred to as Z(5) [185]. A posteriori corroboration of the findings of Reference [89] is found in References [187,188,189].
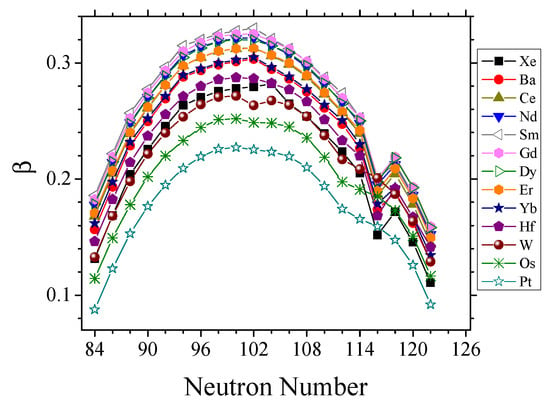
Figure 7.
Proxy-SU(3) predictions for the collective variable , obtained from Equation (10), as described in detail in Reference [89], adapted from Reference [89]. See Section 8.3 for further discussion.
The robustness of this result is emphasized by the fact that it also appears in atomic clusters [190,191,192,193,194,195]. The valence electrons in alkali metal clusters, in particular, are supposed to be free, thus forming shells with major magic numbers 2, 8, 20, 40, 58, 92,… [196,197,198,199,200,201,202,203]. Prolate and oblate shapes in alkali metal clusters were observed experimentally through optical response measurements, finding oblate shapes below cluster sizes 20 and 40 [204,205,206,207], while prolate shapes were seen above cluster sizes 8, 20, 40 [204,205,206,207,208]. In other words, prolate (oblate) shapes are seen above (below) the magic numbers, exactly as in atomic nuclei.
It should be noticed that the shape/phase transition from prolate to oblate shapes is seen equally clearly in the framework of pseudo-SU(3), if the dominance of the hw irreps over the highest irreps is taken into account, as discussed in detail in Reference [209]. Although pseudo-SU(3) and proxy-SU(3) are based on different approximations, involving different unitary transformations, they lead to the same physical conclusion, a fact providing evidence for the compatibility of the two approaches.
The compatibility of the proxy-SU(3) and pseudo-SU(3) approaches has also been pointed out recently [210,211,212] in the framework of the semi-microscopic algebraic quartet model (SAQM) [213], which generates the excitation spectra of shell-like quartets, formed by two protons and two neutrons in a well-defined shell configuration. Based on the SU(3) symmetry, in its initial form [213] the model had been applicable only to light nuclei, based on the Elliott SU(3) symmetry. However, it has recently [210,211,212] been extended to heavy nuclei, based on the proxy-SU(3) symmetry and on the pseudo-SU(3) symmetry, with similar results provided by both approaches. The use of proxy-SU(3) could also be extended in a similar way to the semi-microscopic algebraic cluster model (SACM) [214,215,216], in which the internal structures of the clusters are described in terms of the shell model SU(3) symmetry, while the relative motion is described in terms of the phenomenological algebraic vibron model [60,217,218,219].
9. Islands of Shape Coexistence
9.1. Harmonic Oscillator (HO) and Spin–Orbit (SO) Magic Numbers
The shape coexistence (SC) involves the appearance in a nucleus of two bands lying close in energy but having radically different structures; for example, one of them being spherical and the other deformed, or both of them being spherical, but one of them exhibiting prolate (rugby ball-like) deformation and the other oblate (pancake-like) deformation. Shape coexistence has first been suggested in 1956 by Morinaga [220], in relation to the spectrum of O. Since then many experimental examples were found in both odd and even nuclei, as summarized in the relevant review articles [221,222,223,224]. From the theoretical point of view, SC was attributed to the existence of particle–hole excitations across shell or subshell closures, and was believed to be able to appear all over the nuclear chart, although in Figure 8 of the authoritative review article by Heyde and Wood [223], the regions in which SC was experimentally observed appear to form certain islands on the nuclear chart.
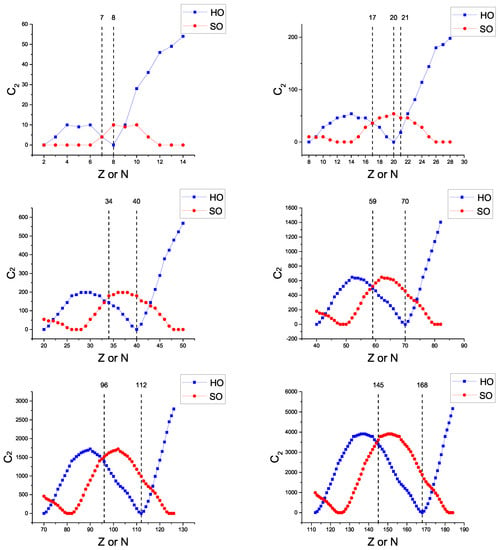
Figure 8.
The eigenvalues of the second-order Casimir operator of SU(3) versus the proton (Z) or neutron number (N). Islands of shape coexistence are predicted by the dual shell mechanism within proton or neutron numbers 7–8, 17–20, 34–40, 59–70, 96–112, 145–168, in which , adapted from Reference [225]. See Section 9.2 for further discussion.
As already mentioned, SC is supposed to be due to particle–hole excitations across shell or subshell closures. However, the magic numbers of the shell models, 2, 8, 20, 28, 50, 82, 126,…, are known to be valid only at zero deformations. These magic numbers originate from the 3D-HO magic numbers 2, 8, 20, 40, 70, 112, 168,…, [8,10] (to be called the HO magic numbers in what follows) because of the action of the spin–orbit interaction [4,5,6,7]. As deformation sets in, the energy gaps separating different shells soon disappear, as one can see in the standard Nilsson diagrams [17,18,19,114] (see also References [122,226] for the evolution of magic numbers away from stability). Furthermore, as seen in Table 3 (see also Reference [227]), in the framework of the proxy-SU(3) symmetry a set of magic numbers 6, 14, 28, 50, 82, 126, 184,… (to be called the SO magic numbers in what follows) appears, corresponding to the strong presence of the spin–orbit interaction everywhere. The standard shell model magic numbers follow the HO magic numbers up to 20, while they follow the SO magic numbers beyond this point.
9.2. A Dual Shell Mechanism for Shape Coexistence
It was suggested [225,228,229] that the interplay between HO and SO magic numbers offers a simple justification for the appearance of islands of SC on the nuclear chart. Let us see how this is occurring.
Because of the collapse of the shell model quantum numbers as deformation sets in, the protons and/or the neutrons of a nucleus can follow either the HO or the SO magic numbers. The same number of protons or neutrons will then correspond to a different irrep in the HO framework and another irrep in the SO framework. These irreps can be seen in Table 8. As an example, let us consider 60 nucleons. In the HO framework, 40 is a magic number; thus, there are 20 nucleons left in the 40–70 shell, which has the U(15) symmetry and, therefore, the 20 nucleons correspond to the (20,0) hw irrep according to Table 6. In the SO framework, 50 is a magic number; thus, there are 10 nucleons left in the 50–82 shell, which in the proxy-SU(3) approximation has the U(15) symmetry; therefore, the 10 nucleons correspond to the (20,4) hw irrep of SU(3) according to Table 6. Indeed, in Table 8 for 60 nucleons, the hw irreps given are (20,4) for the SO case and (20,0) for the HO case.

Table 8.
The highest weight SU(3) irreps for the spin–orbit (SO)-like magic numbers 6, 14, 28, 50, 82, and 126, according to the proxy-SU(3) symmetry and for the harmonic oscillator (HO) magic numbers 2, 8, 20, 40, 70, 112, and 168 according to the Elliott SU(3) symmetry are given for each nucleon number M, as obtained from Table 6, adapted from Reference [225]. See Section 9 for further discussion.
For the band heads of two coexisting bands, one can use the very simple Hamiltonian [225]
where corresponds to the 3D-HO Hamiltonian and to the quadrupole–quadrupole interaction. Both bands should belong to the same U(n) algebra within the SO and HO schemes. From Table 3, we see that this is possible for the nucleon number intervals 6–8, 14–20, 28–40, 50–70, 82–112, 126–168, in which both bands belong to the U(3), U(6), U(10), U(15), U(21), and U(28) algebra, respectively. We remark that the right borders of these regions are the HO magic numbers. The successful parameter-free predictions of the and collective variables for the ground states of nuclei seen in Section 8.2 imply that the ground-state band will belong to the SO irrep, thus the band head of the coexisting band should lie higher in energy. One can easily see that this requirement leads to the condition
the full details of the argument are given explicitly in Section 8 of Reference [225]. From Equation (6), one then sees that this condition is equivalent to the condition
The eigenvalues of the Casimir operator in the SO and HO frameworks are shown for the various shells in Figure 8. We see that the condition of Equation (13) starts being fulfilled at the nucleon numbers 7, 17, 34, 59, 96, and 146, which, therefore, stand for the left borders of the regions in which SC could be possible, with the right borders given by the HO magic numbers mentioned above. Therefore, we conclude that SC can occur only within the nucleon intervals 7–8, 17–20, 34–40, 59–70, 96–112, and 146–168, bearing U(3), U(6), U(10), U(15), U(21), and U(28) symmetry, respectively. These intervals define horizontal and vertical stripes on the nuclear chart, shown in color in Figure 9. One can easily see that the islands of SC seen in Figure 8 of Reference [223] do lie within the stripes predicted by the dual shell mechanism within the proxy-SU(3) framework just found.
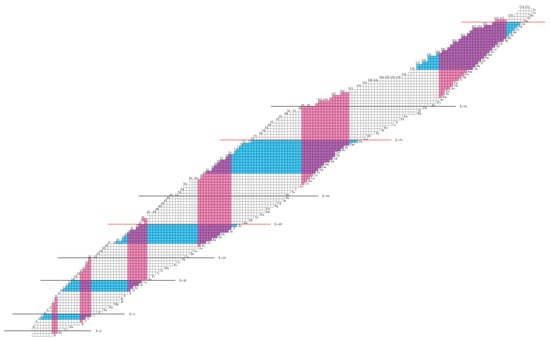
Figure 9.
This map indicates which nuclei have to be examined both theoretically and experimentally for manifesting shape coexistence according to the proposed dual shell mechanism. The colored regions possess proton or neutron numbers (7–8, 17–20, 34–40, 59–70, 96–112, and 145–168). The horizontal stripes correspond to the neutron-induced shape coexistence, while the vertical stripes correspond to the proton-induced shape coexistence, adapted from Reference [225]. See Section 9 for further discussion.
9.3. From Stripes to Islands of Shape Coexistence
The stripes 7–8, 17–20, 34–40, 59–70, 96–112, and 146–168 (determined in the previous subsection) represent necessary conditions for the appearance of SC, but not sufficient ones. Further work is needed in order to narrow down the stripes into islands. A step in this direction was taken within the covariant density functional theory [230,231,232,233,234,235,236], using the DDME2 functional [237] and the code of Reference [238]. A systematic search was made [239,240] for particle–hole excitations, which are believed to be the microscopic mechanisms behind SC. Indeed, specific islands of SC were located [239,240] around the proton shell closures Z = 82 and Z = 50, in which proton particle–hole excitations were caused by the neutrons, characterizing these cases as part of neutron-induced shape coexistence. In addition, specific islands of SC were located [239,240] around the neutron numbers n = 90 and n = 60, in which neutron particle–hole excitations were caused by the protons, therefore characterizing these cases as part of proton-induced shape coexistence. Furthermore, an island of SC was found around , in which both the proton-induced and neutron-induced mechanisms are present simultaneously. All of these islands are consistent with the stripes of the dual shell mechanism within the proxy-SU(3) symmetry, as well as with the empirical islands reviewed in Figure 8 of Reference [223].
Further corroboration of the predictions of the dual shell mechanism was provided by various relativistic microscopic calculations [241,242,243,244,245,246], as well as by calculations using the Bohr Hamiltonian [246,247] and the IBM [248].
The above predictions of specific islands of SC are based on the particle–hole excitation mechanism. Some other microscopic mechanisms may create SC in regions of the nuclear chart outside the islands predicted here. This can be the subject of further investigation.
9.4. Multiple-Shape Coexistence
Recent experimental evidence shows that multiple-shape coexistence (of up to four bands) can be seen in certain nuclei [249,250], while it is also predicted theoretically in others [245]. Multiple-shape coexistence can occur within the dual shell mechanism described above, since the protons can follow either the SO or the HO scheme, and so can (independently) the neutrons. As a result, four different irreps, based on the proton–neutron combinations SO-SO, SO-HO, HO-SO, and HO-HO can occur in general, giving rise to multiple coexistence of four bands, or three bands in the special case in which equal numbers of valence protons and valence neutrons occupy the same shell. This idea, however, still needs to be tested against experimental evidence.
10. Conclusions and Outlook
In this article, we discussed the following: the physical ideas that led to the introduction of the proxy-SU(3) symmetry, the calculations proving its validity and its connection to the shell model framework, the first successful applications in predicting (in a parameter-free way) the values of the collective variables ( and ) for even–even nuclei, the dominance of prolate over oblate shapes in the ground states of even–even nuclei, a prolate to oblate shape/phase transition, and the existence of islands on the nuclear chart in which shape coexistence can appear. Several directions for further investigations are briefly presented below.
The proxy-SU(3) symmetry offers the possibility of making parameter-free predictions for B(E2) transition rates. The value of is known to be connected to the collective variable [148,251]; thus, it can be determined in a parameter-free way from the values calculated as described in Section 8.2. Since ratios of B(E2)s will only depend on angular momentum coupling coefficients of SO(3) [120,121] and SU(3) [252,253,254,255,256,257], parameter-free predictions for all B(E2)s could be obtained in principle. Some first steps in this direction were taken in [151,157].
Based on the experience acquired within the pseudo-SU(3) model [45,46], it is expected that the description of nuclear spectra within the proxy-SU(3) symmetry will require the use of third-order and fourth-order operators. In particular, the O(3) symmetry-preserving three-body operator and four-body operator (their mathematical names being the and shift operators, respectively) [258,259,260,261], will be needed in order to break the degeneracy between the ground state band (GSB) and the band, which in the proxy-SU(3) approach lies within the same SU(3) irrep. This can be seen, for example, in Table 7, where almost all nuclei are characterized by SU(3) irreps with . Since K takes the values [10,26,58], the hw irrep will contain both the (GSB) and () bands [262]. The parameter-free reproduction of the empirical observation (where the energy differences between the band and the ground state band decrease as functions of the angular momentum L in deformed nuclei [263], with an opposite trend seen in vibrational and -unstable nuclei) should be tested. Some first steps in this direction were taken in References [264,265]. The energy scale can be fixed in an even–even nucleus by determining the energy of the first excited state from the value of the , determined in a parameter-free way, as described in Section 8.2. This can be achieved through the microscopically derived [266,267] Grodzins relation [268], connecting the energy of the state and .
Nuclear binding energies and nucleon separation energies are basic nuclear structure quantities, for which extended experimental data [269] and theoretical predictions [147,270,271] exist. It would be an interesting project to examine the degree to which proxy-SU(3) is able to predict these quantities, preferably in a parameter-free way. Some first steps in this direction were taken in References [272,273]. The calculations of two-neutron separation energies are of particular interest due to the recently discovered [274,275] connections between them and the neutron capture cross sections, which are essential for understanding the astrophysical s and r processes.
Author Contributions
Conceptualization, D.B., A.M., S.K.P., T.J.M. and N.M.; methodology, D.B., A.M., S.K.P., T.J.M. and N.M.; writing—original draft preparation, D.B.; writing—review and editing, D.B., A.M., S.K.P., T.J.M. and N.M.; supervision, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bulgarian National Science Fund (BNSF) under contract no. KP-06-N48/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wigner, E. On the consequences of the symmetry of the nuclear Hamiltonian on the spectroscopy of nuclei. Phys. Rev. 1937, 51, 106. [Google Scholar] [CrossRef]
- Franzini, P.; Radicati, L.A. On the validity of the supermultiplet model. Phys. Lett. 1963, 6, 322. [Google Scholar] [CrossRef]
- Hecht, K.T.; Pang, S.C. On the Wigner supermultiplet scheme. J. Math. Phys. 1969, 10, 1571. [Google Scholar] [CrossRef]
- Mayer, M.G. On closed shells in nuclei. Phys. Rev. 1948, 74, 235. [Google Scholar] [CrossRef]
- Mayer, M.G. On closed shells in nuclei. II. Phys. Rev. 1949, 75, 1969. [Google Scholar] [CrossRef]
- Haxel, O.; Jensen, J.H.D.; Suess, H.E. On the “magic numbers” in nuclear structure. Phys. Rev. 1949, 75, 1766. [Google Scholar] [CrossRef]
- Mayer, M.G.; Jensen, J.H.D. Elementary Theory of Nuclear Shell Structure; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Wybourne, B.G. Classical Groups for Physicists; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Moshinsky, M.; Smirnov, Y.F. The Harmonic Oscillator in Modern Physics; Harwood: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Iachello, F. Lie Algebras and Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Bonatsos, D.; Klein, A. Exact boson mappings for nuclear neutron (proton) shell-model algebras having SU(3) subalgebras. Ann. Phys. 1986, 169, 61. [Google Scholar] [CrossRef]
- Nobel Foundation. Nobel Lectures, Physics 1963–1970; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Rainwater, J. Nuclear energy level argument for a spheroidal nuclear model. Phys. Rev. 1950, 79, 432. [Google Scholar] [CrossRef]
- Bohr, A. The coupling of nuclear surface oscillations to the motion of individual nucleons. Mat. Fys. Medd. K. Dan. Vidensk. Selsk. 1952, 26. Available online: http://www.xuantianlinyu.com.cn/Jabref/RefPdf/Bohr1952pp.pdf (accessed on 1 January 2022).
- Bohr, A.; Mottelson, B.R. Nuclear Structure Vol. II: Nuclear Deformations; Benjamin: New York, NY, USA, 1975. [Google Scholar]
- Nobel Foundation. Nobel Lectures, Physics 1971–1980; Lundqvist, S., Ed.; World Scientific: Singapore, 1992. [Google Scholar]
- Nilsson, S.G. Binding states of individual nucleons in strongly deformed nuclei. Mat. Fys. Medd. K. Dan. Vidensk. Selsk. 1955, 29. Available online: http://gymarkiv.sdu.dk/MFM/kdvs/mfm%2020-29/MFM%2029-16.pdf (accessed on 1 January 2022).
- Ragnarsson, I.; Nilsson, S.G.; Sheline, R.K. Shell structure in nuclei. Phys. Rep. 1978, 45, 1. [Google Scholar] [CrossRef]
- Nilsson, S.G.; Ragnarsson, I. Shapes and Shells in Nuclear Structure; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Takahashi, Y. SU(3) shell model in a deformed harmonic oscillator basis. Prog. Theor. Phys. 1975, 53, 461. [Google Scholar] [CrossRef]
- Asherova, R.M.; Smirnov, Y.F.; Tolstoy, V.N.; Shustov, A.P. Algebraic approach to the projected deformed oscillator model. Nucl. Phys. A 1981, 355, 25. [Google Scholar] [CrossRef]
- Rosensteel, G.; Draayer, J.P. Symmetry algebra of the anisotropic harmonic oscillator with commensurate frequencies. J. Phys. A Math. Gen. 1989, 22, 1323. [Google Scholar] [CrossRef]
- Nazarewicz, W.; Dobaczewski, J. Dynamical symmetries, multiclustering, and octupole susceptibility in superdeformed and hyperdeformed nuclei. Phys. Rev. Lett. 1992, 68, 154. [Google Scholar] [CrossRef] [PubMed]
- Nazarewicz, W.; Dobaczewski, J.; Isacker, P.V. Shell model calculations at superdeformed shapes. AIP Conf. Proc. 1992, 259, 30. [Google Scholar]
- Bonatsos, D.; Daskaloyannis, C.; Kolokotronis, P.; Lenis, D. The symmetry algebra of the N-dimensional anisotropic quantum harmonic oscillator with rational ratios of frequencies and the Nilsson model. arXiv 1994, arXiv:hep-th/9411218. [Google Scholar]
- Elliott, J.P. Collective motion in the nuclear shell model. I. Classification schemes for states of mixed configurations. Proc. R. Soc. Lond. Ser. A 1958, 245, 128. [Google Scholar]
- Elliott, J.P. Collective motion in the nuclear shell model. II. The introduction of intrinsic wave-functions. Proc. R. Soc. Lond. Ser. A 1958, 245, 562. [Google Scholar]
- Elliott, J.P.; Harvey, M. Collective motion in the nuclear shell model. III. The calculation of spectra. Proc. R. Soc. Lond. Ser. A 1963, 272, 557. [Google Scholar]
- Wilsdon, C.E. A Survey of the Nuclear s-d Shell Using the SU(3) Coupling Scheme. Ph.D. Thesis, University of Sussex, Brighton, UK, 1965. [Google Scholar]
- Elliott, J.P.; Wildson, C.E. Collective motion in the nuclear shell model. IV. Odd-mass nuclei in the sd shell. Proc. R. Soc. Lond. Ser. A 1968, 302, 509. [Google Scholar]
- Harvey, M. The nuclear SU3 model. Adv. Nucl. Phys. 1968, 1, 67. [Google Scholar]
- Cseh, J. Some new chapters of the long history of SU(3). EPJ Web Conf. 2018, 194, 05001. [Google Scholar] [CrossRef]
- Raychev, P.P. On the broken Sp(3,3) symmetry and the spectra of deformed even–even nuclei. Compt. Rend. Acad. Bulg. Sci. 1972, 25, 1503. [Google Scholar]
- Afanas’ev, G.N.; Abramov, S.A.; Raychev, P.P. Realization of the physical basis for SU(3) and the probabilities of E2 transitions in the SU(3) formalism. Yad. Fiz. 1972, 16, 53, Erratum in Sov. J. Nucl. Phys. 1973, 16, 27. [Google Scholar]
- Raychev, P.P. Parametrization of B(E2) transitions in deformed even–even nuclei within the framework of the SU(3) scheme. Yad. Fiz. 1972, 16, 1171, Erratum in Sov. J. Nucl. Phys. 1973, 16, 643. [Google Scholar]
- Raychev, P.P.; Roussev, R.P. Energy levels and reduced E2-transition probabilities of deformed even–even nuclei in the SU(3) scheme. Yad. Fiz. 1978, 27, 1501, Erratum in Sov. J. Nucl. Phys. 1978, 27, 792. [Google Scholar]
- Minkov, N.; Drenska, S.B.; Raychev, P.P.; Roussev, R.P.; Bonatsos, D. Broken SU(3) symmetry in deformed even–even nuclei. Phys. Rev. C 1997, 55, 2345. [Google Scholar] [CrossRef]
- Minkov, N.; Drenska, S.B.; Raychev, P.P.; Roussev, R.P.; Bonatsos, D. Ground-γ band coupling in heavy deformed nuclei and SU(3) contraction limit. Phys. Rev. C 1999, 60, 034305. [Google Scholar] [CrossRef]
- Minkov, N.; Drenska, S.B.; Raychev, P.P.; Roussev, R.P.; Bonatsos, D. Ground-γ band mixing and odd-even staggering in heavy deformed nuclei. Phys. Rev. C 2000, 61, 064301. [Google Scholar] [CrossRef]
- Afanas’ev, G.N.; Raychev, P.P. Dynamical symmetry groups in nuclei. Fiz. Elem. Chast. At. Yadra 1972, 3, 436, Erratum in Sov. J. Nucl. Phys. 1972, 3, 229. [Google Scholar]
- Hecht, K.T.; Adler, A. Generalized seniority for favored J ≠ 0 pairs in mixed configurations. Nucl. Phys. A 1969, 137, 129. [Google Scholar] [CrossRef]
- Arima, A.; Harvey, M.; Shimizu, K. Pseudo LS coupling and pseudo SU3 coupling schemes. Phys. Lett. B 1969, 30, 517. [Google Scholar] [CrossRef]
- Raju, R.D.R.; Draayer, J.P.; Hecht, K.T. Search for a coupling scheme in heavy deformed nuclei: The pseudo SU(3) model. Nucl. Phys. A 1973, 202, 433. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J.; Hecht, K.T. Strength of the Qπ·Qν interaction and the strong-coupled pseudo-SU(3) limit. Nucl. Phys. A 1982, 381, 1. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J. Shell-model description of the low-energy structure of strongly deformed nuclei. Phys. Rev. Lett. 1983, 51, 1422. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J. Towards a shell model description of the low-energy structure of deformed nuclei I. even–even systems. Ann. Phys. 1984, 156, 41. [Google Scholar] [CrossRef]
- Draayer, J.P. Fermion models. In Algebraic Approaches to Nuclear Structure; Casten, R.F., Ed.; Harwood: Chur, Switzerland, 1993; p. 423. [Google Scholar]
- Castaños, O.; Moshinsky, M.; Quesne, C. Transformations from U(3) to pseudo U(3) basis. In Group Theory and Special Symmetries in Nuclear Physics Ann Arbor, 1991; Draayer, J.P., Jänecke, J., Eds.; World Scientific: Singapope, 1992; p. 80. [Google Scholar]
- Castaños, O.; Moshinsky, M.; Quesne, C. Transformation to pseudo-SU(3) in heavy deformed nuclei. Phys. Lett. B 1992, 277, 238. [Google Scholar] [CrossRef]
- Castaños, O.; Velázquez, A.V.; Hess, P.O.; Hirsch, J.G. Transformation to pseudo-spin-symmetry of a deformed Nilsson hamiltonian. Phys. Lett. B 1994, 321, 303. [Google Scholar] [CrossRef]
- Ginocchio, J.N. Pseudospin as a relativistic symmetry. Phys. Rev. Lett. 1997, 78, 436. [Google Scholar] [CrossRef]
- Ginocchio, J.N. On the relativisitic origins of pseudo-spin symmetry in nuclei. J. Phys. G Nucl. Part. Phys. 1999, 25, 617. [Google Scholar] [CrossRef]
- Janssen, D.; Jolos, R.V.; Dönau, F. An algebraic treatment of the nuclear quadrupole degree of freedom. Nucl. Phys. A 1974, 224, 93. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Collective nuclear states as representations of a SU(6) group. Phys. Rev. Lett. 1975, 35, 1069. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective states I. The vibrational limit. Ann. Phys. 1976, 99, 253. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective nuclear states II. The rotational limit. Ann. Phys. 1978, 111, 201. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective nuclear states IV. The O(6) limit. Ann. Phys. 1979, 123, 468. [Google Scholar] [CrossRef]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Iachello, F.; Isacker, P.V. The Interacting Boson-Fermion Model; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Frank, A.; Isacker, P.V. Symmetry Methods in Molecules and Nuclei; S y G Editores: México, Mexico, 2005. [Google Scholar]
- Rosensteel, G.; Rowe, D.J. Nuclear Sp(3,R) Model. Phys. Rev. Lett. 1977, 38, 10. [Google Scholar] [CrossRef]
- Rosensteel, G.; Rowe, D.J. On the algebraic formulation of collective models III. The symplectic shell model of collective motion. Ann. Phys. 1980, 126, 343. [Google Scholar] [CrossRef]
- Park, P.; Carvalho, J.; Vassanji, M.; Rowe, D.J. The shell-model theory of nuclear rotational states. Nucl. Phys. A 1984, 414, 93. [Google Scholar] [CrossRef]
- Rowe, D.J. Microscopic theory of the nuclear collective model. Rep. Prog. Phys. 1985, 48, 1419. [Google Scholar] [CrossRef]
- Rowe, D.J.; Wood, J.L. Fundamentals of Nuclear Models: Foundational Models; World Scientific: Singapore, 2010. [Google Scholar]
- Wybourne, B.G. The representation space of the nuclear symplectic Sp(6,R) shell model. J. Phys. A Math. Gen. 1992, 25, 4389. [Google Scholar] [CrossRef]
- Escher, J.; Draayer, J.P. Fermion realization of the nuclear Sp(6,R) model. J. Math. Phys. 1998, 39, 5123. [Google Scholar] [CrossRef]
- Ganev, H.G. Shell-model representations of the proton–neutron symplectic model. Eur. Phys. J. A 2015, 51, 84. [Google Scholar] [CrossRef]
- Ganev, H.G. Microscopic shell-model description of transitional nuclei. Eur. Phys. J. A 2022, 58, 182. [Google Scholar] [CrossRef]
- Ganev, H.G. Microscopic shell-model description of strongly deformed nuclei: 158Gd. Int. J. Mod. Phys. E 2022, 31, 2250047. [Google Scholar] [CrossRef]
- Georgieva, A.; Raychev, P.; Roussev, R. Interacting two-vector-boson model of collective motions in nuclei. J. Phys. G Nucl. Phys. 1982, 8, 1377. [Google Scholar] [CrossRef]
- Georgieva, A.; Raychev, P.; Roussev, R. Rotational limit of the interacting two-vector boson model. J. Phys. G Nucl. Phys. 1983, 9, 521. [Google Scholar] [CrossRef]
- Wu, C.-L.; Feng, D.H.; Chen, X.-G.; Chen, J.-Q.; Guidry, M.W. Fermion dynamical symmetry model of nuclei: Basis, Hamiltonian, and symmetries. Phys. Rev. C 1987, 36, 1157. [Google Scholar] [CrossRef]
- Navrátil, P.; Vary, J.P.; Barrett, B.R. Properties of 12C in the ab initio nuclear shell model. Phys. Rev. Lett. 2000, 84, 5728. [Google Scholar] [CrossRef]
- Navrátil, P.; Vary, J.P.; Barrett, B.R. Large-basis ab initio no-core shell model and its application to 12C. Phys. Rev. C 2000, 62, 054311. [Google Scholar] [CrossRef]
- Dytrych, T.; Sviratcheva, K.D.; Bahri, C.; Draayer, J.P.; Vary, J.P. Evidence for symplectic symmetry in ab initio no-core shell model results for light nuclei. Phys. Rev. Lett. 2007, 98, 162503. [Google Scholar] [CrossRef] [PubMed]
- Dytrych, T.; Sviratcheva, K.D.; Bahri, C.; Draayer, J.P.; Vary, J.P. Dominant role of symplectic symmetry in ab initio no-core shell model results for light nuclei. Phys. Rev. C 2007, 76, 014315. [Google Scholar] [CrossRef]
- Dytrych, T.; Sviratcheva, K.D.; Draayer, J.P.; Bahri, C.; Vary, J.P. Ab initio symplectic no-core shell model. J. Phys. G Nucl. Part. Phys. 2008, 35, 123101. [Google Scholar] [CrossRef]
- Tobin, G.K.; Ferriss, M.C.; Launey, K.D.; Dytrych, T.; Draayer, J.P.; Dreyfuss, A.C.; Bahri, C. Symplectic no-core shell-model approach to intermediate-mass nuclei. Phys. Rev. C 2014, 89, 034312. [Google Scholar] [CrossRef]
- Dytrych, T.; Maris, P.; Launey, K.D.; Draayer, J.P.; Vary, J.P.; Langr, D.; Saule, E.; Caprio, M.A.; Catalyurek, U.; Sosonkina, M. Efficacy of the SU(3) scheme for ab initio large-scale calculations beyond the lightest nuclei. Comp. Phys. Commun. 2016, 207, 202. [Google Scholar] [CrossRef]
- Launey, K.D.; Draayer, J.P.; Dytrych, T.; Sun, G.-H.; Dong, S.-H. Approximate symmetries in atomic nuclei from a large-scale shell-model perspective. Int. J. Mod. Phys. E 2015, 24, 1530005. [Google Scholar] [CrossRef]
- Launey, K.D.; Dytrych, T.; Draayer, J.P. Symmetry-guided large-scale shell-model theory. Prog. Part. Nucl. Phys. 2016, 89, 101. [Google Scholar] [CrossRef]
- Dytrych, T.; Launey, K.D.; Draayer, J.P.; Rowe, D.J.; Wood, J.L.; Rosensteel, G.; Bahri, C.; Langr, D.; Baker, R.B. Physics of Nuclei: Key Role of an Emergent Symmetry. Phys. Rev. Lett. 2020, 124, 042501. [Google Scholar] [CrossRef]
- Launey, K.D.; Dytrych, T.; Sargsyan, G.H.; Baker, R.B.; Draayer, J.P. Emergent symplectic symmetry in atomic nuclei. Eur. Phys. J. Spec. Top. 2020, 229, 2429. [Google Scholar] [CrossRef]
- Launey, K.D.; Marcenne, A.; Dytrych, T. Nuclear dynamics and reactions in the ab initio symmetry-adapted framework. Annu. Rev. Nucl. Part. Sci. 2021, 71, 253. [Google Scholar] [CrossRef]
- Kota, V.K.B. SU(3) Symmetry in Atomic Nuclei; Springer: Singapore, 2020. [Google Scholar]
- Bonatsos, D.; Martinou, A.; Assimakis, I.E.; Peroulis, S.K.; Sarantopoulou, S.; Minkov, N. Connecting the proxy-SU(3) symmetry to the shell model. Eur. Phys. J. Web Conf. 2021, 252, 02004. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Proxy-SU(3) symmetry in heavy deformed nuclei. Phys. Rev. C 2017, 95, 064325. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Analytic predictions for nuclear shapes, prolate dominance, and the prolate-oblate shape transition in the proxy-SU(3) model. Phys. Rev. C 2017, 95, 064326. [Google Scholar] [CrossRef]
- Bonatsos, D. Prolate over oblate dominance in deformed nuclei as a consequence of the SU(3) symmetry and the Pauli principle. Eur. Phys. J. A 2017, 53, 148. [Google Scholar] [CrossRef]
- de Shalit, A.; Goldhaber, M. Mixed configurations in nuclei. Phys. Rev. 1953, 92, 1211. [Google Scholar] [CrossRef]
- Talmi, I. Effective interactions and coupling schemes in nuclei. Rev. Mod. Phys. 1962, 34, 704. [Google Scholar] [CrossRef]
- Talmi, I. Generalized seniority and structure of semi-magic nuclei. Nucl. Phys. A 1971, 172, 1. [Google Scholar] [CrossRef]
- Talmi, I. Coupling schemes in nuclei. Riv. Nuovo Cim. 1973, 3, 85. [Google Scholar] [CrossRef]
- Talmi, I. Simple Models of Complex Nuclei; Harwood: Chur, Switzerland, 1993. [Google Scholar]
- Federman, P.; Pittel, S. Towards a unified microscopic description of nuclear deformation. Phys. Lett. B 1977, 69, 385. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S. Hartree-Fock-Bogolyubov study of deformation in the Zr-Mo region. Phys. Lett. B 1978, 77, 29. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S. Unified shell-model description of nuclear deformation. Phys. Rev. C 1979, 20, 820. [Google Scholar] [CrossRef]
- Casten, R.F. Possible Unified interpretation of heavy nuclei. Phys. Rev. Lett. 1985, 54, 1991. [Google Scholar] [CrossRef] [PubMed]
- Casten, R.F. NpNn systematics in heavy nuclei. Nucl. Phys. A 1985, 443, 1. [Google Scholar] [CrossRef]
- Casten, R.F.; Brenner, D.S.; Haustein, P.E. Valence p-n interactions and the development of collectivity in heavy nuclei. Phys. Rev. Lett. 1987, 58, 658. [Google Scholar] [CrossRef] [PubMed]
- Casten, R.F. Nuclear Structure from a Simple Perspective; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Zuker, A.P.; Retamosa, J.; Poves, A.; Caurier, E. Spherical shell model description of rotational motion. Phys. Rev. C 1995, 52, R1741. [Google Scholar] [CrossRef] [PubMed]
- Zuker, A.P.; Poves, A.; Nowacki, F.; Lenzi, S.M. Nilsson-SU(3) self-consistency in heavy n = Z nuclei. Phys. Rev. C 2015, 92, 024320. [Google Scholar] [CrossRef]
- Kaneko, K.; Shimizu, N.; Mizusaki, T.; Sun, Y. Quasi-SU(3) coupling of (1h11/2, 2f7/2) across the n = 82 shell gap: Enhanced E2 collectivity and shape evolution in Nd isotopes. Phys. Rev. C 2021, 103, L021301. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Brenner, D.S.; Casten, R.F.; Millman, E.A. proton–neutron interactions and the new atomic masses. Phys. Rev. Lett. 2005, 94, 092501, Erratum in Phys. Rev. Lett. 2005, 95, 119903. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Casten, R.F. Direct empirical correlation between proton–neutron interaction strengths and the growth of collectivity in nuclei. Phys. Rev. Lett. 2006, 96, 132501. [Google Scholar] [CrossRef]
- Brenner, D.S.; Cakirli, R.B.; Casten, R.F. Valence proton–neutron interactions throughout the mass surface. Phys. Rev. C 2006, 73, 034315. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Casten, R.F.; Winkler, R.; Blaum, K.; Kowalska, M. Enhanced sensitivity of nuclear binding energies to collective structure. Phys. Rev. Lett. 2009, 102, 082501. [Google Scholar] [CrossRef] [PubMed]
- Cakirli, R.B.; Blaum, K.; Casten, R.F. Indication of a mini-valence Wigner-like energy in heavy nuclei. Phys. Rev. C 2010, 82, 061304. [Google Scholar] [CrossRef]
- Bonatsos, D.; Karampagia, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K.; Susam, L.A. Emergent collectivity in nuclei and enhanced proton–neutron interactions. Phys. Rev. C 2013, 88, 054309. [Google Scholar] [CrossRef]
- Stoitsov, M.; Cakirli, R.B.; Casten, R.F.; Nazarewicz, W.; Satula, W. Empirical proton–neutron interactions and nuclear density functional theory: Global, regional, and local comparisons. Phys. Rev. Lett. 2007, 98, 132502. [Google Scholar] [CrossRef] [PubMed]
- Sieja, K. Single-particle and collective structures in neutron-rich Sr isotopes. Universe 2022, 8, 23. [Google Scholar] [CrossRef]
- Lederer, C.M.; Shirley, V.S. (Eds.) Table of Isotopes, 7th ed.; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Davies, K.T.R.; Krieger, S.J. Harmonic-oscillator transformation coefficients. Can. J. Phys. 1991, 69, 62. [Google Scholar] [CrossRef]
- Chasman, R.R.; Wahlborn, S. Transformation scheme for harmonic-oscillator wave functions. Nucl. Phys. A 1967, 90, 401. [Google Scholar] [CrossRef]
- Chacón, E.; de Llano, M. Transformation brackets between cartesian and angular momentum harmonic oscillator basis functions with and without spin–orbit coupling. Tables for the 2s-1d nuclear shell. Rev. Mex. Fís. 1963, 12, 57. [Google Scholar]
- Martinou, A.; Bonatsos, D.; Minkov, N.; Assimakis, I.E.; Peroulis, S.K.; Sarantopoulou, S.; Cseh, J. Proxy-SU(3) symmetry in the shell model basis. Eur. Phys. J. A 2020, 56, 239. [Google Scholar] [CrossRef]
- Edmonds, A.R. Angular Momentum in Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore, 1988. [Google Scholar]
- Sorlin, O.; Porquet, M.-G. Nuclear magic numbers: New features far from stability. Prog. Part. Nucl. Phys. 2008, 61, 602. [Google Scholar] [CrossRef]
- Bonatsos, D.; Sobhani, H.; Hassanabadi, H. Shell model structure of proxy-SU(3) pairs of orbitals. Eur. Phys. J. Plus 2020, 135, 710. [Google Scholar] [CrossRef]
- Castaños, O.; Draayer, J.P.; Leschber, Y. Shape variables and the shell model. Z. Phys. A 1988, 329, 33. [Google Scholar]
- Elliott, J.P.; Evans, J.A.; Isacker, P.V. Definition of the shape parameter γ in the Interacting-Boson Model. Phys. Rev. Lett. 1986, 57, 1124. [Google Scholar] [CrossRef] [PubMed]
- Draayer, J.P.; Park, S.C.; Castaños, O. Shell-model interpretation of the collective-model potential-energy surface. Phys. Rev. Lett. 1989, 62, 20. [Google Scholar] [CrossRef]
- Mayer, M.G. Nuclear configurations in the spin–orbit coupling model. II. Theoretical considerations. Phys. Rev. 1950, 78, 22. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Sarantopoulou, S.; Assimakis, I.E.; Peroulis, S.K.; Minkov, N. Why nuclear forces favor the highest weight irreducible representations of the fermionic SU(3) symmetry. Eur. Phys. J. A 2021, 57, 83. [Google Scholar] [CrossRef]
- Bonatsos, D.; Casten, R.F.; Martinou, A.; Assimakis, I.E.; Minkov, N.; Sarantopoulou, S.; Cakirli, R.B.; Blaum, K. A new scheme for heavy nuclei: Proxy-SU(3). Adv. Nucl. Phys. 2017, 25, 6. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Minkov, N.; Assimakis, I.E.; Sarantopoulou, S.; Peroulis, S. Highest weight SU(3) irreducible representations for nuclei with shape coexistence. arXiv 2018, arXiv:1810.11870. [Google Scholar]
- Guzmán, V.M.B.; Flores-Mendieta, R.; Hernández, J. Contributions of SU(3) higher-order interaction operators to rotational bands in the interacting boson model. Eur. Phys. J. A 2022, 58, 61. [Google Scholar] [CrossRef]
- Hamamoto, I.; Mottelson, B.R. Further examination of prolate-shape dominance in nuclear deformation. Phys. Rev. C 2009, 79, 034317. [Google Scholar] [CrossRef]
- Tajima, N.; Suzuki, N. Prolate dominance of nuclear shape caused by a strong interference between the effects of spin–orbit and l2 terms of the Nilsson potential. Phys. Rev. C 2001, 64, 037301. [Google Scholar] [CrossRef]
- Takahara, S.; Onishi, N.; Shimizu, Y.R.; Tajima, N. The role of spin–orbit potential in nuclear prolate-shape dominance. Phys. Lett. B 2011, 702, 429. [Google Scholar] [CrossRef]
- Takahara, S.; Tajima, N.; Shimizu, Y.R. Nuclear prolate-shape dominance with the Woods-Saxon potential. Phys. Rev. C 2012, 86, 064323. [Google Scholar] [CrossRef]
- Hamamoto, I.; Mottelson, B. Shape deformations in atomic nuclei. Scholarpedia 2012, 7, 10693. [Google Scholar]
- Sugawara, M. Prolate-shape dominance and dual-shell mechanism. Phys. Rev. C 2022, 106, 024301. [Google Scholar] [CrossRef]
- Draayer, J.P.; Leschber, Y.; Park, S.C.; Lopez, R. Representations of U(3) in U(N). Comput. Phys. Commun. 1989, 56, 279. [Google Scholar] [CrossRef]
- Langr, D.; Dytrych, T.; Draayer, J.P.; Launey, K.D.; Tvrdík, P. Efficient algorithm for representations of U(3) in U(N). Comput. Phys. Commun. 2019, 244, 442. [Google Scholar] [CrossRef]
- Alex, A.; Kalus, M.; Huckleberry, A.; von Delft, J. A numerical algorithm for the explicit calculation of SU(N) and SL(N,C) Clebsch–Gordan coefficients. J. Math. Phys. 2011, 52, 023507. [Google Scholar] [CrossRef]
- Assimakis, I.E. Algebraic Models of Nuclear Structure with SU(3) Symmetry. Master’s Thesis, National Technical University of Athens, Athens, Greece, 2015. [Google Scholar] [CrossRef]
- Kota, V.K.B. Simple formula for leading SU(3) irreducible representation for nucleons in an oscillator shell. arXiv 2018, arXiv:1812.01810. [Google Scholar]
- Sarantopoulou, S.; Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Proxy-SU(3) symmetry in heavy nuclei: Prolate dominance and prolate-oblate shape transition. Bulg. J. Phys. 2017, 44, 417. [Google Scholar]
- Vries, H.D.; Jager, C.W.D.; Vries, C.D. Nuclear charge-density-distribution parameters from elastic electron scattering. At. Data Nucl. Data Tables 1987, 36, 495. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Delaroche, J.-P.; Girod, M.; Libert, J.; Goutte, H.; Hilaire, S.; Péru, S.; Pillet, N.; Bertsch, G.F. Structure of even–even nuclei using a mapped collective Hamiltonian and the D1S Gogny interaction. Phys. Rev. C 2010, 81, 014303. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Raman, S.; Ring, P. Ground-state properties of even–even nuclei in the relatitistic mean-field theory. At. Data Nucl. Data Tables 1999, 71, 1. [Google Scholar] [CrossRef]
- Raman, S.; Nestor, C.W., Jr.; Tikkanen, P. Transition probability from the ground to the first-excited 2+ state of even–even nuclides. At. Data Nucl. Data Tables 2001, 78, 1. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Peroulis, S.K.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Proxy-SU(3): A symmetry for heavy nuclei. Bulg. J. Phys. 2017, 44, 385. [Google Scholar]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Parameter-independent predictions for shape variables of heavy deformed nuclei in the proxy-SU(3) model. arXiv 2017, arXiv:1706.05832. [Google Scholar]
- Martinou, A.; Peroulis, S.; Bonatsos, D.; Assimakis, I.E.; Sarantopoulou, S.; Minkov, N.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Parameter-independent predictions for nuclear shapes and B(E2) transition rates in the proxy-SU(3) model. arXiv 2017, arXiv:1712.04134. [Google Scholar] [CrossRef]
- Awwad, N.J.A.; Abusara, H.; Ahmad, S. Ground state properties of Zn, Ge, and Se isotopic chains in covariant density functional theory. Phys. Rev. C 2020, 101, 064322. [Google Scholar] [CrossRef]
- Alstaty, M.I.; Abusara, H. Ground state deformation comparison between covariant density functional theory and proxy-SU(3) model in transitional nuclei. Nucl. Phys. A 2022, 1027, 122504. [Google Scholar] [CrossRef]
- Elsharkawy, H.N.; Kader, M.M.A.; Basha, A.M.; Lotfy, A. Ground state properties of Polonium isotopes using covariant density functional theory. Phys. Scr. 2022, 97, 065302. [Google Scholar] [CrossRef]
- Canavan, R.L.; Rudigier, M.; Regan, P.H.; Lebois, M.; Wilson, J.N.; Jovancevic, N.; Söderström, P.-A.; Collins, S.M.; Thisse, D.; Benito, J.; et al. Half-life measurements in 164,166Dy using γ-γ fast-timing spectroscopy with the ν-Ball spectrometer. Phys. Rev. C 2020, 101, 024313. [Google Scholar] [CrossRef]
- Knafla, L.; Häfner, G.; Jolie, J.; Régis, J.-M.; Karayonchev, V.; Blazhev, A.; Esmaylzadeh, A.; Fransen, C.; Goldkuhle, A.; Herb, S.; et al. Lifetime measurements of 162Er: Evolution of collectivity in the rare-earth region. Phys. Rev. C 2020, 102, 044310. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Parameter free predictions within the proxy-SU(3) model. Bulg. J. Phys. 2017, 44, 407. [Google Scholar]
- Feng, D.H.; Gilmore, R.; Deans, S.R. Phase transitions and the geometric properties of the interacting boson model. Phys. Rev. C 1981, 23, 1254. [Google Scholar] [CrossRef]
- Iachello, F. Dynamic symmetries at the critical point. Phys. Rev. Lett. 2000, 85, 3580. [Google Scholar] [CrossRef]
- Casten, R.F.; Zamfir, N.V. Evidence for a possible E(5) symmetry in 134Ba. Phys. Rev. Lett. 2000, 85, 3584. [Google Scholar] [CrossRef]
- Iachello, F. Analytic description of critical point nuclei in a spherical-axially deformed shape phase transition. Phys. Rev. Lett. 2001, 87, 052502. [Google Scholar] [CrossRef]
- Casten, R.F.; Zamfir, N.V. Empirical realization of a critical point description in atomic nuclei. Phys. Rev. Lett. 2001, 87, 052503. [Google Scholar] [CrossRef]
- Iachello, F. Quantum phase transitions in mesoscopic systems. Int. J. Mod. Phys. B 2006, 20, 2687. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D. Special solutions of the Bohr hamiltonian related to shape phase transitions in nuclei. Rom. Rep. Phys. 2007, 59, 273. [Google Scholar]
- Casten, R.F.; McCutchan, E.A. Quantum phase transitions and structural evolution in nuclei. J. Phys. G Nucl. Part. Phys. 2007, 34, R285. [Google Scholar] [CrossRef]
- Cejnar, P.; Jolie, J.; Casten, R.F. Quantum phase transitions in the shapes of atomic nuclei. Rev. Mod. Phys. 2010, 82, 2155. [Google Scholar] [CrossRef]
- Casten, R.F.; Namenson, A.I.; Davidson, W.F.; Warner, D.D.; Borner, H.G. Low-lying levels in 194Os and the prolate—Oblate phase transition. Phys. Lett. B 1978, 76, 280. [Google Scholar] [CrossRef]
- Alkhomashi, N.; Regan, P.H.; Podolyak, Z.; Pietri, S.; Garnsworthy, A.B.; Steer, S.J.; Benlliure, J.; Caserejos, E.; Casten, R.F.; Gerl, J.; et al. β--delayed spectroscopy of neutron-rich tantalum nuclei: Shape evolution in neutron-rich tungsten isotopes. Phys. Rev. C 2009, 80, 064308. [Google Scholar] [CrossRef]
- Wheldon, C.; Narro, J.G.; Pearson, C.J.; Regan, P.H.; Podolyák, Z.; Warner, D.D.; Fallon, P.; Macchiavelli, A.O.; Cromaz, M. Yrast states in 194Os: The prolate-oblate transition region. Phys. Rev. C 2000, 63, 011304. [Google Scholar] [CrossRef]
- Podolyák, Z.; Steer, S.J.; Pietri, S.; Xu, F.R.; Liu, H.L.; Regan, P.H.; Rudolph, D.; Garnsworthy, A.B.; Hoischen, R.; Gorska, M.; et al. Weakly deformed oblate structures in . Phys. Rev. C 2009, 79, 031305. [Google Scholar] [CrossRef]
- Jolie, J.; Linnemann, A. Prolate-oblate phase transition in the Hf-Hg mass region. Phys. Rev. C 2003, 68, 031301. [Google Scholar] [CrossRef]
- Kumar, K. Prolate-oblate difference and its effect on energy levels and quadrupole moments. Phys. Rev. C 1970, 1, 369. [Google Scholar] [CrossRef]
- Kumar, K. Nuclear shapes, energy gaps and phase transitions. Phys. Scr. 1972, 6, 270. [Google Scholar] [CrossRef]
- Sarriguren, P.; Rodríguez-Guzmán, R.; Robledo, L.M. Shape transitions in neutron-rich Yb, Hf, W, Os, and Pt isotopes within a Skyrme Hartree-Fock + BCS approach. Phys. Rev. C 2008, 77, 064322. [Google Scholar] [CrossRef]
- Robledo, L.M.; Rodríguez-Guzmán, R.; Sarriguren, P. Role of triaxiality in the ground-state shape of neutron-rich Yb, Hf, W, Os and Pt isotopes. J. Phys. G Nucl. Part. Phys. 2009, 36, 115104. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Rodríguez-Guzmán, R.; Robledo, L.M.; Sarriguren, P.; Regan, P.H.; Stevenson, P.D.; Podolyák, Z. Spectroscopic calculations of the low-lying structure in exotic Os and W isotopes. Phys. Rev. C 2011, 83, 054303. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Rodríguez-Guzmán, R.; Robledo, L.M.; Sarriguren, P. Collective structural evolution in neutron-rich Yb, Hf, W, Os, and Pt isotopes. Phys. Rev. C 2011, 84, 054316. [Google Scholar] [CrossRef]
- Sun, Y.; Walker, P.M.; Xu, F.-R.; Liu, Y.-X. Rotation-driven prolate-to-oblate shape phase transition in 190W: A projected shell model study. Phys. Lett. B 2008, 659, 165. [Google Scholar] [CrossRef]
- Jolie, J.; Casten, R.F.; von Brentano, P.; Werner, V. Quantum phase transition for γ-soft nuclei. Phys. Rev. Lett. 2001, 87, 162501. [Google Scholar] [CrossRef]
- Jolie, J.; Cejnar, P.; Casten, R.F.; Heinze, S.; Linnemann, A.; Werner, V. Triple point of nuclear deformations. Phys. Rev. Lett. 2002, 89, 182502. [Google Scholar] [CrossRef]
- Thiamova, G.; Cejnar, P. Prolate–oblate shape-phase transition in the O(6) description of nuclear rotation. Nucl. Phys. A 2006, 765, 97. [Google Scholar] [CrossRef]
- Bettermann, L.; Werner, V.; Williams, E.; Casperson, R.J. New signature of a first order phase transition at the O(6) limit of the IBM. Phys. Rev. C 2010, 81, 021303. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z. The robust O(6) dynamics in the prolate–oblate shape phase transition. J. Phys. G Nucl. Part. Phys. 2013, 40, 105107. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, F.; Liu, Y.-X.; Luo, Y.-A.; Draayer, J.P. Analytically solvable prolate-oblate shape phase transitional description within the SU(3) limit of the interacting boson model. Phys. Rev. C 2012, 85, 064312. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A. Z(5): Critical point symmetry for the prolate to oblate nuclear shape phase transition. Phys. Lett. B 2004, 588, 172. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A.; Yigitoglu, I. γ-rigid solution of the Bohr Hamiltonian for γ = 30o compared to the E(5) critical point symmetry. Phys. Lett. B 2005, 621, 102. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Fortunato, L.; Vitturi, A. Is 198Hg a soft triaxial nucleus with γ = 30o? Eur. Phys. J. Plus 2019, 134, 570. [Google Scholar] [CrossRef]
- Mutsher, S.M.; Sharrad, F.I.; Salman, E.A. Positive parity low-spin states of even–odd 129–133Ba isotopes. Nucl. Phys. A 2022, 1017, 122342. [Google Scholar] [CrossRef]
- Bindra, A.; Mittal, H.M. The magnification of structural anomalies with Grodzins systematic in the framework of Asymmetric Rotor Model. Nucl. Phys. A 2018, 975, 48. [Google Scholar] [CrossRef]
- Clemenger, K. Ellipsoidal shell structure in free-electron metal clusters. Phys. Rev. B 1985, 32, 1359. [Google Scholar] [CrossRef]
- de Heer, W.A. The physics of simple metal clusters: Experimental aspects and simple models. Rev. Mod. Phys. 1993, 65, 611. [Google Scholar] [CrossRef]
- Brack, M. The physics of simple metal clusters: Self-consistent jellium model and semiclassical approaches. Rev. Mod. Phys. 1993, 65, 677. [Google Scholar] [CrossRef]
- Nesterenko, V.O. Metal clusters as a new application field of nuclear-physics ideas and methods. Fiz. Elem. Chastits At. Yadra 1992, 23, 1665, Erratum in Sov. J. Part. Nucl. 1992, 23, 726. [Google Scholar]
- de Heer, W.A.; Knight, W.D.; Chou, M.Y.; Cohen, M.L. Electronic shell structure and metal clusters. Solid State Phys. 1987, 40, 93. [Google Scholar]
- Greiner, W. Summary of the conference. Z. Phys. A Hadr. Nucl. 1994, 349, 315. [Google Scholar] [CrossRef]
- Martin, T.P.; Bergmann, T.; Göhlich, H.; Lange, T. Observation of electronic shells and shells of atoms in large Na clusters. Chem. Phys. Lett. 1990, 172, 209. [Google Scholar] [CrossRef]
- Martin, T.P.; Bergmann, T.; Göhlich, H.; Lange, T. Electronic shells and shells of atoms in metallic clusters. Z. Phys. D At. Mol. Clust. 1991, 19, 25. [Google Scholar] [CrossRef]
- Bjørnholm, S.; Borggreen, J.; Echt, O.; Hansen, K.; Pedersen, J.; Rasmussen, H.D. Mean-field quantization of several hundred electrons in sodium metal clusters. Phys. Rev. Lett. 1990, 65, 1627. [Google Scholar] [CrossRef]
- Bjørnholm, S.; Borggreen, J.; Echt, O.; Hansen, K.; Pedersen, J.; Rasmussen, H.D. The influence of shells, electron thermodynamics, and evaporation on the abundance spectra of large sodium metal clusters. Z. Phys. D At. Mol. Clust. 1991, 19, 47. [Google Scholar] [CrossRef]
- Knight, W.D.; Clemenger, K.; de Heer, W.A.; Saunders, W.A.; Chou, M.Y.; Cohen, M.L. Electronic shell structure and abundances of sodium clusters. Phys. Rev. Lett. 1984, 52, 2141. [Google Scholar] [CrossRef]
- Pedersen, J.; Bjørnholm, S.; Borggreen, J.; Hansen, K.; Martin, T.P.; Rasmussen, H.D. Observation of quantum supershells in clusters of sodium atoms. Nature 1991, 353, 733. [Google Scholar] [CrossRef]
- Bréchignac, C.; Cahuzac, P.; de Frutos, M.; Roux, J.-P.; Bowen, K. Observation of electronic shells in large Lithium clusters. In Physics and Chemistry of Finite Systems: From Clusters to Crystals; NATO Science Series C: Mathematical and Physical Sciences ASIC 374; Jena, P., Khanna, S.N., Rao, B.K.N., Eds.; Kluwer: Dordrecht, The Netherlands, 1992; Volume 1, p. 369. [Google Scholar]
- Bréchignac, C.; Cahuzac, P.; Carlier, F.; de Frutos, M.; Roux, J.P. Temperature effects in the electronic shells and supershells of lithium clusters. Phys. Rev. B 1993, 47, 2271. [Google Scholar] [CrossRef]
- Borggreen, J.; Chowdhury, P.; Kebaïli, N.; Lundsberg-Nielsen, L.; Lützenkirchen, K.; Nielsen, M.B.; Pedersen, J.; Rasmussen, H.D. Plasma excitations in charged sodium clusters. Phys. Rev. B 1993, 48, 17507. [Google Scholar] [CrossRef]
- Pedersen, J.; Borggreen, J.; Chowdhury, P.; Kebaïli, N.; Lundsberg-Nielsen, L.; Lützenkirchen, K.; Nielsen, M.B.; Rasmussen, H.D. Plasmon profiles and shapes of sodium cluster ions. Z. Phys. D At. Mol. Clust. 1993, 26, 281. [Google Scholar] [CrossRef]
- Pedersen, J.; Borggreen, J.; Chowdhury, P.; Kebaïli, N.; Lundsberg-Nielsen, L.; Lützenkirchen, K.; Nielsen, M.B.; Rasmussen, H.D. Optical response and shapes of charged sodium clusters; an analogue of the nuclear giant dipole resonance. In Atomic and Nuclear Clusters; Anagnostatos, G.S., von Oertzen, W., Eds.; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Haberland, H. Metal clusters and nuclei: Some similarities and differences. Nucl. Phys. A 1999, 649, 415. [Google Scholar] [CrossRef]
- Schmidt, M.; Haberland, H. Optical spectra and their moments for sodium clusters, , with 3 ≤ n ≤ 64. Eur. Phys. J. D 1999, 6, 109. [Google Scholar]
- Bonatsos, D.; Martinou, A.; Sarantopoulou, S.; Assimakis, I.E.; Peroulis, S.; Minkov, N. Parameter-free predictions for the collective deformation variables β and γ within the pseudo-SU(3) scheme. Eur. Phys. J. ST 2020, 229, 2367. [Google Scholar] [CrossRef]
- Cseh, J. Shell-like quarteting in heavy nuclei: Algebraic approaches based on the pseudo- and proxy-SU(3) schemes. Phys. Rev. C 2020, 101, 054306. [Google Scholar] [CrossRef]
- Hess, P.O.; Chávez-Nu nez, L.J. A semimicroscopic algebraic cluster model for heavy nuclei. Eur. Phys. J. A 2021, 57, 146. [Google Scholar] [CrossRef]
- Berriel-Aguayo, J.R.M.; Hess, P.O. Approximate projection method for the construction of multi-α-cluster spaces. Phys. Rev. C 2021, 104, 044307. [Google Scholar] [CrossRef]
- Cseh, J. Algebraic models for shell-like quarteting of nucleons. Phys. Lett. B 2015, 743, 213. [Google Scholar] [CrossRef]
- Cseh, J. Semimicroscopic algebraic description of nuclear cluster states. Vibron model coupled to the SU(3) shell model. Phys. Lett. B 1992, 281, 173. [Google Scholar] [CrossRef]
- Cseh, J.; Lévai, G. Semimicroscopic algebraic cluster model of light nuclei. I. Two-cluster-systems with spin-isospin-free interactions. Ann. Phys. 1994, 230, 165. [Google Scholar] [CrossRef]
- Lohr-Robles, D.S.; López-Moreno, E.; Hess, P.O. Quantum phase transitions within a nuclear cluster model and an effective model of QCD. Nucl. Phys. A 2021, 1016, 122335. [Google Scholar] [CrossRef]
- Iachello, F.; Levine, R.D. Algebraic approach to molecular rotation-vibration spectra. I. Diatomic molecules. J. Chem. Phys. 1982, 77, 3046. [Google Scholar] [CrossRef]
- van Roosmalen, O.S.; Iachello, F.; Levine, R.D.; Dieperink, A.E.L. Algebraic approach to molecular rotation-vibration spectra. II. Triatomic molecules. J. Chem. Phys. 1983, 79, 2515. [Google Scholar] [CrossRef]
- Daley, H.J.; Iachello, F. Nuclear vibron model. I. The SU(3) limit. Ann. Phys. 1986, 167, 73. [Google Scholar] [CrossRef]
- Morinaga, H. Interpretation of some of the excited states of 4n self-conjugate nuclei. Phys. Rev. 1956, 101, 254. [Google Scholar] [CrossRef]
- Heyde, K.; Isacker, P.V.; Waroquier, M.; Wood, J.L.; Meyer, R.A. Coexistence in odd-mass nuclei. Phys. Rep. 1983, 102, 291. [Google Scholar] [CrossRef]
- Wood, J.L.; Heyde, K.; Nazarewicz, W.; Huyse, M.; Duppen, P.V. Coexistence in even-mass nuclei. Phys. Rep. 1992, 215, 101. [Google Scholar] [CrossRef]
- Heyde, K.; Wood, J.L. Shape coexistence in atomic nuclei. Rev. Mod. Phys. 2011, 83, 1467. [Google Scholar] [CrossRef]
- Garrett, P.E.; Zielińska, M.; Clément, E. An experimental view on shape coexistence in nuclei. Prog. Part. Nucl. Phys. 2022, 124, 103931. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Mertzimekis, T.J.; Karakatsanis, K.; Assimakis, I.E.; Peroulis, S.K.; Sarantopoulou, S.; Minkov, N. The islands of shape coexistence within the Elliott and the proxy-SU(3) models. Eur. Phys. J. A 2021, 57, 84. [Google Scholar] [CrossRef]
- Otsuka, T.; Gade, A.; Sorlin, O.; Suzuki, T.; Utsuno, Y. Evolution of shell structure in exotic nuclei. Rev. Mod. Phys. 2020, 92, 015002. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D. Magic numbers of cylindrical symmetry. In Nuclear Structure Physics; Shukla, A., Patra, S.K., Eds.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Martinou, A.; Bonatsos, D.; Minkov, N.; Mertzimekis, T.; Assimakis, I.E.; Peroulis, S.; Sarantopoulou, S. Nucleon numbers for nuclei with shape coexistence. HNPS Adv. Nucl. Phys. 2018, 26, 96. [Google Scholar] [CrossRef]
- Martinou, A. A mechanism for shape coexistence. EPJ Web Conf. 2021, 252, 02005. [Google Scholar] [CrossRef]
- Ring, P. Relativistic mean field theory in finite nuclei. Prog. Part. Nucl. Phys. 1996, 37, 193. [Google Scholar] [CrossRef]
- Bender, M.; Heenen, P.-H.; Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.V.; Lalazissis, G.A.; Ring, P. Relativistic Hartree–Bogoliubov theory: Static and dynamic aspects of exotic nuclear structure. Phys. Rep. 2005, 409, 101. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zhou, S.G.; Zhang, S.Q.; Long, W.H.; Geng, L.S. Relativistic continuum Hartree Bogoliubov theory for ground-state properties of exotic nuclei. Prog. Part. Nucl. Phys. 2006, 57, 470. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Mean-field and beyond. Prog. Part. Nucl. Phys. 2011, 66, 519. [Google Scholar] [CrossRef]
- Meng, J.; Zhou, S.G. Halos in medium-heavy and heavy nuclei with covariant density functional theory in continuum. J. Phys. G Nucl. Part. Phys. 2015, 42, 093101. [Google Scholar] [CrossRef]
- Liang, H.; Meng, J.; Zhou, S.-G. Hidden pseudospin and spin symmetries and their origins in atomic nuclei. Phys. Rep. 2015, 570, 1. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Nikšić, T.; Paar, N.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Nikšić, T.; Paar, N.; Vretenar, D.; Ring, P. DIRHB—A relativistic self-consistent mean-field framework for atomic nuclei. Comp. Phys. Commun. 2014, 185, 1808. [Google Scholar] [CrossRef]
- Bonatsos, D.; Karakatsanis, K.E.; Martinou, A.; Mertzimekis, T.J.; Minkov, N. Microscopic origin of shape coexistence in the n = 90, Z = 64 region. Phys. Lett. B 2022, 829, 137099. [Google Scholar] [CrossRef]
- Bonatsos, D.; Karakatsanis, K.E.; Martinou, A.; Mertzimekis, T.J.; Minkov, N. Islands of shape coexistence from single-particle spectra in covariant density functional theory. Phys. Rev. C 2022, 106, 044323. [Google Scholar] [CrossRef]
- Sarma, S.; Devi, R.; Khosa, S.K. Microscopic study of evolution of shape change across even–even mass chain of tellurium isotopes using relativistic Hartree-Bogoliubov model. Nucl. Phys. A 2019, 988, 9. [Google Scholar] [CrossRef]
- Kumar, P.; Dhiman, S.K. Microscopic study of shape evolution and ground state properties in even–even Cd isotopes using covariant density functional theory. Nucl. Phys. A 2020, 1001, 121935. [Google Scholar] [CrossRef]
- Thakur, S.; Kumar, P.; Thakur, V.; Kumar, V.; Dhiman, S.K. Nuclear shape evolution in palladium isotopes. Acta Phys. Pol. B 2021, 52, 1433. [Google Scholar] [CrossRef]
- Thakur, S.; Kumar, P.; Thakur, V.; Kumar, V.; Dhiman, S.K. Shape transitions and shell structure study in zirconium, molybdenum and ruthenium. Nucl. Phys. A 2021, 1014, 122254. [Google Scholar] [CrossRef]
- Yang, X.Q.; Wang, L.J.; Xiang, J.; Wu, X.Y.; Li, Z.P. Microscopic analysis of prolate-oblate shape phase transition and shape coexistence in the Er-Pt region. Phys. Rev. C 2021, 103, 054321. [Google Scholar] [CrossRef]
- Mennana, A.A.B.; Benjedi, R.; Budaca, R.; Buganu, P.; Bassen, Y.E.; Lahbas, A.; Oulne, M. Mixing of the coexisting shapes in the ground states of 74Ge and 74Kr. Phys. Scr. 2021, 96, 125306. [Google Scholar] [CrossRef]
- Mennana, A.A.B.; Benjedi, R.; Budaca, R.; Buganu, P.; Bassen, Y.E.; Lahbas, A.; Oulne, M. Shape and structure for the low-lying states of the 80Ge nucleus. Phys. Rev. C 2022, 105, 034347. [Google Scholar] [CrossRef]
- Hosseinnezhad, A.; Majarshin, A.J.; Luo, Y.A.; Ahmadian, D.; Sabri, H. Deformation in 92-128Pd isotopes. Nucl. Phys. A 2022, 1028, 122523. [Google Scholar] [CrossRef]
- Garrett, P.E.; Rodríguez, T.R.; Varela, A.D.; Green, K.L.; Bangay, J.; Finlay, A.; Austin, R.A.E.; Ball, G.C.; Bandyopadhyay, D.S.; Bildstein, V.; et al. Multiple Shape Coexistence in 110,112Cd. Phys. Rev. Lett. 2019, 123, 142502. [Google Scholar] [CrossRef] [PubMed]
- Garrett, P.E.; Rodríguez, T.R.; Varela, A.D.; Green, K.L.; Bangay, J.; Finlay, A.; Austin, R.A.E.; Ball, G.C.; Bandyopadhyay, D.S.; Bildstein, V.; et al. Shape coexistence and multiparticle-multihole structures in 110,112Cd. Phys. Rev. C 2020, 101, 044302. [Google Scholar] [CrossRef]
- Pritychenko, B.; Birch, M.; Singh, B.; Horoi, M. Tables of E2 transition probabilities from the first 2+ states in even–even nuclei. At. Data Nucl. Data Tables 2016, 107, 1, Erratum At. Data Nucl. Data Tables 2017, 114, 371. [Google Scholar] [CrossRef]
- Draayer, J.P.; Akiyama, Y. Wigner and Racah coefficients for SU3. J. Math. Phys. 1973, 14, 1904. [Google Scholar] [CrossRef]
- Akiyama, Y.; Draayer, J.P. A user’s guide to fortran programs for Wigner and Racah coefficients of SU3. Comput. Phys. Commun. 1973, 5, 405. [Google Scholar] [CrossRef]
- Millener, D.J. A note on recoupling coefficients for SU(3). J. Math. Phys. 1978, 19, 1513. [Google Scholar] [CrossRef]
- Rowe, D.J.; Bahri, C. Clebsch–Gordan coefficients of SU(3) in SU(2) and SO(3) bases. J. Math. Phys. 2000, 41, 6544. [Google Scholar] [CrossRef]
- Bahri, C.; Rowe, D.J.; Draayer, J.P. Programs for generating Clebsch–Gordan coefficients of SU(3) in SU(2) and SO(3) bases. Comput. Phys. Commun. 2004, 159, 121. [Google Scholar] [CrossRef]
- Dytrych, T.; Langr, D.; Draayer, J.P.; Launey, K.D.; Gazda, D. SU3lib: A C++ library for accurate computation of Wigner and Racah coefficients of SU(3). Comput. Phys. Commun. 2021, 269, 108137. [Google Scholar] [CrossRef]
- Hughes, J.W.B. SU(3) in an O(3) basis I. Properties of shift operators. J. Phys. A Math. Nucl. Gen. 1973, 6, 48. [Google Scholar] [CrossRef]
- Hughes, J.W.B. SU(3) in an O(3) basis II. Solution of the state labelling problem. J. Phys. A Math. Nucl. Gen. 1973, 6, 281. [Google Scholar] [CrossRef]
- Judd, B.R.; Miller, W., Jr.; Patera, J.; Winternitz, P. Complete sets of commuting operators and O(3) scalars in the enveloping algebra of SU(3). J. Math. Phys. 1974, 15, 1787. [Google Scholar] [CrossRef]
- Meyer, H.D.; Berghe, G.V.; der Jeugt, J.V. On the spectra of SO(3) scalars in the enveloping algebra of SU(3). J. Math. Phys. 1985, 26, 3109. [Google Scholar] [CrossRef]
- Hosseinnezhad, A.; Sabri, H.; Seidi, M. The correlation of quadrupole transition rates of deformed nuclei by non-parametric approach. Nucl. Phys. A 2022, 1022, 122431. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Martinou, A.; Sarantopoulou, S.; Peroulis, S.K.; Minkov, N. Energy differences of ground state and γ1 bands as a hallmark of collective behavior. Nucl. Phys. A 2021, 1009, 122158. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Martinou, A.; Peroulis, S.K.; Sarantopoulou, S.; Minkov, N. Proxy-SU(3) symmetry for heavy deformed nuclei: Nuclear spectra. Bulg. J. Phys. 2019, 46, 325. [Google Scholar]
- Bonatsos, D.; Assimakis, I.E.; Martinou, A.; Peroulis, S.; Sarantopoulou, S.; Minkov, N. Breaking SU(3) spectral degeneracies in heavy deformed nuclei. arXiv 2020, arXiv:2008.13256. [Google Scholar]
- Jolos, R.V.; Kolganova, E.A. Derivation of the Grodzins relation in collective nuclear model. Phys. Lett. B 2021, 820, 136581. [Google Scholar] [CrossRef]
- Shirokova, N.Y.; Sushkov, A.V.; Malov, L.A.; Kolganova, E.A.; Jolos, R.V. Prediction of the excitation energies of the states for superheavy nuclei based on the microscopically derived Grodzins relation. Phys. Rev. C 2022, 105, 024309. [Google Scholar] [CrossRef]
- Grodzins, L. The uniform behaviour of electric quadrupole transition probabilities from first 2+ states in even–even nuclei. Phys. Lett. 1962, 2, 88. [Google Scholar] [CrossRef]
- Wang, M.; Huang, W.J.; Kondev, F.G.; Audi, G.; Naimi, S. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Fossion, R.; Coster, C.D.; García-Ramos, J.E.; Werner, T.; Heyde, K. Nuclear binding energies: Global collective structure and local shell-model correlations. Nucl. Phys. A 2002, 697, 703. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.J.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM(2012). At. Data Nucl. Data Tables 2016, 109–110, 1. [Google Scholar] [CrossRef]
- Sarantopoulou, S.; Martinou, A.; Bonatsos, D. Two-neutron separation energies within the proxy-SU(3) model. Bulg. J. Phys. 2019, 46, 455. [Google Scholar]
- Martinou, A.; Sarantopoulou, S.; Karakatsanis, K.E.; Bonatsos, D. Highest weight irreducible representations favored by nuclear forces within SU(3)-symmetric fermionic systems. Eur. Phys. J. Web Conf. 2021, 252, 02006. [Google Scholar] [CrossRef]
- Couture, A.; Casten, R.F.; Cakirli, R.B. Simple, empirical approach to predict neutron capture cross sections from nuclear masses. Phys. Rev. C 2017, 96, 061601. [Google Scholar] [CrossRef]
- Couture, A.; Casten, R.F.; Cakirli, R.B. Significantly improved estimates of neutron capture cross sections relevant to the r process. Phys. Rev. C 2021, 104, 054608. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).