New Hermite–Hadamard Integral Inequalities for Geometrically Convex Functions via Generalized Weighted Fractional Operator

Abstract

The main purpose of this research is to concentrate on the development of new definitions for the weighted geometric fractional integrals of the left-hand side and right-hand side of the function ℵ with regard to an increasing function used as an integral kernel. Moreover, the newly developed class of left-hand side and right-hand side weighted geometric fractional integrals of a function ℵ, by applying an additional increasing function, identifies a variety of novel classes as special cases. This is a development of the previously established fractional integrals by making use of the class of geometrically convex functions. Geometrically convex functions in weighted fractional integrals of a function ℵ in the form of another rising function yield the Hermite–Hadamard inequality type. We also establish a novel midpoint identity and the associated inequalities for a class of weighted fractional integral functions known as geometrically convex with respect to an increasing function and symmetric with respect to the geometric mean of the endpoints of the interval. In order to demonstrate the validity of our research, we present examples. Moreover, fractional inequalities and their solutions are applied in many symmetrical domains.

1. Introduction and Preliminaries

The role of simple mathematical inequalities has been rediscovered over the last several decades as a result of their application to various branches of mathematics and applied research. In reality, the evolution of mathematical inequalities is extremely closely tied to the advancements in the theory of convex function. As is well known, the origins of the theory of convex functions may be traced back to the writings of several prominent mathematicians, including Jensen, Hardy, and Hadamard. In recent decades, researchers have been engaged in stimulating arguments over the convex function.

For simplicity, let us define the real function ℵ on a non-empty interval I of the real line $\mathbb{R}.$ If the inequality holds, then the function ℵ is said to be convex on I:

$$\aleph (\tau {\vartheta }_1+(1-\tau ){\vartheta }_2)\le \tau \aleph \left({\vartheta }_1\right)+(1-\tau )\aleph \left({\vartheta }_2\right),$$

(1)

holds for all ${\vartheta }_1,{\vartheta }_2\in I$ and $\tau \in [0,1]$.

On the subject of convex functions, the Hermite–Hadamard integral inequality (also known as the Hadamard-type integral inequality) is perhaps one of the most celebrated conclusions ever presented.

The following inequality is well known in the literature as the Hermite–Hadamard inequality.

Theorem 1.

Let $\aleph :I\subseteq \mathbb{R}\to \mathbb{R}$ be a convex function defined on the interval I of real numbers and ${\vartheta }_1,{\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2.$ The following double inequality holds:

$$\aleph \left(\frac{{\vartheta }_1+{\vartheta }_2}{2}\right)\le \frac{1}{{\vartheta }_2-{\vartheta }_1}{\int }_{{\vartheta }_1}^{{\vartheta }_2}\aleph \left(x\right)dx\le \frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}.$$

(2)

The theory of convex sets and convex functions has received a lot of attention in recent years, and these concepts have been refined and extended in a range of fields. Thus, a wide range of Hermite–Hadamard-type inequalities and their applications have been discovered by a wide range of researchers across a wide range of fields, including mathematics, physics, biology, and chemistry. For important details about how the Hermite–Hadamard uniqueness theorem and basic convex function definitions have been improved, extended, and used, please see [1,2,3,4,5] and references therein.

Fractional calculus originated with a letter from L’Hospital to Leibniz inquiring about the notation that he was employing for the nth derivative of a linear function $\aleph \left(\tau \right)=\tau$, $\frac{D^n\tau }{D^{\tau }n}$. L’Hospital posed the question of what would happen if $n=\frac{1}{2}$. Leibniz said, “A seeming paradox from which practical ramifications will be deduced one day.” Mathematicians are increasingly turning to fractional calculus as a strong tool. According to Sarikaya and colleagues [6], the definitions of Riemannn–Liouville integrals were used to produce a novel version of the Hermite–Hadamard inequality. This finding piqued the interest of numerous researchers, who began investigating the subject further. For further information, as well as recent results and newly discovered properties pertaining to this operator, please see [7,8,9,10,11,12,13,14,15,16].

Definition 1

([17]). A function $\aleph :I\subseteq (0,\infty )\to \mathbb{R}$ is said to be geometrically convex (geometric arithmetically convex) if

$$\aleph \left({\vartheta }_1^{\tau }{\vartheta }_2^{1-\tau }\right)\le \tau \aleph \left({\vartheta }_1\right)+(1-\tau )\aleph \left({\vartheta }_2\right),$$

(3)

for all ${\vartheta }_1,{\vartheta }_2\in I$ and $\tau \in [0,1].$

Theorem 2.

A function $\aleph :I\subseteq (0,\infty )\to \mathbb{R}$ is geometrically convex on I and ${\vartheta }_1,{\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2.$ If $\aleph \in L[{\vartheta }_1,{\vartheta }_2],$ then

$$\begin{array}{c}\hfill \aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\le \frac{1}{ln{\vartheta }_2-ln{\vartheta }_1}{\int }_{{\vartheta }_1}^{{\vartheta }_2}\frac{\aleph \left(\tau \right)}{\tau }d\tau \le \frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}.\end{array}$$

(4)

In [18], the authors introduced the notion of geometrically symmetric functions as follows.

Definition 2.

A function $\varpi :[{\vartheta }_1,{\vartheta }_2]\to \mathbb{R}$, $[{\vartheta }_1,{\vartheta }_2]\subseteq {\mathbb{R}}_{+}$, is said to be geometrically symmetric with respect to $\sqrt{{\vartheta }_1{\vartheta }_2},$ if

$$\varpi \left(\frac{{\vartheta }_1{\vartheta }_2}{\tau }\right)=\varpi \left(\tau \right),\tau \in [{\vartheta }_1,{\vartheta }_2].$$

(5)

The authors in [18] also proved the following Fejér-type integral inequalities, which provide a weighted generalization of (4).

Theorem 3.

A function $\aleph :I\subseteq (0,\infty )\to \mathbb{R}$ is geometrically convex on I and ${\vartheta }_1,{\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2.$ If $\varpi :[{\vartheta }_1,{\vartheta }_2]\to (0,\infty )$ is continuous, positive, and geometrically symmetric to $\sqrt{{\vartheta }_1{\vartheta }_2}$, then

$$\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right){\int }_{{\vartheta }_1}^{{\vartheta }_2}\frac{\varpi \left(\tau \right)}{\tau }d\tau \le {\int }_{{\vartheta }_1}^{{\vartheta }_2}\frac{\aleph \left(\tau \right)\varpi \left(\tau \right)}{\tau }d\tau \le \frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}{\int }_{{\vartheta }_1}^{{\vartheta }_2}\frac{\varpi \left(\tau \right)}{\tau }d\tau .$$

(6)

In [19], İşcan, İ. proved that Hermite–Hadamard inequalities can be represented for geometrically convex functions in fractional integral form as follows:

Theorem 4.

A function $\aleph :I\subseteq (0,\infty )\to \mathbb{R}$ is geometrically convex on I and ${\vartheta }_1,{\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2.$ If ℵ is a geometrically convex function on $[{\vartheta }_1,{\vartheta }_2]$, then the following inequalities for fractional integrals hold:

$$\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\le \frac{\Gamma (\alpha +1)}{2{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\alpha }}\left\{J_{{{\vartheta }_1}^{+}}^{\alpha }\aleph \left({\vartheta }_2\right)+J_{{{\vartheta }_2}^{-}}^{\alpha }\aleph \left({\vartheta }_1\right)\right\}\le \frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}.$$

(7)

In [20], Kunt, proved fractional Hermite–Hadamard–Fejér-type inequalities for geometrically convex functions:

Theorem 5.

A function $\aleph :I\subseteq (0,\infty )\to \mathbb{R}$ is geometrically convex on I and ${\vartheta }_1,{\vartheta }_2\in I$ with ${\vartheta }_1<{\vartheta }_2.$ If $w:[{\vartheta }_1,{\vartheta }_2]\to (0,\infty )$ is continuous, positive, and geometrically symmetric to $\sqrt{{\vartheta }_1{\vartheta }_2}$, then

$$\begin{array}{cc}\hfill \aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left\{J_{{{\vartheta }_1}^{+}}^{\alpha }\varpi \left({\vartheta }_2\right)+J_{{{\vartheta }_2}^{-}}^{\alpha }\varpi \left({\vartheta }_1\right)\right\}& \le \left\{J_{{{\vartheta }_1}^{+}}^{\alpha }\left(\aleph w\right)\left({\vartheta }_2\right)+J_{{{\vartheta }_2}^{-}}^{\alpha }\left(\aleph w\right)\left({\vartheta }_1\right)\right\}\hfill \\ \hfill & \le \frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}\left\{J_{{{\vartheta }_1}^{+}}^{\alpha }\varpi \left({\vartheta }_2\right)+J_{{{\vartheta }_2}^{-}}^{\alpha }\varpi \left({\vartheta }_1\right)\right\}.\hfill \end{array}$$

(8)

In this paper, we will prove the left-hand side and right-hand side weighted fractional and fractional Hermite-Hadamard-Fejér-type inequalities for geometrically convex functions. Moreover, we will obtain the identity for differentiable functions. Using this identity, we will establish some midpoint-type error estimations for geometrically convex functions with respect to an increasing function containing positive weighted geometrically symmetric function forms. Furthermore, we observe the validity of Theorems 6–9 in Figure 1, Figure 2, Figure 3 and Figure 4 respectively.

2. Weighted Fractional Integral

Definition 3.

Let $\aleph \in L[{\vartheta }_1,{\vartheta }_2]$, $[{\vartheta }_1,{\vartheta }_2]\subseteq \left(0,\infty \right).$ Let $\varpi :[{\vartheta }_1,{\vartheta }_2]\to \mathbb{R}$ be positive, integrable, and symmetric weighted functions. If ℘ is an increasing and positive function from $[{\vartheta }_1,{\vartheta }_2)$ onto itself such that its derivative ${\wp }^{\prime }$ is continuous on $({\vartheta }_1,{\vartheta }_2),$ then the left-hand side and right-hand side weighted fractional integrals of order $v>0$, respectively, are given as

$$\left({}_{\varpi }{\mathcal{I}}_{{\vartheta }_1^{+}}^{v,\wp }\aleph \right)\left(\tau \right)=\frac{{\varpi }^{-1}\left(\tau \right)}{\Gamma \left(v\right)}{\int }_{{\vartheta }_1}^{\tau }\frac{{\wp }^{\prime }\left(\kappa \right)}{\wp \left(\kappa \right)}{\left(ln\frac{\wp \left(\tau \right)}{\wp \left(\kappa \right)}\right)}^{v-1}\aleph \left(\kappa \right)\varpi \left(\kappa \right)d\kappa$$

(9)

and

$$\left({}_{\varpi }{\mathcal{I}}_{{\vartheta }_2^{-}}^{v,\wp }\aleph \right)\left(\tau \right)=\frac{{\varpi }^{-1}\left(\tau \right)}{\Gamma \left(v\right)}{\int }_{\tau }^{{\vartheta }_2}\frac{{\wp }^{\prime }\left(\kappa \right)}{\wp \left(\kappa \right)}{\left(ln\frac{\wp \left(\kappa \right)}{\wp \left(\tau \right)}\right)}^{v-1}\aleph \left(\kappa \right)\varpi \left(\kappa \right)d\kappa ,$$

(10)

for ${\varpi }^{-1}\left(\tau \right):=\frac{1}{\varpi \left(\tau \right)}.$

Remark 1. 

(i) Putting $\varpi \left(\tau \right)=1$, the operators (9) and (10) reduce to the fractional integrals of order $v>0$ with regard to the function $\wp \left(\tau \right)$ as follows:

$$\begin{array}{cc}\hfill & \left({\mathcal{I}}_{{\vartheta }_1^{+}}^{v,\wp }\aleph \right)\left(\tau \right)=\frac{1}{\Gamma \left(v\right)}{\int }_{{\vartheta }_1}^{\tau }\frac{{\wp }^{\prime }\left(\kappa \right)}{\wp \left(\kappa \right)}{\left(ln\frac{\wp \left(\tau \right)}{\wp \left(\kappa \right)}\right)}^{v-1}\aleph \left(\kappa \right)d\kappa \hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \left({\mathcal{I}}_{{\vartheta }_2^{-}}^{v,\wp }\aleph \right)\left(\tau \right)=\frac{1}{\Gamma \left(v\right)}{\int }_{\tau }^{{\vartheta }_2}\frac{{\wp }^{\prime }\left(\kappa \right)}{\wp \left(\kappa \right)}{\left(ln\frac{\wp \left(\kappa \right)}{\wp \left(\tau \right)}\right)}^{v-1}\aleph \left(\kappa \right)d\kappa .\hfill \end{array}$$

(ii) 

Putting $\wp \left(\tau \right)=\tau$, the operators (9) and (10) reduce to the weighted fractional integrals of order $v>0$ as follows:

$$\left({}_{\varpi }{\mathcal{I}}_{{\vartheta }_1^{+}}^v\aleph \right)\left(\tau \right)=\frac{{\varpi }^{-1}\left(\tau \right)}{\Gamma \left(v\right)}{\int }_{{\vartheta }_1}^{\tau }{\left(ln\frac{\tau }{\kappa }\right)}^{v-1}\frac{\aleph \left(\kappa \right)\varpi \left(\kappa \right)}{\kappa }d\kappa$$

and

$$\left({}_{\varpi }{\mathcal{I}}_{{\vartheta }_2^{-}}^v\aleph \right)\left(\tau \right)=\frac{{\varpi }^{-1}\left(\tau \right)}{\Gamma \left(v\right)}{\int }_{\tau }^{{\vartheta }_2}{\left(ln\frac{\kappa }{\tau }\right)}^{v-1}\frac{\aleph \left(\kappa \right)\varpi \left(\kappa \right)}{\kappa }d\kappa ,$$

for ${\varpi }^{-1}\left(\tau \right):=\frac{1}{\varpi \left(\tau \right)}.$

(iii) 

Putting $\varpi \left(\tau \right)=1$ and $\wp \left(\tau \right)=\tau$, the operators (9) and (10) reduce to Hadamard fractional integrals of order $v>0$, which is defined by [21]:

$$\left({\mathcal{I}}_{{\vartheta }_1^{+}}^v\aleph \right)\left(\tau \right)=\frac{1}{\Gamma \left(v\right)}{\int }_{{\vartheta }_1}^{\tau }{\left(ln\frac{\tau }{\kappa }\right)}^{v-1}\frac{\aleph \left(\kappa \right)}{\kappa }d\kappa$$

and

$$\left({\mathcal{I}}_{{\vartheta }_2^{-}}^v\aleph \right)\left(\tau \right)=\frac{1}{\Gamma \left(v\right)}{\int }_{\tau }^{{\vartheta }_2}{\left(ln\frac{\kappa }{\tau }\right)}^{v-1}\frac{\aleph \left(\kappa \right)}{\kappa }d\kappa .$$

This work shows how to assess a variety of Hermite–Hadamard–Fejér inequalities using weighted fractional operators with a positive geometrically symmetric weight function in the kernel.

3. Main Results

Throughout this paper, the functions ${\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right),{\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right):I\subset (0,\infty )\to \mathbb{R}$, being a differentiable function on $I^{\circ }$, the interior of I, are defined as:

$${\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)={\vartheta }_1^{\frac{\kappa }{2}}{\vartheta }_2^{\frac{2-\kappa }{2}}$$

and

$${\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)={\vartheta }_1^{\frac{2-\kappa }{2}}{\vartheta }_2^{\frac{\kappa }{2}}.$$

Lemma 1.

The following results hold.

(i)

Let $\varpi :[{\vartheta }_1,{\vartheta }_2]\to \mathbb{R}$ be an integrable function and geometrically symmetric weighted function with respect to $\sqrt{{\vartheta }_1{\vartheta }_2},$ with ${\vartheta }_1<{\vartheta }_2$, and then we have

$$\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)=\varpi \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right),$$

(11)

for every $\kappa \in [0,1].$

(ii)

For order $v>0$ and ℘ is an increasing and positive function from $[{\vartheta }_1,{\vartheta }_2)$ onto itself

$$\begin{array}{cc}\hfill & \left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)=\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\hfill \\ & =\frac{1}{2}\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right].\hfill \end{array}$$

(12)

Proof. 

Suppose that $\tau ={\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)={\vartheta }_1^{\frac{\kappa }{2}}{\vartheta }_2^{\frac{2-\kappa }{2}}$ with $\tau \in \left[{\vartheta }_1,{\vartheta }_2\right]$ and $\kappa \in [0,1],$ and then we have

$$\frac{{\vartheta }_1{\vartheta }_2}{\tau }={\vartheta }_1^{\frac{2-\kappa }{2}}{\vartheta }_2^{\frac{\kappa }{2}}={\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right).$$

Using the geometrically symmetric of $\varpi$ with respect to $\sqrt{{\vartheta }_1{\vartheta }_2}$, we have

$$\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)=\varpi \left(\tau \right)=\varpi \left(\frac{{\vartheta }_1{\vartheta }_2}{\tau }\right)=\varpi \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right).$$

Using the geometrically symmetric of $\varpi ,$ we have

$$\left(\varpi \circ \wp \right)\left(\kappa \right)=\varpi \left(\wp \left(\kappa \right)\right)=\varpi \left(\frac{{\vartheta }_1{\vartheta }_2}{\wp \left(\kappa \right)}\right),\forall \kappa \in \left[{\wp }^{-1}\left({\vartheta }_1\right),{\wp }^{-1}\left({\vartheta }_2\right)\right].$$

Hence, from the above and setting $\wp \left(\tau \right):=\frac{{\vartheta }_1{\vartheta }_2}{\wp \left(\kappa \right)}$, it follows that

$$\begin{array}{cc}\hfill & \left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\hfill \\ \hfill & =\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \hfill \\ \hfill & =\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)}^{v-1}\varpi \left(\frac{{\vartheta }_1{\vartheta }_2}{\wp \left(\kappa \right)}\right)\frac{{\wp }^{\prime }\left(\kappa \right)}{\wp \left(\kappa \right)}d\kappa \hfill \\ \hfill & =\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\kappa \right)\frac{{\wp }^{\prime }\left(\kappa \right)}{\wp \left(\kappa \right)}d\kappa \hfill \\ \hfill & =\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right),\hfill \end{array}$$

which brings the needed equality (12). □

4. Weighted Fractional Hermite–Hadamard-Type Inequalities for Geometrically Convex Functions

It is our goal in this section to develop some novel weighted fractional Hermite–Hadamard-type inequalities for geometrically convex functions with regard to an increasing function that has a positive weighted geometrically symmetric function form that are not previously known.

Theorem 6.

Let $\aleph :[{\vartheta }_1,{\vartheta }_2]\subset (0,\infty )\to \mathbb{R}$ be a geometrically convex function such that $\aleph \in L[{\vartheta }_1,{\vartheta }_2]$ with ${\vartheta }_1,{\vartheta }_2\in I$ and $v>0.$ Let $\varpi :[{\vartheta }_1,{\vartheta }_2]\to \mathbb{R}$ be a positive, integrable, and geometrically symmetric weight function with respect to $\sqrt{{\vartheta }_1{\vartheta }_2}$. If ℘ is an increasing and positive function from $[{\vartheta }_1,{\vartheta }_2)$ onto itself such that its derivative ${\wp }^{\prime }$ is continuous on $({\vartheta }_1,{\vartheta }_2)$, then the following inequalities for fractional integrals hold:

$$\begin{array}{c}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\right.\\ \left.\times \left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\le \varpi \left({\vartheta }_2\right)\left({}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}{\mathcal{I}}_{\varpi \circ \wp }^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\\ +\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\\ \le \left[\frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}\right]\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\right.\\ +\left.\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right].\end{array}$$

(13)

Proof. 

Using the geometric convexity of the function ℵ on $[{\vartheta }_1,{\vartheta }_2]$, we write

$$\aleph \left(\sqrt{{\pi }_1{\pi }_2}\right)\le \frac{\aleph \left({\pi }_1\right)+\aleph \left({\pi }_2\right)}{2},\mathrm{for}\mathrm{all}{\pi }_1,{\pi }_2\in \left[{\vartheta }_1,{\vartheta }_2\right].$$

Choosing ${\pi }_1={\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)$ and ${\pi }_2={\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)$, $\kappa \in [0,1],$ it follows that

$$2\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\le \aleph \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)+\aleph \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right).$$

(14)

Multiplying both sides of (14) by ${\kappa }^{v-1}\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)$ and integrating the resulting inequality with respect to $\kappa$ over $[0,1]$, we obtain

$$\begin{array}{c}2\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right){\int }_0^1{\kappa }^{v-1}\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa \\ \le {\int }_0^1{\kappa }^{v-1}\aleph \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa \\ +{\int }_0^1{\kappa }^{v-1}\aleph \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa .\end{array}$$

(15)

From the left-hand side of the inequality in (15), we use (12) to obtain

$$\begin{array}{c}\frac{\Gamma \left(v\right)}{2{\left(ln\frac{{\vartheta }_2}{{\vartheta }_{{}_1}}\right)}^v}\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\hfill \\ =\frac{\Gamma \left(v\right)}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_{{}_1}}\right)}^v}\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\hfill \\ =\frac{1}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_{{}_1}}\right)}^v}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \hfill \\ ={\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(\frac{ln{\vartheta }_2-ln\wp \left(\tau \right)}{ln{\vartheta }_2-ln{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}\frac{d\tau }{ln\frac{{\vartheta }_2}{{\vartheta }_1}}\hfill \\ ={\int }_0^1{\kappa }^{v-1}\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa ,\left[\mathrm{where}\kappa :=\frac{ln{\vartheta }_2-ln\wp \left(\tau \right)}{ln{\vartheta }_2-ln{\vartheta }_1}\right].\hfill \end{array}$$

(16)

It follows that

$$\begin{array}{c}2\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right){\int }_0^1{\kappa }^{v-1}\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa =\frac{\Gamma \left(v\right)}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^v}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\hfill \\ \times \left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right].\hfill \end{array}$$

(17)

It is possible to prove this by computing the weighted fractional operators,

$$\begin{array}{cc}\hfill & \varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\hfill \\ & =\varpi \left({\vartheta }_2\right)\frac{{\left(\varpi \circ \wp \right)}^{-1}{\wp }^{-1}\left({\vartheta }_2\right)}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\aleph \circ \wp \right)\left(\tau \right)\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \hfill \\ \hfill & +\varpi \left({\vartheta }_1\right)\frac{{\left(\varpi \circ \wp \right)}^{-1}{\wp }^{-1}\left({\vartheta }_1\right)}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\aleph \circ \wp \right)\left(\tau \right)\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \hfill \\ & =\frac{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^v}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(\frac{ln{\vartheta }_2-ln\wp \left(\tau \right)}{ln{\vartheta }_2-ln{\vartheta }_1}\right)}^{v-1}\left(\aleph \circ \wp \right)\left(\tau \right)\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}\frac{d\tau }{ln\frac{{\vartheta }_2}{{\vartheta }_1}}\hfill \\ \hfill & +\frac{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^v}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left(\frac{ln\wp \left(\tau \right)-ln{\vartheta }_1}{ln{\vartheta }_2-ln{\vartheta }_1}\right)}^{v-1}\left(\aleph \circ \wp \right)\left(\tau \right)\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}\frac{d\tau }{ln\frac{{\vartheta }_2}{{\vartheta }_1}}.\hfill \end{array}$$

Setting ${\lambda }_1=\frac{ln{\vartheta }_2-ln\wp \left(\tau \right)}{ln{\vartheta }_2-ln{\vartheta }_1}$ and ${\lambda }_2=\frac{ln\wp \left(\tau \right)-ln{\vartheta }_1}{ln{\vartheta }_2-ln{\vartheta }_1}$, one can deduce that

$$\begin{array}{c}\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^v}{\Gamma \left(v\right)}{\int }_0^1\lambda {{}_1}^{v-1}\aleph \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\lambda {}_1\\ \hfill +\frac{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^v}{\Gamma \left(v\right)}{\int }_0^1\lambda {{}_2}^{v-1}\aleph \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right)d\lambda {}_2.\end{array}$$

By using the geometrically symmetric weighted function of Equation (11), we obtain the required calculation

$$\begin{array}{c}\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^v}{\Gamma \left(v\right)}{\int }_0^1\lambda {{}_1}^{v-1}\aleph \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\lambda {}_1\\ \hfill +\frac{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^v}{\Gamma \left(v\right)}{\int }_0^1\lambda {{}_2}^{v-1}\aleph \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\lambda {}_2.\end{array}$$

As a consequence,

$$\begin{array}{c}{\int }_0^1{\kappa }^{v-1}\aleph \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa +{\int }_0^1{\kappa }^{v-1}\aleph \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa \\ =\frac{\Gamma \left(v\right)}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^v}\left[\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\right.\\ \left.+\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right].\end{array}$$

(18)

The following is the outcome of putting (17) and (18) into (15)

$$\begin{array}{c}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\\ \le \varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\\ +\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right).\end{array}$$

(19)

Finally, it has been established that the left inequality of (13) has been demonstrated. We can show the second inequality of (13) using the geometrically convex function of ℵ, which yields

$$\aleph \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)\le \frac{\kappa }{2}\aleph \left({\vartheta }_1\right)+\frac{2-\kappa }{2}\aleph \left({\vartheta }_2\right).$$

(20)

$$\aleph \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right)\le \frac{2-\kappa }{2}\aleph \left({\vartheta }_1\right)+\frac{\kappa }{2}\aleph \left({\vartheta }_2\right).$$

(21)

Adding (20) and (21), we have

$$\aleph \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)+\aleph \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right)\le \aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right).$$

(22)

Multiplying both sides of (22) by ${\kappa }^{v-1}\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)$, we obtain the following by integrating the resulting inequality in terms of $\kappa$ on $[0,1]$.

$$\begin{array}{cc}\hfill {\int }_0^1{\kappa }^{v-1}\aleph \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa & +{\int }_0^1{\kappa }^{v-1}\aleph \left({\Theta }_{{\vartheta }_2,{\vartheta }_1}\left(\kappa \right)\right)\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa \hfill \\ \hfill & \le \left[\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)\right]{\int }_0^1{\kappa }^{v-1}\varpi \left({\Theta }_{{\vartheta }_1,{\vartheta }_2}\left(\kappa \right)\right)d\kappa .\hfill \end{array}$$

(23)

Then, by using (18) in (23), we have

$$\begin{array}{c}\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\\ +\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\\ \le \left[\frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}\right]\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\right.\\ +\left.\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right].\end{array}$$

(24)

This ends our proof. □

Remark 2. 

From Theorem 6, we can obtain some special cases as follows:

(i) 

If $\wp \left(\tau \right)=\tau$, then inequality (13) becomes

$$\begin{array}{c}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{+}}^v\varpi \right)\left({\vartheta }_2\right)+\left({\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{-}}^v\varpi \right)\left({\vartheta }_1\right)\right]\\ \le \varpi \left({\vartheta }_2\right)\left({}_{\varpi }^v{\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{+}}\aleph \right)\left({\vartheta }_2\right)+\varpi \left({\vartheta }_1\right)\left({}_{\varpi }{\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{-}}^v\aleph \right)\left({\vartheta }_1\right)\\ \le \left[\frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}\right]\left[\left({\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{+}}^v\varpi \right)\left({\vartheta }_2\right)+\left({\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{-}}^v\varpi \right)\left({\vartheta }_1\right)\right],\end{array}$$

(25)

where $\left({\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{+}}^v\varpi \right)\left({\vartheta }_2\right)$ and $\left({\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{-}}^v\varpi \right)\left({\vartheta }_1\right)$ are defined in Remark 1 part(ii).

(ii) 

Assuming that $\wp \left(\tau \right)=\tau$ and $v=1,$ the inequality (13) simplifies to the inequality (6).

(iii) 

Assuming that $\wp \left(\tau \right)=\tau$ and $\varpi \left(\tau \right)=1,$ the inequality (13) simplifies to the inequality (7).

(iv) 

Assuming that $\wp \left(\tau \right)=\tau ,$$\varpi \left(\tau \right)=1$ and $v=1,$ the inequality (13) simplifies to the inequality (4).

Example 1. 

Let $\aleph \left(\tau \right)={\tau }^2$, $\tau \in \left[\frac{1}{2},2\right]$, and then $\varpi \left(\tau \right)={\left(ln\tau \right)}^2$ and $\wp \left(\tau \right)=2\sqrt{\tau }$; hence, ${\wp }^{\prime }\left(\tau \right)=\frac{1}{\sqrt{\tau }}$ and ${\wp }^{-1}\left(\tau \right)=\frac{{\tau }^2}{4}$.

$$\begin{array}{c}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\hfill \\ =\frac{1}{2\Gamma \left(v\right)}\left[{\int }_{{\wp }^{-1}\left(1\right)}^{{\wp }^{-1}\left(2\right)}{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }+{\int }_{{\wp }^{-1}\left(\frac{1}{2}\right)}^{{\wp }^{-1}\left(1\right)}{\left(ln\left(\sqrt{\tau }\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }\right]\\ =\frac{1}{2\Gamma \left(v\right)}\left[{\int }_{\frac{1}{4}}^1{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}{\left(ln\left(2\sqrt{\tau }\right)\right)}^2\frac{d\tau }{\tau }+{\int }_{\frac{1}{16}}^{\frac{1}{4}}{\left(ln\left(\sqrt{\tau }\right)\right)}^{v-1}{\left(ln\left(2\sqrt{\tau }\right)\right)}^2\frac{d\tau }{\tau }\right]\\ \hfill =\frac{2{\left(ln2\right)}^{v+2}}{v\left(v^2+3v+2\right)\Gamma \left(v\right)}+\frac{2^{-v-1}{\left(ln4\right)}^{v+2}}{v\left(v^2+3v+2\right)\Gamma \left(v\right)}=i_1\left(v\right).\end{array}$$

We also observe that

$$\begin{array}{c}\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\hfill \\ =\frac{1}{2\Gamma \left(v\right)}\left[{\int }_{{\wp }^{-1}\left(1\right)}^{{\wp }^{-1}\left(2\right)}{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\aleph \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }+{\int }_{{\wp }^{-1}\left(\frac{1}{2}\right)}^{{\wp }^{-1}\left(1\right)}{\left(ln\left(4\sqrt{\tau }\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\aleph \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }\right]\\ =\frac{2}{\Gamma \left(v\right)}\left[{\int }_{\frac{1}{4}}^1{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}{\left(ln\left(2\sqrt{\tau }\right)\right)}^{2}d\tau +{\int }_{\frac{1}{16}}^{\frac{1}{4}}{\left(ln\left(4\sqrt{\tau }\right)\right)}^{v-1}{\left(ln\left(2\sqrt{\tau }\right)\right)}^{2}d\tau \right]\\ =\frac{1}{\Gamma \left(v\right)}\left[2^{-v-4}\left({(-1)}^{1-v}\left({(-ln\left(4\right))}^v\left(\left(v^2+v+vln\left(16\right)+4{ln}^2\left(2\right)\right)E_{1-v}(-ln\left(4\right))+4v+4+ln\left(256\right)\right)\right.\right.\right.\\ \left.-4{ln}^2\left(2\right)\Gamma \left(v\right)-(v+1+ln\left(16\right))\Gamma (v+1)\right)+16((v+1-2ln\left(4\right))\Gamma (v+1)-\Gamma (v+2,ln\left(4\right))\\ \hfill \left.\left.+ln\left(4\right)(2\Gamma (v+1,ln\left(4\right))+ln(4\left)\right(\Gamma \left(v\right)-\Gamma (v,ln(4\left)\right)\left)\right))\right)\right]=i_2\left(v\right),\end{array}$$

and

$$\begin{array}{c}\left[\frac{\aleph \left({\vartheta }_1\right)+\aleph \left({\vartheta }_2\right)}{2}\right]\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\hfill \\ =\frac{17}{8\Gamma \left(v\right)}\left[{\int }_{{\wp }^{-1}\left(1\right)}^{{\wp }^{-1}\left(2\right)}{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }+{\int }_{{\wp }^{-1}\left(\frac{1}{2}\right)}^{{\wp }^{-1}\left(1\right)}{\left(ln\left(4\sqrt{\tau }\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }\right]\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{17{(ln\left(2\right))}^{v+2}}{2v\left(v^2+3v+2\right)\Gamma \left(v\right)}+\frac{17{\left(ln\left(4\right)\right)}^{v+2}}{2^{v+2}\left(2v^3+6v^2+4v\right)\Gamma \left(v\right)}=i_3\left(v\right).\end{array}$$

We observe the validity of Theorem 6.

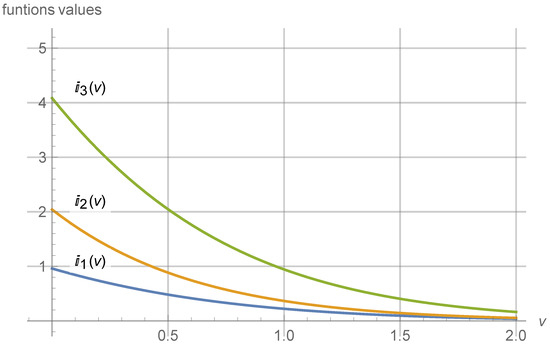
Figure 1. Plot of the values of the functions obtained from the left-most, middle, and right-most terms in the inequality of Theorem 6.

Consider

$$\begin{array}{cc}\hfill & {\mathbb{D}}_1=\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left[{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa .\hfill \\ & {\mathbb{D}}_2=\frac{-1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left[{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa .\hfill \end{array}$$

Lemma 2. 

Let $0<{\vartheta }_1<{\vartheta }_2$ and let $\aleph :[{\vartheta }_1,{\vartheta }_2]\subseteq \left(0,\infty \right)\to \mathbb{R}$ be continuous with derivative ${\aleph }^{\prime }\in L[{\vartheta }_1,{\vartheta }_2]$. If $\varpi :[{\vartheta }_1,{\vartheta }_2]\to \mathbb{R}$ is a positive, integrable, and geometrically symmetric weight function with respect to $\sqrt{{\vartheta }_1{\vartheta }_2}$, and if ℘ is an increasing and positive function from $[{\vartheta }_1,{\vartheta }_2)$ onto itself such that its derivative ${\wp }^{\prime }\left(\tau \right)$ is continuous on $({\vartheta }_1,{\vartheta }_2)$, for $v>0,$ then

$$\begin{array}{c}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\hfill \\ -\left[\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\hfill \\ :={\mathbb{D}}_1+{\mathbb{D}}_2.\hfill \end{array}$$

(26)

Proof. 

Let

$${\mathbb{D}}_1=\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left[{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa .$$

By integration by parts, applying Lemma 1 and Definition 3, we obtain

$$\begin{array}{cc}\hfill & ={\left.\frac{1}{\Gamma \left(v\right)}\left[{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left(\aleph \circ \wp \right)\left(\kappa \right)\right|}_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\hfill \\ \hfill & -\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\kappa \right)\left(\aleph \circ \wp \right)\left(\kappa \right)\frac{{\wp }^{\prime }\left(\kappa \right)}{\wp \left(\kappa \right)}d\kappa \hfill \\ & =\left(\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right)\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)-\varpi \left({\vartheta }_1\right)\hfill \\ \hfill & \times \frac{{\left(\varpi \circ \wp \right)}^{-1}{\wp }^{-1}\left({\vartheta }_1\right)}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left(\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\kappa \right)\left(\aleph \circ \wp \right)\left(\kappa \right)\frac{{\wp }^{\prime }\left(\kappa \right)}{{\wp }^{(}\kappa )}d\kappa \hfill \\ \hfill & =\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)-\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\hfill \\ \hfill & =\frac{1}{2}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\hfill \\ \hfill & -\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right).\hfill \end{array}$$

Similarly, we obtain

$$\begin{array}{cc}\hfill & {\mathbb{D}}_2=\frac{-1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left[{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa \hfill \\ \hfill & ={\left.\frac{-1}{\Gamma \left(v\right)}\left[{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(w\circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left(\aleph \circ \wp \right)\left(\kappa \right)\right|}_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\hfill \\ \hfill & -\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\kappa \right)\left(\aleph \circ \wp \right)\left(\kappa \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\kappa \hfill \\ & =\left(\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right)\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\hfill \\ & -\varpi \left({\vartheta }_1\right)\frac{{\left(w\circ \wp \right)}^{-1}{\wp }^{-1}\left({\vartheta }_2\right)}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\kappa \right)\left(\aleph \circ \wp \right)\left(\kappa \right)\frac{{\wp }^{\prime }\left(\kappa \right)}{\wp \left(\kappa \right)}d\kappa \hfill \\ \hfill & =\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)-\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\frac{1}{2}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\right]\hfill \\ \hfill & -\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right).\hfill \end{array}$$

As a result, we can conclude,

$$\begin{array}{c}{\mathbb{D}}_1+{\mathbb{D}}_2:=\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right.\hfill \\ \left.+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\right]\\ -\left[\varpi \left({\vartheta }_1\right)\left({}_{w\circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right.\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left.+\varpi \left({\vartheta }_2\right)\left({}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}{\mathcal{I}}_{\varpi \circ \wp }^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)\right],\end{array}$$

and we achieve the intended result. □

Remark 3.

If $\wp \left(\tau \right)=\tau ,$ then equality (26) becomes

$$\begin{array}{c}\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{+}}^v\varpi \right)\left({\vartheta }_2\right)+\left({\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{-}}^v\varpi \right)\left({\vartheta }_1\right)\right]\hfill \\ -\left[\varpi \left({\vartheta }_2\right)\left({}_{\varpi }{\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{+}}^v\aleph \right)\left({\vartheta }_2\right)+\varpi \left({\vartheta }_1\right)\left({}_{\varpi }{\mathcal{I}}_{{\sqrt{{\vartheta }_1{\vartheta }_2}}^{-}}^v\aleph \right)\left({\vartheta }_1\right)\right]\\ =\frac{1}{\Gamma \left(v\right)}{\int }_{{\vartheta }_1}^{\sqrt{{\vartheta }_1{\vartheta }_2}}\left[{\int }_{{\vartheta }_1}^{\kappa }{\left(ln\frac{\tau }{{\vartheta }_1}\right)}^{v-1}\varpi \left(\tau \right)\frac{d\tau }{\tau }\right]{\aleph }^{\prime }\left(\kappa \right)d\kappa \\ \hfill -\frac{1}{\Gamma \left(v\right)}{\int }_{\sqrt{{\vartheta }_1{\vartheta }_2}}^{{\vartheta }_2}\left[{\int }_{\kappa }^{{\vartheta }_2}{\left(ln\frac{{\vartheta }_2}{\tau }\right)}^{v-1}\varpi \left(\tau \right)\frac{d\tau }{\tau }\right]{\aleph }^{\prime }\left(\kappa \right)d\kappa .\end{array}$$

We will use the following notations for the rest of this section:

$$\begin{array}{cc}\hfill & {\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)=\aleph \left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right]\hfill \\ & -\left[\varpi \left({\vartheta }_2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_2\right)\right)+\varpi \left({\vartheta }_1\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left({\vartheta }_1\right)\right)\right].\hfill \end{array}$$

Theorem 7.

Consider a scenario in which all of the Lemma 2 criteria are satisfied and $|{\aleph }^{\prime }|$ is geometrically convex on $[{\vartheta }_1,{\vartheta }_2],$ and for $v>0$, we have

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)v\Gamma \left(v\right)}\left[{\mathbb{W}}_1\left({\vartheta }_1,{\vartheta }_2\right)\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|+{\mathbb{W}}_2\left({\vartheta }_1,{\vartheta }_2\right)\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|\right]\\ +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_2\right],\infty }}{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)v\Gamma \left(v\right)}\left[{\mathbb{W}}_3\left({\vartheta }_1,{\vartheta }_2\right)\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|+{\mathbb{W}}_4\left({\vartheta }_1,{\vartheta }_2\right)\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|\right]\\ \le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,{\vartheta }_2\right],\infty }}{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)v\Gamma \left(v\right)}\left\{\left({\mathbb{W}}_1\left({\vartheta }_1,{\vartheta }_2\right)+{\mathbb{W}}_3\left({\vartheta }_1,{\vartheta }_2\right)\right)\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|\right.\\ \left.+\left({\mathbb{W}}_2\left({\vartheta }_1,{\vartheta }_2\right)+{\mathbb{W}}_4\left({\vartheta }_1,{\vartheta }_2\right)\right)\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|\right\},\end{array}$$

(27)

where ${\mathbb{W}}_1\left({\vartheta }_1,{\vartheta }_2\right),$${\mathbb{W}}_2\left({\vartheta }_1,{\vartheta }_2\right),$${\mathbb{W}}_3\left({\vartheta }_1,{\vartheta }_2\right),$ and ${\mathbb{W}}_4\left({\vartheta }_1,{\vartheta }_2\right)$ have the following meanings:

$$\begin{array}{cc}\hfill & {\mathbb{W}}_1\left({\vartheta }_1,{\vartheta }_2\right)=-{\vartheta }_1\Gamma (v+1){(-1)}^{-v-2}\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}+v+1\right)-{\left(\frac{1}{2}ln\frac{{\vartheta }_1}{{\vartheta }_2}\right)}^{v+1}\hfill \\ & \times \left[\frac{1}{2}{\vartheta }_1{\vartheta }_2+{\vartheta }_1{E}_{-v}\left(\frac{1}{2}ln\frac{{\vartheta }_1}{{\vartheta }_2}\right)\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}+v+1\right)\right],\hfill \\ \hfill & {\mathbb{W}}_2\left({\vartheta }_1,{\vartheta }_2\right)={\vartheta }_1{\left(-1\right)}^{-v-2}\Gamma (v+2)-2^{-v-2}{\vartheta }_1{\left(ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}^{v+2}{E}_{-v-1}\left(\frac{1}{2}ln\left(\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right),\hfill \\ \hfill & {\mathbb{W}}_3\left({\vartheta }_1,{\vartheta }_2\right)={\vartheta }_2\left(\Gamma (v+2)-{\left(ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}^{v+2}{E}_{-v-1}\left(\frac{1}{2}ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)\right),\hfill \\ \hfill & {\mathbb{W}}_4\left({\vartheta }_1,{\vartheta }_2\right)=-{\vartheta }_2\Gamma (v+1)\left(ln\frac{{\vartheta }_1}{{\vartheta }_2}+v+1\right)+{\left({\displaystyle \frac{1}{2}}ln\frac{{\vartheta }_1}{{\vartheta }_2}\right)}^{v+1}\left[\frac{1}{2}{\vartheta }_1{\vartheta }_2+{\vartheta }_2{E}_{-v}\left(\frac{1}{2}ln\frac{{\vartheta }_1}{{\vartheta }_2}\right)\left(ln\frac{{\vartheta }_1}{{\vartheta }_2}+v+1\right)\right].\hfill \end{array}$$

Proof. 

We obtain the following result by applying Lemma 2 as well as the characteristics of the modulus and the geometrically convex function of $|{\aleph }^{\prime }|$

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|=\left|\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left[{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa \right.\hfill \\ \left.-\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left[{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa \right|\\ \le \frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|{\wp }^{\prime }\left(\kappa \right)d\kappa \\ \hfill +\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|{\wp }^{\prime }\left(\kappa \right)d\kappa .\end{array}$$

Since $\left|{\aleph }^{{}^{\prime }}\right|$ is a geometrically convex function on $\left[{\vartheta }_1,{\vartheta }_2\right],$ we have

$$\begin{array}{c}\left|({\aleph }^{\prime }\circ \wp )\left(\kappa \right)\right|\le \left|{\aleph }^{\prime }\left({\vartheta }_1^{\frac{ln{\vartheta }_2-ln\wp \left(\kappa \right)}{ln{\vartheta }_2-ln{\vartheta }_1}}{\vartheta }_2^{\frac{ln\wp \left(\kappa \right)-ln{\vartheta }_1}{ln{\vartheta }_2-ln{\vartheta }_1}}\right)\right|\hfill \\ \hfill \le \left(\frac{ln{\vartheta }_2-ln\wp \left(\kappa \right)}{ln{\vartheta }_2-ln{\vartheta }_1}\right)\left|{\aleph }^{{}^{\prime }}\left({\vartheta }_1\right)\right|+\left(\frac{ln\wp \left(\kappa \right)-ln{\vartheta }_1}{ln\left({\vartheta }_2\right)-ln{\vartheta }_1}\right)\left|{\aleph }^{{}^{\prime }}\left({\vartheta }_2\right)\right|.\end{array}$$

Consequently, we obtain

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|\hfill \\ \times \left[\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|+\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)\left|\aleph {}^{\prime }\left({\vartheta }_2\right)\right|\right]{\wp }^{\prime }\left(\kappa \right)d\kappa \\ +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_2\right],\infty }}{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|\\ \hfill \times \left[\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|+\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)\left|\aleph {}^{\prime }\left({\vartheta }_2\right)\right|\right]{\wp }^{\prime }\left(\kappa \right)d\kappa ,\end{array}$$

where

$${\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau =\frac{1}{v}{\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)}^v$$

and

$${\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau =\frac{1}{v}{\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)}^v.$$

Using the computations shown above, we can derive the following integral:

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)v\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left[{\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)}^v\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|\right.\hfill \\ \left.+{\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)}^{v+1}\left|\left({\aleph }^{{}^{\prime }}\right)\left({\vartheta }_2\right)\right|\right]{\wp }^{\prime }\left(\kappa \right)d\kappa +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_2\right],\infty }}{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)v\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\hfill \\ \times \left[{\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)}^{v+1}\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|+{\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right)}^v\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right)\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|\right]{\wp }^{\prime }\left(\kappa \right)d\kappa .\hfill \end{array}$$

(28)

We can derive the required result (27) by performing fundamental integral computations based on the inequality (28). □

Example 2.

Let $\aleph \left(\tau \right)={\tau }^2$, $\tau \in \left[\frac{1}{2},2\right]$, and then $\varpi \left(\tau \right)={\left(ln\tau \right)}^2$ and $\wp \left(\tau \right)=2\sqrt{\tau }$; hence, ${\wp }^{\prime }\left(\tau \right)=\frac{1}{\sqrt{\tau }}$ and ${\wp }^{-1}\left(\tau \right)=\frac{{\tau }^2}{4}$.

$$\begin{array}{c}\aleph \left(1\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left(2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left(\frac{1}{2}\right)\right)\right]\hfill \\ -\left[\varpi \left(2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left(2\right)\right)+\varpi \left(\frac{1}{2}\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left(\frac{1}{2}\right)\right)\right]\hfill \\ \le \frac{{\left|\right|\varpi \left|\right|}_{\left[\frac{1}{2},2\right],\infty }}{ln\left(4\right)\Gamma (v+1)}\left\{\left({\mathbb{W}}_1\left(\frac{1}{2},2\right)+{\mathbb{W}}_3\left(\frac{1}{2},2\right)\right)\left|{\aleph }^{\prime }\left(\frac{1}{2}\right)\right|+\left({\mathbb{W}}_2\left(\frac{1}{2},2\right)+{\mathbb{W}}_4\left(\frac{1}{2},2\right)\right)\left|{\aleph }^{\prime }\left(2\right)\right|\right\}.\hfill \end{array}$$

(29)

We also show that

$$\begin{array}{c}\aleph \left(1\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left(2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left(\frac{1}{2}\right)\right)\right]\hfill \\ =\frac{1}{2\Gamma \left(v\right)}\left[{\int }_{{\wp }^{-1}\left(1\right)}^{{\wp }^{-1}\left(2\right)}{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }+{\int }_{{\wp }^{-1}\left(\frac{1}{2}\right)}^{{\wp }^{-1}\left(1\right)}{\left(ln\left(\sqrt{\tau }\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }\right]\\ =\frac{1}{2\Gamma \left(v\right)}\left[{\int }_{\frac{1}{4}}^1{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}{\left(ln\left(2\sqrt{\tau }\right)\right)}^2\frac{d\tau }{\tau }+{\int }_{\frac{1}{16}}^{\frac{1}{4}}{\left(ln\left(\sqrt{\tau }\right)\right)}^{v-1}{\left(ln\left(2\sqrt{\tau }\right)\right)}^2\frac{d\tau }{\tau }\right]\\ \hfill =\frac{2{\left(ln2\right)}^{v+2}}{v\left(v^2+3v+2\right)\Gamma \left(v\right)}+\frac{2^{-v-1}{\left(ln4\right)}^{v+2}}{v\left(v^2+3v+2\right)\Gamma \left(v\right)},\end{array}$$

and

$$\begin{array}{cc}\hfill & \varpi \left(2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left(2\right)\right)+\varpi \left(\frac{1}{2}\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left(\frac{1}{2}\right)\right)\hfill \\ & =\frac{1}{2\Gamma \left(v\right)}\left[{\int }_{{\wp }^{-1}\left(1\right)}^{{\wp }^{-1}\left(2\right)}{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\aleph \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }+{\int }_{{\wp }^{-1}\left(\frac{1}{2}\right)}^{{\wp }^{-1}\left(1\right)}{\left(ln\left(4\sqrt{\tau }\right)\right)}^{v-1}\varpi \left(2\sqrt{\tau }\right)\aleph \left(2\sqrt{\tau }\right)\frac{d\tau }{\tau }\right]\hfill \\ & =\frac{2}{\Gamma \left(v\right)}\left[{\int }_{\frac{1}{4}}^1{\left(ln\left(\frac{1}{\sqrt{\tau }}\right)\right)}^{v-1}{\left(ln\left(2\sqrt{\tau }\right)\right)}^{2}d\tau +{\int }_{\frac{1}{16}}^{\frac{1}{4}}{\left(ln\left(4\sqrt{\tau }\right)\right)}^{v-1}{\left(ln\left(2\sqrt{\tau }\right)\right)}^{2}d\tau \right]\hfill \\ & =\frac{1}{\Gamma \left(v\right)}\left[2^{-v-4}\left({(-1)}^{1-v}\left({(-ln\left(4\right))}^v\left(\left(v^2+v+vln\left(16\right)+4{ln}^2\left(2\right)\right)E_{1-v}(-ln\left(4\right))+4v+4+ln\left(256\right)\right)\right.\right.\right.\hfill \\ & \left.-4{ln}^2\left(2\right)\Gamma \left(v\right)-(v+1+ln\left(16\right))\Gamma (v+1)\right)+16((v+1-2ln\left(4\right))\Gamma (v+1)-\Gamma (v+2,ln\left(4\right))\hfill \\ & \left.\left.+ln\left(4\right)(2\Gamma (v+1,ln\left(4\right))+ln(4\left)\right(\Gamma \left(v\right)-\Gamma (v,ln(4\left)\right)\left)\right))\right)\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & {\mathbb{W}}_1\left(\frac{1}{2},2\right)=\frac{1}{2}\left(-2{(ln\left(2\right))}^{v+1}-{(-1)}^{-v}(v+1+ln\left(4\right))(\Gamma (v+1)-\Gamma (v+1,-ln\left(2\right)))\right),\hfill \\ & {\mathbb{W}}_2\left(\frac{1}{2},2\right)=\frac{1}{2}{(-1)}^{-v}\left(2{(-1)}^v{(ln\left(2\right))}^{v+1}+\Gamma (v+2)-(v+1)\Gamma (v+1,-ln\left(2\right))\right),\hfill \\ & {\mathbb{W}}_3\left(\frac{1}{2},2\right)=2^{-v-1}\left(2^{v+2}(v+1)(\Gamma (v+1)-\Gamma (v+1,ln\left(2\right)))-{ln}^{v+1}\left(4\right)\right),\hfill \\ & {\mathbb{W}}_4\left(\frac{1}{2},2\right)=-2(v+1-ln\left(4\right))\Gamma (v+1)+2\Gamma (v+2,ln\left(2\right))-4ln\left(2\right)\Gamma (v+1,ln\left(2\right)),\hfill \\ \hfill & {\aleph }^{{}^{\prime }}\left(\frac{1}{2}\right)=1,\hfill \\ \hfill & {\aleph }^{{}^{\prime }}\left(2\right)=4,\hfill \\ \hfill & \aleph \left(1\right)=1.\hfill \end{array}$$

We observe the validity of Theorem 7 by using all the above calculations in (29).

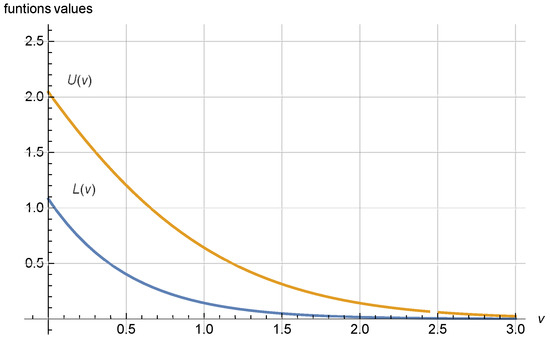
Figure 2. A graph of the error and error bound in the inequality of Theorem 7.

Theorem 8.

Consider a scenario in which all of the Lemma 2 criteria are fulfilled and $|{\aleph }^{\prime }{|}^q$ is geometrically convex on $[{\vartheta }_1,{\vartheta }_2]$ with $q\ge 1$, and the following inequality holds for $v>0$:

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}{v}^{\frac{1}{q}}\Gamma \left(v\right)}\left[{\left({\mathbb{K}}_1\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{1-\frac{1}{q}}{\left({\mathbb{W}}_1\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+{\mathbb{W}}_2\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q\right)}^{\frac{1}{q}}\right]\\ +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_1\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}{v}^{\frac{1}{q}}\Gamma \left(v\right)}\left[{\left({\mathbb{K}}_2\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{1-\frac{1}{q}}{\left({\mathbb{W}}_3\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+{\mathbb{W}}_4\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q\right)}^{\frac{1}{q}}\right]\\ \le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,{\vartheta }_2\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}{v}^{\frac{1}{q}}\Gamma \left(v\right)}\left\{{\left({\mathbb{K}}_1\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{1-\frac{1}{q}}{\left({\mathbb{W}}_1\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+{\mathbb{W}}_2\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q\right)}^{\frac{1}{q}}\right.\\ +\left.{\left({\mathbb{K}}_2\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{1-\frac{1}{q}}{\left({\mathbb{W}}_3\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+{\mathbb{W}}_4\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q\right)}^{\frac{1}{q}}\right\},\end{array}$$

(30)

where

$$\begin{array}{cc}\hfill & {\mathbb{K}}_1\left({\vartheta }_1,{\vartheta }_2\right)=={\vartheta }_1\left(-v{(-1)}^{-v}\Gamma \left(v\right)+\Gamma \left(1+v,\frac{1}{2}ln\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right){\left(ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}^v{\left(ln\left(\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right)}^{-v}\hfill \\ & {\mathbb{K}}_2\left({\vartheta }_1,{\vartheta }_2\right)={\vartheta }_2\left({(-1)}^{-v}\Gamma (1+v)-\Gamma \left(1+v,\frac{1}{2}ln\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right),\hfill \end{array}$$

and ${\mathbb{W}}_1\left({\vartheta }_1,{\vartheta }_2\right),$${\mathbb{W}}_2\left({\vartheta }_1,{\vartheta }_2\right),$${\mathbb{W}}_3\left({\vartheta }_1,{\vartheta }_2\right),$ and ${\mathbb{W}}_4\left({\vartheta }_1,{\vartheta }_2\right)$ are defined in Theorem 7.

Proof. 

Using Lemma 2 as well as the properties of power mean inequality and the geometrically convex function of $|{\aleph }^{\prime }{|}^q$, we obtain

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|=\left|\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left[{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa \right.\hfill \\ \left.-\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left[{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa \right|\\ \le \frac{1}{\Gamma \left(v\right)}{\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{1-\frac{1}{q}}\\ \times {\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|}^q{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}\\ +\frac{1}{\Gamma \left(v\right)}{\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{1-\frac{1}{q}}\\ \hfill \times {\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|}^q{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}.\end{array}$$

Since ${\left|{\aleph }^{\prime }\right|}^q$ is a geometrically convex function on $\left[{\vartheta }_1,{\vartheta }_2\right]$, we have

$$\begin{array}{c}\left|({\aleph }^{\prime }\circ \wp )\left(\kappa \right)\right|\le {\left|{\aleph }^{\prime }\left({\vartheta }_1^{\frac{ln{\vartheta }_2-ln\wp \left(\kappa \right)}{ln{\vartheta }_2-ln{\vartheta }_1}}{\vartheta }_2^{\frac{ln\wp \left(\kappa \right)-ln{\vartheta }_1}{ln{\vartheta }_2-ln{\vartheta }_1}}\right)\right|}^q\hfill \\ \hfill \le \left(\frac{ln{\vartheta }_2-ln\wp \left(\kappa \right)}{ln{\vartheta }_2-ln{\vartheta }_1}\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+\left(\frac{ln\wp \left(\kappa \right)-ln{\vartheta }_1}{ln\left({\vartheta }_2\right)-ln{\vartheta }_1}\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q.\end{array}$$

As a result, we have

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{\Gamma \left(v\right)}{\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{1-\frac{1}{q}}\hfill \\ \times {\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|}^q{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}\\ +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_2\right],\infty }}{\Gamma \left(v\right)}{\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{1-\frac{1}{q}}\\ \hfill \times {\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|}^q{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}},\end{array}$$

where it is obvious that

$$\begin{array}{c}{\mathbb{K}}_1\left({\vartheta }_1,{\vartheta }_2\right)={\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\wp }^{\prime }\left(\kappa \right)d\kappa \hfill \\ \hfill ={\vartheta }_1\left(-v{(-1)}^{-v}\Gamma \left(v\right)+\Gamma \left(1+v,\frac{1}{2}ln\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right){\left(ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}^v{\left(ln\left(\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right)}^{-v}\end{array}$$

$$\begin{array}{c}{\mathbb{K}}_2\left({\vartheta }_1,{\vartheta }_2\right)={\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\wp }^{\prime }\left(\kappa \right)d\kappa \hfill \\ \hfill ={\vartheta }_2\left({(-1)}^{-v}\Gamma (1+v)-\Gamma \left(1+v,\frac{1}{2}ln\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right).\end{array}$$

By using calculations, we obtain the following inequality:

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}{v}^{\frac{1}{q}}\Gamma \left(v\right)}{\left({\mathbb{K}}_1\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{1-\frac{1}{q}}\\ \times {\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|}^q{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}\\ +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_2\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}{v}^{\frac{1}{q}}\Gamma \left(v\right)}{\left({\mathbb{K}}_2\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{1-\frac{1}{q}}\\ \times {\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|{\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|}^q{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}.\end{array}$$

(31)

We can obtain the necessary result (30) by performing basic integral calculations based on inequality (31). □

Example 3.

Let $\aleph \left(\tau \right)={\tau }^3$, $\tau \in \left[\frac{1}{2},2\right]$, then $\varpi \left(\tau \right)={\left(ln\tau \right)}^2$ and $\wp \left(\tau \right)=2\sqrt{\tau }$; hence ${\wp }^{\prime }\left(\tau \right)=\frac{1}{\sqrt{\tau }}$ and ${\wp }^{-1}\left(\tau \right)=\frac{{\tau }^2}{4}$.

$$\begin{array}{c}\aleph \left(1\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left(2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left(\frac{1}{2}\right)\right)\right]\hfill \\ -\left[\varpi \left(2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left(2\right)\right)+\varpi \left(\frac{1}{2}\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left(\frac{1}{2}\right)\right)\right]\\ \le \frac{{\left|\right|\varpi \left|\right|}_{\left[\frac{1}{2},2\right],\infty }}{{\left(ln\left(4\right)\right)}^{\frac{1}{q}}{v}^{\frac{1}{q}}\Gamma \left(v\right)}\left\{{\left({\mathbb{K}}_1\left(\frac{1}{2},2\right)\right)}^{1-\frac{1}{q}}{\left({\mathbb{W}}_1\left(\frac{1}{2},2\right){\left|{\aleph }^{\prime }\left(\frac{1}{2}\right)\right|}^q+{\mathbb{W}}_2\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left(2\right)\right|}^q\right)}^{\frac{1}{q}}\right.\\ +\left.{\left({\mathbb{K}}_2\left(\frac{1}{2},2\right)\right)}^{1-\frac{1}{q}}{\left({\mathbb{W}}_3\left(\frac{1}{2},2\right){\left|{\aleph }^{\prime }\left(\frac{1}{2}\right)\right|}^q+{\mathbb{W}}_4\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left(2\right)\right|}^q\right)}^{\frac{1}{q}}\right\}\\ =\frac{1}{32\Gamma \left(v\right)}\left[\frac{64{ln}^{v+2}\left(2\right)}{v\left(v^2+3v+2\right)}+\frac{2^{5-v}{ln}^{v+2}\left(4\right)}{v^3+3v^2+2v}-3^{-v-2}\left({(-1)}^{-v}\left({ln}^2\left(64\right)\Gamma \left(v\right)+4(v+1+ln\left(64\right))\Gamma (v+1)\right.\right.\right.\\ \left.-{ln}^2\left(64\right)\Gamma (v,-ln\left(8\right))-4\Gamma (v+2,-ln\left(8\right))-12ln\left(4\right)\Gamma (v+1,-ln\left(8\right))\right)+64(4(v+1-3ln\left(4\right))\\ \left.\left.\Gamma (v+1)-4\Gamma (v+2,ln(8\left)\right)+3ln\left(4\right)(ln(64)\Gamma (v)+4\Gamma (v+1,ln\left(8\right))-3ln(4)\Gamma (v,ln\left(8\right)\left)\right))\right)\right]\\ \le \frac{{ln}^2\left(2\right)}{\Gamma \left(v\right){\left(ln\left(4\right)\right)}^{\frac{1}{q}}}\left[{\left(\frac{{(-1)}^{-v}(\Gamma (v+1,-ln\left(2\right))-\Gamma (v+1))}{2v}\right)}^{\frac{q-1}{q}}\left(\frac{{(-1)}^{-v}{2}^{-2q-1}{3}^q(ln\left(4\right)}{v}\right.\right.\\ {\left.\frac{(\Gamma (v+1,-ln\left(2\right))-\Gamma (v+1)))+\left({16}^q-1\right)\Gamma (v+2)-\left({16}^q-1\right)\Gamma (v+2,-ln\left(2\right))}{v}\right)}^{\frac{1}{q}}\\ +{\left(\frac{2(\Gamma (v+1)-\Gamma (v+1,ln\left(2\right)\left)\right)}{v}\right)}^{\frac{q-1}{q}}\left(-\frac{2^{1-2q}{3}^q(v\Gamma \left(v\right)\left(v\left({16}^q-1\right)+{16}^q-{16}^{q}ln\left(4\right)-1\right)}{v}\right.\\ \hfill -\left.{\left.\frac{\left({16}^q-1\right)\Gamma (v+2,ln\left(2\right))+{16}^{q}ln\left(4\right)\Gamma (v+1,ln\left(2\right)))}{v}\right)}^{\frac{1}{q}}\right].\end{array}$$

We observe the validity of Theorem 8.

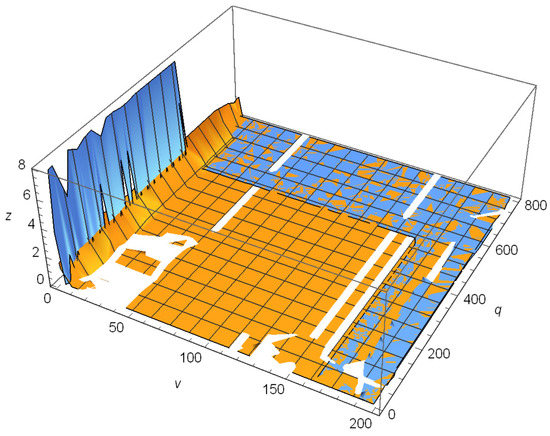
Figure 3. A graph of the error and error bound in the inequality of Theorem 8.

Theorem 9.

Consider a scenario in which all of the Lemma 2 criteria are met and $|{\aleph }^{\prime }{|}^q$ is geometrically convex on $[{\vartheta }_1,{\vartheta }_2]$ with $q>1$, and then we obtain the following inequality for $v>0$:

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}\Gamma \left(v\right)}\left[{\left({\mathbb{H}}_1^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{\frac{1}{p}}{\left({\mathbb{X}}_1\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+{\mathbb{X}}_2\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q\right)}^{\frac{1}{q}}\right]\\ +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_2\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}\Gamma \left(v\right)}\left[{\left({\mathbb{H}}_2^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{\frac{1}{p}}{\left({\mathbb{X}}_3\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+{\mathbb{X}}_4\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q\right)}^{\frac{1}{q}}\right]\\ \le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,{\vartheta }_2\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}\Gamma \left(v\right)}\left\{{\left({\mathbb{H}}_1^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{\frac{1}{p}}{\left({\mathbb{X}}_1\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+{\mathbb{X}}_2\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q\right)}^{\frac{1}{q}}\right.\\ +\left.{\left({\mathbb{H}}_2^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{\frac{1}{p}}{\left({\mathbb{X}}_3\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+{\mathbb{X}}_4\left({\vartheta }_1,{\vartheta }_2\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q\right)}^{\frac{1}{q}}\right\},\end{array}$$

(32)

where ${\mathbb{X}}_1\left({\vartheta }_1,{\vartheta }_2\right),$ ${\mathbb{X}}_2\left({\vartheta }_1,{\vartheta }_2\right),$ ${\mathbb{X}}_3\left({\vartheta }_1,{\vartheta }_2\right),$ ${\mathbb{X}}_4\left({\vartheta }_1,{\vartheta }_2\right),$ ${\mathbb{H}}_1^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)$ and ${\mathbb{H}}_2^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)$ are defined as follows:

$$\begin{array}{cc}\hfill & {\mathbb{X}}_1\left({\vartheta }_1,{\vartheta }_2\right)=\frac{2{\vartheta }_1\left(-1+ln\left(\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right)+\sqrt{{\vartheta }_1{\vartheta }_2}\left(2+ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}{2},\hfill \\ \hfill & {\mathbb{X}}_2\left({\vartheta }_1,{\vartheta }_2\right)=\frac{2{\vartheta }_1+\sqrt{{\vartheta }_1{\vartheta }_2}\left(-2+ln\left(\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right)}{2},\hfill \\ \hfill & {\mathbb{X}}_3\left({\vartheta }_1,{\vartheta }_2\right)=\frac{2{\vartheta }_2+\sqrt{{\vartheta }_1{\vartheta }_2}\left(-2+ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}{2},\hfill \\ \hfill & {\mathbb{X}}_4\left({\vartheta }_1,{\vartheta }_2\right)=\frac{2{\vartheta }_2\left(-1+ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)+\sqrt{{\vartheta }_1{\vartheta }_2}\left(2+ln\left(\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right)}{2},\hfill \\ & {\mathbb{H}}_1^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)={\vartheta }_1{v}^{-p}\left[-{\left(\frac{1}{2}ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}^{vp-1}{E}_{-vp}\left(\frac{1}{2}ln\left(\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right)+{\left(-1\right)}^{-vp-1}\Gamma \left(vp+1\right)\right],\hfill \\ & {\mathbb{H}}_2^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)={\vartheta }_2{v}^{-p}\left[-{\left(\frac{1}{2}ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}^{vp-1}{E}_{-vp}\left(\frac{1}{2}ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)+{\left(-1\right)}^{-vp-1}\Gamma \left(vp+1\right)\right].\hfill \end{array}$$

Proof. 

Using Lemma 2 as well as the properties of Hölder inequality and the geometrically convex function of $|{\aleph }^{\prime }{|}^q$, we obtain

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|=\left|\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left[{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa \right.\hfill \\ \left.-\frac{1}{\Gamma \left(v\right)}{\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left[{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right]\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right){\wp }^{\prime }\left(\kappa \right)d\kappa \right|\\ \le \frac{1}{\Gamma \left(v\right)}{\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|}^p{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{p}}\\ \times {\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|}^q{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}\\ +\frac{1}{\Gamma \left(v\right)}{\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\left(\varpi \circ \wp \right)\left(\tau \right)\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|}^p{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{p}}\\ \hfill \times {\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left|\left({\aleph }^{\prime }\circ \wp \right)\left(\kappa \right)\right|}^q{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}.\end{array}$$

Since ${\left|{\aleph }^{\prime }\right|}^q$ is a geometrically convex function on $\left[{\vartheta }_1,{\vartheta }_2\right]$, we have

$$\begin{array}{c}\left|({\aleph }^{\prime }\circ \wp )\left(\kappa \right)\right|\le {\left|{\aleph }^{\prime }\left({\vartheta }_1^{\frac{ln{\vartheta }_2-ln\wp \left(\kappa \right)}{ln{\vartheta }_2-ln{\vartheta }_1}}{\vartheta }_2^{\frac{ln\wp \left(\kappa \right)-ln{\vartheta }_1}{ln{\vartheta }_2-ln{\vartheta }_1}}\right)\right|}^q\hfill \\ \hfill \le \left(\frac{ln{\vartheta }_2-ln\wp \left(\kappa \right)}{ln{\vartheta }_2-ln{\vartheta }_1}\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+\left(\frac{ln\wp \left(\kappa \right)-ln{\vartheta }_1}{ln\left({\vartheta }_2\right)-ln{\vartheta }_1}\right){\left|{\aleph }^{\prime }\left({\vartheta }_2\right)\right|}^q.\end{array}$$

As a result, we obtain

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}\Gamma \left(v\right)}{\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|}^p{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{p}}\hfill \\ \times {\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left[\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right){\left|\aleph {}^{\prime }\left({\vartheta }_2\right)\right|}^q\right]{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}\\ +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_2\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}\Gamma \left(v\right)}{\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|}^p{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{p}}\\ \hfill \times {\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left[\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right){\left|\aleph {}^{\prime }\left({\vartheta }_2\right)\right|}^q\right]{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}.\end{array}$$

where it is obvious that

$$\begin{array}{c}{\mathbb{H}}_1^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)={\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}{\left|{\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{\kappa }{\left(ln\frac{\wp \left(\tau \right)}{{\vartheta }_1}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|}^p{\wp }^{\prime }\left(\kappa \right)d\kappa \hfill \\ \hfill ={\vartheta }_1{v}^{-p}\left[-{\left(\frac{1}{2}ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}^{vp-1}{E}_{-vp}\left(\frac{1}{2}ln\left(\frac{{\vartheta }_1}{{\vartheta }_2}\right)\right)+{\left(-1\right)}^{-vp-1}\Gamma \left(vp+1\right)\right],\end{array}$$

and

$$\begin{array}{c}{\mathbb{H}}_2^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)={\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left|{\int }_{\kappa }^{{\wp }^{-1}\left({\vartheta }_2\right)}{\left(ln\frac{{\vartheta }_2}{\wp \left(\tau \right)}\right)}^{v-1}\frac{{\wp }^{\prime }\left(\tau \right)}{\wp \left(\tau \right)}d\tau \right|}^p{\wp }^{\prime }\left(\kappa \right)d\kappa \hfill \\ \hfill ={\vartheta }_2{v}^{-p}\left[-{\left(\frac{1}{2}ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)}^{vp-1}{E}_{-vp}\left(\frac{1}{2}ln\left(\frac{{\vartheta }_2}{{\vartheta }_1}\right)\right)+{\left(-1\right)}^{-vp-1}\Gamma \left(vp+1\right)\right].\end{array}$$

By using calculations, we obtain the following inequality:

$$\begin{array}{c}\left|{\Xi }^{v,\wp }({\vartheta }_1,{\vartheta }_2)\right|\le \frac{{\left|\right|\varpi \left|\right|}_{\left[{\vartheta }_1,\sqrt{{\vartheta }_1{\vartheta }_2}\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}\Gamma \left(v\right)}{\left({\mathbb{H}}_1^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{\frac{1}{p}}\hfill \\ \times {\left({\int }_{{\wp }^{-1}\left({\vartheta }_1\right)}^{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}\left[\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right){\left|\aleph {}^{\prime }\left({\vartheta }_2\right)\right|}^q\right]{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}\\ +\frac{{\left|\right|\varpi \left|\right|}_{\left[\sqrt{{\vartheta }_1{\vartheta }_2},{\vartheta }_2\right],\infty }}{{\left(ln\frac{{\vartheta }_2}{{\vartheta }_1}\right)}^{\frac{1}{q}}\Gamma \left(v\right)}{\left({\mathbb{H}}_2^{v,p}\left({\vartheta }_1,{\vartheta }_2\right)\right)}^{\frac{1}{p}}\\ \hfill \times {\left({\int }_{{\wp }^{-1}\left(\sqrt{{\vartheta }_1{\vartheta }_2}\right)}^{{\wp }^{-1}\left({\vartheta }_2\right)}\left[\left(ln\frac{{\vartheta }_2}{\wp \left(\kappa \right)}\right){\left|{\aleph }^{\prime }\left({\vartheta }_1\right)\right|}^q+\left(ln\frac{\wp \left(\kappa \right)}{{\vartheta }_1}\right){\left|\aleph {}^{\prime }\left({\vartheta }_2\right)\right|}^q\right]{\wp }^{\prime }\left(\kappa \right)d\kappa \right)}^{\frac{1}{q}}.\end{array}$$

(33)

In order to achieve the required result (32), we must first perform some fundamental integral calculations on the basis of the inequality (33). □

Example 4.

Let $\aleph \left(\tau \right)={\tau }^2$, $\tau \in \left[\frac{1}{2},2\right]$, and then $\varpi \left(\tau \right)={\left(ln\tau \right)}^2$ and $\wp \left(\tau \right)=2\sqrt{\tau }$; hence, ${\wp }^{\prime }\left(\tau \right)=\frac{1}{\sqrt{\tau }}$ and ${\wp }^{-1}\left(\tau \right)=\frac{{\tau }^2}{4}$.

$$\begin{array}{c}\aleph \left(1\right)\left[\left({\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{+}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left(2\right)\right)+\left({\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{-}}^{v,\wp }\left(\varpi \circ \wp \right)\right)\left({\wp }^{-1}\left(\frac{1}{2}\right)\right)\right]\\ -\left[\varpi \left(2\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{+}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left(2\right)\right)+\varpi \left(\frac{1}{2}\right)\left({}_{\varpi \circ \wp }{\mathcal{I}}_{{\wp }^{-1}{\left(1\right)}^{-}}^{v,\wp }\left(\aleph \circ \wp \right)\right)\left({\wp }^{-1}\left(\frac{1}{2}\right)\right)\right]\\ \le \frac{{\left|\right|\varpi \left|\right|}_{\left[\frac{1}{2},2\right],\infty }}{{\left(ln\left(4\right)\right)}^{\frac{1}{q}}\Gamma \left(v\right)}\left\{{\left({\mathbb{H}}_1^{v,p}\left(\frac{1}{2},2\right)\right)}^{\frac{1}{p}}{\left({\mathbb{X}}_1\left(\frac{1}{2},2\right){\left|{\aleph }^{\prime }\left(\frac{1}{2}\right)\right|}^q+{\mathbb{X}}_2\left(\frac{1}{2},2\right){\left|{\aleph }^{\prime }\left(2\right)\right|}^q\right)}^{\frac{1}{q}}\right.\\ +\left.{\left({\mathbb{H}}_2^{v,p}\left(\frac{1}{2},2\right)\right)}^{\frac{1}{p}}{\left({\mathbb{X}}_3\left(\frac{1}{2},2\right){\left|{\aleph }^{\prime }\left(\frac{1}{2}\right)\right|}^q+{\mathbb{X}}_4\left(\frac{1}{2},2\right){\left|{\aleph }^{\prime }\left(2\right)\right|}^q\right)}^{\frac{1}{q}}\right\}.\end{array}$$

(34)

We observe the validity of Theorem 9.

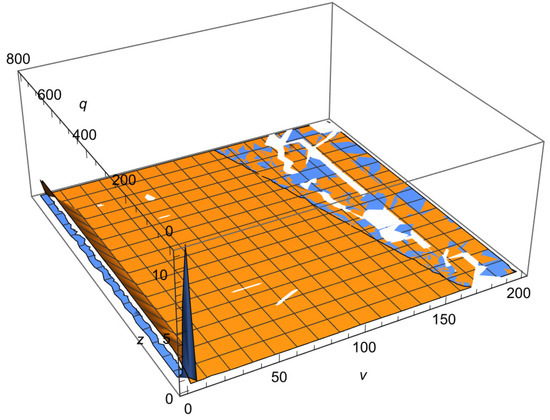
Figure 4. A graph of the error and error bound in the inequality of Theorem 9.

5. Conclusions

In this study, we show highly important and intriguing weighted-type inequalities for a very interesting generalized class of functions, namely geometrically convex functions, using a basic weighted fractional integral operator that depends on an expanding function. Our findings not only generalize a number of findings presented in [17,18,19], but they also enable the production of a number of new results by altering the rising function involved. As a result, both young researchers and those currently working in the field of fractional integral inequality can benefit from the findings, which will open up new areas of investigation in the mathematical sciences.