Star Chromatic Index of 1-Planar Graphs

Abstract

Many symmetric properties are well-explored in graph theory, especially in graph coloring, such as symmetric graphs defined by the automorphism groups, symmetric drawing of planar graphs, and symmetric functions which are used to count the number of specific colorings of a graph. This paper is devoted to studying the star edge coloring of 1-planar graphs. The star chromatic index ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)$ of a graph G is defined as the smallest k for which the edges of G can be colored by using k colors so that no two adjacent edges get the same color and no bichromatic paths or cycles of length four are produced. A graph G is called 1-planar if it can be drawn in the plane such that each edge crosses at most one other edge. In this paper, we prove that every 1-planar graph G satisfies ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 7.75\Delta +166$; and moreover ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le \lfloor 1.5\Delta \rfloor +500$ if G contains no 4-cycles, and ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 2.75\Delta +116$ if G is 3-connected, or optimal, or NIC-planar.

1. Introduction

Symmetry occurs not only in geometry, but also in other branches of mathematics. Graph coloring plays an important role in the whole history of the area of graph theory, in which many symmetric properties are widely studied, such as symmetric graphs defined by the automorphism groups, symmetric drawings of planar graphs. In 1995, Stanley studied graph colorings and related symmetric functions [1], and introduced a homogeneous symmetric function generalization of the chromatic polynomial of a graph. From then, many kind of generalizations have been studied including Tutte symmetric functions [2]. In their book, Gross, Yellen and Anderson [3] wrote a chapter ${}^{\prime \prime }$Graph Colorings and Symmetry${}^{\prime \prime }$ to explore the interplay between a graph’s symmetry and the number of different colorings of that graph.

Throughout this paper, we consider only simple graphs, i.e., without loops and multi-edges. Assume that G is a graph with vertex set $V\left(G\right)$, edge set $E\left(G\right)$, minimum degree $\delta \left(G\right)$, and maximum degree $\Delta \left(G\right)$ (for short, $\Delta$). We say that two edges of G have distance d if their distance is d in the line graph of G. Given a vertex $v\in V\left(G\right)$, we use $d_G\left(v\right)$ and $N_G\left(v\right)$ to denote the degree of v in G and the set of neighbors of v in G, respectively. If $d_G\left(v\right)=k$ or $d_G\left(v\right)\ge k$, then v is called a k-vertex or a $k^{+}$-vertex. The maximum average degree of G, denoted mad$\left(G\right)$, is defined as $max\left\{\frac{2\left|E\right(H\left)\right|}{\left|V\right(H\left)\right|}\right|H\subseteq G\}$.

If a graph G has a mapping $\varphi$ from $E\left(G\right)$ to $\{1,2,\dots ,k\}$ so that any two adjacent edges receive different values, then $\varphi$ is called an edge-k-coloring of G. If, in $\varphi$, each path of length three has distinct colors (or no path or cycle of length four is bichromatic), then $\varphi$ is called a strong edge-coloring (or star edge-coloring). The chromatic index ${\chi }^{\prime }\left(G\right)$ strong chromatic index ${\chi }_{\mathrm{s}}^{\prime }\left(G\right)$, star chromatic index ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)$, respectively) is the least k so that G is edge-k-colorable (strongly edge-k-colorable, star edge-k-colorable, respectively).

It holds trivially that ${\chi }_{\mathrm{s}}^{\prime }\left(G\right)\ge {\chi }_{\mathrm{st}}^{\prime }\left(G\right)\ge {\chi }^{\prime }\left(G\right)\ge \Delta$ for any graph G.

About the strong edge-coloring of graphs, Erdos and Nešetřil raised the following challenging conjecture:

Conjecture 1.

For a graph G,

$${\chi }_{\mathrm{s}}^{\prime }\left(G\right)\le \left\{\begin{array}{cc}1.25{\Delta }^2,\hfill & \mathrm{if}\Delta \mathrm{is}\mathrm{even};\hfill \\ 1.25{\Delta }^2-0.5\Delta +0.25,\hfill & \mathrm{if}\Delta \mathrm{is}\mathrm{odd}.\hfill \end{array}\right.$$

It was shown in [4] that ${\chi }_s^{\prime }\left(G\right)\le 1.998{\Delta }^2$ for a graph G when $\Delta$ is enough large. Very recently, Bonamy et al. [5] improved this upper bound to $1.835{\Delta }^2$. It was shown in [6] that every planar graph G has ${\chi }_{\mathrm{s}}^{\prime }\left(G\right)\le 4\Delta +4$, and there exist planar graphs H such that ${\chi }_{\mathrm{s}}^{\prime }\left(H\right)=4\Delta -4$.

The concept of the star edge-coloring of graphs was introduced by Liu and Deng [7]. They showed that ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le \lceil 16{(\Delta -1)}^{\frac{3}{2}}\rceil$ if G is a graph with $\Delta \ge 7$. In 2013, Dvořák et al. [8] first established the following result for a complete graph $K_n$,

$${\chi }_{\mathrm{st}}^{\prime }\left(K_n\right)\le \frac{2^{2\sqrt{2}(1+o\left(1\right))\sqrt{logn}}}{{(logn)}^{\frac{1}{4}}}n,$$

and then used it to prove that ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le \Delta 2^{O\left(1\right)\sqrt{log\Delta }}$ for any graph G.

Suppose that G is a subcubic graph, i.e., a graph with maximum degree at most three. It was showed in [8] that ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 7$ and conjectured that 6 is enough. This result has been extended from two aspects below. Lužar et al. [9] showed that G is list star edge-7-colorable. Lei et al. [10] proved that ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 6$ if mad$\left(G\right)<\frac{5}{2}$, and ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 5$ if mad$\left(G\right)<\frac{24}{11}$.

In 2016, Bezegová et al. [11] verified: (i) a forest F has ${\chi }_{\mathrm{st}}^{\prime }\left(F\right)\le \lfloor 1.5\Delta \rfloor$; (ii) an outerplanar graph G has ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le \lfloor 1.5\Delta \rfloor +12$. Note that the upper bound $\lfloor 1.5\Delta \rfloor$ of (i) is tight and the number 12 in (ii) was conjectured to be replaced by 1. By using an edge-partition technique, Wang et al. [12] improved and extended the results in [11] as follows:

Theorem 1

([12]). Let G be a planar graph. Then

(1) ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 2.75\Delta +18$.

(2) ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le \lfloor 1.5\Delta \rfloor +18$ if G has no 4-cycles.

(3) ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le \lfloor 1.5\Delta \rfloor +5$ if G is outerplanar.

If a graph G can be drawn in the plane such that each edge crosses at most one other edge, then G is called a 1-planar graph. It was shown in [13] that every 1-planar graph G has $\left|E\right(G\left)\right|\le 4\left|V\right(G\left)\right|-8$, and $\delta \left(G\right)\le 7$. Note that the largest complete graph that is not 1-planar is $K_6$, and there exists a 7-regular 1-planar graph $G^{\prime }$, as shown in Figure 1. Observe that both $K_6$ and $G^{\prime }$ are symmetric with respect to their vertices.

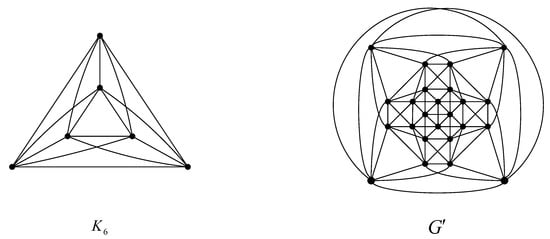
Figure 1. Compete graph $K_6$ and 7-regular 1-planar graph $G^{\prime }$.

Call a 1-planar graph Goptimal if $\left|E\right(G\left)\right|=4\left|V\right(G\left)\right|-8$, NIC-planar if any two pairs of crossing edges have at most one common end-vertices, and IC-planar if any two pairs of crossing edges have no common end-vertices. Recently, Wang et al. [14] studied the strong edge-coloring of 1-planar graphs and obtained the following results:

Theorem 2

([14]). Let G be a 1-planar graph. Then

(1) ${\chi }_{\mathrm{s}}^{\prime }\left(G\right)\le 14\Delta$.

(2) ${\chi }_{\mathrm{s}}^{\prime }\left(G\right)\le 10\Delta +14$ if G is optimal.

(3) ${\chi }_{\mathrm{s}}^{\prime }\left(G\right)\le 6\Delta +20$ if G is IC-planar.

This paper is devoted to discuss the star edge-coloring of 1-planar graphs. The main results obtained are described in the Abstract.

2. Edge-Partition

Suppose that $G_1,G_2$, and G are three graphs with same vertex set. If $E\left(G\right)=E\left(G_1\right)\cup E\left(G_2\right)$ and $E\left(G_1\right)\cap E\left(G_2\right)=\varnothing$, then $(G_1,G_2)$ is said to be an edge-partition of G.

Let G be a 1-planar graph. Ackerman [15] showed that G admits an edge-partition into a planar graph and a forest. We say that G is k-nice, where k is a fixed constant, if G can be edge-partitioned into two planar graphs $G_1$ and $G_2$ such that $\Delta \left(G_2\right)\le k$. It is easy to check that IC-planar graph is 1-nice. Moreover, for our purpose, we list the following more interesting results on k-nice 1-planar graphs.

Lemma 1

([16]). NIC-planar graphs are 3-nice, and the result is the best possible.

Lemma 2

([17]). Optimal 1-planar graphs are 4-nice, and the result is the best possible.

Lemma 3

([18]). All 3-connected 1-planar graphs are 6-nice, and the result is the best possible.

To bind the linear 2-arboricity of 1-planar graphs, Liu et al. [19] established the following structural theorem:

Lemma 4

([19]). Every 1-planar graph G with $\Delta \ge 26$ can be edge-partitioned into two forests $F_1,F_2$ and a graph K such that $\Delta \left(K\right)\le 24$ and $\Delta \left(F_i\right)\le \lceil \frac{\Delta -23}{2}\rceil$ for $i=1,2$.

Corollary 1.

Every 1-planar graph G with $\Delta \ge 26$ can be edge-partitioned into a forest F and a graph H such that $\Delta \left(F\right)\le \lceil \frac{\Delta -23}{2}\rceil$ and $\Delta \left(H\right)\le \lceil \frac{\Delta +25}{2}\rceil$.

Proof. 

By Lemma 4, G has an edge-partition $(F_1,F_2,K)$ such that $F_i$ is a forest with $\Delta \left(F_i\right)\le \lceil \frac{\Delta -23}{2}\rceil$ for $i=1,2$, and K is a graph with $\Delta \left(K\right)\le 24$. Define $F=F_1$ and $H=F_2\cup K$. Then $(F,H)$ is an edge-partition of G such that F is a forest with $\Delta \left(F\right)\le \lceil \frac{\Delta -23}{2}\rceil$ and $\Delta \left(H\right)\le \Delta \left(F_2\right)+\Delta \left(K\right)\le \lceil \frac{\Delta -23}{2}\rceil +24=\lceil \frac{\Delta +25}{2}\rceil$. □

Given a graph G, identifying its vertices x and y means that gluing $x,y$ into a new vertex z such that each of the edges incident to x or y in G is joined to z. An edge e of G is contracted if it is deleted and its end-vertices are identified. Call an edge $e=xy$ of G$(i,j)$-edge if $d_G\left(x\right)=i$ and $d_G\left(y\right)=j$. Set $M\left(e\right)=max\{d_G\left(x\right),d_G\left(y\right)\}$, and define $M^{*}\left(G\right)=min\left\{M\left(e\right)\right|e\in E\left(G\right)\}$.

The following lemma implies the existence of a light edge in a 1-planar graph with minimum degree at least three.

Lemma 5

([20]). Let G be a 1-planar graph with $\delta \left(G\right)\ge 3$. Then $M^{*}\left(G\right)\le 20$.

Let G be a 1-planar graph which is drawn in the plane such that each edge has at most one crossing. Moreover, we may require that the number of crossings in G is as few as possible. Let $X\left(G\right)$ denote the set of crossings in G. Define the associated plane graph H of G as follows:

$$V\left(H\right)=V\left(G\right)\cup X\left(G\right),$$

$$E\left(H\right)=E_0\left(G\right)\cup E_1\left(G\right),$$

where $E_0\left(G\right)$ denotes the set of non-crossed edges in G and

$E_1\left(G\right)=\{xz,zy|xy\in E\left(G\right)\setminus E_0\left(G\right)$ and z is a crossing on $xy\}.$

We say that a vertex $u\in V\left(H\right)$ is true if $u\in V\left(G\right)$, and false if $u\in X\left(G\right)$. Clearly, $d_H\left(u\right)=d_G\left(u\right)$ if $u\in V\left(G\right)$, and $d_H\left(u\right)=4$ if $u\in X\left(G\right)$. Since G is 1-planar, there do not exist two adjacent false vertices in H.

Theorem 3.

If G is a 1-planar graph with $\delta \left(G\right)\ge 2$ and without 4-cycles, then $M^{*}\left(G\right)\le 40$.

Proof. 

If $\delta \left(G\right)\ge 3$, then the result holds from Lemma 5. Thus assume that $\delta \left(G\right)=2$. Suppose that the theorem is not true, i.e., $M^{*}\left(G\right)\ge 41$. Let v be any 2-vertex of G with neighbors x and y. Then $d_G\left(x\right)\ge 41$ and $d_G\left(y\right)\ge 41$. Let H be the associated plane graph of G such that the number of crossings is as few as possible. If $vx$ is a crossing edge of G with crossing $x^{\times }$, then $x^{\times }$ is a false vertex of H that satisfies $v{x}^{\times },x^{\times }x\in E\left(H\right)$ and $vx\notin E\left(H\right)$. Let $\rho \left(v\right)$ denote the number of crossing edges of G in $\{vx,vy\}$. Then $0\le \rho \left(v\right)\le 2$. We say that v is of type 1 if $xy\in E\left(G\right)$ and type 2 if $xy\notin E\left(G\right)$.

We need to define the following operations (OP1)–(OP4):

 (OP1) 

If v is of type 1, then remove the vertex v.

 (OP2) 

If v is of type 2 and $\rho \left(v\right)\le 1$, say $vy\in E\left(H\right)$ by the symmetry of x and y, then contract the edge $vy$.

Assume that v is of type 2 and $\rho \left(v\right)=2$. To introduce (OP3), we define an auxiliary graph B in the following way. Let S denote the set of all type 2 2-vertices u in H with $\rho \left(u\right)=2$. Then each $u\in S$ is adjacent to two false vertices in H. Let T denote the set of false vertices in H which are adjacent to at least one vertex in S. Let $B=H[S\cup T]$, which is an induced subgraph of H on the set $S\cup T$. □

 Claim 1. 

B is a bipartite graph with$\Delta \left(B\right)=2$.

Proof. 

It follows from $M^{*}\left(G\right)\ge 41$ that H contains no adjacent 2-vertices, so no two vertices in S are adjacent. Because H contains no adjacent false vertices, no two vertices in T are adjacent. Hence B is a bipartite graph with bipartitions S and T. Obviously, $d_B\left(x\right)=d_H\left(x\right)=2$ for every $x\in S$. Moreover, because $M^{*}\left(G\right)\ge 41$, every false vertex is adjacent to at most two 2-vertices in H. Hence $\Delta \left(B\right)\le 2$. Noting that $S\ne \varnothing$, we derive that $\Delta \left(B\right)=2$. This completes the proof of Claim 1. □

Let C be a component of B. By Claim 1, C is an even cycle of length at least 4 or a path of length at least 2 from a false vertex to another false vertex.

First, suppose that C is not a path of length 2, say $C=z_1{u}_1{z}_2{u}_2\cdots z_k{u}_k{z}_1$ is an even cycle or $C=z_1{u}_1{z}_2\cdots u_k{z}_{k+1}$ is a path, where $u_1,u_2,\dots ,u_k\in S$, $z_1,z_2,\dots ,z_{k+1}\in T$, and $k\ge 2$.

Let $z_i{u}_i{z}_{i+1}{u}_{i+1}{z}_{i+2}$ be a sub-path of C, where $u_i,u_{i+1}\in S$ and $z_i,z_{i+1},z_{i+2}\in T$. Then $d_H\left(u_i\right)=d_H\left(u_{i+1}\right)=2$ and $d_H\left(z_i\right)=d_H\left(z_{i+1}\right)=d_H\left(z_{i+2}\right)=4$. Let the neighbors of $z_{i+1}$ in H are $u_i,u_{i+1},u_i^{\prime },u_{i+1}^{\prime }$ in a cyclic order. Then $u_i{u}_i^{\prime }$ and $u_{i+1}{u}_{i+1}^{\prime }$ are two crossing edges of G. It is easy to check that no vertex in $\{u_i,u_{i+1}\}$ is joined to any vertex in $\{u_i^{\prime },u_{i+1}^{\prime }\}$. Define the following operation, as shown in Figure 2:

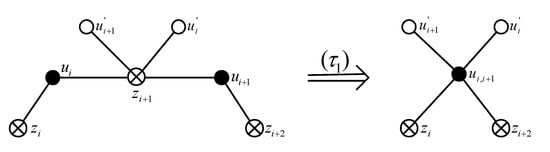
Figure 2. $\left({\tau }_1\right)$ acting on the set $\{u_i,u_{i+1}\}$.

(${\tau }_1$) Remove $z_{i+1}$, identify $u_i$ and $u_{i+1}$ into a new vertex $u_{i,i+1}$, and then join $u_{i,i+1}$ to each of $u_i^{\prime }$ and $u_{i+1}^{\prime }$.

In all figures of this paper, vertices marked • have no edges of H incident with them other than those shown, vertices marked ∘ may have edges connected to other vertices of H not in the configuration, and vertices marked ⊗ are false vertices of H.

We say that $\left({\tau }_1\right)$ is an operator acted on the set $\{u_i,u_{i+1}\}$.

Because $u_i$ and $u_{i+1}$ lie in the boundary of some common face of H, $\left({\tau }_1\right)$ can be reasonably defined, i.e., the resultant graph is a simple 1-planar graph. The following Remark 1 holds obviously.

Remark 1.

Let $H_1$ be the graph obtained from H by acting $\left({\tau }_1\right)$ on the set $\{u_i,u_{i+1}\}$. Then

$\left(1\right)$$d_{H_1}\left(u_{i,i+1}\right)=4$;

$\left(2\right)$ For each vertex $t\in \{z_i,z_{i+2},u_i^{\prime },u_{i+1}^{\prime }\}$, $d_{H_1}\left(t\right)=d_H\left(t\right)$.

Let $z_i{u}_i{z}_{i+1}{u}_{i+1}{z}_{i+2}{u}_{i+2}{z}_{i+3}$ be a sub-path of C, where $u_i,u_{i+1},u_{i+2}\in S$ and $z_i,z_{i+1},z_{i+2},z_{i+3}\in T$. Assume that the neighbors of $z_{i+1}$ in H are $u_i,u_{i+1},u_i^{\prime },u_{i+1}^{\prime }$ in a cyclic order, and the neighbors of $z_{i+2}$ in H are $u_{i+1},u_{i+2},u_{i+1}^{\prime \prime },u_{i+2}^{\prime }$ in a cyclic order. Similarly, no vertex in $\{u_i,u_{i+1}\}$ is adjacent to any vertex in $\{u_i^{\prime },u_{i+1}^{\prime }\}$, and no vertex in $\{u_{i+1},u_{i+2}\}$ is adjacent to any vertex in $\{u_{i+1}^{\prime \prime },u_{i+2}^{\prime }\}$. Note that $u_{i+1}^{\prime }\ne u_{i+1}^{\prime \prime }$, for otherwise G will contain a multi-edge. Moreover, if $u_{i+1}^{\prime }=u_{i+2}^{\prime }$, then G will admit a new plane drawing such that $z_{i+1}$ may not exist, which contradicts the assumption that the number of crossings in G is as few as possible. Hence the only possibility for two vertices in $\{u_i^{\prime },u_{i+1}^{\prime },u_{i+1}^{\prime \prime },u_{i+2}^{\prime }\}$ to be same is that $u_i^{\prime }=u_{i+2}^{\prime }$. To deal with this case, we define the following operation (see Figure 3):

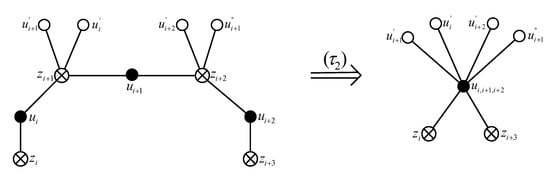
Figure 3. $\left({\tau }_2\right)$ acting on the set $\{u_i,u_{i+1},u_{i+2}\}$.

(${\tau }_2$) Remove $z_{i+1},z_{i+2}$, identify $u_i,u_{i+1},u_{i+2}$ into a new vertex $u_{i,i+1,i+2}$, and then join $u_{i,i+1,i+2}$ to each of $u_i^{\prime },u_{i+1}^{\prime },u_{i+1}^{\prime \prime },u_{i+2}^{\prime }$.

Note that when $u_i^{\prime }=u_{i+2}^{\prime }$, i.e., $u_i^{\prime }$ and $u_{i+2}^{\prime }$ coincide into a vertex w, we connect only one edge between w and $u_{i,i+1,i+2}$. This guarantees that the resultant graph is still a simple plane graph. Similarly, $\left({\tau }_2\right)$ is called an operator acted on the set $\{u_i,u_{i+1},u_{i+2}\}$.

As an easy observation, we have the following:

Remark 2.

Let $H_2$ be the graph obtained from H by acting $\left({\tau }_2\right)$ on the set $\{u_i,u_{i+1},u_{i+2}\}$. Then

$\left(1\right)$$5\le d_{H_2}\left(u_{i,i+1,i+2}\right)\le 6$; and $d_{H_2}\left(u_{i,i+1,i+2}\right)=5$ if and only if $u_i^{\prime }=u_{i+2}^{\prime }$;

$\left(2\right)$ For $j\in \{i,i+2\}$, $d_H\left(u_j^{\prime }\right)-1\le d_{H_2}\left(u_j^{\prime }\right)\le d_H\left(u_j^{\prime }\right)$; and $d_{H_2}\left(u_j^{\prime }\right)=d_H\left(u_j^{\prime }\right)-1$ if and only if $u_i^{\prime }=u_{i+2}^{\prime }$;

$\left(3\right)$ For each vertex $t\in \{z_i,z_{i+3},u_{i+1}^{\prime },u_{i+1}^{\prime \prime }\}$, $d_{H_2}\left(t\right)=d_H\left(t\right)$.

Based on (${\tau }_1$) and (${\tau }_2$), we furthermore define the following operation:

(OP3) If k is even, then act $\left({\tau }_1\right)$ on $\{u_1,u_2\}$, $\{u_3,u_4\}$, …, $\{u_{k-1},u_k\}$, respectively. If k is odd, then act $\left({\tau }_2\right)$ on $\{u_1,u_2,u_3\}$, and $\left({\tau }_1\right)$ on $\{u_4,u_5\}$, …, $\{u_{k-1},u_k\}$, respectively.

Next, suppose that $C=z_1{u}_1{z}_2$ is a path of length 2 with $u_1\in S$ and $z_1,z_2\in T$. Let the neighbors of $z_1$ in H be $u_1,w_1,u_1^{\prime },v_1$ in a cyclic order. Then $w_1,v_1$ are true $3^{+}$-vertices of H, $d_H\left(u_1^{\prime }\right)\ge 41$, and $u_1{u}_1^{\prime },w_1{v}_1\in E\left(G\right)$. Because H is a simple graph, at least one of $w_1$ and $v_1$ is not adjacent to $z_2$, say $z_2{w}_1\notin E\left(H\right)$.

In view of the symmetry of the vertices $z_1$ and $z_2$, we carry out the following operation, see Figure 4:

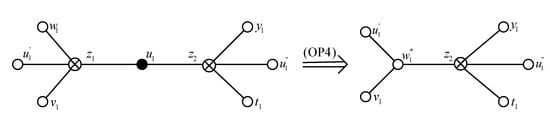
Figure 4. (OP4) acting on the set $\{u_1,w_1\}$.

(OP4) Remove $z_1$, and then identify $u_1$ and $w_1$ into a new vertex $w_1^{*}$. If $u_1^{\prime }{w}_1\in E\left(G\right)$, then join $w_1^{*}$ to $v_1$; otherwise, join $w_1^{*}$ to each of $u_1^{\prime }$ and $v_1$.

Let $H_3$ denote the resultant graph after (OP4) are carried out. It is easy to see that $H_3$ is a simple plane graph. Moreover, the following Remark 3 holds clearly:

Remark 3.

$\left(1\right)$$d_H\left(w_1\right)+1\le d_{H_3}\left(w_1^{*}\right)\le d_H\left(w_1\right)+2$; and $d_{H_3}\left(w_1^{*}\right)=d_H\left(w_1\right)+1$ if and only if $w_1{u}_1^{\prime }\in E\left(H\right)$;

$\left(2\right)$$d_H\left(u_1^{\prime }\right)-1\le d_{H_3}\left(u_1^{\prime }\right)\le d_H\left(u_1^{\prime }\right)$; and $d_{H_3}\left(u_1^{\prime }\right)=d_H\left(u_1^{\prime }\right)-1$ if and only if $w_1{u}_1^{\prime }\in E\left(H\right)$;

$\left(3\right)$$d_{H_3}\left(v_1\right)=d_H\left(v_1\right)$, and $d_{H_3}\left(z_2\right)=d_H\left(z_2\right)$.

By Remark 3(1), $d_{H_3}\left(w_1^{*}\right)\ge d_H\left(w_1\right)+1\ge 3+1=4$.

Let $H^{*}$ denote the resultant graph obtained from H by carrying out (OP1)-(OP4) for all 2-vertices of H. Then $H^{*}$ is a simple plane graph, which is the associated plane graph of some 1-planar graph K. Namely, we can construct a graph K from $H^{*}$ by performing the following operation for each false vertex x: Assuming that the neighbors of x in $H^{*}$ are $x_1,x_2,x_3,x_4$ in a cyclic order, then we remove x and add the diagonal edges $x_1{x}_3$ and $x_2{x}_4$. It is easy to inspect that K is a simple 1-planar graph, and it may contain 4-cycles.

Let $V\left(K\right)=V_1\cup V_2$, where $V_1$ is the set of new vertices added when carrying out (OP3) and (OP4), and $V_2=V\left(K\right)\setminus V_1$. Then $V_2\subseteq V\left(G\right)$.

 Claim 2. 

$\delta \left(K\right)\ge 3$.

Proof. 

It suffices to show that $d_K\left(v\right)\ge 3$ for each vertex $v\in V\left(K\right)$. If $v\in V_1$, i.e., v is a vertex of form $u_{i,i+1},u_{i,i+1,i+2}$ and $w_1^{*}$, then Remarks 1–3 claim that $d_K\left(v\right)\ge 4$. Otherwise, $v\in V_2$. (OP1)-(OP4) imply that $d_G\left(v\right)\ge 3$. Let

$n_3^{+}\left(v\right)=\left|\{x\in N_G\left(v\right)|d_G\left(x\right)\ge 3\}\right|$,

$n_2\left(v\right)=\left|\{x\in N_G\left(v\right)|d_G\left(x\right)=2\}\right|$.

For $i=1,2$, let $n_2^i\left(v\right)$ denote the number of 2-vertices of type i adjacent to v in G. From (OP1)-(OP4), we can see that if $v{v}^{\prime }\in E\left(G\right)$ with $d_G\left(v^{\prime }\right)\ge 3$, then $v^{\prime }\in V\left(K\right)$ and $v{v}^{\prime }$ is still an edge of K. This implies that $d_K\left(v\right)\ge n_3^{+}\left(v\right)$. So, if $n_3^{+}\left(v\right)\ge 3$, then we are done. Otherwise, $n_3^{+}\left(v\right)\le 2$. Because $d_G\left(v\right)\ge 3$, v is adjacent to a 2-vertex y in G. Because $vy\in E\left(G\right)$ and $M^{*}\left(G\right)\ge 41$, it follows that $n_2\left(v\right)=d_G\left(v\right)-n_3^{+}\left(v\right)\ge 41-2=39$. Let $v^{\prime }\in N_G\left(v\right)$ with $d_G\left(v^{\prime }\right)\ge 3$. Because G contains no 4-cycles, there exists at most one 2-vertex, say x, such that $x,v,v^{\prime }$ forms a 3-cycle of G, i.e., x is a 2-vertex of type 1 in G. So it follows that $n_2^1\left(v\right)\le n_3^{+}\left(v\right)\le 2$, and therefore $n_2^2\left(v\right)=n_2\left(v\right)-n_2^1\left(v\right)\ge 39-2=37$.

For $0\le k\le 2$, let $U_k$ denote the set of type 2 2-vertices $x\in N_G\left(v\right)$ with $\rho \left(x\right)=k$. Suppose that $y\in U_0\cup U_1$, and let $y^{\prime }$ be the neighbor of y other than v. Then $v{y}^{\prime }\notin E\left(G\right)$. By (OP2), we need to remove y and then add the edge $v{y}^{\prime }$ to the resultant graph. Then $v{y}^{\prime }\in E\left(K\right)$. So, when $|U_0|+|U_1|\ge 3$, we have that $d_K\left(v\right)\ge |U_0|+|U_1|\ge 3$. Otherwise, $|U_0|+|U_1|\le 2$, so that $|U_2|=n_2^2\left(v\right)-\left(\right|U_0|+|U_1\left|\right)\ge 37-2=35$. Namely, there are at least 35 2-vertices in $U_2$ which are required to carry out (OP3) or (OP4). It is easy to observe that when (OP3) or (OP4) is performed once, the degree of v in K is increased by at least one. It therefore follows that $d_K\left(v\right)\ge ⌊\frac{|U_2|}{3}⌋\ge \lfloor \frac{35}{3}\rfloor =11$. This proves Claim 2. □

By Claim 2 and Lemma 5, K contains an edge $e=xy$ such that $d_K\left(x\right),d_K\left(y\right)\le 20$.

 Claim 3. 

There is an edge $e^{\prime }=x^{\prime }{y}^{\prime }\in E\left(G\right)$such that$d_G\left(x^{\prime }\right),d_G\left(y^{\prime }\right)\le 40$.

Proof. 

The proof is split into two cases as follows. □

Case 1.$xy\in E\left(G\right)$.

There exist $x^{\prime },y^{\prime }\in V\left(G\right)$ such that $x^{\prime }$ corresponds to x, and $y^{\prime }$ corresponds to y. In light of the symmetry of x and y, it suffices to define $x^{\prime }$ and to prove that $d_G\left(x^{\prime }\right)\le 40$. There are two possibilities as follows.

Case 1.1.$x\in V_1$.

Assume that x is generated by acting (${\tau }_1$) on two 2-vertices of G, say $u_i$ and $u_{i+1}$. Then $x=u_{i,i+1}$ and $d_K\left(x\right)=4$ by Remark 1(1). So $x^{\prime }$ can be defined as exactly one of $u_i$ and $u_{i+1}$ such that $d_G\left(x^{\prime }\right)=2$.

Assume that x is generated by acting (${\tau }_2$) on three 2-vertices of G, say $u_i,u_{i+1},u_{i+2}$. Then $x=u_{i,i+1,i+2}$ and $5\le d_K\left(x\right)\le 6$ by Remark 2(1). So $x^{\prime }$ is exactly one of $u_i,u_{i+1}$ and $u_{i+2}$ such that $d_G\left(x^{\prime }\right)=2$.

Assume, by symmetry, that x is generated by carrying out (OP4) for a 2-vertex, say $u_1$, and a $3^{+}$-vertex, say $w_1$, of G. Then $x=w_1^{*}$, and $x^{\prime }$ is exactly one of $u_1$ and $w_1$ such that $d_G\left(x^{\prime }\right)\le max\{d_G\left(u_1\right),d_G\left(w_1\right)\}<d_K\left(x\right)\le 20$ by Remark 3(1).

Case 1.2.$x\in V_2$.

Set $x^{\prime }=x$, and let $z\in N_K\left(x\right)$. There are two possibilities to be handled.

Assume that $z\in V\left(G\right)$ with $d_G\left(z\right)\ge 3$. If $z{x}^{\prime }\in E\left(G\right)$, then because G contains no 4-cycles, there exists at most one 2-vertex $z^{\prime }\in V\left(G\right)$ such that $z{z}^{\prime },z^{\prime }{x}^{\prime }\in E\left(G\right)$. By (OP1), the degree of $x^{\prime }$ in G caused by z is at most two. Otherwise, $z{x}^{\prime }\notin E\left(G\right)$. There exists a 2-vertex $t\in V\left(G\right)$ such that $zt,t{x}^{\prime }\in E\left(G\right)$. In this case, t is a neighbor of $x^{\prime }$ in G. By (OP2), the degree of $x^{\prime }$ in G caused by z stays unchanged.

Assume that $z\in V_1$. Then, by (OP3), (OP4) and Remarks 1-3, z can be split into at most three vertices in G, at most two of which are adjacent to $x^{\prime }$. Thus, the degree of $x^{\prime }$ in G caused by z is at most two.

The above analysis implies that $d_G\left(x^{\prime }\right)\le 2d_K\left(x\right)\le 40$.

Case 2.$xy\notin E\left(G\right)$.

Then there is a 2-vertex $t\in V\left(G\right)$ such that $xt,ty\in E\left(G\right)$ by (OP2)-(OP4). Set $x^{\prime }=x$ and $y=t$. Repeating the proof for Case 1, we can conclude that $d_G\left(x^{\prime }\right)\le 40$. This completes the proof of Claim 3.□

Claim 3 implies that $M\left(x^{\prime }{y}^{\prime }\right)\le 40$, which contradicts the assumption that $M^{*}\left(G\right)\ge 41$. This proves Theorem 3.□

The condition that G contains no 4-cycles in Theorem 3 is essential. For example, $K_{2,n}$ is a 1-planar graph (in fact, planar) with many 4-cycles, so that $M^{*}\left(K_{2,n}\right)=n$ is not bounded by any given constant. Moreover, it should be pointed out that, in the proof of Theorem 3, we employed the symmetry of subgraphs considered many times.

Now, by using Theorem 3 and Theorem 2 in [21], we obtain the following important edge-partition theorem of 1-planar graphs without 4-cycles.

Theorem 4.

Let G be a 1-planar graph with $\Delta \left(G\right)\ge 41$ and without 4-cycles. Then G has an edge-partition $(F,H)$ such that F is a forest with $\Delta \left(F\right)=\Delta \left(G\right)-39$ and H is a graph with $\Delta \left(H\right)=39$.

3. Star Chromatic Index

Let G be a graph and M be a matching of G. M is called strong if $G\left[V\right(M\left)\right]=M$. Note that finding the strong chromatic index ${\chi }_{\mathrm{s}}^{\prime }\left(G\right)$ of G is equivalent to determine the least k such that $E\left(G\right)$ can be partitioned into k edge-disjoint strong matchings. M is said to be partitioned into q strong matchings of G if $M=M_1\cup M_2\cup \cdots \cup M_q$, $M_i\cap M_j=\varnothing$ for $i\ne j$, and each $M_i$ is a strong matching of G. Let ${\rho }_G\left(M\right)$ denote the least q such that M can be partitioned into q strong matchings. By definition, $1\le {\rho }_G\left(M\right)\le \left|M\right|$.

Lemma 6

([14]). If M is a matching of a 1-planar graph G, then ${\rho }_G\left(M\right)\le 14$.

For a subgraph H of a graph G, we use ${\chi }_{\mathrm{s}}^{\prime }\left(H{|}_G\right)$ to denote the least l for which H has an edge-l-coloring such that any two edges of H with at distance at most two in G receive distinct colors.

Lemma 7

([12]). If a graph G has an edge-partition $(K,H)$, then ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le {\chi }_{\mathrm{st}}^{\prime }\left(K\right)+{\chi }_{\mathrm{s}}^{\prime }\left(H{|}_G\right).$

To apply effectively Lemma 7, we need furthermore to evaluate the value of ${\chi }_{\mathrm{s}}^{\prime }\left(H{|}_G\right)$.

Theorem 5.

Suppose that $(K,H)$ is an an edge-partition of a 1-planar graph G. If ${\chi }^{\prime }\left(H\right)=k$, then ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le {\chi }_{\mathrm{st}}^{\prime }\left(F\right)+14k$.

Proof. 

By Lemma 7, ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le {\chi }_{\mathrm{st}}^{\prime }\left(F\right)+{\chi }_{\mathrm{s}}^{\prime }\left(H{|}_G\right)$. To estimate ${\chi }_{\mathrm{s}}^{\prime }\left(H{|}_G\right)$, we first give an edge-k-coloring $\varphi$ of H by using the colors $1,2,\dots ,k$. For $1\le i\le k$, let $E_i$ denote the set of edges in H having the color i. Then $E_i$ is a matching of H. By Lemma 6, ${\rho }_G\left(E_i\right)\le 14$. So it follows easily that ${\chi }_{\mathrm{s}}^{\prime }\left(H{|}_G\right)\le {\rho }_G\left(E_1\right)+{\rho }_G\left(E_2\right)+\cdots +{\rho }_G\left(E_k\right)\le 14k$.

□

The celebrated Vizing theorem says that every simple graph G is edge-$(\Delta +1)$-colorable. That is, the following result holds.

 Lemma 8. 

([22])For a simple graph G, $\Delta \le {\chi }^{\prime }\left(G\right)\le \Delta +1$.

Now, by using the previously preliminary results, we start with proving one of the main results in this paper, i.e., Theorem 6. This theorem tells us that the star chromatic index of some special 1-planar graphs is at most $2.75\Delta$ plus a absolute constant.

Theorem 6.

Let G be a 1-planar graph.

$\left(1\right)$ If G is 3-connected, then ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 2.75\Delta +116$.

$\left(2\right)$ If G is optimal, then ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 2.75\Delta +88$.

$\left(3\right)$ If G is NIC-planar, then ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 2.75\Delta +74$.

$\left(4\right)$ If G is IC-planar, then ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 2.75\Delta +32$.

 Proof. 

(1) Because G is 3-connected, Lemma 3 claims that G has an edge-partition into two planar graphs $G_1$ and $G_2$ such that $\Delta \left(G_2\right)\le 6$. By Theorem 1(1), ${\chi }_{\mathrm{st}}^{\prime }\left(G_1\right)\le 2.75\Delta \left(G_1\right)+18\le 2.75\Delta +18$. By Lemma 8, ${\chi }^{\prime }\left(G_2\right)\le \Delta \left(G_2\right)+1\le 6+1=7$. By Theorem 5, ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le {\chi }_{\mathrm{st}}^{\prime }\left(G_1\right)+14{\chi }^{\prime }\left(G_2\right)\le 2.75\Delta +18+14\times 7=2.75\Delta +166$.

By using Lemmas 1 and 2, we can similarly show (2) and (3). For (4), it suffices to notice that the chromatic index of a matching is at most 1. □

The following Theorem 7 gives actually an almost optimal upper bound (away from a constant) for the star chromatic index of 1-planar graphs without 4-cycles. To show it, we need to introduce two known results.

Lemma 9

([11]). Every forest F has ${\chi }_{\mathrm{st}}^{\prime }\left(F\right)\le \lfloor 1.5\Delta \rfloor$; and the upper bound is tight.

Lemma 10

([23]). Every 1-planar graph G with $\Delta \ge 10$ has ${\chi }^{\prime }\left(G\right)=\Delta$.

Theorem 7.

Every 1-planar graph G without 4-cycles has ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le \lfloor 1.5\Delta \rfloor +500$.

Proof. 

If $\Delta \le 40$, then by Theorem 2(1) we derive that ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le {\chi }_{\mathrm{s}}^{\prime }\left(G\right)\le 14\Delta \le \lfloor 1.5\Delta \rfloor +500$. If $\Delta \ge 41$, then Theorem 4 claims that G can be edge-partitioned into a forest F and a subgraph H such that $\Delta \left(F\right)=\Delta -39$ and $\Delta \left(H\right)=39$. By Lemma 10, ${\chi }^{\prime }\left(H\right)=\Delta \left(H\right)$. It follows from Theorem 5 and Lemma 9 that ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le {\chi }_{\mathrm{st}}^{\prime }\left(F\right)+14{\chi }^{\prime }\left(H\right)\le \lfloor 1.5\Delta \left(F\right)\rfloor +14\Delta \left(H\right)=\lfloor 1.5(\Delta -39)\rfloor +14\times 39<\lfloor 1.5\Delta \rfloor +500.$ □

Finally, we consider the star chromatic index of general 1-planar graphs by giving a linear upper bound about $\Delta$. It is unknown whether or not this upper bound is tight.

Theorem 8.

Let G be a 1-planar graph. Then ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 7.75\Delta +166$.

Proof. 

If $\Delta \le 25$, then it is easy to derive by Theorem 2(1) that ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le {\chi }_{\mathrm{s}}^{\prime }\left(G\right)\le 14\Delta <7.75\Delta +166$. Otherwise, $\Delta \ge 26$. By Corollary 1, G can be edge-partitioned into a forest F and a graph H such that $\Delta \left(F\right)\le \lceil \frac{\Delta -23}{2}\rceil$ and $\Delta \left(H\right)\le \lceil \frac{\Delta +25}{2}\rceil$. Because $\Delta \ge 26$, we deduce that ${\chi }^{\prime }\left(H\right)\le \lceil \frac{\Delta +25}{2}\rceil$ by Lemmas 8 and 10. Hence, by Theorem 5 and Lemma 9, we have the following:

$$\begin{array}{ccc}\hfill {\chi }_{\mathrm{st}}^{\prime }\left(G\right)& \le & {\chi }_{\mathrm{st}}^{\prime }\left(F\right)+14{\chi }^{\prime }\left(H\right)\hfill \\ & \le & \lfloor 1.5\Delta \left(F\right)\rfloor +14⌈\frac{\Delta +25}{2}⌉\hfill \\ & \le & ⌊1.5⌈\frac{\Delta -23}{2}⌉⌋+14⌈\frac{\Delta +25}{2}⌉\hfill \\ & \le & 7.75\Delta +166.\hfill \end{array}$$

□

4. Concluding Remarks

In this paper, we prove that the star chromatic index of 1-planar graphs G is at most $7.75\Delta +166$, but when G is 3-connected, ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le 2.75\Delta +116$. We feel that these results are not best possible, and hence put forward the following problem:

Problem 1.

Determine the smallest constants $a_1$ and $b_1$ such that every 1-planar graph G has ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le a_1\Delta +b_1$.

Because there exists a tree T such that ${\chi }_{\mathrm{st}}^{\prime }\left(T\right)=\lfloor 1.5\Delta \rfloor$, we infer that $a_1\ge 1.5$.

Theorem 7 asserts that if a 1-planar graph G does not contain 4-cycles, then ${\chi }_{\mathrm{st}}^{\prime }\left(T\right)\le \lfloor 1.5\Delta \rfloor +500$. Here the constant 500 seems not best possible.

Problem 2.

Determine the smallest constants $c_1$ such that every 1-planar graph G without 4-cycles has ${\chi }_{\mathrm{st}}^{\prime }\left(G\right)\le \lfloor 1.5\Delta \rfloor +c_1$.

In fact, Theorem 4 extends a result in [24], which says that every planar graph G without 4-cycles has an edge-partition $(F,H)$ such that F is a forest and $\Delta \left(H\right)\le 5$. About other results regarding the vertex-partition of graphs, one can refer to [25,26].

It is unknown whether Theorem 4 is the best possible with respect to the maximum degree of the graph H. Naturally, we raise the following problem.

Problem 3.

Determine the smallest constant $c_2$ such that every 1-planar graph G without 4-cycles can be edge-partitioned into a forest F and a graph H such that $\Delta \left(F\right)=\Delta -c_2$ and $\Delta \left(H\right)=c_2$.

By Theorem 4, we see that $c_2\le 39$ when $\Delta \ge 41$. On the other hand, to discuss the lower bound of $c_2$, we depict the graphs P and $G^{*}$ in Figure 5, either of which is of symmetry with respect to vertices and edges. Note that P is the well-known Petersen graph and is a 1-planar graph without 3-cycles and 4-cycles. If P has an edge-partition $(F,H)$ such that F is a forest; then it is easy to derive that $\Delta \left(H\right)\ge \Delta \left(P\right)-1=2$ because the minimum degree of F is at most one. Observe that $G^{*}$ is a 4-regular planar graph without 4-cycles (of course, it is also 1-planar), and if it has an edge-partition $(F,H)$ such that F is a forest, then $\Delta \left(H\right)\ge 4-1=3$. These two examples show that $c_2\ge 3$.

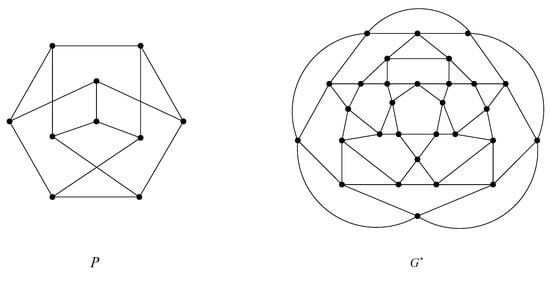
Figure 5. Petersen graph P and planar graph $G^{*}$.