Symmetric Spectral Collocation Method for a Kind of Nonlinear Volterra Integral Equation

Abstract

In this paper, we develop an efficient spectral method for numerically solving the nonlinear Volterra integral equation with weak singularity and delays. Based on the symmetric collocation points, the spectral method is illustrated, and the convergence results are obtained. In the end, two numerical experiments are carried out to confirm the theoretical results.

1. Introduction

Volterra integral equations with weakly singular kernels arise in various areas, including prey–predator and competitive models, superfluidity, stereology, crystal growth, and the radiation of heat from a semi-infinite solid. More information about these equations can be found in [1,2,3,4,5,6,7].

In this paper, we shall investigate the nonlinear weakly singular Volterra integral equation with delays of the following form:

$$\begin{array}{ccc}\hfill & & {\int }_0^X{\int }_0^Y{(X-S)}^{-\mu }{(Y-\xi )}^{-\rho }\tilde{K}(X,Y,S,\xi ,U(pS,q\xi ))d\xi dS\hfill \\ & & =U(X,Y)+G(X,Y),\hfill \end{array}$$

(1)

where $U(X,Y)$ is the unknown function, $X,Y\in [0,T],$ and $\mu ,\rho ,p,q(\in (0,1\left]\right)$ are given constants. $\tilde{K}$ and G are given functions, where

$$\tilde{K}:D\times R\to R,\mathrm{with} D:=\{(X,Y,S,\xi ):0\le S\le X\le T,0\le \xi \le Y\le T\},$$

$$\tilde{G}:T\times T\to R.$$

Assume that all the functions in the above equation are sufficiently smooth. Without loss of generality, we used the prey–predator and competitive models to explain the biological background of this equation. Here, $U(X,Y)$ represents the numbers of eagles and snakes, respectively. On the one hand, eagles prey on snakes. These two kinds of species have different memories of killing and being killed. The parameters p and q depend on the memories of the eagles and snakes, respectively. On the other hand, eagles compete with snakes. They also take mice as prey. This complex relationship between predation and competition is illustrated by the nonlinear kernel function $\tilde{K}$. In the end, the resource function $G(x,y)$ represents the birth rates of the two species.

Research for solving high-dimensional weakly singular Volterra type equations has received much attention. For theoretical results, a class of two-dimensional Volterra type integral equations with singular boundary lines was proposed in [8]. Then, multidimensional Volterra type integral equations with singular boundary domains and kernels were considered by Rajabov [9]. For numerical results, collocation methods [10] were applied for solving two-dimensional weakly singular equations, which arise in the field of electrical engineering. In 2015, accuracy-optimal numerical methods for multidimensional equations were discussed [11]. However, the convergence efficiency in two of the above-mentioned references is not high.

It is well known that the spectral method is an efficient numerical method. One of the main reasons for this is that the method can be exponentially convergent. In [12], a spectral Jacobi collocation method was first proposed for solving linear Volterra integral equations of the second kind with weakly singular kernels, under the condition that the solutions of the equations were sufficiently smooth. Later, Volterra equations with weak singularity approximated by the spectral method received considerable attention. In [13], the authors extended the field of research to weakly singular Volterra integro-differential equations successfully. Spectral approximation for weakly singular Volterra integral equations with pantograph delays was studied in [14]. Chebyshev collocation methods were constructed to approximate weakly singular Volterra integral equations in [15]. A fractional order collocation method for second-kind Volterra integral equations with weakly singular kernels was considered in [16]. However, all these articles mentioned above dealt with the case of a linear situation. Yang et al. [17] discussed spectral collocation methods for the nonlinear Volterra integro-differential equations with weakly singular kernels and presented a rigorous convergence analysis. For more information related to this topic, we refer readers to to [18,19,20,21].

To our knowledge, there are fewer theoretical results from the spectral method available in the literature for nonlinear Volterra integral equations with weak singularity and delays in two-dimensional space. The aim of this paper is to develop the numerical solution of a two-dimensional nonlinear Volterra integral equation with weak singularity and delays. The novelty of our work lies not only in the use of the two-dimensional Gauss quadrature rule to approximate the integral with delays but also in the spectral error analysis for the Jacobi spectral collocation method.

The rest of this paper is organized as follows. In Section 2, we construct a spectral discretization scheme. Some useful spaces and lemmas are given in Section 3. The convergence analysis is proven in Section 4. In Section 5, some numerical examples are presented to verify the theoretical analysis. Section 6 is devoted to some concluding remarks.

2. Spectral Discretization

In this section, a spectral discretization scheme is established to solve Equation (1). First, three transformations are employed so that the Gauss quadrature rule can be applied expediently. Then, we introduce the Lagrange interpolation polynomial and define the approximate solution. Finally, we obtain the nonlinear numerical scheme through the help of spectral discretization.

Let $\mathsf{\Omega }=(-1,1)\times (-1,1)$, where each point is denoted by $(x,y)$ in $\overline{\mathsf{\Omega }}$. In order to use the theory of orthogonal polynomials, we first make the following linear transformations:

$$X=\frac{T}{2}(1+x),Y=\frac{T}{2}(1+y),$$

Then, Equation (1) changes into

$$\begin{array}{ccc}\hfill & & {\int }_0^{\frac{T}{2}(1+x)}{\int }_0^{\frac{T}{2}(1+y)}{\left(\frac{T}{2}(1+x)-S\right)}^{-\mu }{\left(\frac{T}{2}(1+y)-\xi \right)}^{-\rho }\overline{K}\left(x,y,S,\xi ,U(pS,q\xi )\right)d\xi dS\hfill \\ & & =u(x,y)+g(x,y),\hfill \end{array}$$

(2)

where

$$\begin{array}{ccc}& & u(x,y)=U\left(\frac{T}{2}(1+x),\frac{T}{2}(1+y)\right),\hfill \\ & & \overline{K}(x,y,S,\xi ,U(pS,q\xi ))=K\left(\frac{T}{2}(1+x),\frac{T}{2}(1+y),S,\xi ,U(pS,q\xi )\right),\hfill \\ & & g(x,y)=G\left(\frac{T}{2}(1+x),\frac{T}{2}(1+y)\right).\hfill \end{array}$$

Then, we continue to give another couple of variable transformations, where

$$S=\frac{T}{2}(1+s),\xi =\frac{T}{2}(1+\tau ).$$

Here, $s,\tau \in [-1,1],$ and Equation (2) turn into

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\widehat{K}\left(x,y,s,\tau ,u(ps+p-1,q\tau +q-1)\right)d\tau ds\hfill \\ & & =u(x,y)+g(x,y),\hfill \end{array}$$

(3)

where

$$\begin{array}{ccc}& & \widehat{K}\left(x,y,s,\tau ,u(ps+p-1,q\tau +q-1)\right)\hfill \\ & & ={\left(\frac{T}{2}\right)}^{2-\mu -\rho }\overline{K}\left(x,y,\frac{T}{2}(1+s),\frac{T}{2}(1+\tau ),U\left(p\frac{T}{2}(1+s),q\frac{T}{2}(1+\tau )\right)\right).\hfill \end{array}$$

The set of collocation points in the two-dimensional space is denoted by ${\left\{(x_i,y_j)\right\}}_{i,j=0}^N$, where ${\left\{x_i\right\}}_{i=0}^N$ and ${\left\{y_j\right\}}_{j=0}^N$ are the Gauss points in one dimension equipped with the weights ${\omega }_i^x$ and ${\omega }_j^y$, respectively, and they are symmetrical. Obviously, Equation (3) holds at each two-dimensional collocation point such that

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^{x_i}{\int }_{-1}^{y_j}{(x_i-s)}^{-\mu }{(y_j-\tau )}^{-\rho }\widehat{K}\left(x_i,y_j,s,\tau ,u(ps+p-1,q\tau +q-1)\right)d\tau ds\hfill \\ & & =u(x_i,y_j)+g(x_i,y_j).\hfill \end{array}$$

(4)

To apply the Gauss quadrature rule, we need to transform the integral domain of the double integral into $[-1,1]\times [-1,1]$ by the following variable changes:

$$\begin{array}{ccc}\hfill & & s=s\left({\theta }^x\right)=\frac{x_i+1}{2}{\theta }^x+\frac{x_i-1}{2},\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill & & \tau =\tau \left({\theta }^y\right)=\frac{y_j+1}{2}{\theta }^y+\frac{y_j-1}{2},\hfill \end{array}$$

(6)

where $i,j=1,2,\cdots ,N,{\theta }^x,{\theta }^y\in [-1,1]$, and then Equation (4) becomes

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^1{\int }_{-1}^1{(1-{\theta }^x)}^{-\mu }{(1-{\theta }^y)}^{-\rho }\widehat{k}\left(x_i,y_j,s\left({\theta }^x\right),\tau \left({\theta }^y\right),u(ps\left({\theta }^x\right)+p-1,q\tau \left({\theta }^y\right)+q-1)\right)d{\theta }^{y}d{\theta }^x\hfill \\ & & =u(x_i,y_j)+g(x_i,y_j),\hfill \end{array}$$

(7)

where

$$\begin{array}{ccc}\hfill & & \widehat{k}\left(x_i,y_j,s\left({\theta }^x\right),\tau \left({\theta }^y\right),u(ps\left({\theta }^x\right)+p-1,q\tau \left({\theta }^y\right)+q-1)\right)\hfill \\ & & ={\left(\frac{x_i+1}{2}\right)}^{1-\mu }{\left(\frac{y_j+1}{2}\right)}^{1-\rho }\widehat{K}\left(x_i,y_j,s\left({\theta }^x\right),\tau \left({\theta }^y\right),u(ps\left({\theta }^x\right)+p-1,q\tau \left({\theta }^y\right)+q-1)\right).\hfill \end{array}$$

(8)

Using the Gauss integration formula, the integration term in Equation (7) can be approximated by

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^1{\int }_{-1}^1{(1-{\theta }^x)}^{-\mu }{(1-{\theta }^y)}^{-\rho }\widehat{k}\left(x_i,y_j,s\left({\theta }^x\right),\tau \left({\theta }^y\right),u(ps\left({\theta }^x\right)+p-1,q\tau \left({\theta }^y\right)+q-1)\right)d{\theta }^{y}d{\theta }^x\hfill \\ & & \approx \sum _{n,l=0}^N\widehat{k}\left(x_i,y_j,s\left({\theta }_n^x\right),\tau \left({\theta }_l^y\right),u(ps\left({\theta }_n^x\right)+p-1,q\tau \left({\theta }_l^y\right)+q-1)\right){\omega }_n^x{\omega }_l^y.\hfill \end{array}$$

Let $I_{N}u(x,y)$ denote the Lagrange interpolation polynomial such that

$$I_{N}u(x,y)=\sum _{i,j=0}^{N}u(x_i,y_j)L_{ij}(x,y),$$

where $L_{ij}(x,y)=L_i\left(x\right)L_j\left(y\right),L_i,L_j$ are the Lagrange interpolation basis functions associated with the collocation points ${\left\{x_i\right\}}_{i=0}^N$ and ${\left\{y_j\right\}}_{j=0}^N$, respectively, and $I_{N}u$ satisfies

$$I_{N}u(x_i,y_j)=u(x_i,y_j).$$

Let $u_{ij}\approx u(x_i,y_j)$ and $u_N(x,y)\approx u(x,y)$, where

$$\begin{array}{c}\hfill u_N(x,y)=\sum _{i,j=0}^N{u}_{ij}{L}_{ij}(x,y).\end{array}$$

(9)

Then, the spectral collocation method is used to seek a value $u_{ij}$ that satisfies the following nonlinear system:

$$\begin{array}{ccc}\hfill & & \sum _{n,l=0}^N\widehat{k}\left(x_i,y_j,s\left({\theta }_n^x\right),\tau \left({\theta }_l^y\right),\sum _{i,j=0}^N{u}_{ij}{L}_i(ps\left({\theta }_n^x\right)+p-1)L_j(q\tau \left({\theta }_l^y\right)+q-1)\right){\omega }_n^x{\omega }_l^y\hfill \\ & & =u_{ij}+g(x_i,y_j).\hfill \end{array}$$

(10)

We can obtain the values by a proper solver, and at the same time, the approximate solution $u_N$ can also be obtained by the expression in Equation (9).

3. Some Spaces and Lemmas

In this section, we introduce some useful spaces and lemmas which are essential for establishing the Jacobi convergence analysis in the next section.

Now, we introduce three spaces. First, let $L^{\infty }\left(\mathsf{\Omega }\right)$ denote a Banach space in which the measurable functions $v:\mathsf{\Omega }\to R$ are bounded outside a set measuring zero with the following norm:

$${\parallel v\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}=ess\underset{(x,y)\in \mathsf{\Omega }}{sup}\left|v(x,y)\right|.$$

Then, let ${\omega }^{\alpha ,\beta }(x,y)={\left((1-x)(1-y)\right)}^{\alpha }{\left((1+x)(1+y)\right)}^{\beta },\alpha ,\beta \in (-1,0)$, and we can introduce another Banach space:

$$\begin{array}{ccc}& & L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)=\left\{u:{\int }_{-1}^1{\int }_{-1}^1{\left|u(x,y)\right|}^2{\omega }^{\alpha ,\beta }(x,y)dydx<+\infty \right\},\hfill \end{array}$$

(11)

whose inner product and norm are given by

$${(u,v)}_{{\omega }^{\alpha ,\beta }}={\int }_{-1}^1{\int }_{-1}^{1}u(x,y)v(x,y){\omega }^{\alpha ,\beta }(x,y)dydx,$$

$${\parallel u\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}={\left({\int }_{-1}^1{\int }_{-1}^1{\left|u(x,y)\right|}^2{\omega }^{\alpha ,\beta }(x,y)dydx\right)}^{\frac{1}{2}}.$$

The third space is

$$H_{{\omega }^{\alpha ,\beta }}^m\left(\mathsf{\Omega }\right)=\left\{v:{\partial }^{k}v\in L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right),0\le k\le m\right\},$$

which is endowed with the norm

$${\parallel v\parallel }_{H_{{\omega }^{\alpha ,\beta }}^m\left(\mathsf{\Omega }\right)}={\left(\sum _{k=0}^m{\parallel {\partial }^{k}v\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}^2\right)}^{\frac{1}{2}},$$

and the semi-norm

$$\begin{array}{ccc}& & {\left|v\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}={\left(\sum _{k=min(m,N+1)}^m{\parallel {\partial }^{k}v\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}^2\right)}^{\frac{1}{2}}.\hfill \end{array}$$

(12)

Then, we can introduce seven important lemmas. They are essential for the derivation of error analysis in the next section.

Lemma 1

([22] Gronwall inequality). Suppose that nonnegative integrable functions $E(x,y)$ and $G(x,y)$ satisfy

$$E(x,y)\le M{\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }E(s,\tau )d\tau ds+G(x,y),(x,y)\in \mathsf{\Omega },$$

(13)

where M is a nonnegative constant. Then, we have

$$\begin{array}{ccc}\hfill & & {\parallel E\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\le C{\parallel G\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill & & {\parallel E\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\le C{\parallel G\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}.\hfill \end{array}$$

(15)

Remark 1.

Throughout the paper, C denotes a generic positive constant which is independent of N but depends on T and the given functions.

Lemma 2

([23]). Let ${\mathcal{P}}_N$ denote the space of all polynomials of a degree not exceeding N. Assume that the product $v\varphi$ is integrated by the Gauss quadrature formula, where $v\in H_{{\omega }^{\alpha ,\beta }}^m\left(\mathsf{\Omega }\right)$ for some $m>1$ and $\varphi \in {\mathcal{P}}_N$. Then, the following is true:

$$\left|{(v,\varphi )}_{{\omega }^{\alpha ,\beta }}-{(v,\varphi )}_N\right|\le C{N}^{-m}{\left|v\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}{\parallel \varphi \parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)},$$

(16)

where

$${(v,\varphi )}_N=\sum _{i,j=0}^{N}v({\theta }_i^x,{\theta }_j^y)\varphi ({\theta }_i^x,{\theta }_j^y){\omega }_i^x{\omega }_j^y.$$

Lemma 3

([24]). Let $\left|\right|I_N{\left|\right|}_{\infty }=\underset{(x,y)\in \overline{\mathsf{\Omega }}}{max}{\displaystyle \sum _{i,j=0}^N}\left|L_i\left(x\right)L_j\left(y\right)\right|$, and it can be concluded that

$$\begin{array}{c}\hfill \left|\right|I_N{\left|\right|}_{\infty }=\left\{\begin{array}{cc}\mathcal{O}\left({log}^{2}N\right),\hfill & -1<\alpha ,\beta \le -\frac{1}{2},\hfill \\ \mathcal{O}\left(N^{2max(\alpha ,\beta )+1}\right),\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

(17)

Lemma 4

([23,25]). Assume that $u(x,y)\in H_{{\omega }^{\alpha ,\beta }}^m\left(\mathsf{\Omega }\right)$ for $m>1$, and denote $I_{N}u(x,y)$ as its interpolation polynomial associated with the collocation points $\left\{(x_i,y_j),0\le i,j\le N\right\}$. Then, the results of estimates are

$$\begin{array}{ccc}& & \parallel u-I_N{u\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\le C{N}^{4-m}{\left|u\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)},\hfill \end{array}$$

(18)

$$\begin{array}{ccc}& & \parallel u-I_N{u\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\le C{N}^{-m}{\left|u\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}.\hfill \end{array}$$

(19)

Lemma 5

([26,27]). For a nonnegative integer r, and where $\kappa \in (0,1)$, there exists a constant $C_{r,\kappa }>0$ that makes any function $v\in {\mathcal{C}}^{r,\kappa }\left(\overline{\mathsf{\Omega }}\right)$ hold a polynomial function ${\mathcal{J}}_{N}v\in {\mathcal{P}}_N$ such that

$${\displaystyle \parallel }v-{\mathcal{J}}_{N}v{{\displaystyle \parallel }}_{L^{\infty }\left(\mathsf{\Omega }\right)}\le C_{r,\kappa }{N}^{-(r+\kappa )}{\parallel v\parallel }_{{\mathcal{C}}^{r,\kappa }\left(\overline{\mathsf{\Omega }}\right)},$$

(20)

where

$$\begin{array}{ccc}& & {\parallel v\parallel }_{{\mathcal{C}}^{r,\kappa }\left(\overline{\mathsf{\Omega }}\right)}=\underset{\alpha \le r}{max}\underset{(x,y)\in \overline{\mathsf{\Omega }}}{max}\left|{\partial }^{\alpha }v(x,y)\right|+\underset{\alpha \le r}{max}\underset{(x^{\prime },y^{\prime })\ne (x^{″},y^{″})\in \overline{\mathsf{\Omega }}}{sup}\left|\frac{{\partial }^{\alpha }v(x^{\prime },y^{\prime })-{\partial }^{\alpha }v(x^{″},y^{″})}{{[{(x^{\prime }-x^{″})}^2+{(y^{\prime }-y^{″})}^2]}^{\kappa /2}}\right|.\hfill \end{array}$$

Obviously, ${\mathcal{J}}_N$ is a linear operator from ${\mathcal{C}}^{r,\kappa }\left(\overline{\mathsf{\Omega }}\right)$ into ${\mathcal{P}}_N$.

Lemma 6

([28]). Let $0<\kappa <min\{1-\mu ,1-\rho \}$ and ${\mathcal{M}}_{v_1,v_2}$ be defined by

$$\left({\mathcal{M}}_{v_1,v_2}\right)(x,y)={\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\left(\widehat{k}(x,y,s,\tau ,v_1(s,\tau ))-\widehat{k}(x,y,s,\tau ,v_2(s,\tau ))\right)d\tau ds.$$

Then, for any functions $v_1,v_2\in \mathcal{C}\left(\overline{\mathsf{\Omega }}\right)$, there exists a positive constant C such that

$$\frac{|\left({\mathcal{M}}_{v_1,v_2}\right)(x^{\prime },y^{\prime })-\left({\mathcal{M}}_{v_1,v_2}\right)(x^{″},y^{″})|}{{[{(x^{\prime }-x^{″})}^2+{(y^{\prime }-y^{″})}^2]}^{\kappa /2}}\le C\underset{(x,y)\in \overline{\mathsf{\Omega }}}{max}|v_1(x,y)-v_2(x,y)|,$$

(21)

for any different couple of points $(x^{\prime },y^{\prime }),(x^{″},y^{″})\in \overline{\mathsf{\Omega }}$. This implies that

$$\parallel {\mathcal{M}}_{v_1,v_2}{\parallel }_{{\mathcal{C}}^{0,\kappa }\left(\overline{\mathsf{\Omega }}\right)}\le C\underset{(x,y)\in \overline{\mathsf{\Omega }}}{max}|v_1(x,y)-v_2(x,y)|.$$

(22)

Lemma 7

([29]). For every bounded function $v(x,y)$, there is a constant C not relying on $v(x,y)$, leading to

$$\begin{array}{c}\hfill \underset{N}{sup}\parallel \sum _{i,j=0}^{N}v(x_i,y_j)L_{ij}(x,y){\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\le C\underset{(x,y)\in \overline{\mathsf{\Omega }}}{max}\left|v(x,y)\right|.\end{array}$$

(23)

4. Jacobi Convergence Analysis

In this section, Jacobi convergence analysis is carried out. We first obtain the error equation using Equation (7), the discrete numerical scheme in Equation (10), two transformations (Equations (5) and (6)) and the definition of the approximation solution. Then, we present the error estimates precisely and derive the exponential rate of convergence in both the $L^{\infty }$ and $L_{{\omega }^{\alpha ,\beta }}^2$ spaces.

Theorem 1.

Let $u(x,y)$ be the exact solution of Equation (3), which is sufficiently smooth. Assume that $u_N(x,y)$ is the approximate solution and $e(x,y)=u(x,y)-u_N(x,y)$ is the error function. If $m>4$, and $\widehat{k}$ satisfies

$$\begin{array}{ccc}\hfill & & |{\partial }^K\widehat{k}(x,y,s,\tau ,v_1)-{\partial }^K\widehat{k}(x,y,s,\tau ,v_2)|\hfill \\ \hfill & & \le A_K|v_1-v_2|\hfill \\ & & \le A|v_1-v_2|,\hfill \\ \hfill \mathrm{with}& & A=\underset{0\le K\le m}{max}{A}_K.\hfill \end{array}$$

(24)

Then, we obtain the following conclusion:

$$\begin{array}{ccc}\hfill & & {\parallel e\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\le C{N}^{-m}\left\{\begin{array}{cc}{\left(logN\right)}^2{k}^{*}+N^4{\left|u\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)},\hfill & -1<\alpha ,\beta \le -\frac{1}{2},\hfill \\ \left(N^{2max(\alpha ,\beta )+1}\right)k^{*}+N^4{\left|u\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)},\hfill & otherwise,\hfill \end{array}\right.\hfill \end{array}$$

(25)

$$\begin{array}{ccc}& & {\left|\right|e\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\le C{N}^{-m}\left(k^{*}+{\left|u\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}+(N^{-\kappa }+1){\parallel e\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\right),\hfill \end{array}$$

(26)

where

$$\begin{array}{c}\hfill k^{*}=\underset{(x,y)\in \overline{\mathsf{\Omega }}}{max}|\widehat{k}(x,y,s,\tau ,u(s,\tau )){|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}.\end{array}$$

Proof. 

Subtraction between Equations (7) and (10) yields

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^1{\int }_{-1}^1{(1-{\theta }^x)}^{-\mu }{(1-{\theta }^y)}^{-\rho }\widehat{k}\left(x_i,y_j,s\left({\theta }^x\right),\tau \left({\theta }^y\right),u(ps\left({\theta }^x\right)+p-1,q\tau \left({\theta }^y\right)+q-1)\right)d{\theta }^{y}d{\theta }^x\hfill \\ \hfill & & -\sum _{n,l=0}^N\widehat{k}\left(x_i,y_j,s\left({\theta }_n^x\right),\tau \left({\theta }_l^y\right),\sum _{i,j=0}^N{u}_{ij}{L}_i(ps\left({\theta }_n^x\right)+p-1)L_j(q\tau \left({\theta }_l^y\right)+q-1)\right){\omega }_n^x{\omega }_l^y\hfill \\ & & =u(x_i,y_j)-u_{ij}.\hfill \end{array}$$

(27)

If we define

$$\begin{array}{ccc}& & B(x_i,y_j)\hfill \\ & & ={\int }_{-1}^1{\int }_{-1}^1{(1-{\theta }^x)}^{-\mu }{(1-{\theta }^y)}^{-\rho }\widehat{k}\left(x_i,y_j,s\left({\theta }^x\right),\tau \left({\theta }^y\right),u_N(ps\left({\theta }^x\right)+p-1,q\tau \left({\theta }^y\right)+q-1)\right)d{\theta }^{y}d{\theta }^x\hfill \\ & & -\sum _{n,l=0}^N\widehat{k}\left(x_i,y_j,s\left({\theta }_i^x\right),\tau \left({\theta }_j^y\right),\sum _{i,j=0}^N{u}_{ij}{L}_i(ps\left({\theta }_n^x\right)+p-1)L_j(q\tau \left({\theta }_l^y\right)+q-1)\right){\omega }_n^x{\omega }_l^y,\hfill \end{array}$$

then Equation (27) can be rewritten as

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^1{\int }_{-1}^1{(1-{\theta }^x)}^{-\mu }{(1-{\theta }^y)}^{-\rho }\widehat{k}\left(x_i,y_j,s\left({\theta }^x\right),\tau \left({\theta }^y\right),u(ps\left({\theta }^x\right)+p-1,q\tau \left({\theta }^y\right)+q-1)\right)d{\theta }^{y}d{\theta }^x\hfill \\ \hfill & & -{\int }_{-1}^1{\int }_{-1}^1{(1-{\theta }^x)}^{-\mu }{(1-{\theta }^y)}^{-\rho }\widehat{k}\left(x_i,y_j,s\left({\theta }^x\right),\tau \left({\theta }^y\right),u_N(ps\left({\theta }^x\right)+p-1,q\tau \left({\theta }^y\right)+q-1)\right)d{\theta }^{y}d{\theta }^x\hfill \\ \hfill & & +B(x_i,y_j)=u(x_i,y_j)-u_{ij}.\hfill \end{array}$$

Noting Equations (5) and (6), we have that

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^{x_i}{\int }_{-1}^{y_j}{(x_i-s)}^{-\mu }{(y_j-\tau )}^{-\rho }\widehat{K}\left(x_i,y_j,s,\tau ,u(ps+p-1,q\tau +q-1)\right)d\tau ds\hfill \\ \hfill & & -{\int }_{-1}^{x_i}{\int }_{-1}^{y_j}{(x_i-s)}^{-\mu }{(y_j-\tau )}^{-\rho }\widehat{K}\left(x_i,y_j,s,\tau ,u_N(ps+p-1,q\tau +q-1)\right)d\tau ds\hfill \\ & & +B(x_i,y_j)=u(x_i,y_j)-u_{ij}.\hfill \end{array}$$

(28)

By multiplying $L_i\left(x\right)L_j\left(y\right)$ on both sides of Equation (28) and summing up from $i,j=0$ to N, then we obtain the following error equation:

$$\begin{array}{ccc}\hfill & & e(x,y)={\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }(\widehat{K}(x,y,s,\tau ,u(ps+p-1,q\tau +q-1))\hfill \\ \hfill & & -\widehat{K}(x,y,s,\tau ,u_N(ps+p-1,q\tau +q-1)))d\tau ds+\sum _{m=1}^3{B}_m(x,y),\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill & & B_1(x,y)=\sum _{i,j=0}^{N}B(x_i,y_j)L_i\left(x\right)L_j\left(y\right),\hfill \\ \hfill & & B_2(x,y)=u(x,y)-I_{N}u(x,y),\hfill \\ \hfill & & B_3(x,y)=I_N{\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }(\widehat{K}(x,y,s,\tau ,u(ps+p-1,q\tau +q-1))\hfill \\ \hfill & & -\widehat{K}(x,y,s,\tau ,u_N(ps+p-1,q\tau +q-1)))d\tau ds\hfill \\ \hfill & & -{\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }(\widehat{K}(x,y,s,\tau ,u(ps+p-1,q\tau +q-1))\hfill \\ \hfill & & -\widehat{K}(x,y,s,\tau ,u_N(ps+p-1,q\tau +q-1)))d\tau ds.\hfill \end{array}$$

Under the hypothesis of Theorem 1, we arrive at

$$\begin{array}{c}\hfill \left|e(x,y)\right|\le A{\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\left|e(ps+p-1,q\tau +q-1)\right|d\tau ds+\sum _{m=1}^3\left|B_m(x,y)\right|.\end{array}$$

(29)

In addition, through Lemma 1, we obtain that

$$\begin{array}{c}\hfill {\left|\right|e\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}\le C\left(\left|\right|B_1{\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}+\left|\right|B_2{\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}+\left|\right|B_3{\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}\right).\end{array}$$

(30)

Using Lemmas 2 and 3, the following holds true:

$$\begin{array}{ccc}\hfill & & \left|\right|B_1{\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & \le C\left|\right|I_N{\left|\right|}_{\infty }\underset{0\le i,j\le N}{max}\left|B(x_i,y_j)\right|\hfill \\ \hfill & & \le C\left|\right|I_N{\left|\right|}_{\infty }{N}^{-m}\underset{0\le i,j\le N}{max}|\widehat{k}(x_i,y_j,s,\tau ,u_N(s,\tau )){|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)},\hfill \\ & & \le C\left|\right|I_N{\left|\right|}_{\infty }{N}^{-m}\left(k^{*}+{|\widehat{k}(x_i,y_j,s,\tau ,u_N(s,\tau ))-\widehat{k}(x_i,y_j,s,\tau ,u(s,\tau ))|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}\right).\hfill \end{array}$$

(31)

Drawing support from the condition of Equation (24) once more, we find that

$$\begin{array}{ccc}\hfill & & |\widehat{k}(x_i,y_j,s,\tau ,u_N(s,\tau ))-\widehat{k}(x_i,y_j,s,\tau ,u(s,\tau )){|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & \le {\left(\sum _{K=1}^m\left|\right|{\partial }^K\widehat{k}(x_i,y_j,s,\tau ,u_N(s,\tau ))-{\partial }^K\widehat{k}(x_i,y_j,s,\tau ,u(s,\tau )){\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill & & \le \sum _{K=1}^m{A}_K\left|\right|u_N-u{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\hfill \\ & & \le {C\left|\right|e\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}.\hfill \end{array}$$

(32)

By combining Equations (31) with (32), we obtain that

$$\begin{array}{ccc}\hfill & & \left|\right|B_1{\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & \le C{N}^{-m}\left(k^{*}+{C\left|\right|e\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}\right)\left|\right|I_N{\left|\right|}_{\infty }\hfill \\ & & \le C{N}^{-m}\left(k^{*}+{C\left|\right|e\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}\right)\left\{\begin{array}{cc}{log}^{2}N,\hfill & -1<\alpha ,\beta \le -\frac{1}{2},\hfill \\ N^{2max(\alpha ,\beta )+1},\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

(33)

Using the first conclusion in Lemma 4 yields

$$\begin{array}{c}\hfill \left|\right|B_2{\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}\le C{N}^{4-m}{\left|u\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}.\end{array}$$

(34)

Due to Lemmas 5 and 6, we find that

$$\begin{array}{ccc}\hfill & & \parallel B_3{\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & =\parallel (I-I_N){\mathcal{M}}_{u,u_N}{\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & =\parallel (I-I_N){({\mathcal{M}}_{u,u_N}-{\mathcal{J}}_N{\mathcal{M}}_{u,u_N}\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & \le (1+||I_N{\left|\right|}_{\infty })\parallel {\mathcal{M}}_{u,u_N}-{\mathcal{J}}_N{\mathcal{M}}_{u,u_N}{\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & \le C\parallel I_N{\parallel }_{\infty }{N}^{-\kappa }{\parallel {\mathcal{M}}_{u,u_N}\parallel }_{C^{0,\kappa }\overline{\left(\mathsf{\Omega }\right)}}\hfill \\ & & \le C\parallel I_N{\parallel }_{\infty }{N}^{-\kappa }{\parallel e\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}.\hfill \end{array}$$

(35)

Owing to Equations (30)–(35), we reach the conclusion for ${\left|\right|e\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}$ easily. Next, we will carry out the error analysis in the $L_{{\omega }^{\alpha ,\beta }}^2$ space.

With the help of Equation (29) and Gronwall inequality, we have that

$$\begin{array}{c}\hfill {\left|\right|e\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\le C\left(\left|\right|B_1{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}+\left|\right|B_2{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}+\left|\right|B_3{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\right).\end{array}$$

(36)

By virtue of the first lemma and the last lemma, we obtain the following:

$$\begin{array}{c}\hfill \left|\right|B_1{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\le C\underset{(x,y)\in \overline{\mathsf{\Omega }}}{max}\left|B(x,y)\right|\le C{N}^{-m}\left(k^{*}+{\left|\right|e\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\right).\end{array}$$

(37)

Using Lemma 4, we obtain that

$$\begin{array}{c}\hfill \left|\right|B_2{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\le C{N}^{-m}{\left|u\right|}_{H_{{\omega }^{\alpha ,\beta }}^{m;N}\left(\mathsf{\Omega }\right)}.\end{array}$$

(38)

According to Lemmas 5–7, we reach the following:

$$\begin{array}{ccc}\hfill & & \left|\right|B_3{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & =\left|\right|(I-I_N){\mathcal{M}}_{u,u_N}{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & =\left|\right|(I-I_N)({\mathcal{M}}_{u,u_N}-{\mathcal{J}}_N{\mathcal{M}}_{u,u_N}){\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & \le \left|\right|{\mathcal{M}}_{u,u_N}-{\mathcal{J}}_N{\mathcal{M}}_{u,u_N}{\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}+\left|\right|I_N({\mathcal{M}}_{u,u_N}-{\mathcal{J}}_N{\mathcal{M}}_{u,u_N}){\left|\right|}_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & \le C\left|\right|{\mathcal{M}}_{u,u_N}-{\mathcal{J}}_N{\mathcal{M}}_{u,u_N}{\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & & \le C{N}^{-\kappa }\left|\right|{\mathcal{M}}_{u,u_N}{\left|\right|}_{{\mathcal{C}}^{r,\kappa }\left(\overline{\mathsf{\Omega }}\right)}\hfill \\ & & \le C{N}^{-\kappa }{\left|\right|e\left|\right|}_{L^{\infty }\left(\mathsf{\Omega }\right)}.\hfill \end{array}$$

(39)

By combining Equations (36)–(39), we complete the proof. □

5. Numerical Experiments

In this section, we carry out the numerical experiments with a Thinkpad laptop. The environment was a 2.50 GHz Inteli5-3230M CPU with 4.0 GB of memory, and the operating system was Windows XP. Two numerical examples will be provided to confirm the theoretical analysis: one is the special case (i.e., $p=q=1$), and the other is the normal situation. For more details, see the following.

Example 1.

We consider Equation (3) to be

$$\begin{array}{c}\hfill {\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }s\tau d\tau ds=tan\left(xy\right)+g(x,y),\end{array}$$

(40)

where a binary tangent function is selected as the exact solution, and we choose

$$\widehat{K}(x,y,s,\tau ,u(s,\tau ))=arctan\left(u(s,\tau )\right).$$

Therefore, the following is true:

$$g(x,y)=\left(\frac{{(x+1)}^{2-\mu }}{(1-\mu )(2-\mu )}-\frac{{(x+1)}^{1-\mu }}{1-\mu }\right)\left(\frac{{(y+1)}^{2-\rho }}{(1-\rho )(2-\rho )}-\frac{{(y+1)}^{1-\rho }}{1-\rho }\right)-tan\left(xy\right).$$

Starting from $n\ge N$, the system of approximate equations has a unique solution. Here, we let $\mu =1/5$ and $\rho =1/3$ and carried out the numerical experiment supported by Matlab, and the resulting nonlinear discrete numerical scheme in Equation (10) was solved. The CPU time was 11.0953 s. The errors in the $L^{\infty }$ norm and $L_{{\omega }^{\alpha ,\beta }}^2$ norm are found in Table 1.

Table 1. The errors for $\parallel u-u_N{\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}$ and $\parallel u-u_N{\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}$.

N	4	6	8	10	12	14	16
$L^{\infty }$ error	1.77	3.30 × 10${}^{-4}$	1.29 × 10${}^{-5}$	9.24 × 10${}^{-7}$	8.66 × 10${}^{-8}$	8.92 × 10${}^{-9}$	9.28 × 10${}^{-8}$
$L_{{\omega }^{\alpha ,\beta }}^2$ error	1.50	2.96 × 10${}^{-4}$	1.33 × 10${}^{-5}$	9.91 × 10${}^{-7}$	9.63 × 10${}^{-8}$	9.76 × 10${}^{-9}$	1.02 × 10${}^{-9}$
CPU time	0.0156	0.6094	1.6250	4.6719	12.7500	33.5156	72.2188

To show the exponential rate of convergence more visually, we exhibit the errors on the left side of Figure 1. Moreover, the high consistence between the exact solution and the approximate solution is also presented, which is located on the right side of Figure 1.

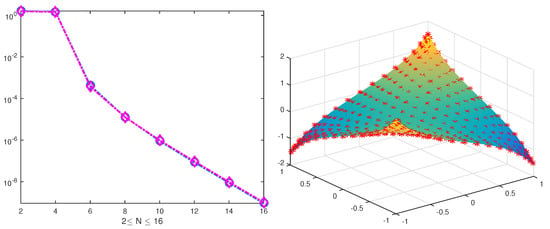
Figure 1. The errors in the $L^{\infty }$ and $L_{{\omega }^{\alpha ,\beta }}^2$ norms (left) and the consistence between the exact solution and approximate solution (right).

Example 1.

Without losing generality, we substitute

$$u(x,y)=e^{(x+1)(y+1)}$$

and

$$\widehat{K}(x,y,s,\tau ,u(ps+p-1,q\tau +q-1))=ln\left(u(ps+p-1,q\tau +q-1)\right)$$

into Equation (3). Please refer to

$$\begin{array}{c}\hfill {\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }(ps+p)(q\tau +q)d\tau ds=u(x,y)+g(x,y).\end{array}$$

Then, after calculation, we have

$$g(x,y)=\frac{pq{(x+1)}^{2-\mu }{(y+1)}^{2-\rho }}{(1-\mu )(2-\mu )(1-\rho )(2-\rho )}-e^{(x+1)(y+1)}.$$

For any given $0<\mu ,\rho ,p,q\le 1$, the approximation solution could be obtained by the spectral method. Then, we chose $\mu =1/4,\rho =\sqrt{2}/2,p=0.8$ and $q=1/3$ as representatives. We carried out the numerical test using Matlab as well. We obtained the result that both kinds of errors decayed exponentially. The corresponding numerical errors are shown in Table 2. It can be seen that the exponential rate of convergence was achieved.

Table 2. The errors for $\parallel u-u_N{\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}$ and $\parallel u-u_N{\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2\left(\mathsf{\Omega }\right)}$.

N	4	6	8	10	12	14	16
$L^{\infty }$ error	45.09172	8.95 × 10${}^{-13}$	9.02 × 10${}^{-13}$	8.03 × 10${}^{-13}$	9.88 × 10${}^{-13}$	7.39 × 10${}^{-13}$	7.53 × 10${}^{-13}$
$L_{{\omega }^{\alpha ,\beta }}^2$ error	51.55358	1.26 × 10${}^{-12}$	1.24 × 10${}^{-12}$	1.10 × 10${}^{-12}$	1.34 × 10${}^{-12}$	1.00 × 10${}^{-12}$	1.02 × 10${}^{-12}$
CPU time	0.0313	0.7813	1.7344	5.5313	13.3594	32.1094	70.7656

Furthermore, in order to show this more clearly, we exhibit the exponential convergence rate in Figure 2, which is illustrated by two subgraphs. The left subgraph demonstrates two kinds of errors, and the excellent consistency between the exact solution and approximate solution is presented in the right subgraph. Based on the shown table and figures, one can easily find that numerical simulation highly agreed with the result obtained by theoretical analysis.

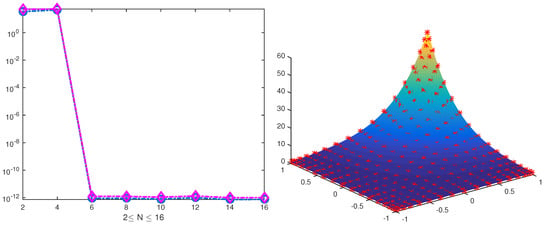
Figure 2. The errors in the $L^{\infty }$ and $L_{{\omega }^{\alpha ,\beta }}^2$ norms (left) and the consistency between the exact solution and approximate solution (right).

6. Concluding Remarks

In this paper, we presented an efficient numerical method for solving the two-dimensional nonlinear Volterra integral equation with weak singularity and delays and developed the spectral approximation schemes carefully. Then, the rigorous convergence results were obtained. Some numerical experiments were carried out to confirm the theoretical analysis. The numerical results demonstrated that the exponential rate of convergence was obtained. It is worth mentioning that our work greatly improved the convergence efficiency compared with those in [10,11]. In the future, we will investigate an efficient numerical method for multidimensional Volterra integral equation with delays.