On Odd Perks-G Class of Distributions: Properties, Regression Model, Discretization, Bayesian and Non-Bayesian Estimation, and Applications

Abstract

In this paper, we present a new univariate flexible generator of distributions, namely, the odd Perks-G class. Some special models in this class are introduced. The quantile function (QFUN), ordinary and incomplete moments (MOMs), generating function (GFUN), moments of residual and reversed residual lifetimes (RLT), and four different types of entropy are all structural aspects of the proposed family that hold for any baseline model. Maximum likelihood (ML) and maximum product spacing (MPS) estimates of the model parameters are given. Bayesian estimates of the model parameters are obtained. We also present a novel log-location-scale regression model based on the odd Perks–Weibull distribution. Due to the significance of the odd Perks-G family and the survival discretization method, both are used to introduce the discrete odd Perks-G family, a novel discrete distribution class. Real-world data sets are used to emphasize the importance and applicability of the proposed models.

1. Introduction

Over the past two decades, a number of generalized classes of statistical models have been developed and explored for the modeling of data in a variety of applications, including in the medical sciences, engineering, environmental and biological studies, life-testing challenges, demographics, actuarial science, and economics. As a result, a number of researchers have presented novel distribution classes that broaden well-known statistical models while also providing a high degree of adaptability for the analysis of data. As a result, various classes have been proposed in the statistical literature for generating new distributions by adding one or more factors. A few famous examples are as follows: the exponentiated Weibull family presented by Mudholkar et al. [1]; the novel approach offered by Marshall Olkin [2], involving the embedding of a parameter into a class of statistical models; the exponentiated T-X family of distributions reported by Alzaghal et al. [3]; Type II half Logistic-G by Hassan et al. [4]; the Weibull-G family by Bourguignon et al. [5]; the beta-generated familyby Eugene et al. [6]; the gamma-generated family by Zografos et al. [7]; the additive Weibull-G family by Hassan et al. [8]; the odd Lindley-G family by Silva et al. [9]; odd inverse power generalized Weibull-G by Al-Moisheer et al. [10]; Marshall-Olkin odd Burr III-G by Afify et al. [11]; Topp–Leone odd Fréchet-G by Al-Marzouki et al. [12]; the transmuted odd Fréchet-G family of distributions by Badr et al. [13]; odd generalized N-H-G by Ahmad et al. [14]; generalized odd Burr III-G by Haq et al. [15] and the odd Fréchet-G family by [16], among others. The Weibull-power Cauchy distribution, presented by Tahir et al. [17], is also worthy of mention.Cordeiro et al. [18] created a new family of generalized distributions. Different authors introduced new distribution to fit COVID-19 data as [19,20,21].

Perks [22] has presented a four-parameter extension of the Gompertz–Makeham distribution with the following hazard rate function:

$$h(x)=\frac{R+S{e}^{\mu x}}{1+M{e}^{-\mu x}+N{e}^{\mu x}}.$$

When $M=N=0$, the Gompertz–Makeham hazard rate function is obtained. The parameters appear to have been designed by Perks to be non-negative, and Marshall and Olkin [23] have demonstrated that $N=0$ cannot be used. However, by setting $M=0$ and choosing $N⟶0$ as the limit, the Gompertz–Makeham distribution can be obtained. Richards [24] has recently introduced a modified version of the Perks distribution, which takes the hazard function of the Perks distribution into account:

$$h(x)=\frac{\lambda \mu e^{\mu x}}{1+\lambda e^{\mu x}}.$$

The Perks distribution has several applications in the field of actuarial science. Haberman et al. [25] and Richards [24] have shown that this distribution is a good fit for pensioner mortality data. The parametric mortality projection is well-described by the Perks distribution, according to Haberman et al. [25]. The cumulative distribution function (cdf) and probability density function (pdf) of the Perks distribution are given as follows:

$$\psi (t;\theta ,\beta )=1-\frac{1+\beta }{1+\beta e^{\theta x}},\beta >0,\theta >0,x>0$$

(1)

and

$$\pi (t;\theta ,\beta )=\beta \theta e^{\theta x}\frac{1+\beta }{{\left(1+\beta e^{\theta x}\right)}^2}.$$

(2)

The authors in [26] defined a new idea for the generation of larger families, making use of any pdf as a generator. The above generator is a member of the $T-X$ distribution family, and its cdf is specified by

$$F(x)={\int }_0^{\mathsf{\Phi }\left[G(x,\delta )\right]}c(t)dt,$$

(3)

where c$(t)$ is the pdf of a random variable (RV) T$\in \left[a,b\right]$ for $-\infty <a<b<\infty$, G$(x,\delta )$ is the cdf of a random variable X, and $\mathsf{\Phi }\left[G(x,\delta )\right]$ is a function of G$(x,\delta )$, which satisfies the following conditions:

(i)

$\mathsf{\Phi }\left[G(x,\delta )\right]\in \left[a,b\right]$;

(ii)

$\mathsf{\Phi }\left[G(x,\delta )\right]$ is differentiable and monotonically non-decreasing;

(iii)

$\mathsf{\Phi }\left[G(x,\delta )\right]⟶a$ as $x⟶-\infty$ and $\mathsf{\Phi }\left[G(x,\delta )\right]⟶b$ as $x⟶\infty$.

The relevant pdf can be obtained as follows:

$$f(x,\beta ,\theta ,\delta )=\left\{\frac{d}{dx}\mathsf{\Phi }\left[G(x,\delta )\right]\right\}c\left\{\mathsf{\Phi }\left[G(x,\delta )\right]\right\}.$$

(4)

Inspired by the T-X concept, we develop a new, broader, and more flexible class of distributions, called the odd Perks-G $(OP)$ class, by combining $\mathsf{\Phi }\left[G(x,\delta )\right]$=$\frac{G(x;\delta )}{1-G(x;\delta )}$ and replacing c $(t)$ by $\beta \theta e^{\theta t}\frac{1+\beta }{{\left(1+\beta e^{\theta t}\right)}^2}$, where $t>0,\theta >0$; $\lambda \ge 0$; $G(x;\delta )$ is the baseline cdf, which depends on a parameter vector $\delta$; and $\overline{G}(x;\delta )=1-G(x;\delta )$ is the baseline reliability function. For each baseline $G(x;\delta ),$ the $OP$ cdf is provided as follows:

$$\begin{array}{cc}\hfill F(x;\beta ,\theta ,\delta )& =\beta \theta (1+\beta ){\int }_0^{\frac{G(x;\delta )}{\overline{G}(x;\delta )}}\frac{e^{\theta t}}{{\left(1+\beta e^{\theta t}\right)}^2}dt\hfill \\ & =1-\frac{(1+\beta )}{1+\beta e^{\theta (\frac{G(x;\delta )}{\overline{G}(x;\delta )})}}.\hfill \end{array}$$

(5)

The associated pdf may be obtained as follows:

$$f(x;\beta ,\theta ,\delta )=\frac{\beta \theta (1+\beta )g(x;\delta )e^{\theta (\frac{G(x;\delta )}{\overline{G}(x;\delta )})}}{\overline{G}{(x;\delta )}^2{\left[1+\beta e^{\theta (\frac{G(x;\delta )}{\overline{G}(x;\delta )})}\right]}^2},$$

(6)

where $g(x;\delta )$ is the baseline pdf of a baseline model. $X\backsim OP-G$ $(\beta ,\theta ,\delta )$ is used to represent an RV X with density function (6). The survival function (SF) of the $OP$-G family is:

$$\overline{F}(x;\beta ,\theta ,\delta )=\frac{(1+\beta )}{1+\beta e^{\theta (\frac{G(x;\delta )}{\overline{G}(x;\delta )})}},$$

(7)

and the hazard rate function (HRF) is defined as

$$\tau (x;\beta ,\theta ,\delta )=\frac{\beta \theta (1+\beta )g(x;\delta )e^{\theta (\frac{G(x;\delta )}{\overline{G}(x;\delta )})}}{\overline{G}{(x;\delta )}^2\left[1+\beta e^{\theta (\frac{G(x;\delta )}{\overline{G}(x;\delta )})}\right]}.$$

(8)

The $OP$-G family can be explained in the following way. Assume Y is a stochastic system’s RV lifetime with a specified continuous G model, where $\frac{G(x;\delta )}{\overline{G}(x;\delta )}$ is the odds ratio that an individual (or item) may not be active (failure or death) at time x following a lifetime Y. If the diversity of this chance of failure is denoted by the RV X and, as such, by the extended exponential model with parameters $\beta$ and $\theta$, then the cdf of X is as follows:

$$P(Y\le x)=P(X\le \frac{G(x;\delta )}{\overline{G}(x;\delta )})=F(x;\beta ,\theta ,\delta ).$$

The primary motives for employing the $OP$-G family in practice are:

(i)

To realize special models for all sorts of HRFs;

(ii)

Under the same baseline distribution, to regularly provide better fits than alternative produced models;

(iii)

Compared to the baseline model, to increase the adjustability of the kurtosis;

(iv)

To construct symmetric, left- and right-skewed, and inverted J-shaped distributions.

The association between survival time and numerous factors, such as sex, weight, blood pressure, and many more, has recently sparked significant attention in the relevant literature. Different parametric regression models, including the log-location-scale regression model, have been employed in a number of applications to quantify the effects of co-variate variables on survival time. As it has been extensively utilized in clinical trials and many other domains of application, the log-location-scale regression model stands out. In many real-world applications involving lifetime data, determining the link between survival time and independent (explanatory) variables is critical. In this context, the regression model method can be applied. The linear log-location-scale regression odd Perks-X model can be stated as follows:

$$y_i=B^{T}X+\sigma z_i,$$

where $z_i;i=1,\cdots ,n$ is the random error, with density function $f(\frac{y-B^{T}X}{\sigma })$; $B=(B_1,B_2,\cdots ,B_k)$ is a vector of unknown parameters of the explanatory variables; $\sigma >0$ is the scale parameter of the regression model; and $X=(X_{i1},X_{i2},\cdots ,X_{ik})$ is the explanatory variable vector, where k is the number of explanatory variables. For more information about linear location-scale regression models, see, for example, [27,28,29,30,31,32].

The remainder of this paper is divided into several sections, structured as follows. In Section 2, a useful expansion of $OP$-G is derived and some special models are obtained by means of the $OP$-G generator. Several mathematical statistical properties, MOMs, probability-weighted moments (PRWMOMs), residual life (RL) and reversed residual life (RRL) FUNs, and entropy (EN) are investigated in Section 3. In Section 4, non-Bayesian estimates of the model’s parameters are obtained. In Section 5, Bayesian estimates of the model’s parameters are obtained. In Section 6, bootstrap confidence intervals for the model’s parameters are obtained. In Section 7, the log-odd Perks–Weibull regression model is introduced. Simulation studies are described in Section 8. Section 9 details the discretization of the $OP$-G family. In Section 10, real-world data sets are used to demonstrate the adaptability of the proposed family. Finally, we present our conclusions.

2. Density of the $\mathit{OP}$-$\mathit{G}$ Class: Useful Expansions

We propose a handy linear representation of the $OP$-G density function in this section. We can write, using the generalised binomial expansion,

$${\left[1+\beta e^{\theta (\frac{G(x;\delta )}{\overline{G}(x;\delta )})}\right]}^{-2}=\sum _{i=0}^{\infty }{(-1)}^i(i+1){\beta }^i{e}^{i\theta (\frac{G(x;\delta )}{\overline{G}(x;\delta )})}.$$

(9)

Applying (9) in (6), we obtain

$$f(x;\beta ,\theta ,\delta )=\frac{\theta (1+\beta )g(x;\delta )}{\overline{G}{(x;\delta )}^2}\sum _{i=0}^{\infty }{(-1)}^i(i+1){\beta }^{i+1}{e}^{\theta (i+1)(\frac{G(x;\delta )}{\overline{G}(x;\delta )})}.$$

(10)

For the exponential function, we can use the power series

$$e^{\theta (i+1)(\frac{G(x;\delta )}{\overline{G}(x;\delta )})}=\sum _{j=0}^{\infty }\frac{{\theta }^j{(i+1)}^j}{j!}\frac{G{(x;\delta )}^{{}^j}}{\overline{G}{(x;\delta )}^{{}^j}}.$$

When we substitute this expansion into Equation (11), we obtain the following:

$$f(x;\beta ,\theta ,\delta )=(1+\beta )g(x;\delta )\sum _{i,j=0}^{\infty }\frac{{(-1)}^i(i+1){\beta }^{i+1}{\theta }^{j+1}{(i+1)}^j}{j!}\frac{G{(x;\delta )}^{{}^j}}{\overline{G}{(x;\delta )}^{{}^{j+2}}}.$$

(11)

If $\mid h\mid <1$ and $f>0$ yield a true non-integer, then the following power series occurs:

$${(1-h)}^{-f}=\sum _{k=0}^{\infty }\frac{\mathsf{\Gamma }(f+k)}{k!\mathsf{\Gamma }(f)}{h}^k.$$

(12)

Applying (12) in (11), for the term $\overline{G}{(x;\delta )}^{i+2}$, the $OP$-G density function can be expressed as an infinite mixture of expo-G density functions, as

$$f(x;\beta ,\theta ,\delta )=\sum _{j,k=0}^{\infty }{\varpi }_{j,k}{h}_{(j+k+1)}(x),$$

(13)

where $h_{\zeta }(x)=\zeta g(x)G^{\zeta -1}(x)$ is the expo-G pdf with power parameter $\zeta$ and

$${\varpi }_{{}_{j,k}}=\frac{(1+\beta ){\theta }^{j+1}}{j!k!\mathsf{\Gamma }(2+j)(j+k+1)}\sum _{i=0}^{\infty }{(-1)}^i(i+1){\beta }^{i+1}{(i+1)}^j.$$

The cdf of the $OP$-G class can also be expressed as a mixture of expo-G cdfs

$$F(x;\beta ,\theta ,\delta )=\sum _{j,k=0}^{\infty }{\varpi }_{j,k}{H}_{(j+k+1)}(x),$$

where $H_{(j+k+1)}(x)$ is the cdf of the exp-G function with power parameter $(j+k+1)$. Thus, several mathematical and statistical properties of the $OP$-G family can be determined obviously from those of the expo-G family.

2.1. Special Models

In this section, we examine four different $OP$-G special models.

2.1.1. Odd Perks Uniform

Let the parent distribution be uniform in the range $(0,\alpha )$, $\alpha >0,G(x;\alpha )=\frac{x}{\alpha }$, and $g(x;\alpha )=\frac{1}{\alpha },0<x<\alpha$. The cdf and pdf of the odd Perks uniform (OPU) are respectively given by

$$F(x;\beta ,\theta ,\alpha )=1-\frac{(1+\beta )}{1+\beta e^{\theta (\frac{\frac{x}{\alpha }}{1-\frac{x}{\alpha }})}}$$

and

$$f(x;\beta ,\theta ,\alpha )=\frac{\beta \theta (1+\beta )e^{\theta (\frac{\frac{x}{\alpha }}{1-\frac{x}{\alpha }})}}{\alpha {(1-\frac{x}{\alpha })}^2{\left[1+\beta e^{\theta (\frac{\frac{x}{\alpha }}{1-\frac{x}{\alpha }})}\right]}^2}.$$

2.1.2. Odd Perks Exponential

The exponential cdf and pdf with parameter $\lambda$ are $G(x;\lambda )=1-e^{-\lambda x}$ and $g(x;\lambda )=\lambda e^{-\lambda x}$. The cdf and pdf of the odd Perks exponential (OPE) are respectively given by

$$F(x;\beta ,\theta ,\lambda )=1-\frac{(1+\beta )}{1+\beta e^{\theta (e^{\lambda x}-1)}}$$

and

$$f(x;\beta ,\theta ,\lambda )=\frac{\beta \theta (1+\beta )\lambda e^{\theta (e^{\lambda x}-1)}}{e^{-\lambda x}{\left[1+\beta e^{\theta (e^{\lambda x}-1)}\right]}^2}.$$

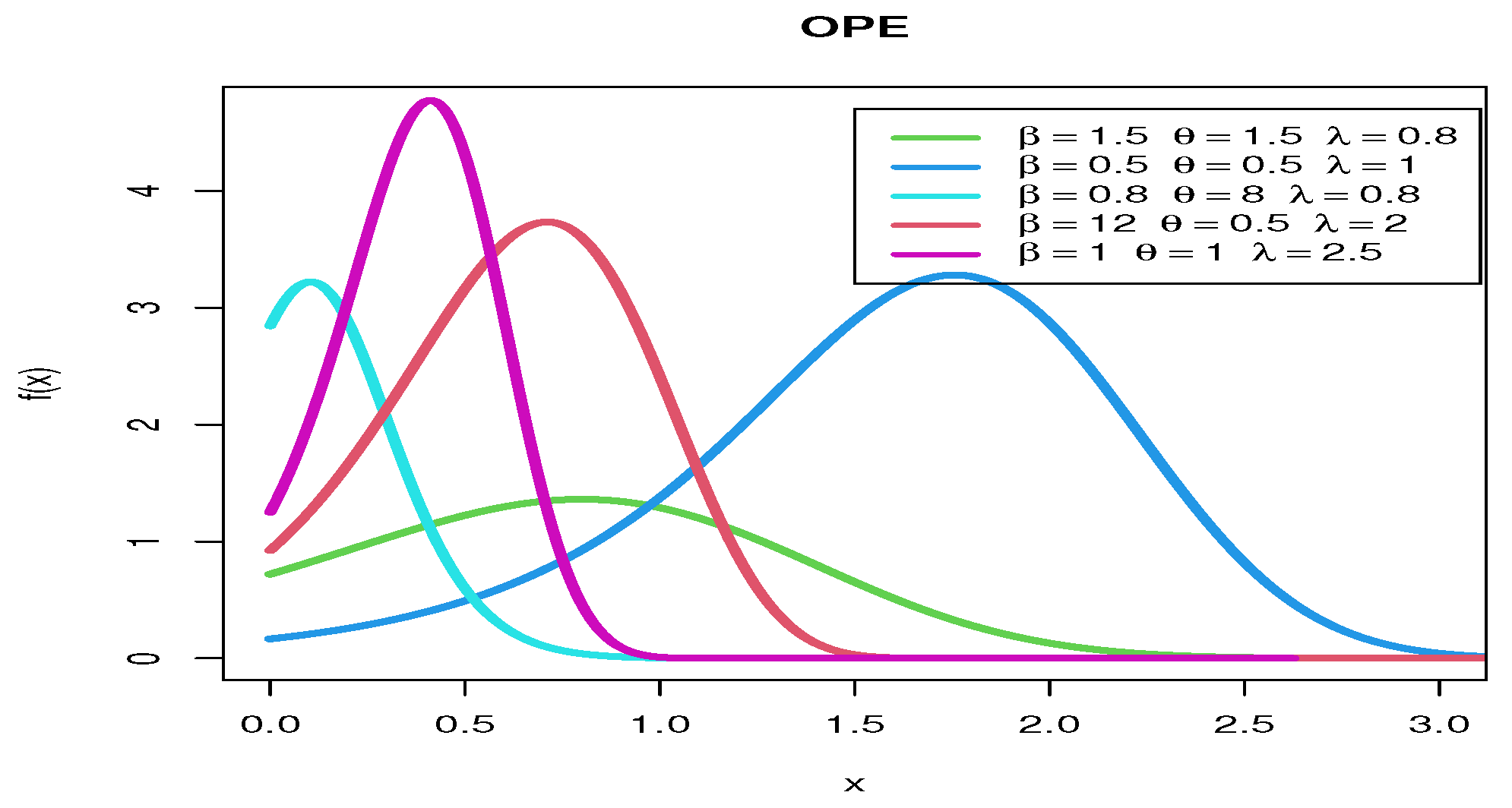
Figure 1 shows various pdf curves for OPE models with different parameter values.

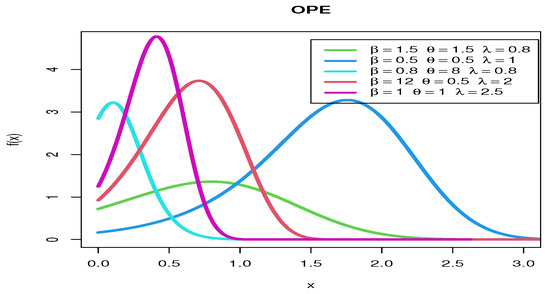
Figure 1. The pdf curves for OPE models with various parameter values.

2.1.3. Odd Perks–Weibull

Let us consider the Weibull distribution with cdf and pdf values given by $G(x;\delta ,\lambda )=1-e^{-{\left(\frac{x}{\lambda }\right)}^{\delta }}$ and $g(x;\delta ,\lambda )=\frac{\delta }{{\lambda }^{\delta }}{x}^{\delta -1}{e}^{-{\left(\frac{x}{\lambda }\right)}^{\delta }},\delta >0,\lambda >0$. The odd Perks–Weibull (OPW) has cdf and pdf given, respectively, by

$$F(x;\beta ,\theta ,\mu ,\gamma )=1-\frac{(1+\beta )}{1+\beta e^{\theta (e^{{\left(\frac{x}{\lambda }\right)}^{\delta }}-1)}}$$

and

$$f(x;\beta ,\theta ,\mu ,\gamma )=\frac{\beta \theta (1+\beta )\frac{\delta }{{\lambda }^{\delta }}{x}^{\delta -1}{e}^{\theta (e^{{\left(\frac{x}{\lambda }\right)}^{\delta }}-1)}}{e^{-{\left(\frac{x}{\lambda }\right)}^{\delta }}{\left[1+\beta e^{\theta (e^{{\left(\frac{x}{\lambda }\right)}^{\delta }}-1)}\right]}^2}.$$

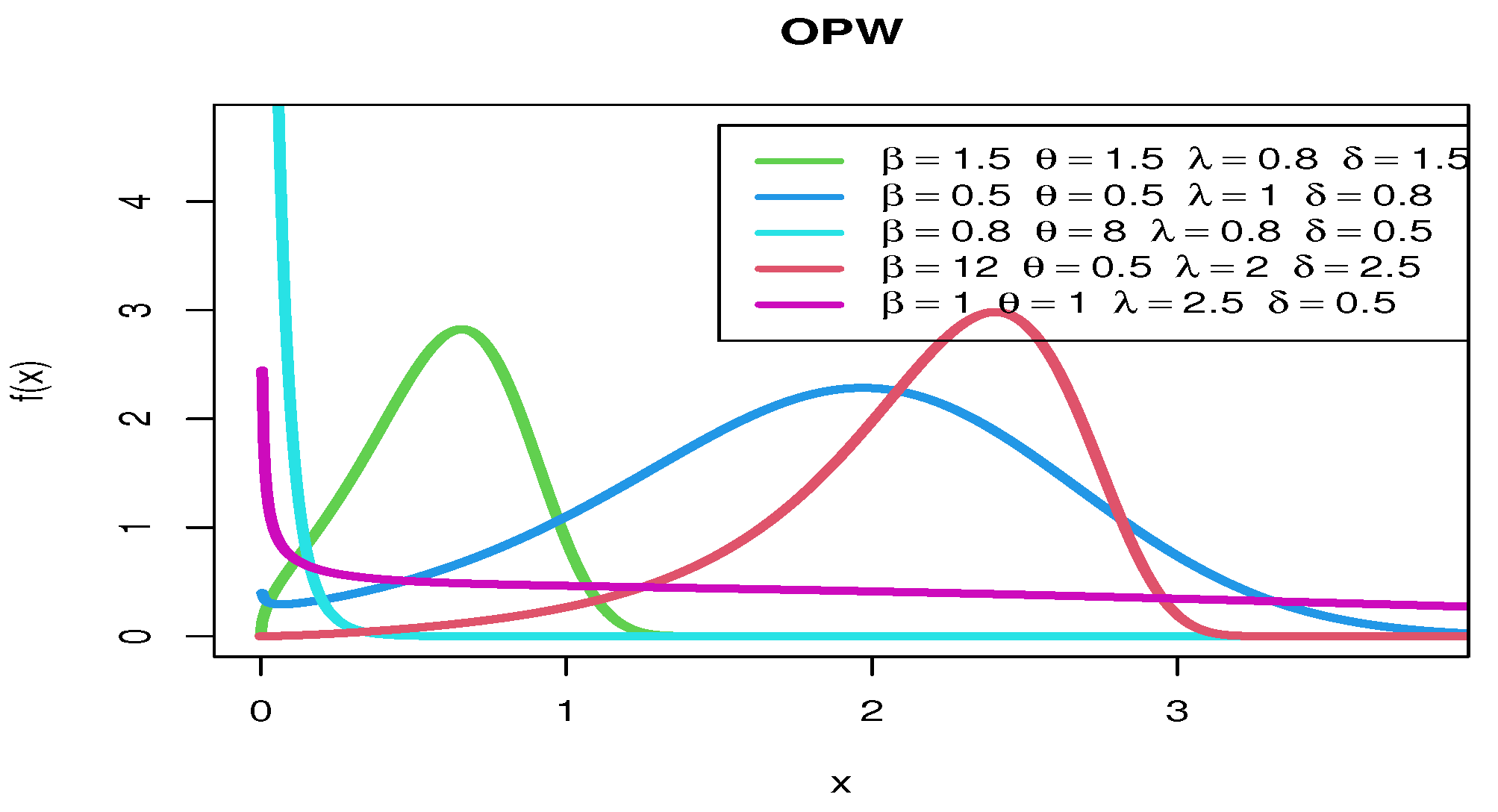
Figure 2 show various pdf curves for OPW models with different parameter values.

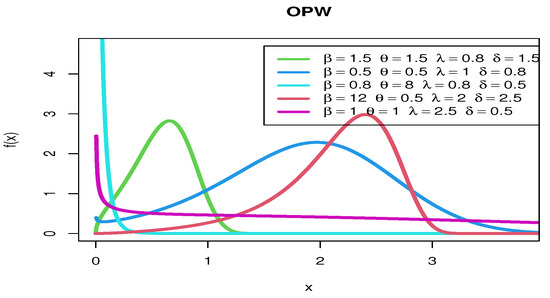
Figure 2. The pdf curves for OPW models with various parameter values.

2.1.4. Odd Perks–Lomax

The Lomax cdf has the parameters $a>0$ and b$>0$, where $G(x;a,b)=1-{(1+\frac{x}{b})}^{-a}$. The odd Perks–Lomax (OPL) model has the cdf

$$F(x;\beta ,\theta ,a,b)=1-\frac{(1+\beta )}{1+\beta e^{\theta ({(1+\frac{x}{b})}^a-1)}},$$

and the associated pdf is given by

$$f(x;\beta ,\theta ,a,b)=\frac{a\beta \theta (1+\beta )e^{\theta ({(1+\frac{x}{b})}^a-1)}}{b{(1+\frac{x}{b})}^{-(a+1)}{\left[1+\beta e^{\theta ({(1+\frac{x}{b})}^a-1)}\right]}^2}.$$

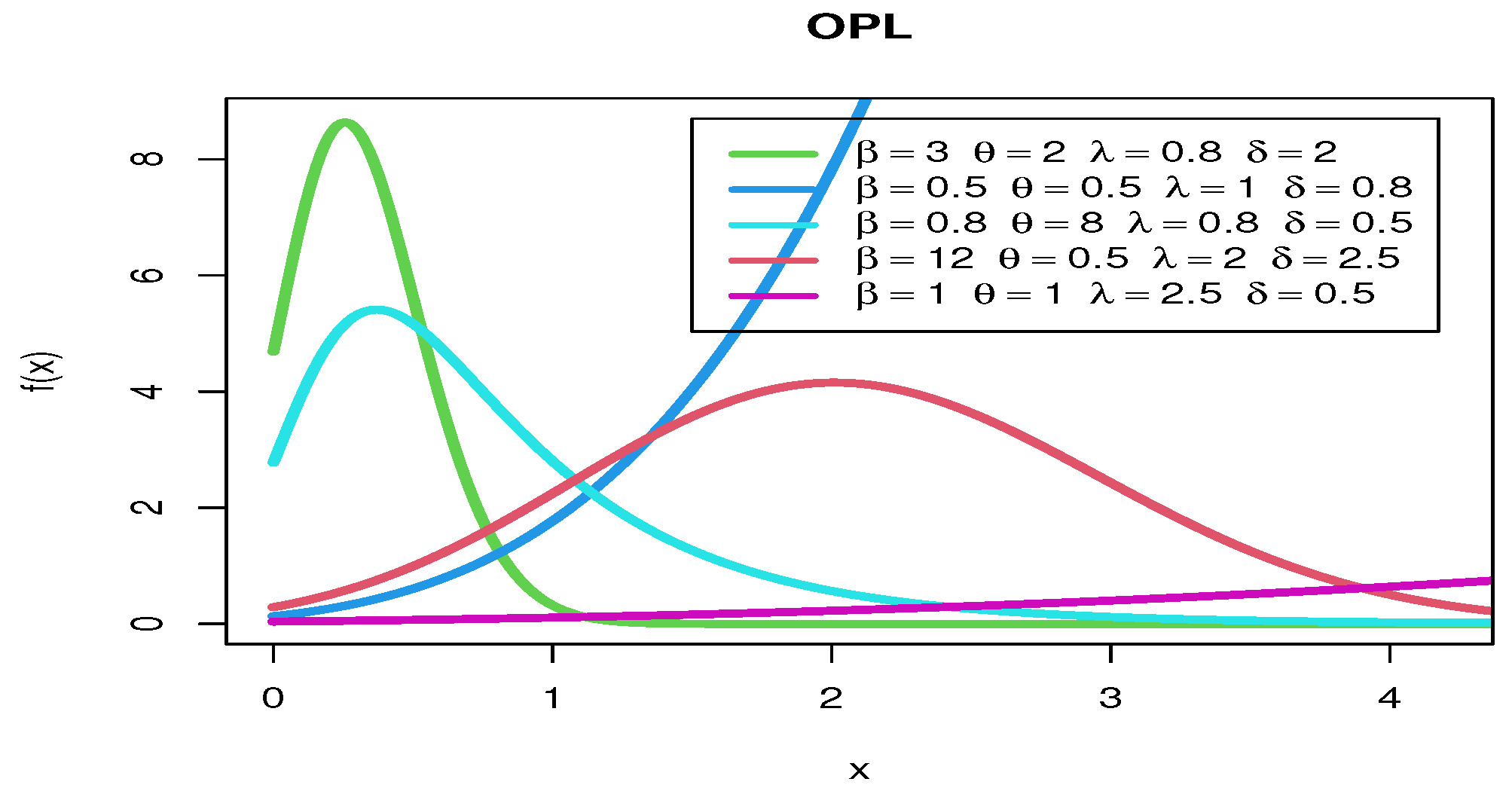
Figure 3 shows various pdf curves for OPL models with different parameter values.

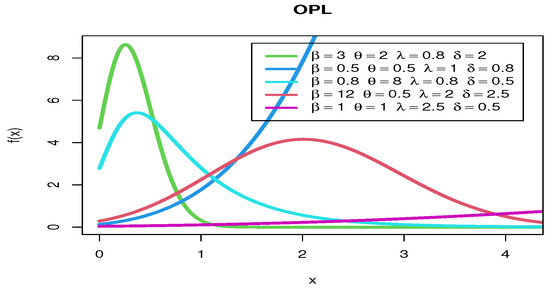
Figure 3. The pdf curves for OPL models with different parameter values.

3. Statistical Features

The statistical features of the $OP$-G family are investigated in this section; specifically, the QFUN, MOMs, incomplete MOMs, PRWMOMs, and RL and RRL FUNs.

3.1. Quantiles

The $OP$-G quantiles (e.g., $x=Q(u)$), may be derived by inverting (5), as shown below

$$F^{-1}(u)=Q_G(u)=G^{-1}\left\{\frac{\frac{1}{\theta }log\left[\frac{\beta +u}{\beta (1-u)}\right]}{\frac{1}{\theta }log\left[\frac{\beta +u}{\beta (1-u)}\right]+1}\right\},$$

(14)

where $Q_{G(u)}$ denotes the QFUN.

3.2. Moments

In this sub-section, the ordinary MOM and MOM GFUNs of the $OP$-G class are derived. Most of the necessary characteristics and features of a distribution can be studied through its MOMs.

Let $Z_{(j+k+1)}$ be an RV having the exp-G pdf $h_{(j+k+1)}(x)$ with power parameter $(j+k+1)$. The rth moment of the $OP$-G family of distributions can be obtained from (13), as follows

$$\mu {}_r^{\prime }=E(X^{{}^r})={\int }_{-\infty }^{\infty }{x}^{r}f(x)dx=\sum _{j,k=0}^{\infty }{\varpi }_{j,k}E(Z_{(j+k+1)}^{{}^r}).$$

(15)

Another formula for the rth MOM follows from (2.5), as $\mu {}_r^{\prime }=E(X^r)={\sum }_{j,k=0}^{\infty }{\varpi }_{j,k}$$E(Z_{(j+k+1)}^{{}^r})$.

Table 1 provides some numerical values of moments for the OPE model, including $\mu {}_1^{\prime }$, $\mu {}_2^{\prime }$, $\mu {}_3^{\prime }$, $\mu {}_4^{\prime }$, variance (var), skewness (SK), kurtosis (KU), and the coefficient of variation (CV).

Table 1. Some numerical values of moments with various parameters in the OPE model.

$(\mathit{\beta },\mathit{\theta },\mathit{\lambda })$	$\mathit{\mu }{{}^{\prime }}_1$	${\mathit{\mu }}_2^{\prime }$	${\mathit{\mu }}_3^{\prime }$	$\mathit{\mu }{}_4^{\prime }$	Var	SK	KU	CV
0.5, 0.5, 0.5	2.523	7.741	26.091	93.614	1.373	−0.23	2.312	0.464
0.8, 0.5, 0.5	2.344	6.863	22.392	78.425	1.369	−0.071	2.224	0.499
1.2, 0.5, 0.5	2.214	6.26	19.944	68.654	1.359	0.042	2.205	0.527
1.5, 0.5, 0.5	2.153	5.987	18.861	64.406	1.353	0.094	2.207	0.54
2.0, 0.5, 0.5	2.085	5.691	17.706	59.929	1.343	0.153	2.219	0.556
2.5, 0.5, 0.5	2.041	5.501	16.974	57.123	1.336	0.191	2.232	0.566
3.0, 0.5, 0.5	2.01	5.369	16.469	55.197	1.33	0.218	2.244	0.574
0.5, 0.8, 0.5	1.989	4.938	13.777	41.633	0.982	0.049	2.373	0.498
0.5, 1.2, 0.5	1.552	3.099	7.081	17.749	0.692	0.216	2.477	0.536
0.5, 1.5, 0.5	1.339	2.349	4.76	10.658	0.556	0.304	2.558	0.557
0.5, 2.0, 0.5	1.096	1.609	2.765	5.303	0.408	0.415	2.698	0.583
0.5, 2.5, 0.5	0.931	1.18	1.771	2.989	0.314	0.499	2.834	0.602
0.5, 3.0, 0.5	0.81	0.907	1.211	1.832	0.25	0.567	2.96	0.618
0.5, 0.5, 0.8	1.614	3.145	6.774	15.629	0.541	−0.12	2.405	0.456
0.5, 0.5, 1.2	1.076	1.398	2.007	3.087	0.24	−0.12	2.405	0.456

For the MOM GFUN, we now introduce two formulas. According to Equation (13), the first formula can be calculated by

$$M_X(t)=E(e^{tX})=\sum _{j,k=0}^{\infty }{\varpi }_{j,k}{M}_{(j+k+1))}(t),$$

(16)

where $M_{(j+k+1))}(t)$ is the MOM-GFUN of $Z_{(j+k+1)}$. As a result, the exp-G GFUN may readily be used to determine $M_X(t)$. The second formula for $M_X(t)$ can be derived from (13) as

$$M_X(t)=\sum _{j,k=0}^{\infty }{\varpi }_{j,k}{M}_{(j+k+1)}(t),$$

where $M_{\kappa }(t)$ is the mgf of the RV $Z_{\varkappa }$, given by

$$\begin{array}{ccc}\hfill M_{\kappa }(t)& =& {\int }_{-\infty }^{\infty }{e}^{tX}g(x)G{(x)}^{\kappa -1},\varkappa >0\hfill \\ & & \\ & =& \kappa {\int }_0^1{u}^{\kappa -1}{e}^{t{Q}_G(u)}du.\hfill \end{array}$$

For each real $s>0$, the sth incomplete MOMs of X, defined by ${\chi }_s(t)$, can be written as

$${\chi }_s(t)={\int }_{-\infty }^t{x}^{s}f(x)dx=\sum _{j,k=0}^{\infty }{\varpi }_{j,k}{\int }_{-\infty }^t{x}^s{\chi }_{s,(j+k+1)}(t)dx,$$

(17)

where

$${\chi }_{s,b}(t)={\int }_0^{G(t)}{u}^{b-1}{Q}_G{(u)}^{s}du,$$

which can be evaluated numerically.

The $(s,r)$th PRWMOMs of the $OP$-G class are provided by:

$${\mathrm{Y}}_{(s,r)}=E\left\{X^{r}F{(x)}^r\right\}={\int }_{-\infty }^{\infty }{x}^{s}F{(x)}^{r}f(x)dx,$$

(18)

based on (5) and (6). Then, after some calculation, we obtain

$$f(x)F{(x)}^r=\sum _{j,k=0}^{\infty }{\mathsf{\Phi }}_{j,k}{h}_{(j+k+1)}(x),$$

where

$$\begin{array}{ccc}\hfill {\mathsf{\Phi }}_{j,k}& =& \frac{{\theta }^{j+1}{\beta }^{m+1}\mathsf{\Gamma }(j+k+2))}{j!k!m!\mathsf{\Gamma }(j+2)\mathsf{\Gamma }(j+k+1)}\sum _{i,m=0}^{\infty }\frac{{(-1)}^{i+m}{(m+1)}^j{(1+\beta )}^{i+1}\mathsf{\Gamma }(i+m+2)}{\mathsf{\Gamma }\left(i+2\right)}.\hfill \end{array}$$

As a result, $(s,r)$th PRWMOMs of the $OP$-G class can be expressed as

$${\mathrm{Y}}_{(s,r)}=\sum _{j,k=0}^{\infty }{\mathsf{\Phi }}_{j,k}^{(r)}{\int }_{-\infty }^{\infty }{x}^s{h}_{(j+k+1)}(x)dx.$$

Thus, the $(s,r)$th PRWMOMs of X may be generated by combining an unlimited number of exp-G MOMs, provided as

$${\mathrm{Y}}_{(s,r)}=\sum _{j,k=0}^{\infty }{\mathsf{\Phi }}_{j,k}^{(r)}E\left(Z_{(j+k+1)}^{{}^s}\right).$$

3.3. Residual Lifetimes

The rth-order MOM of the RL is given as:

$$\begin{array}{cc}\hfill {\mu }_r(t)& =E({(X-t)}^r\mid X>t)=\frac{1}{\overline{F}(t)}{\int }_t^{\infty }{(x-t)}^{r}f(x)dx,r\ge 1\hfill \\ & =\frac{1}{\overline{F}(t)}\sum _{j,k=0}^{\infty }{\varpi }_{j,k}^{*}{\int }_t^{\infty }{x}^r{h}_{(j+k+1)}(x)dx,\hfill \end{array}$$

(19)

where ${\varpi }_{j,k}^{*}={\varpi }_{j,k}$${\sum }_{m=0}^r\left(\genfrac{}{}{0pt}{}{r}{m}\right){(-t)}^{r-m}$. Such a procedure may be used to calculate the rth-order MOM of the RRL.

$$\begin{array}{cc}\hfill m_r(t)& =E({(t-X)}^r\mid X\le t)=\frac{1}{F(t)}{\int }_0^t{(t-x)}^{r}f(x)dx,r\ge 1\hfill \\ & =\frac{1}{F(t)}\sum _{j,k=0}^{\infty }{\varpi }_{j,k}^{*}{\int }_0^t{x}^r{h}_{(j+k+1)}(x)dx.\hfill \end{array}$$

(20)

3.4. Four Different Types of Entropy

The Rényi EN (REN) (see [33]) is characterized by ($\rho >0,\rho \ne 1)$

$$I_R(\rho )=\frac{1}{1-\rho }log\left[{\int }_{-\infty }^{\infty }{f}^{\rho }(x)dx\right].$$

(21)

Again using the binomial expansion (13) in (6), we obtain:

$$f^{\rho }(x)=\sum _{j,k=0}^{\infty }{\mathsf{\Lambda }}_{j,k}g{(x,\delta )}^{\rho }G{(x,\delta )}^{j+k},$$

where

$${\mathsf{\Lambda }}_{j,k}=\sum _{i=0}^{\infty }{(-1)}^i\frac{{\beta }^{\rho +i}{\theta }^{\rho +j}{(1+\beta )}^{\rho }{(i+\rho )}^j\mathsf{\Gamma }(2\rho +i)\mathsf{\Gamma }(2\rho +j+k)}{i!k!\mathsf{\Gamma }(2\rho )\mathsf{\Gamma }(2\rho +j)}.$$

As a result, the REN of the $OP$-G class is given by

$$I_R(\rho )=\frac{1}{1-\rho }log\left\{\sum _{j,k=0}^{\infty }{\mathsf{\Lambda }}_{j,k}{\int }_{-\infty }^{\infty }g{(x)}^{\rho }G{(x)}^{j+k}dx\right\}.$$

(22)

The Tsallis EN (TEN) measure (see [34]) is defined as

$$T_R\left(\rho \right)=\frac{1}{\rho -1}\left[1-\underset{-\infty }{\overset{\infty }{\int }}{\left(f(z)\right)}^{\rho }dz\right],\rho \ne 1,\rho >0.$$

The Havrda and Charvat EN (HCEN) measure (see [35]) is defined as

$$HaC{h}_R\left(\rho \right)=\frac{1}{2^{1-\rho }-1}\left[{\left(\underset{-\infty }{\overset{\infty }{\int }}{\left(f(z)\right)}^{\rho }dz\right)}^{\frac{1}{\rho }}-1\right],\rho \ne 1,\rho >0.$$

The Arimoto EN (AEN) measure (see [36]) of $OP$-G is defined as

$$A{r}_R\left(\rho \right)=\frac{\rho }{1-\rho }\left[{\left(\underset{-\infty }{\overset{\infty }{\int }}{\left(f(z)\right)}^{\rho }dz\right)}^{\frac{1}{\rho }}-1\right],\rho \ne 1,\rho >0.$$

Numerical values of the REN, TEN, HCEN, and AEN under various parameter values in the OPE model are provided in Table 2.

Table 2. Numerical values of the REN, TEN, HCEN, and AEN for the OPE model.

$(\mathit{\beta },\mathit{\theta },\mathit{\lambda })$	$\mathit{\rho }=0.5$				$\mathit{\rho }=1.5$				$\mathit{\rho }=2.5$
	REN	TEN	HCEN	AEN	REN	TEN	HCEN	AEN	REN	TEN	HCEN	AEN
0.5, 0.5, 0.5	0.669	2.802	3.669	2.322	0.651	1.8	1.179	1.054	0.618	1.364	0.957	0.588
0.8, 0.5, 0.5	0.671	2.812	3.686	2.329	0.652	1.803	1.181	1.056	0.626	1.369	0.965	0.59
1.2, 0.5, 0.5	0.669	2.804	3.671	2.323	0.649	1.797	1.177	1.053	0.626	1.369	0.965	0.59
1.5, 0.5, 0.5	0.668	2.795	3.657	2.316	0.646	1.792	1.173	1.05	0.624	1.368	0.963	0.59
2.0, 0.5, 0.5	0.666	2.783	3.635	2.306	0.642	1.784	1.167	1.045	0.621	1.366	0.96	0.589
2.5, 0.5, 0.5	0.664	2.774	3.618	2.298	0.639	1.778	1.163	1.041	0.618	1.364	0.957	0.588
3.0, 0.5, 0.5	0.663	2.766	3.604	2.291	0.636	1.773	1.159	1.039	0.616	1.362	0.955	0.587
0.5, 0.8, 0.5	0.628	2.563	3.25	2.123	0.575	1.652	1.07	0.968	0.549	1.315	0.886	0.567
0.5, 1.2, 0.5	0.557	2.169	2.604	1.797	0.494	1.481	0.946	0.867	0.47	1.242	0.796	0.535
0.5, 1.5, 0.5	0.509	1.925	2.23	1.595	0.442	1.363	0.864	0.798	0.419	1.183	0.732	0.51
0.5, 2.0, 0.5	0.442	1.6	1.765	1.325	0.369	1.181	0.74	0.692	0.344	1.076	0.631	0.464
0.5, 2.5, 0.5	0.385	1.345	1.425	1.114	0.306	1.014	0.628	0.594	0.281	0.96	0.536	0.414
0.5, 3.0, 0.5	0.335	1.137	1.164	0.942	0.252	0.859	0.527	0.503	0.225	0.836	0.445	0.36
0.5, 0.5, 0.8	0.507	1.914	2.214	1.585	0.444	1.366	0.866	0.8	0.414	1.177	0.726	0.507
0.5, 0.5, 1.2	0.331	1.12	1.143	0.927	0.268	0.906	0.558	0.531	0.238	0.866	0.467	0.373

4. Non-Bayesian Estimation

In this section, we examine two different non-Bayesian estimation approaches for the $OP$-G family parameters: The maximum likelihood and maximum product of spacings methods.

4.1. Likelihood Method

Various parameter estimation strategies have been introduced in the literature, the most prominent of which is the maximum likelihood (ML) method, which may be used to create confidence ranges for model parameters, as well as in the testing of statistics. Using complete samples, we can calculate the ML estimates (MLEs) of the parameters for the proposed class. Let $x_1,...,x_n$ be a random sample of size n from the $OP$-G class with parameters $\beta ,\theta$, and $\delta$. The log-likelihood (LL) FUN is given as

$$L_n=nlog(\beta )+nlog(\theta )+nlog(1+\beta )+\sum _{i=1}^{n}logg(x_i;\delta )+\theta t_i-2\sum _{i=1}^{n}log\overline{G}(x_i;\delta )-2\sum _{i=1}^{n}log(1+\beta e^{\theta t_i}),$$

(23)

where $t_i=\frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )}.$ The components of the score vector $U(\mathsf{\Omega })=\frac{\partial L_n}{\partial \mathsf{\Omega }}={\left(\frac{\partial L_n}{\partial \beta },\frac{\partial L_n}{\partial \theta },\frac{\partial L_n}{\partial \delta }\right)}^T$ are given by

$$U_{\beta }=\frac{\partial L_n}{\partial \beta }=\frac{n}{\beta }+\frac{n}{1+\beta }-2\sum _{i=1}^n\frac{e^{\theta t_i}}{1+\beta e^{\theta t_i}},$$

(24)

$$U_{\theta }=\frac{\partial L_n}{\partial \theta }=\frac{n}{\theta }+t_i-2\sum _{i=1}^n\frac{\beta t_i{e}^{\theta t_i}}{1+\beta e^{\theta t_i}},$$

(25)

and

$$U_{{\delta }_k}=\frac{\partial L_n}{\partial {\delta }_k}=\sum _{i=1}^n\frac{g^{\prime }(x_i;\delta )}{g(x_i;\delta )}+\theta \sum _{i=1}^n\frac{G^{\prime }(x_i;\delta )}{{\overline{G}}^2(x_i;\delta )}+2\sum _{i=1}^n\frac{G^{\prime }(x_i;\xi )}{\overline{G}(x_i;\delta )}-2\sum _{i=1}^n\frac{\beta e^{\theta t_i}}{1+\beta e^{\theta t_i}}\partial t_i\partial {\delta }_k,$$

(26)

where $g^{\prime }(x_i;\delta )=\frac{\partial g(x_i;\delta )}{\partial \delta },G^{\prime }(x_i;\delta )=\frac{\partial G(x_i;\delta )}{\partial {\delta }_k},{\overline{G}}^{\prime }(x_i;\delta )=\frac{\partial \overline{G}(x_i;\delta )}{\partial {\delta }_k}$, and ${\underline{\delta }}_k$ is the kth element of the vector of parameters $\underline{\delta }$.

4.2. Maximum Product of Spacings (MPS) Estimation

The authors in [37] developed the MPS methodology as an alternative to the MLE method for estimating the parameters of continuous univariate distributions. They argued that, by replacing the likelihood function with a product of spacings, the MPS approach possesses most of the properties of ML. The authors in [38] also considered the MPS technique as an independent approximation of the Kullback–Leibler information measure.

Let $(X_1<X_2<\cdots <X_n)$ be from the $OP$-G family with cdf (5) and parameters $\beta ,\theta$, and $\delta$. Then, the uniform spacings of this random sample are defined as

$$Gs(\beta ,\theta ,\delta |data)={\left(\prod _{i=1}^{n+1}{D}_i(x_i,\beta ,\theta ,\delta )\right)}^{\frac{1}{n+1}},$$

(27)

where

$$D_i\left(x_i;\beta ,\theta ,\delta \right)=\left\{\begin{array}{cc}F\left(x_1;\beta ,\theta ,\delta \right)\hfill & \mathrm{if}i=1,\hfill \\ F\left(x_i;\beta ,\theta ,\delta \right)-F\left(x_{i-1};\beta ,\theta ,\delta \right)\hfill & \mathrm{if}i=2,\cdots ,n,\hfill \\ 1-F\left(x_n;\beta ,\theta ,\delta \right)\hfill & \mathrm{if}i=n.\hfill \end{array}\right.$$

The MPSEs can be obtained by maximizing the product of spacings, as follows

$$Gs(\beta ,\theta ,\delta |data)={\left\{\left[1-\frac{(1+\beta )}{1+\beta e^{\theta (\frac{G(x_1;\delta )}{\overline{G}(x_1;\delta )})}}\right]\frac{(1+\beta )}{1+\beta e^{\theta (\frac{G(x_n;\delta )}{\overline{G}(x_n;\delta )})}}\prod _{i=2}^n\frac{(1+\beta )}{1+\beta e^{\theta (\frac{G(x_{i-1};\delta )}{\overline{G}(x_{i-1};\delta )})}}-\frac{(1+\beta )}{1+\beta e^{\theta (\frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )})}}\right\}}^{\frac{1}{n+1}}.$$

(28)

The MPSEs of $\beta$, $\theta$, and $\delta$ are calculated by first solving the non-linear equations. The logarithm of the product of spacings in Equation (28) is then differentiated with respect to each parameter. Non-linear optimization algorithms (e.g., the Newton–Raphson method) can be used to numerically solve these equations, as they are difficult to solve analytically. An asymptotic variance–covariance matrix and normal approximation confidence intervals are computed after the ACI.

5. Bayesian Estimation

In this section, we consider the Bayesian estimation of the parameters of the model obtained when data are observed based on the squared error loss function (SELF), defined by

$$\begin{array}{cc}\hfill L_{SELF}=(\mathsf{\Omega },\check{\mathsf{\Omega }})& ={(\check{\mathsf{\Omega }}-\mathsf{\Omega })}^2,\hfill \end{array}$$

where $\check{\mathsf{\Omega }}$ is an estimator of $\mathsf{\Omega }$. We denote the prior and posterior distributions of $\mathsf{\Omega }$ by $\pi (\mathsf{\Omega })$ and ${\pi }^{*}(\mathsf{\Omega }\mid \underline{x})$, respectively. Under the SELF, the Bayesian estimate of any FUN $B(\mathsf{\Omega })$ of $\mathsf{\Omega }$ is given by

$$\begin{array}{cc}\hfill {\tilde{v}}_{SELF}& =E[B(\mathsf{\Omega })\mid \underline{x}]={\int }_0^{\infty }B(\mathsf{\Omega }){\pi }^{*}(\mathsf{\Omega }\mid \underline{x})d\mathsf{\Omega }.\hfill \end{array}$$

(29)

A prior distribution is important for the development of Bayes estimators.

Under the assumption of gamma prior distributions, we investigate this estimation problem. Therefore, it is assumed that $\beta ,\theta$, and $\delta$ follow independent gamma distributions, with ${\beta }_1\sim \mathsf{\Gamma }({\eta }_1,{\zeta }_1)$, $\theta \sim \mathsf{\Gamma }({\eta }_2,{\zeta }_2)$, and $\delta \sim \mathsf{\Gamma }({\eta }_3,{\zeta }_3)$ if $\delta >0$ and if $\delta$ is an individual parameter, with respective pdfs given by

$$\begin{array}{cc}\hfill & \pi (\beta )\propto {\beta }^{{\eta }_1-1}{e}^{-\frac{\beta }{{\zeta }_1}},\beta >0,{\eta }_1,{\zeta }_1>0\hfill \\ & \pi (\theta )\propto {\theta }^{{\eta }_2-1}{e}^{-\frac{\theta }{{\zeta }_2}},\theta >0,{\eta }_2,{\zeta }_2>0\hfill \\ & \pi (\delta )\propto {\delta }^{{\eta }_3-1}{e}^{-\frac{\delta }{{\zeta }_3}},\delta >0,{\eta }_3,{\zeta }_3>0\hfill \end{array}$$

(30)

Using the informative prior (30) and the likelihood FUN (6), the joint posterior density may be calculated as follows:

$${\pi }^{*}(\beta ,\theta ,\delta )\propto {\beta }^{n+{\eta }_1-1}{\theta }^{n+{\eta }_2-1}{(1+\beta )}^n{\delta }^{{\eta }_3-1}{e}^{-\frac{\beta }{{\zeta }_1}-\frac{\delta }{{\zeta }_3}}\prod _{i=1}^n\frac{g(x_i;\delta )e^{-\theta \left[\frac{1}{{\zeta }_2}-\frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )}\right]}}{\overline{G}{(x_i;\delta )}^2{\left[1+\beta e^{\theta \frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )}}\right]}^2}.$$

(31)

The marginal posterior densities of the parameters $\beta ,\theta$, and $\delta$ can be derived as

$${\pi }^{*}(\beta )\propto {\beta }^{n+{\eta }_1-1}{(1+\beta )}^n{e}^{-\frac{\beta }{{\zeta }_1}}\prod _{i=1}^n\frac{1}{{\left[1+\beta e^{\theta \frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )}}\right]}^2}$$

(32)

$${\pi }^{*}(\theta )\propto {\theta }^{n+{\eta }_2-1}\prod _{i=1}^n\frac{e^{-\theta \left[\frac{1}{{\zeta }_2}-\frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )}\right]}}{{\left[1+\beta e^{\theta \frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )}}\right]}^2}$$

(33)

$${\pi }^{*}(\delta )\propto {\delta }^{{\eta }_3-1}{e}^{-\frac{\delta }{{\zeta }_3}}\prod _{i=1}^n\frac{g(x_i;\delta )e^{\theta \frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )}}}{\overline{G}{(x_i;\delta )}^2{\left[1+\beta e^{\theta \frac{G(x_i;\delta )}{\overline{G}(x_i;\delta )}}\right]}^2}.$$

(34)

As the marginal posterior densities in (32), (33) and (34) are not well-known distributions, we utilize the Metropolis–Hastings sampler to produce values for $\beta ,\theta$, and $\delta$, using the normal proposed distribution in (32), (33) and (34).

Furthermore, the approach of Chen and Shao [39] has been widely used to create highest posterior density (HPD) intervals for Bayesian estimates with uncertain benefit distribution parameters. For example, using the two endpoints from MCMC sample outputs, the $2.5\%$ and $97.5\%$ percentiles, a $95\%$ HPD interval can be produced. The Bayesian credible intervals for the parameters $\beta ,\theta$, and $\delta$ are calculated as follows:

• Sort the parameters as ${\tilde{\beta }}^{\left[1\right]}<{\tilde{\beta }}^{\left[2\right]}<...<{\tilde{\beta }}^{\left[N\right]}$, ${\tilde{\theta }}^{\left[1\right]}<{\tilde{\theta }}^{\left[2\right]}<...<{\tilde{\theta }}^{\left[N\right]}$, ${\tilde{\delta }}^{\left[1\right]}<{\tilde{\delta }}^{\left[2\right]}<...<{\tilde{\delta }}^{\left[N\right]}$, and $R^{\left[1\right]}<R^{\left[2\right]}<...<R^{\left[N\right]}$, where N is the length of the generated MCMC.
• The $95\%$ symmetric credible intervals for $\tilde{\beta },\tilde{\theta }$, and $\tilde{\delta }$ become $\left({\tilde{\beta }}^{L\frac{25}{1000}},{\tilde{\beta }}^{L\frac{975}{1000}}\right)$, $\left({\tilde{\theta }}^{L\frac{25}{1000}},{\tilde{\theta }}^{L\frac{975}{1000}}\right)$, and $\left({\tilde{\delta }}^{L\frac{25}{1000}},{\tilde{\delta }}^{L\frac{975}{1000}}\right)$.

6. Bootstrap CI

We propose bootstrap confidence intervals as an alternative to the asymptotic confidence interval for the parameters of the model. For this objective, we created parametric bootstrap samples and discovered two unique bootstrap confidence intervals. First, we employed the Efron [40] percentile bootstrap method (boot-p). Use of the bootstrap-t technique was then proposed, based on the concept of Hall [41] (boot-t). For further information on how these bootstrap confidence intervals work, see [42,43,44].

(i)

Boot-p method

Step 1: Generate $x_1^{*},x_2^{*},....,x_n^{*}$ separate bootstrap samples after computing the MLEs for all parameters, with $\widehat{\beta },\widehat{\theta }$, and $\widehat{\delta }$ as the actual parameters.

Step 2: Calculate the MLEs of all parameters according to the bootstrap samples, denoted by $\widehat{\beta },\widehat{\theta }$, and $\widehat{\delta }$.

Step 3: Repeat Step 2 B times, as needed, in order to obtain a set of bootstrap estimates for $\widehat{\beta },\widehat{\theta }$, and $\widehat{\delta }$.

Step 4: Arrange $({\widehat{\beta }}^1,{\widehat{\theta }}^1,{\widehat{\delta }}^1)$, $({\widehat{\beta }}^2,{\widehat{\theta }}^2,{\widehat{\delta }}^2)$,...,$({\widehat{\beta }}^B,{\widehat{\theta }}^B,{\widehat{\delta }}^B)$ in ascending order, as $({\widehat{\beta }}^{\left[1\right]},{\widehat{\theta }}^{\left[1\right]},{\widehat{\delta }}^{\left[1\right]})$, $({\widehat{\beta }}^{\left[2\right]},{\widehat{\theta }}^{\left[2\right]},{\widehat{\delta }}^{\left[2\right]})$,...,$({\widehat{\beta }}^{\left[B\right]},{\widehat{\theta }}^{\left[B\right]},{\widehat{\delta }}^{\left[B\right]})$.

Step 5: Then, the approximate $100(1-p)\%$ CIs for $\widehat{\beta },\widehat{\theta }$, and $\widehat{\delta }$ are calculated as follows

$$\left({\beta }_{(Boot-p)}^{*\left[B\frac{P}{2}\right]},{\beta }_{(Boot-p)}^{*\left[B(1-\frac{P}{2})\right]}\right),\left({\theta }_{(Boot-p)}^{*\left[B\frac{P}{2}\right]},{\theta }_{(Boot-p)}^{*\left[B(1-\frac{P}{2})\right]}\right),\left({\delta }_{(Boot-p)}^{*\left[B\frac{P}{2}\right]},{\delta }_{(Boot-p)}^{*\left[B(1-\frac{P}{2})\right]}\right).$$

(ii)

Boot-t method

Step 1: The approach is the same as that in the boot-p approach.

Step 2: Compute the bootstrap estimate of $R_F$ by replacing the parameters in Equation (24) with their bootstrap estimates, denoting them by $R_F^{*}$ and the following statistics

$$T_1^{*}=\frac{{\beta }^{*}-\beta }{\sqrt{\widehat{V}({\beta }^{*})}},T_2^{*}=\frac{{\theta }^{*}-\theta }{\sqrt{\widehat{V}({\theta }^{*})}},T_3^{*}=\frac{{\delta }^{*}-\delta }{\sqrt{\widehat{V}({\delta }^{*})}}.$$

Step 3: Step 2 should be repeated B times, as needed.

Step 4: Arrange $(T_j^{*1},T_j^{*2},\cdots ,T_j^{*B})$, where $j=1,2,2+length(\delta )$, in ascending order as $(T_j^{*\left[1\right]},T_j^{*\left[2\right]},\cdots ,T_j^{*\left[B\right]})$.

Step 5: The approximate $100(1-p)\%$ CIs are then obtained by

$$\left(\beta +T_1^{*\left[B\frac{P}{2}\right]}\sqrt{\widehat{V}({\beta }^{*})},\beta +T_1^{*\left[B(1-\frac{P}{2})\right]}\sqrt{\widehat{V}({\beta }^{*})}\right),$$

$$\left(\theta +T_2^{*\left[B\frac{P}{2}\right]}\sqrt{\widehat{V}({\theta }^{*})},\theta +T_2^{*\left[B(1-\frac{P}{2})\right]}\sqrt{\widehat{V}({\theta }^{*})}\right),$$

$$\left(\delta +T_3^{*\left[B\frac{P}{2}\right]}\sqrt{\widehat{V}({\delta }^{*})},\delta +T_3^{*\left[B(1-\frac{P}{2})\right]}\sqrt{\widehat{V}({\delta }^{*})}\right).$$

7. The Log-Odd Perks–Weibull Regression Model

If X is an RV with an odd Perks–Weibull (OPW) distribution, $Y=log(x)$ is an RV with a log-OPW (LOPW) distribution with the transformation parameters $\delta =\frac{1}{\sigma }$ and $\mu =log(\lambda )$. As a result, the pdf and cdf of the LOPW distribution are as follows:

$$F(y;\beta ,\theta ,\mu ,\sigma )=1-\frac{(1+\beta )}{1+\beta e^{\theta \left(e^{e^{\frac{y-\mu }{\sigma }}}-1\right)}}$$

(35)

and

$$f(y;\beta ,\theta ,\mu ,\sigma )=\frac{\beta \theta (1+\beta )\frac{1}{\sigma }{e}^{\frac{y-\mu }{\sigma }}{e}^{\theta \left(e^{e^{\frac{y-\mu }{\sigma }}}-1\right)}}{e^{-e^{\frac{y-\mu }{\sigma }}}{\left[1+\beta e^{\theta \left(e^{e^{\frac{y-\mu }{\sigma }}}-1\right)}\right]}^2},$$

(36)

where $-\infty <\mu <\infty$ is the location parameter, $\beta ,\theta >0$ are the shape parameters, and $\sigma >0$ is the scale parameter. The SF and HRF are provided by

$$\overline{F}(y;\beta ,\theta ,\mu ,\sigma )=\frac{(1+\beta )}{1+\beta e^{\theta \left(e^{e^{\frac{y-\mu }{\sigma }}}-1\right)}}$$

(37)

and

$$\tau (y;\beta ,\theta ,\mu ,\sigma )=\frac{\beta \theta \frac{1}{\sigma }{e}^{\frac{y-\mu }{\sigma }}{e}^{\theta \left(e^{e^{\frac{y-\mu }{\sigma }}}-1\right)}}{e^{-e^{\frac{y-\mu }{\sigma }}}\left[1+\beta e^{\theta \left(e^{e^{\frac{y-\mu }{\sigma }}}-1\right)}\right]}.$$

(38)

If $z=\frac{y-\mu }{\sigma }$ is the standardized RV for y in Equation (36), then z has the following pdf:

$$f(z;\beta ,\theta )=\frac{\beta \theta (1+\beta )e^z{e}^{\theta \left(e^{e^z}-1\right)}}{e^{-e^z}{\left[1+\beta e^{\theta \left(e^{e^z}-1\right)}\right]}^2},-\infty <z<\infty ,$$

(39)

with SF denoted as

$$SF(z)=\frac{(1+\beta )}{1+\beta e^{\theta \left(e^{e^z}-1\right)}}.$$

(40)

Using the linear location-scale regression model in Equation (1), where $\mu =B^{T}X$, the SF of $y_i|X$ can thus be written as:

$$SF(y_i|X)=\frac{(1+\beta )}{1+\beta e^{\theta \left(e^{e^{\frac{y_i-B^T{X}_i}{\sigma }}}-1\right)}}.$$

(41)

MLE Method for Parameters of the Regression Model

The likelihood FUN of the regression model can be expressed as:

$$\begin{array}{cc}\hfill L(\beta ,\theta ,\sigma ,B^T)=& n\left[log(\beta )+log(\theta )+log(1+\beta )\right]+\sum _{i=1}^{n}log(z_i)+\sum _{i=1}^{n}log\left[\theta \left(e^{e^z}-1\right)\right]+\sum _{i=1}^n{e}^{z_i}\hfill \\ & -2\sum _{i=1}^{n}log\left[1+\beta e^{\theta \left(e^{e^{z_i}}-1\right)}\right],\hfill \end{array}$$

(42)

where $z_i=\frac{y_i-B^T{X}_i}{\sigma }$.

By maximizing the log-likelihood function (42), the MLEs $\widehat{\beta },\widehat{\theta },\widehat{\sigma }$, and ${\widehat{B}}^T$ of $\beta ,\theta ,\sigma$, and $B^T$ can be obtained. The survival function for $y_i$ can be computed using the fitted model ():

$$\overline{F}(y;\widehat{\beta },\widehat{\theta },\widehat{\sigma },{\widehat{B}}^T)=\frac{(1+\widehat{\beta })}{1+\widehat{\beta }{e}^{\widehat{\theta }\left(e^{e^{\frac{y-{\widehat{B}}^{T}X}{\widehat{\sigma }}}}-1\right)}}.$$

(43)

The survival function for $t=e^y$ is derived, using the invariance characteristics of the MLE, as follows:

$$\overline{F}(t)=\frac{(1+\widehat{\beta })}{1+\widehat{\beta }{e}^{\widehat{\theta }(e^{{\left(\frac{t}{\widehat{\lambda }}\right)}^{\widehat{\delta }}}-1)}},$$

where $\widehat{\delta }=\frac{1}{\widehat{\sigma }}$ and $\widehat{\lambda }=e^{\left({\widehat{B}}^{T}X\right)}$

The asymptotic distribution of $\sqrt{n}(\widehat{\mathsf{\Theta }}-\mathsf{\Theta })$ is multivariate normal $N(0,I{M}^{-1}(\mathsf{\Theta }))$, where $I{M}^{-1}(\mathsf{\Theta })$ is the information matrix, when the requirements are met for the parameter vector $\mathsf{\Theta }=(\beta ,\theta ,\sigma ,B^T)$ in the interior of the parameter space but not at the boundary. The approximated multivariate normal distribution can be used to build approximate confidence areas for particular parameters in $\mathsf{\Theta }$ in the traditional manner.

8. Simulation Studies

8.1. Simulation for OPE Distribution

To demonstrate the performance of the MLE, MPS, and Bayesian estimation methods with respect to the OPE distribution parameters, we ran a Monte Carlo simulation; that is, for two separate sets of parameter values, we randomly produced 10,000 samples of sizes 30, 70, and 150 from the OPE distribution:

 

In Table 3, $\beta =0.4,\theta =0.5,\lambda =0.6$, $\beta =0.4,\theta =0.5,\lambda =3$, $\beta =0.4,\theta =2,\lambda =0.6$, and $\beta =0.4,\theta =2,\lambda =3$;

Table 3. MLE, MPS, and Bayesian estimation methods for parameters of OPE distribution.

$\mathit{\beta }=0.4$				MLE					MPS			Bayesian
$\mathbf{\theta }$	$\mathbf{\lambda }$	n		Bias	MSE	L.CI	L.BP	L.BT	Bias	MSE	L.CI	Bias	MSE	L.CI
0.5	0.6	30	$\beta$	0.0446	0.0554	0.9067	0.0289	0.0297	0.0979	0.0812	0.9959	0.1079	0.0528	0.7230
			$\theta$	−0.0009	0.0396	0.7808	0.0243	0.0243	0.1134	0.0715	0.8355	0.0660	0.0741	0.9372
			$\lambda$	0.0353	0.0147	0.4541	0.0152	0.0152	−0.0398	0.0137	0.5062	0.0259	0.0175	0.4776
		70	$\beta$	0.0045	0.0129	0.4455	0.0142	0.0143	0.0405	0.0302	0.6271	0.0663	0.0318	0.6188
			$\theta$	0.0023	0.0116	0.4225	0.0132	0.0133	0.0619	0.0258	0.5218	0.0322	0.0397	0.7238
			$\lambda$	0.0116	0.0048	0.2690	0.0088	0.0088	−0.0256	0.0057	0.3164	0.0168	0.0099	0.3732
		150	$\beta$	0.0107	0.0107	0.4038	0.0132	0.0135	0.0151	0.0140	0.4563	0.0251	0.0149	0.4517
			$\theta$	0.0049	0.0159	0.4934	0.0159	0.0157	0.0361	0.0119	0.3719	0.0090	0.0150	0.4616
			$\lambda$	0.0091	0.0042	0.2505	0.0079	0.0078	−0.0154	0.0027	0.2183	0.0094	0.0037	0.2304
	3	30	$\beta$	0.0578	0.1240	1.3625	0.0437	0.0437	0.1456	0.1497	1.3182	0.0887	0.0453	0.6658
			$\theta$	0.0639	0.0623	0.9462	0.0317	0.0318	0.1182	0.0805	0.9572	0.0635	0.0350	0.6478
			$\lambda$	0.0103	0.1448	1.4920	0.0479	0.0470	−0.2354	0.2201	1.8373	−0.0341	0.1352	1.3905
		70	$\beta$	0.0319	0.0566	0.9248	0.0302	0.0303	0.0450	0.0533	0.8748	0.0521	0.0305	0.5807
			$\theta$	0.0425	0.0454	0.8185	0.0254	0.0256	0.0873	0.0448	0.7118	0.0360	0.0191	0.5039
			$\lambda$	0.0161	0.1114	1.3074	0.0410	0.0406	−0.1550	0.1214	1.3947	−0.0133	0.0746	1.0636
		150	$\beta$	0.0182	0.0340	0.7191	0.0237	0.0238	0.0298	0.0281	0.6348	0.0127	0.0118	0.3992
			$\theta$	0.0411	0.0344	0.7097	0.0221	0.0221	0.0525	0.0219	0.5317	0.0150	0.0059	0.2762
			$\lambda$	−0.0204	0.0703	1.0365	0.0349	0.0349	−0.0972	0.0632	0.9861	−0.0007	0.0249	0.6179
2	0.6	30	$\beta$	0.0425	0.0994	1.2251	0.0398	0.0400	0.1859	0.1904	1.4047	0.0869	0.0384	0.6382
			$\theta$	−0.0429	0.0856	1.1353	0.0382	0.0382	0.0509	0.0773	0.9783	−0.0216	0.0803	1.2539
			$\lambda$	0.0405	0.0134	0.4260	0.0130	0.0129	−0.0251	0.0107	0.4585	0.0267	0.0117	0.3827
		70	$\beta$	0.0478	0.0606	0.9473	0.0310	0.0308	0.0983	0.0466	0.8826	0.0619	0.0263	0.5548
			$\theta$	−0.0412	0.0893	1.1611	0.0367	0.0365	0.0494	0.0321	0.5847	−0.0118	0.0790	1.1261
			$\lambda$	0.0241	0.0074	0.3248	0.0101	0.0101	−0.0208	0.0043	0.2886	0.0141	0.0059	0.2877
		150	$\beta$	0.0116	0.0153	0.4822	0.0150	0.0150	0.0502	0.0120	0.5232	0.0216	0.0118	0.3925
			$\theta$	0.0019	0.0037	0.2386	0.0072	0.0072	0.0305	0.0133	0.4067	−0.0155	0.0037	0.2062
			$\lambda$	0.0037	0.0015	0.1490	0.0048	0.0048	−0.0146	0.0019	0.1802	0.0073	0.0011	0.1372
	3	30	$\beta$	0.3058	0.7826	3.2557	0.1044	0.1042	0.2925	0.3949	2.1947	0.1068	0.0491	0.6704
			$\theta$	−0.1049	0.6079	3.0301	0.0951	0.0941	0.0830	0.2070	1.5667	0.0095	0.1283	1.3565
			$\lambda$	0.3745	0.6661	2.8440	0.0907	0.0910	−0.1532	0.2509	2.3979	0.0176	0.1194	1.3171
		70	$\beta$	0.1345	0.6876	3.2091	0.1065	0.0947	0.1228	0.1015	1.1647	0.0643	0.0266	0.5542
			$\theta$	−0.0322	0.3965	2.4663	0.0797	0.0799	0.0900	0.1366	1.2837	0.0154	0.0759	1.0942
			$\lambda$	0.1747	0.3802	2.3193	0.0741	0.0736	−0.1296	0.1323	1.6370	−0.0014	0.0615	0.9628
		150	$\beta$	0.0776	0.0719	1.0063	0.0323	0.0331	0.0566	0.0338	0.7071	0.0225	0.0109	0.3860
			$\theta$	−0.0590	0.2817	2.0688	0.0605	0.0595	0.0586	0.0757	0.9369	0.0111	0.0215	0.5600
			$\lambda$	0.1491	0.2541	1.8886	0.0602	0.0605	−0.0759	0.0642	1.1735	0.0010	0.0210	0.5712

 

In Table 4, $\beta =2,\theta =0.5,\lambda =0.6$, $\beta =2,\theta =0.5,\lambda =3$, $\beta =2,\theta =2,\lambda =0.6$, and $\beta =2,\theta =2,\lambda =3$

Table 4. MLE, MPS, and Bayesian estimation methods for parameters of OPE distribution.

$\mathit{\beta }=2$				MLE					MPS			Bayesian
$\mathbf{\theta }$	$\mathbf{\lambda }$	n		Bias	MSE	L.CI	L.BP	L.BT	Bias	MSE	L.CI	Bias	MSE	L.CI
0.5	0.6	30	$\beta$	0.0353	0.0964	1.2101	0.0408	0.0403	0.0199	0.0124	0.4456	0.0118	0.0377	0.7393
			$\theta$	−0.0025	0.0921	1.1901	0.0377	0.0367	0.1384	0.0910	1.1635	0.0749	0.0718	0.9038
			$\lambda$	0.0731	0.0398	0.7277	0.0230	0.0230	−0.0288	0.0279	0.7468	0.0237	0.0198	0.5344
		70	$\beta$	0.0270	0.0426	0.8021	0.0268	0.0267	0.0092	0.0048	0.2881	0.0003	0.0343	0.7287
			$\theta$	0.0007	0.0455	0.8363	0.0264	0.0264	0.0778	0.0543	0.7847	0.0345	0.0367	0.7005
			$\lambda$	0.0311	0.0157	0.4759	0.0152	0.0151	−0.0235	0.0130	0.4915	0.0157	0.0111	0.3987
		150	$\beta$	0.0032	0.0534	0.9059	0.0280	0.0284	0.0047	0.0009	0.1125	−0.0002	0.0215	0.5613
			$\theta$	0.0029	0.0224	0.5867	0.0179	0.0180	0.0448	0.0234	0.5314	0.0103	0.0128	0.4194
			$\lambda$	0.0157	0.0071	0.3258	0.0101	0.0101	−0.0151	0.0063	0.3368	0.0079	0.0043	0.2467
	3	30	$\beta$	0.0034	0.3211	2.2222	0.0670	0.0668	0.0590	0.1090	1.2186	0.0116	0.0390	0.7513
			$\theta$	0.0675	0.1574	1.5334	0.0490	0.0490	0.2546	0.2976	1.7051	0.0471	0.0313	0.5955
			$\lambda$	0.1402	0.6195	3.0375	0.0976	0.0981	−0.3374	0.7280	3.5511	0.0031	0.1466	1.4590
		70	$\beta$	0.0026	0.1587	1.5624	0.0511	0.0508	0.0138	0.0397	0.7687	0.0091	0.0362	0.7484
			$\theta$	0.0177	0.0633	0.9840	0.0314	0.0315	0.1006	0.0716	0.8896	0.0217	0.0134	0.4037
			$\lambda$	0.1094	0.3170	2.1662	0.0681	0.0680	−0.1599	0.3233	2.4094	0.0048	0.0773	1.0600
		150	$\beta$	0.0144	0.0902	1.1767	0.0357	0.0357	−0.0017	0.0222	0.6009	−0.0051	0.0225	0.5526
			$\theta$	0.0071	0.0187	0.5357	0.0177	0.0177	0.0559	0.0254	0.5360	0.0095	0.0039	0.2356
			$\lambda$	0.0491	0.1425	1.4677	0.0457	0.0460	−0.1084	0.1501	1.6164	−0.0047	0.0235	0.5870
2	0.5	30	$\beta$	0.0167	0.5651	2.9475	0.0874	0.0884	0.1262	0.3467	2.1462	0.0048	0.0418	0.7697
			$\theta$	−0.1275	0.9648	3.8197	0.1137	0.1147	0.2443	0.7177	2.8095	−0.0127	0.1736	1.5779
			$\lambda$	0.1517	0.1161	1.1966	0.0391	0.0388	−0.0016	0.0516	1.0439	0.0349	0.0161	0.4711
		70	$\beta$	−0.0039	0.1432	1.4838	0.0453	0.0453	0.0706	0.1601	1.4701	0.0001	0.0417	0.7755
			$\theta$	−0.0384	0.2948	2.1242	0.0680	0.0678	0.1627	0.3545	2.0451	−0.0283	0.0947	1.1598
			$\lambda$	0.0419	0.0212	0.5466	0.0178	0.0176	−0.0134	0.0207	0.6175	0.0223	0.0074	0.3225
		150	$\beta$	−0.0020	0.1114	1.3092	0.0430	0.0431	0.0317	0.0605	0.9227	0.0031	0.0224	0.5720
			$\theta$	−0.0217	0.2058	1.7772	0.0545	0.0546	0.0914	0.1538	1.3825	−0.0066	0.0284	0.6484
			$\lambda$	0.0254	0.0130	0.4352	0.0136	0.0134	−0.0127	0.0090	0.4066	0.0050	0.0022	0.1816
	3	30	$\beta$	0.0509	1.4323	4.6895	0.1567	0.1567	0.1498	0.8266	3.4183	0.0169	0.0408	0.7719
			$\theta$	0.1807	1.3530	4.5067	0.1437	0.1442	0.4253	0.8080	2.8612	0.0338	0.1195	1.2912
			$\lambda$	0.4268	1.6337	4.7251	0.1509	0.1514	−0.2270	0.6723	3.7438	0.0110	0.1310	1.4191
		70	$\beta$	0.0753	1.3008	4.4633	0.1404	0.1400	0.0511	0.3985	2.4920	0.0152	0.0433	0.7950
			$\theta$	0.2224	1.0997	4.0193	0.1316	0.1306	0.2476	0.3650	2.1360	0.0001	0.0634	0.9824
			$\lambda$	0.1619	0.7878	3.4226	0.1065	0.1071	−0.1647	0.3518	2.5612	0.0053	0.0703	1.0374
		150	$\beta$	0.0299	0.3799	2.4144	0.0767	0.0779	0.0685	0.2049	1.7162	−0.0015	0.0233	0.6047
			$\theta$	0.0961	0.3194	2.1841	0.0690	0.0696	0.2059	0.2005	1.4498	−0.0018	0.0217	0.5667
			$\lambda$	0.0529	0.3443	2.2919	0.0742	0.0733	−0.1644	0.2002	1.8495	0.0045	0.0222	0.5659

The parameter estimates were obtained by computing the bias and mean square error (MSE), as well as the length of the confidence interval (L.CI) for MLE and MPS by asymptotic CI, in addition to the bootstrap CI approach for MLE and the credible CI determined using the HPD interval for Bayesian estimation.The simulation outcomes are shown in Table 3 and Table 4. As a result of these findings, we concluded that as the sample size increased, the empirical means tended to approach the true value of the parameters. Furthermore, as the sample size grew larger, the MSEs and biases decreased.

8.2. Simulation of the LOPW Regression Model

Next, we conducted a Monte Carlo simulation to examine the performance of the ML parameter estimates of the LOPW regression model. The lifetimes were obtained from the OPW distribution, and independent variables $x_{i1},x_{i2}$ were generated using the uniform distribution in the range (0, 1). A total of 1000 samples were created, using the parameters detailed below.

 

In Table 5: multiple regression $\beta =2,\theta =1.6,B_1=1,B_2=0.5,\sigma =0.15$, $\beta =2,\theta =1.6,B_1=1,B_2=0.5,\sigma =0.6$, $\beta =2,\theta =0.6,B_1=1,B_2=0.5,\sigma =0.15$, and $\beta =2,\theta =0.6,B_1=1,B_2=0.5,\sigma =0.6$.

Table 5. Point and interval estimates by MLE for multiple regression.

$\mathit{\beta }=2,{\mathit{B}}_1=1,{\mathit{B}}_2=0.5$			$\mathit{\sigma }=0.15$					$\mathit{\sigma }=0.6$
$\mathbf{\theta }$	n		Bias	MSE	L.CI	L.BP	L.BT	Bias	MSE	L.CI	L.BP	L.BT
0.6	30	$\beta$	0.0092	0.0021	0.1756	0.0056	0.0055	0.0525	1.1150	4.1362	0.1498	0.1346
		$\theta$	0.0495	0.0996	1.2225	0.0386	0.0381	0.1116	0.2449	1.8909	0.0585	0.0577
		$\sigma$	−0.0018	0.0024	0.1904	0.0061	0.0063	0.0019	0.0430	0.8128	0.0265	0.0260
		$B_1$	−0.0039	0.0023	0.1885	0.0058	0.0058	−0.0070	0.0415	0.7987	0.0247	0.0246
		$B_2$	−0.0105	0.0009	0.1090	0.0035	0.0035	−0.0440	0.0205	0.5343	0.0168	0.0166
	70	$\beta$	0.0003	0.0012	0.1376	0.0055	0.0044	0.0162	0.0630	0.9822	0.0321	0.0325
		$\theta$	0.0164	0.0252	0.6192	0.0197	0.0197	0.0244	0.0306	0.6789	0.0218	0.0219
		$\sigma$	−0.0003	0.0008	0.1109	0.0035	0.0035	0.0005	0.0133	0.4516	0.0141	0.0142
		$B_1$	0.0002	0.0009	0.1188	0.0039	0.0039	0.0026	0.0152	0.4827	0.0157	0.0158
		$B_2$	−0.0050	0.0003	0.0610	0.0019	0.0019	−0.0122	0.0141	0.4632	0.0197	0.0137
	150	$\beta$	0.0042	0.0003	0.0696	0.0022	0.0022	−0.0021	0.0400	0.7847	0.0249	0.0248
		$\theta$	0.0061	0.0105	0.4007	0.0133	0.0133	0.0080	0.0131	0.4475	0.0151	0.0153
		$\sigma$	−0.0011	0.0004	0.0782	0.0025	0.0025	−0.0030	0.0077	0.3439	0.0108	0.0106
		$B_1$	0.0005	0.0004	0.0773	0.0024	0.0024	0.0026	0.0064	0.3133	0.0099	0.0099
		$B_2$	−0.0023	0.0001	0.0403	0.0014	0.0014	−0.0198	0.0045	0.2514	0.0080	0.0080
1.6	30	$\beta$	0.0095	0.0113	0.4152	0.0136	0.0134	−0.0057	1.0174	3.9558	0.1865	0.1212
		$\theta$	0.0051	0.2508	1.9638	0.0615	0.0610	0.4050	1.2582	4.1025	0.1290	0.1294
		$\sigma$	−0.0114	0.0031	0.2134	0.0069	0.0068	−0.0171	0.0701	1.0359	0.0315	0.0325
		$B_1$	−0.0133	0.0032	0.2143	0.0066	0.0066	−0.0263	0.0695	1.0290	0.0324	0.0327
		$B_2$	−0.0069	0.0007	0.0975	0.0031	0.0031	0.0011	0.4616	2.6645	0.0880	0.0877
	70	$\beta$	0.0009	0.0051	0.2791	0.0089	0.0087	−0.0320	0.5069	2.7894	0.0959	0.0954
		$\theta$	0.0299	0.1220	1.3647	0.0431	0.0432	0.1741	0.3256	2.1311	0.0689	0.0694
		$\sigma$	−0.0039	0.0012	0.1337	0.0042	0.0042	−0.0111	0.0264	0.6354	0.0208	0.0201
		$B_1$	−0.0034	0.0013	0.1417	0.0046	0.0046	−0.0016	0.0248	0.6182	0.0204	0.0204
		$B_2$	−0.0038	0.0003	0.0649	0.0020	0.0020	−0.0126	0.0359	0.7417	0.0279	0.0221
	150	$\beta$	0.0064	0.0047	0.2675	0.0083	0.0085	0.0011	0.4616	2.6645	0.0880	0.0877
		$\theta$	0.0091	0.0610	0.9677	0.0303	0.0301	0.0707	0.1333	1.4049	0.0445	0.0445
		$\sigma$	−0.0035	0.0006	0.0934	0.0031	0.0030	−0.0039	0.0221	0.5829	0.0181	0.0181
		$B_1$	−0.0011	0.0006	0.0949	0.0031	0.0030	0.0034	0.0130	0.4477	0.0144	0.0144
		$B_2$	−0.0017	0.0001	0.0434	0.0014	0.0014	−0.0257	0.0281	0.6502	0.0210	0.0198

 

In Table 6: simple regression $\beta =2,\theta =1.6,B_1=1,\sigma =0.15$, $\beta =2,\theta =1.6,B_1=1,\sigma =0.6$, $\beta =2,\theta =0.6,B_1=1,\sigma =0.15$, and $\beta =2,\theta =0.6,B_1=1,\sigma =0.6$.

Table 6. Point and interval estimates by MLE for simple regression.

$\mathit{\beta }=2,{\mathit{B}}_1=1$			$\mathit{\sigma }=0.15$					$\mathit{\sigma }=0.6$
$\mathbf{\theta }$	n		Bias	MSE	L.CI	L.BP	L.BT	Bias	MSE	L.CI	L.BP	L.BT
1.6	30	$\beta$	0.0185	0.1410	1.4709	0.0517	0.0445	0.0307	1.0297	3.9779	0.1324	0.1294
		$\theta$	0.1023	0.2396	1.8774	0.0613	0.0611	0.3429	0.7685	3.1642	0.1019	0.1029
		$B_1$	0.0075	0.0033	0.2245	0.0070	0.0071	−0.0002	0.0612	0.9701	0.0312	0.0311
		$\sigma$	−0.0055	0.0043	1.4709	0.0517	0.0445	−0.0130	0.0215	3.9779	0.1324	0.1294
	70	$\beta$	0.0166	0.0166	0.5013	0.0161	0.0161	−0.0301	0.5529	2.9139	0.0910	0.0908
		$\theta$	0.0467	0.1203	1.3479	0.0416	0.0416	0.1416	0.2211	1.7584	0.0524	0.0536
		$B_1$	0.0026	0.0015	0.1496	0.0050	0.0050	0.0017	0.0232	0.5977	0.0199	0.0198
		$\sigma$	−0.0063	0.0007	0.5013	0.0161	0.0161	0.0043	0.0088	2.9139	0.0910	0.0908
	150	$\beta$	0.0023	0.0081	0.3522	0.0111	0.0111	−0.0173	0.3164	2.2052	0.0713	0.0716
		$\theta$	0.0236	0.0551	0.9158	0.0294	0.0294	0.0706	0.0980	1.1964	0.0387	0.0387
		$B_1$	0.0016	0.0008	0.1074	0.0034	0.0034	0.0001	0.0122	0.4333	0.0140	0.0139
		$\sigma$	−0.0011	0.0002	0.3522	0.0111	0.0111	0.0007	0.0034	2.2052	0.0713	0.0716
0.6	30	$\beta$	0.0239	0.4157	2.5269	0.1237	0.0706	0.0992	2.6615	6.3865	0.2204	0.1994
		$\theta$	0.0411	0.0547	0.9033	0.0287	0.0287	0.0559	0.0998	1.2197	0.0397	0.0396
		$B_1$	−0.0008	0.0023	0.1881	0.0059	0.0059	−0.0063	0.0391	0.7748	0.0247	0.0247
		$\sigma$	−0.0028	0.0012	0.1379	0.0055	0.0041	−0.0238	0.0448	0.8251	0.0316	0.0274
	70	$\beta$	−0.0006	0.0060	0.3042	0.0148	0.0091	0.2146	0.9229	5.5153	0.2045	0.2014
		$\theta$	0.0015	0.0256	0.6278	0.0203	0.0200	−0.0036	0.0598	0.9588	0.0316	0.0294
		$B_1$	0.0017	0.0009	0.1192	0.0038	0.0038	0.0076	0.0178	0.5227	0.0175	0.0167
		$\sigma$	−0.0039	0.0009	0.1167	0.0041	0.0037	−0.0347	0.0241	0.5939	0.0192	0.0189
	150	$\beta$	0.0066	0.0043	0.2552	0.0085	0.0082	0.0091	0.0383	0.7670	0.0248	0.0247
		$\theta$	0.0052	0.0075	0.3399	0.0106	0.0107	0.0054	0.0069	0.3249	0.0101	0.0100
		$B_1$	0.0003	0.0009	0.1196	0.0048	0.0038	−0.0023	0.0059	0.3024	0.0096	0.0093
		$\sigma$	−0.0081	0.0007	0.0987	0.0031	0.0031	−0.0066	0.0016	0.1565	0.0049	0.0048

The simulation was conducted using $n=30,70$, and 150.

9. Discretization

There are a variety of approaches in the statistical literature for converting a continuous distribution to a discrete one. The survival discretization method is the most often-used methodology for generating discrete distributions; for further information, see Roy [45]. It requires the existence of a cdf, a continuous and non-negative survival function, and times separated into unit intervals. The discrete distribution PMF is defined as follows:

$$P(X=x)=P(x\le X\le x+1)=\overline{F}(x;\beta ,\theta ,\delta )-\overline{F}(x+1;\beta ,\theta ,\delta );x=0,1,2,...$$

(44)

Then, the PMF of the discrete $OP$-G family can be expressed as

$$P(X=x;\beta ,\theta ,\delta )=\frac{(1+\beta )}{1+\beta e^{\theta \left(\frac{G(x;\delta )}{\overline{G}(x;\delta )}\right)}}-\frac{(1+\beta )}{1+\beta e^{\theta \left(\frac{G(x+1;\delta )}{\overline{G}(x+1;\delta )}\right)}}.$$

(45)

The cdf of the discrete $OP$-G family is given as follows

$$P(X\le x;\beta ,\theta ,\delta )=1-\frac{(1+\beta )}{1+\beta e^{\theta \left(\frac{G(x+1;\delta )}{\overline{G}(x+1;\delta )}\right)}},$$

(46)

and the HRF of the discrete $OP$-G family is

$$h(X=x;\beta ,\theta ,\delta )=1-\frac{1+\beta e^{\theta \left(\frac{G(x;\delta )}{\overline{G}(x;\delta )}\right)}}{1+\beta e^{\theta \left(\frac{G(x+1;\delta )}{\overline{G}(x+1;\delta )}\right)}}.$$

(47)

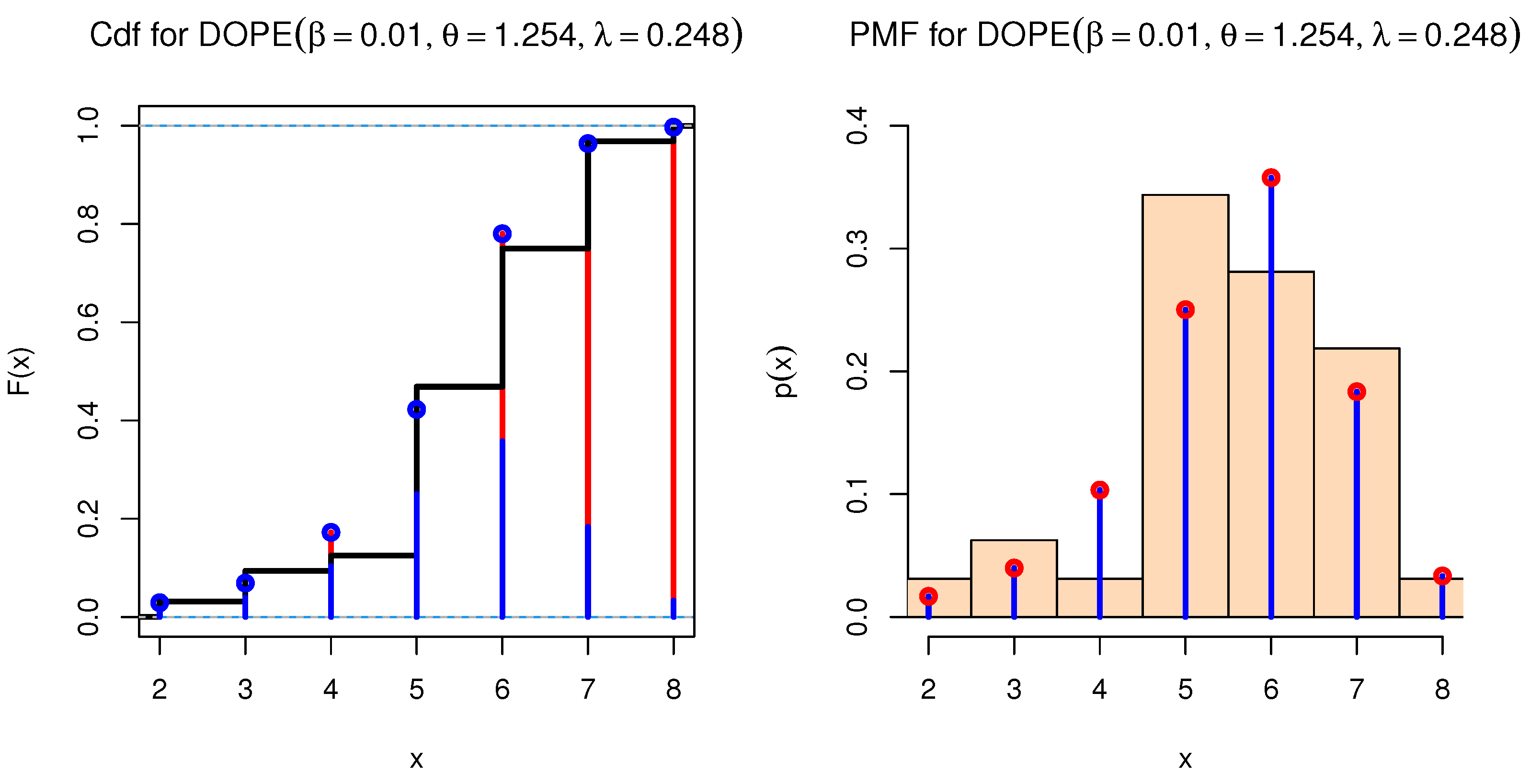
Regarding the OPE distribution, the PMF of the discrete OPE (DOPE) distribution is

$$P(X=x;\beta ,\theta ,\lambda )=\frac{1+\beta }{1+\beta e^{\theta \left(e^{\lambda x}-1\right)}}-\frac{1+\beta }{1+\beta e^{\theta \left(e^{\lambda (x+1)}-1\right)}}.$$

(48)

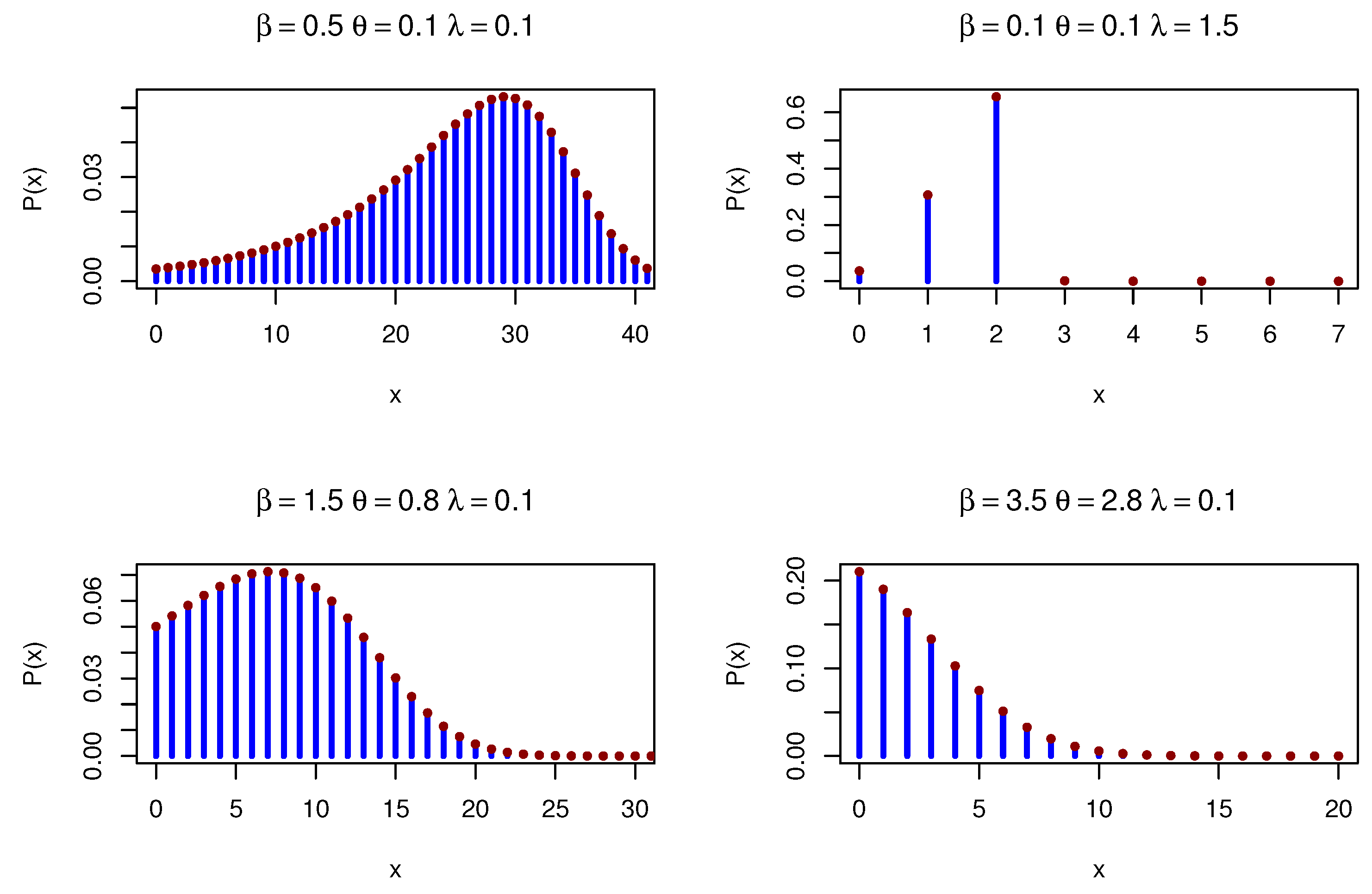
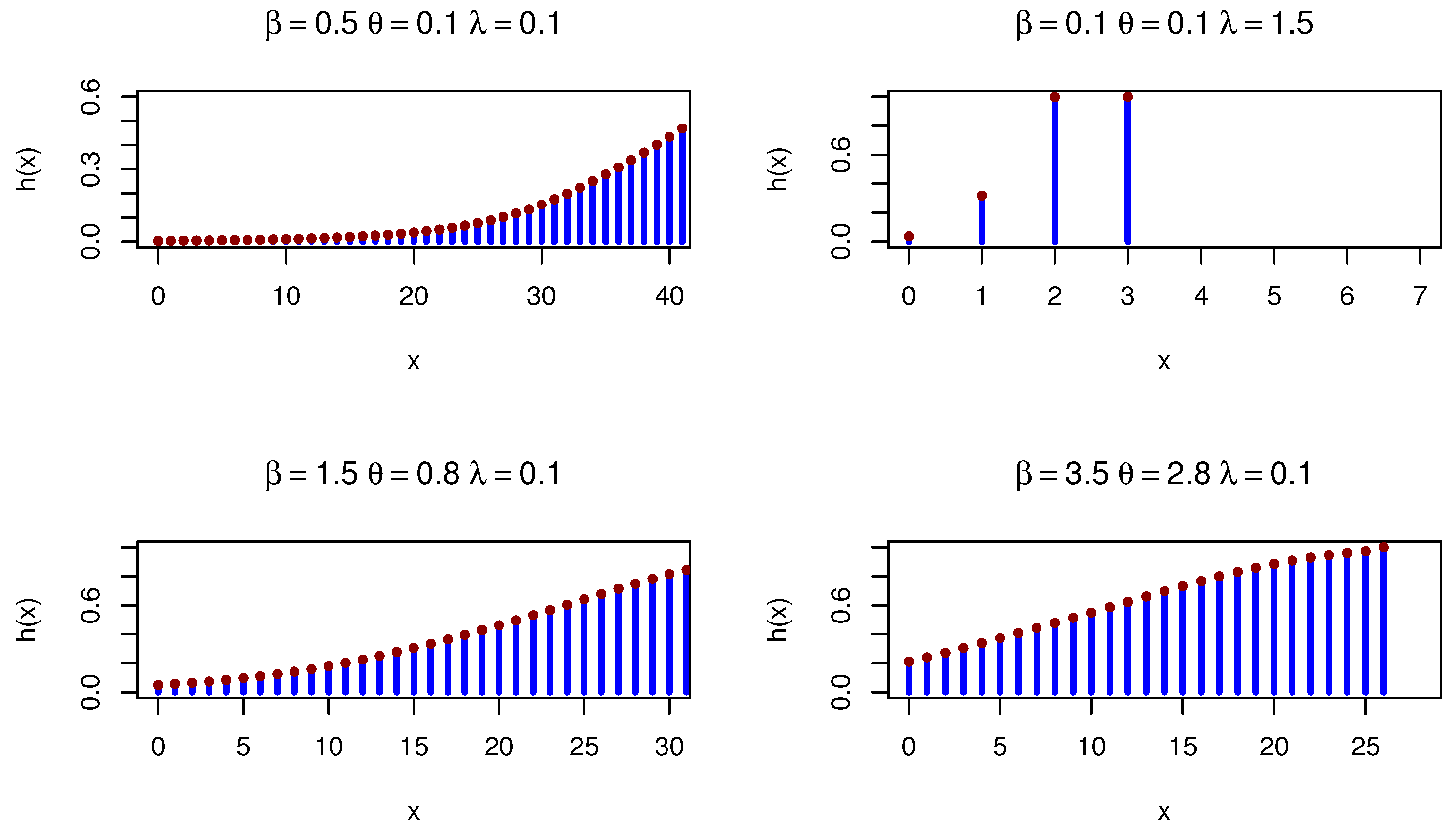
Figure 4 shows various PMFs for the DOPE distribution under various parameters.

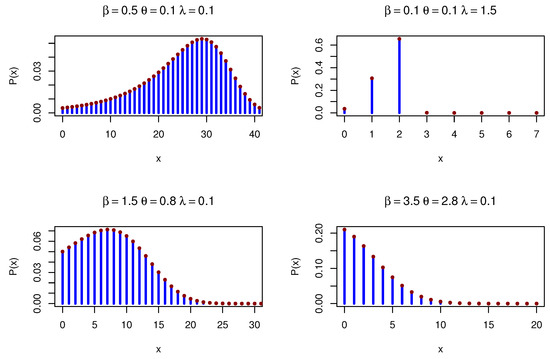
Figure 4. DOPE PMFs under different parameters.

The HRF of the DOPE distribution is given as

$$h(X=x;\beta ,\theta ,\lambda )=1-\frac{1+\beta e^{\theta \left(e^{\lambda x}-1\right)}}{1+\beta e^{\theta \left(e^{\lambda (x+1)}-1\right)}}.$$

(49)

Figure 5 shows various HRFs for the DOPE distribution.

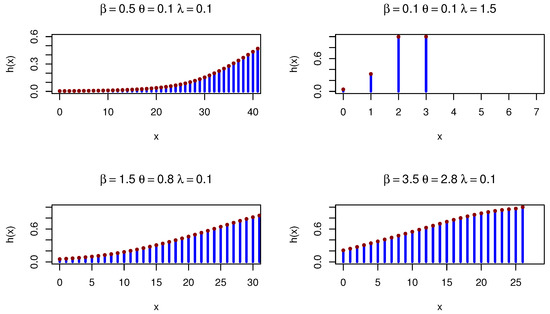
Figure 5. DOPE HRFs under different parameters.

10. Applications

We utilized three real data sets to test the superiority of the continuous distribution, COVID-19 data from Saudi Arabia to test the superiority of the discrete distribution, and Stanford heart transplant data to test the superiority of the regression model. We used various statistical measures, including Kolmogorov–Smirnov (KOS) with p-value (PV), Cramér–von Mises (CVOM), Anderson–Darling (AND), and Chi-squared ($X^2$), using different criteria, including the Akaike information criterion (INC) (AKINC), Bayesian INC (BINC), Hannan–Quinn INC (HQINC), and consistent AKINC (CAKINC) statistics.

10.1. Radiation Failure Mice

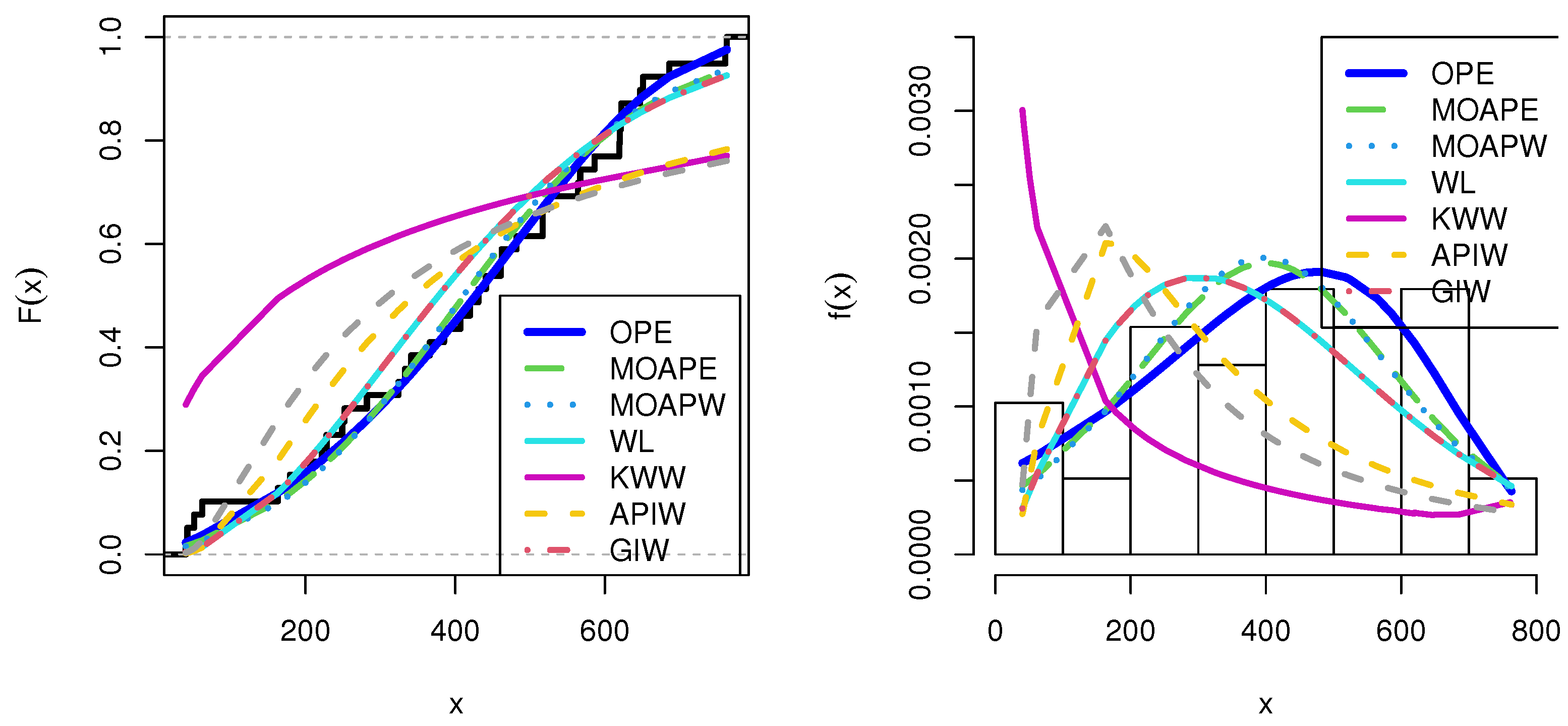
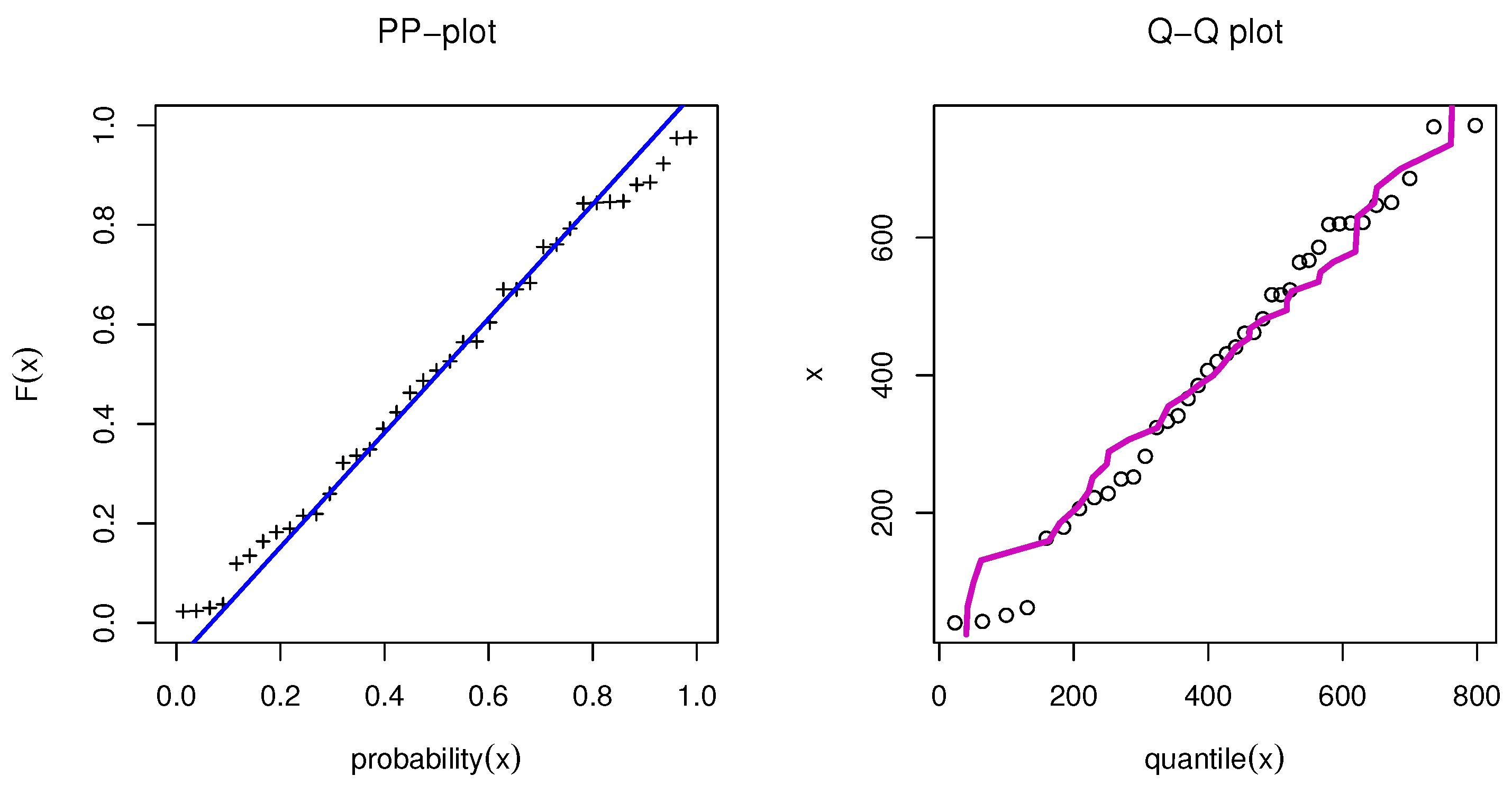
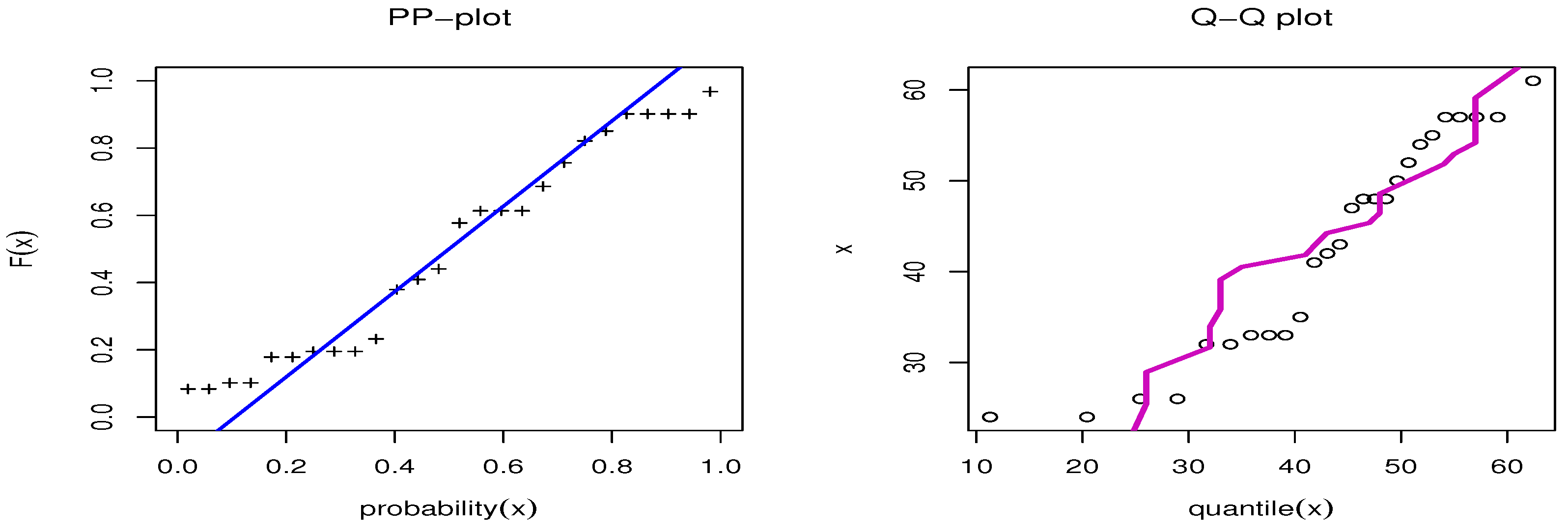
We first examined the genuine data set of radiation failure mice (RFM) reported by Hoel [9], obtained from a laboratory experiment in male mice aged 5–6 weeks that had been exposed to a 300 roentgen radiation dosage. Our goal was to look at other causes of death that were not related to the two main causes of death: Reticulum cell sarcoma and thymic lymphoma. The data were 40, 42, 51, 62, 163, 179, 206, 222, 228, 252, 249, 282, 324, 333, 341, 366, 385, 407, 420, 431, 441, 461, 462, 482, 517, 517, 524, 564, 567, 586, 619, 620, 621, 622, 647, 651, 686, 761, and 763. Table 7 presents the MLE with SE and different measures for the RFM data. Table 7 presents the comparison between our model and different distributions: The Marshall–Olkin alpha power exponential (MOAPEx) introduced by [46], the Marshall–Olkin alpha power Weibull (MOAPW) introduced by [47], the Weibull–Lomax (WL) model introduced by [48], the Kumaraswamy Weibull (KWW) introduced by [49], the alpha power inverse Weibull (APIW) introduced by [50], and the generalized inverse Weibull (GIW) introduced by [51]. Based on these results, we present the measured values of AKINC, BINC, KOS, CVOM, and AND. The smallest values were observed for the OPE distribution, while the largest values were seen with the PV. Based on the results presented in Table 7, we note that OPE can be considered as the best model to fit the RFM data. Figure 6 confirms the results shown in Table 7. Figure 7 shows the PP-plot and QQ-plot for the OPE distribution on the RFM data set.

Table 7. MLE with SE and different measures on RFM data set.

		Estimator	SE	AKINC	BINC	KOS	PV	CVOM	AND
1OPE	$\beta$	4.2151	0.3543	524.9292	529.9199	0.0741	0.9830	0.0223	0.2115
	$\theta$	0.1519	0.0820
	$\lambda$	0.0043	0.0011
MOAPEx	$\alpha$	1.0032	2.4779	530.1173	535.1079	0.0773	0.9740	0.0690	0.5233
	$\beta$	0.0075	0.0012
	$\theta$	21.0635	28.8155
MOAPW	$\alpha$	0.4165	0.6660	532.4730	539.1272	0.0823	0.9542	0.0716	0.5382
	$\beta$	0.9552	0.3223
	$\theta$	42.2525	65.8585
	$\lambda$	117.1953	93.1536
WL	$\alpha$	0.0181	0.0181	536.8698	543.5240	0.1152	0.6786	0.1477	1.0796
	$\beta$	7.8622	0.9723
	$\theta$	0.1518	0.0879
	$\lambda$	0.7153	0.171395
KWW	$\alpha$	1.4444	0.0038	597.8468	604.5011	0.3922	0.0000	0.2680	1.8237
	$\beta$	0.4863	0.0016
	$\theta$	1.1697	0.0118
	$\lambda$	0.0401	0.0064
APIW	$\alpha$	55.910	71.791	560.7260	565.7166	0.0741	0.9830	0.5353	3.3246
	$\beta$	1.3827	0.1509
	$\theta$	593.7153	477.1075
GIW	$\alpha$	12.1509	1.5983	570.1081	570.7938	0.2392	0.0230	0.6934	4.1369
	$\beta$	19.6826	2.2009
	$\theta$	1.0330	0.1118

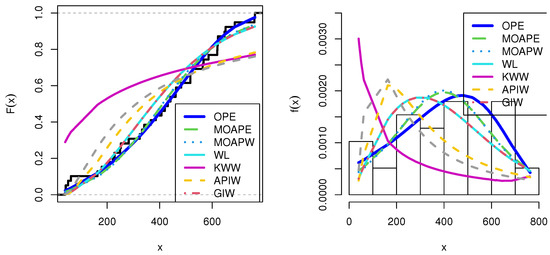
Figure 6. Estimated cdfs and pdfs for RFM data.

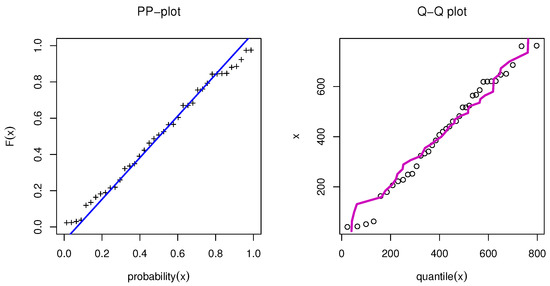
Figure 7. PP-plot and QQ-plot for OPE applied to RFM data.

10.2. Failure Times of a Certain Product

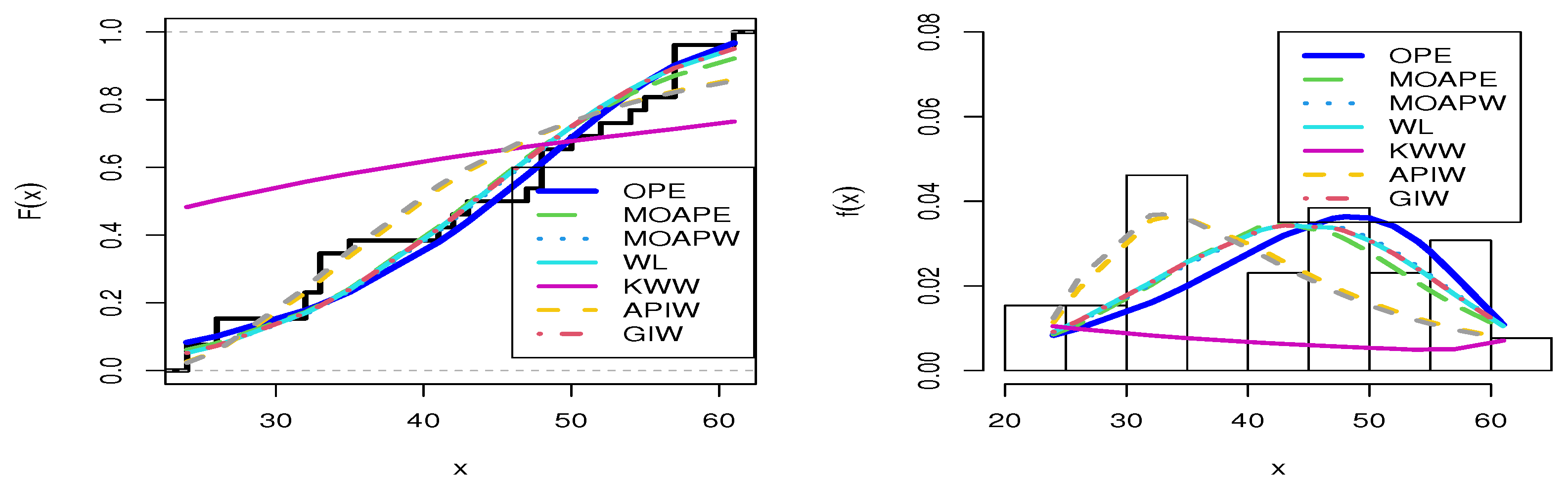
The second data set, that of Gacula and Kubala [52], contains 26 observations and indicates failure times for a specific product. This information has also been utilized by Nassar at al. [46]. The data are 24, 24, 26, 26, 32, 32, 33, 33, 33, 35, 41, 42, 43, 47, 48, 48, 48, 50, 52, 54, 55, 57, 57, 57, 57, and 61. Table 8 presents the MLE with SE and different measures for the failure time data. Table 8 presents a comparison between our model and different distributions, including the MOAPEx, MOAPW, WL, KWW, APIW, and GIW distributions. Based on these results, we found that the measured values of AKINC, BINC, KOS, CVOM, and AND were the smallest for the OPE distribution, while the largest values were obtained with PV. Based on the results in Table 8, we note that the OPE represented the best model to fit the failure time data. Figure 8 confirms the results shown in Table 8. Figure 9 shows the PP-plot and QQ-plot for the OPE distribution on the failure time data set.

Table 8. MLE with SE and different measures on the failure time data set.

		Estimator	SE	AKINC	BINC	KOS	PV	CVOM	AND
OPE	$\beta$	4.2097	12.0939	206.6919	210.4662	0.1525	0.5812	0.0917	0.6362
	$\theta$	0.0131	0.0143
	$\lambda$	0.0924	0.0175
MOAPEx	$\alpha$	28.6726	257.2552	209.6720	213.4463	0.1525	0.5806	0.1243	0.8005
	$\beta$	0.1384	0.0240
	$\theta$	113.0771	323.4044
MOAPW	$\alpha$	1.0028	2.0842	208.2018	213.2342	0.1579	0.5355	0.0976	0.6453
	$\beta$	4.2182	1.2248
	$\theta$	1.1493	1.8492
	$\lambda$	46.4453	7.6819
WL	$\alpha$	0.5025	4.9775	208.2155	213.2479	0.1548	0.5620	0.0987	0.6498
	$\beta$	4.3083	3.0575
	$\theta$	1.0024	2.2157
	$\lambda$	40.4271	172.0853
KWW	$\alpha$	1.7996	0.0017	268.6272	273.6596	0.4831	0.0001	0.1257	0.7863
	$\beta$	0.7313	0.0019
	$\theta$	1.1749	0.0105
	$\lambda$	0.0362	0.0071
APIW	$\alpha$	17786.526	16383.931	214.0297	217.8040	0.1810	0.3621	0.1933	1.2076
	$\beta$	3.6454	0.2983
	$\theta$	49924.7906	24.3221
GIW	$\alpha$	15.4371	0.4222	214.4336	215.5245	0.1845	0.3388	0.2019	1.2680
	$\beta$	16.9912	0.3147
	$\theta$	3.4156	0.4999

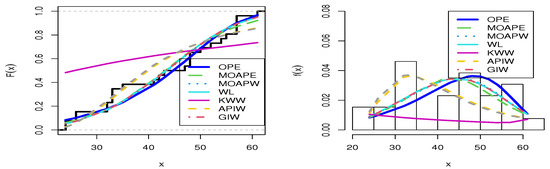
Figure 8. Estimated cdfs and pdfs for the failure time data set.

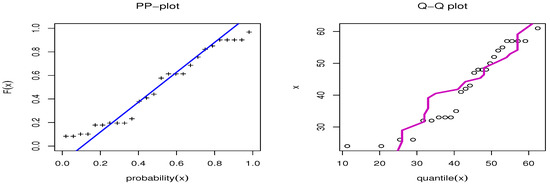
Figure 9. PP-plot and QQ-plot for OPE on the failure time data set.

10.3. Mechanical Data

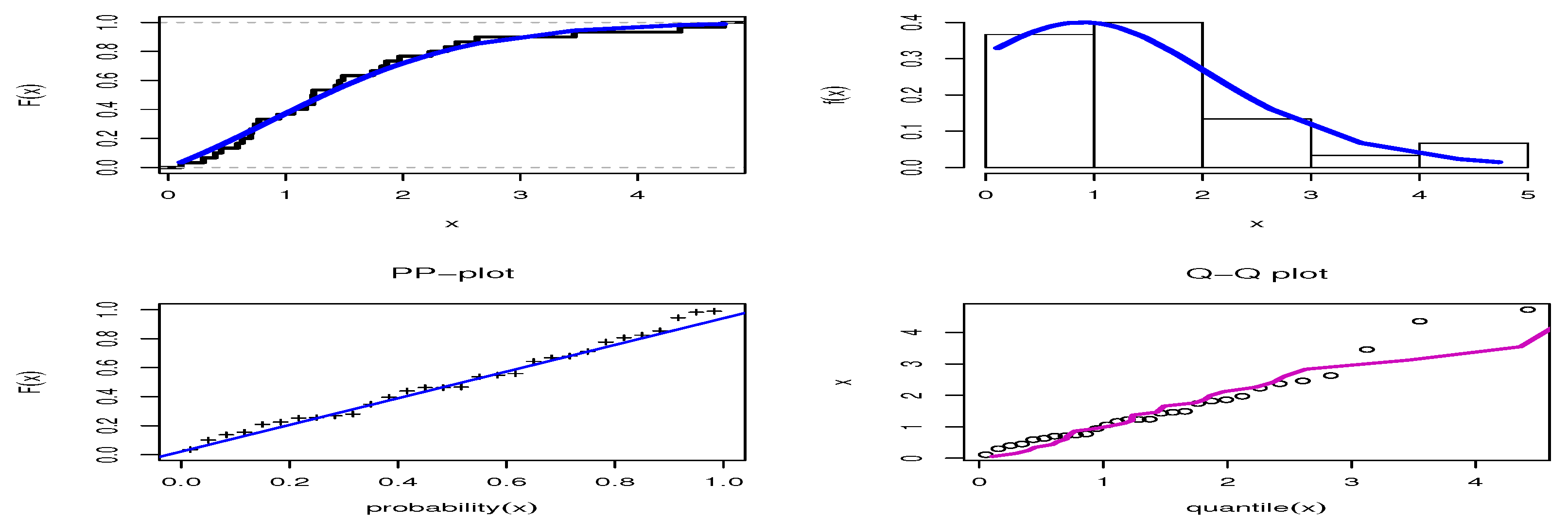
The third data set comprises the times measured between failures for repairable mechanical equipment items, obtained from the work of Seber et al. [53]. The data are 0.11, 0.30, 0.40, 0.45, 0.59, 0.63, 0.70, 0.71, 0.74, 0.77, 0.94, 1.06, 1.17, 1.23, 1.23, 1.24, 1.43, 1.46, 1.49, 1.74, 1.82, 1.86, 1.97, 2.23, 2.37, 2.46, 2.63, 3.46, 4.36, and 4.73. These data have been used to fit the extended inverse Gompertz distribution, which was compared to different distributions by Elshahhat et al. [54]. The results shown in Table 9 indicate that the smallest values of the AKINC, BINC, KOS, CAKINC, and HQINC were obtained by OPE, while the largest values were obtained by the PV for KOS, when comparing our results with those discussed by Elshahhat et al. [54]. Thus, the OPE distribution performed better than the inverse-Weibull, APIW, inverse gamma, generalized inverse Weibull (GIW), exponentiated inverted-Weibull, generalized inverted half-logistic, inverted Kumaraswamy, inverted Nadarajah–Haghighi, alpha-power inverse-Weibull, and extended inverse Gompertz (EIGo), which were discussed in [54]. Figure 10 shows the estimated cdf, estimated pdf, PP-plot, and QQ-plot for the OPE distribution, which confirm the good fit of the OPE distribution to these data.

Table 9. MLE with SE and different measures on the mechanical data set.

		Estimator	SE	AKINC	BINC	KOS	PV	CAKINC	HQINC
OPE	$\beta$	0.3830	0.3571	87.055	88.259	0.076	0.995	87.978	88.400
	$\theta$	32.6162	1.1026
	$\lambda$	0.0345	0.0760
EIGo	$\alpha$	3.5359	1.4251	87.536	88.459	0.089	0.971	88.459	88.459
	$\beta$	2.3986	2.3986
	$\theta$	2.3986	2.3986
GIW	$\alpha$	1.073	0.1314	98.751	102.950	0.134	0.656	99.674	100.100
	$\beta$	0.0761	0.8851
	$\theta$	11.92	148.78
APIW	$\alpha$	99.979	157.11	92.376	92.376	0.113	0.836	2.376	93.721
	$\beta$	1.4079	0.1745
	$\theta$	0.1922	0.0751

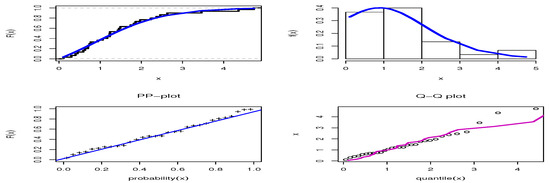
Figure 10. Estimated cdf, pdf, PP-plot, and QQ-plot for the OPE distribution on the mechanical data set.

10.4. Stanford Heart Transplant Data

Data for $n=103$ patients were acquired from the work of Kalbfleisch and Prentice [55]. The number of days between admittance to a heart transplant program and death was used to calculate the patient survival times. Each patient was linked to the following data: $y_i$, log survival follow-up time (days); $x_{i1}$, age (in years); and $x_{i2}$, prior surgery (coded as 0 = No, 1 = Yes). We present the fitting results for the following model:

$$y_i=B_0+B_1{x}_{i1}+B_2{x}_{i2}+\sigma z_i,$$

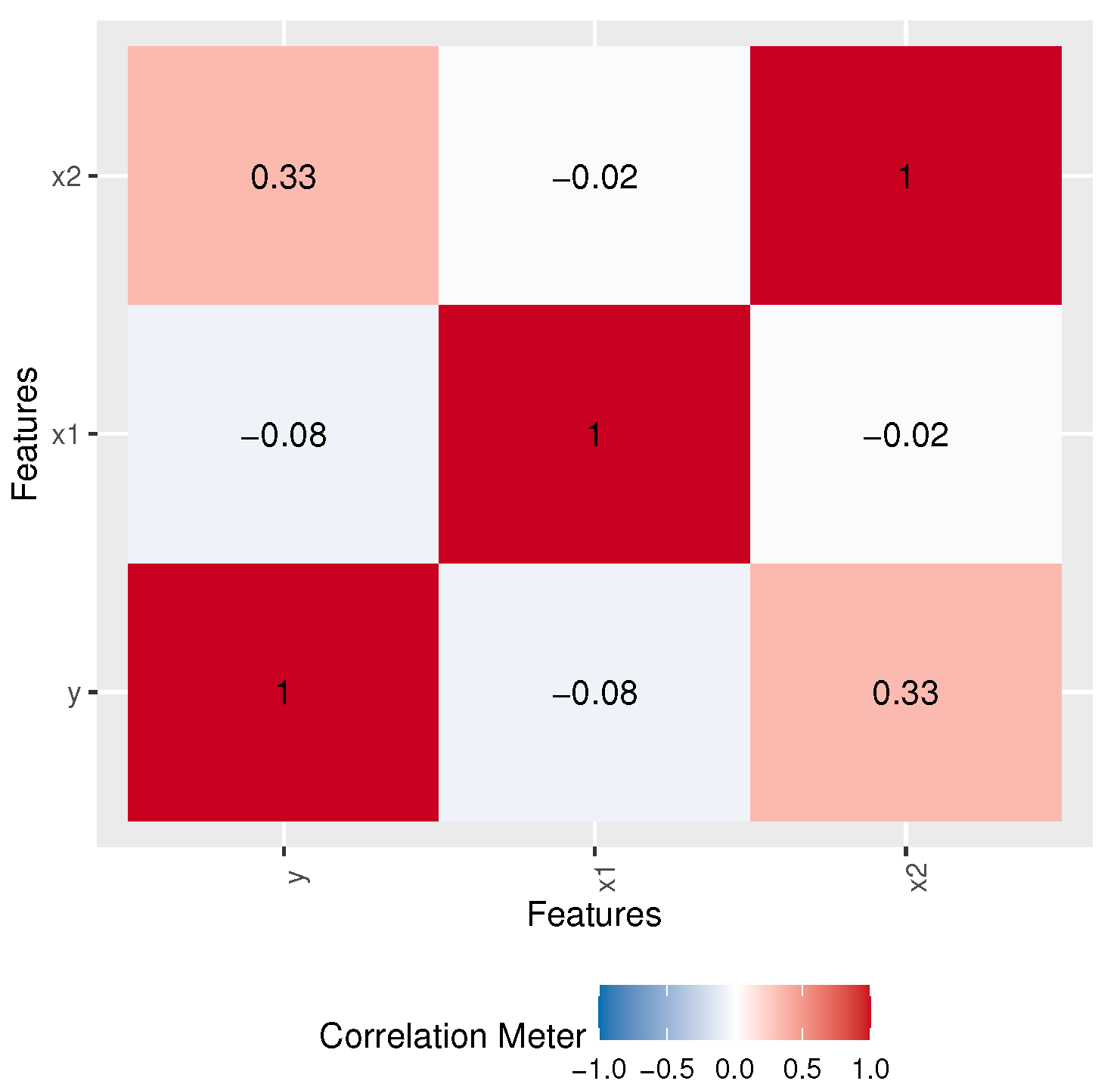
where $y_i$ follows the LOPW distribution. Table 10 shows MLE, SE, and Z-values, as well as PVs, for the LOPW regression model, while Table 11 provides different measures obtained for the LOPW regression model. Figure 11 shows the correlation values.

Table 10. MLE, SE, and Z-values, along with PVs, for the LOPW regression model.

	Estimate	SE	Z-Value	PV
$\beta$	39.5488	0.0002	161,758.8862	2 × 10${}^{-16}$
$\theta$	37.9709	0.0246	1541.6783	2 × 10${}^{-16}$
$B_1$	−0.0218	0.0175	−1.2478	0.2121
$B_0$	10.9676	0.8773	12.5019	2 × 10${}^{-16}$
$B_3$	0.7329	0.3468	2.1136	0.0346
$\sigma$	1.1515	0.1075	10.7146	2 × 10${}^{-16}$

Table 11. Different measures for the LOPW regression model.

	LOG (L)	AKINC	BINC	CAKINC	HQINC
measures	115.7447	243.4894	256.894	244.8442	248.8074

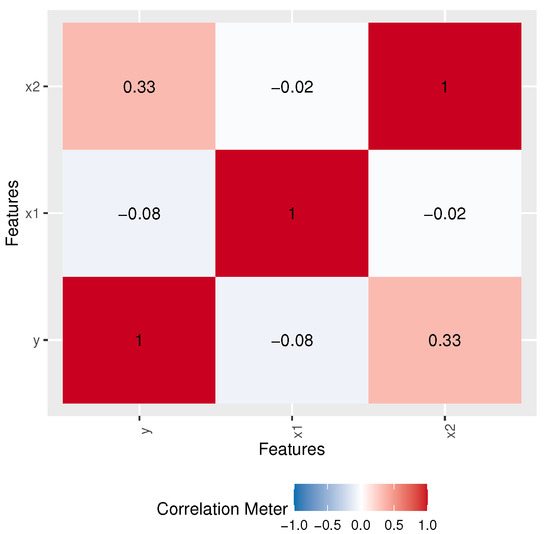
Figure 11. Correlation matrix.

Then,

$${\widehat{y}}_i=10.9676-0.0218x_{i1}+0.7329x_{i2}+1.1515z_i.$$

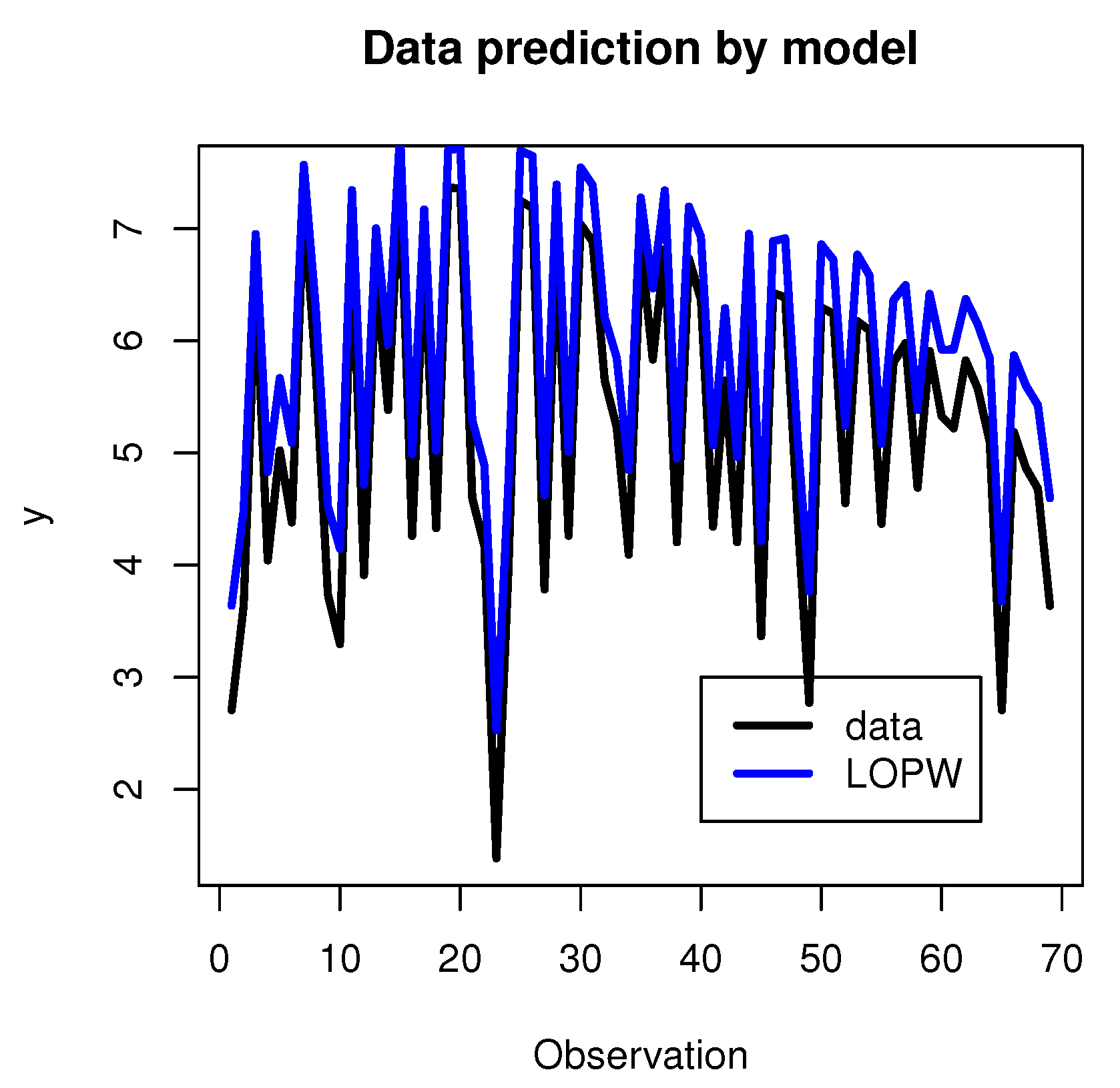
The results regarding the prediction of dependent variables using the regression model are shown in Figure 12.

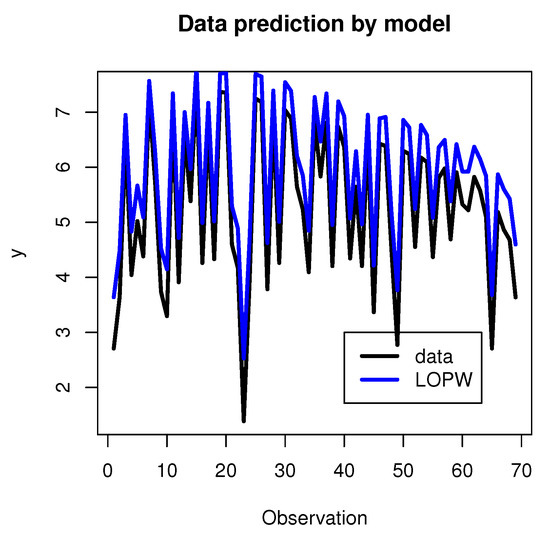
Figure 12. Data prediction using the regression model.

10.5. COVID-19 Data

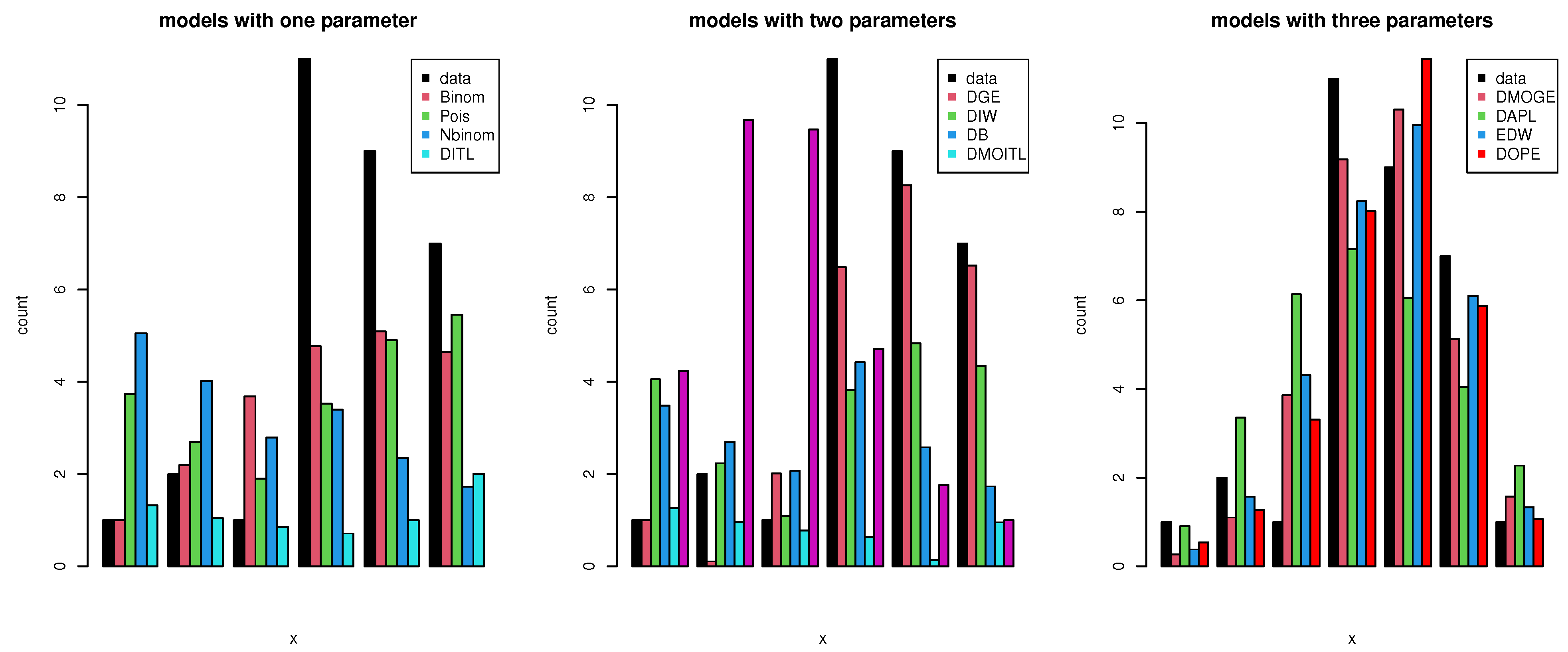
We used a COVID-19 data set from Saudi Arabia that spanned 32 days (from 1 September 2021 to 4 October 2021). This data set was comprised of newly reported instances of daily deaths. The data were as follows: 6, 7, 8, 5, 7, 7, 6, 6, 7, 6, 6, 7, 6, 5, 5, 7, 5, 6, 5, 5, 6, 5, 7, 5, 4, 6, 5, 5, 5, 3, 3, and 2. These data were obtained from the World Health Organization (at https://covid19.who.int/ accessed on 3 March 2022). Table 12 shows the data values, real frequency (count), and frequencies estimated using different discrete distributions. The distributions used for comparison were the discrete Marshall–Olkin inverse Toppe–Leone (DMOITL) introduced by [56], discrete Burr (DB) introduced by [57], discrete inverse Weibull (DIW) introduced by [58], negative binomial distribution (NBinom) introduced by [59], Poisson (Pois), discrete generalized exponential (DGE) suggested by [60], discrete alpha power inverse Lomax (DAPL) introduced by [61], discrete Lindley (DL) introduced by [62], discrete inverse Toppe–Leone (DITL) introduced by [63], exponentiated discrete Weibull introduced by [64], and discrete Marshall–Olkin generalized exponential (DMOGE) introduced by [65]. Figure 13 shows that the DOPE distribution was the best model for fitting these data, with an estimated frequency close to the real frequency. To confirm this conclusion, we used the KS value and Chi-squared ($X^2$) test to determine the best model fit for these data, as well as the AKINC, CAKINC, BINC, and HQINC measures. The results are shown in Table 13. We note that all of these measures had the smallest values with the DOPE distribution. Figure 14 shows the cdf and PMF for the DOPE distribution of these data.

Table 12. Estimated count of values determined by each model.

Value	Count	DMOITL	DB	DIW	NBinom	Poisson	DGE	DAPL	DL	DITL	EDW	DMOGE	DOPE
2	1	0.134	4.425	1.100	2.195	1.903	0.106	0.908	3.564	3.399	0.380	0.270	0.539
3	2	0.955	2.581	3.823	3.684	3.527	2.011	3.355	3.423	2.351	1.570	1.102	1.275
4	1	4.230	1.732	4.832	4.774	4.903	6.485	6.135	3.124	1.725	4.312	3.860	3.309
5	11	9.675	1.262	4.345	5.090	5.453	8.260	7.155	2.756	1.323	8.234	9.181	8.008
6	9	9.469	0.970	3.482	4.648	5.054	6.523	6.054	2.373	1.050	9.954	10.307	11.448
7	7	4.715	0.774	2.692	3.737	4.015	4.052	4.044	2.007	0.855	6.105	5.129	5.871
8	1	1.764	0.636	2.070	2.698	2.790	2.235	2.271	1.674	0.711	1.334	1.571	1.068

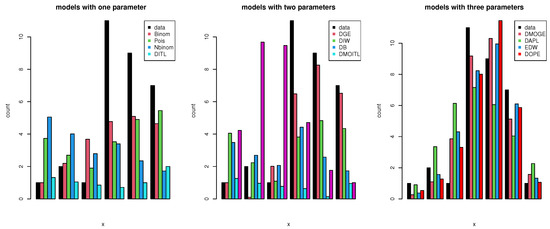
Figure 13. Graphical plots of the expected frequencies and the data obtained using the PMFs of different distributions.

Table 13. MLE with SE and different measures for the compared models.

		Estimator	SE	KS	${\mathit{X}}^2$	PV	AKINC	CAKINC	BINC	HQINC
DOPE	$\beta$	0.0100	0.0166	0.3115	4.6557	0.7937	111.1127	111.9698	115.5099	112.5702
	$\theta$	1.2542	1.9135
	$\lambda$	0.2484	0.1502
DMOITL	$\theta$	357,128.462	4.58 × 10${}^{-7}$	0.2882	7.3500	0.2897	124.3470	124.7340	127.3997	125.3880
	$\lambda$	9.6755	0.2239
DB	$\theta$	8.0592	0.4985	0.5189	57.4840	0.0000	228.7236	229.1107	231.7763	229.7647
	$\lambda$	0.9313	0.0499
DIW	$\theta$	1.83 × 10${}^{-25}$	1	1.0000	15.5424	0.0164	147.5908	147.9779	150.6435	148.6319
	$\lambda$	2.5021	0.76406
NB	$\alpha$	0.8620	0.4002	0.3683	12.5463	0.0508	137.8408	137.9658	139.3672	138.3613
Poisson	$\theta$	5.4427	0.4002	0.3623	10.9623	0.0895	134.3836	134.5086	135.9100	134.9042
DGE	$\theta$	0.4928	0.0474	0.3838	10.7090	0.0978	130.7385	131.1256	133.7912	131.7796
	$\lambda$	40.1642	19.8297
DAPL	$\alpha$	2.11 × 10${}^{-19}$	5.00 × 10${}^{-7}$	0.22901	10.36277	0.11018	122.62439	123.48153	127.02160	124.08194
	$\theta$	1.5680	0.19853
	$\lambda$	4.55 × 10${}^{-8}$	0.000005
DL	$\alpha$	0.7419	0.0273	0.4267	26.0725	0.0002	174.5213	174.6463	176.0477	175.0418
DITL	$\theta$	0.7707	0.1322	0.5156	44.7417	0.0000	223.7540	223.8790	225.2804	224.2745
EDW	$\alpha$	5.9850	0.4457	0.3295	4.9470	0.7632	111.3641	112.2212	115.7613	112.8216
	$\theta$	0.9058	0.0470
	$\lambda$	1.0000	0.1740
DMOGE	$\alpha$	5.9850	1.8723	0.3295	4.9470	0.7632	111.3641	112.2212	115.7613	112.8216
	$\theta$	0.9058	0.3984
	$\lambda$	1.0000	0.0801

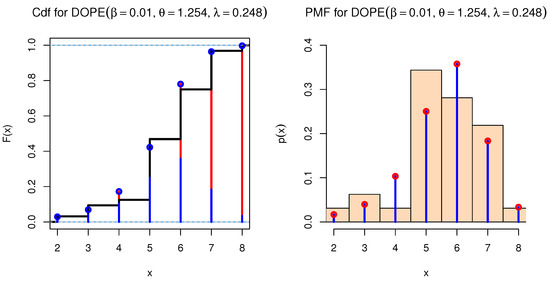
Figure 14. cdf and PMF for DOPE distribution.

11. Concluding Remarks

In this study, we explored the novel odd Perks-G family, and several of its statistical and mathematical features were established. We obtained some of its special models, including the OPU, OPE, OPW, and OPL distributions. The associated model parameters were estimated using the ML technique, the MPS method, and the Bayesian estimation approach, and simulation tests were conducted to evaluate the effectiveness of the OPE estimators using various estimation methods based on biases, MSE, and the CI length. In addition, the OPW distribution was used to develop a new log-location regression model. The unknown parameters of the new regression model were estimated using ML estimation methods. Furthermore, we introduced the discrete odd Perks-G family using the survival discretization method and obtained the DOPE distribution as a special model. Finally, we examined the utility of $OP$-G family distributions using three real data sets, analyzed Stanford heart transplant data using the LOPW regression model, and analyzed COVID-19 data using the discrete model. The OPE distribution outperformed other state-of-the-art distributions in terms of goodness of fit, according to our findings. Furthermore, the LOPW regression model fit the Stanford heart transplant data well. Additionally, the DOPE distribution provided a good fit to the COVID-19 data. In our future research, the new suggested family will be used to generate more new distributions, the statistical properties of which will be explored. We also intend to study the statistical inferences of new models generated using the odd Perks-G family.