Subordination Involving Regular Coulomb Wave Functions

Abstract

The functions $\sqrt{1+z}$, $e^z$, $1+Az$, $A\in (0,1]$ map the unit disc $\mathbb{D}$ to a domain which is symmetric about the x-axis. The Regular Coulomb wave function (RCWF) ${\mathtt{F}}_{L,\eta }$ is a function involving two parameters L and $\eta$, and ${\mathtt{F}}_{L,\eta }$ is symmetric about these. In this article, we derive conditions on the parameter L and $\eta$ for which the normalized form ${\mathtt{f}}_L$ of ${\mathtt{F}}_{L,\eta }$ are subordinated by $\sqrt{1+z}$. We also consider the subordination by $e^z$ and $1+Az$, $A\in (0,1]$. A few more subordination properties involving RCWF are discussed, which leads to the star-likeness of normalized Regular Coulomb wave functions.

1. Introduction

The Regular Coulomb wave function (RCWF) defined in the complex plane is an entire function and closely associated with the well-known classical Bessel function. The Coulomb wave functions have a rich literature (See [1,2,3,4,5,6,7,8,9,10] and references therein) in terms of mathematical and numerical research articles and its applications in various branches of physics, especially in nuclear physics. The symmetrical property of RCWF is established in [11]. Entire functions have good geometric characterizations in the unit disc. In this sense, the exploration of the geometric nature of Coulomb wave functions is limited [4,12]. The aim of this article is to contribute some results on the geometric properties of RCWF.

The Coulomb differential equation [13] is a second-order differential equation of the form

$$\begin{array}{c}\hfill \frac{d^{2}w}{d{z}^2}+\left(1-\frac{2\eta }{z}-\frac{L(L+1)}{z^2}\right)w=0,\eta ,z\in \mathbb{C},\end{array}$$

(1)

that asserts two independent solutions, namely regular and irregular Coulomb wave functions. In terms of Kummer confluent hypergeometric functions ${}_1{F}_1$, the RCWF is defined as

$$\begin{array}{c}\hfill F_{L,\eta }\left(z\right):=z^{L+1}{e}^{-iz}{C}_L\left(\eta \right){}_1{F}_1(L+1+i\eta ,2L+2;2iz)=C_L\left(\eta \right)\sum _{n=0}^{\infty }{a}_{L,n}{z}^{n+L+1}.\end{array}$$

(2)

In this case, $z,\eta ,L\in \mathbb{C}$ and

$$C_L\left(\eta \right)=\frac{2^L{e}^{\frac{\pi \eta }{2}}|\Gamma (L+1+i\eta )|}{\Gamma (2L+2)},$$

$$a_{L,0}=1,a_{L,1}=\frac{\eta }{L+1},a_{L,n}=\frac{2\eta a_{L,n-1}-a_{L,n-2}}{n(n+2L+1)},n\in \{2,3,\dots \}.$$

For the study of the geometric characterization of RCWF, we need a normalized form such as as $h\left(0\right)=1$ or $h\left(0\right)=0=h^{\prime }\left(0\right)-1$. Clearly, $F_{L,\eta }$ defined in (2) does not process such a normalization. Hence, we consider the following two normalizations:

$$\begin{array}{cc}\hfill {\mathtt{f}}_L\left(z\right)& =C_L^{-1}\left(\eta \right)z^{-L-1}{F}_{L,\eta }\left(z\right)=1+\frac{\eta }{L+1}z+\dots \dots \hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathtt{g}}_L\left(z\right)& =C_L^{-1}\left(\eta \right)z^{-L}{F}_{L,\eta }\left(z\right)=z{\mathtt{f}}_L\left(z\right)=z+\frac{\eta }{L+1}{z}^2+\dots \dots \hfill \end{array}$$

(4)

By a calculation, it can be shown from (1) that $f_L$ satisfies the differential equation

$$\begin{array}{c}\hfill z^2{\mathtt{y}}^{″}\left(z\right)+2(L+1)z{\mathtt{y}}^{\prime }\left(z\right)+(z^2-2\eta z)\mathtt{y}\left(z\right)=0,\end{array}$$

(5)

while the function ${\mathtt{g}}_L$ is the solution of the differential equation

$$\begin{array}{c}\hfill z^2{\mathtt{y}}^{″}\left(z\right)+2Lz{\mathtt{y}}^{\prime }\left(z\right)+(z^2-2\eta z-2L)\mathtt{y}\left(z\right)=0.\end{array}$$

(6)

Let $\mathcal{A}$ denote the class of normalized analytic functions f in the open unit disk $\mathbb{D}=\{z:|z|<1\}$ satisfying $f\left(0\right)=0=f^{\prime }\left(0\right)-1$. Denote by ${\mathcal{S}}^{*}$ and $\mathcal{C}$, respectively, the widely studied subclasses of $\mathcal{A}$ consisting of univalent (one-to-one) star-like and convex functions. Geometrically, $f\in {\mathcal{S}}^{*}$ if the linear segment $tw$, $0\le t\le 1,$ lies completely in $f\left(\mathbb{D}\right)$ whenever $w\in f\left(\mathbb{D}\right)$, while $f\in \mathcal{C}$ if $f\left(\mathbb{D}\right)$ is a convex domain. Related to these subclasses is the Cárathèodory class $\mathcal{P}$ consisting of analytic functions p satisfying $p\left(0\right)=1$ and $\mathrm{Re}p\left(z\right)>0$ in $\mathbb{D}$. Analytically, $f\in {\mathcal{S}}^{*}$ if $z{f}^{\prime }\left(z\right)/f\left(z\right)\in \mathcal{P}$, while $f\in \mathcal{C}$ if $1+z{f}^{\prime \prime }\left(z\right)/f^{\prime }\left(z\right)\in \mathcal{P}$.

For two analytic functions f and g in $\mathbb{D}$, the function f is subordinate to g, written as $f\prec g,$ or $f\left(z\right)\prec g\left(z\right),$$z\in \mathbb{D}$, if there is an analytic self-map $\omega$ of $\mathbb{D}$ satisfying $\omega \left(0\right)=0$ and $f\left(z\right)=g\left(\omega \right(z\left)\right)$, $z\in \mathbb{D}$.

Consider now the class $\mathcal{P}\left[\phi \right]$ of analytic functions $p\left(z\right)=1+c_{1}z+\cdots$ in $\mathbb{D}$ satisfying $p\left(z\right)\prec \phi \left(z\right),$ where $\phi$ is an analytic function with a positive real impact on $\mathbb{D}$, $\phi \left(0\right)=1$ and ${\phi }^{\prime }\left(0\right)>0$. This article considers three different $\phi$, namely $\phi \left(z\right)=(1+Az)/(1+Bz)$, $\phi \left(z\right)=\sqrt{1+z}$ and $\phi \left(z\right)=e^z$.

For $-1\le B<A\le 1$ and $\phi \left(z\right)=(1+Az)/(1+Bz)$, denote the class as $\mathcal{P}[A,B]$. This family $\mathcal{P}[A,B]$ has been widely studied by several authors and most notably by Janowski in [14], and the class is also referred to as Janowski class of functions. The class $\mathcal{P}[A,B]$ contains several known classes of functions for judicious choices of A and B. For instance, if $0\le \beta <1$, then $\mathcal{P}[1-2\beta ,-1]$ is the class of functions $p\left(z\right)=1+c_{1}z+\cdots$ satisfying $Rep\left(z\right)>\beta$ in $\mathbb{D}$. In the limiting case $\beta =0$, the class reduces to the classical Cárathèodory class $\mathcal{P}$.

The class of Janowski star-like functions ${\mathcal{S}}^{*}[A,B]$ consists of $f\in \mathcal{A}$ satisfying

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\in \mathcal{P}[A,B],$$

while the Janowski convex functions $\mathcal{C}[A,B]$ are functions $f\in \mathcal{A}$ satisfying

$$1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\in \mathcal{P}[A,B].$$

For $0\le \beta <1$, ${\mathcal{S}}^{*}[1-2\beta ,-1]:={\mathcal{S}}^{*}\left(\beta \right)$ is the classical class of star-like functions of order $\beta$; ${\mathcal{S}}^{*}[1-\beta ,0]:={\mathcal{S}}_{\beta }^{*}=\{f\in \mathcal{A}:|z{f}^{\prime }\left(z\right)/f\left(z\right)-1|<1-\beta \}$, and ${\mathcal{S}}^{*}[\beta ,-\beta ]:={\mathcal{S}}^{*}\left[\beta \right]=\{f\in \mathcal{A}:|z{f}^{\prime }\left(z\right)/f\left(z\right)-1|<\beta |z{f}^{\prime }\left(z\right)/f\left(z\right)+1\left|\right\}$. These are all classes that have been widely studied; see, for example, the works of [14,15,16].

The next important class is related to the right half of lemniscate of Bernoulli given by $\left\{w:|w^2-1|=1\right\}.$ The functions $p\left(z\right)=1+c_{1}z+\cdots$ in $\mathbb{D}$ satisfying $p\left(z\right)\prec \sqrt{1+z}$ are known as lemniscate Cárathèodory function, and the corresponding class is denoted by ${\mathcal{P}}_{\mathcal{L}}$. A lemniscate Cárathèodory function is also Cárathèodory function and hence univalent. The lemniscate star-like class ${\mathcal{S}}_{\mathcal{L}}$ consists of functions $f\in \mathcal{A}$ such that $z{f}^{\prime }\left(z\right)/f\left(z\right)\prec \sqrt{1+z}$. The class ${\mathcal{K}}_{\mathcal{L}}=\left\{f\in \mathcal{A}:1+\left(z{f}^{″}\left(z\right)\right)/f^{\prime }\left(z\right)\prec \sqrt{1+z}\right\}$ is known as a class of lemniscate convex functions.

The third important class that is considered in sequence relates with the exponential functions $e^z$. The functions $p\left(z\right)=1+c_{1}z+\cdots$ in $\mathbb{D}$ satisfying $p\left(z\right)\prec e^z$ is known as the exponential Cárathèodory function, and the corresponding class is denoted by ${\mathcal{P}}_{\mathcal{E}}$. The exponential star-like class ${\mathcal{S}}_{\mathcal{E}}$ consists of functions $f\in \mathcal{A}$ such that $z{f}^{\prime }\left(z\right)/f\left(z\right)\prec e^z$. The class ${\mathcal{K}}_{\mathcal{E}}=\left\{f\in \mathcal{A}:1+\left(z{f}^{″}\left(z\right)\right)/f^{\prime }\left(z\right)\prec e^z\right\}$ is known as a class of exponential convex functions.

The inclusion properties of special functions in the geometric classes are well known [4,12,17,18,19,20,21,22]. However, there are limited articles regarding the inclusion of RCWF in the classes of geometric functions theory. It is proved in [4] that for $L,\eta \in \mathbb{C}$, the function $z\to {\mathtt{g}}_L$ is leminiscate star like provided that

$$(\sqrt{2}-1)|2L-1|+2\left|\eta \right|<\frac{\sqrt{2}}{4}.$$

It is also shown that $z\to {\mathtt{g}}_L$ is exponentially star like provided that

$$(e-1)|2L-1|+2\left|\eta \right|<\frac{e-1}{e^2}.$$

The radius of star-likeness, univalency, is discussed in [12] by using the Weierstrassian canonical product expansion of RCWF. It is proved that for $L>-1$ and $\eta \le 0$, the radius of star-likeness of the order $\beta \in (0,1]$ for the functions $z\to {\mathtt{g}}_L$ is the smallest positive root of

$$(L+\beta ){\mathtt{F}}_{L,\eta }\left(r\right)-r{\mathtt{F}}_{L,\eta }^{\prime }\left(r\right)=0.$$

The star-likeness of ${\mathtt{g}}_L$ is discussed in ([12], Theorem 4). The conditions for which $Re\left({\mathtt{g}}_L\right)>0$ were also found in same results ([12], Theorem 4). However, it seems that the obtained condition for which $Re\left({\mathtt{g}}_L\right)>0$ is not correct with that fact that ${\mathtt{g}}_L\left(0\right)=0$, while as per the requirement of ([12], Lemma 2), it should be ${\mathtt{g}}_L\left(0\right)=1$. The aim of this study is to contribute more results related to the inclusion of normalized RCWF in the classes of univalent functions theory. In Section 2, we state a proof of the results in which the function ${\mathtt{f}}_L$ is subordinated by three functions, $\sqrt{1+z}$, $1+Az$ and $e^z$. We explain our results through a graphical representation in some special cases. The star-likeness for ${\mathtt{g}}_L$ in the shifted disc $1+Az$ is also considered.

Throughout this study, we used the principle of differential subordination [23,24], which is an important tool in the investigation of various classes of analytic functions to proof main result.

Lemma 1

([23,24]). Let $\Omega \subset \mathbb{C}$ and $\Psi :{\mathbb{C}}^2\times \mathbb{D}\to \mathbb{C}$ satisfy

$$\Psi (i\rho ,\sigma ;z)\notin \Omega$$

for $z\in \mathbb{D},$ and real $\rho ,\sigma$ such that $\sigma \le -(1+{\rho }^2)/2$. If p is analytic in $\mathbb{D}$ with $p\left(0\right)=1$, and $\Psi (p\left(z\right),z{p}^{\prime }\left(z\right);z)\in \Omega$ for $z\in \mathbb{D}$, then $Rep\left(z\right)>0$ in $\mathbb{D}$.

Lemma 2

([25]). Let $\Omega \subset \mathbb{C}$, and $\Psi :{\mathbb{C}}^3\times \mathbb{D}\to \mathbb{C}$ satisfy

$$\Psi (r,s,t;z)\notin \Omega$$

whenever $z\in \mathbb{D},$ and for $m\ge n\ge 1$, $-\pi /4\le \theta \le \pi /4$,

$$\begin{array}{c}\hfill r=\sqrt{2cos\left(2\theta \right)}{e}^{i\theta },s=\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}\mathrm{and}Re\left((t+s)e^{-3i\theta }\right)\ge \frac{3m^2}{8\sqrt{2cos\left(2\theta \right)}}.\end{array}$$

(7)

If $\Psi (p\left(z\right),z{p}^{\prime }\left(z\right),z^2{p}^{″}\left(z\right);z)\in \Omega$ for $z\in \mathbb{D}$, then $p\left(z\right)\prec \sqrt{1+z}$ in $\mathbb{D}$.

Lemma 3

([21]). Let $\Omega \subset \mathbb{C}$, and $\Psi :{\mathbb{C}}^3\times \mathbb{D}\to \mathbb{C}$ satisfy $\Psi (r,s,t;z)\notin \Omega$ whenever $z\in \mathbb{D},$ and for $m\ge 1$, $\theta \in (0,2\pi )$,

$$\begin{array}{c}\hfill r=e^{e^{i\theta }},s=m{e}^{i\theta }{e}^{e^{i\theta }}\mathrm{and}Re\left(1+\frac{t}{s}\right)\ge m(1+cos\left(\theta \right).\end{array}$$

(8)

If $\Psi (p\left(z\right),z{p}^{\prime }\left(z\right),z^2{p}^{″}\left(z\right);z)\in \Omega$ for $z\in \mathbb{D}$, then $p\left(z\right)\prec e^z$ in $\mathbb{D}$.

The following Lemma holds for r and s as stated in Lemma 2.

Lemma 4.

Consider s and r as in (7) with $m\ge 1$. For any $\alpha \in \mathbb{R}$, the following inequalities are true:

• $|s+r^2{-\alpha |}^2\ge {\left(\frac{1}{2\sqrt{2}}+2-\alpha \right)}^2$
• ${|r-\alpha |}^2\le {(\alpha -\sqrt{2})}^2$

Proof. 

For the r and s along with $m\ge 1$, we have

$$\begin{array}{cc}\hfill & |s+r^2{-\alpha |}^2\hfill \\ \hfill & ={\left|\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}+2cos\left(2\theta \right)e^{2i\theta }-\alpha \right|}^2\hfill \\ \hfill & ={\left|\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}+2{cos}^2\left(2\theta \right)+isin\left(4\theta \right)-\alpha \right|}^2\hfill \\ \hfill & ={\left|\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}+e^{4i\theta }-(\alpha -1)\right|}^2\hfill \\ \hfill & ={\left|\frac{m}{2\sqrt{2cos\left(2\theta \right)}}+e^{i\theta }-(\alpha -1)e^{-3i\theta }\right|}^2\hfill \\ \hfill & ={\left(\frac{m}{2\sqrt{2cos\left(2\theta \right)}}+cos\left(\theta \right)-(\alpha -1)cos\left(3\theta \right)\right)}^2+{\left(sin\left(\theta \right)+(\alpha -1)sin\left(3\theta \right)\right)}^2\hfill \\ \hfill & \ge {\left(\frac{1}{2\sqrt{2cos\left(2\theta \right)}}+cos\left(\theta \right)-(\alpha -1)cos\left(3\theta \right)\right)}^2+{\left(sin\left(\theta \right)+(\alpha -1)sin\left(3\theta \right)\right)}^2:=g\left(\theta \right)\hfill \end{array}$$

A calculation shows

$$\begin{array}{cc}\hfill g^{\prime }\left(\theta \right)=\frac{1}{4}& \left(2\sqrt{2}{sec}^{\frac{3}{2}}\left(2\theta \right)((2\alpha -1)sin\left(\theta \right)+(\alpha -1)sin\left(5\theta \right))\right.\hfill \\ \hfill & \left.+tan\left(2\theta \right)sec\left(2\theta \right)(8\alpha +8(\alpha -1)cos(4\theta )-7)\right).\hfill \end{array}$$

For a fixed $\alpha >0$, $g^{\prime }\left(\theta \right)$ has a zero only at $\theta =0$ in $(-\pi /4,\pi /4)$, and further for $\alpha >3\left(5+2\sqrt{2}\right)/(16+7\sqrt{2})\approx 0.906785$,

$$g^{″}(\theta =0)=\frac{1}{4}\left(8(\alpha -1)+24\alpha +2\sqrt{2}(7\alpha -6)-22\right)>0.$$

This implies that g has a local minimum at $\theta =0$ and hence

$$\begin{array}{c}\hfill |s+r^2{-\alpha |}^2\ge g\left(0\right)={\left(\frac{1}{2\sqrt{2}}+2-\alpha \right)}^2.\end{array}$$

$$\begin{array}{cc}\hfill {|r-\alpha |}^2=& |\sqrt{2cos\left(2\theta \right)}-\alpha e^{-i\theta }{|}^2\hfill \\ \hfill =& {\left(\sqrt{2cos\left(2\theta \right)}-\alpha cos\left(\theta \right)\right)}^2+{\alpha }^2{sin}^2\left(\theta \right)\hfill \\ \hfill =& 2cos\left(2\theta \right)-2\alpha cos\left(\theta \right)\sqrt{2cos\left(2\theta \right)}+{\alpha }^2\hfill \\ & \le {\alpha }^2-2\sqrt{2}\alpha +2.\hfill \end{array}$$

This complete the proof. □

2. Geometric Properties of Coulomb Wave Functions (CWF)

2.1. Subordination by $\sqrt{1+z}$

In [4], sufficient conditions based on L and $\eta$ is derived for which $z{\mathtt{g}}_L^{\prime }\left(z\right)/{\mathtt{g}}_L\left(z\right)\prec \sqrt{1+z}$, that is ${\mathtt{g}}_L$, is Lemniscate star like. This section derives conditions on L and $\eta$ for which ${\mathtt{f}}_L\left(z\right)\prec \sqrt{1+z}$, which we termed as ${\mathtt{f}}_L$ is the Lemniscate Catathéodory function.

Theorem 1.

For $\eta ,L\in \mathbb{C}$, suppose that

$$\begin{array}{c}\hfill Re(2L+1)>max\left\{0,8\left|\eta \right|+\frac{13}{4}\right\},\end{array}$$

(9)

then ${\mathtt{f}}_L\left(z\right)\prec \sqrt{1+z}$.

Proof. 

Suppose that $\mathtt{p}\left(z\right)={\mathtt{f}}_L\left(z\right)$. Since ${\mathtt{f}}_L$ is the solution of the differential equation (5), $\mathtt{p}$ is the solution of

$$\begin{array}{c}\hfill z^2{\mathtt{p}}^{″}\left(z\right)+2(L+1)z{\mathtt{p}}^{\prime }\left(z\right)+(z^2-2\eta z)\mathtt{p}\left(z\right)=0.\end{array}$$

(10)

Let $\Omega =\left\{0\right\}\subset \mathbb{C}$ and define $\psi :{\mathbb{C}}^3\times \mathbb{D}\to \mathbb{C}$ as

$$\begin{array}{c}\hfill \psi (r,s,t;z):=t+2(L+1)s+(z^2-2\eta z)r.\end{array}$$

(11)

It is clear from (10) that $\psi (p\left(z\right),z{p}^{\prime }\left(z\right),z^2{p}^{″}\left(z\right);z)\in \Omega$. We shall apply Lemma 2 to show $\psi (r,s,t;z)\notin \Omega$, which further implies $p\left(z\right)\prec \sqrt{1+z}$.

For $r,s,t$ as given (7), it follows from (11) that

$$\begin{array}{cc}\hfill \left|\psi \right(r,s,t;z\left)\right|& =|(t+s)+(2L+1)s+(z^2-2\eta z)r|\hfill \\ \hfill & >|(t+s)e^{-3i\theta }+\frac{(2L+1)m}{2\sqrt{2cos\left(2\theta \right)}}|-|z-2\eta |\sqrt{2cos\left(2\theta \right)}\hfill \\ \hfill & >\frac{3m^2}{8\sqrt{2cos\left(2\theta \right)}}+\frac{Re(2L+1)m}{2\sqrt{2cos\left(2\theta \right)}}-|z-2\eta |\sqrt{2cos\left(2\theta \right)}\hfill \\ \hfill & =\frac{1}{8\sqrt{2cos\left(2\theta \right)}}\left[3m^2+4mRe(2L+1)-16-32\left|\eta \right|\right]>0,\hfill \end{array}$$

provided $Re(2L+1)>(13+32|\eta \left|\right)/4$. □

It is well known that for univalent function g, if $f\prec g$, then $f\left(D\right)\subset g\left(D\right)$. Using this fact, we chose some real and complex $\eta$, and validated Theorem 1. For the first case, consider $\eta =1,i$, and L is a real number. Using Theorem 1, in both cases, $L>5.25$. This fact is represented in Figure 1.

Figure 1. Image of ${\mathtt{f}}_L\left(\mathbb{D}\right)$ for $L=5.25$.

We consider another case by taking $\eta =(1+i)$. By Theorem 1, in this case for real $L>6.78185$, and Figure 2 validate the result.

Figure 2. Image of ${\mathtt{f}}_L\left(\mathbb{D}\right)$ for $L=6.78185$.

2.2. Subordination by $1+Az$

In this part we proved that result related to the subordination ${\mathtt{f}}_L\prec 1+Az$ and $z{\mathtt{g}}_L^{\prime }\left(z\right)/{\mathtt{g}}_L\left(z\right)\prec 1+Az$ which describe the nature of ${\mathtt{f}}_L$ and ${\mathtt{g}}_L$ in the disc center at $(1,0)$ and radius A. The results in this section are proved by using Lemma 2.

Theorem 2.

For $\eta ,L\in \mathbb{C}$ and $A\in (0,1]$, suppose that

$$\begin{array}{c}\hfill 4ARe\left(L\right)>2\left|\eta \right|(A+1)-3A+\frac{5}{8}\end{array}$$

(12)

Then, ${\mathtt{f}}_L\left(z\right)\prec 1+Az$.

Proof. 

Consider

$$\begin{array}{c}\hfill q\left(z\right)=\sqrt{\frac{1}{A}\left({\mathtt{f}}_L\left(z\right)+A-1\right)}.\end{array}$$

(13)

A simplification gives

$$\begin{array}{cc}\hfill {\mathtt{f}}_L\left(z\right)& =A{q}^2\left(z\right)-A+1,{\mathtt{f}}_L^{\prime }\left(z\right)=2A{q}^{\prime }\left(z\right)q\left(z\right){\mathtt{f}}_L^{″}\left(z\right)=2A{q}^{″}\left(z\right)q\left(z\right)+2A{\left(q^{\prime }\left(z\right)\right)}^2.\hfill \end{array}$$

From (5), it follows that

$$\begin{array}{c}\hfill 2A{z}^2{q}^{″}\left(z\right)q\left(z\right)+2A{\left(z{q}^{\prime }\left(z\right)\right)}^2+4A(L+1)z{q}^{\prime }\left(z\right)q\left(z\right)+(z^2-2\eta z)(A{q}^2\left(z\right)-A+1)=0.\end{array}$$

Let $\Omega =\left\{0\right\}\subset \mathbb{C}$ and define $\psi :{\mathbb{C}}^2\times \mathbb{D}\to \mathbb{C}$ as

$$\begin{array}{c}\hfill \psi (r,s;z):=2Atr+2A{s}^2+4A(L+1)sr+(z^2-2\eta z)(A{r}^2-A+1).\end{array}$$

(14)

It is clear from (14) that $\psi (q\left(z\right),z{q}^{\prime }\left(z\right);z)\in \Omega$. We shall apply Lemma 2 to show that $\psi (r,s,t;z)\notin \Omega$, which further implies $q\left(z\right)\prec \sqrt{1+z}$.

Now, for $-\pi /4\le \theta \le \pi /4$, let

$$\begin{array}{c}\hfill r=\sqrt{2cos\left(2\theta \right)}{e}^{i\theta },s=\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}.\end{array}$$

It follows by elementary trigonometric identities that

$$r^2-1=2cos\left(2\theta \right)e^{2i\theta }-1=(2{cos}^2\left(2\theta \right)-1)+i2cos\left(2\theta \right)sin\left(2\theta \right)=e^{4i\theta }.$$

Substitute r and s in (18) and a simplification leads to

$$\begin{array}{cc}\hfill \left|\psi \right(r,s,t;z\left)\right|& =|2Atr+2A{s}^2+4A(L+1)sr+(z^2-2\eta z)(A{r}^2-A+1)|\hfill \\ \hfill & =|2Ar(t+s)+2A{s}^2+A(4L+2)sr+(z^2-2\eta z)(A{r}^2-A+1)|\hfill \\ \hfill & >|e^{4i\theta }|\left(\sqrt{2cos\left(2\theta \right)}Re(t+s)e^{-3i\theta }+2A\frac{m^{2}Re\left(e^{2i\theta }\right)}{2cos\left(2\theta \right)}+ARe(4L+2)m\right)\hfill \\ \hfill & -A(1+2|\eta \left|\right)|r^2-1|-(1+2\left|\eta \right|)\hfill \\ \hfill & >\frac{3m^2}{8}+2A{m}^2+ARe(4L+2)m-A(1+2|\eta \left|\right)|e^{4i\theta }|-(1+2\left|\eta \right|)\hfill \\ \hfill & >4ARe\left(L\right)+3A-2\left|\eta \right|(A+1)-\frac{5}{8}>0.\hfill \end{array}$$

By Lemma 2, it is proved that $q\left(z\right)\prec \sqrt{1+z}$ which is equivalent to

$$\begin{array}{c}\hfill \sqrt{\frac{1}{A}\left({\mathtt{f}}_L+A-1\right)}=\sqrt{1+w\left(z\right)},\end{array}$$

(15)

for some analytic function $w\left(z\right)$ such that $\left|w\right(z\left)\right|<1$. A simplification of (15) gives

$$\begin{array}{c}\hfill \frac{1}{A}\left({\mathtt{f}}_L+A-1\right)=1+w\left(z\right)\Rightarrow {\mathtt{f}}_L=1+Aw\left(z\right)\Rightarrow {\mathtt{f}}_L\prec 1+Az.\end{array}$$

This complete the proof. □

Again to validate the Theorem 2, we fix $A=1/2$ and $\eta =1$. Lets L be real and then as per Theorem 2, $L>17/16\approx 1.1$. The Figure 3 indicates that the lower bound for L is possible sharp.

Figure 3. Image of ${\mathtt{f}}_L\left(\mathbb{D}\right)$ for $L=1.1$ and $\eta =1$.

Our next result is about the starlikenes of ${\mathtt{g}}_L$ in the disc $1+Az$.

Theorem 3.

For $\eta ,L\in \mathbb{C}$ and $A\in (0,1]$, suppose that

$$\begin{array}{c}\hfill Re(2L-1)>A-2+\frac{2\left|\eta \right|}{A}.\end{array}$$

(16)

Then, $z{\mathtt{g}}_L^{\prime }\left(z\right)/{\mathtt{g}}_L\left(z\right)\prec 1+Az$.

Proof. 

To prove the result consider

$$\begin{array}{c}\hfill q\left(z\right)=\sqrt{\frac{1}{A}\left(\frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}+A-1\right)}.\end{array}$$

(17)

A calculation yield

$$\begin{array}{cc}\hfill \frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}& =A{q}^2\left(z\right)-A+1\hfill \\ \hfill \frac{z^2{\mathtt{g}}_L^{″}\left(z\right)}{{\mathtt{g}}_L\left(z\right)}& =2Az{q}^{\prime }\left(z\right)q\left(z\right)-(A{q}^2\left(z\right)-A+1)+{(A{q}^2\left(z\right)-A+1)}^2\hfill \end{array}$$

From (6) it follows that

$$\begin{array}{cc}\hfill & \frac{z^2{\mathtt{g}}^{″}\left(z\right)}{\mathtt{g}\left(z\right)}+2L\frac{z{\mathtt{g}}^{\prime }\left(z\right)}{\mathtt{g}\left(z\right)}+(z^2-2\eta z-2L)=0\hfill \\ \hfill \Rightarrow & 2Az{q}^{\prime }\left(z\right)q\left(z\right)+{(A{q}^2\left(z\right)-A+1)}^2+A(2L-1)(q^2\left(z\right)-1)+z^2-2\eta z-1=0\hfill \\ \hfill \Rightarrow & 2Az{q}^{\prime }\left(z\right)q\left(z\right)+A^2{(q^2\left(z\right)-1)}^2+2A(q^2\left(z\right)-1)+A(2L-1)(q^2\left(z\right)-1)+z^2-2\eta z=0.\hfill \end{array}$$

Let $\Omega =\left\{0\right\}\subset \mathbb{C}$ and define $\psi :{\mathbb{C}}^2\times \mathbb{D}\to \mathbb{C}$ as

$$\begin{array}{c}\hfill \psi (r,s;z):=2Ars+A^2{(r^2-1)}^2+2A(r^2-1)+A(2L-1)(r^2-1)+z^2-2\eta z.\end{array}$$

(18)

It is clear from (18) that $\psi (q\left(z\right),z{q}^{\prime }\left(z\right);z)\in \Omega$. We shall apply Lemma 2 and proceed similar to the proof of Theorem 2 to show that $\psi (r,s,t;z)\notin \Omega$. Substitute r and s into (18), and a simplification leads to

$$\begin{array}{cc}\hfill \left|\psi \right(r,s;z\left)\right|& =|2Ars+A^2{(r^2-1)}^2+2A(r^2-1)+A(2L-1)(r^2-1)+z^2-2\eta z|\hfill \\ \hfill & =|m{e}^{4i\theta }+A^2{e}^{8i\theta }+2A{e}^{4i\theta }+A(2L-1)e^{4i\theta }+z^2-2\eta z|\hfill \\ \hfill & >Re(m+A^2{e}^{4i\theta }+2A+ARe(2L-1))-1-2\left|\eta \right|\hfill \\ \hfill & =m+A^{2}cos\left(4\theta \right)+2A+ARe(2L-1)-1-2\left|\eta \right|\hfill \\ \hfill & >-A^2+2A+ARe(2L-1)-2\left|\eta \right|>0,\hfill \end{array}$$

provided $Re(2L-1)>A-2+2\left|\eta \right|/A$.

In view of Lemma 2, it concludes that $q\left(z\right)\prec \sqrt{1+z}$, which is equivalent to

$$\begin{array}{c}\hfill \sqrt{\frac{1}{A}\left(\frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}+A-1\right)}=\sqrt{1+w\left(z\right)}\end{array}$$

for some analytic functions $w\left(z\right)$ such that $\left|w\right(z\left)\right|<1$. A simplification gives

$$\begin{array}{c}\hfill \frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}=1+Aw\left(z\right)\Rightarrow \frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}\prec 1+Az.\end{array}$$

This concludes the result. □

2.3. Subordination by $e^z$

In this part, we derive sufficient conditions on L and $\eta$ for which ${\mathtt{f}}_L\left(z\right)\prec e^z$. The exponential starlikeness of $z{\mathtt{g}}_L^{\prime }\left(z\right)/{\mathtt{g}}_L\left(z\right)$ is discussed in [4]. It is worthy to note here that exponential starlikeness is equivalent to $z{\mathtt{g}}_L^{\prime }\left(z\right)/{\mathtt{g}}_L\left(z\right)\prec e^z$.

Theorem 4.

For $\eta ,L\in \mathbb{C}$, suppose that

$$\begin{array}{c}\hfill Re\left(L\right)\ge \left|\eta \right|\end{array}$$

(19)

Then ${\mathtt{f}}_L\left(z\right)\prec e^z$.

Proof. 

To prove the theorem, it is enough to consider the function $\Psi (r,s,t;z)$ as defined in (11) and then apply Lemma 3 to show that $\Psi (r,s,t;z)\notin \Omega$ for r, s and t as given in (8). For $m\ge 1$ and $Re(2L+1)>0$, it follows that

$$\begin{array}{cc}\hfill \left|\psi \right(r,s,t;z\left)\right|& =|(t+s)+(2L+1)s+(z^2-2\eta z)r|\hfill \\ \hfill & >e^{cos\left(\theta \right)}\left(\left|(t+s)e^{-i\theta }{e}^{-e^{i\theta }}+(2L+1)m\right|-1-2\left|\eta \right|\right)\hfill \\ \hfill & >e^{cos\left(\theta \right)}\left(Re(t+s)e^{-i\theta }{e}^{-e^{i\theta }}+Re(2L+1)m-1-2\left|\eta \right|\right)\hfill \\ \hfill & >e^{cos\left(\theta \right)}\left(m(1+cos(\theta \left)\right)+2Re\left(L\right)m+m-1-2\left|\eta \right|\right)>0,\hfill \end{array}$$

provided $Re\left(L\right)\ge \left|\eta \right|$. Lemma 3 implies $\Psi (r,s,t;z)\notin \Omega$ and hence ${\mathtt{f}}_L\left(z\right)\prec e^z$. This completes the proof. □

We validate this result graphically by taking real L and $\eta$ and $L=\eta =1,10,50,100,500$, and all of the case are presented in Figure 4. It is evident from Figure 4 that ${\mathtt{f}}_L\left(\mathbb{D}\right)\subset e^{\mathbb{D}}$, and for larger $L=\eta$.

Figure 4. Cases for ${\mathtt{f}}_L\left(z\right)\prec e^z$ for $L=\eta$.

2.4. Subordination by $(1+Az)/(1+Bz)$

Theorem 5.

Let $L,\eta \in \mathbb{C}$ and $-1\le B<A\le 1$. Suppose that

$$\begin{array}{cc}\hfill & {(A-B)}^2{\left((1+B)Re\left(L\right)+(1-B)Im\left(L\right)\right)}^2<[\left((1+2|\eta \left|\right){(1+B)}^2-2A-1+B\right)\hfill \end{array}$$

$$\begin{array}{cc}& \times ((1+2|\eta \left|\right){(1-B)}^2-2(A-B)\left((1-B)Re\left(L\right)-(1+B)Im\left(L\right)\right)\hfill \end{array}$$

(20)

$$\begin{array}{cc}& +2(1+AB)-(A-B)+{(1-A)}^2\left)\right]\hfill \end{array}$$

(21)

Then,

$$\frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}\prec \frac{1+Az}{1+Bz},$$

provided $(1+B)z{\mathtt{g}}_L^{\prime }\left(z\right)\ne (1+A){\mathtt{g}}_L\left(z\right)$.

Proof. 

Define the function

$$p\left(z\right):=-\frac{(1-B)z{\mathtt{g}}_L^{\prime }\left(z\right)-(1-A){\mathtt{g}}_L\left(z\right)}{(1+B)z{\mathtt{g}}_L^{\prime }\left(z\right)-(1+A){\mathtt{g}}_L\left(z\right)}.$$

A series of calculation and simplification leads to

$$\begin{array}{cc}\hfill \frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}& =\frac{(1+A)p\left(z\right)+1-A}{(1+B)p\left(z\right)+1-B}\hfill \\ \hfill \frac{z^2{\mathtt{g}}_L^{″}\left(z\right)}{{\mathtt{g}}_L\left(z\right)}& =\frac{2(A-B)z{p}^{\prime }\left(z\right)}{{((1+B)p\left(z\right)+1-B)}^2}-\frac{(1+A)p\left(z\right)+1-A}{(1+B)p\left(z\right)+1-B}+{\left(\frac{(1+A)p\left(z\right)+1-A}{(1+B)p\left(z\right)+1-B}\right)}^2\hfill \end{array}$$

From (6), it follows that

$$\begin{array}{cc}\hfill & \frac{z^2{\mathtt{g}}_L^{″}\left(z\right)}{{\mathtt{g}}_L\left(z\right)}+2L\frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}+(z^2-2\eta z-2L)=0\hfill \\ \hfill \Rightarrow & \frac{2(A-B)z{p}^{\prime }\left(z\right)}{{((1+B)p\left(z\right)+1-B)}^2}+(2L-1)\frac{(A-B)\left(p\right(z)-1)}{(1+B)p\left(z\right)+1-B}\hfill \\ & +{\left(\frac{(1+A)p\left(z\right)+1-A}{(1+B)p\left(z\right)+1-B}\right)}^2+(z^2-2\eta z)=0\hfill \\ \hfill \Rightarrow & 2(A-B)z{p}^{\prime }\left(z\right)+{((1+A)p\left(z\right)+1-A)}^2+(z^2-2\eta z){((1+B)p\left(z\right)+1-B)}^2\hfill \\ \hfill & +\left(\left(2L(A-B)-(1+A)\right)p\left(z\right)-2L(A-B)-A+1\right)\left((1+B)p\left(z\right)+1-B\right)=0\hfill \end{array}$$

Let $\Omega =\left\{0\right\}\subset \mathbb{C}$ and define $\psi :{\mathbb{C}}^2\times \mathbb{D}\to \mathbb{C}$

$$\begin{array}{cc}\hfill \psi (r,s;z)& :=2(A-B)s++{((1+A)r+1-A)}^2+(z^2-2\eta z){((1+B)r+1-B)}^2\hfill \\ \hfill & +\left(\left(2L(A-B)-(1+A)\right)r-2L(A-B)-A+1\right)\left((1+B)r+1-B\right)\hfill \end{array}$$

Denoting $L_1=Re\left(L\right)$ and $L_2=Im\left(L\right)$, we have

$$\begin{array}{cc}\hfill & Re\psi (i\rho ,\sigma ;z)\hfill \\ & <(A-B)(1+{\rho }^2)+Re{((1+A)i\rho +1-A)}^2+Re\left((z^2-2\eta z){((1+B)i\rho +1-B)}^2\right)\hfill \\ \hfill & +Re\left(\left(2L(A-B)-(1+A)\right)i\rho -2L(A-B)-A+1\right)\left((1+B)i\rho +1-B\right)\hfill \\ \hfill & =-(A-B)(1+{\rho }^2)-(1+A){\rho }^2+{(1-A)}^2+(1+2|\eta \left|\right)({(1+B)}^2{\rho }^2+{(1-B)}^2)\hfill \\ \hfill & -2(A-B)((1+B)L_1+(1-B)L_2)\rho -2(A-B)((1-B)L_1+(1+B)L_2)+2(1+AB)\hfill \\ \hfill & =\left(-(A-B)-(1+A)+(1+2|\eta \left|\right){(1+B)}^2\right){\rho }^2-\left(2(A-B)((1+B)L_1+(1-B)L_2)\right)\rho \hfill \\ \hfill & +(1+2|\eta \left|\right){(1-B)}^2-2(A-B)\left((1-B)L_1-(1+B)L_2\right)+2(1+AB)-(A-B)+{(1-A)}^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill \frac{{\Delta }_1}{4}& ={(A-B)}^2{\left((1+B)L_1+(1-B)L_2\right)}^2-[\left((1+2|\eta \left|\right){(1+B)}^2-2A-1+B\right)\hfill \\ \hfill & \times \left((1+2|\eta \left|\right){(1-B)}^2-2(A-B)\left((1-B)L_1-(1+B)L_2\right)+2(1+AB)-(A-B)+{(1-A)}^2\right)]\hfill \end{array}$$

Clearly, by the given hypothesis, ${\Delta }_1<0$, and hence $Re\psi (i\rho ,\sigma ;z)<0$. This implies that $\Psi (r,s,t;z)\notin \Omega$. From Lemma 1 it follows

$$\begin{array}{cc}\hfill p\left(z\right)\prec \frac{1+z}{1-z}& \Rightarrow -\frac{(1-B)z{\mathtt{g}}_L^{\prime }\left(z\right)-(1-A){\mathtt{g}}_L\left(z\right)}{(1+B)z{\mathtt{g}}_L^{\prime }\left(z\right)-(1+A){\mathtt{g}}_L\left(z\right)}\prec \frac{1+z}{1-z}\hfill \\ \hfill & \Rightarrow \frac{z{\mathtt{g}}_L^{\prime }\left(z\right)}{{\mathtt{g}}_L\left(z\right)}\prec \frac{1+Az}{1+Bz}.\hfill \end{array}$$

This completes the proof. □

By choosing $A=-B=1$ in Theorem 5, we have the following result on the star-likeness of ${\mathtt{g}}_L$.

Corollary 1.

For $L,\eta \in \mathbb{C}$, suppose that $\left|\eta \right|<Re\left(L\right)-\frac{1}{3}{(Im\left(L\right))}^2-\frac{1}{4}$. Then, ${\mathtt{g}}_L$ is star like provided that ${\mathtt{g}}_L\ne 0$ for $z\in \mathbb{D}$.

Remark 1.

The condition for the star-likeness of ${\mathtt{g}}_L$ is provided in ([12], Theorem 4) which is the same as stated in Corollary 1.

3. Conclusions

This study finds the conditions for the parameters L and $\eta$ for which the normalized function ${\mathtt{f}}_L\left(z\right)=C_L^{-1}\left(\eta \right)z^{-L-1}{F}_{L,\eta }\left(z\right)$ is subordinated by three different functions $\sqrt{1+z}$, $1+Az$, and $e^z$.

We already interpreted Theorems 1, 2 and 4 graphically. Figure 3 describes the sharpness of Theorem 2. On the other hand, Figure 4 indicates the situation related to Theorem 4. However, we were unable to obtain examples with a similar sharpness using Theorem 1. Thus, it is expected show some improvement in the obtained results. For example, let $\eta =2i$, and then by Theorem 4, ${\mathtt{f}}_L\left(z\right)\prec e^z$ for $Re\left(L\right)>\left|\eta \right|=2$. However, Figure 5 indicates that if L is real, then it can be lower than 1 for $\eta =2i$.

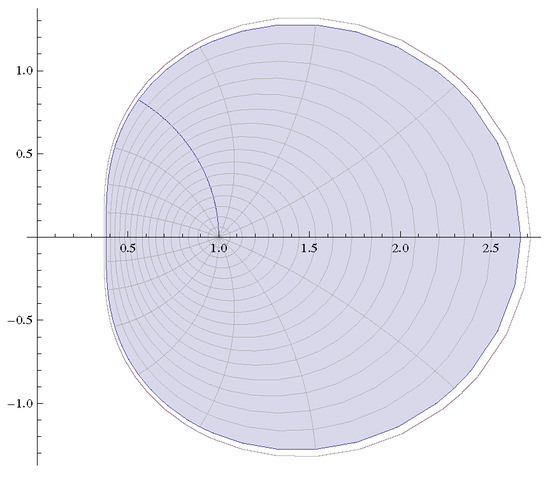
Figure 5. Image of ${\mathtt{f}}_L\left(\mathbb{D}\right)$ for $\eta =2i$ and $L=1.05$.

Similarly, for $\eta =2i$, Theorem 1 implies that ${\mathtt{f}}_L\left(z\right)\prec \sqrt{1+z}$ for

$$Re\left(L\right)>8\left|\eta \right|+\frac{13}{4}=9.125.$$

However, for real L, it follows from Figure 6 that L can be down to $5.5$.

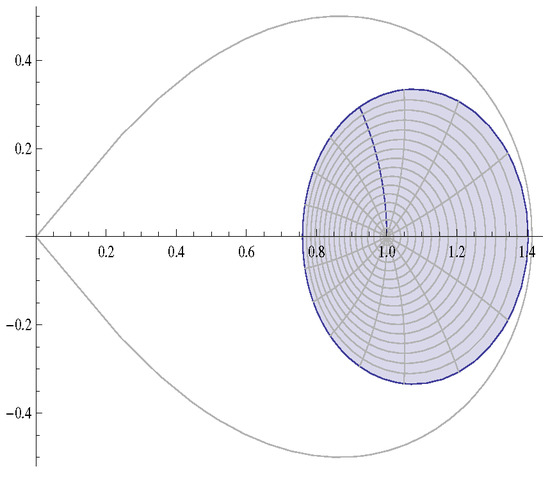
Figure 6. Image of ${\mathtt{f}}_L\left(\mathbb{D}\right)$ for $\eta =2i$ and $L=1.05$.

From the above discussion, we can finally conclude that Theorems 1, 2 and 4 are completely valid with respect to the stated hypothesis. However, for some special choice of parameter $\eta$, there is a possibility for improvement.

This article also derives the conditions for the star-likeness of ${\mathtt{g}}_L$ in the disc $(1+Az)/(1+Bz)$ and $1+Az$. With the special case for $A=1$ and $B=-1$, the results lead to a known result ([12], Theorem 4).