Superpotential for Novel Symmetry in Real and Complex Space

Abstract

We propose a new “superpotential” and find that neither the supersymmetric energy conditions nor the associated shape invariance conditions remain valid. On the other hand, a new energy condition $E_n^{+}-E_n^{(-)}=2\lambda$ between the two partner Hamiltonians $H^{(\pm )}$ emerges. A mathematical proof supports the present findings, with examples being presented. It is observed that when the superpotential is associated with discontinuity or distortion, the SUSY energy conditions and the shape invariance conditions will no longer hold well. The above formalism is also valid in complex space for models involving $PT$-symmetry.

1. Introduction

In physics, symmetry plays a major role in understanding different aspects of physical phenomena. Sometimes the symmetry is either visible or invisible (hidden). Similarly, sometimes symmetry is either broken or unbroken. In fact, Bose-Fermi symmetry or supersymmetry that relates bosons (particles with spin 0 or integer) and fermions (particles with half odd integral spin) were originally used to construct theories for the possible unification of internal symmetry with ordinary space–time symmetry. In 1981, Witten [1] considered a model supersymmetry that remains unbroken at the free level, but broken by small corrections [2]. This promoted many authors at the front level to propose a model to visualize “breaking in supersymmetry (SUSY) [3,4,5,6,7,8,9]”. Some of the interesting analyses on SUSY are: supersymmetry breaking in low-dimensional models [3], supersymmetry breaking in a quantum phase transition [4], dynamical supersymmetry breaking on quantum moduli spaces [5], breaking scale in atomic clocks [6], some experimental evidence of supersymmetry breaking [7], and metastable supersymmetry breaking [8]. Despite this analysis, Feldstein and Yanagida [9] discussed a general method, asking why is the supersymmetry breaking scale unnaturally high, considering CP violation, Peccei–Quinn (PQ) symmetry violation, and the non-conservation of R-parity, etc. However, in a very recent paper by Cai et al. [10], they observed supersymmetry breaking in a trapped ion quantum simulator. Similar papers on SUSY breaking have been discussed using the Rabi model [11,12]. In this context, we would like to point out that Cai et al.’s [10] work explains breaking using the Rabi type of model. On the other hand, supersymmetry in the quantum mechanics (SUSYQM) took a new turn in introducing the “shape invariance” property by Gendeshtein [13] (where the Schroedinger equation need not be solved in finding the supersymmetric energy condition). This novel idea triggers many interesting models [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] such as: harmonic oscillator, Morse oscillator, Rosen–Morse, Eckrat, Poshi-teller, etc., justifying the validity of “shape-invariance” (SI) in nature. However, these model potentials are only confined to real space but not in complex space. In complex space, the operators need to satisfy the PT-symmetry condition, ($[H,PT]=0$). It should be remembered that PT-invariant systems are mainly non-self-adjoint operators [36,37,38,39,40,41,42,43,44] ($H\ne H^{†}$). Here, we highlight the basic features of PT-invariant systems as follows, saying that P stands for a parity invariant operator having the following properties: $Px{P}^{-1}=-x$ and $Pp{P}^{-1}=-p$. Similarly, T stands for the time-reversal operator and has the properties $Tx{T}^{-1}=x$, $Tp{T}^{-1}{T}^{-1}=-p$, and $Ti{T}^{-1}=-i$. In this case, the commutation relation between coordinate $\left(x\right)$ and momentum $\left(p\right)$ remains invariant, i.e., $[x,p]=i$. In fact, in this paper, we formulate a new model of superpotential and a new symmetry that remains valid in real as well as complex space. Further, we study the limitations of supersymmetric energy conditions (SUSYEC) and shape invariance (SI). Below, we first highlight a few important features of supersymmetric energy conditions (SUSYEC), as follows.

2. Supersymmetric Energy Conditions (SUSYEC) and Shape Invariance (SI) Relations

Let us consider an annihilation operator

$$A=\frac{d}{dx}+W\left(x\right)$$

(1)

satisfying the condition

$$A{\varphi }_0^{-}=0$$

(2)

Now, we select another operator B as

$$B=-\frac{d}{dx}+W\left(x\right)$$

(3)

Now, using the above two operators $(A,B)$, we have

$$H^{(-)}=BA=p^2+W^2-\frac{dW}{dx}$$

(4)

and

$$H^{(+)}=AB=p^2+W^2+\frac{dW}{dx}$$

(5)

Here, $H^{\pm },A.B$ are related as per the algebraic structure as

$$H=\left[\begin{array}{cc}{H}^{(-)}& 0\\ 0& H^{(+)}\end{array}\right]$$

(6)

with

$$Q=\left[\begin{array}{cc}0& 0\\ A& 0\end{array}\right]$$

(7)

and

$$Q^{†}=\left[\begin{array}{cc}0& B\\ 0& 0\end{array}\right]$$

(8)

satisfying the following relations as: $[H,Q]=0,[H,Q^{†}]=0$, and $\{Q,Q^{†}\}=H$; and $\{Q,Q\}=0$ and $\{Q^{†},Q^{†}\}=0$.

From the assumed relation $A{\varphi }_0=0$, we can write

$$BA{\varphi }_0^{-}=H^{(-)}{\varphi }_0^{-}=0$$

(9)

This implies

$$E_0^{(-)}=0$$

(10)

Further, let

$$H^{(-)}{\varphi }_n^{-}=E_n^{(-)}{\varphi }_n^{-}$$

(11)

and

$$H^{(+)}{\varphi }_n^{+}=E_n^{(+)}{\varphi }_n^{+}$$

(12)

then

$$H^{(+)}\left(A{\varphi }_n^{-}\right)=AB\left(A{\varphi }_n^{-}\right)=A{H}^{(-)}\varphi n^{-}=E_n^{(-)}\left(A{\varphi }_n^{-}\right)$$

(13)

This means that $\left(A{\varphi }_n^{-}\right)$ is an eigenfunction of $H^{(+)}$ having eigenvalue $E_n^{(-)}$. Similarly, we can write

$$H^{(-)}\left(B{\varphi }_n^{+}\right)=BA\left(B{\varphi }_n^{+}\right)=B{H}^{(+)}\varphi n^{+}=E_n^{(+)}\left(B{\varphi }_n^{+}\right)$$

(14)

In other words, the eigenvalues and eigenfunctions of two Hamiltonians are interrelated, i.e.,

$$E_{n+1}^{(-)}=E_n^{(+)}$$

(15)

$$B{\varphi }_n^{+}={\varphi }_{n+1}^{-}$$

(16)

and

$$A{\varphi }_{n+1}^{-}={\varphi }_n^{+}$$

(17)

The above energy relations are known as supersymmetric energy conditions (SUSYEC).

Shape Invariance Condition

Let

$$\begin{array}{c}{V}_{+}(x,\lambda )=W^2(x,\lambda )+W^{{}^{\prime }}(x,\lambda )\hfill \\ =W^2((x,\beta )-W^{{}^{\prime }}(x,\beta )+R\left(\beta \right)\hfill \\ =V_{-}(x,\beta )+R\left(\beta \right)\hfill \end{array}$$

(18)

Here, $R\left(\beta \right)=f\left(\lambda \right)$ and is independent of x [13]. Here, we present the previous analysis [13] and consider that $\lambda$ is a set of parameters, then one can construct a hierarchy of Hamiltonians as

$$\begin{array}{c}{H}^s=p^2+V_{-}(x,{\beta }_s)+{\sum }_{k=1}^{s}R\left({\beta }_k\right)\hfill \\ =p^2+V_{-}(x,{\beta }_{s-1})+{\displaystyle \sum _{k=1}^{s-1}}R\left({\beta }_k\right)\hfill \end{array}$$

(19)

and considering $H^1=H^{(+)}$ and $H^0=H^{(-)}$, then

$$E_n^{(-)}=\sum _{k=1}^{n}R\left({\beta }_k\right)$$

(20)

or simply

$$E_n^{(-)}=\sum R\left(\beta \right)$$

(21)

To justify this, we consider an exactly solvable model as the simple harmonic oscillator. Here, we chose superpotential $W(x,\lambda )$ as

$$W_1=\lambda x$$

(22)

In Figure 1, we plot the superpotential and reflect its behavior as

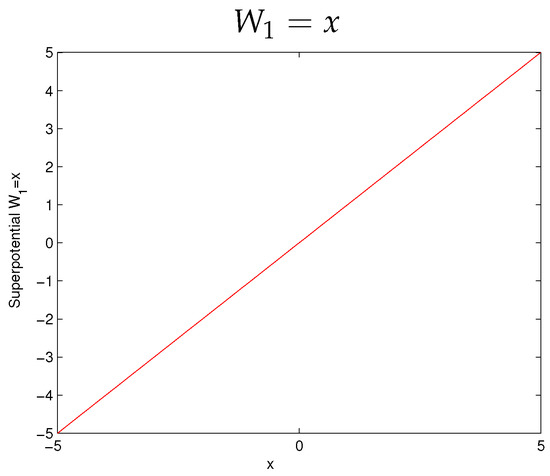
Figure 1. Superpotential: SUSY and SI valid.

Here, superpotential $W_1$ is linear in nature and the above plot is for $\lambda =1$. For this, we have

$$V_{+}(x,\lambda )=V_{-}(x,-\lambda )+2\lambda$$

(23)

Hence,

$$E_n^{(-)}\left(SI\right)=\sum 2\lambda =2n\lambda$$

(24)

Now, we write the Hamiltonian

$$H^{(-)}=p^2+{\lambda }^2{x}^2-\lambda$$

(25)

hence,

$$E_n^{(-)}=(2n+1)\lambda -\lambda =2n\lambda$$

(26)

Hence, we find $E_n^{(-)}\left(SI\right)=E_n^{(-)}$. Here, we would like to say that superpotential W need not be linear to justify SUSYEC and SI; however, its nonlinear nature can also be suitable to justify SUSYEC and SI [13,15,16,17]. Below, we reflect on one such behavior of the superpotential $W_2=tanh\left(x\right)$ in Figure 2.

Figure 2. Superpotential: SUSY and SI are valid.

Let us discuss a few different natures of the superpotential, as given below.

3. A Few Deviated Superpotentials with SUSYEC Being Valid and SI Being Invalid

Here, we consider two different model superpotentials where only SUSYEC remains valid. In this case, we consider the model proposed by Bogie, Gangopadhya, and Mallow [20] as

$$W_3=wx-\frac{a}{x}+[\frac{2wx}{(w{x}^2+2a-1)}-\frac{2wx}{(w{x}^2+2a+1)}]$$

(27)

and claim a few interesting natures connecting to the Euler equation. However, neglecting the extra term, we have

$$W_3\sim wx-\frac{a}{x}=x-\frac{1}{x};w=a=1$$

(28)

Here, SUSY remains valid [27] but the shape invariance is no longer useful in releasing energy $E_n^{(-)}$ because it is practically impossible to visualize the relation

$$V_2^{(+)}=V_2^{(-)}+f\left(\beta \right)$$

(29)

This simple superpotential nature has been reflected in Figure 3 as

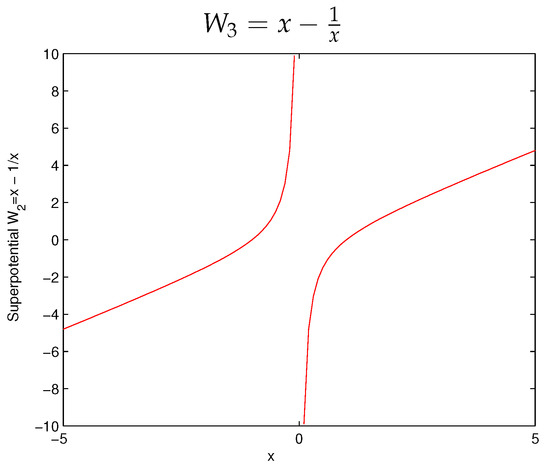
Figure 3. Superpotential: SUSY is valid.

Apart from the above, a similar feature is also seen in the model superpotential proposed by Marques, Negreni, and Da Silva [8] as

$$W_4=\lambda x\left|x\right|=x\left|x\right|;\lambda =1$$

(30)

The nature of $W_4$ is reflected in Figure 4.

Figure 4. Superpotential: SUSY is valid but SI is not valid.

From $W_3$ and $W_4$, we get

$$W_5=x\left|x\right|-\lambda \frac{\left|x\right|}{x}=x\left|x\right|-\frac{\left|x\right|}{x}$$

(31)

Here, neither SUSY nor the shape-invariance remain valid. Below, we present the nature of $W_5$ in Figure 5 as

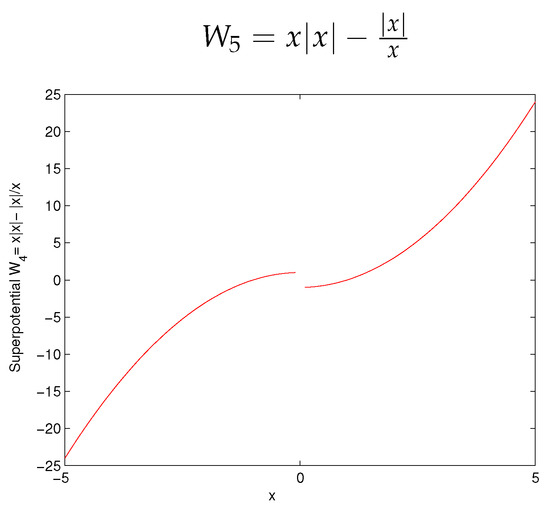
Figure 5. Superpotential: no SUSY and no SI.

Below, we cite the first few energy levels of

$$H^{(-)}=p^2+W_5^2-\frac{d{W}_5}{dx}$$

(32)

in Table 1.

Table 1. Energy levels $E_n^{(-)}$.

${\mathit{E}}_{\mathit{n}}^{(-)}$
−0.333 8
0.553 1
3.821 7
6.961 7

SUSY and SI failure model $W_5$.

3.1. New Superpotential for Novel Symmetry in Real Space

Here, we suggest a new model on superpotential as

$$W_6=x\pm \lambda \frac{\left|x\right|}{x}$$

(33)

whose nature is reflected in Figure 6 as

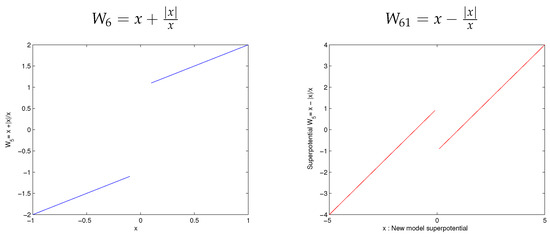
Figure 6. Superpotential: no SUSY and no SI valid.

Further, the Hamiltonians generated from the above new model are

$$H^{\pm }=p^2+x^2+{\lambda }^2\pm 2\lambda \left|x\right|\pm 1$$

(34)

The corresponding SUSY potentials satisfy the relation

$$V_{+}(x,\pm \lambda )=V_{-}(x,\mp \lambda )+2$$

(35)

Hence, using the shape invariance condition, one can easily verify that

$$E_n^{(-)}\ne 2n$$

(36)

Further, the two potentials are different in nature (one is a single well and the other corresponds to a double well potential see Figure 7).

Figure 7. Superpotential: no SUSY and no SI being valid.

Further, both the cases have different natures of the phase-portrait; see Figure 8.

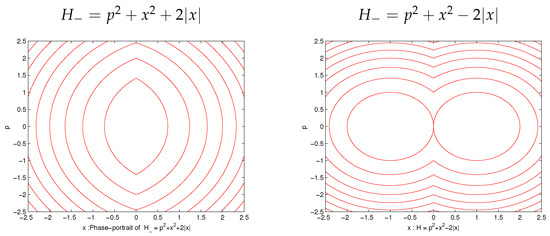
Figure 8. Phase-portrait nature.

In other words, the shape invariance method fails to address the correct energy levels of

$$H^{(-)}=p^2+x^2\pm 2\left|x\right|$$

(37)

and are reflected in Table 2.

Table 2. Novel symmetry: $H^{(-)}$.

${\mathit{H}}^{(-)}={\mathit{p}}^2+{\mathit{x}}^2+2\left|\mathit{x}\right|$	${\mathit{H}}^{(-)}={\mathit{p}}^2+{\mathit{x}}^2-2\left|\mathit{x}\right|$
2.001 1	−0.381 5
5.074 3	0.468 4
7.659 0	1.999 5
10.207 6	3.394 9

Novel symmetry Hamiltonians: superpotential model $W_6$.

Similarly, we consider another superpotential

$$W_7=x+e^{-\left|x\right|/x}$$

(38)

In this case, the nature of the superpotential is reflected in Figure 9 as

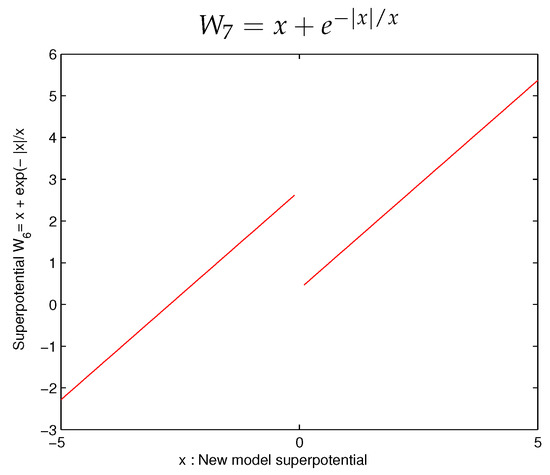
Figure 9. Superpotential: no SUSY and no SI.

Here, we present the corresponding SUSY Hamiltonians as

$$H^{\pm }=p^2+x^2+e^{-2\left|x\right|/x}+2x{e}^{-\left|x\right|/x}\pm 1$$

(39)

In this case, we find the shape-invariance approach is also not valid

$$E_n^{(-)}\ne 2n$$

(40)

Below, we present few energy levels of $H^{(-)}$ corresponding to $W_7\left(x\right)$, as given in Table 3.

Table 3. Energy levels $E_n^{(-)}$.

${\mathit{E}}_{\mathit{n}}^{(-)}$
−0.001 5
1.721 9
2.103 4
4.012 6

Novel symmetry model $W_7$.

3.2. Mathematical Proof of Novel Symmetry

Here, we present the proof of the relation $E_n^{(+)}-E_n^{(-)}=2\lambda$ as follows. Let $E_n$ be the energy of Hamiltonian

$$H=p^2+W^2$$

(41)

and

$$\frac{dW}{dx}=\lambda$$

(42)

then, the energy of

$$H^{(+)}=p^2+W^2+\frac{dW}{dx}$$

(43)

becomes

$$E_n^{(+)}=E_n+\lambda$$

(44)

Similarly,

$$H^{(-)}=p^2+W^2-\frac{dW}{dx}$$

(45)

becomes

$$E_n^{(-)}=E_n-\lambda$$

(46)

Similarly,

$$E_n^{(+)}=E_n+\lambda$$

(47)

Hence, it is easy to equate and to see that

$$E_n^{(+)}-E_n^{(-)}=2\lambda$$

(48)

For $\lambda =1$, we have

$$E_n^{(+)}-E_n^{(-)}=2$$

(49)

4. New Superpotential in Complex Space: $\mathit{P}\mathit{T}$-Symmetry

Here, we extend the above formalism to complex Hamiltonians satisfying the condition

$$[H,PT]=0$$

(50)

In complex, the following conditions must be satisfied

$$[W,PT]=0$$

(51)

and

$$H^{\pm }=p^2-W^2\mp i\frac{dW}{dx}$$

(52)

Now, we define the superpotentials as

4.1. First Model in Complex Space Having $PT$-Symmetry Condition

$$W_8=\lambda ix-i\beta \frac{\left|x\right|}{x}$$

(53)

The corresponding SUSY Hamiltonians [16] become

$$H^{\pm }=p^2+{\lambda }^2{x}^2+{\beta }^2-2\lambda \beta \left|x\right|\pm \lambda$$

(54)

For $\lambda =\beta =1$, it is the same as discussed above in the real case.

4.2. Second Exponential Model in Complex Space Having a $PT$-Symmetry Condition

Let us consider the second model’s superpotential as

$$W_9=\lambda ix-i\frac{\left|x\right|}{x}{e}^{-i\beta \left|x\right|/x}$$

(55)

The corresponding Hamiltonians are

$$H^{\pm }=p^2+{\lambda }^2{x}^2+e^{-2i\beta \left|x\right|/x}-2\lambda \left|x\right|e^{-i\beta \left|x\right|/x}\pm \lambda$$

(56)

Below, we compute the energy levels for $H^{(-)}$, considering $\lambda =1 and \beta =5$, as given in Table 4:

Table 4. Exponential model, few energy levels.

${\mathit{H}}_{\mathit{\lambda }=1;\mathit{\beta }=5}^{(-)}$
0.072 5
2.173 3
4.826 1
7.488 2

Exponential model $H^{(-)};\lambda =1;\beta =5$.

Below, we present its unbroken spectral in PT-symmetry, as in Figure 10.

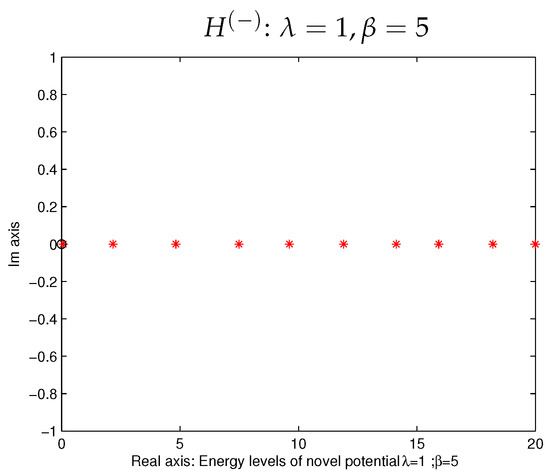
Figure 10. Unbroken spectra in PT-symmetry.

4.3. Third Fractional Model in Complex Space Having $PT$-Symmetry Condition

Similarly, we construct a new fractional model of superpotential satisfying the PT-invariant condition as

$$W_{10}=ix-\frac{i\left(\right|x|/x)}{1+i\left|x\right|/x)}$$

(57)

The corresponding Hamiltonians are

$$H^{\pm }=p^2+x^2+\frac{1}{{(1+i|x|/x)}^2}-2\frac{\left|x\right|}{(1+i|x|/x)}\pm 1$$

(58)

In Table 5, we reflect on the first four energy levels and the spectral nature in Figure 5.

Table 5. Few energy levels of fractional model: $H^{(-)}$.

${\mathit{E}}_{\mathit{n}}^{(-)}$
−0.490 0
1.087 9
2.683 4
4.562 1

Fractional model $H^{(-)}$.

Below, we present its unbroken spectral nature, as in Figure 11.

Figure 11. Unbroken spectra.

5. Method of Calculation

Here, we solve the eigenvalue relation [42,44]

$$H|\mathsf{\Phi }>=E|\mathsf{\Phi }>$$

(59)

where

$$|\mathsf{\Phi }>=\sum A_m|m>$$

(60)

in which $|m>$ satisfies the eigenvalue relation

$$[p^2+x^2]|m>=(2m+1)|m>$$

(61)

with $m=0,1,2,3,4,\dots \dots$

6. Conclusions

In conclusion, the new symmetry operator has no relation with the shape invariance and the traditional supersymmetric energy conditions: $E_n^{(+)}=E_n^{(-)}$ with $E_{-}^{(-)}=0$ in either real or complex space. On the other hand, a new relation has evolved as $E_n^{(+)}-E_n^{(-)}=2\lambda$. This relation remains valid in real and complex space. It should be borne in mind that $R\left(\beta \right)$ in $V_{+}(\lambda ,x)=V_{-}(\beta ,x)+R\left(\beta \right)$ is independent of x. In spite of this, the SUSYEC or SI conditions will no longer be valid. Similarly, many new models can be generated or fabricated using this “novel symmetry”. Interested readers can find many such similar cases as follows:

$$W=x\pm tanh\left(\right|x|/x)$$

(62)

$$W=x\pm sinh\left(\right|x|/x)$$

(63)

and

$$W=tanh\left(x\right)\pm \lambda \left|x\right|/x$$

(64)

Further, the tabulated results presented above are the convergent results from the matrix diagonalization approach used in the MATLAB codes. At this point, the author would like to say that if one selects a superpotential as

$$W=x\frac{<\left|x\right|>}{\sqrt{(<x^2>)}}-\frac{\left|x\right|}{x}$$

(65)

then the new symmetry will be lost, i.e., $E_n^{(+)}-E_n^{(-)}\ne 2$.