Numerical Simulations of the Fractional Systems of Volterra Integral Equations within the Chebyshev Pseudo-Spectral Method

Abstract

In this article, we find the solutions to fractional Volterra-type integral equation nonlinear systems through a Chebyshev pseudo-spectral method (CPM). The fractional derivative is described in the Caputo manner. The suggested method’s accuracy and reliability are confirmed by the results. The proposed method is implemented for solving various nonlinear systems; the results we obtained were compared with the exact solution and other method solutions. The graphical representation and tables show that our method’s error quickly converges as compared to other methods. By comparing the proposed method’s solution with the actual solution and other methods, we can confirm that CPM is more accurate and closer to the exact solution. We display the pointwise solution in the tables, which verifies the proposed method’s accuracy at each point and aids in a better comprehension of the suggested approach. Moreover, the results of using the suggested method at different fractional orders are examined, showing that when a value moves from a fractional order to an integer order, the result is closer to the precise solution. Furthermore, the proposed technique for handling fractional-order linear and non-linear physical problems in science and engineering is straightforward to implement.

1. Introduction

Fractional-order calculus has been around for as long as integer-order calculus. It can be seen in a letter by Leibniz to L’Hopital on 30 September 1695. To this day, the question about $\frac{D^n\psi }{D{\psi }^n}$, the Leibniz notation of the nth derivative of the linear function $\xi \left(\psi \right)=\psi ,$ appears in a letter from L’Hopital. L’Hopital strangely inquired, “What will be the result if $n=\frac{1}{2}?$”, to which Leibniz responded, “An seeming paradox, one day for which a useful result will be drawn”. The integer-order calculus is generalized to the fractional order calculus. Fractional calculus applications include anomalous transports in disordered systems [1], the time-fractional Belousov–Zhabotinsky reaction [2], dielectric relaxation phenomena in polymeric materials [3], long-time memory in a financial time series [4], and transport dynamics in a system governed by anomalous diffusion [5].

Many somatic problems in real life may be demonstrated using mathematical formulations, which convert physical occurrences into sophisticated mathematical formulae. Differential equations are used to simulate various physical phenomena, such as population growth or decay models [6,7,8]. However, some physical phenomena cannot be adequately represented using integer-order differential equations. As a result, the researchers created a new branch of mathematics known as fractional differential equations (FDEs). In comparison to integer-order differential equations, FDEs are employed to accurately simulate a variety of physical phenomena. In recent years, FDEs have gained prominence in the modeling of real-world physical problems, such as colored noise [9], economics [10], earthquake oscillation [11], and bioengineering [12]. The other applications are control theory [13], rheology [14], signal processing [15], damping method [16], polymers [17], and so on [18,19,20,21,22]. Mathematicians are interested in the solutions to these FDEs in order to obtain the objective solution of mathematical models. Analytical and numerical solutions are the most common forms of solutions. However, the analytical solutions we obtain are complex and final for all real-world problems. As a result, mathematicians solve these issues with approximate solutions [23,24]. Symmetry analysis is lovely to study when studying differential equations, more specifically when studying equations from the mathematics of finance. The secret to nature is symmetry, but most observations in the natural world lack it. A powerful technique for disguising symmetry is the occurrence of spontaneous symmetry-breaking. Finite and infinitesimal are two types of symmetries. Finite symmetries may be continuous or discrete. While parity and temporal reversal are discrete natural symmetries, space undergoes continuous modifications. Mathematicians have always been fascinated by patterns. Classifications of spatial and planar patterns made significant achievements in the eighteenth century.

Every branch of engineering and science uses fractional integral- and integro-differential equations. When a physical phenomenon is described using differential equations, the result is a differential equation, integro-differential equation, or integral equation. With these types of equations, some applications are glass-forming processes [25], nanohydrodynamics [26], drop-wise condensation [27], or wind ripples in the desert [28]. In most circumstances, there is no analytical solution to integral- or integro-differential equations. It is difficult to find, even if it exists in some circumstances. For approximating the solutions of integral- and integro-differential equations, various numerical approaches have been developed. To solve these challenges, a variety of approaches have been used, such as the nonstandard difference method (NDM) [29], Adams–Bashforth–Moulton method (ABMM) [30], homotopy analysis method (HAM) [31], generalized differential transform method (GDTM) [32], mixed interpolation collocation method (MICM) [33], collocation method (CM) [34], iterated Galerkin method (IGM) [35], spline collocation method (SCM) [36], Legendre wavelet method (LWM) [37], Newton polynomial (NP) [38], predictor–corrector (PC) [39], and Galerkin method (GM) [40].

To calculate the solutions of FIDEs in this study, we applied a new technique called the Chebyshev pseudo-spectral method (CPM). Our method reduces the proposed models to linear/non-linear systems of algebraic equations, considerably simplifying the problems; an appropriate method is then utilized to solve the resulting system. When compared to other methods, the suggested method has higher accuracy and better convergence. The numerical results show that the suggested technique is effective and reliable. In addition, CPM can be used in a variety of other physical models.

2. Definitions and Preliminaries Concept

This unit introduces the fundamental concepts related to fractional calculus.

Definition 1.

A real function $\xi \left(\psi \right),\psi >0,$ will be in the space ${\mathbb{C}}_{\nu },\nu \in \mathbb{R}$ if a real number exists $p>\nu$, with $\xi \left(\psi \right)={\psi }^p{\xi }_1\left(\psi \right)$ where ${\xi }_1\left(\psi \right)\in [0,\infty ),$ and will be in the space ${\mathbb{C}}_{\nu }^m$ if and only if ${\xi }^{\left(m\right)}\in {\mathbb{C}}_{\nu },$$m\in \mathbb{N}$.

Definition 2.

The fractional Caputo derivative of order α is stated as [41,42]

$$D^{\alpha }\xi \left(\psi \right)=\frac{1}{\mathsf{\Gamma }(n-\alpha )}{\int }_0^{\psi }{(\psi -t)}^{n-\alpha -1}{\xi }^{\left(n\right)}\left(t\right)dt,$$

(1)

for $n-1<\alpha \le n$, $n\in \mathbb{N}$, $\psi >0$, $\xi \in {\mathbb{C}}_{-1}^m$.

Definition 3.

Jin-Hunan’s fractional derivatives are referred to as [42]

$$\frac{D^{\alpha }\xi \left(\psi \right)}{D{\psi }^{\alpha }}=\mathsf{\Gamma }(1+\alpha )\underset{\mathsf{\Delta }\psi ={\psi }_1-{\psi }_2\to L}{lim}\frac{\xi \left({\psi }_1\right)-\xi \left({\psi }_2\right)}{{({\psi }_1-{\psi }_2)}^{\alpha }},$$

(2)

where $\mathsf{\Delta }\psi$ does not approach zero.

Definition 4.

Xiao-Jun defines fractional order derivatives as [42]

$$D_{\psi }^{\alpha }\xi \left({\psi }_0\right)={\xi }^{\alpha }\left({\psi }_0\right)=\frac{d^{\alpha }\xi \left(\psi \right)}{d{\psi }^{\alpha }}{\mid }_{\psi ={\psi }_0}=\underset{\psi \to {\psi }_0}{lim}\frac{{\mathsf{\Delta }}^{\alpha }(\xi \left(\psi \right)-\xi \left({\psi }_0\right))}{{(\psi -{\psi }_0)}^{\alpha }},$$

(3)

where

$${\mathsf{\Delta }}^{\alpha }(\xi \left(\psi \right)-\xi \left({\psi }_0\right))\cong \mathsf{\Gamma }(1+\alpha )\mathsf{\Delta }(\xi \left(\psi \right)-\xi \left({\psi }_0\right))$$

Definition 5.

The integral operator in the Riemann–Liouville sense is stated as [41,42]

$$I^{\alpha }\xi \left(\psi \right)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\psi }{(\psi -t)}^{\alpha -1}\xi \left(t\right)dt,$$

(4)

with the following properties

$$D^{\alpha }{I}^{\alpha }\xi \left(\psi \right)=\xi \left(\psi \right),$$

$$I^{\alpha }{D}^{\alpha }\xi \left(\psi \right)=\xi \left(\psi \right)-\sum _{k=0}^{n-1}\frac{{\xi }^{\left(k\right)}\left(0^{+}\right)}{k!}{\psi }^k,\psi \ge 0n-1<\alpha <n.$$

3. Chebyshev Pseudo-Spectral Method (CPM)

Chebyshev polynomials are defined as the interval $[-1,1]$ and are demonstrated using recurrence equations [43,44].

$${\mathcal{T}}_{n+1}\left(t\right)=2u{\mathcal{T}}_n\left(\psi \right)-{\mathcal{T}}_{n-1}\left(\psi \right),n=1,2,...$$

(5)

where

$${\mathcal{T}}_0\left(\psi \right)=1,{\mathcal{T}}_1\left(\psi \right)=\psi .$$

In order to apply the Chebyshev polynomials in the interval $[0,1]$, Chebyshev’s shifted polynomials are described as ${\hat{\mathcal{T}}}_n\left(\psi \right)$, which explains (in the same way) the Chebyshev polynomials ${\mathcal{T}}_n\left(\psi \right)$ by relation

$${\hat{\mathcal{T}}}_n\left(\psi \right)={\mathcal{T}}_n(2\psi -1).$$

(6)

The recurrence formula is as follows

$${\hat{\mathcal{T}}}_{n+1}\left(\psi \right)=2(2\psi -1)\widehat{{\mathcal{T}}_n}\left(\psi \right)-{\hat{\mathcal{T}}}_{n-1}\left(\psi \right),n=1,2,...$$

(7)

where

$${\hat{\mathcal{T}}}_0\left(\psi \right)=1,{\hat{\mathcal{T}}}_1\left(\psi \right)=2\psi -1.$$

In terms of Chebyshev’s shifted polynomials, a function $\xi \left(\psi \right)\in L_2[0,1]$ is described as

$$\xi \left(\psi \right)=\sum _{n=1}^{\infty }{c}_n{\hat{\mathcal{T}}}_n\left(\psi \right).$$

(8)

The first (m + 1) terms of Chebyshev’s shifted polynomials are considered as

$${\xi }_m\left(\psi \right)=\sum _{n=0}^m{c}_n{\hat{\mathcal{T}}}_n\left(\psi \right),$$

(9)

$${}_0{D}_x^{-\alpha }\left(\sum _{n=0}^m{c}_n{\hat{\mathcal{T}}}_n\left(\psi \right)\right)+\sum _{n=0}^m{c}_n{\hat{\mathcal{T}}}_n\left(\psi \right)=g(\psi ,\xi ).$$

(10)

We have the ability to find a system of equations as

$${}_0{D}_x^{-\alpha }\left(\sum _{n=0}^m{c}_n{\hat{\mathcal{T}}}_n\left({\psi }_i\right)\right)+\sum _{n=0}^m{c}_n{\hat{\mathcal{T}}}_n\left({\psi }_i\right)=g({\psi }_i,\xi ).$$

(11)

Whereas

$${\psi }_i=\frac{i-0.5}{2^{k-1}M}.$$

We used maple software to solve the resultant system, which provides a CPM solution.

4. Applications

Example 1.

Consider the following fractional integral equation nonlinear system

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {}_0{D}_{\psi }^{-\alpha }((1-{\psi }^2+t)+(\xi \left(t\right)+{\zeta }^3\left(t\right))dt=\frac{-1}{12}{\psi }^6-\frac{2}{15}{\psi }^5+\frac{1}{4}{\psi }^4+\frac{1}{3}{\psi }^3,\hfill \\ \hfill & {}_0{D}_{\psi }^{-\alpha }((5+\psi -t)({\xi }^3\left(t\right)-\zeta \left(t\right))dt=\frac{1}{56}{\psi }^8+\frac{5}{7}{\psi }^7-\frac{1}{6}{\psi }^3-\frac{5}{2}{\psi }^2,\hfill \\ \hfill & 0<\alpha \le 1\hfill \end{array}\right.\end{array}$$

(12)

with the exact solution $\xi \left(\psi \right)={\psi }^2,$$\zeta \left(\psi \right)=\psi ,$

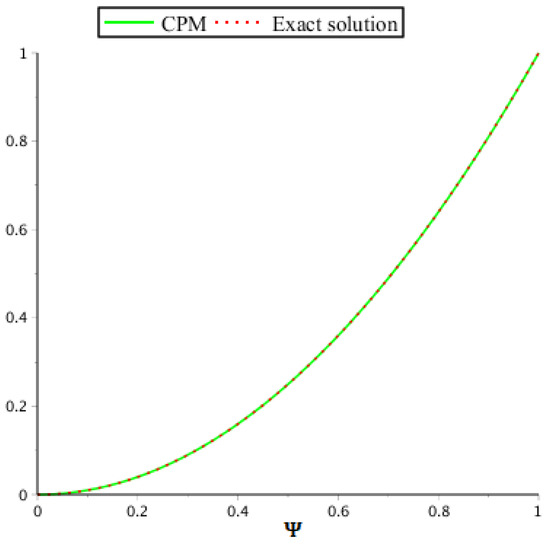
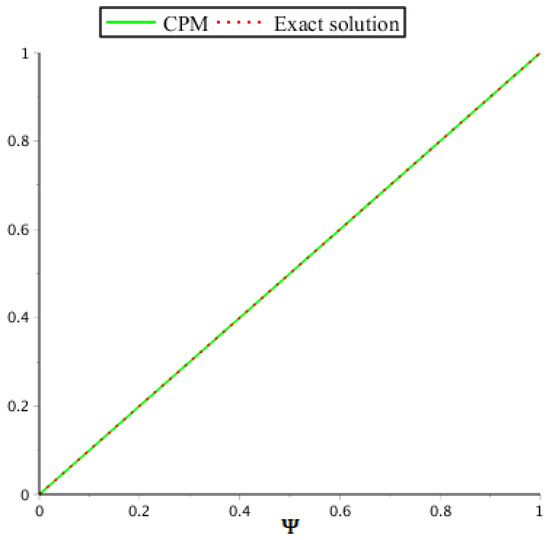
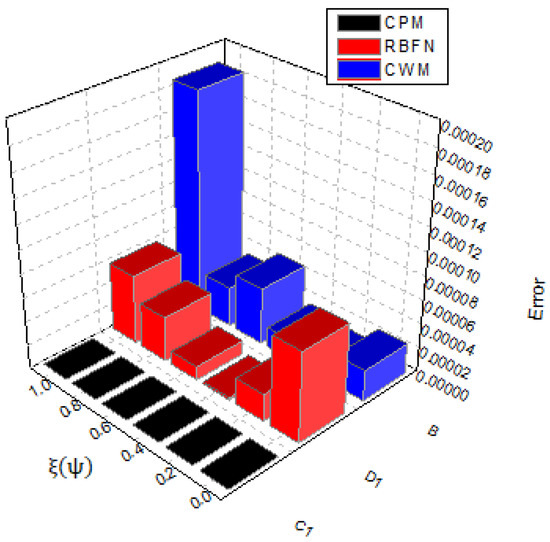
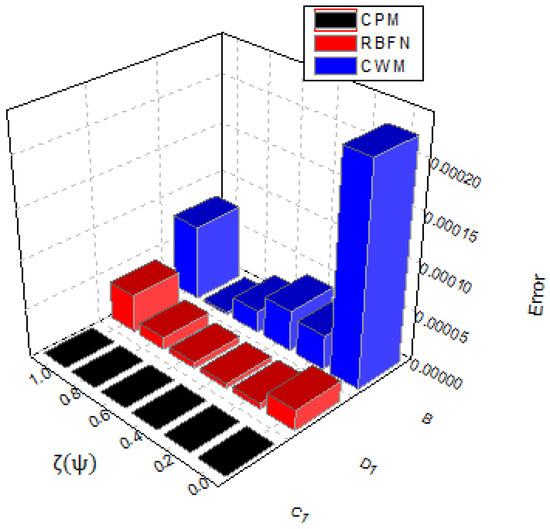
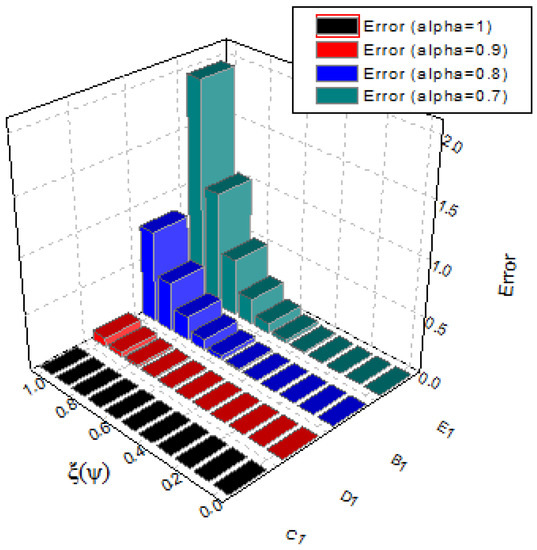
In Table 1, we present the accurate and numerical results obtained by implementing the suggested approach and the results obtained by CWM while Table 2 shows the absolute error comparison of the suggested approach and results obtained through CWM at $m=6$ and the radial basis function network (RBFN) at $m=8$. Figure 1 and Figure 2 show the behavior of the exact solution (E.S) and approximate solution (our technique) of this case when $\alpha =1,$ while Figure 3 and Figure 4 show the error comparison of CPM, CWM, and RBFN. Moreover, Figure 5 demonstrate the graphical behaviors of the solutions for various fractional orders, showing that as the value of α moves toward the integer-order from the fractional order, the solution converges to the exact.

Table 1. Example 1: exact vs. CPM, CWM solution at m = 6.

$\mathit{\psi }$	E.S $\mathit{\xi }\left(\mathit{\psi }\right)$	E.S $\mathit{\zeta }\left(\mathit{\psi }\right)$	CPM $\mathit{\xi }\left(\mathit{\psi }\right)$	CPM $\mathit{\zeta }\left(\mathit{\psi }\right)$	CWM $\mathit{\xi }\left(\mathit{\psi }\right)$	CWM $\mathit{\zeta }\left(\mathit{\psi }\right)$
0	0.0000000	0.0000000	0.0000000000	0.0000000000	−0.000026070	0.000222296
0.2	0.0400000	0.2000000	0.0399999999	0.2000000000	0.039987035	0.199964603
0.4	0.1600000	0.4000000	0.1599999999	0.4000000000	0.159982615	0.400041558
0.6	0.3600000	0.6000000	0.3599999999	0.6000000000	0.360047897	0.599977336
0.8	0.6400000	0.8000000	0.6400000000	0.7999999999	0.639966461	0.799997734
1.0	1.0000000	1.0000000	1.0000000000	0.9999999999	1.000185856	0.999922349

Table 2. CPM versus the CWM error comparison at m = 6 of problem 1.

$\mathit{\psi }$	$\mathit{Error}\left({\mathit{\xi }}_{\mathit{CPM}}\right)$	$\mathit{Error}\left({\mathit{\zeta }}_{\mathit{CPM}}\right)$	$\mathit{Error}\left({\mathit{\xi }}_{\mathit{CWM}}\right)$	$\mathit{Error}\left({\mathit{\zeta }}_{\mathit{CWM}}\right)$	$\mathit{Error}\left({\mathit{\xi }}_{\mathit{RBFN}}\right)$	$\mathit{Error}\left({\mathit{\zeta }}_{\mathit{RBFN}}\right)$
0	0.00000$\times {10}^{+00}$	0.00000$\times {10}^{+00}$	0.00002607	0.0002222	7.54$\times {10}^{-05}$	2.09$\times {10}^{-05}$
0.2	1.60000$\times {10}^{-15}$	1.00000$\times {10}^{-15}$	0.00001296	0.0000353	2.28$\times {10}^{-05}$	5.70$\times {10}^{-06}$
0.4	3.00000$\times {10}^{-15}$	1.00000$\times {10}^{-15}$	0.00001738	0.0000415	1.98$\times {10}^{-06}$	4.79$\times {10}^{-06}$
0.6	3.00000$\times {10}^{-15}$	0.00000$\times {10}^{+00}$	0.00004789	0.0000226	1.16$\times {10}^{-05}$	6.33$\times {10}^{-06}$
0.8	4.00000$\times {10}^{-15}$	2.00000$\times {10}^{-15}$	0.00003353	0.0000022	3.80$\times {10}^{-05}$	1.29$\times {10}^{-05}$
1.0	3.00000$\times {10}^{-14}$	1.30000$\times {10}^{-14}$	0.00018585	0.0000776	5.82$\times {10}^{-05}$	3.89$\times {10}^{-05}$

Figure 1. Example 1 of the solution graph, CPM solution and exact solution for $\xi \left(\psi \right)$.

Figure 2. Example 1 of the solution graph, CPM solution and exact solution for $\zeta \left(\psi \right)$.

Figure 3. Our method, CWM, and RBFN error graph for Example 1.

Figure 4. Our method, CWM, and RBFN error graph for Example 1.

Figure 5. At different fractional orders, the absolute error graph of Example 1.

Example 2.

Consider the following fractional integral equation nonlinear system

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {}_0{D}_{\psi }^{-\alpha }({\xi }^2\left(t\right)-{\zeta }^2\left(t\right))dt=\xi \left(\psi \right)-sin\left(\psi \right)+\psi ,\hfill \\ \hfill & {}_0{D}_{\psi }^{-\alpha }\left(\xi \left(t\right)\zeta \left(t\right)\right)dt=\zeta \left(\psi \right)+\frac{1}{2}{sin}^2\psi +cos\left(\psi \right),\hfill \\ \hfill & 0<\alpha \le 1\hfill \end{array}\right.\end{array}$$

(13)

with the exact solution $\xi \left(\psi \right)=sin\left(\psi \right),$$\zeta \left(\psi \right)=cos\left(\psi \right),$

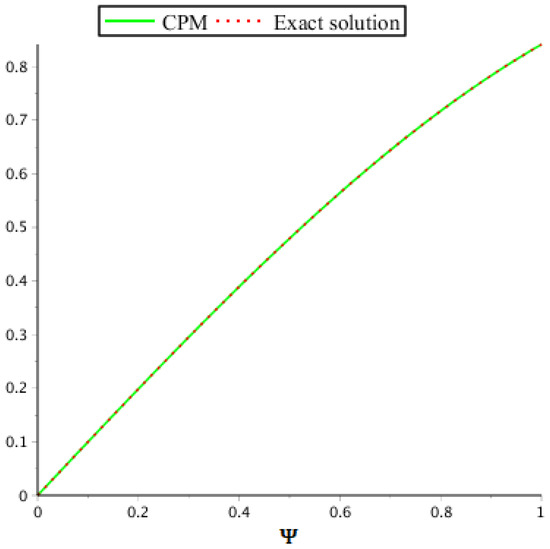
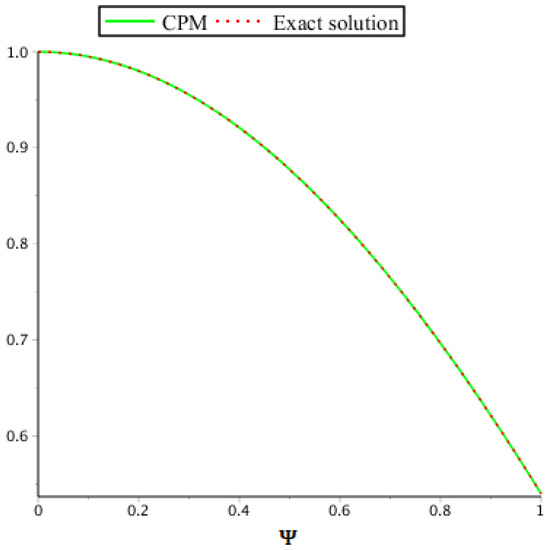
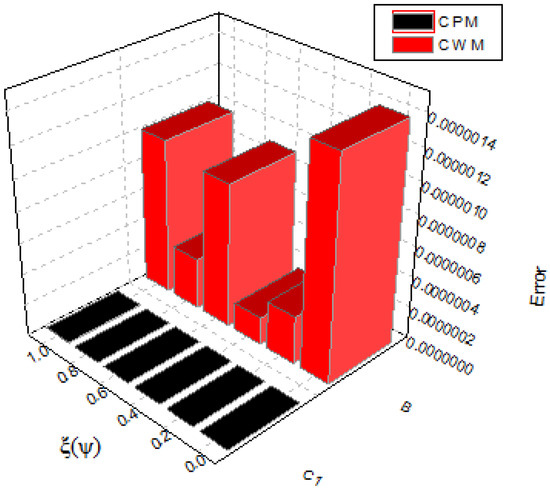
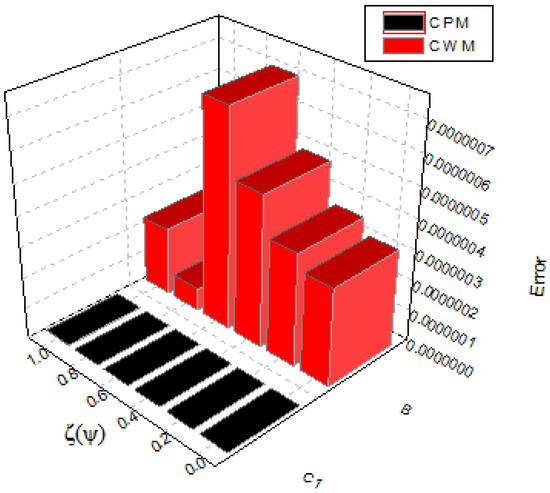
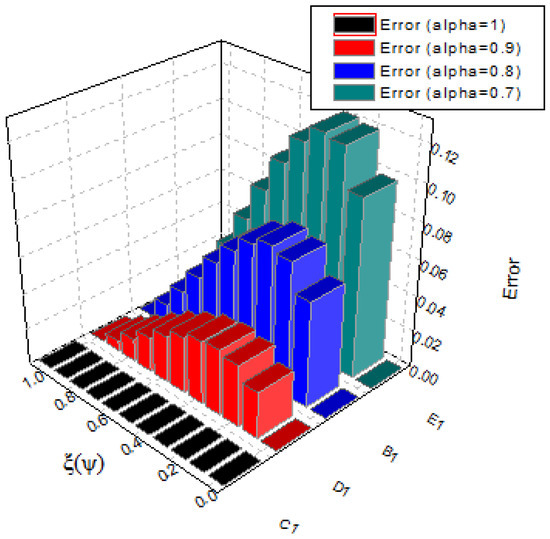
The accurate and numerical results obtained by implementing the suggested approach and results obtained by CWM for $m=6$ are shown in Table 3. In Table 4, the errors implemented by the current approach are compared to those acquired by CWM. In Figure 6 and Figure 7, we compare the accurate results with our method’s results, showing that they are very near to each other. Moreover, Figure 8 and Figure 9 illustrate the CPM and CWM error comparisons, showing that CPM is in good agreement with the exact results, whereas Figure 10 and Figure 11 show graphical representations of the solutions for various fractional orders.

Table 3. Problem 2: exact vs. CPM; CWM solution at m = 6.

$\mathit{\psi }$	E.S $\mathit{\xi }\left(\mathit{\psi }\right)$	E.S $\mathit{\zeta }\left(\mathit{\psi }\right)$	CPM $\mathit{\xi }\left(\mathit{\psi }\right)$	CPM $\mathit{\zeta }\left(\mathit{\psi }\right)$	CWM $\mathit{\xi }\left(\mathit{\psi }\right)$	CWM $\mathit{\zeta }\left(\mathit{\psi }\right)$
0	0.00000000000	1.0000000000	0.00000000000	0.99999999999	−0.000001403	1.000000319
0.2	0.19866933079	0.9800665778	0.19866933072	0.98006657786	0.1986696393	0.9800669460
0.4	0.38941834230	0.9210609940	0.38941834202	0.92106099406	0.3894165787	0.9210604974
0.6	0.56464247339	0.8253356149	0.56464247340	0.82533561482	0.5646433964	0.8253349025
0.8	0.71735609089	0.6967067093	0.71735609079	0.69670670928	0.7173557641	0.6967067839
1.0	0.84147098480	0.5403023058	0.84147098076	0.54030230757	0.8414719842	0.5403020838

Table 4. CPM versus the CWM error comparison at m = 6 of problem 2.

s	$\mathit{Error}\left({\mathit{\xi }}_{\mathit{CPM}}\right)$	$\mathit{Error}\left({\mathit{\zeta }}_{\mathit{CPM}}\right)$	$\mathit{Error}\left({\mathit{\xi }}_{\mathit{CWM}}\right)$	$\mathit{Error}\left({\mathit{\zeta }}_{\mathit{CWM}}\right)$
0	0.0000000000$\times {10}^{+00}$	0.0000000000$\times {10}^{+00}$	0.0000014037	0.000000319
0.2	6.7443073256$\times {10}^{-11}$	1.9129717529$\times {10}^{-11}$	0.0000003085	0.0000003682
0.4	2.8634095988$\times {10}^{-10}$	6.3350567575$\times {10}^{-11}$	0.0000001763	0.0000004966
0.6	1.4540273872$\times {10}^{-11}$	8.3812136477$\times {10}^{-11}$	0.000000923	0.0000007124
0.8	1.0840388114$\times {10}^{-10}$	6.5764647225$\times {10}^{-11}$	0.0000003268	0.0000000746
1.0	4.0385798791$\times {10}^{-9}$	1.7087357128$\times {10}^{-9}$	0.0000009994	0.0000002221

Figure 6. Example 2: CPM solution and exact solution for $\xi \left(\psi \right)$.

Figure 7. Problem 2: CPM solution and exact solution for $\zeta \left(\psi \right)$.

Figure 8. Our method and the CWM error graph for Example 2.

Figure 9. Our method and the CWM error graph for Example 2.

Figure 10. At different fractional orders, the absolute error graph of Example 2.

Figure 11. At different fractional orders, the absolute error graph of Example 2.

Example 3.

Consider the following fractional integral equation nonlinear system:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {}_0{D}_{\psi }^{-\alpha }((5+\psi -t)\xi \left(t\right)+(\frac{{\psi }^2}{2}+t)\zeta \left(t\right)\varphi \left(t\right))=\frac{1}{48}{\psi }^6+\frac{19}{270}{\psi }^5+\frac{19}{72}{\psi }^4+\frac{7}{6}{\psi }^3+{\psi }^2+5\psi ,\hfill \\ \hfill & {}_0{D}_{\psi }^{-\alpha }((\frac{{\psi }^2}{2}+t)\xi \left(t\right)+(3+\psi -t)\zeta \left(t\right)+\frac{1}{4}({\psi }^2-t^2)\varphi \left(t\right))=\frac{1}{24}{\psi }^5+\frac{35}{288}{\psi }^4+\frac{17}{18}{\psi }^3+\frac{5}{4}{\psi }^2\frac{9}{2}\psi ,\hfill \\ \hfill & {}_0{D}_{\psi }^{-\alpha }(t\xi \left(t\right)\zeta \left(t\right)-\psi t{\zeta }^2\left(t\right)-5\varphi \left(t\right))=\frac{1}{72}{x}^6-\frac{1}{4}{\psi }^5-\frac{1}{54}{\psi }^7+\frac{17}{96}{\psi }^4-\frac{9}{8}{\psi }^3-\frac{1}{2}{\psi }^2-\frac{10}{3}\psi ,\hfill \\ \hfill & 0<\alpha \le 1\hfill \end{array}\right.\end{array}$$

(14)

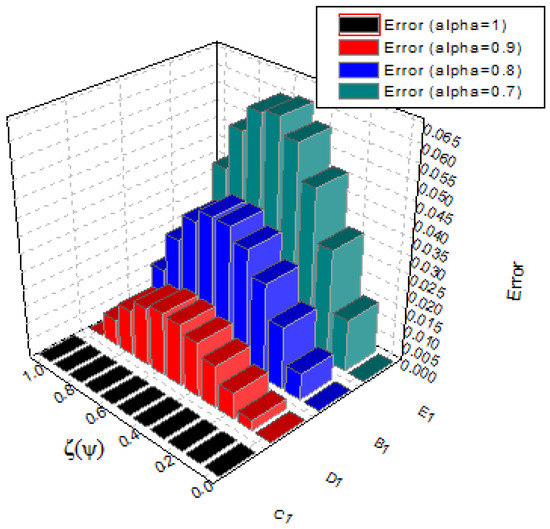
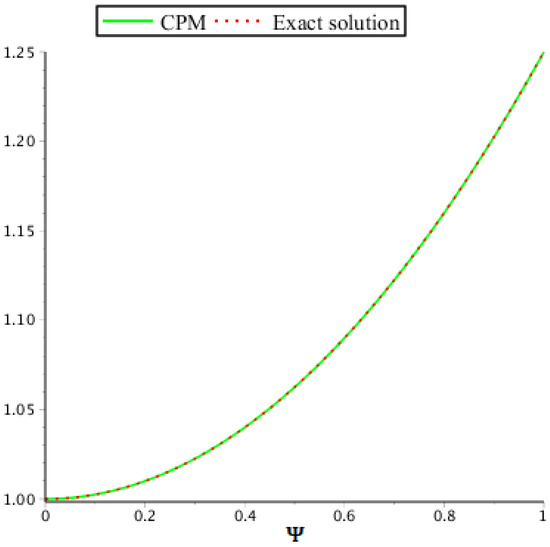
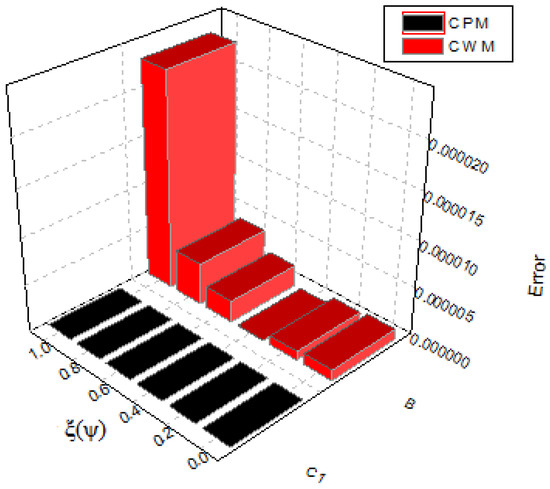
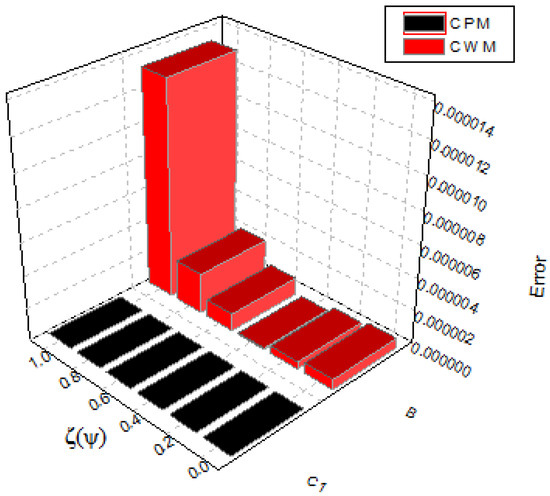
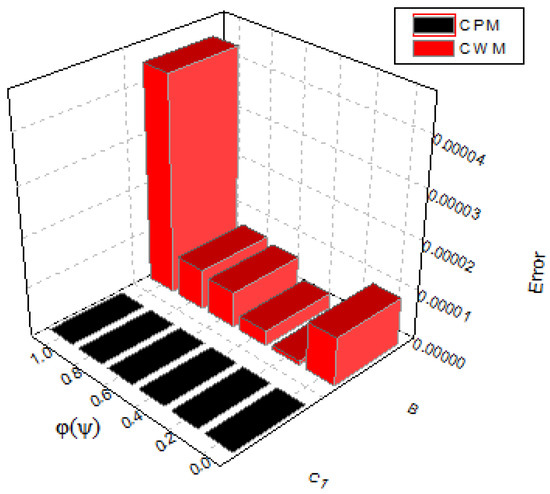
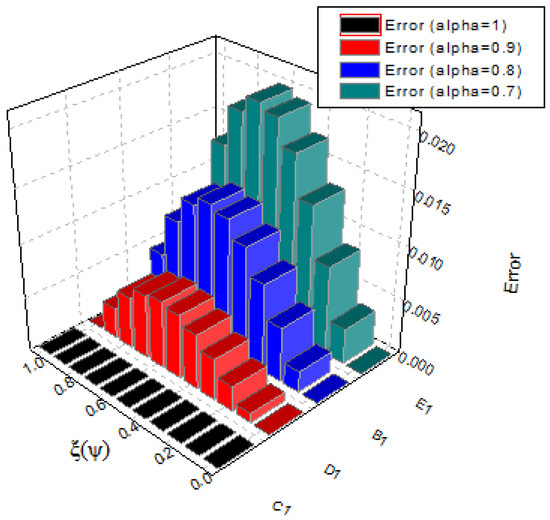
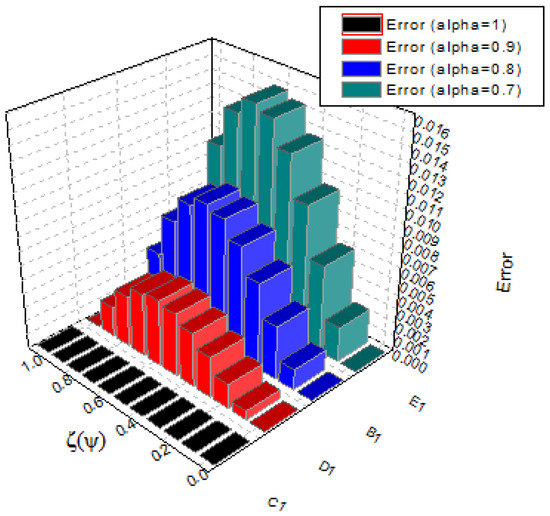
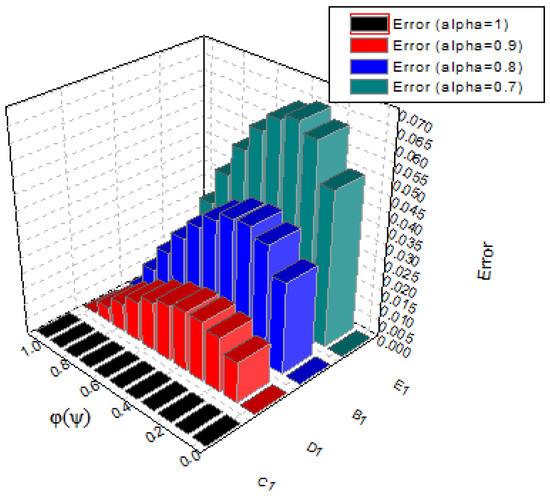
with the exact solution $\xi \left(\psi \right)=1+\frac{1}{4}{\psi }^2,$$\zeta \left(\psi \right)=\frac{3}{2}+\frac{1}{2}{\psi }^2,$ $\varphi \left(\psi \right)=\frac{2}{3}+\frac{1}{2}\psi$ We use the technique described in Section 2 for $\alpha =1$ with $m=6$ to solve this problem. Table 5 shows the exact and CPM estimated solutions. Table 6 compares the absolute error of our technique to that of CWM. The results of the proposed technique are in good agreement with the exact results, as shown in Figure 12 and Figure 13. The error comparison between CPM and CWM is provided in Figure 14, Figure 15 and Figure 16 to demonstrate the usefulness of CPM. In addition, in Figure 17, Figure 18 and Figure 19 we can see the estimated solutions for the various fractional orders.

Table 5. Problem 3: exact vs. CPM solution at m = 6.

$\mathit{\psi }$	E.S $\mathit{\xi }\left(\mathit{\psi }\right)$	E.S $\mathit{\zeta }\left(\mathit{\psi }\right)$	E.S $\mathit{\varphi }\left(\mathit{\psi }\right)$	CPM $\mathit{\xi }\left(\mathit{\psi }\right)$	CPM $\mathit{\zeta }\left(\mathit{\psi }\right)$	CPM $\mathit{\varphi }\left(\mathit{\psi }\right)$
0	1.000000000000	1.50000000	0.6666666666	1.000000000	1.50000000	0.6666666666
0.1	1.002500000000	1.50333333	0.7166666666	1.002500000	1.50333333	0.7166666666
0.2	1.010000000000	1.51333333	0.7666666666	1.009999999	1.51333333	0.7666666666
0.3	1.022500000000	1.53000000	0.8166666666	1.022500000	1.53000000	0.8166666666
0.4	1.040000000000	1.55333333	0.8666666666	1.040000000	1.55333333	0.8666666666
0.5	1.062500000000	1.58333333	0.9166666666	1.062499999	1.58333333	0.9166666666
0.6	1.090000000000	1.62000000	0.9666666666	1.090000000	1.62000000	0.9666666666
0.7	1.122500000000	1.66333333	1.0166666666	1.122500000	1.66333333	1.0166666666
0.8	1.160000000000	1.71333333	0.0666666666	1.160000000	1.71333333	1.0666666666
0.9	1.202500000000	1.77000000	1.1166666666	1.202499999	1.77000000	1.1166666666
1.0	1.250000000000	1.83333333	1.1666666666	1.249999999	1.83333333	1.1666666666

Table 6. CPM versus the CWM error comparison at m = 6 of problem 3.

$\mathit{\psi }$	$\left({\mathit{\xi }}_{\mathit{CPM}}\right)$	$\left({\mathit{\zeta }}_{\mathit{CPM}}\right)$	$\left({\mathit{\varphi }}_{\mathit{CPM}}\right)$	$\left({\mathit{\xi }}_{\mathit{CWM}}\right)$	$\left({\mathit{\zeta }}_{\mathit{CWM}}\right)$	$\left({\mathit{\varphi }}_{\mathit{CWM}}\right)$
0	0.00000$\times {10}^{+00}$	1.00000$\times {10}^{-14}$	3.100000$\times {10}^{-15}$	0.000001158	0.000000642	0.0000097282
0.2	1.00000$\times {10}^{-14}$	0.00000$\times {10}^{+00}$	4.100000$\times {10}^{-15}$	0.000000959	0.000000460	0.0000008219
0.4	1.00000$\times {10}^{-14}$	1.00000$\times {10}^{-14}$	2.100000$\times {10}^{-15}$	0.000000024	0.000000079	0.0000030059
0.6	0.00000$\times {10}^{+00}$	2.00000$\times {10}^{-14}$	3.100000$\times {10}^{-15}$	0.000002301	0.000001072	0.0000071362
0.8	4.00000$\times {10}^{-14}$	0.00000$\times {10}^{+00}$	2.100000$\times {10}^{-14}$	0.000004458	0.000002475	0.0000081324
1.0	6.40000$\times {10}^{-13}$	5.20000$\times {10}^{-13}$	8.100000$\times {10}^{-14}$	0.000022945	0.00001326	0.0000439496

Figure 12. Example 3: CPM solution and exact solution for $\xi \left(\psi \right)$.

Figure 13. Example 3: CPM solution and exact solution for $\varphi \left(\psi \right)$.

Figure 14. Our method and the CWM error graph for Example 3.

Figure 15. Our method and the CWM error graph for Example 3.

Figure 16. Our method and the CWM error graph for Example 3.

Figure 17. At different fractional orders, the absolute error graph of Example 3.

Figure 18. At different fractional orders, the absolute error graph of problem 3.

Figure 19. At different fractional orders, the absolute error graph of Example 3.

5. Conclusions

In this article, we find the solutions to nonlinear fractional equation systems by implementing the Chebyshev pseudo-spectral method. This type of problem is reduced to the solution of a system of linear and nonlinear algebraic equations using the method proposed. The solutions obtained by utilizing the suggested approach are in good agreement with the actual results and are more accurate than those of other methods. Moreover, it can be confirmed from the figures and tables that our method’s error quickly converges compared to other techniques. Maple was used to perform the calculations in this article.