A Wolf Pack Optimization Algorithm Using RASGS and GBA for Multi-Modal Multi-Objective Problems

Abstract

To address multi-modal multi-objective problems (MMOPs), this paper proposes a wolf pack optimization algorithm using random adaptive-shrinking grid search (RASGS) and raid towards global best archive (GBA) for MMOPs. Firstly, RASGS with logical symmetry was adopted to enhance the exploitation of the algorithm in the local area as well as locate a larger number of Pareto-optimal solutions. Moreover, with the help of an existing sorting method composed of the non-dominated sorting scheme and special crowding distance (SCD), the GBA strategy was employed to obtain and maintain the historical global optimal solution of the population as well as induce the population to explore better solutions. The experimental results indicate that the proposed method has obvious superior performance compared with the existing related algorithms.

1. Introduction

In many practical problems, such as economic, management, military, science and engineering design, it is often difficult to judge the quality of a scheme with one index, and more than one uncoordinated or even contradictory objectives must be considered simultaneously. Multi-modal multi-objective optimization problems are defined as the multi-objective optimization problems (MOPs) with at least two similar feasible regions in the decision space corresponding to the same region of the objective space [1]. In real life, it is critical to find all the Pareto optimal solutions in decision space simultaneously for the purpose of decision-making as well as a new challenge; for instance, it is in [2] that the researchers described a real-world scenario: {Option 1, Option 2, Option 3} and {Option4, Option 5, Option 6} are two Pareto sets (PSs) that correspond to the same Pareto front (PF); however, the former go through a gas station while the latter do not. The gas station is needed for some travelers, while it is unnecessary and a nuisance with some potential safety risks for the others, as detailed in Figure 1.

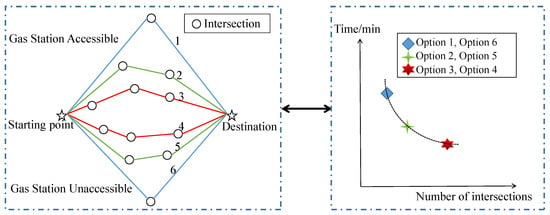
Figure 1. Path planning problem. Option 1, Option 6—1 intersection, 60 min; Option 2, Option 5—2 intersections, 40 min; Option 3, Option 4—3 intersections, 20 min.

People have been active in researching and solving multi-objective problems to meet various emerging needs, such as in [3], where to solve constrained MOPs (CMOPs), Zou et al. proposed a dual population multi-objective optimization evolutionary algorithm that is different from the traditional MOPs. In [4], to solve global optimization problems regarding multiple objective functions, Moghdani R et al. introduced the multi-objective volleyball premier league (MOVPL) algorithm. In [5], Ewees A.A. et al. reported a new multi-objective optimization method (called MWDEO) including improved whale optimization algorithm (WOA) devoted to global exploration as well as the differential evolution (DE) algorithm used to exploit the search space, which enriches the theoretical research in this field. Wang Q et al. adopted multi-objective optimization methods to solve the problems regarding aerospace shell production scheduling in [6]. In [7], researchers proposed a novel particle swarm optimization method named AMPSO by combining dynamic neighborhood-based learning strategy and competition mechanism, committing to solve MMOPs. In [8], researchers introduced a novel and efficient method for solving MOPs inspired by the collision between balls in the game of billiards. In [9], researchers presented a test suite for MOPs including 16 real-world problems, which is used for performance evaluation for multiple-objective optimization algorithms. Some papers showed surveys for methods to solve MOPs, such as in [10], where researchers systematically reviewed and summarized various multi-objective methods devoted to solving MOPs based on hundreds of articles published from 1978 to 2021. In [11], Tian Y et al. gave a comprehensive overview of multi-objective evolutionary algorithms to solve large-scale MOPs.

Recently, the wolf pack optimization algorithm (WPOA) and its variants have been widely applied in many fields owing to their superior optimization performance and robustness. For example, in [12], a novel algorithm named FWPA is proposed to solve a set of static multidimensional knapsack benchmarks as well as several dynamic multidimensional knapsack problems. In [13], researchers adopted a new wolf pack algorithm named HWPA to improve the forecasting performance by obtaining a suitable partition of the universe of discourse. In [14], the authors proposed a new method named DSO-WPOA to promote the coverage rate of movable wireless sensor networks. Especially, in [15], the authors proposed a strategy named ASGS to promote the exploitation ability in local space, which greatly enhances the optimization ability of the WPOA.

Unfortunately, there are few cases where the WPOA or its variants are used to solve MMOPs. Consequently, inspired by the superior performance of the WPOA and the need to address MMOPs, in this paper we propose a wolf pack optimization algorithm using random adaptive-shrinking grid search (RASGS) and raid towards global best archive (GBA) for multi-modal multi-objective problems (MMO-WPOA-RASGS-GBA for short).

This article is organized as follows. Section 2 reviews related works. Section 3 presents an overview of the proposed method. In Section 4, validation experiments are shown. Section 5 concludes the paper.

2. Related Works

2.1. Special Crowding Distance and non-dominated_scd_sort

It is hard to decide which solution is the best one in multi-objective optimization owing to its complexity discussed above, so a dominated relationship [16] was designed to compare the qualities of different solutions which lead to the new concepts: non-dominated solutions, the Pareto optimal set (PS) in decision space as well as the corresponding Pareto front (PF) in objective space [1].

To analyze and manipulate the distribution of the various Pareto optimal sets, researchers proposed the concept of a crowding distance (CD), which is embedded in the omni-optimizer algorithm [17] to compare different non-dominated schemes. Accordingly, the idea of CD has been applied to the following related algorithms, for example, in [1], aiming to obtain more PSs, Liang et al. introduced DN-NSGAII, which utilizes a decision-space CD to sort the same front in objective space, which means the CD of PSs in the decision space can be used to determine which solution is better.

$$\{\begin{array}{c}C{D}_{i,x_j}=\frac{x_j\left(right of i\right)-x_j\left(left of i\right) }{x_j^{max}-x_j^{min}}\\ C{D}_{i,x}={\displaystyle {\displaystyle \sum }_{j=1}^{Num\_D}}C{D}_{i,x_j} , j=1,2,\dots ,Num\_D\end{array}$$

(1)

$$\{\begin{array}{c}C{D}_{i,x_j}=\frac{x_j\left(right of i\right)-x_j\left(left of i\right) }{x_j^{max}-x_j^{min}}\\ C{D}_{i,x}={\displaystyle {\displaystyle \sum }_{j=1}^{Num\_D}}C{D}_{i,x_j} , j=1,2,\dots ,Num\_D\end{array}$$

(2)

where $C{D}_{i,x_j}$ means the CD of the i-th solution in j-th decision space, while $C{D}_{i,f_m}$ means the one in m-th objective space; $C{D}_{i,x}$ means the total CD of the i-th solution in decision space, while $C{D}_{i,f}$ means the one in objective space; Num_D means the dimension number of decision space, while Num_O means the one of objective space.

It should be emphasized that the calculation of CD is different in the decision space and the objective space, and for decision space CD can be obtained from Equation (1) and for objective space from Equation (2). Note that if a solution is a boundary solution in the decision space, the numerator in Equation (1) should be replaced by ($x_j\left(right of i\right)-x_j\left(i\right)$) or ($x_j\left(i\right)-x_j\left(right of i\right)$), as the case may be, and the quantity should be multiplied by a factor of two since this computes only a one-sided difference; otherwise, when a solution is a boundary solution in the objective space, an infinite distance is assigned so as not to lose the solution.

$$C{D}_{avg,f}=\raisebox{1ex}{${\sum }_{i=1}^{Num\_S}C{D}_{i,f}$}\!\left/ \!\raisebox{-1ex}{$Num\_S$}\right.$$

(3)

where $C{D}_{avg,f}$ means the average CD of all solutions in objective space; Num_S means the number of all solutions.

However, CD has shortcomings in that if a solution i is the smallest one in the m-th objective for minimization problems, $C{D}_{i,f}$ is set to ∞, and $C{D}_{avg,f}$ is equal to ∞, so it is unable to compare the $C{D}_{i,f}$ and $C{D}_{avg,f}$. Accordingly, in [2], researchers proposed special crowding distance (SCD) conceived for the purpose of further improving CD along with an obvious adaptation that $C{D}_{i,f_m}$ is assigned to be set to 1 when the i-th solution is the minimum one in the m-th objective space for minimization problems. The SCD can be obtained from the following Equation (4).

$$SC{D}_i=\{\begin{array}{c}max\left(C{D}_{i,x},C{D}_{i,f}\right), \mathrm{when} C{D}_{i,x}>C{D}_{avg,x} \mathrm{or} C{D}_{i,f}>C{D}_{avg,f}\\ min\left(C{D}_{i,x},C{D}_{i,f}\right), \mathrm{other} \mathrm{conditions} \end{array}$$

(4)

where SCD_i means the special crowding distance of the i-th solution; CD_i,x means the crowding distance of the i-th solution about decision space, while CD_i,f means the one about objective space. max(parameter1,parameter2) is a function that returns the parameter with a larger value, while max(parameter1,parameter2) returns the one with a smaller value.

According to the original authors, SCD enhanced genetic diversity of both decision and objective spaces simultaneously owing to the max or min selection procedure reflected in Equation (4).

non-dominated_scd_sort is a function based on non-dominated relation and SCD, which firstly sorts solutions according to non-dominated sorting scheme from Reference [18] and then sorts them in descending order according to their SCD, with the result that the first solution is the non-dominated one with the largest SCD. In fact, non-dominated_scd_sort provides a reference to compare the quality of many different non dominated solutions, which provides support for the GBA strategy discussed later in this paper.

2.2. Strategy of Adaptive-Shrinking Grid Search (ASGS)

In 2007, researchers introduced the wolf swarm algorithm [19] inspired by the hunting process of wolves and composed mainly of the migration, summon-raid, siege, and population renewal mechanism of survival of the fittest. Since the wolf pack optimization algorithm (WPOA) was proposed, it has been widely applied in many different kinds of fields and continuously improved in various forms owing to its strong performance detailed in [15]. As a variant of the WPOA, the excellent performance of ASGS-CWOA [15] mainly benefits from the strategy of ASGS, which inspired us to use it to solve MMOPs. It is briefly described as follows.

Based on the ideas of LWPS [20] and CWOA [21], only one position was examined to determine whether it can become the next traveling position, shown in Equation (5); that is, a searching wolf can investigate one position along a direction, and it is obvious that the method is not suitable for searching for the local neighborhood space centered by the current wolf, which includes numerous locations to be investigated.

$$x_{id-new}=x_{id}+rand\left(-1,1\right)\ast step\_a$$

(5)

where x_id−new means the new location of the i-th wolf about the d-th dimension; rand(−1,1) returns a random value between −1 and 1; step_a means the step size during the stage of migration.

Thus, in [15], the authors proposed the strategy of ASGS conceived for the purpose of covering the whole local domain space centered by the current wolf to be investigated as much as possible, although it is impossible to exhaust all the positions to be investigated for the continuous space problem. The main thought of ASGS is to take the current wolf position as the center and the changing adaptive step size as the measurement scale to generate several inspection points in order to detect the best position in the local region (the position with the best fitness value) for the procedure of migration or siege, as shown in the following Equations (6) and (7).

$$\{\begin{array}{c}a=1-{\left(\raisebox{1ex}{$t-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^2\\ step\_a_{new}=step\_a_0\ast a\\ step\_c_{new}=step\_c_0\ast rand\left(0,1\right)\ast a\end{array}$$

(6)

$$\{\begin{array}{c}k=-K,-K+1,\dots ,0,\dots ,K-1,K\\ \left[k, x_{id-new}\right]=x_{id}+step\_a_{new}\ast k\\ x_{i-new}=\{\left[\left(1~K\right), x_{i1-new}],[\left(1~K\right), x_{i2-new}\left],\dots ,\right[\left(1~K\right), x_{iD-new}\right]\}\end{array}$$

(7)

where $a$ is a factor for step_a_new and step_c_new; step_a_new means the new step size of migration for the t-th iteration, while step_c_new means the one of siege; rand(0,1) returns a random value between 0 and 1; step_c₀ means the initial step size of the stage of siege; K means the number of nodes taken along any direction for a wolf; x_i−new means the new position of i-th wolf while x_id−new means the new one for the d-th dimension.

According to the above formula, each wolf inspects （2×k+1)^D positions in its own local space during hunting and running as shown in Figure 2, where D means the dimension number of solution space. Refer to [15] for a detailed discussion of ASGS.

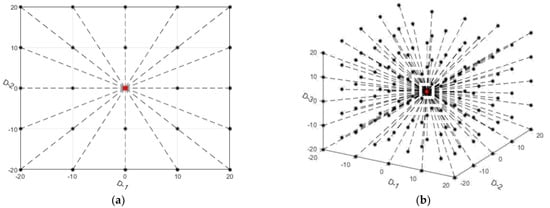
Figure 2. Schematic of the ASGS strategy. (a) Schematic when Dimension is 2 and K is set to 2 for Equation (7). (b) Schematic when Dimension is 3 and K is set to 3.(Red point means the current locaton while the black ones mean the locations to be inspected).

3. Overview of New Proposed Method

3.1. RASGS

It is difficult to solve the MMP problem, while the ASGS greatly improves the optimization performance of the wolf pack optimization algorithm when solving the single objective problem. This encourages us to use the modified ASGS-CWOA to solve the MMP problem. It is undeniable that ASGS-CWOA has excellent performance in solving MMPs (as demonstrated in the experiment in Section 4).

However, we also found that the ASGS strategy extends with the same step size. Although the step size changes adaptively with the advance of iterations, this equidistant expansion greatly limits the flexibility of the ASGS strategy as shown in Figure 2. In order to overcome this deficiency of the ASGS strategy, we propose the random ASGS strategy (RASGS) that introduces a random parameter in the equidistant step size to make the ASGS strategy flexible while maintaining its own basic exploration/extension framework as shown in Figure 3. In Figure 2 and Figure 3, the red point indicates the location of the current wolf, while the black ones represent the positions to be investigated during the stage of migration or siege, and the black dotted lines indicate the potential routes for the current wolf to explore. The RASGS strategy can be illustrated by the following Equation (8).

$$\{\begin{array}{c}{k}_{rand}=k+rand\left(0,1\right),k=-K,-K+1,\dots ,0,\dots ,K-1,K \\ \left[k, x_{id-new}\right]=\{\begin{array}{c}{x}_{id}+step\_a_{new}\ast k_{rand}, k_{rand}<K \\ x_{id}, k_{rand}>K\end{array}\\ x_{i-new}=\{\left[\left(1~K\right), x_{i1-new}],[\left(1~K\right), x_{i2-new}\left],\dots ,\right[\left(1~K\right), x_{iD-new}\right]\}\end{array}$$

(8)

where the variables involved in Equation (8) can be found in the formula already described.

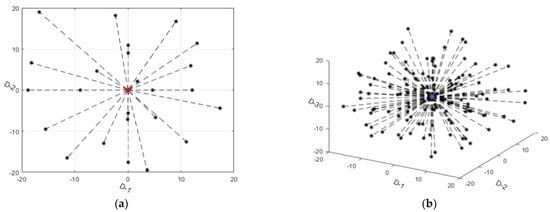
Figure 3. Schematic of the RASGS strategy. (a) Schematic when Dimension is 2 and K is set to 2 for Equation (7). (b) Schematic when Dimension is 3 and K is set to 3. (Both red point and blue point mean the current location while the black ones mean the ones to be inspected).

In essence, solving nonlinear and irregular MMPs requires that the algorithm can not only maintain the stability of the search framework in the hunting and siege stages but also maintain a certain degree of flexibility to deal with the complex and infinite solution space. RASGS inherits the function of the former and introduces random parameters resulting in the implementation of the latter. Similar to ASGS-CWOA, the algorithm based on this new strategy is abbreviated to RASGS-CWOA.

It can also be seen from Figure 3 that although random factors have been added, the locations to be investigated in the local areas are symmetrical and centered on the current wolf position, which is determined by Formula (8).

3.2. GBA

As mentioned above, MMPs have multiple inconsistent goals, making it impossible to compare the quality of different non-dominated solutions through traditional methods, so a global optimal solution like the single objective programming problem cannot be found, as shown in the Figure 4 where for N1, N2 and N3, the best solution cannot be compared due to the two independent evaluation objectives F-1 and F-2. Obviously, solution N1 (corresponding to P1 and P1′ in the decision space) is the best on target F-2 and the worst on F-1 (assuming the larger the better). On the contrary, solution N3 (corresponding to P3 and P3′ in the decision space) is the worst on target F-2 and the best on F-1. Solution N2 (corresponding to P2 and p2′ in the decision space) is in the middle value on objectives F-1 and F-2.

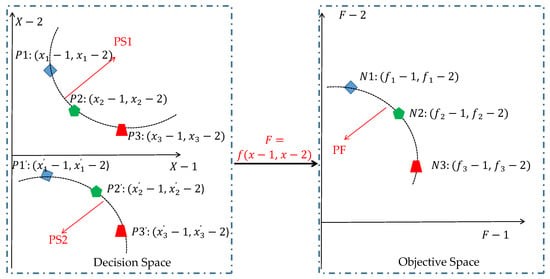
Figure 4. Schematic of non-dominated solutions. Here, PS means Pareto sets, while PF means Pareto front, and P1, P1′—N1, P2, P2′—N2 and P3, P3′—N3.

In [2], the authors adopted SCD to sort the non-dominated solutions so as to obtain a descending order of non-dominated solutions that could not be compared before. The first non-dominated solution in the sequence has the optimal SCD.

According to the idea of ASGS-CWOA, wolves need to raid to the leader wolf; that is, the global optimum, in the summon-raid stage, and the non-dominated solution sorting method proposed in Reference [2] provides the necessary method for obtaining the global optimum required in this stage. In fact, the first non-dominated solution in the sequence obtained after sorting is not really the global optimum in the true sense but a reference, which is enough to induce wolves to gather. In this paper, the method based on SCD to obtain the global optimum and complete the calculation of the summon-raid is called raid to global best archive (GBA) as shown in Figure 5.

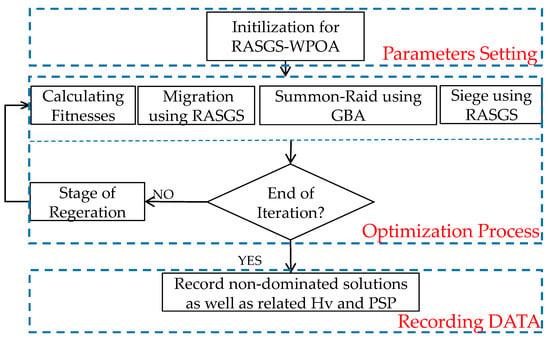
Figure 5. Flow chart of MMO-WPOA-RASGS-GBA.

In particular, in order to compare the support of the GBA strategy for the methods proposed in this paper, this paper proposes the strategy of raid to neighborhood best (RNB for short) based on previous studies, the main idea of which is to establish the local neighborhood optimal archive centered on the current wolf (this paper adopts the ring strategy taking N−1, N and N+1, where N means the current solution while N−1 and N+1 mean the solution before the current solution and the one after the current solution, respectively, detailed in Reference [2]). In the summon-raid stage, wolves rush to the optimal one in their respective neighborhood optimal archive, not the one with the global optimum.

3.3. Overview of Flow Chart of MMO-WPOA-RASGS-GBA

The execution flow of the new algorithm is shown in Figure 5, and the detailed operation details are as described above as well as referring to Reference [15], while the step size during stages of migration, summon-raid and siege are calculated according to Equations (9) and (10).

$$\{\begin{array}{c}step\_a\_basic=\left(VRmax-VRmin\right)/2 \\ step\_b\_basic=\left(VRmax-VRmin\right)/10 \\ step\_c\_max=sum\left(VRmax-VRmin\right)/20\\ step\_c\_min=1e-40 \end{array}$$

(9)

$$\{\begin{array}{c}stepa=\left(1-\left(\left(t-1\right)/T\right)^5\right)\ast step\_a\_basic \\ stepb=\left(1-\left(\left(t-1\right)/T\right)^5\right)\ast step\_b\_basic \\ stepc=step\_c\_min\ast \left(V{R}_{max}-V{R}_{min}\right)\ast exp\left(\left(log\left(step\_c\_min/step\_c\_max\right)\right)\ast \frac{t}{T}\right)\end{array}$$

(10)

where stepa, stepb and stepc mean the step size during stages of migration, summon-raid and siege, respectively. VRmax is the maximum range of solution space, while VRmin means the minimum one in each dimension.

4. Validation Experiment

4.1. Experimental Environment

To verify the feasibility and efficiency of the algorithm proposed in this paper, several groups of comparative experiments were carried out by using the new method: MMO-WPOA-RASGS-GBA, DN-NSGAII, MO-Ring-PSO-SCD, MMO-WPOA-LWPS-GBA, MMO-WPOA-LWPS-RNB, MMO-WPOA-ASGS-GBA, MMO-WPOA-ASGS-RNB and MMO-WPOA-RASGS-RNB. A detailed description is given in the following Table 1.

Table 1. Descriptions of comparative methods.

Order	Name	Description
1	MMO-WPOA-RASGS-GBA	MMO-WPOA-RASGS-GBA was implemented according to the ideas from Section 2 and Section 3 and with the following main parameters. Population size: popsize = 100 × n_var (n_var means the number of dimension in decision space); maximum iterations: Max_Gen = fix (5000 × n_var/popsize), where fix is a function that rounds a given parameter to the nearest integer in the direction of zero.
2	DN-NSGAII	According to the idea from Reference [1], DN-NSGII was designed and implemented.
3	MO-Ring-PSO-SCD	For comparison, the algorithm MO-Ring-PSO-SCD was completely implemented by using the ideas of Reference [2], and the code and data published by the author were fully used.
4	MMO-WPOA-LWPS-GBA	MMO-WPOA-LWPS-GBA was implemented based on LWPS and the strategy of GBA, where LWPS is the concept of Reference [20]. In order to maintain the consistency of comparison, the main parameter settings were the same as the new proposed method MMO-WPOA-RASGS-GBA.
5	MMO-WPOA-LWPS-RNB	MMO-WPOA-LWPS-RNB was implemented based on LWPS and the strategy of RNB. The main parameter settings were the same as the new proposed method MMO-WPOA-RASGS-GBA.
6	MMO-WPOA-ASGS-GBA	MMO-WPOA-ASGS-GBA was implemented based on ASGS-CWOA and the strategy of GBA. The main parameter settings were the same as the new proposed method MMO-WPOA-RASGS-GBA.
7	MMO-WPOA-ASGS-RNB	MMO-WPOA-ASGS-RNB was implemented based on ASGS-CWOA and the strategy of RNB. The main parameter settings were the same as the new proposed method MMO-WPOA-RASGS-GBA.
8	MMO-WPOA-RASGS-RNB	MMO-WPOA-RASGS-RNB was implemented based on RASGS-CWOA and the strategy of RNB. The main parameter settings were the same as the new proposed method MMO-WPOA-RASGS-GBA.

Table 1 shows the numerical experimental configuration and concepts of the eight methods. We conducted all the experiments on a laptop with Windows 7 (64 bit), 12.0 GB memory and an AMD A6-3400 m CPU. In order to meet the following statistical analysis needs, independent experiments were carried out 21 times on 11 test functions as shown in Table 2.

Table 2. Test functions and their features.

Function Name	Numbers of PSs	Overlap in Every Dimension
MMF1	2	✗
MMF2	2	✗
MMF3	2	✓
MMF4	4	✗
MMF5	4	✗
MMF6	4	✓
MMF7	2	✗
MMF8	4	✗
SYM-PART simple	9	✓
SYM-PART rotated	9	✓
Omni-test (n = 3)	27	✓

It must be noted that test functions shown in Table 2 are from Reference [2], which also shows the need for academic verification uniformity.

4.2. Experimental Data and Analysis

In this study, Pareto set proximity (PSP) and hypervolume (Hv) were adopted to test the performance of different methods for MMPs. For a detailed introduction of PSP and HV, please refer to Reference [2]. In order to facilitate simulation experiments and statistics, we used the reciprocal forms of PSP and HV: rPSP and rHV, the smaller the better. On 11 test functions, 21 simulation experiments were carried out for 8 comparison algorithms, and the original data obtained from the experiments are shown in Table 3, which gives the original test data regarding PSP gained by running each comparison algorithm on 11 test functions as well as the data regarding HV. Based on these original test data, some necessary analysis and discussion regarding the performance of different methods are given.

Table 3. PSP and HV obtained from running 8 comparison algorithms on 11 test functions.

Method	Function	Best		Worst		Mean		Standard Deviation
		PSP	HV	PSP	HV	PSP	HV	PSP	HV
DN-NSGAII	1	13.07157454	0.871441292	7.45420489	0.867777461	10.37862956	0.869543972	1.537400748	0.000971016
	2	27.14697376	0.86034517	2.743265272	0.812130676	10.66215106	0.842723622	7.025888613	0.014772512
	3	20.99165336	0.864179667	4.321204324	0.795025678	11.03379399	0.845174252	5.389567687	0.019247749
	4	19.06053311	0.538831423	7.920388234	0.538013489	13.74047358	0.538371962	2.963817426	0.000223549
	5	6.721691985	0.871705041	4.318902002	0.868264371	6.003089379	0.870574743	0.554027273	0.000831438
	6	8.487121963	0.871841635	5.297196162	0.864684655	7.018860458	0.870276462	0.944228126	0.001536351
	7	25.73434643	0.870961261	14.03144506	0.867162762	19.59652068	0.869747436	3.233112307	0.000948028
	8	7.574435284	0.420461536	1.968899546	0.418607833	4.165918029	0.419632606	1.41998449	0.000424649
	9	0.901421457	16.65058558	0.102172245	16.63836026	0.248497916	16.64395359	0.174115453	0.003450843
	10	0.851985453	16.64076529	0.071600353	16.62908329	0.217284248	16.63583674	0.171143405	0.00305863
	11	0.824966497	52.80128767	0.490736377	52.78893019	0.669547795	52.79724749	0.089073764	0.00288194
......	Related data for MO-Ring-PSO-SCD, MMO-WPOA-LWPS-GBA, MMO-WPOA-LWPS-RNB, MMO-WPOA-ASGS-GBA, MMO-WPOA-ASGS-RNB, MMO-WPOA-RASGS-GBA
MMO-WPOA-RASGS-RNB	1	23.93129451	0.872464015	19.78287453	0.871847053	21.41931497	0.872185149	1.080976338	0.000170628
	2	164.1425286	0.871207671	131.6933317	0.869951014	143.0823892	0.870452374	7.876139977	0.000293692
	3	155.8376542	0.871516532	125.5565595	0.870361056	141.025033	0.870966491	7.632984748	0.000359212
	4	44.61290138	0.539158648	37.32542416	0.537586604	41.39526592	0.538390431	2.136074745	0.000416678
	5	14.17445297	0.872425458	11.75215944	0.871841708	12.87865508	0.872182454	0.733297984	0.000160872
	6	16.16825152	0.872555153	13.16557559	0.870727596	14.60809281	0.872027625	0.801278727	0.000459748
	7	44.49262842	0.87165644	34.98611381	0.870040226	40.65581559	0.870956842	2.399970212	0.000453174
	8	21.84212415	0.420854555	18.19303417	0.414828247	20.09382787	0.419980567	0.968923642	0.001257179
	9	18.27235864	16.64725864	12.79305015	16.63366917	15.15875804	16.6406475	1.345772599	0.003929908
	10	13.51032998	16.62859054	10.44428702	16.619417	12.33495567	16.62457421	0.808215646	0.002706662
	11	10.08414621	52.75576581	3.400506796	52.73641053	7.186849936	52.74821071	1.866408547	0.005407196

(1-MMF1, 2-MMF2, 3-MMF3, 4-MMF4, 5-MMF5, 6-MMF6, 7-MMF7, 8-MMF8, 9-SYM_PART_simple, 10-SYM-PART-rotated, 11-Omni-test. Limited to space, only some data are listed; the complete data are shown in the link in Appendix A).

Note: black “*” corresponds to DN-NSGAII; black “.” corresponds to MO-PSO-Ring-SCD; green “*” corresponds to MMO-WPOA-ASGS-GBA; green “.” corresponds to MMO-WPOA-ASGS-RNB; blue “*” corresponds to MMO-WPOA-LWPS-GBA; blue “.” corresponds to MMO-WPOA-LWPS-RNB; red “*” corresponds to MMO-WPOA-RASGS-GBA and red “.” corresponds to MMO-WPOA-RASGS-RNB. Refer to Figure 6 and Figure 7.

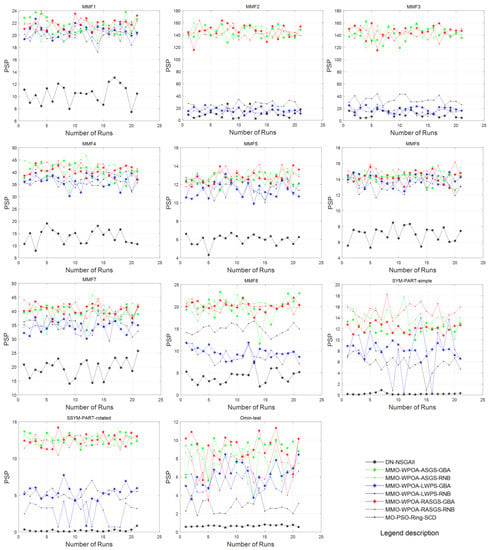
Figure 6. Schematic diagram of the PSP obtained from 21 independent runs.

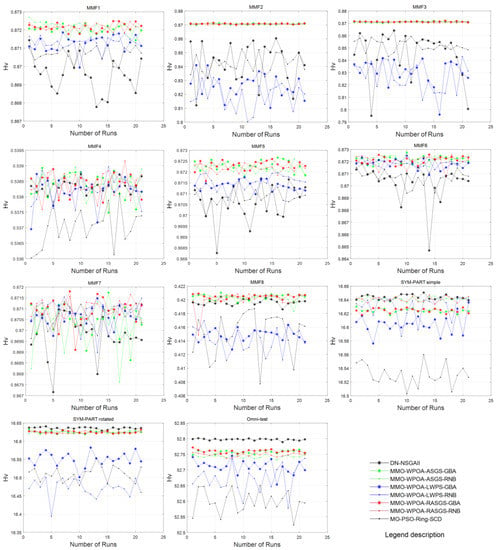
Figure 7. Schematic diagram of the HV obtained from 21 independent runs.

As can be seen from Figure 6 and Figure 7, it is obvious that the red * curve representing the new method MMO-WPOA-RASGS-GBA is at the top except for the last three subgraphs of Figure 7, which shows that this method has good performance on the whole based on PSP and HV indicators.

However, we can also see that green curves and the red “.” curve representing MMO-WPOA-ASGS-RNB, MMO-WPOA-ASGS-GBA and MMO-WPOA-RASGS-RNB are very close, so it is hard to distinguish their performance based on Figure 6 and Figure 7. Accordingly, optimal value, worst value, average value and the standard deviation for PSP and HV are adopted to help us further investigate and analyze the superior performance of the new algorithm, shown in Table 4.

Table 4. Difference between MMO-WPOA-RASGS-GBA and other similar methods.

Item	Order	Difference from PSP				Difference from HV
		Best	Worst	Mean	SD	Best	Worst	Mean	SD
MMO-WPOA-RASGS-GBA vs. MMO-WPOA-ASGS-GBA	1	−0.286	−0.201	0.084	−0.353	0.000058	0.000342	0.000115	−0.000045
	2	5.941	−12.345	2.047	2.514	0.000284	−0.000023	0.000130	0.000023
	3	−2.777	−4.035	4.173	−1.272	0.000314	0.000453	0.000189	0.000008
	4	−0.990	2.557	−0.108	−1.307	−0.000037	0.000320	0.000061	−0.000110
	5	0.729	0.299	0.111	0.154	−0.000069	−0.000219	0.000008	−0.000010
	6	0.736	−0.006	0.083	0.171	−0.000173	0.000001	−0.000058	0.000011
	7	0.981	3.152	0.790	−0.204	0.000058	0.000475	0.000441	−0.000149
	8	−1.288	5.861	0.549	−1.618	−0.000131	0.000218	0.000071	−0.000108
	9	−0.099	0.822	0.153	−0.099	−0.001311	0.000372	0.000426	0.000230
	10	0.566	0.082	−0.141	0.087	−0.000035	0.001645	−0.000159	0.000284
	11	1.103	0.032	0.192	0.187	0.006698	0.003756	0.002740	0.000001
MMO-WPOA-RASGS-GBA vs. MMO-WPOA-ASGS-NBA	1	0.869	1.060	0.804	−0.231	−0.000221	0.000235	0.000014	−0.000087
	2	4.089	−17.950	0.862	3.338	0.000265	0.000293	0.000148	−0.000040
	3	−0.817	−4.143	2.317	−0.095	0.000322	0.000828	0.000234	−0.000070
	4	−2.946	4.975	−0.724	−1.425	−0.000059	0.000023	−0.000037	0.000043
	5	0.388	−0.272	−0.197	0.102	0.000002	−0.000229	0.000138	0.000063
	6	−0.034	0.495	−0.234	−0.013	0.000061	0.000034	−0.000001	0.000002
	7	−2.262	4.520	0.982	−1.514	0.000478	0.001490	0.000664	−0.000318
	8	−0.728	0.804	0.244	−0.238	0.000040	0.001471	0.000181	−0.000241
	9	−4.212	0.752	−1.848	−0.934	−0.016784	−0.017689	−0.016462	0.000119
	10	0.660	−0.231	0.031	0.134	0.001701	0.001232	−0.000149	−0.000082
	11	2.238	1.786	1.685	0.049	0.021988	0.019958	0.017610	0.000246
MMO-WPOA-RASGS-GBA vs. MMO-WPOA-RASGS-NBA	1	−0.430	0.090	0.308	−0.172	0.000022	−0.000070	−0.000037	0.000048
	2	−0.358	−16.393	3.237	3.359	0.000282	−0.000012	0.000376	0.000080
	3	3.775	−10.517	4.956	2.424	0.000630	0.000341	0.000359	−0.000005
	4	−0.922	−0.487	−1.063	−0.329	−0.000263	0.000223	0.000031	−0.000111
	5	−0.087	−0.102	−0.198	−0.062	0.000170	−0.000264	0.000111	0.000079
	6	−0.619	−0.299	−0.322	−0.107	0.000016	0.000874	0.000099	−0.000172
	7	−1.023	1.259	−0.300	−0.466	0.000146	−0.000937	−0.000057	0.000160
	8	0.218	−0.697	0.156	0.068	0.000057	0.004944	0.000502	−0.000967
	9	−4.721	−2.007	−3.041	−0.560	−0.018404	−0.015793	−0.016118	−0.000714
	10	0.730	0.834	0.218	−0.016	0.003227	0.001239	0.000091	0.000453
	11	1.251	2.255	1.949	−0.427	0.016015	0.015172	0.011846	−0.000418

(1-MMF1, 2-MMF2, 3-MMF3, 4-MMF4, 5-MMF5, 6-MMF6, 7-MMF7, 8-MMF8, 9-SYM-PART-Simple, 10-SYM-PART-rotated, 11-Omni-test).

Table 5 was obtained based on the values listed in Table 4 to show the dominance ratios between the newly proposed algorithm and other similar algorithms for PSP and HV.

Table 5. Statistical data for MMO-WPOA-RASGS-GBA and other similar methods.

Item	Index	Statistics for PSP		Statistics for HV
		Number of Advantages	Dominance Ratio (Total: 11)	Number of Advantages	Dominance Ratio (Total: 11)
vs. MMO-WPOA-ASGS-GBA	Best	6	54.55%	5	45.45%
	Worst	7	63.64%	9	81.82%
	Mean	9	81.82%	9	81.82%
	SD	6	54.55%	5	45.45%
vs. MMO-WPOA-ASGS-NBA	Best	5	45.45%	8	72.73%
	Worst	7	63.64%	9	81.82%
	Mean	7	63.64%	7	63.64%
	SD	7	63.64%	6	54.55%
vs. MMO-WPOA-RASGS-NBA	Best	4	36.36%	9	81.82%
	Worst	4	36.36%	6	54.55%
	Mean	6	54.55%	8	72.73%
	SD	8	72.73%	6	54.55%

In terms of the optimal value or maximum value of PSP, it can be clearly seen from Table 5 that six records of MMO-WPOA-RASGS-GBA are better than MMO-WPOA-ASGS-GBA, five records are better than MMO-WPOA-ASGS-RNB and four records are better than MMO-WPOA-RASGS-RNB, and the difference between other records without advantages is very small. In particular, the former has the best performance in the more complex functions SYM-PART-rotated and Omni-test (with 9 and 27 Pareto sets, respectively, as detailed in Table 2). In terms of minimum or worst value for PSP, seven records of MMO-WPOA-RASGS-GBA are better than MMO-WPOA-ASGS-GBA, seven records are better than MMO-WPOA-ASGS-RNB and four records are better than MMO-WPOA-RASGS-RNB, and the difference between other records without advantages is very small, which means that the proposed method

MMO-WPOA-RASGS-GBA has an advantage rate of about 63.64%, 63.64% and 36.36% compared with the other three approximation algorithms. Similarly, in terms of median for PSP, nine records of MMO-WPOA-RASGS-GBA are better than MMO-WPOA-ASGS-GBA, seven records are better than MMO-WPOA-ASGS-RNB and six records are better than MMO-WPOA-RASGS-RNB, and the difference between other records without advantages is very small, which means that MMO-WPOA-RASGS-GBA has an advantage rate of about 81.82%, 63.64% and 54.55% compared with the other three approximation algorithms. Finally, in terms of standard deviation for PSP, six records of MMO-WPOA-RASGS-GBA are better than MMO-WPOA-ASGS-GBA, seven records are better than MMO-WPOA-ASGS-RNB and eight records are better than MMO-WPOA-RASGS-RNB, and the difference between other records without advantages is very small, which means that MMO-WPOA-RASGS-GBA has an advantage rate of about 54.55%, 63.64% and 72.73% compared with the other three approximation algorithms.

Therefore, it can be concluded that the proposed algorithm has overall advantages in terms of PSP index.

In terms of the optimal value or maximum value of HV, it can be clearly seen from Table 5 that five records of MMO-WPOA-RASGS-GBA are better than MMO-WPOA-ASGS-GBA, eight records are better than MMO-WPOA-ASGS-RNB and nine records are better than MMO-WPOA-RASGS-RNB, and the difference between other records without advantages is very small, which means that MMO-WPOA-RASGS-GBA has an advantage rate of about 45.45%, 72.73% and 81.82% compared with the other three approximation algorithms. In terms of minimum or worst value for HV, nine records of MMO-WPOA-RASGS-GBA are better than MMO-WPOA-ASGS-GBA, nine records are better than MMO-WPOA-ASGS-RNB and six records are better than MMO-WPOA-RASGS-RNB, and the difference between other records without advantages is very small, which means that the proposed method MMO-WPOA-RASGS-GBA has an advantage rate of about 81.82%, 81.82% and 54.55% compared with the other three approximation algorithms. Similarly, in terms of median for HV, nine records of MMO-WPOA-RASGS-GBA are better than MMO-WPOA-ASGS-GBA, seven records are better than MMO-WPOA-ASGS-RNB and eight records are better than MMO-WPOA-RASGS-RNB, and the difference between other records without advantages is very small, which means that MMO-WPOA-RASGS-GBA has an advantage rate of about 81.82%, 63.64% and 72.73% compared with the other three approximation algorithms. Correspondingly, in terms of standard deviation for HV, five records of MMO-WPOA-RASGS-GBA are better than MMO-WPOA-ASGS-GBA, six records are better than MMO-WPOA-ASGS-RNB and six records are better than MMO-WPOA-RASGS-RNB, and the difference between other records without advantages is very small, which means that MMO-WPOA-RASGS-GBA has an advantage rate of about 45.45%, 54.55% and 54.55% compared with the other three approximation algorithms.

Accordingly, it can be concluded that the proposed algorithm has overall advantages in terms of HV index, although some performance is not good.

5. Conclusions

To address multi-modal multi-objective problem, a wolf pack optimization algorithm using strategies of random adaptive-shrinking grid search and raid towards global best for MMOPs is proposed, which enriches the method system for using the WPOA to solve MMOPs and makes two key contributions: Firstly, RASGS was adopted to enhance the exploitation of the algorithm in the local area as well as locate a larger number of Pareto-optimal solutions. Moreover, with the help of an existing sorting method composed of the non-dominated sorting scheme and SCD, the strategy of GBA is introduced to obtain and maintain the historical global optimal solution of the population as well as induce the population to explore better solutions. Theoretical research and experimental results indicate that MMO-WPOA-RASGS-GBA has comprehensively superior PSP and HV compared with DN-NSGAII, MO-Ring-PSO-SCD, MMO-WPOA-LWPS-GBA, MMO-WPOA-LWPS-NBA, MMO-WPOA-ASGS-GBA, MMO-WPOA-ASGS-NBA and MMO-WPOA-RASGS-NBA under the same conditions.

However, it needs to be stated that MMO-WPOA-RASGS-GBA is not perfect, and its performance is not optimal in some aspects, such as MMO-WPOA-RASGS-RNB performing better than MMO-WPOA-RASGS-GBA on maximum and minimum values of PSP, as shown in Table 5, which indicates the strategy of RNB is better than GBA in some aspects. Unfortunately, the former performs weakly on median and standard deviation of PSP. On the contrary, this is exactly the advantage of the method proposed in this paper.

Future work will be carried out to continuously improve our related methods to address MMOPs and solve practical engineering problems.