Computational Analysis of Viscoplastic Nanofluid Blending by a Newly Modified Anchorage Impeller within a Stirred Container

Abstract

Several industrial fields require mixing and mechanical agitation processes. This operation is mainly used to enhance heat and mass transfer inside stirred tank systems and improve the degree of homogeneity to obtain a high-quality final product. The main goal of this research paper is to analyze the thermal and hydrodynamic behavior of non-Newtonian nanofluid (Bingham–Papanastasiou–Al₂O₃) inside a symmetrically stirred tank. A 3D numerical study has been conducted for a stationary laminar flow inside a symmetric cylindrical vessel under influencing parameters, including the inertia parameter ($Re=1, 20, 100$) and the volume fraction of nanoparticles ($\mathsf{Ø}=0.02, 0.06, 0.1$) with different geometric configurations, has been introduced into the stirring system. According to the findings, with high inertia ($Re=100$), the heat transfer inside the stirred tank is enhanced. Furthermore, increasing the nanoparticle fraction volume had a significant impact on the acceleration of heat transfer along the stirred vessel. It has been also found that the geometric configuration of an anchor with added arm blade (Case 2) is more efficient compared with the rest of the anchor agitator.

1. Introduction

In many important industrial mechanisms, including chemical science, crystals, polymerization, paint, construction materials, metalworking, gas dispersion, etc., mechanical agitation is one of the most prevalent unit operations used to suspend particles in a liquid in order to promote mass transfer or a chemical reaction, to increase homogeneity to certain degrees, and to speed up the thermal responses and mass transition for attaining a high final superior product with the particular substance [1]. As we study in this research utilizing a novel anchor impeller agitator construction, the efficiency of this activity is dependent on several factors (geometric design of the system of agitation). The proposed format had a favorable impact on the operations that take place in stirred tanks by boosting the flowing of fluid and raising the rate of heat transference inside the swirled tank while also decreasing electricity consumption rates.

Nanofluid flow is of great interest in many areas of modern science, such as engineering and technology, chemical and nuclear industries, and biomechanics. Nanofluids are made by dispersing nanometer-sized particles into a base fluid. Metallic nanoparticles are taken as copper, silver, aluminum, etc., because these particles increase the thermal conductivity and improve the heat transmission capability of pure fluid. These fluids also play a significant role in industry and engineering applications, such as in microelectronics, biomedical devices, nuclear systems cooling, vehicle cooling, power generation, etc. [2]. The study of the thermal behavior inside stirred reactors is very significant since they are crucial in many relevant operations. For example, they are critical to achieving the desired reaction products and preventing the loss control of thermal of reactions, as well as generating the appropriate super-saturation for the product of promising crystals [3].

In fact, CFD technology has become more popular for analyzing and investigating the complicated thermal and fluid flow phenomena in stirred tank systems. The aim of researchers using CFD is to optimize and enhance mixing system parameters such as (flow pattern, power consumption, pumping flow rate vortices sizes, etc.) by adjusting certain factors (geometrical and rheological properties of this stirring system studies). Due to the importance of mechanical agitation and micro-mixing operation in several industry fields, several research papers have involved experimental work and numerical investigation aimed to ameliorate the hydrodynamic structure of these processes. The anchor impeller is often employed for mixing viscous fluids owing to its efficacy with viscous fluids. Several studies have investigated this kind of impeller and its effect on hydrodynamic patterns of stirred tank systems [4,5,6,7,8,9,10].

Ameur et al. [11] used a modified impeller design consisting of a curved blade turbine (CBT) combined with a classical anchor impeller (CAI). They analyze the effect of geometric design, anchor curvature, and shear zone on energy consumption. Studies concerning the yield stress fluid inside agitated tanks equipped with anchor impellers are relatively limited, and most of these studies focus on 2D numerical study. Marouche et al. [12] conducted numerical and experimental research using Newtonian fluid (glucose solution) and yield stress fluid (Carbopol solutions). Significant variances and discrepancies are found between Newtonian fluid and viscoplastic fluid based on the velocity results. Anne-Archard et al. [13] examined the hydrodynamic pattern and power consumption of mixing viscoplastic fluids (Bingham, Herschel–Bulkley, and Casson fluids) using helical and anchor impellers. They found high similarity results that confirmed a Metzner–Otto correlation.

Bertrand et al. [14] and Abid et al. [15] conducted a 3D numerical study on mixing non-Newtonian fluid in laminar flow by inserting an anchor impeller agitator. Their result demonstrates the ineffectiveness of anchor impellers in mixing laminar regimes. Mebarki et al. [16] numerically investigated a novel (round) anchor impeller design for mixing yield stress fluid. They found satisfying results in comparison to the standard anchor impeller, such as the (enhancement flow field pattern and reduced energy consumption cost). Rahmani et al. [17] conducted a comparative analysis of the energy consumed in the mixing tank by various impellers (an anchor agitator, a gate agitator, and a two-blade agitator). The findings revealed that the anchor impeller type has a lower energy consumption than the other types. Kada et al. [1] conducted a 3D numerical research of Bingham–Papanastasiou fluid with varied geometric designs and inclination degrees within a stirred vessel. They discovered that the anchor impeller with an inclination of 60° accelerated the flow inside the stirred system most effectively. The numerical studies on the literature related to the thermal behavior inside the stirred system are relatively limited. Baccar et al. [18] numerically investigated the thermal and hydrodynamic behavior of turbulent flow inside an unbaffled cylindrical agitated vessel by introducing a radial turbine with six blades. According to the findings, the greatest thermal intensity was found to be near the turbine region. Hami et al. [19] investigated the influence of inclination degree on the flow pattern and heat transfer inside the agitated vessel during a thermal and hydrodynamic study of an inclined anchor impeller. In addition, Rahmani et al. [20] and Treveni et al. [21] investigated the thermal behavior of a non-Newtonian fluid inside a stirred tank. Perarasu et al. [22,23] conducted a comparative analysis of two stirring systems (the first contains water, and the second has nanofluids). They observed a significant improvement in heat transfer for the second system with nanofluid, in addition, the increase in the volume fraction of nanoparticles leads to an increase in the heat transfer inside the stirred vessel.

The main purpose of this paper is to contribute to the study of the thermo-hydrodynamic effect of a stationary–laminar flow of a fluid (Bingham–Papanastatiou–Al₂O₃). The influence of adding a nanoparticle volume fraction in the range of (0.02, 0.06, 0.1) has been explored as well as the impact of the inertia value on the flow pattern for different values of $Re=1, 20,$ and $100$. Three different cases have been used to introduce the effect of the new symmetrical anchor impeller design in this study, which are named Case 1 (classical anchor impeller), Case 2 (anchor impeller with one added blade), and Case 3 (anchor with two added symmetric arm blades).

2. Mixing System

The 3D stirred system consists of a cylindrical vessel with a flat bottom equipped with an anchor impeller. The mechanical agitation process was investigated under the condition of hot temperature $T_h$ at the side wall of the tank, and the rest (anchor, bottom) are assumed adiabatic $\frac{\partial T}{\partial n}=0$, as shown in Figure 1.

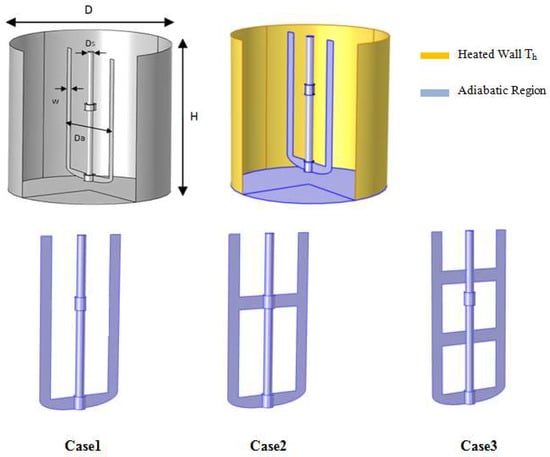
Figure 1. Stirred tank geometry model and boundary conditions.

The dimensionless temperature has 0 initial value in the fluid zone, and the dimensional temperature on the surface of the vessel is posed equally to 1:

• On the impeller and bottom $\frac{\partial T}{\partial n}=0$;
• On the impeller and bottom on the vessel surface $T=1$.

All geometry details of the mixing system are illustrated in Table 1 in addition to the details of nanoparticles shown in Table 2.

Table 1. Geometrical parameter dimensions of the stirred system.

$D$	$H$	$Da$	$w$	$Ds$	$c$
0.3	0.3	0.15	0.03	0.02	0.06

Table 2. Thermal and hydrodynamic properties of alumina nanoparticles.

Properties	Density ($\mathrm{kg}/{\mathrm{m}}^3$)	Thermal Capacity ($\mathrm{J}/\mathrm{kg} \mathrm{K}$)	Thermal Conductivity ($\mathrm{W}/\mathrm{m} \mathrm{K}$)	Dynamic Viscosity ($\mathrm{Pa}·\mathrm{s}$)	Thermal Expansion ($1/\mathrm{K}$)
Al2O3	3970	765	40	-	0.85 × 10−5

3. Mathematical Modeling

For this study, a 3D numerical simulation of the thermo-hydrodynamic flow of a yield stress nanofluid inside a cylindrical stirred tank with a new anchor impeller design was investigated. The mixture consists of a suspension of Al₂O₃ nanoparticles within a Bingham–Papanastasiou base fluid. This study has been performed by using the COMSOL-Multiphysics tools. These software tools solve the system of governing continuity–momentum equation and energy Equations (7)–(11). The finite element method based on the Galerkin’s Discretization was used. The computational domain was defined with an unstructured mesh called tetrahedral mesh, shown in Figure 2, and the residual convergence of the steady state is at least 10⁻⁶ for various variables in this simulation.

Figure 2. Unstructured mesh (Tetrahedral model).

The stirred system was governed by the conservation of mass and momentum equations as follows [24]:

Dimensional equation

Continuity equation

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}+\frac{dW}{dZ}=0$$

(1)

Momentum equation

$${\rho }_{nf}\left(U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}+W\frac{\partial U}{\partial Z}\right)=-\frac{\partial P}{\partial X}+\left[\frac{\partial }{\partial X}\left(2{\mu }_{nf}\frac{\partial U}{\partial X}\right)+\frac{\partial }{\partial Y}\left({\mu }_{nf}\frac{\partial U}{\partial Y}+\frac{\partial V}{\partial X}\right)+\frac{\partial }{\partial z}\left({\mu }_{nf}\frac{\partial U}{\partial Z}+\frac{\partial W}{\partial X}\right)\right],$$

(2)

$${\rho }_{nf}\left(U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}+W\frac{\partial V}{\partial Z}\right)=-\frac{\partial P}{\partial Y}+\left[\frac{\partial }{\partial X}\left({\mu }_{nf}\frac{\partial U}{\partial Y}+\frac{\partial V}{\partial X}\right)+\frac{\partial }{\partial Y}\left(2{\mu }_{nf}\frac{\partial V}{\partial Y}\right)+\frac{\partial }{\partial z}\left({\mu }_{nf}\frac{\partial U}{\partial Z}+\frac{\partial W}{\partial X}\right)\right],$$

(3)

$${\rho }_{nf}\left(U\frac{\partial W}{\partial X}+V\frac{\partial W}{\partial Y}+W\frac{\partial W}{\partial Z}\right)=-\frac{\partial P}{\partial Z}+\left[\frac{\partial }{\partial X}\left({\mu }_{nf}\frac{\partial U}{\partial Y}+\frac{\partial W}{\partial X}\right)+\frac{\partial }{\partial Y}\left({\mu }_{nf}\frac{\partial V}{\partial Z}+\frac{\partial W}{\partial Y}\right)+\frac{\partial }{\partial Z}\left(2{\mu }_{nf}\frac{\partial W}{\partial Z}\right)\right].$$

(4)

Energy equation

$$U\frac{\partial T}{\partial X}+V\frac{\partial T}{\partial Y}+W\frac{\partial T}{\partial Z}={\alpha }_{nf}\left(\frac{{\partial }^{2}T}{\partial X^2}\right)+\left(\frac{{\partial }^{2}T}{\partial Y^2}\right)+\left(\frac{{\partial }^{2}T}{\partial Z^2}\right)$$

(5)

The yield stress fluid can be described by the Bingham–Papanastasiou model [25] as the following relation:

$$\mu ={\mu }_0+\frac{\tau }{\dot{\gamma }}\exp \left(1-m\dot{\gamma }\right)$$

(6)

where ${\mu }_0$ indicates constant viscosity and represents yield stress, $\tau$ refers to the fluid’s shear stress, $m$ is the stress growth exponent, also known as a regularization parameter, and $\dot{\gamma }$ is the shear rate.

Dimensionless parameters [24]

$$X^{*}=\frac{2X}{D},Y^{*}=\frac{2Y}{D}, z^{*}=\frac{2z}{D},U^{*}=\frac{U}{\pi ND},V^{*}=\frac{V}{\pi ND}, W^{*}=\frac{W}{\pi ND}, P^{*}=\frac{P}{\rho {\left(\pi ND\right)}^2}, {\dot{ \gamma }}^{*}=\frac{2}{\pi N{D}^2}\gamma , T^{*}=\frac{T-T_C}{T_h-T_C}$$

(7)

Dimensionless equation

Continuity equation

$$\frac{\partial U^{*}}{\partial X}+\frac{\partial V^{*}}{\partial Y}+\frac{\partial W^{*}}{\partial Z}=0$$

(8)

Momentum equation

$$U^{\ast }\frac{\partial U^{\ast }}{\partial X}+V^{\ast }\frac{\partial U^{\ast }}{\partial Y}+W^{\ast }\frac{\partial U^{\ast }}{\partial Z}=\frac{2}{\pi }{\left(\frac{d}{D}\right)}^2\frac{{\rho }_f}{{\rho }_{nf}}{(1-\varnothing )}^{-2.5}\frac{1}{Re}\left\{\begin{array}{l}\frac{\partial }{\partial X^{\ast }}\left[2\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\frac{\partial U^{\ast }}{\partial X^{\ast }}\right]\hfill \\ +\frac{\partial }{\partial Y^{\ast }}\left[\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\left(\frac{\partial U^{\ast }}{\partial Y^{\ast }}+\frac{\partial V^{\ast }}{\partial X^{\ast }}\right)\right]\hfill \\ +\frac{\partial }{\partial Z^{\ast }}\left[\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\left(\frac{\partial U^{\ast }}{\partial Z^{\ast }}+\frac{\partial W^{\ast }}{\partial X^{\ast }}\right)\right]\hfill \end{array}\right\}$$

(9)

$$U^{\ast }\frac{\partial V^{\ast }}{\partial X}+V^{\ast }\frac{\partial V^{\ast }}{\partial Y}+W^{\ast }\frac{\partial V^{\ast }}{\partial Z}=\frac{2}{\pi }{\left(\frac{d}{D}\right)}^2\frac{{\rho }_f}{{\rho }_{nf}}{(1-\varnothing )}^{-2.5}\frac{1}{Re}\left\{\begin{array}{l}\frac{\partial }{\partial Y^{\ast }}\left[2\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\frac{\partial V^{\ast }}{\partial Y^{\ast }}\right]\hfill \\ +\frac{\partial }{\partial X^{\ast }}\left[\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\left(\frac{\partial U^{\ast }}{\partial Y^{\ast }}+\frac{\partial V^{\ast }}{\partial X^{\ast }}\right)\right]\hfill \\ +\frac{\partial }{\partial Z^{\ast }}\left[\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\left(\frac{\partial V^{\ast }}{\partial Z^{\ast }}+\frac{\partial W^{\ast }}{\partial Y^{\ast }}\right)\right]\hfill \end{array}\right\}$$

(10)

$$U^{\ast }\frac{\partial W^{\ast }}{\partial X}+W^{\ast }\frac{\partial U^{\ast }}{\partial Y}+W^{\ast }\frac{\partial W^{\ast }}{\partial Z}=\frac{2}{\pi }{\left(\frac{d}{D}\right)}^2\frac{{\rho }_f}{{\rho }_{nf}}{(1-\varnothing )}^{-2.5}\frac{1}{Re}\left\{\begin{array}{l}\frac{\partial }{\partial Z^{\ast }}\left[2\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\frac{\partial V^{\ast }}{\partial Z^{\ast }}\right]\hfill \\ +\frac{\partial }{\partial X^{\ast }}\left[\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\left(\frac{\partial U^{\ast }}{\partial Z^{\ast }}+\frac{\partial W^{\ast }}{\partial X^{\ast }}\right)\right]\hfill \\ +\frac{\partial }{\partial Y^{\ast }}\left[\left(1+\frac{Bn}{{\gamma }^{\ast }}\left(1-\exp \left(-M{\dot{\gamma }}^{\ast }\right)\right)\right)\left(\frac{\partial V^{\ast }}{\partial Z^{\ast }}+\frac{\partial W^{\ast }}{\partial Y^{\ast }}\right)\right]\hfill \end{array}\right\}$$

(11)

Energy equation

$$U^{*}\frac{\partial T^{*}}{\partial X^{*}}+V^{*}\frac{\partial T^{*}}{\partial Y^{*}}+W^{*}\frac{\partial T^{*}}{\partial Z^{*}}={\left(\frac{d}{D}\right)}^2\frac{{\alpha }_{nf}}{{\alpha }_f}\frac{1}{Re Pr}\left(\left(\frac{{\partial }^2{T}^{*}}{\partial X^{*2}}\right)+\left(\frac{{\partial }^2{T}^{*}}{\partial Y^{*2}}\right)+\left(\frac{{\partial }^2{T}^{*}}{\partial Z^{*2}}\right)\right)$$

(12)

Fluid base viscosity

$${\mu }_f={\mu }_p+\frac{{\tau }_0}{\gamma }\left(1-\exp \left(-m\gamma \right)\right)$$

(13)

Dimensionless viscosity

$${\mu }_f^{*}=1+\frac{Bn}{{\dot{\gamma }}^{*}}\left(1-\exp \left(-M{\dot{\gamma }}^{*}\right)\right)$$

(14)

The nanofluid viscosity is given by Brinkman’s formula as follows [26]:

$${\mu }_{nf}={\mu }_f{\left(1-\phi \right)}^{2.5}$$

(15)

$${\rho }_{nf}=\phi {\rho }_p+\left(1-\phi \right){\rho }_f$$

(16)

$${(\rho C_p)}_{nf}=\phi {(\rho C_p)}_p+\left(1-\phi \right){(\rho C_p)}_f$$

(17)

The thermal diffusivity of the base fluid and nanofluid are as follows [26]:

$${\alpha }_{nf}=\frac{k_{nf}}{{\left(\rho c_p\right)}_{nf}}, {\alpha }_{bf}=\frac{k_{bf}}{{\left(\rho c_p\right)}_{bf}}$$

(18)

The dimensionless number shown in the dimensionless equation is calculated by the formula as presented in [24,25]:

• Reynolds number:

  $$Re=\frac{\rho N{d}^2}{\mu }$$

  (19)
• Bingham number:

  $$Bn=\frac{\tau D}{{\mu }_{p}N}$$

  (20)
• Nusselt number:

  $$Nu=\frac{k_{nf}}{k_f}{\displaystyle \int }\frac{\partial T}{\partial X}+\frac{\partial T}{\partial Y}+\frac{\partial T}{\partial Z}$$

  (21)
• Power consumption:

  $$Np=\frac{P}{\rho N^3{d}^5}$$

  (22)

  $$P={{\displaystyle \int }}_{A}2\pi N·\left(x{F}_y-y{F}_x\right)·dA$$

  (23)

4. Validation

First of all, in the presentation of our results, it is necessary to validate and check their accuracy by comparing our findings with the previous numerical studies in the literature. In this section, we refer to the work of Ref. [27] on the 2D numerical investigation of mixing viscoplastic fluid inside a stirred tank. We are using the same rheological and geometrical characterization of a stirred system, with the working fluid being Bingham with rheological details $\mu =0.1$, $\tau =0.1$ with inertia value ($Re=13.8$). Our results (Figure 3) are incredibly similar to the previous numerical results of Ref. [27].

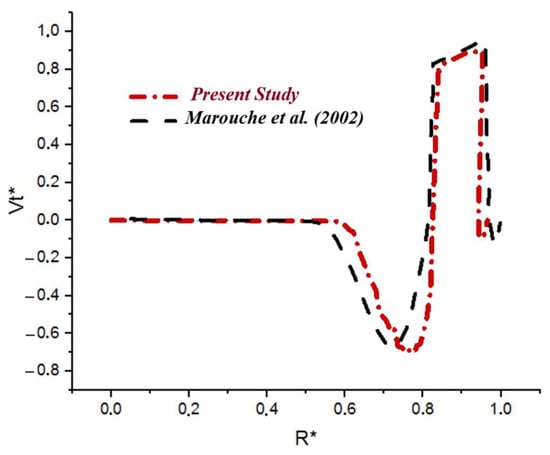
Figure 3. Comparison of tangential velocity distribution outcomes along the impeller plan for $Re=13.8$ with the findings of Ref. [27].

5. Results and Discussions

5.1. Effect of Rheology

The flow pattern is an important criterion for previewing the mixing performance in a stirred tank system. The flow pattern is affected by the rotational speed of the anchor impeller and its design. In this study, different Reynolds values have been investigated. Figure 4a,b illustrate the pattern of streamlined distribution along the stirred tank for different sectors (i.e., 3-dimensions and 2-dimensions sectors). To obtain more accurate analyses of the flow pattern inside the stirred tank, this study investigates different values of inertia ($Re=1, 10,$and$100$). Our finding revealed that there is a significant difference between the three cases, depending on the Reynolds number. The similarity of streamlining along the horizontal part of the vessel for the first inertia case ($Re=1$) is remarkable, which explains the dominance of tangential velocity in stirred vessels with very low axial velocity. In this case, it should be also noted the existence of vortex zones near the shaft of the vessel at low Reynolds values. Similar results were achieved by Ameur and Ghenaim [11].

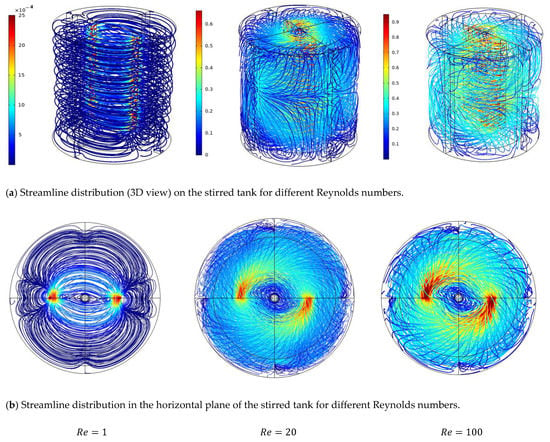
Figure 4. Streamline distribution inside (a) the vessel volume and (b) along the horizontal section.

With the increase in the Reynolds value ($Re=20, 100$) a radical change in the streamline shape was seen with a high-degree angle from the horizontal plane, becoming almost vertical. We also found an increase in the inertia effect on the dead zone region, where the increase in the Reynolds number lead to eliminating this dead zone ($Re=20, 100$). The correlation between the flow intensity and Reynolds numbers is interesting; it can be noted that an increase in the inertia affects the movement of fluids in the vertical direction and resulted in higher axial velocity in a stirred vessel.

Figure 5a,b illustrate the velocity magnitude and vectors filed velocity distribution along the vertical median plane and impeller plane. The results obtained from the preliminary analysis of velocity distribution show that the well-moving zone has been enlarged by the increase in the inertia value ($Re=20, 100$), and high-vector field density around impeller has been remarked, but generally, the flow direction does not deviate tangentially.

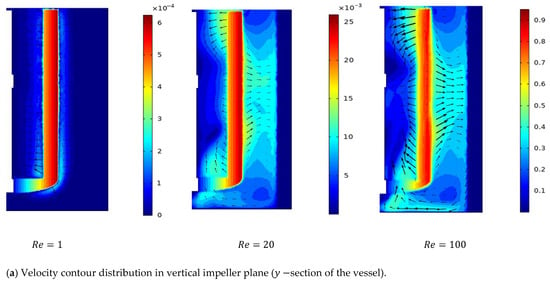
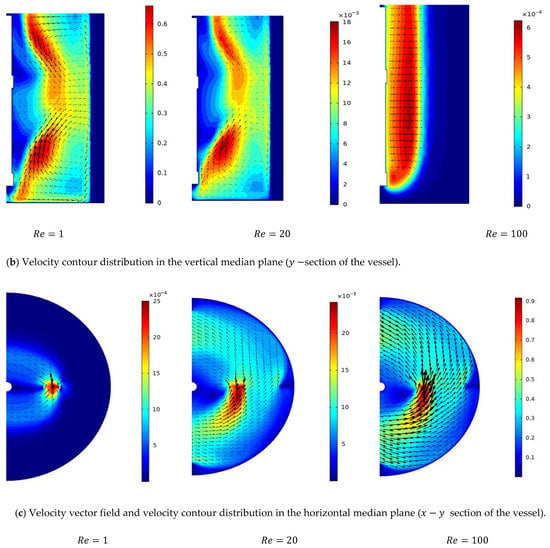
Figure 5. Velocity distribution in (a) the impeller plane, (b) the median plane, and (c) along the horizontal section.

Figure 5c presents the contour velocity on the horizontal section. There was a significant positive correlation between the inertia and moving well zone, and with the increase in the Reynolds number, an increase in the velocity magnitude is recorded in the impeller and median section. This means an important variation in flow intensity occurred along the stirred tank.

Figure 6a,b illustrate the velocity in the radial direction (median plane) and the tangential direction (impeller plane) on the horizontal section of the vessel. We can note that the maximum velocity on the median plane (radial velocity) is 0.15, and in the impeller plane (tangential velocity), it is 0.9. This explains the maximum velocities value at the anchor impeller tip, and it decays at the immediate contact with the side vessel wall. This means that the tangential flow is dominant on the vessel. These obtained results agree well with the finding of Refs. [11,16]. In addition, the obtained results have shown that inertia influences the improvement in fluid flow, expanding the moving zone on the vessel. In addition, the increase in the Reynolds number leads to an increased velocity value along the stirred tank.

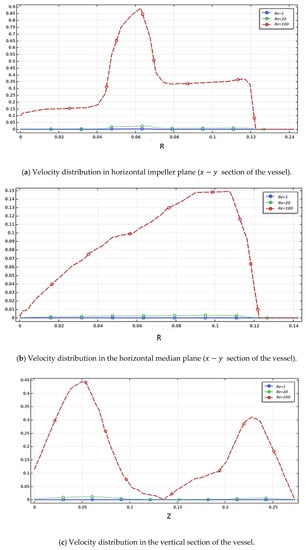
Figure 6. Velocity distribution for different positions inside the vessel.

Figure 6c illustrates the velocity distribution in the vertical axis of the vessel. It is apparent from this result that the increase in the inertia value led to the increase in velocity along the stirred tank, which confirms the impact of high inertia values on the improvement in the flow pattern along the stirred vessel. Figure 7 presents the power consumption as a function of different inertia values (the variation in inertia value is represented by the variation in the rotational speed of anchor impeller $N$). The results showed that with the increase in inertia, the energy consumed is decreased in the mixing system. We can note that this rise in inertia minimizes the cost of energy consumed in this stirred vessel.

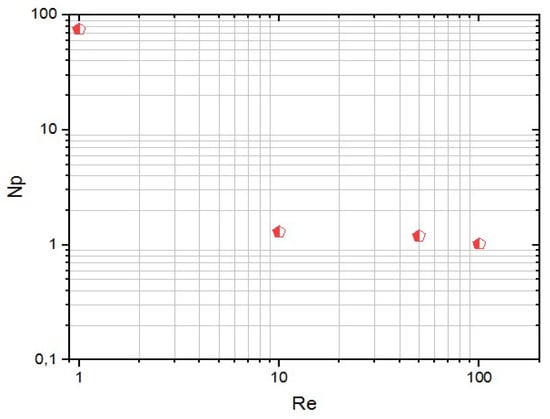
Figure 7. Power number versus the inertia value.

Figure 8a,b show the isothermal distribution in the vertical and the horizontal plane on the stirred tank for different Reynolds numbers ($Re=1, 20, 100$). The thermal contour is shown in Figure 8a,b. We can observe that along the radial direction (from the tank sidewall toward the anchor impeller field), a regularity in the thermal gradient field has been remarked for the Reynolds number ($Re=1, 20$). In these cases, the maximum temperature value is located at the sidewall region. However, a high inertia value ($Re=100$) causes a radical change in the thermal gradient behavior and significant increase in the temperature value on the most of vessel area; especially in the value $Re=100$, a deviation in the thermal line from the vertical direction to the horizontal direction explains the change in the flow pattern inside the stirred tank. This rise in the inertia parameters leads to accelerating the heat transfer and improves the flow pattern inside the stirred system.

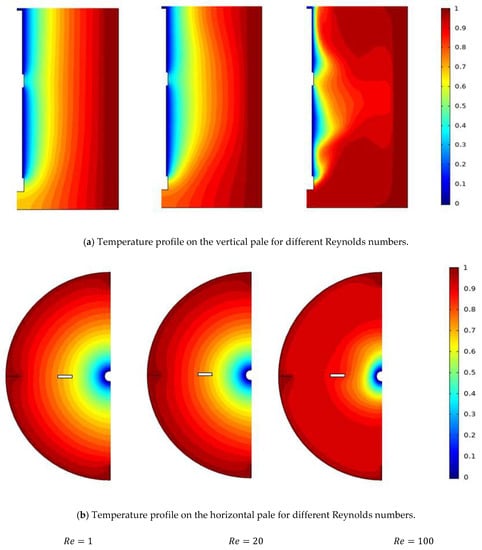
Figure 8. Temperature distribution on the (a) horizontal and (b) vertical position.

5.2. Impeller Design Effect

In this part, different geometrical designs of anchor impellers have been introduced into the mixing system for analyzing their effect on the thermo-hydrodynamics characteristics of stirred tanks. The anchor impeller classic was modified by adding an arm blade in the original shape at different positions. Three geometry configurations have been investigated in this work (Case 1 classical anchor impeller; Case 2 one blade added in the middle of the anchor impeller; Case 3 two blades added in the middle of the anchor impeller). Figure 9a,b show the velocity and vector field distribution on the vertical section in the vessel with different anchor impeller cases. A significant increase in the well-moving zone with an increase in the number of blades was remarked. For Case 1, a horizontal distribution in the vector field was seen, but we can see in Case 2 that the vector fields began to deviate slightly in the vertical direction. In Case 3, with two added blades, a deviation in the vector field from the horizontal direction to the axial direction was seen, which means a change in the flow pattern was found in these two cases (Case 2 and Case 3) in the axial direction. The best performance is for Case 3, which has an impact on changing the flow pattern along the stirred system and accelerating the flow along the vessel.

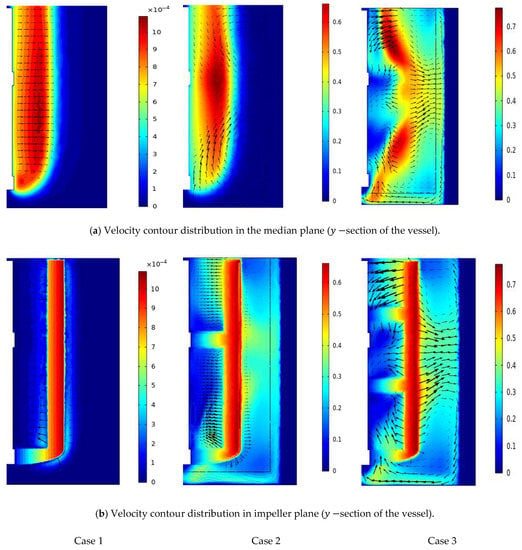
Figure 9. Velocity contour for different positions of (a) vertical section and (b) median plane impeller plane.

Figure 10 shows the isotherm distribution in the vertical section of the tank with different geometric configurations. From the results obtained, we can see that the increase in the number of blades leads to an increase in the temperature value along the stirred tank. The isotherm shown in Figure 10 is proportional to the pattern of streamline; this is related to the effect of forced convection on the stirred tank (deviation in the thermal gradient direction has been remarked for the case, comparatively with Case 1 and Case 2 that have a regularity in the thermal gradient distribution). Case 4 has a big effect on the acceleration of heat transfer and changes in thermal behavior in the stirred system.

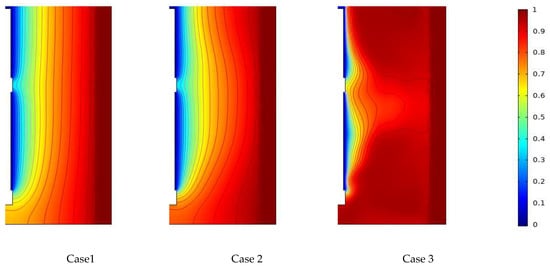
Figure 10. Temperature contour distribution in impeller plane (y-section of the vessel).

5.3. Effect of Adding Nanoparticles

Figure 11a–c represent the impact of adding nanoparticles on the thermal behavior inside the stirred system. We can analyze the distribution of the temperature value along the three axes in the vessel’s $x-y$ and $z$ sections for different volume fractions ($\mathsf{Ø}=0.02, 0.06, 0.1$). From the findings data of Figure 11, we can remark that the increase in the volume fraction leads to an increase in the heat transfer, especially on the impeller plane, contrary to the median plane’s low deference between the temperature for all the volume fraction values ($\mathsf{Ø}=0.02, 0.06, 0.1$).

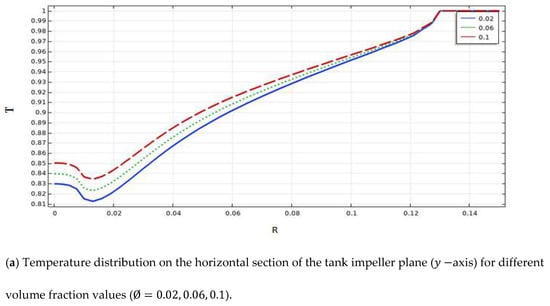
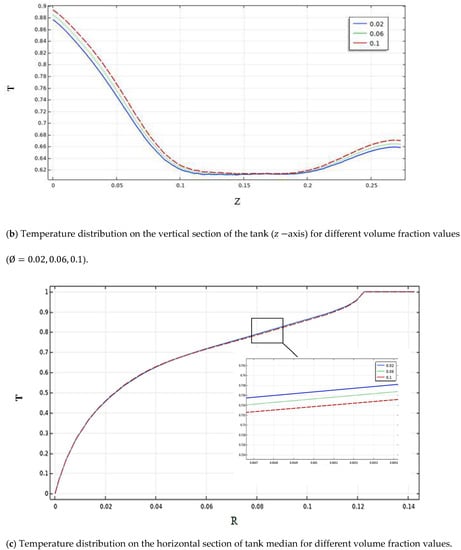
Figure 11. Temperature distribution on the horizontal and vertical positions of the tank.

However, a significant increase in the temperature is related to the increase in the volume fraction in the stirred vessel. Other parameters can describe the rate of heat change inside the stirred system exactly. We can observe by analyzing the Nusselt number variations with different volume fractions and the influence of adding nanoparticles on the thermal behavior inside the stirred tank. From Figure 12, the result showed that with the increase in the nanoparticles density or volume fraction, an increase in the Nusselt value occurs. This explains how the rise in the nanoparticles a positive impact has on enhancing and improving the thermal behavior along the stirred vessel. Figure 13 illustrates the energy consumed as a function of different volume fraction values. From the findings, this results in a low volume fraction (0.02, 0.06) and a decrease in the power consumption along these values; however, for the volume fraction of 0.1, a higher power consumption is required, which explains, in this case, the minimum energy cost found for a lower fraction value.

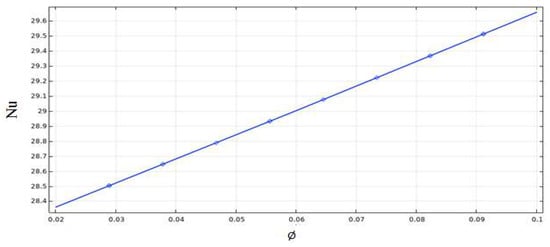
Figure 12. Nusselt average variation versus different volume fractions.

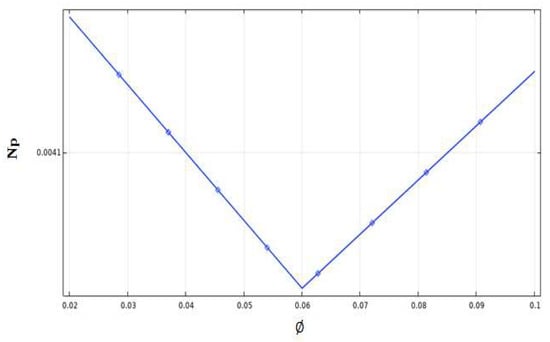
Figure 13. Power consumption as a function of different volume fractions.

6. Conclusions

This paper studied the hydro-thermal analysis of a viscoplastic-nanofluid (Bingham—Papanastasiou base fluid) with Al₂O₃ nanoparticles inside a stirred vessel equipped with different geometric anchor impeller agitator designs. This study aimed to investigate the effect of inertia on the mixing parameters (flow pattern, heat transfer, and power consumption). Various Reynolds numbers ($Re=1, 20, 100$) and volume fractions of nanoparticles ($\mathsf{Ø}=0.02, 0.06, 0.1$) were assessed.

Following the analysis of the findings, the following conclusions are deduced:

• The flow pattern inside the stirred tank shifted in consequence of the inertia parameters; an increase in the velocity was conducive to an increase in inertia inside the stirred tank.
• The tangential flow was relatively dominant in the stirred tank in the case of inertia absence or low Reynolds value ($Re=1, 20$); however, a high Reynolds value ($Re=100$) resulted in shifting the flow pattern from the tangential to the axial direction.
• Heat transfer has been affected by the changing inertia parameter and the volume fraction. Furthermore, with high inertia ($Re=100$), we discovered that the inertia accelerated the heat transfer inside the stirred tank. In addition to the effect of nanoparticle density, however, the high value of the fraction volume led to increasing the heat transfer inside the stirred tank.
• Finally, there was a decrease in energy consumption inside the vessel, which was a consequence of the rise in inertia value.
• Overall, inertia has a high likelihood of improving flow patterns, enhancing heat transfer, and reducing power consumption levels, ultimately being a positive influence on the processes undergone in stirred tanks.

The current technique could be implemented in other fields of science and engineering, especially when related to the simulation of fluid dynamics in the future [28,29,30,31,32,33,34].