Energy of Vague Fuzzy Graph Structure and Its Application in Decision Making

Abstract

Vague graphs (VGs), belonging to the fuzzy graphs (FGs) family, have good capabilities when faced with problems that cannot be expressed by FGs. The notion of a VG is a new mathematical attitude to model the ambiguity and uncertainty in decision-making issues. A vague fuzzy graph structure (VFGS) is the generalization of the VG. It is a powerful and useful tool to find the influential person in various relations. VFGSs can deal with the uncertainty associated with the inconsistent and indeterminate information of any real-world problems where fuzzy graphs may fail to reveal satisfactory results. Moreover, VGSs are very useful tools for the study of different domains of computer science such as networking, social systems, and other issues such as bioscience and medical science. The subject of energy in graph theory is one of the most attractive topics that is very important in biological and chemical sciences. Hence, in this work, we extend the notion of energy of a VG to the energy of a VFGS and also use the concept of energy in modeling problems related to VFGS. Actually, our purpose is to develop a notion of VFGS and investigate energy and Laplacian energy (LE) on this graph. We define the adjacency matrix (AM) concept, energy, and LE of a VFGS. Finally, we present three applications of the energy in decision-making problems.

1. Introduction

In this modern epoch of technology, modeling uncertainties in engineering, computer sciences, social sciences, medical sciences, and economics is growing extensively. Classical mathematical methods are not always useful for dealing with such problems. FG models are advantageous mathematical tools for solving problems in various aspects. Fuzzy graphical models are obviously better than graphical models because of the natural existence of vagueness and ambiguity. The subject of a fuzzy set (FS) was introduced by Zadeh [1] in 1995. After the introduction of fuzzy sets, FS theory has included a large research field. Since then, the theory of FSs has become a vigorous area of research in different disciplines including life sciences, management, statistic, graph theory, and automata theory. The subject of FGs was proposed by Rosenfeld [2]. Kaufmann [3] presented the definitions of FGs from the Zadeh fuzzy relations in 1973. Akram et al. [4,5,6] introduced several concepts in FGs. Some of these product operations on FGs were presented by Mordeson and Peng [7]. Gau and Buehrer [8] proposed the concept of vague set (VS) in 1993 by replacing the value of an element in a set with a subinterval of $[0,1]$. One type of FG is VG. VGs have a variety of applications in other sciences, including biology, psychology, and medicine. Moreover, a VG can concentrate on determining the uncertainties coupled with the inconsistent and indeterminate information of any real-world problems where FGs may not lead to adequate results. Ramakrishna [9] introduced the concept of VGs and studied some of their properties. After that, Akram et al. [10] introduced vague hypergraphs. Borzoei and Rashmanlou [11,12,13] investigated different subjects of VGs. Rao et al. [14,15,16] studied certain properties of domination in vague incidence graphs. Shi et al. [17,18] investigated the domination of product VGs with an application in transportation. Qiang et al. [19] defined novel concepts of domination in vague graphs. New concepts of coloring in vague graphs are presented by Krishna [20]. A graph structure (GS) is a generalization of simple graphs. GSs are very useful in the study of different domains of computer science and computational intelligence. Borzoei and Rashmanlou [21] presented the concept of the maximal product of graphs under a vague environment. Akram et al. [22,23,24] investigated certain types of vague cycles, vague trees, and Cayley vague graphs. First, Sampathkumar [25] introduced the notion of a GS. Fuzzy graph structures (FGSs) are more useful than GSs because they involve the uncertainty and ambiguity of many real-world phenoms. Dinesh [26] introduced the notion of FGSs and investigated some related concepts. Ramakrishna and Dinesh [27] expressed generalized FGSs. Kosari et al. [28,29] presented the notion of VG structure with an application in the medical diagnosis, and they studied a novel description of VG with an application in transportation systems. VGSs are the generalization of FGSs and are powerful tools in the explanation of some structures. Moreover, VFGSs are more applicable than GSs because they confront the uncertainty and ambiguity of many real-world problems. Specific properties of a VFGS are investigated, including the order of a VFGS, the degree of a vertex, and various types of energy in VFGS. Talebi et al. [30] studied the interval-valued fuzzy graph with an application in energy industry management.

Tchier et al. [31] expressed a new group decision-making technique under picture fuzzy soft expert information. Alolaiyan et al. [32] presented a novel MADM framework under q-Rung orthopair fuzzy bipolar soft sets. Akram et al. [33,34] introduced a new notion of pythagorean fuzzy matroids with application and also expressed new results of group decision-making with fermatean fuzzy soft expert knowledge.

Gutman [35], in 1978, presented the notion of graph energy. Certain bounds on energy are discussed in [36,37,38]. The energy of the graph is extended to the energy of FG by Anjali and Sunil Mathew [39] in 2013. Moreover, the energy of an FG is extended to the energy of an intuitionistic fuzzy graph by Praba and Deepa [40] in 2014. Naz et al. [41] extended the energy of an FG to the energy of a bipolar fuzzy graph in 2018. Shi et al. [42] extended the energy on picture fuzzy graphs in 2022. In 2006, Gutman and Zhou [43] defined the Laplacian energy (LE) of a graph as the sum of the absolute deviations (i.e., the distance from the mean) of the eigenvalues of its Laplacian Matrix (LM). Although VGs are better at expressing uncertain variables than FGs, they do not perform well in many real-world situations, such as IT management. Therefore, when the data come from several factors, it is necessary to use VFGSs. Belonging to the FG family, VFGSs have good capabilities when facing problems that cannot be expressed by VGs and GSs. VFGSs have several applications in real-life systems and applications where the level of information inherited in the system varies with time and has different accuracy levels. In this paper, we developed the energy on a VFGS and investigated its properties. We want to solve real problems through the energy applications of this graph. Considering the decision making, a method was suggested to rank the available options using the VFGS and its LE.

2. Preliminaries

Definition 1

([30]). A fuzzy graph on a graph $G^{*}=(W,E)$ is a pair $G=(\xi ,\chi )$ where ξ is a fuzzy set on W, and χ is a fuzzy set on E, such that,

$$\chi \left(vz\right)\le min\left\{\xi \right(v),\xi (z\left)\right\},$$

for all $vz\in E.$

Definition 2

([8]). A vague set (VS) Q is a pair $(t_Q,f_Q)$ on set W, where $t_Q$ and $f_Q$ are real valued functions which can be defined on $W\to [0,1]$ so that, $t_Q\left(v\right)+f_Q\left(v\right)\le 1,\forall v\in W.$

Definition 3

([9,21]). Suppose $G^{*}=(W,E)$ is a graph. A pair $G=(Q,R)$ is named a VG on graph $G^{*}=(W,E)$, where $Q=(t_Q,t_Q)$ is a VS on W and $R=(t_R,f_R)$ is a vague relation on W such that,

$$t_R(v,z)\le min\{t_Q\left(v\right),t_Q\left(z\right)\},$$

$$f_R(v,z)\ge max\{f_Q\left(v\right),f_Q\left(z\right)\},$$

for all $v,z\in W$. Note that R is called vague relation on Q. A VG G is named strong if

$$t_R\left(vz\right)=min\{t_Q\left(v\right),t_Q\left(z\right)\},$$

$$f_R\left(vz\right)=max\{f_Q\left(v\right),f_Q\left(z\right)\},$$

for all $v,z\in W.$

Definition 4

([12]). Suppose $G=(Q,R)$ is a VFG on $G^{*}$, the degree of vertex v is defined as $\mathfrak{D}\left(v\right)=({\mathfrak{D}}_t\left(v\right),{\mathfrak{D}}_f\left(v\right))$, where

$${\mathfrak{D}}_t\left(v\right)=\sum _{v\ne z,z\in W}{t}_R\left(vz\right),{\mathfrak{D}}_f\left(v\right)=\sum _{v\ne z,z\in W}{f}_R\left(vz\right).$$

The order of G is defined as

$$O\left(G\right)=\left(\sum _{v\in W}{t}_Q\left(v\right),\sum _{v\in W}{f}_Q\left(v\right)\right).$$

Definition 5

([25]). A graph structure (GS) $G^{*}=(W,E_1,E_2,\dots ,E_n)$ contains a non-empty set W with relations $E_1,E_2,\dots ,E_n$ on set W that are separated such that each relation $E_i,1\le i\le n$ is symmetric and irreflexive. The GS $G^{*}=(W,E_1,E_2,\dots ,E_n)$ can be described as similar as a graph, where each edge is labeled as $E_i,1\le i\le n$.

Definition 6

([27]). Suppose ζ be the FS on W and ${\tau }_1,{\tau }_2,\dots ,{\tau }_n$ be FSs on $E_1,E_2,\dots ,E_n$, respectively. If $0\le {\tau }_i\left(vz\right)\le min\{\tau \left(v\right),\tau \left(z\right)\}$ for all $v,z\in W,i=1,2,\dots ,n$, then $G=(\zeta ,{\tau }_1,{\tau }_2,\dots ,{\tau }_n)$ is called FGS of GS $G^{*}$.

$G=(Q,R_1,R_2,\dots ,R_n)$ is named a VFGS of a GS $G^{*}=(W,E_1,E_2,\dots ,E_n)$ if $Q=(t_Q,f_Q)$ is a VS on W, and for every $i=1,2,\dots ,n$, $R_i=(t_{R_i},f_{R_i})$ is a VS on $E_i$ such that:

$$t_{R_i}\left(vz\right)\le min\{t_Q\left(v\right),t_Q\left(z\right)\},$$

$$f_{R_i}\ge max\{f_Q\left(v\right),f_Q\left(z\right)\},$$

$\forall vz\in E_i\subset W\times W.$

Note that $t_{R_i}\left(vz\right)=0=f_{R_i}\left(vz\right)$, for all $vz\in W\times W-E_i$ and $0\le t_{R_i}\left(vz\right)\le 1,0\le f_{R_i}\left(vz\right)\le 1$, $vz\in E_i$, where W and $E_i(i=1,2,\dots ,n)$ are named the underlying vertex set and underlying i-edge set of G, respectively.

Example 1.

Consider a graph structure $G^{*}=(W,E_1,E_2,E_3)$, where $W=\{a,b,c,d,e,f\}$, $E_1=\{ab,cd\}$, $E_2=\{bc,ed\}$, and $E_3=\{be,ef\}$. Suppose Q, $R_1$, $R_2$, and $R_3$ is a vague fuzzy subset of W, $E_1$, $E_2$, and $E_3$, respectively, such that

$Q=\{<a,(0.2,0.5)>,<b,(0.2,0.5)>,<c,(0.4,0.7)>,<d,(0.3,0.5)>,<e,(0.1,0.5)>,<,f,(0.4,0.9)>\},$

$R_1=\{<ab,(0.2,0.7)>,<cd,(0.3,0.8)>\},$

$R_2=\{<bc,(0.2,0.7)>,<de,(0.1,0.6)>\},$

$R_3=\{<be,(0.1,0.7)>,<ef,(0.1,0.9)>\}.$

Then, $G=(Q,R_1,R_2,R_3)$ is a VFGS on $G^{*}$ as shown in Figure 1.

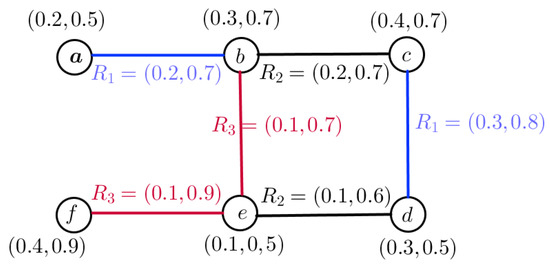
Figure 1. VFGS $G=(Q,R_1,R_2,R_3).$

Definition 7.

Two vertices that are connected by an edge are named adjacent. The AM $\mathcal{A}=\left[v_{pq}\right]$ for a graph $G^{*}=(W,E)$ is a matrix with n rows and m columns, $n=\left|V\right|$, and its entries are defined by

$$v_{pq}=\left\{\begin{array}{cc}1\hfill & if(z_p,z_q)\in E\hfill \\ 0\hfill & ifotherwise.\hfill \end{array}\right.$$

Definition 8.

The spectrum of a matrix is defined as a set of its eigenvalues, and we denote it with $SP\left(G\right)$. The eigenvalues ${\gamma }_p$, $p=1,2,\dots ,l$ of the AM of G are the eigenvalues of G. The spectrum ${\gamma }_1,{\gamma }_2,\dots ,{\gamma }_l$ of the AM of G is the $SP\left(G\right)$; the eigenvalues of the graph satisfy the following relations:

$$\sum _{p=1}^l{\gamma }_p=0,\sum _{p=1}^l{\gamma }_p^2=2k.$$

Definition 9.

The energy of a graph G is denoted by $\mathcal{E}\left(G\right)$ and is defined as the sum of the absolute values of the eigenvalues of $\mathcal{A}$, that is,

$$\mathcal{E}\left(G\right)=\sum _{p=1}^l\left|{\gamma }_p\right|,$$

where ${\gamma }_p$ is an eigenvalues of $\mathcal{A}.$

Theorem 1.

Suppose that G is a graph with l vertices and k edges and $\mathcal{A}$ is the AM of G then

$$\sqrt{2k+{l(l-1)\left|\mathcal{A}\right|}^{\frac{2}{l}}}\le \mathcal{E}\left(G\right)\le \sqrt{2kl}.$$

All the essential notations are shown in Table 1.

Table 1. Some essential notations.

Notation	Meaning
FS	Fuzzy Set
FG	Fuzzy Graph
VS	Vague Set
VG	Vague Graph
GS	Graph Structure
AM	Adjacency Matrix
LE	Laplacian Energy
LM	Laplacian Matrix
FGS	Fuzzy Graph Structure
VFGS	Vague Fuzzy Graph Structure
VFA	Vague Fuzzy Averaging
VFE	Vague Fuzzy Element
VFPR	Vague Fuzzy Preference Relation
VFWA	Vague Fuzzy Weighted Averaging

3. Energy of a Vague Fuzzy Graph Structure

In this section, we express a new notion of the extension of the energy of an FGS called VFGS. We define the notion of energy of a VFGS which can be used in real science.

Definition 10.

The AM $\mathcal{A}\left(G\right)$ of a VFGS, $G=(Q,R_1,R_2,\dots ,R_n)$ is defined as $\mathcal{A}\left(G\right)=(A{R}_1,A{R}_2,\dots ,A{R}_n)$, where $A{R}_i$, $(i=1,2,\dots ,n)$ is a square matrix as $\left[v_{pq}\right]$ in which $v_{pq}^{\left(i\right)}=(t_{pq}^{\left(i\right)},f_{pq}^{\left(i\right)})$, where $t_{pq}^{\left(i\right)}=t_{R_i}\left(z_p{z}_q\right)$ and $f_{pq}^{\left(i\right)}=f_{R_i}\left(z_p{z}_q\right)$ represent the strength of relationship between $z_p$ and $z_q$, respectively.

Definition 11.

The energy of a VFGS $G=(Q,R_1,R_2,\dots ,R_n)$ is defined as the following:

$$\mathcal{E}\left(G\right)=<\mathcal{E}\left(A{R}_i\right)>,1\le i\le n$$

with

$$\mathcal{E}\left(A{R}_i\right)=\left(\sum _{p=1}^l|{\left({\eta }_p\right)}_{R_i}|,\sum _{p=1}^l\left|{\left({\varphi }_p\right)}_{R_i}\right|\right),$$

where ${\left({\eta }_p\right)}_{R_i}$ and ${\left({\varphi }_p\right)}_{R_i}$ are eigenvalues of $\mathcal{A}\left(t_{R_i}\left(z_p{z}_q\right)\right)$ and $\mathcal{A}\left(f_{R_i}\left(z_p{z}_q\right)\right)$, respectively.

Example 2.

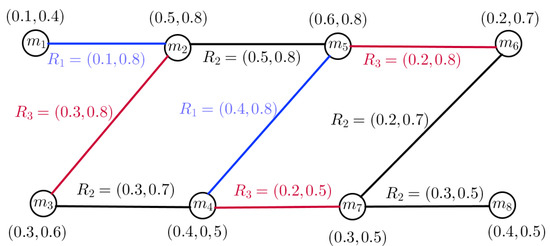
Consider a GS $G^{*}=(W,E_1,E_2,E_3)$, where $W=\{m_1,m_2,m_3,m_4,$ $m_5,m_6,m_7,m_8\},E_1=\{m_1{m}_2,m_4{m}_5\}$, $E_2=\{m_2{m}_5,m_3{m}_4,m_6{m}_7,m_7{m}_8\}$, and $E_3=\{m_5{m}_6,m_2{m}_3,m_4{m}_7\}$. Suppose Q, $R_1$, $R_2$, and $R_3$ is a vague fuzzy subset of W, $E_1$, $E_2$, and $E_3$, respectively, then, $G=(Q,R_1,R_2,R_3)$ is a VFGS on $G^{*}$ as shown in Figure 2, such that

Figure 2. VFGS $G=(Q,R_1,R_2,R_3).$

$$\begin{gathered} Q=\{<m_1(0.1,0.4)>,<m_2(0.5,0.8)>,<m_3(0.3,0.6)>,<m_4(0.4,0.5)>, \\ <m_5(0.6,0.8)>,<m_6(0.2,0.7)>,<m_7(0.3,0.5)>,<m_8(0.4,0.5)>\} \end{gathered}$$

$$R_1=\{<m_1{m}_2(0.1,0.8)>,<m_4{m}_5(0.4,0.8)>\},$$

$$R_2=\{<m_2{m}_5(0.5,0.8)>,<m_3{m}_4(0.3,0.7)>,<m_6{m}_7(0.2,0.7)>,<m_7{m}_8(0.3,0.5)>\},$$

$$R_3=\{<m_5{m}_6(0.2,0.8)>,<m_2{m}_3(0.3,0.8)>,<m_4{m}_7(0.2,0.5)>\}.$$

The AMs and energy of each degree of G are obtained as follows:

$$\mathcal{A}\left(t_{R_1}\right)=\left[\begin{array}{cccccccc}0& 0.1& 0& 0& 0& 0& 0& 0\\ 0.1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0.4& 0& 0& 0\\ 0& 0& 0& 0.4& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_1}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_1}\right|=1$$

$$\mathcal{A}\left(f_{R_1}\right)=\left[\begin{array}{cccccccc}0& 0.8& 0& 0& 0& 0& 0& 0\\ 0.8& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0.8& 0& 0& 0\\ 0& 0& 0& 0.8& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(f_{R_1}\right)\right)=\sum _{p=1}^l\left|{\left({\varphi }_p\right)}_{R_1}\right|=3.2$$

$$\mathcal{A}\left(t_{R_2}\right)=\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0.5& 0& 0& 0\\ 0& 0& 0& 0.3& 0& 0& 0& 0\\ 0& 0& 0.3& 0& 0& 0& 0& 0\\ 0& 0.5& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0.2& 0\\ 0& 0& 0& 0& 0& 0.2& 0& 0.3\\ 0& 0& 0& 0& 0& 0& 0.3& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_2}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_2}\right|=2.32$$

$$\mathcal{A}\left(f_{R_2}\right)=\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0.8& 0& 0& 0\\ 0& 0& 0& 0.7& 0& 0& 0& 0\\ 0& 0& 0.7& 0& 0& 0& 0& 0\\ 0& 0.8& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0.7& 0\\ 0& 0& 0& 0& 0& 0.7& 0& 0.5\\ 0& 0& 0& 0& 0& 0& 0.5& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(f_{R_2}\right)\right)=\sum _{p=1}^l\left|{\left({\varphi }_p\right)}_{R_2}\right|=4.72$$

$$\mathcal{A}\left(t_{R_3}\right)=\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0.3& 0& 0& 0& 0& 0\\ 0& 0.3& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0.2& 0\\ 0& 0& 0& 0& 0& 0.2& 0& 0\\ 0& 0& 0& 0& 0.2& 0& 0& 0\\ 0& 0& 0& 0.2& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_3}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_3}\right|=1.4$$

$$\mathcal{A}\left(f_{R_3}\right)=\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0.8& 0& 0& 0& 0& 0\\ 0& 0.8& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0.5& 0\\ 0& 0& 0& 0& 0& 0.8& 0& 0\\ 0& 0& 0& 0& 0.8& 0& 0& 0\\ 0& 0& 0& 0.5& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(f_{R_3}\right)\right)=\sum _{p=1}^l\left|{\left({\varphi }_p\right)}_{R_3}\right|=4.2$$

Therefore, the energy of a VFGS $G=(Q,R_1,R_2,R_3)$ is equal to

$$\mathcal{E}\left(G\right)=<(1,3.2),(2.32,4.72),(1.4,4.2)>.$$

Theorem 2.

Suppose that $G=(Q,R_1,R_2,\dots ,R_n)$ is a VFGS and $\mathcal{A}\left(G\right)$ is its AM. If ${\left({\eta }_1\right)}_{R_i}\ge {\left({\eta }_2\right)}_{R_i}\ge \dots \ge {\left({\eta }_n\right)}_{R_i}$ and ${\left({\varphi }_1\right)}_{R_i}\ge {\left({\varphi }_2\right)}_{R_i}\ge \dots \ge {\left({\varphi }_n\right)}_{R_i}$ are the eigenvalues of $\mathcal{A}\left(t_{R_i}\left(v_p{v}_q\right)\right)$ and $\mathcal{A}\left(f_{R_i}\left(v_p{v}_q\right)\right)$, respectively, then,

$$I)\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}=0,\sum _{p=1}^l{\left({\varphi }_p\right)}_{R_i}=0.$$

$$II)\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}^2=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2,\sum _{p=1}^l{\left({\varphi }_p\right)}_{R_i}^2=2\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2,$$

Proof. 

(I)

Since ${\mathcal{A}}_{R_i}\left(G\right)$ is a symmetric matrix with zero trace, its eigenvalues are real with a sum equal to zero.

(II)

By effect properties of the matrix, we have

$$tr\left({\left(\mathcal{A}\left(t_{R_i}\left(z_p{z}_q\right)\right)\right)}^2\right)=\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}^2,$$

where

$$tr\left({\left(\mathcal{A}\left(t_{R_i}\left(z_p{z}_q\right)\right)\right)}^2\right)={(0+\left(t_{R_i}\left(z_1{z}_2\right)\right))}^2+\dots +{\left(t_{R_i}\left(z_1{z}_l\right)\right)}^2$$

$$+{\left(t_{R_i}\left(z_2{z}_1\right)\right)}^2+0+\dots +{\left(t_{R_i}\left(z_2{z}_l\right)\right)}^2$$

$$⋮$$

$$+{\left(t_{R_i}\left(z_l{z}_1\right)\right)}^2+{\left(t_{R_i}\left(z_l{z}_2\right)\right)}^2+\dots +0)=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2.$$

Hence,

$$\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}^2=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2.$$

Moreover, we have,

$$tr\left({\left(\mathcal{A}\left(f_{R_i}\left(z_p{z}_q\right)\right)\right)}^2\right)=\sum _{p=1}^l{\left({\varphi }_p\right)}_{R_i}^2,$$

where

$$tr\left({\left(\mathcal{A}\left(f_{R_i}\left(z_p{z}_q\right)\right)\right)}^2\right)=(0+{\left(f_{R_i}\left(z_1{z}_2\right)\right)}^2+\dots +{\left(f_{R_i}\left(z_1{z}_l\right)\right)}^2$$

$$+{\left(f_{R_i}\left(z_2{z}_1\right)\right)}^2+0+\dots +{\left(f_{R_i}\left(z_2{z}_l\right)\right)}^2$$

$$⋮$$

$$+{\left(f_{R_i}\left(z_l{z}_1\right)\right)}^2+{\left(f_{R_i}\left(z_l{z}_2\right)\right)}^2+\dots +0)=2\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2.$$

Hence,

$$\sum _{p=1}^l{\left({\varphi }_p\right)}_{R_i}^2=2\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2.$$

□

Theorem 3.

Let $G=(Q,R_1,R_2,\dots ,R_n)$ be a VFGS and ${\mathcal{A}}_{R_i}\left(G\right)$ be the AM of G. Then,

(I)

$$\sqrt{2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+l(l-1){\left|det\left(\mathcal{A}\left(t_{R_i}\left(z_p{z}_q\right)\right)\right)\right|}^{{\displaystyle \frac{2}{l}}}}$$

$$\le \mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \sqrt{2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}.$$

(II)

$$\sqrt{2\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2+l(l-1){\left|det\left(\mathcal{A}\left(f_{R_i}\left(z_p{z}_q\right)\right)\right)\right|}^{{\displaystyle \frac{2}{l}}}}$$

$$\le \mathcal{E}\left(f_{R_i}\left(z_p{z}_q\right)\right)\le \sqrt{2\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2}.$$

Proof. 

(I) Applying Cauchy–Schwarz inequality to the vectors $(1,1,\dots ,1)$ and $\left(\right|{\left({\eta }_1\right)}_{R_i}|,|{\left({\eta }_2\right)}_{R_i}|,\dots ,|{\left({\eta }_n\right)}_{R_i}\left|\right)$ with n entries, we obtain:

$$\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_i}\right|\le \sqrt{l}\sqrt{\sum _{p=1}^l{\left|{\left({\eta }_p\right)}_{R_i}\right|}^2},\left(1\right)$$

$${\left(\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}\right)}^2=\sum _{p=1}^l{\left|{\left({\eta }_p\right)}_{R_i}\right|}^2+2\sum _{1\le p\le q\le l}{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}.\left(2\right)$$

By comparing the coefficients of ${\left({\eta }_{{}_{R_i}}\right)}^{l-2}$ in the characteristic polynomial

$$\prod _{p=1}^l(\left({\eta }_{{}_{R_i}}\right)-{\left({\eta }_p\right)}_{R_i})=|{\mathcal{A}}_{R_i}\left(G\right)-{\left({\eta }_p\right)}_{R_i}|,$$

we have

$$\sum _{1\le p\le q\le l}{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}=-\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2.\left(3\right)$$

By replacing (3) in (2), we obtain

$$\sum _{p=1}^l{\left|{\left({\eta }_p\right)}_{R_i}\right|}^2=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2,\left(4\right).$$

Replacing (4) in (1), we obtain:

$$\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_i}\right|\le \sqrt{l}\sqrt{2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}=\sqrt{2l\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}.$$

Therefore,

$$\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \sqrt{2l\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}.$$

$${\left(\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\right)}^2=(\sum _{p=1}^l|{\left({\eta }_p\right)}_{R_i}{|)}^2=\sum _{p=1}^l|{\left({\eta }_p\right)}_{R_i}{|}^2+2\sum _{1\le p\le q\le l}|{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}|$$

$$=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+{\displaystyle \frac{2l(l-1)}{2}}AM\left\{\right|{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}\left|\right\}.$$

Since $AM\left\{\right|{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}\left|\right\}\ge GM\left\{\right|{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}\left|\right\},1\le p\le q\le l,$

$$\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\ge \sqrt{2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+l(l-1)GM\left\{\right|{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}\left|\right\}},$$

also, since

$$GM\left\{\right|{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}\left|\right\}={\left(\prod _{1\le p\le q\le l}\left|{\left({\eta }_p\right)}_{R_i}{\left({\eta }_q\right)}_{R_i}\right|\right)}^{{\displaystyle \frac{2}{l(l-1)}}}={\left(\prod _{p=1}^l{\left|{\left({\eta }_p\right)}_{R_i}\right|}^{l-1}\right)}^{{\displaystyle \frac{2}{l(l-1)}}}$$

$$={\left(\prod _{p=1}^l\left|{\left({\eta }_p\right)}_{R_i}\right|\right)}^{{\displaystyle \frac{2}{l}}}={\left|det\left(\mathcal{A}\left(t_{R_i}\left(z_p{z}_q\right)\right)\right)\right|}^{{\displaystyle \frac{2}{l}}},$$

so,

$$\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\ge \sqrt{2l\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+l(l-1)\left|det\right(\mathcal{A}\left(t_{R_i}\left(z_p{z}_q\right)\right){|}^{{\displaystyle \frac{2}{l}}}}.$$

Thus,

$$\sqrt{2l{t}_{R_i}}{\left(z_p{z}_q\right)}^2+l(l-1){\left|det\left(\mathcal{A}\left(t_{R_i}\left(z_p{z}_q\right)\right)\right)\right|}^{{\displaystyle \frac{2}{l}}}\le \mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)$$

$$\le \sqrt{2l\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}.$$

Similarly, we can prove cases (II). □

Theorem 4.

Suppose $G=(Q,R_1,R_2,\dots ,R_n)$ is a VFGS and ${\mathcal{A}}_{R_i}\left(G\right)$ is a AM of $G.$ If $l\le 2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2,l\le 2{\sum }_{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2,$then

$$\left(I\right)\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le {\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}$$

$$+\sqrt{(l-1)\left\{2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2-{\left({\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}\right)}^2\right\}}.$$

$$\left(II\right)\mathcal{E}\left(f_{R_i}\left(z_p{z}_q\right)\right)\le {\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}$$

$$+\sqrt{(l-1)\left\{2\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2-{\left({\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}\right)}^2\right\}}.$$

Proof. 

(I) If ${\mathcal{A}}_{R_i}={\left[v_{pq}\right]}_{n\times n}$ is a symmetric matrix with zero trace, then ${\left({\eta }_{R_i}\right)}_{max}\ge {\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{z}_p{z}_q}{l}}$, where ${\left({\eta }_{R_i}\right)}_{max}$ is the maximum eigenvalue of ${\mathcal{A}}_{R_i}$. If ${\mathcal{A}}_{R_i}\left(G\right)$ is the adjacency matrix of a VFG G, then, ${\eta }_1\ge \frac{2{\sum }_{1\le p\le q\le l}{t}_{R_i}\left(z_p{z}_q\right)}{l}$, where ${\left({\eta }_1\right)}_{R_i}\ge {\left({\eta }_2\right)}_{R_i}\ge \dots \ge {\left({\eta }_l\right)}_{R_i}$. Moreover, since

$$\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}^2=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2$$

$$\sum _{p=2}^l{\left({\eta }_p\right)}_{R_i}^2=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2-{\left({\eta }_1\right)}_{R_i}^2.\left(5\right)$$

Applying Cauchy–Schwarz unequality to the vectors $(1,1,...,1)$ and

$\left(\right|{\left({\eta }_1\right)}_{R_i}|,|{\left({\eta }_2\right)}_{R_i}|,...,|{\left({\eta }_l\right)}_{R_i}\left|\right)$ with $l-1$ entries, we obtain

$$\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)-{\left({\eta }_1\right)}_{R_i}=\sum _{p=2}^l\left|{\left({\eta }_p\right)}_{R_i}\right|\le \sqrt{(l-1)\sum _{p=2}^l{\left|{\left({\eta }_p\right)}_{R_i}\right|}^2}.\left(6\right)$$

Replacing (5) in (6), we must have

$$\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)-{\left({\eta }_1\right)}_{R_i}\le \sqrt{(l-1)\left(2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2-{\left({\eta }_1\right)}_{R_i}^2\right)}$$

$$\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le {\left({\eta }_1\right)}_{R_i}+\sqrt{(l-1)\left(2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2-{\left({\eta }_1\right)}_{R_i}^2\right)}.\left(7\right)$$

Now, the function $M\left(e\right)=e+\sqrt{(l-1)\left(2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2-e^2\right)},$ decreases on the interval $\left(\sqrt{{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}},\sqrt{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}\right).$

Moreover, $l\le 2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2,1\le {\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}.$

So,

$\sqrt{{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}}\le {\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}\le {\displaystyle \frac{2{\sum }_{1\le p\le q\le l}\left(t_{R_i}\left(z_p{z}_q\right)\right)}{l}}$

$\le {\left({\eta }_1\right)}_{R_i}\le \sqrt{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}.$

Therefore, (7) implies

$$\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le {\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}}+$$

$$\sqrt{(l-1)\left\{2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2-{\left(\frac{2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2}{l}\right)}^2\right\}}.$$

Similarly, we can prove cases (II). □

Theorem 5.

Suppose $G=(Q,R_1,R_2,\dots ,R_n)$ is a VFGS. Then, ${\mathcal{E}}_{R_i}\left(G\right)\le {\displaystyle \frac{l}{2}}(1+\sqrt{l}).$

Proof. 

Let $G=(Q,R_1,R_2,\dots ,R_n)$ be a VSFG. If $l\le 2{\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2=2g$, then by usual calculus, it is clear to show that $h\left(g\right)={\displaystyle \frac{2g}{l}}+\sqrt{(l-1)(2g-{\left(\frac{2g}{l}\right)}^2)}$ is maximized when $z=\frac{l^2+l\sqrt{l}}{4}.$ Replacing this value of g in place of $g={\sum }_{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2$, we must have $\mathcal{E}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \frac{l}{2}(1+\sqrt{l})$.

Similarly, it is easy to show that $\mathcal{E}\left(f_{R_i}\left(z_p{z}_q\right)\right)\le \frac{l}{2}(1+\sqrt{l})$. Hence, ${\mathcal{E}}_{R_i}\left(G\right)\le \frac{l}{2}(1+\sqrt{l})$. □

Definition 12.

Suppose $G=(Q,R_1,R_2,\dots ,R_n)$ is a VFGS on n vertices. The degree matrix ${\mathcal{K}}_{R_i}\left(G\right)=\left[k_{pq}^{\left(i\right)}\right]$ of G is an $n\times n$ diagonal matrix, which is defined as:

$${\left(k_{pq}\right)}_{R_i}=\left\{\begin{array}{cc}{d}_G\left(v_p\right)\hfill & p=q\hfill \\ 0\hfill & p\ne q\hfill \end{array}\right.$$

Definition 13.

The $\mathcal{LE}$ of a VFGS $G=(Q,R_1,R_2,\dots ,R_n)$ is defined as ${\mathcal{L}}_{R_i}\left(G\right)={\mathcal{K}}_{R_i}\left(G\right)-{\mathcal{A}}_{R_i}\left(G\right)$, where ${\mathcal{K}}_{R_i}\left(G\right)$ and ${\mathcal{A}}_{R_i}\left(G\right)$ are the degrees matrix and AM of a VFGS, respectively.

Definition 14.

The $\mathcal{LE}$ of a VFGS $G=(Q,R_1,R_2,\dots ,R_n)$ is defined as the following:

$${\mathcal{LE}}_{R_i}\left(G\right)=<\mathcal{LE}\left(t_{R_i}\left(z_p{z}_q\right)\right),\mathcal{LE}\left(f_{R_i}\left(z_p{z}_q\right)\right)>,$$

$${\mathcal{LE}}_{R_i}\left(G\right)=<\sum _{p=1}^l|{\left({\eta }_p\right)}_{R_i}|,\sum _{p=1}^l\left|{\left({\varphi }_p\right)}_{R_i}\right|>,$$

where

$${\left({\eta }_p\right)}_{R_i}={\left({\eta }_p\right)}_{R_i}^{*}-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{t}_{R_i}\left(z_p{z}_q\right)}{l}},$$

$${\left({\varphi }_p\right)}_{R_i}={\left({\varphi }_p\right)}_{R_i}^{*}-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{f}_{R_i}\left(z_p{z}_q\right)}{l}},$$

${\left({\eta }_p\right)}_{R_i}^{*}$ and ${\left({\varphi }_p\right)}_{R_i}^{*}$ are the eigenvalues of $\mathcal{L}\left(t_{R_i}\left(z_p{z}_q\right)\right)$ and $\mathcal{L}\left(t_{R_i}\left(z_p{z}_q\right)\right)$.

Example 3.

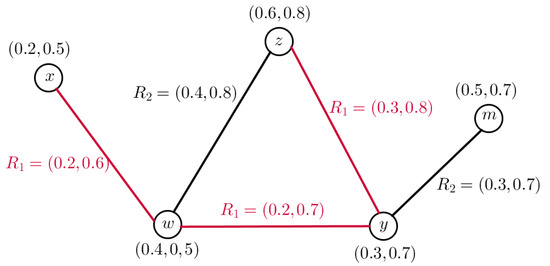
Consider a GS $G^{*}=(W,E_1,E_2)$, where $W=\{x,w,z,y,m\}$, $E_1=\{xw,wy,zy\}$, and $E_2=\{wz,ym\}$. Suppose Q, $R_1$, and $R_2$ are a vague fuzzy subset of W, $E_1$, and $E_2$, respectively, then, $G=(Q,R_1,R_2)$ is a VFGS on $G^{*}$ as shown in Figure 3, such that

Figure 3. VFGS $G=(Q,R_1,R_2).$

$Q=\{<x(0.2,0.5)>,<w(0.4,0.5)>,<z(0.6,0.8)>,<y(0.3,0.7)>,<m(0.5,0.7)>\}$

$R_1=\{<xw(0.2,0.6)>,<wy(0.2,0.7)>,<zy(0.3,0.8)>\},$

$R_2=\{<wz(0.4,0.8)>,<ym(0.3,0.7)>\}.$

The AMs and energy of each degree of G are obtained as follows:

$${\mathcal{A}}_{R_1}=\left[\begin{array}{ccccc}0& (0.2,0.6)& 0& 0& 0\\ (0.2,0.6)& 0& 0& (0.2,0.7)& 0\\ 0& 0& 0& (0.3,0.8)& 0\\ 0& (0.2,0.7)& (0.3,0.8)& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_1}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_1}\right|=1.076$$

$$\mathcal{E}(\mathcal{A}\left(f_{R_1}\right)=\sum _{p=1}^l|{\left({\varphi }_p\right)}_{R_1}|=3.128$$

$${\mathcal{A}}_{R_2}=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& (0.4,0.8)& 0& 0\\ 0& (0.4,0.8)& 0& 0& 0\\ 0& 0& 0& 0& (0.3,0.7)\\ 0& 0& 0& (0.3,0.7)& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_2}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_1}\right|=1.4$$

$$\mathcal{E}(\mathcal{A}\left(f_{R_2}\right)=\sum _{p=1}^l|{\left({\varphi }_p\right)}_{R_1}|=3$$

Therefore, the energy of a VFGS $G=(Q,R_1,R_2)$ is equal to $\mathcal{E}\left(G\right)=<(1.076,3.128),(1.4,3)>$

The degree matrix and $\mathcal{LE}$ are as follows:

$${\mathcal{K}}_{R_1}\left(G\right)=\left[\begin{array}{ccccc}(0.2,0.6)& 0& 0& 0& 0\\ 0& (0.4,1.3)& 0& 0& 0\\ 0& 0& (0.3,0.8)& 0& 0\\ 0& 0& 0& (0.5,1.5)& 0\\ 0& 0& 0& 0& 0\end{array}\right]$$

According to the relationship ${\mathcal{L}}_{R_1}\left(G\right)={\mathcal{K}}_{R_1}\left(G\right)-{\mathcal{A}}_{R_1}\left(G\right)$, we have

$${\mathcal{L}}_{R_1}\left(G\right)=\left[\begin{array}{ccccc}(0.2,0.6)& (-0.2,-0.6)& 0& 0& 0\\ (-0.2,-0.6)& (0.4,1.3)& 0& (-0.2,-0.7)& 0\\ 0& 0& (0.3,0.8)& (-0.3,-0.8)& 0\\ 0& (-0.2,-0.7)& (-0.3,-0.8)& (0.5,1.5)& 0\\ 0& 0& 0& 0& 0\end{array}\right]$$

After computing, we have $\mathcal{LE}\left(\mathcal{A}\left(t_{R_1}\right)\right)=1.39$ and $\mathcal{LE}\left(\mathcal{A}\left(f_{R_1}\right)\right)=4.2.$

$${\mathcal{K}}_{R_2}\left(G\right)=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& (0.4,0.8)& 0& 0& 0\\ 0& 0& (0.4,0.8)& 0& 0\\ 0& 0& 0& (0.3,0.7)& 0\\ 0& 0& 0& 0& (0.3,0.7)\end{array}\right]$$

According to the relationship ${\mathcal{L}}_{R_2}\left(G\right)={\mathcal{K}}_{R_2}\left(G\right)-{\mathcal{A}}_{R_2}\left(G\right)$, we have

$${\mathcal{L}}_{R_2}\left(G\right)=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& (0.4,0.8)& (-0.4,-0.8)& 0& 0\\ 0& (-0.4,-0.8)& (0.4,0.8)& 0& 0\\ 0& 0& 0& (0.3,0.7)& (-0.3,-0.7)\\ 0& 0& 0& (-0.3,-0.7)& (0.3,0.7)\end{array}\right]$$

After computing, we have $\mathcal{LE}\left(\mathcal{A}\left(t_{R_2}\right)\right)=1.4$ and $\mathcal{LE}\left(\mathcal{A}\left(f_{R_2}\right)\right)=3.$

Therefore, the $\mathcal{LE}$ of a VFGS $G=(Q,R_1,R_2)$ is equal to $\mathcal{LE}\left(G\right)=<(1.39,4.2),(1.4,3)>.$

Theorem 6.

Suppose that $G=(Q,R_1,R_2,\dots ,R_n)$ is a VSFG and ${\mathcal{L}}_{R_i}\left(G\right)$ is the ${\mathcal{LE}}_{R_i}$ of G. If ${\left({\eta }_1\right)}_{R_i}^{*}\ge {\left({\eta }_2\right)}_{R_i}^{*}\ge \dots \ge {\left({\eta }_l\right)}_{R_i}^{*}$ and ${\left({\varphi }_1\right)}_{R_i}^{*}\ge {\left({\varphi }_2\right)}_{R_i}^{*}\ge \dots \ge {\left({\varphi }_l\right)}_{R_i}^{*}$ are the eigenvalues of $\mathcal{L}\left(t_{R_i}\left(z_p{z}_q\right)\right)$ and $\mathcal{L}\left(f_{R_i}\left(z_p{z}_q\right)\right)$, then

$$I)\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}^{*}=2\sum _{1\le p\le q\le l}{t}_{R_i}\left(z_p{z}_q\right),\sum _{p=1}^l{\left({\varphi }_p\right)}_{R_i}^{*}=2\sum _{1\le p\le q\le l}{f}_{R_i}\left(z_p{z}_q\right),$$

$$II)\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}^{*2}=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+\sum _{p=1}^l{d}_Q\left(z_p\right).$$

$$\sum _{p=1}^l{\left({\varphi }_p\right)}_{R_i}^{*2}=2\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2+\sum _{p=1}^l{d}_{R_i}^2\left(z_p\right).$$

Proof. 

(I)

Since ${\mathcal{L}}_{R_i}\left(G\right)$ is a symmetric matrix with non-negative Laplacian eigenvalues, therefore,

$$\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}^{*}=tr\left({\mathcal{L}}_{R_i}\left(G\right)\right)=\sum _{p=1}^l{d}_Q\left(z_p\right)=2\sum _{1\le p\le q\le l}\left(t_{R_i}\left(z_p{z}_q\right)\right).$$

Then, ${\sum }_{p=1}^l{\left({\eta }_p\right)}_{R_i}^{*}=2{\sum }_{1\le p\le q\le l}{t}_{R_i}\left(z_p{z}_q\right)$, similarly, ${\sum }_{p=1}^l{\left({\varphi }_p\right)}_{R_i}^{*}=2{\sum }_{1\le p\le q\le l}{f}_{R_i}\left(z_p{z}_q\right)$.

(II)

By tracing the properties of the matrix, we have

$$tr\left({\left(\mathcal{L}\left(t_{R_i}\left(z_p{z}_q\right)\right)\right)}^2\right)=\sum _{p=1}^l{\left({\eta }_p\right)}_{R_i}^{*},$$

where

$$tr\left({\left(\mathcal{L}\left(t_{R_i}\left(z_p{z}_q\right)\right)\right)}^2\right)=\left(d^{2}Q\left(z_1\right)+t_{R_i}^2\left(z_1{z}_2\right)+\dots +t_{R_i}^2\left(z_1{z}_l\right)\right)$$

$$+\left(t_{R_i}^2\left(Z_2{Z}_1\right)+d^{2}Q\left(z_2\right)+\dots +t_{R_i}^2\left(z_2{z}_l\right)\right)$$

$$⋮$$

$$+\left((t_{R_i}^2\left(z_l{z}_1\right)+t_{R_i}^2\left(z_l{z}_2\right)+\dots +d^{2}Q\left(z_l\right)\right)=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+\sum _{p=1}^l{d}_Q^2\left(z_l\right).$$

Hence,

$$\sum _{p=1}^l{\left({\eta }_l\right)}_{R_i}^{*2}=2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+\sum _{p=1}^l{d}_Q^2\left(z_p\right).$$

Similarly, the other relations are fixed. □

Theorem 7.

Suppose $G=(Q,R_1,R_2,\dots ,R_n)$ is a VFGS on n vertices and ${\mathcal{L}}_{R_i}\left(G\right)$ is the $\mathcal{LM}$ of G, then

(I)

$$\mathcal{LE}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \sqrt{2l\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+l\sum _{p=1}^l{\left(d_Q\left(z_p\right)-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}(t_{R_i}\left(z_p{z}_q\right)}{l}}\right)}^2}.$$

(II)

$$\mathcal{LE}\left(f_{R_i}\left(z_p{z}_q\right)\right)\le \sqrt{2l\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2+l\sum _{p=1}^l{\left(d_{R_i}\left(z_p\right)-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}(f_{R_i}\left(z_p{z}_q\right)}{l}}\right)}^2}.$$

Proof. 

(I) Applying Cauchy–Schwarz inequality to the vectors $(1,1,\dots ,1)$ and

$\left(\right|{\left({\eta }_1\right)}_{R_i}|,|{\left({\eta }_2\right)}_{R_i}|,\dots ,|{\left({\eta }_n\right)}_{R_i}\left|\right)$ with n entries, we obtain

$$\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_i}\right|\le \sqrt{l}\sqrt{\sum _{p=1}^l{\left|{\left({\eta }_p\right)}_{R_i}\right|}^2}$$

$$\mathcal{LE}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \sqrt{l}\sqrt{2{\mathcal{A}}_{t_{R_i}}}=\sqrt{2l{\mathcal{A}}_{t_{R_i}}},$$

since

$${\mathcal{A}}_{t_{R_i}}=2l\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+{\displaystyle \frac{1}{2}}\sum _{p=1}^l{\left(d_Q\left(z_p\right)-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}{t}_{R_i}\left(z_p{z}_q\right)}{l}}\right)}^2.$$

Therefore, we have

$$\mathcal{LE}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \sqrt{2l\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+l\sum _{p=1}^l{\left(d_Q\left(z_p\right)-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}(t_{R_i}\left(z_p{z}_q\right)}{l}}\right)}^2}.$$

Similarly, we can prove cases (II). □

Theorem 8.

Suppose $G=(Q,R_1,R_2,\dots ,R_n)$ is a VFGS and ${\mathcal{L}}_{R_i}\left(G\right)$ is a $\mathcal{LE}$ of G. Then

(I)

$\mathcal{LE}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \left|{\left({\eta }_p\right)}_{R_i}\right|$

$$+\sqrt{(l-1)\left(2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+\sum _{p=1}^l{\left(d_Q\left(z_p\right)-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}(t_{R_i}\left(z_p{z}_q\right)}{n}}\right)}^2-{\left({\eta }_p\right)}_{R_i}^2\right)}.$$

(II)

$\mathcal{LE}\left(f_{R_i}\left(z_p{z}_q\right)\right)\le \left|{\left({\varphi }_p\right)}_{R_i}\right|$

$$+\sqrt{(l-1)\left(2\sum _{1\le p\le q\le l}{\left(f_{R_i}\left(z_p{z}_q\right)\right)}^2+\sum _{p=1}^l{\left(d_{R_i}\left(z_p\right)-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}(f_{R_i}\left(z_p{z}_q\right)}{l}}\right)}^2-{\left({\varphi }_p\right)}_{R_i}^2\right)}.$$

Proof. 

Using the Caushy–Schwarz inequality, we obtain

$$I)\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_i}\right|\le \sqrt{l\sum _{p=1}^l{\left|{\left({\eta }_p\right)}_{R_i}\right|}^2},$$

$$\sum _{p=2}^l\left|{\left({\eta }_p\right)}_{R_i}\right|\le \sqrt{(l-1)\sum _{p=2}^l{\left|{\left({\eta }_p\right)}_{R_i}\right|}^2}.$$

$$\mathcal{LE}\left(t_{R_i}\left(z_p{z}_q\right)\right)-\left|{\left({\eta }_1\right)}_{R_i}\right|\le \sqrt{(n-1)(2{\mathcal{A}}_{t_{R_i}}-{\left({\eta }_1\right)}_{R_i}^2)},$$

$$\mathcal{LE}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \left|{\left({\eta }_1\right)}_{R_i}\right|+\sqrt{(n-1)(2{\mathcal{A}}_{t_{R_i}}-{\left({\eta }_1\right)}_{R_i}^2)},$$

Since

$${\mathcal{A}}_{t_{R_i}}=\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+{\displaystyle \frac{1}{2}}\sum _{p=1}^l{\left(d_Q\left(z_p\right)-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}\left(t_{R_i}\left(z_p{z}_q\right)\right)}{l}}\right)}^2.$$

Therefore, $\mathcal{LE}\left(t_{R_i}\left(z_p{z}_q\right)\right)\le \left|{\left({\eta }_p\right)}_{R_i}\right|$

$$+\sqrt{(l-1)\left(2\sum _{1\le p\le q\le l}{\left(t_{R_i}\left(z_p{z}_q\right)\right)}^2+\sum _{p=1}^l{\left(d_Q\left(z_p\right)-{\displaystyle \frac{2{\sum }_{1\le p\le q\le l}(t_{R_i}\left(z_p{z}_q\right)}{l}}\right)}^2-{\left({\eta }_p\right)}_{R_i}^2\right)}.$$

Similarly, we can prove cases (II). □

4. Applications of the Energy VFGS in Decision Making

4.1. Designing an Organizational Communication System

In the real world, communication is very important in every sector, and one of the things we want to talk about is organizational communication. Organizational communication has attracted the attention of many behavioral and organizational science thinkers to the extent that many organizational difficulties have been analyzed and suitable solutions have been found for them. Some thinkers of organizational communication, such as management consultants who have been studying organizational inadequacies in recent years, believe that many of the issues and problems governing organizations are a result of incorrect communication context and lack of attention to the subtleties of organizational communication. If the managers were aware of these issues, they would probably perform their work more effectively and efficiently. With the continuation of interactions between employees, communication networks are formed naturally. Because duties, relations, and memberships are changing, the connections are not fixed and permanent. According to these concepts, we present an example of multiple organizational relationships and examine the importance and impact of multiple relationships in increasing the efficiency and success of an organization.

In this example, we consider education organization as a graph whose vertices include organization management ($z_1$), financial vice president ($z_2$), education unit ($z_3$), educational vice president ($z_4$), technology unit ($z_5$), and research unit ($z_6$). In this educational organization, we want to examine the three desired relationships between the introduced units’ efficient manpower ($R_1$), improving the scientific and educational level ($R_2$), and the relationship between salaries and benefits in raising the quality and efficiency of the organization ($R_3$).

Here, we consider a set of units Q and a set of relations $R_i$. Consider $Q=\{$ organization management, financial vice president, education unit, educational vice president, technology unit, research unit } as a set of units in an education organization and $R_i=\{$ efficient manpower, improving the scientific and educational level, } as sets of relations between units of an education organization.

Now, in Figure 4, we assume $G=(Q,R_1,R_2,R_3)$ is the VFGS, where $Q=\{z_1,z_2,z_3,z_4,z_5,z_6\}$ is the set of vertices and $R_1=\{z_1{z}_6,z_2{z}_3,z_4{z}_6,z_2{z}_5\}$, $R_2=\{z_1{z}_2,z_3{z}_4,z_5{z}_6\}$, and $R_3=\{z_4{z}_5,z_2{z}_6,z_2{z}_4,z_3{z}_6\}$ are sets of relations between vertices in this graph.

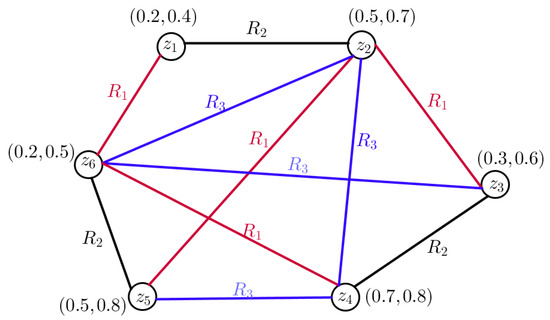
Figure 4. VFGS $G=(Q,R_1,R_2,R_3).$

$Q=\{<z_1(0.2,0.4)>,<z_2(0.5,0.7)>,<z_3(0.3,0.6)>,<z_4(0.7,0.8)>,<z_5(0.5,0.8)>,<z_6(0.2,0.5)>\},$

$R_1=\{<z_1{z}_6(0.2,0.6)>,<z_2{z}_3(0.3,0.7)>,<z_4{z}_6(0.2,0.8)>,<z_2{z}_5(0.4,0.8)>\},$

$R_2=\{<z_1{z}_2(0.2,0.7)>,<z_3{z}_4(0.3,0.8)>,<z_5{z}_6(0.2,0.8)>\},$

$R_3=\{<z_4{z}_5(0.4,0.8)>,<z_2{z}_6(0.2,0.7)>,<z_2{z}_4(0.5,0.8)>,<z_3{z}_6(0.1,0.6)>\}.$

In Figure 4, it is clear that there are three different relationships between the units; we first obtain the energy of each relationship. The AMs and energy of each degree of G are obtained as follows:

$${\mathcal{A}}_{R_1}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& (0.2,0.6)\\ 0& 0& (0.3,0.7)& 0& (0.4,0.8)& 0\\ 0& (0.3,0.7)& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& (0.2,0.8)\\ 0& (0.4,0.8)& 0& 0& 0& 0\\ (0.2,0.6)& 0& 0& (0.2,0.8)& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_1}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_1}\right|=1.56$$

$$\mathcal{E}(\mathcal{A}\left(f_{R_1}\right)=\sum _{p=1}^l|{\left({\varphi }_p\right)}_{R_1}|=4.126$$

$${\mathcal{A}}_{R_2}=\left[\begin{array}{cccccc}0& (0.2,0.7)& 0& 0& 0& 0\\ (0.2,0.7)& 0& 0& 0& 0& 0\\ 0& 0& 0& (0.3,0.8)& 0& 0\\ 0& 0& (0.3,0.8)& 0& 0& 0\\ 0& 0& 0& 0& 0& (0.2,0.8)\\ 0& 0& 0& 0& (0.2,0.8)& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_2}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_2}\right|=1.4$$

$$\mathcal{E}(\mathcal{A}\left(f_{R_2}\right)=\sum _{p=1}^l|{\left({\varphi }_p\right)}_{R_2}|=4.6$$

$${\mathcal{A}}_{R_3}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& (0.5,0.8)& 0& (0.2,0.7)\\ 0& 0& 0& 0& 0& (0.1,0.6)\\ 0& (0.5,0.8)& 0& 0& (0.4,0.8)& 0\\ 0& 0& 0& (0.4,0.8)& 0& 0\\ 0& (0.2,0.7)& (0.1,0.6)& 0& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_3}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_3}\right|=1.634$$

$$\mathcal{E}(\mathcal{A}\left(f_{R_3}\right)=\sum _{p=1}^l|{\left({\varphi }_p\right)}_{R_3}|=3.944$$

Therefore, the energy of a VFGS $G=(Q,R_1,R_2,R_3)$ is equal to $\mathcal{E}\left(G\right)=<(1.56,4.126),(1.4,4.6),(1.634,3.944)>.$

The degree matrix and $\mathcal{LE}$ are as follows:

$${\mathcal{K}}_{R_1}\left(G\right)=\left[\begin{array}{cccccc}(0.2,0.6)& 0& 0& 0& 0& 0\\ 0& (0.7,1.5)& 0& 0& 0& 0\\ 0& 0& (0.3,0.7)& 0& 0& 0\\ 0& 0& 0& (0.2,0.8)& 0& 0\\ 0& 0& 0& 0& (0.4,0.8)& 0\\ 0& 0& 0& 0& 0& (0.4,1.4)\end{array}\right]$$

According to the relationship ${\mathcal{L}}_{R_1}\left(G\right)={\mathcal{K}}_{R_1}\left(G\right)-{\mathcal{A}}_{R_1}\left(G\right)$, we have

$${\mathcal{L}}_{R_1}\left(G\right)=\left[\begin{array}{cccccc}(0.2,0.6)& 0& 0& 0& 0& (-0.2,-0.6)\\ 0& (0.7,1.5)& (-0.3,-0.7)& 0& (-0.4,-0.8)& 0\\ 0& (-0.3,-0.7)& (0.3,0.7)& 0& 0& 0\\ 0& 0& 0& (0.2,0.8)& 0& (-0.2,-0.8)\\ 0& (-0.4,-0.8)& 0& (-0.4,-0.8)& (0.4,0.8)& 0\\ (-0.2,-0.6)& 0& 0& (-0.2,-0.8)& 0& (0.4,1.4)\end{array}\right]$$

After computing, we have $\mathcal{LE}\left(\mathcal{A}\left(t_{R_1}\right)\right)=2.19$ and $\mathcal{LE}\left(\mathcal{A}\left(f_{R_1}\right)\right)=5.8.$

$${\mathcal{K}}_{R_2}\left(G\right)=\left[\begin{array}{cccccc}(0.2,0.7)& 0& 0& 0& 0& 0\\ 0& (0.2,0.7)& 0& 0& 0& 0\\ 0& 0& (0.3,0.8)& 0& 0& 0\\ 0& 0& 0& (0.3,0.8)& 0& 0\\ 0& 0& 0& 0& (0.2,0.8)& 0\\ 0& 0& 0& 0& 0& (0.2,0.8)\end{array}\right]$$

According to the relationship ${\mathcal{L}}_{R_2}\left(G\right)={\mathcal{K}}_{R_2}\left(G\right)-{\mathcal{A}}_{R_2}\left(G\right)$, we have

$${\mathcal{L}}_{R_2}\left(G\right)=\left[\begin{array}{cccccc}(0.2,0.7)& (-0.2,-0.7)& 0& 0& 0& 0\\ (-0.2,-0.7)& (0.2,0.7)& 0& 0& 0& 0\\ 0& 0& (0.3,0.8)& (-0.3,-0.8)& 0& 0\\ 0& 0& (-0.3,-0.8)& (0.3,0.8)& 0& 0\\ 0& 0& 0& 0& (0.2,0.8)& (-0.2,-0.8)\\ 0& 0& 0& 0& (-0.2,-0.8)& (0.2,0.8)\end{array}\right]$$

After computing, we have $\mathcal{LE}\left(\mathcal{A}\left(t_{R_2}\right)\right)=1.4$ and $\mathcal{LE}\left(\mathcal{A}\left(f_{R_2}\right)\right)=4.6.$

$${\mathcal{K}}_{R_3}\left(G\right)=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& (0.7,1.5)& 0& 0& 0& 0\\ 0& 0& (0.1,0.6)& 0& 0& 0\\ 0& 0& 0& (0.9,1.6)& 0& 0\\ 0& 0& 0& 0& (0.4,0.8)& 0\\ 0& 0& 0& 0& 0& (0.3,1.3)\end{array}\right]$$

According to the relationship ${\mathcal{L}}_{R_3}\left(G\right)={\mathcal{K}}_{R_3}\left(G\right)-{\mathcal{A}}_{R_3}\left(G\right)$, we have

$${\mathcal{L}}_{R_3}\left(G\right)=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& (0.7,1.5)& 0& (-0.5,-0.8)& 0& (-0.2,-0.7)\\ 0& 0& (0.1,0.6)& 0& 0& (-0.1,-0.6)\\ 0& (-0.5,-0.8)& 0& (0.9,1.6)& (-0.4,-0.8)& 0\\ 0& 0& 0& (-0.4,-0.8)& (0.4,0.8)& 0\\ 0& (-0.2,-0.7)& (-0.1,-0.6)& 0& 0& (0.3,1.3)\end{array}\right]$$

After computing, we have $\mathcal{LE}\left(\mathcal{A}\left(t_{R_3}\right)\right)=2.39$ and $\mathcal{LE}\left(\mathcal{A}\left(f_{R_3}\right)\right)=5.79.$

Therefore, the $\mathcal{LE}$ of a VFGS $G=(Q,R_1,R_2,R_3)$ is equal to $\mathcal{LE}\left(G\right)=<(2.19,5.8),(1.4,4.6),(2.39,5.79)>$.

In this application, we can clearly see that if the amount of energy in the relationships between the units is greater, the units have a greater impact on each other. Here, it is clear that the energy in $R_3$ is more than others. Therefore, the educational vice president unit and technology unit, education unit and research unit, education unit and educational vice president unit, and education unit and research unit have a greater effect on each other.

4.2. Role of Virtual Social Networks on Cultural Communication

Virtual space has entered many areas of life in different human societies in such a way that it is used for various purposes, including business, games and entertainment, and similar work activities, and the beneficiaries of individuals and institutions use these virtual spaces to facilitate work or provide special services. Currently, social networks are the inhabitants of the turbulent ocean of the Internet. Networks play an essential role in the world’s media equations with virtual socialism. The virtual space is formed depending on social constructions, and technological growth, media convergence, and related issues are different outputs in different social conditions. Virtual social networks, such as Twitter, Instagram, Facebook, WhatsApp, Telegram, etc., which provide the opportunity to meet people from different cultures with different languages and ethnicities, are very important in intercultural communication, and since in Iran the application of virtual social networks is widespread, these virtual social networks are considered an important source for the intercultural communication of Iranians. Due to the fact that today’s era is the era of communication and virtual space, it is not possible to communicate in this space without accepting cultures and accepting cultures without taking into account customs and beliefs and, ultimately, creating a common culture. Therefore, the main issue of this application is the role of virtual social networks in cultural communication in Iran.

We used five platforms $z_p(p=1,2,3,4,5)$: Twitter ($z_1$), Instagram ($z_2$), Facebook ($z_3$), WhatsApp ($z_4$), and Telegram ($z_5$) to investigate the role of virtual space in cultural communication. Meanwhile, we invited four experts $e_l(l=1,2,3,4)$ in the field of cultural issues to examine each of these platforms’ vague fuzzy preference relations (VFPRs) ${\mathcal{M}}_l={\left(m_{pq}^l\right)}_{5\times 5}(l=1,2,3,4)$ as follows:

$${\mathcal{M}}_1=\left[\begin{array}{ccccc}(0.3,0.3)& (0.6,0.5)& (0.3,0.6)& (0.7,0.5)& (0.3,0.5)\\ (0.5,0.6)& (0.3,0.3)& (0.4,0.3)& (0.8,0.7)& (0.4,0.6)\\ (0.6,0.3)& (0.3,0.4)& (0.3,0.3)& (0.2,0.8)& (0.5,0.2)\\ (0.5,0.7)& (0.7,0.8)& (0.8,0.2)& (0.3,0.3)& (0.7,0.1)\\ (0.5,0.3)& (0.6,0.4)& (0.5,0.2)& (0.7,0.1)& (0.3,0.3)\end{array}\right]$$

$${\mathcal{M}}_2=\left[\begin{array}{ccccc}(0.3,0.3)& (0.3,0.5)& (0.3,0.6)& (0.2,0.8)& (0.3,0.6)\\ (0.5,0.3)& (0.3,0.3)& (0.4,0.6)& (0.5,0.4)& (0.4,0.8)\\ (0.6,0.3)& (0.6,0.4)& (0.3,0.3)& (0.2,0.7)& (0.3,0.7)\\ (0.8,0.2)& (0.4,0.5)& (0.7,0.2)& (0.3,0.3)& (0.2,0.4)\\ (0.6,0.3)& (0.8,0.4)& (0.7,0.3)& (0.4,0.2)& (0.3,0.3)\end{array}\right]$$

$${\mathcal{M}}_3=\left[\begin{array}{ccccc}(0.3,0.3)& (0.2,0.5)& (0.3,0.9)& (0.5,0.8)& (0.2,0.8)\\ (0.5,0.1)& (0.3,0.3)& (0.4,0.7)& (0.3,0.4)& (0.4,0.8)\\ (0.9,0.3)& (0.7,0.4)& (0.3,0.3)& (0.2,0.7)& (0.3,0.5)\\ (0.5,0.8)& (0.4,0.3)& (0.7,0.2)& (0.3,0.3)& (0.2,0.1)\\ (0.8,0.2)& (0.8,0.4)& (0.5,0.3)& (0.1,0.2)& (0.3,0.3)\end{array}\right]$$

$${\mathcal{M}}_4=\left[\begin{array}{ccccc}(0.3,0.3)& (0.5,0.6)& (0.3,0.6)& (0.2,0.8)& (0.3,0.1)\\ (0.6,0.5)& (0.3,0.3)& (0.8,0.6)& (0.8,0.3)& (0.4,0.7)\\ (0.6,0.3)& (0.6,0.8)& (0.3,0.3)& (0.2,0.8)& (0.2,0.4)\\ (0.8,0.2)& (0.3,0.8)& (0.8,0.2)& (0.3,0.3)& (0.2,0.1)\\ (0.1,0.3)& (0.7,0.4)& (0.4,0.2)& (0.1,0.2)& (0.3,0.3)\end{array}\right]$$

The VFDGs ${\mathcal{M}}_l$ corresponding to VFPRs given in matrices ${\mathcal{M}}_l,(l=1,2,3,4)$ are shown in Figure 5, Figure 6, Figure 7 and Figure 8, respectively

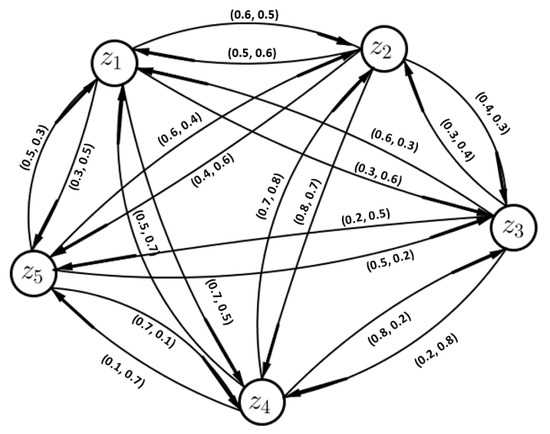
Figure 5. Platforms’ vague fuzzy preference relation ${\mathcal{M}}_1.$

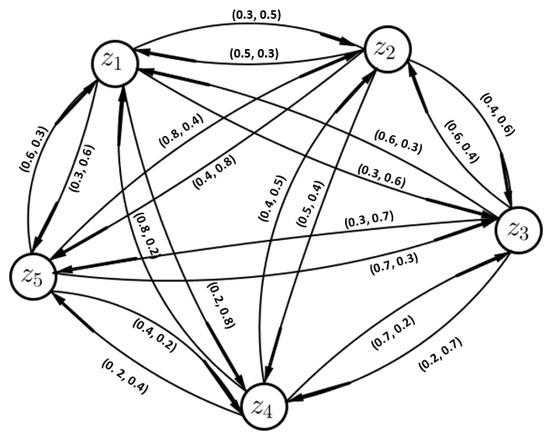
Figure 6. Platforms’ vague fuzzy preference relation ${\mathcal{M}}_2.$

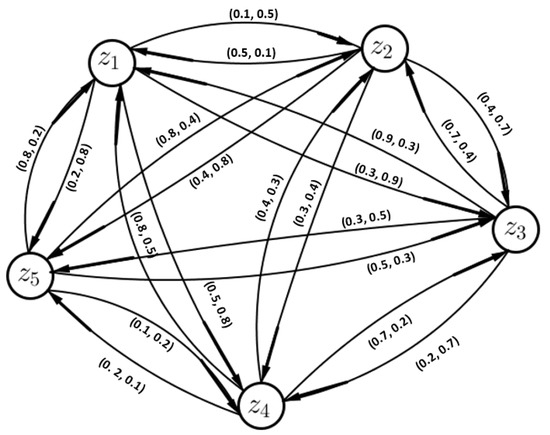
Figure 7. Platforms’ vague fuzzy preference relation ${\mathcal{M}}_3.$

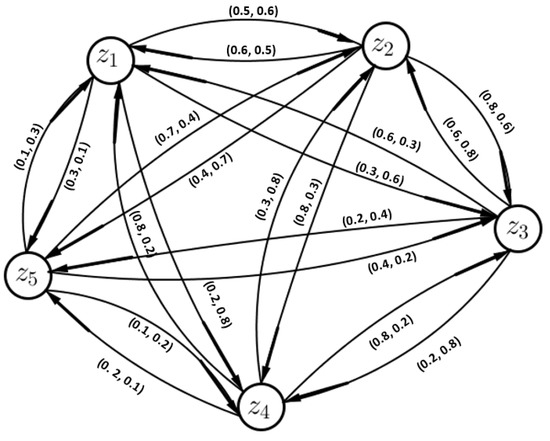
Figure 8. Platforms’ vague fuzzy preference relation ${\mathcal{M}}_4.$

The energy of each VFDG is calculated as:

$\mathcal{E}\left({\mathcal{M}}_1\right)=(3.367,3.044),\mathcal{E}\left({\mathcal{M}}_2\right)=(2.596,2.596),$$\mathcal{E}\left({\mathcal{M}}_3\right)=(2.764,3.295)$, and $\mathcal{E}\left({\mathcal{M}}_4\right)=(2.692,2.692).$

Then, the weight of each expert can be calculated as:

$$w_l=\left(w_l,w_l\right),l=1,2,3,4$$

$$w_l=\left({\displaystyle \frac{\mathcal{E}\left({\left({\mathcal{M}}_t\right)}_l\right)}{{\sum }_{k=1}^4\mathcal{E}({\left({\mathcal{M}}_t\right)}_k}}),{\displaystyle \frac{\mathcal{E}\left({\left({\mathcal{M}}_f\right)}_l\right)}{{\sum }_{k=1}^4\mathcal{E}({\left({\mathcal{M}}_f\right)}_k}})\right).$$

Here,

$$w_1=(0.294,0.261),w_2=(0.227,0.223),w_3=(0.242,0.283),w_4=(0.235,0.231).$$

Therefore, the weight vector of four experts $e_l(l=1,2,3,4)$ is:

$w=\left(\right(0.294,0.261),(0.227,0.223),(0.242,0.283),(0.235,0.231\left)\right).$

Compute the averaged vague fuzzy element (VFE) $v_p^l$ of the platforms $z_p$ (Twitter ($z_1$), Instagram($z_2$), Facebook ($z_3$), WhatsApp ($z_4$), and Telegram ($z_5$)) over all the other testing venues for the experts $e_l(l=1,2,3,4)$ by the vague fuzzy averaging (VFA) operator:

$$v_p^l=VFA(v_{p1}^l,v_{p2}^l,\dots ,v_{pn}^l)=\left(\sqrt{1-{\left(\prod _{q=1}^n(1-t_{pq}^2\right)}^{{\displaystyle \frac{1}{n}}}},{\left(\prod _{q=1}^n{f}_{pq}\right)}^{{\displaystyle \frac{1}{n}}}\right)$$

$p=1,2,\dots ,n.$

The aggregation results are listed in Table 2.

Table 2. The aggregation results of the experts.

Experts	The Overall Results of the Experts
$e_1$	$v_1^1=(0.4946,0.4661)$
	$v_2^1=(0.6967,0.4661)$
	$v_3^1=(0.4186,0.3465)$
	$v_4^1=(0.6505,0.3129)$
	$v_5^1=(0.5485,0.2338)$
$e_2$	$v_1^2=(0.2833,0.5334)$
	$v_2^2=(0.4294,0.4441)$
	$v_3^2=(0.4484,0.4459)$
	$v_4^2=(0.5748,0.2992)$
	$v_5^2=(0.6184,0.293)$
$e_3$	$v_1^3=(0.3163,0.6127)$
	$v_2^3=(0.3901,0.3676)$
	$v_3^3=(0.6334,0.4169)$
	$v_4^3=(0.4944,0.2701)$
	$v_5^3=(0.621,0.2701)$
$e_4$	$v_1^4=(0.3394,0.3866)$
	$v_2^4=(0.6517,0.4521)$
	$v_3^4=(0.4387,0.4704)$
	$v_4^4=(0.6044,0.2491)$
	$v_5^4=(0.4184,0.2701)$

Compute a collective VFE $v_p(p=1,2,3,4,5)$ of the platforms $z_p$ ( Twitter ($z_1$), Instagram ($z_2$), Facebook ($z_3$), WhatsApp($z_4$), and Telegram ($z_5$)) over all the other platforms using the vague fuzzy weighted averaging (VFWA) operator [32]:

$$v_p^l=VFWA(v_p^1,v_p^2,\dots ,v_p^s)=\left(\sqrt{1-\prod _{l=1}^s{(1-t_l^2)}^{w_l}},\prod _{l=1}^s{\left(f_l\right)}^{w_l}\right)$$

Therefore, Twitter ($v_1)=(0.3584,0.4997)$, Instagram ($v_2)=(0.5419,0.4324)$, Facebook ($v_3)=(0.4847,0.4199)$, Whatsapp ($v_4)=(0.581,0.2828)$, and Telegram ($v_5)=(0.5515,0.2667).$

Compute the score functions $s\left(v_p\right)=t_p^2-f_p^2$ [33] of $v_p(p=1,2,3,4,5)$ and rank all the platforms $z_p$ ( Twitter ($z_1$), Instagram ($z_2$), Facebook ($z_3$), WhatsApp ($z_4$), and Telegram ($z_5$)) according to the values of $s\left(v_p\right)(p=1,2,3,4,5)$ (Twitter ($s\left(v_1\right)$), Instagram ($s\left(v_2\right)$), Facebook ($s\left(v_3\right)$), WhatsApp ($s\left(v_4\right)$), and Telegram($s\left(v_5\right)$)).

$$s\left(v_1\right)=-0.1212,s\left(v_2\right)=0.2225,s\left(v_3\right)=0.0586,s\left(v_4\right)=0.2575,s\left(v_5\right)=0.233.$$

Then, $s\left(v_4\right)>s\left(v_5\right)>s\left(v_2\right)>s\left(v_3\right)>s\left(v_1\right).$ Thus, the best platform is WhatsApp.

4.3. Role of Advertising Tools in Raising the Quality Level of Advertising Companies

An advertising company is a company that creates, plans, and manages all aspects of advertising for its customers. Advertising companies can specialize in a specific field and branch of advertising, such as interactive advertising, or comprehensively provide services and use all advertising tools such as websites, social media, online advertising, etc. Brochures, catalogs, instant messaging with direct mail, print media, television ads, sales invitations, etc., are among the advertising tools that the advertising company uses to operate in this field. In this part, four advertising companies signed contracts among themselves to raise the quality level of their work. In these contracts, the companies defined relationships between themselves. In their meeting, these four companies expressed the factors that can affect their work promotion, among which are the right price regarding the quality, the professional production group, company services, and customer orientation. We assume that there are four advertising companies with the names $A,B,C$, and D. We define the relationships between them as follows,

Consider $Q=\{A,B,C,D\}$ as a set of advertising companies and $R_i=\{$ creating television teasers ($R_1$), designing and printing billboards ($R_2$), advertising photography ($R_3$) } as sets of relations between advertising companies.

Now, in Figure 9, we assume $G=(Q,R_1,R_2,R_3)$ is the VFGS, where $Q=\{A,B,C,D\}$ is the set of vertices and $R_1=\left\{AD\right\}$, $R_2=\{AB,CD\}$ and $R_3=\{BC,BD\}$ are sets of relations between vertices in this graph.

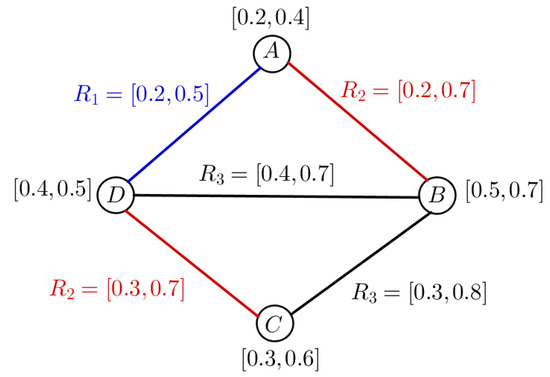
Figure 9. VFGS $G=(Q,R_1,R_2,R_3).$

$Q=\{<A(0.2,0.4)>,<B(0.5,0.7)>,<C(0.3,0.6)>,<D(0.4,0.5)>\},$

$R_1=\{<AD(0.2,0.5)>\},$$R_2=\{<AB(0.2,0.7)>,<CD(0.3,0.7)>\},$

$R_3=\{<BC(0.3,0.8)>,<BD(0.4,0.7)>\}.$

In Figure 9, it is clear that there are three different relationships between the advertising companies; we first obtain the energy of each relationship. The AMs and energy of each degree of G are obtained as follows:

$${\mathcal{A}}_{R_1}=\left[\begin{array}{cccc}0& 0& 0& (0.2,0.5)\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ (0.2,0.5)& 0& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_1}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_1}\right|=0.4$$

$$\mathcal{E}(\mathcal{A}\left(f_{R_1}\right)=\sum _{p=1}^l|{\left({\varphi }_p\right)}_{R_1}|=1$$

$${\mathcal{A}}_{R_2}=\left[\begin{array}{cccc}0& (0.2,0.7)& 0& 0\\ (0.2,0.7)& 0& 0& 0\\ 0& 0& 0& (0.3,0.7)\\ 0& 0& (0.3,0.7)& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_2}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_2}\right|=1$$

$$\mathcal{E}(\mathcal{A}\left(f_{R_2}\right)=\sum _{p=1}^l|{\left({\varphi }_p\right)}_{R_2}|=2.8$$

$${\mathcal{A}}_{R_3}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& (0.3,0.8)& (0.4,0.7)\\ 0& (0.3,0.8)& 0& 0\\ 0& (0.4,0.7)& 0& 0\end{array}\right]$$

$$\mathcal{E}\left(\mathcal{A}\left(t_{R_3}\right)\right)=\sum _{p=1}^l\left|{\left({\eta }_p\right)}_{R_3}\right|=1$$

$$\mathcal{E}(\mathcal{A}\left(f_{R_3}\right)=\sum _{p=1}^l|{\left({\varphi }_p\right)}_{R_3}|=2.12$$

Therefore, the energy of a VFGS $G=(Q,R_1,R_2,R_3)$ is equal to $\mathcal{E}\left(G\right)=<(0.4,1),(1,2.8),(1,2.12)>.$

The degree matrix and $\mathcal{LE}$ are as follows:

$${\mathcal{K}}_{R_1}\left(G\right)=\left[\begin{array}{cccc}(0.2,0.5)& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& (0.2,0.5)\end{array}\right]$$

According to the relationship ${\mathcal{L}}_{R_1}\left(G\right)={\mathcal{K}}_{R_1}\left(G\right)-{\mathcal{A}}_{R_1}\left(G\right)$, we have

$${\mathcal{L}}_{R_1}\left(G\right)=\left[\begin{array}{cccc}(0.2,0.5)& 0& 0& (-0.2,-0.5)\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ (-0.2,-0.5)& 0& 0& (0.2,0.5)\end{array}\right]$$

After computing, we have $\mathcal{LE}\left(\mathcal{A}\left(t_{R_1}\right)\right)=0.4$ and $\mathcal{LE}\left(\mathcal{A}\left(f_{R_1}\right)\right)=1.$

$${\mathcal{K}}_{R_2}\left(G\right)=\left[\begin{array}{cccc}(0.2,0.7)& 0& 0& 0\\ 0& (0.2,0.7)& 0& 0\\ 0& 0& (0.3,0.7)& 0\\ 0& 0& 0& (0.3,0.7)\end{array}\right]$$

According to the relationship ${\mathcal{L}}_{R_2}\left(G\right)={\mathcal{K}}_{R_2}\left(G\right)-{\mathcal{A}}_{R_2}\left(G\right)$, we have

$${\mathcal{L}}_{R_2}\left(G\right)=\left[\begin{array}{cccc}(0.2,0.7)& (-0.2,-0.7)& 0& 0\\ (-0.2,-0.7)& (0.2,0.7)& 0& 0\\ 0& 0& (0.3,0.7)& (-0.3,-0.7)\\ 0& 0& (-0.3,-0.7)& (0.3,0.7)\end{array}\right]$$

After computing, we have $\mathcal{LE}\left(\mathcal{A}\left(t_{R_2}\right)\right)=1$ and $\mathcal{LE}\left(\mathcal{A}\left(f_{R_2}\right)\right)=2.8.$

$${\mathcal{K}}_{R_3}\left(G\right)=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& (0.7,1.5)& 0& 0\\ 0& 0& (0.3,0.8)& 0\\ 0& 0& 0& (0.4,0.7)\end{array}\right]$$

According to the relationship ${\mathcal{L}}_{R_3}\left(G\right)={\mathcal{K}}_{R_3}\left(G\right)-{\mathcal{A}}_{R_3}\left(G\right)$, we have

$${\mathcal{L}}_{R_3}\left(G\right)=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& (0.7,1.5)& 0& (-0.3,-0.8)& (-0.4,-0.7)\\ 0& (-0.3,-0.8)& (0.3,0.8)& 0\\ 0& (-0.4,-0.7)& 0& (0.4,0.7)\end{array}\right]$$

After computing, we have $\mathcal{LE}\left(\mathcal{A}\left(t_{R_3}\right)\right)=0.74$ and $\mathcal{LE}\left(\mathcal{A}\left(f_{R_3}\right)\right)=2.25.$

Therefore, the $\mathcal{LE}$ of a VFGS $G=(Q,R_1,R_2,R_3)$ is equal to

$\mathcal{LE}\left(G\right)=<(0.4,1),(1,2.8),(0.74,2.25)>$.

In this application, we can clearly see that if the amount of energy in the relationships between the advertising companies is greater, they have a greater impact on each other. Here, it is clear that the energy in $R_2$ is more than others. Therefore, in order to raise the quality level of their work, two companies A and B, and also two companies C and D, can cooperate in the field of designing and printing advertising billboards.

5. Conclusions

Graph theory has many applications in solving different problems of several domains, including networking, planning, and scheduling. VGSs are very valuable tools for the study of various domains of computational intelligence and computer science. Optimization, neural networks, and operations research can be mentioned among the applications of VGSs in different sciences. Since many parameters in real-world networks are specifically related to the concept of energy, this concept has become one of the most extremely used concepts in graph theory. However, the energy in FG is so important because of the confrontation with uncertain and ambiguous topics. This concept becomes more interesting when we know that we are dealing with an FG called VFGS. This led us to examine the energy in VFGSs. So, in this work, we presented the notion of the energy of a VFGS and investigated some of its properties. We obtained the energy of the VFGS by using the eigenvalues of the AM and calculating its spectrum. Moreover, we expanded the concept of the LE on a VFGS. Finally, three applications of the VFGS in decision making are presented. In our future work, we will investigate the concepts of domination set, vertex covering, and independent set in VGSs and give applications of different types of domination in VGSs and other sciences.