Quadratic-Phase Wave-Packet Transform in L²($\mathbb{R}$)

Abstract

Wavelet transform is a powerful tool for analysing the problems arising in harmonic analysis, signal and image processing, sampling, filtering, and so on. However, they seem to be inadequate for representing those signals whose energy is not well concentrated in the frequency domain. In pursuit of representations of such signals, we propose a novel time-frequency transform coined as quadratic-phase wave packet transform in $L^2\left(\mathbb{R}\right)$. The proposed transform is aimed at rectifying the conventional wavelet transform by employing a quadratic-phase Fourier transform with extra degrees of freedom. Besides the formulation of all the fundamental results, including the orthogonality relation, reconstruction formula and the characterization of range, we also derive a direct relationship between the well-known Wigner-Ville distribution and the proposed transform. In addition, we study the quadratic-phase wave-packet transform in the framework of almost periodic functions. Finally, we extend the scope of the present work by investigating the composition of quadratic-phase wave packet transforms.

1. Introduction

Time-frequency analysis has witnessed a giant leap with the birth of the Gabor transform, in which the Gaussian distribution function is used as a window function to construct efficient time-frequency localization of finite energy signals [1]. Gabor systems are generated by modulations ${\mathcal{M}}_c\psi \left(t\right)=e^{ict}\psi \left(t\right),c\in \mathbb{R}$ and translations ${\mathcal{T}}_b\psi \left(t\right)=\psi (t-b),b\in \mathbb{R}$ of a single function $\psi \left(t\right)\in L^2\left(\mathbb{R}\right)$ and hence, can be viewed as the set of time-frequency shifts of $\psi$ in a time-frequency plane. Although the Gabor transforms catered much to the needs of scientific and engineering communities, however, due to the rigid window function, they can only provide the time-frequency content of a signal with constant frequency and time resolution. This is often not the most desired resolution, which led to the birth of wavelet transform [1]. Wavelet systems are generated by a set of dilations ${\mathcal{D}}_a\psi \left(t\right)=a^{-1/2}\psi \left(t/a\right),a\in {\mathbb{R}}^{+}$ and translations ${\mathcal{T}}_b\psi \left(t\right)=\psi (t-b),b\in \mathbb{R}$ of a single window function $\psi \left(t\right)\in L^2\left(\mathbb{R}\right)$. The wavelet transform can be viewed as a time-scale analysis tool, which provides a better description of the signal than the Gabor transform [2]. Moreover, the symmetry property of wavelets is often desirable in practical applications, and as such, wavelets can reveal different patterns and singularities of highly nonstationary signals, such as Brownian motions, patterns on the water surfaces, fractal properties of the velocity field, computations of Renyi dimensions, Hurst and Hölder exponents. Some prominent examples of the symmetric wavelets include biorthogonal wavelets, quincunx wavelets, and carinal Bsplines [3]. Despite the fact that the wavelet transforms have captivated the scientific, engineering, and research communities with their wide range of applications and simple mathematical underpinning, however, they could not perform satisfactorily while analyzing signals whose energy is not well concentrated in the frequency domain. To circumvent this defect, Labate et al. [4] introduced wave packet systems $\left\{{\mathcal{D}}_a{\mathcal{T}}_b{\mathcal{M}}_c\psi \left(t\right):a\in {\mathbb{R}}^{+},b,c\in \mathbb{R}\right\}$ by incorporating all three of the operations, that is, translation, dilation, and modulation, to a family of functions in $L^2\left(\mathbb{R}\right)$. The wave-packet transform can be thought of as the Fourier transform of the signal f windowed with the kernel of the wavelet transform [5]. Indeed, the wave-packet transformation has gained respectable status in the research community and has been successfully applied across diverse fields of science and engineering, particularly in de-noising, image compression and encryption in wireless communication [6,7,8].

The most recent generalisation of the Fourier transform appeared via the theory of reproducing kernels underneath the guise of the quadratic-phase Fourier transform. The off-shoots of Fourier transform include the fractional Fourier transform, linear canonical transform, and the special affine Fourier transform. For a given collection of real parameters $\Lambda =(A,B,C,D,E),B\ne 0$, the quadratic-phase Fourier transform of any $f\in L^2\left(\mathbb{R}\right)$ is defined by [9]

$$\begin{array}{c}\hfill {\mathcal{F}}_{\Lambda }\left[f\right]\left(\omega \right)={\int }_{\mathbb{R}}f\left(t\right){\mathcal{K}}_{\Lambda }(t,\omega )dt,\end{array}$$

(1)

where ${\mathcal{K}}_{\Lambda }(t,\omega )$ denotes the quadratic-phase Fourier kernel and is given by

$$\begin{array}{c}\hfill {\mathcal{K}}_{\Lambda }(t,\omega )=exp\left\{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)\right\}.\end{array}$$

(2)

It is worth noting that (1) is indeed a cluster of transformations which includes the prominent signal processing tools ranging from Fourier to much recent special affine Fourier transforms [10]. Owing to the arbitrariness of the real parameters $\Lambda =(A,B,C,D,E)$, the QPFT ha a lot of flexibility and is of critical significance in tackling problems requires higher degrees of freedom [11]. The quadratic-phase Fourier transform has rectified almost all the limitations of preceding transforms; nonetheless, in some cases, QPFT is inadequate for analysing the signals having high-frequency components for short durations and low-frequency components for long durations. Therefore, in order to obtain joint time-frequency representations, Shah and Lone [12] first introduced the quadratic-phase wavelet transform in the pursuit of time-frequency analysis. The quadratic-phase wavelet transform inherits the excellent mathematical properties of the wavelet transform and the QPFT along with some fascinating properties of its own. As of now, this transformation has received immense attention in many aspects of science and engineering, including harmonic analysis, differential equations, sampling and so on [13,14]. However, much to dismay, one of the severe limitations is that their signal analyzing capability is restricted in the time-frequency plane and hence, are incompetent for localized analysis of those signals whose energy is not well concentrated in the quadratic-phase frequency domain, for instance the chirp like signal which is ubiquitous in nature.

The sole aim of this paper is to introduce the notion of quadratic-phase wave packet transform in $L^2\left(\mathbb{R}\right)$ originated by the combined action of dilations, modulations, and translations of a single function. This novel integral transform can efficiently localize any non-transient signal at different scales and locations in the time-frequency plane with more degrees of freedom. At first, we formulate the quadratic-phase wave-packet transform, braced with an example. In the aftermath, we investigate the orthogonal property of the proposed transform and then establish a natural relationship between the Wigner-Ville distribution and the quadratic-phase wave-packet transform. To broaden the scope of the present study, we shall investigate the composition of quadratic-phase wave-packet transformations in $L^2\left(\mathbb{R}\right)$.

The space of almost periodic function on $\mathbb{R}$ is a closed subspace of $L_{\infty }\left(\mathbb{R}\right)$ spanned by the set of functions of the form $e^{i\lambda t},\lambda \in \mathbb{R}$. EIn other words, we say that the space of almost periodic functions is the uniform closure of the trigonometric polynomials of the form ${\sum }_1^m{h}_k{e}^{i{\lambda }_{k}t}$, where $h_k\in \mathbb{C},{\lambda }_k\in \mathbb{R}$ and $m\in \mathbb{N}$. All almost periodic functions are uniformly continuous and bounded in nature. These functions have received considerable attention across various disciplines of science and technology such as quantum mechanics, optics, geophysics, differential equations, harmonic analysis, and so on [15,16]. Keeping the exciting developments of almost periodic functions in hindsight, it is desirable to study the behaviour of almost periodic functions in the framework of quadratic-phase wave-packet transform. The main contributions of the article are itemized below:

• To introduce the notion of quadratic-phase wave packet transform.
• To study mathematical properties of the proposed transform.
• To study of quadratic-phase wave packet transform on the space of almost periodic functions.
• To study the composition of quadratic-phase wave-packet transforms.

The rest of the paper is structured into four main sections. In Section 2, we formulate the concept of quadratic-phase wave packet transform and study its basic properties. Section 3 deals with the study of quadratic-phase wave packet transform on the space of almost periodic functions. Section 4 is completely devoted to the formulation of the composition of quadratic-phase wave packet transforms. Finally, a conclusion is extracted in Section 5.

2. Quadratic-Phase Wave-Packet Transform in $L^2\left(\mathbb{R}\right)$

In this section, we formally introduce the notion of quadratic-phase wave-packet transform in $L^2\left(\mathbb{R}\right)$ and then study the fundamental properties of the proposed transform including the orthogonality relation, an inversion formula and the characterization of range. In the sequel, we derive a direct relationship between the well-known Wigner distribution and the quadratic-phase wave packet transform. To accomplish our objectives, we shall define a couple of unitary operators acting on the space of square-integrable functions.

For any function $\psi \in L^2\left(\mathbb{R}\right)$ and $\alpha \in {\mathbb{R}}^{+},\beta ,\omega \in \mathbb{R}$, we define the translation operator ${\mathcal{T}}_{\beta }$, dilation operator ${\mathcal{D}}_{\alpha }$ and a generalized modulation operator ${\mathcal{M}}_{\omega }^{\Lambda }$ by $\left({\mathcal{T}}_{\beta }\psi \right)\left(t\right)=\psi (t-\beta )$, $\left({\mathcal{D}}_{\alpha }\psi \right)\left(t\right)={\alpha }^{-1/2}\psi \left(t/\alpha \right)$ and $\left({\mathcal{M}}_{\omega }^{\Lambda }\psi \right)\left(t\right)=e^{i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\psi \left(t\right),A,B,C,D,E\in \mathbb{R},B\ne 0$, respectively.

We now define the family of analyzing functions by implementing the above defined unitary operators together with the parametric set $\Lambda =\left(A,B,C,D,E\right),B\ne 0$ on a square integrable function $\psi$ as:

$$\begin{array}{c}\hfill {\mathcal{D}}_{\alpha }{\mathcal{T}}_{\beta }{\mathcal{M}}_{\omega }^{\Lambda }\psi \left(t\right)={\psi }_{\omega ,\alpha ,\beta }^{\Lambda }\left(t\right)={\displaystyle \frac{1}{\sqrt{\alpha }}}\psi \left({\displaystyle \frac{t-\beta }{\alpha }}\right)e^{i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)},\alpha \in {\mathbb{R}}^{+},\beta ,\omega \in \mathbb{R}.\end{array}$$

(3)

Having constructed the collection of analyzing functions, we are ready to introduce the definition of the quadratic-phase wave packet transform.

Definition 1.

Given a parametric set $\Lambda =(A,B,C,D,E),B\ne 0$, the quadratic-phase wave packet transform of any function $f\in L^2\left(\mathbb{R}\right)$ is defined by

$$\begin{array}{c}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )=⟨f,{\psi }_{\omega ,\alpha ,\beta }^{\Lambda }⟩,\alpha \in {\mathbb{R}}^{+},\beta ,\omega \in \mathbb{R},\end{array}$$

(4)

where ${\psi }_{\omega ,\alpha ,\beta }^{\Lambda }$ is given by (3).

Define ${\psi }_{\alpha }\left(t\right)=\frac{1}{\sqrt{\alpha }}\psi \left(\frac{t}{\alpha }\right)$, then the quadratic-phase wave packet transform (4) can be recast as

$$\begin{array}{c}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )={\int }_{\mathbb{R}}f\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}.\end{array}$$

(5)

Or, equivalently

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )& =e^{-i\left(C{\omega }^2+E\omega \right)}{\int }_{\mathbb{R}}f\left(t\right)e^{-i\left(A{t}^2+Dt\right)}\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-iBt\omega }\mathrm{dt}\hfill \\ \hfill & =e^{-i\left(C{\omega }^2+E\omega \right)}{\int }_{\mathbb{R}}F\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-it\left(B\omega \right)}\mathrm{dt}\hfill \\ \hfill & =e^{-i\left(C{\omega }^2+E\omega \right)}{WPT}_F(B\omega ,\alpha ,\beta ),\hfill \end{array}$$

(6)

where $F\left(t\right)=f\left(t\right)e^{-i\left(A{t}^2+Dt\right)}$ and ${WPT}_F(B\omega ,\alpha ,\beta )$ denoted the classical wave packet transform of a signal $F\left(t\right)$ with its argument scaled by a parameter B. From (6), we observe that the computation of the quadratic-phase wave packet transform performs the following three actions in unison:

(i).

A product by a chirp signal, i.e., $f\left(t\right)\to F\left(t\right)=f\left(t\right)e^{-i\left(A{t}^2+Dt\right)}$.

(ii).

A classical wave-packet transform (with its argument scaled by B), that is, $F\left(t\right)\to {WPT}_F(B\omega ,\alpha ,\beta )$.

(iii).

Another product by a chirp signal, that is, ${WPT}_F(B\omega ,\alpha ,\beta )\to \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )=$$e^{-i\left(C{\omega }^2+E\omega \right)}{WPT}_F(B\omega ,\alpha ,\beta )$.

Hence the computational load of the quadratic-phase wave packet transform is essentially dictated by the classical wave packet transform. Moreover, the aformentioned scheme is depicted in Figure 1.

Figure 1. Structure of computing the proposed quadratic-phase wave packet transform.

We can draw the following observations from the Definition 1:

(i).

For the parametric set $\Lambda =\left(-A/2B,1/B,0,-D/2B,0\right)$ and multiplying the right side of (5) by $1/\sqrt{2\pi iB}$, Definition 1 boils down to the linear canonical wave packet transform

$$\begin{array}{c}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )={\displaystyle \frac{1}{\sqrt{2\pi iB}}}{\int }_{\mathbb{R}}f\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{i\left(A{t}^2-2Bt\omega +D{\omega }^2\right)/2B}\mathrm{dt}.\end{array}$$

(7)

(ii).

For the parametric set $\Lambda =\left(-cot\theta /2,csc\theta ,-cot\theta /2,0,0\right)$, $\theta \ne n\pi$ and multiplying the right side of (5) by $1/\sqrt{1-icot\alpha }$, Definition 1 reduces to the fractional wave packet transform

$$\begin{array}{c}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )={\displaystyle \frac{1}{\sqrt{1-icot\alpha }}}{\int }_{\mathbb{R}}f\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{i\left(t^2+{\omega }^2\right)cot\theta /2-it\omega csc\theta }\mathrm{dt}.\end{array}$$

(8)

(iii).

For the parametric set $\Lambda =(0,1,-1,0:0,0)$, Definition 1 boils down to the classical wave packet transform

$$\begin{array}{c}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )={\int }_{\mathbb{R}}f\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\omega t}\mathrm{dt}.\end{array}$$

(9)

We now present an example for the lucid illustration of the proposed quadratic-phase wave packet transform given by (4).

Example 1.

Consider the wavelet function $\psi \left(t\right)=e^{-\pi t^2}$. Then, we shall compute the quadratic-phase wave packet transform (5) of the function $f\left(t\right)=e^{ikt},k>0$ with respect to an analyzing function $\psi \left(t\right)$ as:

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )& ={\int }_{\mathbb{R}}f\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{\alpha }}}{\int }_{\mathbb{R}}{e}^{ikt}{e}^{-\pi {\left(\frac{t-\beta }{\alpha }\right)}^2}{e}^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{\alpha }}}{e}^{-\pi {\left(\frac{\beta }{\alpha }\right)}^2-i\left(C{\omega }^2+E\omega \right)}{\int }_{\mathbb{R}}{e}^{-\left(iA+\frac{\pi }{{\alpha }^2}\right)t^2+\left(ik+\frac{2\pi \beta }{\alpha }-B\omega -D\right)t}\mathrm{dt}\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{\pi \alpha }{\pi +iA{\alpha }^2}}}exp\left\{-\pi {\left(\frac{\beta }{\alpha }\right)}^2-i\left(C{\omega }^2+E\omega \right)\right\}\hfill \\ \hfill & \times exp\left\{\frac{{\left(ik+\frac{2\pi \beta }{\alpha }-B\omega -D\right)}^2}{4\left(iA+\frac{\pi }{{\alpha }^2}\right)}\right\}.\hfill \end{array}$$

(10)

It is immediate from (10) that the quadratic-phase wave packet transform (4) can be visualized as a three-parameter representation of a signal $f\in L^2\left(\mathbb{R}\right)$. Simultaneous visualization of quadratic-phase wave packet transform in all three variables is hardly possible. Hence, in order to have a sound visualization, some variables must either be fixed or eliminated, so that one is restricted to a particular section of the parameter space determined by $\alpha \in {\mathbb{R}}^{+},\omega ,\beta \in \mathbb{R}$.

(i).

Position Representation: In case the frequency and scale parameters ω and α are kept fixed in (10); that is $\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )$ is rendered as a function of translation parameter β only, the quadratic-phase wave packet transform yields a position representation system. For $k=1$, the position representation $\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(·,·,\beta )$ of (10) corresponding to different parameters are presented in Figure 2.

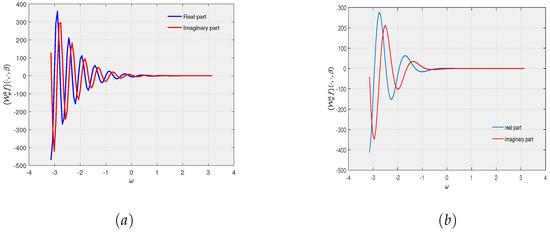Figure 2. (a) Position-representation of Example 1 for $\omega =3,\alpha =7/2$ and $\Lambda =(1,3,5/2,2,1/2)$. (b) Position-representation of Example 1 for $\omega =1/2,\alpha =1$ and $\Lambda =(1,1/2,0,3,0)$.

(ii).

Scale Representation: If $\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )$ is solely regarded as a function of scale variable α, then the quadratic-phase wave packet transform boils down to a scale representation $\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(·,\alpha ,·)$. For the case $k=1$, the scale representation of (10) corresponding to different parameters are depicted in Figure 3.

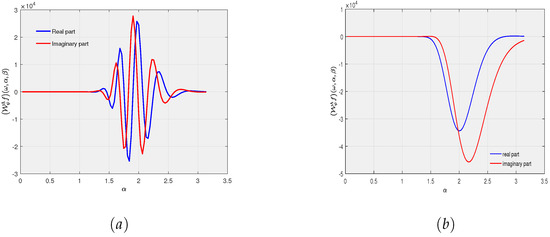Figure 3. (a) Scale-representation of Example 1 $\omega =4,\beta =1$ and $\Lambda =(1,3,5/2,2,1/2)$. (b) Scale-representation of Example 1 $\omega =4,\beta =1$ and $\Lambda =(0,5/2,1,3/2,1/2)$.

(iii).

Frequency Representation: The quadratic-phase wave packet transform yields a frequency representation of a transformed signal when the scale and translation variables α and β are kept constant. The frequency representation is especially useful in situations where frequency behaviour is important. Figure 4 represents the frequency representation $\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,·,·)$ of the Example 1 with respect to different set of parameters.

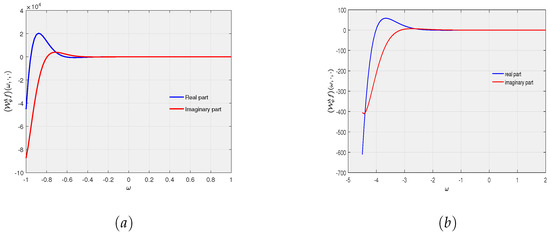Figure 4. (a) Frequency-presentation of Example 1 for $k=1,\alpha =5,\beta =1$ and $\Lambda =(1,3,5/2,2,1/2)$. (b) Frequency-representation of Example 1 with respect to $k=1,\alpha =4,\beta =1$ and $\Lambda =(1,3/2,0,2,1)$.

In the following theorem, we assemble some basic properties of the quadratic-phase wave packet transform Definition 1.

Theorem 1.

For any $f,g\in L^2\left(\mathbb{R}\right)$, $\gamma ,\delta \in \mathbb{R}$, $\mu \in {\mathbb{R}}^{+}$ and an admissible ψ, the quadratic-phase wave packet transform $\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )$ satisfies the following properties:

(i).

Linearity: $\left({\mathcal{W}}_{\psi }^{\Lambda }(\gamma f+\delta g)\right)(\omega ,\alpha ,\beta )=\gamma \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )+\delta \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )$,

(ii).

Translation: $\left({\mathcal{W}}_{\psi }^{\Lambda }\left({\mathcal{T}}_{k}f\right)\right)(\omega ,\alpha ,\beta )=e^{-i\left(A{k}^2+Bk\omega +Dk\right)}\left({\mathcal{W}}_{\psi }^{\Lambda }\left({\mathcal{M}}_{-2Ak}f\right)\right)(\omega ,\alpha ,\beta -k)$,

(iii).

Modulation: $\left({\mathcal{W}}_{\psi }^{\Lambda }\left({\mathcal{M}}_{{\omega }^{\prime }}f\right)\right)(\omega ,\alpha ,\beta )=e^{2\pi i\left(\alpha t+C{\alpha }^2/B^2-2\alpha \omega /B-E\alpha /B\right)}\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )$,

(iv).

Scaling: $\left({\mathcal{W}}_{\psi }^{\Lambda }f\left(\mu t\right)\right)(\omega ,\alpha ,\beta )=\frac{1}{\sqrt{\left|\mu \right|}}\left({\mathcal{W}}_{\psi }^{{\Lambda }^{\prime }}f\right)\left(\frac{\omega }{\mu },\mu \alpha ,\mu \beta \right),{\Lambda }^{\prime }=\left(A/{\mu }^2,B,C{\mu }^2,D/\mu ,E\mu \right)$,

(v).

Conjugation: $\left({\mathcal{W}}_{\psi }^{\Lambda }\overline{f}\right)(\omega ,\alpha ,\beta )=\overline{\left({\mathcal{W}}_{\psi }^{-\Lambda }f\right)(\omega ,\alpha ,\beta )}$.

Proof. 

For the sake of brevity, we omit the proof. □

Next, we derive the orthogonality relation for the proposed quadratic-phase wave packet transform given by (4).

Theorem 2.

For any $f,g\in L^2\left(\mathbb{R}\right)$ and admissible wavelets ${\psi }_1$ and ${\psi }_2$, we have

$$\begin{array}{c}\hfill ⟨\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta ),\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )⟩={\displaystyle \frac{1}{\left|B\right|}}\parallel \psi {\parallel }^2⟨f,g⟩.\end{array}$$

(11)

Proof. 

Invoking the well-known Fubini theorem, we have,

$$\begin{array}{cc}\hfill & {\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )\overline{\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )}\mathrm{d}\omega \mathrm{d}\beta \hfill \\ \hfill & ={\int }_{\mathbb{R}}\left\{{\int }_{\mathbb{R}}f\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\right\}\hfill \\ \hfill & \times \left\{{\int }_{\mathbb{R}}\overline{g\left(z\right)}{\psi }_{\alpha }(z-\beta )e^{i\left(A{z}^2+Bz\omega +C{\omega }^2+Dz+E\omega \right)}\mathrm{dz}\right\}\mathrm{d}\omega \mathrm{d}\beta \hfill \\ \hfill & ={\int }_{\mathbb{R}}\left\{{\int }_{\mathbb{R}}{e}^{-i\left(B(t-z)\omega \right)}\mathrm{d}\omega \right\}\left\{{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}f\left(t\right)\overline{g\left(z\right)}{\psi }_{\alpha }(z-\beta )\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\left(A\left(t^2-z^2\right)+D(t-z)\right)}\mathrm{dt}\mathrm{dz}\right\}\mathrm{d}\beta \hfill \\ \hfill & ={\displaystyle \frac{1}{\left|B\right|}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}f\left(t\right)\overline{g\left(z\right)}{\psi }_{\alpha }(z-\beta )\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\left(A\left(t^2-z^2\right)+D(t-z)\right)}\delta (t-z)\mathrm{dt}\mathrm{dz}\mathrm{d}\beta \hfill \\ \hfill & ={\displaystyle \frac{1}{\left|B\right|}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}f\left(t\right)\overline{g\left(t\right)}{\psi }_{\alpha }(t-\beta )\overline{{\psi }_{\alpha }(t-\beta )}\mathrm{dt}\mathrm{d}\beta \hfill \\ \hfill & ={\displaystyle \frac{1}{\left|B\right|}}{\int }_{\mathbb{R}}{\psi }_{\alpha }(t-\beta )\overline{{\psi }_{\alpha }(t-\beta )}\mathrm{d}\beta {\int }_{\mathbb{R}}f\left(t\right)\overline{g\left(t\right)}\mathrm{dt}\hfill \\ \hfill & ={\displaystyle \frac{1}{\left|B\right|}}\parallel \psi {\parallel }^2⟨f,g⟩.\hfill \end{array}$$

This completes the proof of Theorem 2. □

Remark 1. (i). For $f=g$, Theorem 2 collapses to the following identity:

$$\begin{array}{c}\hfill {\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{\left|\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )\right|}^2\mathrm{d}\omega \mathrm{d}\beta ={\displaystyle \frac{1}{\left|B\right|}}\parallel \psi {\parallel }^2\parallel f{\parallel }^2.\end{array}$$

(12)

(ii). For the case $\parallel \psi \parallel =1$, relation (12) yields

$$\begin{array}{c}\hfill {\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{\left|\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )\right|}^2\mathrm{d}\omega \mathrm{d}\beta ={\displaystyle \frac{1}{\left|B\right|}}\parallel f{\parallel }^2,\end{array}$$

(13)

which, except for the parameter B, gives the energy preserving relation corresponding to the quadratic-phase wave packet transform.

In our next theorem, we demonstrate that the quadratic-phase wave packet transform ${\mathcal{W}}_{\psi }^{\Lambda }f$ of any function $f\in L^2\left(\mathbb{R}\right)$ is reversible in the sense that f can be easily recovered from the transformed space $L^2(\mathbb{R}\times \mathbb{R})$.

Theorem 3.

Let $\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )$ be the quadratic-phase wave packet transform of any arbitrary square integrable function f and $\parallel \psi \parallel =1$, then f can be reconstructed via:

$$\begin{array}{c}\hfill f\left(t\right)=\left|B\right|{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta ){\psi }_{\omega ,\alpha ,\beta }^{\Lambda }\left(t\right)\mathrm{d}\omega \mathrm{dt},\end{array}$$

(14)

where ${\psi }_{\omega ,\alpha ,\beta }^{\Lambda }\left(t\right)$ is given by (3).

Proof. 

We have,

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )& ={\int }_{\mathbb{R}}f\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\hfill \\ \hfill & =e^{-i\left(C{\omega }^2+E\omega \right)}{\int }_{\mathbb{R}}f\left(t\right)e^{-i\left(A{t}^2+Dt\right)}\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-iBt\omega }\mathrm{dt}\hfill \\ \hfill & =e^{-i\left(C{\omega }^2+E\omega \right)}{\int }_{\mathbb{R}}F\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-iBt\omega }\mathrm{dt}\hfill \\ \hfill & =e^{-i\left(C{\omega }^2+E\omega \right)}\left({\mathcal{G}}_{{\psi }_{\alpha }}F\right)(B\omega ,\beta ),\hfill \end{array}$$

(15)

where $F\left(t\right)=f\left(t\right)e^{-i\left(A{t}^2+Dt\right)}$ and $\left({\mathcal{G}}_{{\psi }_{\alpha }}F\right)(B\omega ,\beta )$ is the Gabor transform of $F\left(t\right)$ with respect to the window function ${\psi }_{\alpha }$. Since $F\left(t\right)\in L^2\left(\mathbb{R}\right)$ whenever $f\left(t\right)\in L^2\left(\mathbb{R}\right)$; therefore, the inverse of the function $F\left(t\right)\in L^2\left(\mathbb{R}\right)$ is given by

$$\begin{array}{c}\hfill F\left(t\right)={\displaystyle \frac{\left|B\right|}{⟨{\psi }_1,{\psi }_2⟩}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{G}}_{{\psi }_1}F\right)(B\omega ,\beta ){\psi }_2(t-\beta )e^{iB\omega t}\mathrm{d}\omega \mathrm{d}\beta .\end{array}$$

(16)

For ${\psi }_1={\psi }_2$ and ${\psi }_{\alpha }$ as the window function, relation (16) yields

$$\begin{array}{c}\hfill F\left(t\right)={\displaystyle \frac{\left|B\right|}{\parallel {\psi }_{\alpha }{\parallel }^2}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{G}}_{{\psi }_1}F\right)(B\omega ,\beta ){\psi }_{\alpha }(t-\beta )e^{iB\omega t}\mathrm{d}\omega \mathrm{d}\beta .\end{array}$$

(17)

Implementing (15) in (17), we obtain

$$\begin{array}{c}\hfill f\left(t\right)e^{-i\left(A{t}^2+Dt\right)}={\displaystyle \frac{\left|B\right|}{{\parallel \psi \parallel }^2}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )e^{i\left(C{\omega }^2+E\omega \right)}{\psi }_{\alpha }(t-\beta )e^{iB\omega t}\mathrm{d}\omega \mathrm{d}\beta .\end{array}$$

Or equivalently,

$$\begin{array}{cc}\hfill f\left(t\right)& =\left|B\right|{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta ){\psi }_{\alpha }(t-\beta )e^{i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{d}\omega \mathrm{d}\beta \hfill \\ \hfill & =\left|B\right|{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta ){\psi }_{\omega ,\alpha ,\beta }^{\Lambda }\mathrm{d}\omega \mathrm{d}\beta .\hfill \end{array}$$

This completes the proof of Theorem 3. □

In the following, we investigate the characterization of the range for the quadratic-phase wave packet transform given by (5).

Theorem 4.

If $f\in L^2\left(\mathbb{R}\right)$ and ${\psi }_{\alpha }\in L^2\left(\mathbb{R}\right)$ such that $\parallel \psi \parallel =1$, then f belongs to the range ${\mathcal{W}}_{\psi }^{\Lambda }\left(L^2\left(\mathbb{R}\right)\right)$ if and only if

$$\begin{array}{c}\hfill f\left({\omega }^{\prime },\alpha ,{\beta }^{\prime }\right)={\int }_{\mathbb{R}}{\int }_{\mathbb{R}}f(\omega ,\alpha ,\beta )⟨{\psi }_{\omega ,\alpha ,\beta }^{\Lambda },{\psi }_{{\omega }^{\prime },\alpha ,{\beta }^{\prime }}^{\Lambda }⟩\mathrm{d}\omega \mathrm{d}\beta ,\end{array}$$

(18)

where ${\psi }_{\omega ,\alpha ,\beta }^{\Lambda }$ is defined in (3).

Proof. 

Assume that $f\in {\mathcal{W}}_{\psi }^{\Lambda }\left(L^2\left(\mathbb{R}\right)\right)$. Then, there exists $g\in L^2\left(\mathbb{R}\right)$ such that ${\mathcal{W}}_{\psi }^{\Lambda }g=f$. In order to show that f satisfies (18), we proceed as

$$\begin{array}{cc}\hfill f\left({\omega }^{\prime },\alpha ,{\beta }^{\prime }\right)& =\left({\mathcal{W}}_{\psi }^{\Lambda }g\right)\left({\omega }^{\prime },\alpha ,{\beta }^{\prime }\right)\hfill \\ \hfill & ={\int }_{\mathbb{R}}g\left(t\right)\overline{{\psi }_{{\omega }^{\prime },\alpha ,{\beta }^{\prime }}^{\Lambda }\left(t\right)}\mathrm{dt}\hfill \\ \hfill & ={\int }_{\mathbb{R}}\left\{{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{W}}_{\psi }^{\Lambda }g\right)(\omega ,\alpha ,\beta ){\psi }_{\omega ,\alpha ,\beta }^{\Lambda }\left(t\right)\mathrm{d}\omega \mathrm{d}\beta \right\}\overline{{\psi }_{{\omega }^{\prime },\alpha ,{\beta }^{\prime }}^{\Lambda }\left(t\right)}\mathrm{dt}\hfill \\ \hfill & ={\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{W}}_{\psi }^{\Lambda }g\right)(\omega ,\alpha ,\beta )\left\{{\int }_{\mathbb{R}}{\psi }_{\omega ,\alpha ,\beta }^{\Lambda }\left(t\right)\overline{{\psi }_{{\omega }^{\prime },\alpha ,{\beta }^{\prime }}^{\Lambda }\left(t\right)}\mathrm{dt}\right\}\mathrm{d}\omega \mathrm{d}\beta \hfill \\ \hfill & ={\int }_{\mathbb{R}}{\int }_{\mathbb{R}}f(\omega ,\alpha ,\beta )⟨{\psi }_{\omega ,\alpha ,\beta }^{\Lambda },{\psi }_{{\omega }^{\prime },\alpha ,{\beta }^{\prime }}^{\Lambda }⟩\mathrm{d}\omega \mathrm{d}\beta ,\hfill \end{array}$$

which evidently verifies our claim. Conversely, suppose that the function f satisfies (18). To verify that $f\in {\mathcal{W}}_{\psi }^{\Lambda }\left(L^2\left(\mathbb{R}\right)\right)$, it is sufficient to find out a function $g\in L^2\left(\mathbb{R}\right)$ such that ${\mathcal{W}}_{\psi }^{\Lambda }g=f$. Therefore, the desired function g will be constructed as follows:

Let

$$\begin{array}{c}\hfill g\left(t\right)={\int }_{\mathbb{R}}{\int }_{\mathbb{R}}f(\omega ,\alpha ,\beta ){\psi }_{\omega ,\alpha ,\beta }^{\Lambda }\left(t\right)\mathrm{d}\omega \mathrm{d}\beta .\end{array}$$

(19)

Then, it is straightforward to get $\parallel g{\parallel }_2\le \parallel f{\parallel }_2<\infty$; that is $g\in L^2\left(\mathbb{R}\right)$. Furthermore, by virtue of Fubini theorem, we have

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }g\right)\left({\omega }^{\prime },\alpha ,{\beta }^{\prime }\right)& ={\int }_{\mathbb{R}}g\left(t\right)\overline{{\psi }_{{\omega }^{\prime },\alpha ,{\beta }^{\prime }}^{\Lambda }\left(t\right)}\mathrm{dt}\hfill \\ \hfill & ={\int }_{\mathbb{R}}\left\{{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}f(\omega ,\alpha ,\beta ){\psi }_{\omega ,\alpha ,\beta }^{\Lambda }\left(t\right)\mathrm{d}\omega \mathrm{d}\beta \right\}\overline{{\psi }_{{\omega }^{\prime },\alpha ,{\beta }^{\prime }}^{\Lambda }}\left(t\right)\mathrm{dt}\hfill \\ \hfill & ={\int }_{\mathbb{R}}{\int }_{\mathbb{R}}f(\omega ,\alpha ,\beta )⟨{\psi }_{\omega ,\alpha ,\beta }^{\Lambda },{\psi }_{{\omega }^{\prime },\alpha ,{\beta }^{\prime }}^{\Lambda }⟩\mathrm{d}\omega \mathrm{d}\beta \hfill \\ \hfill & =f\left({\omega }^{\prime },\alpha ,{\beta }^{\prime }\right).\hfill \end{array}$$

This completes the proof of Theorem 4. □

The classic Wigner-Ville distribution, which is defined as the Fourier transform of the instantaneous autocorrelation function $f\left(t+\frac{\tau }{2}\right)\overline{f\left(t-\frac{\tau }{2}\right)}$, is one of the most prominent tools for analysing signals whose energy is not well concentrated in the time-frequency domains. Several areas of science and engineering, such as quantum physics, optics, sonar, radar, and signal processing in general, have made extensive the use of Wigner-Ville distribution [1,14]. The vast applicability of the Wigner-Ville distribution in time-frequency analysis has sparked considerable attention and is one of the most active areas of contemporary research. As such, it is essential to establish a relationship between the conventional Wigner-Ville distribution and the proposed quadratic-phase wave packet transforms.

Definition 2.

The Wigner-Ville distribution of any finite energy signal $f\in L^2\left(\mathbb{R}\right)$ is defined by

$$\begin{array}{c}\hfill {\mathit{W}}_f(t,\omega )={\int }_{\mathbb{R}}f\left(t+{\displaystyle \frac{\tau }{2}}\right)\overline{f\left(t-{\displaystyle \frac{\tau }{2}}\right)}{e}^{-i\omega \tau }\mathrm{d}\tau .\end{array}$$

(20)

Towards the end of this section, we obtain a direct relationship between the classical Wigner-Ville distribution (20) and the proposed quadratic-phase wave packet transform (5).

Theorem 5.

Let ${\mathit{W}}_f(t,\omega )$ be the Wigner-Ville distribution of any $f\in L^2\left(\mathbb{R}\right)$ and ψ be an admissible wavelet. Then, we have

$$\begin{array}{cc}\hfill {\mathit{W}}_f(t,\omega )& =2\left|B\right|e^{2i\left(\omega t+2A{t}^2-Dt\right)}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{e}^{-2iBt\xi }\left({\mathcal{W}}_{\psi }^{\Lambda }\left({\mathcal{M}}_{-2\omega }f\right)\right)(\xi ,\alpha ,\beta )\hfill \\ \hfill & \times \overline{\left({\mathcal{W}}_{\psi }^{{\Lambda }^{\prime }}\left({\mathcal{M}}_{-4At}f\right)\right)\left(-\xi ,-\alpha ,-(\beta +2t)\right)}\mathrm{d}\xi \mathrm{d}\beta ,\hfill \end{array}$$

(21)

where ${\Lambda }^{\prime }=(A,B,C,-D,-E)$.

Proof. 

The Wigner-Ville distribution of any $f\in L^2\left(\mathbb{R}\right)$ is given by

$$\begin{array}{c}\hfill {\mathit{W}}_f(t,\omega )={\int }_{\mathbb{R}}f\left(t+{\displaystyle \frac{\tau }{2}}\right)\overline{f\left(t-{\displaystyle \frac{\tau }{2}}\right)}{e}^{-i\omega \tau }\mathrm{d}\tau ,\end{array}$$

or equivalently,

$$\begin{array}{c}\hfill {\mathit{W}}_f(t,\omega )=2e^{2i\omega t}{\int }_{\mathbb{R}}f\left(z\right)\overline{f(2t-z)}{e}^{-2i\omega z}\mathrm{dz}.\end{array}$$

(22)

By virtue of inversion Formula (14) and Theorem 1, we have

$$\begin{array}{cc}\hfill f(2t-z)& =\left|B\right|{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{W}}_{\psi }^{\Lambda }f(-z+2t)\right)(\xi ,\alpha ,\beta ){\psi }_{\xi ,\alpha ,\beta }^{\Lambda }\left(z\right)\mathrm{d}\xi \mathrm{d}\beta \hfill \\ \hfill & =\left|B\right|{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{e}^{-2i\left(2A{t}^2-Bt\xi -Dt\right)}\left({\mathcal{W}}_{\psi }^{\Lambda }\left({\mathcal{M}}_{4At}f(-z)\right)\right)(\xi ,\alpha ,\beta +2t){\psi }_{\xi ,\alpha ,\beta }^{\Lambda }\left(z\right)\mathrm{d}\xi \mathrm{d}\beta \hfill \\ \hfill & =\left|B\right|{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{e}^{-2i\left(2A{t}^2-Bt\xi -Dt\right)}\left({\mathcal{W}}_{\psi }^{{\Lambda }^{\prime }}\left({\mathcal{M}}_{-4At}f\right)\right)\left(-\xi ,-\alpha ,-(\beta +2t)\right){\psi }_{\xi ,\alpha ,\beta }^{\Lambda }\left(z\right)\mathrm{d}\xi \mathrm{d}\beta ,\hfill \end{array}$$

(23)

where ${\Lambda }^{\prime }=(A,B,C,-D,-E)$. Implementing the estimate (23) in (22) and using the well-known Fubini theorem, we obtain

$$\begin{array}{cc}\hfill {\mathit{W}}_f(t,\omega )& =2\left|B\right|e^{2i\omega t}{\int }_{\mathbb{R}}f\left(z\right)e^{-2i\omega z}\hfill \\ \hfill & \times \left\{{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{e}^{2i\left(2A{t}^2-Bt\xi -Dt\right)}\overline{\left({\mathcal{W}}_{\psi }^{{\Lambda }^{\prime }}\left({\mathcal{M}}_{-4At}f\right)\right)\left(-\xi ,-\alpha ,-(\beta +2t)\right){\psi }_{\xi ,\alpha ,\beta }^{\Lambda }\left(z\right)}\mathrm{d}\xi \mathrm{d}\beta \right\}\mathrm{dz}\hfill \\ \hfill & =2\left|B\right|e^{2i\left(\omega t+2A{t}^2-Dt\right)}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{e}^{-2iBt\xi }\overline{\left({\mathcal{W}}_{\psi }^{{\Lambda }^{\prime }}\left({\mathcal{M}}_{-4At}f\right)\right)\left(-\xi ,-\alpha ,-(\beta +2t)\right)}\hfill \\ \hfill & \times \left\{{\int }_{\mathbb{R}}\left({\mathcal{M}}_{-2\omega }f\right)\left(z\right)\overline{{\psi }_{\xi ,\alpha ,\beta }^{\Lambda }\left(z\right)}\mathrm{dz}\right\}\mathrm{d}\xi \mathrm{d}\beta \hfill \\ \hfill & =2\left|B\right|e^{2i\left(\omega t+2A{t}^2-Dt\right)}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{e}^{-2iBt\xi }\left({\mathcal{W}}_{\psi }^{\Lambda }\left({\mathcal{M}}_{-2\omega }f\right)\right)(\xi ,\alpha ,\beta )\hfill \\ \hfill & \times \overline{\left({\mathcal{W}}_{\psi }^{{\Lambda }^{\prime }}\left({\mathcal{M}}_{-4At}f\right)\right)\left(-\xi ,-\alpha ,-(\beta +2t)\right)}\mathrm{d}\xi \mathrm{d}\beta .\hfill \end{array}$$

This completes the proof of Theorem 4. □

3. Quadratic-Phase Wave-Packet Transform for Almost Periodic Functions

In this Section, our main goal is to extend the theory of quadratic-phase wave-packet transformation to the space of almost periodic functions. Almost periodic functions are a natural generalization of the usual periodic functions on $\mathbb{R}$. Let ${\mathcal{T}}_p$ represent the space of all trigonometric polynomials on $\mathbb{R}$ and is of the form

$$\begin{array}{c}\hfill {\mathcal{T}}_p=\left\{f\left(t\right)=\sum _{k=1}^m{h}_k{e}^{i{\lambda }_{k}t}:h_k\in \mathbb{C},{\lambda }_k\in \mathbb{R},m\in \mathbb{N}\right\}.\end{array}$$

(24)

The space ${\mathcal{T}}_p$ is equipped with the sup norm given by ${\parallel f\parallel }_{\infty }={sup}_{t\in \mathbb{R}}\left|f\left(t\right)\right|$. The completion of the space ${\mathcal{T}}_p$ with respect to this sup norm turns out to be the space of almost periodic functions and is denoted by ${\mathcal{A}}_p$.

Let ${\mathcal{Q}}_{\mathbb{R}}$ represents the family of functions q of the form

$$\begin{array}{c}\hfill q\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \sum _{\ell =1}^n{\lambda }_{\ell }{t}^{\alpha \ell },}\hfill & t\ge 0,\hfill \\ {\displaystyle -\sum _{\ell =1}^n{\lambda }_{\ell }{(-t)}^{\alpha \ell },}\hfill & t<0\hfill \end{array}\right.,\end{array}$$

(25)

where $n\in \mathbb{R}$, ${\lambda }_{\ell }\in \mathbb{R},\ell =1,2,\dots ,n$ and ${\alpha }_1>{\alpha }_2>\cdots >{\alpha }_n>0$. A function P of the form ${\displaystyle P\left(t\right)=\sum _{k=1}^m{h}_k{e}^{i{q}_k\left(t\right)},q\left(t\right)\in {\mathcal{Q}}_{\mathbb{R}}}$ is called a generalized trigonometric polynomial on $\mathbb{R}$.

Definition 3.

A function f defined on $\mathbb{R}$ is said to have a strong limit power if for every $\epsilon >0$, there exists a generalized trigonometric polynomial $P_{\epsilon }$ such that

$$\begin{array}{c}\hfill \parallel f-P_{ϵ}\parallel =sup\left\{|f\left(t\right)-P_{\epsilon }\left(t\right)|:t\in \mathbb{R}\right\}<\epsilon .\end{array}$$

(26)

We denote the space of all functions with strong limit power by $\mathcal{G}\left(\mathbb{R}\right)$ and the inner product associated with $\mathcal{G}\left(\mathbb{R}\right)$ is defined by

$$\begin{array}{c}\hfill ⟨f,g⟩=\underset{T\to \infty }{lim}{\displaystyle \frac{1}{2T}}{\int }_{-T}^{T}f\left(t\right)\overline{g\left(t\right)}\mathrm{dt}.\end{array}$$

(27)

Moreover, it is worthwhile to mention that ${\mathcal{A}}_p\subset \mathcal{G}\left(\mathbb{R}\right)$ and ${\parallel f\parallel }_{{\mathcal{A}}_p}={\parallel f\parallel }_{\mathcal{G}}$. Both the spaces ${\mathcal{A}}_p$ and $\mathcal{G}\left(\mathbb{R}\right)$ are closed subspaces of $L^{\infty }\left(\mathbb{R}\right)$.

We are now in a position to investigate the quadratic-phase wave packet transform (5) on the space of almost periodic functions.

Theorem 6.

Let f be an almost periodic function. Then, the quadratic-phase Fourier transform of f with respect to a parametric set $\Lambda =(A,B,C,D,E),B\ne 0$ is a strong limit power function.

Proof. 

We shall begin the proof in case f is a trigonometric polynomial. That is, f is of the form

$$\begin{array}{c}\hfill f\left(t\right)=\sum _{k=1}^m{h}_k{e}^{i{\lambda }_{k}t}.\end{array}$$

(28)

An application of QPFT (1) on (28) yields

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\Lambda }\left[f\right]\left(\omega \right)& ={\int }_{\mathbb{R}}f\left(t\right)e^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\hfill \\ \hfill & =\sum _{k=1}^m{h}_k{\int }_{\mathbb{R}}{e}^{i{\lambda }_{k}t}{e}^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\hfill \\ \hfill & =\sum _{k=1}^m{h}_k{e}^{-i\left(C{\omega }^2+E\omega \right)}{\int }_{\mathbb{R}}{e}^{-iA{t}^2+i\left({\lambda }_k-B\omega -D\right)t}\mathrm{dt}\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{1}{iA}}}\sum _{k=1}^m{h}_k{e}^{-i\left(C{\omega }^2+E\omega \right)}{e}^{i{\left({\lambda }_k-B\omega -D\right)}^2/4A}\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{1}{A}}}\sum _{k=1}^m{h}_k{e}^{-i\left(C{\omega }^2+E\omega -\frac{{({\lambda }_k-B\omega -D)}^2}{4A}+\frac{\pi }{4}\right)},\hfill \end{array}$$

(29)

which is a generalized trigonometric series in $\omega$. Moreover, if f is an almost periodic function, there exist a sequence $\left\{f_n\right\}$ of trigonometric polynomials converging uniformly to f. Therefore, it suffices to verify that, if $\parallel f_n{-f\parallel }_{\infty }\to 0$, then $\parallel {\mathcal{F}}_{\Lambda }\left[f_n\right]\left(\omega \right)-{\mathcal{F}}_{\Lambda }\left[f\right]\left(\omega \right){\parallel }_{\infty }\to 0$.

We observe that

$$\begin{array}{cc}\hfill |{\mathcal{F}}_{\Lambda }\left[f_n\right]\left(\omega \right)-{\mathcal{F}}_{\Lambda }\left[f\right]\left(\omega \right)|& =\left|{\mathcal{F}}_{\Lambda }\left[f_n-f\right]\left(\omega \right)\right|\hfill \\ \hfill & =\left|{\int }_{\mathbb{R}}\left(f_n-f\right)e^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\right|\hfill \\ \hfill & \le {\int }_{\mathbb{R}}|f_n\left(t\right)-f\left(t\right)|\mathrm{dt}\to 0.\hfill \end{array}$$

Consequently, we have

$$\begin{array}{c}\hfill \parallel {\mathcal{F}}_{\Lambda }\left[f_n\right]\left(\omega \right)-{\mathcal{F}}_{\Lambda }\left[f\right]\left(\omega \right){\parallel }_{\infty }=\underset{\omega \in \mathbb{R}}{sup}|{\mathcal{F}}_{\Lambda }\left[f_n\right]\left(\omega \right)-{\mathcal{F}}_{\Lambda }\left[f\right]\left(\omega \right)|\to 0.\end{array}$$

This completes the proof of Theorem 6. □

In our next theorem, we shall demonstrate that the assumption $\psi \in L^1\left(\mathbb{R}\right)$ suffices to conclude that the quadratic-phase wave packet transform is a strong limit power function.

Theorem 7.

Let $\psi \in L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$ be an admissible wavelet and $\Lambda =(A,B,C,D,E)$ with $B\ne 0$. Then for any almost periodic function f, the quadratic-phase wave packet transform ${\mathcal{W}}_{\psi }^{\Lambda }$ of f is a strong limit function in ω.

Proof. 

Let $f\left(t\right)$ be a trigonometric polynomial of the form

$$\begin{array}{c}\hfill f\left(t\right)=\sum _{k=1}^m{h}_k{e}^{i{\lambda }_{k}t}.\end{array}$$

(30)

Then, the quadratic-phase wave packet transform of f given by (30) is computed as

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )& ={\int }_{\mathbb{R}}f\left(t\right)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{\alpha }}}\sum _{k=1}^m{h}_k{e}^{-i\left(C{\omega }^2+E\omega \right)}{\int }_{\mathbb{R}}\overline{\psi \left({\displaystyle \frac{t-\beta }{\alpha }}\right)}{e}^{-i\left(-{\lambda }_{k}t+A{t}^2+Bt\omega +Dt\right)}\mathrm{dt}\hfill \\ \hfill & =\sqrt{\alpha }\sum _{k=1}^m{h}_k{e}^{-i\left(C{\omega }^2+E\omega \right)}{\int }_{\mathbb{R}}\overline{\psi \left(z\right)}{e}^{-i\left((D-{\lambda }_k)(\alpha z+\beta )+A{(\alpha Z+\beta )}^2+B(\alpha Z+\beta )\omega \right)}\mathrm{dz}\hfill \\ \hfill & =\sqrt{\alpha }\sum _{k=1}^m{h}_k{e}^{-i\left(A{\beta }^2+B\omega \beta +(D-{\lambda }_k)\beta \right)}\hfill \\ \hfill & \times {\int }_{\mathbb{R}}{e}^{i\alpha {\lambda }_{k}z}\overline{\psi \left(z\right)}{e}^{-i\left({\alpha }^{2}A{z}^2+\alpha Bz\omega +C{\omega }^2+\alpha (D+2\beta A)z+E\omega \right)}\mathrm{dz}\hfill \\ \hfill & =\sqrt{\alpha }\sum _{k=1}^m{h}_k{\mathcal{F}}_{{\Lambda }^{☆}}\left[\Psi \right]\left(\omega \right)e^{-i\left(A{\beta }^2+B\omega \beta +(D-{\lambda }_k)\beta \right)},\hfill \end{array}$$

where $\Psi \left(t\right)=e^{i\alpha {\lambda }_{k}t}\overline{\psi \left(t\right)}$ and ${\Lambda }^{★}=\left({\alpha }^{2}A,\alpha B,C,\alpha (D+2\beta A),E\right),B\ne 0$.

Hence, for any fixed $\alpha$, we infer that the quadratic-phase wave packet transform $\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )$ turns out to be a generalized trigonometric polynomial in $\omega$. Moreover, since f is an almost periodic function, there exist a sequence $\left\{f_n\right\}$ of trigonometric polynomials converging uniformly to f. Thus, it is sufficient to verify that, if $\parallel f_n{-f\parallel }_{\infty }\to 0$, then $\parallel \left({\mathcal{W}}_{\psi }^{\Lambda }{f}_n\right)(\omega ,\alpha ,\beta )-\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta ){\parallel }_{\infty }\to 0$. To verify our claim, we proceed as:

$$\begin{array}{cc}\hfill {∥\left({\mathcal{W}}_{\psi }^{\Lambda }{f}_n\right)(\omega ,\alpha ,\beta )-\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )∥}_{\infty }& =\underset{\omega \in \mathbb{R}}{sup}\left|\left({\mathcal{W}}_{\psi }^{\Lambda }{f}_n\right)(\omega ,\alpha ,\beta )-\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )\right|\hfill \\ \hfill & =\underset{\omega \in \mathbb{R}}{sup}\left|\left({\mathcal{W}}_{\psi }^{\Lambda }(f_n-f)\right)(\omega ,\alpha ,\beta )\right|\hfill \\ \hfill & \le \underset{\omega \in \mathbb{R}}{sup}\left|{\int }_{\mathbb{R}}(f_n-f)\overline{{\psi }_{\alpha }(t-\beta )}{e}^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}\mathrm{dt}\right|\hfill \\ \hfill & \le \underset{\omega \in \mathbb{R}}{sup}\sqrt{\alpha }{\int }_{\mathbb{R}}|f_n(\alpha z+\beta )-f(\alpha z+\beta )|\left|\psi \left(z\right)\right|\mathrm{dz}\hfill \\ \hfill & \le \parallel f_n-f{\parallel }_{\infty }\parallel \psi {\parallel }_1\to 0.\hfill \end{array}$$

Thus, we conclude that the quadratic-phase wave packet transform $\left({\mathcal{W}}_{\psi }^{\Lambda }{f}_n\right)(\omega ,\alpha ,\beta )$ of an almost periodic function f is a strong limit power function in $\omega$. □

4. Composition of Quadratic-Phase Wave-Packet Transforms

The main objective of this section is to study the composition of quadratic-phase wave packet transforms, which can be thought of as the successive application of two quadratic-phase wave packet transforms with respect to a distinct pair of wavelets. The idea is to compose a pair of wave packet transforms concerning two different admissible wavelets to yield a new four-parameter wave packet transform determined by a pair of scaling parameters and one common translation and frequency parameters. We intend to examine the behaviour of the composition of quadratic-phase wave packet transforms and study the associated properties, including the orthogonality relation and the inversion formula.

Let

$$\begin{array}{c}\hfill f_{\omega }^{\Lambda }\left(t\right)=f\left(t\right)e^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}.\end{array}$$

(31)

Then, the application of QPFT on (31) yields

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\Lambda }\left[f_{\omega }^{\Lambda }\left(t\right)\right]\left(\xi \right)& ={\int }_{\mathbb{R}}f\left(t\right)e^{-i\left(A{t}^2+Bt\omega +C{\omega }^2+Dt+E\omega \right)}{e}^{-i\left(A{t}^2+Bt\xi +C{\omega }^2+Dt+E\xi \right)}\mathrm{dt}\hfill \\ \hfill & =e^{2iC\omega \xi }{\int }_{\mathbb{R}}f\left(t\right)e^{-i\left(2A{t}^2+Bt(\omega +\xi )+C{(\omega +\xi )}^2+2Dt+E(\omega +\xi )\right)}\mathrm{dt}\hfill \\ \hfill & =e^{2iC\omega \xi }{\int }_{\mathbb{R}}f\left(t\right)e^{-i\left(2A{t}^2+Bt(\omega +\xi )+C{(\omega +\xi )}^2+2Dt+E(\omega +\xi )\right)}\mathrm{dt}\hfill \\ \hfill & =e^{2iC\omega \xi }{\mathcal{F}}_{\Lambda }\left[f\right](\omega +\xi ).\hfill \end{array}$$

(32)

Furthermore, we have

$$\begin{array}{cc}\hfill & {\mathcal{F}}_{\Lambda }\left[{\psi }_{\alpha }(t-\beta )\right]\left(\xi \right)\hfill \\ \hfill & ={\int }_{\mathbb{R}}{\psi }_{\alpha }(t-\beta )e^{-i\left(A{t}^2+Bt\xi +C{\xi }^2+Dt+E\xi \right)}\mathrm{dt}\hfill \\ \hfill & =\sqrt{\alpha }{\int }_{\mathbb{R}}\psi \left(z\right)e^{-i\left(A{(\alpha Z+\beta )}^2+B(\alpha Z+\beta )\xi +C{\xi }^2+D(\alpha Z+\beta )+E\xi \right)}\mathrm{dz}\hfill \\ \hfill & =\sqrt{\alpha }{e}^{-i\left(A{\beta }^2+B\beta \xi +D\beta \right)}{\int }_{\mathbb{R}}{e}^{-2iA\alpha \beta z}\psi \left(z\right)e^{-i\left({\alpha }^{2}A{z}^2+Bz\left(\alpha \xi \right)+\frac{c}{{\alpha }^2}{\left(\alpha \xi \right)}^2+\alpha Dz+\frac{E}{\alpha }\left(\alpha \xi \right)\right)}\mathrm{dz}\hfill \\ \hfill & =\sqrt{\alpha }{e}^{-i\left(A{\beta }^2+B\beta \xi +D\beta \right)}{\int }_{\mathbb{R}}\Psi \left(z\right)e^{-i\left({\alpha }^{2}A{z}^2+Bz\left(\alpha \xi \right)+\frac{C}{{\alpha }^2}{\left(\alpha \xi \right)}^2+\alpha Dz+\frac{E}{\alpha }\left(\alpha \xi \right)\right)}\mathrm{dz}\hfill \\ \hfill & =\sqrt{\alpha }{e}^{-i\left(A{\beta }^2+B\beta \xi +D\beta \right)}{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left(\alpha \xi \right),\hfill \end{array}$$

(33)

where $\Psi \left(t\right)=e^{-2iA\alpha \beta z}\psi \left(z\right)$ and $\tilde{\Lambda }=\left({\alpha }^{2}A,B,\frac{C}{{\alpha }^2},\alpha D,\frac{E}{\alpha }\right),B\ne 0$.

The quadratic-phase wave packet transform (4) can be recast in terms of inner product of functions $f_{\omega }^{\Lambda }\left(t\right)$ and ${\psi }_{\alpha }(t-\beta )$ as:

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )& =⟨f_{\omega }^{\Lambda }\left(t\right),{\psi }_{\alpha }(t-\beta )⟩\hfill \\ \hfill & =\left|B\right|⟨{\mathcal{F}}_{\Lambda }\left[f_{\omega }^{\Lambda }\left(t\right)\right]\left(\xi \right),{\mathcal{F}}_{\Lambda }\left[{\psi }_{\alpha }(t-\beta )\right]\left(\xi \right)⟩\hfill \\ \hfill & =\sqrt{\alpha }\left|B\right|{\int }_{\mathbb{R}}{e}^{2iC\omega \xi }{\mathcal{F}}_{\Lambda }\left[f\right](\omega +\xi )e^{i\left(A{\beta }^2+B\beta \xi +D\beta \right)}\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left(\alpha \xi \right)}\mathrm{d}\xi \hfill \\ \hfill & =\sqrt{\alpha }\left|B\right|{\int }_{\mathbb{R}}{e}^{i\left(2C\omega \xi -C{\xi }^2-E\xi \right)}{\mathcal{F}}_{\Lambda }\left[f\right](\omega +\xi )\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left(\alpha \xi \right)}\overline{{\mathcal{K}}_{\Lambda }(\beta ,\xi )}\mathrm{d}\xi \hfill \\ \hfill & ={\mathcal{F}}_{\Lambda }^{-1}\left[\sqrt{\alpha }{e}^{i\left(2C\omega \xi -C{\xi }^2-E\xi \right)}{\mathcal{F}}_{\Lambda }\left[f\right](\omega +\xi )\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left(\alpha \xi \right)}\right]\left(\beta \right).\hfill \end{array}$$

Consequently,

$$\begin{array}{c}\hfill {\mathcal{F}}_{\Lambda }\left[\left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,\alpha ,\beta )\right]\left(\xi \right)=\sqrt{\alpha }{e}^{i\left(2C\omega \xi -C{\xi }^2-E\xi \right)}{\mathcal{F}}_{\Lambda }\left[f\right](\omega +\xi )\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left(\alpha \xi \right)}.\end{array}$$

(34)

By virtue of relation (34), we can write

$$\begin{array}{c}\hfill \left({\mathcal{W}}_{\psi }^{\Lambda }f\right)(\omega ,{\alpha }_1,\beta )=\sqrt{{\alpha }_1}\left|B\right|{\int }_{\mathbb{R}}{e}^{i\left(2C\omega \xi -C{\xi }^2-E\xi \right)}{\mathcal{F}}_{\Lambda }\left[f\right](\omega +\xi )\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left({\alpha }_1\xi \right)}\overline{{\mathcal{K}}_{\Lambda }(\beta ,\xi )}\mathrm{d}\xi \end{array}$$

(35)

and

$$\begin{array}{c}\hfill {\mathcal{F}}_{\Lambda }\left[\left({\mathcal{W}}_{\varphi }^{\Lambda }f\right)\left(\xi ,{\alpha }_2,{\beta }^{\prime }\right)\right]\left(\omega \right)=\sqrt{{\alpha }_2}{e}^{i\left(2C\xi \omega -C{\omega }^2-E\omega \right)}{\mathcal{F}}_{\Lambda }\left[f\right](\xi +\omega )\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Phi \right]\left({\alpha }_2\omega \right)},\end{array}$$

(36)

where $\Psi \left(t\right)=e^{-2iA{\alpha }_1\beta t}\psi \left(t\right)$ and $\Phi \left(t\right)=e^{-2iA{\alpha }_2{\beta }^{\prime }t}\varphi \left(t\right)$. Based on (35) and (36), we shall define the product of transforms as follows:

$$\begin{array}{c}\hfill \left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )={\mathcal{W}}_{\psi }^{\Lambda }\left[\left({\mathcal{W}}_{\varphi }^{\Lambda }f\right)\left(\xi ,{\alpha }_2,{\beta }^{\prime }\right)\right](\omega ,{\alpha }_1,\beta ).\end{array}$$

(37)

With the aid of (35) and (36), we can express the composition of quadratic-phase wave packet transforms as follows:

$$\begin{array}{cc}\hfill \left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )& =\sqrt{{\alpha }_1}\left|B\right|{\int }_{\mathbb{R}}{e}^{i\left(2C\omega \xi -C{\xi }^2-E\xi \right)}{\mathcal{F}}_{\Lambda }\left[\left({\mathcal{W}}_{\varphi }^{\Lambda }f\right)\left(\xi ,{\alpha }_2,{\beta }^{\prime }\right)\right](\omega +\xi )\hfill \\ \hfill & \times \overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left({\alpha }_1\xi \right)}\overline{{\mathcal{K}}_{\Lambda }(\beta ,\xi )}\mathrm{d}\xi \hfill \\ \hfill & =\sqrt{{\alpha }_1{\alpha }_2}\left|B\right|{\int }_{\mathbb{R}}{e}^{i\left(2C\omega \xi -C{\xi }^2-E\xi \right)}{e}^{i\left(2C\xi (\omega +\xi )-C{(\omega +\xi )}^2-E(\omega +\xi )\right)}\hfill \\ \hfill & \times {\mathcal{F}}_{\Lambda }\left[f\right](2\xi +2\omega )\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Phi \right]\left({\alpha }_2(\omega +\xi )\right)}\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left({\alpha }_1\xi \right)}\overline{{\mathcal{K}}_{\Lambda }(\beta ,\xi )}\mathrm{d}\xi \hfill \\ \hfill & =\sqrt{{\alpha }_1{\alpha }_2}\left|B\right|{\int }_{\mathbb{R}}{e}^{i\left(C\left(4\omega \xi -{\omega }^2\right)-2\omega \xi -E(\omega +2\xi )\right)}{\mathcal{F}}_{\Lambda }\left[f\right](2\xi +2\omega )\hfill \\ \hfill & \times \overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Phi \right]\left({\alpha }_2(\omega +\xi )\right)}\overline{{\mathcal{F}}_{\tilde{\Lambda }}\left[\Psi \right]\left({\alpha }_1\xi \right)}\overline{{\mathcal{K}}_{\Lambda }(\beta ,\xi )}\mathrm{d}\xi .\hfill \end{array}$$

(38)

Equation (38) serves as an explicit expression for the composition of quadratic-phase wave packet transforms.

Next, we shall derive an analogue of orthogonality relation (11) for the composition of quadratic-phase wave packet transforms defined in (38).

Theorem 8.

Let $\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )$ and $\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }g\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )$ be the quadratic-phase wave packet transforms of f and g belonging to $L^2\left(\mathbb{R}\right)$, respectively. Then, we have

$$\begin{array}{c}\hfill {\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )\overline{\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }g\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )}\mathrm{d}\omega \mathrm{d}\beta ={\displaystyle \frac{1}{\left|B\right|}}⟨\psi ,\varphi ⟩⟨f,g⟩.\end{array}$$

(39)

Proof. 

The proof directly follows from the Theorem 2, hence omitted. □

Remark 2. (i). For $f=g$ and $\psi =\varphi$, Theorem 8 yields the energy preserving relation associated with the quadratic-phase wave packet transforms defined in (38).

$$\begin{array}{c}\hfill {\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )\overline{\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }g\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )}\mathrm{d}\omega \mathrm{d}\beta ={\displaystyle \frac{1}{\left|B\right|}}\parallel \psi {\parallel }^2\parallel f{\parallel }^2.\end{array}$$

(40)

(ii). The operator ${\mathcal{P}}_{\psi ,\varphi }^{\Lambda }$ is bounded and linear. Moreover, for the normalized ψ and $\left|B\right|=1$, relation (40) becomes an isometry from $L^2\left(\mathbb{R}\right)$ to $L^2(\mathbb{R}\times \mathbb{R})$.

Towards the culmination of this section, we shall demonstrate that the input signal $f\in L^2\left(\mathbb{R}\right)$ can be recovered from the corresponding composition of wave packet transforms $\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)$.

Theorem 9.

If $\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )$ is the quadratic-phase wave packet transforms corresponding to a function $f\in L^2\left(\mathbb{R}\right)$, then f can be reconstructed via the following formula:

$$\begin{array}{c}\hfill f\left(t\right)={\displaystyle \frac{\left|B\right|}{⟨\psi ,\varphi ⟩}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )\overline{\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }\delta (·-t)\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )}\mathrm{d}\omega \mathrm{d}\beta .\end{array}$$

(41)

Proof. 

Let $g\left(t\right)=\delta (z-t)$ denotes the well-known Dirac delta function. Then using the definition of QPFT (1), it can be easily deduced that

$$\begin{array}{c}\hfill \delta (z-t)={\int }_{\mathbb{R}}{\mathcal{K}}_{-\Lambda }(z,\omega )\overline{{\mathcal{K}}_{-\Lambda }(z,\omega )}\mathrm{d}\omega ,\end{array}$$

(42)

so that $\mathcal{F}\left[g\right]\left(\omega \right)=\overline{{\mathcal{K}}_{-\Lambda }(z,\omega )}$. Invoking the inversion formula of the QPFT, we have

$$\begin{array}{cc}\hfill f\left(t\right)& ={\displaystyle \frac{1}{\left|B\right|}}{\int }_{\mathbb{R}}\mathcal{F}\left[f\right]\left(\omega \right){\mathcal{K}}_{-\Lambda }(t,\omega )\mathrm{d}\omega \hfill \\ \hfill & ={\displaystyle \frac{1}{\left|B\right|}}{\int }_{\mathbb{R}}\mathcal{F}\left[f\right]\left(\omega \right)\overline{\mathcal{F}\left[g\right]\left(\omega \right)}\mathrm{d}\omega \hfill \\ \hfill & ={\displaystyle \frac{\left|B\right|}{⟨\psi ,\varphi ⟩}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )\overline{\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }g\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )}\mathrm{d}\omega \mathrm{d}\beta .\hfill \end{array}$$

(43)

As a consequence of (43), we conclude that the desired reconstruction formula takes the following form:

$$\begin{array}{c}\hfill f\left(t\right)={\displaystyle \frac{\left|B\right|}{⟨\psi ,\varphi ⟩}}{\int }_{\mathbb{R}}{\int }_{\mathbb{R}}\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }f\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )\overline{\left({\mathcal{P}}_{\psi ,\varphi }^{\Lambda }\delta (·-t)\right)(\omega ,{\alpha }_1,{\alpha }_2,\beta )}\mathrm{d}\omega \mathrm{d}\beta .\end{array}$$

This completes the proof of Theorem 9. □

5. Conclusions

In the present study, we intertwined the advantages of the classical wavelet and quadratic-phase fourier transforms, and introduced the notion of the novel quadratic-phase wave packet transform in $L^2\left(\mathbb{R}\right)$. The prime advantage of this intertwining lies in the fact that the proposed transform enjoys certain extra degrees of freedom and thus achieves higher flexibility, which in turn can be employed in optimizing the concentration of the higher frequency spectrum. As such, the proposed transform serves as a significant addition to the contemporary tools of signal and image processing. Besides the study of all the fundamental properties, we also obtained a direct relationship between the Wigner-Ville distribution and the proposed transform. Moreover, we also investigated the quadratic-phase wave packet transform on the space of almost periodic functions. Finally, we carried out the analysis of composition of quadratic-phase wave packet transforms in $L^2\left(\mathbb{R}\right)$. Nevertheless, the present study, in itself, leads to several ramifications and developments.