Abstract
A horizontally symmetric all-metallic vibration isolator (AM-VI) is proposed to further investigate the dynamic mechanical performance. The novel AM-VI was constructed by combining hat-shaped metal rubber and oblique springs, which were connected in parallel. The springs were arranged symmetrically relative to the support. The elliptic method and the frequency sweeping method were used to compare the dynamic stiffness and the loss factor of the AM-VI. The results demonstrated that the dynamic stiffness and the loss factor calculated by two distinct test methodologies were considerably different, indicating that the inertial force effect of the dynamic testing equipment should be taken into count when adopting the elliptic method. Furthermore, when the vibration isolation performance was evaluated by utilizing mechanical impedance and force transmissibility, the AM-VI achieved excellent vibration isolation performance within a broad frequency range.
1. Introduction
Vibration isolators are widely used to suppress the effect of unwanted vibrations on equipment and components [1,2]. Passive vibration isolation does not have an external energy supply, and it has the advantages of simple structure, high reliability, low cost, and a remarkable high-frequency vibration suppression effect [3], so passive vibration isolation is widely used for vibration suppression in many areas, such as spacecraft [4], vehicle seats [5], vessels [6], and high-accuracy equipment. Some efforts have been made regarding the development and innovation of passive vibration isolation for this purpose. In addition, many vibration isolators and systems with innovative structures have been developed to achieve passive vibration isolation; these include the wipe rope isolator [7], spring vibration isolator [8], metal rubber vibration isolator [9,10], and pipeline bracket system [11]. Although the abovementioned vibration isolators have characteristics of a good damping effect or stiffness that meets the requirements, they do not meet the dual requirements of suitable stiffness and excellent damping ability at the same time. To solve the dilemma discussed above, the work proposes an all-metallic vibration isolator (AM-VI) whose key elements are composed of four rectangular springs and hat-shaped metal rubber.
To further explore the performance of the vibration isolator, many theoretical and experimental studies have been conducted. Cao et al. [12] studied the fatigue damage characteristics of metal rubber isolators. Yan et al. [13] designed a new type of shape memory alloy metal rubber (SMA-MR) damper and investigated the law of mechanical properties with temperature through experimental methods. Using annular metal rubber and shape memory alloy actuators, Shen et al. [14] developed a resonant frequency-tunable vibration isolator and demonstrated the reliability of the tunable resonant frequency with a resonant frequency identification experiment in a sine sweep test ranging from 5 to 500 Hz. Liu et al. [15] designed an integrated quasi-zero stiffness isolator (IQZS) composed of a single elastic structure and studied its dynamic characteristics through theoretical analysis and experimentation. A dynamic characteristic analysis of inertia-based vibration isolators was conducted, and the vibration performance of the vibration isolators was evaluated through performance criteria [16,17]. Wang et al. [18] considered three configurations that incorporate a negative stiffness element and extra inerter in parallel connection into the conventional isolator to study their vibration characteristics through resonant frequency and displacement transmissibility. Roncen et al. [19] conducted experimental research and a numerical simulation of a nonlinear rubber isolator subjected to both harmonic and broadband excitations. Tang et al. [20] studied the vibration transmission characteristics of a single-degree-of-freedom passive vibration isolation system with two nonlinear dampers. The results indicated that nonlinear systems performed better than linear systems when force transmissibility was considered, and the damper and spring parallel system showed ideal characteristics when displacement transmissibility was considered, while the damper and spring perpendicular system did not.
Although extensive investigations have been conducted on the dynamic characteristics and vibration isolation performance of passive vibration isolators through theoretical analysis, numerical simulation, and experimental verification, few studies have addressed the influence of different experimental methods on the dynamic characteristics of vibration isolators, to the best of the authors’ knowledge. This work proposed an AM-VI and then investigated its dynamic performance through different experimental methods.
The work is divided into three main sections and is structured as follows. In Section 2, the novel AM-VI is proposed, and its main component’s parameters are described. In Section 3, the dynamic performance characterization parameters of the AM-VI (such as dynamic stiffness, loss factor, mechanical impedance, and force transmissibility) are introduced. In Section 4, the effects of the elliptic method and the frequency sweeping method on the dynamic stiffness and loss factor of the AM-VI are compared, and the AM-VI’s vibration isolation performance is further studied.
2. Development of an All-Metallic Vibration Isolator
2.1. Structural Design
The AM-VI was designed as shown in Figure 1. it primarily consistes of an elastic component, a damping element, a limiting element, and other basic components. It is combined the superior vibration isolation property of rubber isolators with the better service environment adaptability of metallic materials. Four oblique rectangular springs were arranged symmetrically relative to the support and deployed to provide stiffness as stiffness support elements. This comprised the elastic components. The damping element consisted of an upper and lower hat-shaped metal rubber, respectively. It was capable of sustaining lateral and vertical tensile pressure loads. Figure 2 depicts its structure, and Table 1 lists the appropriate geometric parameters. Compared with the traditional stiffness elements and damping elements, the two aforementioned elements exhibit excellent properties of consistency, reliability, and creep. Limiting metal rubber constituted the limiting element. The limiting metal rubber, which was positioned in the middle of the base beneath the support, protected the AM-VI from shock. One shell, one base, and one support constituted the fundamental parts of the AM-VI. In addition, assembling the different parts of the AM-VI was made easier by the availability of numerous standard parts.
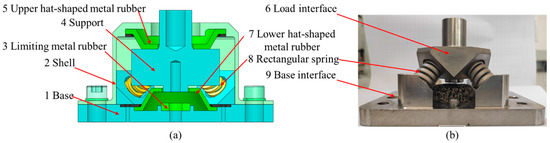
Figure 1.
The diagram of the AM-VI: (a) the sectional diagram of structure; (b) the internal AM-VI without installing shell.
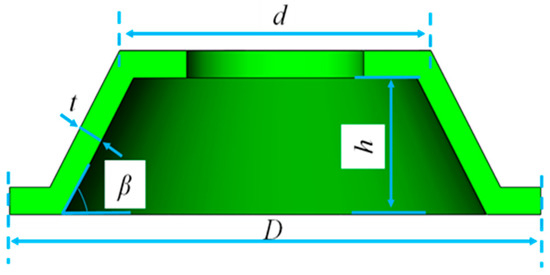
Figure 2.
Schematic diagram of the hat-shaped metal rubber structure.

Table 1.
Geometric dimensions of hat-shaped metal rubber.
2.2. Material Selection and Main Component Parameters
The AM-VI needs to be treated with anti-corrosion treatment because it must function under demanding situations, such as high temperature, low temperature, wet heat, salt spray, etc. Consequently, the actions taken were as follows. First, 304 stainless steel was used as the raw material for the processing of the main parts. Second, the oblique spring’s surface was nickel-plated after processing 55CrSi as the raw material. Second, 304 stainless steel wire with a wire diameter of 0.3 mm was spiral wound, blank prepared, and cold stamped to form the metal rubber [21,22]. Since the metal rubber structure for hats was unique, pre-pressing the metal rubber blank before cold stamping was essential for achieving consistency in molding.
Additionally, the AM-VI weighed 4.3 kg and had a load rating of 2 kN. Its weight was calculated using the material parameters given in the 3D modeling program SOLIDWORKS. The mounting interface of the AM-VI was designed to guarantee accurate installation when used. According to the request, the load interface was intended for M18, whereas the base interface was designed for M14. The main component parameters of the AM-VI are listed in Table 2.

Table 2.
The main component parameters of the AM-VI.
3. Dynamic Test Methods and Performance Characterization
3.1. The Elliptic Method
When the elliptic method was conducted to perform the dynamic test, the dynamic stiffness and loss factor were computed on the basis of the transmission force-displacement curve that was obtained. As shown in Figure 3a, X0 is the displacement’s amplitude and the maximum value in the elliptic curve’s X coordinate. FT is the elastic force amplitude and the corresponding transmission force when the displacement is the maximum X0. FD is the maximum damping force, namely the transmission force when the displacement is zero. The main components of the dynamic testing apparatus were a computer, a controller, and a dynamic testing machine with a force sensor positioned on top of the upper grip. A schematic representation of the vibration isolator dynamic test is shown in Figure 3b. It should be noted that before the test started, the vertical load rating of the AM-VI was preloaded by the testing machine to guarantee that the AM-VI was always under pressure during the test.
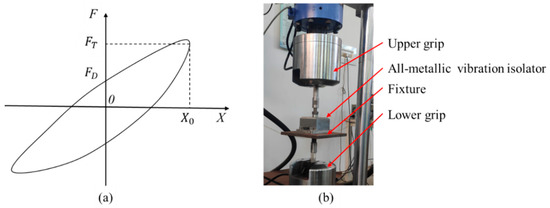
Figure 3.
The schematic of dynamic test of the elliptic method. (a) Transmission force-displacement curve. (b) The dynamic testing machine and designed fixtures for measurement of transmission force.
3.2. The Frequency Sweeping Method
A frequency sweeping test was also applied to investigate the dynamic performance of the AM-VI. The experimental equipment and system for the frequency sweeping test are shown in Figure 4. The constructed test platform is displayed in Figure 5. Constant force excitation can be used to test an AM-VI’s dynamic performance, and mechanical impedance and force transmissibility can be obtained by computation. As depicted in Figure 5, when dynamic stiffness and loss factor are measured, a force sensor and a displacement sensor were used. Similarly, when mechanical impedance and force transmissibility were measured, a force sensor and an acceleration sensor were utilized. The test platform was excited with a 10 N constant force sweeping throughout a frequency range of 5 Hz to 1000 Hz, and the attached counterweight was 198 kg.
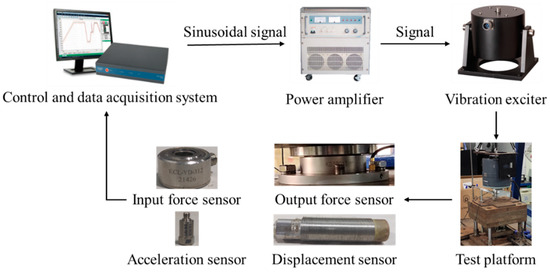
Figure 4.
The experimental equipment and system for the frequency sweeping test.

Figure 5.
Dynamic test platform for the frequency sweeping test.
3.3. Performance Characterization
3.3.1. Characterization of Dynamic Stiffness
When the elliptic method is used to calculate the dynamic stiffness Kd, it can be expressed as [23]:
According to vibration theory, the dynamic test system of the AM-VI can be simplified to a hysteresis dynamic model, as demonstrated in Figure 6. Then, the corresponding vibration equation is established, which can be written as [24]:
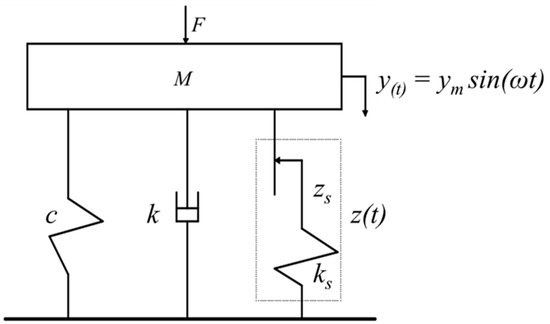
Figure 6.
Hysteresis dynamics model of the AM-VI.
Introducing the non-dimensional parameters:
Substituting Equation (3) into Equation (2), Equation (2) can be rewritten as:
In Figure 6, F is the sinusoidal excitation force applied to the AM-VI by the testing machine, M is the inertial mass of the AM-VI’s input (mainly the mass of the test system tooling and fixture), ym is the vibration amplitude, y is the vibration excitation function about time, k is the dynamic stiffness of the test system (mainly the stiffness of the AM-VI’s spring and metal rubber), and c is the equivalent viscoelastic damping coefficient of the test system, z(t) is a nonlinear restoring force with memory characteristics, zs is the memory restoring force when slipping, and ks is the linear stiffness before slippage.
The analysis of the test system revealed that the force sensor’s measuring value included the elastic recovery force of the AM-VI, the damping force of the measuring system, and the inertia force of the testing machine. This is in accordance with the principle of the test system and the installation position of the force sensor. Therefore, it was suggested that the inertial force effect of the dynamic test machine should be taken into consideration when incorporating Equation (4). Afterward, the following equations were summarized by integrating elastic recovery forces, damping forces, and inertial forces [23]:
where Fd is the actual elastic recovery force of the AM-VI, Fa is the inertia force, Fc is the damping force, and f is the excitation frequency. FT is the load force equivalent to the excitation amplitude ym. It is apparent in Equation (5) that the inertial force and the corresponding load force determine the actual elastic recovery force. Consequently, Equation (5) can be simplified as:
where KT is the measured dynamic stiffness after considering the inertial force effect of the dynamic testing machine, and Kd is the actual dynamic stiffness.
In addition, when the frequency sweeping method is used for the dynamic test, the dynamic stiffness can be expressed as [23]:
where m is the mass of the test system; f is the natural frequency of the test system; and K0 is the sum of the dynamic stiffness of other elastic elements in the excitation system except the isolator—usually K0 = 0, but K0 ≠ 0 in variable load excitation. The model for calculating the dynamic stiffness of the AM-VI is presented in Table 3.

Table 3.
Model for calculating the dynamic stiffness of the AM-VI.
3.3.2. Characterization of Loss Factor
When the elliptic method is used for the dynamic test, the loss factor η can be expressed as [23]:
When the frequency sweeping method is used for the dynamic test, the loss factor can be calculated for isolators with small damping (approximately symmetrical relative to the resonant point), which can be expressed as [25]:
where ωn is the natural circular frequency, and ω1 and ω2 are the circular frequencies for the half-power point. The model for calculating the loss factor of the AM-VI is presented in Table 4.

Table 4.
Model for calculating the loss factor of the AM-VI.
3.3.3. Characterization of Vibration Isolation Performance
The input force sensor was attached to the counterweight block with a threaded connection in the test platform, which was connected to the vibration exciter via an exciter rod lifted by a flexible rope. The AM-VI and the output force sensor were screwed to the base platform. The input force and output force sensor recorded the input and output force, respectively. The counterweight block’s acceleration can be regarded as the input acceleration because it was screw-fastened to the AM-VI.
The relationship between the dynamic force at both ends of the AM-VI and the vibration speed can be expressed as follows [26] since the AM-VI vibrates unidirectionally during the frequency sweeping test:
where Z11, Z22 and Z12, Z21 are the input and transfer impedance, respectively; V1 and V2 are the vibration speed at the input and output, respectively; and FZ1 and FZ2 are the dynamic force at the input and output, respectively.
The output speed of the isolator could be regarded as zero because the output of the tested system was fixed to the output force sensor, which seemed to be fixed to a sizable inflexible mass block. Thus, Equation (11) can be simplified as:
Considering that the test was performed by the acceleration sensor, Equation (12) can be expressed as:
where α1 is the acceleration of the isolator’s input, and ω is the circular frequency.
The force transmissibility was calculated to visually show the AM-VI’s performance in vibration isolation. Considering that the test system can be viewed as a single-degree-of-freedom vibration system, the force transmissibility [3] of the AM-VI is given by:
with the non-dimensional parameters:
where is the damping, βi is the dimensionless circular frequency, m is the load rating of the isolator, ci is the damping coefficient, and ki is the dynamic stiffness of the AM-VI. The calculation model of the corresponding vibration isolation performance parameters is presented in Table 5.

Table 5.
Model for calculating the vibration isolation performance parameter of the AM-VI.
4. Results and Discussion
4.1. Effect of the Elliptic Method and the Frequency Sweeping Method on Dynamic Stiffness
We performed investigations into how the elliptic method and the frequency sweeping method affected the dynamic stiffness of the AM-VI. Figure 7a displays the displacement-frequency response curve acquired by the frequency sweeping method. According to vibration theory, a system with one degree of freedom vibrates in a single, one-order mode. Figure 7a shows that the displacement–frequency response curve only exhibits the first-order modal, verifying the accuracy of the experimental result. The results reveal that the tested system’s resonance frequency was 9.31 Hz, and the dynamic stiffness of the AM-VI was calculated to be 677.52 N/mm by putting the weight mass and resonant frequency of the tested system into Equation (8).
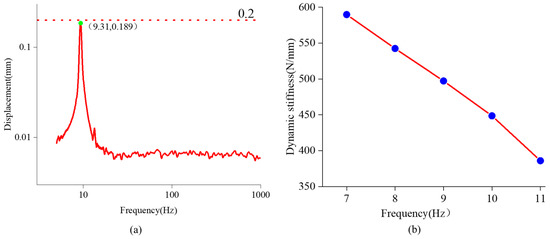
Figure 7.
Experimental results of dynamic stiffness under the elliptic method and the frequency sweeping method. (a) displacement-frequency response curve (b) dynamic stiffness-frequency curve.
Figure 7b demonstrates the relationship between the dynamic stiffness and excitation frequency as measured by the elliptic method. It can be seen that the dynamic stiffness decreased with an increase in excitation frequency. It should be noted that the resonant frequency was closest to 9 Hz. Then, the dynamic stiffness (at 9 Hz excitation frequency) and the frequency sweep results were used to investigate the effect of diverse excitation methods on the dynamic stiffness of the AM-VI. The relevant experimental results are listed in Table 6.

Table 6.
Dynamic stiffness of the AM-VI under different dynamic experimental methods.
Table 6 demonstrates that the dynamic stiffness of the AM-VI was significantly lower when utilizing the elliptic method than it was when utilizing the frequency sweeping method. The reasons for the above experimental results can be explained as follows.
Since the test system’s actual load was slightly smaller than its rating load, the resonant frequency of the AM-VI was slightly larger for the frequency sweeping testing. Similar to the results above, a large difference was found between the dynamic stiffness predicted by Equation (8) and the actual dynamic stiffness because the test system’s load was slightly lower than the rated load. The rated load of the AM-VI was applied by the dynamic testing machine for elliptic dynamic testing. Considering the force sensor‘s position on the dynamic testing machine and the fact that the force sensor recorded data that included the machine’s inertial force, it is crucial to think about how the inertial force effect affects the dynamic stiffness. Comparing the experimental results obtained by considering the inertial force effect of the dynamic testing machine, the relationship between the dynamic stiffness and the excitation frequency is shown in Figure 8. The dynamic stiffness of the AM-VI without considering the inertial force effect was obtained by the dynamic test of the elliptic method. The dynamic stiffness of the AM-VI considering the inertial force effect was obtained by bringing the experimental data into Equation (7) and then fitting it with MATLAB. The inertial mass of the AM-VI was determined to be 70 kg by fitting. It can be seen that regardless of whether the inertial force effect of the dynamic testing machine was considered, the dynamic stiffness had the same tendency, and both decreased with an increase in excitation frequency. The corresponding dynamic stiffness parameters are listed in Table 7.
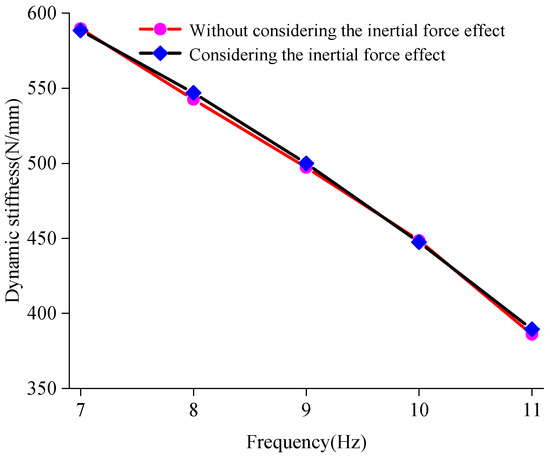
Figure 8.
Dynamic stiffness-frequency curves with and without considering inertial force effect.

Table 7.
Dynamic stiffness parameters with and without considering the inertial force effect.
Since the resonant frequency was 9.31 Hz, the actual dynamic stiffness under the excitation of the 9 Hz frequency was calculated. The actual dynamic stiffness of the AM-VI was equal to 721.05 N/mm by bringing the dynamic stiffness at a frequency of 9 Hz and considering the inertial force effect in Equation (7). The corresponding results are listed in Table 8.

Table 8.
The corresponding dynamic stiffness of the AM-VI under different dynamic test methods.
After considering the inertial force effect of the dynamic testing machine, the dynamic stiffnesses of the AM-VI obtained by the elliptic method and the frequency sweeping method were not very different, which might be due to errors caused by the accuracy of the equipment and the installation of the test platform. The test results demonstrate the necessity of considering the inertial force effect of the testing machine when using the elliptic method for the dynamic test of the isolator, and it is recommended that the inertial force effect of the testing machine should be considered during the test.
4.2. Effect of the Elliptic Method and the Frequency Sweeping Method on Loss Factor
Investigations into how the elliptic method and frequency sweeping method affected the loss factor of the AM-VI were performed. Figure 9 displays the displacement–frequency response curve that was acquired using the frequency sweeping method. The loss factor of the AM-VI was calculated to be 0.060 by putting the data into Equation (10).
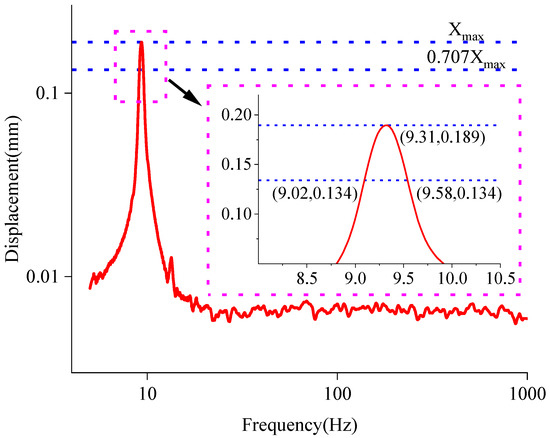
Figure 9.
Displacement-frequency response curve by the frequency sweeping method.
The experimental results of the loss factor at each excitation frequency by the elliptic method are listed in Table 9. It should be noted that the loss factor did not change significantly, and the maximum variation was just 0.01 in the frequency range from 7 Hz to 11 Hz, indicating that the excitation frequency had less of an effect on the damping performance of the AM-VI.

Table 9.
Loss factor of the AM-VI under different excitation frequencies.
Similarly, the loss factor of the AM-VI obtained at the 9 Hz excitation frequency and the experimental results obtained by the frequency sweeping test were used to analyze the influence of different excitation methods on the loss factor. The corresponding loss factor is listed in Table 10.

Table 10.
Loss factor of the AM-VI under different dynamic test methods.
It can be seen in Table 10 that the loss factor of the AM-VI obtained by the elliptic method was larger than that obtained by the frequency sweeping method. The reasons for the above test results can be explained as follows. Since the inertial force effect of the dynamic testing machine was not considered in the dynamic test of the elliptic method, the elastic recovery force of the AM-VI was smaller than the actual value, and the loss factor calculated by Equation (9) was larger than the actual loss factor. When the frequency sweeping test began, the metal wires inside the metal rubber changed from no slip to coil spring contact, and this was accompanied by slip generation, resulting in damping energy consumption. However, the excitation magnitude applied to the test system was relatively small at only 10 N, resulting in less wire contact and slippage inside the metal rubber, so the damping energy consumption was low and the loss factor was small to some extent. Increasing the amplitude of the excitation force applied to the tested system increased the contact and sliding between the wires inside the metal rubber, consuming more energy and thereby increasing the loss factor of the AM-VI.
4.3. Analysis of Force Transmissibility Characteristics
Because the counterweight and the input force sensor were threaded fixed, and the force sensor was fixed with a threaded rod and the vibration exciter, the dynamic force Fz1 at the AM-VI’s input can be viewed as the excitation force of the vibration exciter. The mechanical impedance curve of the tested AM-VI is shown in Figure 10. The mechanical impedance curve in Figure 10 shows that the AM-VI has excellent vibration isolator performance to a great extent.
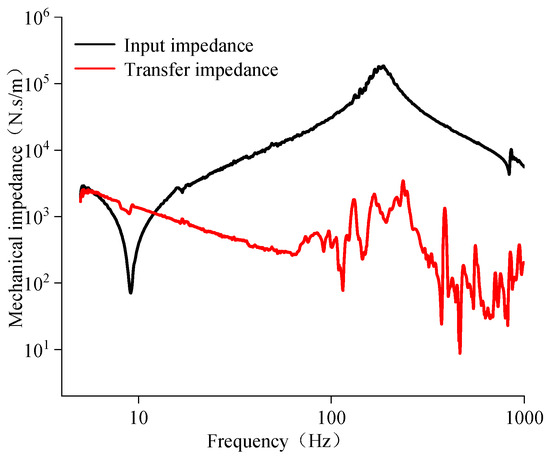
Figure 10.
Mechanical impedance-frequency curves of the tested AM-VI.
The force transmissibility was calculated to further evaluate the vibration isolation performance of the AM-VI, as shown in Figure 11. It can be seen that the force transmissibility was greater than 1 when the excitation frequency was less than 14.60 Hz, which indicates the vibration amplification of the AM-VI in the low-frequency band. The AM-VI gradually started to perform its vibration isolation effect as the frequency increased. It also can be noted that the force transmissibility was less than 1 when the excitation frequency was more than 14.60 Hz, which means that the AM-VI was beginning to exert its vibration isolation effect. The theoretical and experimental curves of the force transmissibility had the same trend within 100 Hz, and their values were relatively close. It can be seen in Figure 11 that the actual resonant frequency was offset from the theoretical resonant frequency to the low frequency, and the initial frequency of vibration isolation measured by the test was slightly larger than the initial frequency of theoretical vibration isolation. The cause of the abovementioned results may be the manufactured and installed error of the AM-VI and the experimental error of the test. With the excitation frequency exceeding 100 Hz, the experimental curve of the force transmissibility showed an oscillating trend. It was different from the downward trend of the theoretical curve. This discrepancy may be due to the test conditions. The force transmissibility reached 0.01 with the increase in the excitation frequency, which indicates excellent vibration isolator performance of the AM-VI within a wide frequency range. The isolator with nonlinear damping had better vibration isolation performance than the isolator with linear damping at high frequencies [27,28]. The metal rubber damping element of the AM-VI is a type of nonlinear damping material [21], and the force transmissibility shows that the AM-VI has excellent vibration isolation performance within a broad frequency. This demonstrates the validity of previous research to some extent.
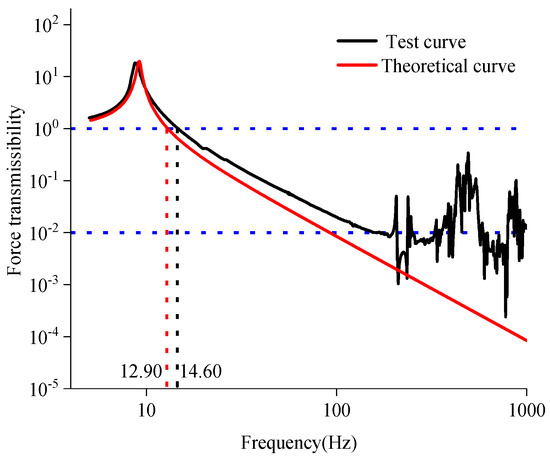
Figure 11.
Force transmissibility-frequency curves of the tested AM-VI.
5. Conclusions
Combining the superior vibration isolation property of the rubber isolator and the advantage of metallic materials (better service environment adaptability), a novel AM-VI was constructed. The AM-VI was constructed by the parallel connection of four oblique rectangular springs and hat-shaped metal rubber. The dynamic performance of the AM-VI (such as dynamic stiffness, loss factor, mechanical impedance, and force transmissibility) was investigated. The main conclusions and contributions of the work are as follows:
- (1)
- The dynamic stiffness of the AM-VI calculated by the elliptic method was smaller than that calculated by the frequency sweeping method. However, the loss factor was the opposite. After taking the inertial force effect of the dynamic testing machine into account, the dynamic stiffness calculated by the two methods was similar.
- (2)
- There were significant differences in the dynamic stiffness and the loss factor calculated by two distinct test methodologies. It is suggested that the inertial force effect of the dynamic testing equipment should be considered when the elliptic method is used for dynamic testing.
- (3)
- The AM-VI achieved excellent vibration isolation performance within a broad frequency range. With increased excitation frequency, the force transmissibility reached 0.01.
Author Contributions
Conceptualization, X.X. and L.Z.; methodology, X.X.; validation, C.Z.; formal analysis, Z.Z.; writing—original draft preparation, X.X. and L.Z.; writing—review and editing, F.H. and Y.S.; supervision, Y.S. and X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 12272094), the National Natural Science Foundation of Fujian Province (No. 2022J01541) and the Key Project of National Defence Innovation Zone of Science and Technology Commission of CMC, which are gratefully appreciated.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Acknowledgments
The authors would like to express many thanks to engineer Zilin Ren of Zhuhai Gree Electric Company, China, for his valuable comments and motivating discussion.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, C.C.; Jing, X.J.; Daley, S.; Li, F.M. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56–57, 55–80. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Kamesh, D.; Pandiyan, R.; Ghosal, A. Passive vibration isolation of reaction wheel disturbances using a low frequency flexible space platform. J. Sound Vib. 2012, 331, 1310–1330. [Google Scholar] [CrossRef]
- Kwon, S.C.; Jo, M.S.; Oh, H.U. Experimental validation of fly-wheel passive launch and on-orbit vibration isolation system by using a superelastic SMA mesh washer isolator. Int. J. Aerosp. Eng. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat. J. Sound Vib. 2011, 330, 6311–6335. [Google Scholar] [CrossRef]
- Song, Y.B.; Wen, J.H.; Yu, D.L.; Liu, Y.Z.; Wen, X.S. Reduction of vibration and noise radiation of an underwater vehicle due to propeller forces using periodically layered isolators. J. Sound Vib. 2014, 333, 3031–3043. [Google Scholar] [CrossRef]
- Salvatore, A.; Carboni, B.; Chen, L.Q.; Lacarbonara, W. Nonlinear dynamic response of a wire rope isolator: Experiment, identification and validation. Eng. Struct. 2021, 238, 111121. [Google Scholar] [CrossRef]
- Liu, S.Y.; Su, P.; Yang, L.H.; Feng, X.J.; Liu, H.S. Experimental investigation of a five-spring vibration isolator. J. Phys. Conf. Ser. 2020, 1707, 12007. [Google Scholar] [CrossRef]
- Cao, X.B.; Wei, C.; Liang, J.Q.; Wang, L.X. Design and dynamic analysis of metal rubber isolators between satellite and carrier rocket system. Mech. Sci. 2019, 10, 71–78. [Google Scholar] [CrossRef]
- Jin, S.Z.; Jiang, G.H.; Wu, G.; Chen, B.W.; Zou, X.Y. Simulation calculation and research of double layer metal rubber vibration isolator. Am. J. Sci. Res. Essays 2019, 4, 19. [Google Scholar]
- Xue, X.; Ruan, S.X.; Li, A.X.; Bai, H.B.; Xiao, K. Nonlinear dynamic modelling of two-point and symmetrically supported pipeline brackets with elastic-porous metal rubber damper. Symmetry 2019, 11, 1479. [Google Scholar] [CrossRef]
- Cao, F.L.; Bai, H.B.; Yang, J.C.; Ren, G.Q. Analysis on fatigue damage of metal rubber vibration isolator. Adv. Mater. Res. 2012, 1700, 490–495. [Google Scholar] [CrossRef]
- Yan, H.; Yan, X.; Zhao, Y.L.; Su, H.Y.; Jiang, H.Y.; Yang, D.S. Study on temperature mechanical properties of SMA-MR material dampers. Rare Met. Mater. Eng. 2020, 49, 1140–1143. [Google Scholar]
- Shen, X.; Chen, Y.C.; Wang, J.Q.; Li, J.F.; Chang, L.L.; Sun, Y.Y. Design, experiment and verification of resonant frequency-tunable vibration isolator based on annular metal rubbers and shape memory alloy actuators. J. Vib. Eng. Technol. 2019, 7, 277–289. [Google Scholar] [CrossRef]
- Liu, H.P.; Xiao, K.L.; Lv, Q.; Ma, Y.L. Analysis and experimental study on dynamic characteristics of an integrated quasi-zero stiffness isolator. J. Vib. Acoust.-Trans. ASME. 2022, 144, 1–28. [Google Scholar] [CrossRef]
- Dai, J.G.; Wang, Y.; Wei, M.X.; Zhang, W.W.; Zhu, J.H.; Jin, H.; Jiang, C. Dynamic characteristic analysis of the inerter-based piecewise vibration isolator under base excitation. Acta Mech. 2022, 233, 513–533. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.X.; Cheng, C.; Ding, H.; Chen, L.Q. Dynamic performance analysis of a mixed-connected inerter-based quasi-zero stiffness vibration isolator. Struct. Control. Health Monit. 2020, 27, e2604. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.F.; Ouyang, H.J.; Zheng, X.; Ye, J.P. Vibration analyses of linear isolators incorporating a quasi-zero stiffness and an inerter simultaneously. Vibroengineering Procedia 2020, 32, 69–74. [Google Scholar]
- Roncen, T.; Sinou, J.J.; Lambelin, J.P. Experiments and nonlinear simulations of a rubber isolator subjected to harmonic and random vibrations. J. Sound Vib. 2019, 451, 71–83. [Google Scholar] [CrossRef]
- Tang, B.; Brennan, M.J. A comparison of two nonlinear damping mechanisms in a vibration isolator. J. Sound Vib. 2013, 332, 510–520. [Google Scholar] [CrossRef]
- Xue, X.; Ruan, S.X.; Bai, H.B.; Chen, X.C.; Shao, Y.C.; Lu, C.H. An enhanced constitutive model for the nonlinear mechanical behavior of the elastic-porous metal rubber. Mech. Mater. 2020, 148, 103447. [Google Scholar] [CrossRef]
- Xue, X.; Yang, P.; Shao, Y.C.; Bai, H.B. Manufacture technology and anisotropic behavior of elastic-porous metal rubber. Int. J. Lightweight Mater. Manuf. 2019, 3, 88–99. [Google Scholar]
- Haym, B.; Mark, L.; Nagurka, S.M.H. Mechanical Vibration; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wang, S.L.; Bai, H.B.; Lu, C.H. The research progress and application expectation of metal rubber vibration isolator. Int. Conf. Mater. 2015, 10, 687–692. [Google Scholar]
- Yerrawar, R.N.; Arakerimath, R.R. Experimental investigations of damping characteristic for MR strut by half-power bandwidth method. J. Meas. Eng. 2018, 6, 163–172. [Google Scholar] [CrossRef]
- Valiente-Blanco, I.; Perez-Diaz, J.L.; Cristache, C. Potential reduction of the inertial mass of tuned vibration absorbers by means of mechanical impedance matching. J. Sound Vib. 2018, 442, 90–107. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Brennan, M.; Ding, H.; Chen, L.Q. High-static-low-dynamic-stiffness vibration isolation enhanced by damping nonlinearit. Sci. China 2019, 62, 1103–1110. [Google Scholar] [CrossRef]
- Lang, Z.Q.; Jing, X.J.; Billings, S.A.; Tomlinson, G.R.; Peng, Z.K. Theoretical study of the effects of nonlinear viscous damping on vibration isolation of SDOF systems. J. Sound Vib. 2009, 323, 352–365. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).