A Novel Shuffled Frog-Leaping Algorithm for Unrelated Parallel Machine Scheduling with Deteriorating Maintenance and Setup Time

Abstract

Unrelated parallel machine scheduling problems (UPMSP) with various processing constraints have been considered fully; however, a UPMSP with deteriorating preventive maintenance (PM) and sequence-dependent setup time (SDST) is seldom considered. In this study, a new differentiated shuffled frog-leaping algorithm (DSFLA) is presented to solve the problem with makespan minimization. The whole search procedure consists of two phases. In the second phase, quality evaluation is done on each memeplex, then the differentiated search processes are implemented between good memeplexes and other ones, and a new population shuffling is proposed. We conducted a number of experiments. The computational results show that the main strategies of DSFLA were effective and reasonable and DSFLA was very competitive at solving UPMSP with deteriorating PM and SDST.

1. Introduction

The parallel machine scheduling problem (PMSP) is a typical scheduling problem that can be categorized into three types: identical PMSP, uniform PMSP, and unrelated PMSP (UPMSP). As the generalization of the other two types, UPMSP has attracted great attention, and a number of results have been obtained to solve UPMSP with various processing constraints, such as random breakdown and random rework [1,2,3,4].

Preventive maintenance (PM) often exists in many actual manufacturing cases, can effectively prevent potential failures and serious accidents in parallel machines, and is often required to be considered in UPMSP. Regarding UPMSP with maintenance, Yang et al. [5] studied UPMSP with aging effects and PM to minimize the total machine load and proved that the problem remained polynomially solvable when a maintenance frequency on every machine is given.

Tavana et al. [4] presented a three-stage maintenance scheduling model for UPMSP with aging effects and multi-maintenance activities. Wang and Liu [6] proposed an improved non-dominated sorting genetic algorithm-II for multi-objective UPMSP with multi-resources PM. Gara-Ali et al. [7] provided several performance criteria and different maintenance systems and gave a new method to solve the problem with deteriorating and maintenance. Lei and Liu [8] proposed an artificial bee colony (ABC) with division for distributed UPMSP with PM.

Deteriorating maintenance means that the length of maintenance activity is not constant and depends on the running time of the machine. UPMSP with deteriorating maintenance has also been studied. Cheng et al. [9] and Hsu et al. [10] provided some polynomial solutions. Lu et al. [11] considered UPMSP with parallel-batching processing, deteriorating jobs, and deteriorating maintenance and presented a mixed integer programming model and a hybrid ABC with tabu search (TS).

In many real-life industries, such as the chemical, printing, metal processing, and semiconductor industries, SDST often cannot be ignored [12]. UPMSP with SDST has been extensively addressed since the pioneering work of Parker et al. [13]. Kurz and Askin [14] proposed several heuristics. Arnaout et al. [15] designed an improved ant colony optimization with a pheromone re-initialization method. Vallada and Ruiz [16] presented a genetic algorithm to minimize the makespan. Lin and Ying [17] developed a hybrid ABC for UPMSP with machine-dependent setup times and SDST.

Caniyilmaz et al. [18] applied an ABC algorithm to solve UPMSP with processing set restrictions, an SDST, and a due date. Diana et al. [19] presented an improved immune algorithm by introducing a local search and a new selection operator. Wang and Zheng [20] proposed an estimation of distribution algorithm and gave five local search strategies. Ezugwu and Akutsah [21] proposed an improved firefly algorithm refined with a local search. Fanjul-Peyro et al. [22] presented an exact algorithm. Bektur and Sarac [23] introduced a TS and a simulated annealing algorithm for UPMSP with SDST, machine eligibility restrictions and a common server. Cota et al. [24] developed a multi-objective smart pool search algorithm for green UPMSP with SDST.

For UPMSP with PM and SDST, Avalos-Rosales et al. [25] developed an efficient meta-heuristic based on a multi-start strategy to minimize the makespan, and Wang and Pan [26] presented a novel imperialist competitive algorithm with an estimation of distribution algorithm to optimize the makespan and total tardiness.

SDST and deteriorating maintenance are common processing constraints and often exist simultaneously in the real-life production process; however, the previous works mainly deal with UPMSP with one of these two constraints, few papers focus on UPMSP with maintenance and SDST [25,26] and UPMSP with deteriorating PM and SDST is hardly studied. It is necessary to investigate UPMSP with deteriorating PM and SDST due to their extensive existences in production. On the other hand, meta-heuristics, including ABC, have been applied to solve UPMSP with various processing constraints, such as PM and SDST. As a meta-heuristic, by observing, imitating, and modeling the search behavior of frogs for the location with the maximum amount of available food, the shuffled frog-leaping algorithm (SFLA) is seldom used to handle UPMSP.

SFLA has a fast convergence speed and effective algorithm structure containing local search and global information exchanges [27]. It has been widely applied to solve various optimization problems, such as topology optimization and production scheduling problems [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. The existing works on scheduling problems revealed that SFLA has great potential in solving UPMSP with deteriorating PM and SDST. On the other hand, the same search process and parameters are adopted in all memeplexes, and the differentiated search process is seldom used, which can effectively intensify the exploration ability and avoid falling local optima; thus, it is necessary to investigate the possible applications of SFLA with new optimization mechanisms for UPMSP with SDST and PM.

In this study, UPMSP with deteriorating PM and SDST is considered, and a new differentiated shuffled frog-leaping algorithm (DSFLA) is applied to minimize the makespan. The entire search procedure is composed of two phases. In the second phase, the memeplex quality is evaluated on each memeplex to divide all memeplexes into good memeplexes and others, then the differentiated search processes are implemented between good memeplexes and others, and a new population shuffling is proposed. We conduct experiments to test the effect of the main strategies and the search advantages for DSFLA.

The remainder of the paper is organized as follows. The problem is described in Section 2 followed by an introduction to SFLA in Section 3. DSFLA for the considered problem is reported in Section 4. Numerical experiments on DSFLA are reported in Section 5, the conclusions are summarized in the final section, and some topics of future research are provided.

2. Problem Description

UPMSP with deteriorating PM and SDST is composed of n jobs $J_1,J_2,\cdots ,J_n$ and m unrelated parallel machines $M_1,M_2,\cdots ,M_m$. Each job can be processed on any one of m machines. The processing time $p_{kj}$ of job $J_j$ depends on the performance of its processing machine $M_k$. The processing times on different machines are usually different.

On machine $M_k$, job is processed in a time interval between two consecutive maintenance activities, and the length of the interval is indicated as $u_k$, and $w_k$ denotes the duration of each maintenance. For deteriorating maintenance, $w_k$ is not constant and depends on $M_k$ and the starting time of maintenance, $w_k=c_k+d_k\times t_k$, where $c_k,d_k$ are constant, and $t_k$ indicates the starting time of maintenance on $M_k$. There are some intervals for processing on each machine. If the processing of a job cannot be completed in a processing interval, the job cannot be processed in the current interval and should be moved to the next interval.

For SDST, $s_{kij}$ is the setup time for processing job $J_j$ after job $J_i$ on machine $M_k$, $s_{k0j}$ indicates the setup time of machine $M_k$ to process the first job $J_j$ after a maintenance activity, and $s_{kj0}$ is the setup time of machine $M_k$ to perform a maintenance activity after the job $J_j$.

There have the following constraints on jobs and machines.

■

Each job and machine is available at time zero.

■

Each job can be processed on only one machine at a time.

■

Operations cannot be interrupted.

■

Preemption is not allowed.

The problem is composed of the scheduling sub-problem and machine assignment sub-problem. The goal of the problem is to minimize the makespan.

Let $C_{\pi \left(j\right)}$ be a completion time of job j in schedule $\pi$, and the makespan can be defined by $C_{max}\left(\pi \right)={max}_{j=1,\dots ,n}\left\{C_{\pi \left(j\right)}\right\}$. Thus, the objective is to find a schedule $\pi$ that minimizes the makespan $C_{max}^{*}={min}_{\pi \in \mathsf{\Pi }}\left\{C_{max}\left(\pi \right)\right\}$, where $\mathsf{\Pi }$ is the set of all feasible schedules $\pi$.

An illustrative example is provided. Table 1 and Table 2 give the processing time and setup time. There are two machines and eight jobs. Data on deteriorating PM are shown in Figure 1, where $c_k=1$ and $d_k=0.1$ for all machines.

Table 1. Processing time.

Job	1	2	3	4	5	6	7	8
$M_1$	56	57	51	30	70	38	42	62
$M_2$	58	55	34	69	34	57	69	50

Table 2. Setup times $s_{1jk}$ and $s_{2jk}$.

${\mathit{s}}_{1\mathit{j}\mathit{k}}$	$\mathit{k}=0$	1	2	3	4	5	6	7	8	${\mathit{s}}_{2\mathit{j}\mathit{k}}$	$\mathit{k}=0$	1	2	3	4	5	6	7	8
$j=0$	0	6	10	6	9	8	8	6	7	j = 0	0	10	9	6	9	5	8	8	7
1	8	0	10	5	7	10	8	10	7	1	5	0	7	9	9	7	9	8	6
2	8	5	0	6	7	9	8	5	8	2	8	7	0	8	10	6	7	7	5
3	7	7	9	0	7	5	9	9	7	3	10	6	7	0	6	10	8	5	5
4	5	7	7	10	0	6	10	6	9	4	6	10	9	5	0	7	9	10	7
5	8	10	6	7	10	0	9	6	5	5	10	7	10	9	9	0	8	6	6
6	8	7	7	9	8	6	0	8	10	6	6	6	10	7	7	6	0	5	8
7	6	9	8	9	3	9	7	0	10	7	6	7	9	5	8	8	6	0	8
8	8	10	10	5	7	5	5	6	0	8	10	9	8	6	7	6	7	9	0

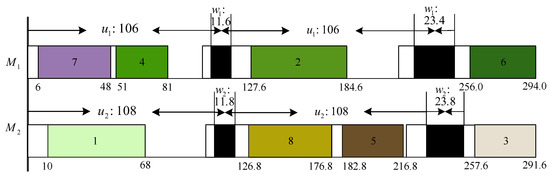
Figure 1. A schedule of the example.

When no PM is considered, any two jobs on any one machine are symmetrical, that is, exchanging them does not change the makespan. When PM is handled, any two jobs on a machine between time 0 and the first PM or two consecutive PMs, because of the above, are reasonable; thus, the consideration of PM has impact on the optimization of the considered UPMSP.

3. Introduction to SFLA

In SFLA, a solution is defined as the position of a frog, and there is a population of possible solutions defined by a set of virtual frogs. After the initial population P is produced, the following steps, which are population division, memeplex search, and population shuffling, are repeated until the stopping condition is met.

Population division is as follows. After all solutions are sorted, suppose that $Fi{t}_1\ge Fi{t}_2\ge \cdots \ge Fi{t}_N$, and then solution $x_k$ is allocated into memeplex $k\left(mods\right)+1$, where $k\left(mods\right)$ indicates the remainder of $k/\phantom{ks}s$, $Fi{t}_i$ is the fitness of solution $x_i$, and s indicates the number of memeplexes.

The search process in memeplex ${\mathcal{M}}_l$ is shown below. $x_w$ is used as optimization object, then a new solution $x_w^{\prime }$ is produced by Equation (2) with $x_w$ and $x_b$. If the new one is better than $x_w$, then replace $x_w$ with $x_w^{\prime }$; otherwise, $x_w$ and $x_g$ are used to generate a solution $x_w^{\prime }$ by Equation (3). If $x_w^{\prime }$ has better fitness than $x_w$, then $x_w^{\prime }$ becomes the new $x_w$; otherwise, a randomly obtained solution directly substitutes for $x_w$, where $x_w$, $x_b$ and $x_g$ are the worst solution and best solution in memeplex ${\mathcal{M}}_l$ and the best solution of P.

$$x_w^{\prime }=x_w+rand\times (x_b-x_w)$$

(1)

$$x_w^{\prime }=x_w+rand\times (x_g-x_w)$$

(2)

where $rand$ is a random number following uniform distribution in [0.1].

A new population P is constructed by shuffling all evolved memeplexes.

As stated above, all memeplexes are often evolved by the same search process and parameters [29,32,33] and the differentiated search in memeplexes is seldom considered. When the differentiated search operators and parameters are introduced, the search ability will be intensified, and local optima can be effectively avoided, as a result, the search efficiency is greatly improved. In this study, DSFLA is presented to solve UPMSP with deteriorating PM and SDST.

4. DSFLA for UPMSP with Deteriorating PM and SDST

DSFLA is composed of two phases, and the differentiated search is implemented in the second phase.

4.1. Initialization, Population Division, and the First Phase

UPMSP consists of two sub-problems: machine assignment and scheduling, and two-string representation is often applied to indicate the solution of UPMSP [46,47]; however, two strings are often dependent each other, and it is difficult to design and apply global search or local search on each string independently. In this study, a solution of the problem is represented as a machine assignment string $\left[M_{{\theta }_1},M_{{\theta }_2},\cdots ,M_{{\theta }_n}\right]$ and a scheduling string $\left[q_1,q_2,\cdots ,q_n\right]$, where $M_{{\theta }_j}$ is the assigned parallel machine for job $J_j$, $j=1,2,\cdots ,n$, and $q_l$ is real number and corresponds to $J_l$. These two strings are independent.

Lei and Liu [8] analyzed why a scheduling string is introduced because of the above mentioned changes of symmetry. The decoding process is described below. First, we decide on a machine for each job according to each machine assignment string, and then on each machine $M_k$, for all jobs $J_i,J_{i+1},\cdots ,J_j$ allocated on $M_k$—that is, $M_{{\theta }_i}=M_{{\theta }_{i+1}},\cdots ,=M_{{\theta }_j}=M_k$. The processing sequence of these jobs is decided by the ascending order of $q_l,l\in [i,j],i<j$, and they process jobs and deal with maintenance on $M_k$ sequentially.

After the initial population P is randomly produced, population division is performed in the following way. Decide the best s solutions from P and sort them in the descending order of their objective. Then, the first solution is allocated into memeplex ${\mathcal{M}}_1$, the second solution is assigned into ${\mathcal{M}}_2$, and so on. Then, binary tournament selection is used to allocate other solutions into memeplexes: randomly select two solutions $x_i$ and $x_j$, and then, if $x_i$ ($x_j$) is better than $x_j$ ($x_i$). Then, $x_i$ ($x_j$) is included into ${\mathcal{M}}_1$. If two solutions have the same objective, then stochastically choose one of them and add it into ${\mathcal{M}}_1$. The unchosen solution goes back to population P. Repeat the above steps for deciding a solution for ${\mathcal{M}}_2$, ${\mathcal{M}}_3$, $\cdots ,{\mathcal{M}}_s$, and then repeat the above procedure until all solutions are assigned. Obviously, $N=s\times \theta$, where $\theta$ denotes the size of each memeplex.

There are two phases in the search process of DSFLA. The steps of the first phase are identical with SFLA in Section 3. The search process in ${\mathcal{M}}_i$ is shown below. Repeat the following steps $R_1$ times: decide $x_w,x_b\in {\mathcal{M}}_i$, execute two-point crossover on machine assignment string of $x_w$ and $x_b$, if the obtained solution x is better than $x_w$, then replace $x_w$ with x; otherwise, apply two-point crossover on a scheduling string between $x_w$ and $x_b$. If the generated solution x has a smaller makespan than $x_w$, x becomes the new $x_w$, where $R_1$ is an integer.

In the first phase, global search is only used because of its good exploration ability in the early search stage. In the second phase, the differentiated search processes are implemented based on memeplex quality evaluation.

4.2. The Second Phase

The evaluation of memeplex quality is seldom considered in SFLA. In this study, memeplex quality is evaluated according to solution quality and evolution quality. For memeplex ${\mathcal{M}}_l$, its quality $Me{q}_l$ is defined by

$$Me{q}_l={\alpha }_1\times \frac{ms{q}_{max}-ms{q}_l}{ms{q}_{max}-ms{q}_{min}}+{\alpha }_2\times \frac{mv{q}_l-mv{q}_{min}}{mv{q}_{max}-mv{q}_{min}}$$

(3)

where ${\alpha }_1,{\alpha }_2$ are real number, $ms{q}_l$ and $mv{q}_l$ indicate solution quality and evolution quality of ${\mathcal{M}}_l$, respectively, $ms{q}_{max}=\underset{l=1,2,\cdots ,s}{max}\left\{ms{q}_l\right\}$, $ms{q}_{min}=\underset{l=1,2,\cdots ,s}{min}\left\{ms{q}_l\right\}$, $mv{q}_{\max }$ and $mv{q}_{\min }$ represent the maximum and minimum evolution quality of all memeplexes, respectively.

After all solutions in ${\mathcal{M}}_l$ are sorted in the ascending order of makespan, let $H_1$ indicate the set of the first $\theta /2$ solutions except $x_b$ and $H_2$ is the set of the remained $\theta /2$ solutions in ${\mathcal{M}}_l$,

$$ms{q}_l=C_{max}\left(x_b\right)+{\beta }_1\times {\overline{C}}_{max}\left(H_1\right)+{\beta }_2\times {\overline{C}}_{max}\left(H_2\right)$$

(4)

where ${\overline{C}}_{max}\left(H_i\right)$ is the average makespan of all solutions in $H_i$, $i=1,2$, ${\beta }_i, i=1,2$ is a real number.

Solutions of $H_1$ are better than those of $H_2$; therefore, we set ${\beta }_1>{\beta }_2$ to reflect this feature. ${\beta }_1=0.4$ and ${\beta }_2=0.1$ are obtained by experiments.

Let $I{m}_x$ indicate the improved number of x between the first generation and the current generation. When $x\in {\mathcal{M}}_l$ is chosen as an optimization object, such as $x_w$, in general SFLA, if an obtained solution $x^{\prime }$ is better than x, then $I{m}_x=I{m}_x+1$. $S{e}_x$ is the total search times from the first generation to the current generation.

$$mv{q}_l={\sum }_{x\in {\mathcal{M}}_l}{Im}_x/\phantom{{\sum }_{x\in {\mathcal{M}}_l}{Im}_x{\sum }_{x\in {\mathcal{M}}_l}S{e}_x}{\sum }_{x\in {\mathcal{M}}_l}S{e}_x$$

(5)

For solution $x_i$, its $ac{t}_{x_i}$ is used to evaluate its evolution quality and is computed by

$$ac{t}_{x_i}=I{m}_{x_i}/S{e}_{x_i}$$

(6)

The second phase is shown as follows.

(1)

Perform population division, compute $Me{q}_l$ for all memeplexes, sort them in descending order of $Me{q}_l$, and construct set $\Theta =\left\{{\mathcal{M}}_l\left|Me{q}_l>\overline{Meq},l\le \eta \times \theta \right.\right\}$.

(2)

For each memeplex ${\mathcal{M}}_l$, ${\mathcal{M}}_l\notin \Theta$, repeat the following steps $R_1$ times if $\left|\mathcal{T}\right|>0$, execute global search between $x_b$ and a randomly chosen $y\in \mathcal{T}$; else perform global search between $x_b$ and a solution $y\in {\mathcal{M}}_l$ with $ac{t}_y\ge ac{t}_x$ for all $x\in {\mathcal{M}}_l$.

(3)

For each memeplex ${\mathcal{M}}_l\in \Theta$,

1

sort all solutions in ${\mathcal{M}}_l$ in the ascending order of makespan, suppose $C_{max}\left(x_1\right)\le C_{max}\left(x_2\right)\le \cdots \le C_{max}\left(x_{\theta }\right)$, and construct a set $\phi =\left\{x_i\left|dis{t}_{x_i}<\overline{dist},i\le \theta /\phantom{\theta 2}2\right.\right\}$.

2

Repeat the following steps $R_2$ times, and randomly choose a solution $x_i\in {\mathcal{M}}_l\setminus \phi$; if $ac{t}_{x_i}>0.5$, then select a solution $y\in \phi$ by roulette selection based on $P{r}_y$, execute global search between $x_i$ and y, and update memory $\mathcal{T}$; else execute global search between $x_i$ and a solution z with $ac{t}_z\ge ac{t}_{x_i}$ for all $x_i\in {\mathcal{M}}_l$ and update memory $\mathcal{T}$.

(4)

Execute multiple neighborhood searches on each solution $x\in \phi$.

(5)

Perform new population shuffling.

where $dis{t}_{x_i}=|C_{max}\left(x_i\right)-C_{max}\left(x_b\right)|$ is defined for each solution $x_i\in {\mathcal{M}}_l$ and $\overline{dist}$ is the average value of all $dis{t}_{x_i}$ in ${\mathcal{M}}_l$. $\eta$ is a real number and set to be 0.4 by experiments, $\overline{Meq}$ indicates the average quality of all memeplexes, $\Theta$ is the set of good memeplexes, and $P{r}_y$ is a probability and defined by

$$P{r}_y=\frac{\left|\phi \right|-ran{k}_y}{\left|\phi \right|}\times \frac{{Im}_y}{{\sum }_{x\in \phi }{Im}_x}$$

(7)

where $ran{k}_y$ is an integer and decided by ranking according to makespan in the first step of step (3) in the above Algorithm.

In the second phase, after all memeplexes are sorted in the descending order of $Me{q}_l$, suppose $Me{q}_1\ge Me{q}_2\ge \cdots Me{q}_s$.

Memory $\mathcal{T}$ is used to store the intermediate solutions. The maximum size ${\left|\mathcal{T}\right|}_{max}$ is given in advance. We set ${\left|\mathcal{T}\right|}_{max}$ to be 200 by experiments. When the number of solutions exceeds ${\left|\mathcal{T}\right|}_{max}$, a solution x can be added into $\mathcal{T}$ when x is better than the worst solution of $\mathcal{T}$ and substitutes for the worst one.

Six neighborhood structures are used. ${\mathcal{N}}_1$ is shown below. Randomly select a job from the machine $M_k$ with the largest $C_{max}^k$ and move it into the machine $M_g$ with the smallest $C_{max}^g$, where $C_{max}^k$ and $C_{max}^g$ are the completion time of the last processed job on $M_k$ and $M_g$, respectively. ${\mathcal{N}}_2$ is performed in the following way. Decide on a machine $M_k$ with the largest $C_{max}^k$ and a job $J_i$ with the largest processing time $p_{ki}$ on $M_k$, randomly choose a machine $M_g,g\ne k$ and a job $J_j$ with the largest $p_{gj}$ and exchange $J_i$ and $J_j$ between $M_k$ and $M_g$.

${\mathcal{N}}_3$ is described as follows. Randomly select two machines $M_k$ and $M_g$ and exchange a job $J_i$ with the largest $p_{ki}$ and a job $J_j$ with the largest $p_{gj}$ between these two machines. ${\mathcal{N}}_1,{\mathcal{N}}_2,{\mathcal{N}}_3$ only act on the machine assignment string.

${\mathcal{N}}_4$,${\mathcal{N}}_5$,${\mathcal{N}}_6$ are performed on a scheduling string by swapping two randomly chosen genes, inserting a randomly selected gene into a new randomly decided position, and inverting genes between two stochastically positions $k_1,k_2,k_1<k_2$.

Multiple neighborhood search is performed in the following way. For solution x, let $u=1$, repeat the following steps V times: produce a solution $z\in {\mathcal{N}}_u\left(x\right)$, $u=u+1$, let $u=1$ if $u=7$, and if z is better than x, then replace x with z and $I{m}_x=I{m}_x+1$.

Global search is executed in the same way of the first phase.

In the existing SFLA [29,32,33], a new population P is constructed by using s evolved memeplexes. In this study, new population shuffling is done in the following way: $\gamma$ best solutions of $\mathcal{T}$ and s memeplexes are added into new population P, and $\gamma$ worst solutions of P are removed. We test by experiments and set $\gamma =0.1\times {\left|\mathcal{T}\right|}_{max}$.

Some worst solutions of P can be updated by solutions of $\mathcal{T}$, that is, solutions of P can be improved by memeplex search or shuffling.

In the second phase, the set $\Theta$ is composed of good memeplexes with better quality than other memeplexes, in the search process for a good memeplex, a global search of optimization object x is implemented according to $ac{t}_x$, and then multiple neighborhood search acts on the solutions in $\phi$. Only global search is executed for other memeplexes; moreover, different parameters, $R_1,R_2,R_1\ne R_2$, are used, and, as a result, differentiated search is implemented.

4.3. Algorithm Description

The detailed steps of DSFLA are shown below.

(1)

Initialization. Randomly produce initial population P with N solutions, and let initial $\mathcal{T}$ be empty.

(2)

Population division. execute search process within each memeplex.

(3)

Perform population shuffling.

(4)

If the stopping condition of the first phase is not met, then go to step (2).

(5)

Execute the second phase until the stopping condition is met.

The computational complexity is $O(N\times R_1\times L)$, where L is the repeated number of steps 2–3.

Unlike the previous SFLA [29,32,33], DSFLA has the following features. (1) Quality evaluation is done for all memeplexes according to the solution quality and evolution quality and all memeplexes are categorized into two types: good memeplexes and other memeplexes. (2) The differentiated search is implemented by different search strategies and parameters for two types of memeplexes; as a result, the exploration ability is intensified; and the possibility of falling into local optima diminishes greatly.

5. Computational Experiments

Extensive experiments were conducted on a set of instances to test the performance of DSFLA for UPMSP with deteriorating PM and SDST. All experiments were implemented by using Microsoft Visual C++ 2019 and run on 8.0 G RAM 2.30 GHz CPU PC.

5.1. Instances and Comparative Algorithms

We used 70 instances, which has $n\in \left\{15,20,25,30,35\right\}$ and $m\in \left\{2,4,6,8\right\}$, or $n\in \left\{50,70,90,100,120,150,170,200,220,250\right\}$ and $m\in \left\{10,15,20,25,30\right\}$, $p_{ki}\in [50,70]$, setup time from [5,10], $c_k=1$, $d_k=0.1$, and $u_k={max}_{1\le i\le n}\left\{p_{ki}+s_{k0i}+s_{ki0}\right\}$ for machine $M_k$.

We proposed a hybrid particle swarm optimization and genetic algorithm (HPSOGA) [48] for UPMSP. It can be applied to our UPMSP after the decoding procedure of DSFLA is adopted, and thus we selected it as a comparative algorithm. Lu et al. [11] presented ABC-TS for an unrelated parallel-batching machine scheduling problem with deteriorating jobs and maintenance. Avalos-Rosales et al. [25] applied a multi-start algorithm (MSA) to solve UPMSP with PM and SDST. These two algorithms can be directly used to solve UPMSP with SDST and deteriorating PM and possess good performance; therefore, they are chosen as comparative algorithms.

The general SFLA in Section 3 was also implemented, in which global search between two solutions is performed in the same way as the first stage of DSFLA. The comparison between DSFLA and SFLA is to show the effect of the main strategies of DSFLA.

5.2. Parameter Settings

In DSFLA, the stopping condition is the maximum number $max\_it$ of objective function evaluations. We found that DSFLA can converge fully. We also tested this condition for other comparative algorithms when $max\_it$ is ${10}^5$. We also found that the above $max\_it$ was appropriate; thus, we used this stopping condition.

DSFLA possesses other main parameters: N, s, $R_1$, $R_2$, V, and $max\_i{t}_1$, where $max\_i{t}_1$ denotes the maximum number of objective function evaluations in the first phase.

The Taguchi method [49] was used to decide the settings for parameters. We selected instance $150\times 20$ for parameter tuning. The levels of each parameter are shown in Table 3. There were 27 parameter combinations according to the orthogonal array $L_{27}\left(3^6\right)$.

Table 3. Parameters and their levels.

Parameters		Factor Level
	1	2	3
N	60	80	100
s	4	5	10
$R_1$	30	50	70
$R_2$	80	100	120
V	220	240	260
$max\_i{t}_1$	5000	10,000	15,000

DSFLA with each combination run 10 times independently for the chosen instance. The results of $MIN$ and the $S/N$ ratio are shown in Figure 2, in which the $S/N$ ratio is defined as $-10\times {log}_{10}\left(MI{N}^2\right)$ and $MIN$ is the best solution found in 10 runs. From Figure 2, DSFLA with following combination $N=80$, $s=5$, $R_1=50$, $R_2=100$, $V=240$ and $max\_i{t}_1={10}^4$ obtained better results than DSFLA with other combinations; therefore, the above combination was adopted.

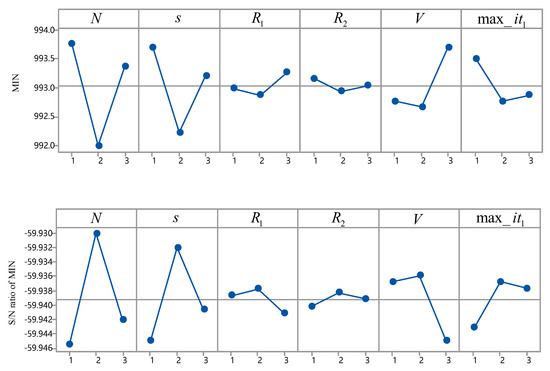
Figure 2. Results of $MIN$ and the $S/N$ ratio.

5.3. Results and Analyses

DSFLA was compared with SFLA, ABC-TS, HPSOGA, and MSA. All parameters except the stopping conditions of ABC-TS, HPSOGA, and MSA were directly adopted from the original references. For SFLA, there were no $R_1,R_2,V$ and $max\_i{t}_1$, and the other parameters were given the same settings as DSFLA. Each algorithm randomly ran 10 times for each instance. Table 4, Table 5 and Table 6 show the computational results of all algorithms, in which $AVG$ is the average value of the obtained 10 elite solutions in 10 runs, and $SD$ is the standard deviation of 10 elite solutions.

Table 4. Computational results of five algorithms on the metric MIN.

Instance	DSFLA	SFLA	HPSOGA	ABC-TS	MSA	Instance	DSFLA	SFLA	HPSOGA	ABC-TS	MSA
15 × 2	942	963	946	976	947	120 × 10	1889	2085	1908	2188	1889
15 × 4	365	368	379	381	375	120 × 15	1005	1151	1165	1403	1008
15 × 6	251	259	252	263	256	120 × 20	667	812	813	995	667
15 × 8	153	156	164	165	157	120 × 25	510	645	646	822	521
20 × 2	1343	1368	1340	1395	1404	120 × 30	391	519	516	677	388
20 × 4	500	509	504	514	514	150 × 10	2854	3097	2858	3543	2854
20 × 6	367	375	367	379	368	150 × 15	1413	1617	1614	1884	1413
20 × 8	258	260	260	267	258	150 × 20	985	1150	1166	1184	994
25 × 2	2031	2076	2076	2061	2078	150 × 25	673	825	810	1008	673
25 × 4	779	794	804	794	755	150 × 30	526	664	673	821	521
25 × 6	491	499	498	499	493	170 × 10	3650	3977	3650	4534	3654
25 × 8	365	367	365	376	368	170 × 15	1867	1881	1877	2422	1872
30 × 2	2730	2765	2796	2804	2736	170 × 20	1177	1358	1207	1613	1176
30 × 4	943	962	963	979	952	170 × 25	827	989	1010	1179	827
30 × 6	515	517	517	623	517	170 × 30	682	820	824	988	668
30 × 8	380	382	380	391	382	200 × 10	5171	5721	5176	5638	5179
35 × 2	3888	3978	3931	3945	3933	200 × 15	2480	2491	2513	2753	2485
35 × 4	1162	1164	1163	1175	1164	200 × 20	1418	1620	1636	1869	1419
35 × 6	645	653	650	665	657	200 × 25	1011	1196	1204	1389	1004
35 × 8	494	504	500	517	499	200 × 30	822	991	999	1168	829
50 × 10	514	524	523	667	516	220 × 10	6458	7046	7131	7936	6459
50 × 15	376	379	381	507	379	220 × 15	2853	3138	2856	3989	2865
50 × 20	260	268	273	368	260	220 × 20	1650	1894	1897	2443	1652
50 × 25	162	262	259	276	163	220 × 25	1184	1405	1600	1633	1202
50 × 30	159	160	170	271	160	220 × 30	994	1166	1191	1397	983
70 × 10	820	829	828	986	820	250 × 10	8908	9685	9784	9680	8916
70 × 15	511	520	519	658	514	250 × 15	3614	4020	4076	4079	3651
70 × 20	382	389	386	520	379	250 × 20	2175	2440	2488	2777	2177
70 × 25	267	375	276	395	269	250 × 25	1418	1841	1888	1891	1420
70 × 30	263	269	273	389	264	250 × 30	1189	1389	1422	1615	1173
100 × 10	1398	1566	1401	1647	1399	300 × 10	14,919	16,333	14,924	16,359	14,919
100 × 15	814	829	824	1004	819	300 × 15	5175	5726	6387	6241	5175
100 × 20	524	650	643	818	520	300 × 20	2859	3524	3615	3598	2861
100 × 25	390	513	502	652	393	300 × 25	1908	2484	2495	2503	1908
100 × 30	382	393	395	523	376	300 × 30	1420	1882	1909	2145	1422

Table 5. Computational results of five algorithms on the metric AVG.

Instance	DSFLA	SFLA	HPSOGA	ABC-TS	MSA	Instance	DSFLA	SFLA	HPSOGA	ABC-TS	MSA
15 × 2	942	963	946	976	947	120 × 10	1889	2098	1910	2198	1890
15 × 4	365	368	380	382	375	120 × 15	1005	1178	1168	1419	1008
15 × 6	251	260	254	267	256	120 × 20	669	819	818	1007	668
15 × 8	153	160	165	173	158	120 × 25	511	662	658	826	523
20 × 2	1343	1368	1342	1395	1404	120 × 30	393	523	522	681	389
20 × 4	500	509	506	517	514	150 × 10	2855	3103	2861	3569	2856
20 × 6	367	375	369	383	369	150 × 15	1413	1626	1624	1905	1414
20 × 8	258	261	262	268	258	150 × 20	993	1162	1168	1195	996
25 × 2	2031	2076	2076	2062	2078	150 × 25	673	831	818	1026	673
25 × 4	779	794	804	797	755	150 × 30	526	668	691	826	521
25 × 6	491	499	498	505	493	170 × 10	3653	3984	3650	4539	3655
25 × 8	365	367	365	381	368	170 × 15	1868	1896	1881	2433	1872
30 × 2	2730	2765	2796	2805	2736	170 × 20	1179	1372	1218	1619	1185
30 × 4	943	963	965	983	953	170 × 25	827	1001	1013	1191	828
30 × 6	515	518	518	625	518	170 × 30	684	825	837	1005	669
30 × 8	380	383	384	400	383	200 × 10	5172	5723	5177	5678	5179
35 × 2	3888	3978	3931	3946	3934	200 × 15	2480	2504	2520	2783	2485
35 × 4	1162	1164	1163	1177	1164	200 × 20	1421	1641	1644	1886	1420
35 × 6	646	654	651	667	658	200 × 25	1012	1202	1215	1401	1005
35 × 8	495	505	503	519	501	200 × 30	827	998	1007	1188	829
50 × 10	515	524	525	674	517	220 × 10	6459	7049	7133	7947	6459
50 × 15	377	379	384	515	380	220 × 15	2853	3141	2858	3995	2890
50 × 20	261	268	275	385	261	220 × 20	1650	1912	1919	2459	1653
50 × 25	163	262	264	280	165	220 × 25	1185	1410	1616	1645	1204
50 × 30	159	167	171	273	160	220 × 30	996	1176	1196	1410	984
70 × 10	821	829	831	1003	822	250 × 10	8909	9691	9788	9701	8918
70 × 15	512	520	521	667	515	250 × 15	3615	4029	4084	4087	3651
70 × 20	382	389	391	524	380	250 × 20	2177	2471	2498	2784	2177
70 × 25	268	375	278	396	270	250 × 25	1419	1855	1899	1906	1421
70 × 30	263	269	276	392	267	250 × 30	1190	1404	1429	1621	1173
100 × 10	1400	1566	1403	1652	1400	300 × 10	14,921	16,335	14,927	16,364	14,920
100 × 15	815	829	827	1019	823	300 × 15	5176	5734	6388	6269	5175
100 × 20	526	650	651	825	521	300 × 20	2860	3546	3618	3627	2862
100 × 25	390	513	513	667	394	300 × 25	1909	2502	2502	2508	1909
100 × 30	384	393	397	529	378	300 × 30	1421	1897	1916	2165	1423

Table 6. Computational results of five algorithms on the metric SD.

Instance	DSFLA	SFLA	HPSOGA	ABC-TS	MSA	Instance	DSFLA	SFLA	HPSOGA	ABC-TS	MSA
15 × 2	0.00	0.00	0.00	0.00	0.60	120 × 10	0.00	8.72	1.20	10.06	0.75
15 × 4	0.00	0.00	0.90	0.46	0.66	120 × 15	1.50	9.40	2.84	5.83	0.00
15 × 6	0.65	1.20	1.77	2.22	0.30	120 × 20	0.87	3.50	5.10	5.85	0.66
15 × 8	1.50	2.21	1.04	2.30	1.57	120 × 25	0.66	5.83	11.31	2.75	1.64
20 × 2	0.00	0.00	2.10	0.00	0.46	120 × 30	1.47	2.21	5.76	3.10	0.94
20 × 4	0.00	0.00	2.29	2.32	0.49	150 × 10	1.25	3.69	4.27	9.70	1.86
20 × 6	0.00	0.43	1.73	1.61	1.75	150 × 15	0.80	7.45	10.06	11.95	0.54
20 × 8	0.64	0.60	2.28	0.83	0.54	150 × 20	2.80	5.70	2.49	5.55	1.18
25 × 2	0.00	0.00	0.00	0.80	1.20	150 × 25	0.00	3.24	3.75	7.00	1.31
25 × 4	0.00	0.00	0.00	1.04	0.00	150 × 30	0.00	2.46	7.35	3.10	0.30
25 × 6	0.40	0.00	0.30	2.92	0.00	170 × 10	0.98	5.54	2.02	2.76	2.19
25 × 8	0.00	0.30	0.00	2.27	0.40	170 × 15	0.49	8.59	4.23	6.99	0.00
30 × 2	0.00	0.00	0.00	0.40	0.00	170 × 20	0.60	5.84	10.41	5.12	2.97
30 × 4	0.00	0.92	2.40	1.60	1.36	170 × 25	1.20	5.24	3.67	4.68	1.72
30 × 6	0.00	0.66	1.03	1.20	1.09	170 × 30	1.86	3.87	11.79	6.68	0.64
30 × 8	0.63	0.93	3.78	4.61	1.81	200 × 10	1.10	1.26	1.15	13.37	3.25
35 × 2	0.00	0.00	0.00	0.49	0.64	200 × 15	0.30	9.48	5.87	10.91	0.30
35 × 4	0.00	0.30	0.00	3.15	0.60	200 × 20	1.99	10.41	6.59	5.95	1.36
35 × 6	1.18	0.84	0.23	1.43	0.30	200 × 25	0.30	3.81	8.62	6.43	0.50
35 × 8	0.77	0.91	3.22	1.75	1.94	200 × 30	3.33	5.29	5.41	7.42	0.78
50 × 10	0.49	2.68	1.94	3.68	0.80	220 × 10	0.40	1.75	1.84	6.78	0.30
50 × 15	0.40	1.52	3.03	4.76	0.87	220 × 15	1.02	2.96	3.16	3.11	11.20
50 × 20	0.15	1.65	2.19	5.80	0.38	220 × 20	0.30	8.56	8.77	11.27	3.04
50 × 25	2.70	1.64	5.19	2.26	1.89	220 × 25	1.94	3.22	7.75	5.72	2.69
50 × 30	0.00	1.62	1.16	1.71	0.49	220 × 30	0.48	5.39	5.05	6.95	0.98
70 × 10	1.02	3.75	1.11	9.89	2.12	250 × 10	1.19	3.81	4.67	7.66	0.81
70 × 15	1.10	2.56	2.94	4.61	1.76	250 × 15	0.46	4.72	5.90	4.36	0.00
70 × 20	0.49	1.92	4.85	2.87	1.30	250 × 20	1.08	13.19	8.65	4.07	0.90
70 × 25	2.77	2.03	1.01	1.76	0.89	250 × 25	2.10	7.69	9.60	9.52	1.76
70 × 30	0.65	2.00	2.46	2.09	1.36	250 × 30	0.49	6.70	8.72	7.08	0.49
100 × 10	1.85	5.68	1.20	2.17	0.54	300 × 10	1.37	2.27	3.41	4.04	0.66
100 × 15	1.50	1.90	2.70	5.06	3.36	300 × 15	0.46	5.14	3.67	9.68	0.30
100 × 20	1.30	2.83	5.44	4.52	1.25	300 × 20	1.56	8.65	2.39	14.59	1.81
100 × 25	0.35	2.25	11.52	5.51	1.34	300 × 25	0.50	11.93	4.63	4.57	1.40
100 × 30	0.53	3.76	1.59	3.95	1.46	300 × 30	0.50	7.12	3.73	6.80	1.04

Table 7 describes the computational times of DSFLA and its comparative algorithms, in which the unit of time is seconds. Figure 3 gives a box plot of all algorithms, in which $DM$ ($DA$) ($DS$) indicates the $MIN$ ($AVG$) ($SD$) of an algorithm minus the $MIN$ ($AVG$) ($SD$) of DSFLA. Figure 4 reveals the convergence curves of two instances.

Table 7. The computational times of DSFLA, HPSOGA, ABC-TS, and MSA.

Instance	DSFLA	HPSOGA	ABC-TS	MSA	Instance	DSFLA	HPSOGA	ABC-TS	MSA
15 × 2	0.25	0.19	0.63	0.10	120 × 10	3.56	3.88	12.42	3.04
15 × 4	0.22	0.20	0.35	0.17	120 × 15	3.28	3.77	7.53	4.50
15 × 6	0.24	0.23	0.27	0.20	120 × 20	2.94	3.73	5.70	5.64
15 × 8	0.33	0.23	0.23	0.20	120 × 25	2.77	3.86	4.69	7.43
20 × 2	0.20	0.31	1.22	0.28	120 × 30	2.74	4.02	4.77	9.53
20 × 4	0.28	0.40	0.59	0.30	150 × 10	4.79	5.10	20.41	4.90
20 × 6	0.27	0.40	0.43	0.36	150 × 15	4.12	5.29	14.93	5.91
20 × 8	0.22	0.40	0.36	0.29	150 × 20	3.82	5.38	10.08	7.10
25 × 2	0.24	0.41	2.10	0.31	150 × 25	3.27	5.55	7.71	11.27
25 × 4	0.19	0.46	0.93	0.38	150 × 30	3.55	5.53	7.18	12.94
25 × 6	0.27	0.47	0.66	0.38	170 × 10	5.60	6.64	28.42	5.26
25 × 8	0.20	0.47	0.55	0.40	170 × 15	4.80	6.42	18.54	6.23
30 × 2	0.22	0.48	3.25	0.41	170 × 20	4.06	7.30	12.97	8.32
30 × 4	0.37	0.49	1.36	0.46	170 × 25	3.59	8.62	10.17	10.86
30 × 6	0.37	0.57	0.94	0.57	170 × 30	3.95	8.20	9.06	12.14
30 × 8	0.23	0.56	0.73	0.58	200 × 10	7.31	10.33	39.29	7.85
35 × 2	0.33	0.55	5.81	1.36	200 × 15	5.76	8.48	25.82	9.22
35 × 4	0.33	0.65	1.97	1.34	200 × 20	5.00	8.57	19.34	9.60
35 × 6	0.27	0.62	1.29	1.30	200 × 25	4.64	8.88	14.62	10.07
35 × 8	0.35	0.70	1.21	1.39	200 × 30	4.77	9.11	13.03	11.11
50 × 10	1.85	0.97	2.20	1.72	220 × 10	8.50	10.66	48.66	8.03
50 × 15	1.63	1.01	1.29	1.93	220 × 15	6.70	8.98	33.07	9.93
50 × 20	1.70	1.20	1.08	0.86	220 × 20	5.64	8.94	24.60	10.01
50 × 25	1.58	1.21	6.04	1.81	220 × 25	5.03	9.03	18.63	11.16
50 × 30	1.80	0.96	5.86	2.24	220 × 30	5.20	9.06	16.30	11.54
70 × 10	2.22	1.62	3.45	2.27	250 × 10	10.17	11.91	69.33	10.14
70 × 15	2.01	1.78	2.49	2.43	250 × 15	8.16	10.08	42.52	10.95
70 × 20	2.06	1.78	1.98	2.59	250 × 20	6.94	10.45	31.35	11.06
70 × 25	1.98	1.83	1.74	2.73	250 × 25	5.86	10.40	25.25	10.96
70 × 30	2.12	2.02	1.63	2.02	250 × 30	6.11	10.59	22.36	11.62
100 × 10	3.06	2.63	7.95	2.49	300 × 10	13.85	15.42	103.58	13.51
100 × 15	2.67	2.78	5.27	2.67	300 × 15	10.31	14.77	79.38	14.03
100 × 20	2.61	2.74	3.94	2.37	300 × 20	8.87	14.23	59.08	14.16
100 × 25	2.46	3.19	3.35	3.01	300 × 25	7.88	14.02	54.39	14.58
100 × 30	2.50	3.24	3.09	3.62	300 × 30	7.73	14.99	56.85	15.04

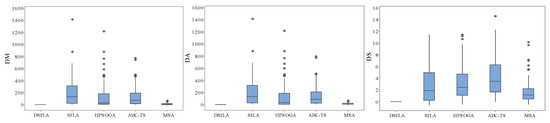
Figure 3. Box plot of all algorithms.

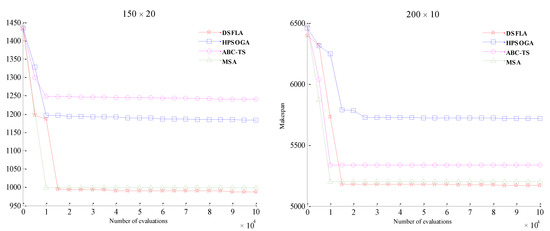
Figure 4. Convergence curves of DSFLA and its comparative algorithms.

As shown in Table 4, Table 5 and Table 6, SFLA could not produce better $MIN$ than DSFLA on any instances and obtains bigger $MIN$ than SFLA by at least 100 for most instances. DSFLA had better convergent performance than SFLA. DSFLA generated smaller $AVG$ than SFLA on all instances, and the differences of $AVG$ between the two algorithms were significant.

DSFLA performed better than SFLA for the average performance. The $SD$ of SFLA was also worse than that of DSFLA for most instances, and SFLA was inferior to DSFLA regarding search stability. DSFLA performed notably better when compared with SFLA. This conclusion can also be drawn from Figure 3; thus, new strategies, such as differentiated search, had a positive impact on the performance of DSFLA.

It can be seen from Table 4 that DSFLA produced smaller $MIN$ compared with HPSOGA and ABC-TS for nearly all instances and generated a worse $MIN$ than MSA for only 11 instances. DSFLA converged better than its comparative algorithms. The convergence performance differences between DSFLA and its comparative algorithm can also be seen from the box plot and convergence curves in Figure 3 and Figure 4.

The results in Table 5 show that DSFLA obtained a better $AVG$ over HPSOGA and ABC-TS for nearly all instances and possessed a smaller $AVG$ than MSA for most instances. DSFLA had a better average performance than its three comparative algorithms. This conclusion can also be drawn from Figure 3. Table 6 and Figure 3 reveal that DSFLA had better stability than its three comparative algorithms; thus, we concluded that DSFLA can provide promising results for solving UPMSP with deteriorating PM and SDST.

The good performances of DSFLA mainly resulted from its new strategies in the second phase. The differentiated search was implemented by memeplex quality evaluation and different search combinations of global search and multiple neighborhood search. These strategies effectively intensified the exploration ability and avoided the search falling into local optima. As a result, a high search efficiency was obtained; thus, DSFLA is a very competitive method for the considered UPMSP.

6. Conclusions

UPMSP with various processing constraints has been extensively considered. This paper addressed UPMSP with deteriorating PM and SDST and provided a new algorithm named DSFLA to minimize the makespan. In DSFLA, two search phases exist, memeplex quality evaluation is performed, and the differentiated search processes between two kind of memeplexes are implemented in the second phase. A new population shuffling was also presented. A number of computational experiments were conducted. The computational results demonstrated that DSFLA had promising advantages, such as good convergence and stability in solving the considered UPMSP.

UPMSP with at least two actual constraints, such as PM, SDST, and learning effects, may attract attention. We will continue to focus on these UPMSP by using meta-heuristics, including ABC and the imperialist competitive algorithm. Uncertainty often cannot be neglected and should be added into scheduling problems. UPMSP with uncertainty and energy-related elements, etc. is our future topic. Reinforcement learning has been used to solve scheduling problems and we will pay attention to meta-heuristics with reinforcement learning for UPMSP with various processing constraints.