Bright–Dark Soliton Waves’ Dynamics in Pseudo Spherical Surfaces through the Nonlinear Kaup–Kupershmidt Equation

Abstract

The soliton waves’ physical behavior on the pseudo spherical surfaces is studied through the analytical solutions of the nonlinear (1+1)–dimensional Kaup–Kupershmidt $\left(\mathcal{KK}\right)$ equation. This model is named after Boris Abram Kupershmidt and David J. Kaup. This model has been used in various branches such as fluid dynamics, nonlinear optics, and plasma physics. The model’s computational solutions are obtained by employing two recent analytical methods. Additionally, the solutions’ accuracy is checked by comparing the analytical and approximate solutions. The soliton waves’ characterizations are illustrated by some sketches such as polar, spherical, contour, two, and three-dimensional plots. The paper’s novelty is shown by comparing our obtained solutions with those previously published of the considered model.

1. Introduction

A significant and prominent portion of the nonlinear partial differential Equation (NLPDE) has recently played a role in describing many physical, chemical, biological, mechanical, optical, and other phenomena in engineering [1,2]. This image aims to identify the new features of each model by finding their moving wave solutions to construct the original and soundscapes for semi-analytical and numerical schemes [3,4,5]. Therefore, the analytical findings’ precision can be verified by contrasting the analytical to estimated solutions for displaying the matching results [6,7]. Thus, several mathematicians and physics researchers have focused on the drawing up of accurate analytical, semi–analytical, and numerical schemes such as Khater method, modified Khater method, generalized Khater method, exp–function method, Hirota’s method, the bi–linear method, Adomian degradation method, b-spline schemes, and the Sine Gordon expansion method [8,9,10,11,12,13,14,15]. These schemes have dealt with many phenomena and some novel properties that allow many great applications [16,17,18,19,20] to use these solutions.

This research paper investigates the analytical and approximate solutions of (1+1)–D $\mathcal{KK}$ equation through the modified F–expansion (MFE), Novel auxiliary Equation (NAE), and variational iteration (VI) methods [21,22,23,24,25]. This model is given by [26,27,28,29,30]

$$q_1{\mathcal{K}}_t+{\mathcal{K}}_{5x}+q_2\mathcal{K}{\mathcal{K}}_{x x x}+q_3 {\mathcal{K}}_x{\mathcal{K}}_{x x}+q_4{\mathcal{K}}^2{\mathcal{K}}_x=0,$$

(1)

where $q_g,g=1,2,3,4$ are arbitrary constants applying the following wave traveling transformation $\mathcal{K}(x,t)=\mathcal{R}\left(\mathcal{G}\right), \mathcal{G}=x+\lambda t$, where $\lambda$ is the arbitrary constant to be evaluated through the suggested analytical methods, converts the NLPDE into the following ordinary differential Equation (ODE)

$${\mathcal{R}}^{\left(5\right)}+q_2 {\mathcal{R}}^{\left(3\right)} \mathcal{R}+\lambda q_1 {\mathcal{R}}^{\prime }+q_3 {\mathcal{R}}^{\prime } {\mathcal{R}}^{″}+q_4 {\mathcal{R}}^2 {\mathcal{R}}^{\prime }=0.$$

(2)

Applying the homogeneous balance principles to Equation (2) for evaluating the value of balance between the ODE’s model form, finds that $s=2$. Consequently, the considered model’s general solutions are given by

$$\mathcal{R}\left(\mathfrak{G}\right)=\left\{\begin{array}{l}{\displaystyle \sum _{i=-s}^n}{a}_i {(\mathcal{Q}\left(\mathcal{G}\right)+\varrho )}^i=a_2 {(\mathcal{Q}\left(\mathcal{G}\right)+\varrho )}^2+a_1 (\mathcal{Q}\left(\mathcal{G}\right)+\varrho )+a_0,\\ \hspace{1em}{\displaystyle \sum _{i=1}^s}{a}_i \mathsf{\Lambda }{\left(\mathcal{G}\right)}^i+a_0=a_2 \mathsf{\Lambda }{\left(\mathcal{G}\right)}^2+a_1 \mathsf{\Lambda }\left(\mathcal{G}\right)+a_0,\end{array}\right.$$

(3)

where s is the value of balance, while $a_2, a_1, a_0$ are arbitrary constants to be evaluated along with the suggested methods’ framework.

The remaining parts of the article are provided in the order below; Section 2 offers the wave’s solitary versions by introducing the analytical schemes indicated. The analytical solutions obtained are often examined to achieve the requested criteria for applying the semi-analytical methods suggested. Finally, the estimated solutions are determined, and analytical, semi-analytical, and total errors between the solutions are shown. Specific alternatives are displayed by sure distinct illustrations that demonstrate the novel properties of the model. The findings and creativity of the paper are seen in Section 3. The description of all results obtained in the whole study paper is explained in Section 4.

2. Distinct Solutions

Here, many various kinds of solutions are obtained and employ two recent analytical schemes then using their solutions for evaluating the approximate solutions of the considered model. This investigation aims to illustrate the dynamical behavior of the soliton waves on pseudo-spherical surfaces. Additionally, it seeks to show the accuracy of the obtained solutions by estimating the value of error between both solutions.

2.1. Soliton Wave Solution

Employing the suggested computational (MFE and NAE) methods investigates the solitary wave solutions of the proposed model.

2.1.1. MFE Method’s Investigation

Employing the MFE method’s framework with the following auxiliary equation ${\mathcal{Q}}^{\prime }\left(\mathcal{G}\right)=\mathcal{Q}{\left(\mathcal{G}\right)}^2+\varrho$, where $\varrho$ is arbitrary constant, and the above-mention general solution, finds the following value of the previous-shown parameters:

• Set A

  $$a_0=\frac{1}{3}{a}_2\varrho (3\varrho +2),a_1=-2a_2\varrho ,q_1=-\frac{{\varrho }^2\left(a_2^2{q}_4+12a_2{q}_2+144\right)}{9\lambda },q_3=-\frac{a_2{q}_4}{6}-\frac{60}{a_2}-2q_2.$$
• Set B

  $$a_1=\frac{12q_2\varrho }{q_4},a_2=-\frac{6q_2}{q_4},q_1=-\frac{4q_4\varrho \left(a_0{q}_2(3\varrho +2)+4\varrho \right)+a_0^2{q}_4^2+12q_2^2{\varrho }^2(\varrho +1)(3\varrho +1)}{\lambda q_4},q_3=\frac{10q_4}{q_2}-q_2.$$

Thus, the solitary solution’s of the nonlinear (1+1)–D $\mathcal{KK}$ equation are given by For $\varrho <0$, we have

$${\mathcal{K}}_{\mathrm{A},1}(x,t)=a_2\left(\varrho {\tan }^2\left(\sqrt{\varrho }(\lambda t+x)\right)+\frac{2\varrho }{3}\right)+\frac{a_{-1}\left(\sqrt{\varrho }\tan \left(\sqrt{\varrho }(\lambda t+x)\right)+\varrho \right)+a_{-2}}{{\left(\sqrt{\varrho }\tan \left(\sqrt{\varrho }(\lambda t+x)\right)+\varrho \right)}^2},$$

(4)

$${\mathcal{K}}_{\mathrm{A},2}(x,t)=\frac{1}{3}{a}_2\varrho \left(3{\cot }^2\left(\sqrt{\varrho }(\lambda t+x)\right)+2\right)+\frac{a_{-1}\left(\varrho -\sqrt{\varrho }\cot \left(\sqrt{\varrho }(\lambda t+x)\right)\right)+a_{-2}}{{\left(\varrho -\sqrt{\varrho }\cot \left(\sqrt{\varrho }(\lambda t+x)\right)\right)}^2},$$

(5)

$${\mathcal{K}}_{\mathrm{B},1}(x,t)=\frac{a_{-1}\left(\sqrt{\varrho }\tan \left(\sqrt{\varrho }(\lambda t+x)\right)+\varrho \right)+a_{-2}}{{\left(\sqrt{\varrho }\tan \left(\sqrt{\varrho }(\lambda t+x)\right)+\varrho \right)}^2}+a_0+\frac{6q_2\varrho \left(\varrho -{\tan }^2\left(\sqrt{\varrho }(\lambda t+x)\right)\right)}{q_4},$$

(6)

$${\mathcal{K}}_{\mathrm{A},2}(x,t)=\frac{a_{-1}\left(\varrho -\sqrt{\varrho }\cot \left(\sqrt{\varrho }(\lambda t+x)\right)\right)+a_{-2}}{{\left(\varrho -\sqrt{\varrho }\cot \left(\sqrt{\varrho }(\lambda t+x)\right)\right)}^2}+a_0+\frac{6q_2\varrho \left(\varrho -{\cot }^2\left(\sqrt{\varrho }(\lambda t+x)\right)\right)}{q_4}.$$

(7)

For $\varrho >0$, we have

$${\mathcal{K}}_{\mathrm{A},3}(x,t)=a_2\left(\varrho {\tan }^2\left(\sqrt{\varrho }(\lambda t+x)\right)+\frac{2\varrho }{3}\right)+\frac{a_{-2}}{\varrho {\left(\tan \left(\sqrt{\varrho }(\lambda t+x)\right)+\sqrt{\varrho }\right)}^2}+\frac{a_{-1}}{\sqrt{\varrho }\tan \left(\sqrt{\varrho }(\lambda t+x)\right)+\varrho },$$

(8)

$${\mathcal{K}}_{\mathrm{A},4}(x,t)=\frac{1}{3}{a}_2\varrho \left(3{\cot }^2\left(\sqrt{\varrho }(\lambda t+x)\right)+2\right)+\frac{a_{-2}}{\varrho {\left(\sqrt{\varrho }-\cot \left(\sqrt{\varrho }(\lambda t+x)\right)\right)}^2}+\frac{a_{-1}}{\varrho -\sqrt{\varrho }\cot \left(\sqrt{\varrho }(\lambda t+x)\right)},$$

(9)

$${\mathcal{K}}_{\mathrm{B},3}(x,t)=\frac{a_{-1}\left(\sqrt{\varrho }\tan \left(\sqrt{\varrho }(\lambda t+x)\right)+\varrho \right)+a_{-2}}{{\left(\sqrt{\varrho }\tan \left(\sqrt{\varrho }(\lambda t+x)\right)+\varrho \right)}^2}+a_0+\frac{6q_2\varrho \left(\varrho -{\tan }^2\left(\sqrt{\varrho }(\lambda t+x)\right)\right)}{q_4},$$

(10)

$${\mathcal{K}}_{\mathrm{B},4}(x,t)=\frac{a_{-1}\left(\varrho -\sqrt{\varrho }\cot \left(\sqrt{\varrho }(\lambda t+x)\right)\right)+a_{-2}}{{\left(\varrho -\sqrt{\varrho }\cot \left(\sqrt{\varrho }(\lambda t+x)\right)\right)}^2}+a_0+\frac{6q_2\varrho \left(\varrho -{\cot }^2\left(\sqrt{\varrho }(\lambda t+x)\right)\right)}{q_4}.$$

(11)

For $\varrho =0$, we have

$${\mathcal{K}}_{\mathrm{A},5}(x,t)=\frac{a_{-2}}{{\left(\frac{1}{\lambda t+x}-\varrho \right)}^2}+\frac{a_{-1}}{\varrho -\frac{1}{\lambda t+x}}+a_2\left(\frac{1}{{(\lambda t+x)}^2}+\frac{2\varrho }{3}\right),$$

(12)

$${\mathcal{K}}_{\mathrm{B},5}(x,t)=\frac{a_{-2}}{{\left(\frac{1}{\lambda t+x}-\varrho \right)}^2}+\frac{a_{-1}}{\varrho -\frac{1}{\lambda t+x}}+a_0+\frac{6q_2\left({\varrho }^2-\frac{1}{{(\lambda t+x)}^2}\right)}{q_4}.$$

(13)

2.1.2. NAE Method’s Soliton Solutions

Employing the NAE method’s framework with the following auxiliary equation ${\mathsf{\Lambda }}^{\prime }\left(\mathcal{Q}\right)={\mathcal{P}}_3 \mathsf{\Lambda }{\left(\mathcal{Q}\right)}^2+{\mathcal{P}}_2 \mathsf{\Lambda }\left(\mathcal{Q}\right)+{\mathcal{P}}_1$, where ${\mathcal{P}}_j,j=1,2,3$ are arbitrary constants, and the above-mentioned general solution, give the following value of the previously shown parameters:

• Set A

  $$\begin{array}{l}{a}_0\to \frac{a_2\left({\mathcal{P}}_2^2+8{\mathcal{P}}_1{\mathcal{P}}_3\right)}{12{\mathcal{P}}_3^2},a_1\to \frac{a_2{\mathcal{P}}_2}{{\mathcal{P}}_3},q_1\to -\frac{{\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right)}^2\left(12a_2{\mathcal{P}}_3^2{q}_2+a_2^2{q}_4+144{\mathcal{P}}_3^4\right)}{144\lambda {\mathcal{P}}_3^4},\\ q_3\to -\frac{a_2{q}_4}{6{\mathcal{P}}_3^2}-\frac{60{\mathcal{P}}_3^2}{a_2}-2q_2.\end{array}$$
• Set B

  $$\begin{array}{l}{a}_1\to -\frac{6{\mathcal{P}}_2{\mathcal{P}}_3{q}_2}{q_4},a_2\to -\frac{6{\mathcal{P}}_3^2{q}_2}{q_4},q_1\to -\frac{1}{\lambda q_4}(q_4\left(a_0\left({\mathcal{P}}_2^2+8{\mathcal{P}}_1{\mathcal{P}}_3\right)q_2+{\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right)}^2\right)\\ +a_0^2{q}_4^2+6{\mathcal{P}}_1{\mathcal{P}}_3\left({\mathcal{P}}_2^2+2{\mathcal{P}}_1{\mathcal{P}}_3\right)q_2^2),q_3\to \frac{10q_4}{q_2}-q_2.\end{array}$$

Thus, the solitary solutions of the nonlinear (1+1)–D $\mathcal{KK}$ equation are given by

For ${\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3>0, {\mathcal{P}}_2{\mathcal{P}}_3\ne 0$, we get

$${\mathcal{K}}_{\mathrm{A},1}(x,t)=-\frac{a_2\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right)}{12{\mathcal{P}}_3^2}\left(3 {\mathrm{sech}}^2\left(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)-1\right),$$

(14)

$${\mathcal{K}}_{\mathrm{A},2}(x,t)=\frac{a_2\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right)}{12{\mathcal{P}}_3^2}\left(3 {\mathrm{csch}}^2\left(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)+1\right),$$

(15)

$${\mathcal{K}}_{\mathrm{B},1}(x,t)=a_0+\frac{3q_2}{2q_4}\left(4 {\mathcal{P}}_1{\mathcal{P}}_3+\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right){\mathrm{sech}}^2\left(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)\right),$$

(16)

$${\mathcal{K}}_{\mathrm{B},2}(x,t)=a_0+\frac{3q_2}{2q_4}\left(4 {\mathcal{P}}_1{\mathcal{P}}_3-\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right){\mathrm{csch}}^2\left(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)\right).$$

(17)

For ${\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3<0, {\mathcal{P}}_2{\mathcal{P}}_3\ne 0$, we get

$${\mathcal{K}}_{\mathrm{A},3}(x,t)=-\frac{a_2\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right)}{12{\mathcal{P}}_3^2}\left(3{\sec }^2\left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)-1\right),$$

(18)

$${\mathcal{K}}_{\mathrm{A},4}(x,t)=-\frac{a_2\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right)}{12{\mathcal{P}}_3^2}\left(3{\csc }^2\left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)-1\right),$$

(19)

$${\mathcal{K}}_{\mathrm{B},3}(x,t)=a_0+\frac{3q_2}{2q_4}\left(4{\mathcal{P}}_1{\mathcal{P}}_3+\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right){\sec }^2\left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right),$$

(20)

$${\mathcal{K}}_{\mathrm{B},4}(x,t)=a_0+\frac{3q_2}{2q_4}\left(4{\mathcal{P}}_1{\mathcal{P}}_3+\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right){\csc }^2\left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right).$$

(21)

For ${\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3>0, {\mathcal{P}}_1{\mathcal{P}}_3\ne 0$, we get

$$\begin{array}{cc}\hfill {\mathcal{K}}_{\mathrm{A},5}(x,t)=& a_2\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right)(-10{\mathcal{P}}_1{\mathcal{P}}_3+\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}{\mathcal{P}}_2\left(-\sinh \left(\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)\right)\hfill \\ & +\left({\mathcal{P}}_2^2-2{\mathcal{P}}_1{\mathcal{P}}_3\right)\cosh \left(\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right))/(12{\mathcal{P}}_3^2\left({\mathcal{P}}_2\cosh \right(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\hfill \\ & (\lambda t+x))-\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\sinh \left(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right){)}^2),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\mathcal{K}}_{\mathrm{A},6}(x,t)=& a_2\left({\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3\right)(10{\mathcal{P}}_1{\mathcal{P}}_3+\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}{\mathcal{P}}_2\left(-\sinh \left(\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)\right)\hfill \\ & +\left({\mathcal{P}}_2^2-2{\mathcal{P}}_1{\mathcal{P}}_3\right)\cosh \left(\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right))/(12{\mathcal{P}}_3^2\left({\mathcal{P}}_2\sinh \right(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\hfill \\ & (\lambda t+x))-\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\cosh \left(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right){)}^2),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\mathcal{K}}_{\mathrm{B},5}(x,t)=& a_0+6{\mathcal{P}}_1{\mathcal{P}}_3{q}_2({\mathcal{P}}_2^2-2{\mathcal{P}}_1{\mathcal{P}}_3-\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}{\mathcal{P}}_2\sinh \left(\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)\hfill \\ & +\left({\mathcal{P}}_2^2-2{\mathcal{P}}_1{\mathcal{P}}_3\right)\cosh \left(\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right))/(q_4\left({\mathcal{P}}_2\cosh \right(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\hfill \\ & (\lambda t+x))-\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\sinh \left(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right){)}^2),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\mathcal{K}}_{\mathrm{B},6}(x,t)=& a_0-6{\mathcal{P}}_1{\mathcal{P}}_3{q}_2({\mathcal{P}}_2\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\sinh \left(\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)\hfill \\ & -\left({\mathcal{P}}_2^2-2{\mathcal{P}}_1{\mathcal{P}}_3\right)\left(\cosh \left(\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right)-1\right))/(q_4\left({\mathcal{P}}_2\sinh \right(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\hfill \\ & (\lambda t+x))-\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}\cosh \left(\frac{1}{2}\sqrt{{\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3}(\lambda t+x)\right){)}^2).\hfill \end{array}$$

(25)

For ${\mathcal{P}}_2^2-4{\mathcal{P}}_1{\mathcal{P}}_3<0, {\mathcal{P}}_1{\mathcal{P}}_3\ne 0$, we get

$$\begin{array}{l}{\mathcal{K}}_{\mathrm{A},7}(x,t)=\frac{1}{12}{a}_2(\frac{{\mathcal{P}}_2^2}{{\mathcal{P}}_3^2}\\ -\frac{24{\mathcal{P}}_1{\mathcal{P}}_2\cos \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)}{{\mathcal{P}}_3\left(\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}\sin \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)+{\mathcal{P}}_2\cosh \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right)}\\ +8{\mathcal{P}}_1(\frac{1}{{\mathcal{P}}_3}\\ +\frac{3{\mathcal{P}}_1\left(\cos \left(\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)+1\right)}{{\left(\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}\sin \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)+{\mathcal{P}}_2\cosh \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right)}^2}\left)\right),\end{array}$$

(26)

$$\begin{array}{l}{\mathcal{K}}_{\mathrm{A},8}(x,t)=\frac{1}{12}{a}_2(\frac{{\mathcal{P}}_2^2}{{\mathcal{P}}_3^2}+8{\mathcal{P}}_1(\frac{1}{{\mathcal{P}}_3}\\ -\frac{3{\mathcal{P}}_1\left(\cos \left(\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)-1\right)}{{\left({\mathcal{P}}_2\sinh \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)-\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}\cos \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right)}^2})\\ +\frac{24{\mathcal{P}}_1{\mathcal{P}}_2\sin \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)}{{\mathcal{P}}_3\left(\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}\cos \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)-{\mathcal{P}}_2\sinh \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right)}),\end{array}$$

(27)

$$\begin{array}{l}{\mathcal{K}}_{\mathrm{B},7}(x,t)=a_0+\left(12{\mathcal{P}}_1{\mathcal{P}}_3{q}_2\cos \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right(\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}{\mathcal{P}}_2\sin (\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}\\ (\lambda t+x))-2{\mathcal{P}}_1{\mathcal{P}}_3\cos \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)+{\mathcal{P}}_2^2\cosh \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)))/(q_4\\ \times (\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}\sin \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)+{\mathcal{P}}_2\cosh \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right){)}^2),\end{array}$$

(28)

$$\begin{array}{l}{\mathcal{K}}_{\mathrm{B},8}(x,t)=a_0-\left(12{\mathcal{P}}_1{\mathcal{P}}_3{q}_2\sin \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right(2{\mathcal{P}}_1{\mathcal{P}}_3\sin \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\\ +\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}{\mathcal{P}}_2\cos \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)+{\mathcal{P}}_2^2\left(-\sinh \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right)\left)\right)\\ /\left(q_4{\left({\mathcal{P}}_2\sinh \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)-\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}\cos \left(\frac{1}{2}\sqrt{4{\mathcal{P}}_1{\mathcal{P}}_3-{\mathcal{P}}_2^2}(\lambda t+x)\right)\right)}^2\right).\end{array}$$

(29)

For ${\mathcal{P}}_1=0\&{\mathcal{P}}_2{\mathcal{P}}_3\ne 0$, we get

$${\mathcal{K}}_{\mathrm{A},9}(x,t)=\frac{1}{12}{a}_2{\mathcal{P}}_2^2\left(\frac{1}{{\mathcal{P}}_3^2}+\frac{12{\mathsf{\Omega }}^2}{{\beta }^2{\left(e^{{\mathcal{P}}_2(-(\lambda t+x))}+\mathsf{\Omega }\right)}^2}-\frac{12\mathsf{\Omega }}{\beta {\mathcal{P}}_3\left(e^{{\mathcal{P}}_2(-(\lambda t+x))}+\mathsf{\Omega }\right)}\right),$$

(30)

$${\mathcal{K}}_{\mathrm{A},10}(x,t)=\frac{1}{12}{a}_2{\mathcal{P}}_2^2\left(\frac{1}{{\mathcal{P}}_3^2}+\frac{12e^{2{\mathcal{P}}_2(\lambda t+x)}}{{\beta }^2{\left(e^{{\mathcal{P}}_2(\lambda t+x)}+\mathsf{\Omega }\right)}^2}-\frac{12}{{\mathcal{P}}_3\left(\beta +\beta \mathsf{\Omega }{e}^{{\mathcal{P}}_2(-(\lambda t+x))}\right)}\right),$$

(31)

$${\mathcal{K}}_{\mathrm{B},9}(x,t)=a_0+\frac{6{\mathcal{P}}_3{\mathcal{P}}_2^2{q}_2\mathsf{\Omega }\left(\beta \left(e^{{\mathcal{P}}_2(-(\lambda t+x))}+\mathsf{\Omega }\right)-{\mathcal{P}}_3\mathsf{\Omega }\right)}{{\beta }^2{q}_4{\left(e^{{\mathcal{P}}_2(-(\lambda t+x))}+\mathsf{\Omega }\right)}^2},$$

(32)

$${\mathcal{K}}_{\mathrm{B},10}(x,t)=a_0+\frac{6{\mathcal{P}}_3{\mathcal{P}}_2^2{q}_2{e}^{{\mathcal{P}}_2(\lambda t+x)}\left(\beta \mathsf{\Omega }+\left(\beta -{\mathcal{P}}_3\right)e^{{\mathcal{P}}_2(\lambda t+x)}\right)}{{\beta }^2{q}_4{\left(e^{{\mathcal{P}}_2(\lambda t+x)}+\mathsf{\Omega }\right)}^2}.$$

(33)

2.2. Semi–Analytical Solutions

Here, we apply the VI method to the considered model along with the above-obtained analytical solutions. These solutions are used to construct the requested conditions for the suggested approximate schemes. The aims of this section are evaluating the numerical solutions of the nonlinear VP model and investigating the accuracy of the obtained analytical solutions. Handling the considered model via the VI method gives

$${\mathcal{K}}_{\mathrm{Semi}-\mathrm{analytical}}=\left\{\begin{array}{l}\frac{1}{12{(\tanh \left(2x\right)+2)}^7}(1536t(405\tanh \left(2x\right)+4358){\mathrm{sech}}^{10}\left(2x\right)-48\\ \times {\mathrm{sech}}^8\left(2x\right)((616784t-1)\tanh \left(2x\right)+2(778544t-7))+2{\mathrm{sech}}^6\left(2x\right)\\ \times (16(3090480t-131)\tanh \left(2x\right)+52179036t-7831)+{\mathrm{sech}}^4\left(2x\right)\\ \times (3(6477327t+12092)\tanh \left(2x\right)+75298110t+65290)-{\mathrm{sech}}^2\left(2x\right)\\ \times \left(\right(111084189t+61352\left)\tanh \right(2x)+110984790t+67562)+2(6194\\ \times \tanh \left(2x\right)+6199\left)\right),\\ \frac{\hspace{1em}\hspace{1em}-66t\tanh \left(\frac{x}{2}\right)+\cosh \left(x\right)-5}{3\left(\cosh \right(x)+1)}{|}_{\mathrm{NAE}}.\end{array}\right.{\mid }_{\mathrm{MKE} \mathrm{method}},$$

(34)

Investigating the analytical and semi-analytical solutions concerning different values of x of the considered model along with the above-shown approximate solutions is represented by the following Table 1 and Table 2.

Table 1. Absolute error between analytical and approximate solutions through the MFE and VI methods for $x \in \{10,11,\cdots ,29,30\}, t\in \{1,2,3,4,5\}$.

Value of x	$\mathit{t}=1$	$\mathit{t}=2$	$\mathit{t}=3$	$\mathit{t}=4$	$\mathit{t}=5$
10	1.4432899320127 × 10−13	2.88213897192691 × 10−13	4.32098801184111 × 10−13	5.75539615965681 × 10−13	7.19424519957101 × 10−13
11	3.10862446895044 × 10−15	5.77315972805081 × 10−15	8.43769498715119 × 10−15	1.11022302462516 × 10−14	1.37667655053519 × 10−14
12	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
13	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
14	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
15	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
17	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
18	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
19	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
20	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
21	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
22	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
23	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
24	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
25	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
26	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
27	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
28	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
29	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16
30	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16	4.44089209850063 × 10−16

Table 2. Absolute error between analytical and approximate solutions through the MFE and VI methods for $x\in \{10,11,\cdots ,29,30\}, t\in \{5,7,9,11,13\}$.

Value of x	t = 5	t = 7	t = 9	t = 11	t = 13
10	0.0164244725343919	0.16654441640775	0.768291042082899	0.764296573715769	0.15456101130636
11	0.00612510388391158	0.0654402400876814	0.413294105364588	0.991850112266608	0.41035480239668
12	0.00226461467607447	0.0246752792399448	0.17824901408163	0.783449430725106	0.782908753326303
13	0.000834641432710226	0.0091608207257004	0.0697467012240005	0.418871310795438	0.998698061991988
14	0.000307255579977739	0.003381448617511	0.0262596162962896	0.180300854252883	0.785968774011267
15	0.000113061194247033	0.00124550927506378	0.00974367638621276	0.0705015447026717	0.419798142092268
16	0.0000415967037510345	0.000458406440250525	0.00359587067076089	0.0265373095425168	0.180641818692087
17	0.0000153030884371685	0.00016866662738646	0.00132439093487935	0.00984583427270436	0.0706269788158394
18	5.62976149848238 × 10−6	0.0000620528182497249	0.000487425407530773	0.00363345249082281	0.0265834542153602
19	2.07108297073377 × 10−6	0.0000228284749557162	0.000179342112418768	0.00133821651842542	0.00986280995476424
20	7.61910125712806 × 10−7	8.39819683040588 × 10−6	0.0000659801102002033	0.000492511556099862	0.00363969749601051
21	2.80291244492137 × 10−7	3.08953346023211 × 10−6	0.0000242732449891592	0.000181213201995989	0.00134051392754658
22	1.03113409810618 × 10−7	1.13657712896842 × 10−6	8.92969803173438 × 10−6	0.0000666684455996602	0.000493356725697391
23	3.79333067179743 × 10−8	4.18123533130199 × 10−7	3.28506182639687 × 10−6	0.0000245264694327396	0.000181524122517152
24	1.39548841371351 × 10−8	1.53819075254802 × 10−7	1.20850799517624 × 10−6	9.02285409870585 × 10−6	0.0000667828268674509
25	5.13371495314274 × 10−9	5.6586878571796 × 10−8	4.44585419978605 × 10−7	3.31933202823986 × 10−6	0.0000245685479496327
26	1.88858823024773 × 10−9	2.08171497262377 × 10−8	1.63553859455767 × 10−7	1.22111529793356 × 10−6	9.03833392007503 × 10−6
27	6.94772794851417 × 10−10	7.65820140635753 × 10−9	6.01681055534264 × 10−8	4.49223387488651 × 10−7	3.32502673627832 × 10−6
28	2.5559265814934 × 10−10	2.81729489737259 × 10−9	2.21346095341524 × 10−8	1.65260072348961 × 10−7	1.22321026396754 × 10−6
29	9.40272304461587 × 10−11	1.03642483484379 × 10−9	8.14286776895656 × 10−9	6.0795786183121 × 10−8	4.49994082385441 × 10−7
30	3.45907191778849 × 10−11	3.81279452454919 × 10−10	2.99559366201407 × 10−9	2.23655203246409 × 10−8	1.65543595165296 × 10−7

3. Results’ Discussion

Here, the article’s results are illustrated by comparing them with previously published solutions. In contrast, the paper’s contribution is also explained by showing the result’s novelty and shown figures and tables. Additionally, this section shows the obtained solution’s accuracy by estimating the matching between obtained analytical and approximate solutions. The formulated solutions are different from the constructed solutions by numerous researchers who have applied some distinct analytical schemes.

This paper has applied the MFE and NAE analytical schemes to the considered model for constructing novel solutions. Both computational methods depend on the above-shown auxiliary equations that are different from the previous techniques. These auxiliary equations provide some distinct solutions by giving a specific value of parameters. The considered model is studied by utilizing some analytical and numerical schemes such as the homotopy perturbation method (HPM) [26], different methods of fixed-point theorem together with the concept of Piccard L-stability [27], the deep geometric theory of Krasil’shchik and Vinogradov that is known with a nonlocal symmetries theory [28], the q-homotopy analysis transform method (q-HATM) [29], the modified auxiliary equation of direct algebraic method [30], the Adomian decomposition method (ADM) [31], perturbation scheme and the Hirota bi-linear formalism [32]. However, all these are studies of the considered model, but our paper has constructed novel solutions that have not been obtained in previously published articles.

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 show the dynamical behavior of the obtained solutions through the pseudo spherical surfaces, respectively, kink, bright, dark, bright, dark, and dark waves. These figures have been plotted by using the following values of the above-shown parameters in its represented solution $[a_2=4, a_{-2}=2, a_{-1}=5, \lambda =3, \varrho =-16 \& a_0=0.3, a_2=0.5, a_{-2}=0.1, a_{-1}=0.9, \lambda =7, q_2=0.8, q_4=0.4, \varrho =-4 \& a_2=5, \lambda =7, {\mathcal{P}}_1=1, {\mathcal{P}}_2=3, {\mathcal{P}}_3=2 \& a_2=5, \lambda =7, {\mathcal{P}}_1=1, {\mathcal{P}}_2=3, {\mathcal{P}}_3=2 \& a_0=5, \lambda =7, {\mathcal{P}}_1=1, {\mathcal{P}}_2=3, {\mathcal{P}}_3=2, q_2=6, q_4=8 \& a_0=5, \lambda =7, {\mathcal{P}}_1=1, {\mathcal{P}}_2=3, {\mathcal{P}}_3=2, q_2=6, {\mathcal{P}}_4=8]$. For further explanation of the sketched solutions Equations (4), (6), (14), (16), (22), and (24), three, two-dimensional, contour, polar, and spherical plots have been figured to show more novel properties of the wave’s dynamical behavior on the considered surface.

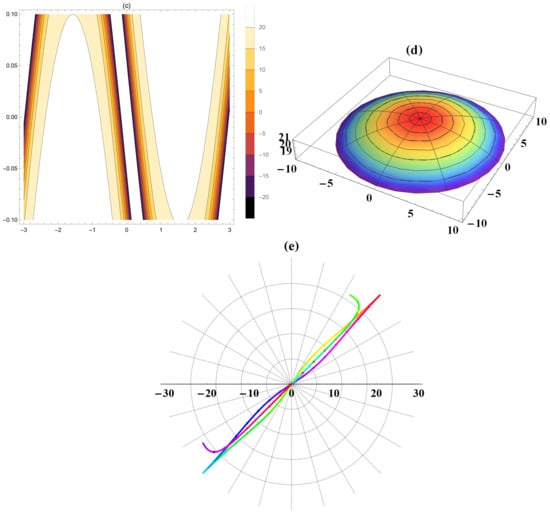
Figure 1. Distinct kink waves’ sketches of Equation (4) in various formulas (three (a), two (b), contour (c), spherical (d), polar plots (e)) for $a_2=4, a_{-2}=2, a_{-1}=5, \lambda =3, \varrho =-16$.

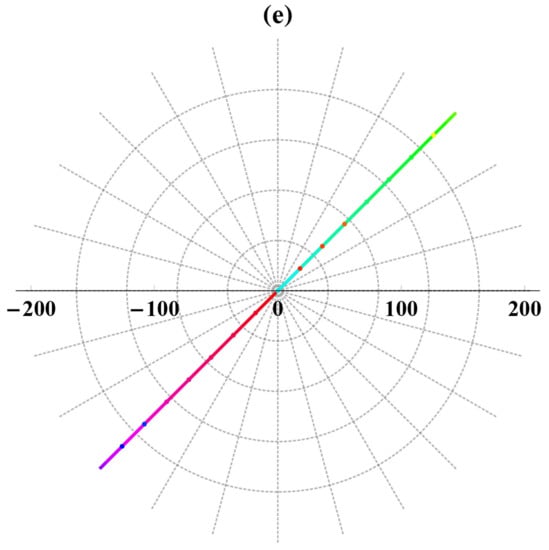
Figure 2. Distinct bright waves’ sketches of Equation (6) in various formulas (three (a), two (b), contour (c), spherical (d), polar plots (e)) for $a_0=0.3, a_2=0.5, a_{-2}=0.1, a_{-1}=0.9, \lambda =7, q_2=0.8, q_4=0.4, \varrho =-4$.

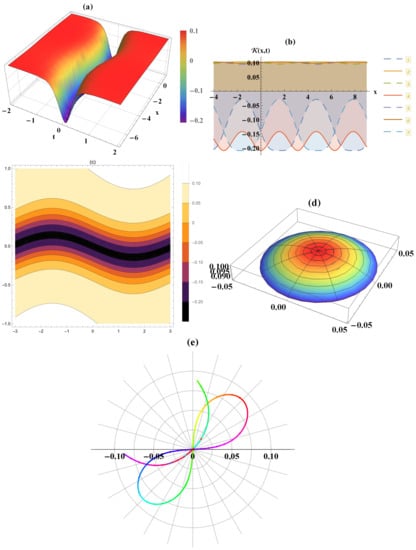
Figure 3. Distinct dark waves’ sketches of Equation (14) in various formulas (three (a), two (b), contour (c), spherical (d), polar plots (e)) for $a_2=5, \lambda =7, {\mathcal{P}}_1=1, {\mathcal{P}}_2=3, {\mathcal{P}}_3=2$.

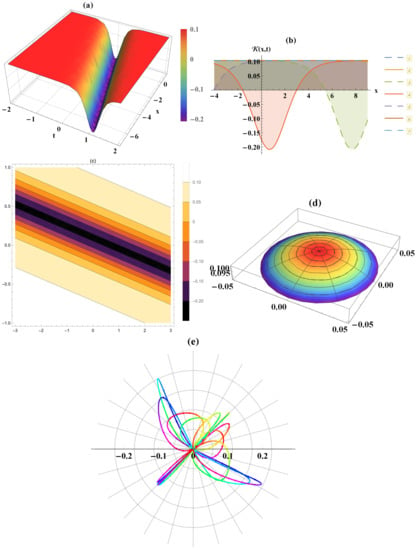
Figure 4. Distinct bright waves’ sketches of Equation (22) in various formulas (three (a), two (b), contour (c), spherical (d), polar plots (e) for $a_2=5, \lambda =7, {\mathcal{P}}_1=1, {\mathcal{P}}_2=3, {\mathcal{P}}_3=2$.

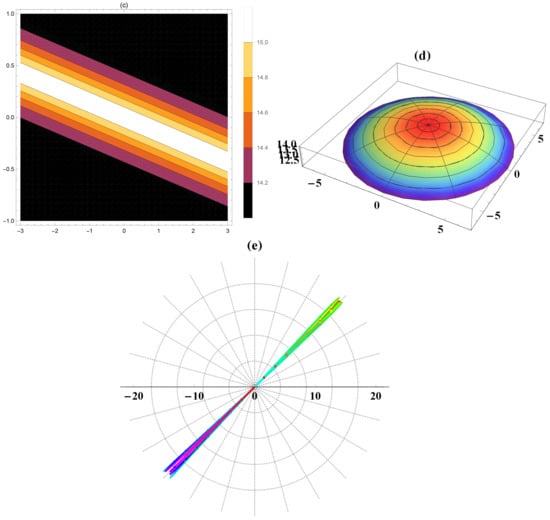
Figure 5. Distinct dark waves’ sketches of Equation (16) in various formulas (three (a), two (b), contour (c), spherical (d), polar plots (e)) for $a_0=5, \lambda =7, {\mathcal{P}}_1=1, {\mathcal{P}}_2=3, {\mathcal{P}}_3=2, q_2=6, q_4=8$.

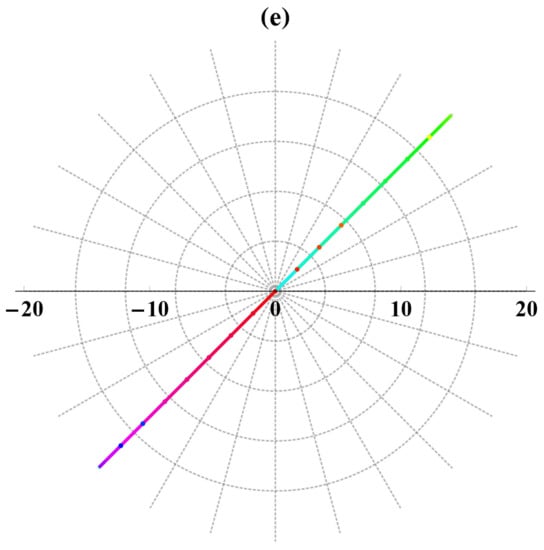
Figure 6. Distinct dark waves’ sketches of Equation (24) in various formulas (three (a), two (b), contour (c), spherical (d), polar plots (e)) for $a_0=5, \lambda =7, {\mathcal{P}}_1=1, {\mathcal{P}}_2=3, {\mathcal{P}}_3=2, q_2=6, {\mathcal{P}}_4=8$.

Estimating the matching between analytical and approximate solutions by using the analytical obtained solutions for constructing the requested conditions allows applying the VI method. The approximate solutions of the considered model are also sketched in distinct forms (Figure 7 and Figure 8). While the matching between the analytical and approximate solutions is discussed through Table 1 and Table 2 and Figure 9 and Figure 10. Additionally, The MFE method’s accurate is greater than the NAE method, and this superiority is explained by Figure 11:

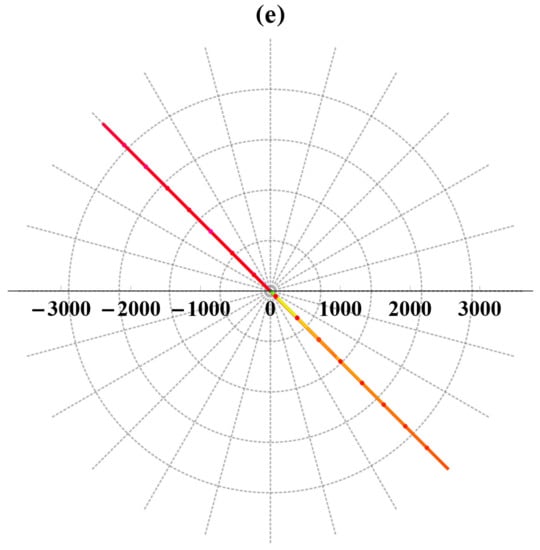
Figure 7. Distinct bright waves’ sketches of the obtained approximate solution by the calculated data from the MFE method’s solutions in various formulas (three (a), two (b), contour (c), spherical (d), polar plots (e)).

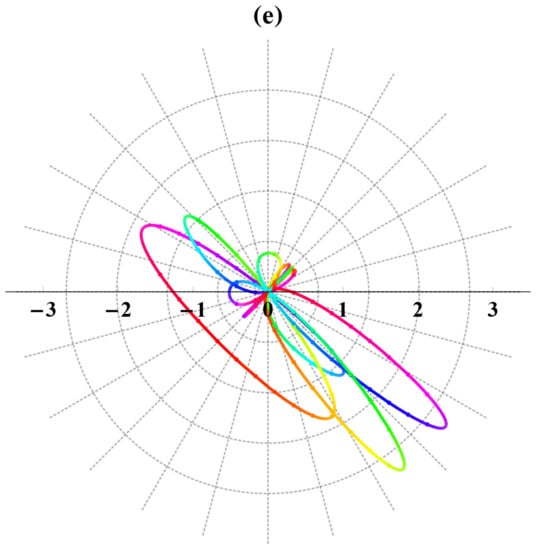
Figure 8. Distinct bright waves’ sketches of the obtained approximate solution by the calculated data from the NAE method’s solutions in various formulas (three (a), two (b), contour (c), spherical (d), polar plots (e)).

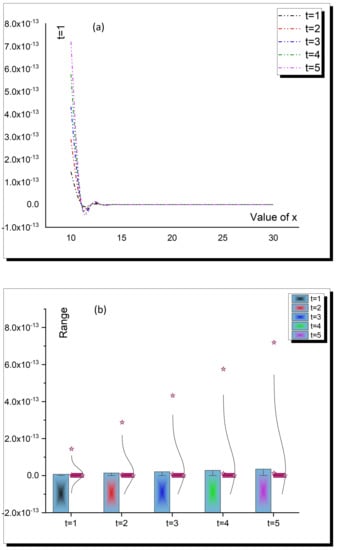
Figure 9. Absolute error through Table 1, through (a) two-dimensional, and (b) bar normal plots.

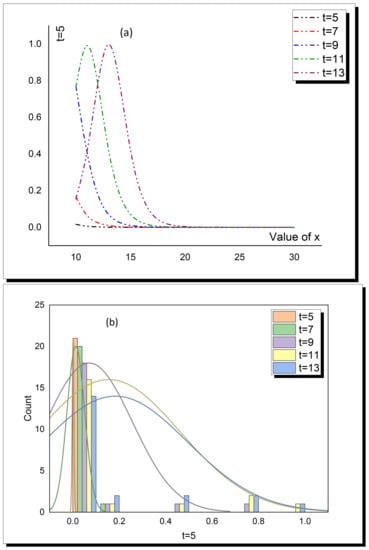
Figure 10. Absolute error through Table 2., through (a) two-dimensional, and (b) distribution plots.

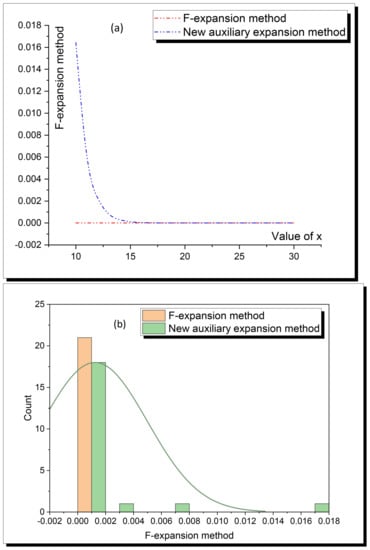
Figure 11. Accuracy of the MFE expansion method over NAE method through (a) two-dimensional, and (b) distribution plots.

4. Conclusions

This paper has successfully implemented two recent analytical schemes for obtaining novel solutions of the nonlinear $\mathcal{KK}$-model. Many computational wave solutions have been formulated through the used schemes. These solutions have been checked for their accuracy by employing the VI approximate schemes. The solutions have been represented in some different sketches to explain the physical and dynamical characterizations of the waves on pseudo-spherical surfaces. The paper’s novelty and contribution are demonstrated by comparing its solutions with the previously published results of the considered model.