Bounds on the Arithmetic-Geometric Index

Abstract

The concept of arithmetic-geometric index was recently introduced in chemical graph theory, but it has proven to be useful from both a theoretical and practical point of view. The aim of this paper is to obtain new bounds of the arithmetic-geometric index and characterize the extremal graphs with respect to them. Several bounds are based on other indices, such as the second variable Zagreb index or the general atom-bond connectivity index), and some of them involve some parameters, such as the number of edges, the maximum degree, or the minimum degree of the graph. In most bounds, the graphs for which equality is attained are regular or biregular, or star graphs.

1. Introduction

In chemical graph theory, a topological descriptor is a function that associates each molecular graph with a real value. If it correlates well with some chemical property, then it is called a topological index. Since Winer’s work (see [1]), numerous topological indices have been defined and discussed, the growing interest in their study is because there are several applications in theoretical chemistry, especially in QSPR/QSAR research (see [2,3,4]).

In particular, vertex-degree-based topological indices belong to one of the largest and most studied classes of topological descriptors. The Randić index [5] and the Zagreb indices [6] are probably the best known such descriptors.

In [7,8,9], the first and second variable Zagreb indices are defined, for each $\alpha \in \mathbb{R}$, as

$$M_1^{\alpha }\left(G\right)=\sum _{u\in V\left(G\right)}{d}_u^{\alpha },M_2^{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{\left(d_u{d}_v\right)}^{\alpha },$$

where $d_u$ denotes the degree of $u\in V\left(G\right)$.

Note that, for $\alpha =2$, $\alpha =-1$ and $\alpha =3$, the index $M_1^{\alpha }$ is the first Zagreb index $M_1$, the inverse index $ID$, and the forgotten index F, respectively; also, for $\alpha =1$, $\alpha =-1/2$ and $\alpha =-1$, the index $M_2^{\alpha }$ is the second Zagreb index $M_2$, the Randić index R and the modified Zagreb index.

The geometric-arithmetic index|$GA$ is defined in [10] as

$$GA\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{2\sqrt{d_u{d}_v}}{d_u+d_v}.$$

There are many papers studying the mathematical and computational properties of the $GA$ index (see [10,11,12,13,14,15,16,17]).

In 2015, the arithmetic-geometric index [18] was defined as

$$AG\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}.$$

The $AG$ index of path graphs with pendant vertices attached was discussed in the papers [18,19]. Additionally, the arithmetic-geometric index of graphene, which is the most conductive and effective material for electromagnetic interference shielding, was computed in [20]. The paper [21] studied the spectrum and energy of arithmetic-geometric matrix, in which the sum of all elements is equal to 2$AG$. Other bounds of the arithmetic-geometric energy appeared in [22,23]. The paper [24] studies extremal $AG$-graphs for various classes of simple graphs, and it includes inequalities that involve $AG+GA$, $AG-GA$, $AG·GA$, and $AG/GA$. In [25,26,27,28], there are more bounds on the $AG$ index and a discussion on the effect of deleting an edge from a graph on the arithmetic-geometric index.

Along the paper, we denote, by G, a simple graph without isolated vertices.

An important subject in the study of topological indices is to bind them in terms of some parameters. Reference [29] proves that many upper bounds of $GA$ are not useful, and it shows the importance of obtaining upper bounds of $GA$ less than the number of edges m. In a similar way, it is important to find lower bounds of $AG$ that are greater than m. With this aim, in this paper we obtain several new lower bounds of $AG$, which are greater than m, and we characterize the extremal graphs.

2. Bounds Involving Other Indices

A graph is said biregular if it is bipartite and the degree of any vertex in one side of the bipartition is the maximum degree $\Delta$ and the degree of any vertex in the other side is the minimum degree $\delta$.

One can check that the following result holds.

Lemma 1.

Let g be the function $g(x,y)=\frac{x+y}{2\sqrt{xy}}$ with $0<a\le x,y\le b$. Then

$$1\le g(x,y)\le \frac{a+b}{2\sqrt{ab}}.$$

The equality in the upper bound is attained if and only if either $x=a$ and $y=b$, or $x=b$ and $y=a$, and the equality in the lower bound is attained if and only if $x=y$.

The following inequalities follow from Lemma 1:

$$m\le AG\left(G\right)\le \frac{\Delta +\delta }{2\sqrt{\Delta \delta }}m.$$

(1)

The lower bound in (1) also follows from the inequalities $GA\left(G\right)·AG\left(G\right)\ge m^2$ and $GA\left(G\right)\le m$, see [11],12]. The upper bound in (1) appears in [27].

The following result improves the lower bound in (1), see Remark 1.

Theorem 1.

If G is a graph with m edges, maximum degree Δ, and minimum degree δ, then

$$m+\frac{M_1\left(G\right)-2M_2^{1/2}\left(G\right)}{2\Delta }\le AG\left(G\right)\le m+\frac{M_1\left(G\right)-2M_2^{1/2}\left(G\right)}{2\delta }.$$

The equality in each bound is attained if and only if G is a regular graph.

Proof. 

We have

$$\begin{array}{cc}\hfill \frac{d_u+d_v}{2\sqrt{d_u{d}_v}}& =1+\frac{{\left(\sqrt{d_u}-\sqrt{d_v}\right)}^2}{2\sqrt{d_u{d}_v}},\hfill \\ \hfill AG\left(G\right)& =m+\sum _{uv\in E\left(G\right)}\frac{{\left(\sqrt{d_u}-\sqrt{d_v}\right)}^2}{2\sqrt{d_u{d}_v}}.\hfill \end{array}$$

Because

$$\begin{array}{cc}\hfill \sum _{uv\in E\left(G\right)}\frac{{\left(\sqrt{d_u}-\sqrt{d_v}\right)}^2}{2\sqrt{d_u{d}_v}}& \ge \frac{1}{2\Delta }\sum _{uv\in E\left(G\right)}{\left(\sqrt{d_u}-\sqrt{d_v}\right)}^2\hfill \\ & =\frac{1}{2\Delta }\left(\sum _{uv\in E\left(G\right)}\left(d_u+d_v\right)-2\sum _{uv\in E\left(G\right)}\sqrt{d_u{d}_v}\right)\hfill \\ & =\frac{M_1\left(G\right)-2M_2^{1/2}\left(G\right)}{2\Delta },\hfill \end{array}$$

we conclude

$$AG\left(G\right)\ge m+\frac{M_1\left(G\right)-2M_2^{1/2}\left(G\right)}{2\Delta }.$$

Because

$$\begin{array}{cc}\hfill \sum _{uv\in E\left(G\right)}\frac{{\left(\sqrt{d_u}-\sqrt{d_v}\right)}^2}{2\sqrt{d_u{d}_v}}& \le \frac{1}{2\delta }\sum _{uv\in E\left(G\right)}{\left(\sqrt{d_u}-\sqrt{d_v}\right)}^2\hfill \\ & =\frac{1}{2\delta }\left(\sum _{uv\in E\left(G\right)}\left(d_u+d_v\right)-2\sum _{uv\in E\left(G\right)}\sqrt{d_u{d}_v}\right)\hfill \\ & =\frac{M_1\left(G\right)-2M_2^{1/2}\left(G\right)}{2\delta },\hfill \end{array}$$

we conclude

$$AG\left(G\right)\le m+\frac{M_1\left(G\right)-2M_2^{1/2}\left(G\right)}{2\delta }.$$

If G is regular, then both bounds are the same, and they are equal to $AG\left(G\right)$.

If the equality in some bound is attained, then we have either $d_u{d}_v={\Delta }^2$ for every $uv\in E\left(G\right)$ or $d_u{d}_v={\delta }^2$ for every $uv\in E\left(G\right)$, so $d_u=\Delta$ for every $u\in V\left(G\right)$ or $d_u=\delta$ for every $u\in V\left(G\right)$, and G is a regular graph. □

Remark 1.

Because Cauchy–Schwarz inequality gives

$$\begin{array}{cc}\hfill M_1\left(G\right)-2M_2^{1/2}\left(G\right)& =\sum _{uv\in E\left(G\right)}{\left(\sqrt{d_u}-\sqrt{d_v}\right)}^2\hfill \\ & =\sum _{uv\in E\left(G\right)}{\left(\sqrt{d_u}-\sqrt{d_v}\right)}^2\frac{1}{m}\sum _{uv\in E\left(G\right)}{1}^2\hfill \\ & \ge \frac{1}{m}{\left(\sum _{uv\in E\left(G\right)}|\sqrt{d_u}-\sqrt{d_v}|\right)}^2,\hfill \end{array}$$

we have $M_1\left(G\right)-2M_2^{1/2}\left(G\right)\ge 0$ and, so, Theorem 1 improves the lower bound in (1).

The misbalance rodeg index [30] is

$$MR\left(G\right)=\sum _{uv\in E\left(G\right)}|\sqrt{d_u}-\sqrt{d_v}|.$$

Theorem 1 and Remark 1 have the following consequence.

Corollary 1.

If G is a graph with m edges, maximum degree Δ, and minimum degree δ, then

$$m+\frac{MR{\left(G\right)}^2}{2\Delta m}\le AG\left(G\right),$$

and the equality is attained if and only if G is regular graph.

The following fact is elementary.

Lemma 2.

Let us consider the function $f(x,y)={\left(xy\right)}^{\alpha }$ with $\delta \le x,y\le \Delta$. Then

$$\begin{array}{c}\hfill f(x,y)\le {\delta }^{2\alpha },\mathrm{if}\alpha \le 0,\\ \hfill f(x,y)\le {\Delta }^{2\alpha },\mathrm{if}\alpha \ge 0.\end{array}$$

The following result provides bounds that relate the arithmetic-geometric and the second variable Zagreb indices.

Theorem 2.

If G is a graph with maximum degree Δ and minimum degree δ, and $\alpha \in \mathbb{R}$, then

$$\begin{array}{cc}\hfill AG\left(G\right)\le \Delta {\delta }^{2\alpha -1}{M}_2^{-\alpha }\left(G\right),& if\alpha \le 1/2,\hfill \\ \hfill AG\left(G\right)\le {\Delta }^{2\alpha }{M}_2^{-\alpha }\left(G\right),& if\alpha \ge 1/2,\hfill \end{array}$$

and the equality in each bound is attained for some fixed α if and only if G is regular.

Proof. 

We have

$$\sum _{uv\in E\left(G\right)}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\le \Delta \sum _{uv\in E\left(G\right)}{\left(d_u{d}_v\right)}^{\alpha -1/2}{\left(d_u{d}_v\right)}^{-\alpha }.$$

If $\alpha \le 1/2$, then Lemma 2 gives

$$AG\left(G\right)\le \Delta {\delta }^{2\alpha -1}\sum _{uv\in E\left(G\right)}{\left(d_u{d}_v\right)}^{-\alpha }.$$

If $\alpha \ge 1/2$, then we have, by Lemma 2

$$AG\left(G\right)\le {\Delta }^{2\alpha }\sum _{uv\in E\left(G\right)}{\left(d_u{d}_v\right)}^{-\alpha }.$$

If G is regular, then $AG\left(G\right)=m$, $M_2^{-\alpha }\left(G\right)={\delta }^{-2\alpha }m={\Delta }^{-2\alpha }m$ and $\Delta {\delta }^{2\alpha -1}={\Delta }^{2\alpha }$, and the equality in each bound is attained.

If the equality is attained, then $d_u+d_v=2\Delta$ for every $uv\in E\left(G\right)$; thus, $d_u=\Delta$ for every $u\in V\left(G\right)$, and G is a regular graph. □

The symmetric division deg index

$$SDD\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{d_u^2+d_v^2}{d_u{d}_v}=\sum _{uv\in E\left(G\right)}\left(\frac{d_u}{d_v}+\frac{d_v}{d_u}\right).$$

is another Adriatic index that appears in [30,31], see also [32].

We need the following inequality (see e.g., [14], Lemma 4) in the proof of Theorem 3 below.

Lemma 3.

Let $(X,\mu )$ be a measure space and $f,g:X\to \mathbb{R}$ measurable functions. If there exist positive constants $\omega ,\mathrm{\Omega }$ with $\omega \left|g\right|\le \left|f\right|\le \mathrm{\Omega }\left|g\right|$μ-a.e., then

$${\parallel f\parallel }_2{\parallel g\parallel }_2\le \frac{1}{2}\left(\sqrt{\frac{\mathrm{\Omega }}{\omega }}+\sqrt{\frac{\omega }{\mathrm{\Omega }}}\right){\parallel fg\parallel }_1.$$

(2)

If these norms are finite, the equality in the bound is attained if and only if $\omega =\mathrm{\Omega }$ and $\left|f\right|=\omega \left|g\right|$μ-a.e. or $f=g=0$μ-a.e.

We have the following direct consequence.

Corollary 2.

If $a_j,b_j\ge 0$ and $\omega b_j\le a_j\le \mathrm{\Omega }{b}_j$ for $1\le j\le m$, then

$${\left(\sum _{j=1}^m{a}_j^2\right)}^{1/2}{\left(\sum _{j=1}^m{b}_j^2\right)}^{1/2}\le \frac{1}{2}\left(\sqrt{\frac{\mathrm{\Omega }}{\omega }}+\sqrt{\frac{\omega }{\mathrm{\Omega }}}\right)\sum _{j=1}^m{a}_j{b}_j.$$

If $a_j>0$ for some $1\le j\le m$, then the equality holds if and only if $\omega =\mathrm{\Omega }$ and $a_j=\omega b_j$ for every $1\le j\le m$.

The following result provides an inequality relating the arithmetic-geometric and the symmetric division deg indices.

Theorem 3.

Let G be a graph with m edges, maximum degree Δ, and minimum degree δ. Subsequently,

$$\frac{\sqrt{2\sqrt{\Delta \delta }(\Delta +\delta )}}{{\left(\sqrt{\Delta }+\sqrt{\delta }\right)}^2}\sqrt{m\left(SDD\left(G\right)+2m\right)}\le AG\left(G\right)\le \frac{1}{2}\sqrt{m\left(SDD\left(G\right)+2m\right)}.$$

The equality in the lower bound is attained if and only if G is a regular graph. The equality in the upper bound is attained if G is a regular or biregular graph.

Proof. 

Let us consider

$$a_j:=\frac{d_u+d_v}{2\sqrt{d_u{d}_v}},b_j:=1.$$

We have, by Corollary 1,

$$1\le \frac{a_j}{b_j}\le \frac{\Delta +\delta }{2\sqrt{\Delta \delta }}.$$

Thus, Corollary 2 gives

$$\begin{array}{cc}\hfill \left(\sum _{uv\in E\left(G\right)}1\right)\left(\sum _{uv\in E\left(G\right)}\frac{{(d_u+d_v)}^2}{4d_u{d}_v}\right)& \le \frac{1}{4}{\left(\sqrt{\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}}+\sqrt{\frac{2\sqrt{\Delta \delta }}{\Delta +\delta }}\right)}^2{\left(\sum _{uv\in E\left(G\right)}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\right)}^2\hfill \\ & =\frac{1}{4}{\left(\frac{{\left(\sqrt{\Delta }+\sqrt{\delta }\right)}^2}{\sqrt{2\sqrt{\Delta \delta }(\Delta +\delta )}}\right)}^{2}AG{\left(G\right)}^2.\hfill \end{array}$$

Because

$$\begin{array}{cc}\hfill \sum _{uv\in E\left(G\right)}1=m,\sum _{uv\in E\left(G\right)}\frac{{(d_u+d_v)}^2}{4d_u{d}_v}& =\frac{1}{4}\sum _{uv\in E\left(G\right)}\frac{d_u^2+d_v^2}{d_u{d}_v}+\sum _{uv\in E\left(G\right)}\frac{1}{2}\hfill \\ & =\frac{1}{4}SDD\left(G\right)+\frac{1}{2}m,\hfill \end{array}$$

we conclude

$$\begin{array}{cc}\hfill \frac{m}{4}\left(SDD\left(G\right)+2m\right)& \le \frac{1}{4}{\left(\frac{{\left(\sqrt{\Delta }+\sqrt{\delta }\right)}^2}{\sqrt{2\sqrt{\Delta \delta }(\Delta +\delta )}}\right)}^{2}AG{\left(G\right)}^2,\hfill \\ \hfill AG\left(G\right)& \ge \frac{\sqrt{2\sqrt{\Delta \delta }(\Delta +\delta )}}{{\left(\sqrt{\Delta }+\sqrt{\delta }\right)}^2}\sqrt{m\left(SDD\left(G\right)+2m\right)}.\hfill \end{array}$$

If the equality in this bound is attained, then Corollary 2 gives

$$1=\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}.$$

Thus, Corollary 1 gives $\Delta =\delta$, and, so, G is regular.

If G is regular, then

$$\begin{array}{cc}& \frac{\sqrt{2\sqrt{\Delta \delta }(\Delta +\delta )}}{{\left(\sqrt{\Delta }+\sqrt{\delta }\right)}^2}\sqrt{m\left(SDD\left(G\right)+2m\right)}=\frac{\sqrt{2\delta 2\delta }}{4\delta }\sqrt{m\left(2m+2m\right)}=m=AG\left(G\right).\hfill \end{array}$$

On the other hand, the Cauchy–Schwarz inequality gives

$$\begin{array}{c}\hfill AG{\left(G\right)}^2={\left(\sum _{uv\in E\left(G\right)}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\right)}^2\le \left(\sum _{uv\in E\left(G\right)}1\right)\left(\sum _{uv\in E\left(G\right)}\frac{{(d_u+d_v)}^2}{4d_u{d}_v}\right).\end{array}$$

Because

$$\begin{array}{cc}\hfill \sum _{uv\in E\left(G\right)}1=m,\sum _{uv\in E\left(G\right)}\frac{{(d_u+d_v)}^2}{4d_u{d}_v}& =\frac{1}{4}SDD\left(G\right)+\frac{1}{2}m,\hfill \end{array}$$

we conclude

$$\begin{array}{c}\hfill AG{\left(G\right)}^2\le \frac{m}{4}\left(SDD\left(G\right)+2m\right).\end{array}$$

If G is regular or biregular, then

$$\begin{array}{cc}\hfill \frac{1}{2}\sqrt{m\left(SDD\left(G\right)+2m\right)}& =\frac{1}{2}\sqrt{m\left(\left(\frac{\Delta }{\delta }+\frac{\delta }{\Delta }\right)m+2m\right)}\hfill \\ & =\frac{m}{2}\sqrt{\frac{{\Delta }^2+{\delta }^2+2\Delta \delta }{\Delta \delta }}=\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}m=AG\left(G\right).\hfill \end{array}$$

□

The atom-bond connectivity index [33] is

$${\displaystyle ABC\left(G\right)=\sum _{uv\in E\left(G\right)}\sqrt{\frac{d_u+d_v-2}{d_u{d}_v}}.}$$

Furtula et al. [34] made a generalization of $ABC$ index, defined as

$${\displaystyle AB{C}_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{\left(\frac{d_u+d_v-2}{d_u{d}_v}\right)}^{\alpha },\mathrm{where}\alpha \in \mathbb{R}.}$$

They showed that the $AB{C}_{\alpha }$ defined in this way, for $\alpha =-3$, has better predictive power than the original $ABC$ index.

The three following results relate the arithmetic-geometric and the general atom-bond connectivity indices.

Theorem 4.

Let G be a graph with maximum degree Δ and without isolated edges, and $\alpha >0$. Then

$$AG\left(G\right)\le \frac{{(\Delta -1)}^{\alpha }(\Delta +1)}{2{\Delta }^{\alpha +\frac{1}{2}}}AB{C}_{-\alpha }\left(G\right),$$

and the equality in the inequality holds if and only if G is a union of stars $S_{\Delta +1}$.

Proof. 

Note that $(d_u,d_v)\ne (1,1)$, since G does not have isolated edges, hence $\Delta \ge 2$. First of all, we are going to compute the minimum value of

$$W(x,y)={\left(\frac{x+y-2}{xy}\right)}^{-\alpha }\frac{2\sqrt{xy}}{x+y}=2{(x+y-2)}^{-\alpha }{(x+y)}^{-1}{x}^{\alpha +\frac{1}{2}}{y}^{\alpha +\frac{1}{2}}$$

on $\{1\le x\le y,2\le y\le \Delta \}$. We have

$$\begin{array}{cc}\hfill \frac{\partial W}{\partial x}& =2y^{\alpha +\frac{1}{2}}\left[-\alpha {(x+y-2)}^{-\alpha -1}{(x+y)}^{-1}{x}^{\alpha +\frac{1}{2}}-{(x+y-2)}^{-\alpha }{(x+y)}^{-2}{x}^{\alpha +\frac{1}{2}}\right.\hfill \\ & \left.+\left(\alpha +\frac{1}{2}\right){(x+y-2)}^{-\alpha }{(x+y)}^{-1}{x}^{\alpha -\frac{1}{2}}\right]\hfill \\ & =2y^{\alpha +\frac{1}{2}}{x}^{\alpha -\frac{1}{2}}{(x+y-2)}^{-\alpha -1}{(x+y)}^{-2}\left[-\alpha (x+y)x-(x+y-2)x\right.\hfill \\ & \left.+\left(\alpha +\frac{1}{2}\right)(x+y-2)(x+y)\right]\hfill \\ & =2y^{\alpha +\frac{1}{2}}{x}^{\alpha -\frac{1}{2}}{(x+y-2)}^{-\alpha -1}{(x+y)}^{-2}\left[\alpha (x+y)(x+y-2-x)\right.\hfill \\ & \left.+(x+y-2)\left(\frac{x+y}{2}-x\right)\right]\hfill \\ & =2y^{\alpha +\frac{1}{2}}{x}^{\alpha -\frac{1}{2}}{(x+y-2)}^{-\alpha -1}{(x+y)}^{-2}\left[\alpha (x+y)(y-2)+\frac{1}{2}(x+y-2)(y-x)\right]\ge 0,\hfill \end{array}$$

so, $W(x,y)$ is strictly increasing on $x\in [1,y]$ for every fixed $y\ge 2$ and, so, $W(1,y)\le W(x,y)$. Consider

$$a\left(y\right)=W(1,y)=2{(y-1)}^{-\alpha }{(1+y)}^{-1}{y}^{\alpha +1/2}.$$

Subsequently,

$$\begin{array}{cc}\hfill a^{\prime }\left(y\right)& =2\left[-\alpha {(y-1)}^{-\alpha -1}{(y+1)}^{-1}{y}^{\alpha +\frac{1}{2}}-{(y-1)}^{-\alpha }{(y+1)}^{-2}{y}^{\alpha +\frac{1}{2}}\right.\hfill \\ & \left.+\left(\alpha +\frac{1}{2}\right){(y-1)}^{-\alpha }{(y+1)}^{-1}{y}^{\alpha -\frac{1}{2}}\right]\hfill \\ & =2{(y-1)}^{-\alpha -1}{(y+1)}^{-2}{y}^{\alpha -\frac{1}{2}}\left[-\alpha (y+1)y-(y-1)y+\left(\alpha +\frac{1}{2}\right)(y-1)(y+1)\right]\hfill \\ & =2{(y-1)}^{-\alpha -1}{(y+1)}^{-2}{y}^{\alpha -\frac{1}{2}}\left[\alpha (y+1)(y-1-y)+(y-1)\left(\frac{y+1}{2}-y\right)\right]\hfill \\ & =2{(y-1)}^{-\alpha -1}{(y+1)}^{-2}{y}^{\alpha -\frac{1}{2}}\left[-\alpha (y+1)-\frac{1}{2}{(y-1)}^2\right]<0,\hfill \end{array}$$

so, w is strictly decreasing on $y\in [2,\Delta ]$. Thus, we have $a(\Delta )\le a\left(y\right)=W(1,y)\le W(x,y)$ for every $1\le x\le y$, $2\le y\le \Delta$ and the equalities hold if and only if $x=1$ and $y=\Delta$. Therefore,

$$\frac{2{\Delta }^{\alpha +\frac{1}{2}}}{{(\Delta -1)}^{\alpha }(\Delta +1)}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\le {\left(\frac{d_u+d_v-2}{d_u{d}_v}\right)}^{-\alpha }\mathrm{for}\mathrm{every}uv\in E\left(G\right),$$

and the equality is attained if and only if $d_u=1$ and $d_v=\Delta$ or vice versa for each edge $uv\in E\left(G\right)$, i.e., every connected component of G is a star $S_{\Delta +1}$. □

Remark 2.

The argument in the proof of Theorem 4 (with the same hypotheses) allows for obtaining the following lower bound of $AG$, but it is elementary:

$$\frac{{(2\Delta -2)}^{\alpha }}{{\Delta }^{2\alpha }}AB{C}_{-\alpha }\left(G\right)\le AG\left(G\right),$$

and the equality in the inequality holds if and only if G is regular.

We can improve Theorem 4 when $\delta \ge 2$.

Theorem 5.

Let G be a graph with maximum degree Δ and minimum degree $\delta \ge 2$, and $\alpha >0$. Afterwards,

$$AG\left(G\right)\le max\left\{\frac{{(2\delta -2)}^{\alpha }}{{\delta }^{2\alpha }},\frac{{(\Delta +\delta -2)}^{\alpha }(\Delta +\delta )}{2{(\Delta \delta )}^{\alpha +\frac{1}{2}}}\right\}AB{C}_{-\alpha }\left(G\right).$$

The equality in the inequality holds if G is regular.

Proof. 

Consider the notation in the proof of Theorem 4, and the function

$$\begin{array}{cc}\hfill c\left(y\right)& =W(\delta ,y)=2{\delta }^{\alpha +\frac{1}{2}}{(y+\delta -2)}^{-\alpha }{(y+\delta )}^{-1}{y}^{\alpha +\frac{1}{2}},\hfill \end{array}$$

with $2\le \delta \le y\le \Delta$. The argument in the proof of Theorem 4 gives that $c\left(y\right)=W(\delta ,y)\le W(x,y)$ for every $\delta \le x\le y\le \Delta$.

We have

$$\begin{array}{cc}\hfill c^{\prime }\left(y\right)& =2{\delta }^{\alpha +\frac{1}{2}}\left[-\alpha {(y+\delta -2)}^{-\alpha -1}{(y+\delta )}^{-1}{y}^{\alpha +\frac{1}{2}}-{(y+\delta -2)}^{-\alpha }{(y+\delta )}^{-2}{y}^{\alpha +\frac{1}{2}}\right.\hfill \\ & +\left.\left(\alpha +\frac{1}{2}\right){(y+\delta -2)}^{-\alpha }{(y+\delta )}^{-1}{y}^{\alpha -\frac{1}{2}}\right]\hfill \\ & =2{\delta }^{\alpha +\frac{1}{2}}{(y+\delta -2)}^{-\alpha -1}{(y+\delta )}^{-2}{y}^{\alpha -\frac{1}{2}}[-\alpha (y+\delta )y-(y+\delta -2)y\hfill \\ & \left.+\left(\alpha +\frac{1}{2}\right)(y+\delta -2)(y+\delta )\right]\hfill \\ & =2{\delta }^{\alpha +\frac{1}{2}}{(y+\delta -2)}^{-\alpha -1}{(y+\delta )}^{-2}{y}^{\alpha -\frac{1}{2}}[\alpha (y+\delta )(-y+y+\delta -2)\hfill \\ & \left.+(y+\delta -2)\left(-y+\frac{y+\delta }{2}\right)\right]\hfill \\ & =2{\delta }^{\alpha +\frac{1}{2}}{(y+\delta -2)}^{-\alpha -1}{(y+\delta )}^{-2}{y}^{\alpha -\frac{1}{2}}\left[\alpha (y+\delta )(\delta -2)-\frac{1}{2}(y+\delta -2)(y-\delta )\right].\hfill \end{array}$$

Consider first the case $\delta =2$. We have

$$\begin{array}{cc}\hfill c^{\prime }\left(y\right)& =2{\delta }^{\alpha +\frac{1}{2}}{(y+\delta -2)}^{-\alpha -1}{(y+\delta )}^{-2}{y}^{\alpha -\frac{1}{2}}\left[\alpha (y+\delta )(\delta -2)-\frac{1}{2}(y+\delta -2)(y-\delta )\right]\hfill \\ & =-{\delta }^{\alpha +\frac{1}{2}}{(y+\delta -2)}^{-\alpha }{(y+\delta )}^{-2}{y}^{\alpha -\frac{1}{2}}(y-\delta )\le 0.\hfill \end{array}$$

Thus, ${min}_{y\in [\delta ,\Delta ]}c\left(y\right)=c(\Delta )$.

Now, assume that $\delta \ge 3$. Let us consider the second degree polynomial

$$P\left(y\right)=\alpha (y+\delta )(\delta -2)-\frac{1}{2}(y+\delta -2)(y-\delta ).$$

Because

$$P\left(0\right)=\alpha \delta (\delta -2)-\frac{1}{2}(\delta -2)(-\delta )=\left(\alpha +\frac{1}{2}\right)\delta (\delta -2)\ge 0,$$

there exists at least a non-positive zero of P. Hence, there exists at most a zero of P in the interval $[\delta ,\Delta ]$. Additionally, $P\left(\delta \right)=2\delta (\delta -2)>0$.

Thus, there exists, at most, a zero of $c^{\prime }$ in the interval $[\delta ,\Delta ]$ and $c^{\prime }\left(\delta \right)>0$. Consequently,

$$\underset{y\in [\delta ,\Delta ]}{min}c\left(y\right)=min\left\{c\left(\delta \right),c(\Delta )\right\},$$

for every $\delta \ge 3$ and, so, for every $\delta \ge 2$. Therefore,

$$\begin{array}{cc}\hfill W(x,y)& \ge W(\delta ,y)\ge c\left(y\right)\ge min\left\{c\left(\delta \right),c(\Delta )\right\}\hfill \\ & =min\left\{{\delta }^{2\alpha }{(2\delta -2)}^{-\alpha },2{(\Delta \delta )}^{\alpha +\frac{1}{2}}{(\Delta +\delta -2)}^{-\alpha }{(\Delta +\delta )}^{-1}\right\},\hfill \end{array}$$

for every $\delta \le x\le y\le \Delta$ and, by symmetry, for every $\delta \le x,y\le \Delta$. Consequently,

$$min\left\{\frac{{\delta }^{2\alpha }}{{(2\delta -2)}^{\alpha }},\frac{2{(\Delta \delta )}^{\alpha +\frac{1}{2}}}{{(\Delta +\delta -2)}^{\alpha }(\Delta +\delta )}\right\}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\le {\left(\frac{d_u+d_v-2}{d_u{d}_v}\right)}^{-\alpha }$$

for every $uv\in E\left(G\right)$, and

$$AG\left(G\right)\le max\left\{\frac{{(2\delta -2)}^{\alpha }}{{\delta }^{2\alpha }},\frac{{(\Delta +\delta -2)}^{\alpha }(\Delta +\delta )}{2{(\Delta \delta )}^{\alpha +\frac{1}{2}}}\right\}AB{C}_{-\alpha }\left(G\right).$$

If G is regular, thus $\Delta =\delta$ and

$$\begin{array}{cc}& max\left\{\frac{{(2\delta -2)}^{\alpha }}{{\delta }^{2\alpha }},\frac{{(\Delta +\delta -2)}^{\alpha }(\Delta +\delta )}{2{(\Delta \delta )}^{\alpha +\frac{1}{2}}}\right\}AB{C}_{-\alpha }\left(G\right)\hfill \\ & max\left\{\frac{{(2\delta -2)}^{\alpha }}{{\delta }^{2\alpha }},\frac{{(2\delta -2)}^{\alpha }2\delta }{2{\delta }^{2\alpha +1}}\right\}\frac{{\delta }^{2\alpha }}{{(2\delta -2)}^{\alpha }}m=m=AG\left(G\right),\hfill \end{array}$$

and the equality in the inequality holds. □

Now, we relate the arithmetic-geometric and general atom-bond connectivity indices with parameter greater than or equal to $1/2$.

Theorem 6.

If G is a graph with minimum degree $\delta \ge 2$ and maximum degree Δ, and $\beta \ge 1/2$, then

$$AG\left(G\right)\le {\left(\frac{{\Delta }^2}{2\Delta -2}\right)}^{\beta }AB{C}_{\beta }\left(G\right),$$

and the equality in the inequality is attained if and only if G is regular.

Proof. 

Define $\alpha =-\beta \le -1/2$. As in the proof of Theorem 4, let us consider

$$W(x,y)={\left(\frac{x+y-2}{xy}\right)}^{-\alpha }\frac{2\sqrt{xy}}{x+y}=2{(x+y-2)}^{-\alpha }{(x+y)}^{-1}{x}^{\alpha +\frac{1}{2}}{y}^{\alpha +\frac{1}{2}}$$

on $\{2\le \delta \le x\le y\le \Delta \}$. We have

$$\begin{array}{cc}\hfill \frac{\partial W}{\partial x}& =2y^{\alpha +\frac{1}{2}}{x}^{\alpha -\frac{1}{2}}{(x+y-2)}^{-\alpha -1}{(x+y)}^{-2}\left[\alpha (x+y)(y-2)+\frac{1}{2}(x+y-2)(y-x)\right]\hfill \\ & \le 2y^{\alpha +\frac{1}{2}}{x}^{\alpha -\frac{1}{2}}{(x+y-2)}^{-\alpha -1}{(x+y)}^{-2}\left[-\frac{1}{2}(x+y)(y-2)+\frac{1}{2}(x+y-2)(y-x)\right]\hfill \\ & =2y^{\alpha +\frac{1}{2}}{x}^{\alpha -\frac{1}{2}}{(x+y-2)}^{-\alpha -1}{(x+y)}^{-2}\left[-\frac{1}{2}(x-2)-(y-x)\right]\le 0,\hfill \end{array}$$

on $\{\delta \le x\le y\le \Delta \}$. Hence, $W(y,y)\le W(x,y)$ when $\delta \le x\le y\le \Delta$. We define now

$$\begin{array}{cc}\hfill b\left(y\right)& =W(y,y)=2^{-\alpha }{\left(\frac{y-1}{y^2}\right)}^{-\alpha }.\hfill \end{array}$$

Subsequently,

$$\begin{array}{cc}\hfill b^{\prime }\left(y\right)& =\alpha 2^{-\alpha }{\left(\frac{y-1}{y^2}\right)}^{-\alpha -1}\frac{y-2}{y^3}\le 0.\hfill \end{array}$$

Consequently, b is a strictly decreasing function on $\delta \le y\le \Delta$, and

$$W(\Delta ,\Delta )=b(\Delta )\le b\left(y\right)=W(y,y)\le W(x,y)$$

when $\delta \le x\le y\le \Delta$. Hence, by symmetry,

$${\left(\frac{2\Delta -2}{{\Delta }^2}\right)}^{\beta }=W(\Delta ,\Delta )\le W(x,y)$$

for each $\delta \le x,y\le \Delta$, and

$${\left(\frac{2\Delta -2}{{\Delta }^2}\right)}^{\beta }\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\le {\left(\frac{d_u+d_v-2}{d_u{d}_v}\right)}^{\beta }\mathrm{for}\mathrm{every}uv\in E\left(G\right),$$

$${\left(\frac{2\Delta -2}{{\Delta }^2}\right)}^{\beta }AG\left(G\right)\le AB{C}_{\beta }\left(G\right).$$

□

Remark 3.

The arguments in the proof of Theorem 6 (with the same hypotheses) allow to obtain the following lower bound of $AG$, but it is elementary:

$${\left(\frac{{\delta }^2}{2\delta -2}\right)}^{\beta }AB{C}_{\beta }\left(G\right)\le AG\left(G\right),$$

and the equality in the inequality holds if and only if G is regular.

3. General Bounds on the $\mathit{AG}$ Index

In this section we obtain additional lower bounds of $AG$ improving the lower bound in (1), which do not involve other topological indices. The two following bounds involve m and the minimum degree.

Theorem 7.

If G is a graph with m edges, minimum degree δ, maximum degree $\delta +1$, and α is the number of edges $uv$ with $d_u\ne d_v$, then α is an even integer and

$$AG\left(G\right)=m+\alpha \left(\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}-1\right).$$

Proof. 

Let $D=\left\{uv\in E\left(G\right):d_u\ne d_v\right\}$, then $\alpha$ is the cardinality of D. Because $\delta$ is the minimum degree of G and $\delta +1$ is its maximum degree, if $uv\in D$, then $d_u=\delta$ and $d_v=\delta +1$ or vice versa and, therefore,

$$\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}=\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}.$$

If $uv\in D^c$, then $d_u=d_v=\delta$ or $d_u=d_v=\delta +1$, and therefore

$$\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}=1.$$

Because there are exactly $\alpha$ edges in D and $m-\alpha$ edges in $D^c$, we have

$$\begin{array}{cc}\hfill AG\left(G\right)& =\sum _{uv\in E\left(G\right)}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\hfill \\ & =\sum _{uv\in D^c}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}+\sum _{uv\in D}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\hfill \\ & =\sum _{uv\in D^c}1+\sum _{uv\in D}\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}\hfill \\ & =m-\alpha +\alpha \frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}.\hfill \end{array}$$

Assume, for contradiction, that $\alpha$ is an odd integer.

Let $G_1$ be a subgraph of G induced by the $n_1$ vertices with degree $\delta$ in $V\left(G\right)$, and denote by $m_1$ the number of edges of $G_1$. Handshaking Lemma gives $n_1\delta -\alpha =2m_1$. Because $\alpha$ is an odd integer, $\delta$ is also an odd integer. Thus, $\delta +1$ is an even integer.

Let $G_2$ be a subgraph of G that is induced by the $n_2$ vertices with degree $\delta +1$ in $V\left(G\right)$, and denote, by $m_2$, the number of edges of $G_2$. Handshaking Lemma gives $n_2(\delta +1)-\alpha =2m_2$, a contradiction, since $\alpha$ is an odd integer and $\delta +1$ is an even integer.

Thus, we conclude that $\alpha$ is an even integer. □

Theorem 8.

If G is a connected graph with m edges, minimum degree δ and maximum degree $\delta +1$, then

$$AG\left(G\right)\ge m+\frac{2\delta +1}{\sqrt{\delta (\delta +1)}}-2,$$

and the equality is attained for each δ.

Proof. 

Let $\alpha$ be the number of edges $uv\in E\left(G\right)$ with $d_u\ne d_v$. Theorem 7 gives that $\alpha$ is an even integer. Because G is a connected graph, we have $\alpha \ne 0$ and so, $\alpha \ge 2$. Since

$$\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}>1$$

and $\alpha \ge 2$, Theorem 7 gives

$$\begin{array}{cc}\hfill AG\left(G\right)& =m+\alpha \left(\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}-1\right)\hfill \\ & \ge m+2\left(\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}-1\right)\hfill \\ & =m-2+\frac{2\delta +1}{\sqrt{\delta (\delta +1)}}.\hfill \end{array}$$

Given a fixed $\delta$, let us consider the complete graphs $K_{\delta +1}$ and $K_{\delta +2}$ with $\delta +1$ and $\delta +2$ vertices, respectively. Fix $u_1,u_2\in V\left(K_{\delta +1}\right)$ and $v_1,v_2\in V\left(K_{\delta +2}\right)$, and denote by $K_{\delta +1}^{\prime }$ and $K_{\delta +2}^{\prime }$ the graphs obtained from $K_{\delta +1}$ and $K_{\delta +2}$ by deleting the edges $u_1{u}_2$ and $v_1{v}_2$, respectively. Let ${\mathrm{\Gamma }}_{\delta }$ be the graph with $V\left({\mathrm{\Gamma }}_{\delta }\right)=V\left(K_{\delta +1}^{\prime }\right)\cup V\left(K_{\delta +2}^{\prime }\right)$ and $E\left({\mathrm{\Gamma }}_{\delta }\right)=E\left(K_{\delta +1}^{\prime }\right)\cup E\left(K_{\delta +2}^{\prime }\right)\cup \left\{u_1{v}_1\right\}\cup \left\{u_2{v}_2\right\}$. Thus, ${\mathrm{\Gamma }}_{\delta }$ has ${\delta }^2+2\delta +1$ edges, minimum degree $\delta$, maximum degree $\delta +1$, and Theorem 7 give

$$AG\left({\mathrm{\Gamma }}_{\delta }\right)={\delta }^2+2\delta -1+\frac{2\delta +1}{\sqrt{\delta (\delta +1)}}.$$

Hence, the equality is attained for each $\delta$. □

A chemical graph is a graph with $\Delta \le 4$.

Corollary 3.

If G is a connected chemical graph with m edges, minimum degree δ, and maximum degree $\delta +1$, then Then

$$AG\left(G\right)\ge m-2+\frac{7\sqrt{3}}{6}.$$

Furthermore, the equality in the bound is attained.

Proof. 

Because G is a chemical graph, we have $1\le \delta \le 3$. Since

$$\underset{1\le \delta \le 3}{min}\frac{2\delta +1}{\sqrt{\delta (\delta +1)}}=min\left\{\frac{3}{\sqrt{2}},\frac{5}{\sqrt{6}},\frac{7}{\sqrt{12}}\right\}=\frac{7\sqrt{3}}{6},$$

Theorem 8 gives the desired inequality.

The graph ${\mathrm{\Gamma }}_3$ in the proof of Theorem 8 provides that the equality is attained. □

We need some definitions. Let G be a graph with maximum degree $\Delta$ and minimum degree $\delta <\Delta -1$. We denote, by ${\alpha }_0,{\alpha }_1,{\alpha }_2$, the cardinality of the subsets of edges

$$\begin{array}{cc}\hfill A_0& =\{uv\in E\left(G\right):d_u=\delta ,d_v=\Delta \},\hfill \\ \hfill A_1& =\{uv\in E\left(G\right):d_u=\delta ,\delta <d_v<\Delta \},\hfill \\ \hfill A_2& =\{uv\in E\left(G\right):d_u=\Delta ,\delta <d_v<\Delta \},\hfill \end{array}$$

respectively.

We need the following result ([28], Theorem 5).

Lemma 4.

If G is a graph with m edges, maximum degree Δ, and minimum degree $\delta <\Delta -1$, then

$$AG\left(G\right)\le \frac{\Delta +\delta }{2\sqrt{\Delta \delta }}m-{\alpha }_1\left(\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}-\frac{\delta +\Delta -1}{2\sqrt{\delta (\Delta -1)}}\right)-{\alpha }_2\left(\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}-\frac{\Delta +\delta +1}{2\sqrt{\Delta (\delta +1)}}\right),$$

$$AG\left(G\right)\ge m+{\alpha }_0\left(\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}-1\right)+{\alpha }_1\left(\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}-1\right)+{\alpha }_2\left(\frac{2\Delta -1}{2\sqrt{\Delta (\Delta -1)}}-1\right).$$

We are going to use Lemma 4 to obtain the following lower bound of $AG$ involving m and the minimum and maximum degree.

Theorem 9.

Let G be a connected graph with m edges, maximum degree Δ and minimum degree $\delta <\Delta -1$. Subsequently,

$$AG\left(G\right)\ge m+min\left\{\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}+\frac{2\Delta -1}{2\sqrt{\Delta (\Delta -1)}}-2,\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}-1\right\}.$$

The equality in the bound is attained.

Proof.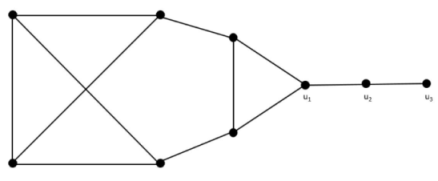 

Because G is connected, we have two possibilities: $A_0\ne \varnothing$, or $A_1\ne \varnothing$ and $A_2\ne \varnothing$.

In the first case, ${\alpha }_0\ge 1$ and, since

$$\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}\ge 1,$$

Lemma 4 gives

$$\begin{array}{cc}\hfill AG\left(G\right)& \ge m+{\alpha }_0\left(\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}-1\right)+{\alpha }_1\left(\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}-1\right)+{\alpha }_2\left(\frac{2\Delta -1}{2\sqrt{\Delta (\Delta -1)}}-1\right)\hfill \\ & \ge m+\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}-1.\hfill \end{array}$$

In the second case, ${\alpha }_1,{\alpha }_2\ge 1$ and Lemma 4 give

$$\begin{array}{cc}\hfill AG\left(G\right)& \ge m+{\alpha }_0\left(\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}-1\right)+{\alpha }_1\left(\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}-1\right)+{\alpha }_2\left(\frac{2\Delta -1}{2\sqrt{\Delta (\Delta -1)}}-1\right)\hfill \\ & \ge m+\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}+\frac{2\Delta -1}{2\sqrt{\Delta (\Delta -1)}}-2.\hfill \end{array}$$

Let G be the graph in the figure.

We have $m=12$, $\Delta =3$, $\delta =1$, $A_0=\varnothing$, ${\alpha }_0=0$, $A_1=\left\{u_2{u}_3\right\}$, ${\alpha }_1=1$, $A_2=\left\{u_1{u}_2\right\}$ and ${\alpha }_2=1$. Additionally, if $uv\notin A_0\cup A_1\cup A_2$, then $d_u=d_v$. Thus,

$$\begin{array}{cc}\hfill AG\left(G\right)& =\sum _{uv\in E\left(G\right)\backslash A_0\cup A_1\cup A_2}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}+\sum _{uv\in A_0}\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}+\sum _{uv\in A_1}\frac{\delta +d_v}{2\sqrt{\delta d_v}}+\sum _{uv\in A_2}\frac{\Delta +d_v}{2\sqrt{\Delta d_v}}\hfill \\ & =10+\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}+\frac{2\Delta -1}{2\sqrt{\Delta (\Delta -1)}}=10+\frac{3}{2\sqrt{2}}+\frac{5}{2\sqrt{6}}\approx 12.0813\hfill \end{array}$$

The lower bound is

$$\begin{array}{cc}\hfill m+& min\left\{\frac{2\delta +1}{2\sqrt{\delta (\delta +1)}}+\frac{2\Delta -1}{2\sqrt{\Delta (\Delta -1)}}-2,\frac{\Delta +\delta }{2\sqrt{\Delta \delta }}-1\right\}\hfill \\ \hfill 12+& min\left\{\frac{3}{2\sqrt{2}}+\frac{5}{2\sqrt{6}}-2,\frac{2}{\sqrt{3}}-1\right\}\hfill \\ & \approx 12+min\{0.0813,0.1547\}=12.0813\hfill \end{array}$$

and so, this graph attains the equality in the inequality. □

4. Conclusions

Topological indices have become a useful tool for the study of theoretical and practical problems in different areas of science. An important line of research that is associated with topological indices is to find optimal bounds and relations between known topological indices. In particular, to obtain bounds for the topological indices that are associated with invariant parameters of a graph.

We have the following nine results for the arithmetic-geometric index $AG$:

• An upper and lower bound of $AG$ based on the first and second variable Zagreb indices (Theorem 1).
• An upper bound of $AG$ that is based on the second variable Zagreb index $M_2^a$ (Theorem 2).
• An upper and lower bound of $AG$ based on $SDD$ (Theorem 3).
• An upper bound of $AG$ based on the general atom-bond connectivity index $AB{C}_a$ (Theorem 4).
• Another upper bound of $AG$ based on the general atom-bond connectivity index $AB{C}_a$ for graphs with minimum degree $\delta \ge 2$ (Theorem 5).
• A further upper bound of $AG$ based on the general atom-bond connectivity index $AB{C}_a$ for graphs with minimum degree $\delta \ge 2$ (Theorem 6).
• An exact formula of $AG$ based on the number of edges m and the minimum degree $\delta$ if the maximum degree is $\delta +1$ (Theorem 7).
• A lower bound of $AG$ based on the number of edges m and the minimum degree $\delta$ if the maximum degree is $\delta +1$ (Theorem 8). We provide a family of graphs for which the equality is attained.
• A lower bound of $AG$ that is based on the number of edges m, the minimum degree $\delta$, and the maximum degree $\Delta$ (Theorem 9). We provide a graph for which the equality is attained.

Because the arithmetic-geometric index is useful from a practical point of view, to know extremal graphs for each bound involving this index allows for detecting chemical compounds that could satisfy desirable properties. Hence, these extremal graphs should correspond to molecules with a extremal value of a desired property correlated well with this index.

In the case of centrality indices, the generalization of degree has turned out to be a useful approach: the role of a more interconnected node can differ from a node that is connected to nodes having a lower degree [35]. We would like to purpose as a direction for future research to study similar problems for centrality indices.