Construction of an S-Box Based on Chaotic and Bent Functions

Abstract

An S-box is the most important part of a symmetric encryption algorithm. Various schemes are put forward by using chaos theory. In this paper, a construction method of S-boxes with good cryptographic properties is proposed. The output of an S-box can be regarded as a group of Boolean functions. Therefore, we can use the different properties of chaos and Bent functions to generate a random Bent function with a high nonlinearity. By constructing a set of Bent functions as the output of an S-box, we can create an S-box with good cryptological properties. The nonlinearity, differential uniformity, strict avalanche criterion and the independence criterion of output bits are then analyzed and tested. A security analysis shows that the proposed S-box has excellent cryptographic properties.

1. Introduction

With the rapid development of modern information technology, the popularity of computer and communication networks is more and more extensive. The problem of information security is becoming more and more prominent and is gradually becoming a problem that people cannot ignore. Information encryption technology plays an important role in modern information security communication, as a powerful weapon to protect the security of information. An S-box [1,2,3,4,5,6] is the only nonlinear component in many block cipher algorithms, which has the effect of scrambling the whole block cipher algorithm. Therefore, its cipher strength determines the security strength of the whole block cipher algorithm.

In recent years, many achievements have been made in the construction of chaotic S-boxes [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. In 2018, Eesa et al. [31] proposed a new method to construct a strong cryptographic bijective S-box based on the complex dynamics of a new hyperchaotic system. Lambić [32] proposed an S-box design method based on an improved one-dimensional discrete chaotic map, which took advantage of the special case of Lambić’s chaotic map based on a permutation synthesis. In 2019, Zahid et al. [33] proposed an innovative technique to construct an S-box using cubic fractional transformation (CFT). Lu et al. [34] proposed a novel S-box design algorithm based on a new compound chaotic system, which was constructed by a concatenated Tent and Logistic chaotic system. In 2020, Chew et al. [35] proposed an S-box structure based on a linear fractional transformation and permutation function. Wang et al. [36] proposed a genetic algorithm for constructing biological S-boxes with a high nonlinearity. The main idea was to construct an S-box by combining the characteristics of a chaotic system and a swarm intelligence algorithm. Han et al. [37] superimposed the two chaotic maps Tent and Henon and introduced the idea of image scrambling into the design of the S-box, which enhanced the randomness of the key sequence of the ZUC stream cipher algorithm.

This paper presents an effective method to obtain chaotic S-boxes with important cryptographic properties. The principal innovation of this paper is to use a chaotic function to generate a chaotic Bent function [38,39,40,41]. This method considers that an S-box can be regarded as a group of Boolean functions. Therefore, we will design a finite number of random Bent functions by using the random distribution characteristics of logistic mapping. The output of several Bent functions then composes the S-box. In our research, the nonlinearity, differential uniformity, strict avalanche criterion and the independence criterion of output bits are analyzed and tested. A security analysis shows that the proposed S-box has important cryptographic properties.

Outline: in the second part, the definition and construction of the Bent function and the logistic discrete chaotic system are introduced. The third part introduces the construction method of the S-box based on the Bent function and logistic and the balancing method. The fourth part compares and analyzes the cryptographic characteristics of different S-box construction methods. Finally, in the fifth part, the paper is summarized.

2. Basic Knowledge

2.1. Bent Function

2.1.1. Definition of Boolean Function

Definition 1.

Let $F_2$ be a binary finite field and $n$ be a positive integer and the mapping $f:F_2^n\to F_2$ be a Boolean function.

The algebraic normal form of an n-dimensional Boolean function:

$$\mathrm{y}=f(x_1,x_2,\dots ,x_n)=\mathrm{a}(0)+\mathrm{a}(1)x_1+\dots +\mathrm{a}\left(1,2,\dots ,n\right)x_1{x}_2\dots x_n$$

(1)

If the set of all n-dimensional Boolean functions is recorded as $B_n$, let $x\in F_2^n$. The number of $f(x)=1$ is called the weight of the function $f$, which is recorded as $W_H(f)$. If an n-dimensional Boolean function $f$ satisfies $W_H(f)=2^{n-1}$, then the function is said to be balanced.

Let $f,g\in B_n$, the Hamming distance of $f$ and $g$, be defined as:

$$d(f,g)=\left|\left\{x\in F_2^n|f\left(x\right)\ne \mathrm{g}\left(x\right)\right\}\right|$$

(2)

where $\left|A\right|$ represents the number of elements in set $A$.

It is easy to find: $d(f,g)=W_H(f-g)$.

2.1.2. Definition of a Bent Function

Let $f\in B_n$, the Fourier transform of function ${(-1)}^{f(x)}$, be:

$$F\left(\lambda \right)=\frac{1}{2^{n/2}}{\displaystyle \sum }_{x\in F_2^n}{\left(-1\right)}^{f\left(x\right)\oplus \lambda ,x}$$

(3)

where $\lambda ,x\in F_2^n$, the inner product of $\lambda ,x$, is defined as $⟨\lambda ,x⟩={\lambda }_1{x}_1\oplus \dots \oplus {\lambda }_n{x}_n$.

Definition 2.

Let $f\in B_n$, if $\left|F(\lambda )\right|=1$ for any $\lambda \in F_2^n$, then $f(x)$ is called a Bent function.

Let $f\in B_n$, then the Walsh transformation of $f$ is:

$$W_f\left(\omega \right)={\displaystyle \sum }_{x\in F_2^n}{\left(-1\right)}^{f\left(x\right)\oplus \omega ,x}$$

(4)

According to Definition 2 and Formula (4), if $f$ satisfies $\left|W_f(\omega )\right|=2^{n/2}$, then $f$ is a Bent function.

2.1.3. Maiorana MC Farland Type Multi Output Bent Function

The Maiorana MC Farland type Bent function is one of the most well-known basic construction types of Bent function. Rothaus [42], Maiorana, MC Farland [43] and Dillon [44] have made in-depth studies on the construction of this type of Bent function.

If $n,m\ge 1$ are positive integers, then $F:F_2^n\to F_2^m$ functions can be expressed as a set of Boolean functions, $F=(f_1,f_2,\dots ,f_m),f_i\in B_n,i=1,2,\dots ,m$ and function $F$ can be called multiple output Boolean functions, where $f_i,i=1,2,\dots ,m$ is called the coordinate function of $F$.

Definition 3.

If the Boolean function $f:F_2^{n/2}\times F_2^{n/2}\to F_2$ has the form of Formula (5), then $f$ is called the Maiorana MC Farland type Bent function.

$$f\left(x\right)=f(x_1,x_2)=⟨\pi \left(x_1\right),x_2⟩\oplus \mathrm{g}\left(x_1\right)$$

(5)

where $\pi$ is the permutation in $F_2^{n/2}$ and $g(x)$ is the Boolean function in any $F_2^{n/2}$.

$${\pi }_i\left(x\right)=A^{i-1}x,x\in F_2^n,1\le i\le m$$

(6)

where A is a state transition matrix of a $\frac{n}{2}$ level linear feedback shift register.

If all $f_i,i=1,2,\dots ,m$ are Maiorana MC Farland type Bent functions, $F$ is called the Maiorana MC Farland type multi output Bent function.

2.2. Logistic Discrete Chaotic System

The proposed algorithm is based on the Bent functions incorporating chaos. We employed a one-dimensional logistic chaotic map due to its simplicity. The difference iteration equation of the logistic chaotic map is expressed as:

$$x_{n+1}=\mathsf{\mu }{x}_n(1-x_n)$$

(7)

In the formula (7), the initial value $x_0\in (0,1)$ and system parameter is $\mu \in (0,4]$ of the logistic chaotic map. The dynamic behavior of the logistic chaotic map is closely related to the system parameter $\mu$.

The bifurcation characteristics of a logistic chaotic map are shown in Figure 1, which shows the two-dimensional relationship between the numerical distribution of the iterative chaotic sequence and the system parameter $\mu$. Previous studies have shown that when $3.56994568\le \mu \le 4$, most of the Lyapunov exponents of logistic chaotic maps are greater than 0 and they are in a chaotic state. At this time, with the increase of the $\mu$ value, the complexity of its dynamic behavior increases and the logistic map reaches the chaotic state through periodic doubling. In this range, there are several times when the Lyapunov exponent is less than 0. In this case, a period window will appear; that is, the mapping oscillates between certain values. Only when the system parameter $\mu =4$ will the iterative values be mapped to the whole [0,1] interval, which is called the full mapping state.

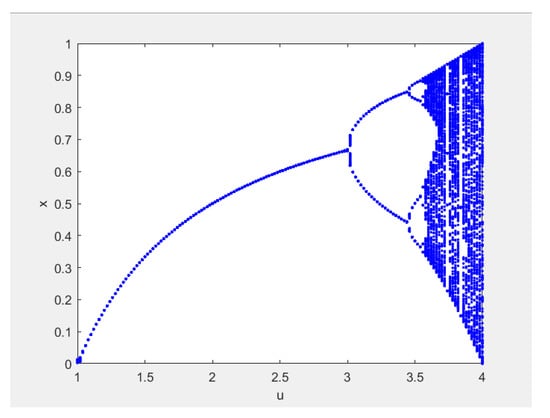
Figure 1. Bifurcation characteristics of a logistic chaotic map.

The two-dimensional phase diagram of a logistic chaotic map is shown in Figure 2. When $\mu =4$, the logistic chaotic map is in the shape of a steel helmet and its iterative values are distributed in the [0,1] interval. As the number of iterations increases, the chaotic trajectory becomes unpredictable and spreads to the whole phase space. Therefore, based on the above characteristics of the logistic chaotic map, we chose $\mu =4$ to construct our discrete chaotic system.

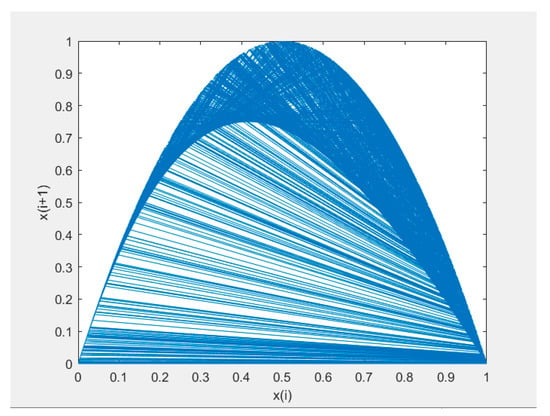
Figure 2. The two-dimensional phase diagram of a logistic chaotic map.

2.2.1. Randomness Test

The randomness of digital chaotic sequences is an important index. The special publication 800-22 test set published by NIST was used to detect the different properties of random sequences. The test set has become the basic standard of sequence randomness testing and has been adopted by many chaotic sequence researchers. In this paper, the threshold quantization method was used to quantify the logistic chaotic system. The NIST randomness test was carried out on the generated digital chaotic sequence and the influence of system parameters and sequence length on the randomness performance was studied so as to provide a theoretical support for the construction of a digital chaotic sequence in an S-box.

Every index of NIST testing was obtained through a certain testing algorithm. Whether the $P\in [0,1]$ value of each index was greater than or equal to 0.01 was taken as the test result. If the $P$ value met the test requirements, the specific value would be displayed. If the p value did not meet the test requirements, it would be displayed as “$*$”. A larger p value indicated a better randomness of the tested sequence. Considering the size of running memory and the speed of running, the sample size was 100 and the test length was 1000 and 10,000 bits, respectively. To avoid contingency, three parameters of the system were selected for the logistic chaotic mapping.

The NIST test results of the logistic chaotic map under three sets of system parameters are shown in Table 1. When $\mu =4$ and $\mu =3.9999$, digital chaotic sequences of 1000 and 10,000 bits could pass ten NIST tests; when $\mu =3.9$, digital chaotic sequences of 1000 bits could pass ten NIST tests while the digital chaotic sequences of 10,000 bits could only pass three NIST tests.

Table 1. NIST test of a logistic chaotic map threshold quantization.

(a) System parameter μ = 4
Test Items Sequence Length	1000	10,000
	p Value	p Value
Approximate Entropy	0.999162	0.991535
Block Frequency	0.964295	0.494392
Cumulative Sums	0.584261	0.664283
FFT	0.121488	0.121488
Frequency	0.122325	0.080519
Linear Complexity	0.984623	0.918243
Longest Run	0.924076	0.678686
Rank	0.69372	0.69372
Runs	0.964295	0.102526
Serial	0.404221	0.00513
(b) System parameter μ = 3.9999
Test Items Sequence Length	1000	10,000
	p Value	p Value
Approximate Entropy	0.896754	0.634582
Block Frequency	0.01265	0.006
Cumulative Sums	0.258134	0.065482
FFT	0.056842	0.026271
Frequency	0.779188	0.051942
Linear Complexity	0.728834	0.435813
Longest Run	0.924076	0.383827
Rank	0.239113	0.073452
Runs	0.289667	0.085587
Serial	0.142273	0.00182
(c) System parameter μ = 3.9
Test Items Sequence Length	1000	10,000
	p Value	p Value
Approximate Entropy	0.261183	0.027351
Block Frequency	0.01265
Cumulative Sums	0.058153
FFT	0.034271
Frequency	0.051942
Linear Complexity	0.139426	0.001453
Longest Run	0.383827	0.085587
Rank	0.068134
Runs	0.289667
Serial	0.037261

A NIST test showed that the one-dimensional discrete chaotic map logistic could achieve a better quantization effect when it was close to the full map and its random performance gradually decreased with the decrease of system parameters and the increase of the sequence length. Therefore, this paper chose $\mu =4$ to construct a logistic discrete chaotic system, which could meet the requirement of the randomness of a digital sequence.

3. Construction of an S-Box Based on a Bent Function and a Logistic Chaotic System

3.1. The Construction of a Multi Output Bent Function Based on a Logistic Chaotic System

The main idea of this method was to construct a pseudo-random sequence generator by using the advantages of logistic mapping such as a high complexity, large parameter space and sensitivity to initial values. A large number of pseudo-random sequences with a good performance and great difference could be obtained by slightly changing the initial values and parameters. The pseudo-random sequence was quantized into a binary sequence to construct the Maiorana MC Farland type Bent function and then the highly nonlinear S-box was constructed.

The threshold quantization method was used in the selection of the value quantization method of the chaotic sequence. The specific quantization method can be expressed as the chaotic value in the interval (0,0.5) is quantized as 0 and the value in the interval [0.5,1) is quantized as 1. In Section 2.2.1, we tested the digital sequence generated by the threshold quantization method with NIST and the results showed that the sequence generated when $\mu =4$ met the requirement of randomness. The quantized binary sequence was taken as the constants and coefficients of $g(x)$ in Equation (8).

$$g(x_{1,1},x_{1,2},\dots ,x_{1,n})=\mathrm{a}(0)+\mathrm{a}(1)x_{1,1}+\dots +\mathrm{a}\left(1,2,\dots ,n\right)x_{1,1}{x}_{1,2}\dots x_{1,n}.$$

(8)

Based on the Boolean function constructed by a chaotic sequence, eight Bent functions were constructed as the output of an 8 ∗ 8 S-box.

$$f_1\left(x\right)=f_1(x_1,x_2)=⟨\pi \left(x_1\right),x_2⟩\oplus {\mathrm{g}}_1\left(x_1\right)$$

(9)

3.2. Balancing Method

The S-box constructed in Section 3.1 did not meet the balance requirements. Therefore, the S-box needed to be processed.

The first step was to traverse all of the elements in the S-box. All duplicate outputs were found and all elements with the same output except the first element were replaced with 256.

The second step was to store the elements that did not exist in the S-box in the array $B$. $B_i$ was the $i$ element in $B$.

Finally, we filled the elements in array $B$ into the elements containing 256 in turn.

3.3. Construction of Chaotic S-Boxes with a High Nonlinearity

The structure of an S-box module based on an Maiorana MC Farland type Bent function and a discrete chaotic system is shown in Figure 3.

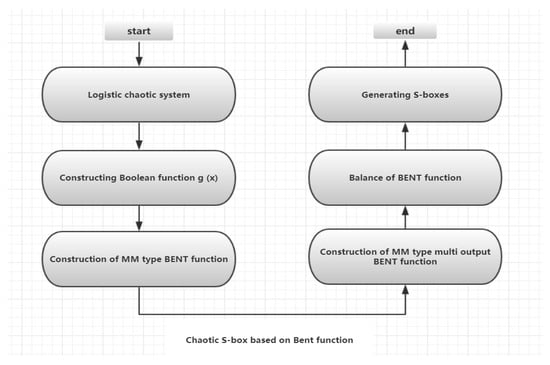
Figure 3. An S-box generation module based on the Bent function and discrete chaotic system.

According to the above method, the S-box generated based on a logistic chaotic system and a Bent function output is shown in Table 2. When the input was 00101000, the first four bits 0010 were 2 and the last four bits 1000 were 8. The corresponding output was the second row and the eighth column in the Table. The output data 1E were converted into the 8-bit binary number 00011110.

Table 2. The chaotic S-box based on a Bent function.

No.	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	98	34	93	C	8C	DF	F6	91	EC	35	F0	A8	74	DC	A2	B8
1	87	63	C6	12	65	DB	B2	A5	C4	11	32	3D	7D	68	D1	2A
2	CC	2D	9B	B6	16	6C	D7	AC	1E	43	A0	55	31	25	C8	C7
3	7F	1F	E0	14	99	FC	BE	2C	75	76	53	45	B7	C2	9E	0F
4	9C	06	FB	7E	CE	A4	59	C0	E3	22	66	4F	D5	2B	4C	01
5	05	B0	AA	6D	C5	8D	21	67	20	57	51	5C	3C	E2	B9	61
6	F3	77	0B	E9	5B	9F	26	E1	B5	D9	AF	C3	1A	F9	96	10
7	D0	84	AD	86	40	ED	97	92	FA	47	0E	F1	6B	69	BB	CF
8	17	58	4B	BD	13	1B	04	EB	0D	4A	08	9D	5A	71	9A	DD
9	C1	A	44	B1	95	AE	00	02	A6	E8	42	4E	83	BC	DE	BA
A	07	39	90	41	24	37	6A	D8	8E	60	E4	2F	CB	3F	7A	CA
B	82	AB	7C	78	62	A9	1D	DA	46	F2	80	F4	72	D4	D2	54
C	F7	73	30	B4	1C	CD	5F	A3	23	6F	64	EA	D6	70	C9	50
D	28	36	E5	2E	F8	E7	BF	3A	FE	FD	3E	8A	FF	8B	18	5D
E	89	33	49	7B	27	8F	85	6E	29	79	A1	3B	D3	15	03	38
F	88	EF	56	EE	4D	09	B3	94	81	F5	19	A7	48	E6	5E	52

4. Performance Analysis of an S-Box

4.1. Nonlinearity

The nonlinearity of the Boolean function refers to the distance between the Boolean function and the affine function. In order to resist the attack of linear cryptography, the distance between the Boolean function and the affine function should be as large as possible. The nonlinearity represented by the Walsh cyclic spectrum is defined as:

$$N_f=2^{n-1}-\frac{1}{2}\underset{\alpha \in F_2^n}{\max }\left|W_f\left(\alpha \right)\right|$$

(10)

It can be seen from the results in Table 3 that Ni was the nonlinearity of the Boolean function corresponding to each bit of the S-box. Compared with the S-box constructed by other chaotic systems, the proposed method had a higher than average nonlinearity. It could better resist the attack of optimal linear approximation.

Table 3. The nonlinearity of an S-box.

S-Box	S-Box in This Paper	Lambić S-Box [32]	Lu et al. S-Box [34]	Han et al. S-Box [37]
N1	108	108	108	106
N2	106	104	106	106
N3	104	108	104	104
N4	106	106	104	106
N5	108	106	104	106
N6	108	108	106	104
N7	108	106	108	106
N8	106	106	110	104
Average nonlinearity	106.75	106.5	106.3	105.25

4.2. Differential Uniformity

The uniformity of differential distribution is an important security index of the cryptographic function. The success of a differential cryptoanalysis is realized by the nonuniformity of the differential distribution of the Boolean function. The better the uniformity of difference, the stronger the ability to resist a differential attack. The index used to describe the uniformity of the differential distribution of the Boolean function is the differential uniformity. Generally, the differential approximation probability $D{P}_f$ is used to describe the input/output XOR distribution of $f$.

$${\mathrm{DP}}_f=\underset{△x\ne 0,△y}{\max }\left(\frac{\left\{x\in X|f\left(x\right)\oplus f\left(x\oplus \right)△x\right\}}{2^n}=△y\right)$$

(11)

The smaller the difference uniformity $D{P}_f$, the higher the security of the S-box.

The following conclusion can be drawn from Table 4. It can be seen from Table 4a that the maximum value was 10 except in the first row and first column in the difference distribution table of the S-box in this paper. As can be seen from Table 4b, compared with other chaotic S-boxes, the differential approximation probability of the S-box in this paper was moderate, which showed that the S-box had a strong ability to resist a differential attack.

Table 4. The differential uniformity of an S-box.

(a) Partial input output differential distribution of an S-box
6	0	0	2	2	0	2	0	2	0	2	0	4	0	0	0
2	0	0	0	0	10	0	0	0	6	0	2	0	0	0	0
0	0	4	0	2	2	2	0	2	2	2	2	2	2	0	0
2	0	2	0	2	0	0	2	0	0	2	0	2	0	0	2
2	0	4	0	0	2	0	2	0	0	2	0	2	0	0	0
2	0	2	2	2	0	2	2	2	0	6	0	0	2	2	2
0	0	0	0	2	2	0	6	0	0	0	0	0	0	0	0
0	0	0	0	0	0	2	0	0	2	0	0	0	0	2	2
2	0	0	0	0	2	0	0	4	0	0	0	0	0	0	0
0	2	0	0	0	2	0	2	2	0	0	2	2	0	0	0
2	2	0	2	0	2	2	0	0	2	0	6	0	0	0	2
0	4	0	0	2	0	0	0	2	0	0	2	2	2	2	0
4	2	2	2	2	0	0	2	0	2	0	4	2	0	0	2
0	0	0	0	0	0	2	0	0	0	2	0	0	2	4	2
2	2	0	0	0	2	0	0	0	0	0	2	2	2	0	0
0	0	0	4	0	2	0	6	0	0	2	0	0	0	0	0
(b) The comparison of the differential uniformity
S-Box				S-Box in This Paper			Lambić S-Box [32]			Lu et al. S-Box [34]			Han et al. S-Box [37]
Differential maximum				10			10			10			10
Differential approximation probability				0.0390625			0.0390625			0.0390625			0.0390625

4.3. Strict Avalanche Criterion

The strict avalanche criterion is used to measure the randomness of the input change of an S-box to the output change. The avalanche characteristics indicates that if any bit in the input vector is flipped, the probability of the output bit flipping is close to 0.5 and then the S-box satisfies the strict avalanche criterion.

The following conclusions can be drawn from Table 5. Table 5a shows that there was no case where the input changed but the output did not change. As can be seen from Table 5b, compared with other chaotic S-boxes, the average value of the correlation matrix was closer to 0.5 so the S-boxes proposed in this paper satisfied more strict avalanche criteria than the others.

Table 5. The strict avalanche criterion of an S-box.

(a) The correlation matrix of an S-box
No.	1	2	3	4	5	6	7	8
1	0.4844	0.5	0.625	0.4688	0.4688	0.4688	0.5	0.5156
2	0.4844	0.5156	0.5938	0.4531	0.4844	0.4531	0.5625	0.5469
3	0.4219	0.5	0.5	0.4531	0.5	0.5313	0.4688	0.4688
4	0.4844	0.5625	0.5	0.4844	0.4375	0.5	0.5	0.4063
5	0.5313	0.5156	0.4375	0.4531	0.5313	0.4688	0.4688	0.5313
6	0.5156	0.5	0.4844	0.5156	0.4844	0.5313	0.5313	0.4688
7	0.5313	0.5625	0.5	0.5469	0.4688	0.4688	0.4688	0.4375
8	0.5	0.5156	0.4844	0.4844	0.5	0.5313	0.5469	0.4844
(b) The comparison of strict avalanche criterion
S-Box		S-Box in This Paper	Lambić S-Box [32]		Lu et al. S-Box [34]		Han et al. S-Box [37]
The average value of the correlation matrix		0.4976	0.4937		0.5050		0.4981

4.4. Independence Criterion of Output Bits

The method of measuring the output bit independence of an S-box was first proposed by Adams [45]. The definition of correlation is as follows. For the two output bits $f_i$ and $f_j$$(i\ne j,1\le i,j\le n)$ of an S-box. If $f_i\oplus f_j$ is highly nonlinear and satisfies the correlation requirement of the strict avalanche effect, the correlation coefficient of each output bit pair is close to 0 when one input bit is reversed. Therefore, the BIC performance of an S-box can be measured by calculating the nonlinearity of $f_i\oplus f_j$ and its satisfaction to SAC.

The following conclusions can be drawn from Table 6. From the nonlinear values of the matrix in Table 6a, we could see that the S-box satisfied the nonlinear characteristics. The elements of the matrix in Table 6b were closer to 0.5 so the S-box in this paper satisfied the strict avalanche effect more than other chaotic S-boxes. Compared with other chaotic S-boxes in Table 6c, the proposed S-box had excellent output bit independence.

Table 6. The independence criterion of output bits of an S-box.

(a)The BIC nonlinearity of an S-box
-	106	102	102	104	98	102	106
106	-	100	104	106	106	106	106
102	100	-	104	100	104	108	102
102	104	104	-	100	108	102	104
104	106	100	100	-	104	100	104
98	106	104	108	104	-	100	106
102	106	108	102	100	100	-	106
106	106	102	104	104	106	106	-
(b) The BIC-SAC of an S-box
-	0.5039	0.4883	0.4668	0.5215	0.5137	0.5195	0.5137
0.5039	-	0.4824	0.5039	0.502	0.5039	0.5137	0.4746
0.4883	0.4824	-	0.5078	0.4785	0.5195	0.5137	0.4961
0.4668	0.5039	0.5078	-	0.5059	0.5176	0.4941	0.5137
0.5215	0.502	0.4785	0.5059	-	0.5234	0.4922	0.4883
0.5137	0.5039	0.5195	0.5176	0.5234	-	0.5078	0.498
0.5195	0.5137	0.5137	0.4941	0.4922	0.5078	-	0.498
0.5137	0.4746	0.4961	0.5137	0.4883	0.498	0.498	-
(c) The comparison of the independence criterion of output bits
S-Box	S-Box in This Paper	Lambić S-Box [32]		Lu et al. S-Box [34]		Han et al. S-Box [37]
Maximum of BIC nonlinearity	108	108		108		106
Minimum of BIC nonlinearity	98	100		98		104
Maximum of BIC-SAC	0.5234	0.578125		0.5254		0.543
Minimum of BIC-SAC	0.4668	0.4375		0.4707		0.4687

5. Conclusions

In this paper, we proposed the chaotic S-boxes to be used in symmetric encryption algorithms. The logistic chaotic map was employed along with Bent functions to give the elements of the S-boxes. This method made full use of the properties of chaotic functions. Logistic mapping was mainly used to generate Bent functions with high nonlinear values. We verified several security analyses such as nonlinearity, difference uniformity, strict avalanche criterion and the independence criterion of output bits. The results of the obtained S-box showed that all of the criteria for a good S-box were approximately fulfilled.