An Efficient Approach for Sidelobe Level Reduction Based on Recursive Sequential Damping
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Paper Contribution
1.3. Paper Organization
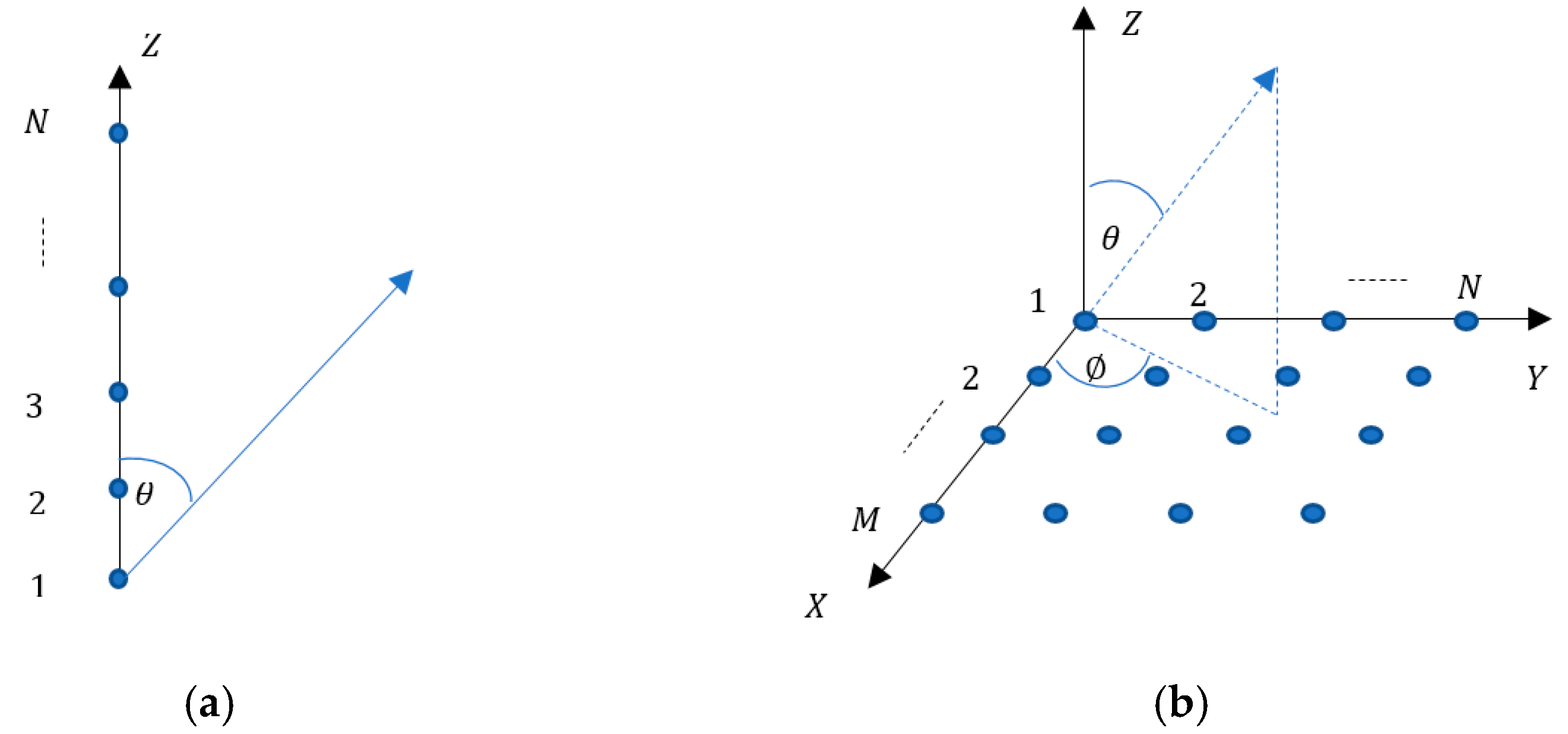
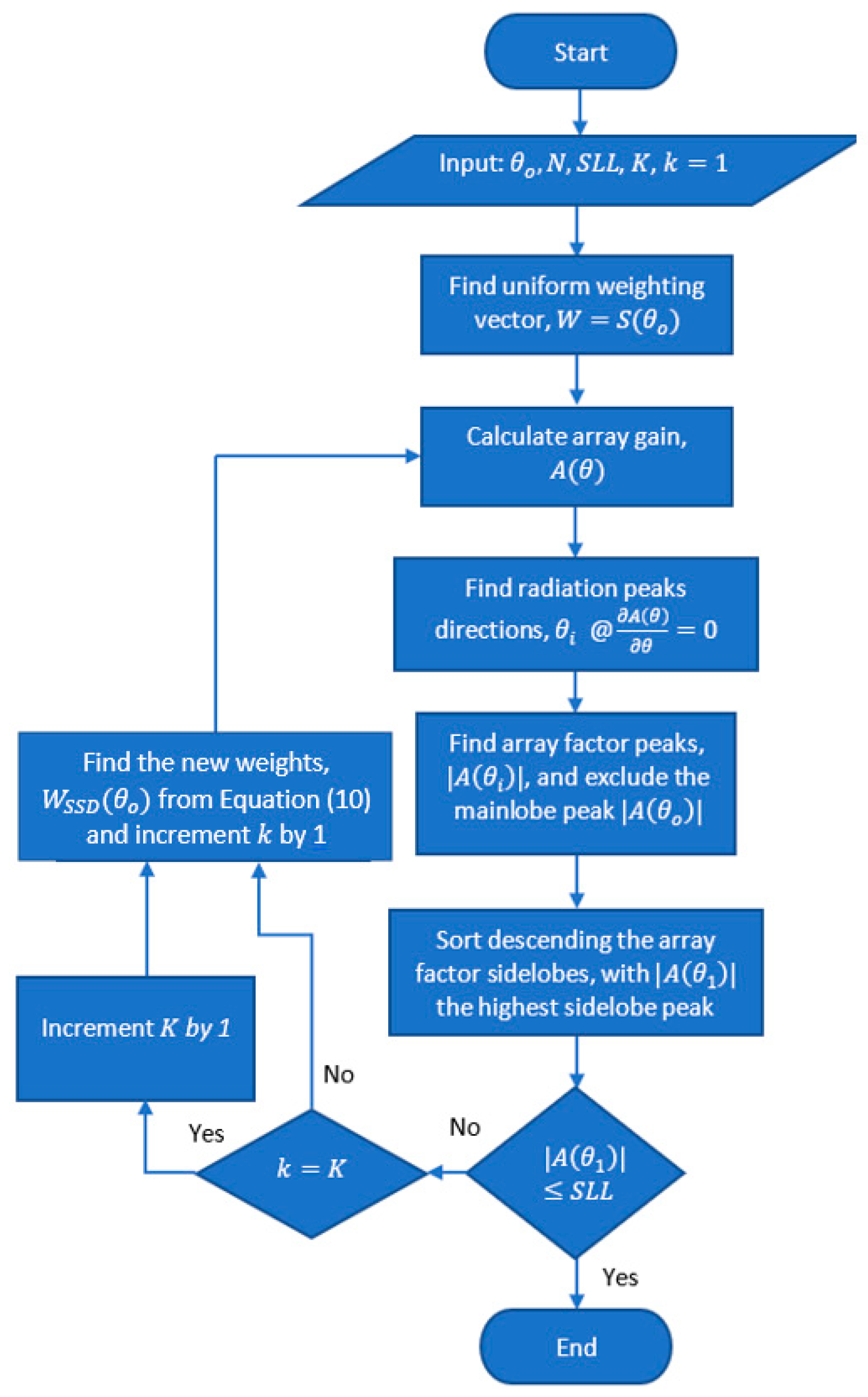
2. Modelling of the Proposed SSD Technique
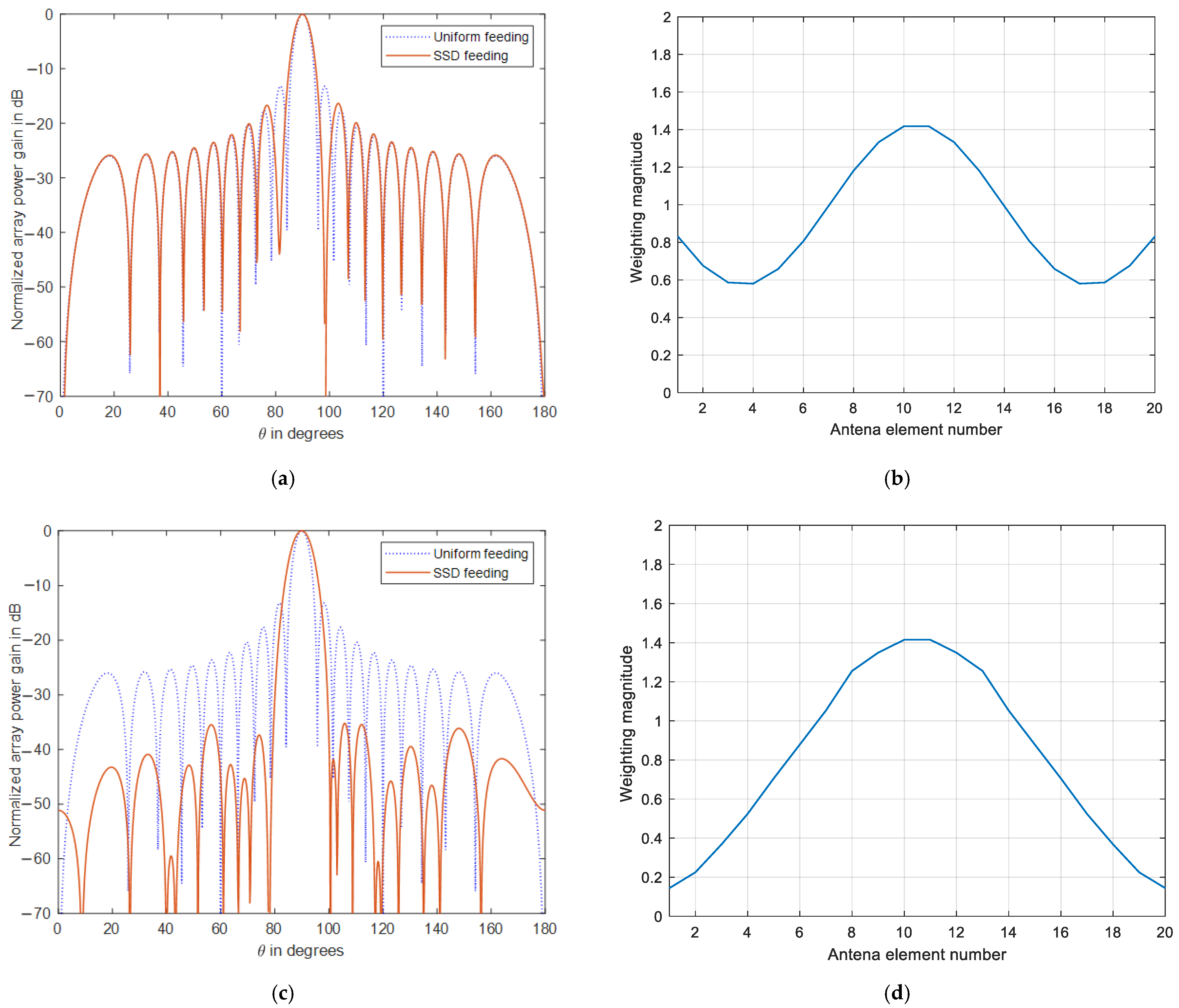
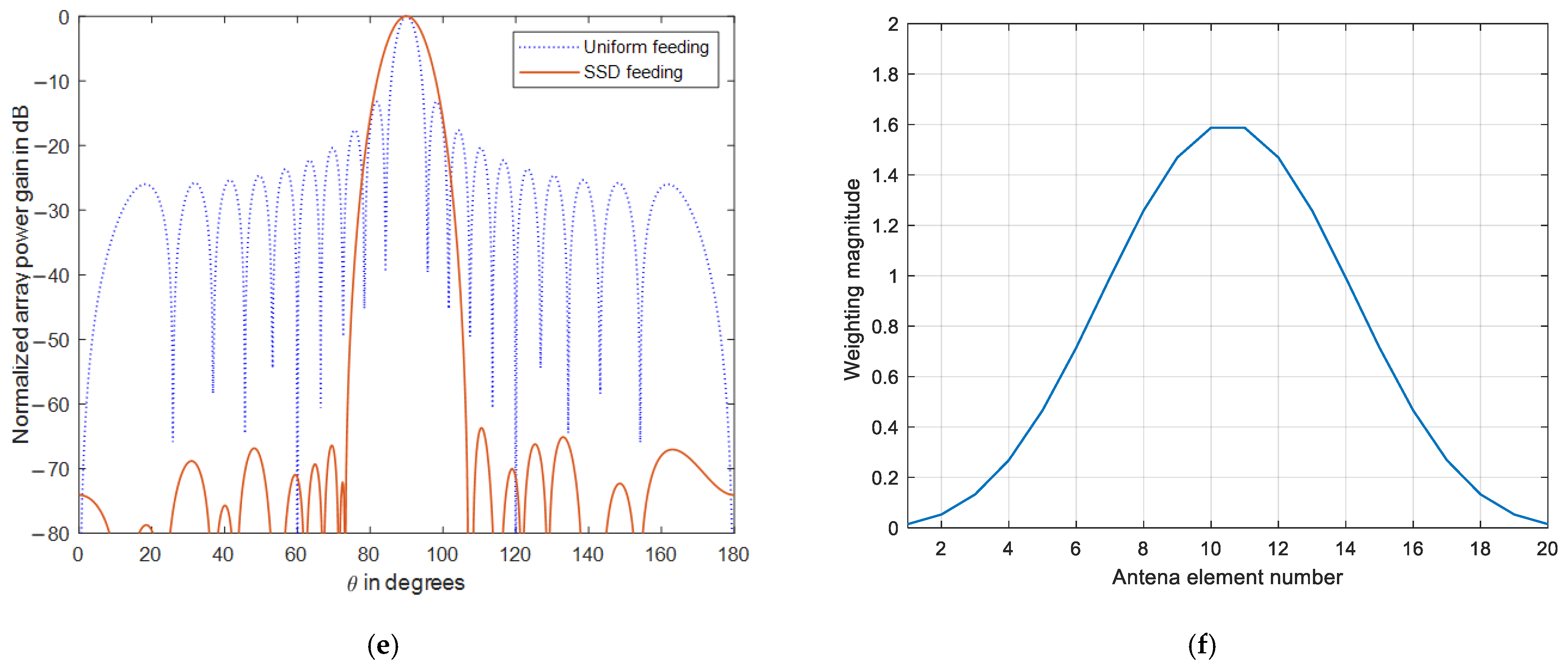
3. SSD Performance Analysis
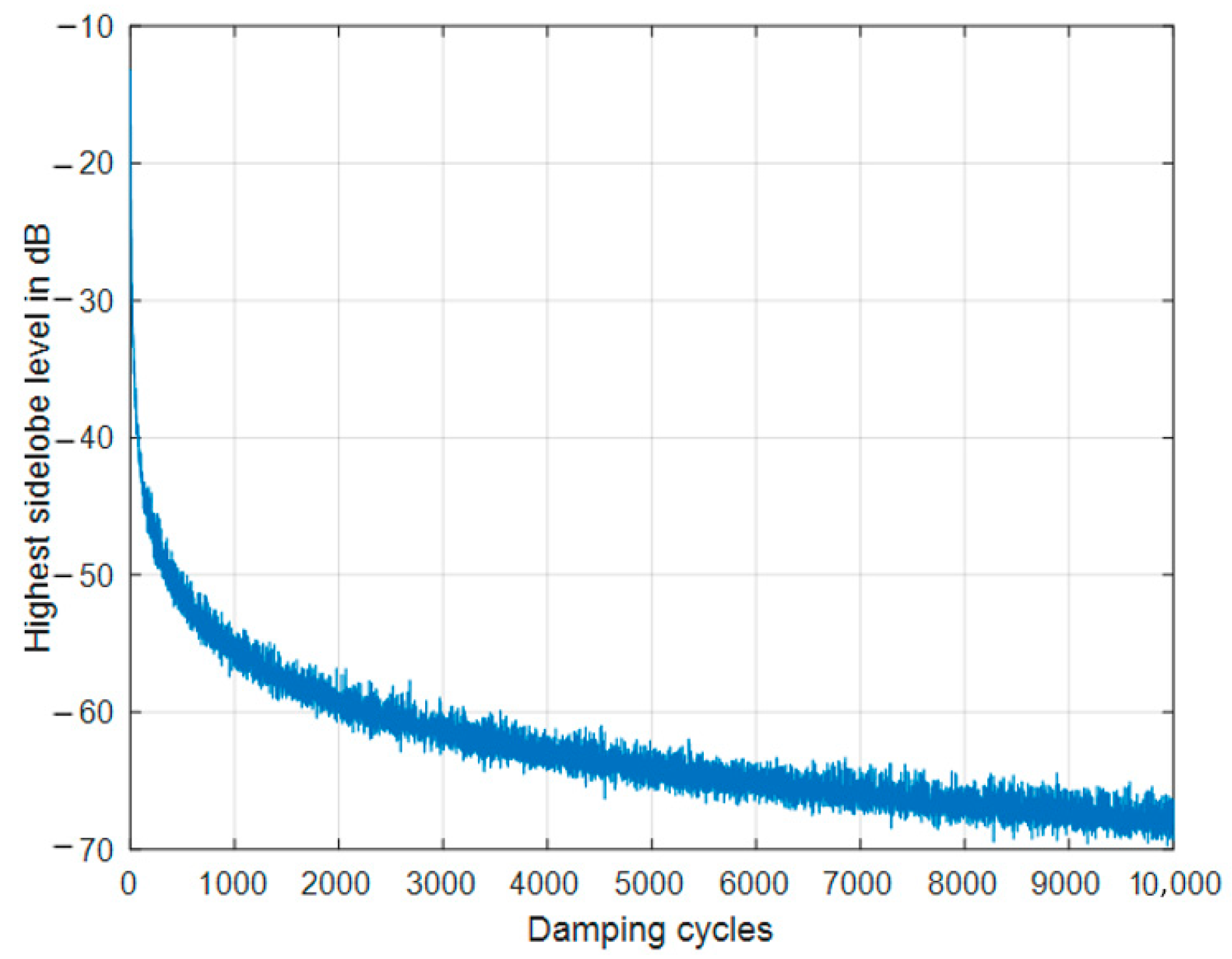
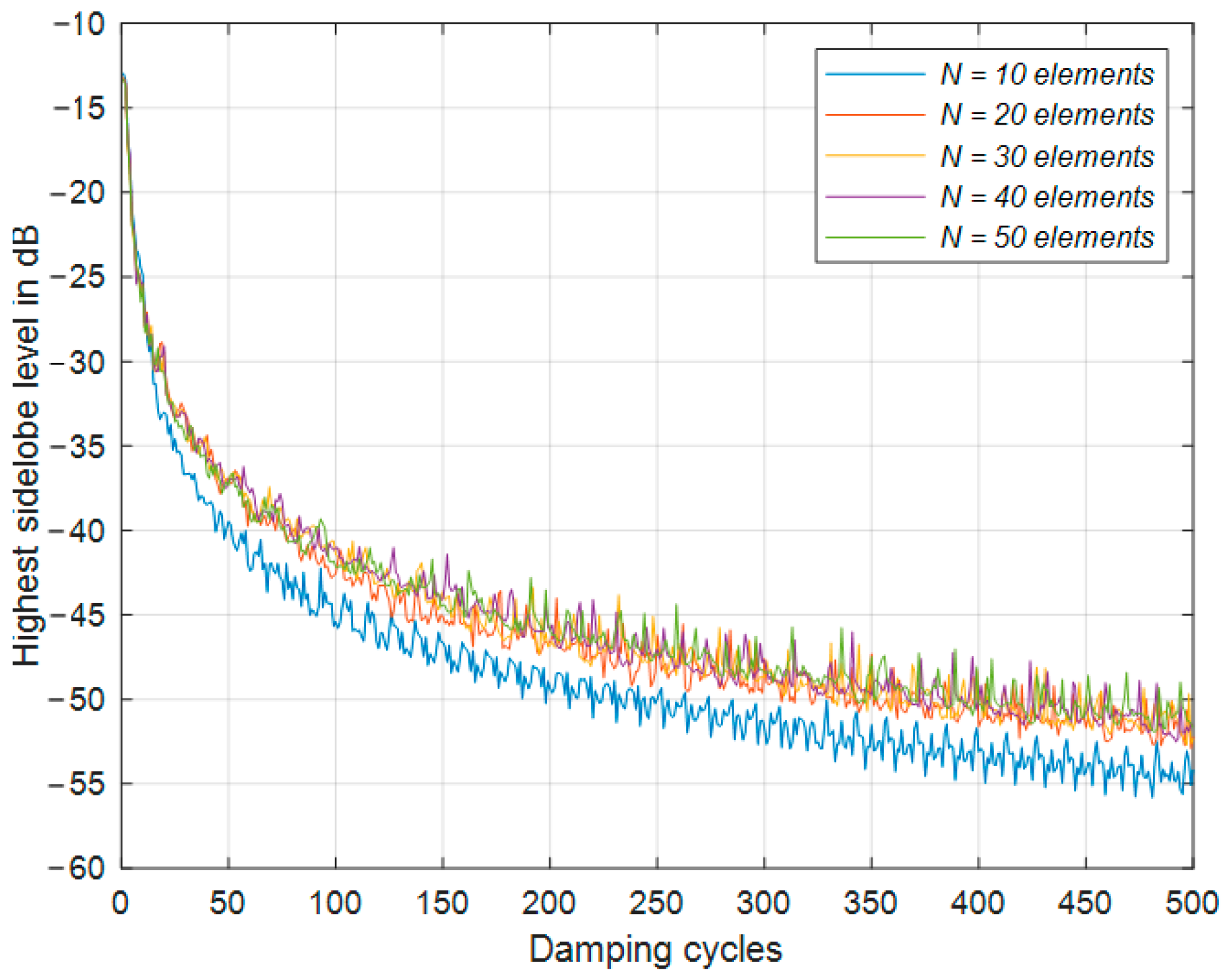
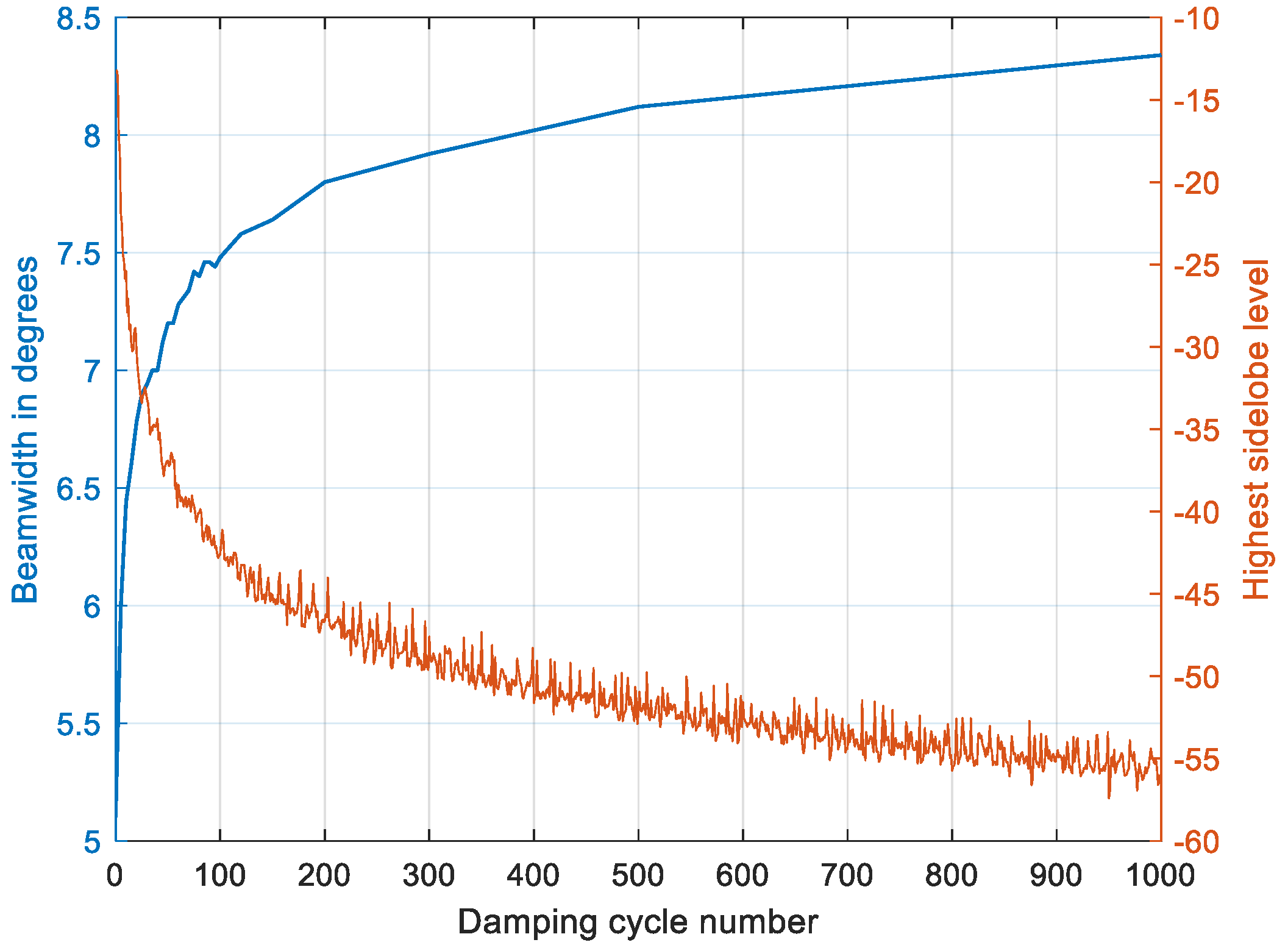
3.1. SSD Damping Behavior
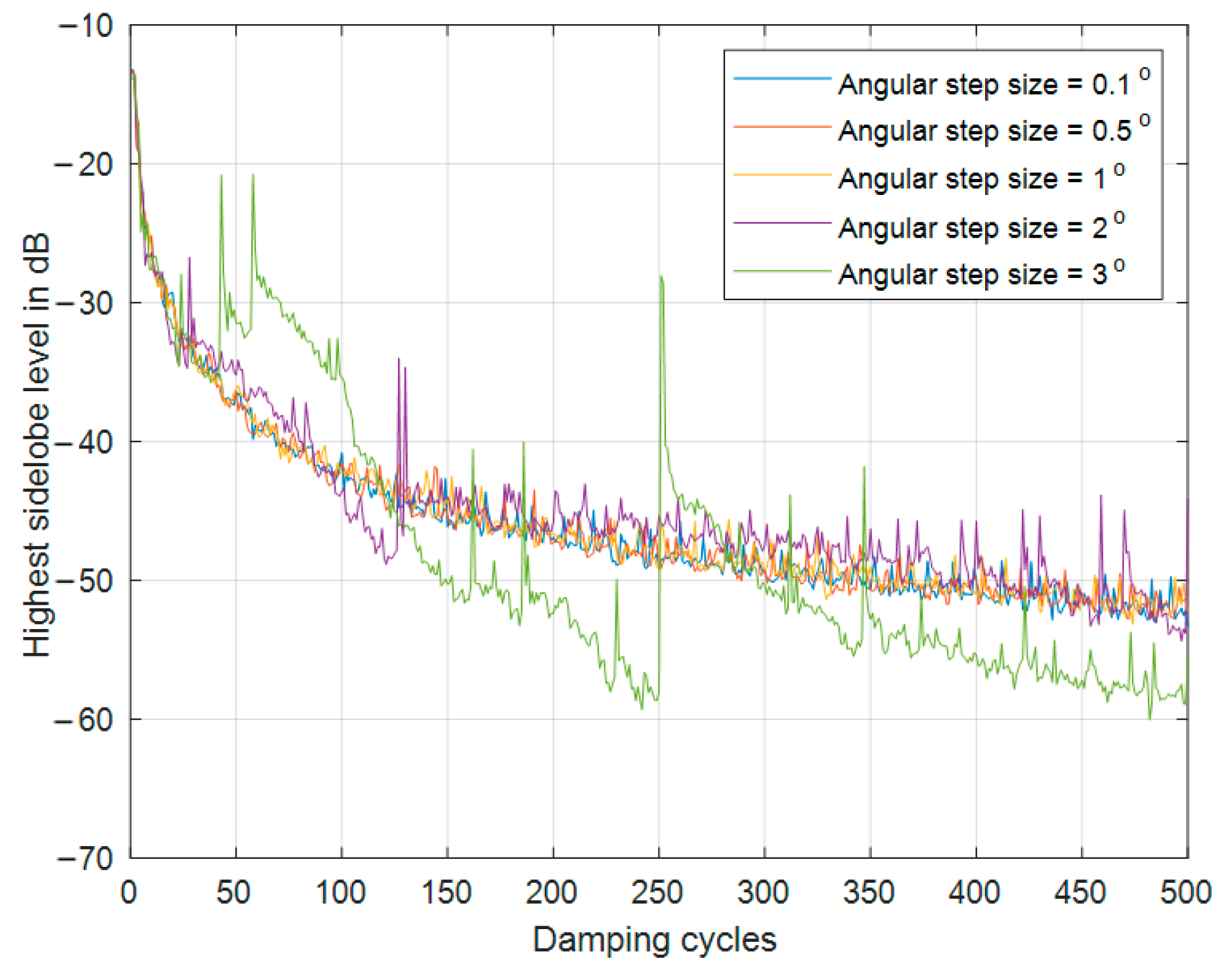
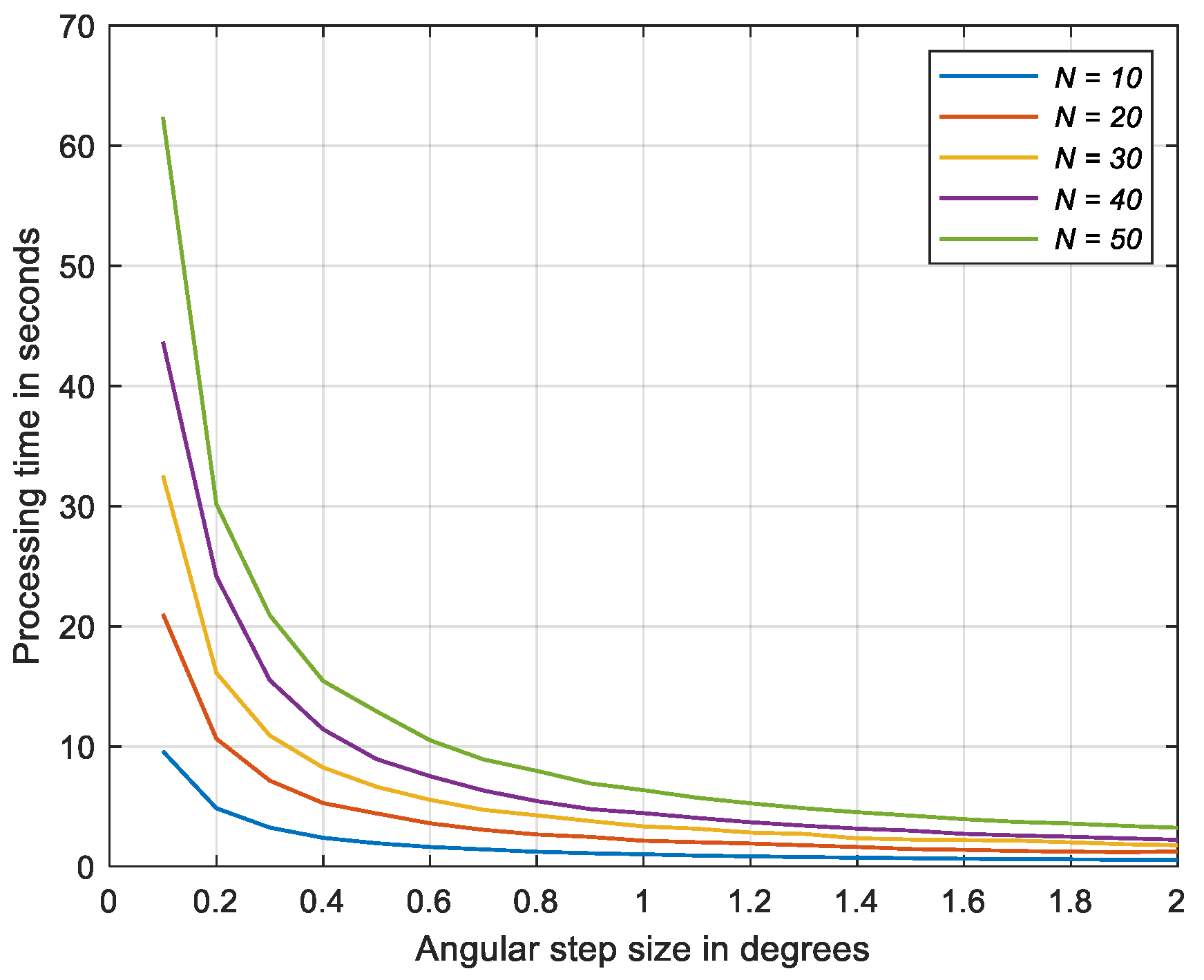
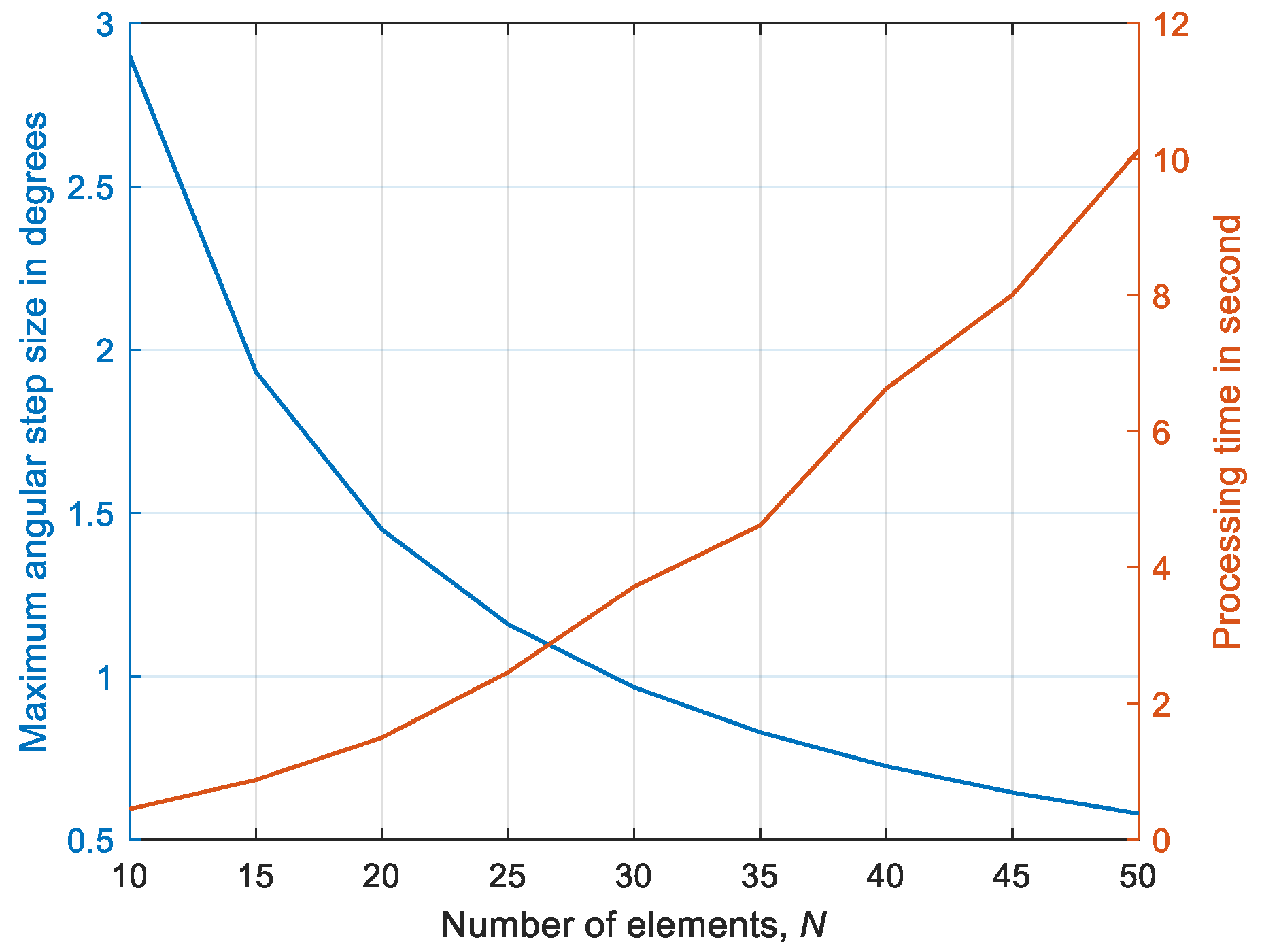
3.2. SSD Behavior at Different Angular Step Sizes
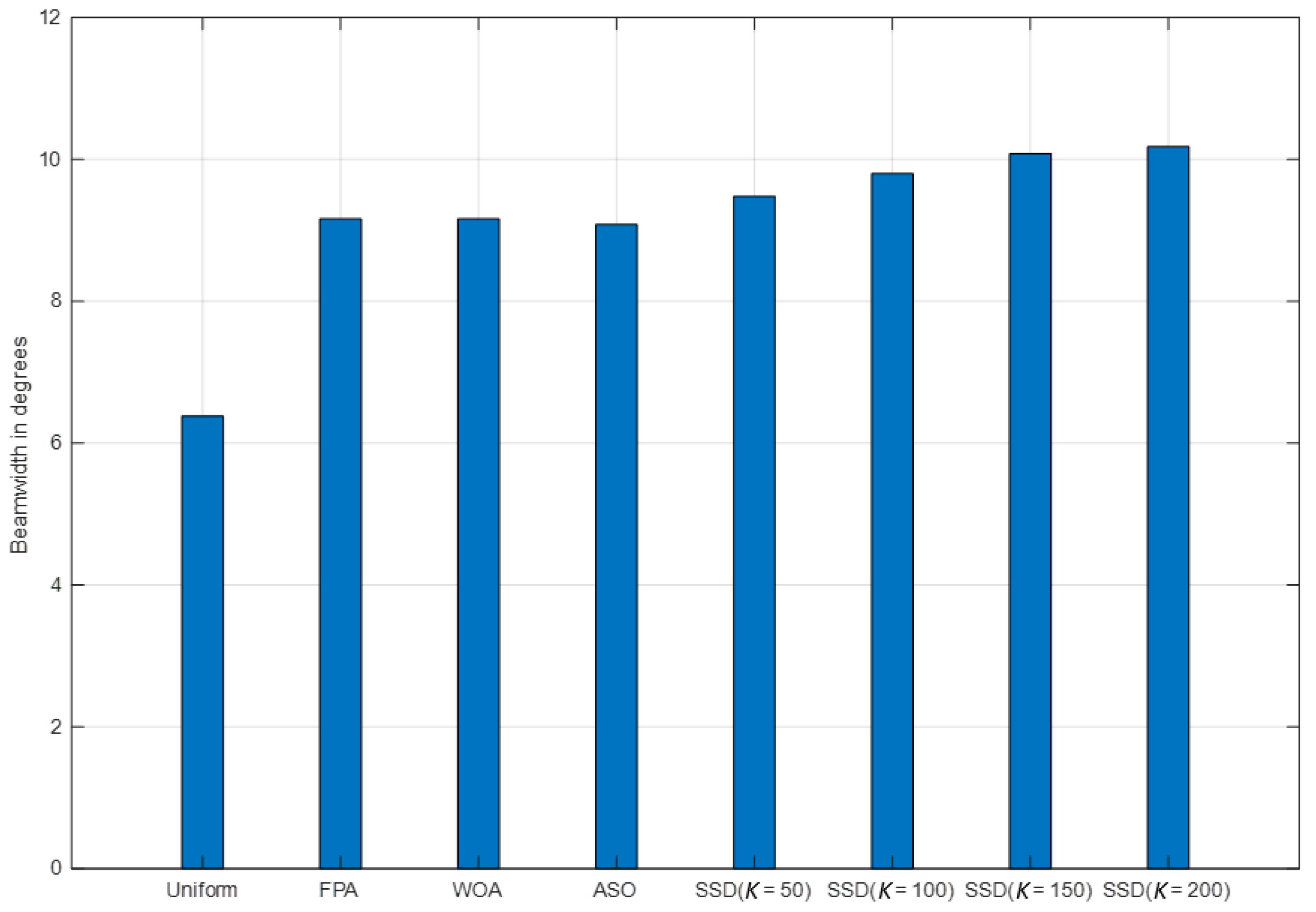
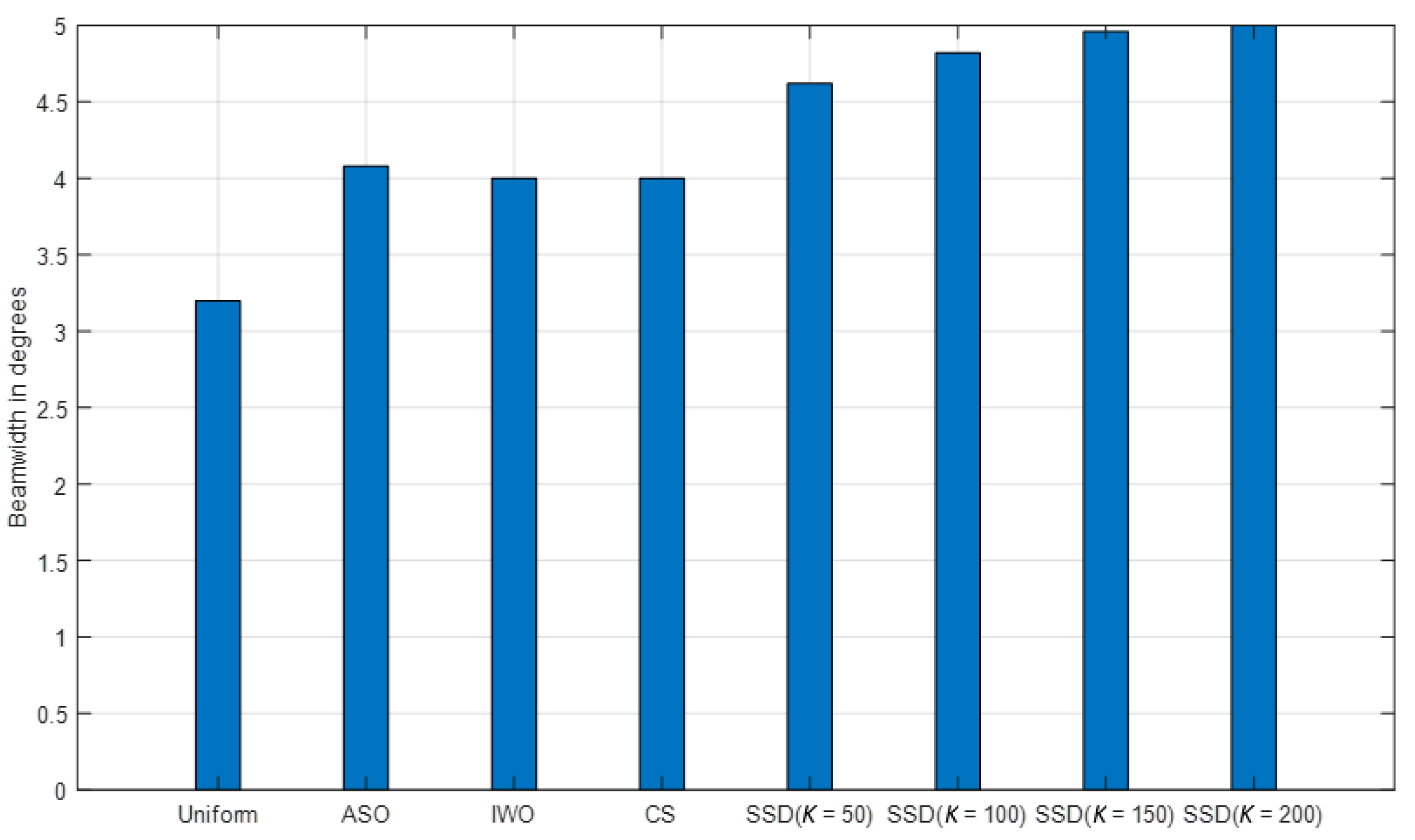
3.3. Impact of SSD on the Beamwidth
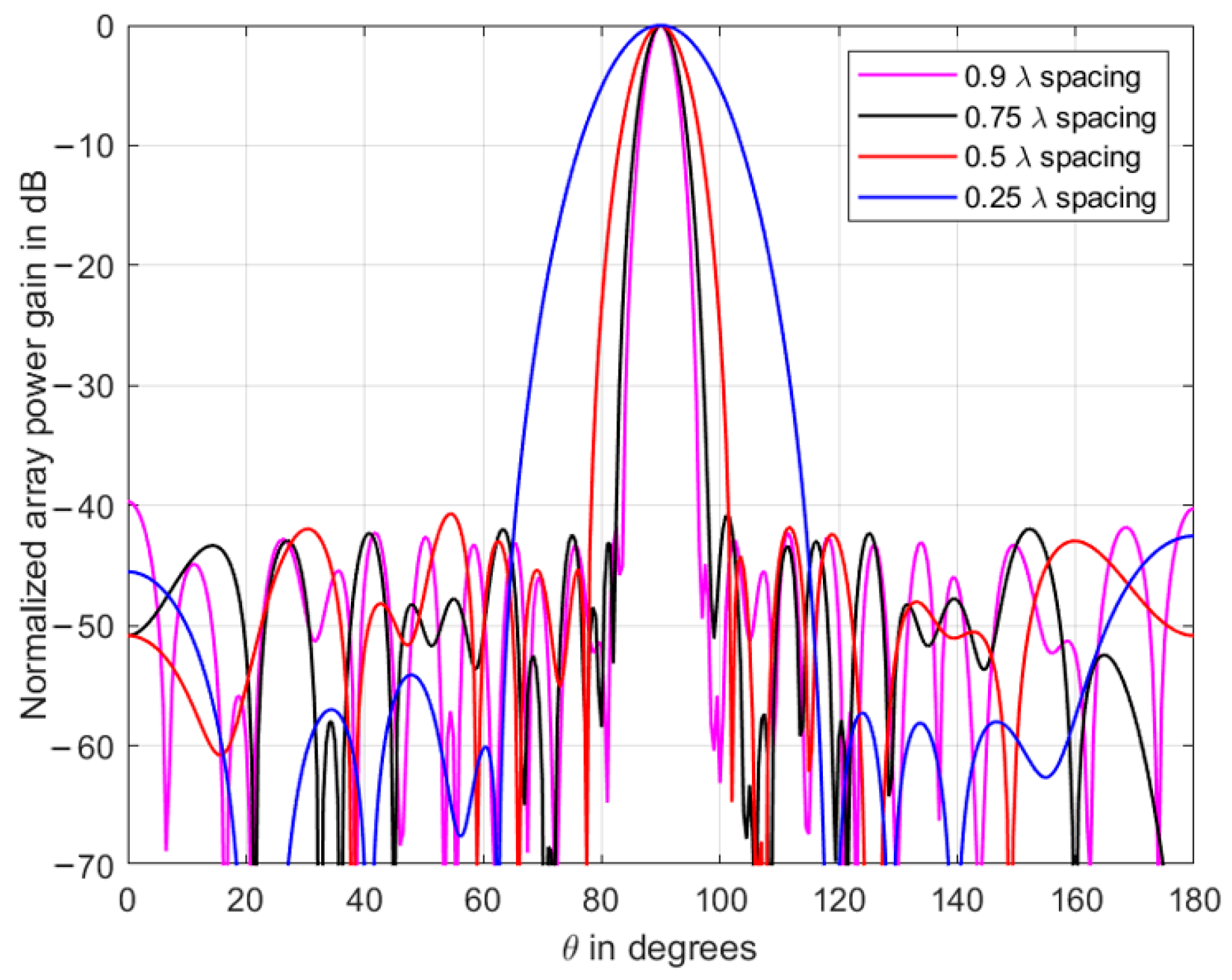
3.4. SSD Performance with Interelement Spacing
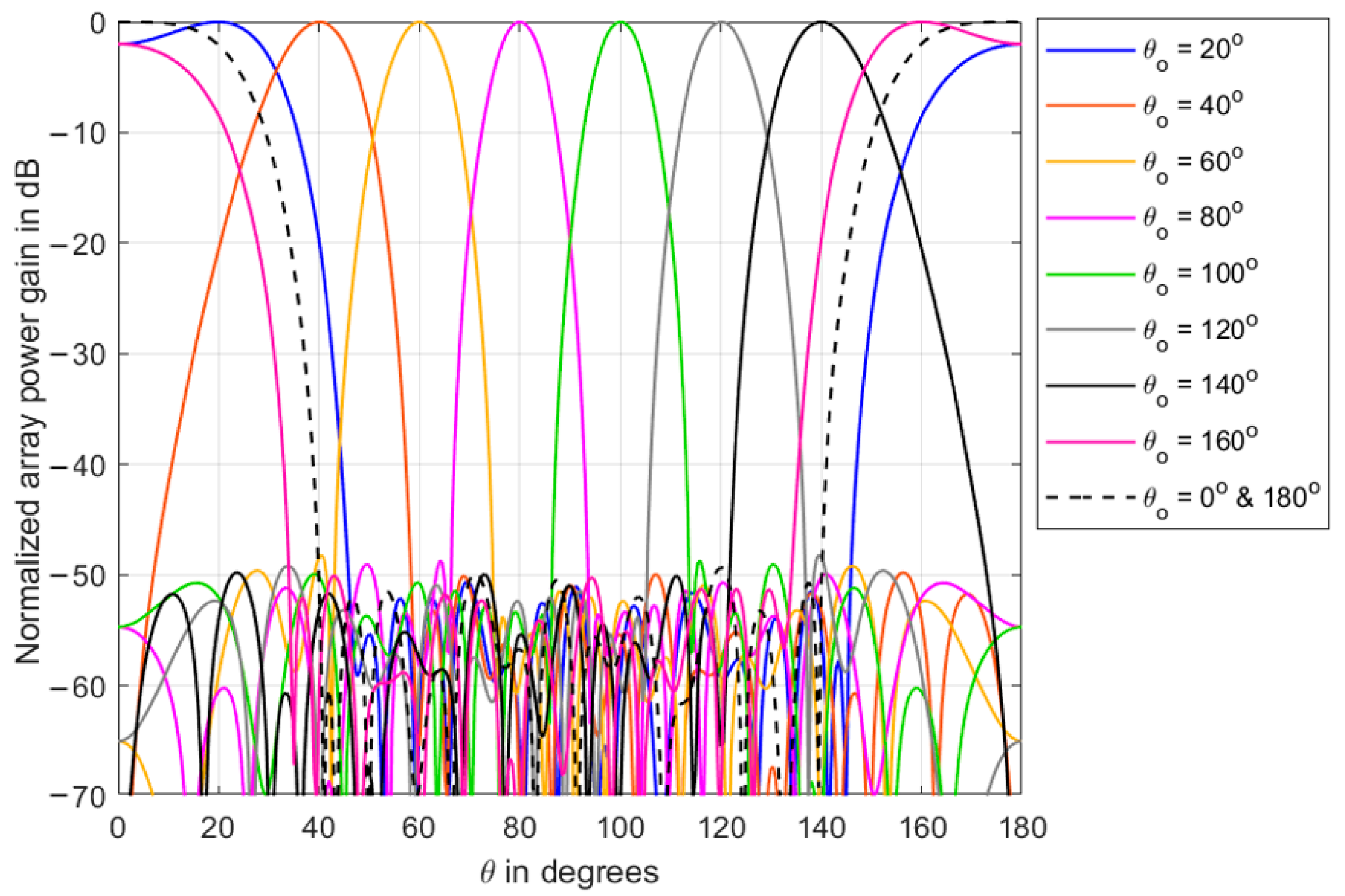
3.5. SSD Performance with the Mainlobe Direction
4. SSD Performance Comparisons and Discussions
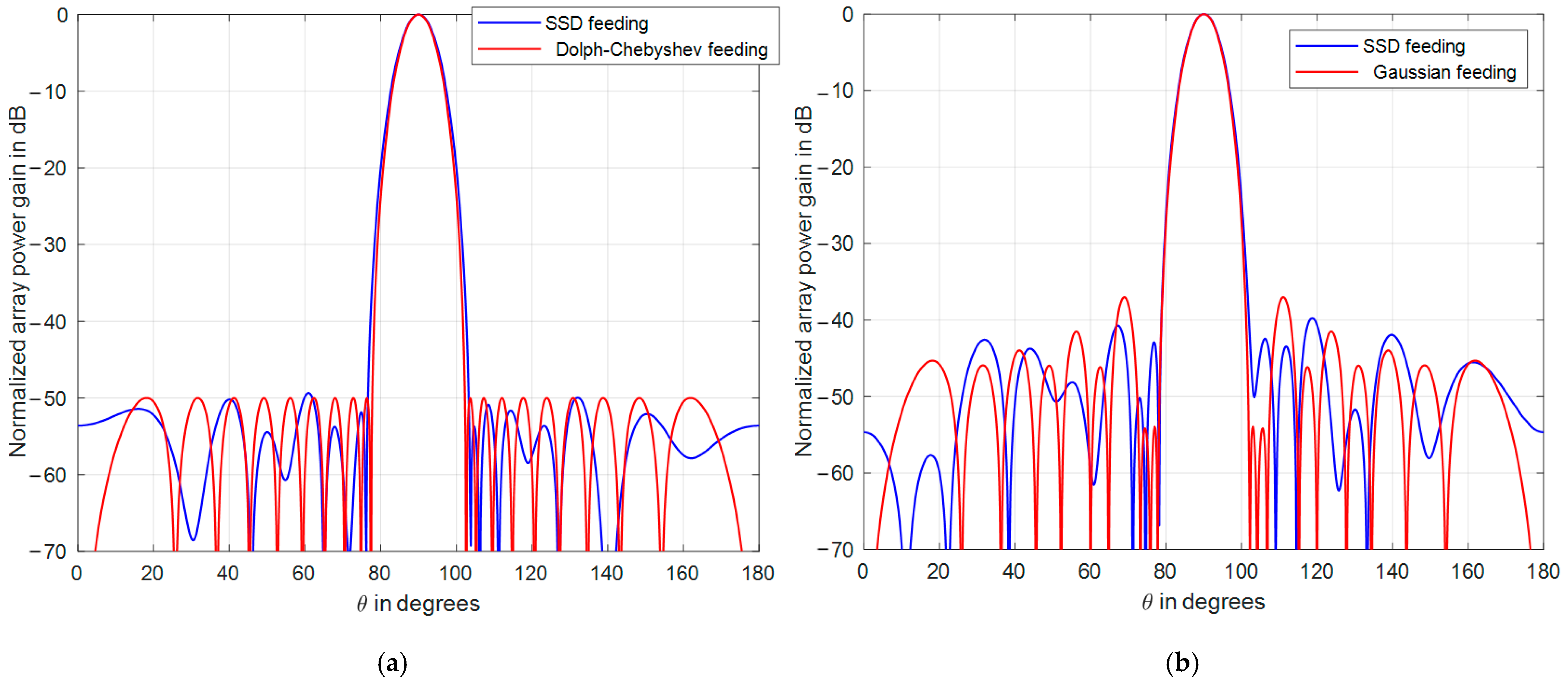
4.1. Comparisons with Conventional Tapering Windows
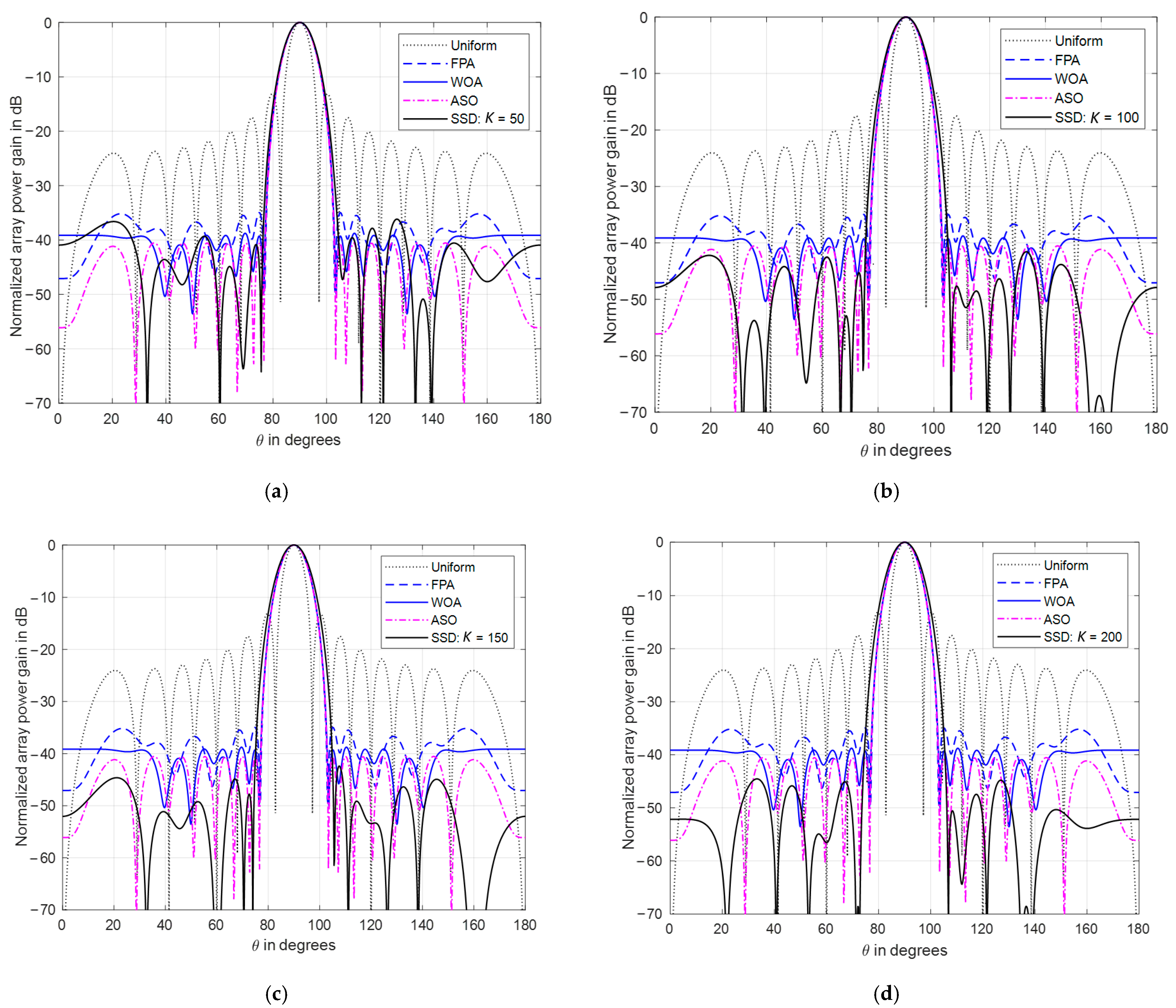
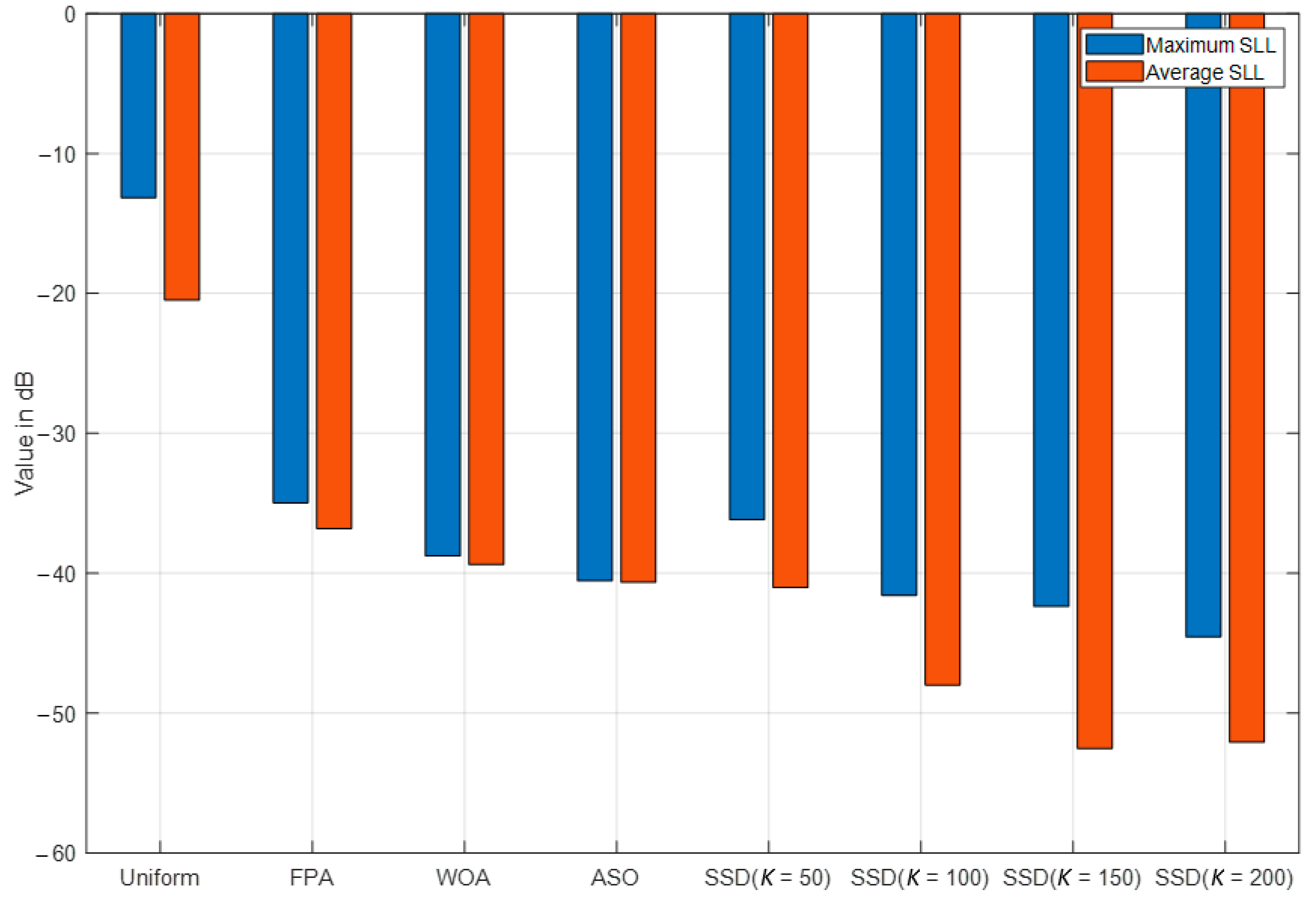
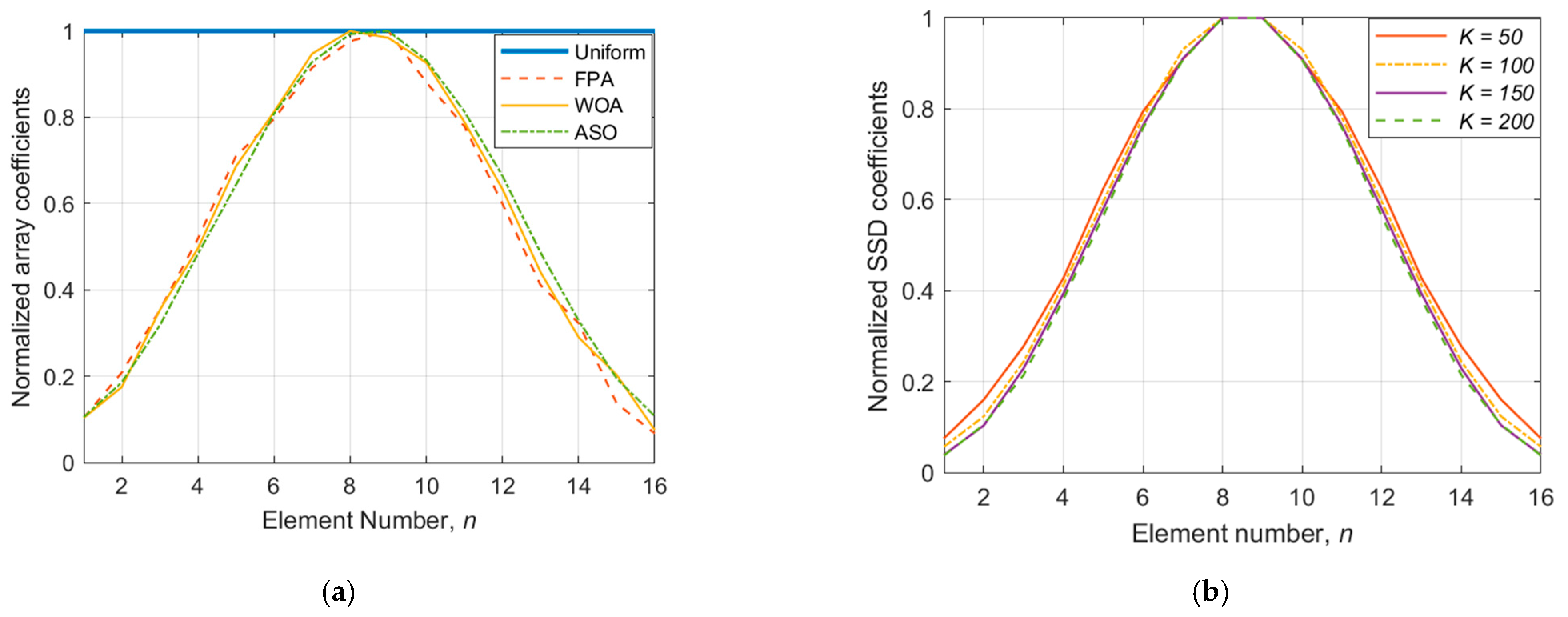
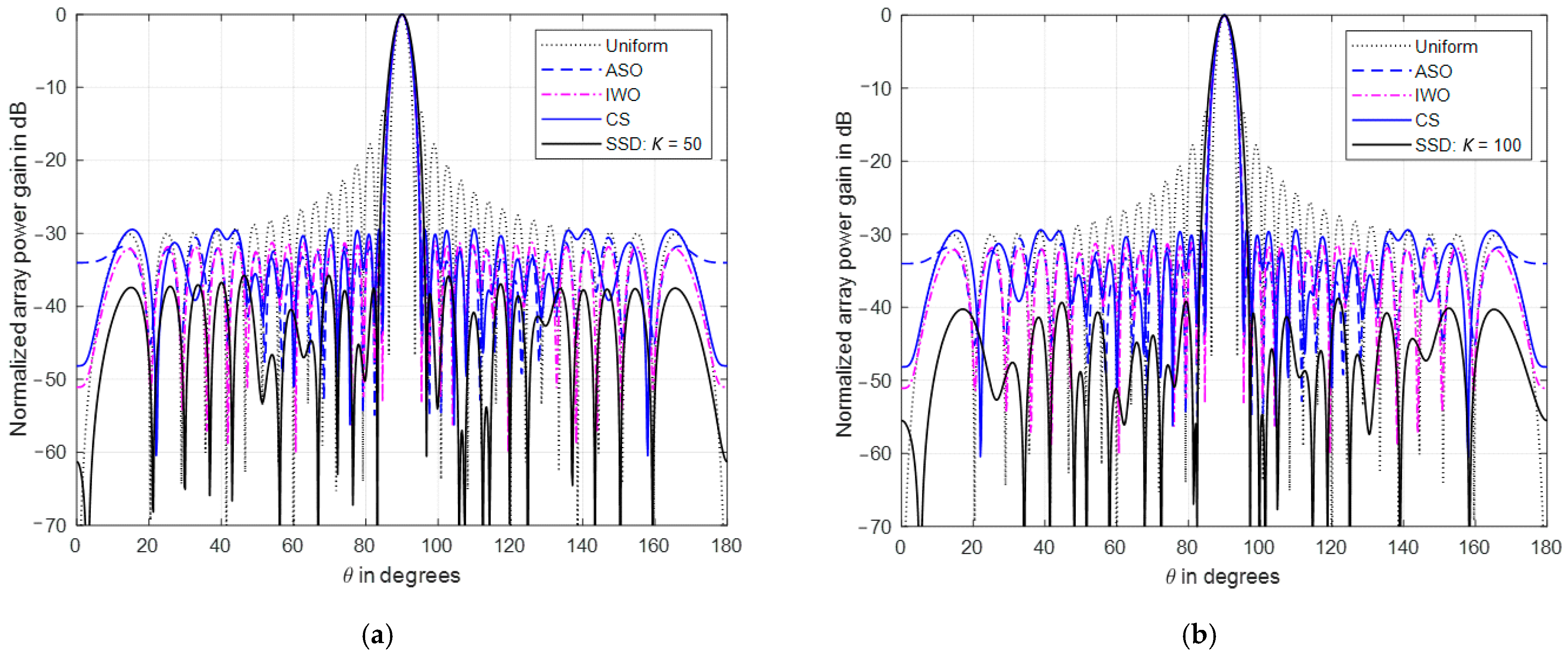
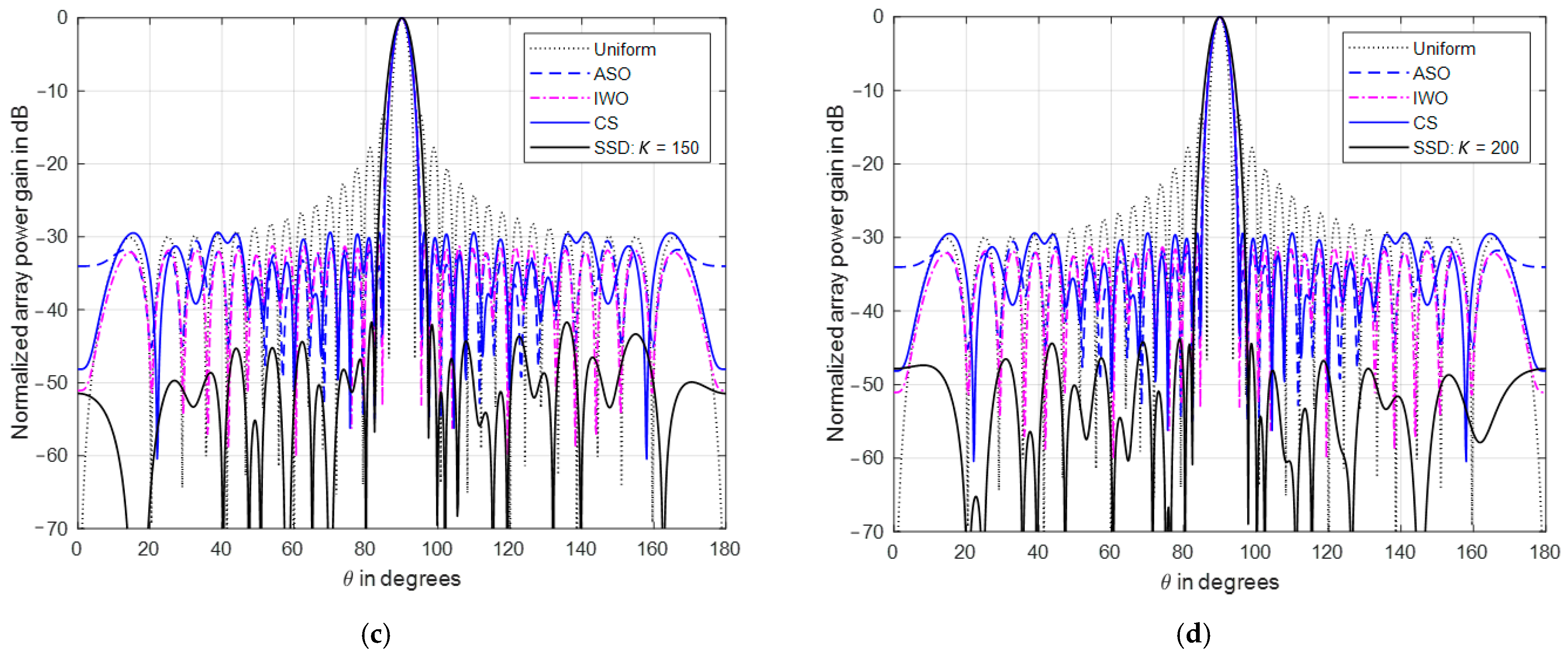
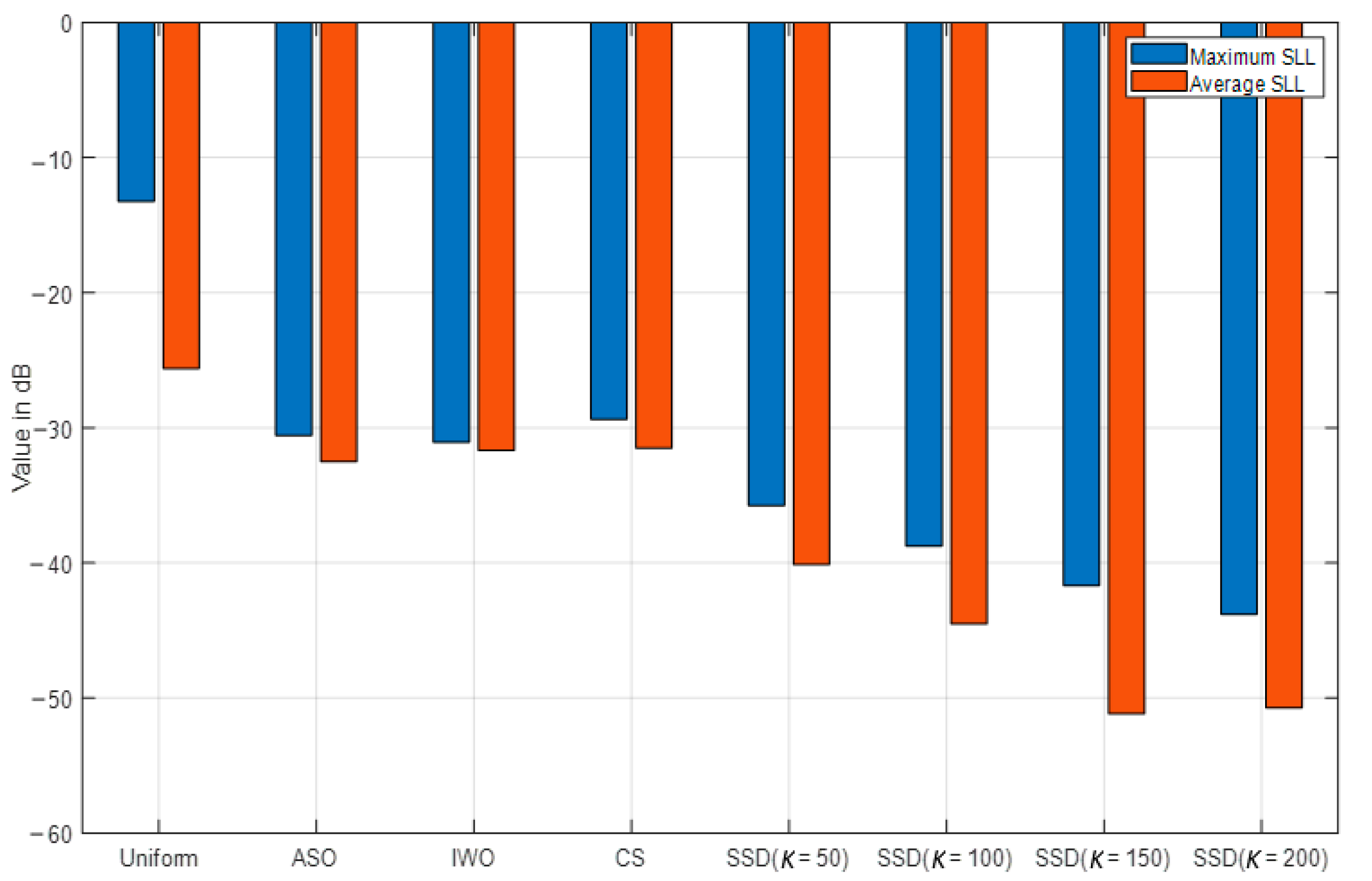
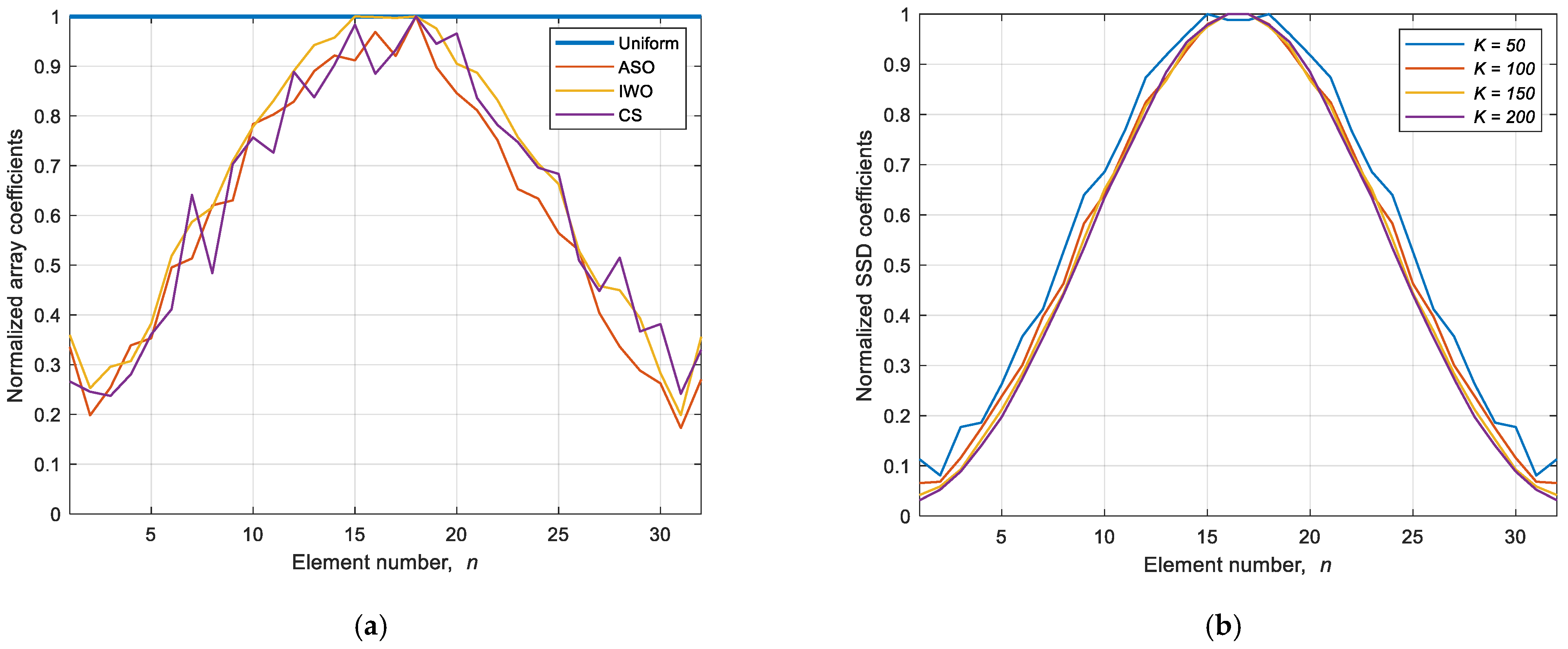
4.2. Comparisons with Optimization Techniques
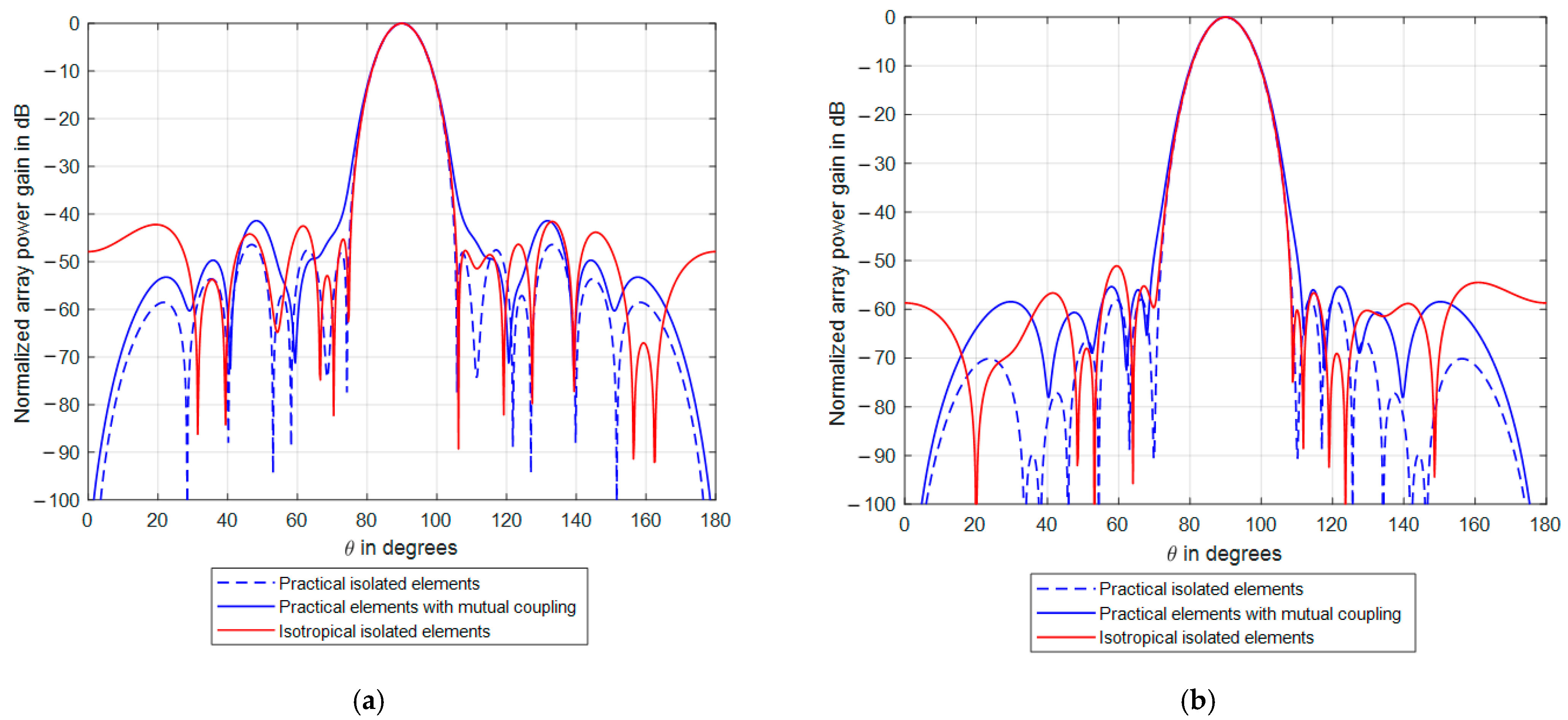
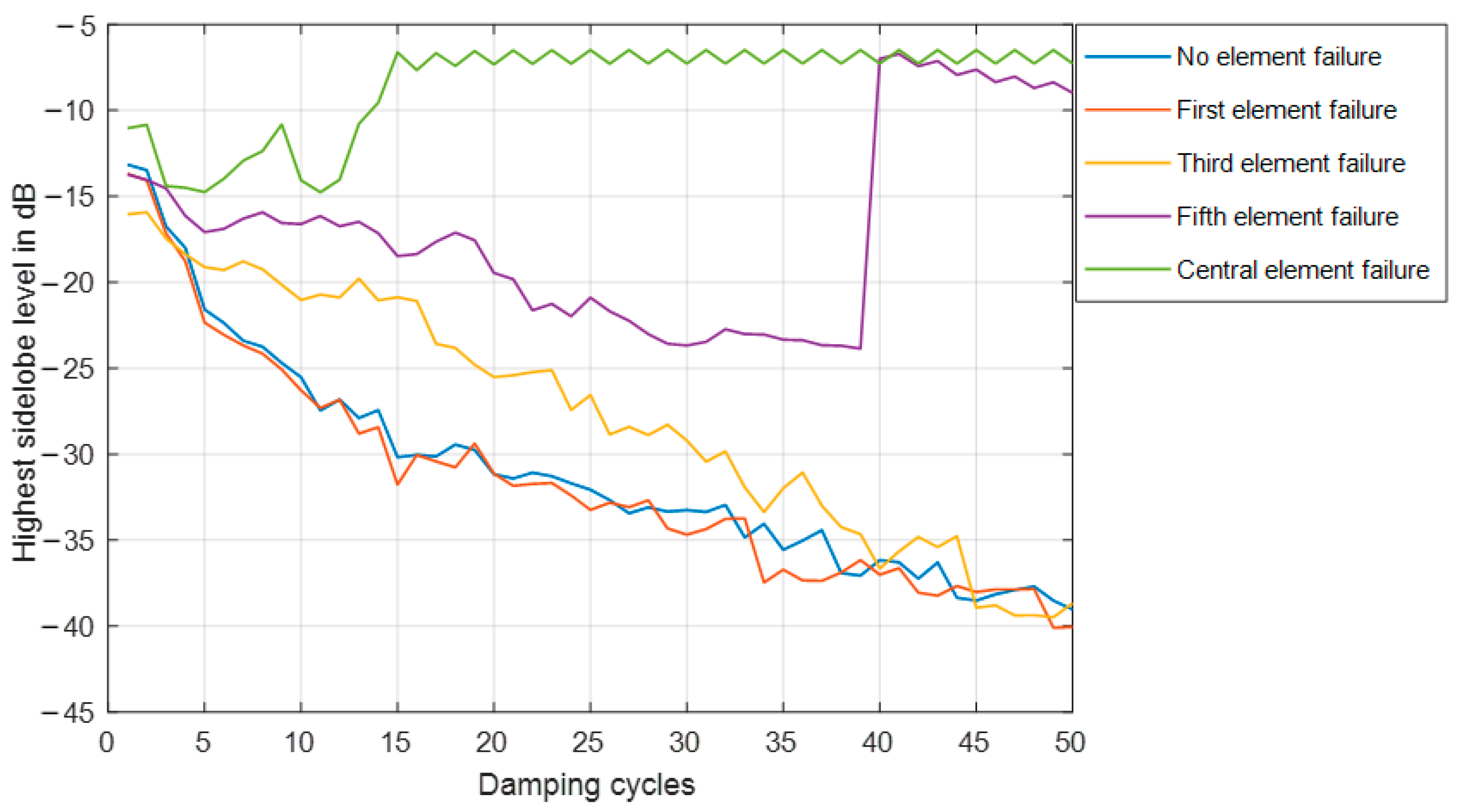
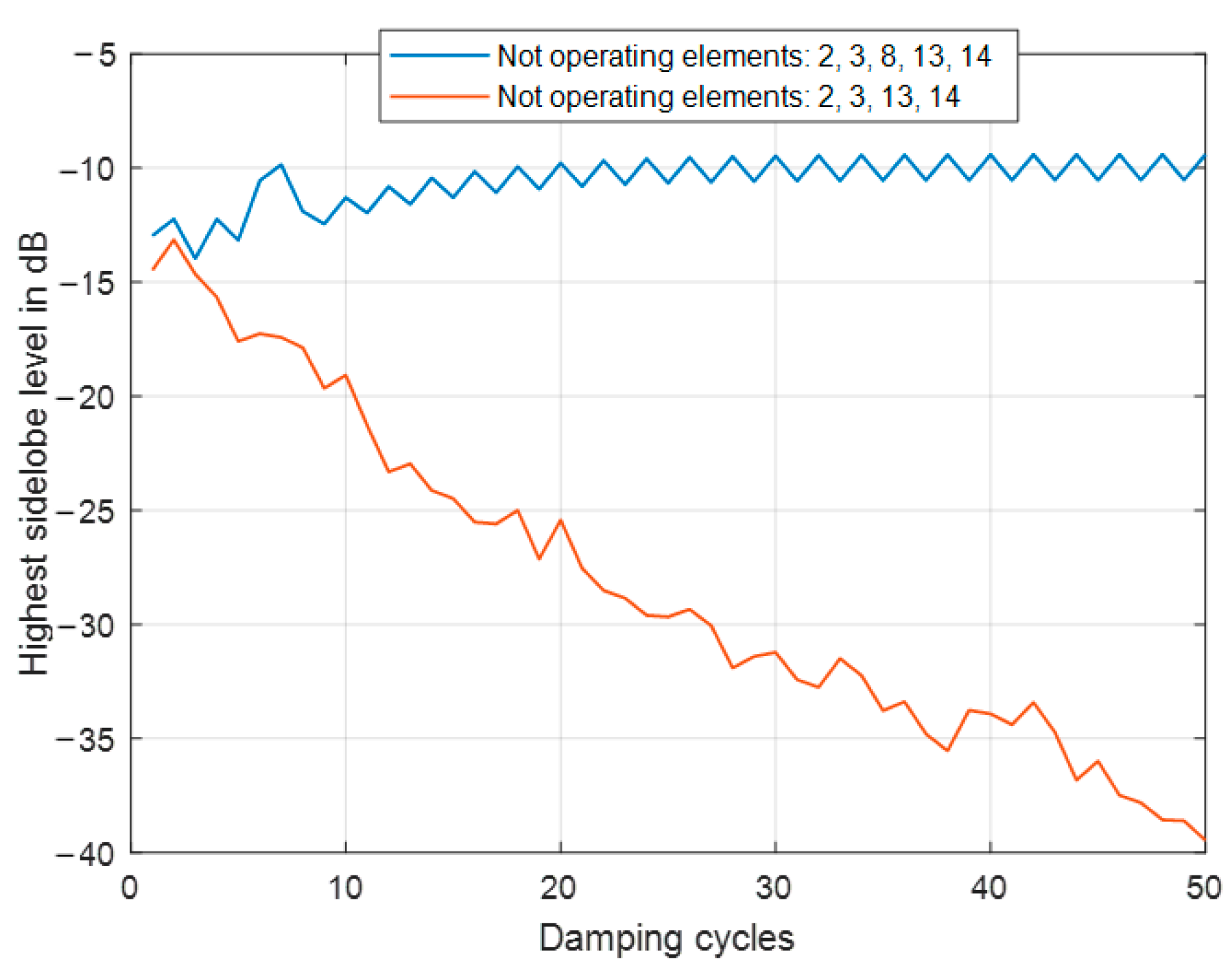
5. Mutual Coupling Effects on the SSD Performance
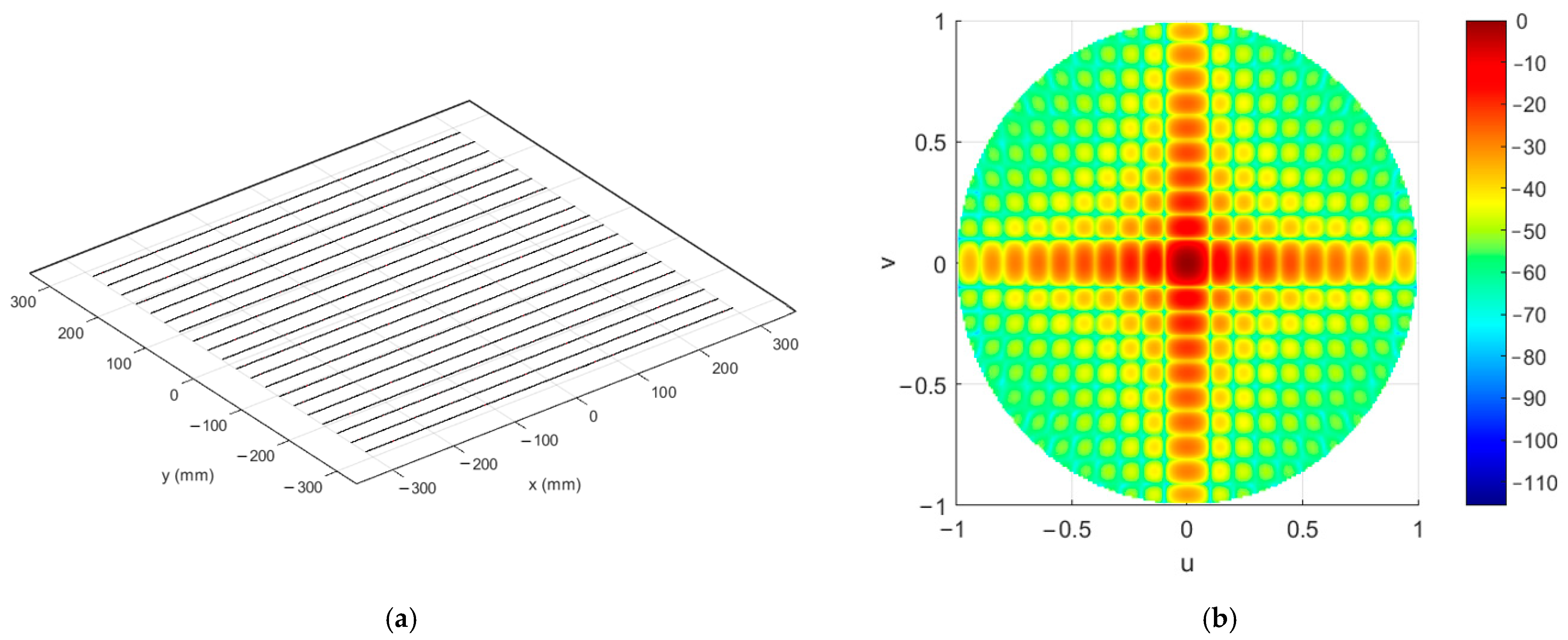
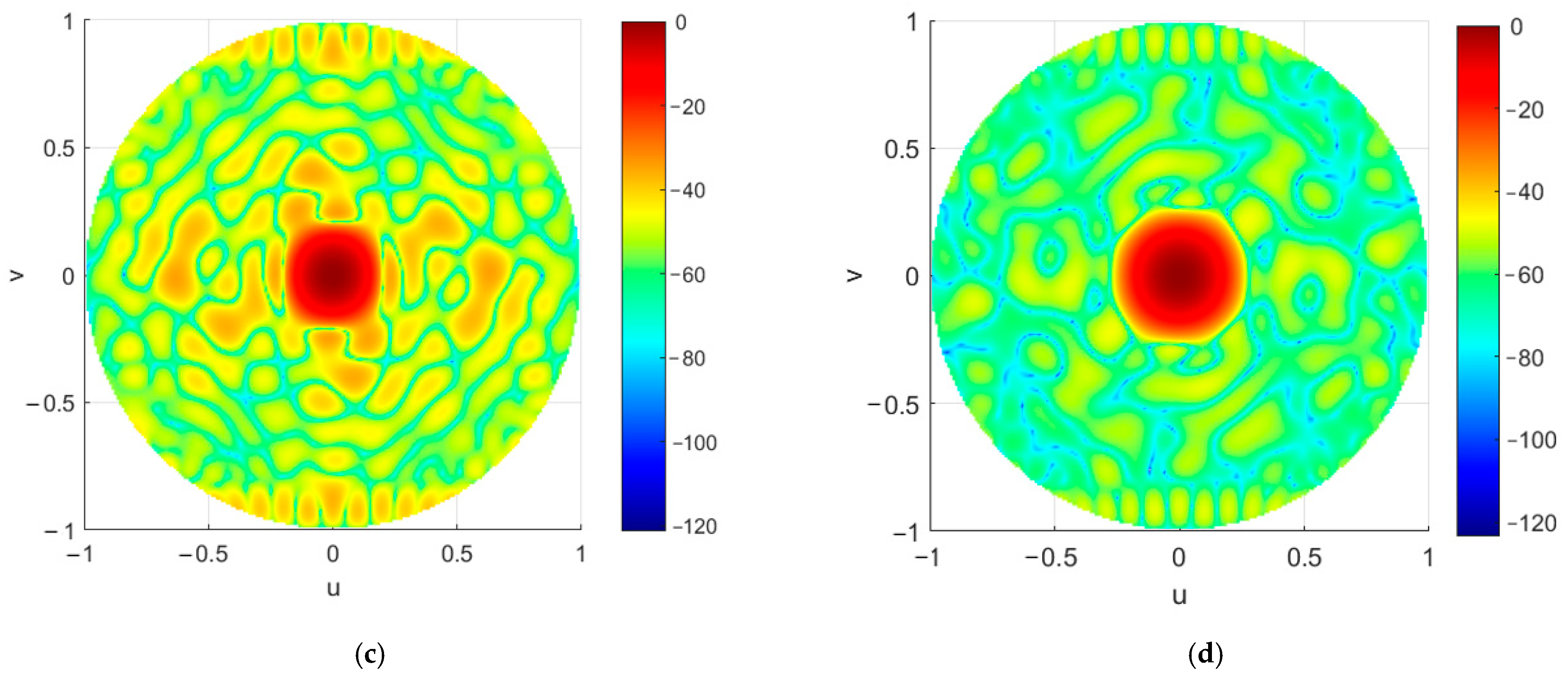
6. SSD for Two-Dimensional Planar Arrays
7. SSD Operational Constraints and Limitations Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akyildiz, I.F.; Nie, S.; Lin, S.-C.; Chandrasekaran, M. 5G roadmap: 10 key enabling technologies. Comput. Netw. 2016, 106, 17–48. [Google Scholar] [CrossRef]
- Li, J.; Ma, Z.; Mao, L.; Wang, Z.; Wang, Y.; Cai, H.; Chen, X. Broadband Generalized Sidelobe Canceler Beamforming Applied to Ultrasonic Imaging. Appl. Sci. 2020, 10, 1207. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, W.; Chen, J.; Kuang, H.; Liu, W.; Li, C. Azimuth Sidelobes Suppression Using Multi-Azimuth Angle Synthetic Aperture Radar Images. Sensors 2019, 19, 2764. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.Z.; Al-Rizzo, H. Beamforming Optimization in Internet of Things Applications Using Robust Swarm Algorithm in Conjunction with Connectable and Collaborative Sensors. Sensors 2020, 20, 2048. [Google Scholar] [CrossRef]
- Nguyen, A.H.; Cho, J.-H.; Bae, H.-J.; Sung, H.-K. Side-lobe Level Reduction of an Optical Phased Array Using Amplitude and Phase Modulation of Array Elements Based on Optically Injection-Locked Semiconductor Lasers. Photonics 2020, 7, 20. [Google Scholar] [CrossRef]
- Issa, K.; Fathallah, H.; Ashraf, M.A.; Vettikalladi, H.; Alshebeili, S. Broadband High-Gain Antenna for Millimetre-Wave 60-GHz Band. Electronics 2019, 8, 1246. [Google Scholar] [CrossRef]
- Albagory, Y. An efficient WBAN aggregator switched-beam technique for isolated and quarantined patients. AEU-Int. J. Electron. Commun. 2020, 123, 153322. [Google Scholar] [CrossRef]
- Albagory, Y. Direction-independent and self-reconfigurable spherical-cap antenna array beamforming technique for massive 3D MIMO systems. Wirel. Netw. 2020, 26, 6111–6123. [Google Scholar] [CrossRef]
- Prabhu, K.M.M. Window Functions and Their Applications in Signal Processing; Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Juárez, E.; Panduro, M.A.; Reyna, A.; Covarrubias, D.H.; Mendez, A.; Murillo, E. Design of Concentric Ring Antenna Arrays Based on Subarrays to Simplify the Feeding System. Symmetry 2020, 12, 970. [Google Scholar] [CrossRef]
- Nofal, M.; Aljahdali, S.; Albagory, Y. Tapered beamforming for concentric ring arrays. AEU-Int. J. Electron. Commun. 2013, 67, 58–63. [Google Scholar] [CrossRef]
- Dessouky, M.; Sharshar, H.; Albagory, Y. Optimum normalized-Gaussian tapering window for side lobe reduction in uni-form concentric circular arrays. Prog. Electromagn. Res. 2007, 69, 35–46. [Google Scholar] [CrossRef]
- Dessouky, M.; Sharshar, H.; Albagory, Y. An Approach for Dolph-Chebyshev Uniform Concentric Circular Arrays. J. Electromagn. Waves Appl. 2007, 21, 781–794. [Google Scholar] [CrossRef]
- Dessouky, M.I.; Sharshar, H.A.; Albagory, Y.A. Efficient sidelobe reduction technique for small-sized concentric circular arrays. Prog. Electromagn. Res. 2006, 65, 187–200. [Google Scholar] [CrossRef]
- Nofal, M.; Aljahdali, S.; Albagory, Y. Simplified Sidelobe Reduction Techniques for Concentric Ring Arrays. Wirel. Pers. Commun. 2013, 71, 2981–2991. [Google Scholar] [CrossRef]
- Lau, B.; Leung, Y. A Dolph-Chebyshev approach to the synthesis of array patterns for uniform circular arrays. In Proceedings of the 2000 IEEE International Symposium on Circuits and Systems, Emerging Technologies for the 21st Century, Proceedings (IEEE Cat No. 00CH36353), Geneva, Switzerland, 28–31 May 2000; Volume 1, pp. 124–127. [Google Scholar]
- Sarker, M.A.; Hossain, M.S.; Masud, M.S. Robust beamforming synthesis technique for low side lobe level using taylor excited antenna array. In Proceedings of the 2016 2nd International Conference on Electrical, Computer & Telecommunication Engineering (ICECTE), Rajshahi, Bangladesh, 8–10 December 2016; pp. 1–4. [Google Scholar]
- Aljahdali, S.; Nofal, M.; Albagory, Y. A modified array processing technique based on Kaiser window for concentric circular arrays. In Proceedings of the 2012 International Conference on Multimedia Computing and Systems, ICMCS 2012, Tangiers, Morocco, 10–12 May 2012. [Google Scholar]
- Singh, U.; Salgotra, R. Synthesis of linear antenna array using flower pollination algorithm. Neural Comput. Appl. 2018, 29, 435–445. [Google Scholar] [CrossRef]
- Chakravarthy, V.; Rao, P.M. Circular array antenna optimization with scanned and unscanned beams using novel particle swarm optimization. Indian J. Appl. Res. 2015, 5, 790–793. [Google Scholar]
- Mehrabian, A.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Sharaqa, A.; Dib, N. Circular antenna array synthesis using firefly algorithm. Int. J. RF Microw. Comput. Aided Eng. 2014, 24, 139–146. [Google Scholar] [CrossRef]
- Sun, G.; Liu, Y.; Chen, Z.; Zhang, Y.; Wang, A.; Liang, S. Thinning of concentric circular antenna arrays using improved discrete cuckoo search algorithm. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Li, H.; Liu, Y.; Sun, G.; Wang, A.; Liang, S. Beam pattern synthesis based on improved biogeography-based optimization for reducing sidelobe level. Comput. Electr. Eng. 2017, 60, 161–174. [Google Scholar] [CrossRef]
- Van Luyen, T.; Giang, T.V.B. Interference Suppression of ULA Antennas by Phase-Only Control Using Bat Algorithm. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3038–3042. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Almagboul, M.A.; Shu, F.; Qian, Y.; Zhou, X.; Wang, J.; Hu, J. Atom search optimization algorithm based hybrid antenna array receive beamforming to control sidelobe level and steering the null. AEU-Int. J. Electron. Commun. 2019, 111, 152854. [Google Scholar] [CrossRef]
- Liang, S.; Fang, Z.; Sun, G.; Liu, Y.; Qu, G.; Zhang, Y. Sidelobe Reductions of Antenna Arrays via an Improved Chicken Swarm Optimization Approach. IEEE Access 2020, 8, 37664–37683. [Google Scholar] [CrossRef]
- Sun, G.; Liu, Y.; Li, H.; Liang, S.; Wang, A.; Li, B. An Antenna Array Sidelobe Level Reduction Approach through Invasive Weed Optimization. Int. J. Antennas Propag. 2018, 2018, 4867851. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley: Hoboken, NJ, USA, 2016; ISBN 978-1-118-64206-1. [Google Scholar]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A New Bio-inspired Algorithm: Chicken Swarm Optimization. In Advances in Swarm Intelligence; Tan, Y., Shi, Y., Coello, C.A.C., Eds.; ICSI: Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8794. [Google Scholar] [CrossRef]
- Saxena, P.; Kothari, A. Optimal Pattern Synthesis of Linear Antenna Array Using Grey Wolf Optimization Algorithm. Int. J. Antennas Propag. 2016, 2016, 1205970. [Google Scholar] [CrossRef]
- Guney, K.; Durmus, A.; Basbug, S. Antenna Array Synthesis and Failure Correction Using Differential Search Algorithm. Int. J. Antennas Propag. 2014, 2014, 276754. [Google Scholar] [CrossRef]
- Weng, W.-C.; Yang, F.; Elsherbeni, A.Z. Linear antenna array synthesis using Taguchi’s method: A novel optimization technique in electromagnetics. IEEE Trans. Antennas Propag. 2007, 55, 723–730. [Google Scholar] [CrossRef]
- Guney, K.; Durmus, A. Pattern Nulling of Linear Antenna Arrays Using Backtracking Search Optimization Algorithm. Int. J. Antennas Propag. 2015, 2015, 713080. [Google Scholar] [CrossRef]
| Benchmarking Window | Window SLL (dB) | SSD SLL (dB) | Relative Reduction in the Maximum SLL (dB) | Beamwidth (Degrees) |
|---|---|---|---|---|
| Triangular window | −26.39 | −32.32 | 6.32 | 7.12° |
| Hamming | −27.89 | −30.5 | 2.61 | 7.14° |
| Hanning | −27.6 | −30.6 | 3 | 7.14° |
| Blackman | −37.74 | −44.83 | 7.09 | 8.06° |
| Dolph-Chebyshev | −50 | −52 | 2 | 8.38° |
| Kaiser | −35.96 | −46.55 | 10.59 | 8.2° |
| Gaussian | −37.19 | −40.02 | 2.83 | 7.74° |
| Cosine square | −28 | −40 | 12 | 7.74° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albagory, Y.; Alraddady, F. An Efficient Approach for Sidelobe Level Reduction Based on Recursive Sequential Damping. Symmetry 2021, 13, 480. https://doi.org/10.3390/sym13030480
Albagory Y, Alraddady F. An Efficient Approach for Sidelobe Level Reduction Based on Recursive Sequential Damping. Symmetry. 2021; 13(3):480. https://doi.org/10.3390/sym13030480
Chicago/Turabian StyleAlbagory, Yasser, and Fahad Alraddady. 2021. "An Efficient Approach for Sidelobe Level Reduction Based on Recursive Sequential Damping" Symmetry 13, no. 3: 480. https://doi.org/10.3390/sym13030480
APA StyleAlbagory, Y., & Alraddady, F. (2021). An Efficient Approach for Sidelobe Level Reduction Based on Recursive Sequential Damping. Symmetry, 13(3), 480. https://doi.org/10.3390/sym13030480






