A Puzzle-Based Data Sharing Approach with Cheating Prevention Using QR Code

Abstract

The information technique has developed rapidly. The technique of QR codes is widely applied in our daily life, and the mechanism is suitable to share data. A QR code uses symmetric encryption to store and retrieve data efficiently. However, the security issues of QR codes are seldom discussed by the wider community. Moreover, if the sender wishes only the authorized participant to attain the private data which are shared, the data must be encrypted. Furthermore, we do not know who should be censured when problems arise. In view of this, to maintain the integrity and the confidentiality of information security, this paper proposed a new puzzle-based data sharing scheme to share the private information safely. Firstly, we generated the digital signature of the information, then applied the random grids algorithm to obtain the shares. Then, we disarrayed the shares which contain the information and the digital signature with a puzzle-based encoding method. Afterwards, we concealed them into the cover QR codes. With the QR code mechanism of error correction, the marked QR code remain meaningful. Finally, we could send marked QR codes via transmission. The receiver could use XOR operation to obtain the private information after solving the puzzles and verify whether it was tampered with by the digital signature. The proposed system can recover the lossless data and protect them from being divulged. To deal with the potential hazard of transmission in a public environment, there are more and more studies on data hiding and image authentication.

1. Introduction

With the rapid development of the Internet and information technology, the amount of people using smart phones has risen. Additionally, it is notable that the usage of smart phones has been enriched with functions such as sending e-mails, searching information on the Internet, or shopping on websites, paying online or credit transferring with confidential information features. Therefore, the security when transferring sensitive data should be ensured, otherwise people might suffer from the theft of personal property.

It is noteworthy that QR codes can store data and be used for obtaining data when the device is offline. They have been used widely in daily life for functions such as ticketing systems, product tracing, electronic transactions, social networks, etc. However, people usually scan them directly, without confirming their trustworthiness. Cryptography is a common method to assure the information security in the digital transmission. There are two ways to encrypt private data via cryptography, symmetric cryptography and asymmetric cryptography [1]. A QR code uses an asymmetric encryption scheme to store and retrieve data efficiently [2,3]; QR codes are not readable with the naked eye and people usually rely on optical instruments when scanning for data. When operating the information obtained from public environments, it is possible that the users might expose their sensitive information, as they are not aware that the QR code might have been tampered with, and the website address they are accessing could possibly be a phishing website [4,5,6,7,8]. Therefore, it is necessary that people have a way to validate if the website address is issued by the publisher. If paying information is usurped, it might bring about financial losses. Moreover, if the personal and private information is leaked to a phishing website, it could endanger the personal safety of the user. In other words, it is more and more important to verify the data or website addresses from QR codes in this information based society we live in.

Owing to the designed mechanism, anyone who has a camera built into their smart phone and installs QR code scanning software could scan a QR code to acquire the information of it. That shows the potential risks: it is possible that the information of QR code might be divulged to hackers. For the most part, to protect the private data that would be shared by QR code, the administrator will store the message in the database in the cloud, and replace the message with an URL showing a website address that could link to the backend database. Only a user who has right to pass the access permission can retrieve the data. However, this method of showing the database website address may attract attackers’ attention to try to access the secret message.

Recently, in order to prevent the data which have to be hidden from exposure to the public, many studies have focused on QR codes. In 2009, Chen et al. [9] proposed a scheme that utilizes steganography. It firstly generates a QR code with a text, then removes some functional patterns of QR code. As a result of removing the position detecting pattern and alignment pattern, the QR code would only retain the important information, such as version, error correction level, data and error correction codewords, etc. Then, flatten them from a 2-D bit stream into 1-D bit stream. Finally, after choosing the coefficients of discrete cosine transform (DCT), the 1-D bit stream would be embedded into the cover image. The secret payload would depend on the version of QR code image. However, this scheme would cost lots of computational resources.

On the other hand, Sun et al. [10] proposed a watermarking scheme applied to QR codes. There are two algorithms in the scheme; both of them are utilized with Discrete Wavelet Transform (DWT). One firstly generates random serial numbers as secret key, then embeds them into the cover of the QR code for authentication. The other one embeds a binary image, such as a logo, into the cover of the QR code, preventing counterfeits. However, neither algorithm modifies modules in the QR code, which would make the cover QR code, and the fact that it is embedded with some information, easily found.

There are distributed data sharing schemes [11,12,13,14,15,16,17] that allow the message to be segmented into numerous shadows. The original message can be recovered when the participants hold enough shares which contain the shadows. Furthermore, these data sharing schemes use QR codes as cover images, and all of them modify the modules to share the data (except Chuang et al.’s scheme [13]). Utilizing the error correction characteristic of QR codes, the schemes could allow the marked QR code to remain meaningful. However, Lin et al.’s scheme [12] would cause additional issues on distributing the keys, though it could hold more space for data. In [15], Huang et al. proposed an efficient QR code data embedding mechanism based on the Hamming code. The (8, 4) Hamming code is utilized for embedding the secret message into the cover of a QR code. In [16], Alajmi et al. proposed a steganographic system that adopts the notion of quick response (QR) code as a container for hiding the payload. By doing so, misleading information can easily be exposed to the adversary.

Although Chuang et al.’s scheme [13] and Huang et al.’s scheme [15] can share data without additional information, the message would be obtained as a meaningless number stream by anyone who has a QR code reader. It would be a serious problem if everyone can access the shadow of secret bits without any permission or requirement. In another aspect, Lin’s scheme can make the marked QR codes be meaningful, but it needs to manage key distribution. Without knowing the keys, the scheme cannot recover the original message.

To overcome the above-mentioned issues, Huang et al. [11] proposed a scheme that utilizes a Sudoku puzzle to encode secret message and embed it into QR codes. However, using Sudoku puzzle to encode data would raise two issues: (1) a low capacity for the message and (2) a limited position of the puzzle. The issue of low capacity for the message is due to the fact that embedding a whole Sudoku puzzle would cost lots of bits. However, using a Sudoku puzzle to encode a message may cost a lot of digits of QR code for embedding the puzzle into QR code. For example, it could be referred that novenary $\times$ Sudoku puzzle size = 4 bits $\times$ (9 $\times$ 9) = 364 bits for each share when we embed a message with 0 bits. Moreover, the method of Sudoku puzzle encoding is coordinate-like, which leads to the issue of a limited position of the puzzle. As a result, it would cost additional bits to represent the coordinates of each cell of the Sudoku embedded in QR codes. As shown in Huang et al.’s work [11], when the secret message is “2015”, firstly transform it into novenary: ${\left(2015\right)}_{10}={\left(2678\right)}_9$. Then, it would be represented as $\left(6\mathrm{DA}122\mathrm{EC}\right)$ accordingly. Finally, it will cost 4 bits hexadecimal $\times$8 = 32 bits, simply for sharing a 4-digit number. To address the issues raised by the Sudoku puzzle-based QR code scheme, in this paper, we propose a new breed of puzzle which is coordinate-free. Based on our proposed coordinate-free puzzle, we propose a new scheme which can preserve more capacity for data. Through a series of experiments, we provide sufficient evidence to prove that our proposal outperforms state-of-the-art QR code data embedding schemes.

The rest of this paper is organized as follows. We first introduce some related work in Section 2. Section 3 explains the deep learning-based approaches for Image Authentication and Recovery System. Section 4 presents the experiment and discussion, and Section 5 contains the conclusion.

2. Related Works

2.1. Technique of QR Code

The QR code (Quick Response code) is a public standard published in ISO/IEC18004. It is a two-dimensional barcode, and features high data storage, error correcting, and quick response. Since its invention in 1994 by Japanese company Denso Wave [18], it has become a part of daily life in activities such as exchanging business cards, object identification, stocks marketing, policy publicizing, advertising, etc. Meeting the demand of quickly exchanging data, QR codes offer a substantial decrease in time, compared to keying in a website address or data input by hand. QR codes provide a way to obtain data quickly, becoming a common way of marketing. Compared to a one-dimensional barcode, there are more resemblances to an image with the two-dimensional QR barcode. Moreover, as there are two dimensions, the QR barcode can carry more data, and also correct the failure of some errors even if it was damaged. Moreover, unlike one-dimensional barcodes which require straight aim, the QR code can be scanned at different angles and still obtain the data.

The most basic element of the QR code is the modules; the white represents 0 and the black is 1. Several modules can compose a codeword, which can represent characters depending on which encode mode is used. For instance, the byte mode will use 8 modules to compose one codeword and represent one character. Moreover, to improve the capability of scanning, the position detecting pattern will be a part of the QR code image. If the version of QR code is larger, the alignment pattern might be used to support the process of scanning.

There are many tools and open-source software nowadays, such as Zxing [19], which offer users the ability to produce and scan QR codes conveniently. When producing a standard QR code, there are many choices of versions and error correcting levels available. If the data stream is too big to fit in the QR code, a higher version is a better option. However, a higher version means a larger size of QR code image, and it is not easy to scan for data if the QR code image is too large. Another way could be a substitute plan: choosing a lower error correction level.

Although a lower error correction level could make the storage of QR code increase, it indicates that the capacity of restoring original data when the QR code is damaged will drop, as Table 1 shows. After choosing the version and error correcting level, depending what type of data are input, an encoding type would be selected. The data would be stored in different ways according to the form of data. They are: numeric, alphanumeric, byte encoding, and Kenji. Each type needs a distinct data bit to represent themselves.

Table 1. Comparison of different error correction levels.

Error Correction Level	Capacity of Recovering Data of QR Code
Level L	Approximately 7%
Level M	Approximately 15%
Level Q	Approximately 25%
Level H	Approximately 30%

Afterwards, the error correcting code would be generated by the Reed Solomon algorithm, referring to the selected error correcting level being used to try to recover original data when QR code image is damaged in the future. Then, the encoded data stream and error correcting code would be put to the data blocks and error correcting blocks of QR code, as Figure 1 shows. To enhance the readability, the program will calculate every pixel of the QR code image and decide which mask to use, then apply the best mask to the QR code image.

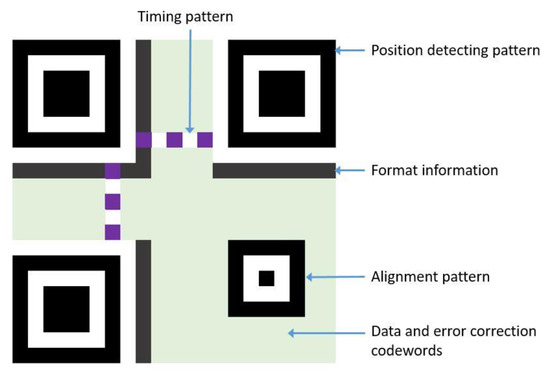
Figure 1. Structure of a QR code.

2.2. Encryption of Pictures and Shapes by Random Grids by Kafri et al.

The random grids algorithm is one kind of visual data sharing technique. It was proposed by Kafri et al. [20] in 1987. The algorithm is described as Algorithm 1. Briefly, for a secret image $S$ with a size of $W\times H$, it will generate two shares, $S{C}_1$ and $S{C}_2$, with the same size according to the algorithm. The pixels of $S{C}_1$ are randomly chosen to be black or white, and the pixels of $S{C}_2$ refer to the pixel value of the position in $S$; if the position indicates a bit which calls for a black pixel, then the pixel of same position in $S{C}_2$ would be set as the opposite value in same position of $S{C}_1$, otherwise set it as same value of $S{C}_1$. By stacking $S{C}_1$ and $S{C}_2$, there might be a 50% chance that the white pixel of original secret image will be white in the recovered image, while the black pixels have 100% chance of being black in the recovered image.

Applying the random grids algorithm could not only solve the problem of pixel expansion [21], but also utilize the randomness for preventing those unauthorized from stealing the secret directly. This design of algorithm makes the secret image remain confidential and safe, as the process of recovering needs to have two shares at the same time. It would not be 100% recovery when stacking the shares.

Algorithm 1 The random grids secret sharing [20]

Input: secret image S with size of W × H

for the pixel of S(i, j), 0 ≤ i ≤ W, 0 ≤ j ≤ H

SC1(i, j) = random of {0, 1}

if S(i, j) = 0

SC2(i, j) = SC1(i, j)

else

SC2(i, j) = !SC1(i, j)

Output: share 1 SC1 and share 2 SC2

Besides recovering secret image by stacking shares, there are other systems [22,23] could restore 100% secret bits by applying XOR operation with shares. By operating (2,2)-threshold XOR-based random grids algorithm, a 100% recovery rate can be achieved when restoring the original secret image. It is a lossless recovery technique of data sharing and it will not leak the confidentiality by holding just one share.

2.3. Digital Signature

The technique of the digital signature was first proposed by Rives et al. [24] in 1978. It utilizes the public-key cryptosystem by Diffie and Hellman (1976) [25]. The process of producing a digital signature is shown in Figure 2. First, the message digest would be generated by passing the data (document, data, etc.) to the hash function, e.g., SHA-256, MD5, etc. A hash function must be in keeping with the definitions [26]:

(a)

Output should have a fixed length data stream for any length input.

(b)

It is hard to find a same value by given different inputs.

(c)

Without knowing the input, it is hard to search out the input by given the message digest.

Then, the message digest is encrypted by public-key cryptosystem, e.g., RSA, with a private key which should be kept carefully by the publisher. The theorem of the RSA algorithm is using two large primes to make the encrypted message be difficult to decrypt due to the computational complexity [27]. The concept of RSA is described as following [24]:

(a)

Let N be the multiplied result of two not equal primes p and q.

(b)

Find r and choose e, which is coprime with r by formula $\left(1\right)$.

(c)

Use formula $\left(2\right)$ to find d, which is modular multiplicative inverse of e.

(d)

Let the e be the public key and d the private key.

$$r=\lambda \left(N\right)=\mathrm{lcm}\left(\lambda \left(p\right),\lambda \left(q\right)\right)=\mathrm{lcm}\left(p-1,q-1\right)$$

(1)

$$d\times e \mathrm{mod} \lambda \left(N\right)=1$$

(2)

By finishing the digital signature, a client can validate the data which are sent via untrusted internet by comparing the hash values of the digital signature and original document. The safety of the algorithm will raise when the length of chosen primes increased [25].

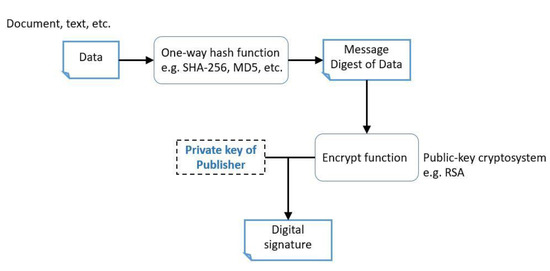
Figure 2. The process of digital signature [28].

3. Proposed Method

The proposed method is a (2,2)-threshold random grids data sharing system based on the QR code technique and a new method, which is puzzle based, to encode a bit stream. The secret sharing procedure of the proposed system is shown in Figure 3. There would be one dealer and two participants in the proposed system. The dealer is in charge of generating the digital signature and appending it to the message, then transforming it into a binary bit stream. Afterwards, the dealer encrypts it into two shares then encodes them as puzzles, which will be discussed in Section 3.1.2, and conceals them to in two QR codes. Finally, the dealer distributes them to the participants. The shared data can be restored by solving the puzzles when both marked QR code images are obtained. It will not leak any secret message if there is a marked QR code image missing, or without knowing the solution of puzzles. Moreover, the proposed system can achieve cheater prevention by comparing the technique of digital signature.

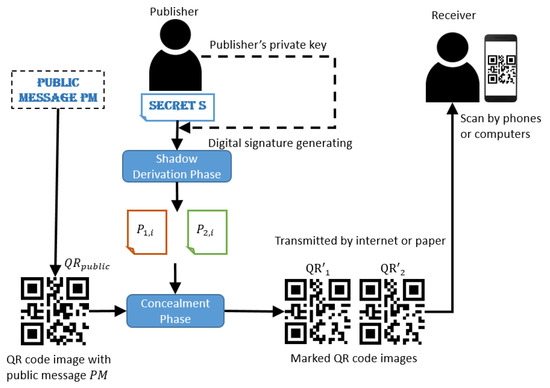
Figure 3. The secret sharing procedure of the proposed system.

3.1. Secret Sharing Procedure

In this section, the process of generating marked QR codes will be described clearly, with some instances for illustration.

3.1.1. Shadow Derivation Phase

Step 1. Generate public key and private key.

For instance, two random prime numbers: p = 13,990,592,845,718,003,597 and q = 15,765,429,783,677,334,361 then determine e = 65,537. Afterwards, d could be calculated as 147,609,429,104,525,097,256,750,152,470,343,671,393 by formula (1) and (2). Finally, e is the public key and d is the private key.

Step 2. Generate message digest by one-way hash function.

$$V=hash\left(S\right)$$

(3)

There would be a one-way hash process to do in the process of a digital signature. Take MD5 as example; it would output a 128-bit length message digest, no matter how long the input is [29], and the output bit stream can be represented as characters. For instance, regard “NCHU” as input then the message digest $V=\mathrm{MD}5\left(“\mathrm{NCHU}”\right)= \mathrm{beca}06031\mathrm{f}14907\mathrm{b}$.

Step 3. Encrypt the hash value by RSA encrypting function to Generate digital signature

$$D=RSA\left(d,V\right)$$

(4)

For instance, the digital signature should be produced as below:

$$D=V^{\mathrm{d}} mod \left(p\times q\right)=332\mathrm{d}82590\mathrm{cc}95078\mathrm{abd}5\mathrm{a}7\mathrm{eb}5\mathrm{f}9\mathrm{e}9\mathrm{a}66$$

Notice that the public key is distributed, and the private key is kept carefully by the publisher.

Step 4. Let $B=(S\Vert D)$ and convert it into a binary bit stream.

Step 5. Calculate the length of $B$ as $l_B$ then apply random grids algorithm described below where $i=0, 1,\dots ,l_B-1$.

$$Shar{e}_1\left(i\right)=random\left(\left\{0,1\right\}\right)$$

$$Shar{e}_2\left(i\right)=\{\begin{array}{c}Shar{e}_1\left(i\right) \mathrm{if} B\left(i\right)=0\\ !Shar{e}_1\left(i\right) \mathrm{if} B\left(i\right)=1\end{array}$$

(5)

3.1.2. Puzzle-Based Encoding

In this section, the process of generating marked QR codes will be described clearly with some instances for illustration.

Preliminary Phase

Step 1. The idea of puzzle: let 8 digital bits with 0 or 1, which mean white and black, respectively, be put into a size of $3\times 3$ grids in sequence, but skip the middle center to fit its size, as shown in Figure 4b. The sequence is arranged as the order of codeword, which is read by zig-zag, as shown in Figure 4a, then regard it as the puzzle.

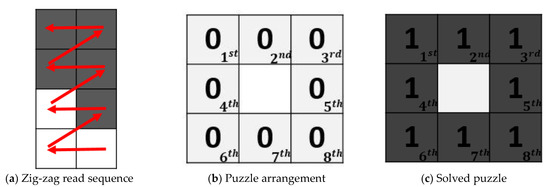
Figure 4. Basic idea of puzzle.

Step 2. The rules of the puzzle: the solution of the puzzle is making it to be full of 1 (black), as shown in Figure 4a show, by choosing the position in the grids to change its state. If we choose the $n^{th}$ position of the grids to change, then the neighbors of the $n^{th}$ which means $n-1^{th}$, $n+1^{th}$ and itself would change the state of them, e.g., if the state of the $n^{th}$ position is 0 then it would be change into 1, otherwise 1 would do so into 0. When the puzzle is full of 1, it has been solved with the rules. Then, we consider those grids we have chosen is the original secret.

For example: there is an unsolved puzzle, and the bit stream is “00101111”; to solve it, the $1^{th}$ grid should be chosen, and the other grids are not selected. Then, mapping those grids which is chosen into 1, the others are 0. There will be an 8-bit stream and find out the original secret is “10000000”.

Step 3. Examine the collision: generate whole set and check the solutions of itself whether there are collisions of it. Firstly, produce two sets with all possibilities of the 8-bit stream: one is for the puzzle set and the other is the solution set. Then, apply Algorithm 2 described below:

Algorithm 2 Examine the collision

Produce two set, Setp and Sets and an empty set Setc for mapping

for i in each Setp:

for j in each Sets:

solve Setp(i) by applying Sets(j)

candicate_answer = Sets(j)

if (candicate_answer could be the solution of Setp(i))

solution_count++

end for

if solution_count < 1:

alert “no solution”

else if solution_count > 1:

alert “collision”

else put the candicate_answer into Setc(i)

end for

The result shows that there is only one solution for each puzzle, so it can be regarded as a one-to-one mapping encoding method.

Phase I. Encoding Phase:

Step 1. Generate $Block{s}_n\left(i\right)$ by splitting every 8 bits of $Shar{e}_n, i=0, 1,\dots ,l, n=1, 2$ where $l$ = $\left(\mathrm{length} \mathrm{of} Shar{e}_1\right)/8-1$ which would be same as ${{Share}^{\prime }}_2$.

Step 2. Produce $P_{n,i}$ = puzzle of $Block{s}_n\left(i\right)$ by mapping each bit stream blocks, $i=0, 1,\dots ,l, n=1, 2$

$$P_{n,i}=Se{t}_p\left(\mathrm{index} \mathrm{of} Block{s}_n\left(i\right) in Se{t}_c\right)$$

(6)

Step 3. Append each block value of $P_{n,i}$ into bit steam as $B_n$ where $i=0, 1,\dots ,l, n=1, 2$

$$B_n=(P_{n,1} \Vert P_{n,2} \Vert \dots \Vert P_{n,i})$$

(7)

Phase II. Concealment Phase:

Step 1. Calculate the length of $B_n$ then choose the best version and EC level for generating public QR code image $Q{R}_{public}$ with public message $PM$.

Step 2. Replace the data codewords of $Q{R}_{public}$ with bit stream $B_n$ which is in compliance with the codewords format of QR code.

• Then, there would be two marked QR codes, ${{QR}^{\prime }}_1$ and ${{QR}^{\prime }}_2$. Both of them could be scanned with a QR code decoder and only come up with public message of $Q{R}_{public}$ instead of the camouflage bit stream $B_n$.
• Notice that if someone replaces the data codewords of a QR code, it will lead to massive errors of the QR code. Therefore, make sure that the numbers of error correction codes which belongs to $Q{R}_{public}$ could work with the amount of those replaced data codewords; in other words, the marked QR code should still be able to be decoded by a common QR code decoder and bring out the public message.

3.2. Secret Retrieval Procedure

Firstly, scan the marked QR codes, then obtain the public messages and ${B^{\prime }}_n$. Note that ${B^{\prime }}_n$ are separated from the data codeword blocks of ${{QR}^{\prime }}_n$ by the QR code decoder.

3.2.1. Phase I. Puzzle Decoding Phase:

Step 1. Convert ${B^{\prime }}_n$ into ${P^{\prime }}_{n,i}$ by splitting with every 8 bits of it.

Step 2. Generate ${{Blocks}^{\prime }}_n\left(i\right)$ by mapping ${P^{\prime }}_{n,i}$ with $Se{t}_c$

$${{Blocks}^{\prime }}_n\left(i\right)=Se{t}_c\left(\mathrm{index} \mathrm{of} {P^{\prime }}_{n,i} in Se{t}_p\right)$$

(8)

3.2.2. Phase II. Secret Recovering Phase:

Step 1. Recover ${{Share}^{\prime }}_n$ by appending ${{Blocks}^{\prime }}_n\left(i\right)$

$${{Share}^{\prime }}_n=({{Blocks}^{\prime }}_n\left(1\right) \Vert {{Blocks}^{\prime }}_n\left(2\right) \Vert \dots \Vert {{Blocks}^{\prime }}_n\left(i\right))$$

(9)

Step 2. Restore $B^{\prime }$ by random grids algorithm.

$$B^{\prime }={{Share}^{\prime }}_1 \oplus {{Share}^{\prime }}_2$$

(10)

Step 3. Transform $B^{\prime }$ with ASCII table and obtain $S^{\prime }$ and $D^{\prime }$

3.2.3. Phase III. Cheater Identification:

Step1. Generate authentication bit stream value by hash the $S^{\prime }$.

$$V^{\prime }= \mathrm{Hash}\left(S^{\prime }\right)$$

(11)

Step 2. Decrypt the digital signature $D^{\prime }$ into $\overline{V}$ by applying RSA decrypting function.

For instance, the digital signature should be decoded as follows:

$${D^{\prime }}^e mod \left(p\times q\right)= \mathrm{beca}06031\mathrm{f}14907\mathrm{b}$$

Step 3. Compare $\overline{V}$ to $V^{\prime }$; if $\overline{V}$ is different from $V^{\prime }$, that means the secret message $S^{\prime }$ has been tampered with, and it is not the original secret message $S$. Then, $S^{\prime }$ is not trustworthy, and should be discarded. If not, we can trust $S^{\prime }$ is same as $S$.

4. Experimental Result

To evaluate the practical applicability of the proposed scheme, an application is developed with the open-source library, ZXing library [19] which is based on Java program language and used to generate and decode QR codes. According to the QR code standard, the 5-H version of QR code consists of 134 codewords. There would be 46 data codewords and 88 error correction codewords in the QR code. We choose the byte mode to generate QR code images in the proposed system. Then, Figure 5 shows the other example of the proposed scheme with version 10, and the error correction level is Q. Figure 5a,b show the public message of QR codes with “https://www.nchu.edu.tw/” (accessed date: 9 September 2021) and http://mis.nchu.edu.tw/ (accessed date: 28 September 2021), the website addresses to the homepages of National Chung Hsing University and Management Information System Department of National Chung Hsing University. Figure 5c,d are the marked QR codes. The result shows that the higher version of QR code may cause delay time as the camera of smart phone needs to focus on the QR code image when the size of itself is fixed.

Figure 5. Examples of the proposed scheme with version 10 and error correction level with Q. (a) Cover QR code 1. (b) Cover QR code 2. (c) Marked QR code of (a). (d) Marked QR code of (b).

The feature of meaningful QR codes could decrease the curiosity of common QR code users when scanning in public environment. Moreover, the designed scheme, which is puzzle-based and cheater preventing, could protect the secret message from a malicious attack of altering the QR code image. According to the cheater identification phase of the proposed scheme, the digital signature will be obviously different, as the technique can distinguish if even one bit from the real marked QR code is modified. In addition, the designed puzzle in the proposed scheme would be totally changed if there is a bit different from original bit stream of puzzle.

Table 2 illustrates the capacity of private data storage of the proposed scheme. The digital signature is composed of 32 bytes which is equal to at least 256 bits. The more bits of public and private keys chosen, the more bytes the digital signature would need. Additionally, the minimum secret message is one character; in other words, 1 byte of secret message is needed. Then, the digital signature appended after the minimal secret message will result in a 33-bytes camouflage message. Beside the least length calculation, the mechanism of error correction of the QR code is generated by the Reed Solomon Code algorithm [30], therefore, there should be two error correction codewords to recover one data codeword for the marked QR code.

Table 2. The capacity of secret storage of the marked QR code applied with proposed scheme, in different versions, and the error correction levels according to the QR code standard.

Version	Error Correction Level	# of Codewords	# of Error Correction Codewords	Max Number of the Modified Codewords	Max Numbers of the Secret Shadow Bits
1	L	19	7	3	0
	M	16	10	5	0
	Q	13	13	6	0
	H	9	17	8	0
5	L	108	26	13	0
	M	86	48	24	0
	Q	62	72	36	32
	H	46	88	44	96
10	L	274	72	36	32
	M	216	130	65	264
	Q	154	192	96	512
	H	122	224	112	640
20	L	861	224	112	640
	M	669	416	208	1408
	Q	485	600	300	2144
	H	385	700	350	2544
30	L	1735	450	225	1544
	M	1373	812	406	2992
	Q	985	1200	600	4544
	H	745	1440	720	5504
40	L	2956	750	375	2744
	M	2334	1372	686	5232
	Q	1666	2040	1020	7904
	H	1276	2430	1215	9464

In a drastic situation, the 33 bytes of camouflage message with the minimum amount of data, there must be more than 66 error correction codewords on the QR code image. By calculating with the QR code standard, it can be found that version 5, with error correction level Q, could be in accordance with the minimum that the bytes of the least camouflaged message needs. The schemes mentioned in Section 2 will be discussed and compared to the proposed scheme. Table 3 shows the summary of feature comparison among them. To overcome the drawback brought from the Sudoku puzzle, a new puzzle-based scheme has been proposed in this paper. By applying the puzzle algorithm, the shadows can be protected in an efficient way, and there is no need to put additional information with it. In addition, the technique of a digital signature could not only verify the publisher, but also procure the purpose of authentication. Though it requires more bits than only utilizing the one-way hash function, it can protect the information with better security.

Table 3. Feature comparisons among the previous schemes and the proposed method.

Functionality	Chuang’s Scheme [13]	Lin’s Scheme [12]	Huang’s Scheme [11]	The Proposed Scheme
Meaningful marked results	No	Yes	Yes	Yes
Module-based modifying	No	Yes	Yes	Yes
Utilizing the error correction capability	No	Yes	Yes	Yes
Cheating prevention	No	Yes	Yes	Yes
Identify the cheater	No	It depends	Yes	Yes
Measures to identify the cheater	None	Message digest of the keys	Message digest of the Sudoku table and shadows	Digital signature of the secret
Reveal the secret without additional information	No	No	Yes	Yes
Minimum version and EC level of QR codes	It depends	It depends	7-H	5-H
Capacity of secret message	Numbers of data codewords	Adjustable 24~9720 bits	Adjustable 20~9260 bits	Adjustable 32~9464 bits

Aside from providing an efficient encoding method, the marked QR code can resist many kinds of defects which may be caused by the transmission process. Table 4 shows that the marked QR code version 10, with error correction level Q, suffered from Gaussian noise by standard deviations of 10 to 100, and can still be scanned for data. Table 5 points out that the same mark QR code could still be decodable after Gaussian blur with different radii of pixels. Table 6 indicates that the marked QR code can perform well under JPEG compression with disparities of compression rates. Table 7 illustrates the fact that the marked QR code can still be scanned for information from different angles of rotation. Figure 6a shows the tempered marked QR code with different blocks alteration. Figure 6b indicates the tempered marked QR code with a large block modification. All could be decoded for a meaningful message.

Table 4. The results of the marked QR code of Figure 5d after Gaussian noise.

Standard Deviation	10	30	50	70	100
Distorted QR code

Table 5. The results of the marked QR code of Figure 5d after Gaussian blur.

Radius	3 Pixels	6 Pixels	9 Pixels	12 Pixels	15 Pixels
Distorted QR code

Table 6. The results of the marked QR code of Figure 5c after JPEG compression.

Compression	20%	40%	60%	80%	100%
Distorted QR code

Table 7. The results of the marked QR code of Figure 5d after different angles rotated.

Rotation	45°	90°	135°	270°	315°
Distorted QR code

Figure 6. Results of marked QR code after different blocks alteration.

The feature comparison among the proposed method and previous schemes is shown in Table 3. The proposed scheme can not only ensure the marked QR code remains meaningful, but can also accomplish cheater identification. Moreover, the proposed scheme can use a lower version of QR code, which means the size of QR code image could be smaller. The capacity of the proposed scheme can hold more data than the others, except Lin’s scheme. Though Lin’s scheme could hold more bits than ours, the ability of identifying cheater is varied down to nothing. Notice that in the data capacity of Huang’s scheme, the maximum is 9260 bits with careful calculation, and not 9260 guaranteed, which is pointed out in Huang et al.’s scheme.

5. Conclusions

This paper presents a new puzzle based QR code data embedding scheme to share the private information safely. To enhance the capacity for embedding private data, we propose a new breed of puzzle which is coordinate-free. Instead of a Sudoku puzzle, our proposed puzzle is utilized for encoding the shadows in an efficient way without any collisions. As a result, our proposal can offer the capability of cheater identification and feasibility of adjustable secret message. According to experimental results, we can see that our proposed puzzle-based encoding method has low computational complexity but still promises a certain extent of security when encoding. Concealing the shadows into the QR codes with the characteristic of error correction can keep the shares meaningful. For future work, we plan to design a new breed of puzzle to integrate the notion of homomorphic encryption, so that QR codes can represent one character with higher security, meaning retention, and cheater identification.