A Single-Key Variant of LightMAC_Plus

Abstract

LightMAC_Plus proposed by Naito (ASIACRYPT 2017) is a blockcipher-based MAC that has beyond the birthday bound security without message length in the sense of PRF (Pseudo-Random Function) security. In this paper, we present a single-key variant of LightMAC_Plus that has beyond the birthday bound security in terms of PRF security. Compared with the previous construction LightMAC_Plus1k of Naito (CT-RSA 2018), our construction is simpler and of higher efficiency.

1. Introduction

A MAC (Message Authentication Code) is a fundamental symmetric-key primitive that produces a tag to authenticate a message. MACs are often based on a blockcipher (e.g., CBC-MAC [1], PMAC [2], OMAC [3], LightMAC [4]) so that these become secure PRFs (Pseudo-Random Functions) under the standard assumption that the underlying keyed blockciphers are pseudo-random permutations because of the well known observation that PRFs are secure MACs [1]. Most blockcipher-based MACs have a security bound that is called birthday security, i.e., against up to $O\left(2^{n/2}\right)$ adversarial queries (here n is the block length of the underlying blockcipher).

However the birthday bound security may not be enough for blockciphers with short block sizes such as TripleDES and lightweight blockciphers such as PRESENT [5], LED [6], GIFT [7]. Therefore, designing a MAC with beyond birthday-bound security is an important research of MAC design. This kind of MACs contribute not only to the longevity of 128-bit blockciphers but also to blockciphers with short block sizes. To go beyond birthday-bound security, a series of blockcipher-based MACs have been proposed, including SUM-ECBC [8], PMAC_Plus [9] and 3kf9 [10].

LightMAC [4] is a variant of PMAC [2] and the first blockcipher-based MAC with birthday security without message length. In LightMAC, for each n-bit blockcipher call, an m-bit counter and an $(n-m)$-bit message block are input. By the presence of counters, LightMAC becomes a secure PRF up to $O\left(2^{n/2}\right)$ tagging queries. LightMAC, adopts the counter-based construction used in the protected counter sum [11] and XOR MAC [12] to avoid the input collision. So the input for the i-th blockcipher call is ${⟨i⟩}_m\parallel M_i$, where ${⟨i⟩}_m$ represents the corresponding m-bit binary number of i and $M_i$ represents the i-th message block of $n-m$ bits. For LightMAC, the xor value of the blockcipher outputs becomes a hash value, and then a tag is defined by encrypting the hash value. LightMAC_Plus proposed by Naito [13] is a blockcipher-based MAC which is beyond birthday secure up to roughly $2^{2n/3}$ (tagging or verification) queries. LightMAC_Plus follows the Double-Block Hash-then-Sum (DbHtS), where a message is first mapped into a $2n$-bit string by a double-block hash function and then the two encrypted values of each n-bit half is xor-summed to generate the tag. Datta et al.  [14] have proved that both three-key and two-key DbHtS constructions can achieve beyond-birthday-bound security with a bound $q^3/2^{2n}$ where q is the number of MAC queries. Leurent et al.   [15] show attacks on all three-key DbHtS constructions with query complexity $2^{3n/4}$. Very recently, Kim et al.  [16] give a tight provable bound $q^{4/3}/2^n$ for three-key DbHtS constructions. Compared with LightMAC, LightMAC_Plus has a better security bound but the key size is increased and the efficiency is degraded.

Naito also proposed LightMAC_Plus1k [17] which is a single key variant of LightMAC_Plus. LightMAC_Plus1k has been proved the same level of security as LightMAC_Plus. To reduce the number of the keys from three to one, Naito use the first two bits for the domain separation: in the hash part, the most significant bit of an input to the blockcipher is set to zero; in the finalization function, the most significant two bits are 10 and 11. Moreover, by using of the domain separation, a 4-bit security degradation is compromised from LightMAC_Plus to LightMAC_Plus1k.

Our Contributions

Our main contribution in this paper is to design a simpler and more efficient single key variant of LightMAC_Plus, but with the same secure level as LightMAC_Plus1k. The new construction is called 1k-LightMAC_Plus. In order to reduce the key size, we also use the domain separation technique. Different from LightMAC_Plus1k, the hash function for 1k-LightMAC_Plus remains the same with LightMAC_Plus. In the finalization function, the least significant bit of an input to one of two keyed blockciphers is fixed to zero and the other is fixed to one. Due to the domain separation, the two blockciphers calling with the same key in the finalization function have completely distinct input sets. What is more, we proved that 1k-LightMAC_Plus has the same security level as LightMAC_Plus1k in the sense of PRF security.

2. Preliminaries

2.1. Notations

${\{0,1\}}^n$ represents the set of all strings of length n. For any two strings $X,Y\in {\{0,1\}}^{*}$, denote their concatenation as $X\left|\right|Y$, and donote their bitwise exclusive or as $X\oplus Y$. . $\left|X\right|$ denotes the bit length of string X. We use $N=2^n$. We use $\mathbf{1}$ and $\mathbf{0}$ to denote the $n-$bit binary string $0^{n-1}\parallel 1$ and $0^n$, respectively. Moreover we denote $a\in \{b,b\oplus 1\}$ as $a{=}_{1}b$ for $a,b\in {\{0,1\}}^n$. That is, $a{=}_{1}b$ implies either $a=b$ or $a=b\oplus 1$ but not both. The natural index set $\{1,2,\cdots ,q\}$ is denoted as $\left[q\right]:=[1\cdots q]$ for a positive integer q. For a given ordered set $\mathcal{S}$ we use $\min \mathcal{S}$ to denote the minimum element of $\mathcal{S}$. $\mathcal{X}\cap \mathcal{Y}$ denotes the intersection of set $\mathcal{X}$ and $\mathcal{Y}$. If $\mathcal{X}\cap \mathcal{Y}=\varnothing$ then we write $\mathcal{X}\bigsqcup \mathcal{Y}$ to denote the disjoint union. The set of all functions from $\mathcal{X}$ to $\mathcal{Y}$ is denoted as $\mathrm{Func}(\mathcal{X},\mathcal{Y})$ and the set of all permutations over $\mathcal{X}$ is denoted as $\mathrm{Perm}\left(\mathcal{X}\right)$. The notation $X\stackrel{\$}{\leftarrow }\mathcal{S}$ means that X is chosen uniformly at random from a finite set $\mathcal{S}$ and independently of all other random variables defined so far. We also denote $\mathbf{P}(a,b)$ as the number of permutations of taking b objects from a distinct objects at a time, which means that $\mathbf{P}(a,b)={\prod }_{i=1}^b(a-(i-1))$. For a list $\mathcal{L}=\{(a_1,b_1),\cdots ,(a_{\ell },b_{\ell })\}$, $\mathrm{Dom}\left(\mathcal{L}\right):=\{a_1,\cdots ,a_{\ell }\}$, $\overline{\mathrm{Dom}\left(\mathcal{L}\right)}:={\{0,1\}}^n\backslash \{a_1,\cdots ,a_{\ell }\}$ and $\mathrm{Rng}\left(\mathcal{L}\right):=\{b_1,\cdots ,b_{\ell }\}$, $\overline{\mathrm{Rng}\left(\mathcal{L}\right)}:={\{0,1\}}^n\backslash \{b_1,\cdots ,b_{\ell }\}$.

2.2. Security Definitions

$F:\mathcal{K}\times \mathcal{X}\to \mathcal{Y}$ is a keyed function with domain $\mathcal{X}\subseteq {\{0,1\}}^{*}$, range $\mathcal{Y}$ and key space $\mathcal{K}$. We also write $F_K\left(X\right)$ for $F(K,X)$. A $(q,t,\sigma )$-distinguisher in the presence of F is an algorithm $\mathcal{A}$ that has oracle access to a function with domain $\mathcal{X}$ and range $\mathcal{Y}$. Assume that $\mathcal{A}$ makes at most q queries and totally $\sigma$ blocks one whose running time is at most t, and finally outputs a single bit. The PRF-security of F, i.e., distinguishing F from R that is randomly uniformly chosen from $\mathrm{Func}(\mathcal{X},\mathcal{Y})$, is defined as

$${Adv}_F^{\mathrm{prf}}\left(\mathcal{A}\right)\stackrel{\mathrm{def}}{=}\left|\mathrm{Pr}\left[K\stackrel{\$}{\leftarrow }\mathcal{K}:{\mathcal{A}}^{F_K}=1\right]-\mathrm{Pr}\left[R\stackrel{\$}{\leftarrow }Func(\mathcal{X},\mathcal{Y}):{\mathcal{A}}^R=1\right]\right|.$$

$F_K\left(X\right)$ becomes a permutation When $\mathcal{X}=\mathcal{Y}$. Then the PRP-security of F can be defined as follows.

$${Adv}_F^{\mathrm{prp}}\left(\mathcal{A}\right)\stackrel{\mathrm{def}}{=}\left|\mathrm{Pr}\left[K\stackrel{\$}{\leftarrow }\mathcal{K}:{\mathcal{A}}^{F_K}=1\right]-\mathrm{Pr}\left[R\stackrel{\$}{\leftarrow }Perm\left(\mathcal{X}\right):{\mathcal{A}}^R=1\right]\right|.$$

When $atk\in \{prf,prp\}$, we define

$${Adv}_F^{\mathrm{atk}}(q,t,\sigma )\stackrel{\mathrm{def}}{=}\underset{\mathcal{A}}{max}{Adv}_F^{\mathrm{atk}}\left(\mathcal{A}\right)$$

2.3. H-Coefficient Technique

Now we introduce a proof technique named the H-Coefficient technique [18,19]. Here just a brief description is provided, and interested readers can refer to [18,19] for a complete explanation. We assume that the distinguisher $\mathcal{A}$ is information-theoretic, which is computationally not bounded. Therefore, without loss of generality we assume $\mathcal{A}$ is deterministic. Suppose $\mathcal{A}$ interacts with one of two oracles, the “real world” oracle $\mathcal{O}$ or the “ideal world” oracle $\mathcal{Q}$. The query-response tuples that $\mathcal{A}$ receives is called a view. Let X (resp. Y) be the probability distribution of the view when $\mathcal{A}$ interacts with $\mathcal{O}$ (resp. $\mathcal{Q}$). Let $\mathcal{T}$ be the set of all attainable views $\tau$ when interacting with $\mathcal{Q}$, that is $\mathcal{T}=\{\tau \mid \mathrm{Pr}[Y=\tau ]>0\}$.

The H-Coefficient technique partitions $\mathcal{T}$ into two subsets ${\mathcal{T}}_{\mathrm{good}}$ and ${\mathcal{T}}_{\mathrm{bad}}$ which are disjoint such that $\mathcal{T}={\mathcal{T}}_{\mathrm{good}}\bigcup {\mathcal{T}}_{\mathrm{bad}}$. If there exist $0\le {ϵ}_1,{ϵ}_2\le 1$ so that

•

For $\forall \tau \in {\mathcal{T}}_{\mathrm{good}}$, it holds that

$$\frac{\mathrm{Pr}[X=\tau ]}{\mathrm{Pr}[Y=\tau ]}\ge 1-{ϵ}_1.$$

•

For a view $\tau \stackrel{\$}{\leftarrow }\mathcal{T}$, it holds that

$$\mathrm{Pr}[\tau \in {\mathcal{T}}_{\mathrm{bad}}]\le {ϵ}_2.$$

Then the advantage of $\mathcal{A}$ can be bounded as

$$\mathbf{Adv}\left(\mathcal{A}\right)\le {ϵ}_1+{ϵ}_2.$$

3. 1k-LightMAC_Plus

3.1. Specification

In this section, we introduce our single-key variant of LightMAC_Plus, which is called 1k-LightMAC_Plus. The XOR of two independent permutations is a “natural” PRP-to-PRF method. If only a single permutation is to be used, one can simulate this independence through domain separation. Therefore, domain separation can be used to reduce the number of keys. We process the finalization function of LightMAC_Plus with a same key but the least significant bit of an input to one of two keyed blockciphers is fixed to 0 and the other is fixed to 1.

The details for 1k-LightMAC_Plus is presented in Algorithm 1 (the subfunction used in Algorithm 1 is defined as Algorithm 2) and depicted in Figure 1.

Algorithm 1 1k-LightMAC_Plus$\left[E_K\right]\left(M\right)$.

1: $(v,w)\leftarrow$ InternalHash$\left[E_K\right]\left(M\right)$ 2: $T_1\leftarrow E_K\left(v\right)$ 3: $T_2\leftarrow E_K\left(w\right)$ 4: $T\leftarrow T_1\oplus T_2$ 5: ReturnT

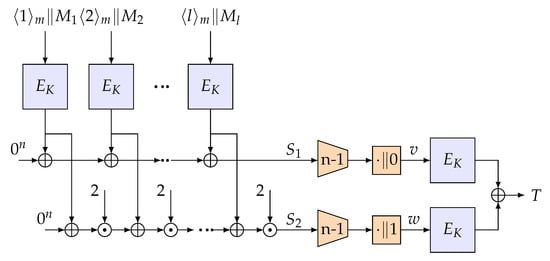
Figure 1. Illustration of 1k-LightMAC_Plus.

Algorithm 2 InternalHash$\left[E_K\right]\left(M\right)$.

1: $M\leftarrow M\parallel {10}^{*}$ 2: $M_1{M}_2\cdots M_L\leftarrow \mathbf{Partition}\left(M\right),S_1=0^{n-1},S_2=0^{n-1}$ 3: for$i=1,2\cdots l$do 4:     $B_i\leftarrow {⟨i⟩}_m\parallel M_i;C_i\leftarrow E_K\left(B_i\right)$ 5:     $S_1\leftarrow S_1\oplus C_i;S_2\leftarrow S_2\oplus 2^{l-i+1}·C_i$ 6: end for 7: $v_0\leftarrow {\mathbf{lsb}}_{n-1}\left(S_1\right);w_0\leftarrow {\mathbf{lsb}}_{n-1}\left(S_2\right)$ 8: $v\leftarrow v_0\parallel 0;w\leftarrow w_0\parallel 1$ 9: Return$(v,w)$

3.2. Security Bound

Theorem 1.

Any distinguisher with running time t, making q-tuple of distinct messages with an aggregate of total σ-many blocks, can distinguish 1k-LightMAC_Plus[E] from a uniform random function by

$${\mathbf{Adv}}_{1\mathrm{k}-\mathrm{LightMAC}\_\mathrm{Plus}\left[\mathrm{E}\right]}^{\mathrm{prf}}(q,t,\sigma )\le {\mathbf{Adv}}_E^{\mathrm{prp}}(2q+\sigma +2,t^{\prime })+\frac{147q^2{\sigma }^2}{N^3}+\frac{114q{\sigma }^2}{N^2}+\frac{16\sigma }{N}+\frac{q}{N}$$

where $t^{\prime }=t+O(2q+\sigma +2)$.

The proof is provided in next section.

4. Proof of Theorem 1

In this section, we prove Thereom 1 with the H-coefficient technique.

4.1. Initialization

We assume that the distinguisher $\mathcal{A}$ interacts with either the ideal oracle or the real oracle 1k-LightMAC_Plus with a random permutation $\Pi$ and that the distinguisher $\mathcal{A}$ always makes deterministic and non-repeating queries.

4.1.1. Ideal Oracle

The ideal oracle defined here is comprised of two phases: (a) One is called online phase. For each query $M^i$ made by $\mathcal{A}$, the oracle samples the response $T^i\stackrel{\$}{\leftarrow }{\{0,1\}}^n$ and then returns it to the distinguisher $\mathcal{A}$. (b) The other is called offline phase. In this phase, the oracle samples the internal hash value for each query in a without-replacement manner from ${\{0,1\}}^n$. During the sampling, if some specific event happens, then the oracle aborts the process. The ideal oracle is formally shown in Figure 2.

Figure 2. Ideal Oracle: boxed items denote bad events. ⊥ and ⊤ denote the abort symbol and an undefined variable, respectively.

4.1.2. Views

At the end of $\mathcal{A}$ interacting with the oracle and before $\mathcal{A}$ outputting the bit, we reveal the values of internal computations $(X,Y,{\widehat{v}}^{\left[q\right]},{\widehat{w}}^{\left[q\right]})$ to $\mathcal{A}$. Thus, the view of $\mathcal{A}$ is in the form

$$\begin{array}{c}\hfill \tau =\left(M^{\left[q\right]},T^{\left[q\right]},X,Y,{\widehat{v}}^{\left[q\right]},{\widehat{w}}^{\left[q\right]}\right).\end{array}$$

For two block tuples $X,Y$, if there exist permutations $\pi \in \mathrm{Perm}$ such that $\pi \left(x^i\right)=y^i$, we call X and Y permutation compatible, denoted as $X\stackrel{\pi }{\to }Y$. It is straightforward that in the real world an attainable transcript must satisfy the following two conditions at the same time.   

$$\begin{array}{cc}\hfill & {\widehat{v}}^i\oplus {\widehat{w}}^i=T^i,\forall i\in \left[q\right]\mathrm{and}\hfill \\ \hfill & (X,v^{\left[q\right]},w^{\left[q\right]})\stackrel{\pi }{\to }(Y,{\widehat{v}}^{\left[q\right]},{\widehat{w}}^{\left[q\right]}).\hfill \end{array}$$

The notation $X_{id}$ represents the probability distribution of transcript $\tau$ induced by the ideal world, while $X_{re}$ represents that induced by the real world. We call a transcript $\tau$ attainable if $\mathrm{Pr}[X_{id}=\tau ]>0$. All such attainable views contribute to a set $\mathcal{T}$. Besides, we partition $\mathcal{T}$ into two disjoint subsets ${\mathcal{T}}_{\mathrm{good}}$ and ${\mathcal{T}}_{\mathrm{bad}}$ such that $\mathcal{T}={\mathcal{T}}_{\mathrm{good}}\bigcup {\mathcal{T}}_{\mathrm{bad}}$.

4.2. Analysis of Bad Events

We define bad events in the ideal world according to the freshness of $v^i$ and $w^i$, which consists of four different cases. Here we first introduce a definition.

Definition 1.

Let X be the set of all the inputs $X_j^i$ of internal hash part for $\forall i\in \left[q\right]$ and $\forall j\in \left[l_i\right]$. If there exists an $i\in \left[q\right]$ s.t. $v^i$ is non-fresh in the union set $v^{\left[q\right]}\cup X$ and simultaneously $w^i$ is non-fresh in the union set $w^{\left[q\right]}\cup X$, then the tuple $\left(v^{\left[q\right]},w^{\left[q\right]}\right)$ is called “an extended covered tuple". Otherwise, the tuple is said to be “an e.c.f tuple" (short for “an extended cover free tuple").

Both $v^i$ and $w^i$ are non-fresh

In this case, a bad event ECF occurs (defined in Figure 2). For 1k-lightMAC_Plus, “Non-fresh” $v^i$ can collide with some previous v or some input blocks and so is $w^i$.

$v^i$ is fresh and $w^i$ is non-fresh

In this case, bad events PCF1 PCF2 and RCOLL happen.

$v^i$ is non-fresh and $w^i$ is fresh

This is similar to the “$v^i$ is fresh and $w^i$ is non-fresh” case.

Both $v^i$ and $w^i$ are fresh.

Owing to the computation of the internal hash part there may exist some inputs–output couples of the random permutation $\Pi$ that have been defined previously. In this case, the final part is the sum of two identical random permutations under conditional distribution. Here we introduce an observation on the conditional distribution of the sum of two identical random permutations by Datta et al. [20].

Lemma 1

([20], Section 3). For any set Y with size d and a k tuple $t^{\left[k\right]}:=(t^1,\cdots ,t^k)$ of non zero n bit strings, let

$$\mathcal{H}={(h_0^i,h_1^i)}_i:h_0^i\oplus h_1^i=t^i,\forall i\in \left[k\right],{(h_0^i,h_1^i)}_i\in {(\mathbb{N}\setminus Y)}^{\left(2k\right)}.$$

Then, $\left|\mathcal{H}\right|\ge \frac{\mathbf{P}(N-d,2k)}{N^k}(1-{\mu }_2)$ where ${\mu }_2=\frac{k{d}^2+2d{k}^2+4k^3/3}{{(N-d-2k)}^2}.$ Moreover, if $d+2k\le \frac{N}{2}$, then ${\mu }_2\le \frac{4k{d}^2+8d{k}^2+6k^3}{N^2}.$

Interested readers can refer to Section 3 of paper [20] for full proof. We define the event

$$\mathtt{Bad}:=\mathtt{ZeroT}\vee \mathtt{ECF}\vee \mathtt{PCF}\mathtt{1}\vee \mathtt{PCF}\mathtt{2}\vee \mathtt{RCOLL},$$

then it follows that

$$\begin{array}{cc}\hfill \mathrm{Pr}[X_{id}\in {\mathcal{T}}_{bad}]\le & \mathrm{Pr}\left[\mathtt{ZeroT}\right]+\mathrm{Pr}\left[\mathtt{ECF}\right|\overline{\mathtt{ZeroT}}]+\mathrm{Pr}\left[\mathtt{PCF}\mathtt{1}\right|\overline{\mathtt{ZeroT}}]\hfill \\ \hfill & +\mathrm{Pr}\left[\mathtt{PCF}\mathtt{2}\right|\overline{\mathtt{ZeroT}}]+\mathrm{Pr}\left[\mathtt{RCOLL}\right|\overline{\mathtt{ZeroT}}]\hfill \end{array}$$

(1)

At first we bound $\mathrm{Pr}\left[\mathtt{ZeroT}\right]$. If $\exists i\in \left[q\right]$ s.t. $T^i=0$, then the bad flag ZeroT is set to 1. For a fixed $i\in \left[q\right]$ it is obvious that $\mathrm{Pr}[T^i=0]=\frac{1}{N}$ because each $T^i$ is chosen uniformly and independently in the ideal oracle. Therefore, we get

$$\begin{array}{c}\hfill \mathrm{Pr}\left[\mathtt{ZeroT}\right]=\mathrm{Pr}\left[{\vee }_{i=1}^q{T}^i=\mathbf{0}\right]\le \sum _{i=1}^q\mathrm{Pr}\left[T^i=\mathbf{0}\right]=\frac{q}{N}.\end{array}$$

(2)

Then we focus on $\mathrm{Pr}\left[\mathtt{ECF}\right|\overline{\mathtt{ZeroT}}]$. If the bad tag ECF is set to 1, at least one of the following cases happens: (1)$v^i{=}_1{X}_{\alpha }^j,w^i{=}_1{X}_{\beta }^k$; (2)$v^i{=}_1{X}_{\alpha }^j,w^i=w^k$; (3)$v^i=v^j,w^i{=}_1{X}_{\beta }^k$; and (4)$v^i=v^j,w^i=w^k$. We denote these four cases as ECF${}_1$, ECF${}_2$, ECF${}_3$ and ECF${}_4$ in order. Note that $v^i=v^j$ is equivalent to $S_1^i{=}_1{S}_1^j$ and $w^i=w^j$ is equivalent to $S_2^i{=}_1{S}_2^j$ (line 4 in Figure 2 for the definition of $S_1$ and $S_2$).

Now we concentrate on the upper bound of $\mathrm{Pr}\left[{\mathtt{ECF}}_1\right|\overline{\mathtt{ZeroT}}]$. For different indices $i,j\in \left[q\right]$ we define the set ${\mathtt{NEQ}}_{i,j}:=\{\alpha \in [min{l}_i,l_j]:M_{\alpha }^i\ne M_{\alpha }^j\}\cup \{\alpha :min\{l_i,l_j\}+1\le \alpha \le max\{l_i,l_j\}\}$. It means that the set ${\mathtt{NEQ}}_{i,j}$ consists of all the index couples for which the two corresponding message blocks are not equal. Assume that $\gamma =min{\mathtt{NEQ}}_{i,j}$ and $l_i\le l_j$ and it is straightforward that $\gamma \le l_j$. The equations $v^i{=}_1{X}_{\alpha }^j$ and $w^i{=}_1{X}_{\beta }^k$ can be rewritten in matrix form with respect to variable Y as follows:

$$\left(\begin{array}{ccc}\mathbf{1}& b& \cdots \\ 2^{l_i-\gamma +1}& X_{\beta }^k\oplus b^{\prime }& \cdots \end{array}\right)·\left(\begin{array}{c}{Y}_{\gamma }^i\\ \mathbf{1}\\ ⋮\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right)$$

where $b,b^{\prime }\in \{\mathbf{0},\mathbf{1}\}$. If $b=\mathbf{1}$ and $2^{l_i-\gamma +1}=X_{\beta }^k\oplus b^{\prime }$ hold, then $rank\ge 1$, otherwise $rank=2$. To analyze the solution of the matrix, another lemma [20] is introduced here.

Lemma 2

([20], Section 2.4). Assume that $\mathcal{S}\subseteq \mathbb{N}$ and the size of $\mathcal{S}$ is $N^{\prime }$. $Y_i$ is sampled from $\mathcal{S}$ in a without-replacement manner for $1\le i\le s$ and Let $Y:=\left(Y_1,\dots ,Y_s\right)$. A is a fixed $b\times s$ matrix with rank n. For any $b\times 1$ vector v, the following inequality holds.

$$\mathrm{Pr}\left[{\left(A\right)}_{b\times s}·Y^{\mathrm{T}}=v\right]\le \frac{1}{\mathbf{P}\left(N^{\prime }-s+n,n\right)}.$$

Interested readers can refer to Section 2 of paper [20] for full proof.

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[{\mathtt{ECF}}_1\right|\overline{\mathtt{ZeroT}}]& \le \sum _{i,j,k}\sum _{\alpha ,\beta }\mathrm{Pr}[v^i{=}_1{X}_{\alpha }^j\wedge w^i{=}_1{X}_{\beta }^k|\overline{\mathtt{ZeroT}}]\hfill \\ \hfill & \le \sum _{i,j,k}\sum _{\alpha ,\beta }\mathrm{Pr}\left[w^i{=}_1{X}_{\beta }^k\right|\overline{\mathtt{ZeroT}}]·\mathrm{Pr}\left[v^i{=}_1{X}_{\alpha }^j\right|\overline{\mathtt{ZeroT}}]\hfill \\ \hfill & \le \sum _{i,j,k}\sum _{\alpha ,\beta }\frac{4}{N}·\frac{4}{N}\hfill \\ \hfill & \le \frac{16q{\sigma }^2}{N^2}\hfill \end{array}$$

$\mathrm{Pr}\left[{\mathtt{ECF}}_2\right]$,$\mathrm{Pr}\left[{\mathtt{ECF}}_3\right]$ and $\mathrm{Pr}\left[{\mathtt{ECF}}_4\right]$ can be proven in a similar analysis:

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[{\mathtt{ECF}}_2\right|\overline{\mathtt{ZeroT}}]& \le \frac{16q{\sigma }^2}{N^2}\hfill \\ \hfill \mathrm{Pr}\left[{\mathtt{ECF}}_3\right|\overline{\mathtt{ZeroT}}]& \le \frac{16q{\sigma }^2}{N^2}\hfill \\ \hfill \mathrm{Pr}\left[{\mathtt{ECF}}_4\right|\overline{\mathtt{ZeroT}}]& \le \frac{16q{\sigma }^2}{N^2}\hfill \end{array}$$

In total, we have

$$\mathrm{Pr}\left[\mathtt{ECF}\right|\overline{\mathtt{ZeroT}}]\le \frac{64q{\sigma }^2}{N^2}$$

(3)

Next, we bound $\mathrm{Pr}\left[\mathtt{PCF}\mathtt{1}\right|\overline{\mathtt{ZeroT}}]$. The bad flag $\mathtt{PCF}\mathtt{1}$ occurs in Case A or Case B (refer to Figure 2). We separate event $\mathtt{PCF}\mathtt{1}$ into two disjointed events in terms of Case A or Case B. We define $\mathtt{PCF}{\mathtt{1}}_1:=\left(v^i{=}_1{X}_{\alpha }^j\right)\wedge (Y_{\alpha }^j\oplus Y_{\beta }^k=T^i)$ and $\mathtt{PCF}{\mathtt{1}}_2:=\left(w^i{=}_1{X}_{\alpha }^j\right)\wedge (Y_{\alpha }^j\oplus Y_{\beta }^k=T^i)$.

Now we bound the probability of $\mathtt{PCF}{\mathtt{1}}_1$. The equations $v^i{=}_1{X}_{\alpha }^j$ and $Y_{\alpha }^j\oplus Y_{\beta }^k=T^i$ can be rewritten as:

$$\left(\begin{array}{ccc}\mathbf{1}& X_{\alpha }^j\oplus b& \cdots \\ \mathbf{0}/\mathbf{1}& T^i& \cdots \end{array}\right)·\left(\begin{array}{c}{Y}_{\gamma }^{l_i}\\ \mathbf{1}\\ ⋮\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right)$$

where $b\in \{\mathbf{0},\mathbf{1}\}$. If $X_{\alpha }^j\oplus b$ and $Y_{\gamma }^{l_i}=Y_{\alpha }^j$ holds or $X_{\alpha }^j\oplus b$ and $Y_{\gamma }^{l_i}=Y_{\beta }^k$ holds, then $rank\ge 1$, otherwise $rank=2$. Then we bound the probability in the following.

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[\mathtt{PCF}{\mathtt{1}}_1\right|\overline{\mathtt{ZeroT}}]& \le \sum _{i,j,k}\sum _{\alpha ,\beta }\mathrm{Pr}[v^i{=}_1{X}_{\alpha }^j\wedge Y_{\alpha }^j\oplus Y_{\beta }^k=T^i|\overline{\mathtt{ZeroT}}]\hfill \\ \hfill & =\sum _{i,j,k}\sum _{\alpha ,\beta }\mathrm{Pr}\left[v^i{=}_1{X}_{\alpha }^j\right|\overline{\mathtt{ZeroT}}]·\mathrm{Pr}[Y_{\alpha }^j\oplus Y_{\beta }^k=T^i|v^i{=}_1{X}_{\alpha }^j\wedge \overline{\mathtt{ZeroT}}]\hfill \\ \hfill & \le \sum _{i,j,k}\sum _{\alpha ,\beta }\frac{4}{N}·\frac{2}{N}\hfill \\ \hfill & \le \frac{8q{\sigma }^2}{N^2}\hfill \end{array}$$

$\mathrm{Pr}\left[\mathtt{PCF}{\mathtt{1}}_2\right]$ can be proven in a similar analysis:

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[\mathtt{PCF}{\mathtt{1}}_2\right|\overline{\mathtt{ZeroT}}]& \le \frac{16q{\sigma }^2}{N^2}\hfill \end{array}$$

To sum up, we can obtain the following result

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[\mathtt{PCF}\mathtt{1}\right|\overline{\mathtt{ZeroT}}]& \le \frac{32q{\sigma }^2}{N^2}\hfill \end{array}$$

(4)

Next we concentrate on $\mathrm{Pr}\left[\mathtt{PCF}\mathtt{2}\right|\overline{\mathtt{ZeroT}}]$. The bad flag $\mathtt{PCF}\mathtt{2}$ occurs in Case A or Case B (refer to Figure 2). We separate event $\mathtt{PCF}\mathtt{2}$ into three disjointed events. We define $\mathtt{PCF}{\mathtt{2}}_1:=\left(v^i{=}_1{X}_{\alpha }^j\right)\wedge \left(v^k{=}_1{X}_{\beta }^l\right)\wedge (Y_{\alpha }^j\oplus Y_{\beta }^l=T^i\oplus T^k)$, $\mathtt{PCF}{\mathtt{2}}_2:=\left(v^i{=}_1{X}_{\alpha }^j\right)\wedge \left(w^k{=}_1{X}_{\beta }^l\right)\wedge (Y_{\alpha }^j\oplus Y_{\beta }^l=T^i\oplus T^k)$ and $\mathtt{PCF}{\mathtt{2}}_3:=\left(w^i{=}_1{X}_{\alpha }^j\right)\wedge \left(w^k{=}_1{X}_{\beta }^l\right)\wedge (Y_{\alpha }^j\oplus Y_{\beta }^l=T^i\oplus T^k)$.

To obtain a good bound, we introduce a property [20].

Property 1

([20], Appendix B). $M^i$ and $M^j$ are two different messages. On condition that $\sigma \le \frac{N}{2}$ the following inequalities hold.

$$\left(a\right)\mathrm{Pr}\left[v^i{=}_1{v}^j\wedge \overline{\mathrm{ZeroT}}\right]\le \frac{4\left(max\left\{l_i,l_j\right\}+1\right)}{N},\left(b\right)\mathrm{Pr}\left[w^i{=}_1{w}^j\wedge \overline{\mathrm{ZeroT}}\right]\le \frac{4}{N}.$$

Interested readers can refer to Appendix B of paper [20] for full proof.

Firstly, we bound the probability of $\mathrm{Pr}\left[\mathtt{PCF}{\mathtt{2}}_1\right|\overline{\mathtt{ZeroT}}]$. We analyze it by whether the condition $T_i$ equals $T^k$ or not. If $T_i=T^k$, then $Y_{\alpha }^j=Y_{\beta }^l$. Because Y’s are the outputs of a permutation, we obtain that $X_{\alpha }^j=X_{\beta }^l$. Furthermore, $v^i=v^k$. Therefore,

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[\mathtt{PCF}{\mathtt{2}}_1\right|\overline{\mathtt{ZeroT}}\wedge (T^i=T^k)]& =\mathrm{Pr}[v^i=v^k|\overline{\mathtt{ZeroT}}]\hfill \\ \hfill & \le \frac{4(max\{l_i,l_j\}+1)}{N}\hfill \\ \hfill & \le \frac{4\sigma }{N}\hfill \end{array}$$

The first inequality is deduced from the property.

Furthermore, when $T^i\ne T^k$, the three included events $\left(v^i{=}_1{X}_{\alpha }^j\right)\wedge \left(v^k{=}_1{X}_{\beta }^l\right)\wedge (Y_{\alpha }^j\oplus Y_{\beta }^l=T^i\oplus T^k)$ of $\mathtt{PCF}{\mathtt{2}}_1$ can be written as the following matrix equality with respect to variable Y:

$$\underset{A}{\underbrace{\left(\begin{array}{cccc}\mathbf{1}& \mathbf{0}/\mathbf{1}& X_{\alpha }^j\oplus b& \cdots \\ \mathbf{0}& \mathbf{1}& X_{\beta }^l\oplus b^{\prime }& \cdots \\ \mathbf{0}/\mathbf{1}& \mathbf{1}& T^i\oplus T^j& \cdots \end{array}\right)}}·\left(\begin{array}{c}{Y}_{\gamma }^i\\ Y_{\beta }^l\\ \mathbf{1}\\ ⋮\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\hfill \\ \mathbf{0}\hfill \\ \mathbf{0}\hfill \end{array}\right)$$

where $b\in \{0,1\}$. Define event $\mathtt{E}:=(X_{\alpha }^j\oplus b\oplus T^i\oplus T^k=0)$. If $\mathtt{E}$ holds and $\left(A\right[1\left]\right[2],A[3\left]\right[1\left]\right)$ equals to$(1,1)$ simultaneously, then $rank\left(A\right)\ge 2$, otherwise $rank\left(A\right)=3$. Therefore,

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[\mathtt{PCF}{\mathtt{2}}_1\right|\overline{\mathtt{ZeroT}}\wedge (T^i\ne T^k)]& \le \mathrm{Pr}\left[\mathtt{PCF}{\mathtt{2}}_1\right|\overline{B}\wedge \overline{\mathtt{ZeroT}}\wedge (T^i\ne T^k)]+\hfill \\ \hfill & \mathrm{Pr}\left[\mathtt{PCF}{\mathtt{2}}_1\right|B\wedge \overline{\mathtt{ZeroT}}\wedge (T^i\ne T^k)]·\mathrm{Pr}\left[B\right|(T^i\ne T^k)]\hfill \\ \hfill & \le \sum _{i,j,k,l}\sum _{\alpha ,\beta }\frac{49}{N^3}\le \frac{49q^2{\sigma }^2}{N^3}\hfill \end{array}$$

Therefore, we can obtain

$$\mathrm{Pr}\left[\mathtt{PCF}{\mathtt{2}}_1\right|\overline{\mathtt{ZeroT}}]\le \frac{49q^2{\sigma }^2}{N^3}+\frac{4\sigma }{N}.$$

$\mathrm{Pr}\left[{\mathtt{PCF}}_2\right]$ and $\mathrm{Pr}\left[{\mathtt{PCF}}_3\right]$ can be proven in a similar analysis:

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[\mathtt{PCF}{\mathtt{2}}_2\right|\overline{\mathtt{ZeroT}}]& \le \frac{49q^2{\sigma }^2}{N^3}+\frac{\sigma }{N}\hfill \\ \hfill \mathrm{Pr}\left[\mathtt{PCF}{\mathtt{2}}_3\right|\overline{\mathtt{ZeroT}}]& \le \frac{49q^2{\sigma }^2}{N^3}+\frac{2\sigma }{N}\hfill \end{array}$$

In total, we have

$$\mathrm{Pr}\left[\mathtt{PCF}\mathtt{2}\right|\overline{\mathtt{ZeroT}}]\le \frac{147q^2{\sigma }^2}{N^3}+\frac{7\sigma }{N}.$$

(5)

Finally we analyze the bounding of $\mathrm{Pr}\left[\mathtt{RCOLL}\right|\overline{\mathtt{ZeroT}}]$. The bad flag RCOLL occurs in Case C or Case D (refer to Figure 2). We separate RCOLL into ${\mathtt{RCOLL}}_1$ and ${\mathtt{RCOLL}}_2$ and define ${\mathtt{RCOLL}}_1:=\left(v^i{=}_1{v}^j\right)\wedge ({\widehat{w}}^i\in Ran\left({\mathcal{L}}_2\right))$ and ${\mathtt{RCOLL}}_2:=\left(w^i{=}_1{w}^j\right)\wedge ({\widehat{v}}^i\in Ran\left({\mathcal{L}}_2\right))$.   

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[{\mathtt{RCOLL}}_1\right|\overline{\mathtt{ZeroT}}]& =\sum _{i,j}\mathrm{Pr}[v^i{=}_1{v}^j\wedge {\widehat{w}}^i\in Ran\left({\mathcal{L}}_2\right)|\overline{\mathtt{ZeroT}}]\hfill \\ \hfill & =\sum _{i,j}\mathrm{Pr}\left[v^i{=}_1{v}^j\right|\overline{\mathtt{ZeroT}}]·\mathrm{Pr}[{\widehat{w}}^i\in Ran\left({\mathcal{L}}_2\right)]\hfill \\ \hfill & \stackrel{*}{\le }\sum _{i,j}\frac{2(max\{l_i,l_j\}+1)}{N}·\frac{2q+\eta }{N}\hfill \\ \hfill & \le \frac{6\sigma }{N}\hfill \end{array}$$

Because the number of elements in $Ran\left({\mathcal{L}}_2\right))$ is at most $2q+\eta$, the inequality (*) holds from the property. The last inequality holds owing to $q\le \sigma \le N^2$. Similarly one can show

$$\mathrm{Pr}\left[{\mathtt{RCOLL}}_2\right|\overline{\mathtt{ZeroT}}]\le \frac{3\sigma }{N}$$

So we can obtain

$$\mathrm{Pr}\left[\mathtt{RCOLL}\right|\overline{\mathtt{ZeroT}}]\le \frac{9\sigma }{N}$$

(6)

From inequalities (1)–(6), we can obtain

$$\begin{array}{c}\hfill \mathrm{Pr}[X_{id}\in {\mathcal{T}}_{bad}]\le \frac{147q^2{\sigma }^2}{N^3}+\frac{96q{\sigma }^2}{N^2}+\frac{16\sigma }{N}+\frac{q}{N}\end{array}$$

(7)

4.3. Analysis of Good Transcripts

Having defined bad events and computed the upper bound of the probability of each bad transcript in the ideal world, it remains to lower bound $\mathrm{Pr}[X_{re}=\tau ]/\mathrm{Pr}[X_{id}=\tau ]$ for a good transcript $\tau$.

Firstly, we discuss in an ideal oracle what properties a good transcript have. For each $i\in \mathcal{F}$ (line 10 of Figure 2), both $v^i$ and $w^i$ are fresh; therefore, it is the same case with the corresponding ${\widehat{v}}^i$ and ${\widehat{w}}^i$. As ECF is not set to one, for each $i\notin \mathcal{F}$ either ${\widehat{v}}^i$ or ${\widehat{w}}^i$ is fresh (but not both). Assume the size of $\mathcal{F}$ is f, then there are $q-f$ non-fresh message blocks and $q+f$ fresh message blocks.

Denote ${\mathcal{F}}_v^{\prime }$ as the set of all the indices i s.t. $v^i$ is in collision with some input of the hash computation and ${\mathcal{F}}_w^{\prime }$ is defined in a similar way. Then we define an equivalence relation ${\sim }_v$ on ${\mathcal{F}}_v:=\left[q\right]\backslash ({\mathcal{F}}_v^{\prime }\cup \mathcal{F})$ (line 6 of Figure 2) as $i{\sim }_{v}j$ if $v_i=v_j$. Also the equivalence relation $i{\sim }_{w}j$ on ${\mathcal{F}}_w:=\left[q\right]\backslash ({\mathcal{F}}_w^{\prime }\cup \mathcal{F})$ is defined similarly. Here, we would like to point out that we cannot have $v_j=w_j$ because we have applied domain-separation technique by setting the most significant bit as 0 and 1, respectively. ${\sim }_v$ and ${\sim }_w$ are equivalence relations on ${\mathcal{F}}_v$ and ${\mathcal{F}}_w$, respectively. We partition the set ${\mathcal{F}}_v$ as $C_1\bigsqcup \cdots C_{t^{\prime }}$ where each $C_j$ is a subset of ${\mathcal{F}}_v$ and the set ${\mathcal{F}}_w$ as $C_1^{\prime }\bigsqcup \cdots C_t^{\prime }$ where $C_j^{\prime }$ is a subset of ${\mathcal{F}}_w$. The equivalence class $C_j$ is called “the v-class" and $C_j^{\prime }$ “the w-class". We point that each part contains at least two elements. Let $c_j=min{C}_j$ be the minimum value of partition $C_j$ and so is $c_j^{\prime }=min{C}_{j^{\prime }}^{\prime }$. So, when $i=c_j$ or $i=c_j^{\prime }$ for some $j\in \left[t\right]$ or $j^{\prime }\in \left[t^{\prime }\right]$, we sample the output ${\mathcal{L}}_2(·)$ (Case C or Case D, respectively in Figure 2), which dominates the outputs for each element with respect to the corresponding equivalent class $C_j$ or $C_{j^{\prime }}^{\prime }$, respectively.

Upon the above analysis, we can obtain that different elements in tuple $(v^{\left[q\right]},w^{\left[q\right]})$ have different corresponding elements in $({\widehat{v}}^{\left[q\right]},{\widehat{w}}^{\left[q\right]})$ for a good transcript. Hence there exists a permutation $\Pi$ such that the two tuples $(v^{\left[q\right]},w^{\left[q\right]})$ and $({\widehat{v}}^{\left[q\right]},{\widehat{w}}^{\left[q\right]})$ are part of its inputs and outputs, respectively.

Lemma 3.

Assuming that $\tau =(M^{\left[q\right]},T^{\left[q\right]},X,Y,{\widehat{v}}^{\left[q\right]},{\widehat{w}}^{\left[q\right]})$ is a good transcript, we can obtain

$$\frac{\mathrm{Pr}[X_{re}=\tau ]}{\mathrm{Pr}[X_{id}=\tau ]}\ge 1-\frac{18q{\sigma }^2}{N^2}$$

(8)

Proof. 

Define a set $\mathcal{I}=\mathcal{F}\cup {\mathcal{F}}_v\cup {\mathcal{F}}_w$. In addition, assume that the size of ${\mathcal{L}}_1$ is $\eta$.

$$\begin{array}{cc}\hfill \mathrm{Pr}[X_{id}=\tau ]& =\mathrm{Pr}[T^{\left[q\right]}\wedge {\mathcal{L}}_1\left(X_j^i\right)=Y_j^i\wedge {\mathcal{L}}_2\left(v^{i^{\prime }}\right)={\widehat{v}}^{i^{\prime }}\wedge {\mathcal{L}}_2\left(w^{i^{\prime }}\right)={\widehat{w}}^{i^{\prime }},\forall i^{\prime }\in \mathcal{I}]\hfill \\ \hfill & =\frac{1}{N^q}\times \mathrm{Pr}[\underset{\mathrm{B}1}{\underbrace{{\mathcal{L}}_1\left(X_j^i\right)=Y_j^i}}\wedge \underset{\mathrm{B}2}{\underbrace{{\mathcal{L}}_2\left(v^{i^{\prime }}\right)={\widehat{v}}^{i^{\prime }}}}\wedge \underset{\mathrm{B}3}{\underbrace{{\mathcal{L}}_2\left(w^{i^{\prime }}\right)={\widehat{w}}^{i^{\prime }}}},\forall i^{\prime }\in \mathcal{I}]\hfill \\ \hfill & =\frac{1}{N^q}\times \mathrm{Pr}\left[\mathrm{B}1\right]\times \mathrm{Pr}[\mathrm{B}2\wedge \mathrm{B}3|\mathrm{B}1]\hfill \\ \hfill & =\frac{1}{N^q}\times \frac{1}{\mathbf{P}(N,\eta )}\times \mathrm{Pr}[\mathrm{B}2\wedge \mathrm{B}3|\mathrm{B}1]\hfill \end{array}$$

(9)

Now we focus on the item $\mathrm{Pr}[\mathrm{B}2\wedge \mathrm{B}3|\mathrm{B}1]$.

$$\begin{array}{cc}\hfill \mathrm{Pr}[\mathrm{B}2\wedge \mathrm{B}3|\mathrm{B}1]& =\mathrm{Pr}[\underset{B4}{\underbrace{\mathrm{B}2\wedge \mathrm{B}3,\forall i^{\prime }\in \mathcal{I}\backslash \mathcal{F}}}|\mathrm{B}1]\times \mathrm{Pr}[\mathrm{B}2\wedge \mathrm{B}3,\forall i^{\prime }\in \mathcal{F}|\mathrm{B}1\wedge \mathrm{B}4].\hfill \\ \hfill & =\frac{1}{\mathbf{P}(N-(2f+\eta ),t+t^{\prime })}\times \mathrm{Pr}[\mathrm{B}2\wedge \mathrm{B}3,\forall i^{\prime }\in \mathcal{F}|\mathrm{B}1\wedge \mathrm{B}4]\hfill \end{array}$$

(10)

Assuming that $\eta +2f\le \frac{N}{2}$, $\eta \le \sigma$ and $f\le q\le \sigma$, with Lemma 1 we have

$$\begin{array}{cc}\hfill \mathrm{Pr}[\mathrm{B}2\wedge \mathrm{B}3,\forall i^{\prime }\in \mathcal{F}|\mathrm{B}1\wedge \mathrm{B}4]& \le \frac{N^f}{\mathbf{P}(N-\eta ,2f)\times (1-\frac{4f{\eta }^2+8f^2\eta +6f^3}{N^2})}\hfill \\ \hfill & \le \frac{N^f}{\mathbf{P}(N-\eta ,2f)\times (1-\frac{18q{\sigma }^2}{N^2})}.\hfill \end{array}$$

(11)

Following (9)–(11), we can obtain

$$\mathrm{Pr}[X_{id}=\tau ]\le \frac{1}{N^q}\times \frac{1}{\mathbf{P}(N,\eta )}\times \frac{1}{\mathbf{P}(N-(2f+\eta ),t+t^{\prime })}\times \frac{N^f}{\mathbf{P}(N-\eta ,2f)\times (1-\frac{18q{\sigma }^2}{N^2})}$$

(12)

Next, for a good transcript $\tau$ the interpolation probability in the real world is computed.

$$\begin{array}{cc}\hfill \mathrm{Pr}[X_{re}=\tau ]& =\frac{1}{P(N,\eta )}\times \frac{1}{P(N-\eta ,t+t^{\prime }+q+f)}\hfill \end{array}$$

(13)

Following the Equations (12) and (13), we have that

$$\begin{array}{cc}\hfill \frac{\mathrm{Pr}[X_{re}=\tau ]}{\mathrm{Pr}[X_{id}=\tau ]}& \ge \frac{N^q\times P(N-(2f+\eta ),t+t^{\prime })\times P(N-\eta ,2f)\times (1-\frac{18q{\sigma }^2}{N^2})}{P(N-\eta ,t+t^{\prime }+q+f)\times N^f}\hfill \\ \hfill & =\frac{N^{q-f}}{P(N-(t+t^{\prime }+q+2f),q-f)}\times \left(1-\frac{18q{\sigma }^2}{N^2}\right)\hfill \\ \hfill & \ge 1-\frac{18q{\sigma }^2}{N^2}\hfill \end{array}$$

(14)

Finally, by applying the H-coefficient technique in Section 2.3 with the Equations (7) and (14), we conclude the proof for Theorem 1. □