1. Introduction
Over the past few decades, the Vehicle Routing Problem (VRP) and its variants have been the subject of massive investigations in operations research. This fact is due to the importance of its applications in different domains, such as logistics, supply chain management, scheduling, inventory, finance, etc. The main purpose of the vehicle routing problem is to find a set of least cost routes, beginning and ending at a depot, that together cover a set of customers (see, e.g., [
1,
2,
3]). In real-world applications, several operational constraints must be taken into account, as for example considering the travel and service times with time-window limitations [
4]. Then, the considered problem becomes the Vehicle Routing Problem with Time Windows (VRPTW) [
5].
A challenging topic in solving the VRPTW problem consists of considering uncertain parameters. Different approaches have been proposed in order to handle uncertain events in a VRPTW, in demand, displacement time, and service time. From the literature, we distinguish between stochastic and robust approaches. The stochastic variant can be regarded as a methodology that aims at finding a near-best solution for the objective function responding to all uncertain events that are characterized by their probability distributions [
6,
7,
8]. On the other hand, the purpose of the robust approach is to find a solution that protects against the impact of data uncertainties, taking into consideration several technical criteria challenges such as the worst case, best case, min-max deviation, etc. The choice of a mathematical model of uncertain data is a crucial step to provide robust solutions. This kind of approach was the subject of a series of papers (see, e.g., [
9]). In this context, Rouky et al. [
10] introduced the uncertainties to the travel times of locomotives and the transfer times of shuttles as a model of the Rail Shuttle Routing Problem (RSRP) at Le Havre port. The authors proposed the Robust Ant Colony Optimization (RACO) as an efficient technique to deal with the problem. In the same spirit, Wu et al. [
11] proposed a robust model tested on a set of random instances for the vehicle routing problem with uncertain travel time to improve the robustness of the solution, which enhances its quality compared with the worst case in a majority of scenarios. For instance, we split the resolution methods of this last approach into two major categories: exact and heuristic methods.
Due to the NP-hard nature of such problems, we cannot expect to use exact methods for the resolution (see, e.g., [
12,
13]). Indeed, the heuristics are solution methods that yield very good solutions in a limited time at the expense of ensuring the optimal solution. A generic class called the metaheuristic is used to exploit the best capabilities to achieve better solutions to solve a wide range of problems, since the mechanism to avoid getting trapped in local minima is present. In this regard, the literature covers a considerable number of metaheuristics conceived of to solve the VRPTW such as Simulated Annealing (SA) [
14,
15], Variable Neighborhood Search (VNS) [
16,
17], Ant Colony Optimization Algorithm (ACO) [
18,
19], Genetic Algorithm (GA) [
20], and Tabu Search (TS) [
21,
22,
23].
The need for parallel computing becomes inevitable despite the good results obtained with metaheuristics, due to the huge scale of the input data and the unexpected way of its change, which makes the objective function time-consuming. However, it is important to notice that the quality of the solution can be influenced. For instance, the major challenge is to find a parallelization strategy that solves larger problem instances in reasonable computing times and offers a consistently high level of performance over a wide variety of problem characteristics. In this context, several authors have proposed parallel techniques to tackle the combinatorial problems. Following these ideas, Bouthillier et al. [
24] proposed a multi-thread parallel cooperative multi-search method founded on a solution warehouse strategy to deal with the deterministic VRPTW. Their method is based mainly on two cooperating classes of heuristics, namely tabu search and the evolutionary algorithms. In this regard, Røpke (2009) [
25] applied a parallel ALNS to the traveling salesman problem with pickup and delivery and the capacitated vehicle routing problem such that each worker thread obtains a copy of the current solution and performs destroy and repair operations on its local copy in order to produce the best global solution. In the same spirit, Hemmelmayr (2014) [
26]) proposed a parallel variant of the Large Neighborhood Search (LNS) to solve the periodic location routing problem. On the same topic, Pillac [
27] presented a parallel version of the ALNS by adding a set covering post-optimization model that combines the tours generated throughout the search to assemble a better solution. It is worth mentioning here that the longer a heuristic is run, the better the quality of the solution is. Our contribution in this work is to study the balance between the quality of the solution and the corresponding execution time. Therefore, we suggest through our investigation a compromise between the required running time and the objective function. This can be viewed as a multi-criteria optimization problem.
Thus, the goal of this work is to study the effect of multithreading parallelization of the resolution approach blocks on the running time and the objective function. The optimization problem considered here is a variant of the Robust Vehicle Routing Problem with Time Windows (RVRPTW) including both uncertainties in travel and service times. Our contribution to all previous works lies first on the choice of the efficient Parallel Adaptive Large Neighborhood Search (PALNS) metaheuristic of Ropke [
25], which leads to a reduced running time. Moreover, we used our parallel version of the Metropolis Monte Carlo algorithm to generate all possible realizations and to transform the problem under uncertainties to a set of deterministic sub-problems. For more detail about this splitting process, see for instance the previous work [
9] and the references therein. Based on the efficient implementation of [
25], different combinations (sequential/parallel) of the Monte Carlo algorithm and ALNS are performed. In this way, our strategy offers to decision makers the choice of the combination depending on their preferences and the situation at hand.
To the best of our knowledge, this contribution is the first work to be devoted to the study of VRPTW considering the uncertainties on travel times and service times for different sizes of instances in terms of both the execution time and the objective value.
The outline of this paper is organized as follows. The problem statement and mathematical model is provided in the second section. The sequential robust approach used to solve the problem is the subject of the third section. Within
Section 4, we present the parallel Monte Carlo algorithm to generate all possible scenarios and the parallel ALNS algorithm to solve each sub-problem corresponding to each scenario. Finally, a detailed computational and comparative study is given before the concluding remarks and perspectives.
2. Problem Statement
The mathematical formulation of the problem can be represented on a graph
, where
is the set of nodes and
is the set of arcs. The node
o represents the depot, and each other node is affected by a customer
i. Each arc
is assigned to the travel cost
, which, in general, is proportional to the travel time
or the distance
between
i and
j. For the rest of this paper, we consider only the travel time cost
. It is worth mentioning that this travel time
is subject to uncertainty
. The nominal service time is denoted by
for each vehicle
k and node
i within the time window
and depends on uncertainty
. According to the work of [
9], we identify the uncertainty sets related to these times by:
and
We denote the subset of arcs that are dependent on uncertainty by with a cardinal and the subset of nodes depending on uncertainty by with a cardinal .
The binary decision variables take the value one if vehicle k travels between the pairs of nodes and zero otherwise.
We introduce the model of our problem, which tries to find a solution optimizing the total travel time taking into account the minimization of the worst evaluation over all scenarios:
subject to:
where M is a great value and
and
are two indicator functions. When
,
takes the value of one. When
,
takes one.
The constraint (1) stipulates that each customer must be visited once. The constraint (2) guarantees that each tour starts from the depot. The constraint (3) ensures that the same vehicle arrives and leaves from each node it serves. The constraint (4) ensures that each tour ends at the depot. The constraint (5) guarantees that the service time at any customer i by vehicle k starts inside a specified time interval . The last constraint (6) prohibits the violation of the time windows. Then, if the vehicle arrives ahead of time at a customer i, it must wait until the time window opens, and besides, it is not allowed to arrive late.
3. Robust Optimization
In real-world applications of operations research, we cannot ignore the fact that in the presence of uncertainties, an optimal solution could become worse or even unreachable from a practical point of view. Therefore, the need to develop models that immunize against those uncertainties has become indispensable.
In general, the uncertain parameters are represented by closed, convex, and bounded uncertainty sets, which can be also estimated from the historic data. Thereby, constructing the adequate uncertainty set has a crucial role in identifying the conservativeness of the model.
In this section, we present briefly the most important sets of uncertainties and the corresponding robust optimization models.
In this regard, we consider the following uncertain linear programming problem:
For the remainder of this section, only the coefficients
of the matrix
A are the object of uncertainties, and their values belong to a bounded set of uncertainties called
U. Accordingly,
takes a value in the interval
where
is the nominal value and
represents the maximum positive deviation. Therefore, we can define
as:
Generally, is a random variable that is subject to uncertainty and varies between −1 and one.
For instance, three types of uncertainty sets can be distinguished [
28].
3.1. Box Uncertainty Set
The box uncertainty set is an uncertainty structure that takes its name from the box formed by the interaction of perturbations. It aims at finding a conservative solution for a robust problem where the value of all uncertain coefficient perturbations is less than a perturbation bound
(see, e.g., [
29]). Its uncertainty set can be described as follows:
The robust counterpart of the problem is given by the following:
It is worth pointing out that the problem becomes more conservative as the value of increases.
3.2. Ellipsoidal Uncertainty Set
The ellipsoidal uncertainty set comes to avoid over conservativeness and to limit the uncertainty space by eliminating a subset of uncertainty. The level of robustness can be controlled by modifying the value of the parameter
, which defines the borders of the set [
30]. This uncertainty set can be given as:
The robust counterpart model is expressed in the following way:
The inconvenience of this robust counterpart model lies in the generation of a convex nonlinear programming problem, with a greater computational requirement in contrast to linear models.
3.3. Polyhedral Uncertainty Set
The polyhedral uncertainty set corresponds to the most frequent case of uncertainty sets defined as the set of solutions, which are protected against all situations in which at most
coefficients of the
ith constraints are perturbed. In this case, the robust counterpart is equivalent to a linear optimization problem.
The robust counterpart of the problem can be defined as below:
where
represents the set of coefficients
of the
ith constraint, which are uncertain. We define for each
i a parameter
that varies in the interval
. The solution of this model is immunized against all cases where coefficients up to
will change, and one coefficient
changes by
as reported by [
31].
4. The Robust Approach for the VRPTW with Uncertain Travel and Service Times
In this section, we present the robust resolution approach proposed by [
9] to deal with the VRPTW under uncertain travel and service times. We assume that the uncertainty in travel times and service times is directed by two parameters
and
, which belong respectively to the intervals
and
. Those parameters are called budgets of uncertainty and are defined to control the number of travel times and service times, which are allowed to vary from their nominal values. Thus, the major challenge of this approach is to derive, for each scenario (
,
) considered, a robust solution that protects against time window violation or reduces the waiting times.
In order to explain the robust approach, we define some notations to be used in this approach:
: A possible realization
: The best robust solution
: The solution found at the Nth realization
: The total traveled time of a solution
: The worst evaluation of a solution
= : The tour of the vehicle k
= : A path of the tour
: A set of arcs within the larger deviations of travel time
: A set of nodes within the larger deviations of service time
: All of the nodes that constitute
: The set of the arcs that constitute the path
: The maximum date of arrival of the vehicle k at customer
To understand the idea behind this approach, we propose a simplified presentation in four steps summarized in Algorithm 1:
| Algorithm 1. The robust approach algorithm. |
Parameters: Set , set Outputs: Solution for each do solutions.add(solution) end for for each do if then solutions.remove(solution) return NULL end if if then solutions.remove(solution) return NULL end if end for return
|
In the first step, the robust algorithm generates a set of realizations using the Metropolis Monte Carlo sampling. Each realization corresponds to a possible scenario in which travel times of a subset of arcs achieves their maximum values , and service times related to a subset of vehicles take their maximum values ; whereas the other arcs and nodes take respectively their and nominal values.
The objective of the second step is to obtain for each realization
a feasible solution
that satisfies the related sub-problem. For this purpose, we apply the Adaptive Large Neighborhood Search (ALNS) metaheuristic [
32], which presents an adaptive specialization of the notion of local search, so-called large neighborhoods. It aims to enhance an incumbent solution by diversifying the search process on large neighborhoods. This can be done by applying a pair of destroy and repair operators to the solution and then accepting or rejecting the new solution. In this context, we use three different destroy operators, which contribute to ruin a part of the current solution, namely: the proximity operator, the route portion operator, and the longest detour operator. Then, we recreate a complete solution using the greedy insertion heuristic. The destroy and repair neighborhoods are selected by a roulette wheel mechanism that uses the search history of each operator to favor the best performing one.
The third step depicts a mechanism conceived of to verify the feasibility of the solution achieved by using the ALNS approach in the preceding step, by examining the time windows associated with each visited customer. The last step is devoted to the evaluation of the robustness of the solution, according to the worst case criterion. In practice, we evaluate the solution
on the worst of possible cases, which relates to the realization where the
travel times of this solution reach at the same time their maximum values. The pseudocodes of those methods are shown in Algorithms 2 and 3, respectively.
| Algorithm 2. Check for robustness. |
for to do for to do calculate and for to do if and then else end if end for for to do if and then end if end for for to l do end for if then feasible takes false, and the algorithm ends end if end for end for
|
| Algorithm 3. Evaluation on the worst case. |
put in descending order all the arcs of according to their maximum deviations. for to do end for for to do end for return
|
For a detailed description of this robust approach, we refer the reader to the study of [
9] and the references therein.
5. The Parallel Robust Approach for the VRPTW with Uncertain Travel and Service Times
In this section, we provide a detailed exposition of the multi-threading parallel approach used in this paper. We start by giving some insights into the motivation before handling the complete description of the proposed approach.
The first challenge of such an approach is to derive the best robust solution that responds to to all uncertainties with a reduced running time. However, the sequential robust approach suffers from lengthy computational times; partly because the generation of scenarios is time-consuming, as well as the research of the solution block. Unlike those blocks, the check of robustness and the evaluation of the worst case blocks are not time-consuming, generally because they are restricted to evaluating the obtained solution.
Table 1 confirms our assertion that the Monte Carlo and the ALNS blocks take considerable time compared to the other blocks. This can be explained by the fact that the first phase is responsible for generating all the possible scenarios in which
displacement times take their maximum values and
service times take their maximum values. The ALNS block is also time-consuming, since it chooses at each iteration a neighborhood to explore, based on a score that reflects its past performance. This is possible by the application of several destroy and repair operators. Oppositely, the other blocks are not time-consuming, considering that the first mechanism verifies the feasibility of our solution by investigating the related time windows of each visited customer, and the second mechanism is dedicated to the evaluation of the robustness of the solution based on the worst case robust criterion. As an alternative to overcome this impediment, we propose a multithreading parallelization of the costly blocks as detailed in the next subsections.
5.1. The Parallel Monte Carlo Sampling
The parallel Metropolis Monte Carlo algorithm described below is a scenario generation technique that uses a defined number of worker threads to generate in a parallel way a predefined number
n of independent identically distributed scenarios. In practice, each worker thread produces a realization
that corresponds to a deterministic VRPTW problem, in which
displacement times and
service times reach simultaneously their maximum values. The pseudocodes of this parallel method is shown in Algorithm 4:
| Algorithm 4. Parallel Monte Carlo. |
Input: , , n Output: scenarios for to n in parallel do for to do Select randomly two clients i and j end for for to do Select randomly a client i end for Generate a scenario Add to end for return
|
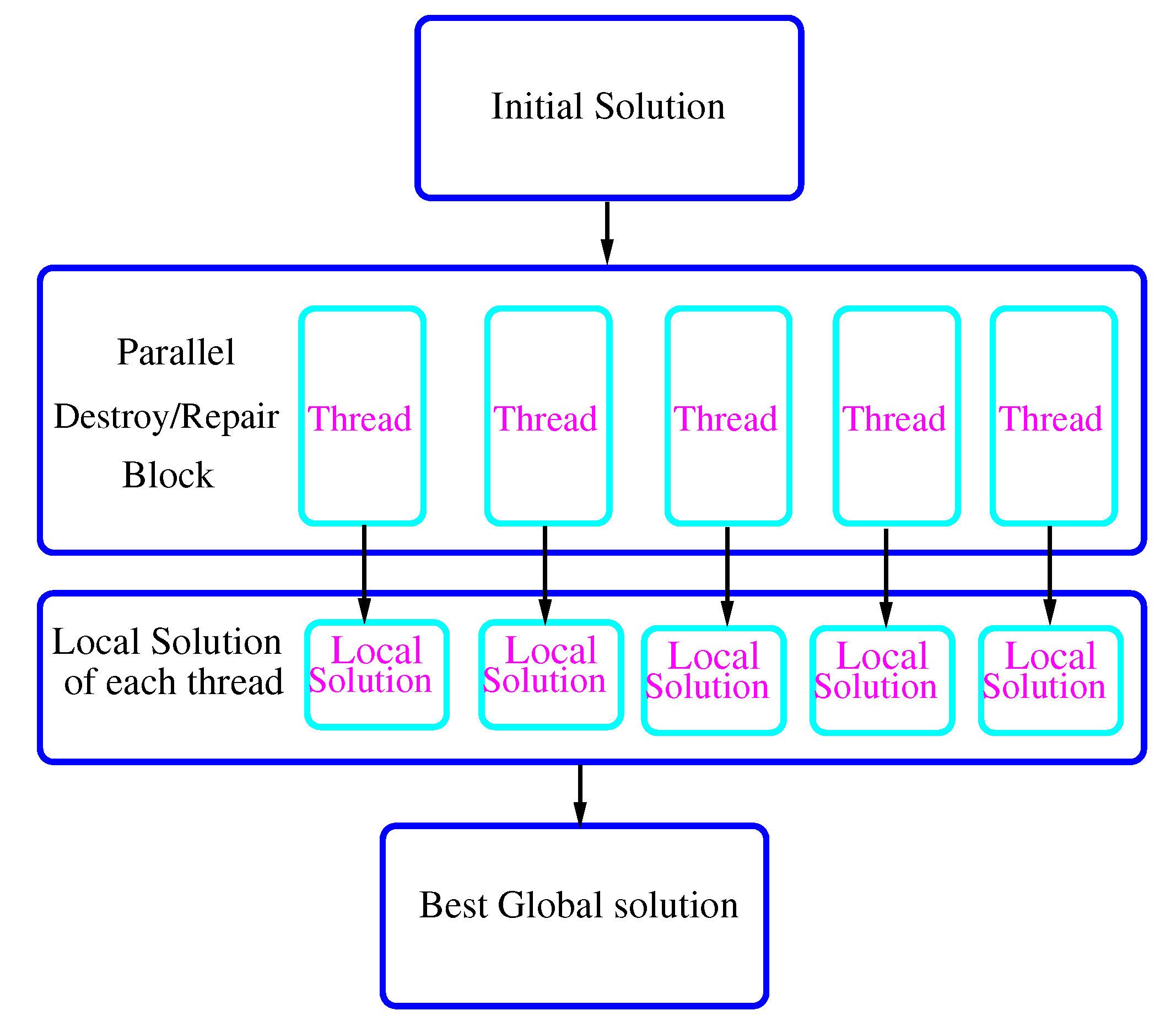
5.2. The Parallel ALNS
In this subsection, we present the Parallel Adaptive Large Neighborhood Search (PALNS) method developed by [
25]. This method can be presented in three phases (see
Figure 1).
At the first level, we generate an initial feasible solution by using the greedy insertion metaheuristic [
33]. The main idea behind this method is to select the best feasible insertion place in the incumbent route for each non-inserted node taking into account two major factors: the increase in total cost of the current route after the insertion and the delay of the service start time of the customer succeeding the newly inserted customer.
The second phase is related to a set of destroy and repair operators designed to enhance the incumbent solution. In this context, each worker thread deals with a copy of the current solution and executes destroy and repair methods on this local copy in order to improve it.
The third phase collects the routes of different local solutions that each thread has obtained, for the purpose of combining it into a new better temporary global solution and sending it to be improved. At this stage, we will accept or reject the generated solution, based on a hill climbing acceptance criterion. It is worth mentioning that only the current and global best solutions are shared between worker threads, in order to update them as necessary by repeating the process until a stop criterion is met.
We should point out here that the ALNS uses a flexible layer with a set of destruction heuristics (proximity operator, route portion operator, and longest detour operator) and an insertion heuristic (the greedy insertion) and applies them by a roulette wheel selection that highlights the corresponding performance obtained during the search. On the other hand, the LNS heuristic does not use this scoring mechanism.
For a completed description of the used PALNS, we refer the reader to the study of [
25] and the references therein.
6. Computational Experiments
In this section, we summarize a few of the results obtained by evaluating different robust approaches conceived of to solve the vehicle routing problem with time windows with uncertain service and travel times.
We explore the effect of applying the thread parallelism to the Monte Carlo and ALNS blocks, on the execution time and the objective value. This leads to four different robust combinations: the sequential approach that uses sequential Monte Carlo and sequential ALNS (MC sequential and ALNS sequential), the approach employing sequential Monte Carlo and parallel ALNS (MC sequential and ALNS parallel), the approach that uses parallel Monte Carlo and sequential ALNS (MC parallel and ALNS sequential), and the parallel approach combining parallel Monte Carlo and parallel ALNS (MC parallel and ALNS parallel). We should note here that the sequential approach (MC sequential and ALNS sequential) coincides with the only method from the literature [
9] that deals with the considered problem.
It is important to mention that the notion of thread parallelism used in our context can be defined as the capability of a processing unit to execute multiple processes contemporaneously or with time slicing. By means of a thread, the smallest unit of processing can be performed in an operating system in order to accelerate the execution time and manage the code over time. In our study, we use four threads in order to establish the comparison between the different approaches. The choice of four threads is not restrictive, and we can use as many threads as possible. Our assumption is that using more threads leads to the improvement of the average execution time, but it slightly decreases the quality of the obtained solution. For more details, see, e.g., [
25].
The robust approaches studied in this paper were tested on a classical set of instances in reference to Solomon’s benchmark (1987) [
33] and Gehring and Homberger’s benchmark [
34]:
Set R contains problems with randomized customers.
Set C contains problems with clustered customers.
Set contains problems with both clustered and randomized customers.
In order to simulate the uncertainty of RVRPTW by discrete scenarios, the uncertain travel time and uncertain service time are generated at random, so that they go from 0 to 10. We denote the used instances as follows: , where and present respectively the number of travel times and service times considered uncertain and refers to the instance of Solomon and Gehring and Homberger’s benchmark or the size of larger instances.
For small instances (Solomon and Homberger’s instances), we chose 15,600 iterations as a stop criterion in order to diversify the research, which may ameliorate the quality of our solution, because the solution has a greater chance to escape from a local minimum. As far as we are aware, the maximal number of iterations for instances is falling in the literature. With a view toward examining the capability of our approaches for tackling that problem, we judge it based on the average performance over 10 multiple independent runs.
For the set of instances larger than 1000, we generate random representative instances in such a manner that the travel time between each pair of nodes is between 0 and 100, and the same for the service time. The time interval has a capacity of 200 between the start and the end of the service at each customer. We forced a stop condition of about 20 min, which allows a good comparison between the proposed methods in terms of the number of reached iterations for the same time interval. Then, we present the measurements achieved for a single run.
The proposed algorithms were implemented in Java 7, compiled with Intel compiler Celeron 1.80 GHz core i5 with 8 GB RAM.
6.1. Execution Time
Table 2 presents a comparison of the execution time for each instance group between different robust approaches with the maximal number of iterations of 15,600. As expected, the results show that the approaches containing the parallel ALNS succeeded by those containing parallel Monte Carlo lead to the improvement of the average execution time compared to other sequential approaches. This can be explained by the fact that the ALNS block succeeded by the Monte Carlo block consumes most of the execution time compared to other blocks.
In the same spirit, we report in
Table 3 a comparison of different approaches according to the number of reached iterations when the stopping limit time is about 20 min for the group of instances 2500–4500. The approach containing more parallel blocks attained more iterations for the same time interval since it reduced the execution time of the consuming blocks.
Table 4 depicts the improvement results in execution time for Solomon’s instances. The conclusion from this table is clear: the running time is much faster for the approaches using parallel ALNS succeeded by those employing the parallel Monte Carlo algorithm.
6.2. Objective Function
Table 5 presents the objective function of different robust approaches for the group of instances 2500–4500. When the size of the instance increases, the cost function of the approaches containing parallel and sequential ALNS solution converges. Then, we compute the mean absolute percent deviation (MAPD), which is the absolute difference between the cost function of the approach containing the sequential ALNS and the parallel ALNS divided by the magnitude of the objective function in the approach with sequential ALNS. This indicator (MAPD) goes from
for the instance of size 1000 to
for the instance of size 4500. We can conclude that incorporating the parallel ALNS in the approaches is efficient for large instances.
Table 6 depicts the results of the objective value for some of Solomon’s instances. We observe that the ALNS controls the solution quality. Then, the approaches that contain a sequential ALNS yield better results than those that contain parallel ALNS. The ALNS is responsible for finding the solution of each scenario, in contrast with the Monte Carlo algorithm, which is limited to generating the possible scenarios. When we increase the instance size, the quality of the solution of the parallel approach becomes more interesting.
7. Conclusions
In this work, we study the robust vehicle routing problem with time windows where travel times and service times are both the subject of uncertainty. For this purpose, we opt for the robust technique proposed by [
9] to deal with the problem. As far as the adopted approach derives the best robust solution that responds to all uncertainties, it still suffer from lengthy computational times; partly because the generation of scenarios, as well as the research of the solution block are time-consuming. As an alternative to remedy this problem, we introduce a procedure for the thread parallelism in the Monte Carlo block, and we use the parallel ALNS proposed by [
25]. This leads to four different robust approaches combining the (sequential/parallel) Monte Carlo algorithm and the (sequential/parallel) ALNS.
The considered approaches are tested on Solomon’s benchmark instance of VRPTW and lager instances generated randomly. Accordingly, we can offer a decision-making solution that provides great protection against delays in a reasonable running time. However, we should note that the related counterpart of using the parallel ALNS, which is the objective value, can be influenced, since the parallel ALNS slightly reduces the quality of the solution, especially for small instances.
In future works, we intend to include a pre-processing step based on different clustering techniques such as K-means, K-medoids, density-based spatial, etc., in order to ensure the commitment of the solutions. These techniques will not change the structure of the suggested approach drastically, and our assumption is that they will enhance the solution quality obtained with the parallel ALNS.