Induction Motor Multiclass Fault Diagnosis Based on Mean Impact Value and PSO-BPNN
Abstract
1. Introduction
2. Signal Analysis Method and Classifier
2.1. S-Transform (ST)
2.2. Neural Network
3. Methodology
3.1. Mean Impact Value
- Step (1)
- Select all features as feature set
- Step (2)
- Train the model of PSO-BPNN.
- Step (3)
- Assume adjustment rate and adjust , get and .
- Step (4)
- Respectively input and to BPNN.
- Step (5)
- Get the output and .
- Step (6)
- Calculate impact value of , .
- Step (7)
- Calculate mean impact value, .
3.2. Particle Swarm Optimization-BP Neural Network
- Step (1)
- Set number of particles i, number of iterations t, the maximum number of iterations tmax, the acceleration constants c1 and c2, and the inertia weights w.
- Step (2)
- Assume that the coordinates of each particle in space , and the speed of each particle in space .
- Step (3)
- Calculate the fitness values of all particles by BPNN, and obtain the best solution Pbest for individuals and the best solution Gbest for groups.
- Step (4)
- Correct flight speed of the particle
- Step (5)
- Correct the particle position .
- Step (6)
- if , and repeat step (3) to step (5).
- Step (7)
- Obtain the best position of the groups as the best solution.
- Step (8)
- Get PSO-BP model.
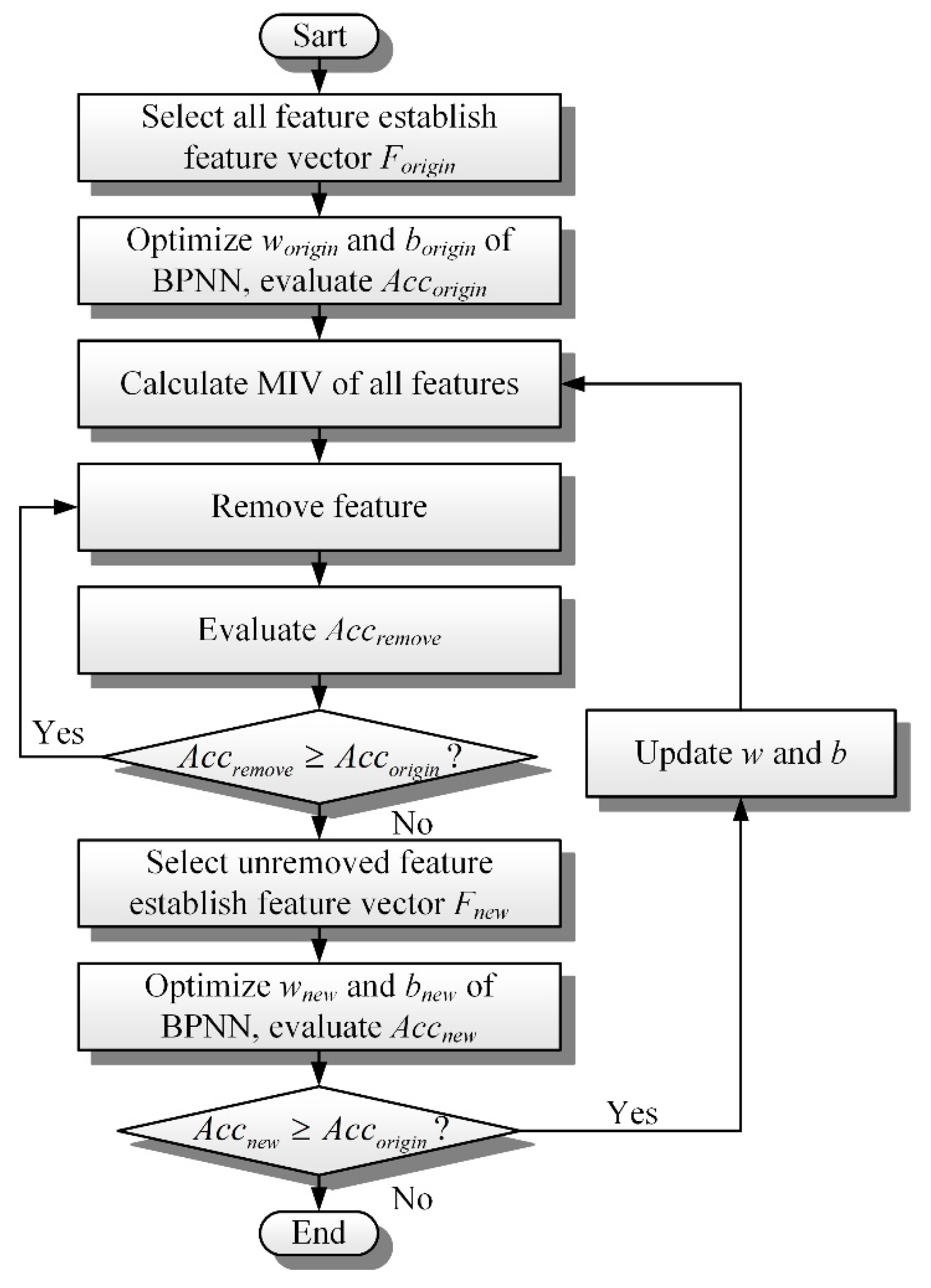
3.3. Feature Selection
- Step (1)
- Select all features to establish feature vector Forigin and set dimension D = 50.
- Step (2)
- Use PSO to optimize the initial weights worigin and bias borigin of BPNN.
- Step (3)
- Record the optimized result and evaluate the accuracy Accremove of BPNN.
- Step (4)
- Calculate MIV of all features.
- Step (5)
- Arrange MIV from the minimum to the maximum and remove a feature corresponding to the smallest MIV. D = D − 1.
- Step (6)
- Select unremoved features to create a new feature vector Fnew, and evaluate the accuracy Accremove. If Accremove > Accorigon, go back to Step (5).
- Step (7)
- Select the features that have not been removed to create a new feature vector , and use PSO to optimize the initial weight wnew and bnew bias of BPNN. To evaluate the accuracy Accnew.
- Step (8)
- If Accnew > Accorigin, go back to Step (5).
4. Experimental Measurements and Analysis of IM
4.1. Experiment Device
4.2. Experiment Structure
4.3. Analysis Current of IM
4.3.1. Healthy Motor
4.3.2. Bearing Failure Motor
4.3.3. Stator Short Circuit Fault Motor
4.3.4. Rotor Drilling Fault Motor
4.4. Feature Extraction
- (1)
- Tmax: maximum value of each column of ST matrix.
- (2)
- Tmin: minimum value of each column of ST matrix.
- (3)
- Tmean: average value of each column of ST matrix.
- (4)
- Tmse: mean square error of each column of ST matrix.
- (5)
- Tstd: standard deviation of each column of ST matrix.
- (6)
- Fmax: maximum value of each row of ST matrix.
- (7)
- Fmin: minimum value of each row of ST matrix.
- (8)
- Fmean: average value of each row of ST matrix.
- (9)
- Fmse: mean square error of each row of ST matrix.
- (10)
- Fstd: standard deviation of each row of ST matrix.
4.5. Classifier
5. Results
5.1. Motor Current Signal Measurement
5.2. Feature Selection Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brkovic, A.; Gajic, D.; Gligorijevic, J.; Savic Gajic, I.; Georgieva, O.; Gennaro, S.-D. Early fault detection and diagnosis in bearings for more efficient operation of rotating machinery. Energy 2017, 136, 63–71. [Google Scholar] [CrossRef]
- Ro, H.S.; Kim, D.H.; Jeong, H.G.; Lee, K.-B. Tolerant control for power transistor faults in switched reluctance motor drives. IEEE Trans. Ind. Appl. 2015, 51, 3187–3197. [Google Scholar] [CrossRef]
- Tobon-Mejia, D.A.; Medjaher, K.; Zerhouni, N. CNC machine tool’s wear diagnostic and prognostic by using dynamic Bayesian networks. Mech. Syst. Signal Process. 2012, 28, 167–182. [Google Scholar] [CrossRef]
- Resendiz-Ochoa, E.; Osornio-Rios, R.A.; Benitez-Rangel, J.P.; De Romero-Troncoso, R.J.; Morales-Hernandez, L.A. Induction motor failure analysis: An automatic methodology based on infrared imaging. IEEE Access 2018, 6, 76993–77003. [Google Scholar] [CrossRef]
- Hsueh, Y.-M.; Ittangihal, V.R.; Wu, W.-B.; Chang, H.-C.; Kuo, C.-C. Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform. Symmetry 2019, 11, 1212. [Google Scholar] [CrossRef]
- Korkua1, S.; Jain, H.; Lee, W.-J.; Kwan, C. Wireless Health Monitoring System for Vibration Detection of Induction Motors. In Proceedings of the 2010 IEEE Industrial and Commercial Power Systems Technical Conference, Tallahassee, FL, USA, 9–13 May 2010. [Google Scholar]
- Ge, M.; Wand, J.; Xu, Y.; Zhang, F.; Bai, K.; Ren, X. Rolling Bearing Fault Diagnosis Based on EWT Sub-Modal Hypothesis Test and Ambiguity Correlation Classification. Symmetry 2018, 10, 730. [Google Scholar] [CrossRef]
- Yang, T.; Pen, H.; Wang, Z.; Chang, C.S. Feature Knowledge Based Fault Detection of Induction Motors through the Analysis of Stator Current Data. IEEE Trans. Instrum. Meas. 2016, 65, 549–558. [Google Scholar] [CrossRef]
- Oyamada, M. Extracting feature engineering knowledge from data science notebooks. In Proceedings of the IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019. [Google Scholar]
- Rauber, T.W.; de Boldt, F.A.; Varejão, F.M. Heterogeneous feature models and feature selection applied to bearing fault diagnosis. IEEE Trans. Ind. Electron. 2014, 62, 637–646. [Google Scholar] [CrossRef]
- Gligorijevic, J.; Gajic, D.; Brkovic, A.; Savic Gajic, I.; Georgieva, O.; Gennaro, S.-D. Online Condition Monitoring of Bearings to Support Total Productive Maintenance in the Packaging Materials Industry. Sensors 2016, 16, 316. [Google Scholar] [CrossRef]
- Huang, Z.-L.; Zhang, J.; Zhao, T.-H.; Sun, Y. Synchrosqueezing S-transform and its application in seismic spectral decomposition. IEEE Trans. Geosci. Remote Sens. 2016, 54, 817–825. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, D. EEG time-frequency analysis based on the improved S-transform. In Proceedings of the 25th Chinese Control and Decision Conference, Guiyang, China, 25–27 May 2013. [Google Scholar]
- Feng, Z.P.; Chen, X.W.; Liang, M. Iterative generalized synchrosqueezing transform for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Mech. Syst. Signal Process. 2015, 52, 360–375. [Google Scholar] [CrossRef]
- Wu, H.T.; Chan, Y.H.; Lin, Y.T.; Yeh, Y.H. Using synchrosqueezing transform to discover breathing dynamics from ECG signals. Appl. Comput. Harmon. Anal. 2014, 36, 354–359. [Google Scholar] [CrossRef]
- Wang, Z.-C.; Ren, W.-X.; Liu, J.-L. A synchrosqueezed wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction. J. Sound Vib. 2013, 332, 6016–6028. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Wang, Y.; Cai, G.; Ding, B.; Zhang, X. Nonlinear squeezing time-frequency transform for weak signal detection. Signal Process. 2015, 113, 195–210. [Google Scholar] [CrossRef]
- Ahrabian, A.; Looney, D.; Stanković, L.; Mandic, D.P. Synchrosqueezing-based time-frequency analysis of multivariate data. Signal Process. 2015, 106, 331–341. [Google Scholar] [CrossRef]
- Kwan, C.; Zhang, X.; Xu, R.; Haynes, L. A novel approach to fault diagnostics and prognostics. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 604–609. [Google Scholar]
- Yang, C.; Lu, L.; Lin, H.; Guan, R.; Shi, X.; Liang, Y. A Fuzzy-Statistics-Based Principal Component Analysis (FS-PCA) Method for Multispectral Image Enhancement and Display. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3937–3947. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Z. A hybrid model for blood pressure prediction from a PPG signal based on MIV and GA-BP neural network. In Proceedings of the 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery, Guilin, China, 29–31 July 2017. [Google Scholar]
- Lee, C.-Y.; Shen, Y.-X. Optimal feature selection for power-quality disturbances classification. IEEE Trans. Power Deliv. 2006, 26, 2342–2351. [Google Scholar] [CrossRef]
- Qian, T.; Li, X.; Ayhan, B.; Xu, R.; Kwan, C.; Griffin, T. Application of Support Vector Machines to Vapor Detection and Classification for Environmental Monitoring of Spacecraft. In ISNN 2006. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Liu, N.; Gao, J.; Zhang, B.; Li, F.; Wang, Q. Time-Frequency Analysis of Seismic Data Using a Three Parameters S Transform. IEEE Geosci. Remote Sens. Lett. 2018, 15, 142–146. [Google Scholar] [CrossRef]
- Brown, R.A.; Lauzon, M.L.; Frayne, R. A general description of linear time-frequency transforms and formulation of a fast, invertible transform that samples the continuous S-transform spectrum nonredundantly. IEEE Trans. Signal Process. 2010, 58, 281–290. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Liu, X.; Tang, J. Mass classification in mammograms using selected geometry and texture features and a new SVM-based feature selection method. IEEE Syst. J. 2014, 8, 910–920. [Google Scholar] [CrossRef]
- Fernandez-Martinez, J.L.; Garcia-Gonzalo, E. Stochastic Stability Analysis of the Linear Continuous and Discrete PSO Models. IEEE Trans. Evol. Comput. 2011, 15, 405–423. [Google Scholar] [CrossRef]











| Tmax | Tmin | Tmean | Tmse | Tstd | Fmax | Fmin | Fmean | Fmse | Fstd | |
|---|---|---|---|---|---|---|---|---|---|---|
| MAX + MIN | F1 | F6 | F11 | F16 | F21 | F26 | F31 | F36 | F41 | F46 |
| MAX − MIN | F2 | F7 | F12 | F17 | F22 | F27 | F32 | F37 | F42 | F47 |
| Mean | F3 | F8 | F13 | F18 | F23 | F28 | F33 | F38 | F43 | F48 |
| Mse | F4 | F9 | F14 | F19 | F24 | F29 | F34 | F39 | F44 | F49 |
| Std | F5 | F10 | F15 | F20 | F25 | F30 | F35 | F40 | F45 | F50 |
| Classfier | Accuaracy |
|---|---|
| PNN | 86.12% |
| BPNN | 96.3% |
| PSO-BPNN | 100% |
| Feature Number | Number of Features | Accuracy | Computing Time |
|---|---|---|---|
| F1, F2, F3, …, F48, F49, F50 | 50 | 100% | 21.03 |
| F11, F13, F24, F27, F31, F32, F34, F35, F39, F40, F42, F43, F46, F47, F49, F50 | 16 | 100% | 19.43 |
| F24, F31, F32, F39, F40, F43, F46, F47, F49, F50 | 10 | 100% | 19.11 |
| F24, F31, F32, F40, F43, F46, F47, F49, F50 | 9 | 99.4% | 19.07 |
| Feature Number | Number of Features | Accuracy | Computing Time |
|---|---|---|---|
| F1, F2, F3, …, F48, F49, F50 | 50 | 86.5% | 21.09 |
| F9, F20, F24, F26, F27, F30, F32, F36, F38, F39, F40, F44, F45, F46, F47, F50 | 16 | 88.6% | 19.43 |
| F36, F38, F39, F40, F44, F46, F50 | 7 | 86.5% | 19.08 |
| F38, F39, F40, F44, F46, F50 | 6 | 86.2% | 18.90 |
| Feature Number | Number of Features | Accuracy | Computing Time |
|---|---|---|---|
| F1, F2, F3,…, F48, F49, F50 | 50 | 64.0% | 21.07 |
| F1, F3, F5, F7, F8, F9, F11, F12, F13, F14, F20, F23, F24, F25, F26, F28, F32, F35, F36, F37, F38, F39, F42, F43, F45, F49, F50 | 27 | 71% | 19.95 |
| F42, F43, F45 | 3 | 67.3% | 18.71 |
| F42, F45 | 2 | 63.2% | 18.76 |
| Feature Selection Methods | Number of Features | Accuaracy of Healthy Motor | Accuaracy of Bearing Failure Motor | Accuaracy of Stator Short Circuit Fault Motor | Accuaracy of Rotor Drilling Fault Motor | Total Accuaracy |
|---|---|---|---|---|---|---|
| All features | 50 | 100% | 100% | 100% | 100% | 100% |
| MIV base on PSO-BPNN | 9 | 97.7% | 100% | 99.9% | 100% | 99.4% |
| Feature Selection Methods | Number of Features | Accuracy |
|---|---|---|
| All features | 50 | 100% |
| GA | 28 | 100% |
| ReliefF | 9 | 98.5% |
| MIV base on PSO-BPNN | 9 | 99.4% |
| Healthy Motor | Bearing Failure Motor | Stator Short Circuit Fault Motor | Rotor Drilling Fault Motor | Total | |
|---|---|---|---|---|---|
| Healthy motor | 48.85 | 0 | 0.05 | 0 | 99.8% 0.2% |
| Bearing failure motor | 0 | 50 | 0 | 0 | 100% 0% |
| Stator short circuit fault motor | 0.1 | 0 | 49.9 | 0 | 100% 0% |
| Rotor drilling fault motor | 0.2 | 0 | 0 | 50 | 97.8% 2.2% |
| Total | 97.7% 2.3% | 100% 0% | 99.8% 0.2% | 100% 0% | 99.4% 0.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-Y.; Ou, H.-Y. Induction Motor Multiclass Fault Diagnosis Based on Mean Impact Value and PSO-BPNN. Symmetry 2021, 13, 104. https://doi.org/10.3390/sym13010104
Lee C-Y, Ou H-Y. Induction Motor Multiclass Fault Diagnosis Based on Mean Impact Value and PSO-BPNN. Symmetry. 2021; 13(1):104. https://doi.org/10.3390/sym13010104
Chicago/Turabian StyleLee, Chun-Yao, and Hong-Yi Ou. 2021. "Induction Motor Multiclass Fault Diagnosis Based on Mean Impact Value and PSO-BPNN" Symmetry 13, no. 1: 104. https://doi.org/10.3390/sym13010104
APA StyleLee, C.-Y., & Ou, H.-Y. (2021). Induction Motor Multiclass Fault Diagnosis Based on Mean Impact Value and PSO-BPNN. Symmetry, 13(1), 104. https://doi.org/10.3390/sym13010104




