Advanced Algorithms and Common Solutions to Variational Inequalities

Abstract

The paper aims to present advanced algorithms arising out of adding the inertial technical and shrinking projection terms to ordinary parallel and cyclic hybrid inertial sub-gradient extra-gradient algorithms (for short, PCHISE). Via these algorithms, common solutions of variational inequality problems (CSVIP) and strong convergence results are obtained in Hilbert spaces. The structure of this problem is to find a solution to a system of unrelated VI fronting for set-valued mappings. To clarify the acceleration, effectiveness, and performance of our parallel and cyclic algorithms, numerical contributions have been incorporated. In this direction, our results unify and generalize some related papers in the literature.

1. Introduction

In this manuscript, we discuss the problem of finding fixed points which also solve VI via a Hilbert space (Hs). Let ¥ be a nonempty closed convex subset (ccs) of Hs ℸ under the induced norm$∥.∥$ and the inner product $⟨.,.⟩.$

The structure of the variational inequality problem (VIP) was built by the authors [1], for finding ${\wp }^{\ast }\in$ such that

$$⟨\gimel {\wp }^{\ast },\wp -{\wp }^{\ast }⟩\ge 0\mathrm{for}\mathrm{all}\wp \in \yen ,$$

(1)

where $\gimel :\daleth \to \daleth$ be a nonlinear mapping. They refer to the set of solutions of VIP (1) as $VI(\gimel ,\yen )$.

VI is involved in many interesting fields like, transportation, economics, engineering mechanics, mathematical programming. It is considered an indispensable tool in such specializations (see, for example, [2,3,4,5,6,7,8]). VI widely spread in optimization problems (OPs), where the algorithms were used solving it, see [7,9].

Under suitable stipulation to talk VIPs there is a two-way: projection modes and regularized manners. According to these lines, many iterative schemes have been presented and discuss for solving VIPs. Here, We focused on the first type. One of the easiest ways is using the gradient projection method, because when calculating it only needs one projection on the feasible set. However, the convergence of this method requires slightly strong assumptions that operators are strongly monotone or inverse strongly monotone. Via Lipschitz continuous and monotone mappings ℷ for solving saddle point problems and generalizing VIPs. Another projection method called the extra-gradient method has been presented by Korpelevich [10], which is built as below:

$$\left\{\begin{array}{c}{\wp }_n=P_{\yen }({⅁}_n-\ell \gimel \left({⅁}_n\right)),\hfill \\ {⅁}_{n+1}=P_{\yen }({⅁}_n-\ell \gimel \left({\wp }_n\right)),\hfill \end{array}\right.$$

for a suitable parameter ℓ and the metric projection $P_{\yen }$ onto ¥. Finding a projection and simplicity of the method depend on ¥ if it simple the extra-gradient method is computable and very useful otherwise the extra-gradient method is more complicated. The extra-gradient method used to solve two distance OPs if ¥ is a cc set.

In a Hs, the weak convergence of a solution of the VIPs is incorporated under the sub-gradient extra-gradient method [11] by the below algorithm:

$$\left\{\begin{array}{c}{\wp }_n=P_{\yen }({⅁}_n-\ell \gimel \left({⅁}_n\right)),\hfill \\ {⅁}_{n+1}=P_{{\xi }_n}({⅁}_n-\ell \gimel \left({\wp }_n\right)),\hfill \end{array}\right.$$

where ${\xi }_n$ is a half-space defined as follows:

$${\xi }_n=\{\theta \in \daleth :⟨({⅁}_n-\ell \gimel \left({⅁}_n\right))-{\wp }_n,\theta -{\wp }_n⟩\le 0\}.$$

Authors [12] accelerate the speed of convergence of the algorithm by building the following algorithm:

$$\left\{\begin{array}{c}{\wp }_n=P_{\yen }({⅁}_n-\ell \gimel \left({⅁}_n\right)),\hfill \\ {\mathsf{\Lambda }}_n={\eta }_n{⅁}_n+(1-{\eta }_n)P_{{\xi }_n}{⅁}_n,\hfill \\ {\yen }_n=\{\mathsf{\Lambda }\in \daleth :∥{\mathsf{\Lambda }}_n-\mathsf{\Lambda }∥\le ∥{⅁}_n-\mathsf{\Lambda }∥\},\hfill \\ {\mho }_n=\{\mathsf{\Lambda }\in \daleth :⟨{⅁}_n-\mathsf{\Lambda },{⅁}_0-{⅁}_n⟩\ge 0\},\hfill \\ {⅁}_{n+1}=P_{{\yen }_n\cap {\mho }_n}{⅁}_0.\hfill \end{array}\right.$$

Our paper is interested in finding CSVIP. The CSVIP here is to find a point ${\wp }^{\ast }\in \Re ={\cap }_{i=1}^N{\Re }_i$ such that

$$⟨{\gimel }_i\left({\wp }^{\ast }\right),\wp -{\wp }^{\ast }⟩\ge 0\mathrm{for}\mathrm{all}\wp \in {\Re }_i,i=1,..,N.$$

(2)

where ${\Re }_i:\daleth \to \daleth$ be a nonlinear mapping and ${\Re }_i$ be a finite family of non-empty ccs of ℸ such that ${\cap }_{i=1}^N{\Re }_i\ne \varnothing .$ Please note that If $N=1,$ CSVIP (2) reduce to VIP (1). Here CSVIPs takes many forms such as: Convex feasibility problem (CFP), if we consider all ${\gimel }_i=0$, then we find a point ${\wp }^{\ast }\in {\cap }_{i=1}^N{\Re }_i$ in the non-empty intersection of a finite family of cc sets. Common fixed point problem (CFPP) If we take the sets ${\Re }_i$ are the fixed point sets in (CFP). These problems have been studied in-depth and expansion, and their numerous applications have become the focus of attention of many researchers see [13,14,15,16,17,18,19].

For multi-valued mappings of ${\gimel }_i:\daleth \to 2^{\daleth },$ $i=1,..,N$, an algorithm for solving the CSVIP is given by [20]. For simplicity we list the below algorithm for ${\gimel }_i$ is a single-valued: Choose ${\wp }_1\in \daleth$ and compute

$$\left\{\begin{array}{c}{\wp }_n^i=P_{{\Re }_i}({⅁}_n-{\ell }_n^i{\gimel }_i\left({⅁}_n\right)),\hfill \\ {\mathsf{\Lambda }}_n^i=P_{{\Re }_i}({⅁}_n-{\ell }_n^i{\gimel }_i\left({\wp }_n\right))\hfill \\ {\yen }_n^i=\{\mathsf{\Lambda }\in \daleth :⟨{⅁}_n-{\mathsf{\Lambda }}_n^i,\mathsf{\Lambda }-{⅁}_n-{\gamma }_n^i({\mathsf{\Lambda }}_n^i-{⅁}_n)⟩\},\hfill \\ {\yen }_n={\cap }_{i=1}^N{\yen }_n^i,\hfill \\ {\pounds }_n=\{\mathsf{\Lambda }\in \daleth :⟨{⅁}_1-{⅁}_n,\mathsf{\Lambda }-{⅁}_n⟩\le 0\},\hfill \\ {⅁}_{n+1}=P_{{\yen }_n\cap {\pounds }_n}{⅁}_1.\hfill \end{array}\right.$$

(3)

the approximation ${⅁}_{n+1}$ of the algorithm (3), can be found by constructing $N+1$ subsets ${\yen }_n^1,$${\yen }_n^2$,..,${\yen }_n^i$ and ${\pounds }_n$ and solve the following minimization problem:

$$\left\{\begin{array}{c}min{∥\mathsf{\Lambda }-{⅁}_1∥}^2,\\ \mathrm{such}\mathrm{that}\mathsf{\Lambda }{\in }_n^1\cap ..\cap {\yen }_n^i\cap {\pounds }_n.\end{array}\right.$$

(4)

when N is large, this task can be very costly. Respect to the power of the number of half-spaces, the number of subcases in the explicit solution formula of the problem (4) is two.

In Banach spaces, for finding a common element of the set of fixed points via a family of asymptotically quasi $\varphi -$non-expansive mappings the authors [21,22] derived two strongly convergent parallel hybrid iterative methods. This algorithm can be formulated in Hilbert spaces as follows:

$$\left\{\begin{array}{c}{⅁}_0\in \yen ,\hfill \\ {\wp }_n^i={\eta }_n{⅁}_n+(1-{\eta }_n)S_{{\yen }_i}{⅁}_n,i=1,..,N,\hfill \\ i_n=argmax\{∥{\wp }_n^i-{⅁}_n∥:i=1,..,N\},\stackrel{-}{{\wp }_n}={\wp }_n^{i_n},\hfill \\ {\yen }_{n+1}=\{v\in {\yen }_n:∥v-\stackrel{-}{{\wp }_n}∥\le ∥v-{⅁}_n∥\},\hfill \\ {⅁}_{n+1}=P_{{\yen }_{n+1}}{⅁}_0.\hfill \end{array}\right.$$

where ${\eta }_n\in (0,1),$$lim{sup}_{n\to \infty }{\eta }_n<1.$ According to this algorithm, the approximation ${⅁}_{n+1}$ is defined as the projection of ${⅁}_0$ onto ${\yen }_{n+1}$, and finding the explicit form of the sets ${\yen }_n$ and perform numerical experiments seems complicated. By the same scenario, Hieu [23], introduced two PCHSE algorithms for CSVIPs in Hilbert spaces and analyze their convergence by numerical results.

Our main goal in this paper is to present iterative procedures for solving CSVIPs and prove its strong convergence. We called it, PCHISE algorithms. Our algorithms generates a sequence that converges strongly to the nearest point projection of the starting point onto the solution set of the CSVIP. To simplify this convergence, we use the inertial technical and shrinking projection methods. Also, some numerical experiments to support our results are given.

The outline of this work is as follows: In the next section, we give a definition and lemmas that we will use in study of the strong convergence analysis. Strong convergence results are obtained bu these procedures in Section 3, and at the ending, in Section 4, non-trivial two computational examples to discuss the performance of our algorithms and support theoretical results are incorporated.

2. Definition and Necessary Lemmas

In this section, we recall some definitions and results which will be used later.

Definition 1.

[24] For all $⅁,\wp \in \daleth ,$ a nonlinear operator ℷ is called

(i)

monotone if

$$⟨⅁-\wp ,\gimel ⅁-\gimel \wp ⟩\ge 0,$$

(ii)

pseudomonotone if $⟨⅁-\wp ,\gimel ⅁-\gimel \wp ⟩\ge 0$ leads to

$$⟨\wp -⅁,\gimel \wp -\gimel ⅁⟩\le 0,$$

(iii)

$\eta -$inverse strongly monotone ($\eta -$ism) if there exists $\eta >0$ such that

$$⟨⅁-\wp ,\gimel ⅁-\gimel \wp ⟩\ge \eta {∥\gimel ⅁-\gimel \wp ∥}^2;$$

(iv)

maximal monotone if it is monotone and its graph

$$G(\gimel )=\left\{\right(⅁,\gimel ⅁):⅁\in \daleth \}$$

is not a proper subset of one of any other monotone mapping,

(v)

L-Lipschitz continuous if there exists a positive constant L such that

$$\left|\right|\gimel (⅁)-\gimel (\wp )\left|\right|\le L\left|\right|⅁-\wp \left|\right|;$$

(vi)

nonexpansive if

$$\left|\right|\gimel (⅁)-\gimel (\wp )\left|\right|\le \left|\right|⅁-\wp \left|\right|.$$

Here, the set $\mathsf{\Theta }(\gimel )=\{⅁\in \daleth :\gimel ⅁=⅁\}$ is referred to the set of all fixed points of a mapping ℷ.

It’s obvious that a monotone mapping $\gimel :\daleth \to \daleth$ is maximal iff, for each $(⅁,\wp )\in \daleth \times \daleth$ such that $⟨⅁-u,\wp -v⟩\ge 0$ for all $(u,v)\in G(\gimel )$, it follows that $\wp =\gimel (⅁)$.

Lemma 1.

[25] Let ℸ be a real Hilbert space (rHs). Then for each $⅁,\wp \in \daleth$ and $\tau \in [0,1],$

(i) ${∥⅁-\wp ∥}^2\le {∥⅁∥}^2+{∥\wp ∥}^2-2⟨⅁,\wp ⟩,$

(ii) ${∥⅁+\wp ∥}^2\le {∥⅁∥}^2-2⟨\wp ,⅁+\wp ⟩,$

(iii) ${∥\tau ⅁-(1-\tau )\wp ∥}^2=\tau {∥⅁∥}^2+(1-\tau ){∥\wp ∥}^2-\tau (1-\tau ){∥⅁-\wp ∥}^2.$

For each $⅁\in \daleth$, the projection $P_{\yen }⅁$ defined by $P_{\yen }⅁=argmin\{∥\wp -⅁∥:\wp \in \yen \}$. Also, $P_{\yen }⅁$ exists and is unique because is nonempty ccs of ℸ. The projection $P_{\yen }:\daleth \to \yen$ has the following properties:

Lemma 2.

[24] Assume that $P_{\yen }:\daleth \to \yen$ is a projection. Then

(i) $P_{\yen }$ is 1-ism, i.e., for each $⅁,\wp \in \daleth$,

$$⟨P_{\yen }⅁-P_{\yen }\wp ,⅁-\wp ⟩\ge {∥P_{\yen }⅁-P_{\yen }\wp ∥}^2.$$

(ii) For all ℘$\in \daleth ,$⅁$\in \yen ,$

$${∥⅁-P_{\yen }⅁∥}^2+{∥P_{\yen }\wp -\wp ∥}^2\le {∥⅁-\wp ∥}^2.$$

(iii) $\mathsf{\Lambda }=P_{\yen }⅁$ if and only if

$$⟨⅁-\mathsf{\Lambda },\mathsf{\Lambda }-\wp ⟩\ge 0,\forall \wp \in \yen .$$

Lemma 3.

[25] Suppose that ℷ is a monotone, hemi-continuous mapping form onto ℸ, where ¥ is a non-empty ccs of a Hs ℸ, then

$$VI(\gimel ,\yen )=\{u\in \yen :⟨v-u,\gimel (v)⟩\ge 0,\forall v\in \yen \}.$$

Lemma 4.

[26] Suppose that $\yen \ne \varnothing$ is a ccs of a Hs ℸ. Given that $⅁,\wp ,\mathsf{\Lambda }\in \daleth$ and $\iota \in \mathbb{R},$ the set

$$\{v\in \daleth :{∥\wp -v∥}^2\le {∥⅁-v∥}^2+⟨\mathsf{\Lambda },v⟩+\iota \}$$

is cc.

The normal cone $N_{\yen }$ to a set at a point $⅁\in \yen$ defined by

$$N_{\yen }⅁=\{{⅁}^{\ast }\in \daleth :⟨⅁-\wp ,{⅁}^{\ast }⟩\ge 0,\forall \wp \in \yen \}.$$

Thus, the following result is very important.

Lemma 5.

[27] Suppose that ℷ is a monotone, hemi-continuous mapping form ¥ onto ℸ, where ¥ is a non-empty ccs of a Hs ℸ, with $D(\gimel )=\yen .$ Let ℑ be a mapping defined by

$$\Im (⅁)=\left\{\begin{array}{c}\gimel ⅁+N_{\yen }⅁\mathrm{if}⅁\in \yen \\ \varnothing \mathrm{if}⅁\notin \yen \end{array}\right.$$

Then ℑ is a maximal monotone and ℑ${}^{-1}\left(0\right)=VI(\gimel ,\yen ).$

3. Main Theorems

This part is devoted to discuss the strong converges for our proposed algorithms under the following considerations: The collection ${\left\{{\gimel }_i\right\}}_{i=1}^N$ is Lipschitz continuous with the same constant L$>0$. Via $L=max\{L_i:i=1,...,N\}$, ${\gimel }_i$ is also L-Lipschitz continuous for each $i=1,..,N$. Finally, we consider $\mathsf{\Theta }={\cap }_{i=1}^{N}VI({\gimel }_i,{\Re }_i)$ is non-empty.

Theorem 1.

(PHISE algorithm)

Assume that ℸ is a rHs and $\Re ={\cap }_{i=1}^N{\Re }_i\ne \varnothing$, where ${\Re }_i,$$i=1,..,N$ be ccs of ℸ. Let ${\left\{{\gimel }_i\right\}}_{i=1}^n:\daleth \to \daleth$ be a finite collection of monotone and L-Lipschitz continuous mappings and the solution set Θ is nonempty. Let $\left\{{⅁}_n\right\}$ be a sequence generated by ${⅁}_0,{⅁}_1\in {\yen }_1^i=\yen =\daleth$, for all $i=1,..,N$ and

$$\left\{\begin{array}{c}{{\rm Y}}_n={⅁}_n+{\pi }_n({⅁}_n-{⅁}_{n-1}),\hfill \\ {\wp }_n^i=P_{{\Re }_i}({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({{\rm Y}}_n\right)),\hfill \\ {\mathsf{\Lambda }}_n^i=P_{{\xi }_n^i}({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({\wp }_n^i\right)),\hfill \\ {\yen }_{n+1}^i=\{v\in \daleth :{∥{\mathsf{\Lambda }}_n^i-v∥}^2\le {∥{⅁}_n-v∥}^2+(1-r){\pi }_n^2{∥{⅁}_n-{⅁}_{n-1}∥}^2\},\hfill \\ {\yen }_{n+1}={\bigcap }_{i=1}^N{\yen }_{n+1}^i,\hfill \\ {⅁}_{n+1}=P_{{\yen }_{n+1}}{⅁}_1,n\ge 1.\hfill \end{array}\right.$$

(5)

where ${\wp }_n^i\in {\Re }_i,$${\mathsf{\Lambda }}_n^i\in {\xi }_n^i=\{v\in \daleth :⟨({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({{\rm Y}}_n\right))-{\wp }_n^i,v-{\wp }_n^i⟩\le 0\},$${\ell }_n\in (0,\frac{1}{2L})$ and ${\pi }_n\in [0,1).$ Assume that ${\sum }_{i=1}^{\infty }{\pi }_n∥{⅁}_n-{⅁}_{n-1}∥<\infty .$ Then the sequence $\left\{{⅁}_n\right\}$ converges strongly to $\varpi =P_{\mathsf{\Theta }}{⅁}_1.$

Proof. 

The proof is divided into the below steps

Step 1. Show that

$${∥{\mathsf{\Lambda }}_n^i-{⅁}^{\ast }∥}^2\le {∥{⅁}_n-{⅁}^{\ast }∥}^2+(1-r){\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2-r\left({∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{⅁}_n∥}^2\right),$$

(6)

where ${⅁}^{\ast }\in \mathsf{\Theta }$ and $r=1-{\ell }_{n}L>0.$

Let ${⅁}^{\ast }\in \mathsf{\Theta },$ then by Lemma 1 (i), we can write

$$\begin{array}{ccc}\hfill {∥{{\rm Y}}_n-{⅁}^{\ast }∥}^2& =& {∥({⅁}_n-{⅁}^{\ast })-{\pi }_n({⅁}_{n-1}-{⅁}_n)∥}^2\hfill \\ & =& {∥{⅁}_n-{⅁}^{\ast }∥}^2+{\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2-2{\pi }_n⟨{⅁}_n-{⅁}^{\ast },{⅁}_{n-1}-{⅁}_n⟩\hfill \\ & \le & {∥{⅁}_n-{⅁}^{\ast }∥}^2+{\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2.\hfill \end{array}$$

(7)

Also, by simple calculations, we can find

$${∥{\wp }_n^i-{{\rm Y}}_n∥}^2\le {∥{\wp }_n^i-{⅁}_n∥}^2+{\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2.$$

(8)

Similarly,

$${∥{\mathsf{\Lambda }}_n^i-{{\rm Y}}_n∥}^2\le {∥{\mathsf{\Lambda }}_n^i-{⅁}_n∥}^2+{\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2.$$

Since, ${\gimel }_i$ is monotone on ${\Re }_i$ and ${\wp }_n^i\in {\Re }_i$, we can get

$$⟨{\gimel }_i\left({\wp }_n^i\right)-{\gimel }_i\left({⅁}^{\ast }\right),{\wp }_n^i-{⅁}^{\ast }⟩\ge 0,\mathrm{for}\mathrm{all}{⅁}^{\ast }\in \mathsf{\Theta }.$$

This together with ${⅁}^{\ast }\in VI({\gimel }_i,{\Re }_i),$ yields

$$⟨{\gimel }_i\left({\wp }_n^i\right),{\wp }_n^i-{⅁}^{\ast }⟩\ge 0.$$

So

$$⟨{\gimel }_i\left({\wp }_n^i\right),{\mathsf{\Lambda }}_n^i-{⅁}^{\ast }⟩\ge ⟨{\gimel }_i\left({\wp }_n^i\right),{\mathsf{\Lambda }}_n^i-{\wp }_n^i⟩.$$

(9)

From definition of the metric projection onto ${\xi }_n^i$, one can obtain

$$⟨{\mathsf{\Lambda }}_n^i-{\wp }_n^i,({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({{\rm Y}}_n\right))-{\wp }_n^i⟩\le 0.$$

(10)

Thus, by (10), we get

$$\begin{array}{ccc}\hfill ⟨{\mathsf{\Lambda }}_n^i-{\wp }_n^i,({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({{\rm Y}}_n\right))-{\wp }_n^i⟩& =& ⟨{\mathsf{\Lambda }}_n^i-{\wp }_n^i,({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({{\rm Y}}_n\right))-{\wp }_n^i⟩\hfill \\ & +& {\ell }_n⟨{\mathsf{\Lambda }}_n^i-{\wp }_n^i,{\gimel }_i\left({{\rm Y}}_n\right)-{\gimel }_i\left({\wp }_n^i\right)⟩\hfill \\ & \le & {\ell }_n⟨{\mathsf{\Lambda }}_n^i-{\wp }_n^i,{\gimel }_i\left({{\rm Y}}_n\right)-{\gimel }_i\left({\wp }_n^i\right)⟩.\hfill \end{array}$$

(11)

Put $s_n^i={{\rm Y}}_n-{\ell }_n{\gimel }_i\left({\wp }_n^i\right)$ and write again ${\mathsf{\Lambda }}_n^i=P_{{\xi }_n^i}\left(s_n^i\right).$ From Lemma 2 (ii) and (9), one can write

$$\begin{array}{cc}\hfill {∥{\mathsf{\Lambda }}_n^i-{⅁}^{\ast }∥}^2& \le {∥s_n^i-{⅁}^{\ast }∥}^2-{∥P_{{\xi }_n^i}\left(s_n^i\right)-s_n^i∥}^2\hfill \\ \hfill & ={∥{{\rm Y}}_n-{\ell }_n{\gimel }_i\left({\wp }_n^i\right)-{⅁}^{\ast }∥}^2-{∥{\mathsf{\Lambda }}_n^i-({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({\wp }_n^i\right))∥}^2\hfill \\ \hfill & ={∥{{\rm Y}}_n-{⅁}^{\ast }∥}^2-{∥{\mathsf{\Lambda }}_n^i-{{\rm Y}}_n∥}^2+2{\ell }_n⟨{⅁}^{\ast }-{\mathsf{\Lambda }}_n^i,{\gimel }_i\left({\wp }_n^i\right)⟩\hfill \\ \hfill & \le {∥{{\rm Y}}_n-{⅁}^{\ast }∥}^2-{∥{\mathsf{\Lambda }}_n^i-{{\rm Y}}_n∥}^2+2{\ell }_n⟨{\wp }_n^i-{\mathsf{\Lambda }}_n^i,{\gimel }_i\left({\wp }_n^i\right)⟩.\hfill \end{array}$$

(12)

From (11), we have

$$\begin{array}{cc}\hfill & {∥{\mathsf{\Lambda }}_n^i-{{\rm Y}}_n∥}^2-2{\ell }_n⟨{\wp }_n^i-{\mathsf{\Lambda }}_n^i,{\gimel }_i\left({\wp }_n^i\right)⟩\hfill \\ \hfill =& {∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i+{\wp }_n^i-{{\rm Y}}_n∥}^2-2{\ell }_n⟨{\wp }_n^i-{\mathsf{\Lambda }}_n^i,{\gimel }_i\left({\wp }_n^i\right)⟩\hfill \\ \hfill =& {∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{{\rm Y}}_n∥}^2-2⟨{\mathsf{\Lambda }}_n^i-{\wp }_n^i,({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({\wp }_n^i\right)-{\wp }_n^i)⟩\hfill \\ \hfill =& {∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{{\rm Y}}_n∥}^2-2{\ell }_n⟨{\mathsf{\Lambda }}_n^i-{\wp }_n^i,{\gimel }_i\left({{\rm Y}}_n\right)-{\gimel }_i\left({\wp }_n^i\right)⟩\hfill \\ \hfill \ge & {∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{{\rm Y}}_n∥}^2-2{\ell }_n∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥∥{\gimel }_i\left({{\rm Y}}_n\right)-{\gimel }_i\left({\wp }_n^i\right)∥\hfill \\ \hfill \ge & {∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{{\rm Y}}_n∥}^2-2{\ell }_{n}L∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥∥{{\rm Y}}_n-{\wp }_n^i∥\hfill \\ \hfill \ge & {∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{{\rm Y}}_n∥}^2-{\ell }_{n}L\left({∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{{\rm Y}}_n-{\wp }_n^i∥}^2\right)\hfill \\ \hfill \ge & (1-{\ell }_{n}L)\left({∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{{\rm Y}}_n∥}^2\right).\hfill \end{array}$$

(13)

From (13) in (12) and applying (7), (8), we can get

$$\begin{array}{ccc}\hfill {∥{\mathsf{\Lambda }}_n^i-{⅁}^{\ast }∥}^2& \le & ∥{{\rm Y}}_n-{⅁}^{\ast }∥-(1-{\ell }_{n}L)\left({∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{{\rm Y}}_n∥}^2\right)\hfill \\ & \le & {∥{⅁}_n-{⅁}^{\ast }∥}^2+{\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2\hfill \\ & & -(1-{\ell }_{n}L)\left({∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{⅁}_n∥}^2+{\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2\right)\hfill \\ & =& {∥{⅁}_n-{⅁}^{\ast }∥}^2+(1-r){\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2-r\left({∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{⅁}_n∥}^2\right).\hfill \end{array}$$

Hence, we have the inequality (6).

Step 2. Show that ${⅁}_{n+1}$ is well-defined for all ${⅁}_1\in \daleth$ and $\mathsf{\Theta }{\subset }_{n+1}.$ Since ${\gimel }_i$ is Lipschitz continuous, thus, Lemma 3 confirm that $VI({\gimel }_i,{\Re }_i)$ is too for all $i=1,..,N$. Hence, $\mathsf{\Theta }$ is closed and convex. It follows from the definition of ${\yen }_{n+1}$ and Lemma 4 that, ${\yen }_{n+1}$ is closed and convex for each $n\ge 1.$

Let $v\in \mathsf{\Theta },$ thus we obtain from Step 1 that

$$\begin{array}{ccc}\hfill {∥{\mathsf{\Lambda }}_n^i-v∥}^2& \le & {∥{⅁}_n-v∥}^2+(1-r){\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2-r\left({∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2+{∥{\wp }_n^i-{⅁}_n∥}^2\right)\hfill \\ & \le & {∥{⅁}_n-v∥}^2+(1-r){\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2.\hfill \end{array}$$

Therefore, we have $v{\in }_{n+1}.$ Thus, $\mathsf{\Theta }{\subset }_{n+1}$ and ${⅁}_{n+1}=P_{\mathsf{\Theta }}{⅁}_1$ is will-defined.

Step 3. Prove that ${lim}_{n\to \infty }∥{⅁}_{n-1}-{⅁}_n∥$ exists. Since $\mathsf{\Theta }\ne \varnothing$ is ccs of $\daleth ,$ then there is a unique $u\in \mathsf{\Theta }$ such that

$$u=P_{\mathsf{\Theta }}{⅁}_1$$

From ${⅁}_n=P_{{\yen }_n}{⅁}_1,$${\yen }_{n+1}{\subset }_n$ and ${⅁}_{n+1}\in {\yen }_n,$ we can get

$$∥{⅁}_n-{⅁}_1∥\le ∥{⅁}_{n+1}-{⅁}_1∥,\mathrm{for}\mathrm{all}n\ge 1.$$

(14)

On the other hand, as $\mathsf{\Theta }\subset {\in }_n,$ we have

$$∥{⅁}_n-{⅁}_1∥\le ∥u-{⅁}_1∥,\mathrm{for}\mathrm{all}n\ge 1.$$

This proves that $\left\{{⅁}_n\right\}$ is bounded and non-decreasing. Hence, ${lim}_{n\to \infty }∥{⅁}_{n-1}-{⅁}_n∥$ exists.

Step 4. Prove that for all $i=1,..,N.$, the following relation holds

$$\underset{n\to \infty }{lim}∥{⅁}_{n+1}-{⅁}_n∥=\underset{n\to \infty }{lim}∥{\mathsf{\Lambda }}_n^i-{⅁}_n∥=\underset{n\to \infty }{lim}∥{\wp }_n^i-{⅁}_n∥=\underset{n\to \infty }{lim}∥{\wp }_n^i-{{\rm Y}}_n∥=0.$$

From ${⅁}_{n+1}\in {\yen }_{n+1}\subset {\yen }_n$ and ${⅁}_n=P_{{\yen }_n}{⅁}_1,$ we can get

$${∥{⅁}_n-{⅁}_{n+1}∥}^2\le {∥{⅁}_{n+1}-{⅁}_1∥}^2-{∥{⅁}_n-{⅁}_1∥}^2.$$

For this inequality, letting $n\to \infty$ and using Step 3, we find

$$\underset{n\to \infty }{lim}∥{⅁}_{n+1}-{⅁}_n∥=0.$$

(15)

Since ${\sum }_{i=1}^{\infty }{\theta }_n∥{⅁}_n-{⅁}_{n-1}∥<\infty$, then we have

$$\underset{n\to \infty }{lim}∥{{\rm Y}}_n-{⅁}_n∥=\underset{n\to \infty }{lim}∥{⅁}_n-{⅁}_{n-1}∥=0.$$

(16)

From (15) and the definitions of ${\yen }_{n+1}^i$, ${⅁}_{n+1}\in {\yen }_{n+1}$, we have

$${∥{\mathsf{\Lambda }}_n^i-{⅁}_{n+1}∥}^2\le {∥{⅁}_n-{⅁}_{n+1}∥}^2+(1-r){\pi }_n^2{∥{⅁}_n-{⅁}_{n-1}∥}^2\to 0$$

(17)

as $n\to \infty$ for all $i=1,..,N.$ By triangle inequality and using (15) and (17), one can obtain that

$$∥{\mathsf{\Lambda }}_n^i-{⅁}_n∥\le ∥{\mathsf{\Lambda }}_n^i-{⅁}_{n+1}∥+∥{⅁}_{n+1}-{⅁}_n∥\to 0$$

(18)

as $n\to \infty$ for all $i=1,..,N.$ From Step 1 and the triangle inequality, for each $v\in \mathsf{\Theta },$ one has

$$\begin{array}{ccc}\hfill r{∥{\wp }_n^i-{⅁}_n∥}^2& \le & {∥{⅁}_n-v∥}^2+(1-r){\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2-r{∥{\mathsf{\Lambda }}_n^i-{\wp }_n^i∥}^2-{∥{\mathsf{\Lambda }}_n^i-v∥}^2\hfill \\ & \le & {∥{⅁}_n-v∥}^2+(1-r){\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2-{∥{\mathsf{\Lambda }}_n^i-v∥}^2\hfill \\ & \le & \left(∥{⅁}_n-v∥+∥{\mathsf{\Lambda }}_n^i-v∥\right)∥{⅁}_n-{\mathsf{\Lambda }}_n^i∥+(1-r){\pi }_n^2{∥{⅁}_{n-1}-{⅁}_n∥}^2.\hfill \end{array}$$

(19)

Applying (16) and (18) in (19) and the boundedness of $\left\{x_n\right\}$, $\left\{{\mathsf{\Lambda }}_n^i\right\}$, yields

$$\underset{n\to \infty }{lim}∥{\wp }_n^i-{⅁}_n∥=0,i=1,..,N.$$

(20)

By triangle inequality and using (16) and (20), one can write

$$∥{\wp }_n^i-{{\rm Y}}_n∥\le ∥{\wp }_n^i-{⅁}_n∥+∥{⅁}_n-{{\rm Y}}_n∥\to 0$$

(21)

as $n\to \infty$ for all $i=1,..,N.$

Step 5. Show that the strongly convergent of $\left\{{⅁}_n\right\},\left\{{\wp }_n^i\right\}$ and $\left\{{\mathsf{\Lambda }}_n^i\right\}$ generated by (5) to $\varpi =P_{\mathsf{\Theta }}{⅁}_1$. Let $\left\{{⅁}_n\right\}$ has a weak cluster point $\varpi$, and has a subsequence converging weakly to $\varpi$, i.e., ${⅁}_n\rightharpoonup \varpi ,$ from (20), ${\wp }_n^i\rightharpoonup \varpi .$

Now we show that $\varpi \in {\cap }_{i=1}^{N}VI({\gimel }_i,{\Re }_i).$ Lemma 5, ensures that the mapping

$${\Im }_i(⅁)=\left\{\begin{array}{c}{\gimel }_i⅁+N_{{\Re }_i}(⅁)\mathrm{if}⅁\in \yen \\ \varnothing \mathrm{if}⅁\notin \yen \end{array}\right.$$

is a maximal monotone, where $N_{{\Re }_i}(⅁)$ is the normal cone to ${\Re }_i$ at $⅁\in {\Re }_i.$ For all $(⅁,\wp )\in G\left({\Im }_i\right),$ we have $\wp -{\gimel }_i⅁\in N_{{\Re }_i}(⅁),$ where $G\left({\Im }_i\right)$ is the graph of ${\Im }_i.$ By the definition of $N_{{\Re }_i}(⅁),$ we find that

$$⟨⅁-\mathsf{\Lambda },\wp -{\gimel }_i(⅁)⟩\ge 0$$

for all $\mathsf{\Lambda }\in {\Re }_i.$ Since ${\wp }_n^i\in {\Re }_i,$

$$⟨⅁-{\wp }_n^i,\wp -{\gimel }_i(⅁)⟩\ge 0.$$

Therefore,

$$⟨⅁-{\wp }_n^i,\wp ⟩\ge ⟨⅁-{\wp }_n^i,{\gimel }_i(⅁)⟩.$$

(22)

Considering ${\wp }_n^i=P_{{\Re }_i}({{\rm Y}}_n-{\ell }_n{\gimel }_i\left({{\rm Y}}_n\right))$ and Lemma 2 (iii), we can get

$$⟨⅁-{\wp }_n^i,{\wp }_n^i-{{\rm Y}}_n+{\ell }_n{\gimel }_i\left({{\rm Y}}_n\right)⟩\ge 0,$$

or

$$⟨⅁-{\wp }_n^i,{\gimel }_i\left({{\rm Y}}_n\right)⟩\ge ⟨⅁-{\wp }_n^i,\frac{{{\rm Y}}_n-{\wp }_n^i}{{\ell }_n}⟩.$$

(23)

Therefore, from (22), (23) and the monotonicity of ${\gimel }_i,$ we have

$$\begin{array}{ccc}\hfill ⟨⅁-{\wp }_n^i,\wp ⟩& \ge & ⟨⅁-{\wp }_n^i,{\gimel }_i(⅁)⟩\hfill \\ & =& ⟨⅁-{\wp }_n^i,{\gimel }_i(⅁)-{\gimel }_i\left({\wp }_n^i\right)⟩+⟨⅁-{\wp }_n^i,{\gimel }_i\left({\wp }_n^i\right)-{\gimel }_i\left({{\rm Y}}_n\right)⟩+⟨⅁-{\wp }_n^i,{\gimel }_i\left({{\rm Y}}_n\right)⟩\hfill \\ & \ge & ⟨⅁-{\wp }_n^i,{\gimel }_i\left({\wp }_n^i\right)-{\gimel }_i\left({{\rm Y}}_n\right)⟩+⟨⅁-{\wp }_n^i,\frac{{{\rm Y}}_n-{\wp }_n^i}{{\ell }_n}⟩.\hfill \end{array}$$

(24)

Applying (21) in (24) and ${\gimel }_i$ is L-Lipschitz continuous,

$$\underset{n\to \infty }{lim}∥{\gimel }_i\left({\wp }_n^i\right)-{\gimel }_i\left({{\rm Y}}_n\right)∥=0.$$

(25)

Taking the limit in (24) as $n\to \infty$ and using (25), ${\wp }_n^i\rightharpoonup \varpi ,$ we have $⟨⅁-\varpi ,\wp ⟩\ge 0$ for all $(⅁,\wp )\in G\left({\Im }_i\right).$ Taking into account the maximal monotonicity of ${\Im }_i$ implies that for all $i=1,..,N,$$\varpi \in {\Im }_i^{-1}\left(0\right)=VI({\gimel }_i,{\Re }_i)$.

Finally, we show that ${⅁}_n\to \varpi =\zeta =P_{\mathsf{\Theta }}{⅁}_1.$ From (14) and $\zeta \in \mathsf{\Theta },$ we can get

$$∥{⅁}_n-{⅁}_1∥\le ∥\zeta -{⅁}_1∥,\mathrm{for}\mathrm{all}n\ge 1.$$

(26)

By (26) and lower weak semi-continuity of the norm, we can write

$$∥\varpi -{⅁}_1∥\le lim\underset{n\to \infty }{inf}∥{⅁}_n-{⅁}_1∥\le lim\underset{n\to \infty }{sup}∥{⅁}_n-{⅁}_1∥\le ∥\zeta -{⅁}_1∥.$$

By the definition of $\zeta ,$$\varpi =\zeta$ and ${lim}_{n\to \infty }∥{⅁}_n-{⅁}_1∥=∥\zeta -{⅁}_1∥.$ Thus, from ${⅁}_n-{⅁}_1\rightharpoonup \zeta -{⅁}_1$ and the Kadec-Klee property of ℸ, one can get ${⅁}_n-{⅁}_1\to \zeta -{⅁}_1,$ and so ${⅁}_n\to \varpi .$ Also, Steps 2, 4 ensures that the sequences $\left\{{\wp }_n^i\right\}$, $\left\{{\mathsf{\Lambda }}_n^i\right\}$ converge strongly to $P_{\mathsf{\Theta }}{⅁}_1.$ This completes the proof. □

Theorem 2.

(CHISE algorithm)

Suppose that all requirements of Theorem 1 are fulfilled. Let $\left\{{⅁}_n\right\}$ be a sequence generated by ${⅁}_0,{⅁}_1\in =\daleth$, for all $i=1,..,N$ and

$$\left\{\begin{array}{c}{{\rm Y}}_n={⅁}_n+{\pi }_n({⅁}_n-{⅁}_{n-1}),\hfill \\ {\wp }_n=P_{{\Re }_{\left[n\right]}}({{\rm Y}}_n-{\ell }_n{\gimel }_{\left[n\right]}\left({{\rm Y}}_n\right)),\hfill \\ {\mathsf{\Lambda }}_n=P_{{\xi }_{\left[n\right]}}({{\rm Y}}_n-{\ell }_n{\gimel }_{\left[n\right]}\left({\wp }_n\right)),\hfill \\ {\yen }_{n+1}=\{v\in {\yen }_n:{∥{\mathsf{\Lambda }}_n-v∥}^2\le {∥{⅁}_n-v∥}^2+(1-r){\pi }_n^2{∥{⅁}_n-{⅁}_{n-1}∥}^2\},\hfill \\ {⅁}_{n+1}=P_{{\yen }_{n+1}}{⅁}_1,n\ge 1.\hfill \end{array}\right.$$

where ${\wp }_n\in {\Re }_{\left[n\right]},$${\mathsf{\Lambda }}_n\in {\xi }_{\left[n\right]}=\{v\in \daleth :⟨({{\rm Y}}_n-{\ell }_n{\gimel }_{\left[n\right]}\left({{\rm Y}}_n\right))-{\wp }_n,v-{\wp }_n⟩\le 0\},$${\ell }_n\in (0,\frac{1}{2L}),\left[n\right]=n\left(modN\right)+1$ with the mod function here taking values in $\{1,2,..,N\}$ and ${\pi }_n\in [0,1).$ Assume that ${\sum }_{i=1}^{\infty }{\pi }_n∥{⅁}_n-{⅁}_{n-1}∥<\infty .$ Then the sequence $\left\{{⅁}_n\right\}$ converges strongly to $\varpi =P_{\mathsf{\Theta }}{⅁}_1.$

Proof. 

By arguing similarly as in the proof of Theorem 1, we obtain that $\mathsf{\Theta }$ and ${\yen }_{n+1}$ are cc and $\mathsf{\Theta }\subset {\in }_{n+1}$ for all $n\ge 1$. We have demonstrated that before $\left\{{⅁}_n\right\},$$\left\{{\wp }_n\right\}$ and $\left\{{\mathsf{\Lambda }}_n\right\}$ are bounded and

$$\underset{n\to \infty }{lim}∥{⅁}_{n+1}-{⅁}_n∥=\underset{n\to \infty }{lim}∥{\mathsf{\Lambda }}_n-{⅁}_n∥=\underset{n\to \infty }{lim}∥{\wp }_n-{⅁}_n∥=\underset{n\to \infty }{lim}∥{\wp }_n-{{\rm Y}}_n∥=0.$$

(27)

Now, let the sequence $\left\{{⅁}_n\right\}$ has some weak cluster points $\varpi$ and subsequence $\left\{{⅁}_{n_k}\right\}$. For $i\in \{1,2,...,N\}$ be fixed, the set of indexes i is finite, this leads to ${⅁}_{n_k}\rightharpoonup p$ and $\left[n_k\right]=i$ for all $k.$ also (27) gives ${\wp }_{n_k}\rightharpoonup \varpi$ as $k\to \infty$. By the same scenario of (22)–(25), one can get $\varpi \in VI({\gimel }_i,{\Re }_i)$. for all $i,$ and $\varpi \in \mathsf{\Theta }.$ The rest of the proof comes immediately from proof Theorem 1.  □

Remark  1.

(i)

The projection ${⅁}_{n+1}=P_{{\yen }_{n+1}}\left({⅁}_1\right)$ computed explicitly as in Theorem 1 because ${\yen }_{n+1}$ is either half-spaces or the whole space ℸ.

(ii)

If ℷ is $\eta -$ism mapping, then ℷ is $\frac{1}{\eta }-$Lipschitz continuous. Thus, for $i=1,..,N,$ our algorithms can use to solve the CSVIP for the $\eta -$ism mappings ${\gimel }_i$.

4. Numerical Experiments

In this section, we consider two numerical examples to explain the efficiency of the proposed algorithms. The MATLAB codes run in MATLAB version 9.5 (R2018b) on Intel(R) Core(TM)i5-6200 CPU PC @ 2.30 GHz 2.40 GHz, RAM 8.00 GB. We use the Quadratic programming to solve the minimization problems.

(1)

For Van Hieu results in [23] Algorithm 3.1 (Alg. 1) we use $\lambda =\frac{1}{2L}.$

(2)

For our proposed algorithms (Alg. 2) we use ${\ell }_n=\frac{1}{2L}$ and ${\pi }_n=0.2.$

Example 1.

Let the operators ${\beth }_i$ can be define on the convex set $\yen \subset {\mathbb{R}}^m$ as follows:

$${\beth }_i(⅁)=(B_i{B}_i^T+S_i+D_i)⅁+q_i,\forall i=1,\cdots ,N,$$

where $q_i\in {\mathbb{R}}^m,$$B_i$ is an $m\times m$ matrix, $S_i$ is an $m\times m$ skew-symmetric matrix and $D_i$ is an $m\times m$ diagonal matrix whose diagonal entries are non-negative. All these above mentioned matrices and vectors $q_i$ are randomly generated ($B=rand\left(m\right),$$C=rand\left(m\right),$$S=0.5C-0.5C^T,$$D=diag\left(rand\right(m,1\left)\right)$) between $(0,1).$ The feasible set ${\yen }_i=\yen \subset {\mathbb{R}}^m$ is cc set and defined as:

$$\yen =\{⅁\in {\mathbb{R}}^m:A⅁\le d\},$$

where A is an $20\times m$ matrix and d is a non-negative vector. It is clear that ${\beth }_i$ is monotone and L-Lipschitz continuous with $L=max\left\{\parallel B_i{B}_i^T+S_i+D_i\parallel :i=1,\cdots ,m\right\}.$ In this example, we choose $q_i=0.$ Thus, the solution set $\Omega =\left\{0\right\}.$ During Example 1, we use $x_0=x_1=(1,1,\cdots ,1)$ and $D_n=\parallel {⅁}_n\parallel .$

Example 2.

Suppose that $\daleth =L^2\left([0,1]\right)$ is a Hs with the norm

$$\parallel ⅁\parallel =\sqrt{{\int }_0^1{|⅁\left(t\right)|}^{2}dt}$$

and the inner product

$$⟨⅁,\wp ⟩={\int }_0^1⅁\left(t\right)\wp \left(t\right)dt,\mathrm{for}\mathrm{all}⅁,\wp \in \daleth .$$

Assume that ${\yen }_i:=\{⅁\in L^2\left([0,1]\right):\parallel ⅁\parallel \le 1\}$ be the unit ball. Let us define an operator ${\beth }_i:{\yen }_i\to \daleth$ by

$${\beth }_i(⅁)\left(t\right)={\int }_0^1\left(⅁\left(t\right)-H_i(t,s)f_i(⅁\left(s\right))\right)ds+g_i\left(t\right)$$

for all $⅁\in$, $t\in [0,1]$ and i = 1, 2, where

$$H_1(t,s)=\frac{2ts{e}^{(t+s)}}{e\sqrt{e^2-1}},f_1(⅁)=cos⅁,g_1\left(t\right)=\frac{2t{e}^t}{e\sqrt{e^2-1}}.$$

$$H_2(t,s)=\frac{\sqrt{21}}{7}(t+s),f_2(⅁)=exp(-{⅁}^2),g_2\left(t\right)=\frac{\sqrt{21}}{7}(t+0.5).$$

As shown in [14] the ${\beth }_i$ is monotone (hence pseudo-monotone) and L-Lipschitz-continuous with $L=2.$ Moreover, the solution set of the CSVIPs for the operators ${\beth }_i$ on ${\yen }_i$ is $\Omega =\left\{0\right\}.$ During example 2, we use $x_0=x_1=t$ and $D_n=\parallel {⅁}_n\parallel .$

5. Discussion

We have the following observations concerning the above-mentioned experiments:

(i)

Figure 1 and Figure 2 and Table 1 demonstrates the behavior of both algorithms as the size of the problem m varies. We can see that the performance of the algorithm depends on the size of the problem. More time and a significant number of iterations are required for large dimensional problems. In this case, we can see that the inertial effect strengthens the efficiency of the algorithm and improves the convergence rate.

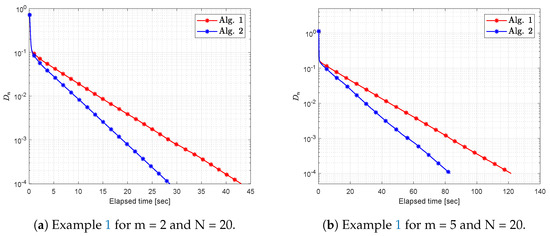Figure 1. Example 1: Numerical comparison for the values of m = 2, 5 and N = 20.

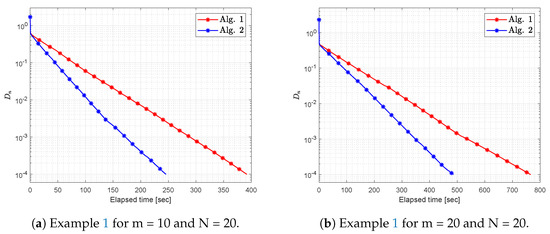Figure 2. Example 1: Numerical comparison for the values of m = 10, 20 and N = 20.

Table 1. Numerical results for Figure 1 and Figure 2.

N	m	Algorithm 1		Algorithm 2
		Number of Iter.	CPU (s)	Number of Iter.	CPU (s)
20	2	269	43.01771	185	28.6043
20	5	788	121.0213	529	83.1379
20	10	2493	391.9032	1066	245.6833
20	20	7780	765.5070	3038	485.9237

(ii)

Figure 3 and Table 2 display the behavior of both algorithms while the number of problems N varies. It could be said that the performance of algorithms also depends on the number of problems involved. In this scenario, we can see that roughly the same number of iterations are required, but the execution time depends entirely on the number of problems N.

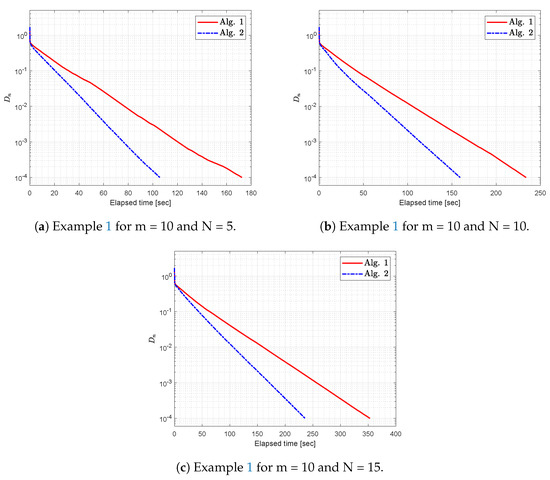Figure 3. Example 1 for m = 10 and different values of N = 5, 10, 15.

Table 2. Numerical results for Figure 3.

N	m	Algorithm 1		Algorithm 2
		Number of Iter.	CPU (s)	Number of Iter.	CPU (s)
5	10	3101	172.4298	2267	105.7254
10	10	3009	233.6499	2340	159.1928
15	10	3254	353.0176	2109	235.8372

(iii)

Figure 4, Figure 5 and Figure 6 and Table 3 shows the behavior of both algorithms as tolerance $ϵ$ varies. In this case, we can see that, as tolerance $ϵ$ is closer to zero, iteration and elapsed time also increase.

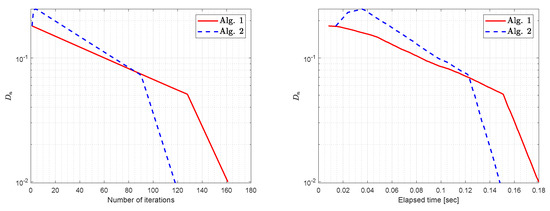Figure 4. Example 2: Numerical comparison by letting TOL = ${10}^{-2}$.

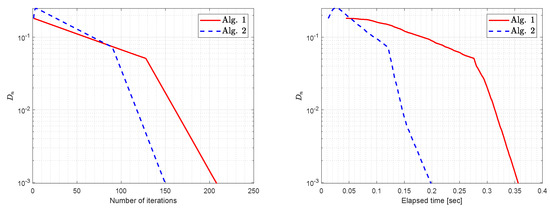Figure 5. Example 2: Numerical comparison by letting TOL = ${10}^{-3}$.

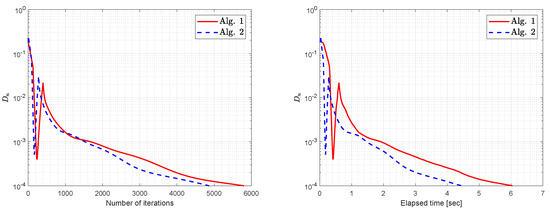Figure 6. Example 2: Numerical comparison by letting TOL = ${10}^{-4}$.

Table 3. Numerical results for Figure 4, Figure 5 and Figure 6.

N	TOL	Algorithm 1		Algorithm 2
		Number of Iter.	CPU (s)	Number of Iter.	CPU (s)
2	10−2	161	0.1799	118	0.1483
2	10−3	208	0.3563	150	0.1985
2	10−4	5801	6.0405	4863	4.4441

(iv)

Based on the progress of the numerical results, we find that our methods are effective and successful in finding solutions for VIP and our algorithms converges faster than the algorithms of Hieu [19].

6. Conclusions

In this manuscript, we propose two strongly convergent parallel and cyclic hybrid inertial CQ-sub-gradient extra-gradient algorithms for finding common the CSVIP. This problem consists of finding a common solution to a system of unrelated variational inequalities corresponding to set-valued mappings in a Hs. The algorithms presented in this article are a hybrid of synthesis the inertial technical, shrinking projection and CQ-terms to parallel and cyclic hybrid inertial sub-gradient extra-gradient algorithms to develop possible practical numerical methods when the number of sub-problems is large. Finally, non-trivial numerical examples are given here to verify the efficiency of the proposed parallel and cyclic algorithms.