On Ulam–Hyers Stability for a System of Partial Differential Equations of First Order

Abstract

The aim of this paper is to investigate generalized Ulam–Hyers stability and generalized Ulam–Hyers–Rassias stability for a system of partial differential equations of first order. More precisely, we consider a system of two nonlinear equations of first order with an unknown function of two independent variables, which satisfy the corresponding compatibility condition. The study method is that of differential inequalities of the Gronwall type.

1. Introduction

Ulam–Hyers stability is an important problem in functional equations theory, which was studied by many authors who can be found in the monograph [1].

The problem was posed by Ulam in 1940 (cf. [2,3]) in the following way. Let G be a group and H a metric group with metric d and $f:G\to H.$ For every $\epsilon >0,\exists \delta >0$ such that, if $f:G\to H$ verifies

$$d\left(f\left(xy\right),f\left(x\right)f\left(y\right)\right)\le \delta ,x,y\in G,$$

then $\exists g:G\to H$ a homomorphism with

$$d\left(f\left(x\right),g\left(x\right)\right)\le \epsilon ,x\in G?$$

Firstly, Hyers [3] gaves an answer for additive Cauchy equation in Banach spaces, as follows.

Let $X_1,X_2$ be Banach spaces, $\delta >0$ and $f:X_1\to X_2$ such that

$$∥f\left(x+y\right)-f\left(x\right)-f\left(y\right)∥\le \delta ,\forall x,y\in X_1.$$

There exists a unique additive mapping $g:X_1\to X_2$ verifying

$$∥f\left(x\right)-g\left(x\right)∥\le \delta ,\forall x\in X_1.$$

Ulam–Hyers stability of differential equations was firstly investigated by Alsina and Ger [4] in the following way. Let $\epsilon >0,$ $I\subset \mathbb{R}$ be an open interval and $f:I\to \mathbb{R}$ differentiable. If f satisfies

$$\left|f^{\prime }\left(x\right)-f\left(x\right)\right|\le \epsilon ,\forall x\in I,$$

then $\exists g:I\to \mathbb{R}$ differentiable such that $g^{\prime }\left(x\right)=g\left(x\right)$ and

$$\left|f\left(x\right)-g\left(x\right)\right|\le 3\epsilon ,\forall x\in I.$$

The stability of differential linear equations of first order was studied in the papers [4,5]. Bernoulli equations were studied in [6] and Riccati equations in [7]. In [8], systems of first order linear differential equations were studied. Some results regarding linear differential equations of higher order were established in [9].

The first authors who studied Hyers-Ulam stability of partial differential equations were Prastaro and Rassias [10]. After that, a few results in this direction were given by other authors, regarding partial differential equations of first order [11,12], of order two [13], or of order three [14].

Recently, in a set of papers, Rus [13,15], has opened a new direction of study of the Ulam stability using Gronwall type inequalities and Picard operators technique. This will be used in this paper. Another direction of stability research is that in which results regarding fixed point theory are used [16].

In this paper, we will study the stability of a system of partial differential equations of order one, nonlinear. We mention that those are not studied yet in literature.

The general form of a system of n partial differential equations of first order for a function $u=u\left(x_1,x_2,\cdots ,x_n\right)$ is

$$\frac{\partial u}{\partial x}=f\left(x,u\right),$$

where $f=\left(f_1,f_2,\cdots ,f_n\right),f_i=f_i\left(x_1,x_2,\cdots ,x_n\right),x=\left(x_1,x_2,\cdots ,x_n\right),i=\overline{1,n}.$

The normal form of this system is

$$\left\{\begin{array}{c}\frac{\partial u}{\partial x_1}=f_1\left(x_1,x_2,\cdots ,x_n\right)\hfill \\ \cdots \hfill \\ \frac{\partial u}{\partial x_n}=f_n\left(x_1,x_2,\cdots ,x_n\right)\hfill \end{array}\right..$$

(1)

If the functions $f_i,i=\overline{1,n}$ admits continuous partial derivatives of order two, then $\frac{{\partial }^{2}u}{\partial x_k\partial x_i}=\frac{{\partial }^{2}u}{\partial x_i\partial x_k},i\ne k.$ These are the compatibility conditions and are not always identities.

We will consider the system in the case of functions of two variables, denoted by $x,y$. Let $u=u\left(x,y\right).$

Example 1.

We consider the system

$$\left\{\begin{array}{c}\frac{\partial u}{\partial x}=-y\hfill \\ \frac{\partial u}{\partial y}=\frac{u}{y}\hfill \end{array}\right.,y\ne 0,u\left(0,1\right)=2.$$

The compatibility condition is identically verified, $\forall u\in C^2\left(\Omega \right),\Omega \subset {\mathbb{R}}^2,y\ne 0.$ The solution is $u=\left(2-x\right)y.$

Example 2.

We consider the system

$$\left\{\begin{array}{c}\frac{\partial u}{\partial x}=u+yu\hfill \\ \frac{\partial u}{\partial y}=u^2+2xu\hfill \end{array}\right..$$

In this case, the compatibility condition is reduced to the equation $u\left[1+u\left(1+y\right)\right]=0.$ Only two solutions are possible, namely $u=0$ and $u=-\frac{1}{1+y}.$ Verifying, we get that $u=0$ is the single solution.

Example 3.

We consider the system

$$\left\{\begin{array}{c}\frac{\partial u}{\partial x}=y-u\hfill \\ \frac{\partial u}{\partial y}=xu\hfill \end{array}\right..$$

The compatibility condition is not verified, hence the system has no solution.

From these examples, we see that Ulam stability for a system can be studied only for those which verify identical compatibility condition.

In the following lines, we will consider the system:

$$\left\{\begin{array}{c}\frac{\partial u}{\partial x}=f\left(x,y,u\right)\hfill \\ \frac{\partial u}{\partial y}=g\left(x,y,u\right),\hfill \end{array}\right.$$

(2)

where $f,g\in C^1\left({\overline{\Omega }}_1\right),{\overline{\Omega }}_1=\left[x_0,x_0+a\right]\times \left[y_0,y_0+a\right]\times \left[u_0,u_0+b\right],$ $a,b\in \left(0,\infty \right)$ and $\left(x_0,y_0,u_0\right)\in {\mathbb{R}}^3$. Let $\overline{D}=\left[x_0,x_0+a\right]\times \left[y_0,y_0+a\right],$ $u\in C^2\left(\overline{D}\right)$. We consider $C\left(\overline{D}\right)$ endowed with Chebyshev norm that is $∥u∥=\underset{x\in \overline{D}}{max}\left|u\left(x\right)\right|.$ Let $\overline{B}\left(u_0,b\right)\subset C\left(\overline{D}\right)$.

We will study the problem (2) + (3)

$$u\left(x_0,y_0\right)=u_0.$$

(3)

From $\frac{{\partial }^{2}u}{\partial x\partial y}=\frac{{\partial }^{2}u}{\partial y\partial x}$, the compatibility condition of the system is

$$\frac{\partial g}{\partial x}+\frac{\partial g}{\partial u}f=\frac{\partial f}{\partial y}+\frac{\partial f}{\partial u}g.$$

(4)

2. Preliminaries

We will formulate the problem (2) + (3) as an integral equation, if condition (4) is satisfied. Since $du=fdx+gdy$, the problem (2) + (3) is equivalent with the integral equation

$$u\left(x,y\right)=u_0+{\int }_{x_0}^{x}f\left(s,y_0,u\left(s,y_0\right)\right)ds+{\int }_{y_0}^{y}g\left(x,t,u\left(x,t\right)\right)dt.$$

(5)

Let $\epsilon >0$ and $\phi \in C\left(\overline{D},{\mathbb{R}}_{+}\right)$, nondecreasing in x and y. Let the inequalities

$$\left|v\left(x,y\right)-u_0-{\int }_{x_0}^{x}f\left(s,y_0,v\left(s,y_0\right)\right)ds-{\int }_{y_0}^{y}g\left(x,t,v\left(x,t\right)\right)dt\right|\le \epsilon ,\forall \left(x,y\right)\in \overline{D},$$

(6)

$$\left|v\left(x,y\right)-u_0-{\int }_{x_0}^{x}f\left(s,y_0,v\left(s,y_0\right)\right)ds-{\int }_{y_0}^{y}g\left(x,t,v\left(x,t\right)\right)dt\right|\le \phi \left(x,y\right),\forall \left(x,y\right)\in \overline{D}.$$

(7)

Definition 1.

Equation (5) is generalized Ulam–Hyers stable if there exist the real numbers $c_1,c_2$ such that, for each $\epsilon >0$ and for each solution v of (6), there exists a solution u of (5) with:

$$\left|v\left(x,y\right)-u\left(x,y\right)\right|\le c_1\epsilon +c_2,\forall \left(x,y\right)\in \overline{D}.$$

Definition 2.

Equation (5) is generalized Ulam–Hyers–Rassias stable with respect to φ if there exist the real numbers $c_1,c_2$ such that for each solution v of (7) there exists a solution u of (5) with:

$$\left|v\left(x,y\right)-u\left(x,y\right)\right|\le c_1\phi \left(x,y\right)+c_2,\forall \left(x,y\right)\in \overline{D}.$$

Remark 1.

A function v is a solution of (6) if and only if there exists a function $k\in C\left(\overline{D},\mathbb{R}\right)$ such that

(i) 

$\left|k\left(x,y\right)\right|\le \epsilon ,\forall \left(x,y\right)\in \overline{D};$

(ii) 

$v\left(x,y\right)=u_0+{\int }_{x_0}^{x}f\left(s,y_0,v\left(s,y_0\right)\right)ds+{\int }_{y_0}^{y}g\left(x,t,v\left(x,t\right)\right)dt+k\left(x,y\right),\forall \left(x,y\right)\in \overline{D}.$

Remark 2.

A function v is a solution of (7) if and only if there exists a function $k\in C\left(\overline{D},\mathbb{R}\right)$ such that

(i) 

$\left|k\left(x,y\right)\right|\le \phi \left(x,y\right),\forall \left(x,y\right)\in \overline{D};$

(ii) 

$v\left(x,y\right)=u_0+{\int }_{x_0}^{x}f\left(s,y_0,v\left(s,y_0\right)\right)ds+{\int }_{y_0}^{y}g\left(x,t,v\left(x,t\right)\right)dt+k\left(x,y\right),\forall \left(x,y\right)\in \overline{D}.$

3. Generalized Ulam–Hyers Stability

The first result is the following.

Theorem 1.

If

(i) 

$f,g\in C^1\left({\overline{\Omega }}_1\right)$, and $M_1,M_2\in \mathbb{R}$ such that $\left|f\left(x,y,u\right)\right|\le M_1,$ $\left|g\left(x,y,u\right)\right|\le M_2$ on ${\overline{\Omega }}_1$;

(ii) 

$\exists L_g>0$ such that

$$\left|g\left(x,y,u_1\right)-g\left(x,y,u_2\right)\right|\le L_g\left|u_1-u_2\right|,\forall \left(x,y\right)\in \overline{D},\forall u_1,u_2\in \mathbb{R};$$

(iii) 

$a\le \frac{b}{M_1+M_2};$

(iv) 

the compatibility condition (4) is satisfied;

then:

(a) 

problems (2) + (3) have a unique solution in $\overline{B}\left(u_0,b\right)$.

(b) 

Equation (5) is generalized Ulam–Hyers stable.

Proof. 

(a) This is a consequence from the existence and uniqueness theorem (Rus [17], p. 210), since the conditions (i)–(iv) appear there.

(b) Let v be a solution to the inequality (6). Let u be the unique solution in $\overline{B}\left(u_0,b\right)$ to the problem (2) + (3). Using Remark 1, we obtain

$$\begin{array}{cc}\hfill & \left|v\left(x,y\right)-u\left(x,y\right)\right|\le \left|v\left(x,y\right)-u_0-{\int }_{x_0}^{x}f\left(s,y_0,v\left(s,y_0\right)\right)ds-{\int }_{y_0}^{y}g\left(x,t,v\left(x,t\right)\right)dt\right|\hfill \\ \hfill & +{\int }_{x_0}^x\left|f\left(s,y_0,v\left(s,y_0\right)\right)-f\left(s,y_0,u\left(s,y_0\right)\right)\right|ds+{\int }_{y_0}^y\left|g\left(x,t,v\left(x,t\right)\right)-g\left(x,t,u\left(x,t\right)\right)\right|dt\hfill \\ \hfill & \le \epsilon +2M_{1}a+L_g{\int }_{y_0}^y\left|v\left(x,t\right)-u\left(x,t\right)\right|dt,\forall \left(x,y\right)\in \overline{D}.\hfill \end{array}$$

Using Gronwall lemma ([18], p. 3) now, we get

$$\left|v\left(x,y\right)-u\left(x,y\right)\right|\le \left(\epsilon +2M_{1}a\right)e^{L_{g}a},\forall \left(x,y\right)\in \overline{D},$$

hence $\left|v\left(x,y\right)-u\left(x,y\right)\right|\le c_1\epsilon +c_2,$ where $c_1=e^{L_{g}a},c_2=2M_{1}a{e}^{L_{g}a}$. Hence, Equation (5) is generalized Ulam–Hyers stable. □

Example 4.

Let $\left(x_0,y_0,u_0\right)=\left(1,1,1\right)$, ${\overline{\Omega }}_1=\left[1,1+a\right]\times \left[1,1+a\right]\times \left[1,1+b\right],$ $\overline{D}=\left[1,1+a\right]\times \left[1,1+a\right],$ $a=\frac{1}{9},b=\frac{1}{2}.$ We consider the system

$$\left\{\begin{array}{c}\frac{\partial u}{\partial x}=\frac{u}{x}\hfill \\ \frac{\partial u}{\partial y}=\frac{2u}{y}\hfill \end{array}\right.$$

(8)

and the initial condition

$$u\left(1,1\right)=1.$$

(9)

The corresponding solution is $u=x{y}^2.$ The problem (8) + (9) is equivalent with the integral Equation (5), which became

$$u\left(x,y\right)-1-{\int }_1^x\frac{u\left(s,1\right)}{s}ds-{\int }_1^y\frac{2u\left(s,t\right)}{t}dt=0.$$

(10)

We consider the inequality

$$\left|v\left(x,y\right)-1-{\int }_1^x\frac{v\left(s,1\right)}{s}ds-{\int }_1^y\frac{2v\left(s,t\right)}{t}dt\right|\le \epsilon .$$

(11)

Let $\epsilon =\frac{1}{3}.$ The function $v\left(x,y\right)=x{y}^2+\frac{3x}{10}$ is a solution of (11). We apply Theorem 1. We have

$$f\left(x,y,u\right)=\frac{u}{x},g\left(x,y,u\right)=\frac{2u}{y},x_0=y_0=1,u_0=1,$$

$$\left|f\left(x,y,u\right)\right|=\left|\frac{u}{x}\right|\le 1+b=\frac{3}{2}=M_1,$$

$$\left|g\left(x,y,u\right)\right|=\left|\frac{2u}{y}\right|\le 2\left(1+b\right)=3=M_2,$$

$$\left|g\left(x,y,u_1\right)-g\left(x,y,u_2\right)\right|=\left|\frac{2u_1}{y}-\frac{2u_2}{y}\right|=\frac{2}{y}\left|u_1-u_2\right|\le 2\left|u_1-u_2\right|,$$

hence $L_g=2.$

Hence, $\left|v\left(x,y\right)-u\left(x,y\right)\right|\le \left(\epsilon +2M_{1}a\right)e^{L_{g}a}=\left(\epsilon +2\left(1+b\right)a\right)e^{2a}=\frac{2}{3}{e}^{\frac{2}{9}}$ on $\overline{D}.$ Thus, Equation (10) is generalized Ulam–Hyers stable.

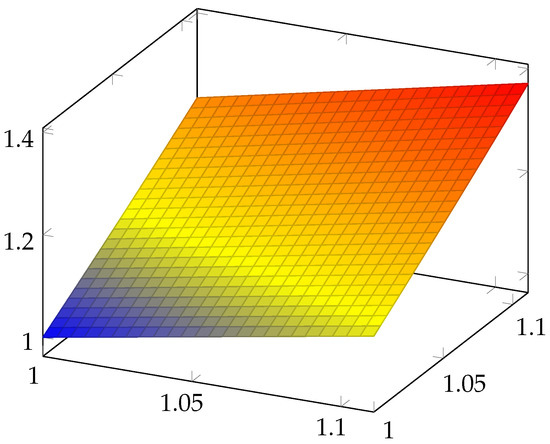
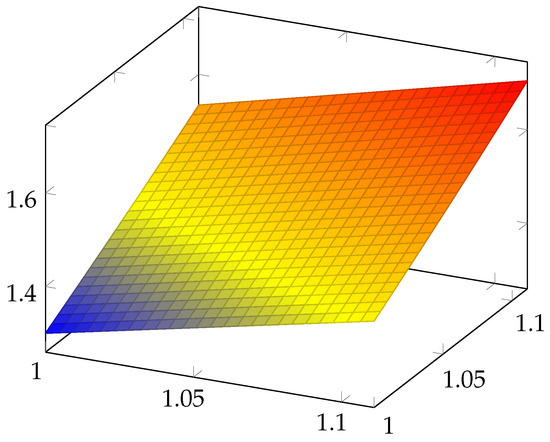
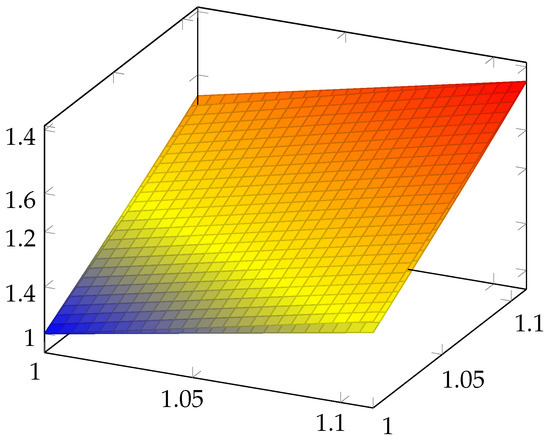
We remark that $u\left(x,y\right)=x{y}^2$ and $v\left(x,y\right)=x{y}^2+\frac{3x}{10}$ represent two surfaces. We have drawn these surfaces in Figure 1 and Figure 2, respectively, and, in Figure 3, both of them are overlapping. We can see that these surfaces are close to one another.

Figure 1. Representation of the surface $u=x{y}^2$ on $\overline{D}.$

Figure 2. Representation of the surface $u=x{y}^2+\frac{3x}{10}$ on $\overline{D}.$

Figure 3. Representation of the surfaces $u=x{y}^2,u=x{y}^2+\frac{3x}{10}$, on $\overline{D}$ together.

4. Generalized Ulam–Hyers–Rassias Stability

We study, now, generalized Ulam–Hyers–Rassias stability of system (2).

Theorem 2.

If

(i) 

$f,g\in C^1\left({\overline{\Omega }}_1\right)$, and $M_1,M_2\in \mathbb{R}$ such that $\left|f\left(x,y,u\right)\right|\le M_1,$ $\left|g\left(x,y,u\right)\right|\le M_2$ on ${\overline{\Omega }}_1$;

(ii) 

$\exists L_g\in C\left(\overline{D},{\mathbb{R}}_{+}\right)$ such that

$$\left|g\left(x,y,u_1\right)-g\left(x,y,u_2\right)\right|\le L_g\left(x,y\right)\left|u_1-u_2\right|,\forall \left(x,y\right)\in \overline{D},\forall u_1,u_2\in \mathbb{R};$$

(iii) 

$a\le \frac{b}{M_1+M_2};$

(iv) 

the compatibility condition (4) is satisfied;

(v) 

$\phi \in C\left(\overline{D},{\mathbb{R}}_{+}\right)$ is nondecreasing in y;

(vi) 

${\int }_{y_0}^{y_0+a}{L}_g\left(x,y\right)dy$ is convergent and there exists a real number M such that ${\int }_{y_0}^{y_0+a}{L}_g\left(x,y\right)dy\le M,$ $\forall x\in \left[x_0,x_0+a\right]$.

Then, Equation (5) is generalized Ulam–Hyers–Rassias stable.

Proof. 

Let v be a solution to the inequality (7). Denote by u the unique solution in $\overline{B}\left(u_0,b\right)$ to problems (2) + (3). From Remark 2, we get

$$\begin{array}{cc}\hfill & \left|v\left(x,y\right)-u\left(x,y\right)\right|\le \left|v\left(x,y\right)-u_0-{\int }_{x_0}^{x}f\left(s,y_0,v\left(s,y_0\right)\right)ds-{\int }_{y_0}^{y}g\left(x,t,v\left(x,t\right)\right)dt\right|\hfill \\ \hfill & +{\int }_{x_0}^x\left|f\left(s,y_0,v\left(s,y_0\right)\right)-f\left(s,y_0,u\left(s,y_0\right)\right)\right|ds+{\int }_{y_0}^y\left|g\left(x,t,v\left(x,t\right)\right)-g\left(x,t,u\left(x,t\right)\right)\right|dt\hfill \\ \hfill & \le \phi \left(x,y\right)+2M_{1}a+{\int }_{y_0}^y{L}_g\left(x,y\right)\left|v\left(x,t\right)-u\left(x,t\right)\right|dt,\forall \left(x,y\right)\in \overline{D}.\hfill \end{array}$$

We use Gronwall lemma ([18], p. 6) and we obtain

$$\left|v\left(x,y\right)-u\left(x,y\right)\right|\le \left(\phi \left(x,y\right)+2M_{1}a\right)e^{M}dt,\forall \left(x,y\right)\in \overline{D},$$

hence

$$\left|v\left(x,y\right)-u\left(x,y\right)\right|\le c_1\phi \left(x,y\right)+c_2,$$

where $c_1=e^M,c_2=2a{M}_1{e}^M.$

Consequently, the generalized Ulam–Hyers–Rassias stability of Equation (5) is proved. □

5. Conclusions

In this paper, we have studied generalized Ulam–Hyers and respectively Ulam–Hyers–Rassias stability of system (2), if condition (4) is satisfied, with initial condition (3). We have reduced this problem to Equation (5). We have used the method of differential inequalities, Gronwall types inequalities, and Picard operators technique. It is well known that these systems have many applications in the study of some partial differential equations of higher order, as in physics, chemistry, and other domains of science. Many problems from the domain Symmetry are modeled by differential equations and partial differential equations and those are approached in the stability point of view. The future study could be the stability of general system (1).