Abstract
In this study, the resultant forces and moments acting on infinite symmetric FGPs with a triangular hole subject to uniaxial tensile load were examined via an analytical method using the complex variable approach. The mechanical properties of graded plates are hypothesized to vary throughout the thickness exponentially. The impact of various factors, namely hole orientation, hole aspect ratio as well as the hole corner curve on stress distribution and moment resultants is considered. In order to approve the credibility of the analytical approach, its outcomes are compared to numerical results acquired from ABAQUS finite element modeling. This comparison showed a favorable agreement level among the acquired analytical and numerical outcomes. Based on these results, the mentioned factors entail a considerable effect on the distribution of resultant forces and moments at the proximity of the hole and the load bearing tolerance of functional grated plates with holes may be enhanced by suitable selection of the aforementioned parameters.
1. Introduction
Openings and holes are vital sections of structural models, and control of their adverse effects on the structure stability and failure probability around these geometric discontinuities is crucial to design procedures. In order to reliably predict the behavior of a hole structure, designers must cautiously examine stress distribution at the hole proximity and estimate stress distribution in order to avoid the concentration of stress. Currently, structural models may be enhanced using functionally graded materials (FGMs), where mechanical or thermal attributes vary gradually across one of the fundamental sizes. Such materials may have a prominent impact on the structural members’ robustness subjected to different loadings. In the past few decades, designers and engineers have focused on FGMs which present great heat resistance at one part and substantial mechanical characteristics at the opposing part. For present research, the effect of various factors on resultant forces and moments distribution at the proximity of a triangular hole in FGPs (FGPs), is examined.
The initial function of the comprehensive variable approach to solve boundary value issues for isotropic bodies is accredited to Muskhelishvili []. Savin [] utilized this approach to examine infinite isotropic and anisotropic plates with various holes. Subsequently, Muskhelishvili’s approach was extended to 2D issues related to anisotropic elastic materials by Lekhnitskii []. Lekhnitskii’s purpose of this theory was to present an overall solution regarding infinite anisotropic plates consisting of circular holes of varying sizes. For the sake of simplicity, he initially created a formulation specific to orthotropic plates. Sharma [,] examined the factor for stress concentration at the proximity of various holes. Rezaeepazhand and Jafari [] used a mapping function derived from Lekhnitiskii’s theory to get the stress concentration factor of different rectangular holes and curvature radii in anisotropic plates. In this study, they managed to decrease stress concentration factor by adjusting the hole angle orientation. Ukadgaonker and Rao [] studied stress in asymmetrical laminated plates consisting of various shaped holes which included squares and circles in addition to abnormal shapes. Jafari and Byati [] examined optimizing orthotropic infinite plate with quasi-triangular hole by utilizing the dragonfly algorithm. Furthermore, by utilizing a genetic algorithm, Jafari et al. [] acquired favorable values of the factors that affect the stress distribution at the proximity of different holes in orthotropic and laminated plates. Chen et al. [] examined stress distribution within a FGP (with differing characteristics across the radial direction) consisting of a circular hole. Regarding the research, the outcomes were acquired by considering homogenous characteristics for every angle lamina of the plate. These researchers studied the functionally graded infinite plates at the radial direction and consisting of circular holes []. Sharma [] obtained stress functions to determine stress distribution at the proximity of special holes within infinitely laminated plates under arbitrary biaxial loading at infinity by utilizing Muskhelishvili’s complex variable method. The impact of fiber orientation, loading factor, stacking pattern, loading angle and hole geometry on stress distribution at the proximity of holes in anisotropic/orthotropic plates was examined. Pan [] presented a comprehensive solution for FGPs consisting of a circular hole. Reid and Paskaramoorthy [] implemented the classical theory to develop a resolution for FGPs. Sharma and Dave [] presented a solution for moments and stress resultant at the proximity of elliptical and circular hole in infinite FGP with through thickness material characteristic deviance. In this research, the complex variable approach was utilized to examine the impact of factors, namely the dispersion of materials characteristics and the load angle of resultant and of moments. Mohammadi and Dirang [] obtained the stress concentration in FGPs containing a circular hole for biaxial loading. They used an exponential function to model their plate in a radial direction. Enab [] studied the stress concentration evaluation on FGPs with elliptical holes acted by biaxial loads, using finite element method to model their plate. Mehrparvar and Ghannadpour [,] examined the post-buckling and nonlinear demeanors of perforated plates with circular, elliptic or rectangular holes under in-plane compressive mode. Craciun et al. [,,]—using a complex potential method—studied the equilibrium states of the anisotropic elastic body containing an elliptic hole by using conformal mappings and obtained solution in a closed, compact form.
Ashoori and Jafari [] examined the impact of various factors on stress resultant and moments distribution at the vicinity of non-circular cutouts within asymmetric laminates. Jafari et al. [,] using complex potential method obtained the forces and moments per unit length in infinite FGPs with rectangular cutout.
Most prior research on FGP with loads had a focus on circular and elliptically shaped holes and did not pay attention to other factors, namely orientation angle and corner curvature of non-circular holes, in spite of their possible effects on the structure strength. In this study, the impact of hole orientation angle, hole corner curvature and aspect ratio on stress distribution in the neighborhood of the triangular hole in FGPs is studied. The hole is not subjected to external loading and we consider that the plate is greater than the hole.
2. Analytical Formulations
In order to further develop Lekhnitskii’s relation and to acquire forces and moments per unit length distribution at the proximity of the quasi-triangular hole, as well as calculate Cauchy’s integral in a simplistic manner amidst calculating the resultants, it is more favorable to turn the quasi-triangular hole into a single circle. This study is conducted by considering the plane stress state without body forces. More, the plate is in its linear elastic domain. The dimension of the cutout is small in comparison with the plate (infinite plate). By utilizing a mapping function, the quasi-triangular exterior area in the physical coordinate of z may be converted to the exterior area of the unit circle in plane . The utilized mapping function, following [], is given by:
with:
Concerning the above equations, denote the roots of the properties equation of generally orthotropic plate and will later be discussed; ascertains the hole size and is assumed as ; is the aspect ratio of the hole (determines hole elongation or compression along y-axis); n shows the hole geometry (in this study, ). As presented in Figure 1, the parameter ω () represents the curve of hole corner; a larger ω creates a sharper edge while a less ω creates a sleeker corner. At the least value of ω (i.e., ), hole turns into a circle. The impact of this parameter on the evolution of hole geometry from triangular toward circle is illustrated in Figure 1. The parameter in the equations above denotes the hole orientation angle.
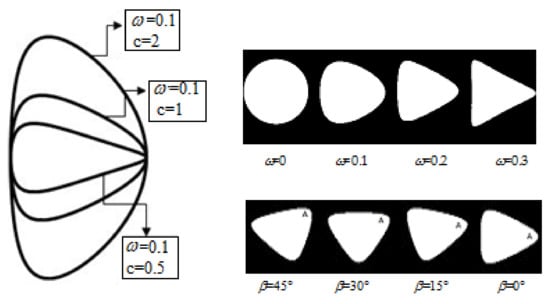
Figure 1.
The influence of ω,β on the hole geometry ()
Regarding composite laminates, due to various orientations for every layer, the 2D stress–strain relationship ascertained by the decreased stiffness matrix concerning the kth layer is:
The matrix is symmetric and dependent on the fiber orientation and engineering constants for every layer. The stress components of the kth layer as function of the mid surface curvatures (kx, ky and kxy) and mid surface strain (, and ) are in accordance with Equation (4) []:
Following [], we have:
with (kx, ky, kxy) and , , are the kth layer mid surface curvatures and strains.
Forces and moments per unit length originating from subjected load may be calculated by stress integration in every layer across the laminate thickness []:
where, and represent the space between upper and lower limits of the kth layer to to the middle surface (Figure 2). Every layer has a fixed thickness . For a laminate that possesses layers, the overall thickness is:
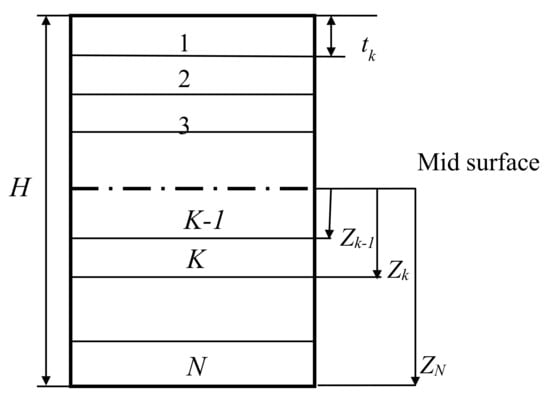
Figure 2.
Laminate with N layers.
Using Equations (4)–(6), we get forces and moments per unit length, []:
The extensional stiffness coefficients the bending-extension coupling coefficients and the is bending stiffness coefficients are expressed, as follows []:
Perforated FGPs considered in this study are exponential FGP, i.e., Young’s modulus, Poisson’s ratio and shear modulus of the point residing at the distance z relative to the total thickness are provided via the exponential function below:
Such that is the gap from the X-Y plane at the plate center within the mid surface, M. P(z) is the substance characteristic at distance z, , H is the total thickness, is the material property in the top layer of the FGP and the material property in the bottom layer of the FGP, as in Figure 3. In the present composite material, top and bottom laminates have a 90-degree and 0-degree fiber angle, correspondingly.
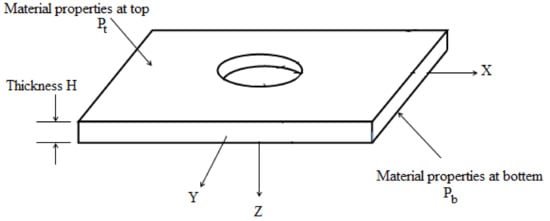
Figure 3.
FGP with a hole [].
The forces and moments per unit length are obtained in terms of the stress function as relations (11) and (12), []:
where Re [.] represents real part of [.]. In the above relations following [] we get
where:
being anisotropy factor [].
The stress functions may be computed using the superposition approach by aggregating the stress functions in two conditions. For the initial condition, a complete plate is assumed (excluding a hole) under a load on outer edges. Such load creates an internal load on the points on the hole limits. Regarding the main issue, the hole boundary is not subjected to a load. For the second condition, it is assumed that an opposing force to the hole boundary internal hole offsets its impact. When there is no hole, the stress function corresponding to first condition has a constant complex value:
For the second state, the potential functions of the first state are used to compute the internal forces and and the transverse force and the bending moment generated at the hole boundary. Using the equilibrium equations in the and directions, the internal forces are related to the resultants , and as follows []:
Following [], in the second case, we have the following equations:
where fx, fy, p(Γ), m(Γ) and respectively Γ are internal forces, transverse force, bending moment, and arc hole length to the current point, respectively.
Now using Equations (12,13) in (17)–(20) we get the boundary conditions:
Due to the hole boundary being considered to be free from traction, regarding the second condition, it is assumed that at the hole boundary, an opposing force to the internal load stemming from the external load of the initial condition offsets its impact. Therefore, the boundary conditions are:
Using the Schwartz formula concerning the holomorphic function and the substitution of the mapping function (1) in Equations (25) to (28) yields:
where
From Equations (29)–(32) we get the solution :
Such that is the initial derivative of the mapping function in regard to . Ultimately, by implementing Equation (33) in Equations (12) and (13), the forces and moments per unit length are acquired.
3. Numerical Results
At first, to validate the used method, the results of presented analytical study are evaluated using the finite element method (in ABAQUS). For that, the hole geometry was modeled with the following values for the studied parameters: β = 0° (the orientation angle of the hole), c = 1(aspect ratio of the hole) and ω = 0.125 (bluntness parameter). To simulate FGP, it is considered to include 100 layers with marginally differing characteristics that altogether create the eventual variances in characteristics along the thickness. The mechanical characteristics considered for FGM are provided in Table 1.

Table 1.
Mechanical properties.
The implemented load was . For the purpose of obtaining optimal mesh grid and enhancing the preciseness of FEM outcomes, the region at the hole’s proximity was modeled using a smaller mesh compared to farther regions. Meshing took place using S8R elements in regard to the physics and geometry of the issue at hand. Figure 4 provides a comparison of the stress resultant Ny acquired from the provided analytical solution including one provided by the numerical solution. Figure 5 presents a resembling comparison of the stress resultant Nxy. The angle α denotes the points’ position on the hole boundary in regard to the horizontal axis. The mesh and loading patterns are depicted in Figure 6 and Figure 7, correspondingly. The maximum resultant forces’ ratio at the hole corner to the implemented load is considered as the normalized stress resultant. Evidently, when the implemented load is 1, i.e., (), hence the normalized stress resultant is the resultant forces. Furthermore, the normalized moment resultants ( and ) are defined as (,,) correspondingly [], such that H is the overall laminate thickness.
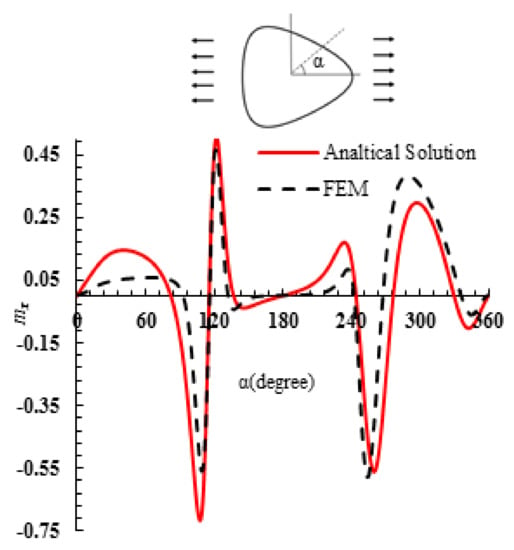
Figure 4.
Comparing the moments mx provided by the analytical approach and the numerical solution (ω = 0.125).
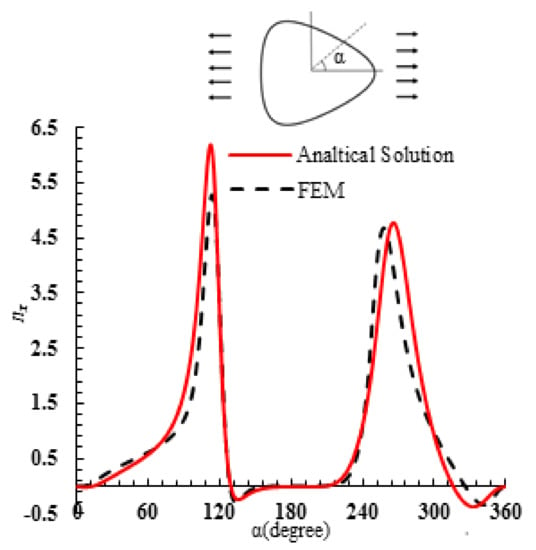
Figure 5.
Comparing the resultant force nx provided by the analytical approach and the numerical solution (ω = 0.125).

Figure 6.
Mesh refinement for plate with quasi-triangular hole.
Figure 7.
Loading situation in ABAQUS software.
4. Results
In this section, we investigate the forces and moments per unit length of FGPs with quasi-triangular hole. In Figure 8, the maximum resultant forces acquired around a triangular hole in asymmetric laminate from modeling with 20 to 140 layers are presented. Evidently, as the number of laminate (N) is increased, the stress resultant primarily increases, and subsequently decreases until gradually reaching a constant value at N = 90. Consequently, every research outcome was calculated with N = 100 layer number, which is accordance to dimensionless ply thickness of 0.01.
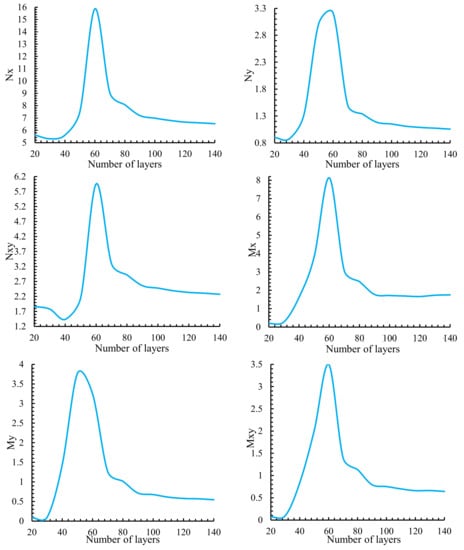
Figure 8.
Forces and moments per unit length.
Figure 9 presents the discrepancies of the normalized forces and moments per unit length with the rotation angle of triangular hole (β) in various values of bluntness parameter (ω). Because the difference of resultant forces with hole orientation are periodical, the outcomes are provided for β values of up to 90 degrees. Based on this figure, for all values of ω, by decreasing the value of ω, the forces and moments per unit length is reduced. In each value of ω, the minimum normalized resultant forces (nx, ny, nxy) occur at approximately rotation angle of 45° and the rotation angle of 20° leads to the maximum normalized resultant forces. For example, the normalized resultant forces (nxy) presented in Figure 9.
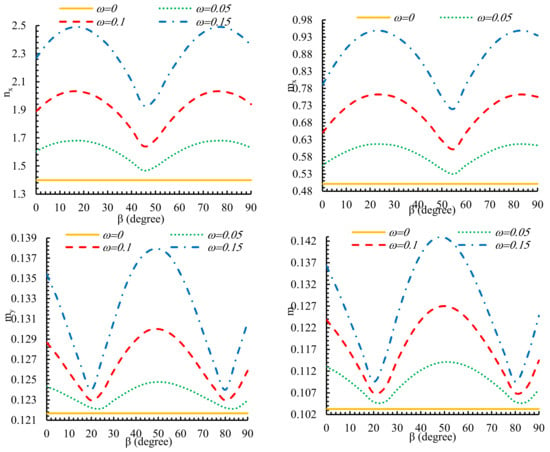
Figure 9.
Discrepancies of the normalized forces and moments per unit length with the rotation angle of triangular hole (β).
Moreover, for moments, the minimum value of happens at hole orientation of 55°. The minimum values of and occur at rotation angle of 20°; and behave differently compared to . The rotation angle of 50° leads to the maximum value of and . Due to the difference between the three modes, all three charts of normalized moments are placed.
The aforementioned parameter c guides the hole’s aspect ratio and solely influences the outcomes along the y-direction. The impact of this factor on the maximum resultant forces acquired with various curvature factors at zero-degree orientation (β = 0) are shown by Figure 10. Evidently, as c is increased, all resultants enhanced linearly. This is evident in all values of bluntness parameter. As shown in this figure, the lowest values of forces and moments per unit length happen in ω = 0 which is equivalent to a circular hole. Regarding the similarity of linear behavior in both cases, two samples of the vector (ny, my) are selected excellently.
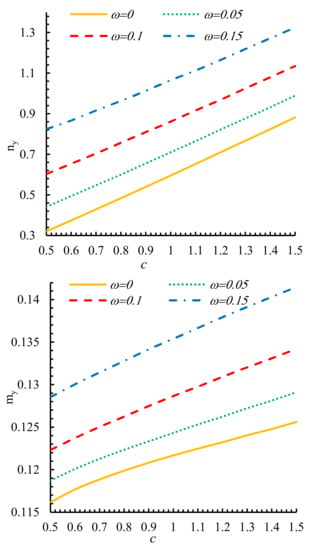
Figure 10.
The effect of c on the normalized forces and moments per unit length in different values of ω.
Figure 11 depicts the impact of bluntness parameter (ω) on the normalized resultant force at β = 0 and c = 1. This figure shows that as we increased ω to sharpen the hole corners, the maximum resultant forces increased. The minimum value of normalized forces and moments per unit length occur at ω = 0. As previously stated, ω = 0 is the equivalent of a circular hole. As illustrated in this figure, the rotation angle of 45° compared to two other angles leads to the minimum values of normalized resultant forces. The maximum values of nx and ny occur at rotation angle of 30° however, for ny this value occurs at rotation angle of zero degrees. The rotation angle of 30° causes the minimum values of and , however, the minimum value of occurs at rotation angle of zero degrees.
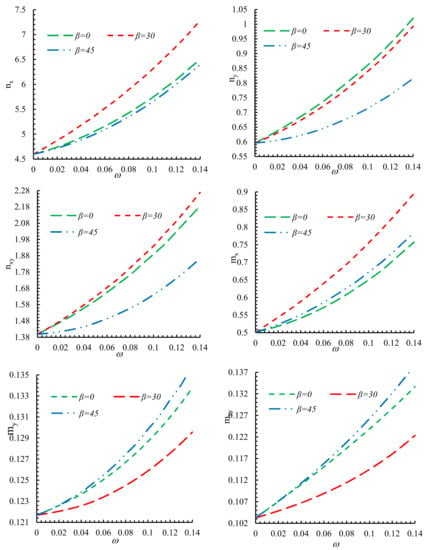
Figure 11.
The effect of ω on the normalized forces and moments per unit length.
5. Conclusions
This study provided an analytical approach on the basis of Lekhnitskii’s formalism and a conformal mapping to assess the stress distribution of FGPs consisting of triangular holes. The impact of hole geometry on forces and moments per unit length to be created at the proximity of the hole boundary was examined. An overall assessment indicated that:
- (1)
- By comparing the provided analytical solution in addition to the numerical solution acquired via finite element modeling, favorable compatibility was exhibited between these outcomes.
- (2)
- When a perforated plate subjected to uniaxial loading along the x-direction, the normalized forces and moments per unit length at the proximity of the holes of various aspect rations will be greater at the loading direction compared to other directions.
- (3)
- The hole corner’s curvature radius does not only determine the values of the forces and moments per unit length, but also hole orientation and aspect ratio have substantial roles in this regard. Therefore, cautious modifications of such parameters may substantially decrease the forces and moments concerning every hole at all provided corner curvatures.
- (4)
- Most forces and moments per unit length change linearly with aspect ratio of triangular hole (c).
- (5)
- The lowest values of the normalized forces and moments occur in ω = 0 which is equivalent to a circular hole this means that for a triangular hole, the values of the normalized forces and moments are not less than the circular hole in any value of the parameters discussed.
- (6)
- As bluntness parameter (ω) increases, the normalized forces and moments increase at different rotation angles.
Author Contributions
Writing—review and editing: M.J., M.H.B.C., H.A., E.-M.C. and L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Mapping function | |
| Complex variable | |
| ,, , | Complex constants related to the roots of the characteristic equation |
| Bluntness | |
| Hole geometry | |
| Imaginary constant | |
| Counter | |
| Shear strain | |
| Layers counter | |
| Reduced stiffness matrix | |
| Mid-plate shear strain | |
| Thickness | |
| Total thickness | |
| Distance to mid plane | |
| Thickness of each layer | |
| Exponential function | |
| Material properties in the upper layers | |
| Material properties in the lower layers | |
| Napier number (2.718) | |
| Exponential function constant | |
| Real part | |
| Potential function | |
| Hole aspect ratio | |
| The roots of the characteristic equation | |
| Hole rotation angle | |
| The hole size | |
| , | Normal stress |
| Shear stress | |
| , | Longitudinal strain |
| , | Midline longitudinal strains |
| ,, | Intra-curvature curvature |
| ,, | Resultant forces |
| , , | Moments resultants |
| Number of layers | |
| Tensile stiffness matrix | |
| Coupling matrix | |
| Bending stiffness matrix | |
| , , | Complex constant in calculating force and moments |
| Anisotropy factor | |
| Components of internal force | |
| Force at the boundary of hole | |
| Normal bending at the boundary of hole | |
| Transverse force at the boundary of hole | |
| length of the hole arc |
References
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity, 2nd ed.; Cambridge University Press: Cambridge, UK, 1962. [Google Scholar]
- Savin, G.N. Stress Concentration Around Holes; Pergamon Press: New York, NY, USA, 1961. [Google Scholar]
- Lekhnitskii, S.G. Anisotropic Plates, 2nd ed.; Gordon and Breach Science: New York, NY, USA, 1968. [Google Scholar]
- Sharma, D.S. Stress distribution around polygonal holes. Int. J. Mech. Sci. 2012, 65, 115–124. [Google Scholar] [CrossRef]
- Sharma, D.S. Moment distribution around polygonal holes in infinite plate. Int. J. Mech. Sci. 2014, 78, 177–182. [Google Scholar] [CrossRef]
- Rezaeepazhand, J.; Jafari, M. Stress Analysis of Composite Plates with a Quasi-Square Cutout Subjected to Uniaxial Tension. J. Reinf. Plast. Compos. 2009, 29, 2015–2026. [Google Scholar] [CrossRef]
- Ukadgaonker, V.G.; Rao, D.K.N. A general solution for stress resultants and moments around holes in unsymmetric laminates. Compos. Struct. 2000, 49, 27–39. [Google Scholar] [CrossRef]
- Jafari, M.; Chaleshtari, M.H.B. Using dragonfly algorithm for optimization of orthotropic infinite plates with a quasi-triangular cut-out. Eur. J. Mech. A/Solids 2017, 66, 1–14. [Google Scholar] [CrossRef]
- Jafari, M.; Moussavian, H.; Chaleshtari, M.H.B. Optimum Design of Perforated Orthotropic and Laminated Composite Plates under in-plane loading by genetic algorithm. Struct. Multidiscip. Optim. 2017, 57, 341–357. [Google Scholar] [CrossRef]
- Yang, Q.; Gao, C.F.; Chen, W. Stress analysis of a functional graded material plate with a circular hole. Arch. Appl. Mech. 2009, 80, 895–907. [Google Scholar] [CrossRef]
- Yang, Q.; Gao, C.; Chen, W. Stress concentration in a finite functionally graded material plate. Sci. China Ser. G Phys. Mech. Astron. 2012, 55, 1263–1271. [Google Scholar] [CrossRef]
- Sharma, D.S. Stress concentration around circular/elliptical/triangular cutouts in infinite composite plate. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011. [Google Scholar]
- Pan, E. Exact Solution for Functionally Graded Anisotropic Elastic Composite Laminates. J. Compos. Mater. 2003, 37, 1903–1920. [Google Scholar] [CrossRef]
- Reid, R.G.; Paskaramoorthy, R. An extension to classical lamination theory for use with FGPs. Compos. Struct. 2011, 93, 639–648. [Google Scholar] [CrossRef]
- Dave, J.; Sharma, D.S. Stresses and moments in through-thickness FGP weakened by circular/elliptical cut-out. Int. J. Mech. Sci. 2016, 105, 146–157. [Google Scholar] [CrossRef]
- Mohammadi, M.; Dryden, J.R.; Jiang, L. Stress concentration around a hole in a radially inhomogeneous plate. Int. J. Solids Struct. 2011, 48, 483–491. [Google Scholar] [CrossRef]
- Enab, T. Stress concentration analysis in FGPs with elliptic holes under biaxial loadings. Ain Shams Eng. J. 2014, 5, 839–850. [Google Scholar] [CrossRef]
- Mehrparvar, M.; Ghannadpour, S. Plate assembly technique for nonlinear analysis of relatively thick FGPs containing rectangular holes subjected to in-plane compressive load. Compos. Struct. 2018, 202, 867–880. [Google Scholar] [CrossRef]
- Ghannadpour, S.; Mehrparvar, M. Energy effect removal technique to model circular/elliptical holes in relatively thick composite plates under in-plane compressive load. Compos. Struct. 2018, 202, 1032–1041. [Google Scholar] [CrossRef]
- Craciun, E.-M.; Soós, E. Anti-plane States in an Anisotropic Elastic Body Containing an Elliptical Hole. Math. Mech. Solids 2005, 11, 459–466. [Google Scholar] [CrossRef]
- Craciun, E.M.; Barbu, L. Compact closed form solution of the incremental plane states in a pre-stressed elastic composite with an elliptical hole. ZAMM 2013, 95, 193–199. [Google Scholar] [CrossRef]
- Marin, M.; Abbas, I.; Vlase, S.; Craciun, E.-M. A Study of Deformations in a Thermoelastic Dipolar Body with Voids. Symmetry 2020, 12, 267. [Google Scholar] [CrossRef]
- Savadkoohi, H.S.A.; Jafari, M. Studying the effect of different parameters on stress resultant and moments distribution around non-circular cutouts in unsymmetric laminates. ZAMM 2017, 97, 1317–1330. [Google Scholar] [CrossRef]
- Jafari, M.; Chaleshtari, M.H.B.; Abdolalian, H. General solution of stress field in exponential functionally graded material plates containing a quasi-rectangular cutout. J. Compos. Mater. 2018, 53, 405–421. [Google Scholar] [CrossRef]
- Moussavian, H.; Jafari, M. Optimum design of laminated composite plates containing a quasi-square cutout. Struct. Multidiscip. Optim. 2016, 55, 141–154. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).