Abstract
The article is an original insight into interdisciplinary challenges of shaping innovative unconventional complex free form buildings roofed with multi-segment shell structures arranged with using novel parametric regular networks. The roof structures are made up of nominally plane thin-walled folded steel sheets transformed elastically and rationally into spatial shapes. A method is presented for creating such symmetric structures based on the regular spatial polyhedral networks created as a result of a composition of many complete reference tetrahedrons by their common flat sides and straight side edges arranged regularly and symmetrically in the three-dimensional Euclidean space. The use of the regularity and symmetry in the process of shaping different forms of (a) single tetrahedral meshes and whole consistent polyhedral structures, (b) individual plane walls and complex elevations, (c) single transformed folds, entire corrugated shell roofs, and their structures allow a creative search for attractive rational parametric solutions using a few author’s parametric algorithms and their implementation as built-in commands of the AutoCAD visual editor or applications of the Rhino/Grasshopper program.
1. Introduction
Thin-walled steel sheets are profiled in one direction to use them as members and coverings for roofing. The rationality of using such sheets results from the very favorable ratio of self-weight to load-bearing capacity or covering surface area, and from quick roof assembly [1]. Due to the orthotropic properties of the sheeting, including very different stiffness in two orthogonal directions, flat profiled sheets have been elastically deformed into two shell forms, i.e., rotational cylinder [2,3], Figure 1, and central sectors of right hyperbolic paraboloids [3,4], Figure 2.
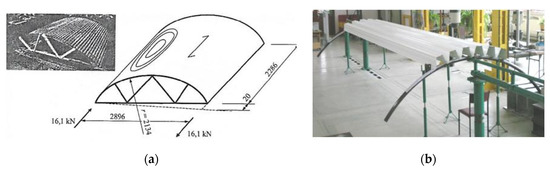
Figure 1.
Elastically bent corrugated cylindrical steel shells: (a) by Abdel_Sayed [2]; (b) by Abramczyk [3].

Figure 2.
Elastically twisted hyperbolic paraboloid steel shells: (a) two-layer by J.E. Parker [4]; (b) one-layer by Abramczyk [3].
Geometric and mechanical changes of the transformed sheets depend on the imposed boundary conditions including the type and degree of the shape transformations. The possibility of using elastically deformed folded sheets as roof coverings depends primarily on the amount of the initial stresses caused by the shape transformations. Therefore, shallow hyperbolic paraboloid sheeting shaped as a result of small twist transformations are most often used [2], Figure 2.
Thin-walled steel sheets having open profiles and folded in one direction can be joined with their longitudinal edges into nominally flat sheeting and transformed into ruled shell shapes as a result of spreading onto at least two skew roof directrices, Figure 3a. The shell shape of each transformed sheeting depends on a mutual position and curvature of two edge directrices. The sheeting can be modeled with a regular smooth ruled undevelopable surface called a warped surface [1], Figure 3b.
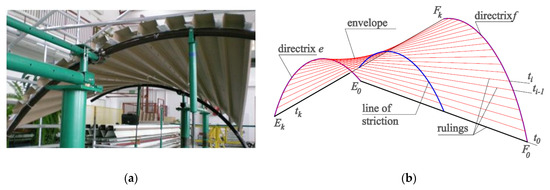
Figure 3.
(a) An axis-symmetric experimental thin-walled corrugated steel shell supported by two curved skew directrices; (b) elements of a smooth model used for shaping the transformed shells.
The analyses related to a static strength work of such deformed and loaded corrugated shells are based on analytical methods leading to calculations of critical forces [5] or FEM describing the entire behavior of these shells [6]. All spatial shape transformations investigated in the present article are effective because freedom of the transverse width increments of each shell fold diversified along its length is ensured [7]. The effective shape transformations are accomplished to obtain a rational static strength work of each shell fold and then very attractive visual building forms [8]. Each shell sheeting transformed effectively, Figure 4, is characterized by a line of contraction passing through the half-length of each shell fold and the smallest possible pre-stresses [9].
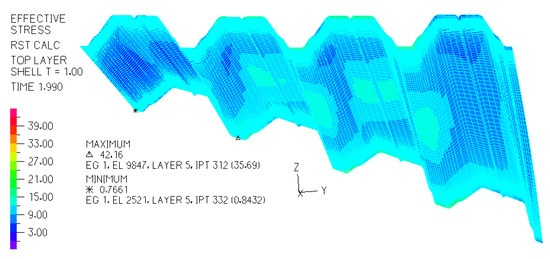
Figure 4.
An accurate mechanical thin-walled folded model of a nominally plane folded sheet transformed elastically into a shell shape and the graphical expression of the “effective” stresses in MPa on its top surface.
The specific feature of the investigated effective shape transformations is that they particularly provide an easy shaping of various symmetric unconventional and rational shell-free forms of roofs, entire buildings, and their structural systems [10], Figure 5a,b. In this way, very attractive free forms of buildings having oblique eaves, girders, and elevations can be shaped [11].

Figure 5.
Two unconventional symmetric shell-free forms: (a) an erected roof shell by Reichhart [10]; (b) a computer model of a bar structural system intended for the transformed shell roof sheeting.
The aforementioned basic properties and restrictions of a rational shaping of single corrugated ruled shell-free forms transformed effectively, concerning the complexity of their shapes, including the contractions, results in the fact that two complete corrugated shell sheets cannot be joined with their crosswise ends, that is perpendicular to their fold’s direction, to obtain one resultant smooth shell [3]. Straight or curved edges must appear between two individual shell sheeting joined transversally towards their folds, Figure 6a. Thus, such shells must be modeled by means of complex multi-segment roof shell structures, Figure 6b.

Figure 6.
A symmetric shell structure roofing the experimental hall at Rzeszow University of Technology: (a) an internal view; (b) an external view.
2. State of the Art
Thin-walled folded steel sheets of open profiles allow easy deformations of their folds, including their flat rectangular walls and inclination angles between flanges and webs. Nilson studied the possibilities of the sheet’s deformations into hyperbolic paraboloid shells and published his research in 1962 [12]. He showed that double-layered fold sheeting transformed elastically into a central sector of a hyperbolic paraboloid or a symmetrical arrangement of four quarters of such a sector is more economical than a reinforced concrete hyperbolic paraboloid shell.
The research conducted under the guidance of Winter [13] confirmed the most important Nilson’s conclusions. It was associated with a greater variety of the sheet profiles and dimensions of two-layer hyperbolic paraboloid shells. Central sectors and compositions of quarters of the hyperbolic paraboloid shells were examined. Parker studied roof structures consisting of four folded quarters of a right hyperbolic paraboloid. The analyzed segments were made of two layers of sheets located orthogonally and stiffened with a circumference frame. He analyzed the behavior of the transformed sheeting, including the changes in stiffness and potential energy of these sheets [4]. The Muscat’s research [14] concerned primarily critical loads and stability of the sheeting of the type analogous with the one investigated by Parker and Nilsen. Banavalkar made a thorough analysis of the static strength work of these shells [15].
A comprehensive summary of the research performed at Cornwell University is the report made by Gergely et al., [16]. The authors carried out a complete detailed analysis of the static strength work of single and complex profiled hyperbolic paraboloid shells. These shells were made up of plane sheets profiles located in two mutually orthogonal layers, which enables these researches to analyze the shells as isotropic. They examined folded shells of different profiles.
Behavior of a central sector of a folded steel hyperbolic paraboloid stiffened with a circumferential frame was studied by McDermott [17]. Gioncu and Petcu [18] studied the work of the analogous hyperbolic paraboloid shells using traditional analytical analyses of strength and critical loads. They finally developed a novel HYPBUCK computer program for calculating critical loads. They also studied umbrella shell sheeting composed of four symmetrical right hyperbolic paraboloid quarters in various configurations, Figure 7a,b.
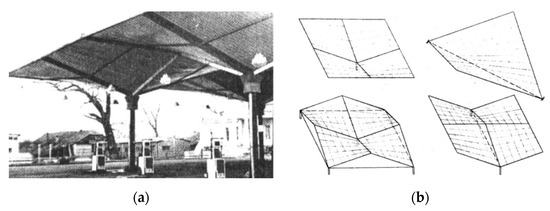
Figure 7.
Symmetrically arranged hyperbolic paraboloid units by Petcu and Gioncu [5]: (a) an erected corrugated umbrella shed; (b) various configurations of umbrella shell structures.
Parallel studies and analyzes related to the static strength work of single and complex hyperbolic paraboloid shells made up of flat folded sheets of different profiles were conducted by Egger et al. [19]. Their method is based on the performed tests, conventional analyses, and analytical calculations of strength and critical loads.
The shells investigated by the aforementioned researchers were undergone forced shape transformations causing relatively big pre-stresses due to the imposed boundary conditions, including the joints between two orthogonal layers arranged over the whole area of the transformed shells and the frames stiffen the quadrangular edges of the shells, so only shallow hyperbolic paraboloid shells called hypars could be created, Figure 8a,b. In addition, the adjustment of all longitudinal shell fold’s axes to the calculated rulings of the designed hyperbolic paraboloid quarters imposes a significant change in the width of the transverse fold’s ends passing along each shell directrix affecting important initial stresses. To limit the level of the pre-stresses, a maximum deformation degree has to be introduced. Initial forced deformations of the nominally plane folded sheets have been used by Dawydov in prefabrication of long-span roof panels [20].

Figure 8.
Two symmetric experimental hyperbolic paraboloid shells: (a) a single shell by McDermott [17]; (b) an umbrella structure of four quarters by Banavalkar and Parker [16].
Davis and Bryan [21] described the most important geometrical and mechanical characteristics of flat and thin-walled transformed shell folds. They presented a complete way of analyzing and designing shells and structures made up of two-layer corrugated sheets located orthogonally. Two most important general conclusions given by these authors and regarding the transformed roof shells are as follows. The researchers found that, theoretically, it is possible to shape many different types of the transformed folded shell sheeting. Practically, however, it is possible to build only cylindrical and hyperbolic paraboloid types of the transformed folded steel shells for roofing due to the available technology.
The use of the well-known conventional design methods [1,16,19,21], known from the traditional courses of theory of thin-walled shells, in shaping of such transformed shell roofs is ineffective because it usually results in high values of normal and shear stresses, local buckling and distortion of thin-walled walls: flanges and webs. The assembly of each designed shell sheeting into skewed roof directrices is often impossible because of the plasticity of the fold’s edges between flanges and webs. Reichhart developed a specific method for calculating the arrangement and the length of the supporting lines of all folds in transformed one-layer corrugated shell sheeting [10], Figure 5a and Figure 6a,b. The method is based on the orthotropic geometric and mechanic properties of the folded sheets and limits the value of the pre-stresses. His method enables one to shaped right hyperbolic paraboloids or other deep right ruled surfaces [22].
The Reichhart’s method is effective only for the cases where the fold’s longitudinal axes are perpendicular to roof directrices or very close to those [3]. The method leads to serious errors as it is demonstrated by Abramczyk [3]. These errors result from the lack of conditions providing similar values of stresses at both transverse ends of the same fold. Abramczyk significantly improved the Reichhart’s concept and has proposed an innovative method [3,8], so that the transformation would cause the smallest possible initial stresses on the shell folds resulting from this transformation. The visible result of different stress values at both transverse ends of the same shell fold is that the transverse contraction of the fold does not pass halfway along its length, on the contrary, it is shifted closer to one of these ends.
In order to create a method for shaping the considered type of the roof shells transformed rationally, Abramczyk [3] proposed a condition requiring the contraction of each entire shell to pass halfway along the length of each shell fold, Figure 3a,b. The condition has to be ensured to obtain a shell fold characterized by the effectiveness of the shape transformations [23]. The Abramczyk’s method employs some specific geometric properties of warped surfaces, primarily their lines of striction. The second condition utilized by Abramczyk relates to calculations of the respective surface areas modeling compressing and stretching zones on the transformed folds [24]. Both conditions are based on the results of his experimental tests and computer simulations [25], Figure 1 and Figure 2. They are implemented in the Abramczyk’s application [23] developed in the Rhino/Grasshopper program used for parametric modeling of engineering objects.
Simple shell structures composed of a few complete corrugated shells were used in different architectural configurations, most often as shells supported by stiff constructions based on very few columns [24,25]. Such shell structures are used for achieving (a) large spans; (b) greater architectural attractiveness; and (c) skylights letting sunlight into the building interior. Reichhart arranged the complete corrugated shells on horizontal or oblique planes [10] to achieve continuous ribbed structures, Figure 6 and Figure 9. He developed a simple method for geometrical and strength shaping of the transformed shell roofs. He designed a few corrugated shell sheeting supported by very stiff frameworks or planar girders with additional intermediate directrices, members, and roof bracings.

Figure 9.
The external view of one elevation of the experimental hall at Rzeszow University of Technology roofed with the shell structure.
In the 70s, Biswas and Iffland [26] presented two concepts of two continuous regular roof structures composed of many identical hyperbolic paraboloid segments made up of transformed folded steel sheets arranged on two various spheres. In the first concept, Figure 10a,b, they proposed triangular shell segments having three-segment edge lines. Another important feature of this concept is that the proposed plane system, dividing the roof structure into tetrads of triangular shell segments, which is based on a sphere. This concept requires significant oblique cuts and big transformation degree of all rectangular folded sheets.
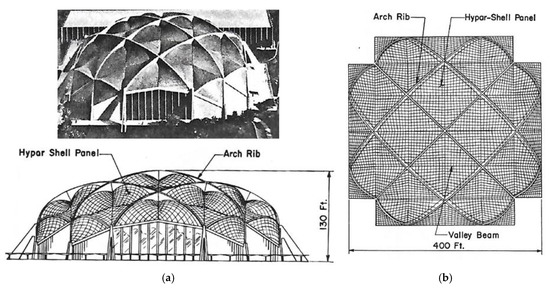
Figure 10.
The first Field House structure proposed by Biswas and Iffland [26]: (a) concept and elevation; (b) plan.
In the second concept, typical quadrilateral transformed hyperbolic paraboloid segments are used, Figure 11a,b. This concept is more realistic, but the degree of twisting and deflection of the complete hyperbolic paraboloid segments are small.
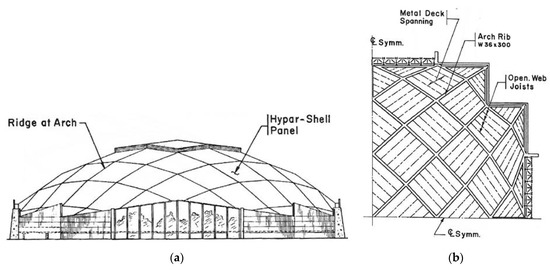
Figure 11.
The second structure proposed by Biswas and Iffland [26]: (a) elevation; (b) framing plan of a quarter of the structure.
At present, shell structures consisting solely of steel decks are not visually appealing. In order to increase their attractiveness, it is possible to use: (1) areas of discontinuity between the metal steel segments, filled with, e.g., glass panels, (2) green plant gardens on the transformed segments, (3) coat the segments with different plastic membranes, (4) communication routes between the segments, (5) a coherent connection of glass facades and steel shell roof.
In order to create medium and long span free form building structures roofed with complex corrugated shells, Abramczyk [27,28] has proposed certain types of the so-called reference tetrahedrons to model complete free forms covered with folded glass elevations and roofed with complete transformed corrugated steel shell sectors. These tetrahedrons can be arranged regularly in the three-dimensional space to model complex building free forms, Figure 12a,b. Prokopska [29,30] has drawn drew attention to the architectural aspects of shaping such forms.
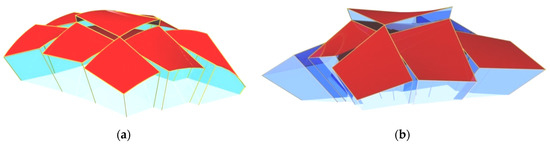
Figure 12.
Two complex building free forms covered with multi-segment roof shell structures and plane-walled folded glass elevations characterized by (a) curved roof directrices; (b) straight roof directrices.
One of the Abramczyk’s methods [31] relates to positioning of many aforementioned reference tetrahedrons along ellipses t0 and w0 contained in two orthogonal principal planes (x,z) and (y,z) of symmetry of a reference ellipsoid ωr, Figure 13a. The method allows the investigated form of a polyhedral structure to be a regular network and precisely take into account by the designer the variable curvature of ωr. The method replaces a finite number of the selected straight lines ti,j normal to ωr with side edges ki,j of the sought-after reference tetrahedrons. A specific feature of the reference tetrahedrons is that two their subsequent straight side edges ki,j and ki+1,j belonging to the same side must intersect, while two corresponding straight lines ti,j and ti+1,j normal to ωr do not intersect to each other, Figure 13b. The positions of ti,j and ti+1,j have to be replaced by ki,j and ki+1,j, so that the positions of ki,j and ki+1,j have to be defined based on the geometric properties of ωr. An architectural study of a free form created with the help of the method is presented in Figure 14.
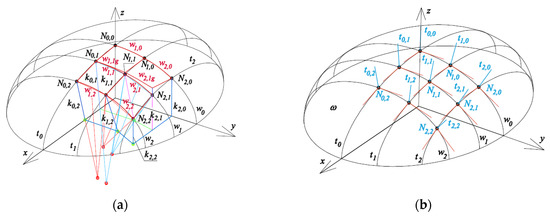
Figure 13.
Creation of a coherent complex free form arranged over a double-curved reference ellipsoid: (a) a quarter of the final structure; (b) normals to the reference ellipsoid.
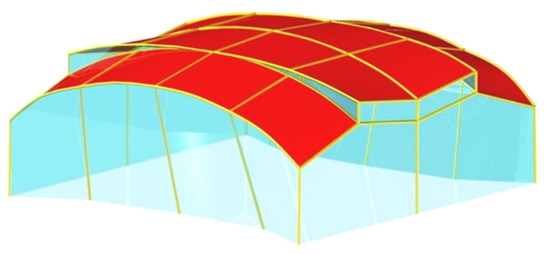
Figure 14.
The architectural study of a free form optimized on the basis of the investigated reference ellipsoid.
Parameterization of the reference tetrahedrons enables to computationally search for attractive unconventional building free forms [23,27] and innovative structural systems intended for the investigated complex building free forms. In the analyses of these systems, the supported himself with the following works Obrębski [32] developed a few methods for shaping very diversified shell rod structures. Rebielak [33] developed steel rod structural systems supporting flat roof covers composed of corrugated sheets. A team of researchers led by Abel and Mungan [34] published comprehensively many examples of the construction systems associated with shaping very diversified roof shells and building free forms. A parametric method for shaping rod shells in the form of Catalan surfaces using the Rhino/Grasshopper program is presented by Dźwierzyńska and Prokopska [35]. The exact geometrical characteristics and methods for determining regular curves and surfaces have been presented by Carmo [36] and Gray [37].
Transformed folded steel sheets are also used as curved supports for shell panels of individual roof covers [38], Figure 15. Convex roof shells characterized by the positive Gaussian curvature can be created in this way.

Figure 15.
Two steel structural systems supporting transformed folded sheets by Żwirek [38]: (a) the erection of the final shell roof; (b) experimental tests.
3. Aim
The aim is to present a novel method for parametric shaping of building complex free forms based on the innovative spatial polyhedral networks. The presentation is focused on using symmetry for (1) obtaining attractive complex shapes of shell roof structures, folded multi-plane elevations and entire free form buildings, (2) reducing the number of the variables required to define the geometric objects employed, (3) making the proposed algorithm very intuitive, (4) getting rationality of the transformed shell roof forms and their structural systems. The shell roof structures designed with the help of the method are composed of many complete shell sectors arranged in conformity with shapes of various regular reference surfaces. In addition, each elevation should be composed of many planar and oblique walls coherent with the designed shell roof structure.
4. Concept of the Method
The algorithm of the investigated method allows a rational use of the shape transformations of nominally flat thin-walled open folded steel sheets to achieve visually attractive shell roofs whose shapes determine unconventional building free forms as well as their innovative structural systems. Since any two roof directrices are mutually skew straight or curved lines, it is convenient to contain these directrices in the planes of façade walls or in the planes of roof girders. The directrices should be assumed as segments of the roof shell eaves. In addition, a controlled inclination of all elevations to the vertical makes it possible to increase the attractiveness of the created free form buildings.
A smooth resultant shell cannot be the result of a composition of two transformed individual shells with their transverse edges due to the location of the fold’s contraction of each effectively transformed roof shell with respect to the roof directrices. Thus, both smooth shells must be separated by a common rib disturbing the smoothness of the resultant complex structure. The ribs- between many complete transformed shells can be taken for common directrices of many pairs of the adjacent shells in the complex roof shell structure.
Following the method’s algorithm, a system of the planes separating all roof shell segments and containing the aforementioned edges, including directrices, has to be adopted. Such a spatial system is called a polyhedral reference network Γ. Each reference network Γ is characterized by the following geometrical properties. Each complete mesh Γij of Γ is limited by four adjacent planes of the system defined by means of four vertices WABij, WCDij, WADij, and WBCij, Figure 16. Each single shell segment Ωij and each complete free form Σij are located in one mesh Γij, so that façade walls, roof directrices and eaves segments are included in the aforementioned quadruple of planes of Γij.
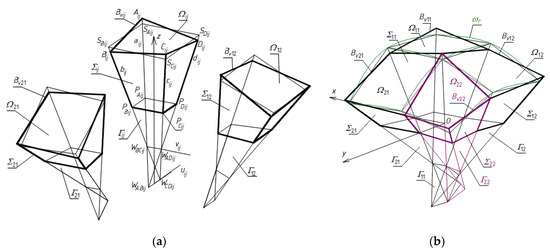
Figure 16.
Creation of a complex free form by means of a reference network Γ composed of tetrahedral meshes Γij (i = j = 1): (a) Γij before setting (b) Γij after setting in Γ.
Every two adjacent planes of each single mesh Γij intersect in the side edges: aij, bij, cij, dij, and, every two opposite planes intersect in the axes uij or vij of Γij. The side edges and axes of Γij are defined by means of four vertices WABij, WCDij, WADij, WBCij, Figure 16a. Thus, each possible triple of these vertices determines one plane of Γij. On the basis of these vertices, four points SAij, SBij, SCij and SDij are constructed on four side edges aij, bij, cij, dij. These points are vertices of a spatial quadrangle SAijSBijSCijSDij determining a certain piece of a reference surface ωr, Figure 16b. In relation to ωr, four vertices Aij, Bij, Cij, Dij of single eaves Bvij are determined to obtain mutually skew roof directrices. Vertices PAij, PBij, PCij, PDij, Figure 16a, belonging to a flat horizontal base of the sought-after free form Σ are constructed in relation to the aforementioned four vertices WABij, WCDij, WADij, WBCij. The complex free form Σ created on the basis of such a reference network Γ is a sum of all individual free forms Σij. Finally, a resultant z-axis symmetric free form structure can be achieved, Figure 17a,b.
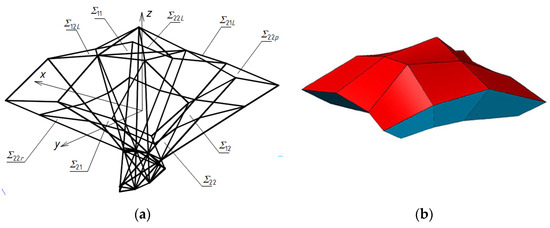
Figure 17.
A complex free form building structure Σ roofed with a continuous shell structure: (a) edge model; (b) architectural stadium.
Parameterization realized in the process of the geometric shaping of such free forms Σ is based on a definition of a finite set of variables entering into computer application in the form of either the measures of stiff motions, like rotations and translations, or division coefficients of all pairs of the adopted vertices of Γ. An algorithm of the stiff motions leading to the creation of Σ is presented in Section 5. An example of using the division coefficients in creating a spatial reference network is presented in Section 6.
5. Method’s Algorithm
In the first step of the method’s algorithm, the first mesh Γ11 of a reference network Γ is created so that the positions of its four vertices WAB11, WCD11, WAD11, and WBC11 are defined in the three-dimensional space. For this purpose, a global coordinate system [x,y,z] must be taken, Figure 18a, where a point O is the origin of [x,y,z]. These vertices are arranged symmetrically in relation to the principal planes of [x,y,z], so the sought-after mesh must be symmetric. The first set of initial data is formed from the measures of the vectors and angles employed to determine all characteristic points of Γ11.
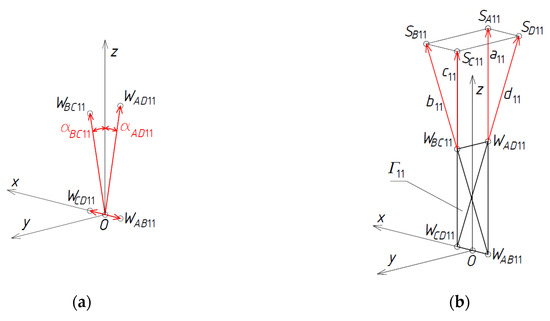
Figure 18.
Creation of Γ11: (a) vertices: WCD11, WAB11, WAD11 and WBC11; (b) side edges: a11 = (WAD11, WAB11), b11 = (WBC11, WAB11), c11 = (WCD11, WBC11) and d11 = (WAD11, WCD11).
On the basis of the aforementioned set of initial data, four vertices of Γ11 are determined as follows. The position of vertex WCD11 is the result of the translation TOCD11 of the point O by the vector OWCD11 whose measure is defined by means of one element of the first initial set. In an analogous way, the position of vertex WAB11 is defined by means of the translation TOAB11 of the point O by the vector OWAB11 so that its location is on opposite side of O on the x-axis.
The position of vertex WAD11 is the result of a composition of the rotation OCD11_ AB11 of the z-axis about the x-axis by the angle αAD11 and the translation TOAD11 of O by the vector OWAD11, where the measures of αAD11 and OWAD11 are two elements of the first set of initial data. The position of vertex WBC11 can be obtained in an analogous way, that is, by means of the rotation OAB11_CD11 of the z-axis about the x-axis by the angle αBC11 opposite to αAD11 and the translation TOBC11 of O. If we want to achieve a z-axis-symmetric reference tetrahedron, the absolute values of the above vectors and angles must be equal to each other, respectively.
The obtained vertices WAB11, WCD11, WAD11 and WBC11 determine four straight side edges: a11, b11, c11 and d11 of Γ11. In order to obtain four points SA11, SB11, SC11 and SD11 of a reference surface and four vertices A11, B11, C11 and D11 of eaves Bv11 of a shell roof structure, four vectors have to be measured along the side edges a11, b11, c11 and d11, Figure 19a,b, so that SA11= TSA11(WAD11), SB11 = TSB11(WBC11), SC11 = TSC11(WBC11), and = TSD11(WAD11), and A11 = TA11(SA11), B11 = TB11(SB11), C11 = TC11(SC11), and D11 = TD11(SD11). The measures of these vectors belong to the set of initial data.
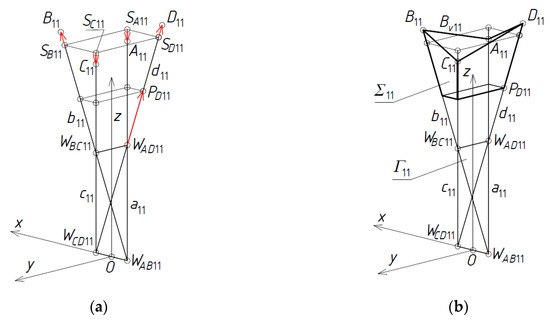
Figure 19.
Two subsequent steps of the creation of Σ11: (a) vertices A11, B11, C11 and D11; (b) eaves Bv11.
In order to determine a horizontal plane base of the complete free form Γ11, a point PD11 = TPD11(WCD11) has to be defined on d11. The measure of the vector WCD11PD11 must be one of the elements of the first set of initial data. Other points of this base can be calculated as the intersection of the horizontal base plane passing through the point PD11 and the four side edges of Γ11.
The second step of the algorithm relates to the determination of the reference tetrahedron Γ12, Figure 20a,b. At first, a second set of initial data must be adopted. The set is composed of the measures of the angles and vectors employed in the algorithm to define the positions of all characteristic points of Γ12.
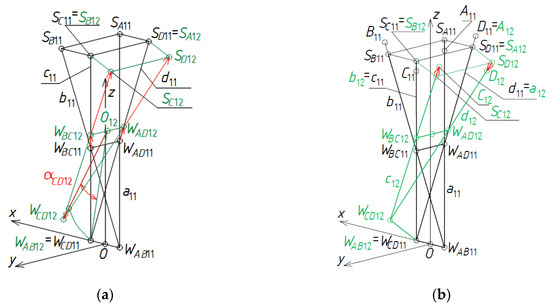
Figure 20.
Two subsequent steps of the determination of (a) the vertices WAB12, WBC12, WAD12, WCD12 of Γ12; (b) the vertices A12, B12, C12, D12 of Bv12.
Four vertices of Γ12 are determined as follows. Vertex WAB12 is identical with WCD11 of Γ11 introduced previously. Positions of the vertices WBC12 = TBC12(WBC11), WAD12 = TAD12(WAD11) are defined on two side edges b12 = c11, a12 = d11 so that the measures of the vectors WAD11WAD12 and WBC11WBC12 are elements of the second set of initial data. The position of vertex WCD12 is obtained as a result of a composition of the rotation OWAD12_WBC12 of O12WAB11 about the axis WAD12WBC12 by the angle αCD12 and the translation TCD12 of O12 by the vector O12WCD12, where O12 is a point of the (WAD12, WBC12) straight line. If the reference tetrahedron Γ12 is to be symmetrical about the z-axis, WBC12 and WAD12 have to be symmetric to each other towards the (x,z)-plane and O12 has to be the middle point of the edge WBC12WAD12. Four vertices WAB12, WCD12, WAD12, and WBC12 determine four straight side edges: a12, b12, c12, and d12 of Γ12.
Four auxiliary points belonging to a reference surface ωr and Γ are constructed so that SA12 = SD11, SB12 = SC11, SC12 = TSC12(WBC12), SD12 = TSD12(WAD12), where the measures of the vectors WBC12SC12 and WAD12SD12 are two elements of the second set of initial data. On the basis of two other elements of the second set, four points A12 = D11, B12 = C11, C12 = TC12(SC12), D12 = TD12(SD12), Figure 20b, constituting the vertices of a closed spatial quadrilateral line modeling shell roof eaves are constructed.
The third step of the method’s algorithm relates to determination of the reference tetrahedron Γ21, Figure 21a,b. The third set of initial data, composed of the measures of the respective angles and vectors employed to define all specific points of Γ21 is adopted.
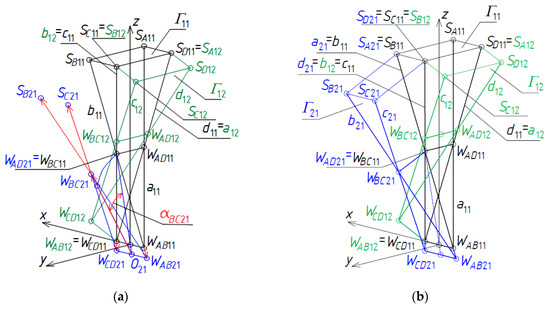
Figure 21.
Two subsequent steps of the method’s algorithm related to the construction of; (a) the vertices of Γ21; (b) the eaves side edges of Σ21.
Four vertices WAB21, WCD21, WAD21, and WBC21 of Γ21 are determined as follows, Figure 21a. The vertex WAD21 = WBC11. The positions of vertices WAB21 = TAB21(WAB11), WCD21 = TCD21(WCD11) are defined on two side edges a21 = b11, d21 = c11, Figure 21b, so that the measures of the vectors WAB11WAB21 and WCD11WCD21 are two elements of the third set of initial data. The position of WBC21 = TBC21OWCD21_WAB21(WBC11) is obtained as a result of a composition of the rotation OWCD21_WAB21 of O21WAD21 about the axis WCD21WAB21 by the angle αBC21 and the translation TBC21 of O21 by the vector O21WBC21, where O21 is a point of the straight line WCD21WAB21. If the reference tetrahedron Γ21 is to be symmetrical towards the (y,z)-plane, the positions of points WCD21 and WAB21 have to be symmetric to each other towards the (y,z)-plane and O21 has to be the middle point of the segment WCD21WAB21. Four vertices WAB21, WCD21, WAD21, and WBC21 determine four straight side edges: a21, b21, c21 and d21 of Γ21.
Four auxiliary points belonging to ωr are determined on the side edges of Γ21 so that SA21 = SB11, SD21 = SC11, SC21 = TSC21(WBC21) and SB21 = TSB21(WBC21), where the measures of the vectors WBC21SC21 and WBC21SB21 belong to the third set of initial data.
The fourth step of the method’s algorithm concerns a determination of the reference tetrahedron Γ22, Figure 22a,b. The fourth set composed of the measures of the vectors and angles employed in this step is adopted.
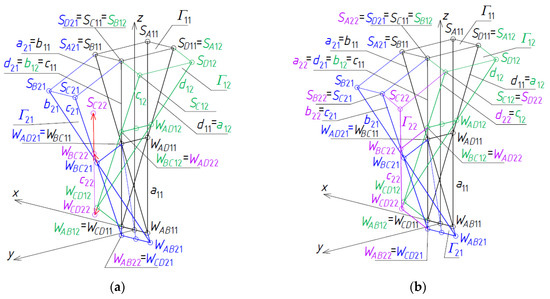
Figure 22.
Two subsequent steps of the method’s algorithm related to the construction of (a) all vertices of Γ22; (b) all side edges of Σ22.
Four vertices WAD22 = WBC12, WAB22 = WCD21, WBC22 = TBC22(WBC21), WCD22 = TCD22(WCD12) of Γ12, Figure 22a, are defined so that the measures of the vectors WBC21WBC22 and WCD21WCD22 are two elements of the fourth set of initial data. Four vertices WAB22, WCD22, WAD22, and WBC22 determine four straight side edges: a22, b22, c22, and d22 and two axes u22 and v22 of Γ22 Figure 23a.
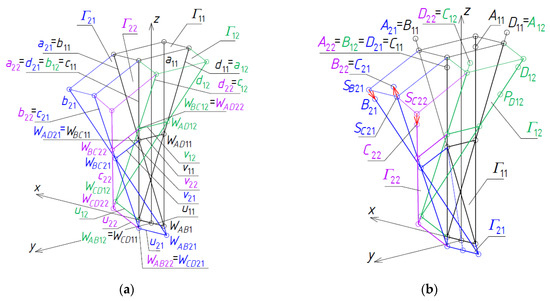
Figure 23.
Subsequent steps of the method’s algorithm concerning: (a) definition of the Γ’s axes; (b) creation of the vertices of Σ21, Σ22.
Four auxiliary points of Γ belonging to ωr are constructed so that SA22 = SC11, SD22 = SC12, SB22 = SC21, and SC22 = TC22(WBC22), Figure 23b, where the measure of the vector WBC22SC22 is a value belonging to the fourth set of the initial data. On the basis of these points of ωr, four points A22 = C11, B22 = C21, C22 = TC22(SC22), D22 = C12 constituting the vertices of a closed spatial quadrilateral line modeling complete shell roof eaves are constructed.
The result of adding up the four reference tetrahedrons Γij constructed above is a subnet Γ1 constituting about one-fourth of the designed reference network Γ. The other three parts of Γ can be built using z-axis symmetry and two (x,z)- and (y,z)-plane symmetries called 3D-mirrors, Figure 24a,b, in the way described Section 6 with the help of a certain example. All obtained points SAij, SBij, SCij, and SDij, Figure 24a, and their images obtained as a result of the aforementioned symmetries are the selected vertices of a certain net defining ωr, Figure 24b. In relation to this net, a roof structure Ω composed of nine sectors Ωij is positioned. Thus, the vertices of the eaves of each Ωij segment of the roof structure Ω are defined on the basis of ωr, Figure 25.
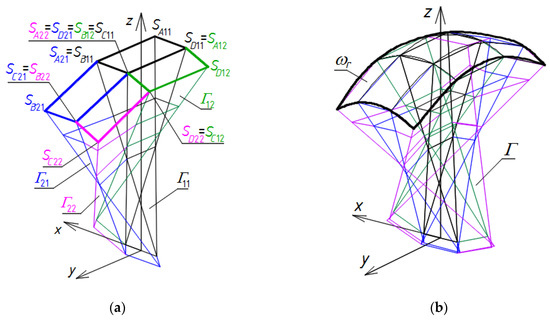
Figure 24.
Subsequent steps of the method’s algorithm related to the creation: (a) a quarter of Γ; (b) the entire network Γ and the reference surface ωr symmetrical about the z-axis.
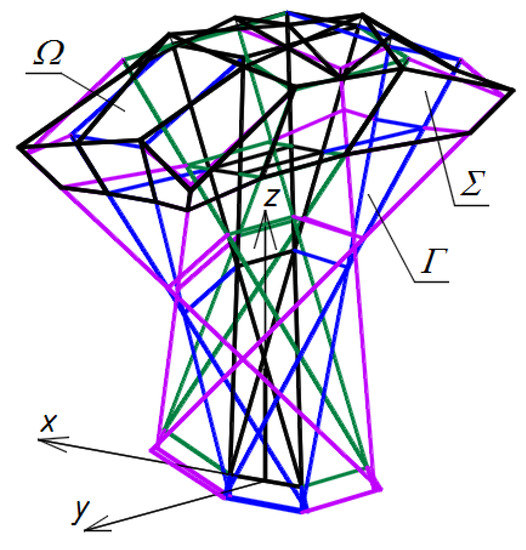
Figure 25.
The final step of creating Σ and Ω symmetrical about the z-axis.
In addition, it is worth paying attention to the following properties of the reference network Γ built so far. The vertices of each reference tetrahedron Γij designate side edges aij, bij, cij, and dij and planes of Γ. Each new reference tetrahedron Γi+1j or Γij+1 is created as a spatial mesh having four sought-after vertices defined in the selected side edges of the previously constructed tetrahedrons Γij to obtain subsequent pairs of the adjacent meshes having common planes. In the aforementioned planes of Γ, the locations of roof directrices are determined.
In the case of creating a reference tetrahedron contained in any of the two orthogonal directions related to the first z-axially symmetrical tetrahedron Γ11, one its vertex is laid outside the side edges of the already created subnet of Γ. This vertex determines a new plane of Γ passing through the already constructed axis of this tetrahedron. However, in the case of two directions diagonal in relation to the first Γ11, each new reference tetrahedron has to have two vertices identical to two from the four previously constructed vertices of Γ and two other new vertices have to be determined on two side edges of the previously created subnet of Γ.
This way of constructing the subsequent reference tetrahedrons located in these orthogonal and diagonal directions leads to the fact that each inner side edge of Γ is shared by four adjacent reference tetrahedrons and eight vertices of these four tetrahedrons belong to this side edge. In a general case, these vertices occupy four different positions, in pairs.
Therefore, it seems rational to carry out a process of a geometric parameterization of this type of reference networks, especially the mutual positions of their vertices and other characteristic points. An example of using such an algorithm for a parametric determination of reference polyhedral networks Γ and eaves nets Bv is given in Section 6, where certain division coefficients of the selected pairs of some adjacent vertices by other vertices of the reference network are employed. In addition, some points belonging to a reference surface and vertices of the eaves edge line of each individual roof shell segment are defined at each side edge of the network Γ. It is also advisable to use analogous division coefficients of pairs of the reference network’s vertices in determining these points of the reference surface and the eaves limiting the individual roof shell segments. An example of making such a parameterization is included in Section 6.
6. Parametric Shaping of an Example Reference Network and a Free Form Shell Roof
The algorithm assisted computationally leads to creation of intuitive engineering parametric and regular models of attractive and rational building free forms. To create such models stiff motions including translations and rotations of points and planes presented in the previous section are going to be replaced by slightly more complex actions related to the division coefficients and proportions of some elements of the reference Γ and eaves Bv networks. These coefficients and proportions allow us to define the positions of (1) the sought-after vertices of Γ with respect to the adopted or calculated at one of the previous steps pairs of other vertices of Γ, (2) the subsequent planes of Γ, (3) the points SAir, SBij, SCij, and SDij belonging to a reference surface wr, (4) the vertices Aij Bij, Cij and Dij of Bv relative to the already determined vertices of Γ and these points of wr.
A use of the method for determining a quarter Γ1 of a reference network Γ, Figure 26, and a quarter Bv1 of Bv consisting of closed spatial quadrangles Bvij, is presented below. It is based on some adopted proportions. All vertices of the other three quarters Γ2L, Γ3p, Γ4r of Γ, Figure 26, and Bv2L, Bv3p, Bv4r of Bv are determined using: (1) a z-axial symmetry, in the case of Γ2L, (2) a (x,z)-plane symmetry called 3D-mirror, where Γ3p is constructed, (3) a (y,z)―plane symmetry for Γ4r.
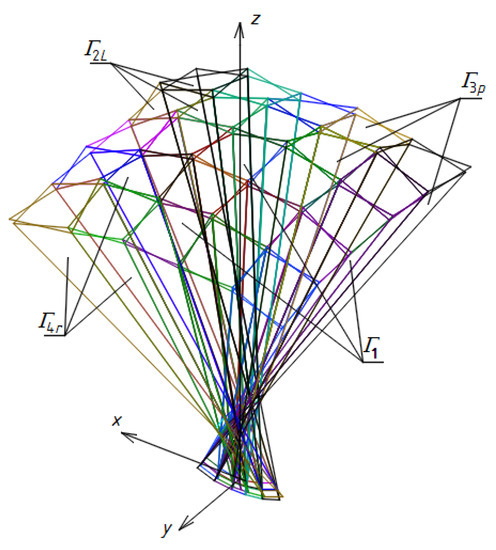
Figure 26.
A multi-segment reference network Γ composed of four symmetric subnets Γ1, Γ2L, Γ3p, and Γ4r.
Creating the z-axially symmetric network Γ is started with defining the first z-axially symmetric mesh Γ11, Figure 27. The subsequent meshes Γij are determined in the order presented in the previous section, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25. In order to build the mesh Γ11, the following quantities and proportions are adopted. The values of these variables are given in Table 1.
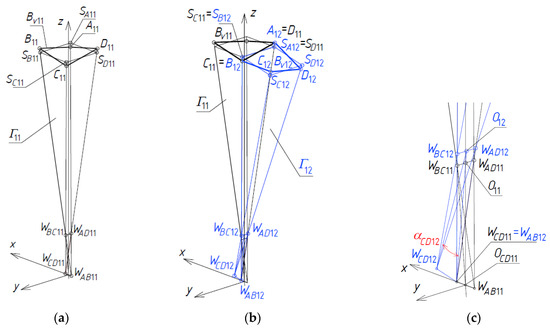
Figure 27.
Creation of two initial reference tetrahedrons: (a) Γ11; (b) Γ12; and (c) a detail of Γ12.

Table 1.
The initial data defining the shapes of the meshes Γ11 and Bv11 of Γ and Bv.
Two opposite planes (WAB11, WCD11, WBC11) and (WAB11, WCD11, WAD11), Figure 27a–c, are inclined to each other at an angle α11 = 2 αBC11 = 2 αAD11, Figure 19. The length of the edge WCD11WAB11 contained in the u1-axis was adopted in accordance with the values given in Table 1.
The WBC11WAD11’s length results from the adopted values of the angle α11 and the height OWBC11 of the triangle <WAB11, WCD11, WBC11> as well as the proportion.
dOW11= OWAD11/OWBC11
The positions of points SA11, SV11, SC11, and SD11 are defined with the same constant dS11 listed in Table 1 as follows
where is the vector starting with WAB11 and ending at WAD11, m() is the measure of , is the vector whose starting point is WAB11 and ending point is SA11, etc. Thus, the location of points SA11, SB11, SC11 and SD11 is defined on the basis of the adopted division coefficients of all pairs {WAB11, WAD11}, {WAB11, WBC11}, {WCD11, WBC11} and {WCD11, WAD11} of the vertices of the Γ11 mesh. The subsequent four points SA11, SB11, SC11 and SD11 usually form a flat rectangle determining the reference surface ωr in relation to which the shell segments of the designed multi-segment shell roof are arranged in the three-dimensional space.
dSB11 = dSA11 = dSC11 = dSD11 = dS11
The locations of the vertices A11, B11, C11 and D11 of Γ11, Figure 27a, are defined by means of the following proportions
where is the vector having the starting point at WAB11 and the end point at A11, etc. Points A11, B11, C11, and D11 determine a spatial quadrangle Bv11 constituting the eaves of a single, smooth, shell segment Ω11 modeling a single shell of a complex roof structure. It was adopted a constant dd11 to calculate the values of four division coefficients dA11, dB11, dC11, and dD11. This constant is used with positive or negative sign depending on whether the points A11, B11, C11, and D11 lie above or below ωr defined in the corresponding area by means of the quadrangle SA11SB11SC11SD11, Figure 27a. The ratios dA11, dB11, dC11, and dD11 are calculated as follows
dA11 = dSA11 + ddA11
dB11 = dSB11 + ddB11
dC11 = dSC11 + ddC11
dD11 = dSD11 + ddD11
ddB11 = −ddA11 = −ddC11 = ddD11 = dd11

Table 2.
The initial data defining the shapes of Γ12 and Bv12.
The angle αCD12 is defined by means of the angle α11 adopted in the previous step and the following formula.
dαCD12 = αCD12/α11
In order to determine WCD12, it was also adopted the following relationship
where O12 is the middle of the segment WAD12WBC12. The aforementioned values are listed in Table 2. Two new division coefficients dWBC12 and dWAD12 are adopted as follows
where m() is the measure of the vector having the starting point at WCD11 and the end point at WBC12, and m() is the measure of the vector , etc.
The positions of points SA12 and SB12 are similar to the positions of SD11 and SC11 determined previously for Γ11. The positions of SC12 and SD12 result from the following proportions
dSC12 = dSD12 = dS11
The assumed values of these proportions are given in Table 2. The positions of points A12 = D11, B12 = C11 are calculated previously for Γ11. The positions of points C12 and D12 can determined by means of the following proportions
where the considered values are listed in Table 2.
dC12 = dSC12 + ddC12
dD12 = dSD12 + ddD12
ddC12 = −ddD12 = dd12 = dd11
The sought-after vertices WAB13, WAD13, WCD13, and WBC13 of Γ13 constituting one mesh of Γ1, Figure 28a, the points SA13, SB13, SC13, and SD13 of ωr and the vertices A13, B13, C13, and D13 of the closed eaves quadrangle Bv13, Figure 28b, can be defined analogously as for Γ12 and Bv12 using the following formula
where O13 is the middle point of WAD13WBC13.
dαCD13 = αCD13/α11
dSC13 = dSD13 = dS11
dC13 = dSC13 + ddC13
dD13 = dSD13 + ddD13
ddD13 = −ddC13 = dd13 = dd11
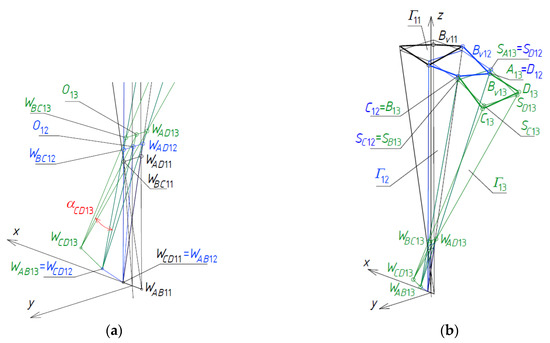
Figure 28.
The step related to creation of Γ13: (a) vertices; (b) a general shape.
The mutual position of the adjacent meshes Bv12 and Bv13 results from the relationships adopted for all meshes of Bv, which are as follows SA13 = SD12, SB13 = SC12, A13 = D12, B13 = C12, Figure 28a. The values of the adopted new proportions are given in Table 3.

Table 3.
The initial data defining the shapes of the meshes Γ13 and Bv13 of Γ and Bv.
Compared to the investigated way for creating Γ1j and Bv1j meshes (for j = 1 to 3) of the first orthogonal direction in Γ, the manner of determining the subsequent Γi1 and Bvi1 meshes (for i = 1 to 3) of the second orthogonal direction in Γ, Figure 29a, needs a slight modification.
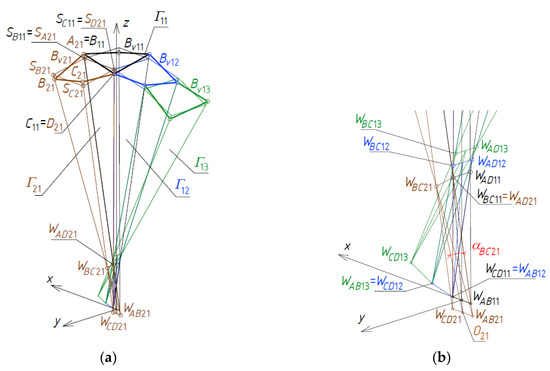
Figure 29.
The step related to creation of Γ21: (a) a general shape; (b) vertices.
The angle αBC21 is a function of the angle α11, defined with the help of the following formula
dαBC21 = α BC21/α11
The following relations were adopted
where O21 is the middle point of the edge WCD21WAB21, Figure 29b. The positions of points SA21 and SD21 are similar to the positions of points SB11 and SC11 obtained previously for Γ11. The positions of points SB21 and SC21, Figure 29a, result from adopting of the following proportions
whose values are given in Table 4. The positions of points A21 = B11 and D21 = C11. The positions of the points B21 and C21 result from adopting of the following proportions
dSB21 = dSC21 = dS11
dB21 = dSB21 + ddB21
dC21 = dSC21 + ddC21
ddC21 = −ddB21 = dd21 = dd11

Table 4.
The initial data defining the meshes Γ21 and Bv21.
All vertices WAB31, WAD31, WCD31 and WBC31 of Γ31, four points SA31, SB31, SC31, and SD31 of ωr and all vertices A31, B31, C31, and D31 of Bv31 are determined like for Γ21, Figure 30a,b. For this purpose, the following proportions are defined
where O31 is the middle point of WCD31WAB31. The locations of points SA31 = SB21, SD31 = SC21, A31 = B21, and D31 = C21. All values of the proportions defined above are shown in Table 5.
dαBC31 = α BC31/α BC21
dSB31 = dSC31 = dS11
dB31 = dSB31 + ddB31
dC31 = dSC31 + ddC31
ddB31 = −ddC31 = dd31 = dd21
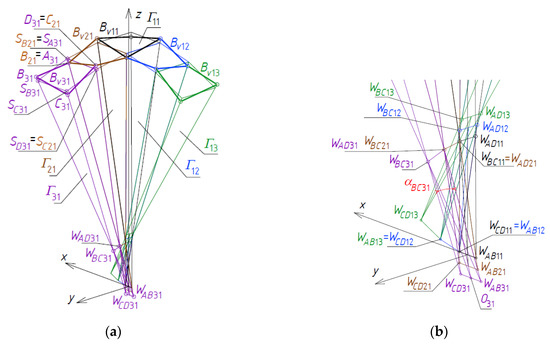
Figure 30.
The step related to the creation of the reference tetrahedron Γ31: (a) a general shape; (b) vertices.

Table 5.
The initial data defining the meshes Γ31 and Bv31.
To create the tetrahedron Γ22 and the quadrangle Bv22, Figure 31a, the values listed in Table 6 are adopted. To determine the position of WCD22 on the straight line c22, Figure 31a,c, a coefficient dWCD22 defining the division of the edge WBC12WCD12 by the point WCD22 is defined as follows
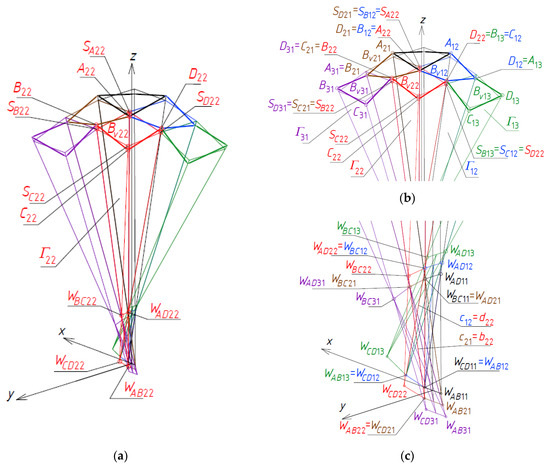
Figure 31.
Determination of Γ22: (a) a general shape; (b) vertices of Bv22; (c) vertices of Γ22.

Table 6.
The initial data defining the shapes of the meshes Γ22 and Bv22.
To determine the location of WBC22 on b22 = c21, a coefficient dWBC22 defining the division of the edge WCD21WBC21 by the point WBC22 is assumed, Figure 31c, so that
In addition, WAB22 = WCD21, WAD22 = WBC12. Similarly, the values of two coefficients dSC22 and ddC22 are adopted. The first value defines a division ratio of the edge WCD22WBC22 by SC22, Figure 31c,
The second proportion together with the first one enables one to define a division ratio of the edge WCD22WBC22 by C22
where
dC22 = dSC22 + ddSC22
Analogous proportions as for Γ22 positioned diagonally towards Γ11 are defined for: (1) Γ23 and Γ32, located diagonally in relation to Γ12 and Γ22. (2) Γ33 located diagonally towards Γ22. Values of these proportions are listed in Table 7. A sum of all Γij (for i = 1–3) achieved so far is a subnet Γ1 constituting about one quarter of Γ. It is contained in the dihedral angle limited by the planes (x,z) and (y,z) containing the positive y-axis and negative x-axis, Figure 32.

Table 7.
The initial data defining the meshes Γ23, Γ32, Γ33 and Bv23, Bv32, Bv33.
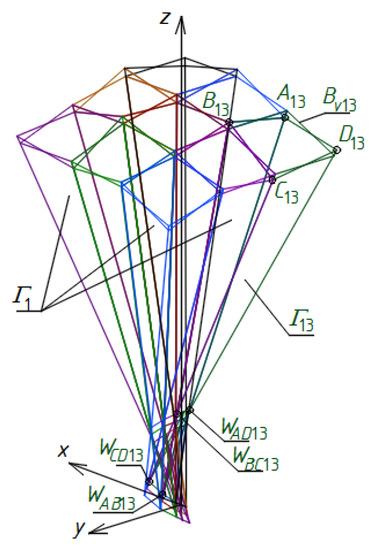
Figure 32.
A quarter Γ1 of the entire reference network Γ.
The reference tetrahedrons Γ1j and Γi1 for (for i, j = 1 to 3) of the subnet Γ1 were arranged in two orthogonal directions along the principal planes (x,z) and (y,z) of [x,y,z]. However, other tetrahedrons Γij (for i, j = 2 to 3) are arranged in diagonal directions towards the Γ11 mesh. To construct these tetrahedrons, a relatively small number of the respective proportions is employed.
The calculated coordinates of all vertices of the subnets Γ1 and Bv1 are given in Table A1, Table A2 and Table A3 posted in Appendix A. Table A1 applies to all vertices WABij, WCDij, WADij, and WBCij of Γ1 (for i, j = 1 to 3). Table A2 relates to the vertices SAij, SBij, SCij, and SDij of ωr. Table A3 concerns all vertices Aij, Bij, Cij, and Dij of Bv1.
In order to create the second pair of subnets Γ2L and Bv2L of Γ and Bv, the z-axis-symmetry of all characteristic points WABij, WCDij, WADij, WBCij, Aij, Bij, Cij, Dij, SAij, SBij, SCij, and SDij of the previously constructed subnets Γ1 and Bv1 is used. As a result of this transformation, the vertices WABijL, WCDijL, WADijL and WBCijL of Γ2L, the vertices AijL, BijL, CijL, and DijL of BvijL as well as the points SAijL, SBijL, SCijL, and SDijL of ωr are determined so that SAijL, SBijL, SCijL, SDijL, AijL, BijL, CijL, and DijL belong to the dihedral angle located between the (x,z)-plane and (y,z)-plane and including the positive x-half-axis and the negative y-half-axis, Figure 33. Examples of a single reference tetrahedron Γ13L of the subnet Γ2L and a mesh Bv13L of the subnet Bv2L are shown in Figure 33.
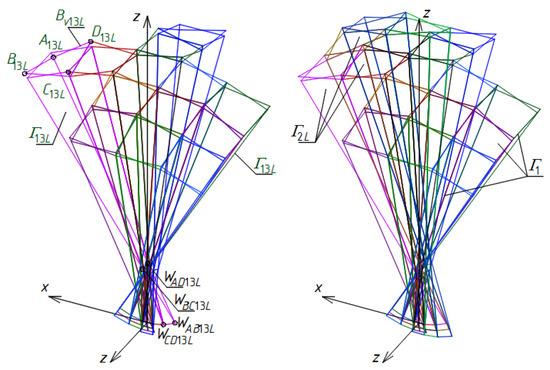
Figure 33.
Two steps of the determination of the second quarter Γ2L of the designed z-axis-symmetric reference network Γ.
For the subnets Γ2L and Bv2L, there are many proportions between the lengths of their side edges and axes and the measures of their angles, identical to those obtained for Γ1 and Bv1. Some selected relations resulting from the z-axis-symmetry of the vertices of Γ2L and Bv2L and the corresponding vertices of Γ1 and Bv1 are listed in Table A4, Table A5 and Table A6 posted in Appendix A. Table A4 applies to the vertices WABijL, WCDijL, WADijL, and WBCijL of Γ2L. Table A5 relates to the vertices SAijL, SBijL, SCijL, and SDijL of ωr. Table A6 consists of the coordinates of the vertices AijL, BijL, CijL, and DijL belonging to Bv2L.
To create the third pair of the subnets Γ3p and Bv3p of Γ and Bv, a (x,z)-plane-symmetry, of the previously constructed nets Γ1 and Bv1 is used. Based on this symmetry, the following are transformed: (1) all vertices WABij, WCDij, WADij, and WBCij of Γ1, (2) all vertices Aij, Bij, Cij, and Dij of Bv1, (3) the points SAij, SBij, SCij, and SDij of ωr. As a result of this transformation, the vertices WABijp, WCDijp, WADijp, and WBCijp of Γ3p, the vertices Aijp, Bijp, Cijp, and Dijp of Bvijp and the points SAijp, SBijp, SCijp, and SDijp of ωr are determined, Figure 34. The obtained points SAijp, SBijp, SCijp, SDijp, Aijp, Bijp, Cijp, and Dijp belong to the subspace contained between the planes (x,z) and (y,z), so that both the negative x-half-axis and the negative y-half-axis are included in this subspace. Examples of the reference tetrahedron Γ23p of Γ3p and the mesh Bv23p of Bv3p are shown in Figure 34.

Figure 34.
Three quarters Γ1, Γ2L and Γ3p of the reference network Γ.
For the subnets Γ3p and Bv3p, many specific proportions between their side edge and axis lengths and angle measures similar to those obtained for Γ1 and Bv1 can be found. Some relations resulting from the (x,z)-plane-symmetry of the vertices of Γ3p and Bv3p and the corresponding vertices of Γ1 and Bv1 created previously are listed in Table A7, Table A8 and Table A9 posted in Appendix A. Table A7 relates to the vertices WABijp, WCDijp, WADijp, and WBCijp of Γ3p. Table A8 concerns the points SAijp, SBijp, SCijp, and SDijp of ωr. Table A9 applies to the vertices Aijp, Bijp, Cijp, and Dijp of Bv3p.
To determine the fourth subset Γ4r of Γ and subnet Bv4r of Bv, a (y,z)-plane-symmetry of Γ1 and Bv1 is used. The positions of the vertices WABijr, WCDijr, WADijr, and WBCijr of Γ4r, the vertices Aijr, Bijr, Cijr, and Dijr of Bvijr and the points SAij, SBij, SCij, and SDij of ωr are determined as a result of the transformations of (1) the vertices WABij, WCDij, WADij, and WBCij of Γ1, (2) the vertices Aij, Bij, Cij, and Dij of Bv1, (3) the points SAij, SBij, SCij, and SDij of ωr, so that SAijr, SBijr, SCijr, SDijr, Aijr, Bijr, Cijr, and Dijr belong to the dihedral angle limited by the (x,z)-half-plane and (y,z)-half-plane containing the positive x-half-axis and the positive y-half-axis, Figure 26.
Some selected relations between the vertices of Γ4r and Bv4r and the corresponding vertices of Γ1 and Bv1, resulting from the (y,z)-plane-symmetry of Γ and Bv are given in Table A10, Table A11 and Table A12 included in Appendix A. Table A10 relates to the WABijr, WCDijr, WADijr, and WBCijr vertices of Γ4r. Table A11 concerns the points SAijr, SBijr, SCijr, and SDijr of ωr. Table A12 applies to the vertices Aijr, Bijr, Cijr, and Dijr of Bv4r. Finally, the sought-after nets Γ and Bv are created as the sums of the respective symmetric subnets Γ1, Bv1, Γ2L, Bv2L, Γ3p, Bv3p, Γ4r, and Bv4r have already been constructed. These nets have to be supplemented with roof shell sectors and a plain base to obtain complete building free form model.
7. Discussion
The proposed method for creating parametric spatial networks enables implementation of the novel algorithms in computer programs to conveniently and intuitively search for unconventional shapes and position of elevation walls and roof shells. The benefits of the parameterization include (1) the possibility of defining and reducing a number of the independent variables entered into the method’s algorithm, (2) specifying the special relations between dependent and independent variables to obtain the intuitiveness of the free form shaping, the regularity and respective curvature of the resultant complex shell roofs, (3) interesting outside roof and elevation patterns in an arrangement of many complete shell roof sectors and plane walls facets. The shape and mutual position parameterization of all reference tetrahedrons constituting the meshes of the investigated reference networks allowed developing various types of the innovative polyhedral reference networks. The activity aims at making a parametric description of these networks by means of the smallest possible number of independent variables so that such networks become regular and consistent, as well as determine diversified geometrical properties of the employed reference surfaces, including the negative, positive or zero Gaussian curvature, Figure 35 and Figure 36.
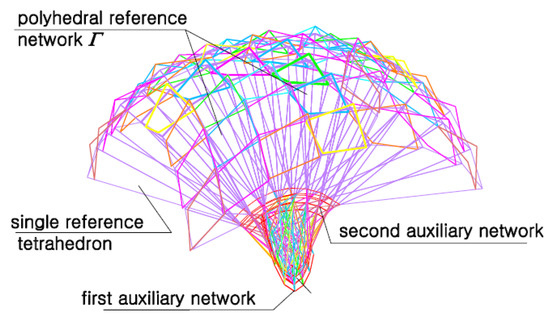
Figure 35.
A sum of many spatial quadrangular meshes arranged compatible with a regular surface of the positive Gaussian curvature by means of a polyhedral reference network determined on the basis of the pair of auxiliary orthogonal networks composed of plane meshes.
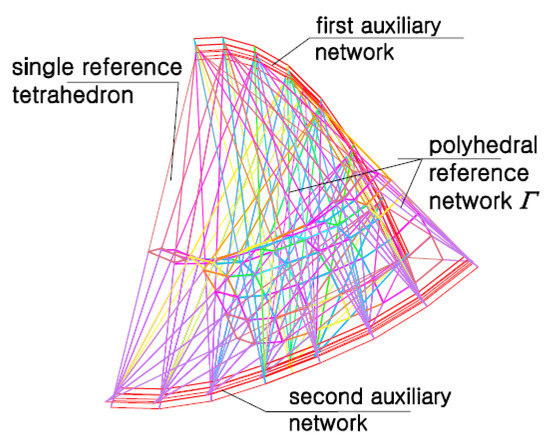
Figure 36.
A sum of many spatial quadrangular meshes arranged compatible with a regular surface of the negative Gaussian curvature by means of a polyhedral reference network determined on the basis of the pair of auxiliary orthogonal networks composed of plane meshes.
The points SAijk, SBijk, SCijk, and SDijk (for i, j = 1–3, k = ϕ, L, p, r, where ϕ is the empty set) used in the example presented in the previous section designate a regular double-curved surface ωr characterized by the positive Gaussian curvature, Figure 26 and Figure 35, because the values of the proportions dSAijk, dSBijk, dSCijk, and dSDijk are bigger than 1.0. Double-curved surfaces having the negative Gaussian curvature can be obtained when the coefficients range from 0.0 to 1.0, Figure 36. The investigated method allows one to enter certain points to determine such networks Γ and Bv for which the resultant reference surface is a single-curved surface having the zero Gaussian curvature. For this case, selected groups of the axes of some reference tetrahedrons Γij have to be contained in the same straight lines. This problem is going to be presented in further publications.
In the presented example, it was shown how to create a regular, spatial, polyhedral reference network Γ on the basis of which eaves quadrilateral network Bv determining an unconventional shell roof structure can be built. All Γijk (for i, j = 1–3, k = ϕ, L, p, r) of Γ are tetrahedrons whose vertices, side edges, planes and axes take specific mutual positions influencing diversified types of the created reference surfaces ωr and eaves roof networks Bv. Meshes Γijk affect the rationality of the designed building free form structures due to the specific mutual positions of the side edges aijk, bijk, cijk and dijk of Γ. Bvijk (for i, j = 1–3, k = ϕ, L, p, r) of Bv are closed spatial quadrangles whose two opposite sides can be taken as roof directrices. The parametric shapes and mutual positions of the directrices may positively affect a process of designing the attractive building structures by automatically changing the proportions dAij, dBij, dCij, and dDij defining the positions of the Bvijk‘s vertices on aijk, bijk, cijk and dijk in accordance with ωr.
The investigated method relies on special setting all subsequent reference tetrahedrons together, so that each pair of two adjacent tetrahedrons has one plane in common. Many reference tetrahedrons can be set together to obtain an edge roof shell structures having regular edge patterns on its surfaces and attractive patterns of folded plane areas on its elevations. The analyzed specific properties of the innovative spatial reference networks should lead to a creative intuitive computational shaping of attractive, rational complex-building free forms of medium and large span and novel structural systems intended for these forms.
The network Bv introduced in Section 6, Figure 26, and the network shown in Figure 36 are characterized by the fact that each pair of their adjacent quadrilateral meshes Bvijk and Bvmns arranged orthogonally in relation to the mesh Bv11 (for i = 1 or j = 1 and m = 1 or n = 1 and k, s = ϕ, L, p, r) has one common edge, including their directrix, and two common vertices. In addition, each tetrad of adjacent quadrilaterals Bvijk has one common vertex. In contrast, the Bv network shown in Figure 35 was created so that each of the two adjacent quadrangles Bvijk and Bvmns arranged in any of the orthogonal directions compatible with the principal planes (x,z) and (y,z) do not have a common edge, but their corresponding edges are inclined to each other and intersect in one point. In this case, each two adjacent meshes-quadrangles arranged diagonally in Bv have only one common vertex.
The shell roof structure Ω presented in Section 6 is continuous and has many edges between smooth sectors Ωijk limited by eaves quadrangles Bvijk (for i = 1 or j = 1 and m = 1 or n = 1 and k = ϕ, L, p, r). The edges model a set of ribs between the complete transformed shells of a roof structure. In the parametric description of Γ implemented to computer applications, it is possible to easily change the positions of all vertices Aijk, Bijk, Cijk, Dijk of the meshes Bvijk along the side edges of Γ, relative to reference surface ωr by modifying the division coefficients of some specific pairs of—the vertices of Γ. The change may cause the resultant structure Ω to become discontinuous, Figure 35. The structure Ω can contain many empty flat areas dividing the roof shell sectors Ωijk. These openings should be built by windows illuminating the interior of the designed building with the sunlight. This problem is also going to be analyzed in the further publications.
The author has developed some activities leading to minimize the number of independent parameters describing the geometrical properties of the presented reference networks. For this purpose, symmetrical forms of buildings must be sought. The possibility of adopting one parameter constituting only one independent variable used in defining all proportions between the selected roof and elevation elements is also developed by the author to find similar and different types of various free forms.
8. Conclusions
There are significant limitations in creating building free forms roofed with transformed corrugated shell sheeting concerning the complicated orthotropic geometrical and mechanical properties of thin-walled folded steel sheets. To overcome these limitations, the novel method based on the polyhedral reference networks and quadrilateral eaves nets helpful in shaping individual free forms and their specific multi-plane and multi-shell structures were carried out. As a result, the intuitive method supported by novel computer applications uses the presented relatively great possibilities of searching for diverse and innovative building structures based on the proposed shape transformations.
The main goals of combining the complete transformed shells in any roof structure include increasing the span of the roof and entire building, integrating the roof and façade forms, increasing the visual attractiveness of the entire building free form, and making it sensitive to the natural or built environments. The most common concept used in a shaping of such transformed folded shell structures is a combination of central sections of right hyperbolic paraboloids, their halves or quadrants set in various configurations, and joined along their common edges. The author developed many coherent rules for creating such complex structures covered with plane-walled folded elevations and multi-segment transformed shell roof structures. The developed algorithms allowed a radical increase in the variety of the shapes employed in design.
The presented method uses the novel vector and parametric descriptions of shaping complex building free forms characterized by the shape integration of their complex multi-shell roofs and multi-plane façades. The method’s algorithm requires entering specific sets of parameters defining the general shapes of the investigated complex free forms and their individual roof and elevation elements. The parameters are either the measures of the vectors and angles of stiff motions such as translations and rotations, or the division coefficients of certain characteristic points, of the proposed novel networks by their other characteristic points.
Many proportions between geometric properties of all roof and elevations elements can be defined using functions based on the measures of the investigated types of stiff motions to achieve diversified attractive patterns on multi-plane folded elevations and multi-shell roof structures. More comprehensive studies seem to be targeted at an assignment of (a) the possible types of the independent and dependent variables, (b) the specific proportions between the dependent parameters to obtain such specific groups of the architectural free forms that are characterized by similar or different properties, (c) the search for some ranges of the values of the selected independent parameters defining attractive building free forms.
Achieving optimal, rational and attractive solutions appearing as the result of the process of shaping building free forms roofed with transformed corrugated shells and their complete elements require using regularity and symmetry of (a) single reference tetrahedrons and entire reference polyhedral networks, (b) plane walls and entire elevations of the designed complex building free forms, (c) some strips of the transformed folded sheets and entire complete transformed roofs shells and their structures, (d) structural systems intended for these forms. The research initiated and developed by the author on parametric process of architectural, geometrical, and static strength shaping of the regular free form structures roofed with transformed corrugated shell structures, and their structural systems is very extensive and requires a certain number of complete steps. One of these steps associated with geometrical and computational shaping such forms was elaborated by the author and the obtained results are presented in this paper.
Funding
This research was funded by Rzeszow University of Technology.
Acknowledgments
I am very grateful to A. Prokopska the head of my Department and to M. Gosztyła the Dean of my Faculty for the support.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A

Table A1.
The coordinates of the vertices WABij, WCDij, WADij, WBCij (for i, j = 1, 2, 3) of the polyhedral reference network Γ1 shown in Figure 27.
Table A1.
The coordinates of the vertices WABij, WCDij, WADij, WBCij (for i, j = 1, 2, 3) of the polyhedral reference network Γ1 shown in Figure 27.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| WAB11 | 4500.0 | −4793.6 | 54,790.7 |
| WCD11 | 4500.0 | 4880.7 | 55,786.9 |
| WAD11 | −4500.0 | 4793.6 | 54,790.7 |
| WBC11 | −4500.0 | −4880.7 | 55,786.9 |
| WAB12 | xWCD11 | yWCD11 | zWCD11 |
| WCD12 | 3254.3 | 0.0 | 468.2 |
| WAD12 | −100.0 | −958.7 | 10,958.1 |
| WBC12 | −100.0 | 958.7 | 10,958.1 |
| WAB13 | xWCD12 | yWCD12 | zWCD12 |
| WCD13 | 5572.7 | 0.0 | zSC12 |
| WAD13 | −435.4 | −1054.6 | 12,007.1 |
| WBC13 | −435.4 | 1054.6 | 12,007.1 |
| WAB21 | −1100.0 | −87.2 | −996.2 |
| WCD21 | 1100.0 | −87.2 | −996.2 |
| WAD21 | xWBC11 | yWBC11 | zWBC11 |
| WBC21 | 0.0 | 2574.0 | 9677.1 |
| WAB31 | −1210.0 | −353.3 | −2063.5 |
| WCD31 | 1210.0 | 353.3 | −2063.5 |
| WAD31 | −xWBC21 | yWBC21 | zWBC21 |
| WBC31 | 0.0 | 4374.6 | 9074.6 |
| WAB22 | xWCD21 | yWCD21 | zWCD21 |
| WCD22 | 3589.7 | 0.0 | −580.8 |
| WAD22 | xWBC12 | yWBC12 | zWBC12 |
| WBC22 | −110.0 | 2840.1 | 10,744.4 |
| WAB23 | xWCD22 | yWCD22 | zWCD22 |
| WCD23 | 6173.6 | −105.5 | 435.5 |
| WAD23 | xWBC13 | yWBC13 | zWBC13 |
| WBC23 | −480.0 | 3133.7 | 11,876.9 |
| WAB32 | xWCD31 | yWCD31 | zWCD31 |
| WCD32 | 3959.7 | −389.5 | −1713.3 |
| WAD32 | xWBC22 | yWBC22 | zWBC22 |
| WBC32 | −121.0 | 4847.4 | 10,188.4 |
| WAB33 | xWCD32 | yWCD32 | zWCD32 |
| WCD33 | 6838.9 | −429.4 | −708.6 |
| WAD33 | xWBC23 | yWBC23 | zWBC23 |
| WBC33 | −529.1 | 5371.0 | 11,378.6 |

Table A2.
The coordinates of the points SAij, SBij, SCij, SDij for (i,j = 1, 2, 3) of the reference surface ωr.
Table A2.
The coordinates of the points SAij, SBij, SCij, SDij for (i,j = 1, 2, 3) of the reference surface ωr.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| SA11 | 4500.0 | −4793.6 | 54,790.7 |
| SB11 | 4500.0 | 4880.7 | 55,786.9 |
| SC11 | −4500.0 | 4793.6 | 54,790.7 |
| SD11 | −4500.0 | −4880.7 | 55,786.9 |
| SA12 | xSD11 | ySD11 | zSD11 |
| SB12 | xSC11 | ySC11 | zSC11 |
| SC12 | −13,517.1 | 4793.6 | 52,918.0 |
| SD12 | −13,517.1 | −4793.6 | 52,918.0 |
| SA13 | xSD12 | ySD12 | zSD12 |
| SB13 | xSC12 | ySC12 | zSC12 |
| SC13 | −21,737.1 | 4793.6 | 49,304.2 |
| SD13 | −21,737.1 | −4793.6 | 49,304.2 |
| SA21 | xSB11 | ySB11 | zSB11 |
| SB21 | 4500.0 | 13,460.5 | 53,340.4 |
| SC21 | −4500.0 | 13,460.5 | 53,340.4 |
| SD21 | xSC11 | ySC11 | zSC11 |
| SA31 | xSB21 | ySB21 | zSB21 |
| SB31 | 4500.0 | 21,957.5 | 50,497.3 |
| SC31 | −4500.0 | 21,957.5 | 50,497.3 |
| SD31 | xSC21 | ySC21 | zSC21 |
| SA22 | xSC11 | ySC11 | zSC11 |
| SB22 | xSC21 | ySC21 | zSC21 |
| SC22 | −13,675.6 | 13,605.3 | 52,270.2 |
| SD22 | xSC12 | ySC12 | zSC12 |
| SA23 | xSC12 | ySC12 | zSC12 |
| SB23 | xSC22 | ySC22 | zSC22 |
| SC23 | −22,104.0 | 13,660.9 | 49,061.5 |
| SD23 | xSC13 | ySC13 | zSC13 |
| SA32 | xSC21 | ySC21 | zSC21 |
| SB32 | xSC31 | ySC31 | zSC31 |
| SC32 | −13,692.4 | 22,263.8 | 49,770.7 |
| SD32 | xSC22 | ySC22 | zSC22 |
| SA33 | xSC22 | ySC22 | zSC22 |
| SB33 | xSC32 | ySC32 | zSC32 |
| SC33 | −22,428.4 | 22,611.2 | 47,304.5 |
| SD33 | xSC23 | ySC23 | zSC23 |

Table A3.
The coordinates of the vertices Aij, Bij, Cij, Dij (for i, j = 1, 2, 3) of the eaves edge net Bv1.
Table A3.
The coordinates of the vertices Aij, Bij, Cij, Dij (for i, j = 1, 2, 3) of the eaves edge net Bv1.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| A11 | 4,400.0 | −4,706.4 | 53,794.5 |
| B11 | 4,600.0 | 4,880.7 | 55,786.9 |
| C11 | −4,400.0 | 4,706.4 | 53,794.5 |
| D11 | −4,600.0 | −4,880.7 | 55,786.9 |
| A12 | −4,390.0 | −4,697.7 | 53,694.9 |
| B12 | −4,610.0 | 4,889.4 | 55,886.5 |
| C12 | −13,517.1 | 4,697.9 | 51,869.0 |
| D12 | −13,852.6 | −4,889.4 | 53,967.0 |
| A13 | −13,148.2 | −4,688.1 | 51,764.1 |
| B13 | −13,886.1 | 4,899.0 | 54,071.9 |
| C13 | −21,136.3 | 4,688.1 | 48,252.2 |
| D13 | −22,338.0 | −4,899.0 | 50,356.2 |
| A21 | 4,390.0 | 4,697.7 | 53,694.9 |
| B21 | 4,610.0 | 13,726.6 | 54,407.7 |
| C21 | −4,390.0 | 13,194.4 | 52,273.0 |
| D21 | xB12 | yB12 | zB12 |
| A31 | 4,379.0 | 13,167.7 | 52,166.3 |
| B31 | 4,621.0 | 22,430.3 | 51611.1 |
| C31 | −4,379.0 | 21,484.7 | 49,383.5 |
| D31 | −4,621.0 | 13,753.2 | 54,514.4 |
| A22 | xC11 | yC11 | zC11 |
| B22 | xD31 | yD31 | zD31 |
| C22 | −13,367.3 | 13,360.7 | 51,326.4 |
| D22 | xB13 | yB13 | zB13 |
| A23 | xC12 | yC12 | zC12 |
| B23 | −13,983.9 | 13,850.0 | 53,213.9 |
| C23 | −21,549.5 | 13,391.0 | 48,108.1 |
| D23 | −22,338.0 | 4,899.0 | 50,356.2 |
| A32 | xC21 | yC21 | zC21 |
| B32 | −4,621.0 | 22,430.3 | 51,611.1 |
| C32 | −13,352.3 | 21,827.4 | 48,778.9 |
| D32 | xB23 | yB23 | zB23 |
| A33 | xC22 | yC22 | zC22 |
| B33 | −14,032.4 | 22,700.2 | 50,762.6 |
| C33 | −21,916.7 | 22,208.4 | 46,465.1 |
| D33 | −22,658.4 | 13,930.9 | 50,015.0 |

Table A4.
The coordinates of the vertices WABijL, WCDijL, WADijL, WBCijL (for i, j = 1, 2, 3) of the polyhedral reference network Γ2L shown in Figure 28.
Table A4.
The coordinates of the vertices WABijL, WCDijL, WADijL, WBCijL (for i, j = 1, 2, 3) of the polyhedral reference network Γ2L shown in Figure 28.
| Vertex | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| WAB12L | −xWCD12 | −yWCD12 | zWCD12 |
| WCD12L | xWAB11 | yWAB11 | zWAB11 |
| WAD12L | −xWBC12 | −yWBC12 | zWBC12 |
| WBC12L | −xWAD12 | −yWAD12 | zWAD12 |
| WAB13L | −xWCD13 | −yWCD13 | zWCD13 |
| WCD13L | xWAB12 L | yWAB12 L | zWAB12 L |
| WAD13L | −xWBC13 | −yWBC13 | zWBC13 |
| WBC13L | −xWAD13 | −yWAD13 | zWAD13 |
| WAB21L | −xWCD21 | −yWCD21 | zWCD21 |
| WCD21L | −xWAB21 | −yWAB21 | zWAB21 |
| WAD21L | −xWBC21 | −yWBC21 | zWBC21 |
| WBC21L | −xWAD21 | −yWAD21 | zWAD21 |
| WAB31L | −xWCD31 | −yWCD31 | zWCD31 |
| WCD31L | −xWAB31 | −yWAB31 | zWAB31 |
| WAD31L | −xWBC31 | −yWBC31 | zWBC31 |
| WBC31L | −xWAD31 | −yWAD31 | zWAD31 |
| WAB22L | −xWCD22 | −yWCD22 | zWCD22 |
| WCD22L | −xWAB22 | −yWAB22 | zWAB22 |
| WAD22L | −xWBC22 | −yWBC22 | zWBC22 |
| WBC22L | −xWAD22 | −yWAD22 | zWAD22 |
| WAB23L | −xWCD23 | −yWCD23 | zWCD23 |
| WCD23L | −xWAB23 | −yWAB23 | zWAB23 |
| WAD23L | −xWBC23 | −yWBC23 | zWBC23 |
| WBC23L | −xWAD23 | −yWAD23 | zWAD23 |
| WAB32L | −xWCD32 | −yWCD32 | zWCD32 |
| WCD32L | −xWAB32 | −yWAB32 | zWAB32 |
| WAD32L | −xWBC32 | −yWBC32 | zWBC32 |
| WBC32L | −xWAD32 | −yWAD32 | zWAD32 |
| WAB33L | −xWCD33 | −yWCD33 | zWCD33 |
| WCD33L | −xWAB3 | −yWAB3 | zWAB3 |
| WAD33L | −xWBC33 | −yWBC33 | zWBC33 |
| WBC33L | −xWAD33 | −yWAD33 | zWAD33 |

Table A5.
The coordinates of the points SAijL, SBijL, SCijL, SDijL (for i, j = 1, 2, 3) of the reference surface ωr.
Table A5.
The coordinates of the points SAijL, SBijL, SCijL, SDijL (for i, j = 1, 2, 3) of the reference surface ωr.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| SA12L | −xSC12 | −ySC12 | zSC12 |
| SB12L | −xSD12 | −ySD12 | zSD12 |
| SC12L | −xSA12 | −ySA12 | zSA12 |
| SD12L | −xSB12 | −ySB12 | zSB12 |
| SA13L | −xSC12 | −ySC13 | zSC13 |
| SB13L | −xSD13 | −ySD13 | zSD13 |
| SC13L | −xSA13 | −ySA13 | zSA13 |
| SD13L | −xSB13 | −ySB13 | zSB13 |
| SA21L | −xSC21 | −ySC21 | zSC21 |
| SB21L | −xSD21 | −ySD21 | zSD21 |
| SC21L | −xSA21 | −ySA21 | zSA21 |
| SD21L | −xSB21 | −ySB21 | zSB21 |
| SA31L | −xSC31 | −ySC31 | zSC31 |
| SB31L | −xSD31 | −ySD31 | zSD31 |
| SC31L | −xSA31 | −ySA31 | zSA31 |
| SD31L | −xSB31 | −ySB31 | zSB31 |
| SA22L | −xSC22 | −ySC22 | zSC22 |
| SB22L | −xSD22 | −ySD22 | zSD22 |
| SC22L | −xSA22 | −ySA22 | zSA22 |
| SD22L | −xSB22 | −ySB22 | zSB22 |
| SA23L | −xSC23 | −ySC23 | zSC23 |
| SB23L | −xSD23 | −ySD23 | zSD23 |
| SC23L | −xSA23 | −ySA23 | zSA23 |
| SD23L | −xSB23 | −ySB23 | zSB23 |
| SA32L | −xSC32 | −ySC32 | zSC32 |
| SB32L | −xSD32 | −ySD32 | zSD32 |
| SC32L | −xSA32 | −ySA32 | zSA32 |
| SD32L | −xSB32 | −ySB32 | zSB32 |
| SA33L | −xSC33 | −ySC33 | zSC33 |
| SB33L | −xSD33 | −ySD33 | zSD33 |
| SC33L | −xSA33 | −ySA33 | zSA33 |
| SD33L | −xSB33 | −ySB33 | zSB33 |

Table A6.
The coordinates of the vertices AijL, BijL, CijL, DijL (for i, j = 1, 2, 3) of the eaves edge net Bv2L.
Table A6.
The coordinates of the vertices AijL, BijL, CijL, DijL (for i, j = 1, 2, 3) of the eaves edge net Bv2L.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| A12L | −xC12 | −yC12 | zC12 |
| B12L | −xD12 | −yD12 | zD12 |
| C12L | −xA12 | −yA12 | zA12 |
| D12L | −xB12 | −yB12 | zB12 |
| A13L | −xC13 | −yC13 | zC13 |
| B13L | −xD13 | −yD13 | zD13 |
| C13L | −xA13 | −yA13 | zA13 |
| D13L | −xB13 | −yB13 | zB13 |
| A21L | −xC21 | −yC21 | zC21 |
| B21L | −xD21 | −yD21 | zD21 |
| C21L | −xA21 | −yA21 | zA21 |
| D21L | −xB21 | −yB21 | zB21 |
| A31L | −xC31 | −yC31 | zC31 |
| B31L | −xD31 | −yD31 | zD31 |
| C31L | −xA31 | −yA31 | zA31 |
| D31L | −xB31 | −yB31 | zB31 |
| A22L | −xC22 | −yC22 | zC22 |
| B22L | −xD22 | −yD22 | zD22 |
| C22L | −xA22 | −yA22 | zA22 |
| D22L | −xB22 | −yB22 | zB22 |
| A23L | −xC23 | yC23 | zC23 |
| B23L | −xD23 | −yD23 | zD23 |
| C23L | −xA23 | −yA23 | zA23 |
| D23L | −xB23 | −yB23 | zB23 |
| A32L | −xC32 | −yC32 | zC32 |
| B32L | −xD32 | −yD32 | zD32 |
| C32L | −xA32 | −yA32 | zA32 |
| D32L | −xB32 | −yB32 | zB32 |
| A33L | −xC33 | −yC33 | zC33 |
| B33L | −xD33 | −yD33 | zD33 |
| C33L | −xA33 | −yA33 | zA33 |
| D33L | −xB330 | −yB33 | zB33 |

Table A7.
The coordinates of the vertices WABijp, WCDijp, WADijp, WBCijp (for i, j = 1, 2, 3) of the polyhedral reference network Γ3p shown in Figure 29.
Table A7.
The coordinates of the vertices WABijp, WCDijp, WADijp, WBCijp (for i, j = 1, 2, 3) of the polyhedral reference network Γ3p shown in Figure 29.
| Vertex | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| WAB22p | xWAB22 | −yWAB22 | zWAB22 |
| WCD22p | xWCD22 | −yWCD22 | zWCD22 |
| WAD22p | xWBC22 | −yWBC22 | zWBC22 |
| WBC22p | xWAD22 | −yWAD22 | zWAD22 |
| WAB23p | xWAB23 | −yWAB23 | zWAB23 |
| WCD23p | xWCD23 | −yWCD23 | zWCD23 |
| WAD23p | xWBC23 | −yWBC23 | zWBC23 |
| WBC23p | xWAD23 | −yWAD23 | zWAD23 |
| WAB32p | xWAB32 | −yWAB32 | zWAB32 |
| WCD32p | xWCD32 | −yWCD32 | zWCD32 |
| WAD32p | xWBC32 | −yWBC32 | zWBC32 |
| WBC32p | xWAD32 | −yWAD32 | zWAD32 |
| WAB33p | xWAB33 | −yWAB33 | zWAB33 |
| WCD33p | xWCD33 | −yWCD33 | zWCD33 |
| WAD33p | xWBC33 | −yWBC33 | zWBC33 |
| WBC33p | xWAD33 | −yWAD33 | zWAD33 |

Table A8.
The coordinates of the points SAijp, SBijp, SCijp, SDijp for (i, j = 1, 2, 3) of the reference surface ωr.
Table A8.
The coordinates of the points SAijp, SBijp, SCijp, SDijp for (i, j = 1, 2, 3) of the reference surface ωr.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| SA22p | xSB22 | −ySB22 | zSB22 |
| SB22p | xSA22 | −ySA22 | zSA22 |
| SC22p | xSD22 | −ySD22 | zSD22 |
| SD22p | xSC22 | −ySC22 | zSC22 |
| SA23p | xSB23 | −ySB23 | zSB23 |
| SB23p | xSA23 | −ySA23 | zSA23 |
| SC23p | xSD23 | −ySD23 | zSD23 |
| SD23p | xSC23 | −ySC23 | zSC23 |
| SA32p | xSB32 | −ySB32 | zSB32 |
| SB32p | xSA32 | −ySA32 | zSA32 |
| SC32p | xSD32 | −ySD32 | zSD32 |
| SD32p | xSC32 | −ySC32 | zSC32 |
| SA33p | xSB33 | −ySB33 | zSB33 |
| SB33p | xSA33 | −ySA33 | zSA33 |
| SC33p | xSD33 | −ySD33 | zSD33 |
| SD33p | xSC33 | −ySC33 | zSC33 |

Table A9.
The coordinates of the vertices Aijp, Bijp, Cijp, Dijp, (for i, j = 1, 2, 3) of the eaves edge net Bv3p.
Table A9.
The coordinates of the vertices Aijp, Bijp, Cijp, Dijp, (for i, j = 1, 2, 3) of the eaves edge net Bv3p.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| A22p | xA32 | −yA32 | zA32 |
| B22p | xB12 | −yB12 | zB12 |
| C22p | xC12 | −yC12 | zC12 |
| D22p | xD32 | −yD32 | zD32 |
| A23p | xA33 | −yA33 | zA33 |
| B23p | xB13 | −yB13 | zB13 |
| C23p | xC13 | −yC13 | zC13 |
| D23p | xD33 | −yD33 | zD33 |
| A32p | xC31 | −yC31 | zC31 |
| B32p | xB22 | −yB22 | zB22 |
| C32p | xC22 | −yC22 | zC22 |
| D32p | xB33 | −yB33 | zB33 |
| A33p | xC32 | −yC32 | zC32 |
| B33p | xB23 | −yB23 | zB23 |
| C33p | xC23 | −yC23 | zC23 |
| D33p | −22,940.0 | 23,014.0 | 48,143.90 |

Table A10.
The coordinates of the vertices WABijr, WCDijr, WADijr, WBCijr (for i, j = 1, 2, 3) of the polyhedral reference network Γ4r shown in Figure 21.
Table A10.
The coordinates of the vertices WABijr, WCDijr, WADijr, WBCijr (for i, j = 1, 2, 3) of the polyhedral reference network Γ4r shown in Figure 21.
| Vertex | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| WAB22r | −xWCD22 | yWCD22 | zWCD22 |
| WCD22r | −xWAB22 | yWAB22 | zWAB22 |
| WAD22r | −xWAD22 | yWAD22 | zWAD22 |
| WBC22r | −xWBC22 | yWBC22 | zWBC22 |
| WAB23r | −xWCD23 | yWCD23 | zWCD23 |
| WCD23r | −xWAB23 | yWAB23 | zWAB23 |
| WAD23r | −xWAD23 | yWAD23 | zWAD23 |
| WBC23r | −xWBC23 | yWBC23 | zWBC23 |
| WAB32r | −xWCD32 | yWCD32 | zWCD32 |
| WCD32r | −xWAB32 | yWAB32 | zWAB32 |
| WAD32r | −xWAD32 | yWAD32 | zWAD32 |
| WBC32r | −xWBC32 | yWBC32 | zWBC32 |
| WAB33r | −xWCD33 | yWCD33 | zWCD33 |
| WCD33r | −xWAB33 | yWAB33 | zWAB33 |
| WAD33r | −xWAD33 | yWAD33 | zWAD33 |
| WBC33r | −xWBC33 | yWBC33 | zWBC33 |

Table A11.
The coordinates of the points SAijr, SBijr, SCijr, SDijr for (i, j = 1, 2, 3) of the reference surface ωr.
Table A11.
The coordinates of the points SAijr, SBijr, SCijr, SDijr for (i, j = 1, 2, 3) of the reference surface ωr.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| SA22r | −xSD22 | ySD22 | zSD22 |
| SB22r | −xSC22 | ySC22 | zSC22 |
| SC22r | −xSB22 | ySB22 | zSB22 |
| SD22r | −xSA22 | ySA22 | zSA22 |
| SA23r | −xSD23 | ySD23 | zSD23 |
| SB23r | −xSC23 | ySC23 | zSC23 |
| SC23r | −xSB23 | ySB23 | zSB23 |
| SD23r | −xSA23 | ySA23 | zSA23 |
| SA32r | −xSD32 | ySD32 | zSD32 |
| SB32r | −xSC32 | ySC32 | zSC32 |
| SC32r | −xSB32 | ySB32 | zSB32 |
| SD32r | −xSA32 | ySA32 | zSA32 |
| SA33r | −xSD33 | ySD33 | zSD33 |
| SB33r | −xSC33 | ySC33 | zSC33 |
| SC33r | −xSB33 | ySB33 | zSB33 |
| SD33r | −xSA33 | ySA33 | zSA33 |

Table A12.
The coordinates of the vertices Aijr, Bijr, Cijr, Dijr (for i, j = 1, 2, 3) of the eaves edge net Bv4r.
Table A12.
The coordinates of the vertices Aijr, Bijr, Cijr, Dijr (for i, j = 1, 2, 3) of the eaves edge net Bv4r.
| Point | x-Coordinate [mm] | y-Coordinate [mm] | z-Coordinate [mm] |
|---|---|---|---|
| A22r | −xA23 | yA23 | zA23 |
| B22r | −xB23 | yB23 | zB23 |
| C22r | −xC21 | yC21 | zC21 |
| D22r | −xD21 | yD21 | zD21 |
| A23r | −xC13 | yC13 | zC13 |
| B23r | −xD33 | yD33 | zD33 |
| C23r | −xC22 | yC22 | zC22 |
| D23r | −xD22 | yD22 | zD22 |
| A32r | −xA33 | yA33 | zA33 |
| B32r | −xB33 | yB33 | zB33 |
| C32r | −xC31 | yC31 | zC31 |
| D32r | −xD31 | yD31 | zD31 |
| A33r | −xC23 | yC23 | zC23 |
| B33r | −xD33p | −yD33p | zD33p |
| C33r | −xC32 | yC32 | zC32 |
| D33r | −xD32 | yD32 | zD32 |
References
- Yu, W.-W.; LaBoube, R.A.; Chen, H. Cold Formed Steel Design; John Wiley and Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Abdel_Sayed, G. Critical shear loading of curved panels of corrugated sheets. Proc. ASCE J. Struct. Div. 1970, 96, 1279–1294. [Google Scholar]
- Abramczyk, J. Shell Free Forms of Buildings Roofed with Transformed Corrugated Sheeting, Monograph; Publishing House of Rzeszow University of Technology: Rzeszów, Poland, 2017. [Google Scholar]
- Parker, J.E. Behavior of Light Gauge Steel Hyperbolic Paraboloid Shells. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1969. [Google Scholar]
- Petcu, V.; Gioncu, D. Corrugated hypar structures. In Proceedings of the I International Conference on Lightweight Structures in Civil Engineering, Warsaw, Poland, 1 December 1995; pp. 637–644. [Google Scholar]
- Yang, H. A Finite Element Formulation for Stability Analysis of Doubly Curved Thin Shell Structures. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1969. [Google Scholar]
- Prokopska, A.; Abramczyk, J. Parametric Creative Design of Building Free Forms Roofed with Transformed Shells Introducing Architect’s and Civil Engineer’s Responsible Artistic Concepts. Buildings 2019, 9, 58. [Google Scholar] [CrossRef]
- Abramczyk, J. Shape transformations of folded sheets providing shell free forms for roofing. In Proceedings of the 11th Conference on Shell Structures: Theory and Applications, Gdańsk, Poland, 11–13 October 2017; Pietraszkiewicz, W., Witowski, W., Taylor and Francis Group, Eds.; Routledge: London, UK, 2017; Volume 4, pp. 409–412. [Google Scholar]
- Prokopska, A.; Abramczyk, J. Shape Transformations of Plane Folded Sheets for Shell Roofing. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 082064. [Google Scholar] [CrossRef]
- Reichhart, A. Geometrical and Structural Shaping Building Shells Made up of Transformed Flat Folded Sheets; Hhouse of Rzeszow University of Technology: Rzeszów, Poland, 2002. (In Polish) [Google Scholar]
- Abramczyk, J. Building Structures Roofed with Multi-Segment Corrugated Hyperbolic Paraboloid Steel Shells. Procedia Eng. 2016, 161, 1545–1550. [Google Scholar] [CrossRef]
- Nilson, V.E. Testing a light gauge steel hyperbolic paraboloid shell. Proc. ASCE J. Struct. Div. 1962, 88, 51–66. [Google Scholar]
- Winter, G. Strength of thin steel compression flanges. Trans. ASCE 1974, 112, 895–912. [Google Scholar]
- Muskat, R. Buckling of Light Gage Steel Hyperbolic Paraboloid Roofs. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1968. [Google Scholar]
- Banavalkar, P.V. Analysis and Behavior of Light Gauge Hyperbolic Paraboloid Shells. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1971. [Google Scholar]
- Gergely, P.; Banavalkar, P.V.; Parker, J.E. The Analysis and Behavior of Thin-Steel Hyperbolic Paraboloid Shells; A Research Project Sponsored by the America Iron and Steel Institute, Report No. 338; Civil, Architectural and Environmental Engineering: Ithaca, NY, USA, September 1971. [Google Scholar]
- McDermott, J.F. Single layer corrugated steel sheet hypars. Proc. ASCE J. Struct. Div. 1968, 94, 1279–1294. [Google Scholar]
- Gioncu, V.; Petcu, D. Corrugated Hypar Structures. In Proceedings of the International Conference LSCE, Warsaw, Poland, 25–29 September 1995; pp. 637–644. [Google Scholar]
- Egger, H.; Fischer, M.; Resinger, F. Hyperschale aus Profilblechen. Stahlbau 1971, 12, 353–361. [Google Scholar]
- Dawydov, J.U. House foods of Hyperbolic steel panel-shells. In Proceedings of the 12th International Conference on Supercomputing, ICS 1998, Melbourne, Australia, 13–17 July 1998; Volume II, pp. 500–550. [Google Scholar]
- Davis, J.M.; Bryan, E.R. Manual of Stressed Skin Diaphragm Design; Granada Publishing Ltd.: London, UK, 1982. [Google Scholar]
- Reichhart, A. Corrugated Deformed Steel Sheets as Material for Shells. In Proceedings of the International Conference on Lightweight Structures in Civil Engineering, Warsaw, Poland, 25–29 December 1995; pp. 625–636. [Google Scholar]
- Prokopska, A.; Abramczyk, J. Responsive Parametric Building Free Forms Determined by Their Elastically Transformed Steel Shell Roofs Sheeting. Buildings 2019, 9, 46. [Google Scholar] [CrossRef]
- Abramczyk, J. Transformed Shell Roof Structures as the Main Determinant in Creative Shaping Building Free Forms Sensitive to Man-Made and Natural Environments. Buildings 2019, 9, 74. [Google Scholar] [CrossRef]
- Abramczyk, J. Symmetric Shape Transformations of Folded Shell Roofs Determining Creative and Rational Shaping of Building Free Forms. Symmetry 2019, 11, 1438. [Google Scholar] [CrossRef]
- Biswas, M.; Iffland, J.S.B. Metal deks used to form hypar-shell panels. In Proceedings of the 2nd Speciality Conference on Cold-Formed Steel Structures, Rolla, MO, USA, 15–17 August 1973. [Google Scholar]
- Abramczyk, J. Parametric shaping of consistent architectural forms for buildings roofed with corrugated shell sheeting. J. Archit. Civ. Eng. Environ. 2017, 10, 5–18. [Google Scholar]
- Abramczyk, J. Principles of geometrical shaping effective shell structures forms. JCEEA 2014, XXXI, 5–21. [Google Scholar] [CrossRef]
- Prokopska, A.; Abramczyk, J. Innovative systems of corrugated shells rationalizing the design and erection processes for free building forms. J. Archit. Civ. Eng. Environ. 2017, 29–40. [Google Scholar] [CrossRef]
- Prokopska, A. Methodology of Architectural Design Preliminary Phases of the Architectural Process; Publishing House of Rzeszow University of Technology: Rzeszów, Poland, 2018. [Google Scholar]
- Abramczyk, J. Integrated building forms covered with effectively transformed folded sheets. J. Int. Assoc. Shell Spat. Struct. 2016, 57, 121–132. [Google Scholar] [CrossRef]
- Obrębski, J.B. Observations on Rational Designing of Space Structures. In Proceedings of the Symposium Montpellier Shell and Spatial Structures for Models to Realization IASS, Montpellier, France, 20–24 September 2004; pp. 24–25. [Google Scholar]
- Rębielak, J. Morphology of roof structure systems designer by means of lenticular girder. In Spatial Structures–Temporary and Permanent, Proceedings of the International Symposium of the International Association for Shell and Spatial Structures, Shanghai, China, 8–12 November 2010; Zhang, Q., Yang, L., Hu, Y., Eds.; China Architecture & Building Press: Shanghai, China, 2010; pp. 1249–1256. [Google Scholar]
- Abel, J.F.; Mungan, I. Fifty Years of Progress for Shell and Spatial Structures; International Association for Shell and Spatial Structures: Madrid, Spain, 2011. [Google Scholar]
- Dzwierzynska, J.; Prokopska, A. Pre-rationalized parametric designing of roof shells formed by repetitive modules of Catalan surfaces. Symmetry 2018, 10, 105. [Google Scholar] [CrossRef]
- Carmo, M.P. Differential Geometry of Curves and Surfaces; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Grey, A. Modern Differential Geometry of Curves and Surfaces with Mathematica; CRC Press LCC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Żwirek, P. Selected issues of using nominally flat folded sheets and self-bearing panels for curved. In Proceedings of the 9th Scientific and Technical Conference on Shaping Structures. Thin-walled Structures, Rzeszów, Poland, 11–12 September 2015. (In Polish). [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).