Time-Varying Delayed H_∞ Control Problem for Nonlinear Systems: A Finite Time Study Using Quadratic Convex Approach

Abstract

In this manuscript, we consider the finite-time $H_{\infty }$ control for nonlinear systems with time-varying delay. With the assistance of a novel Lyapunov-Krasovskii functional which includes some integral terms, a matrix-based on quadratic convex approach, combined with Wirtinger inequalities and some useful integral inequalities, a sufficient condition of finite-time boundedness is established. A novel feature presents in this paper is that the restriction which is necessary for the upper bound derivative is not restricted to less than 1. Further a $H_{\infty }$ controller is designed via memoryless state feedback control and a new sufficient conditions for the existence of finite-time $H_{\infty }$ state feedback for the system are given in terms of linear matrix inequalities (LMIs). At the end, some numerical examples with simulations are given to illustrate the effectiveness of the obtained result.

1. Introduction

The occurrence of time delays is an important fact in many of the networking and processing control systems. Such delays can have the capacity to destabilize the control systems and also make some crucial disintegration in the performance of the closed-loop systems, see the references cited therein [1,2,3,4,5,6,7]. While modeling a real control system, the existence of time delays is always taken to be a time-varying one that satisfies the condition $d_1\le d\left(t\right)\le d_2$ and $d_1$ which is not necessarily restricted to be 0. In recent years, the study on finite-time stability (FTS) has increased the research interest from various researches around the world due to the wider applications in mathematical control theory, which has been studied by different approaches in various kinds of systems, see for instance [8,9,10,11,12,13,14,15]. To this extent, the author Dorato in [8], explained the fundamental concepts of stability theory of dynamical systems in finite-time sense. Generally, the given system leads to be finite-time stable if the considered state of the system should be within the bounded limit for a fixed interval of time. From this, one can observe that the concept of finite-time stability mainly attracts the boundedness of a system during a fixed interval of time period. Some of the exciting results for finite-time stability and stabilization with the existence of time-delay have been obtained in [8,9,10,11,12]. Moreover, in some practical systems, there is a need to outline the system that guarantees a maximum $H_{\infty }$ performance rather than the finite-time stability. Hence this motivates us to concentrate on the present study of research.

On the other hand, the study on $H_{\infty }$ control problem will make a sense in reducing the consequences of the external disturbances from both inside and outside the system. The main theme of the $H_{\infty }$ problem is to design a controller from outside the system and to obtain the robust stability (i.e., to minimize the errors). Also this will result in minimizing the guaranteeing disturbance attenuation level $\gamma$ in the $H_{\infty }$ sense for the system. Hence this finite-time $H_{\infty }$ control concerns in the design of feedback controller which ensures the FTS of the closed-loop system and guarantees a maximum $H_{\infty }$ performance bound.

Recently, the authors [10,11,16,17] have enhanced the results on finite time stability and $H_{\infty }$ performance analysis. In [10], finite-time $H_{\infty }$ control for a continuous system with norm-bounded disturbance has been studied but a continuous system is not a nonlinear system. Robust finite-time $H_{\infty }$ control of linear time-varying delay systems with bounded control has been considered in [11] based on Riccati Equations. In [12], the problem of robust finite-time stabilization with guaranteed cost control was studied based on the Lyapunov functional method and generalized Jensen integral inequality. These techniques allow us to design the state feedback controllers which stabilize the closed-loop system in the finite time. In [18], authors used an improved Lyapunov-Krasovskii functional (LKF) with triple-integral terms, augment terms and convex combination technique to show the effectiveness of the obtained results. Hao et al. [19] developed a novel problem on time-varying delayed nonlinear systems with finite-time stability and stabilization by employing the integral inequality and some free fuzzy by weighting metrices, which are less conservative than other existing ones. In [20], delay-dependent finite-time stability criteria for an uncertain continuous-time system with time varying delays has been studied but a continuous-time system is not a nonlinear system and without $H_{\infty }$ performance analysis. In [21], improved results on delay-dependent $H_{\infty }$ control for uncertain systems with time-varying delays have been considered by using bounding techniques for some cross-term of the LKF method and the free-weighting matrix method.

Several approaches that reduce the conservatism for the system with time delay have been reported in the literature. They are namely an appropriate Lyapunov-Krasovskii functional method by using bounding techniques while finding the time-derivative, delay decomposition approach; free weighting matrices approach and reciprocally convex optimization techniques, see [21,22,23,24]. Of all the above mentioned approaches, a novel method to reduce the conservatism is matrix-based quadratic convex approach. This approach will gives a better maximum allowable upper bound for time-varying delay over some existing ones, see for references [25,26,27].

So with the intuition from the above evidences, in this paper, we have followed a matrix-based quadratic convex approach to obtain a better maximum bound value. This is the first time that we have incorporated this method to study the finite-time $H_{\infty }$ problem for the considered control system with time-varying delay. Further, the purposes of this paper are given as follows:

I.

We consider some new Lyapunov-Krasovskii functional which has not been considered yet in stability analysis of finite-time $H_{\infty }$ control. The new Lyapunov-Krasovskii functional includes some integral terms of the form ${\int }_{t-h}^t{(h-t-s)}^j{\dot{x}}^T\left(s\right)R_j\dot{x}\left(s\right)ds(j=1,2)$ which the integrands are polynomial multiplied by ${\dot{x}}^T\left(s\right)R_j\dot{x}\left(s\right)ds(j=1,2)$ and one may estimate an upper bound of the integral by employing some techniques from [22,25], the matrix based quadratic convex approach, the use of a tighter bounding technique and useful integral inequality such as Wirtinger inequality.

II.

Lyapunov-Krasovskii with the matrix based quadratic convex approach is introduced to formulate finite-time stability criteria and $H_{\infty }$ performance level where the time-varying delay satisfies $0\le d_1\le d\left(t\right)\le d_2,{\mu }_1\le \dot{d}\left(t\right)\le {\mu }_2.$ Moreover, the restriction of upper bound derivative is not necessary restricted less than 1 compared with [20]

III.

Two numerical examples are given to demonstrate the effectiveness of theoretical result.

2. Problem Statement

In this section, we consider a system with time-varying delay and control input as

$$\begin{array}{c}\hfill \left.\begin{array}{c}\dot{x}\left(t\right)=Ax\left(t\right)+Dx(t-d\left(t\right))+Bu\left(t\right)+Cw\left(t\right)+f(x\left(t\right),t)+g(x(t-d\left(t\right)),t)\\ z\left(t\right)=Ex\left(t\right)+Gx(t-d(t\left)\right)+Fu\left(t\right)+f\left(x\right(t),t)+g\left(x\right(t-d\left(t\right)),t),\end{array}\right\}\\ \hfill x(t_0+\theta )=\varphi \left(\theta \right),\theta \in [-d_2,0],(t_0,\varphi )\in {\mathcal{R}}^{+}\times \mathcal{C}([-d_2,t_0],{\mathcal{R}}^n),\end{array}$$

(1)

where $x\left(t\right)\in {\mathcal{R}}^n$ is the state; $u\left(t\right)\in {\mathcal{R}}^m$ is the control input, $w\left(t\right)\in {\mathcal{L}}_2([0,\infty ],{\mathcal{R}}^r)$ is a disturbance input and $z\left(t\right)\in {\mathcal{R}}^s$ is the observation output. The delay $d\left(t\right)$ is time-varying continuous function which satisfies

$$\begin{array}{c}\hfill 0\le d_1\le d\left(t\right)\le d_2,{\mu }_1\le \dot{d}\left(t\right)\le {\mu }_2.\end{array}$$

In this paper, we consider the nonlinear functions satisfying

$$\begin{array}{c}f(x\left(t\right),t)={(f_1(x_1\left(t\right),t),f_2(x_2\left(t\right),t),\dots ,f_n(x_n\left(t\right),t))}^T\in {\mathcal{R}}^n\\ g(x(t-d\left(t\right)),t)=(g_1(x_1(t-d\left(t\right)),t),g_2\left(x_2(t-t)\right),t),\dots ,g_n(x_n(t-d\left(t\right)),t){)}^T\in {\mathcal{R}}^n,\end{array}$$

$f,g:{\mathcal{R}}^n\times [-d_M,\infty )\to {\mathcal{R}}^n$ are nonlinear function satisfying the Lipschitz conditions; namely, there exist positive constants ${\beta }_1,{\beta }_2,\forall x,y\in {\mathcal{R}}^n,$ such that

$$\begin{array}{c}\hfill {\parallel f(y,t)-f(x,t)\parallel }^2\le {\beta }_1{\parallel y\left(t\right)-x\left(t\right)\parallel }^2,\\ \hfill {\parallel g(y,t)-g(x,t)\parallel }^2\le {\beta }_2{\parallel y\left(t\right)-x\left(t\right)\parallel }^2.\end{array}$$

We assume the following restrictions on the nonlinear perturbations

$$\begin{array}{cc}\hfill f^T(x\left(t\right),t)f(x\left(t\right),t)& \le {\beta }_1{x}^T\left(t\right)x\left(t\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill g^T(x(t-d\left(t\right)),t)g(x(t-d\left(t\right)),t)& \le {\beta }_2{x}^T(t-d\left(t\right))x(t-d\left(t\right)).\hfill \end{array}$$

(3)

The initial condition, $\varphi (.):={\sup }_{t\in [-d_M,0]}\{\parallel \varphi \left(t\right)\parallel ,\parallel \dot{\varphi \left(t\right)}\parallel \}.$ The disturbance is a continuous function satisfying

$$\begin{array}{c}\hfill \exists k>0:{\int }_0^T{w}^T\left(t\right)w\left(t\right)dt\le k.\end{array}$$

(4)

Under the above assumptions on $d(.),f(.),g(.)$ and the initial function $\varphi \left(t\right)$, the system (2) has a unique solution $x(t,\varphi )$ on $[0,T].$ For a prescribed scalar $\gamma >0$, we define the performance index as

$$\begin{array}{c}\hfill J\left(t\right)={\int }_0^{\infty }[z^T\left(s\right)z\left(s\right)-{\gamma }^2{w}^T\left(s\right)w\left(s\right)]ds.\end{array}$$

(5)

The objective of this paper is to design a memoryless state feedback controller $u\left(t\right)=Kx\left(t\right)$.

3. Preliminaries

The following definition and lemma are necessary in the proof of the main results:

Definition 1.

[9] The nonlinear system (2) where $w\left(t\right)$ is a perturbation satisfying (4). The system (2) is said to be finite-time bounded with respect to $(c_1,c_2,T,R,d)$ with $0<c_1<c_2,$ and $R>0$, if

$$\begin{array}{c}\hfill {\sup }_{-{\tau }_2\le s\le 0}\left\{{\varphi }^T\left(s\right)R\varphi \left(s\right){\dot{\varphi }}^T\left(s\right)R\dot{\varphi }\left(s\right)\right\}\le c_1\Rightarrow x^T\left(t\right)Rx\left(t\right)<c_2,\forall \in [0,T].\end{array}$$

(6)

Definition 2.

[9] The nonlinear system (2) is said to be finite-time $H_{\infty }$ bounded with respect to $(c_1,c_2,T,R,d,\gamma )$ with $0<c_1<c_2,d\ge 0,\gamma >0,$$R>0$ and a memoryless state feedback controller $u\left(t\right)=Kx\left(t\right)$, following conditions should be satisfied:

(i)

The zero solution of the closed-loop system, where $w\left(t\right)=0$,

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=-(A-BK)x\left(t\right)+f\left(x\left(t\right)\right)+g\left(x(t-\tau \left(t\right))\right)+Cw\left(t\right),\end{array}$$

(7)

is finite-time bounded.

(ii)

Under zero-initial condition $\varphi \left(t\right)=0,\forall \in [-d_2,0]$ the output $z\left(t\right)$ satisfies

$$\begin{array}{c}\hfill {\int }_0^T{z}^T\left(t\right)z\left(t\right)dt<{\gamma }^2{w}^T\left(t\right)w\left(t\right)dt.\end{array}$$

(8)

We introduce the following technical lemmas, which will be used in the proof of our results.

Proposition 1.

[11] Let $P\in M^{n\times n},R\in M^{n\times n}$ be symmetric positive definite matrices. We have

(i)

${\lambda }_{\mathit{min}}\left(P\right)\left(R\right)>0,{\lambda }_{\mathit{max}}\left(P\right)\left(R\right)>0\mathrm{and}{\lambda }_{\mathit{min}}\left(P\right)x^{T}x\le x^{T}Px\le {\lambda }_{\mathit{max}}\left(P\right)x^{T}x,\forall x\in {\mathcal{R}}^n$

(ii)

$x^{T}x\le {\lambda }_{\mathit{max}}\left(R^{-1}\right)x^{T}Rx,\forall x\in {\mathcal{R}}^n$

(iii)

$x^{T}Px\le {\lambda }_{\mathit{max}}\left(P\right){\lambda }_{\mathit{max}}\left(R^{-1}\right)x^{T}Rx,\forall x\in {\mathcal{R}}^n$.

Lemma 1.

[22] For a given matrix $R>0$, the following inequality holds for any continuously differentiable function $w:[a,b]\to {\mathcal{R}}^n$

$${\int }_a^b{\dot{\omega }}^T\left(u\right)R\dot{\omega }du\ge \frac{1}{b-a}({\mathsf{\Gamma }}_1^{T}R{\mathsf{\Gamma }}_1+3{\mathsf{\Gamma }}_2^{T}R{\mathsf{\Gamma }}_2)$$

(9)

where ${\mathsf{\Gamma }}_1:=\omega \left(b\right)-\omega \left(a\right),{\mathsf{\Gamma }}_2:=\omega \left(b\right)+\omega \left(a\right)-\frac{2}{b-a}{\int }_a^b\omega \left(u\right)du$.

Remark 1.

: From the above inequality, it can be observed that the inequality in Lemma 1 gives a firm lower bound for ${\int }_a^b{\dot{\omega }}^T\left(u\right)R\dot{\omega }\left(u\right)du$ than Jensen’s inequality since $3{\mathsf{\Gamma }}_2^{T}R{\mathsf{\Gamma }}_2>0$ for ${\mathsf{\Gamma }}_2\ne 0.$ Hence it shows that the inequality (9) is improved than the Jensen’s inequality.

Before we introduce some useful integral inequalities, we denote

$$\left.\begin{array}{c}{\nu }_1\left(t\right):=\frac{1}{d_2-d\left(t\right)}{\int }_{t-d_2}^{t-d\left(t\right)}y\left(s\right)ds\\ {\nu }_2\left(t\right):=\frac{1}{d\left(t\right)-d_1}{\int }_{t-d\left(t\right)}^{t-d_1}y\left(s\right)ds\\ {\nu }_3\left(t\right):=\frac{1}{d_1}{\int }_{t-d_1}^{t}y\left(s\right)ds.\end{array}\right\}$$

(10)

Lemma 2.

[25] For a given scalar $d_1\ge 0$ and any $n\times n$ real matrices $Y_1>0$ and $Y_2>0$ and a vector $\dot{y}:[-d_1,0]\to {\mathcal{R}}^n$ such that the integration concerned below is well defined, the following inequality holds for any vector-valued function ${\pi }_1\left(t\right):[0,\infty )\to {\mathcal{R}}^k$ and matrices $M_1\in {\mathcal{R}}^{k\times k}$ and $N_1\in {\mathcal{R}}^{k\times n}$ satisfying $\left[\begin{array}{cc}{M}_1& N_1\\ N_1^T& Y_1\end{array}\right]\ge 0,$

$$\begin{array}{cc}\hfill {\wp }_1& :={\int }_{t-d_1}^t(d_1-t+s){\dot{y}}^T\left(s\right)Y_1\dot{y}\left(s\right)ds\hfill \\ \hfill & \ge -\frac{d_1^2}{2}{\pi }_1^T\left(t\right)M_1{\pi }_1\left(t\right)-2d_1{\pi }_1^T{N}_1[y\left(t\right)-{\nu }_3\left(t\right)],\hfill \\ \hfill {\wp }_2& :={\int }_{t-d_1}^t{(d_1-t+s)}^2{\dot{y}}^T\left(s\right)Y_2\dot{y}\left(s\right)ds\hfill \\ \hfill & \ge d_1{[y\left(t\right)-{\nu }_3\left(t\right)]}^T{Y}_2[y\left(t\right)-{\nu }_3\left(t\right)]\hfill \end{array}$$

where ${\nu }_3\left(t\right)$ is defined in (10).

Lemma 3.

[26] Let $d\left(t\right)$ be a continuous function satisfying $0\le d_1\le d\left(t\right)\le d_2$. For any $n\times n$ real matrix $R_2>0$ and a vector $\dot{y}:[-d_2,0]\to {\mathcal{R}}^n$ such that the integration concerned below is well defined, the following inequality holds for any ${\varphi }_{i1}\in {\mathcal{R}}^q$ and real matrices $Z_i\in {\mathcal{R}}^{q\times q},$$F_i\in {\mathcal{R}}^{q\times n}$ satisfying $\left[\begin{array}{cc}{Z}_i& F_i\\ F_i^T& R_2\end{array}\right]\ge 0,(i=1,2),$

$$\begin{array}{ccc}\hfill -{\int }_{t-d_2}^{t-d_1}(d_2-t+s){\dot{y}}^T\left(s\right)R_2\dot{y}\left(s\right)ds& \le & \frac{1}{2}{(d_2-d\left(t\right))}^2{\varphi }_{11}^T{Z}_1{\varphi }_{11}+2(d_2-d\left(t\right)){\varphi }_{11}^T{F}_1{\varphi }_{12}\hfill \\ \hfill & +& \frac{1}{2}[{(d_2-d_1)}^2-{(d_2-d\left(t\right))}^2]{\varphi }_{21}^T{Z}_2{\varphi }_{21}\hfill \\ \hfill & +& 2{\varphi }_{21}^T{F}_2[(d_2-d\left(t\right)){\varphi }_{22}+(d\left(t\right)-d_1){\varphi }_{23}]\hfill \end{array}$$

where ${\varphi }_{12}:=y(t-d\left(t\right))-{\nu }_1\left(t\right),{\varphi }_{22}:=y(t-d_1)-x(t-d\left(t\right)),{\varphi }_{23}:=y(t-d_1)-{\nu }_2\left(t\right)$ with ${\nu }_i\left(t\right)(i=1,2)$ being defined in (10).

Lemma 4.

[25] Let $d\left(t\right)$ be a continuous function satisfying $0\le d_1\le d\left(t\right)\le d_2.$ For any $n\times n$ real matrix $R_1>0$ and a vector $\dot{y}:[-d_2,0]\to {\mathcal{R}}^n$ such that the integration concerned below is well defined, the following inequality holds for any $2n\times 2n$ real matrix $S_1$ satisfying $\left[\begin{array}{cc}{\tilde{R}}_1& S_1\\ S_1^T& {\tilde{R}}_1\end{array}\right]\ge 0,$

$$\begin{array}{c}\hfill -(d_2-d_1){\int }_{t-d_2}^{t-d_1}{\dot{y}}^T\left(s\right)R_1\dot{y}\left(s\right)ds\le 2{\psi }_{11}^T{S}_1{\psi }_{21}-{\psi }_{11}^T{\tilde{R}}_1{\psi }_{11}-{\psi }_{21}^T{\tilde{R}}_1{\psi }_{21},\end{array}$$

where $\widetilde{R_1}:=\mathrm{diag}\{R_1,3R_1\};$ and

$$\begin{array}{c}\hfill {\psi }_{11}:=\left[\begin{array}{c}y(t-d\left(t\right))-y(t-d_2)\\ y(t-d\left(t\right))+y(t-d_2)-2{\nu }_1\left(t\right)\end{array}\right],{\psi }_{21}:=\left[\begin{array}{c}y(t-d_1)-y(t-d\left(t\right))\\ y(t-d_1)+y(t-d\left(t\right))-2{\nu }_2\left(t\right)\end{array}\right].\end{array}$$

Remark 2.

If we substitute $d_1=0$, in Lemma 4, then the inequality can be reduced and it is similar to that of the one in [22]. Also, the dimensions of the slack matrix variables of $S_1$ is $2n\times 2n$ compared to the dimension $2n\times 5n$ introduced in [23].

Lemma 5.

[25] Let ${\chi }_0,{\chi }_1$ and ${\chi }_2$ be $m\times m$ real symmetric matrices and a continuous function d satisfy $d_1\le d\le d_2,$ where $d_1$ and $d_2$ are constants satisfying $0\le d_1\le d_2$. If ${\chi }_0\ge 0,$ then

$$\begin{array}{c}\hfill d^2{\chi }_0+d{\chi }_1+{\chi }_2<0(\le 0),\forall d\in [d_1,d_2]\\ \hfill \iff d_i^2{\chi }_0+d_i{\chi }_1+{\chi }_2<0(\le 0),(i=1,2)\\ \hfill or{d}^2{\chi }_0+d{\chi }_1+{\chi }_2>0(\ge 0),\forall d\in [d_1,d_2]\\ \hfill \iff d_i^2{\chi }_0+d_i{\chi }_1+{\chi }_2>0(\ge 0),(i=1,2).\end{array}$$

4. Main Results

In this section, we firstly design a memoryless $H_{\infty }$ feedback control for the addressed system (2) with the inclusion of time-varying delays and then obtain the finite-time stabilizability analysis conditions. Here we derive a novel finite-time stability for the system (2) by using the matrix-based quadratic convex approach with some integral inequalities in [25]. To achieve this status, we choose the following Lyapunov-Krasovskii functional:

$$\begin{array}{c}\hfill V(t,x_t,{\dot{x}}_t)=V_1\left(t\right)+V_2\left(t\right)+V_3\left(t\right)\end{array}$$

where $x_t$ denotes the function $x\left(t\right)$ defined on the interval $[t-d_2,t]$. Setting $P_1=P^{-1}$, $y\left(t\right)=P_{1}x\left(t\right),$ $d_{21}:=d_2-d_1$ and

$$\begin{array}{cc}{V}_1\left(t\right)\hfill & :=e^{\alpha t}{y}^T\left(t\right)Py\left(t\right)+e^{\alpha t}{\int }_{t-d_1}^t{\dot{y}}^T\left(s\right)Q_0\dot{y}\left(s\right)ds,\hfill \\ V_2\left(t\right)\hfill & :=e^{\alpha t}{\int }_{t-d_1}^t\left[y^T\left(t\right)y^T\left(s\right)\right]Q_1{\left[y^T\left(t\right)y^T\left(s\right)\right]}^{T}ds+e^{\alpha t}{\int }_{t-d\left(t\right)}^{t-d_1}\left[y^T\left(t\right)y^T\left(s\right)\right]Q_2{\left[y^T\left(t\right)y^T\left(s\right)\right]}^{T}ds\hfill \\ \hfill & +e^{\alpha t}{\int }_{t-d_2}^{t-d\left(t\right)}\left[y^T\left(t\right)y^T\left(s\right)\right]Q_3{\left[y^T\left(t\right)y^T\left(s\right)\right]}^{T}ds,\hfill \\ V_3\left(t\right)\hfill & :=e^{\alpha t}{\int }_{t-d_1}^t[(d_1-t+s){\dot{y}}^T\left(s\right)d_1{W}_1\dot{y}\left(s\right)+{(d_1-t+s)}^2{\dot{y}}^T\left(s\right)W_2\dot{y}\left(s\right)]ds\hfill \\ \hfill & +d_{21}{e}^{\alpha t}{\int }_{t-d_2}^{t-d_1}[(d_1-t+s){\dot{y}}^T\left(s\right)R_1\dot{y}\left(s\right)+{(d_1-t+s)}^2{\dot{y}}^T\left(s\right)R_2\dot{y}\left(s\right)]ds\hfill \end{array}$$

where $Q_j>0,(j=0,1,2,3),W_1>0,W_2>0,R_1>0,R_2>0$ and P are real matrices to be determined. Before introducing the main result, the following notations of several matrix variables are defined for simplicity: ${\tilde{R}}_1=\mathrm{diag}\{R_1,3R_1\};$

$$\begin{array}{cc}\hfill {\Xi }_2(d\left(t\right),\dot{d}\left(t\right)):=& {\Xi }_{20}+[d\left(t\right)-d_1]{\Xi }_{21}+[d_2-d\left(t\right)]{\Xi }_{22},\hfill \end{array}$$

(11)

$$\begin{array}{cc}{\Xi }_3\left(d\left(t\right)\right):=\hfill & {\tilde{\phi }}_1^T{S}_1{\tilde{\phi }}_2+{\tilde{\phi }}_2^T{S}_1^T{\tilde{\phi }}_1-{\tilde{\phi }}_1^T{\tilde{R}}_1^T{\tilde{\phi }}_1+{(d_2-d\left(t\right))}^2(Z_1-Z_2)+(d_2-d\left(t\right)){\Xi }_{31}\hfill \\ \hfill & +(d\left(t\right)-d_1){\Xi }_{32}+d_{21}^2{Z}_2-{\tilde{\phi }}_2^T{\tilde{R}}_1{\tilde{\phi }}_2,\hfill \end{array}$$

(12)

$$\begin{array}{ccc}{\widehat{\Xi }}_4:\hfill & =\hfill & d_1^2{Z}_3-{\tilde{\phi }}_3^T{\tilde{W}}_1{\tilde{\phi }}_3+e_9^T(d_1^2{W}_1+d_1^2{W}_2)e_9+2d_1{N}_3(e_1-e_7)+e_8^T(d_{21}^T{R}_1+d_{21}^T{R}_2)e_8\hfill \\ \hfill & +\hfill & 2d_1{(e_1-e_7)}^T{N}_3^T+e_1^T(AP+P{A}^T+(BY+Y^T{B}^T)+\epsilon I)e_1\hfill \\ \hfill & +\hfill & e_1^T\left(PD\right)e_2+e_2^T\left(D^{T}P\right)e_1+e_1^T(AP+Y{B}^T)e_9+e_9^T(P{A}^T+Y^{T}B)e_1\hfill \\ \hfill & +\hfill & e_2^T\left(DP\right)e_9+e_9^T\left(P{D}^T\right)e_2+e_8^T\left(Q_0\right)e_8+e_9^T(-2P+\epsilon I+Q_0)e_9\hfill \\ \hfill & +\hfill & e_{10}^T\left(I\right)e_{10}+e_{11}^T\left(I\right)e_{11}+e_1^T\left(P{E}^T\right)e_{12}+e_{12}^T\left(EP\right)e_1\hfill \\ \hfill & +\hfill & e_2^T\left(P{G}^T\right)e_{13}+e_{13}^T\left(GP\right)e_2+e_{14}^T\left(Y{F}^T\right)e_{14}+e_{11}^T\left(Y\right)e_1+e_{15}^T(-{\gamma }^{2}I)e_{15},\hfill \end{array}$$

(13)

with $e_i\in {\mathcal{R}}^{n\times 15n}(i=1,2,\dots ,15)$ denoting the i-th row-block vector of the $14n\times 14n$ identity matrix ${\tilde{W}}_1=\mathrm{diag}\{W_1,3W_1\};$ and

$$\begin{array}{cc}\hfill {\Xi }_{20}:=& \left[e_1^T{e}_3^T\right](Q_2-Q_1){\left[e_1^T{e}_3^T\right]}^T\hfill \\ \hfill & +{\tau }_1\left[e_9^{T}0\right]Q_1{\left[e_1^T{e}_7^T\right]}^T+{\tau }_1\left[e_1^T{e}_7^T\right]Q_1{\left[e_9^{T}0\right]}^T\hfill \\ \hfill & -(1-\dot{\tau }\left(t\right))\left[e_1^T{e}_2^T\right](Q_2-Q_3){\left[e_1^T{e}_2^T\right]}^T\hfill \\ \hfill & -\left[e_1^T{e}_4^T\right]Q_3{\left[e_1^T{e}_4^T\right]}^T+\left[e_1^T{e}_1^T\right]Q_1{\left[e_1^T{e}_1^T\right]}^T\hfill \\ \hfill {\Xi }_{21}:=& \left[e_1^T{e}_6^T\right]Q_2{\left[e_9^{T}0\right]}^T+\left[e_9^{T}0\right]Q_2{\left[e_1^T{e}_6^T\right]}^T\hfill \\ \hfill {\Xi }_{22}:=& \left[e_1^T{e}_5^T\right]Q_3{\left[e_9^{T}0\right]}^T+\left[e_9^{T}0\right]Q_3{\left[e_1^T{e}_5^T\right]}^T\hfill \\ \hfill {\Xi }_{31}:=& 2N_1(e_2-e_5)+2N_2(e_3-e_2)+2{(e_3-e_2)}^T{N}_2^T+2{(e_2-e_5)}^T{N}_1^T\hfill \\ \hfill {\Xi }_{32}:=& 2N_1(e_3-e_6)+2{(e_3-e_6)}^T{N}_1^T\hfill \\ \hfill {\tilde{\phi }}_1:=& \mathrm{col}\{e_2-e_4,e_2+e_4-2e_5\}\hfill \\ \hfill {\tilde{\phi }}_2:=& \mathrm{col}\{e_3-e_2,e_3+e_2-2e_6\}\hfill \\ \hfill {\tilde{\phi }}_3:=& \mathrm{col}\{e_1-e_3,e_1+e_3-2e_7\}.\hfill \end{array}$$

Theorem 1.

Consider $\gamma >0.$ Then system (2) is finite-time $H_{\infty }$ control with respect to $(c_1,c_2,T,R,d,\gamma )$ and satisfies ${\parallel z\left(t\right)\parallel }_2<\gamma {\parallel w\left(t\right)\parallel }_2$ for all nonzero $w\in {\mathcal{L}}_2[0,\infty )$ if there exist positive definite matrices $P,Q_j>0,(j=0,1,2,3),W_1,W_2,R_1,R_2,S_1,Z_1,Z_2,Z_3,N_1,N_2,N_3$ and Y such that the following linear matrix inequalities $\left(LMIs\right)$ hold

$$\begin{array}{c}\left[\begin{array}{cc}{\tilde{R}}_1& S_1\\ S_1^T& {\tilde{R}}_1\end{array}\right]\ge 0,\left[\begin{array}{cc}{Z}_i& N_i\\ N_i^T& R_2\end{array}\right]\ge 0,(i=1,2)\\ \left[\begin{array}{cc}{Z}_3& N_2\\ N_3^T& W_2\end{array}\right]\ge 0,Z_1\ge Z_2,\end{array}$$

$$\begin{array}{c}\hfill \left.\begin{array}{c}{\Xi }_2(d_1,{\mu }_1)+{\Xi }_3\left(d_1\right)+{\widehat{\Xi }}_4<0\\ {\Xi }_2(d_1,{\mu }_2)+{\Xi }_3\left(d_1\right)+{\widehat{\Xi }}_4<0\\ {\Xi }_2(d_2,{\mu }_1)+{\Xi }_3\left(d_2\right)+{\widehat{\Xi }}_4<0\\ {\Xi }_2(d_2,{\mu }_2)+{\Xi }_3\left(d_2\right)+{\widehat{\Xi }}_4<0\end{array}\right\}\end{array}$$

(14)

and

$$\begin{array}{c}\hfill {\displaystyle \frac{{\alpha }_2{c}_1+{\gamma }^{2}k}{{\alpha }_1}}\le e^{-\alpha T}{c}_2\end{array}$$

(15)

For this problem, the feedback control is taken to be of

$$u\left(t\right)=Y{P}^{-1}x\left(t\right),t\ge 0.$$

(16)

Proof. 

By finding the time-derivative of V for the considered system (2), we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_1=& 2e^{\alpha t}{y}^T\left(t\right)P\dot{y}\left(t\right)+\alpha e^{\alpha t}{y}^T\left(t\right)Py\left(t\right)+e^{\alpha t}\{{\dot{y}}^T\left(t\right)Q_0\dot{y}\left(t\right)-{\dot{y}}^T(t-d_1)Q_0\dot{y}(t-d_1)\}+\alpha V_1(.)\hfill \end{array}$$

(17)

$$\begin{array}{ccc}{\dot{V}}_2\hfill & =\hfill & e^{\alpha t}\{\left[y^T\left(t\right)y^T\left(t\right)\right]Q_1{\left[y^T\left(t\right)y^T\left(t\right)\right]}^T-\left[y^T\left(t\right)y^T(t-d_1)\right]Q_1{\left[y^T\left(t\right)y^T(t-d_1)\right]}^T\hfill \\ \hfill & +\hfill & {\int }_{t-d_1}^{t}2[y^T\left(t\right)y^T\left(s\right)Q_1{\left[\dot{y}{\left(t\right)}^{T}0\right]}^{T}ds+\left[y^T\left(t\right)y^T(t-d_1)\right]Q_2{\left[y^T\left(t\right)y^T(t-d_1)\right]}^T\hfill \\ \hfill & -\hfill & (1-\dot{d\left(t\right)})\left[y^T\left(t\right)y^T(t-d\left(t\right))\right]Q_2{\left[y^T\left(t\right)y^T(t-d\left(t\right))\right]}^T\hfill \\ \hfill & +\hfill & 2{\int }_{t-d\left(t\right)}^{t-d_1}\left[y^T\left(t\right)y^T\left(s\right)\right]Q_2{\left[{\dot{y}}^T\left(t\right)0\right]}^{T}ds-\left[y^T\left(t\right)y^T(t-d_2)\right]Q_3{\left[y^T\left(t\right)y^T(t-d_2)\right]}^T\hfill \\ \hfill & +\hfill & (1-\dot{d\left(t\right)})\left[y^T\left(t\right)y^T(t-d\left(t\right))\right]Q_3{\left[y^T\left(t\right)y^T(t-d\left(t\right))\right]}^T\hfill \\ \hfill & +\hfill & {\int }_{t-d_2}^{t-d\left(t\right)}2\left[y^T\left(t\right)y^T\left(s\right)\right]Q_3{\left[{\dot{y}}^T\left(t\right)0\right]}^{T}ds\}+\alpha V_2(.)\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\dot{V_3}\hfill & =\hfill & e^{\alpha t}\{{\dot{y}}^T\left(t\right)d_1{W}_1\dot{y}\left(t\right)+d_1^2{\dot{y}}^T\left(t\right)W_2\dot{y}\left(t\right)-{\int }_{t-d_1}^t{\dot{y}}^T\left(s\right)d_1{W}_1\dot{y}\left(s\right)ds\hfill \\ \hfill & -\hfill & 2{\int }_{t-d_1}^t(d_1-t+s){\dot{y}}^T\left(s\right)W_2\dot{y}\left(s\right)ds+{\left(d_{21}\right)}^2{\dot{y}}^T(t-d_1)R_1\dot{y}(t-d_1)\hfill \\ \hfill & +\hfill & {\left(d_{21}\right)}^2{\dot{y}}^T(t-d_1)R_2\dot{y}(t-d_1)-d_{21}{\int }_{t-d_2}^{t-d_1}{\dot{y}}^T\left(s\right)R_1\dot{y}\left(s\right)ds\hfill \\ \hfill & -\hfill & 2{\int }_{t-d_2}^{t-d_1}(d_2-t+s){\dot{y}}^T\left(s\right)R_2\dot{y}\left(s\right)ds\}+\alpha V_3(.).\hfill \end{array}$$

(19)

From (2) and Cauchy inequality, we get the following equality:

$$\begin{array}{c}\hfill -2{\dot{x}}^T\left(t\right)P_1[\dot{x}\left(t\right)-Ax\left(t\right)-Dx(t-d\left(t\right))-Bu\left(t\right)-Cw\left(t\right)-f(x\left(t\right),t)-g(x(t-d\left(t\right)),t)]=0\end{array}$$

we obtain the following

$$\begin{array}{cc}\hfill 0=& -2{\dot{x}}^T\left(t\right)P_1[\dot{x}\left(t\right)-Ax\left(t\right)-Dx(t-\tau \left(t\right))-Bu\left(t\right)-Cw\left(t\right)-f(x\left(t\right),t)-g(x(t-d\left(t\right)),t)]\hfill \\ \hfill =& -2{\dot{y}}^T\left(t\right)P\dot{y}\left(t\right)+2{\dot{y}}^T\left(t\right)APy\left(t\right)+2{\dot{y}}^T\left(t\right)DPy(t-d\left(t\right))+2{\dot{y}}^T\left(t\right)2BYy\left(t\right)+2{\dot{y}}^T\left(t\right)CPw\left(t\right)\hfill \\ \hfill & +2{\dot{y}}^T\left(t\right)Pf\left(y\left(t\right)\right)+2{\dot{y}}^T\left(t\right)Pg\left(y(t-d\left(t\right))\right)\hfill \end{array}$$

(20)

From (17) and (20), we have ${\dot{V}}_1$ is

$$\begin{array}{cc}\hfill {\dot{V}}_1=& 2e^{\alpha t}{y}^T\left(t\right)P\dot{y}\left(t\right)+\alpha e^{\alpha t}{y}^T\left(t\right)Py\left(t\right)+e^{\alpha t}\{{\dot{y}}^T\left(t\right)Q_0\dot{y}\left(t\right)-{\dot{y}}^T(t-d_1)Q_0\dot{y}(t-d_1)\}\hfill \\ \hfill & -2{\dot{y}}^T\left(t\right)P\dot{y}\left(t\right)+2{\dot{y}}^T\left(t\right)APy\left(t\right)+2{\dot{y}}^T\left(t\right)DPy(t-d\left(t\right))+2{\dot{y}}^T\left(t\right)2BYy\left(t\right)+2{\dot{y}}^T\left(t\right)CPw\left(t\right)\hfill \\ \hfill & +2{\dot{y}}^T\left(t\right)Pf\left(y\left(t\right)\right)+2{\dot{y}}^T\left(t\right)Pg\left(y(t-d\left(t\right))\right)\hfill \\ \hfill =& e^{\alpha t}{\xi }^T\left(t\right){\Xi }_1\xi \left(t\right)+\alpha V_1(.).\hfill \end{array}$$

(21)

where $\xi \left(t\right):=\mathrm{col}\&\{y\left(t\right),y(t-d\left(t\right)),y(t-d_1),y(t-d_2),{\nu }_1\left(t\right),{\nu }_2\left(t\right),{\nu }_3\left(t\right),\dot{y}(t-d_1),\dot{y}\left(t\right),f\left(y\left(t\right)\right),g\left(y(t-d\left(t\right))\right)\}$,

$$\begin{array}{cc}\hfill {\Xi }_1:=& 2e_1^T\left(P\right)e_9+\alpha e_1^T\left(P\right)e_1+e_9^T\left(Q_0\right)e_9-e_8^T\left(Q_0\right)e_8-2e_9^T\left(P\right)e_9+2e_9^T(AP+4BY)e_1+2e_9^{T}DP{e}_2\hfill \\ \hfill & +2e_9^{T}CP{e}_{12}+2e_{9}P{e}_{10}+2e_{9}P{e}_{11}.\hfill \end{array}$$

With the consideration of the three terms of ${\dot{V}}_2\left(t\right)$, we obtained the following inequalities:

$$\begin{array}{cc}\hfill & {\int }_{t-d_1}^{t}2\left[y^T\left(t\right)y^T\left(s\right)\right]Q_1{\left[\dot{y}{\left(t\right)}^{T}0\right]}^{T}ds\le 2d_1\left[y^T\left(t\right){\nu }_3^T\right]Q_1{\left[{\dot{y}}^T\left(t\right)0\right]}^T,\hfill \\ \hfill & {\int }_{t-d\left(t\right)}^{t-d_1}2\left[y^T\left(t\right)y^T\left(s\right)\right]Q_2{\left[\dot{y}{\left(t\right)}^{T}0\right]}^{T}ds\le 2(d\left(t\right)-d_1)\left[y^T\left(t\right){\nu }_2^T\right]Q_2{\left[{\dot{y}}^T\left(t\right)0\right]}^T\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\int }_{t-d_2}^{t-d\left(t\right)}2\left[y^T\left(t\right)y^T\left(s\right)\right]Q_3{\left[\dot{y}{\left(t\right)}^{T}0\right]}^{T}ds\le 2(d_2-d\left(t\right))\left[y^T\left(t\right){\nu }_1^T\right]Q_3\left[{\dot{y}}^T\left(t\right)0\right].\hfill \end{array}$$

Therefore, the estimation of ${\dot{V}}_2\left(t\right)$ is estimated as

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)& \le {\Xi }_{20}+(d\left(t\right)-d_1){\Xi }_{21}+(d_2-d\left(t\right)){\Xi }_{22}+\alpha V_2\hfill \\ \hfill & =e^{\alpha t}{\xi }^T\left(t\right){\Xi }_2(d\left(t\right),\dot{d}\left(t\right))\xi \left(t\right)+\alpha V_2.\hfill \end{array}$$

(22)

where ${\Xi }_2$ is given as the same as that of in (11). Further, ${\dot{V}}_3\left(t\right)$ is estimated as

$$\begin{array}{c}\hfill {\dot{V}}_3\left(t\right)=e^{\alpha t}\{{\xi }^T\left(t\right){\Xi }_{30}{\xi }^T\left(t\right)+{\delta }_1\left(t\right)+{\delta }_2\left(t\right)\}+\alpha V_3\end{array}$$

where

$$\begin{array}{cc}\hfill {\Xi }_{30}:=& e_9^T(d_1^2{W}_1+d_1^2{W}_2)e_9+e_8^T(d_{21}^2{R}_1+d_{21}^2{R}_2)e_8,\\ \hfill {\delta }_1\left(t\right)=& -{\int }_{t-d_2}^{t-d_1}{\dot{y}}^T\left(s\right)d_{21}{R}_1\dot{y}\left(s\right)ds-2{\int }_{t-d_2}^{t-d_1}(d_2-t+s){\dot{y}}^T\left(s\right)R_2\dot{y}\left(s\right)ds,\\ \hfill {\delta }_2\left(t\right)=& -{\int }_{t-d_1}^t{\dot{y}}^T\left(s\right)d_1{W}_1\dot{y}\left(s\right)ds-2{\int }_{t-d_1}^t(d_1-t+s){\dot{y}}^T\left(s\right)W_2\dot{y}\left(s\right)ds.\end{array}$$

By Lemma 3 and Lemma 4, we obtain the following

$$\begin{array}{c}\hfill -(d_2-d_1){\int }_{t-d_2}^{t-d_1}{\dot{y}}^T\left(s\right)R_1\dot{y}\left(s\right)ds\le 2{\psi }_{11}^T{S}_1{\psi }_{21}-{\psi }_{11}^T{\tilde{R}}_1{\psi }_{11}-{\psi }_{21}^T{\tilde{R}}_1{\psi }_{21},\end{array}$$

where $\widetilde{R_1}:=\mathrm{diag}\{R_1,3R_1\};$ and

$$\begin{array}{c}\hfill {\psi }_{11}:=\left[\begin{array}{c}y(t-d\left(t\right))-y(t-d_2)\\ y(t-d\left(t\right))+y(t-d_2)-2{\nu }_1\left(t\right)\end{array}\right],\\ \hfill {\psi }_{21}:=\left[\begin{array}{c}y(t-d_1)-y(t-d\left(t\right))\\ y(t-d_1)+y(t-d\left(t\right))-2{\nu }_2\left(t\right).\end{array}\right],\end{array}$$

and

$$\begin{array}{cc}\hfill -2{\int }_{t-d_2}^{t-d_1}(d_2-t+s){\dot{y}}^T\left(s\right)R_2\dot{y}\left(s\right)ds& \le -2\{\frac{1}{2}{(d_2-d\left(t\right))}^2{\xi }^T\left(t\right)Z_1\xi \left(t\right)\hfill \\ \hfill & +2(d_2-d\left(t\right)){\xi }^T\left(t\right)N_1[y(t-d\left(t\right))-{\nu }_3]\hfill \\ \hfill & +\frac{1}{2}\left[{(d_2-d_1)}^2{(d_2-d\left(t\right))}^2\right]{\xi }^T\left(t\right)Z_2\xi \left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)N_2[(d_2-d\left(t\right))[y(t-d_1)-y(t-d\left(t\right))]\hfill \\ \hfill & +(d\left(t\right)-d_1)[y(t-d_1)-{\nu }_2]\left]\right\}.\hfill \end{array}$$

Thus, we get

$$\begin{array}{cc}\hfill {\delta }_1\left(t\right)\le & [2{\psi }_{11}^T{S}_1{\psi }_{21}-{\psi }_{11}^T{\tilde{R}}_1{\psi }_{11}-{\psi }_{21}^T{\tilde{R}}_1{\psi }_{21}-2\{\frac{1}{2}{(d_2-d\left(t\right))}^2{\xi }^T\left(t\right)Z_1\xi \left(t\right)\hfill \\ \hfill & +2(d_2-d\left(t\right)){\xi }^T\left(t\right)N_1[y(t-d\left(t\right))-{\nu }_3]+\frac{1}{2}\left[{(d_2-d_1)}^2{(d_2-dd\left(t\right))}^2\right]{\xi }^T\left(t\right)Z_2\xi \left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)N_2[(d_2-d\left(t\right))[y(t-d_1)-y(t-d\left(t\right))]+(d\left(t\right)-d_1)[y(t-d_1)-{\nu }_2]]\}.\hfill \\ \hfill =& {\xi }^T\left(t\right){\Xi }_3\left(d\left(t\right)\right)\xi \left(t\right),\hfill \end{array}$$

(23)

where ${\Xi }_3\left(d\left(t\right)\right)$ is given in (12). From Lemma 1 and Lemma 2, we obtain

$$\begin{array}{cc}\hfill -{\int }_{t-d_1}^t{\dot{y}}^T\left(s\right)d_1{W}_1\dot{y}\left(s\right)ds\le & {[y\left(t\right)-y(t-d_1)]}^T{W}_1[y\left(t\right)-y(t-d_1)]+3{\widetilde{{\mathsf{\Omega }}_1}}^T{W}_1\widetilde{{\mathsf{\Omega }}_1}\hfill \end{array}$$

and

$$\begin{array}{c}\hfill -2{\int }_{t-d_1}^t(d_1-t+s){\dot{y}}^T\left(s\right)W_2\dot{y}\left(s\right)ds\le -d_1^2{\xi }^T\left(t\right)M_1\xi \left(t\right)-2d_1{\xi }^T\left(t\right)N_3[y\left(t\right)-{\nu }_3].\end{array}$$

From which it follows that

$$\begin{array}{cc}\hfill {\delta }_2\left(t\right)\le & {[y\left(t\right)-y(t-d_1)]}^T{W}_1[y\left(t\right)-y(t-d_1)]\hfill \\ \hfill & +3{\widetilde{{\mathsf{\Omega }}_1}}^T{W}_1\widetilde{{\mathsf{\Omega }}_1}-d_1^2{\xi }^T\left(t\right)M_1\xi \left(t\right)-2d_1{\xi }^T\left(t\right)N_1[y\left(t\right)-{\nu }_3],\hfill \\ \hfill =& {\xi }^T\left(t\right){\Xi }_{33}\xi \left(t\right)\hfill \end{array}$$

(24)

where $\widetilde{{\mathsf{\Omega }}_1}=y\left(t\right)+y(t-d_1)-2{\nu }_3,\widetilde{{\mathsf{\Omega }}_2}=y(t-d\left(t\right))+y(t+d_2)-{\nu }_1,\widetilde{{\mathsf{\Omega }}_3}=y(t-d_1)+y(t-d\left(t\right))-{\nu }_2$,

$$\begin{array}{cc}\hfill {\Xi }_{33}:=& -{\tilde{\phi }}_3^T\mathrm{diag}\{W_1,3W_1\}{\tilde{\phi }}_3+d_1^2{Z}_3+2d_1{N}_3(e_1-e_7)+2d_1{(e_1-e_7)}^T{N}_3^T\hfill \end{array}$$

Hence, from (23) and (24), we obtain

$$\begin{array}{c}\hfill {\dot{V}}_3\le e^{\alpha t}\left\{{\xi }^T\left(t\right)[{\Xi }_3\left(d\left(t\right)\right)+{\Xi }_4]\xi \left(t\right)\right\}+\alpha V_3\end{array}$$

(25)

where ${\Xi }_4:={\Xi }_{30}+{\Xi }_{33}.$ From (21), (22) and (25), we obtain $\dot{V}(t,y_t,{\dot{y}}_t)$ along the solution of the system (2) as

$$\begin{array}{c}\hfill \dot{V}(t,x_t)\le \alpha V(t,x_t)+e^{\alpha t}{\xi }^T\mathsf{\Delta }(d\left(t\right),\dot{d}\left(t\right))\xi \left(t\right)\end{array}$$

where

$$\begin{array}{c}\hfill \mathsf{\Delta }(d\left(t\right),\dot{d}\left(t\right))={\Xi }_2(d\left(t\right),\dot{d}\left(t\right))+{\Xi }_3\left(d\left(t\right)\right)+({\Xi }_1+{\Xi }_4).\end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill \dot{V}(t,x_t)\le & \alpha V_{(}.)+{\xi }^T\left(t\right)\widehat{\mathsf{\Delta }}(d\left(t\right),\dot{d}\left(t\right))\xi \left(t\right)+\gamma {\parallel w\left(t\right)\parallel }^2-y^T\left(t\right)[P{E}^{T}EP+Y{F}^{T}FY]y\left(t\right)\hfill \\ \hfill & -y^T(t-d\left(t\right))\left[P{G}^{T}GP\right]y(t-d\left(t\right))-f^T\left(x\left(t\right)\right)f\left(x\left(t\right)\right)-g^T\left(x(t-d\left(t\right))\right)g\left(x(t-d\left(t\right))\right)\hfill \end{array}$$

(26)

where

$$\begin{array}{cc}\hfill \widehat{\mathsf{\Delta }}(d\left(t\right),\dot{d}\left(t\right))& ={\Xi }_2(d\left(t\right),\dot{d}\left(t\right))+{\Xi }_3\left(d\left(t\right)\right)+({\widehat{\Xi }}_1+{\Xi }_4)\hfill \\ \hfill & ={\Xi }_2(d\left(t\right),\dot{d}\left(t\right))+{\Xi }_3\left(d\left(t\right)\right)+{\widehat{\Xi }}_4,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\widehat{\Xi }}_1=& {\Xi }_1+e_1^T[P{E}^{T}EP+Y{F}^{T}FY]e_1+e_2^T\left[P{G}^{T}GP\right]e_2+e_{10}^T\left[I\right]e_{10}+e_{11}^T\left[I\right]e_{11},\hfill \end{array}$$

and ${\widehat{\Xi }}_4={\widehat{\Xi }}_1+{\Xi }_4$ is defined in ([23]). $\widehat{\mathsf{\Delta }}(d\left(t\right),\dot{d}\left(t\right))$ may be rewritten as

$$\widehat{\mathsf{\Delta }}(d\left(t\right),\dot{d}\left(t\right))=d^2\left(t\right){\mathsf{\Delta }}_0+d\left(t\right){\mathsf{\Delta }}_1+{\mathsf{\Delta }}_2$$

(27)

where ${\mathsf{\Delta }}_0=Z_1-Z_2$ and ${\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2$ are $d\left(t\right)$-independent real matrices. By Lemma (5), if $Z_1-Z_2\ge 0$ and the inequality in (14) holds, then $\widehat{\mathsf{\Delta }}(d\left(t\right),\dot{d}\left(t\right))<0,\forall d\left(t\right)\in [d_1,d_2],\forall \dot{d}\left(t\right)\in [{\mu }_1,{\mu }_2].$ Moreover, the terms $\widehat{\mathsf{\Delta }}(d\left(t\right),\dot{d}\left(t\right))$ can be recast in the sense of convex combination of $\dot{d}\left(t\right)$ as follows:

$$\begin{array}{c}\hfill \widehat{\mathsf{\Delta }}(d\left(t\right),\dot{d}\left(t\right))=(1-\dot{d}\left(t\right)){⟡}_0+\dot{d}\left(t\right){⟡}_1+{⟡}_2\end{array}$$

(28)

where ${⟡}_0=Q_2-Q_3$ and ${⟡}_1,{⟡}_2$ are $\dot{d}\left(t\right)$-independent real matrices. Hence by making use of the Schur complement lemma, it follows from (27), (28) and (6) that the inequality $\widehat{\mathsf{\Delta }}(d\left(t\right),\dot{d}\left(t\right))<0$ holds. Therefore, we have from inequality (26) that

$$\begin{array}{c}\hfill \dot{V}(t,x_t)\le \alpha V(t,x_t)\gamma w{\left(t\right)}^{T}w\left(t\right)-z{\left(t\right)}^{T}z\left(t\right)\end{array}$$

(29)

and hence

$$\begin{array}{c}\hfill \dot{V}(t,x_t)\le \alpha V(t,x_t)+{\gamma }^2{w}^T\left(t\right)w\left(t\right).\end{array}$$

because of $z{\left(t\right)}^{T}z\left(t\right)\ge 0$. Multiplying both sides with $e^{-\alpha t},$ we obtain

$$\begin{array}{c}\hfill e^{-\alpha t}\dot{V}(t,x_t)-\alpha e^{-\alpha t}V(t,x_t)<e^{-\alpha t}{\gamma }^2{w}^T\left(t\right)w\left(t\right).\end{array}$$

Hence, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\left(e^{-\alpha t}V(t,x_t)\right)=e^{-\alpha t}\dot{V}(t,x_t)-\alpha e^{-\alpha t}V(t,x_t).\end{array}$$

So,

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\left(e^{-\alpha t}V(t,x_t)\right)<e^{-\alpha t}{\gamma }^2{w}^T\left(t\right)w\left(t\right).\end{array}$$

Integrating both sides from 0 to t, we get

$$\begin{array}{c}\hfill \left(e^{-\alpha t}V(t,x_t)\right)-V(0,x_0)<{\gamma }^2{\int }_0^t{e}^{-\alpha t}{w}^T\left(s\right)w\left(s\right)ds,\end{array}$$

which can be reformulated as

$$\begin{array}{c}\hfill e^{-\alpha t}V(t,x_t))<V(0,x_0)+{\gamma }^2{\int }_0^t{e}^{-\alpha t}{w}^T\left(s\right)w\left(s\right)ds,\end{array}$$

note that

$$\begin{array}{c}\hfill {\alpha }_1{x}^T\left(t\right)Rx\left(t\right)\le V(t,x_t),\forall :0\le T.\end{array}$$

(30)

Hence, we have

$$\begin{array}{cc}\hfill V_1(t,x_t)& =e^{\alpha t}{x}^T\left(t\right)P^{-1}x\left(t\right)\hfill \\ \hfill & =e^{\alpha }t{x}^T\left(t\right)R^{{\displaystyle \frac{1}{2}}}{R}^{{\displaystyle \frac{-1}{2}}}{P}^{-1}{R}^{{\displaystyle \frac{-1}{2}}}{R}^{{\displaystyle \frac{1}{2}}}x\left(t\right)\hfill \\ \hfill & =e^{\alpha t}{x}^T\left(t\right)R^{{\displaystyle \frac{1}{2}}}{\widehat{P}}^{-1}{R}^{{\displaystyle \frac{1}{2}}}x\left(t\right)\hfill \\ \hfill & \ge x^T\left(t\right)R^{{\displaystyle \frac{1}{2}}}{\widehat{P}}^{-1}{R}^{{\displaystyle \frac{1}{2}}}x\left(t\right)\hfill \\ \hfill & \ge {\lambda }_{min}{\left(\widehat{P}\right)}^{-1}{x}^T\left(t\right)Rx\left(t\right)\hfill \end{array}$$

(31)

and ${\alpha }_1={\lambda }_{min}{\left(\widehat{P}\right)}^{-1}$.

Consider

$$\begin{array}{ccc}V(0,x_0)\hfill & =\hfill & y^T\left(0\right)Py\left(0\right)+{\int }_{-d_1}^0{\dot{y}}^T\left(s\right)Q_0\dot{y}\left(s\right)ds,+{\int }_{-d_1}^0\left[y^T\left(0\right)y^T\left(s\right)\right]Q_1{\left[y^T\left(0\right)y^T\left(s\right)\right]}^{T}ds\hfill \\ \hfill & +\hfill & {\int }_{-d\left(t\right)}^{-d_1}\left[y^T\left(0\right)y^T\left(s\right)\right]Q_2{\left[y^T\left(0\right)y^T\left(s\right)\right]}^{T}ds+{\int }_{-d_2}^{-d\left(t\right)}\left[y^T\left(0\right)y^T\left(s\right)\right]Q_3{\left[y^T\left(0\right)y^T\left(s\right)\right]}^{T}ds,\hfill \\ \hfill & +\hfill & {\int }_{-d_1}^0[(d_1+s){\dot{y}}^T\left(s\right)d_1{W}_1\dot{y}\left(s\right)+{(d_1+s)}^2{\dot{y}}^T\left(s\right)W_2\dot{y}\left(s\right)]ds\hfill \\ \hfill & +\hfill & d_{21}{\int }_{-d_2}^{-d_1}[(d_1+s){\dot{y}}^T\left(s\right)R_1\dot{y}\left(s\right)+{(d_1+s)}^2{\dot{y}}^T\left(s\right)R_2\dot{y}\left(s\right)]ds\hfill \\ \hfill & \hfill \le & {\lambda }_{max}{\left(P\right)\parallel \varphi \parallel }^2+{\lambda }_{max}\left(Q_0\right){\parallel \varphi \parallel }^2+{\lambda }_{max}\left(Q_1\right){\parallel i\parallel }^2+{\lambda }_{max}\left(Q_2\right){\parallel \varphi \parallel }^2+{\lambda }_{max}\left(Q_3\right){\parallel \varphi \parallel }^2\hfill \\ \hfill & +\hfill & {\lambda }_{max}\left(W_1\right)d_1^2{\parallel \varphi \parallel }^2+{\lambda }_{max}\left(W_2\right)d_1^2{\parallel \varphi \parallel }^2+{\lambda }_{max}\left(R_1\right)d_{21}^2{\parallel \varphi \parallel }^2+{\lambda }_{max}\left(R_2\right)d_{21}{\parallel \varphi \parallel }^2,\hfill \end{array}$$

so we have

$$\begin{array}{cc}\hfill V(0,x_0)\le & ({\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q_0\right)+{\lambda }_{max}\left(Q_1\right)+{\lambda }_{max}\left(Q_2\right)+{\lambda }_{max}\left(Q_3\right)\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & +{\lambda }_{max}\left(W_1\right)d_1^2+{\lambda }_{max}\left(W_2\right){\pi }_6+{\lambda }_{max}\left(R_1\right)d_{21}^2+{\lambda }_{max}\left(R_2\right)d_{21}^3)c_1,\hfill \\ \hfill & ={\alpha }_2{c}_1\hfill \end{array}$$

(33)

where ${\alpha }_2={\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q_0\right)+{\lambda }_{max}\left(Q_1\right)+{\lambda }_{max}\left(Q_2\right)+{\lambda }_{max}\left(Q_3\right)+{\lambda }_{max}\left(W_1\right)d_1^2+{\lambda }_{max}\left(W_2\right){\pi }_6+{\lambda }_{max}\left(R_1\right)d_{21}^2+{\lambda }_{max}\left(R_2\right)d_{21}^3$.

Therefore, from (31), (33), it follows that

$$\begin{array}{c}\hfill {\alpha }_1{e}^{-\alpha t}{x}^T\left(t\right)Rx\left(t\right)<e^{-\alpha t}V(t,x\left(t\right))\le {\alpha }_2{c}_1+{\gamma }^{2}k,\forall t\in [0,T].\end{array}$$

and hence from (30), we have

$$\begin{array}{c}\hfill x^T\left(t\right)Rx\left(t\right)<\left({\displaystyle \frac{{\alpha }_2{c}_1+{\gamma }^2\beta k}{{\alpha }_1}}\right)e^{\alpha t}\le c_2,\forall t\in [0,T],\end{array}$$

which implies that the closed-loop system is finite-time stable w.r.t $(c_1,c_2,T,R,d,\gamma ).$ To complete the proof of the theorem, it remains to show the $\gamma$ optimal level condition (5). For this, we consider the following relation

$$\begin{array}{c}\hfill \dot{V}(t,x_t)+z^T\left(t\right)z\left(t\right)-{\gamma }^2{w}^T\left(t\right)w\left(t\right)<0.\end{array}$$

Integrating both sides of above equation from $t_0$ to t, we get

$$\begin{array}{c}\hfill {\int }_{t_0}^t\left[\dot{V}(t,x_t)+z^T\left(t\right)z\left(t\right)-{\gamma }^2{w}^T\left(t\right)w\left(t\right)\right]dt<0.\end{array}$$

It follows that

$$\begin{array}{cc}\hfill {\int }_{t_0}^t\left[z^T\left(t\right)z\left(t\right)-{\gamma }^2{w}^T\left(t\right)w\left(t\right)\right]dt& \le V(t_0,x_{t_0})-V(t,x_t)\hfill \\ \hfill & \le 0.\hfill \end{array}$$

(34)

Therefore, under zero initial condition $x\left(t\right)=0$, $t\in [-{\tau }_2,t_0]$, by letting $t\to +\infty$ in (34), we get

$$\begin{array}{c}\hfill {\int }_{t_0}^{\infty }{z}^T\left(t\right)z\left(t\right)dt<{\gamma }^2{\int }_{t_0}^{\infty }{w}^T\left(t\right)w\left(t\right)dt\end{array}$$

which gives ${\parallel z\parallel }_2<\gamma {\parallel w\parallel }_2$. This completes the proof. □

5. Numerical Examples

In this section, we provide two numerical examples with their simulations to demonstrate the effectiveness of our results.

Example 1.

Consider the nonlinear system with interval time-varying delays which was considered in [7]

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =Ax\left(t\right)+Dx(t-d(t\left)\right)+Bu\left(t\right)+Cw\left(t\right)+f\left(x\right(t),t)+g\left(x\right(t-d\left(t\right)),t)\hfill \\ \hfill z\left(t\right)& =Ex\left(t\right)+Gx(t-d(t\left)\right)+Fu\left(t\right)+f\left(x\right(t),t)+g\left(x\right(t-d\left(t\right)),t).\hfill \end{array}$$

We have used theorem 1 to evaluated the value of minimum γ for $H_{\infty }$ control condition. Where

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}-1.3& 0.3\\ 0.5& 0.1\end{array}\right],D=\left[\begin{array}{cc}-0.01& 0.02\\ 0.03& -0.04\end{array}\right],\\ \hfill B=\left[\begin{array}{cc}0.2& 0\\ 0.3& 0\end{array}\right],C=\left[\begin{array}{cc}-0.02& 0.01\\ 0.02& -0.03\end{array}\right],\\ \hfill E=G=\left[\begin{array}{cc}0.06& -0.06\\ -0.08& 0.08\end{array}\right],F=\left[\begin{array}{cc}0.8& 0\\ 0.6& 0\end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill f(·)=g(·)=0.01\left[\begin{array}{c}\sqrt{x_1^2\left(t\right)+x_2^2(t-\tau \left(t\right))}\\ \sqrt{x_2^2\left(t\right)+x_1^2(t-\tau \left(t\right))}\end{array}\right],\end{array}$$

${\beta }_1={\beta }_2=0.01$, ${\tau }_1=0.3,{\tau }_2=0.5,{\mu }_1=-0.1,{\mu }_2=0.1,\gamma =4$$k=2$. And the condition (15) is satisfied with $\alpha =0.6,T=10,c_1=1,c_1=50\gamma =4.$ By using LMI Toolbox in Matlab, it can be shown that the constructed LMI in Theorem (1) is feasible. Further the $H_{\infty }$ controller feedback gain matrix is obtained as:

$$\begin{array}{c}\hfill K=Y{P}^{-1}=\left[\begin{array}{cc}-3.4638& -6.8069\\ -4.3243& -4.1846\end{array}\right].\end{array}$$

Table 1, shows the value of minimum γ with ${\mu }_1=-0.1$ and ${\mu }_2=0.1$ by using Theorem (1). In Table 2, we show the value of minimum γ with ${\mu }_1=0.05$ and ${\mu }_2=0.1$ by using Theorem (1)

Table 1. The value of the minimum allowable disturbance attenuation γ with ${\mu }_1=-0.1$ and ${\mu }_2=0.1$.

			$\overline{{\mathit{\beta }}_1={\mathit{\beta }}_2=0.01}$
Method	${\tau }_1$	${\tau }_2$	${\gamma }_{min}$
By Theorem 1	0.1	0.3	0.2377
	0.1	0.5	0.2474
			$\overline{{\mathbf{\beta }}_{\mathbf{1}}={\mathbf{\beta }}_{\mathbf{2}}=\mathbf{0}.\mathbf{05}}$
Method	${\tau }_1$	${\tau }_2$	${\gamma }_{min}$
By Theorem 1	0.1	0.3	0.8991
	0.1	0.5	0.9643

Table 2. The value of the minimum allowable disturbance attenuation γ with ${\mu }_1=0.05$ and ${\mu }_2=0.1$.

			$\overline{{\mathit{\beta }}_1={\mathit{\beta }}_2=0.01}$
Method	${\tau }_1$	${\tau }_2$	${\gamma }_{min}$
By Theorem 1	0.1	0.5	0.2487

Example 2.

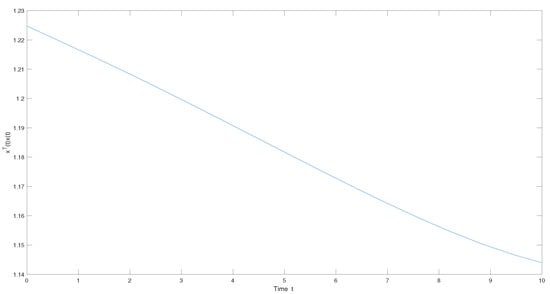
[20] Consider the following nonlinear system with interval time-varying delay which was considered in

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=Ax\left(t\right)+Dx(t-d\left(t\right))+Bu\left(t\right)+Cw\left(t\right)+f(x\left(t\right),t)+g(x(t-d\left(t\right)),t)\end{array}$$

with

$$\begin{array}{c}\hfill A=\left[\begin{array}{ccc}0.01& 0.01& 0.01\\ 0.01& 0.01& 0.02\\ 0.02& 0.01& 0.02\end{array}\right],D=\left[\begin{array}{ccc}0.01& 0.01& 0.01\\ 0.01& 0.01& 0.01\\ 0.01& 0.01& 0.01\end{array}\right],\\ \hfill B=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],C=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill f(x\left(t\right),t)=0.0025sin\left(0.05\right)x\left(t\right){\left[001\right]}^T\\ \hfill g(x(t-d\left(t\right)),t)=0.0025sin\left(0.05\right)x\left(t\right){\left[100\right]}^T\end{array}$$

we investigate delay function $d\left(t\right)=0.5|sin(3t\left)\right|+0.1$. Consider the finite-time of nonlinear system with respect to $(c_1,c_{2,},T,d,\gamma )$ with different fixed times $(T=2,4,6,8,10)$. The maximum values of the norm of state vector are $1.1780,0.5706,0.8510,0.3974,4.8264,0.2091$ and $0.0558$ for $T=2,4,6,8,10$, respectively. We have Figure 1 to show the trajectories of $x^T\left(t\right)x\left(t\right)$ of the closed-loop system with the condition $\varphi \left(t\right)=[0.5,-0.5].$ Moreover, we set $\gamma =0.5,d=2$ and the initial function ${\varphi }^T=[0.1t+0.2,0.1t+0.2,0.1t+0.2],\forall t\in [-0.6,0],$$d_1=1\le d_2=2,$${\beta }_1={\beta }_2=1.25\times {10}^{-4}$ ${\varphi }^T\left(t\right)\varphi \left(t\right)=0.5\le 0.5=c_1$. From (31) and (33), we obtain ${\alpha }_1=0.9227$ and ${\alpha }_2=8.0883.$ By solving Theorem using MATLAB toolbox a feasible solution (show some solution) is

$$\begin{array}{c}\hfill P=\left[\begin{array}{ccc}1.1153& -0.0597& -0.0872\\ -0.0597& 1.1062& -0.0932\\ -0.0872& -0.0932& 1.0498\end{array}\right],Q_0=\left[\begin{array}{ccc}0.569877& -0.0011& -0.0013\\ -0.0011& 0.5690& -0.0019\\ -0.0013& -0.0019& 0.5682\end{array}\right],\\ \hfill R_1=\left[\begin{array}{ccc}0.2088& -0.0003& -0.0004\\ -0.0003& 0.2087& -0.0005\\ -0.0004& -0.0005& 0.2085\end{array}\right],R_2=\left[\begin{array}{ccc}0.0551& -0.0006& -0.0009\\ -0.0006& 0.0550& -0.0010\\ -0.0009& -0.0010& 0.0544\end{array}\right],\\ \hfill W_1=\left[\begin{array}{ccc}0.3957& 0.0005& 0.0007\\ 0.0005& 0.3959& 0.0008\\ 0.0007& 0.0008& 0.3964\end{array}\right],W_2=\left[\begin{array}{ccc}4.8208& -0.0112& -0.0110\\ -0.0112& 4.8039& -0.0223\\ -0.0110& -0.0223& 4.7988\end{array}\right],\\ \hfill Q_1=\left[\begin{array}{cccccc}0.5284& -0.0012& -0.0015& -0.0000& -0.0000& -0.0000\\ -0.0012& 0.5276& -0.0021& -0.0000& 0.0000& -0.0000\\ -0.0015& -0.0021& 0.5266& -0.0000& 0.0000& 0.0000\\ -0.0000& -0.0000& -0.0000& 0.8473& 0.0009& 0.0010\\ -0.0000& 0.0000& 0.0000& 0.0009& 0.8485& 0.0018\\ -0.0000& -0.0000& 0.0000& 0.0010& 0.0018& 0.8490\end{array}\right],\\ \hfill Q_2=\left[\begin{array}{cccccc}0.4602& -0.0017& -0.0025& 0.0000& -0.0000& -0.0000\\ -0.0017& 0.4598& -0.0028& 0.0000& -0.0000& -0.0000\\ -0.0025& -0.0028& 0.4582& -0.0000& -0.0000& 0.0000\\ 0.0000& 0.0000& -0.0000& 0.8663& 0.0146& 0.0224\\ -0.0000& -0.0000& -0.0000& 0.0146& 0.8649& 0.0214\\ -0.0000& -0.0000& 0.0000& 0.0224& 0.0214& 0.8802\end{array}\right],\\ \hfill Q_3=\left[\begin{array}{cccccc}1.8321& 0.0103& 0.0167& -0.0000& -0.0000& -0.0000\\ 0.0103& 1.8297& 0.0151& 0.0000& 0.0000& -0.0000\\ 0.0167& 0.0151& 1.8413& -0.0000& 0.0000& -0.0000\\ -0.0000& 0.0000& -0.0000& 2.0919& 0.0091& 0.0141\\ -0.0000& 0.0000& 0.0000& 0.0091& 2.0907& 0.0133\\ -0.0000& -0.0000& -0.0000& 0.0141& 0.0133& 2.1004\end{array}\right].\end{array}$$

the $H_{\infty }$ controller feedback gain can be computed as

$$\begin{array}{c}\hfill K=Y{P}^{-1}=\left[\begin{array}{ccc}-36.12& 21.03& -16.49\\ -1.34& -9.32& -5.16\\ 22.59& -15.59& 4.45\end{array}\right].\end{array}$$

Figure 1. Trajectories of $x^T\left(t\right)x\left(t\right)$ in Example 2, the unit of T which is second.

Table 3 to shows the smallest value of $c_2$ with different $T=2,4,6,8,10$

Table 3. Shows the smallest value of $c_2$ with different $T=2,4,6,8,10$

T	2	4	6	8	10
By Theorem 1	5.5527	6.2606	7.0589	7.9589	8.9736
Stojanovic [20]	NF	NF	NF	NF	NF

Remark 3.

From Table 3, the table lists the smallest values of $c_2$ with different $T=2,4,6,8,10$. It is obvious that condition in [20] is not-feasible (NF) because $\dot{d}\left(t\right)=1.5$ for all T. It not consistent with the conditions $\dot{d}\left(t\right)=1.5<\rho <1$ in [20].

6. Conclusions

In this paper, finite-time $H_{\infty }$ control for nonlinear systems with time-varying delay is studied. By using a set of improved Lyapunov-Krasovskii functional including with some integral terms, a matrix-based on quadratic convex, combined with Wirtinger inequalities and some useful integral inequalities were proposed which illustrate the effectiveness of the obtained result in the numerical part. However, the improved method for the restriction on the upper bound of the delay derivative should be considered which means that a fast time-varying delay is allowed without any requirement on the derivative. New sufficient conditions of finite-time boundedness for above-mentioned class of system were given in term of linear matrix inequalities (LMIs).