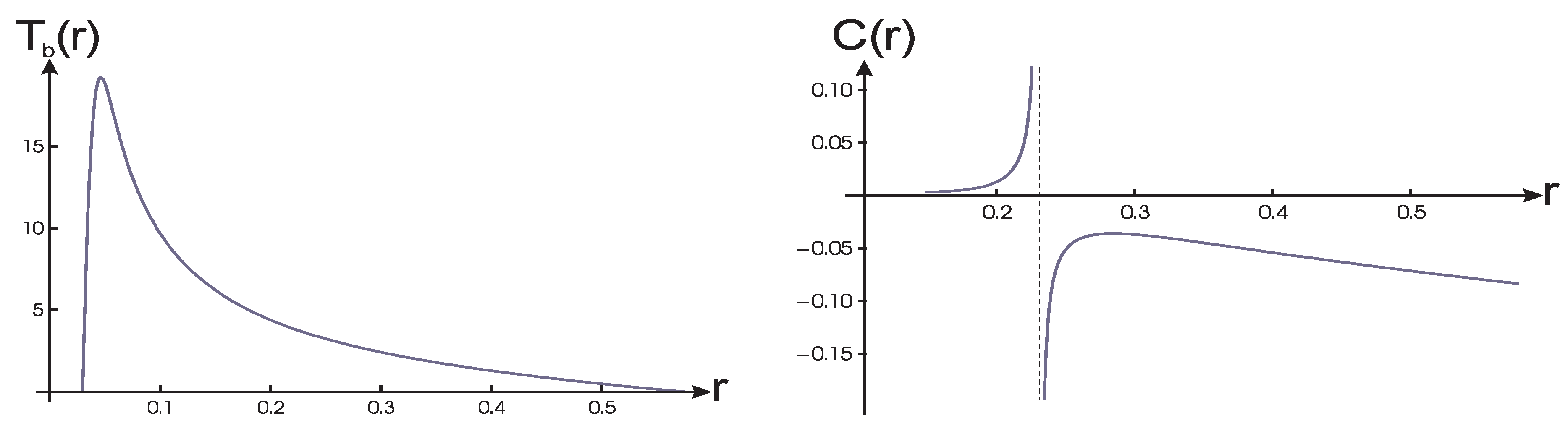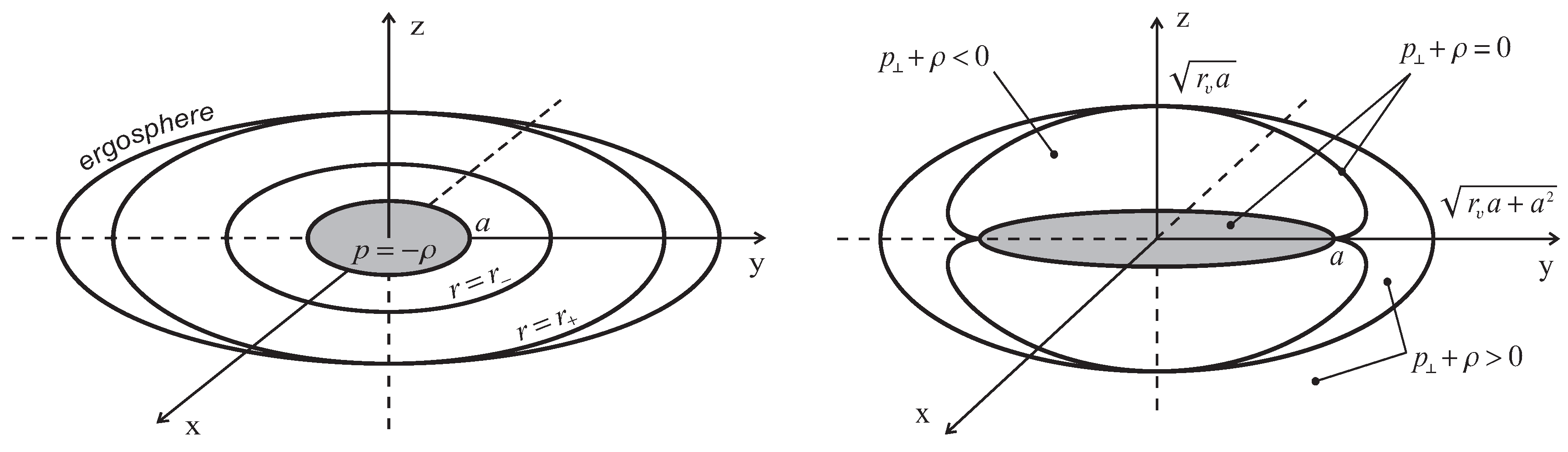1. Introduction
Regular spherical black holes with the de Sitter interiors and self-gravitating solitons replacing naked singularities are described by the Einstein equations with source terms specified by [
1,
2]
and satisfying the weak energy condition (WEC) which requires non-negativity of density for any observer on a time-like curve.
The early hypotheses concerning replacement of a singularity with a de Sitter core related appearance of the de Sitter vacuum with the self-regulation of geometry due to vacuum polarization effects [
3], with the existence of the limiting curvature [
4], and with the symmetry restoration at the GUT scale in the final stage of the gravitational collapse [
1,
5]. Appearance of a de Sitter core instead of the Schwarzschild singularity was found in the frame of a loop quantum gravity [
6,
7], of renormalization group improving [
8], and of a noncommutative geometry approach [
9].
Dark energy is defined by the equation of state
with
responsible for accelerated expansion
. The best fit,
at 68% CL [
10], distinguishes the cosmological constant
related to the vacuum density
as
.
The Einstein cosmological term
associated with the maximally symmetric de Sitter vacuum
can power the inflationary dynamics in the early Universe and at present but cannot provide a description of a
evolution because of
by virtue of the Einstein equations. Alternative models propose a dark energy of a non-vacuum origin (for a review see Reference [
11]).
A time-dependent and spatially inhomogeneous vacuum dark energy is suggested by the algebraic classification for the stress-energy tensors as defined by the algebraic structure of its stress-energy tensor [
1,
12], in which the maximal symmetry
is reduced to a partial symmetry
with the vacuum equation of state
in not more than two spatial directions. Introduced in this way vacuum dark fluid [
13] can be both evolving and clustering. Solutions to the Einstein equations present, dependently on coordinate mapping, regular cosmological models with variable
including initial, final and intermediate (if necessary) de Sitter stages [
14,
15,
16] (for a review, see Reference [
17]), and regular black holes (RBHs) and self-gravitating solitons G-lumps (particlelike structures without horizons replacing naked singularities) with the de Sitter interiors [
13,
18] (for a review, see Reference [
19]). Mass
M of an object is related to spacetime symmetry breaking from the de Sitter group at the origin [
2]. It can be presented as
where
,
, and
. The length scale
is intrinsic for de Sitter-Schwarzschild geometry matching the Schwarzschild exterior to the de Sitter interior directly [
3] or continuously [
1].
Black hole remnants, the end-products of the Hawking evaporation, have been discussed as a reliable source of dark matter for above forty years [
20,
21,
22] (for a recent review see Reference [
23]). In the case of a singular black hole there is no symmetry or quantum number which would prevent a black hole from a complete evaporation [
24,
25], while the complete evaporation would inevitably produce a crucial change in the spacetime structure [
26] as well as would lead to a fundamental open question—how to evaporate a singularity? [
27]. Quantum evaporation of a regular black hole involves a 2-nd order phase transition followed by quantum cooling and resulting in thermodynamically stable double-horizon remnant [
28,
29,
30] (for a review see Reference [
31]) free of the existential problems.
Primordial RBHs, their remnants and G-lumps can be considered as heavy dark matter candidates generically related to a vacuum dark energy via their de Sitter interiors [
18,
32]. In their GUT scale false vacuum interiors baryon and lepton numbers are not conserved, as a result they can induce proton decay in an underground detector like IceCUBE, which would present their observational signature in heavy dark matter searches [
32]. They can form graviatoms with electrically charged particles [
33]. Electromagnetic radiation of graviatoms which provides their observational signature, depends essentially on the energy density of the interior de Sitter vacuum and fits within the range available for observations [
33].
Spherical solutions specified by Equation (
1) belong to the Kerr-Shild class [
34]. General approach for obtaining axially symmetric solutions from spherical solutions of this class was developed by Gürses and Gürsey [
35]. It includes the Newman-Janis algorithm and allows to transform spherical solutions to the axially symmetric solutions which describe regular rotating black holes and spinning G-lumps replacing naked singularities [
36,
37,
38] (for a review see Reference [
39]). The de Sitter center is transformed to the equatorial de Sitter vacuum disk which is the generic property of all axial solutions obtained with the Newman-Janis algorithm [
36,
39].
Energy conditions distinguish two types of interiors. The 1-st type interior satisfies WEC and reduces to the de Sitter vacuum disk. The 2-nd type interior includes an additional two-dimensional closed S-surface of the de Sitter vacuum which contains the de Sitter disk as a bridge. WEC is violated in the internal cavities between the S-surface and the disk, which are thus filled with a phantom energy [
38,
39] specified by the equation of state
(
in
) [
40] (for a review see Reference [
41]). For solutions of the the Kerr-Schild class
;
.
Geometry of rotating objects includes ergoregions where processes of extraction of rotational energy can occur (see, e.g., a topical review in Reference [
42]). Spinning G-lump can have two ergospheres and ergoregion between them, or one ergosphere and ergoregion beyond it [
38].
For a G-lump with 2-nd kind interior a phantom energy is not screened by the horizon. This would make possible extraction of a phantom energy and lead to additional observational signatures for spinning G-lumps and graviatoms as heavy dark matter (DM) candidates providing a source of information about the scale and properties of a phantom energy.
In
Section 2 we outline the basic features of spherically symmetric objects, and their observational signatures as heavy DM candidates.
Section 3 is devoted to spinning compact objects with de Sitter interiors and additional opportunities following from existence of two types of their interiors with different dark energy (DE) contents.
Section 4 contains summary and discussion.
2. Spherical Objects with de Sitter Vacuum Interiors
The Einstein equations admit the class of regular spherically symmetric solutions with the de Sitter centers due to the algebraic structure of their source terms Equation (
1) satisfying WEC which ensures non-negativity of density [
1,
2,
12,
43]. They are described by the metrics [
1,
12]
Regularity at the origin is guaranteed by the de Sitter asymptotic as
where the metric function
tends to the de Sitter metric
with the de Sitter radius
related to the central density
as
; a source term Equation (
1) responsible for a metric Equation (
2) takes the de Sitter value
, and the spacetime symmetry restores to the de Sitter group [
2]. It can be confirmed by direct calculation of the Kretschmann curvature invariant
where
is the Riemann curvature tensor (see, e.g., Reference [
44]). For the geometries with the metrics Equation (
2) it reduces to
where
The Kretschmann curvature invariant tends to the de Sitter value as .
The number of spacetime horizons is directly related to the number of the de Sitter vacuum scales,
[
16]. In the case of two vacuum scales, at the origin and at infinity, a stress-energy tensor evolves between two de Sitter vacua, and the metric function
tends to the Schwarzschild-de Sitter metric
.
Spacetime with 2 vacuum scales can have not more than 3 horizons and admits 5 possible configurations shown in
Figure 1: regular cosmological black hole with mass constrained by
and confined by the event horizon
and the internal horizon
in the universe with the cosmological horizon
(
Figure 1 Left); two double-horizon states,
and
, and two one-horizon states (
Figure 1 Right) [
45]
De Sitter-Schwarzschild spacetime with one vacuum scale—at the de Sitter center—has two horizons. The metric function
in Equation (
2) tends to the Schwarzschild metric for
and to the Minkowski metric
as
. Spacetime is asymptotically flat and admits three possible configurations including a regular black hole with
, an extreme regular black hole with the double horizon
and G-lump with
.
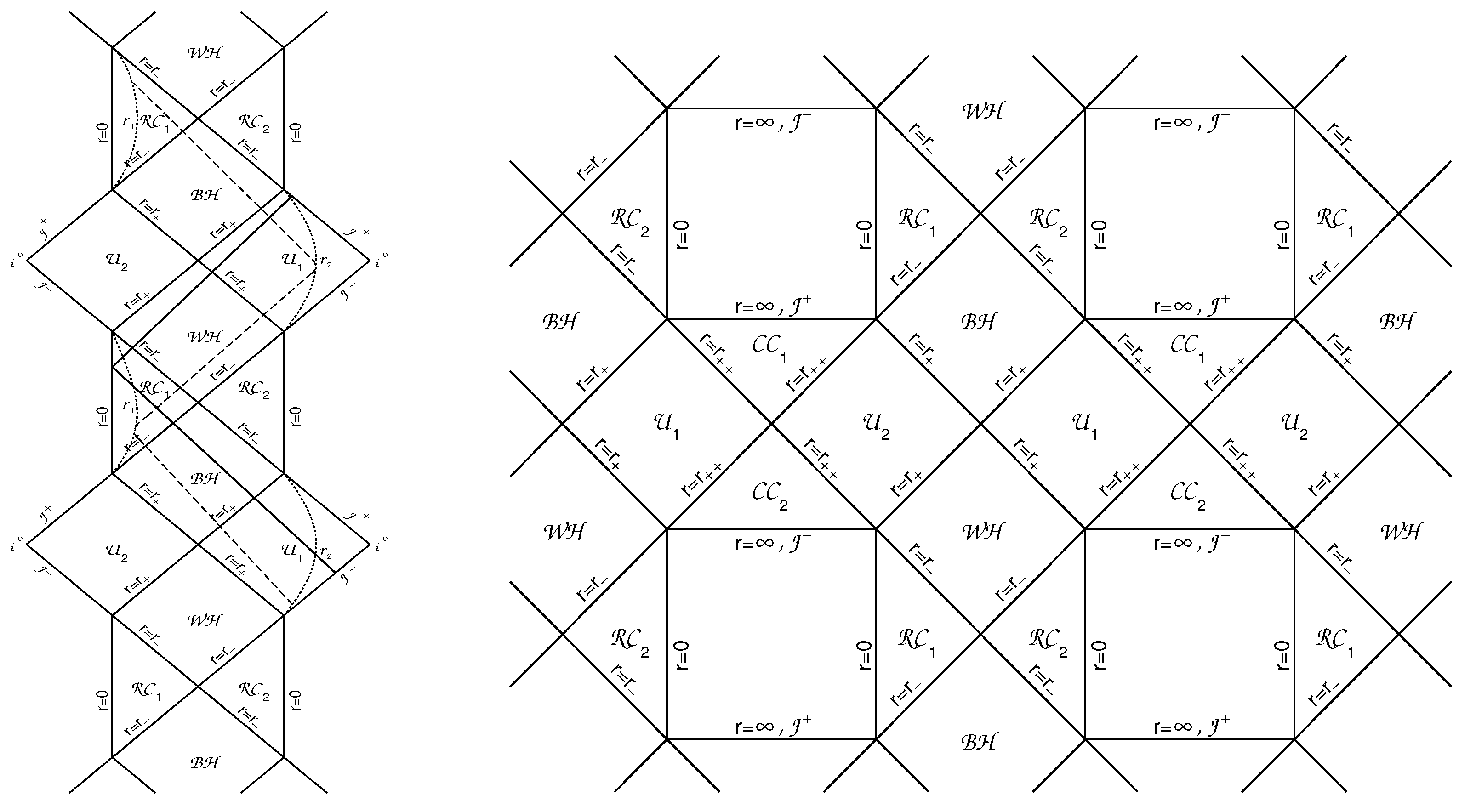
Global structure of regular spacetime with the de Sitter center is shown in
Figure 2 Left for the de Sitter-Schwarzschild spacetime and in
Figure 2 Right for spacetime with two vacuum scales.
Global structure is presented by the Penrose-Carter conformal diagrams which represent the maximal analytic extension for solutions Equation (
2), and contains an infinite sequence of regular black and white holes,
and
, whose future and past singularities are replaced with regular asymptotically de Sitter cores
, and parallel (not causally connected) universes
,
. The horizons are denoted by
,
,
. The surfaces
and
are the null (
) boundaries of the manifold, and
represents the spacelike infinities (see Reference [
14] and references therein).
Extension of diagrams in both directions (up and down) satisfies the requirement of
geodesic completeness of manifold, which means that all geodesics can be infinitely continued to both future and past except those which terminate in a singularity [
46].
In regular spacetime, geodesics never terminate. All infalling particles travel towards future regions of the Penrose-Carter diagram. Radial timelike geodesics satisfy the equation
where the dot denotes derivative with respect to the proper time. For the asymptotically flat spacetime they are shown in
Figure 2 Left [
47]. A particle with
arrives at the center where the type of geodesic changes, ingoing geodesic becomes outgoing (see
Figure 2 Left), and travel includes "reflections" from the regular timelike surfaces
in the future [
47]. A particle with
meets a turning point
at a surface
(dotted lines in
Figure 2 Left), and continues its motion towards growing
r. (Geodesics of this type exist also in the Reissner-Nordström spacetime where not all infalling particles terminate in a singularity [
46].)
Photons whose wave length is much less than a characteristic scale of geometry, propagate along the null geodesics guided by
, directed from
towards
and oriented under the angle
. In spacetime with two vacuum scales shown in
Figure 2 Right, geodesics behavior is similar.
In the field of a G-lump, test particles on radial geodesics penetrate the point and move outward it in the same space.
For the metrics from the class Equation (
2) the quantum temperature of any horizon reads [
48]
The partition function
calculated as the path integral sum for a canonical ensemble of spacetime metrics from the class Equation (
2) at the constant temperature of the horizon, entropy
and internal energy
are given by [
49]
The specific heat of a horizon can be written in the form [
30]
which allows to determine stability of a product of evaporation directly by its metric function.
Process of the quantum evaporation of RBH from its 3 horizons (shown in
Figure 1 Left) occurs with decreasing mass
M and is directed towards the double-horizon state,
(the curve
in
Figure 1 Right), where the temperature vanishes [
30]. Behavior of temperature-horizon dependence (shown in
Figure 3 Left) is generic, because the temperature evolves between two zero values, at the double horizons
and
, hence it must have a maximum somewhere in between, where specific heat
(shown in
Figure 3 Right) is inevitably broken and changes the sign [
28], which testifies for the 2-nd order phase transition followed by the quantum cooling [
28,
29,
30]. Maximum of the temperature is achieved at the phase transition and is given by
with
[
28].
Evaporation stops at the double-horizon state
where the temperature vanishes and specific heat becomes positive by virtue of Equation (
8), hence the end-product of evaporation is the thermodynamically stable remnant generically related to vacuum dark energy via its interior de Sitter vacuum ([
30,
50] and references therein). Its mass is determined by
[
28,
30] where the coefficient
depends on the form of the density profile.
For the pictures in this Section we applied the density profile [
1]
calculated in the simple semiclassical model of vacuum polarization effects in the gravitational field to which contribute all fields involved in a collapse, which results in
, where
is the gravitational (tidal) force, and
is the critical (de Sitter) force [
1,
2,
28].
For the density profile Equation (
9) with
and
GeV, the temperature at the phase transition
; the mass of the remnant
[
28].
The process of regular RBH evaporation is free of the existential problem crucial for a singular black hole due to the absence of a mechanism preventing complete evaporation [
24,
25], which involves an essential change in the spacetime structure from a spacetime with the distinguished (by the singularity) center to the globally regular maximally symmetric de Sitter or Minkowski spacetime. As a result, the question—how to evaporate a singularity?—also becomes irrelevant [
27].
Regular object without the event and internal horizons (the upper curve,
, in
Figure 1 Right) is identified as a self -gravitating soliton G-lump [
2,
28], which can be presented as a spherical bubble with decreasing from the center density (WEC requires
[
2]) and is described by the mini-superspace model with a single degree of freedom [
51] in the gravitational potential
. Energy spectrum of G-lump,
, is shifted down by the minimum of the potential
in
which corresponds to the binding energy. Here
is the transversal pressure (normalized to
). The energy of the zero-point vacuum mode
is remarkably similar to the energy of the Hawking radiation from the de Sitter horizon,
, which would be emitted in the presence of the horizon [
2]. For the density profile Equation (
9)
.
Regular primordial black holes and G-lumps can arise during the early inflationary stage(s) in the processes of collapse of quantum fluctuations arising from primordial inhomogeneities. For this reason their observational signatures as heavy dark matter candidates provide the signatures for inhomogeneity of the early universe [
32]. Probability of their formation in a quantum collapse and masses are constrained by [
33]
Possibilities of formation of compact objects with the de Sitter interior depend on the scales of the interior vacuum
and of the inflationary vacuum
. At the first inflation the scale of inflationary vacuum can be adopted as the GUT scale
. In the case of interior de Sitter vacuum of the GUT scale [
5],
, mass of an arising object is constrained by
, and most probable is formation of primordial RBHs. In the case of the Planck scale for interior de Sitter vacuum [
3,
4], mass range for collapsing objects admits production of G-lumps. Objects with small masses are produced with the bigger probability (for a detailed analysis see Reference [
33]).
One more possibility implied by the standard model is production of compact objects with the de Sitter interiors during the second inflationary stage in the early Universe. The standard model of particle physics predicts a phase transition at the QCD scale of 100–200 MeV which can lead to a second inflationary stage with duration of about 7–10 e-foldings (see Reference [
52] and references therein). In this case the formation constraints Equation (
10) admit any mass.
Primordial RBH remnants and G-lumps can capture charged particles and form graviatoms—gravitationally bound (
) quantum systems ([
33] and references therein). Conditions needed for the formation of graviatoms [
33] constrain the masses of particles by
GeV for
. This constraint admits GUT scale particles arising after the first inflation and leptoquarks survived in galactic haloes [
53].
Observational signatures of RBH remnants, G-lumps and graviatoms as heavy DM candidates provide information about the scale of the interior de Sitter vacuum. Objects with the GUT scale interiors, where baryon and lepton numbers are not conserved, may induce a proton decay in an underground detector. The rough estimate for the cross-section of such a process by the geometrical size of a nucleon (
cm
), would lead to one event per
years in one ton of a detector matter. In the 1 km
detector, like IceCUBE, there could be expected up to 300 events per year [
32] which can be observational signature of DM candidates with the de Sitter interiors in heavy dark matter searches at the IceCUBE experiment [
32].
Observational signature for graviatoms is provided by their electromagnetic radiation with the characteristic frequency essentially depending on the scale of the interior de Sitter vacuum. Most promising is the oscillatory radiation [
33]. For the density profile Equation (
9) the energy
GeV
appears within the range of observational possibilities (for cosmic photons up to
GeV [
54]).
3. Regular Spinning Compact Objects with DE Interiors
The spherically symmetric metrics Equation (
2) belong to the Kerr-Schild class [
34] and can be transformed to the axially symmetric metrics in general, model-independent form as was established by Gürses and Gürsey [
35] who have shown that the metrics of this class can be presented in the Lorentz covariant coordinate system, and developed the general approach based on the complex Trautman-Newman translations which include the Newman-Janis algorithm typically applied for constructing axially symmetric solutions describing spinning objects (for a review [
39]).
In the Boyer-Lindquist coordinates the Gürses-Gürsey metric reads [
35]
in the units
. The Lorentz signature is [- + + +], and
where
a is the angular momentum. The metric Equation (
11) contains a master function
which directly relates an axial solution with a spherical solution from which it originates. In the asymptotically flat case considered here the metric Equation (
11) reduces to that for the Kerr geometry,
as
[
35]. The mass parameter
coming from a spherical solution, is the finite positive mass generically related to the interior de Sitter vacuum and breaking of space-time symmetry from the de Sitter group for any solution from the class specified by Equation (
1) [
2].
In the axially symmetric geometry surfaces of constant
r are the oblate confocal ellipsoids [
46]
which degenerate, for
, to the equatorial disk
centered on the symmetry axis and bounded by the ring
. The Cartesian coordinates
are related to the Boyer-Lindquist coordinates
by
.
The asymptotically flat spacetime with the metric Equation (
11) can have not more than two horizons [
38]. They are defined by the equation
where
and
is the internal and event horizons, respectively.
Ergosphere is a surface of a static limit
. It satisfies the equation
Ergoregions are defined by
(which makes possible extraction of rotational energy). For black holes ergospheres and ergoregions exist for any density profile. In the case of a spinning G-lump the existence of ergospheres depends on the density profile. G-lumps can have two ergospheres and ergoregion between them, one ergosphere and ergoregion involving the whole interior, or no ergospheres [
38].
The stress-energy tensor responsible for the geometry Equation (
11) can be written in the form [
35]
in the orthonormal tetrad
The sign plus refers to the R-regions outside the event horizon and inside the internal horizon where the vector is time-like. The sign minus refers to the regions between the horizons where the vector is time-like. The vectors and are space-like in all regions.
The eigenvalues of the stress-energy tensor Equation (
18) in the co-rotating frame where ellipsoidal layers rotate with the angular velocity
, are defined by
in the regions outside the event horizon and inside the intern horizon where density is defined as the eigenvalue corresponding to the time-lik eigenvector
. They are expressed via a related spherical function
as
[
35]. With using Equation (
13) and definition of a mass function in Equation (
2) we obtain the relation between the density
and transversal pressure
and the density
and pressure
[
1,
3] for a related spherical solution
This gives the master relation basic for investigation of energy conditions for the class of regular spinning objects described by the metrics Equation (
11) obtained from the metrics Equation (
2) [
37,
38]
On the equatorial disk Equation (
15),
and
, the equation of state takes the form
and represents the rotating de Sitter vacuum in the co-rotating frame [
36,
37,
38].
Regular axially symmetric solutions satisfy the condition Equation (
1) and describe regular spinning black holes and solitons with the de Sitter vacuum interiors, asymptotically Kerr for a distant observer [
38]. The existence of interior de Sitter vacuum disk is the generic property of all regular spinning objects described by solutions obtained with using the Newman-Janis algorithm [
39].
Energy conditions distinguish two kinds of their interior regions. In the case when a spherical solution violates the dominant energy condition (DEC),
, we have
, and the function
in Equation (
22) vanishes only at approaching the de Sitter disk Equation (
15). The 1-st type interior of spinning objects satisfies WEC. It is shown in
Figure 4 Left, where we also plotted the horizons
,
, and the ergosphere.
The 1-st type interior of spinning objects satisfies WEC and looks as shown in
Figure 4 Left, where we also plotted the event horizon
, the internal horizon
and the ergosphere.
In the case when a spherical solution satisfies DEC,
, we have
and there can exist the closed de Sitter surface,
-surface
with the de Sitter disk as a bridge. In the cavities between the upper and down boundaries of the
-surface and the bridge WEC is violated,
,
, and cavities are filled with a phantom fluid. It is the 2-nd type interior shown in
Figure 4 Right, where
is a characteristic regularization parameter [
37,
38].
In a black hole with the 2-nd type interior the phantom region can be screened by the event horizon. In the case of a G-lump the phantom region is open to the outside region. Its -surface is located beyond the ergosphere, a phantom region fits within the ergoregion, as a result the processes of energy extraction can involve also the phantom energy.
For spinning G-lumps extraction of both rotational and phantom energy from their ergoregions is facilitated by the absence of the horizons. In
Figure 5 we show the
-surface (Left) plotted for
(where
a is the angular momentum normalized to
), and dependence of horizons on
a (Right) for different values
where
.
Pictures in this Section are plotted for the particular exact solution, originated from the spherically symmetric solution with the phenomenologically regularized Newtonian profile [
38]
where
is the density of the de Sitter vacuum on the disk
and
.
The cut-off length scale
in Equation (
23) is proportional to the de Sitter radius
. The parameter
gives the interior density at
and represents the energy density of self-interaction directly related to
(
), in accordance with the Zel’dovich idea [
55] to associate the cosmological constant with self-interaction [
38].
The cut-off parameter
allows us to present the mass of an object by the formula
, which corresponds to the volume in the closed de Sitter world, and displays the relation of the mass for rotating regular compact objects with the interior de Sitter vacuum revealed for the spherical objects of this class [
2].
For the density profile Equation (
9)
(
), and the condition
in Equation (
22) reduces to
. The width of the
-surface
as the function of
z has two maxima at
[
37,
38]. The relation between the width of the
-surface in the equatorial plane
and its height
defines the form of the
-surface by the oblateness parameter
.
The parameter
in Equation (
23) can be presented as
, where the dimensionless parameter
. Detailed form of the
-surface depends on the parameters
and on the specific angular momentum
. The quantities
,
and the oblateness parameter
are given by
The case
corresponds to
and to the oblate
-surface shown in
Figure 4. For
, we have
and the
-surface becomes prolate [
38].
4. Summary and Discussion
We considered the basic features of regular compact objects with DE interiors as predicted by analysis of regular solutions to dynamical equations governing their behavior. Such an approach yields the information about generic properties without model assumptions and constraints.
Algebraic classification of stress-energy tensors allows to introduce in general setting dynamical vacuum dark energy by reducing maximal symmetry of the Einstein cosmological term keeping the vacuum equation of state only in one or two spatial directions. In the considered here case the algebraic structure of a source term in the Einstein equations is specified by . Regular solutions of this class describe regular black holes, stable remnants of their quantum evaporation and self-gravitating vacuum solitons G-lumps replacing naked singularities. The basic generic feature of these objects is the de Sitter vacuum interiors.
For spinning regular objects of this class dynamical equations predict the existence of two kinds of regular interiors, one preserving and the other violating the weak energy condition. The 1-st type interior satisfies WEC and reduces to the equatorial disk of the de Sitter vacuum. In the 2-nd type the interior de Sitter region is presented by a closed -surface of the de Sitter vacuum with the equatorial de Sitter disk as the bridge. The cavities between the -surface are filled with a phantom substance () where WEC is violated.
Phantom energy defined by
with
was introduced as kind of a dark energy which could be responsible for the observed acceleration of our universe in default of a time evolving cosmological constant [
40]. In the most of models phantom energy originates from scalar field(s) with negative kinetic energy and may involve extra dimensions (for a review [
41]).
As follows from the general analysis, a phantom fluid appears inside the regular spinning objects described by regular axially symmetric solutions of the Kerr-Schild class obtained with using the Gürsey-Gürses approach including the Newman-Janis algorithm. In this case a phantom fluid is essentially anisotropic, the phantom equation of state is valid for a transversal pressure, with . It violates the weak energy condition (which implies a non-negative energy density for any local observer on a timelike curve) and can have negative energy density for a certain class of observers. A phantom energy appears in these objects without explicit introduction of additional entities as generic ingredient directly related to the algebraic structure of their stress-energy tensors. This question needs further investigation for deeper understanding of the physical nature of a phantom energy.
Primordial regular black holes and G-lumps appear from primordial quantum fluctuations during early inflationary stages when they can capture charged particles and form graviatoms.
Regular black hole remnants, G-lumps and graviatoms can be considered heavy DM candidates with DE interiors responsible for their additional observational signatures. They can induce proton decay in an underground detector which can serve as their observational signature for heavy dark matter searches at the IceCUBE experiment. For the charged remnants [
37] one can expect much stronger effect of falling down its center and in consequence a much stronger effect of induced proton decay [
32].
Graviatoms radiate within the range of the ultra-high energy ∼10 GeV which in principle can be observed and serve as observational signature for graviatoms as heavy DM candidates and as a source of information about the energy scale of the interior de Sitter vacuum. Information about the scale and properties of a phantom energy can in principle come from observational signatures for spinning remnants, G-lumps and graviatoms with the 2-nd kind interiors, which contain phantom energy.
Efficiency of energy extraction from G-lumps ergoregions is facilitated by the absence of the horizons. For spinning G-lumps with the 2-nd kind interiors the phantom regions are not screened by the horizons. Open character of the phantom interiors for spinning G-lumps suggests the existence of mechanisms of extraction of a phantom energy from their ergoregions and of related astrophysical consequences. These questions need further investigation.