Image Zooming Based on Two Classes of C1-Continuous Coons Patches Construction with Shape Parameters over Triangular Domain
Abstract
1. Introduction
2. Materials and Methods
2.1. Rational Quadratic Trigonometric Hermite Functions with Shape Parameters
- and ,
- Monotonicity: For fixed , , , and , are monotonically increasing for ; is monotonically decreasing for ,
- End-point properties:
2.2. Two Classes of Coons Patches Constructions over Triangular Domain
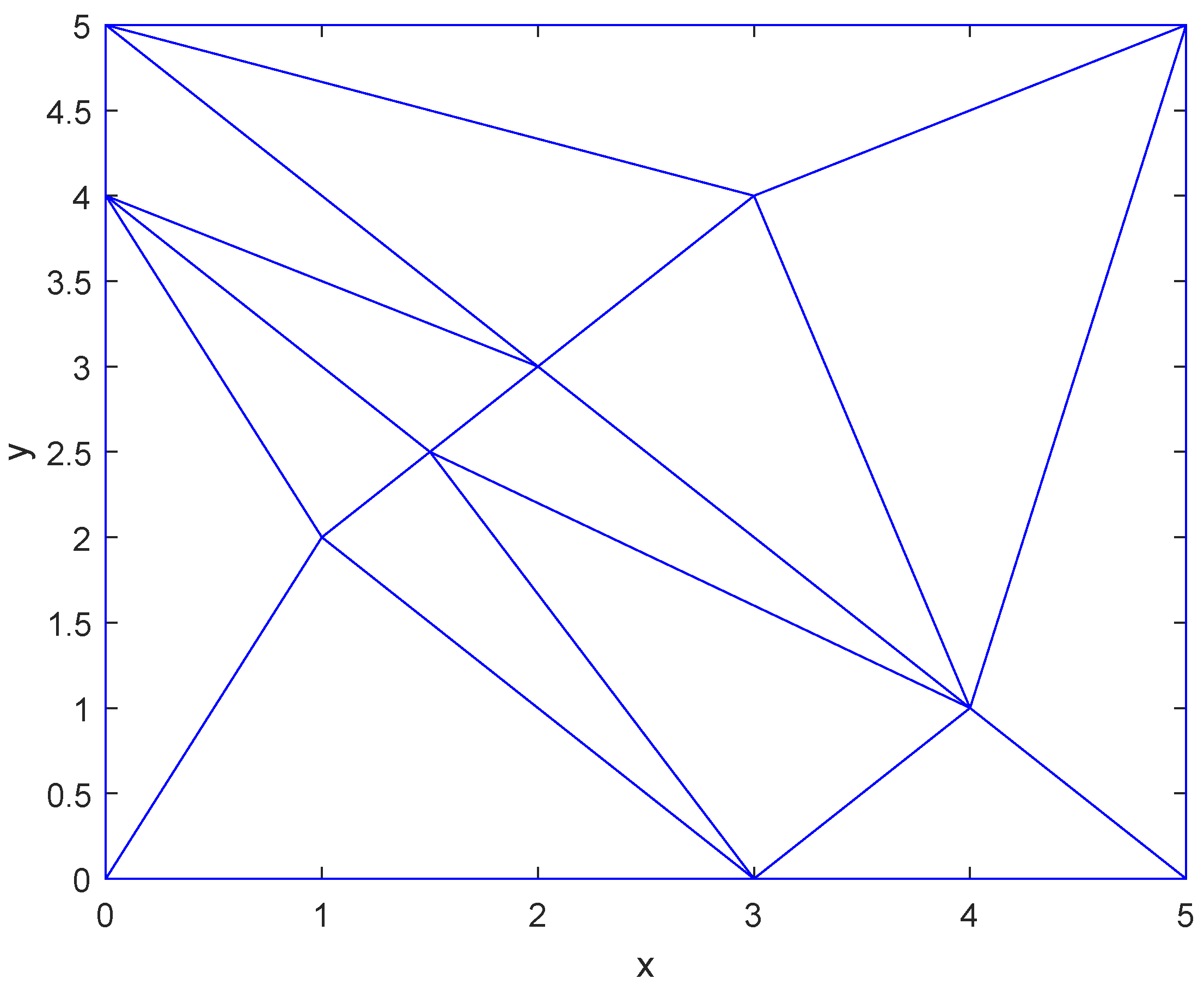
2.2.1. Relationship between Barycentric Coordinates and Cartesian Coordinates
2.2.2. Coons Patch Construction Based on Side–Side Method
2.2.3. Coons Patch Construction Based on Side–Vertex Method
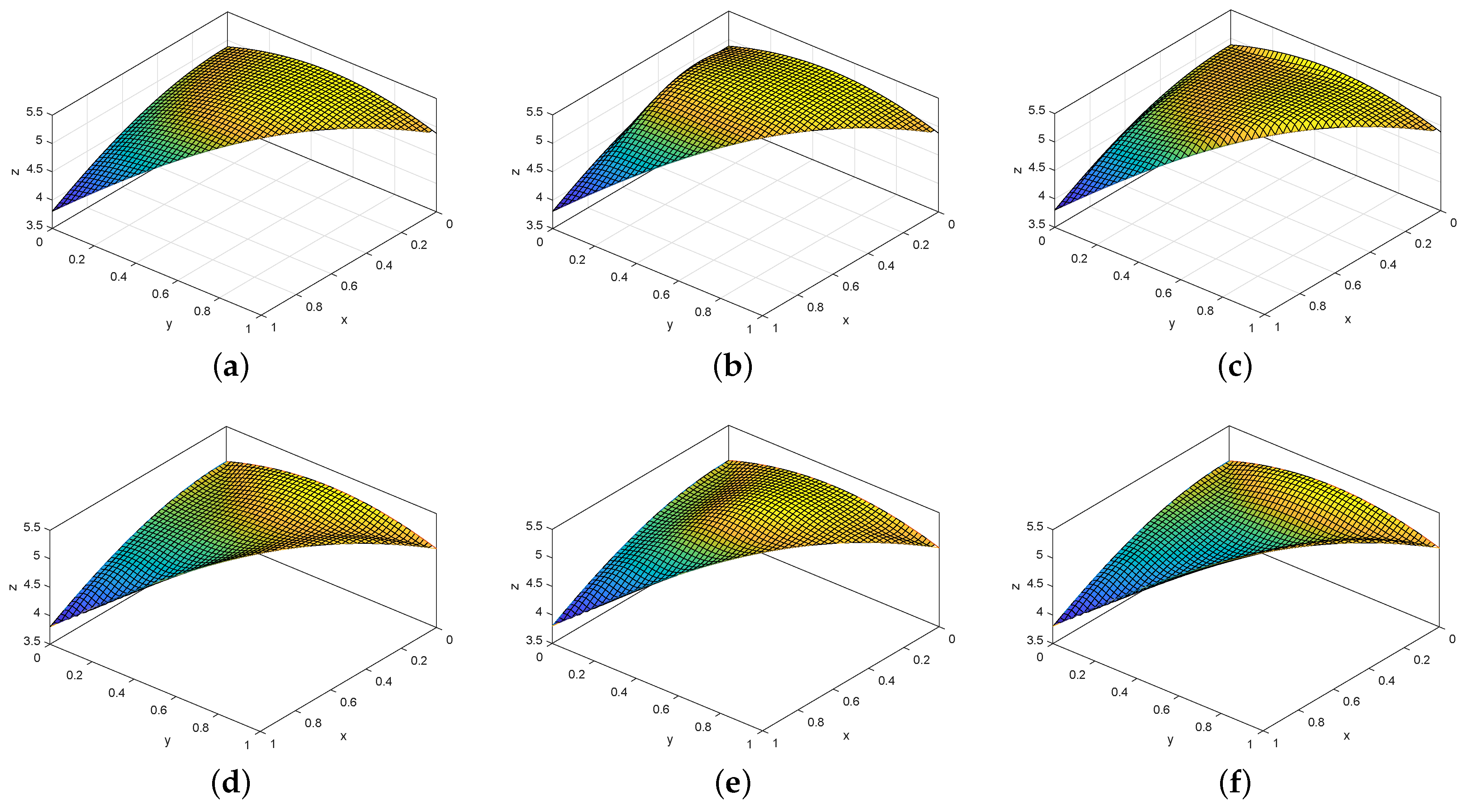
2.3. Region Control of Shape Parameters
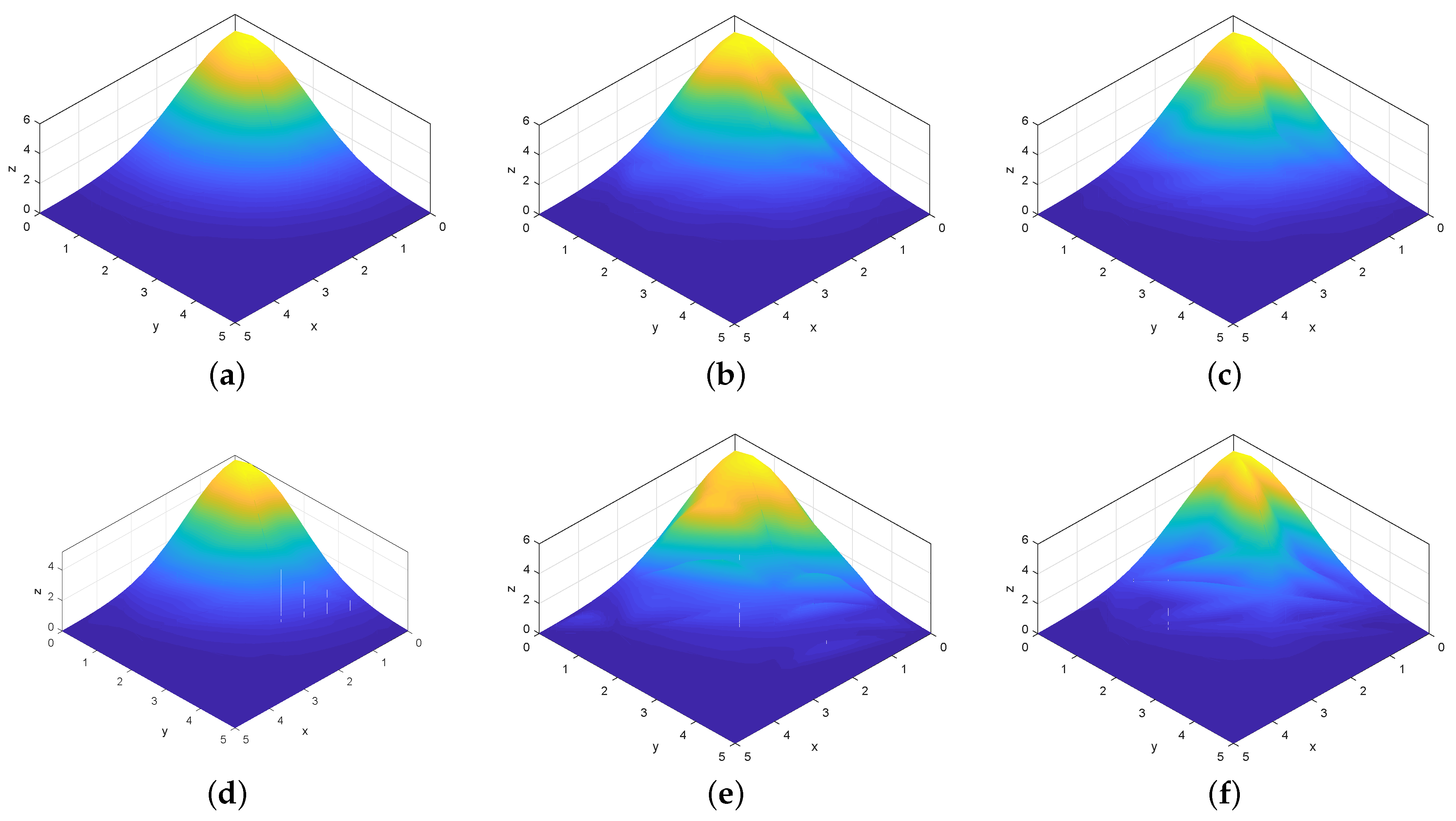
2.4. Image Zooming Based on Two Classes of Coons Patches Construction over Triangular Domain
Method of Image Zooming by Coons Patch Construction
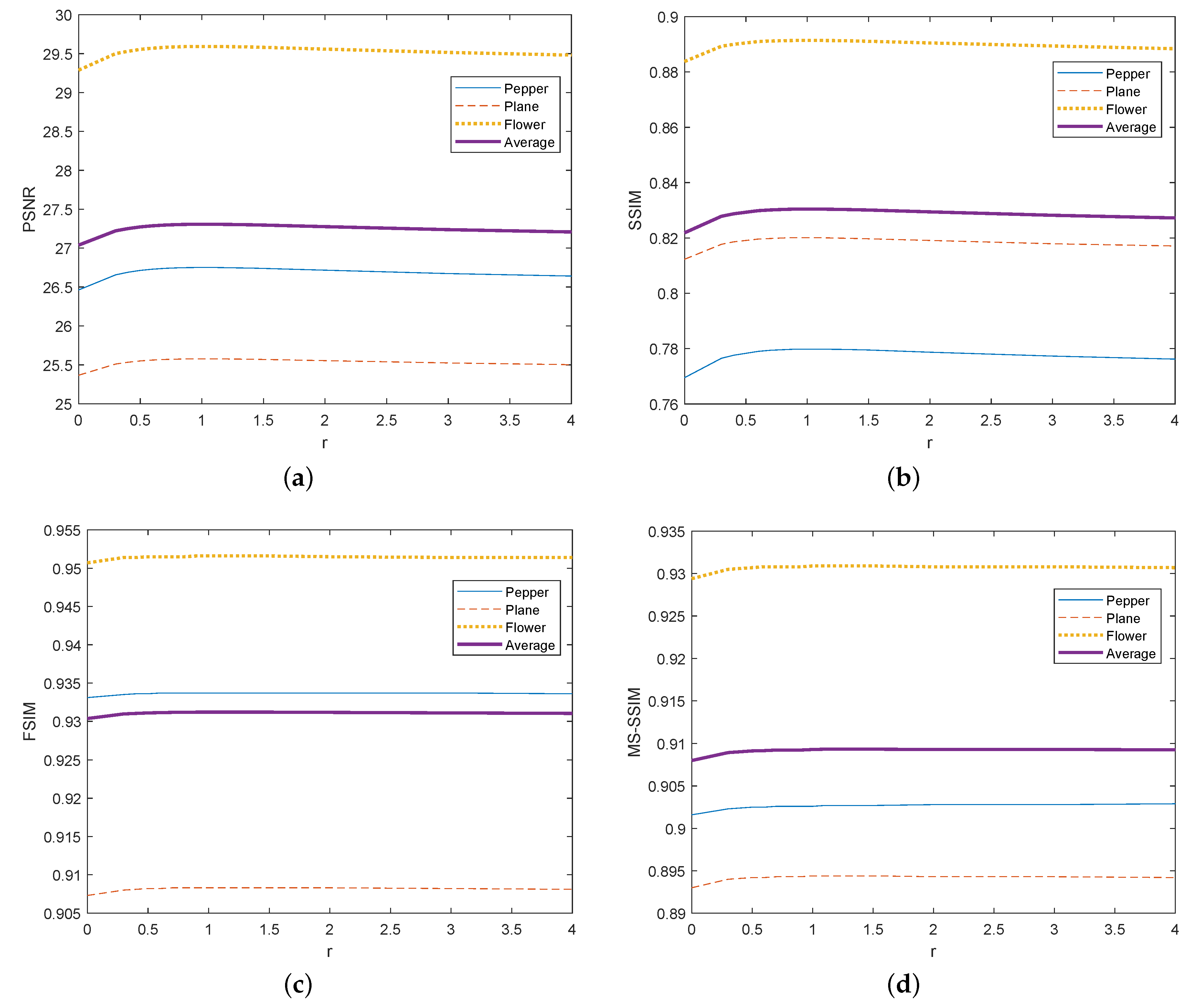
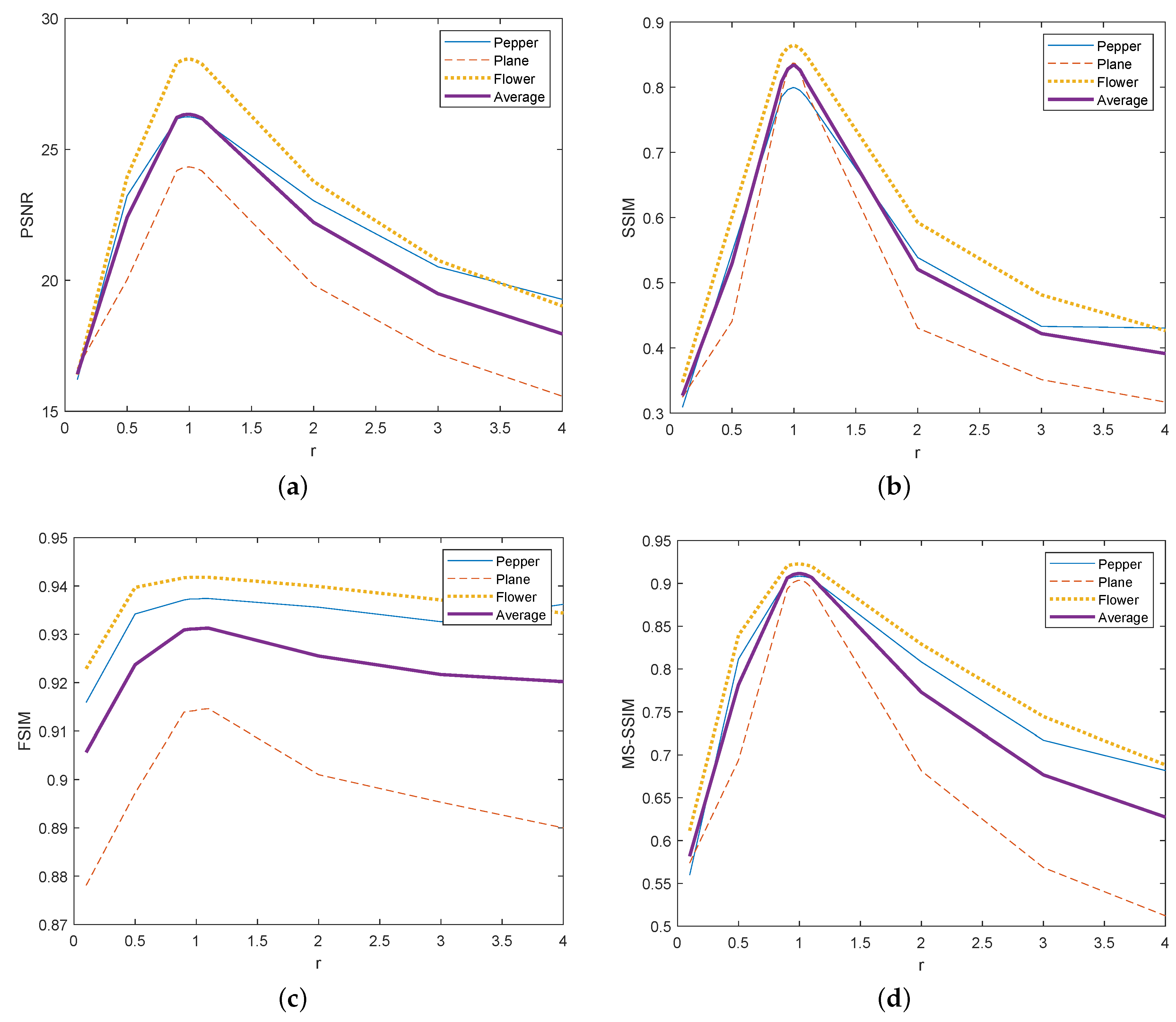
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PSNR | Peak Signal to Noise Ratio |
| SSIM | Structural Similarity |
| FSIM | Feature Similarity |
| MS-SSIM | Multiscale Structural Similarity |
| SS | Side–side Method Based on the Rational Quadratic Trigonometric Hermite Functions |
| SV | Side-vertex Method Based on the Rational Quadratic Trigonometric Hermite Functions |
References
- Gonzalez, R.C.; Woods, R.E. Image Enhancement in the spatial Domain. In Digital Image Processing; Dworkin, A., Ed.; Prentice Hall: New York, NY, USA, 2002; pp. 76–142. [Google Scholar]
- Keys, R.G. Cubic convolution interpolation for digitalimage processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Park, S.K.; Schowengerdt, R.A. Image reconstruction by parametric cubic convolution. Comput. Vis. Graph. Image Process. 1983, 23, 258–272. [Google Scholar] [CrossRef]
- Lehmann, T.M.; Gonner, C.; Spitzer, K. Survey: Interpolation methods in medical image processing. IEEE Trans. Med. Imaging 2000, 18, 1049–1075. [Google Scholar] [CrossRef] [PubMed]
- Muresan, D.D.; Parks, T.W. Adaptively quadratic (AQua) image interpolation. IEEE Trans. Image Process. 2004, 13, 690–698. [Google Scholar] [CrossRef]
- Han, P.; Su, Z.; Liu, X. Image interpolation using Coons surface patch with shape control parameters. J. Comput.-Aided Des. Comput. Graph. 2005, 17, 976–980. [Google Scholar]
- Li, J.; Zhao, D.; Lu, Y. Image Zooming Using Rational Coons Interpolation patch with shape Parameters. J. Comput.-Aided Des. Comput. Graph. 2011, 23, 1853–1859. [Google Scholar]
- Barnhill, R.E.; Birkhoff, G.; Gordon, W.J. Smooth interpolation in triangles. J. Approx. Theory 1973, 8, 114–128. [Google Scholar] [CrossRef]
- Barnhill, R.E.; Gregory, J.A. Compatible smooth interpolation in triangles. J. Approx. Theory 1975, 15, 214–225. [Google Scholar] [CrossRef]
- Barnhill, R.E.; Gregory, J.A. Polynomial interpolation to boundary data on triangle. Math. Comput. 1975, 29, 726–735. [Google Scholar] [CrossRef]
- Gregory, J.A. Smooth interpolation without twist constraints. In Computer Aided Geometric Design; Barnhill, R.E., Resenfeld, R.F., Eds.; Academic Press: New York, NY, USA, 1974; pp. 71–88. [Google Scholar]
- Gregory, J.A. A blending function interpolant for triangles. In Multivariate Approximation; Handscomb, D.C., Ed.; Academic Press: New York, NY, USA, 1978; pp. 279–287. [Google Scholar]
- Gregory, J.A. C1 rectangular and nonrectangular surface patches. In Surfaces in Computer Aided Geometric Design; Barnhill, R.E., Boehm, W., Eds.; North-Holland: Amsterdam, The Netherlands, 1983; pp. 25–33. [Google Scholar]
- Nielson, G.M. The side vertex method for interpolation in triangles. J. Approx. Theory 1979, 25, 318–336. [Google Scholar] [CrossRef][Green Version]
- Hagen, H. Geometric surface patches without twist constraints. Comput. Aided Geom. Des. 1986, 3, 179–184. [Google Scholar] [CrossRef]
- Hagen, H. Curvature continuous triangular interpolants. In Methods in CAGD; Lyche, T., Schumaker, L., Eds.; Academic Press: Oslo, Norway, 1989; pp. 373–384. [Google Scholar]
- Nielson, G.M. A transfinite, visually continuous, triangular interpolant. In Geometric Modeling, Applications and New Trends; Farin, G., Ed.; SIAM: Philadelphia, PA, USA, 1987; pp. 235–246. [Google Scholar]
- Tang, Y.; Wu, X.; Han, X. C1-Continuous H-Type Coons Patches on Triangles. J. Eng. Graph. 2010, 31, 97–103. [Google Scholar]
- Wu, X.; Han, X.; Luo, S. C1-Continuous triangular Coons Patches with shape parameters. Comput. Appl. 2008, 28, 3123–3125. [Google Scholar]
- Wu, X.; Han, X.; Luo, S.; Wang, J. C1-Continuous C-Type Coons Patches on Triangles. Appl. Res. Comput. 2009, 26, 1538–1540. [Google Scholar]
- Wu, X.; Han, X.; Tang, Y. C1-Continuous T-Type Coons Patches on Triangles. Comput. Eng. Appl. 2010, 46, 173–176. [Google Scholar]
- Giachetti, A.; Asuni, N. Real-time artifact-free image upscaling. IEEE Trans. Image Process. 2011, 20, 1538–1540. [Google Scholar] [CrossRef]
- Li, X.; Orchard, M.T. New edge-directed interpolation. IEEE Trans Image Process. 2001, 10, 1521–1527. [Google Scholar]
- Hung, K.W.; Siu, W.C. Single-image super-resolution using iterative Wiener filter based on nonlocal means. Signal Process. Image Commun. 2015, 39, 26–45. [Google Scholar] [CrossRef]
- Abbas, S.; Hussain, M.Z.; Irshad, M. Image interpolation by rational ball cubic B-spline representation and genetic algorithm. Alex. Eng. J. 2017, 57, 931–937. [Google Scholar] [CrossRef]
- Coons, S.A. Surfaces in Computer-Aided Design of Space Forms; Technical report MAC-TR-41; MIT: Cambridge, MA, USA, 1967. [Google Scholar]
- Zhu, Y.P. C2 positivity-preserving rational interpolation splines in one and two dimensions. Appl. Math. Comput. 2018, 316, 186–204. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.Q.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Simoncelli, E.; Bovik, A. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A Database of Human Segmented Natural Images and its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision (ICCV 2001), Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar]


| Parameter | ||||||
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | |
| 0.9 | 1 | 2 | 3 | 1 | 4 | |
| 1 | 1.01 | 1 | 1.06 | 1 | 1.05 |
| Image | Bilinear | Bicubic | ICBI | NEDI | SR-NLM | RBC | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pepper | ||||||||||
| Plane | ||||||||||
| Flower | ||||||||||
| Average |
| Image | Bilinear | Bicubic | ICBI | NEDI | SR-NLM | RBC | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pepper | ||||||||||
| Plane | ||||||||||
| Flower | ||||||||||
| Average |
| Image | Bilinear | Bicubic | ICBI | NEDI | SR-NLM | RBC | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pepper | ||||||||||
| Plane | ||||||||||
| Flower | ||||||||||
| Average |
| Image | Bilinear | Bicubic | ICBI | NEDI | SR-NLM | RBC | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pepper | ||||||||||
| Plane | ||||||||||
| Flower | ||||||||||
| Average |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Zhu, Y. Image Zooming Based on Two Classes of C1-Continuous Coons Patches Construction with Shape Parameters over Triangular Domain. Symmetry 2020, 12, 661. https://doi.org/10.3390/sym12040661
Tang Y, Zhu Y. Image Zooming Based on Two Classes of C1-Continuous Coons Patches Construction with Shape Parameters over Triangular Domain. Symmetry. 2020; 12(4):661. https://doi.org/10.3390/sym12040661
Chicago/Turabian StyleTang, Yunyi, and Yuanpeng Zhu. 2020. "Image Zooming Based on Two Classes of C1-Continuous Coons Patches Construction with Shape Parameters over Triangular Domain" Symmetry 12, no. 4: 661. https://doi.org/10.3390/sym12040661
APA StyleTang, Y., & Zhu, Y. (2020). Image Zooming Based on Two Classes of C1-Continuous Coons Patches Construction with Shape Parameters over Triangular Domain. Symmetry, 12(4), 661. https://doi.org/10.3390/sym12040661





