Abstract
For a scalar field in an exponentially expanding universe, constituent modes of elementary excitation become unstable consecutively at shorter wavelength. After canonical quantization, a Bogoliubov transformation reduces the minimally coupled scalar field to independent 1D modes of two inequivalent types, leading eventually to a cosmological partitioning of energy. Due to accelerated expansion of the coupled space-time, each underlying mode transits from an attractive oscillator with discrete energy spectrum to a repulsive unit with continuous unbounded energy spectrum. The underlying non-autonomous Schrödinger equation is solved here as the wave function evolves through the attraction-repulsion transition and ceases to oscillate.
1. Introduction
Due to the accelerated expansion of the universe, fundamental modes of a weakly coupled scalar field eventually become unstable. It is shown here that a Bogoliubov transformation may reduce the system to a collection of oscillators with time dependent frequencies that become pure imaginary at times of attraction–repulsion transition. The main question to be answered here is what the Schrödinger wave function looks like as it evolves across the attraction–repulsion transition. That is answered by solving the non-autonomous Schrödinger equation exactly. Before that, the spectral properties of the quantum field are analysed in the Fock picture. Possible implications in cosmology and in the mathematical representation theory of Boson fields, are discussed.
Over the last decade it has become generally accepted that over intergalactic scales the universe is isotropic, spatially flat, expanding, and accelerating [1,2,3,4,5,6,7,8]. These assumptions lead to a simple form of the Friedmann equation (e.g., [9]). Neglecting the radiation component of energy,
where G is the universal gravitational constant, is the mass density of matter, and is the cosmological constant which is assumed to be positive to produce an accelerating universe. The energy density of the dark component is . As time increases and the universe expands, the mass density will decrease. Therefore at large times, will be asymptotic to . Carroll and Chatwin-Davies [10] view this as a consequence of the second law of thermodynamics, even without reference to general relativity. The FLRW universe with this scale factor is equivalent by a change of coordinates to half of the maximally symmetric de Sitter space which can be defined as a four dimensional hyper-surface satisfying
and embedded in 1+4-dimensional flat Minkowski space (e.g., Chap. 5.4 of [11].)
The field equations are routinely solved exactly in terms of a discrete expansion of spherical harmonics satisfying appropriate boundary conditions. The consideration of boundary conditions is not straightforward [12]. The choice of boundary conditions, and its relativistic consequences, are discussed in Appendix B. Consideration of the canonical stress-energy tensor constructed from a de Sitter-invariant Lagrangian, lead to a boundary condition that is unusual in this context. The set-up of the classical boundary value problem and its standard solution by separation of variables are given in Section 2.1 and Appendix A. This construction is well known but it is needed to explain the origin of repulsive modes.
Section 2.2 is concerned with the energy spectrum. After second quantization, a Bogoliubov transformation is applied to reduce the Hamiltonian to that of a sum of independent subsystems of minimal degrees of freedom. However, unlike in usual free Boson field theory (e.g., [13]) and unlike in the many-body theory of condensed matter (e.g., [14]), the Hamiltonian is not a sum of quasi-particle number operators. The indefinite Hamiltonian involves two of the six types of Broadbridge’s inequivalent normal forms [15] for quadratic Boson operators. After canonical quantization, the Hamiltonian is composed of light and a dark components, quantum oscillators as well as quantum repulsive units . The repulsive units have a continuous spectrum of energy eigen-distributions akin to Schroer’s “jelly states” [16]. As time increases, modes of progressively high wave number cease to be oscillatory and join the collection of unbounded repulsive units. The fundamental non-autonomous modes are analysed in two ways. The first is to classify the spectrum of the modal Hamiltonian that is frozen in time (Section 2.2). The second, which is the main objective, is to directly solve the non-autonomous Schrödinger equation that evolves from a harmonic oscillator to a repulsive unit (Section 2.3). Initializing from the well defined vacuum in the distant past, it is demonstrated that the expectation value of each quantum field mode progresses through a finite number of oscillations before it remains on one side or another of . The solution is readily extended to other initial conditions in the distant past. The example is given of a linear combination of the past vacuum with a past single particle state.
The covariant massless Klein-Gordon field develops unstable modes when it is minimally coupled to an exponentially accelerating de Sitter universe [17,18]. However when unstable classical modes are quantized the Fock representation is no longer physically relevant [19,20,21,22]. The absence of number operators [23] in the commutant of the Hamiltonian is associated with the breakdown of the Fock-Cook representation of the quantum algebra. It has been proven [24] that no de Sitter-invariant Fock vacuum state exists for a massless minimally coupled field on de Sitter space. Allen concludes that either (1) the standard Fock space construction must be abandoned or (2) the vacuum state must break full de Sitter invariance. Since breaking invariance is a far less radical idea than the abandonment of the familiar Fock representation, there has been much investigation into possible vacua for the massless minimally coupled field that are invariant under a subgroup of [24,25,26,27]. This is in contradistinction with the weakly coupled massive scalar field for which there are many fully invariant states, including the Bunch-Davies vacuum [28] which coincides with the minimum energy state in the distant past. One may instead, consider Allen’s first option: the abandonment of the Fock space construction. The break-down of the Fock representation is entirely due to the unstable modes and as we will show, there are only finitely many of these modes at any time. The repulsive modes that are discussed further in Section 3 are dark in the sense that they have no particle or radiation interpretation and so cannot be detected by usual methods that rely on absorption and scattering of particles and oscillatory waves. This phenomenon occurs already at the level of semi-classical quantization wherein the scalar field is quantized but the gravitational tensor field is classical.
The inflationary period is most simply represented by a scalar inflaton field [29] that was coupled to a universe that was expanding exponentially as , with very large [30,31]. The radius of the observable universe is estimated to be 47 billion light years compared to only 14 billion light years for the Hubble radius [32]. The favoured explanation is expansion that is evidenced by correlations over large space-like separations observed in the cosmic microwave background [33]. The inflationary exponential time scale must be several orders of magnitude smaller than the duration of the inflation period, which is supposed to be . After the sharp big bang, dynamical fields should have a broad frequency spectrum. As discussed in Section 3.1, after many dynamical modes have been destabilised at successively higher energy, the critical radial wave number is proportional to . As is familiar from spherical harmonic expansions, the principal quantum energy levels have degeneracy of order . These two facts combined, ensure that the dark energy density is approximately constant in time during inflation.
Section 3.2 is a discussion on the existence of a preferred physical representation of the quantum field algebra of observables, which is conventionally taken to be a C*-algebra generated by the Weyl operators [34]. Use of a countable basis of exact field solutions in a finite universe has resulted in the number of repulsive units remaining finite, although increasing with time. This means that although the repulsive modes have neither a natural vacuum representation nor a particle interpretation, Stone’s theorem guarantees that the Hilbert space representation is unique, modulo a unitary automorphism. This preferred physical representation enables meaningful calculations and predictions about the system. This result is significantly different from that of the approximate continuous Fourier expansion [18], since approximation of finite space by spatially infinite space, artificially leads to a problematic infinite number of unstable modes. The remaining infinitely many quantum oscillator modes still have a unique Fock-Cook representation, so overall there is still a well defined preferred physical representation.
2. Canonical Field Quantization and Unstable Modes
2.1. Classical Klein-Gordon Field in an Accelerating Space-Time
Assuming the geometry of a spatially isotropic expanding universe, the standard metric is
Here, , are to be interpreted as material coordinates that maintain fixed values on matter that is moving with the mean expansion of the universe and t is cosmic time that would be measured in such a reference frame. The generally covariant Klein-Gordon equation is
where represents the covariant derivative, m is the particle rest mass, is the coupling constant for matter wave-gravity interaction, and is the Ricci Scalar.
is the divergence of the gradient or the Laplace-Beltrami operator,
Changing to a conformal time coordinate,
then the metric conforms to that of Minkowski,
From here on, attention will be focussed on exponential expansion with Hubble time
Defining , as explained in [18], (1) is expressed as
where
and □ is the standard d’Alembertian operator. In these coordinates, the Klein-Gordon equation resembles the standard Lorentz-invariant scalar wave equation, allowing one to develop an illustrative quantum field theory using the familiar notation of canonical quantization.
For minimal coupling, and . In that case the ratio of the mass-dependent term to the mass-independent term within is . Even for the massive Higgs particle, during the inflation period this ratio is smaller than , due to the large value of . During inflation, particle rest mass has little influence on field dynamics. For illustrative purposes, we will consider . Then with minimal coupling ,
The focus from here will be on separated modes with distinct radial wave number k. This analysis will make no further assumptions about the effective potential energy function of the mean inflaton field that would allow for development of observed structures. In fact, in the minimal chaotic inflaton field model, the effective potential is indeed quadratic at small- but it needs a higher-order plateau at large- (e.g., [35] ).
When examining the analytic structure of relativistic wave equations, it is convenient to assume that ℏ (Planck’s constant divided by ), speed of light c and reference radius have been scaled to unity. The length scale , time scale and mass scale may be chosen so that
After this choice of scaling, other important constants such as G and will be scaled to non-unit dimensionless values:
The reference radius is the universal radius at a particular reference time. In epochs well after inflation, the reference time is usually taken to be the present, labelled here as . For studies of inflation dynamics, a more appropriate reference time would be around after the singularity at . From the perspective of de Sitter space, the singularity at may be viewed as a coordinate singularity. The standard FLRW coordinate system covers only half of de Sitter space. There is another coordinate patch that covers an earlier period of FLRW contraction. There is no consideration here of the structure of the inflaton field prior to exponential expansion when the de Sitter model is inappropriate. For convenience, the circumflex will be left off dimensionless variables , and . However, the numerical values of dimensional quantities will be recalled in later discussions when necessary.
As discussed in Appendix B, there exists a reference frame with a system of co-moving (material) space-like coordinates, by which the universe is described as the interior of a sphere within which the de Sitter metric applies. The scalar field will be supplemented by the boundary condition
It can be seen by constructing the canonical stress-energy tensor that this condition guarantees zero flux of energy across the material boundary which is a moving boundary in another system of physical coordinates.
By separation of variables (Appendix A), the solution to (7) may be expanded in terms of spherical harmonic basis functions
where and are expansion coefficients. are solutions of
wherein are eigenvalues of the radial wave number, to be determined from the boundary conditions. satisfies a non-autonomous differential equation whose solutions are nevertheless well known in terms of Hankel functions or equivalently as Bessel functions,
, with
and
where and are Bessel functions of order , of the first and second kind respectively. are well-known spherical Bessel functions
As recounted in Appendix A, the classical time-dependence of a dynamical mode with radial wave number k may be expressed in terms of a time-dependent angular frequency ,
This leads to a time dependent dispersion relation (Figure 1),
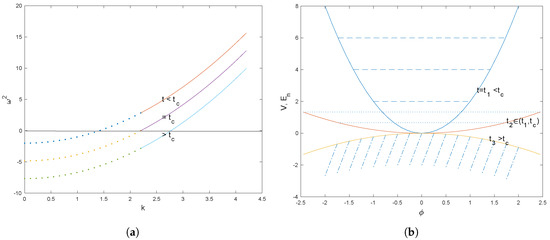
Figure 1.
(a) Time dependent dispersion relation (schematic) for minimally coupled Klein-Gordon equation. for the minimum discrete wave number k becomes negative at critical time . (b) Classical potential energy and quantum energy levels for time-dependent Hamiltonian. As time increases, the attractive force weakens and discrete energy gaps narrow between bound eigenstates. At times , the force is repulsive and the Hamiltonian has continuous spectrum with no lower bound.
Since the Bessel function of the second kind is singular at , a finite-valued requires . A is absorbed into and . Equation (13) with the boundary condition (10) determines that in Equation (11), covers the set of eigenvalues of a Sturm-Liouville problem, satisfying
It follows that the set of admissible eigenvalues is the set of zeros of the derivative spherical Bessel function,
where ℓ is any non-negative integer. k can take one of a discrete set of values being the s’th positive zero of . In the notation of Antosiewicz [36], k can be . It is known that the zeros of and of are interlaced [37]:
This statement requires to be interpreted as 0. The ordering of zeros of is not fully understood. However from Sec. 10.1.58 of [36], for ,
which is approximately a monotonic function of the integer part n of ,
It is convenient to choose
The ordering in the following summation is complete, covering all positive zeros of derivative spherical Bessel functions within the factor . It is practically monotonic in n and has the advantage of simple enumeration.
This expansion is analogous to that which uses the standard ordered basis of energy eigenfunctions of central force systems [38]. n is analogous to the principal quantum number but the r-dependence is different because the assumed material surface boundary condition replaces square integrability on . The time dependence is not merely trigonometric since the governing equation is non-autonomous. The basis functions are chosen to be complex, so that canonical second quantization may proceed just as in the autonomous free field case for which are complex sinusoids
The number of independent basis eigenfunctions with quantum number n is . Hence, the number of radial wave number eigenvalues that are less than or equal to is similarly of order .
2.2. Reduction of Time-Frozen Hamiltonian by Bogoliubov Transformation
The method of canonical quantization will be the long established approach, similar to that of Pauli [13]. For aspects of coupling with curved space-times, the reader is referred to the standard texts [11,39,40].
Under canonical quantization, the field becomes a self-adjoint operator of the same form as (11) but with and now operators.
Noting that , the requirement that be self adjoint implies , where superscript dagger represents the operator adjoint. Therefore the second quantized field is
Now the field Equation (7) is the Euler-Lagrange equation generated by the Lagrangian density
so the canonical conjugate field variable is
with . For Boson fields the field variable and its corresponding canonical conjugate field variable will obey the equal-time commutation relations:
which taken with (20) and (21) imply
where is the Wronskian and from (Equation 11.4.5 of Luke [41]),
Since is a real constant and is a purely imaginary constant, one can normalize to
so that whereby (25)–(27) are the standard Boson commutation relations and we may interpret and as Boson creation and annihilation operators respectively.
The canonical Hamiltonian is
where is the sectioned 3-space given by constant and is the spatial volume element. To avoid the difficulty of integrating the second term we note that the boundary condition (10) with Green’s identity
where is the surface of all space, implies that
The Hamiltonian is a sum of commuting quadratic Boson terms
and
where
The eigenvalues of , where , that are invariants of the group of Bogoliubov transformations, are
These eigenvalues are real when and purely imaginary when . These are the same criteria for real and imaginary frequency found by Mijic [17]. By the theory of equivalence classes of quadratic Hamiltonians [15], there exists a Bogoliubov transformation by which the Hamiltonian in terms of new annihilation operators is
with
and
We can regard and respectively as a collection of quantum oscillators with time dependent frequency and quantum repulsive units with time dependent Hooke coefficient . An analogous partitioning occurs between propagating and evanescent modes in optics [42]. Note that and commute and they each may be further decomposed into a sum of commuting Hamiltonian components for independent elementary modes of one degree of freedom. Unlike , cannot be transformed to a linear combination of number operators since the frequencies are purely imaginary for all wave numbers .
The expansion in terms of the countable basis of spherical harmonics results in the number of repulsive modes, although increasing with time, remaining finite since for any finite value of there are only finitely many solutions to (15) with . The basis modes in (20) have an r-dependent factor
In this sense, resembles a wave number. However, at any time, a field dynamical mode with radial wave number less than will be non-oscillatory, reaching its last extremum near to the time that becomes negative. At the level of second quantization, that dynamical mode is a harmonic oscillator with time dependent squared angular frequency that becomes negative at some finite time. The Pauli formulation [13] represents a quantized field as an infinite system of harmonic oscillators. When the field is minimally coupled to an accelerating expanding space-time, there is also a finite number of quantum field modes that may be represented as repulsive units with pure imaginary frequency.
In the Fock representation of quantum mechanics, a single harmonic oscillator is represented by the Hamiltonian
with This can be expressed as
However if the decreasing angular frequency becomes zero, the above correspondence between canonical variables and creation/annihilation operators breaks down. When the real angular frequency becomes pure imaginary , the self-adjoint time-frozen Hamiltonian H has a continuous spectrum instead of a discrete spectrum (Figure 1) and it can no longer be written in terms of a number operator . Instead, the normal form [15] for such a repulsive dynamical mode is as in the components of in (36).
2.3. Non-Autonomous Quantum Evolution: Solution with Finitely Many Extrema
The spectral properties of the time-frozen Hamiltonian do not give the complete picture of the dynamics of a single component non-autonomous oscillator. In the next section, operators q and p will be represented in the usual Schrödinger picture as operators on with and . Thereafter, the relevant non-autonomous Schrödinger equation will be solved exactly. Full spatial dependence of the field is temporarily disregarded as attention is focused on a dynamical mode with a single degree of freedom labelled by , with a single pair of canonical variables that are now operators. In the following section, if x is to be regarded as the classical version of quantum variable q, then that variable is associated with the displacement of a single independent dynamical mode of the field . However, as in the Pauli construction by Fourier inversion, after each of those separate quantum dynamical modes have been solved exactly, they may be recombined to construct the full space-time-dependent field, even though this reconstruction is no longer standard Fourier inversion.
2.3.1. Transforming to an Autonomous Schrödinger Equation
The aim is to solve the non-autonomous Schrödinger equation
where
with , , and is the cosmological constant, where and Note that time evolution, under the non-autonomous equation, is still unitary. In Dirac notation,
where is self adjoint and time dependent. If evolves under the same time evolution,
By analogous results of Bluman and Kumei [43] on non-autonomous diffusion equations, it is possible to transform to a new function
satisfying the autonomous Schrödinger equation
in terms of transformed variables of the form
with inverse transformation
The above transformation can be made to approach the identity transformation in the distant past, so that the non-autonomous Equation (37) agrees asymptotically with the autonomous Equation (38). Initial conditions for the original pde and the transformed pde will coincide, at a time taken sufficiently far back in the past. We need to find suitable functions and .
Now the target autonomous PDE (38) implies
Equating coefficients with those of original Schrödinger equation (37) gives the following set of PDEs that we must solve, in order to find and .
The ratio of the coefficient of the term to the coefficient of the term in (37) must agree with that in (39). Therefore,
where T is an unknown function of only. Then this gives
where S is some function of . Consequently,
With a primed variable denoting a total derivative with respect to , we also have
Now matching the terms:
for some function F.
This establishes the form of the three functions and G but we need to specify the three newly introduced functions T, S and F. From (42) we find
and
Now compare coefficients with those of the previous expression (43) for .
From the x-coefficient:
which has general solution
but we will simply choose , because this will be most convenient.
From the - coefficient:
which is the Ermakov-Pinney equation with solution
where satisfies
We take the simplest non-zero solution for u,
Then
The singularities due to the zeros in the denominator are cancelled by part of the Bessel term when we multiply by u, resulting in T being a well behaved function. We would also like to remove the oscillatory behaviour in T due to the trigonometric and Bessel functions, so that the transformations to and are one-to-one and invertible. This can be done by choosing and , so that
which is 1-1 for all times in the domain .
From the -coefficient:
With the choice, ,
We can now substitute these into the transformations.
To ensure that the transformation approaches the identity in the distant past (ie as or ) we choose
Next we simply have
which approaches x in the distant past, as desired.
Letting also simplifies G so we have
which approaches 1 in the distant past, as desired.
2.3.2. Harmonic Oscillator Initially in Ground State
We take W to have the form of a simple harmonic oscillator in the ground state with frequency k (in the distant past, the frequency approaches k). , so
The probability density is
Compared to the usual stationary Gaussian probability density of the time-independent oscillator in its ground state, the Gaussian probability density spreads as the particle wave number effectively decreases in time, as
2.3.3. Superposition of Harmonic Oscillator Ground State and First Excited State
As an example of an oscillating asymmetric state, we take the solution to (38) to be a superposition of the ground state and the first excited state. We choose the probability density to be predominantly on one side initially.
which is automatically normalised for any value of . With ,
and
In the original coordinates, the probability density is
where
which will approach , a constant between −1 and 1 that is related to the exact value of the cosmological constant, since .
Now using
the total probability to the right of the origin is
The probabilistically favoured location oscillates from side to side but eventually the oscillations cease. The extrema in the probability of occur at times
The final extremum occurs at time , where P is the largest integer less than The final distribution will depend on the cosmological constant and the limit of . In that final distribution, the probability of x being positive is
3. Discussion
3.1. Cosmological Implications
The highest radial wave number for an unstable mode is given by
for some index . Combining this with (17), . With n fixed, the number of independent basis functions is approximately . Hence the number of independent unstable non-particulate modes, is approximately the number of basis functions with , which is
The number of independent non-oscillatory modes is of order . If one assumes equipartition of energy among modes originating from a broad-spectrum sharp explosion, then the energy density summed over non-particulate modes will remain approximately constant during the expansion. In more detail, the critical radial wave number is
The number of independent unstable modes is
If the dimensionless mean energy distributed to each unstable mode is E, then the dark energy density is
This could not account for all dark energy that is consistent with the Friedmann equation unless the energy per unstable mode were to be
E diverges as approaches zero, consistent with unstable quantum field modes not being prevalent when accelerated expansion is negligible. Conversely, when is very large, the dark energy is allocated in small amounts among very many unstable discrete modes, consistent with the classical continuum approximation that is inherent in the Friedmann equation.
The above presentation includes a number of assumptions that may be rough approximations. The eigenvalue label n is not exactly proportional to . The Hamiltonian is not constant but decreasing in time. Similarly, may be decreasing in time as would be the case at thermal equilibrium with radiation at decreasing temperature. Assume that the best-fit power law is
Then the dark energy density will be
This agrees with the Friedmann equation if and only if
In the unlikely event that dark energy modes remain in thermal equilibrium with radiation modes whose temperature decreases as , would be . In the more likely event that dark energy modes do not freely interact with radiation modes so that they are not in thermal equilibrium, but remain near the energy levels at which they became unstable, would be much less than , consistent with the approximation of being proportional to N.
A scalar inflaton field would have converted a large amount of energy to non-particulate form. This is not the case for the expansion rate that is inferred at the present age of the universe. The Hubble time is currently estimated to be 14 billion years and the estimated age is 13.7 billion years. Due to expansion, the radius of the observable universe is much greater than , around 47 billion light years [32]. Since the material radius is scaled here to , the dimensionless Hubble radius is less than 14/47. The first positive zero of the spherical Bessel functions is . This mode becomes unstable when . Equivalently from (9) in dimensionless form,
which occurred at around 0.23 times the age of the universe which is within the matter-dominated era which lasted until about 0.7 times current age [44]. Here, denotes the present time when . At the present time, the critical radial wave number is If there were already a large number of unstable modes, then we would have . This implies which contradicts the assumption of large N unless material radius is much larger than observable radius.
Destabilization of the classical field has been examined in detail here only for a massless spin-0 scalar field but we expect that this effect is indicative of more general integer-spin fields. We expect that a similar effect will occur for a massless spin-1 field and that Bose quantization of the unstable modes will again require a representation with non-particulate eigenstates of the Hamiltonian. The black body spectrum of the cosmic microwave background peaks at 1.07 μm. In the scalar field, according to (53), modes of this wavelength will become repulsive after an exponential expansion of approximately 100 duration. Although at the present time, large-scale cosmogenic field instability is barely incipient and therefore has no practical consequence, the unstable non-particulate quantum modes might dominate the energy spectrum in the far-distant future.
3.2. Existence of Preferred Physical Representation
There is no preferred Fock representation of the Weyl quantum algebra of observables for fields that are unstable. Even if we freeze the form of the Hamiltonian at a particular time, there is no time-invariant vacuum state of zero energy, there is no number operator that commutes with the total Hamiltonian [23] and the energy spectrum of each quantized unstable mode is unbounded below. This is more dramatic than the Unruh effect [45] in which observers in different accelerating reference frames ascribe different vacuum states and different n-particle states in the same Hilbert space. It is more dramatic than the van Hove effect [46] (which in turn is stronger than the Unruh effect), in which the strength of interaction requires unitarily inequivalent vacuum representations of the quantum algebra at different times. When a classical mode becomes exponentially unstable, the cyclic representation of the quantum algebra based on a time invariant vacuum state is no longer possible [19,20,22]. Each independent unstable mode contributes a continuous spectrum with corresponding generalized eigenfunctions of the Hamiltonian that are distributions in the dual of the Hilbert space. These eigenfunctions are neither oscillatory nor particulate in character, but related to Schroer’s “jelly” states [16].
Despite these technical difficulties, there are only finitely many unstable modes at any given time, so that for the unstable subsystem, the Stone-von Neumann theorem will guarantee an irreducible separable quantum Hilbert space representation that is unique up to unitary equivalence. In this sense, Isidro and Fernández Córdoba [47] are correct to say that the finite extent of the universe allows for unambiguous measurement of universal quantities such as the total Boltzmann entropy. Since the remaining countably infinite set of stable modes can be represented in terms of simultaneous eigenstates of number operators and of the Hamiltonian, they can be interpreted as absorption of any number of quanta above the vacuum level. The usual preferred Fock-Cook representation [34,48,49] of the stable field component can be extended in a uniquely defined way simply by taking a direct product with the representation of the unstable component that has finite degrees of freedom and whose Hilbert space representation is uniquely determined by the Stone-von Neumann theorem [50,51].
4. Conclusions
The effectively massless scalar field minimally coupled to a spatially flat but rapidly expanding FLRW universe with positive cosmological constant, is an example of an exactly solvable quantum field theory. It has been shown how each of the contributing non-autonomous quantum dynamical modes may be solved exactly even when they evolve from being attractive to repulsive. Like all well-known successful 20th Century quantum field theories, the model is semi-classical in the sense that the primary fields are operators but the space-time background is classical. The pseudo-Riemannian space-time is associated with a classical gravitational field. Because of the exponential expansion of the universe, the fundamental dynamical modes of the system become unstable at progressively shorter material wavelengths at progressively later times. Much of the energy of the inflaton field would have been converted to a non-oscillatory form. Apart from the inflation period, the current universe would admit a relatively small number of unstable Klein-Gordon modes. The simple model with minimal coupling already demonstrates the influence of unstable modes on the quantized energy spectrum. A single unstable mode contributes a continuous spectrum of the quantized time-frozen Hamiltonian, associated with eigenstates that can be viewed as neither oscillatory radiation nor particles. There is no particle number operator that commutes with the time-frozen Hamiltonian of an unstable mode. This non-oscillatory character pertains also when the full non-autonomous system is solved; wave components eventually cease to oscillate in time. The destabilised energy eigenstates are dark in the sense that neither particle detectors nor wave detectors are designed to interact with them. The appearance of these states follows from nothing more than the standard canonical field quantization procedure that has been used for more than 75 years. It requires no additional physical postulates.
The increasing number of independent unstable modes remains finite, whereas the number of stable modes is countably infinite. This allows one to specify a preferred Hilbert space representation with a Fock representation accounting for all of the stable modes. By considering cosmological effects in semi-classical quantization we have focused on effects at extremely long wavelengths. However it is conceivable that a similar mechanism of dark energy generation at short wavelengths may occur in a quantum gravity theory. The conformal metric is expanding exponentially so one would not expect all dynamical modes of the gravitational field to be expressible in terms of gravitational waves and graviton particles.
Author Contributions
The authors contributed equally to this project. All authors have read and agreed to the published version of the manuscript.
Funding
The second author gratefully acknowledges support of the Australian Research Council for project DP160101366.
Acknowledgments
Kerry Hinton guided the authors on the physics literature. Sarah Becirevic assisted with a literature search and classification of non-autonomous Schrödinger equations.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| FLRW | Friedmann Lemaitre Robertson Walker |
| PDE | partial differential equation |
Appendix A. Separation of Variables
From the non-autonomous Klein-Gordon Equation (7),
In spherical polar coordinates ,
Consider a separated solution satisfying
In order for to be -periodic, m can be any integer; consequently . Now separating the independent variable ,
The separated equation for is equivalent to Legendre’s equation
where L is finite for all if and only if ℓ is a non-negative integer. Then , a Legendre function of z.
Separating the remaining independent variables and r,
The separated equation for is equivalent to
where . Hence the solutions are linear combinations of
Finally, satisfies
satisfies Bessel’s equation, resulting in the solutions for F being spherical Bessel functions This neglects the second kind that is undefined at .
Appendix B. Choice of Boundary Conditions
Boundary conditions in relativistic field theories are guided by symmetry principles. The exponentially expanding FLRW universe may be embedded in de Sitter space (e.g., Chap. 5.4 of [11] ), which is flat 1+4 -dimensional Minkowski space coordinatised as and restricted to the isometry-invariant hyperbolic surface
Here, are grouped together because they are closely related to FLRW material coordinates:
This then results in the FLRW metric with exponential expansion:
In material polar coordinates ,
The coordinate patch given by covers only half of de Sitter space. In the context of de Sitter space, the singularity at is merely a coordinate singularity, not a geometric singularity. The other half of de Sitter space could be covered by a second FLRW patch in which is decreasing. This second patch is currently well beyond the realm of practical science.
It is straightforward to calculate Killing vectors, being tangent vectors of isometries in de Sitter space. A coordinate transformation then results in ten independent Killing vectors for the FLRW space. This was done by Schrödinger [52], neatly summarised by Hari Dass and Desiraju [53] who related the isometries to zero modes of the Laplace-Beltrami operator. Because of the exponential form of expansion, the maximally invariant de Sitter version of FLRW has an additional scaling isometry
The radius of a sphere is not even invariant under this simplest of isometries. The spherical surface is not invariant under Lorentz transformations that contract lengths in the direction of an observer’s velocity. The invariant surface containing the points with and is the space-time hyperboloid given by . However in continuum mechanics the boundary is physically defined by parcels of co-moving matter each of which, by definition, has a constant location in material coordinates . Hence in order to state a boundary condition on the sphere, one needs an additional postulate that the isotropic space-time has a special locally Lorentz frame in which each time-section is a sphere. It is an anathema to the principle of relativity that there should be a physically distinguished frame. However it has recently been demonstrated that the cosmic microwave background is isotropic only in a special reference frame. Relative to that frame, the earth has a speed of 370 km s [54].
Standard physical boundary conditions are commonly stated in terms of components of the canonical stress-energy tensor which is constructed from the de Sitter-invariant Lagrangian density
In terms of polar radial coordinates and in units chosen so that and =1, the Lagrangian density for the scalar field equation is
The component of the stress energy tensor is which must be equal to the energy flux in the radial direction. In the material coordinate system, an expanding spherical boundary has a constant material radius coordinate . Since this is in a material coordinate system, zero-transport across the location really means zero-transport relative to a moving location in terms of a system of physical coordinates. The material coordinate system is convenient for expressing a moving boundary condition in a simple way. In that case the required physical condition of no transport of energy across the boundary implies either or . There is no generally agreed boundary condition for the universe. The viewpoint here is that each fundamental single-particle mode will have only a finite number of oscillations in time before it transitions to a dark non-oscillatory mode. At any time instant, each propagating mode will have only a finite number of local extrema. If the boundary condition is imposed, then the last of the finite number of extrema of each mode will occur at the boundary. Since zeros of are interlaced between extrema, the mode decomposition will be virtually the same if the boundary condition were given as .
References
- Aldrovandi, R. Nonrelativistic spacetimes with cosmological constant. Class. Quantum Grav. 1999, 16, 495–506. [Google Scholar] [CrossRef]
- Balbi, A. Constraints on cosmological parameters from MAXIMA-1. Astrophys. J. 2000, 545, L1–L5. [Google Scholar] [CrossRef]
- De Bernardis, P. A flat Universe from high-resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955–959. [Google Scholar] [CrossRef] [PubMed]
- Peacock, J.A.; Cole, S.; Norberg, P.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.D.; Colless, M.; Collins, C.; Couch, W.; et al. (Hubble Space Telescope Project Consortium). A measurement of the cosmological mass density from clustering in the 2dF. Galaxy Redshift Survey. Nature 2001, 410, 169–173. [Google Scholar] [CrossRef] [PubMed]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. (Supernova Cosmology Project Consortium). Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–587. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia supernova discoveries at z > 1 from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665–688. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. (WMAP Team). First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Supp. 2003, 148, 175–195. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; et al. (WMAP team). Cosmological parameters from SDSS and WMAP. Phys. Rev. D. 2004, 69, 103501-1–103501-26. [Google Scholar] [CrossRef]
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Benjamin Cummings: San Francisco, CA, USA, 2003. [Google Scholar]
- Carroll, S.M.; Chatwin-Davies, M. Cosmic equilibration: A holographic no-hair theorem from the generalized second law. Phys. Rev. D 2017, 97, 046012. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Esposito, G.; Kamenshchik, A.Y.; Pollifrone, G. Euclidean Quantum Gravity on Manifolds with Boundary; Kluwer/Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Pauli, W. Relativistic field theory of elementary particles. Rev. Mod. Phys. 1941, 13, 203–232. [Google Scholar] [CrossRef]
- Thouless, D.J. The Quantum Mechanics of Many-Body Systems, 2nd. ed.; Dover Publications: New York, NY, USA, 1992. [Google Scholar]
- Broadbridge, P. Normal forms for classical and Boson systems. Phys. A 1979, 99, 494–512. [Google Scholar] [CrossRef]
- Schroer, B. Quantization of m2 < 0 field equations. Phys. Rev. D 1971, 3, 1764–1770. [Google Scholar]
- Mijic, M. Particle production and classical condensates in de Sitter space. Phys. Rev. D 1998, 57, 2138–2146. [Google Scholar] [CrossRef]
- Broadbridge, P.; Zulkowski, P. Dark Energy States from Quantization of Boson Fields in a Universe with Unstable Modes. Rep. Math. Phys. 2006, 57, 27–40. [Google Scholar] [CrossRef]
- Broadbridge, P.; Hurst, C.A. Existence of a complex Structure for Quadratic Hamiltonians? Ann. Phys. 1981, 131, 104–117. [Google Scholar] [CrossRef]
- Paneitz, S.M. Unitarization of symplectics and stability for causal differential equations in Hilbert space. J. Funct. Anal. 1981, 41, 315–326. [Google Scholar] [CrossRef][Green Version]
- Broadbridge, P. Problems in the quantization of quadratic Hamiltonians. Hadron. J. 1981, 4, 899–948. [Google Scholar]
- Broadbridge, P. Existence Theorems for Segal Quantization via Spectral Theory in Krein Space. J. Austral. Math. Soc. B 1983, 24, 439–460. [Google Scholar] [CrossRef][Green Version]
- Chaiken, J.M. Number operators for representations of the canonical commutation relations. Commun. Math. Phys. 1968, 8, 164–184. [Google Scholar] [CrossRef]
- Allen, B. Vacuum states in de Sitter space. Phys. Rev. D 1985, 32, 3136–3149. [Google Scholar] [CrossRef]
- Allen, B.; Folacci, A. Massless minimally coupled scalar field in de Sitter space. Phys. Rev. D 1987, 35, 3771–3778. [Google Scholar] [CrossRef]
- Kirsten, K.; Garriga, J. Massless minimally coupled fields in de Sitter space: O(4)-symmetric states versus de Sitter-invariant vacuum. Phys. Rev. D 1993, 48, 567–577. [Google Scholar] [CrossRef] [PubMed]
- Polarski, D. Infrared divergences in de Sitter space. Phys. Rev. D 1991, 43, 1892–1895. [Google Scholar] [CrossRef] [PubMed]
- Bunch, T.S.; Davies, P.C.W. Quantum field theory in de Sitter space—Renormalization by point-splitting. Proc. Roy. Soc. A. 1978, 360, 117–134. [Google Scholar]
- Guth, A.H. Inflation. Proc. Natl. Acad. Sci. USA 1993, 90, 4871–4877. [Google Scholar] [CrossRef] [PubMed]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. 1980, 91B, 99–102. [Google Scholar] [CrossRef]
- Kazanas, D. Dynamics of the universe and spontaneous symmetry breaking. Astrophys. J. 1980, 241, L59–L63. [Google Scholar] [CrossRef]
- Taylor Redd, N. How Big is the Universe? Available online: https://www.space.com/24073-how-big-is-the-universe.html (accessed on 10 June 2017).
- Adam, R.; Ade, P.A.; Aghanim, N.; Akrami, Y.; Alves, M.I.R.; Argüeso, F.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; et al. (The Planck Collaboration). Planck 2015 results. I. Overview of products and scientific results. Astron. Astrophys. 2016, 594, A16. [Google Scholar]
- Segal, I.E. Mathematical Problems of Relativistic Physics; American Mathematical Soc.: Providence, RI, USA, 1963. [Google Scholar]
- Harigaya, K.; Ibe, M.; Kawasaki, M.; Yanagida, T.T. Revisiting the minimal chaotic inflation model. Phys. Lett. B 2016, 756, 113–117. [Google Scholar] [CrossRef]
- Antosiewicz, H.A. Bessel Functions of Fractional Order. In Handbook of Mathematical Functions; Abramowicz, M., Stegun, I.A., Eds.; National Bureau of Standards: Washington, DC, USA, 1964; pp. 435–478. [Google Scholar]
- Liu, H.; Zou, J. Zeros of the Bessel and spherical Bessel functions and their applications for uniqueness in inverse acoustic obstacle scattering. IMA J. Appl. Math. 2007, 72, 817–831. [Google Scholar] [CrossRef][Green Version]
- Messiah, A. Quantum Mechanics; North-Holland: Amsterdam, The Netherlands, 1961; Volume 1, Chapter 9. [Google Scholar]
- Fulling, S.A. Aspects of Quantum Field Theory in Curved Space-Time; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Mukhanov, V.F.; Winitski, S. Introduction to Quantum Effects in Gravity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Luke, Y.L. Integrals of Bessel Functions. In Handbook of Mathematical Functions; Abramowicz, M., Stegun, I.A., Eds.; National Bureau of Standards: Washington, DC, USA, 1964; p. 485. [Google Scholar]
- Aiello, A. Field theory of monochromatic optical beams. 1. Classical fields. J. Opt. 2019, 22, 014001. [Google Scholar] [CrossRef]
- Bluman, G.W.; Kumei, S. Symmetry-based algorithms to relate partial differential equations. 1. Local symmetries. Euro. J. Appl. Math. 1990, 1, 189–216. [Google Scholar] [CrossRef]
- Ryden, B. Introduction to Cosmology; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1984, 14, 870–892. [Google Scholar] [CrossRef]
- Van Hove, L. Les difficultés de divergences pour un modele particulier de champ quantifié. Physica 1952, 18, 145–159. [Google Scholar] [CrossRef]
- Isidro, J.M.; Fernández de Córdoba, P. On the Holographic Bound in Newtonian Cosmology. Entropy 2018, 20, 83. [Google Scholar] [CrossRef]
- Fock, V. Konfigurationsraum und zweite Quantelung. Z. Phys. 1932, 75, 622–647. [Google Scholar] [CrossRef]
- Cook, J. The mathematics of second quantization. Trans. Am. Math. Soc. 1953, 74, 222–245. [Google Scholar] [CrossRef]
- Stone, M.H. On one-parameter unitary groups in Hilbert Space. Ann. Math. 1932, 33, 643–648. [Google Scholar] [CrossRef]
- Von Neumann, J. Die Eindeutigkeit der Schrödingerschen Operatoren. Math. Ann. 1931, 104, 570–578. [Google Scholar] [CrossRef]
- Schrödinger, E. Expanding Universes; Cambridge University Press: Cambridge, UK, 1956. [Google Scholar]
- Hari Dass, N.D.; Desiraju, H. Killing vectors of FLRW metric (in comoving coordinates) and zero modes of the scalar Laplacian. arXiv, 2016; arXiv:1511.07142v3. [Google Scholar]
- Collaboration, P.; Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. (The Planck Collaboration). Planck 2018 results. I. Overview, and the cosmological legacy of Planck. arXiv, 2018; arXiv:180706205P. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).