Abstract
This paper focuses on advances in the understanding of both the fundamental and applied aspects of nanomaterials. Nanoparticles (titania and graphene oxide) in water-based fluid lying on a surface incorporating the leading edge accretion (or ablation) are analyzed. Entropy generation rate is also considered. The Hall current effect is induced in the flow of hybrid nanofluid, due to which the two-dimensional study converts into three-dimensional space. Similarity transformations convert the equations of momentum, heat transfer, nanoparticles volume fraction and boundary conditions into non-dimensional form. Mathematica software is used to obtain the computation through homotopy analysis method. Analysis is provided through the effects of different parameters on different profiles by sketching the graphs. Flow, heat transfer and nanoparticles concentration in TiO/HO, as well as GO-TiO/HO, are decreased with increasing the Stefan blowing effect, while entropy generation rate elevates upon increasing each parameter. Both of the velocity components are reduced with increasing the Hall parameter. Streamlines demonstrate that trapping is increased at the left side of the surface. The obtained results are compared with the published work which show the authentication of the present work.
1. Introduction
When an electrically conducting fluid is under an ionization process and the strength of the applied magnetic field is high, then the normal conductivity of the magnetic field is reduced to the free spiraling of electrons and ions about the magnetic lines force before suffering collisions. In such a situation, a current is induced in a normal direction to both the electric and magnetic fields. This phenomenon is known as the Hall current effect. When the strength of the magnetic field is strong, the effects of Hall currents cannot be neglected. It is highly important and interesting to know how the results of hydrodynamical problems get modified by the effects of Hall currents. The Hall effect generates a cross flow, making the flow three-dimensional in a two-dimensional system. The magnetohydrodynamic flows with Hall effect have important applications in Hall accelerators, power generators, flight magnetohydrodynamics, refrigeration coils, transmission lines, electric transformers. Shateyi and Motsa [1] analyzed the problem of magnetohydrodynamic flow and heat transfer of a viscous, incompressible and electrically conducting fluid past a semi-infinite unsteady stretching sheet. Hayat et al. [2] investigated the viscous dissipation effects on mixed convection three-dimensional flow of Jeffery fluid past a vertical stretching surface taking into account the Hall and ion effects. Ahmed and Zueco [3] obtained the exact solution to the problem of heat and mass transfer in a rotating vertical porous channel in the presence of Hall current. Gaffar et al. [4] presented the nonlinear, non-isothermal, magnetohydrodynamic free convection boundary layer flow, heat and mass transfer of non-Newtonian Eyring–Powell fluid from a vertical surface in a non-Darcy, isotropic, homogeneous porous medium considering Hall currents and ionslip currents. Abdelaziz [5] worked on the steady boundary layer magnetohydrodynamic slip flow past a stretching sheet in a water-based nanofluid in the presence of the Hall effect. Hayat et al. [6] investigated the Hall effect on the peristaltic transport of couple stress fluid in an inclined channel.
Structure and dynamics, particularly surfaces and interfaces, have long been fields of fruitful research. This field has changed profoundly since the discovery of nanoparticles. While nanoparticles continue to dazzle the research community with recent discoveries such as superconductivity and highly correlated electron physics, a plethora of other materials have emerged, covering an entire spectrum of electronic properties. Moreover, the possibility of stacking these materials to create artificial structures, interfaces, and with tunable twisting angles, opens the door to unprecedented control of structure, dynamics, and properties. We now possess exquisite control in designing new model systems, exploring new properties, and studying new physical/chemical processes. Recently, the focus has been on advances in the understanding of both the fundamental and applied aspects of nanoparticles and nanofluids for researchers and practicing engineers from different disciplines to interact and exchange their latest understandings. Khan [7] analyzed the nanobioconvection model to explore that Brownian motion parameter increases the thermal conductivity and creates resistance to the flow of microorganisms. Bahiraei and Heshmation [8] presented a review examining the graphene family nanofluids for the capabilities of graphene-based nanofluids, innovations in preparing techniques, stability analysis and types of surfactants used. They provided future work and also investigated the second law analysis for graphene-family nanofluids, thermophysical properties, hydrodynamic attributes, boiling and convective heat transfer, as well as the applications such as in car radiators, electronic coolings, heat exchangers, energy storage, in addition to molecular dynamics and artificial intelligence. Briffa et al. [9] worked on the physical and chemical transformations of zirconium-doped ceria nanoparticles in the presence of phosphate. Khan et al. [10] used rheological equations of an isotropic Casson nanofluid and Williamson nanofluid to asses the flow, heat transfer, nanoparticles concentration and gyrotactic microorganisms. Bahiraei [11] attempted to work on the past studies related to nanofluids in review and summary form, considering particle migration, Buongiorno model, molecular dynamics simulation, and other theoretical studies. He concluded about the research related to nanofluids (mentioned in his paper) that among other reasons, particle migration is the reason which causes inconsistencies in the previous studies results. Saba et al. [12] studied hybrid nanofluid (CNT-FeO/HO) in asymmetric long channel with dilating/squeezing walls by implementing the active method coupled with the RK–Fehlberg algorithm for the solution of non-dimensional equations. Bahiraei et al. [13] reviewed and summarized the present investigations for nanofluids in heat exchangers. They found that excessive reports have proven that nanofluids provide an enhanced heat transfer rate which increases by incrementing the concentration and Reynolds number. Waini et al. [14] investigated dual solutions and temporal stability analysis of the dual solutions for the unsteady flow and heat transfer in a hybrid nanoflid past a stretching/shrinking sheet. Bahiraei and Heshmation et al. [15] reviewed the use of nanofluids in electronics cooling by considering several aspects like block type, nanoparticle material, numerical approach, energy consumption and second law of thermodynamical system to show the challenges offered in the field under study. Gulzar et al. [16] presented an experimental study on the rheological behaviour and stability analysis of AlO-TiO Therminol-55 hybrid nanofluid using varying concentrations of 0.05 wt%, 0.075 wt%, 0.1 wt%, 0.25 wt% and 0.5 wt% in two-step method. Dalkilic et al. [17] worked experimentally on the turbulent heat transfer characteristics of Graphite-SiO/HO hybrid nanofluid flow in a horizontal smooth tube with and without quad-channel twisted tape inserts of length between 0 and 42 cm with constant ratios of 5. Khan et al. [18] discussed the effective thermal conductivity, particle’s conventional static and a Brownian motion which describes the influences of size, volume fraction, temperature dependency, the type of particle and base fluid combination. Rosca et al. [19] used Buongiorno’s nanofluid model to investigate the unsteady boundary layer flow of a nanofluid past a moving surface in an external uniform free stream. More studies on fluids and analytical solutions are presented in the references [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37].
Entropy generation reduces the performance of engineering systems due to irreversibilities which exists in heat and mass transfer flows. The first attention to the entropy generation was paid by Bejan [38]. Ahmad and Nadeem [39] used the Thomson and Troian auxiliary conditions to investigate the entropy minimization in stagnation point flow of a hybrid nanofluid with Cattaneo–Christov heat and mass flux theory, variable mass diffusivity and viscosity, activation energy past a nonlinear porous stretching sheet. Khan et al. [40] applied the shooting method to compute the solution of entropy generation in axisymmetric flow of non-Newtonian nanofluid between two parallel rotating disks where Bejan number was noted to decrease with increasing the parameter of Casson nanofluid. Khan et al. [41] examined the entropy generation for single/multi walled carbon nanotubes with homogeneous–heterogeneous chemical reactions and heat transfer. Zaib et al. [42] proposed a mathematical model for entropy generation considering micropolar magnetite-FeO ferro liquid to compute the first and second solutions of the problem. Khan et al. [43] worked for the first time in the literature to measure the entropy generation in the presence of gyrotatic microorganisms whose investigations showed that entropy generation was increased with the microorganisms concentration difference parameter. Shahsavar et al. [44] applied the two-phase mixture model to simulate the hydrothermal and irreversibility behavior of biological water–Ag nanofluid by finding that with decreasing the average nanofluid temperature, thermal conductivity was decreased, which resulted in the decrement of entropy generation. Khan et al. [45] used the series solution to analyze the entropy generation in the presence of the Hall effect, buoyancy effects, thermal radiation, Soret and Dofour effects. Sohail et al. [46] communicated through the entropy generation of three-dimensional flow of Maxwell nanofluid containing gyrotactic microorganisms and homogeneous–heterogeneous chemical reactions in the presence of Cattaneo–Christov heat and mass flux theory, which showed that entropy generation increased with high values of thermal radiation. Shah et al. [47] reported the entropy generation in non-Newtonian Casson nanofluid flow with thermal radiation, Arrhenius activation energy and binary chemically reaction past a nonlinear stretching surface. Khan et al. [48] investigated hybrid nanofluid flow with entropy generation. The references [49,50,51,52] provide a few other studies on the entropy subject.
The aforementioned discussion rests on the analysis of different features of fluids, but still there is a gap in the discussion of hybrid nanofluids with Hall effect and entropy generation in the literature. The objective of the present study is to investigate further the hybrid nanofluid. Hence, the authors have attempted to model and solve the problem for hybrid nanofluid with leading edge accretion or ablation, Hall effect and entropy generation, whose solution is accomplished through HAM [53].
2. Methods
An incompressible viscous fluid flow is investigated with free stream velocity U, nanoparticles concentration C and temperature T. In water-based fluid, two types of nanoparticles, namely TiO (titania) and GO (graphene oxide), with volume fractions = 0.03 and = 0.04 are considered respectively. Magnetic field B = [0, B, 0] is applied perpendicularly to the heat and mass transfer flow. It is assumed that the strength of electric charge and magnetic field are maximum. The schematic diagram of the problem is shown in Figure 1.
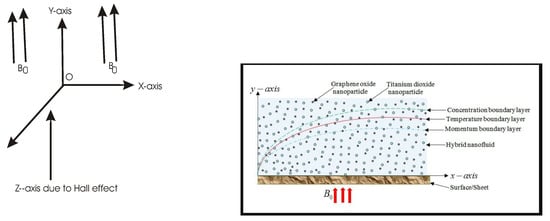
Figure 1.
Schematic diagram of the problem.
The problem has the following governing equations for hybrid nanofluid as in [19,45]
where u, v, w are the velocity components in the x, y, z directions and m is the Hall parameter. The subscript hnf denotes the hybrid nanofluid. , , and are respectively the dynamic viscosity, density, thermal conductivity and heat capacity of hybrid nanofluid.
Boundary conditions are used as
where u is the external velocity and is the stretching/shrinking parameter. > 0 is used for stretching sheet, < 0 is used for shrinking sheet and = 0 denotes the static surface. (T, C) and (T, C) are the hybrid nanofluid temperature and volume fractions at surface and infinity respectively. The thermophysical properties of water, titania and graphene oxide nanoparticles are given in Table 1, while the mathematical forms of the thermophysical properties of nanofluid and hybrid nanofluid are given in Table 2.

Table 1.
Thermophysical properties of water and nanoparticles [12,14,39].

Table 2.
Formulations of thermophysical properties of nanofluid and hybrid nanofluid [12,14,39].
In Table 1, s and s are used respectively for the solid nanoparticles of TiO (titania) and GO (graphene oxide). f is used for the base fluid.
Introducing the similarity transformations for (f, g), , , and as the non-dimensional velocities, variable, temperature and nanoparticles concentration respectively as
where is the stream function. is the kinematic viscosity. is the leading edge accretion or ablation parameter where () must be greater than zero [19].
The continuity Equation (1) is identically satisfied through Equation (8). Information is deducted from Table 1 and Table 2 and Equation (8) to get the following equations from Equations (2)–(7)
where = , = , = , = , = 1 + . () represents the derivative with respect to . M = is the magnetic field parameter, Pr = is the Prandtl number, Ec = is the Eckert number, Sc = is the Schmidt number, and f = is the suction/injection parameter (or Stefan blowing) respectively. It is noted that for = 0.00 and = 0.00, the problem becomes about viscous fluid. If = 0.00, GO/HO is obtained and if = 0.00, TiO/HO is made.
It is important to investigate the physical quantities having extensive applications in industries like the local skin friction coefficients (C, C), Nusselt number Nu, and wall mass flux Q as
where
Note that (, ), q, and q are known as wall frictions, heat transfer, and mass transfer on the surface respectively.
3. Entropy Generation
The equation representing the entropy generation [39,40,42,46] is
where R is the ideal gas constant while D is the diffusivity. In Equation (18), the first and second terms are respectively entropy generation due to heat transfer and viscous dissipation. The third and fourth terms are the diffusivity effects due to nanoparticles.
The characteristic entropy generation is
So
where Re = is the Reynolds number, = is the temperature difference parameter, Br = is the Brinkman number, = is the diffusion constant parameter due to nanoparticles concentration and = is the concentration difference parameter due to nanoparticles concentration.
4. Results and Discussion
The analytical solution of Equations (9)–(14) is obtained via the homotopy analysis method (HAM) [53] and then Equation (21) is solved. All the numerical values of thermophysical properties are used from Table 1 and Table 2 in computing the solution. For the influential role of parameters in flow, heat and mass transfer as well as entropy generation, m = 0.10, M = 1.00, = 1.00, Sc = 1.00, f = 0.001, = , Pr = 6.20, Re = 1.00, Br = 1.00, = 1.00, = 1.00 and = 1.00 are used. A comparison is made with the existing literature [19], which can be seen in Table 3. The physical sketch of the problem is shown in Figure 1. The h-curves are given in Figure 2, Figure 3 and Figure 4. The parameters’ effects are depicted in graphs through Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18.

Table 3.
Comparison values of f(0) in terms of parameter .
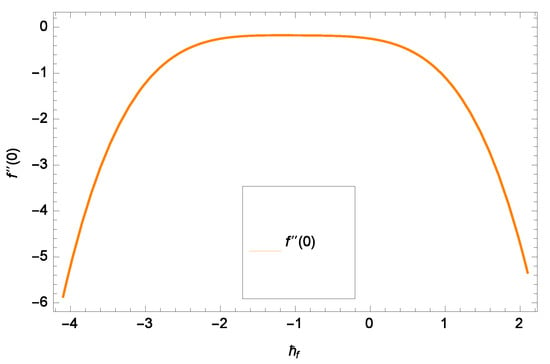
Figure 2.
Representation of the curve of f().
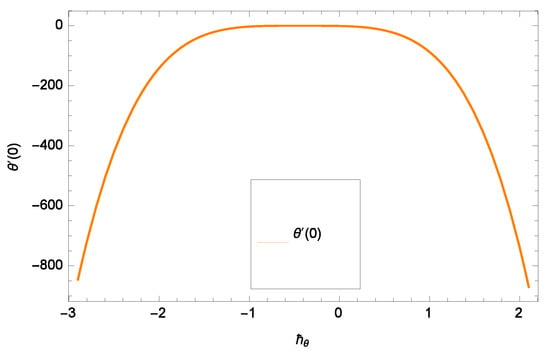
Figure 3.
Representation of the curve of ().
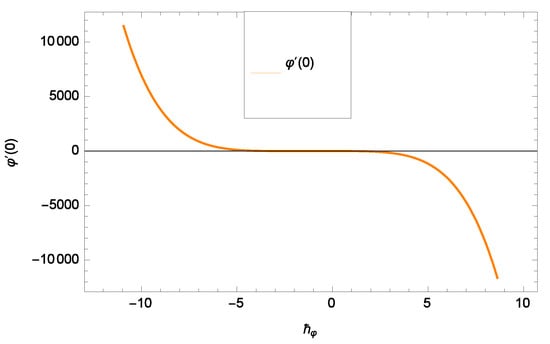
Figure 4.
Representation of the curve of ().
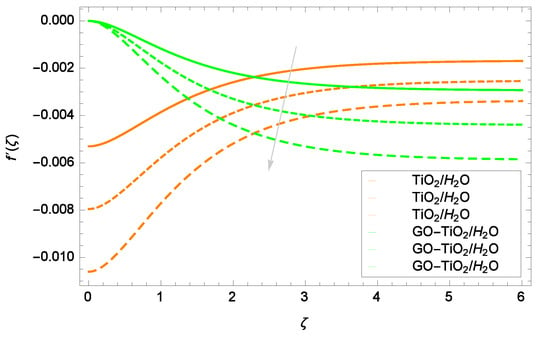
Figure 5.
Representation of the influence of a magnetic field parameter M = 1.00, 1.50, 2.00 on velocity f.
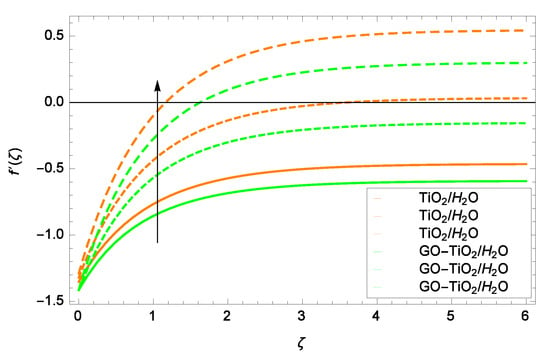
Figure 6.
Representation of the influence of a stretching/shrinking = 1.00, 1.50, 2.00 on velocity f.
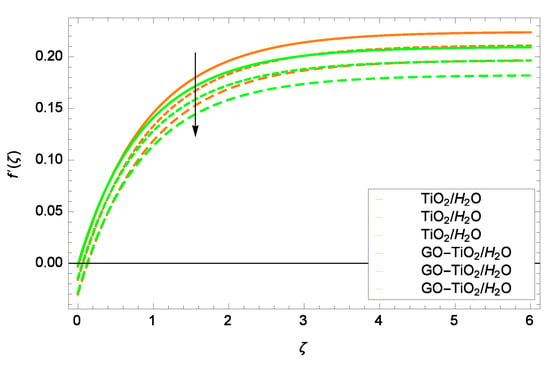
Figure 7.
Representation of the influence of a Stefan blowing parameter f = 0.001, 0.001, 0.002 on velocity f.
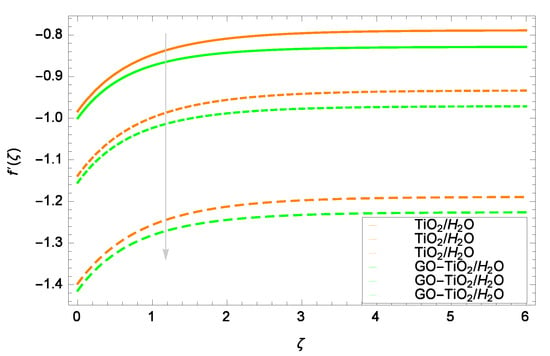
Figure 8.
Representation of the influence of an accretion/ablation parameter = , , on velocity f.
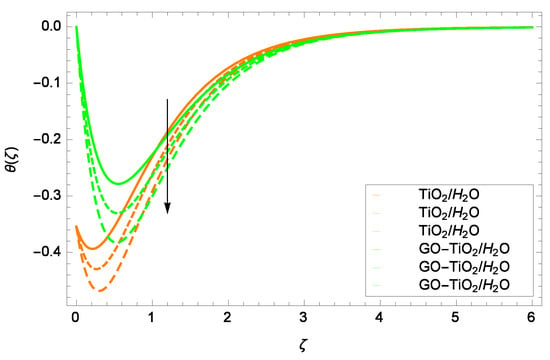
Figure 9.
Representation of the influence of a Prandtl number Pr = 6.20, 8.20, 10.20 on temperature ().
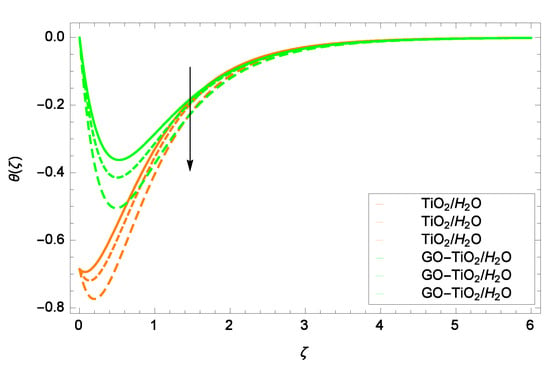
Figure 10.
Representation of the influence of a stretching/shrinking parameter = 1.00, 1.50, 2.00 on temperature ().
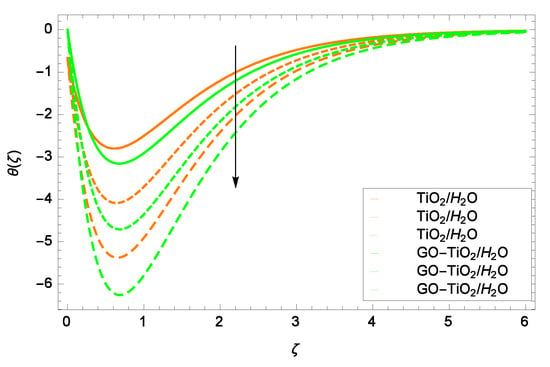
Figure 11.
Representation of the influence of a Stefan blowing parameter f = 1.00, 1.50, 2.00 on temperature ().
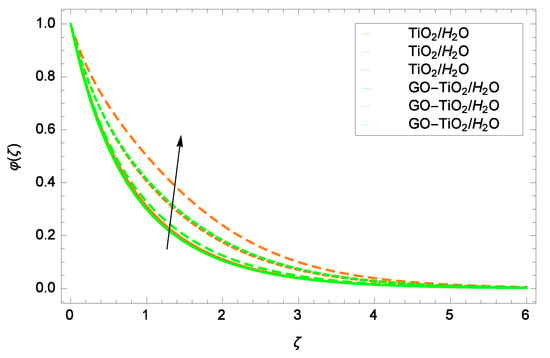
Figure 12.
Representation of the influence of a Schmidt number Sc = 1.00, 5.00, 9.00 on nanoparticles concentration ().
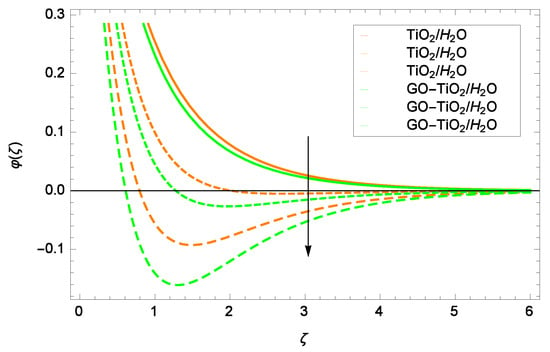
Figure 13.
Representation of the influence of a Stefan blowing parameter f = 1.00, 5.00, 9.00 on nanoparticles concentration ().
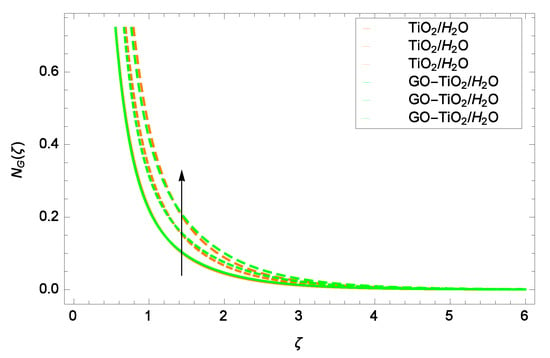
Figure 14.
Representation of the influence of a Reynolds number Re = 1.00, 1.50, 2.00 on entropy generation rate N().
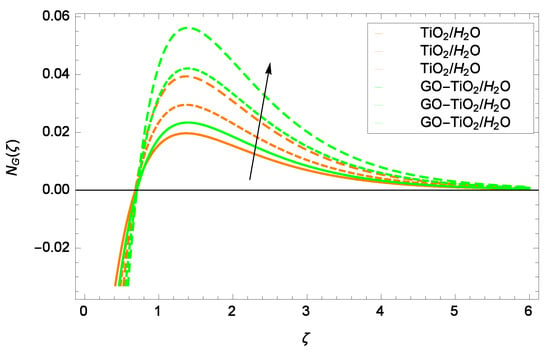
Figure 15.
Representation of the influence of a Brinkman number Br = 1.00, 1.50, 2.00 on entropy generation rate N().
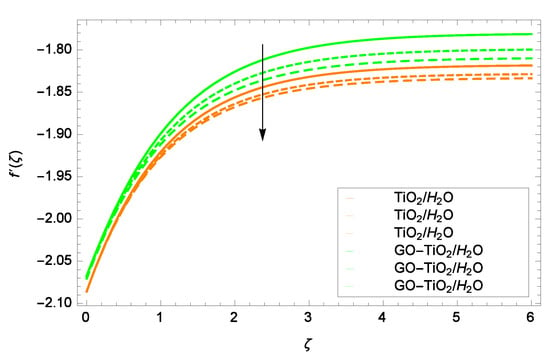
Figure 16.
Representation of the influence of a Hall parameter m = 1.00, 1.50, 2.00 on velocity f.
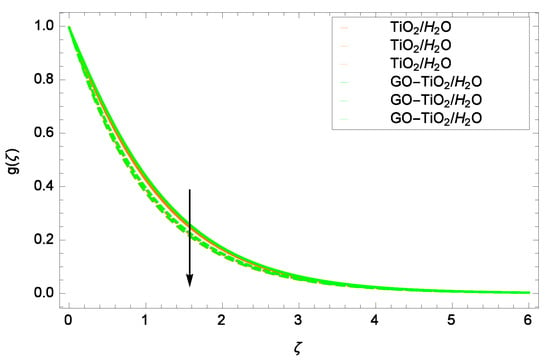
Figure 17.
Representation of the influence of a Hall parameter m = 1.00, 1.50, 2.00 on velocity g.
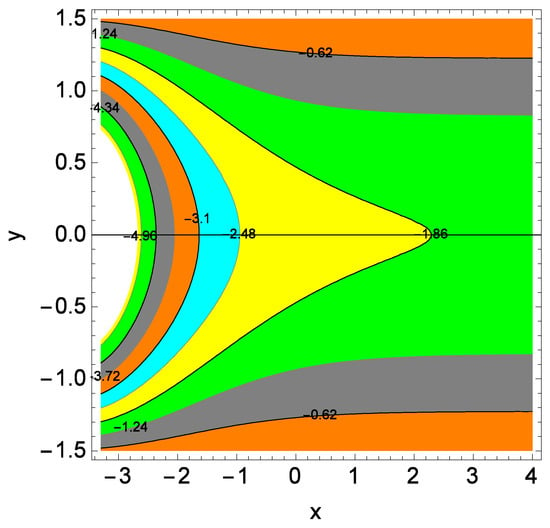
Figure 18.
Representation of the influence of a Hall parameter m = 0.60, = 0.03, = 0.04 on streamlines.
Figure 5 is presented to show the influence of Lorentz forces on velocity f. Observation from the graph reveals that velocity is decelerated for TiO/HO and GO-TiO/HO when the magnetic field parameter M increases on 1.00, 1.50 and 2.00. TiO/HO and GO-TiO/HO attain maximum velocity near the surface. Lorentz forces decrease the flow of TiO/HO and GO-TiO/HO. Figure 6 exhibits the effect of stretching/shrinking parameter on velocity f. Analysis is made for the stretching case, i.e., for > 0. When the surface stretches at the positive values of , the flow of mono nanoliquid and hybrid nanoliquid is accelerated. There is almost no distinct influential effect on velocity. Anyhow, the velocity of GO-TiO/HO is a little bit less in magnitude compared to that of TiO/HO. The reason is that the flow of TiO/HO is high due to the inclusion of one nanopaticle, while the flow of GO-TiO/HO is comparatively slow on account of two nanoparticles. Moreover, GO-TiO/HO has high viscosity compared to that of TiO/HO. The suction/injection or Stefan blowing parameter f effect on velocity f is portrayed in Figure 7. Due to suction (f> 0), near to the wall a vacant space is made. Fluid enters this vacant area to occupy it completely, consequently velocity f of TiO/HO and GO-TiO/HO is decreased. It is noted that in the central area of the channel, the velocity f is stable. Figure 8 reports that with the decreasing values of accretion/ablation parameter , the velocity of TiO/HO and GO-TiO/HO is also decreased. Interesting results are obtained for various values of . On adopting the positions 0 <<, it happens to achieve a leading edge ablation of the magnitude Ucot. On becoming the situation ≤< 0, in the backward boundary layer with trailing edge an accretion phenomenon is obtained. Implementing the case = 0 and = , the system becomes similar to familiar work, such as the Blasius flat plate study and Rayleigh–Stokes study in case of hybrid nanofluid.
Figure 9 examines the influence of Prandtl number Pr on the nanoparticles temperature distribution (). With higher values of Pr, () is diminished. Viscous forces exert a uniform effect on heat transfer for the whole of location of the channel. Figure 10 is designed to show the effect of stretching/shrinking parameter on temperature (). Both of the TiO/HO and GO-TiO/HO have shown decrement in temperature for the increasing values of . The temperature of the GO-TiO/HO is comparatively a little bit higher than that of TiO/HO in stretching phenomena. Figure 11 exposes that as the Stefan blowing parameter f increases, the temperature of TiO/HO and GO-TiO/HO is decreased. Close to the wall, the decrement in heat transfer is most prominent. Sucking extracts the heat from both of the fluids.
Figure 12 reveals that the addition in Schmidt number Sc increases the concentration. Through high values of Sc, viscosity is enhanced. Since the viscosity is the characteristic on account of cohesive forces within different layers of TiO/HO and GO-TiO/HO which have relative movement, the nanoparticles concentration is enhanced. By dispersing the nanoparticles into the water, the viscosity enhances, resulting in an increase in the cohesive forces. Figure 13 displays the suction/injection parameter f, which has a dominant role in diminishing the nanoparticles concentration . Due to suction (f > 0), the nanoparticles close to the wall remained in lower numbers, so the nanoparticles concentration is dilute. Therefore, the nanoparticles concentration decreases with increasing the suction parameter f.
Entropy generation rate N() and Reynolds number Re are projected in Figure 14. Keeping the consideration of the definition of Re, it is observed that there is an increase in entropy generation for the entire range of . This is due to the addition of nanoparticles and the drag associated with them. Figure 15 is designed to show the effect on entropy generation rate by Brinkman number Br. The enhancements in Br contribute to the dynamic viscosity of TiO/HO and GO-TiO/HO. Strong cohesive forces are generated, which enhance the entropy generation rate N().
The Hall effect is exists on behalf of boosting the intensity of the magnetic field. Increasing the intensity of the magnetic field generates the Lorentz force resistance to the motion of mono and hybrid nanofluids (TiO/HO and GO-TiO/HO). For the clarification of the aforementioned statement, Figure 16 is drawn, where it is noticed that the flows of the fluids decrease. Flow with all its components (f, g()) reduces, which provides the deficiency of convection into the surface. Lorentz forces latent power boosts the nanoparticles volume fraction. During these conditions, the Lorentz forces work strongly on the flow, which ultimately reduces it. The irrelevance of the magnetic field for the flow for minimum value of magnetic field parameter M is likely that the enhancement of the convection through nanoparticles is at once removed via the applicability of the magnetic field. The last term in Equation (9) in non-dimensional form provides the proof that at low magnetic field strength and velocity g(), the Hall current parameter m controls fluids motion completely. Similarly, it is evident from the last term in Equation (10) that the velocity g() is decreased by improving the Hall current parameter m. Figure 17 authenticates that the flow component is extremely slow with the positive values of m. It may vanish completely to zero if m is enlarged.
Streamlines investigation shows the flow internal behaviors. Streamline behaviors are noticed for the Hall parameter m. The effect of this parameter shows the trapping mainly on the upper and lower portions of the surface. Figure 18 demonstrates that the trapping is same at the lower and upper portions on flow surface as the Hall parameter m assumes the value 0.60. The trapping is high to the left of the channel compared to the right portion of the surface. It is evident that the compression of streamlines are at a distance from the wall.
Solution Validation
The validation of the solution is extremely important for achieving the correct results. For that purpose, the results of the present problem are compared with the study [19], although the published paper [19] has the investigations on mono nanofluid with dual solutions via bvp4c from MATLAB while the authors’ study is on hybrid nanofluid, in addition to innovations like boundary conditions, entropy generation, etc. using HAM solution. But still there exists a nice agreement in computing f(0) in terms of leading edge accretion or ablation parameter under some conditions.
5. Conclusions
The nanomaterials titania and graphene oxide are used to model the heat and mass transfer flow of TiO/HO and GO-TiO/HO with Hall current effect, leading edge accretion (or ablation) and entropy generation. HAM is used to generate the solution of the problem. The effects of all the parameters on different profiles are discussed in detail. The summary is presented as
- (1)
- Velocity decreases with increasing the parameters M, f, and increases with increasing the parameter .
- (2)
- Temperature decreases with increasing the parameters Pr, , f.
- (3)
- Nanoparticles concentration decreases with increasing the parameter f and increases with increasing the parameter Sc.
- (4)
- Entropy generation increases with increasing the parameters Re and Br.
- (5)
- Both the velocity components decrease with the Hall effect parameter m.
- (6)
- Streamlines show that the trapping increases at the left side of the surface for the parameter m.
Author Contributions
Conceptualization, N.S.K.; methodology, N.S.K.; software, P.K.; validation, Q.S. and A.B.; formal analysis, P.K.; investigation, N.S.K.; resources, P.T.; data curation, A.S.; writing—original draft preparation, N.S.K.; writing—review and editing, N.S.K.; visualization, Z.U.; supervision, N.S.K.; project administration, N.S.K.; funding acquisition, P.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
Acknowledgments
The authors are cordially thankful to the honorable reviewers for their constructive comments to improve the quality of the paper. This research is supported by the Postdoctoral Fellowship from King Mongkut’s University of Technology Thonburi (KMUTT), Thailand. This project is supported by the Theoretical and Computational Science (TaCS) Center under Computational and Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shatey, S.; Mosta, S. Variable viscosity on magnetohydrodynamic fluid flow and heat transfer over an unsteady stretching surface with Hall effect. Bound. Value Probl. 2010, 2010, 257568. [Google Scholar] [CrossRef]
- Hayat, T.; Awais, M.; Nawaz, M.; Iram, S.; Alsaedi, A. Mixed convection three-dimensional flow with Hall and ion-slip effects. Int. J. Nonlinear Sci. Numer. Simul. 2013, 14, 167–177. [Google Scholar] [CrossRef]
- Ahmed, S.; Zueco, J. Modeling of heat and mass transfer in a rotating vertical porous channel with Hall current. Chem. Eng. Commun. 2011, 198, 1294–1308. [Google Scholar] [CrossRef]
- Gaffar, S.A.; Prasad, V.R.; Reddy, E.K. MHD free convection flow of Eyring-Powell fluid from vertical surface in porous media with Hall/ionslip currents and Ohnic dissipation. Alex. Eng. J. 2016, 55, 875–905. [Google Scholar] [CrossRef]
- El-Aziz, M.A. Effects of Hall current on the flow and heat transfer of a nanofluid over a stretching sheet with partial slip. Int. J. Mod. Phys. C 2013, 24, 1350044. [Google Scholar] [CrossRef]
- Hayat, T.; Iqbal, M.; Yasmin, H.; Alsaadi, F. Hall Hall effects on peristaltic flow of couple stress fluid in an inclined asymmetric channel. Int. J. Biomath. 2014, 7, 1450057. [Google Scholar] [CrossRef]
- Khan, N.S. Bioconvection in second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Braz. J. Phys. 2018, 43, 227–241. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Graphene family nanofluids: A critical review and future research directions. Energy Convers. Manag. 2019, 196, 1222–1256. [Google Scholar] [CrossRef]
- Briffa, S.M.; Lynch, I.; Hapiuk, D.; Valsami-Jones, E. Physical and chemical transformations of zirconium doped ceria nanoparticles in the presence of phosphate: Increasing realism in environmental fate and behaviour experiments. Environ. Pollut. 2019, 252, 974–981. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Khan, M.A.; Bonyah, E.; Islam, S. Mixed convection in gravity-driven thin film non-Newtonian nanofluids flow with gyrotactic microorganisms. Results Phys. 2017, 7, 4033–4049. [Google Scholar] [CrossRef]
- Bahiraei, M. Particle migration in nanofluids: A critical review. Int. J. Therm. Sci. 2016, 109, 90–113. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Khan, U.; Mohyud-Din, S.T. A novel coupling of (CNT-Fe3O4/H2O) hybrid nanofluid for improvements in heat transfer for flow in an asymmetric channel with dilating/squeezing walls. Int. J. Heat Mass Transf. 2019, 136, 186–195. [Google Scholar] [CrossRef]
- Bahiraei, M.; Rahmani, R.; Yaghoobi, A.; Khodabandeh, E.; Mashayekhi, R.; Amani, M. Recent research contributions concerning use of nanofluids in heat exchangers: A critical review. Appl. Therm. Eng. 2018, 133, 137–159. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Electronic cooling with nanofluids: A critical review. Energy Convers. Manag. 2018, 172, 438–456. [Google Scholar] [CrossRef]
- Gulzar, O.; Qayoum, A.; Gupta, R. Experimental study on stability and rheological behaviour of hybrid Al2O3-TiO2 Therminol-55 nanofluids for considering solar collectors. Powder Technol. 2019, 352, 436–444. [Google Scholar] [CrossRef]
- Dalkilic, A.S.; Turk, O.A.; Mercan, H.; Nakkaew, S. An experimental investigation on heat transfer characteristics of graphite-SiO2/water hybrid nanofluid flow in horizontal tube with various quad-channel twisted tape inserts. Int. Commun. Heat Mass Transf. 2019, 107, 1–13. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, I.; Alqahtani, A.M.; Alshomrani, A.S. Magnetohydrodynamic nanoliquid thin film sprayed on a stretching cylinder with heat transfer. J. Appl. Sci. 2017, 7, 271. [Google Scholar] [CrossRef]
- Rosca, N.C.; Pop, I. Unsteady boundary layer flow of a nanofluid past a moving surface in an external uniform free stream using Buongiorno’s model. Comput. Fluids 2014, 95, 49–55. [Google Scholar] [CrossRef]
- Zuhra, S.; Khan, N.S.; Khan, M.A.; Islam, S.; Khan, W.; Bonyah, E. Flow and heat transfer in water based liquid film fluids dispensed with graphene nanoparticles. Results Phys. 2018, 8, 1143–1157. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, W. Thermophoresis and thermal radiation with heat and mass transfer in a magnetohydrodynamic thin film second-grade fluid of variable properties past a stretching sheet. Eur. Phys. J. Plus 2017, 132, 11. [Google Scholar] [CrossRef]
- Palwasha, Z.; Khan, N.S.; Shah, Z.; Islam, S.; Bonyah, E. Study of two dimensional boundary layer thin film fluid flow with variable thermo-physical properties in three dimensions space. AIP Adv. 2018, 8, 105318. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, A.; Shah, Z. Brownian motion and thermophoresis effects on MHD mixed convective thin film second-grade nanofluid flow with Hall effect and heat transfer past a stretching sheet. J. Nanofluids 2017, 6, 812–829. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S.; Shah, Z.; Bonyah, E.; Khan, W.; Islam, S. Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv. 2019, 8, 115302. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Kumam, P.; Shah, Z.; Islam, S.; Khan, W.; Zuhra, S.; Sohail, A. Influence of inclined magnetic field on Carreau nanoliquid thin film flow and heat transfer with graphene nanoparticles. Energies 2019, 12, 1459. [Google Scholar] [CrossRef]
- Khan, N.S. Study of two dimensional boundary layer flow of a thin film second grade fluid with variable thermo-physical properties in three dimensions space. Filomat 2019, 33, 5387–5405. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S. Boundary layer unsteady flow and heat transfer in a second grade thin film nanoliquid embedded with graphene nanoparticles past a stretching sheet. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, W.; Khan, I.; Ali, L. Thin film flow of a second-grade fluid in a porous medium past a stretching sheet with heat transfer. Alex. Eng. J. 2017, 57, 1019–1031. [Google Scholar] [CrossRef]
- Zuhra, S.; Khan, N.S.; Alam, A.; Islam, S.; Khan, A. Buoyancy effects on nanoliquids film flow through a porous medium with gyrotactic microorganisms and cubic autocatalysis chemical reaction. Adv. Mech. Eng. 2020, 12, 1–17. [Google Scholar] [CrossRef]
- Palwasha, Z.; Islam, S.; Khan, N.S.; Ayaz, H. Non-Newtonian nanoliquids thin film flow through a porous medium with magnetotactic microorganisms. Appl. Nanosci. 2018, 8, 1523–1544. [Google Scholar] [CrossRef]
- Khan, N.S. Mixed convection in MHD second grade nanofluid flow through a porous medium containing nanoparticles and gyrotactic microorganisms with chemical reaction. Filomat 2019, 33, 4627–4653. [Google Scholar] [CrossRef]
- Zuhra, S.; Khan, N.S.; Shah, Z.; Islam, Z.; Bonyah, E. Simulation of bioconvection in the suspension of second grade nanofluid containing nanoparticles and gyrotactic microorganisms. AIP Adv. 2018, 8, 105210. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Z.; Shutaywi, M.; Kumam, P.; Thounthong, P. A comprehensive study to the assessment of Arrhenius activation energy and binary chemical reaction in swirling flow. Sci. Rep. 2020, 10, 7868. [Google Scholar] [CrossRef] [PubMed]
- Zuhra, S.; Khan, N.S.; Islam, S. Magnetohydrodynamic second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Comput. Appl. Math. 2018, 37, 6332–6358. [Google Scholar] [CrossRef]
- Zuhra, S.; Khan, N.S.; Islam, S.; Nawaz, R. Complexiton solutions for complex KdV equation by optimal homotopy asymptotic method. Filomat 2020, 33, 6195–6211. [Google Scholar] [CrossRef]
- Zahra, A.; Mahanthesh, B.; Basir, M.F.M.; Imtiaz, M.; Mackolil, J.; Khan, N.S.; Nabwey, H.A.; Tlili, I. Mixed radiated magneto Casson fluid flow with Arrhenius activation energy and Newtonian heating effects: Flow and sensitivity analysis. Alex. Eng. J. 2020, 57, 1019–1031. [Google Scholar]
- Liaqat, A.; Asifa, T.; Ali, R.; Islam, S.; Gul, T.; Kumam, P.; Mukhtar, S.; Khan, N.S.; Thounthong, P. A new analytical approach for the research of thin-film flow of magneto hydrodynamic fluid in the presence of thermal conductivity and variable viscosity. ZAMM J. Appl. Math. Mech. Z. Angewwandte Math. Mech. 2020, 1–13. [Google Scholar] [CrossRef]
- Bejan, A. Second law analysis in heat transfer. Energy 1980, 5, 720–732. [Google Scholar] [CrossRef]
- Ahmad, S.; Nadeem, S. Flow analysis by Cattaneo-Christov heat flux in the presence of Thomson and Troian slip condition. Appl. Nanosci. 2020. [Google Scholar] [CrossRef]
- Khan, N.; Riaz, I.; Hashmi, M.S.; Musmar, S.A.; Khan, S.U.; Abdelmalek, Z.; Tlili, I. Aspects of chemical entropy generation in flow of Casson nanofluid between radiative stretching disks. Entropy 2020, 22, 495. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S.; Shah, Q. Entropy generation in two phase model for simulating flow and heat transfer of carbon nanotubes between rotating stretchable disks with cubic autocatalysis chemical reaction. Appl. Nanosci. 2019, 9, 1797–1822. [Google Scholar] [CrossRef]
- Zaib, A.; Khan, U.; Shah, Z.; Kumam, P.; Thounthong, P. Optimization of entropy generation in flow of micrpolar mixed convective magnetite (Fe3O4) ferroparticle over a vertical plate. Alex. Eng. J. 2019, 58, 1461–1470. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Z.; Islam, S.; Khan, I.; Alkanhal, T.A.; Tlili, I. Entropy generation in MHD mixed convection non-Newtonian second-grade nanoliquid thin film flow through a porous medium with chemical reaction and stratification. Entropy 2019, 21, 139. [Google Scholar] [CrossRef]
- Shahsavar, A.; Baseri, M.M.; Al-Rashed, A.A.A.A.; Afrand, M. Numerical investigation of forced convection heat transfer and flow irreversibility in a novel heat sink with helical microchannels working with biologically synthesized water-silver nano-fluid. Int. Commun. Heat Mass Transf. 2019, 108, 104324. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S.; Shah, Z.; Bonyah, E.; Khan, W.; Islam, S.; Khan, A. Hall current and thermophoresis effects on magnetohydrodynamic mixed convective heat and mass transfer thin film flow. J. Phys. Commun. 2019, 3, 035009. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R.; Abdelsalam, S.I. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Phys. Scr. 2019, 95, 045206. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Deebani, W. Radiative MHD Casson nanofluid flow with activation energy and chemical reaction over nonlinear stretching surface through entropy generation. Sci. Rep. 2020, 10, 4402. [Google Scholar] [CrossRef]
- Khan, N.S.; Kumam, P.; Thounthong, P. Renewable energy technology for the sustainable development of thermal system with entropy measures. Int. J. Heat Mass Transf. 2019, 145, 118713. [Google Scholar] [CrossRef]
- Khan, N.S.; Kumam, P.; Thounthong, P. Second law analysis with effects of Arrhenius activation energy and binary chemical reaction on nanofluid flow. Sci. Rep. 2020, 10, 1226. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Q.; Bhaumik, A.; Kumam, P.; Thounthong, P.; Amiri, I. Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Sci. Rep. 2020, 10, 4448. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Q.; Sohail, A. Dynamics with Cattaneo-Christov heat and mass flux theory of bioconvection Oldroyd-B nanofluid. Adv. Mech. Eng. 2020. [Google Scholar] [CrossRef]
- Rahila, N.; Noor, M.; Shah, Z.; Sohail, M.; Kumam, P.; Thounthong, P. Entropy generation optimization in MHD pseudoplastic fluid comprising motile microorganisms with stratification effect. Alex. Eng. J. 2020, 59, 485–496. [Google Scholar]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).