Abstract
A micromechanical model is developed to study the creep phenomena with neat and carbon-fiber-reinforced PEEK (Polyetheretherketon) and epoxy. The model considers that the continuous elastic circular fibers form a regular array inside the matrix material. In this study, the fibers are considered to be linear elastic and anisotropic, while the matrix has a nonlinear viscoelastic behavior. The approach describes the time-dependent response of unidirectional viscoelastic composites subjected to various types of loading conditions. A comparison between the finite element analysis and the proposed micromechanical model shows a good agreement. Experimental tests validate the results obtained using the proposed theoretical model.
1. Introduction
Creep phenomenon in viscoelastic materials is defined as primary, secondary, and tertiary creep and represents a time-dependent deformation of the material subjected to a certain applied load [1,2] (see Figure 1). Generally, this phenomenon occurs at high temperature but can be seen in certain materials, too, at the room temperature. In time, the studied material can increase in length and this can be dangerous in service.
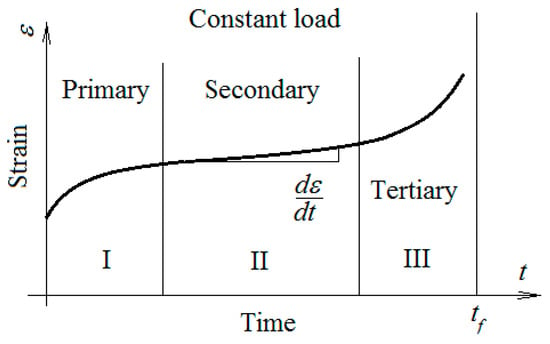
Figure 1.
The primary, secondary, and tertiary creep (adapted after [2]).
Usually, engineering applications refer to the primary and secondary stages, when the creep strain rate is much larger. The creep strain (deformation) rate is defined as the slope of the creep strain–time curve. Generally, this is dependent on stress, temperature, and time. The primary creep starts with a rapid rate that slows with time. The secondary creep has a relatively uniform rate. The tertiary creep region is attributed to a rapid increase in creep strain rate. Here, we have an accelerated creep rate and it ends when the material breaks. This third stage is usually brief and is normally associated with geometric instabilities, leading quickly to failure and, therefore, is not of much interest in engineering analysis. In practice, it is necessary to know the rate of deformation, provided by a creep test, in order to be implemented directly in the design stage [2,3]. Studies on the creep phenomenon are numerous [4,5,6] and the history of the field will be briefly reviewed in the following.
Different materials, such as metals, plastics, rubber, or concrete, have different behavior, and creep in service can be influenced by existing loads and temperatures. To determine experimentally the creep behavior of a material, measurements of dimensional changes at constant high temperature and constant load must be performed. A comparison with the measurements at room temperature offers an image of difference in behavior at different temperatures. The creep models are useful for long-term service devices (pieces) which are strain limited and can provide a prediction of life expectancy. Because the creep generally occurs at high temperatures, it is necessary to use an environmental chamber to ensure precise heating control. This is critical to minimize the effects of the thermal expansion.
Brinson et al. [7] proposed an accelerated characterization scheme to predict the viscoelastic behavior of general laminated composite materials. Their analysis is based on a reduced amount of experimental measurements. In other words, the tests utilize short-term observation of the unidirectional material at elevated temperature to predict long-term response based upon the time–temperature superposition principle (TTSP) [8,9].
In this way, based on short-term measurements of the composite material at elevated temperature, the long-term response of the material can be predicted based upon the time–temperature superposition principle (TTSP) [10].
Studying nonlinear viscoelastic behavior of unidirectional composites has been the subject of investigation by Schaffer and Adams [11]. Their analysis is based on an elastoplastic finite element micromechanics program to model a unidirectional composite material. The authors used the symmetry arguments of the fiber packing arrangement of the unidirectional composite, hence, simplifying the analysis so that only one-quarter of the circular fibers is to be modeled. Finite element method proves to be an important tool to determine the overall moduli of a composite. This method can be applied not only for a bi-phase material with a simple geometry of the fiber but also for a complex topology of the constituent material of composite. Any combination of longitudinal and transversal, as well as hygrothermal, loading history may be analyzed. Nonlinear viscoelastic constitutive equations developed by Schapery [12,13,14] were used to account for the viscoelastic material behavior. Further, the analysis provides an examination of the internal stresses of the composite under a variety of external conditions. In this approach, thermal- and moisture-dilatational effects were included by means of initial stress. Mohan and Adams [15] utilized the above program to determine the response of the unidirectional graphite- and glass-reinforced composites. They were able to find a good correlation between the time-dependent response and the predictions achieved by the finite-element micromechanics program of Schaffer and Adams [11].
Findley et al. [16,17,18] developed a procedure to accurately model the nonlinear creep compliance of a variety of materials. By applying the Findley approach, the nonlinear creep behavior of viscoelastic materials can be characterized using an empirical model. The technique is based on a creep power law. The method may conveniently be implemented into a numerical procedure.
Dillard et al. [19,20] used a nonlinear viscoelastic model based on the Findley approach to represent the creep of graphite/epoxy composites. This model, together with uniaxial tension tests on 0°, 90°, and 10° off-axis specimens, allows complete characterization of the nonlinear viscoelastic compliance matrix of an orthotropic material, such as a unidirectional lamina. Furthermore, the basic procedure was also utilized to characterize the long-term nonlinear behavior of general laminates.
In another study [21], creep behavior of carbon epoxy laminates was investigated by tensile creep test on [+/−45]2s coupons. The authors reviewed the effects of temperature, moisture, and stress levels on the time-dependent shear modulus for two carbon epoxy laminate systems. This study has shown that a moisture concentration of about 1% may be considered as the critical limit for the investigated system. In other words, the viscoelastic deformation occurs much more rapidly beyond this limit. It was further demonstrated that for the above laminate, shear stresses in excess of 50% of the ultimate tensile strength could lead to irreversible deformation during creep.
Measurement concerning the elastic/viscoelastic behavior of a unidirectional aramid fiber-reinforced epoxy at room and elevated temperatures were performed by Walrath [22]. The “power law” was chosen as the appropriate mathematical model to describe linear, as well as nonlinear, viscoelastic compliance. For the nonlinear characterization, the nonlinear viscoelastic coefficients, which in general were shown to be functions of both stress and temperature, were introduced into the model. This was in accordance with the Schapery [12] nonlinear viscoelastic model, which was believed to adequately fit the response of the material to uniaxial loading.
Hashin [23] and Hashin et al. [24,25,26] used a variational principle in order to convert from elastic to time-dependent behavior through comparatively simple equations. This formulation assumes that a composite can be modeled as a random distribution of continuous fibers of varying diameters with a constant fiber volume fraction throughout. Each circular fiber is surrounded by a circular matrix bounded rigidly to it. It is, in fact, a collection of composite cylinders with differing sizes. The requirement is that the strain energy stored in a representative element is equal to that existing in an element of homogeneous material with the same effective properties. As a result of this, the stresses and strains in a representative cylinder are representative of those in the real composite, but in the average sense.
Bowles and Griffin [27] investigate the thermally induced stress fields in the two constituents of polymer-based composites at cold temperatures which are typical for spacecraft operating temperature. The study of the influence of microstructural geometry showed that this factor does indeed affect the distributions and magnitudes of the induced stresses depending on whether a composite cylinder, square, or hexagonal array of microstructural geometry is assumed. Furthermore, it was shown that fiber properties did not strongly influence the matrix stresses, yet the absolute value of the latter increased with higher values of fiber volume ratio .
In a study undertaken by Zhao et al. [28], all elastic constants which characterize an orthotropic and a transversely isotropic composite were derived. It was shown that for the transversely isotropic case, among the various investigations by Hill [29,30,31,32], the upper and lower bounds presented in reference [32] and those of Hashin [23] could very well be used to estimate the effective elastic moduli, when the ribbons are harder or softer than the matrix material, respectively.
Weng and Wang [33] extended the Mori–Tanaka method [34] into the Laplace domain to investigate the viscoelastic behavior of an isotropic composite containing randomly oriented inclusions.
The nonlinear viscoelastic/viscoplastic behavior of IM6/5260 graphite/bismaleimide has been the subject of investigation by Pasricha et al. [35]. Schapery’s nonlinear formulation [12] was used to characterize the response of the above material at 93 °C by testing the 0-, 90-, and 45-degree specimens. The 90-degree specimen showed a nonlinearly elastic but linearly viscoelastic behavior, while the 45-degree specimen was both nonlinearly elastic as well as nonlinearly viscoelastic.
A micromechanical analysis to investigate the overall viscoelastic behavior of a unidirectional composite has been proposed by Aboudi [36,37]. Good agreement has been shown to exist between the finite element results obtained by Schaffer and Adams ([11]) and the proposed micromechanical analysis.
The subject related to the properties of biphasic materials has been studied by numerous papers in recent years [38,39,40,41,42,43,44,45,46,47,48,49].
In the paper, the authors propose a micromechanical model in order to study the creep behavior of a composite material reinforced with carbon fiber. The model was used to obtain the creep curve for different load applied to the test specimen. An experimental procedure was used to verify the obtained results.
2. Micromechanical Model
In a micromechanical approach, the global composite properties are determined from the properties of the individual constituents, i.e., fiber and matrix, as well as the interaction between them. Indeed, in a unidirectional composite, the fibers are distributed randomly in the matrix material. However, it is reasonable to consider some periodicity in the distribution of the fibers. The symmetries and the periodicity help us to simplify the proposed model. An example of this situation is depicted by the square array in Figure 2. The following assumptions are made in the present micromechanical analysis:
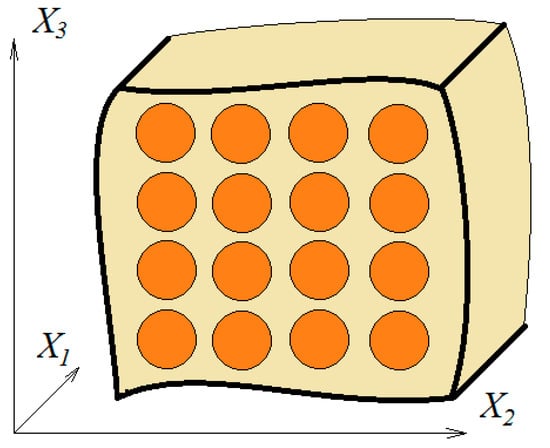
Figure 2.
Square fiber packing geometry of a unidirectional composite.
- Continuous fibers, circular in cross section and extended in the X1-direction, are arranged in a rectangular array in the X2–X3 plane.
- The fibers are supposed to be linearly elastic and anisotropic while the polymeric matrix is nonlinearly viscoelastic but isotropic.
- The interaction between fibers and matrix is merely mechanical and no crack or holes may develop under load.
The above regular and periodic packing allows the analysis of a representative cell and thereby reduces the size and complexity of the problem. Note that Figure 3 shows one of the repeating units of the periodical pattern shown in Figure 2. Thus, the representative unit cell (RUC) can consist of two subcells modeling only one-quarter of a fiber with the corresponding matrix material as shown in Figure 4. Moreover, the unit cells are considered to be small in size compared to all dimensions in the composite.
Figure 3.
The repeating unit of a square fiber array geometry.
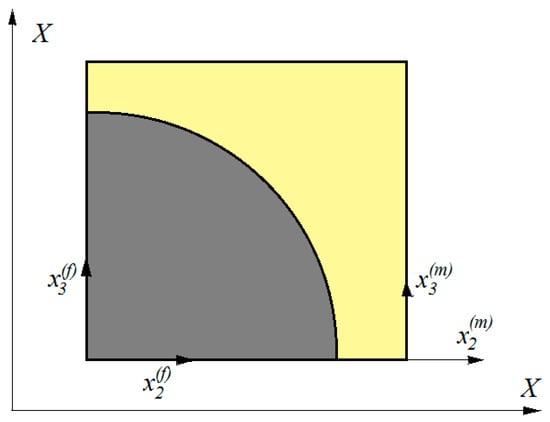
Figure 4.
The representative unit cell with local coordinates.
For each subcell in the representative cell, a local reference frame (X1, , ) with its origin located as shown in Figure 4 is introduced. Furthermore, the displacement in each of the two subcells is expressed in a first-order linear expansion as a function of the distance from the origin to the local coordinate axes [27,28]. This means that the displacement at any point in the subcell is:
In this equation, represents the displacement components of the origin of the local coordinate axes. The functions and are used to represents linear dependence of the displacements at any point in the subcell in and directions, respectively. It should be pointed out the ““ is used to symbolically represent both fiber () and matrix () constituents in the representative cell. An example of this is the expression given by Equation (1) which applies to both phases, fiber as well as matrix. For an expression applying exclusively to only one of the constituents in the representative cell, the proper notation “f” or “m” is used.
It is now necessary to establish a relation between the average stresses and average strains in the composite from which the overall behavior of the composite can be determined. The familiar strain–displacement relations of anisotropic bodies,
Applied to each subcell of the representative cell and written in an alternative form, yields
If we have the notation:
where is the engineering shear strain.
Substituting Equation (1) into Equation (2) and considering Equation (3a,b) yields:
The constitutive equation of a linear and transversely isotropic material is:
or:
where and are the Young’s moduli, and are the shear moduli and and are the Poisson’s ratio. It is appropriate to write this equation in the inverse form as it applies to the elastic fiber material (). Note that X1 is the direction of anisotropy and the X2–X3 plane is the plane of isotropy.
with:
The other components of the stiffness matrix are obtained from Equation (10b). In compact form, Equation (10c) can be written as:
Due to the presence of polymeric matrix in composite materials, the overall behavior of the fiber-reinforced plastics should be considered as viscoelastic. The viscoelastic material response of the composite, for a creep type loading in which the applied stress is kept constant, can be described with the help of the Boltzmann’s superposition principle.
For the nonlinear viscoelastic material behavior under uniaxial creep loading and isothermal conditions, however, Schapery’s equation [12], written here in a modified form yields:
where:
For the isotropic nonlinear viscoelastic material, (subcell “m” in the representative cell) under multiaxial loading, the constitutive equations can be written in a tensor form as follows:
In Equation (14), is given by Equation (13), is the time-dependent Poisson’s ration, and is the Kronecker’s delta. For the materials examined in the present study, it has been determined experimentally that Poisson’s ratio is a very weak function of time so that it can be taken to be practically time independent.
The problem is now reduced to the following steps to determine the overall behavior of the composite. First, the induced stresses in each subcell resulting from an externally applied constant load are to be determined. Continuity of tractions along the interfaces of the phases has to be satisfied. Then, the strains in the representative cell need to be calculated using the induced strains in each subcell. It should be noted that all stresses and strains are evaluated in an average sense. Continuity of displacements throughout the composite requires that all displacements be continuous over the boundary of the subcells inside the unit cell, as well as between the adjacent cells. Finally, the overall behavior of the composite is determined by relating the average stresses and the average strains evaluated above.
3. Calculation of the Average Stresses in the Unit Cell
The composite specimen under consideration is in the shape of a rectangular parallelepiped with edges parallel to the coordinate axes (X1, X2, X3) and has a volume V. The problem to be discussed now is that of computing the average stress in the representative volume cell. This is a sample of the whole composite which contains a sufficient number of the constituent materials and, at the same time, is representative of the bulk material, as far as the structural point of view is concerned. Therefore, the representative volume cell retains the same properties as those of the entire composite. The volume average of the stress distribution can be written as:
For the representative cell containing one-quarter of a fiber and the corresponding matrix, the above equation is written in an alternative form as:
where are the average stresses in the subcells and A and are the areas of the representative cell and of the subcells, respectively. Note that for the sake of simplicity in computation, a unit depth of the composite has been considered, i.e., V = A × 1. It follows from Figure 3 that
The average stress in each of the two subcells is written in a similar way as:
It seems appropriate at this point to change the variables of integration in the above double integral and perform the integration in polar coordinate system. This is achieved by using the following Jacobian transformation:
Equation (19) for subcell “f” can therefore be written in the polar coordinate system as follows:
where for the transversely isotropic fiber has the components introduced in Equation (12). Substitution of Equations (4)–(9) and (10b) into Equation (21) leads to the following average stresses in the fiber material:
This is written in an alternative form as:
Next, the average stresses for subcell “m” are determined. For this purpose, it is convenient to calculate the total stress in the unit cell as if it consisted only of matrix material. Subsequently, the stress in subcell “m” is computed by subtracting that of subcell “f” from the total stress of the unit cell as computed above. Based on the local coordinate of subcell “m”, the following relation is obtained:
This equation together with Equations (4)–(9) and (14) yields:
Note that Equations (25)–(30) is a system of nonlinear equations relating the subcell stresses in the matrix indirectly to the micro-variables and .
4. Determination of the Continuity Conditions
As mentioned earlier, throughout the representative cell, the continuity conditions of displacements at the interface between the subcells and the adjacent unit cells must be fulfilled. This turn means that the continuity conditions must be satisfied in both ×2 and ×3 directions within the composite, as it will be described below.
It is obvious from Figure 5 that for subcells “f” and “m”, the following relations hold
and:
where is to imply the location of the interface between the subcells of the representative cell in the direction and located points on the interface.
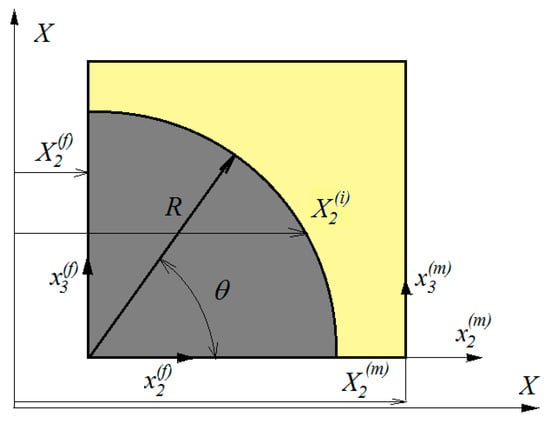
Figure 5.
Representative cell used for the continuity conditions.
Upon substitution of Equations (31) and (32) into Equation (1) for and , viz.
where:
The condition for continuity of displacements at the interface between the two subcells must be considered in the average sense. This means:
The above integration is simplified to:
Attention is drawn to the fact that the above quantities are as yet evaluated at and .
Addition and subtraction of the above equations provides the continuity conditions of displacements described above in direction as:
Equation (39) is the expression which describes the continuity of displacement for the two neighboring cells, and .
5. Calculation of the Average Strains in the Unit Cell
For the composite specimen introduced earlier and making use of the continuity of displacements just discussed, the volume average of the internal strain can be shown to be:
and, for the representative cell under investigation
where and have the same definition as before and are the strain components in the subcells as defined in Equations (4)–(9).
Substituting Equation (1) in (3) leads to the following relation for
This equation together with Equation (41) yields:
which can be simplified to:
Having established all the necessary equations for the prediction of the overall behavior of the composite, it is now appropriate to work out examples to examine the applicability of the analysis. It was mentioned earlier that even in a uniaxial test, the specimen experiences a three-axial state of stress which is very complex. It is, therefore, appropriated to have be octahedral shear stress in the matrix to let the stress-dependent material properties and depend on a single invariant rather than the applied stress given in Equations (12)–(13). This so-called equivalent stress was introduced to be the octahedral shear stress in matrix. The same analogy can be used here to let the material properties be a function of , an equivalent stress in the subcell “m” defined below, since the analysis is performed on the micro-level.
It should be noted that the procedure by which the unknowns are solved for is of an incremental nature. This means that the unknown variables are evaluated stepwise in time and that the procedure is continued until the variables of interest are determined at the requested time. At each time step, however, a system of 13 algebraic equations is to be solved. These equations are summarized below and contain the following as unknown variables:
- the six subcell stresses , , and ;
- the four micro-variables and ;
- and the three composite strains , , and .
As mentioned earlier, it is desired to establish a relation between the average stress in the matrix and that of the fiber in the representative unit cell. It should be pointed out that the assumption of equal average stresses in the neighboring subcells of the representative unit cell (RUC) in Aboudi’s model [36,37] may be an oversimplification of the real case. In reality, the average stresses and strains in the two phases of the unit cell may be different. In general, if the unidirectional composite is under a biaxial state of stress transverse to the fiber direction, namely in the (X2, X3) plane, the relations which can be applied in the X2 direction are
and:
which are written in a simplified form as:
A similar relation can be obtained in X3 direction:
It should be mentioned at this point that the concentration factors and should satisfy the relation:
And
For the special case when the composite is loaded in only one of the directions, X2 or X3, the relation corresponding to the direction with no applied load should be replaced accordingly by either:
or:
For the biaxial loading conditions as described above, the concentration values in an average sense have to be determined accordingly. A few biaxial cases were examined, but since all the experiments carried out in the present study were under uniaxial tension test, only these values are considered here.
The 13 equations containing the 13 unknowns listed before are the following:
However, the relations above containing and should be modified when necessary. The properties for the two types of fibers together with the associated resins are given in Table 1. For the fibers, the longitudinal elastic modulus El was supplied by the manufacturer. Since the transverse properties of the fibers (i.e., Et, ) are not available, their values were computed based on an inverse technique.

Table 1.
Elastic constituent material properties.
In order to verify the applicability of the presented procedure, a creep curve of the glass/epoxy system used in Schaffer and Adams’s study [11] was obtained. This together with the results computed with the finite element method is shown in Figure 6. It is readily seen that the results of the proposed micromechanical approach agree very well with those obtained using Finite Element Method.
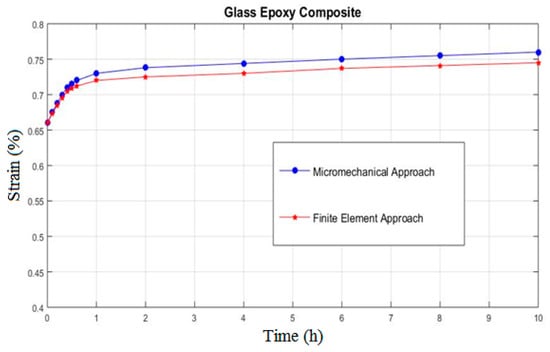
Figure 6.
Comparison between micromechanical and Finite Element prediction for of glass epoxy composite subjected to and
For the purpose of illustration, in Figure 7 through 11, the above micromechanics procedure was used to obtain the creep curve at different temperatures and stress levels for the two composites and resin materials mentioned earlier. It can be easily observed that the proposed micromechanical analysis can be used for accurate predictions of the experimental data under various loading conditions (temperature 23 °C, see Figure 7; temperature 80 °C, see Figure 8). We mention that 23 °C represents the room temperature where the reference experiments were made. The temperature of 80 °C is the temperature at which the experiments were done for this study and represents a temperature that is found in some practical applications of carbon fibers. It should be pointed out that the present analysis, as opposed to the one presented in [15,16], assumes the fibers have a circular cross section. Calculus was performed in the environment programming MATLAB. The studied cases are summarized in Table 2.
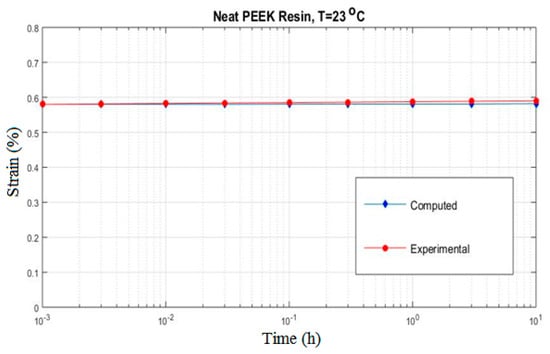
Figure 7.
The creep strain for neat PEEK resin subjected to at 23 °C.
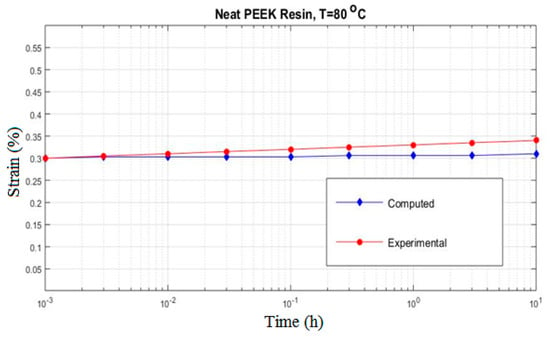
Figure 8.
The creep strain for neat PEEK resin subjected to at 80 °C.

Table 2.
Cases verified by experimental tests.
6. Results and Discussion
In Figure 7, the response of the neat PEEK resin subjected to an applied uniaxial stress of at 23 °C is shown together with the experimental result. Examination of Figure 7 indicates that a good prediction of the experimental results is achieved by using the proposed micromechanical approach. In Figure 8, the same tests performed at 80 °C is presented. A significant difference can be observed. The temperature changes the creep diagram and the strain in the specimen is half as much as in the first case.
In Figure 9, the overall creep response of a one-dimensional carbon/PEEK composite subjected to a transverse stress of at 80 °C is shown along with the experimental result. It is readily seen that the deviation of the present micromechanical prediction from the experimental result is around 5%. The effect of non-linearity can be seen in Figure 10 where the applied stress is increased to while the temperature is kept unchanged. Fair to good agreement seems to exist between the experimental and computed results for the presented loading condition. Analogous results are obtained for the transverse creep response of carbon/epoxy composite for which the graphs are shown in Figure 11 and Figure 12.
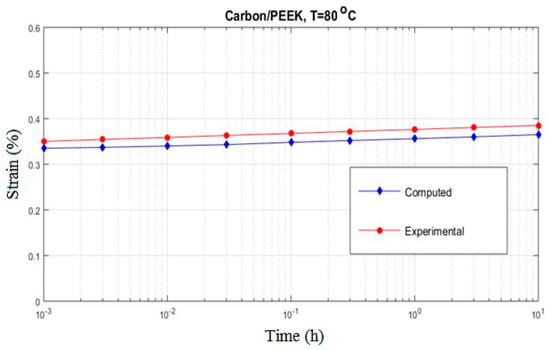
Figure 9.
The creep strain for carbon/PEEK subjected to at 80 °C.
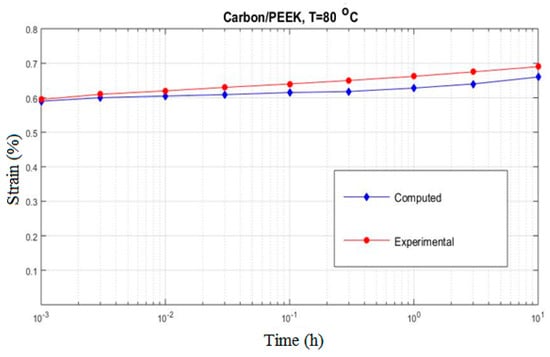
Figure 10.
The creep strain for carbon/PEEK subjected to at 80 °C.
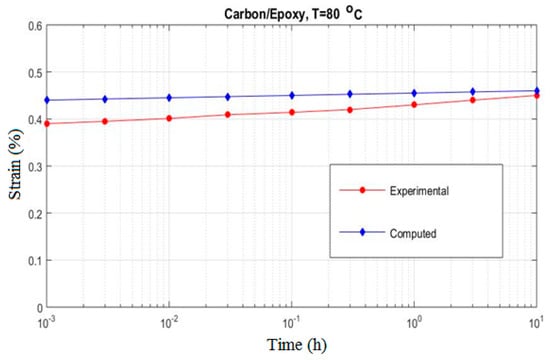
Figure 11.
The creep strain for carbon/epoxy subjected to at 80 °C.
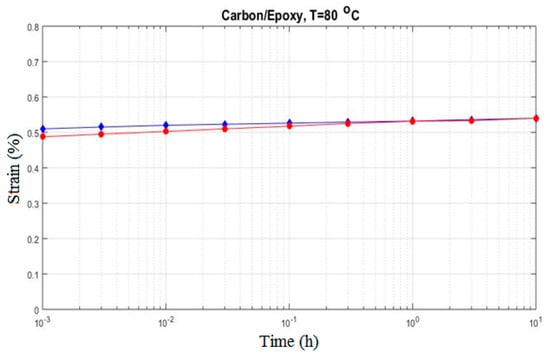
Figure 12.
The creep strain for carbon/epoxy subjected to at 80 °C.
It is shown that excellent modeling of the experiments is possible by using Schapery’s approach for nonlinear viscoelastic characterization. The results show that the stress range, in which linear viscoelasticity can be assumed, is shifted to lower values with increasing temperature. This is true for the meat resins and the laminates investigated. However, temperature seems to have a much lower effect on the linear viscoelastic limit of the laminates. The influence of the temperature on the time-dependent response was found to be nonlinear.
7. Conclusions
A combined experimental–analytical study to investigate the temperature dependence of the nonlinear viscoelastic response of two composite materials—a thermoset and a thermoplastic matrix system—was undertaken. The following remarks are made with regard to the results presented in the paper.
An excellent modeling is possible using Schapery’s result [11] for nonlinear and creep response of viscoelastic materials. For the temperature considered in the paper (80 °C), it can be assumed that the instantaneous response is linear and temperature independent over the range of stress levels relevant in practical applications. This result can be useful in the study of thermoviscoelastic response analysis of composite materials.
Concerning the micromechanics procedure of the present study, the analysis is capable of modeling a unidirectional composite subjected to longitudinal and/or transversal normal loading. A finite element procedure is used to model an RVE(representative volume element). The constitutive material parameters which are functions of time and temperature are input to the program through appropriate subroutines. Schapery’s nonlinear constitutive equation for isothermal uniaxial loading condition is incorporated into the analysis to account for nonlinear viscoelastic behavior. From the numerous experimental results, the several examples presented demonstrate the potential application of the present method. For the three-axial state of stress which is presented in the composite as a result of uniaxial loading, the equivalent stress in the matrix is considered so that all viscoelastic parameters are dependent on a single invariant. Poisson’s ratio has been shown to be a very weak function of time or nearly time independent, an observation which has greatly simplified the constitutive equations.
In summary, the creep data generated through the use of the above micromechanical approach show good correlation with those obtained experimentally.
Author Contributions
Conceptualization, M.K. and S.V.; methodology, M.K.; software, M.K. and S.V.; validation, M.K. and S.V.; writing—original draft preparation, M.K. and S.V.; writing—review and editing, M.K. and S.V.; visualization, M.K. and S.V.; supervision, M.K.; project administration, M.K. and S.V.; funding acquisition, M.K. and S.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors thank Technical University Munich for the administrative and technical support concerning the experiments. We want to thank the reviewers who have read the manuscript carefully and have proposed pertinent corrections that have led to an improvement in our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cristescu, N.; Craciun, E.-M.; Gaunaurd, G. Mechanics of Elastic Composites (CRC Series in Modern Mechanics and Mathematics). Appl. Mech. Rev. 2004, 57, B27. [Google Scholar] [CrossRef]
- Zaoui, A. Homogeneization Techniques for Composite Media’, dans ‘Lecture Notes in Physics’; Springer: Berlin, Germany, 1987; Volume 272. [Google Scholar]
- Garajeu, M. Contribution à L’étude du Comportement non Lineaire de Milieu Poreaux Avec ou Sans Renfort. Ph.D. Thesis, Aix-Marseille University, Marseille, France, 1995. [Google Scholar]
- Brauner, C.; Herrmann, A.S.; Niemeier, P.M.; Schubert, K. Analysis of the non-linear load and temperature-dependent creep behaviour of thermoplastic composite materials. J. Thermoplast. Compos. Mater. 2016, 30, 302–317. [Google Scholar] [CrossRef]
- Fett, T. Review on Creep-Behavior of Simple Structures. Res. Mech. 1988, 24, 359–375. [Google Scholar]
- Sá, M.F.; Gomes, A.; Correia, J.; Silvestre, N. Creep behavior of pultruded GFRP elements—Part 1: Literature review and experimental study. Compos. Struct. 2011, 93, 2450–2459. [Google Scholar] [CrossRef]
- Brinson, H.F.; Morris, D.H.; Yeow, Y.I. A New Method for the Accelerated Characterization of Composite Materials. In Proceedings of the Sicth International Conference on Experimental Stress Analysis, Munich, Germany, 18–22 September 1978. [Google Scholar]
- Jinsheng, X.; Hongli, W.; Xiaohong, Y.; Long, H.; ChangSheng, Z. Application of TTSP to non-linear deformation in composite propellant. Emerg. Mater. Res. 2018, 7, 19–24. [Google Scholar] [CrossRef]
- Nakano, T. Applicability condition of time–temperature superposition principle (TTSP) to a multi-phase system. Mech. Time-Depend. Mater. 2012, 17, 439–447. [Google Scholar] [CrossRef]
- Achereiner, F.; Engelsing, K.; Bastian, M. Accelerated Measurement of the Long-Term Creep Behaviour of Plastics. Superconductivity 2017, 247, 389–402. [Google Scholar]
- Schaffer, B.G.; Adams, D.F. Nonlinear Viscoelastic Behavior of a Composite Material Using a Finite Element Micromechanical Analysis; Dept. Report UWME-DR-001-101-1, Dep. Of Mech. Eng.; University of Wyoming: Laramie, WY, USA, 1980. [Google Scholar]
- Schapery, R. Nonlinear viscoelastic solids. Int. J. Solids Struct. 2000, 37, 359–366. [Google Scholar] [CrossRef]
- Violette, M.G.; Schapery, R. Time-Dependent Compressive Strength of Unidirectional Viscoelastic Composite Materials. Mech. Time-Depend. Mater. 2002, 6, 133–145. [Google Scholar] [CrossRef]
- Hinterhoelzl, R.; Schapery, R. FEM Implementation of a Three-Dimensional Viscoelastic Constitutive Model for Particulate Composites with Damage Growth. Mech. Time-Depend. Mater. 2004, 8, 65–94. [Google Scholar] [CrossRef]
- Mohan, R.; Adams, D.F. Nonlinear creep-recovery response of a polymer matrix and its composites. Exp. Mech. 1985, 25, 262–271. [Google Scholar] [CrossRef]
- Findley, W.N.; Adams, C.H.; Worley, W.J. The Effect of Temperature on the Creep of Two Laminated Plastics as Interpreted by the Hyperbolic Sine Law and Activation Energy Theory. In Proceedings of the Proceedings-American Society for Testing and Materials, Conshohocken, PA, USA, 1 January 1948; Volume 48, pp. 1217–1239. [Google Scholar]
- Findley, W.N.; Khosla, G. Application of the Superposition Principle and Theories of Mechanical Equation of State, Strain, and Time Hardening to Creep of Plastics under Changing Loads. J. Appl. Phys. 1955, 26, 821. [Google Scholar] [CrossRef]
- Findley, W.N.; Peterson, D.B. Prediction of Long-Time Creep with Ten-Year Creep Data on Four Plastics Laminates. In Proceedings of the American Society for Testing and Materials, Sixty-first(61th) Annual Meeting, Boston, MA, USA, 26–27 June 1958. [Google Scholar]
- Dillard, D.A.; Brinson, H.F. A Nonlinear Viscoelastic Characterization of Graphite Epoxy Composites. In Proceedings of the 1982 Joint Conference on Experimental Mechanics, Oahu, HI, USA, 23–28 May 1982. [Google Scholar]
- Dillard, D.A.; Morris, D.H.; Brinson, H.F. Creep and Creep Rupture of Laminated Hraphite/Epoxy Composites. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 30 September 1980. [Google Scholar]
- Charentenary, F.X.; Zaidi, M.A. Creep Behavior of Carbon-Epoxy (+/−45o)2s Laminates. In Progess in Sciences and Composites; Hayashi, K., Umekawa, S., Eds.; ICCM-IV; The Japan Society for Composite Materials, c/o Business Center for Academic Societies Japan 2-4-6, Yayoi, Bunkyo-ku, Tokyo 113: Tokyo, Japan, 1982. [Google Scholar]
- Walrath, D.E. Viscoelastic response of a unidirectional composite containing two viscoelastic constituents. Exp. Mech. 1991, 31, 111–117. [Google Scholar] [CrossRef]
- Hashin, Z. On Elastic Behavior of Fibre Reinforced Materials of Arbitrary Transverse Phase Geometry. J. Mech. Phys. Solids 1965, 13, 119–134. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. On some variational principles in anisotropic and nonhomogeneous elasticity. J. Mech. Phys. Solids 1962, 10, 335–342. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A Variational Approach to the Theory of the Elastic Behavior of Multiphase Materials. J. Mech. Phyds. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Hashin, Z.; Rosen, B.W. The Elastic Moduli of Fiber-Reinforced Materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Bowles, D.E.; Griffin, O.H., Jr. Micromecjanics Analysis of Space Simulated Thermal Stresses in Composites. Part I: Theory and Unidirectional Laminates. J. Reinf. Plast. Compos. 1991, 10, 504–521. [Google Scholar]
- Zhao, Y.H.; Weng, G.J. Effective Elastic Moduli of Ribbon-Reinforced Composites. J. Appl. Mech. 1990, 57, 158–167. [Google Scholar] [CrossRef]
- Hill, R. Theory of Mechanical Properties of Fiber-strengthened Materials: I Elastic Behavior. J. Mech. Phys. Solids 1964, 12, 199–212. [Google Scholar] [CrossRef]
- Hill, R. Theory of Mechanical Properties of Fiber-strengthened Materials: II Inelastic Behavior. J. Mech. Phys. Solids 1964, 12, 213–218. [Google Scholar] [CrossRef]
- Hill, R. Theory of Mechanical Properties of Fiber-strengthened Materials: III Self-Consistent Model. J. Mech. Phys. Solids 1965, 13, 189–198. [Google Scholar] [CrossRef]
- Hill, R. Continuum Micro-Mechanics of Elastoplastic Polycrystals. J. Mech. Phys. Solids 1965, 13, 89–101. [Google Scholar] [CrossRef]
- Weng, Y.M.; Wang, G.J. The Influence of Inclusion Shape on the Overall Viscoelastic Behavior of Compoisites. J. Appl. Mech. 1992, 59, 510–518. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average Stress in the Matrix and Average Elastic Energy of Materials with Misfitting Inclusions. Acta Metal. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Pasricha, A.; Van Duster, P.; Tuttle, M.E.; Emery, A.F. The Nonlinear Viscoelastic/Viscoplastic Behavior of IM6/5260 Graphite/Bismaleimide. In Proceedings of the VII International Congress on Experimental Mechanics, Las Vegas, NV, USA, 8–11 June 1992. [Google Scholar]
- Aboudi, J. Micromechanical characterization of the non-linear viscoelastic behavior of resin matrix composites. Compos. Sci. Technol. 1990, 38, 371–386. [Google Scholar] [CrossRef]
- Aboudi, J. Mechanics of Composite Materials—A Unified Micromechanical Approach; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Abd-Elaziz, E.M.; Marin, M.; Othman, M.I. On the Effect of Thomson and Initial Stress in a Thermo-Porous Elastic Solid under G-N Electromagnetic Theory. Symmetry 2019, 11, 413. [Google Scholar] [CrossRef]
- Abbas, I.A.; Marin, M. Analytical solution of thermoelastic interaction in a half-space by pulsed laser heating. Phys. E Low-Dimensional Syst. Nanostruct. 2017, 87, 254–260. [Google Scholar] [CrossRef]
- Vlase, S.; Teodorescu-Draghicescu, H.; Motoc, D.L.; Scutaru, M.L.; Serbina, L.; Calin, M.R. Behavior of Multiphase Fiber-Reinforced Polymers Under Short Time Cyclic Loading. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 419–423. [Google Scholar]
- Teodorescu-Draghicescu, H.; Stanciu, A.; Vlase, S.; Scutaru, L.; Calin, M.R.; Serbina, L. Finite Element Method Analysis of Some Fibre-Reinforced Composite Laminates. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 782–785. [Google Scholar]
- Stanciu, A.; Teodorescu-Drǎghicescu, H.; Vlase, S.; Scutaru, M.L.; Cǎlin, M.R. Mechanical behavior of CSM450 and RT800 laminates subjected to four-point bend tests. Optoelectron. Adv. Mater. Rapid Commun. 2012, 6, 495–497. [Google Scholar]
- Niculiţă, C.; Vlase, S.; Bencze, A.; Mihălcică, M.; Calin, M.R.; Serbina, L. Optimum stacking in a multi-ply laminate used for the skin of adaptive wings. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 1233–1236. [Google Scholar]
- Katouzian, M.; Vlase, S.; Calin, M.R. Experimental procedures to determine the viscoelastic parameters of laminated composites. J. Optoelectron. Adv. Mater. 2011, 13, 1185–1188. [Google Scholar]
- Teodorescu-Draghicescu, H.; Vlase, S.; Stanciu, M.D.; Curtu, I.; Mihalcica, M. Advanced Pultruded Glass Fibers-Reinforced Isophtalic Polyester Resin. Mater. Plast. 2015, 52, 62–64. [Google Scholar]
- Fliegener, S.; Hohe, J. An anisotropic creep model for continuously and discontinuously fiber reinforced thermoplastics. Compos. Sci. Technol. 2020, 194, 108168. [Google Scholar] [CrossRef]
- Xu, B.; Xu, W.; Guo, F. Creep behavior due to interface diffusion in unidirectional fiber-reinforced metal matrix composites under general loading conditions: A micromechanics analysis. Acta Mech. 2020, 231, 1321–1335. [Google Scholar] [CrossRef]
- Lal, H.M.M.; Xian, G.-J.; Thomas, S.; Zhang, L.; Zhang, Z.; Wang, H. Experimental Study on the Flexural Creep Behaviors of Pultruded Unidirectional Carbon/Glass Fiber-Reinforced Hybrid Bars. Materials 2020, 13, 976. [Google Scholar] [CrossRef]
- Wang, Z.; Smith, D.E. Numerical analysis on viscoelastic creep responses of aligned short fiber reinforced composites. Compos. Struct. 2019, 229, 111394. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).