Abstract
In this research, we study the non-parametric portfolio selection problem with Value at Risk (VaR) minimization and establish a new enhanced Mixed Integer Linear Programming (MILP) formulation to obtain the optimal solutions considering the symmetric property of VaR. We identify that the new MILP formulation can significantly reduce the computation burden of the MILP solver CPLEX. To solve larger-scale practical portfolio selection problems in reasonable computation time, we also develop the Particle Swarm Optimization (PSO) algorithm integrating an efficient Fast Feasible Solution Detection (FFSD) scheme to obtain the near-optimal solutions. Using the simulated datasets with different distribution parameters and skewness and kurtosis patterns, some preliminary numerical results are provided to show the efficiency of the new formulation and FFSD scheme.
1. Introduction
Portfolio optimization is a fundamental financial problem that aims at optimally allocating limited capital to available assets by making a balance between maximal reward and minimal risk [1]. As investors consider the return as a favorable gain and meanwhile try to avoid bearing the undesirable losses, risk management has received much attention from practitioners and researchers in modern portfolio theory. To acquire a beneficial financial asset allocation strategy from limited capital resources under various uncertainties, a quantitative risk measurement that characterizes the potential return and loss should be established. In 1952, Markowitz firstly formulated a Mean-Variance (MV) model to maximize the expected return for a certain level of risk [2]. However, the MV model works only when the investor’s utility function is quadratic or the portfolio revenue follows a normal distribution. Due to people’s different attitudes about the desirable positive returns and undesirable negative risks, the semi-variance risk measurement was proposed correspondingly [3]. In addition, since it is difficult to calculate the effective frontiers, such risk measures have been widely criticized by practitioners. However, inspired by the initial work of Markowitz, many extensions to the MV method also have been investigated subsequently, such as [4,5,6,7,8].
To properly express the investors’ attitude towards the under-performance and over-performance of a portfolio, a popular down-side risk indicator called Value at Risk (VaR) was developed [9]. Given a confidence level over a fixed horizon, VaR measures the maximum possible loss of a portfolio from the market risk. For example, given a daily VaR valued as x with a confidence level of 99%, it measures the risk that the loss will be greater than x with a chance of 1%. Without loss of generality, a higher confidence level means a smaller loss of a portfolio. Since then, VaR has gradually gained popularity in the academic field of risk management and financial engineering owing to its simplicity and applicability [10,11,12,13,14,15,16,17,18]. By now, VaR is widely used in banks and insurance companies for estimating the exposure of a certain portfolio to high losses. However, VaR has also been criticized by financial regulators and academic researchers due to the non-additivity and non-convexity property [19]. In addition, as VaR is non-convex, VaR is rarely used as a risk measurement in real-world asset allocation because optimizing a risk-reward capital allocation problem with the objective of VaR minimization often requires a large computation time. To consider the potential losses ignored by VaR, many improved modifications have been investigated, including the most commonly used measure termed as Conditional VaR (CVaR) [20]. Specifically, CVaR aims to investigate the expected losses that occur beyond the VaR threshold and has been extensively studied in the research field [21,22,23].
Although VaR is a controversial risk management tool, as it is a major tool in banks and investment companies for estimating risk, the researcher still concentrates on developing various methods to solve the VaR based portfolio optimization problem. In this study, we briefly introduce the scientific notation of VaR and establish the corresponding portfolio optimization model. To reduce the computation burden of minimizing VaR via a commercial MILP solver, such as CPLEX, a new MILP model based on the symmetric property of VaR is proposed. Since optimizing practical large-scale MILP problems requires huge computing time, we propose to utilize the PSO algorithm with an Fast Feasible Solution Detection (FFSD) scheme to obtain near-optimal solutions in affordable computation time. The PSO algorithm is a typical representative of the swarm intelligence algorithm that dominates the field of nature-inspired meta-heuristics. The swarm intelligence algorithm solves complex optimization problems by simulating the collective behavior of decentralized and self-organizing biological individuals in nature [24]. In recent years, a representative swarm intelligence algorithm called particle swarm optimization has been demonstrated to be an efficient optimization tool in solving non-convex complicated problems [25,26,27,28]. A comparison study of the PSO algorithm with a genetic algorithm in finding optimal portfolio solutions has been presented in [29] where several strategies for handling the constraints are designed.
Based on the above analysis and review of the related research work, the major contributions of this research include the following:
- We propose a new enhanced MILP formulation with symmetric consideration to significantly reduce the computational burden of finding the optimal portfolios through the CPLEX software.
- We propose an FFSD scheme embedded in the PSO algorithm (PSO-FFSD) to further improve the performance of the PSO algorithm for tackling large-scale computational instances.
2. Formulation of the Non-Parametric Portfolio Selection Problem with VaR Minimization
In this section, we develop the formulation of the non-parametric VaR minimization portfolio selection problem. According to the definition of VaR, it measures the exposure of an investment strategy to the potential high losses. Specifically, the of a portfolio is expressed as the quantile of the portfolio’s loss under a given confidence level (usually taking values in the range of ). We assume there exist n assets to be invested in the financial market, and its corresponding uncertain loss rates in a certain period, usually from Time 0 to the fixed time T, are represented by a random variable . Let represent a possible portfolio on the n assets. Then, the confidence level of the portfolio , denoted as , is the -quantile of and can be formally stated as:
where is the -quantile of the portfolio’s loss distribution. We also use and to represent probability and expectation, respectively. Then, the expected portfolio return in the investment period is given by .
The VaR minimization portfolio selection problem aims at searching for the best portfolio to minimize whilst a given minimum expected return and the sum of each asset allocation percentage being equal to one are met, respectively. Correspondingly, the general formulation of the minimization portfolio selection problem is as follows.
As mentioned before, Formulation (2) can be solved by two approaches called the parametric approach and the non-parametric approach. In this research, we adopt the non-parametric approach to solve Formulation (2) by using a finite m number of samples to represent the random variable . Then, Formulation (2) can be rewritten as:
In Formulation (3), we utilize symbol as the k-th () smallest element in the set , and it is configured to a free decision variable z. Then, the variable z exactly represents the , and the vector of average return denoted as can be estimated as . Furthermore, Formulation (3) is equivalent to an MILP formulation by adding m auxiliary binary decision variables, and it can also be represented as:
where M is a big enough constant number. For the simplicity of description, Formulation (4) is abbreviated as VaR-MILP.
Next, we present an important theorem of the VaR proposed by Pflug [30] that will be used later in the paper.
Theorem 1.
Proof of Theorem 1.
We define the Probability Density Function (PDF) of as . Similarly, we also define the negative form of as:
and the PDF of as . Then, we can obtain the following relationship of and , the -quantile property of , respectively.
Equation (6b) can be extended to the following form by substituting for , that is:
Considering the -quantile property of and formula (7), we can obtain the following relationship:
and then □
Theorem 1 will be useful in the next section when we develop an enhanced optimization model with symmetric consideration.
A New Enhanced MILP Formulation with Symmetric Consideration
In this section, we propose an enhanced MILP formulation for solving the VaR minimization portfolio selection problem. The newly developed formulation is rooted in Theorem 1, which indicates that the VaR value has two ways of evaluation. One of them is the original definition in VaR, and the other is based on the symmetrical property of VaR. The new enhanced MILP formulation is also motivated by the research of Sherali and Smith [31], who suggested constructing a good MILP formulation with symmetrical considerations. A recent study by Lalla-Ruiz and Voß [32] also demonstrated that changes in mathematical formulations may largely influence the solvability and quality of the optimization results. They showed that the optimization solver exhibits notably different behavior if extra constraints or variables are used. In other words, formulating the same problem with different descriptions may bring an immense performance improvement during its execution. Klotz et al. also showed that carefully formulating the model and tuning standard integer programming algorithms often result in significantly faster solve times, in some cases, admitting a feasible or near-optimal solution that could otherwise elude the practitioner [33]. The implementation process of the new enhanced MILP formulation of the non-parametric portfolio selection problem can be described in detail as the VaR value can be calculated by in a symmetrical way, that is changing the original random variable to its negative form and altering the confidence level to correspondingly. As the VaR possesses the inherent symmetric information in the problem itself, implementing the VaR-MILP formulation with the symmetric consideration may notably accelerate the optimizing process.
Since the MILP formulation is often resolved via the branch-and-cut or branch-and-bound method to obtain the optimal solution, appropriately imposing extra relevant decision variables and symmetric constraints will significantly reinforce the computational efficiency by exploring the fewer feasible regions and trial nodes. The enhanced VaR-MILP with symmetric consideration is capable of generating dual solutions to the VaR-MILP formulation with extra disaggregated constraints. Thus, we utilize the introduced symmetric decision variables and constraints to generate tighter representations to the VaR-MILP formulation by which the overall optimizing performance is improved by reducing the bounding procedure in the search process even for some larger models.
Next, we describe the detailed idea of utilizing symmetric consideration to optimize VaR-MILP. The VaR-MILP formulation determines the optimal value by firstly obtaining the intermediate loss set for all the scenarios and then locating the proper position value in L; that is, adopting the first and second constraints in Formulation (4) to restrict variable z as the VaR. Instead of applying only the original one way optimizing strategy in the VaR-MILP formulation, we introduce another symmetric direction acceleration scheme: simultaneously performing optimization on the intermediate set L and its corresponding opposite set , which contains the negative form of L. The symmetric direction optimizing strategy can be considered as the complementary operation that is applied to the opposite intermediate set . Although the two operations optimize their own intermediate set in their directions cooperatively, the intrinsic complementary features of the two sets L and guarantee that the bi-direction optimization process achieves the same optimum.
Based on the above approach that tries to optimize VaR in the symmetrical direction, we propose to integrate the bi-directional operations with dual complementary binary variables to accelerate the optimization process of the VaR-MILP formulation. Below is the proposed enhanced MILP formulation with symmetric consideration to minimize VaR, denoted as VaR-MILP-Symmetric (Sym). In the Appendix A, we will also prove the optimal portfolios of the new proposed enhanced formulation is the same as that resulting from the VaR-MILP approach.
In the next section, we introduce our proposed PSO algorithm, denoted as VaR-PSO, to solve the large-scale VaR minimization problem.
3. Minimizing VaR by PSO
In this section, we provide a swarm intelligence algorithm called PSO to efficiently obtain the optimal portfolios measured by VaR. Note that the VaR minimization portfolio selection problem presented in Formulation (4) is highly none smooth, and traditional optimization methods cannot provide high-quality feasible solutions quickly and effectively. Although Formulation (4) can be transformed into the VaR-MILP-Sym formulation, tackling the practical problem of simulation number and stock number will still take much calculation time. Meanwhile, the practical investment scenarios often require the investors to make an effective asset allocation strategy among a large number of assets. For example, the United States has three major securities exchange markets, namely NYSE, NASDAQ, and AMEX. Currently, a total number of 7679 companies conduct daily stock transactions in the three markets. Until 14 Sep, 2020, the number of listed companies in the A-share market of China exceeded 4000. To select the optimal investment plan among so many assets, it will require huge computation costs utilizing traditional optimization methods.
PSO is a population based optimization method where a group of randomly generated solutions evolves in a behavioral framework drawn on the collective behavior of social animals, e.g., schools of fish or flocks of birds, to search for the optimal solution iteratively. The PSO conceives of a large group of particles, often in the form of n-dimensional real-valued vectors, moving into the solution space. Each particle i is characterized by its position and an n-dimensional velocity vector , which represents the change in position degree. In each updating iteration t, each particle moves as follows:
where is called the inertial weight, which controls the impact of the previous iteration’s particle velocity on the current one, and are two randomly generated variables within the range of (0, 1), and and are two positive constant parameters, called acceleration coefficients.
In Equation (10), the best previously visited position of particle i is denoted as , and the position of the best individual of the whole group is denoted as the global best position . The fitness of each particle can be evaluated according to the objective function defined in the present optimization problem. Hence, the updated position of each particle depends on the direction of its movement, its velocity, the best preceding position, and the best position among the swarm. PSO uses Equation (11) to calculate the new velocity according to its previous velocity and two-part distances that include the current position of each particle in reference to both its own best historical position and the best position of the entire swarm. Then, each particle flies toward a new position by Equation (11). This process is repeated until a predefined stopping criterion is met.
Applying PSO to solve the portfolio optimization problem has been studied in the literature. Wang et al. proposed the VaR based fuzzy-portfolio selection model and used the improved particle swarm optimization algorithm to search for the approximate optimal solutions [34]. Zhu et al. adopted Particle Swarm Optimization (PSO) to solve the constrained portfolio optimization problem [35]. Cura used the cardinality constrained mean-variance model, and the computation results showed that the particle swarm optimization approach is successful in portfolio optimization [36]. Finding the optimal solutions to the non-parametric portfolio selection problem by the PSO algorithm requires focusing on the following issues.
- Solution representation:
For the VaR minimization problem, the natural representation of a PSO solution is to use real numbers to denote the investment proportions. In our implementation, each particle is represented by an n-dimensional vector, where the number of dimensions corresponds to the total number of investment stocks in a portfolio. The kth component of particle , i.e., , denotes the investment proportion of stock k.
- Initial solution and particle evaluation criterion:
To minimize , we first randomly generate the initial population with real numbers in the range . Since in Formulation (4), decision variables must satisfy the constraint that the sum is equal to one, a normalization step is applied to each randomly generated particle and can be stated as follows:
At the same time, to make the decision variables meet the request of minimum revenue, each particle is evaluated by a penalty function as follows:
where M is a big positive constant number.
Based on the above particle representation, initialization, and evaluation procedures, the pseudo-code of the VaR-PSO algorithm for solving the optimal VaR portfolios problem described previously is given in Algorithm 1. The termination criterion is controlled by the maximum number of generations. Furthermore, the newly visited position of each particle needs to be normalized by Equation (12). This guarantees that the search process is always performed in the potential area of satisfying the constraint that all decision variables are summed to one. In our computational experiments, we follow the model of Shi et al. [37].
| Algorithm 1 Framework of VaR-PSO. |
| Input: The max number of generations (MaxGen), population size (), Output: Best portfolio solution
|
A Fast Feasible Solution Detection Scheme
In the above section, we adopted a simple penalty function method to establish the new particle evaluation function, hoping that the algorithm searches within the feasible domain. The new evaluation function contains two corresponding parts, one of which is the original VaR definition function, and the other is the penalty item added. The construction of the penalty item is based on the extent to which the current solution violates the constraint. The VaR-PSO algorithm also introduces a normalization step, thus ensuring that the search process is only performed in the space that requires the sum of all decision variables being equal to one. As VaR-PSO evolves in searching the optimal portfolios, infeasible solutions are granted much larger objective values while feasible solutions much smaller ones to propel all the particles flying to the feasible region quickly. The difficulty in solving the non-parametric portfolio selection problem by the PSO algorithm is dealing with the constraint that a feasible solution must satisfy the minimum expected revenue rate , which is . However, solving the linear inequality constraint that satisfies the minimum reward margin with many decision variables by a simple penalty function method is rather inefficient. Especially in the initial searching procedure, the PSO is an aimless searcher since all particles fly blindly in the non-feasible domains, resulting in very low search efficiency. Moreover, the size of the feasible domain space also depends on the parameter . When investors tend to get a higher reward margin, it will inevitably lead to a further reduction of the feasible domain space. Under such an investment situation, how to quickly obtain a feasible portfolio solution will greatly affect the overall search efficiency of the PSO algorithm. In recent years, researchers have proposed to convert constrained optimization problems into multi-objective optimization problems to deal with some difficult constraints [38,39]. Using multi-objective optimization techniques to address constrained optimization problems generally transforms the original problem into a multi-objective optimization problem with two objectives. The first one is the original problem objective function, and the second one is the degree to which the solution violates the constraints. In this research, the two objectives are defined in the following form:
The essence of using the multi-objective optimization method to deal with the constrained optimization problem is that it uses the original objective function value and the degree of violation to the constraint to compare some of the obtained solutions, with the hope to guide the algorithm to quickly move to the feasible domain consisting of the optimal solution. Since the two target values exist in the PSO algorithm, the traditional mechanism for evaluating individuals with a single objective value is no longer applicable.
This paper uses a tournament selection operator proposed by Deb [40] to compare solutions, that is:
- When comparing two particles with one feasible and the other infeasible, choose the feasible solution.
- When the two compared particles are both feasible solutions, select the particle with a smaller objective function value.
- When both particles are infeasible, choose the particle with the least degree of constraint violation, which is the particle with a smaller objective function value.
The procedure of Deb’s tournament selection strategy in our research is outlined in Algorithm 2.
| Algorithm 2 Deb’s tournament selection strategy. |
|
Although the selection strategy proposed by Deb is suitable for the PSO algorithm performing multi-objective searches whilst guiding the search direction towards the feasible domain, too few Pareto solutions in the current swarm will ultimately degrade its searching performance. Besides, the main drawback of the above comparison criteria lies in that it is difficult to play the role of infeasible solutions, especially when the infeasible solution is very close to the boundary of the feasible domain. Hence, we propose a fast feasible solution detection scheme that is based on the assumption that the centroid of some infeasible solutions with near-optimal VaR evaluation values around the feasible domain boundary will be located in the feasible domain with a high probability. To ensure that a sufficient number of detected solutions are generated in the potential feasible domain, the mechanism by which we generate the centroid solutions will be constructed by enumerating all possible combinations of different solutions in the Pareto solution set. Specifically, we can generate the required number of central solutions based on two solutions, three solutions, and even more solutions in the Pareto set. See Figure 1 below for an explanation.
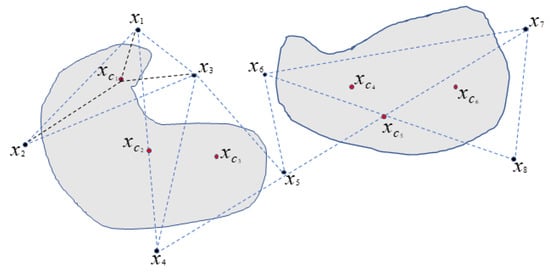
Figure 1.
Illustration of the Pareto set based fast feasible solution detection scheme.
Suppose the non-dominated infeasible solutions are located near the feasible space boundary represented by , respectively. We define as the polyhedral centroids consisting of points , ,,, and as vertices, correspondingly. We define the Pareto set as P and the generated detected solution set as . If the number of solutions in the set is still insufficient due to too few non-dominated solutions in the Pareto set, we will add some randomly generated solutions to the set. Note that the maximum number of solutions generated by our proposed fast feasible solution detection scheme is if the present Pareto set has p solutions. As the number of elements in the Pareto solution set exceeds 10, the number of generated detected solutions will exceed 1000. In that case, we modify the detection method by randomly selecting partial solutions in the Pareto solution set P and calculate their corresponding centers. The whole procedure of our proposed fast feasible solution detection scheme is outlined in Algorithm 3.
We take advantage of the fast feasible solution detection scheme together with the VaR-PSO algorithm to efficiently explore feasible near-optimality portfolios. To strengthen the exploration ability of the algorithm, especially in the later stage of the search, once the solutions found in the population are all feasible, we will reinitialize the entire swarm. We name the VaR-PSO algorithm integrated with an FFSD scheme as VaR-PSO-FFSD, and it is presented in Algorithm 4.
| Algorithm 3 The fast feasible solution detection scheme. |
|
| Algorithm 4 Framework of VaR-PSO-FFSD. |
|
4. Computation Experiment
In this section, we compare the performance differences of the two MILP formulations and PSO algorithms for solving the non-parametric portfolio selection problem. To be specific, we first present the numerical results to compare the performance of the fundamental MILP formulation and the modified MILP formulation. Subsequently, we carry out the comparison tests by using the PSO algorithm and the PSO algorithm with an FFSD scheme for addressing even larger computational instances with simulation number m, and stock number n is up to 3000 and 100, respectively.
Due to the NP-hard characteristic of the MILP model and limited computation resources, we restrict the size of the problem to a certain extent to obtain the optimal solution in an acceptable time. In these cases, we generate 14 typical simulated computation instances that include different stock combination numbers and simulation numbers. In Figure 2, we show the distribution of Instance 6 and Instance 13 together with the skewness and kurtosis values. The implementation of the VaR-MILP and VaR-MILP-Sym formulations was coded in the C# language, which calls the optimization engine of IBM ILOG CPLEX with Version 12.9 to obtain the optimal VaR values. All the computational experiments were carried out on a PC with an Intel Core-i7 8700 CPU and 16Gb RAM running on Windows 10.
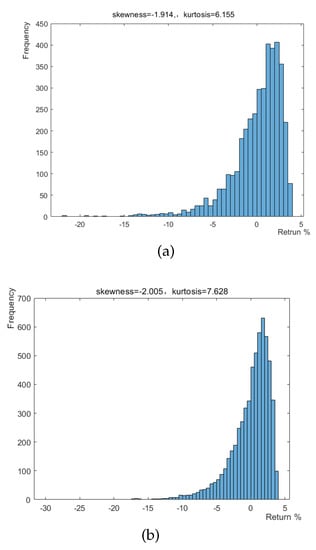
Figure 2.
(a,b) are the histogram plots of Instances 6 and 13.
4.1. Performance Comparison of the Two MILP Formulations
We adopt the CPU times and explored nodes as the evaluation metrics to validate the performance differences of the two versions of the proposed MILP formulations to obtain the optimal portfolios. In the case of each testing instance, the obtained optimal VaR value, CPU times, and explored nodes using different formulation types are listed in Table 1 considering the normal confidence level .

Table 1.
The VaR value with confidence level , CPU times, and explored nodes for different testing instances.
From the results shown in Table 1, it can generally be observed that all the formulations converge to the same global optimal VaR value. This verifies the accuracy of the proposed MILP formulation with the symmetric consideration acceleration strategy. It can be observed that under the confidence level, the optimum value of all instances can be obtained within around 20 to 2560 s concerning different parameter . In tackling Instance 12, the computation times by using two formulations all exceed 1100 s. However, for solving Instance 11, even the simulation numbers m and n reach 1500 and 4, respectively, and the maximum execution time is 265.11s for the basic VaR-MILP. We also observe that the stock combination number n is also the key parameter that determines the optimization efficiency of the MILP formulation. For optimizing Instances 6 and 7, although the instance parameter m is identical, the computation time is quite different. It seems that the simulated dataset information also affects the computation efficiency of the MILP formulations. In general, the optimization times of the two formulations have significant differences: VaR-MILP-Sym exhibits a superior performance to the basic VaR-MILP approach. The average speedup ratio of formulation VaR-MILP-Sym compared with VaR-MILP for solving instance under is . An interesting phenomenon is that although the optimization time of the VaR-MILP-Sym model is less than VaR-MILP, there is no regular rule in the number of nodes explored by the two formulations; that is to say, in some cases, the number of nodes that need to be explored to find the optimal solution using the VaR-MILP-Sym model is less than using the model VaR-MILP, while other examples are just the opposite.
Note that in some cases, VaR-MILP performs rather poorly because of the large number of nodes that must be explored and eliminated by the branch-and-bound process. Comparing the explored nodes of the related instances, VaR-MILP-Sym performs most efficiently in cutting no promising branches since it adds a set of constraints to the basic model with extra complementary binary variables and constraints, which tends to encourage finding a high-quality solution during the enumeration process. Furthermore, the VaR-MILP-Sym formulation shows the promising ability of further exploration. On the other hand, VaR-MILP does not perform as well as VaR-MILP-Sym, perhaps because the symmetric consideration scheme integrated into the VaR-MILP-Sym formulation enables CPLEX to find a relatively better upper bound at the root node. Generally speaking, in all tests, VaR-MILP-Sym appears to be the most efficient formulation, offering substantial time savings in performing the computation.
For resolving practical applications, investment institutions often select portfolios on a large set of stock combinations. From the above computation tests, we find that obtaining the optimal solution of the VaR minimization based non-parametric portfolio selection problem is rather time consuming when the larger stock combination number n reaches five. For example, solving Instance 12 under , we need 1160.58 s to reach the optimum by the most efficient formulation. This situation indicates that obtaining the optimized solution by utilizing the MILP formulation is inappropriate in real-world applications. In the next section, we provide a near-optimal solution generation method by the PSO algorithms. Next, we will compare the computation results of tackling some larger problems with simulation number and stock number .
4.2. Performance Comparison of the Proposed PSO Algorithms
In this section, we present the numerical results of comparing the performances of the two PSO based algorithms to efficiently obtain high-quality portfolios. The proposed VaR-PSO and VaR-PSO-FFSD algorithms were also coded in the C# programming language and run on the same platform as described in the previous section for solving the MILP formulations. To investigate the performances of the two PSO algorithms, we carried out the experiments by generating daily return prices for up to 100 stocks with different skewness and kurtosis patterns. From these data, each computation instance was formed by having the number of stocks and number of scenarios . Since investors also consider the minimum rate of return in the actual investment process, we increased the regular value to 90% of the maximum in the set , that is . Thus, we generated a total number of large-scale computation instances. For all the experiments, the parameter in VaR-PSO and VaR-PSO-FFSD was set according to Shi and Eberhart [37], who recommended a linearly decreasing form from 0.9 to 0.4. The population size and max number of iterations of two PSO algorithms were set to and , respectively. The acceleration constants and were both set to 2.0. We used the average VaR values and execution times of the PSO algorithm randomly running 10 times as its performance index. We used and to represent the optimized VaR values obtained by using the two PSO algorithms, respectively. In addition to the VaR value, we also recorded the running time of each algorithm. The VaR confidence parameter was set to the popular value of . All the computation results are listed in Table 2.

Table 2.
The obtained VaR values and execution times by using PSO algorithms for solving instances under confidence level . FFSD, Fast Feasible Solution Detection.
From Table 2, some conclusions can be drawn. In all instances, the VaR-PSO algorithm takes the shortest time to solve the portfolio selection problem, and all of the average VaR values obtained by VaR-PSO are inferior to the VaR-PSO-FFSD algorithm. In all the computational instances, the average time spent in VaR-PSO-FFSD is 476.016/308.501 ≈1.319 times that of the VaR-PSO. VaR-PSO-FFSD takes more time than VaR-PSO mainly due to the introduction of the FFSD scheme and the inclusion of the process of finding the Pareto set in VaR-PSO-FFSD. In solving the instances with the fixed stock number, the time spent by the two PSO algorithms increases significantly with the increase of the simulation number. This observation is similar to the computational results obtained by adopting the VaR-MILP formulations. Furthermore, when the number of simulation m is fixed, increasing the number of stocks n will also increase the optimization time of the two PSO algorithms. During the tests, we also discovered that when the expected yield was set to , all PSO algorithms can find a feasible solution at the end of the iteration. This also indicates that it is not difficult to find a feasible investment solution when the value in the proposed portfolio optimization model is set relatively small. It needs to be pointed out that the VaR-PSO algorithm may not find a feasible solution at the beginning of the iteration in solving the instances of large stock number n, e.g., . However, as the iteration continues, the VaR-PSO algorithm will soon discover the feasible regions.
However, when the value is increased to , the quality of the solution obtained by the VaR-PSO algorithm changes dramatically. Especially when the stock number n is greater than 200 and the simulation number m increases to 3000, the VaR-PSO algorithm does not guarantee that a feasible solution can be found at the end of the iteration in each random trial. In addressing such computational instances, even increasing the number of iterations of the VaR-PSO algorithm does not help it quickly find a feasible investment solution. However, the VaR-PSO-FFSD algorithm is capable of finding multiple feasible solutions after a few iterations. In this research, to compare the average searching performance of the two PSO algorithms, we set the maximum n to 100. In general, compared with the results obtained by the VaR-PSO algorithm, the average VaR value is reduced by 6.9% when using the VaR-PSO-FFSD algorithm. The computational results demonstrate that the adoption of an FFSD scheme in the PSO algorithm provides a better balance between the solution quality and computation time. Therefore, the VaR-PSO-FFSD algorithm is a better solution approach to solve large non-parametric portfolio selection problems.
5. Conclusions
This paper considers the non-parametric portfolio selection problem, and a new MILP formulation integrating the advantage of the symmetric information of VaR is proposed to speed up the optimum searching process. Numerical experiments show that the new formulation can lead to the same optimum with a shorter computation time compared with the basic MILP formulation in solving small-scale instances, and the speedup ratio is approximately 1.58. Subsequently, we developed a PSO algorithm integrating the FFSD procedure to solve large computational instances. Although the execution time of VaR-PSO-FFSD is 1.38 times that of VaR-PSO, it can reduce VaR by an average of 6.9% in the testing instances. We find that the new MILP model with symmetric characteristics can be used to quickly obtain the optimal portfolio solutions for small-scale problems, e.g., the simulation number and stock number , and the improved PSO algorithm with the FFSD scheme is more suitable for solving large-scale non-parametric portfolio selection problems wherein the stock number and simulation number . There may be some possible limitations in this study. The empirical results of the two MILP formulations reported herein should be considered in light of a broad range of computational instances. In the future, the superiority of the enhanced MILP formulation with symmetric consideration will continue to be verified against a wider range of testing data. In addition, we plan to design an efficient heuristic search strategy for solving practical ultra-large-scale non-parametric VaR minimization portfolio selection problems.
Author Contributions
D.W. proposed the idea and the models and wrote the original draft; Y.C. implemented the two MILP formulations that call the CPLEX solver engine to find the optimal portfolio solutions; H.W. implemented the two PSO algorithms; M.H. checked the methodology and computational results. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Fundamental Research Funds for the Central Universities of China under Grant No. N150404016; the NSFC Major International (Regional) Joint Research Project Grant No.71620107003; the Liaoning Revitalizing Talent Program No. XLYC1802115; the Fundamental Research Funds for the State Key Laboratory of Synthetical Automation for Process Industries Grant No. 2013ZCX11; the 111 Incubating Program of Overseas Expert Introduction (BC2018010); the “High-level Overseas Expert” Introduction Program (G20190006026).
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
Appendix A
Let denote the optimal solution of VaR-MILP, denote the optimal value of VaR-MILP, and denote the optimal value of VaR-MILP-Sym. First, we apply some conversions to the VaR-MILP-Sym formulation. Assume and , then VaR-MILP-Sym can be expressed in the following form, denoted as VaR-MILP-Sym-T1.
Since VaR-MILP-Sym-T1 is the equivalent form of VaR-MILP-Sym, is also the optimal objective value of VaR-MILP-Sym-T1. Compared with the basic VaR-MILP formulation, VaR-MILP-Sym-T1 includes the added constraint (A1b). In addition to this, all the constraints in VaR-MILP-Sym-T1 are identical to those of VaR-MILP. Supposing represents any feasible solution to VaR-MILP, then we can also find a proper value for that satisfies constraint (A1c). That is, is also the feasible solution of VaR-MILP-Sym-T1. According to the above analysis, we can conclude that the optimal solution () to VaR-MILP is also a feasible solution of VaR-MILP-Sym-T1.
Assume . When , then according to the constraint in VaR-MILP, we deduce that the relationship also holds. Moreover, the constraint indicates that there exists a total number of components that satisfy . Suppose , , then we obtain that and . Otherwise, is not the optimal solution of VaR-MILP, and is not the optimal objective value of VaR-MILP, correspondingly.
The objective function of VaR-MILP-Sym-T1 contains two independent components, called z and , respectively. When we input the optimal solution into the formulation for VaR-MILP-Sym-T1, we can conclude that , in which z represents the first part of the objective value under any feasible solution. In other words, the first objective part of formulation VaR-MILP-Sym-T1 reaches the optimum at .
In addition, we can also find a value for that satisfies the inequality relationship of , i.e., . The above relationship can also be expressed in the present form, . Then, we derive the relationship .
Since , we conclude that the objective also reaches the optimum at .
In summary, two respective parts of the objective function in VaR-MILP-Sym-T1, i.e., z and , reach the same optimum . Accordingly, we assert that is the optimal solution to formulation VaR-MILP-Sym-T1 and . Furthermore, the optimal value of VaR-MILP-Sym is strictly twice as large as that of VaR-MILP. Since formulation VaR-MILP-Sym-T1 is equivalent to VaR-MILP-Sym, then VaR-MILP-Sym is also equivalent to VaR-MILP and .
References
- Kolm, P.N.; Tütüncü, R.; Fabozzi, F.J. 60 Years of portfolio optimization: Practical challenges and current trends. Eur. J. Oper. Res. 2014, 234, 356–371. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Nawrocki, D. A Brief History of Downside Risk Measures. J. Investig. 1999, 8, 9–25. [Google Scholar] [CrossRef]
- Konno, H.; Yamazaki, H. Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market. Manag. Sci. 1991, 37, 519–531. [Google Scholar] [CrossRef]
- Speranza, M.G. Linear programming models for portfolio optimization. Finance 1993, 37, 107–123. [Google Scholar]
- Young, M.R. A minimax portfolio selection rule with linear programming solution. Manag. Sci. 1998, 44, 673–683. [Google Scholar] [CrossRef]
- Teo, K.L.; Yang, X. Portfolio selection problem with minimax type risk function. Ann. Oper. Res. 2001, 101, 333–349. [Google Scholar] [CrossRef]
- Wang, L.; Wu, H.; Li, G.; Lu, W. An Improved MV Method for Stock Allocation Based on the State-Space Measure of Cognitive Bias with a Hybrid Algorithm. Symmetry 2020, 12, 1036. [Google Scholar] [CrossRef]
- Morgan, J. RiskMetrics-Technical Document; Morgan Guaranty Trust Company of New York: New York, NY, USA, 1996. [Google Scholar]
- Benati, S.; Rizzi, R. A mixed integer linear programming formulation of the optimal mean/value-at-risk portfolio problem. Eur. J. Oper. Res. 2007, 176, 423–434. [Google Scholar] [CrossRef]
- Gaivoronski, A.A.; Pflug, G. Value-at-risk in portfolio optimization: Properties and computational approach. J. Risk 2004, 7, 1–31. [Google Scholar] [CrossRef]
- Glasserman, P.; Heidelberger, P.; Shahabuddin, P. Variance reduction techniques for estimating value-at-risk. Manag. Sci. 2000, 46, 1349–1364. [Google Scholar] [CrossRef]
- Kaplanski, G.; Kroll, Y. VaR risk measures versus traditional risk measures: An analysis and survey. J. Risk 2002, 4, 1–27. [Google Scholar] [CrossRef]
- Ghaoui, L.E.; Oks, M.; Oustry, F. Worst-case value-at-risk and robust portfolio optimization: A conic programming approach. Oper. Res. 2003, 51, 543–556. [Google Scholar] [CrossRef]
- Natarajan, K.; Pachamanova, D.; Sim, M. Constructing risk measures from uncertainty sets. Oper. Res. 2009, 57, 1129–1141. [Google Scholar] [CrossRef]
- Wozabal, D. Value-at-risk optimization using the difference of convex algorithm. OR Spectr. 2012, 34, 861–883. [Google Scholar] [CrossRef]
- Huang, X.; Xu, J.; Wang, S.; Xu, C. Minimization of the k-th maximum and its application on LMS regression and VaR optimization. J. Oper. Res. Soc. 2012, 63, 1479–1491. [Google Scholar] [CrossRef]
- Lwin, K.T.; Qu, R.; MacCarthy, B.L. Mean-VaR portfolio optimization: A nonparametric approach. Eur. J. Oper. Res. 2017, 260, 751–766. [Google Scholar] [CrossRef]
- Artzner, P.; Delbaen, F.; Eber, J.M.; Heath, D. Coherent measures of risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–42. [Google Scholar] [CrossRef]
- Yao, H.; Li, Z.; Lai, Y. Mean-CVaR portfolio selection: A nonparametric estimation framework. Comput. Oper. Res. 2013, 40, 1014–1022. [Google Scholar] [CrossRef]
- Lim, A.E.; Shanthikumar, J.G.; Vahn, G.Y. Conditional value-at-risk in portfolio optimization: Coherent but fragile. Oper. Res. Lett. 2011, 39, 163–171. [Google Scholar] [CrossRef]
- Kibzun, A.I.; Kuznetsov, E.A. Analysis of criteria VaR and CVaR. J. Bank. Financ. 2006, 30, 779–796. [Google Scholar] [CrossRef]
- Dreżewski, R.; Doroz, K. An agent-based co-evolutionary multi-objective algorithm for portfolio optimization. Symmetry 2017, 9, 168. [Google Scholar] [CrossRef]
- Kumar, S.K.; Tiwari, M.; Babiceanu, R.F. Minimisation of supply chain cost with embedded risk using computational intelligence approaches. Int. J. Prod. Res. 2010, 48, 3717–3739. [Google Scholar] [CrossRef]
- Ma, Z.; Yuan, X.; Han, S.; Sun, D.; Ma, Y. Improved Chaotic Particle Swarm Optimization Algorithm with More Symmetric Distribution for Numerical Function Optimization. Symmetry 2019, 11, 876. [Google Scholar] [CrossRef]
- Kumar, R.S.; Kondapaneni, K.; Dixit, V.; Goswami, A.; Thakur, L.S.; Tiwari, M. Multi-objective modeling of production and pollution routing problem with time window: A self-learning particle swarm optimization approach. Comput. Ind. Eng. 2016, 99, 29–40. [Google Scholar] [CrossRef]
- Du, Y.; Xu, F. A Hybrid Multi-Step Probability Selection Particle Swarm Optimization with Dynamic Chaotic Inertial Weight and Acceleration Coefficients for Numerical Function Optimization. Symmetry 2020, 12, 922. [Google Scholar] [CrossRef]
- Dallagnol, V.; van den Berg, J.; Mous, L. Portfolio management using value at risk: A comparison between genetic algorithms and particle swarm optimization. Int. J. Intell. Syst. 2009, 24, 766–792. [Google Scholar] [CrossRef]
- Pflug, G.C. Some remarks on the value-at-risk and the conditional value-at-risk. In Probabilistic Constrained Optimization; Springer: Boston, MA, USA, 2000; pp. 272–281. [Google Scholar]
- Sherali, H.D.; Smith, J.C. Improving discrete model representations via symmetry considerations. Manag. Sci. 2001, 47, 1396–1407. [Google Scholar] [CrossRef]
- Lalla-Ruiz, E.; Voß, S. Improving solver performance through redundancy. J. Syst. Sci. Syst. Eng. 2016, 25, 303–325. [Google Scholar] [CrossRef]
- Klotz, E.; Newman, A.M. Practical guidelines for solving difficult mixed integer linear programs. Surv. Oper. Res. Manag. Sci. 2013, 18, 18–32. [Google Scholar] [CrossRef]
- Wang, B.; Wang, S.; Watada, J. Fuzzy-portfolio-selection models with value-at-risk. IEEE Trans. Fuzzy Syst. 2011, 19, 758–769. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Wang, K.; Chen, Y. Particle Swarm Optimization (PSO) for the constrained portfolio optimization problem. Expert Syst. Appl. 2011, 38, 10161–10169. [Google Scholar] [CrossRef]
- Cura, T. Particle swarm optimization approach to portfolio optimization. Nonlinear Anal. Real World Appl. 2009, 10, 2396–2406. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Cai, Z.; Wang, Y. A multiobjective optimization-based evolutionary algorithm for constrained optimization. IEEE Trans. Evol. Comput. 2006, 10, 658–675. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z. Combining multiobjective optimization with differential evolution to solve constrained optimization problems. IEEE Trans. Evol. Comput. 2012, 16, 117–134. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).